Multi-Criteria Optimization of Yarn Guide Manufacturing Processes
Abstract
1. Introduction
- Have a low coefficient of friction when interacting with the yarn, which mainly depends on the Surface Geometrical Structure (SGP) resulting from the treatment;
- Not cause the formation of electrostatic charges and not transfer these charges to the yarn;
- Be sufficiently resistant to wear.
2. Multi-Criteria Evaluation Method
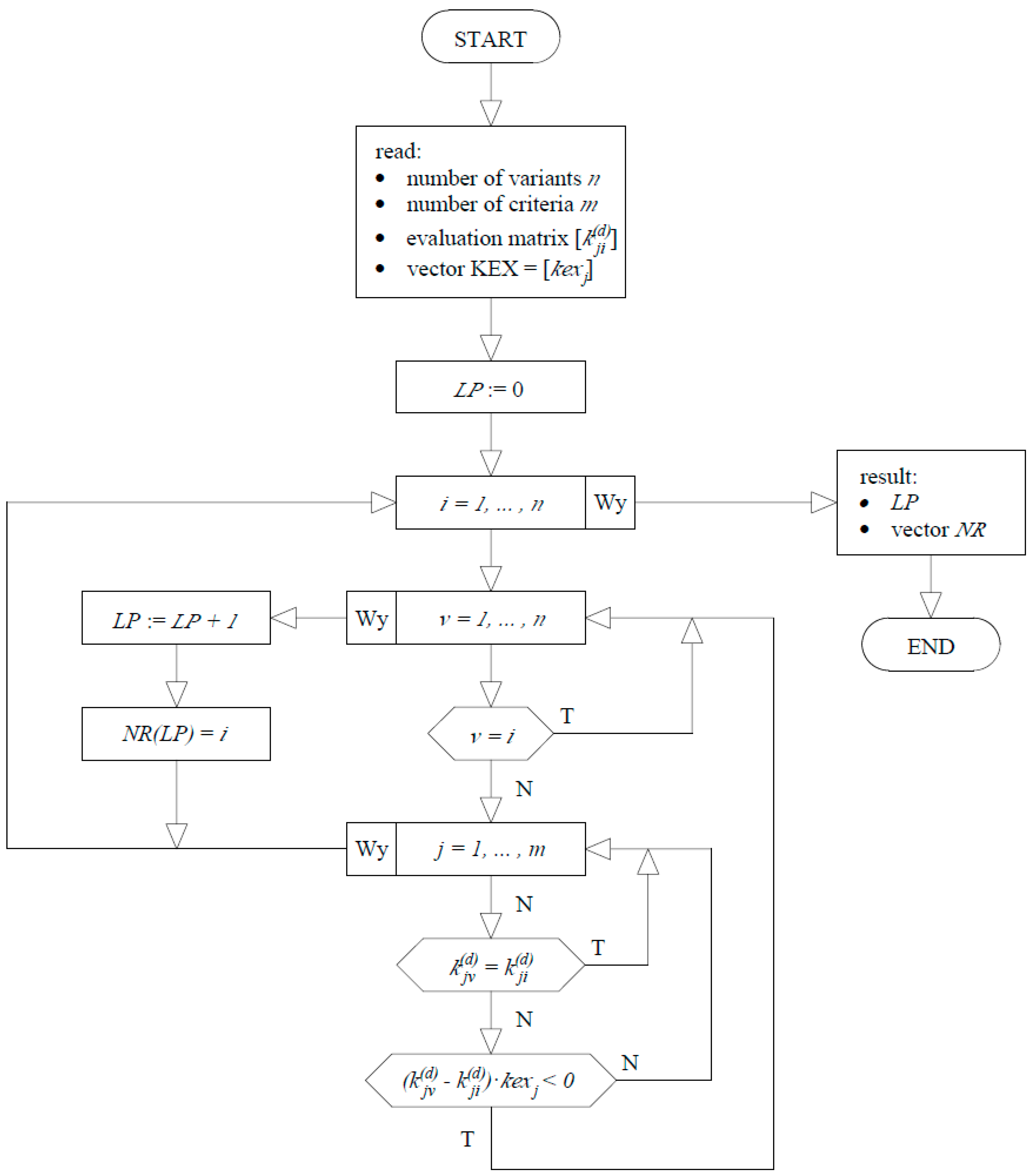
2.1. Optimum Method in the Pareto Sense
- The table of evaluations of variants of the manufacturing process of the yarn guide of the ring spinning frame with respect to deterministic criteria , where—the number of variants of the manufacturing process of the yarn guide;—the number of criteria;
- The extremum direction vector .
2.2. Selection of the Best Option from the Set of Optimal Solutions in the Pareto Sense
3. An Example of the Selection of a Variant of the Optimal Yarn Guide Manufacturing Process in View of the Unit Manufacturing Cost and Manufacturing Quality Criteria
3.1. A Set of Acceptable Variants of the Yarn Guide Manufacturing Process
- Selecting guides from the production range of companies engaged in such production and almost completely reconstructing their mounting on the ring spinning frame;
- Aiming to leave the mounting of the guide unchanged, which involved developing a new shape of the guide from the aforementioned materials.
3.2. A Set of Criteria for Evaluating the Yarn Guide of Ring Spinning Frame
- Unit manufacturing cost Kw, PLN;
- Mean square deviation of the profile Rq, µm;
- Maximum profile elevation Rp, µm;
- Mean square profile inclination RΔq, rad;
- Mean radius of curvature of profile vertices rw, µm;
- Maximum hardness at the surface of the surface layer HV0.1;
- Depth of hardening of the surface layer gww, µm.
3.3. Selection of the Optimal Variant of the Yarn Guide Manufacturing Process in View of the Unit Manufacturing Cost and Manufacturing Quality Criteria
4. Conclusions
- First stage, the determination of a set of optimal variants in the Pareto sense;
- Second stage, the determination of the best variant from this set using a distance function.
- Variant a12 () for which the semi-finished product is a drawn bar (ø6 mm) of C45 steel, quenched and tempered to a hardness of 350 HB, with a spiral insert made of glazed porcelain.The values of the criteria evaluations are Kw = 11.05 PLN/pcs.; Rq = 0.145 µm;Rp = 0.686 µm; RΔq = 0.0240 rad; rw = −0.200 µm; HV0.1 = 1130; and gww = 105 µm
- Variant a13 () for which the value of the distance function is slightly higher, by 0.0967, is the variant with the Al2O3 ceramic sinter insert.The values of the criteria evaluations are Kw = 13.02 PLN/pcs.; Rq = 0.542 µm;Rp = 1.191 µm; RΔq = 0.0617 rad; rw = −0.137 µm; HV0.1 = 1450; and gww = 205 µm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SGP | Structure of geometrical surfaces |
References
- Emmerich, M.; Deutz, A. Multicriteria optimization and decision making: Principles, algorithms and case studies. arXiv 2024, arXiv:2407.00359. [Google Scholar] [CrossRef]
- Chong, E.K.; Lu, W.S.; Zak, S.H. An Introduction to Optimization: With Applications to Machine Learning; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Mardani, A.; Jusoh, A.; MDNor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraživanja 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Liang, J.; Ban, X.; Yu, K.; Qu, B.; Qiao, K.; Yue, C.; Chen, K.; Tan, K.C. A survey on evolutionary constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2022, 27, 201–221. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Li, Y.; Zhang, J. Multiple tasks for multiple objectives: A new multiobjective optimization method via multitask optimization. IEEE Trans. Evol. Comput. 2023, 29, 172–186. [Google Scholar] [CrossRef]
- Lukic, D.; Milosevic, M.; Antic, A.; Borojevic, S.; Ficko, M. Multi-criteria selection of manufacturing processes in the conceptual process planning. Adv. Prod. Eng. Manag. 2017, 12, 151–162. [Google Scholar] [CrossRef]
- He, Z.; Tran, P.K.; Thomassey, S.; Zeng, X.; Xu, J.; Yi, C. A deep reinforcement learning based multi-criteria decision support system for optimizing textile chemical process. Comput. Ind. 2021, 125, 103373. [Google Scholar] [CrossRef]
- Das, S.; Ghosh, A.; Majumdar, A.; Banerjee, D. Yarn engineering using hybrid artificial neural network-genetic algorithm model. Fibers Polym. 2013, 14, 1220–1226. [Google Scholar] [CrossRef]
- Mwasiagi, J.I.; Huang, X.; Wang, X. The use of hybrid algorithms to improve the performance of yarn parameters prediction models. Fibers Polym. 2012, 13, 1201–1208. [Google Scholar] [CrossRef]
- Khan, M.K.; Khan, M.S.A.; Kamran; Popa, I.L. Intuitionistic hesitant fuzzy rough aggregation operator-based EDAS method and its application to multi-criteria decision-making problems. Axioms 2025, 14, 21. [Google Scholar] [CrossRef]
- Zhu, S.; Zeng, L.; Cui, M. Symmetrical generalized Pareto dominance and adjusted reference vector cooperative evolutionary algorithm for many-objective optimization. Symmetry 2024, 16, 1484. [Google Scholar] [CrossRef]
- He, Z.; Tran, K.P.; Thomassey, S.; Zeng, X.; Xu, J.; Yi, C. Multi-objective optimization of the textile manufacturing process using deep-Q-network based multi-agent reinforcement learning. J. Manuf. Syst. 2022, 62, 939–949. [Google Scholar] [CrossRef]
- Kaplan, S.; Araz, C.; Göktepe, Ö. A multicriteria decision aid approach on navel selection problem for rotor spinning. Text. Res. J. 2006, 76, 896–904. [Google Scholar] [CrossRef]
- Szadkowski, J. Artifical intelligence approach to structural and parametrical optimization of multi–tool–machinning processes. Gepgyartastechnologia 1992, 9–10, 359–366. [Google Scholar]
- Płonka, S. Metody Oceny i Wyboru Optymalnej Struktury Procesu Technologicznego [Methods of Assessing and Selecting the Optimal Structure of the Technological Process]; Wydawnictwo Politechniki Łódzkiej: Bielsko-Biała, Poland, 1998. [Google Scholar]
- Mittemeijer, E.J.; Somers, M. Thermochemical Surface Engineering of Steels; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Dobrzański, L.A.; Dobrzańska-Danikiewicz, A.D. Obróbka Powierzchni Materiałów Inżynierskich [Engineering Materials Surface Treatment]; International OCSCO World Press: Gliwice, Poland, 2011. [Google Scholar]
- Posmyk, A. Warstwy Powierzchniowe Aluminiowych Tworzyw Konstrukcyjnych [Surface Layers of Aluminium Engineering Materials]; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2010. [Google Scholar]
- Lawrence, C.A. Fundamentals of Spun Yarn Technology; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Rauschert GmbH. Ceramic Thread Guides Rapal® Catalogue. Available online: https://rauschert.com.pl/img/files/PDF/prowadnice/Rapal_Katalog_2013.pdf (accessed on 3 September 2024).
- Płonka, S. Wielokryterialna Optymalizacja Procesów Wytwarzania Części Maszyn [Multi-Criteria Optimization of Machine Parts Manufacturing Processes]; WNT: Warszawa, Poland, 2017. [Google Scholar]
- Nowicki, B.W. Struktura Geometryczna: Chropowatość i Falistość Powierzchni [Geometric Structure: Surface Roughness and Waviness]; WNT: Warszawa, Poland, 1991. [Google Scholar]
- Osyczka, A. Evolutionary Algorithms for Single and Multicriteria Design Optimization; Physica–Verlag: Heidelberg, Germany, 2002. [Google Scholar]
- Montusiewicz, J. Ewolucyjna Analiza Wielokryterialna w Zagadnieniach Technicznych. [Evolutionary Multi-Criteria Analysis in Technical Matters]. Postdoctoral Dissertation, Politechnika Lubelska (Lublin University of Technology), Lublin, Poland, 2004. Available online: https://rcin.org.pl/Content/9112/PDF/WA727_9272_57263-5-2004_Ewolucyjna-analiza.pdf (accessed on 3 September 2024).
- Breiing, A.; Knosala, R. Bewerten Technischer Systeme: Theoretische und Methodische Grundlagen Bewertungstechnischer Entscheidungshilfen [Evaluating Technical Systems: Theoretical and Methodological Foundations of Evaluation-Related Decision-Making Aids]; Springer: Berlin, Germany, 2013. [Google Scholar]
- Ganesan, T.; Elamvazuthi, I.; Vasant, P.; Shaari, K.Z.K. Multiobjective optimization of bioactive compound extraction process via evolutionary strategies. In Intelligent Information and Database Systems, Proceedings of the 7th Asian Conference, ACIIDS 2015, Bali, Indonesia, 23–25 March 2015; Nguyen, N., Trawiński, B., Kosala, R., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9012, pp. 13–21. [Google Scholar] [CrossRef]
- Płonka, S.; Postrożny, J.; Drobina, R. Methodology of optimum selection of material and semi-folded products for rotors of open-end spinning machine. Autex Res. J. 2021, 21, 393–402. [Google Scholar] [CrossRef]
- Montusiewicz, J. Wspomaganie Procesów Projektowania i Planowania Wytwarzania w Budowie i Eksploatacji Maszyn Metodami Analizy Wielokryterialnej [Assistance for Design and Manufacturing Planning Processes in the Construction and Operation of Machines Using Multi-Criteria Analysis]; Wydawnictwo Politechniki Lubelskiej: Lublin, Poland, 2012. [Google Scholar]
- H’mida, F.; Martin, P.; Vernadat, F. Cost estimation in mechanical production: The Cost Entity approach applied to integrated product engineering. Int. J. Prod. Econ. 2006, 103, 17–35. [Google Scholar] [CrossRef]
- Wang, Z.; Nabavi, S.R.; Rangaiah, G.P. Multi-criteria decision making in chemical and process engineering: Methods, progress, and potential. Processes 2024, 12, 2532. [Google Scholar] [CrossRef]
- Lindroth, P.; Patriksson, M.; Strömberg, A.-B. Approximating the Pareto optimal set using a reduced set of objective functions. Eur. J. Oper. Res. 2010, 207, 1519–1534. [Google Scholar] [CrossRef]
- Henkel Ltd. “Loctite® Maintenance, Repair & Overhaul. Solutions Guide & Product Selector”. Available online: https://airstart.com.au/pdf/LOCTITE-FULL_PRODUCT_CATALOGUE.pdf (accessed on 3 September 2024).
- Klimczak, K.M.; Mleczko, J.; Więcek, D. Działalność Gospodarcza Przedsiębiorstw w Warunkach Przemysłu 4.0 [Economic Activity of Enterprises in the Context of Industry 4.0]; Polskie Wydawnictwo Ekonomiczne: Warszawa, Poland, 2023. [Google Scholar]
- Więcek, D.; Więcek, D. Production costs of machine elements estimated in the design phase. In Intelligent Systems in Production Engineering and Maintenance—ISPEM 2017: Proceedings of the First International Conference on Intelligent Systems in Production Engineering and Maintenance, Wrocław, Poland, 28–29 September 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 380–391. [Google Scholar] [CrossRef]
- PN-EN ISO 21920-2; Specyfikacje Geometrii Wyrobów (GPS)—Struktura Geometryczna Powierzchni: Profil—Część 2: Terminy, Definicje i Parametry Struktury Geometrycznej Powierzchni. [Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters]. Polish Committee for Standardization: Warszawa, Poland, 2022.
- Oczoś, K.E.; Liubimov, V. Struktura Geometryczna Powierzchni [Geometric Structure of the Surface]; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2003. [Google Scholar]
- Adamczak, S. Metrologia Geometryczna Powierzchni Technologicznych. Zarysy Kształtu—Falistość—Mikro- i Nanochropowatość [Geometric Metrology of Technological Surfaces: Outlines of Shape—Waviness—Micro- and Nanoroughness]; PWN: Warszawa, Poland, 2023. [Google Scholar]
- Zieliński, R.; Zieliński, W. Tablice Statystyczne [Statistical Tables]; PWN: Warszawa, Poland, 1990. [Google Scholar]
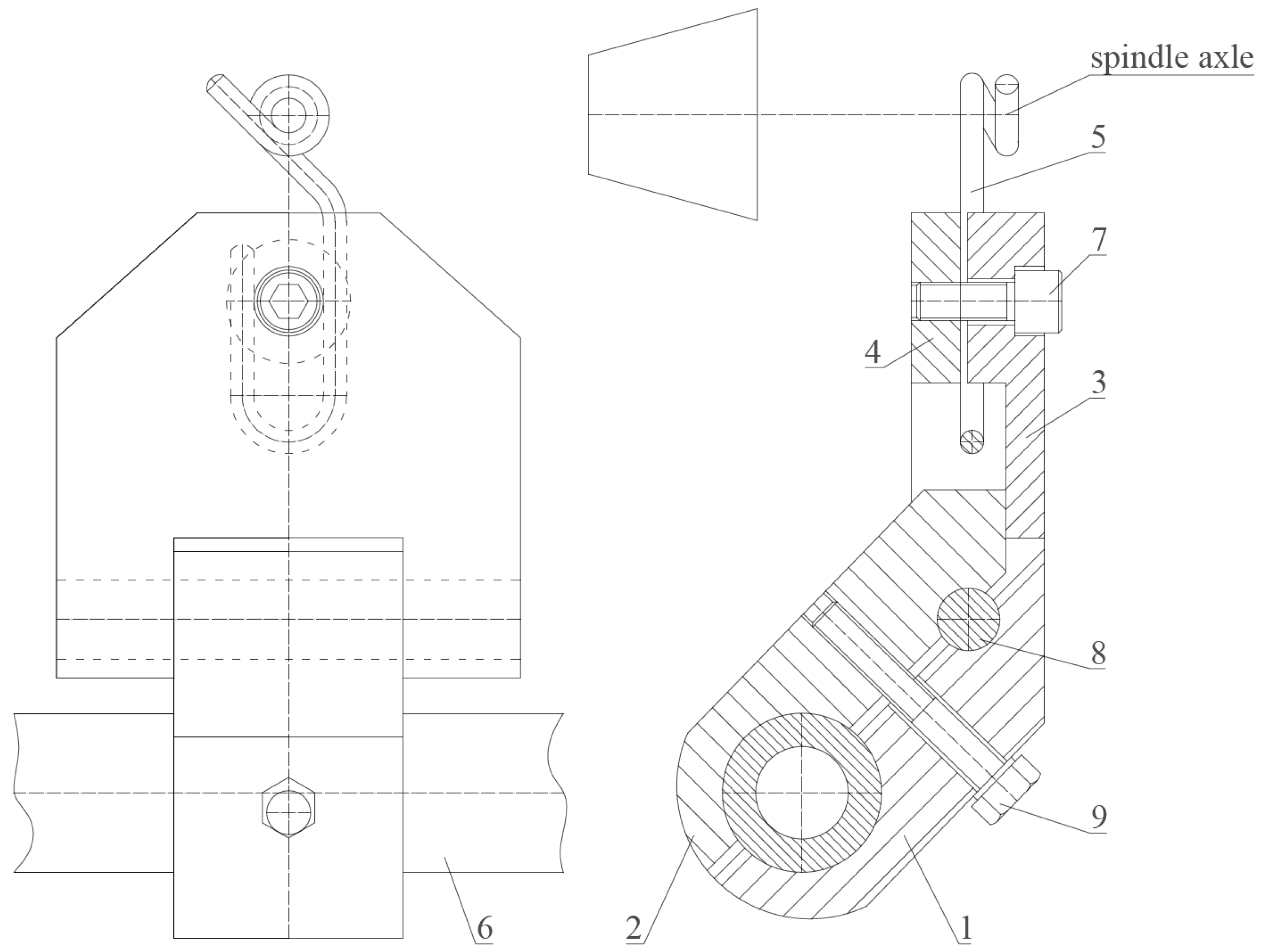
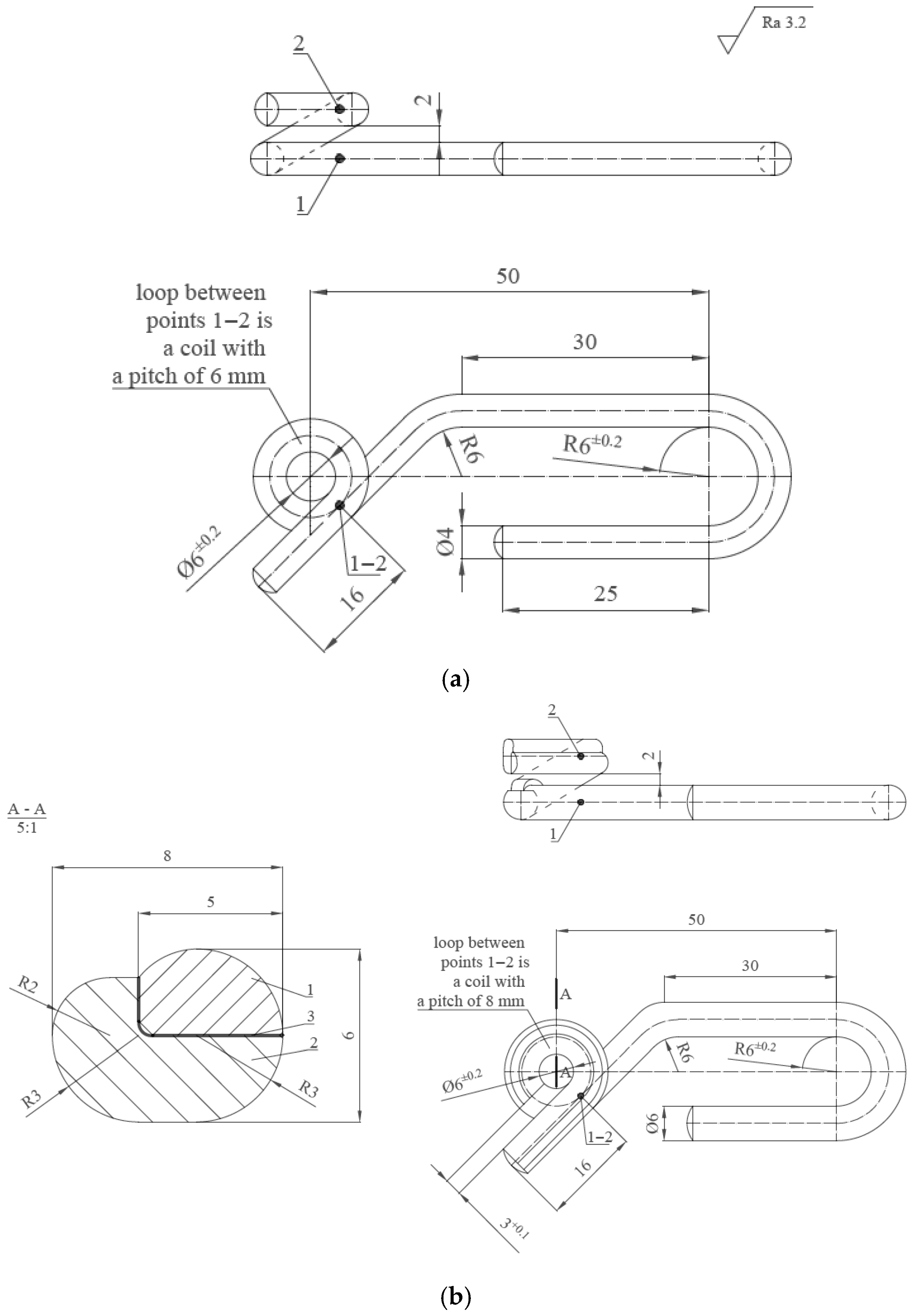

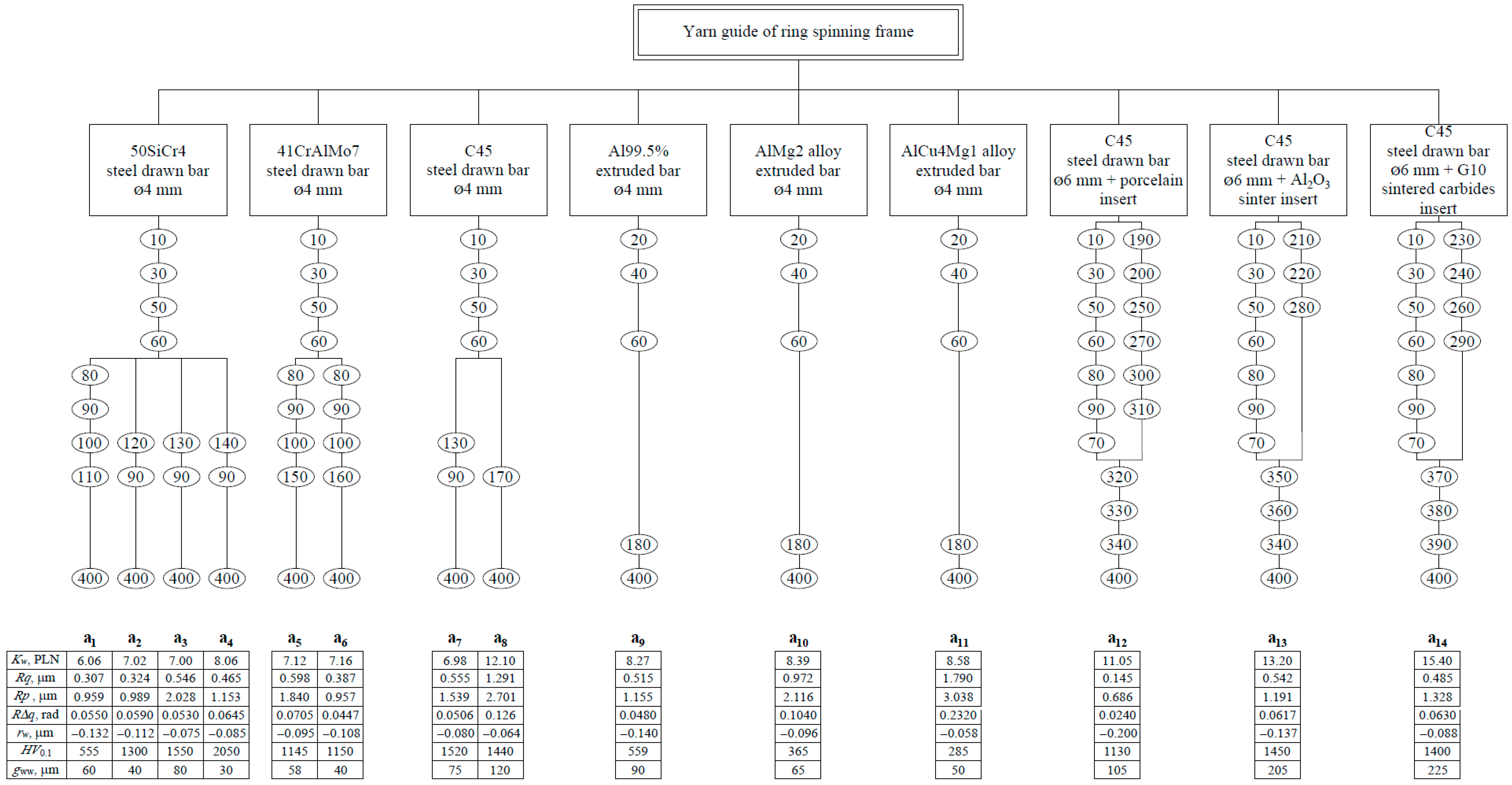
| Op. No. | Name of Operation | Station |
|---|---|---|
| 10 | Cutting steel drawn rod ø4 to a length of 130 mm or rod ø6 mm to a length of 162 mm | PHS-160 press |
| 20 | Cutting an extrusion bar made of Al or its alloys ø4 mm to a length of 145 mm | Hand press |
| 30 | Chamfering the ends of the steel bar ø4 mm or ø6 on both sides to 0.5 × 45° | 06-TSZ special grinder |
| 40 | Chamfering the ends of the bar of Al or its alloys ø4 mm on both sides to 0.5 × 45° | Belt grinder (abrasive cloth belt) |
| 50 | Soft annealing | PEC-90 electric stove |
| 60 | Straightening, bending in the device according to the drawing | Locksmith table + special instrument |
| 70 | Milling the end of the guide of C45 steel with a diameter of ø6 mm to a dimension of 3 mm, keeping the dimension 2+0.1 (according to Figure 3b). Refracting the sharp edges to a dimension of 0.5 × 45° | Precision milling machine |
| 80 | PEC-90 electric stove | |
| 90 | PEC-90 electric stove | |
| 100 | Removing scale by vibration | “Bolton” vibratory smoothing machine |
| 110 | Blacking | Bath: NaOH 100 g/L + NaNO3 130 g/L |
| 120 | VFC furnace | |
| 130 | VFC furnace | |
| 140 | VFC furnace | |
| 150 | Retort stove | |
| 160 | Retort stove | |
| 170 | Plasma spraying with Al2O3 powder | PLANCER device type PN-110 |
| 180 | Bath: electrolyte in the form of sulfuric acid 6% + sulfosalicylic acid 3% + lactic acid 2% + glycerin 2% | |
| 190 | Preparing the porcelain paste according to the recipe | Mixer AG-015 |
| 200 | Pressing the porcelain mass in the mold | Hydraulic press |
| 210 | Preparing the mass of aluminum powder Al2O3 | Mixer AG-015 |
| 220 | Pressing the mass of aluminum powder Al2O3 into a mold | Hydraulic press |
| 230 | Preparing the mass from tungsten carbide powder WC 94%/Co 6% according to the recipe | Mixer |
| 240 | Pressing in the form of a mass of powder WC 94%/Co 6% | Hydraulic press |
| 250 | Drying the porcelain molding at 120 °C | Chamber dryer |
| 260 | Evaporating the molding with WC 94%/Co 6% | SEL 13 dryer |
| 270 | Burning the porcelain molding at 900 °C | Chamber gas stove |
| 280 | Burning the Al2O3 molding at 1800 °C | Chamber gas stove |
| 290 | Burning the molding with WC 94%/Co 6% at 1280 °C | Chamber gas stove |
| 300 | Covering the porcelain molding with glaze | Bathtub with liquid glaze |
| 310 | Burning the glazed porcelain molding at 1410 °C | Chamber gas stove |
| 320 | Fitting the porcelain molding in the eyelet of the C45 steel guide | Locksmith table + special grinder |
| 330 | Embedding the porcelain molding with Loctite 3090 2K 10 g adhesive into the eyelet of the C45 steel guide | Locksmith table |
| 340 | Drying of the adhesive at 22 °C—about 5 h | Dryer |
| 350 | Fitting the Al2O3 sintered molded part in the mesh of a C45 steel guideway | Locksmith table + special grinder |
| 360 | Embedding the Al2O3 sintered molding on Loctite 3090 2K 10 g adhesive in the eyelet of the C45 steel guide | Locksmith table |
| 370 | Fitting the WC molding 94%/Co 6% into the eyelet of the C45 steel guide | Locksmith table + special grinder |
| 380 | Embedding the WC 94%/Co 6% molding on Loctite EA 3425 adhesive in the eyelet of the C45 steel guide | Locksmith table |
| 390 | Drying the adhesive at 22 °C—about 3 h | Dryer |
| 400 | Final inspection | Inspection stand |
| kj | a1 | a2 | a3 | a4 | a5 | a6 | |
| k1 | 0.1000 | 0.1822 | 0.1805 | 0.2713 | 0.1908 | 0.1942 | |
| k2 | 0.2131 | 0.2250 | 0.3799 | 0.3234 | 0.4162 | 0.2689 | |
| k3 | 0.2084 | 0.2203 | 0.6328 | 0.2854 | 0.5582 | 0.2076 | |
| k4 | 0.3431 | 0.3745 | 0.3275 | 0.4176 | 0.4647 | 0.2624 | |
| k5 | 0.5000 | 0.3824 | 0.1647 | 0.2235 | 0.2824 | 0.3588 | |
| k6 | 0.1000 | 0.5000 | 0.6333 | 0.9000 | 0.4173 | 0.4200 | |
| k7 | 0.2231 | 0.1410 | 0.3051 | 0.1000 | 0.2149 | 0.1410 | |
| kj | a7 | a8 | a9 | a12 | a13 | a14 | |
| k1 | 0.1788 | 0.6173 | 0.2893 | 0.5274 | 0.7116 | 0.9000 | |
| k2 | 0.3862 | 0.9000 | 0.3583 | 0.1000 | 0.3771 | 0.3373 | |
| k3 | 0.4387 | 0.9000 | 0.2862 | 0.1000 | 0.3005 | 0.3549 | |
| k4 | 0.3086 | 0.9000 | 0.2882 | 0.1000 | 0.3957 | 0.4059 | |
| k5 | 0.1941 | 0.1000 | 0.5471 | 0.9000 | 0.5294 | 0.2412 | |
| k6 | 0.6173 | 0.5747 | 0.1048 | 0.4093 | 0.5800 | 0.5533 | |
| k7 | 0.2846 | 0.4692 | 0.3462 | 0.4077 | 0.8179 | 0.9000 |
| Variant Number | a1 | a2 | a3 | a4 | a5 | a6 |
| Value of the distance function | 1.1584 | 1.0493 | 1.1774 | 1.1455 | 1.2389 | 1.0838 |
| Variant number | a7 | a8 | a9 | a12 | a13 | a14 |
| Value of the distance function | 1.0969 | 1.7661 | 1.1119 | 0.8116 | 0.9083 | 1.1870 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarco, A.; Płonka, S.; Zyzak, P. Multi-Criteria Optimization of Yarn Guide Manufacturing Processes. Appl. Sci. 2025, 15, 9055. https://doi.org/10.3390/app15169055
Jarco A, Płonka S, Zyzak P. Multi-Criteria Optimization of Yarn Guide Manufacturing Processes. Applied Sciences. 2025; 15(16):9055. https://doi.org/10.3390/app15169055
Chicago/Turabian StyleJarco, Aleksandra, Stanisław Płonka, and Piotr Zyzak. 2025. "Multi-Criteria Optimization of Yarn Guide Manufacturing Processes" Applied Sciences 15, no. 16: 9055. https://doi.org/10.3390/app15169055
APA StyleJarco, A., Płonka, S., & Zyzak, P. (2025). Multi-Criteria Optimization of Yarn Guide Manufacturing Processes. Applied Sciences, 15(16), 9055. https://doi.org/10.3390/app15169055






