A Fourth-Order Moment Method Based on Back Propagation Neural Network for High-Dimensional Nonlinear Reliability Analysis
Abstract
1. Introduction
2. Methods
2.1. Improved Fourth-Order Moment Method for Reliability Index
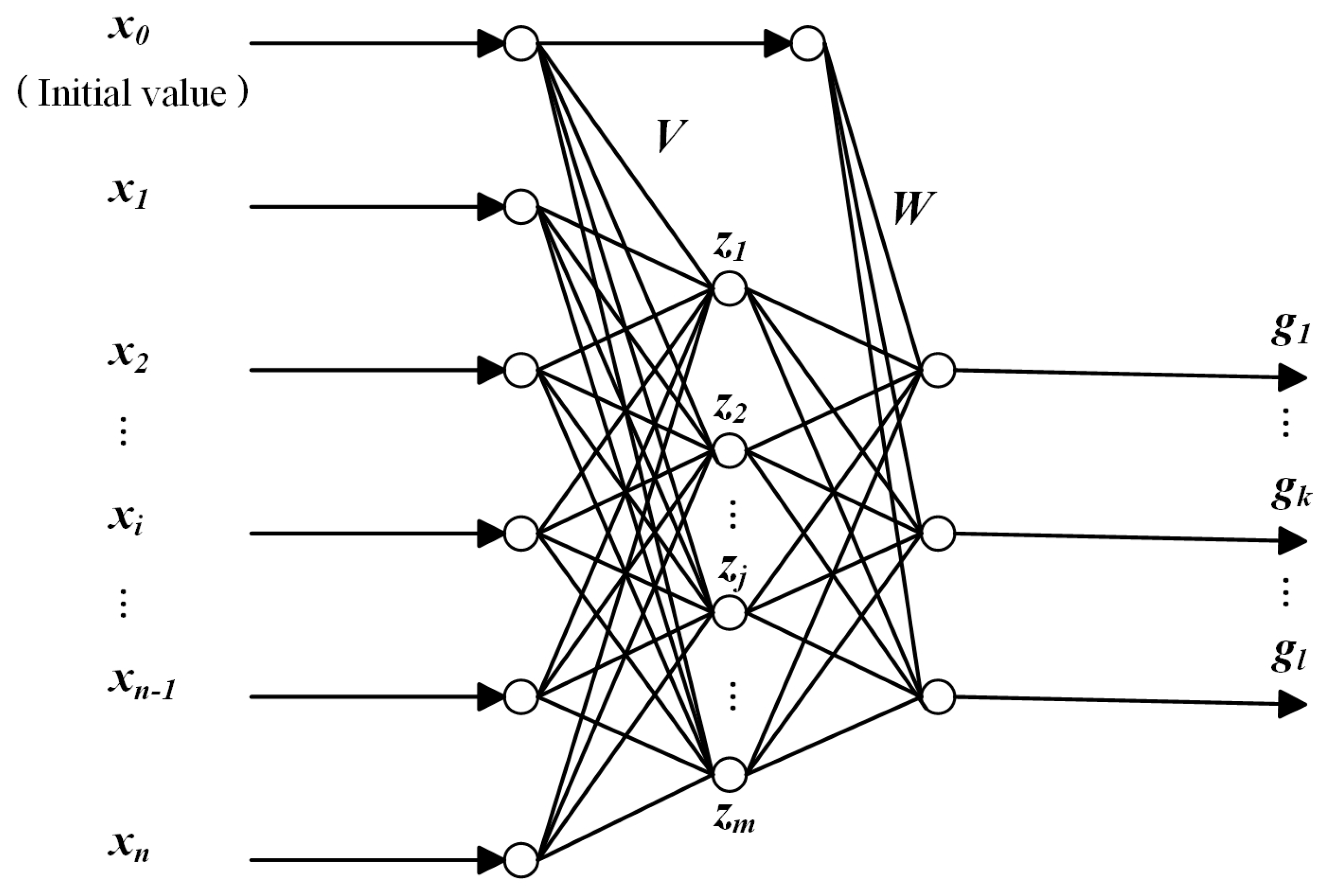
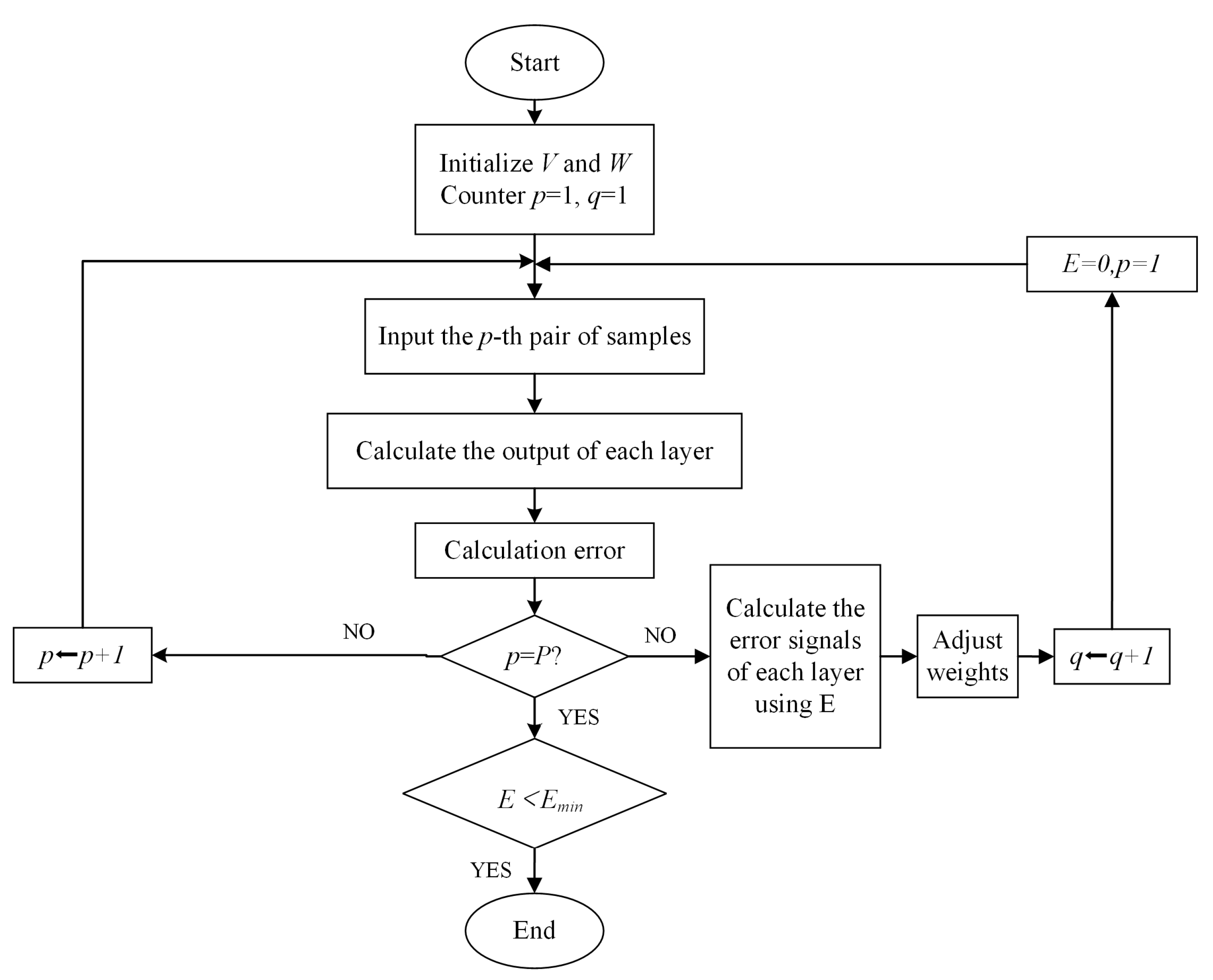
2.2. State Function Surrogate Model Based on BP Neural Network
3. Results
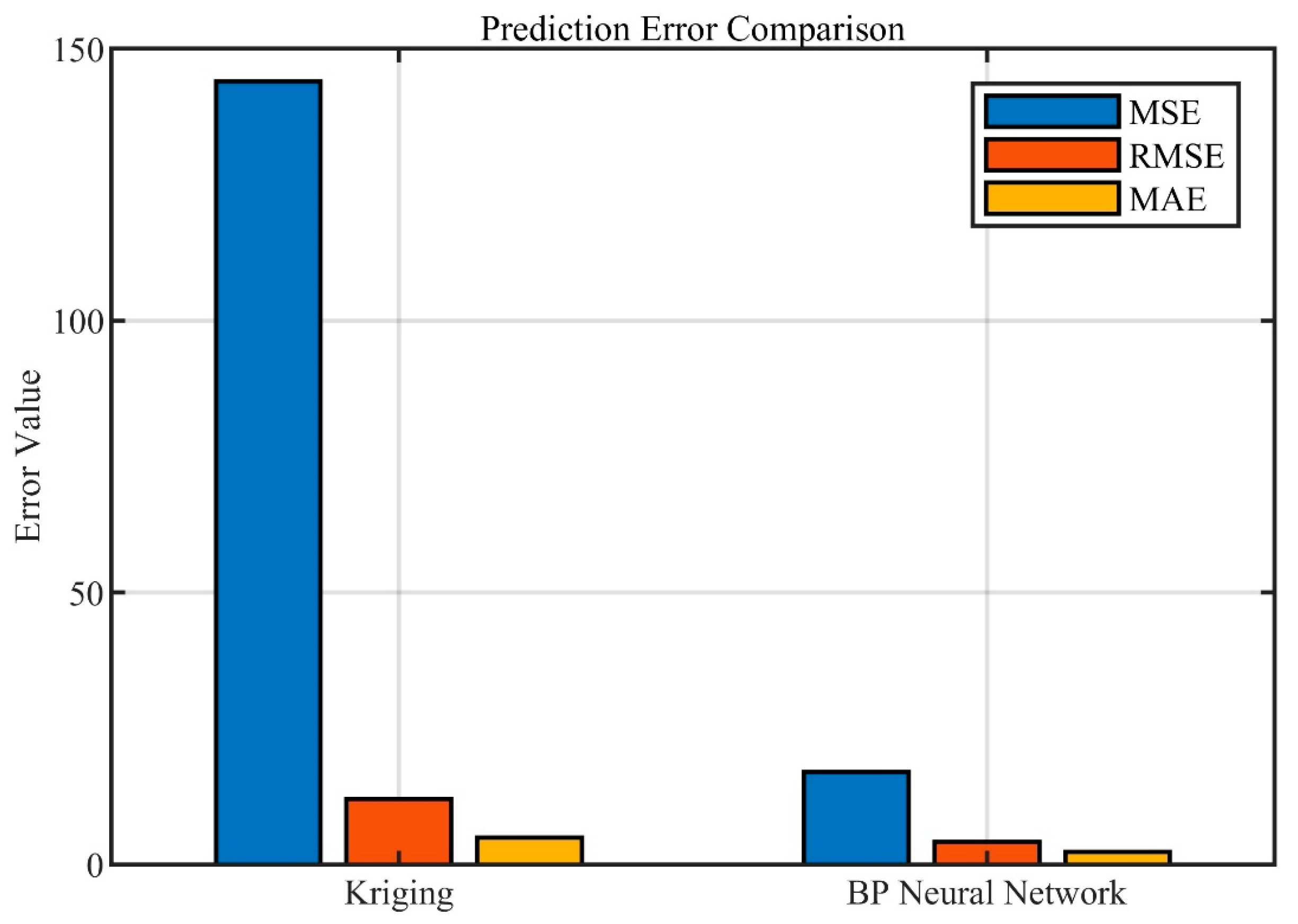
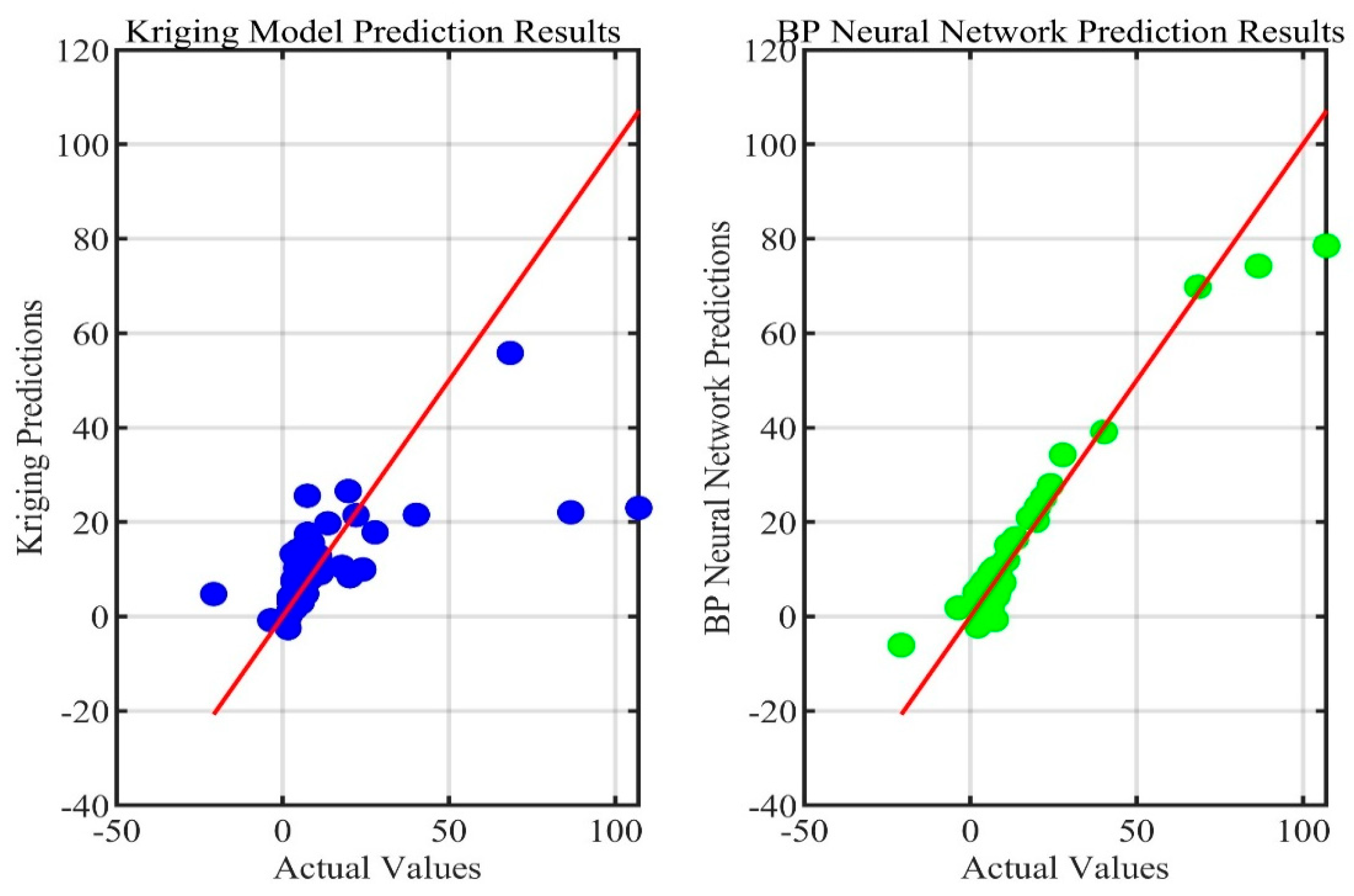
3.1. Comparison of Prediction Performance of Surrogate Models
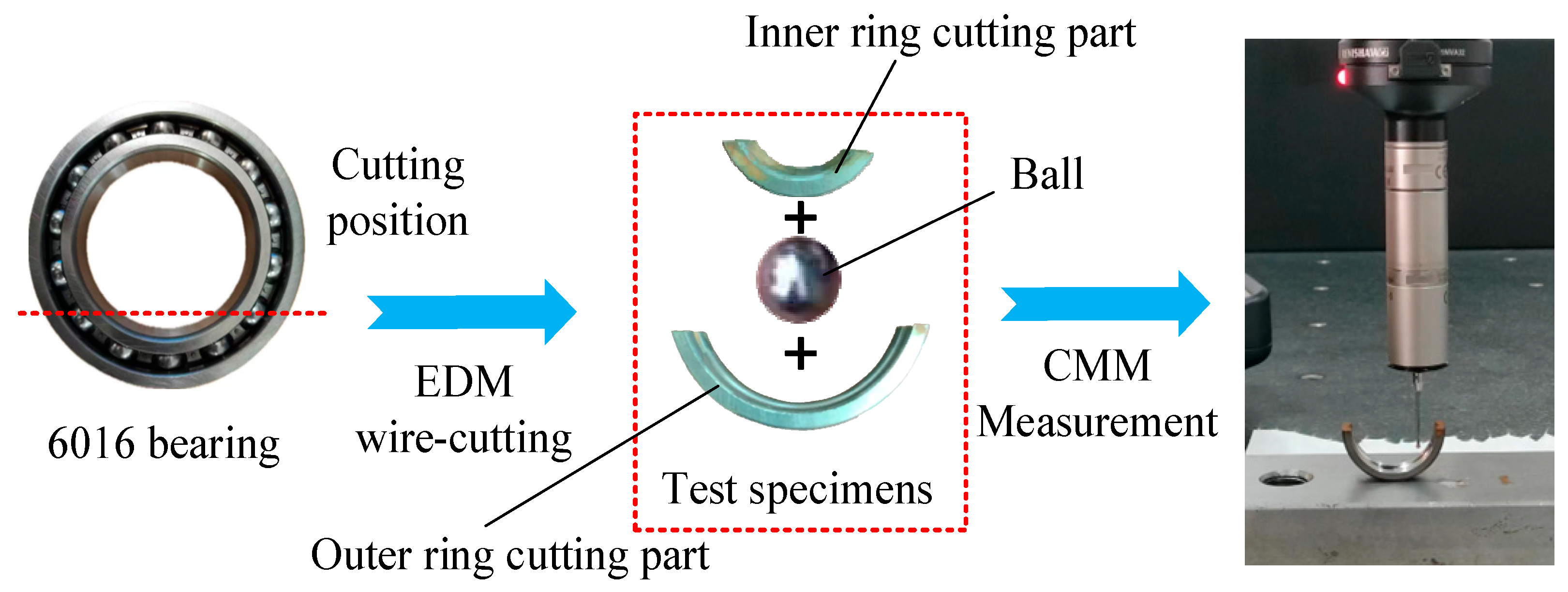
3.2. Reliability Analysis of 6016 Bearing Strength
3.3. Reliability Analysis of Stable Time-Varying Fatigue of 6016 Bearings
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BP | Back-Propagation |
| MCS | Monte Carlo Simulation |
| SORM | Second-Order Reliability Method |
| MPP | Most Probable Point |
| NN | Neural Networks |
| SVM | Support Vector Machines |
| PCE | Polynomial Chaos Expansion |
| ANN | Artificial Neural Network |
| DNNs | Deep Neural Networks |
| RBF | Radial Basis Function |
| CNNs | Convolutional Neural Networks |
| BP-FM | Back Propagation—Fourth-order Moment |
| FOSM | First-Order Second-Moment |
| FEM | Finite Element Method |
| MSE | Mean Square Error |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| EDM | Electrical Discharge Machining |
| CMM | Coordinate Measuring Machine |
Appendix A
References
- Al-Mosawe, D.; Neves, L.; Owen, J. Accelerating reliability analysis of deteriorated simply supported concrete beam with a newly developed approach: MCS, FORM and ANN. Structures 2024, 60, 105962. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Wang, G.; Lu, N.; Cui, J.; Wang, H. Fatigue Reliability Assessment for Orthotropic Steel Decks: Considering Multicrack Coupling Effects. Metals 2024, 14, 272. [Google Scholar] [CrossRef]
- Song, L.; Yu, X.; Xu, B.; Pang, R.; Zhang, Z. 3D slope reliability analysis based on the intelligent response surface methodology. Bull. Eng. Geol. Environ. 2021, 80, 735–749. [Google Scholar] [CrossRef]
- Kumar, A.; Pandit, B.; Tiwari, G. Reliability-based stability analysis of large rock slopes with different failure mechanisms using response surface methodology. Environ. Earth Sci. 2022, 81, 51121. [Google Scholar] [CrossRef]
- Shao, Z.; Li, X.; Xiang, P. A new computational scheme for structural static stochastic analysis based on Karhunen-Loeve expansion and modified perturbation stochastic finite element method. Comput. Mech. 2023, 71, 917–933. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Q.; Cao, H.; Ma, J. Structural Reliability Analysis Using Stochastic Finite Element Method Based on Krylov Subspace. Algorithms 2024, 17, 424. [Google Scholar] [CrossRef]
- Amalnerkar, E.; Lee, T.H.; Lim, W. Reliability analysis using bootstrap information criterion for small sample size response functions. Struct. Multidiscip. Optim. 2020, 62, 2901–2913. [Google Scholar] [CrossRef]
- de la Cruz, R.; Salinas, H.S.; Meza, C. Reliability Estimation for Stress-Strength Model Based on Unit-Half-Normal Distribution. Symmetry 2022, 14, 837. [Google Scholar] [CrossRef]
- Xie, H.; Li, J.; Liao, D. A new structural reliability analysis method under non-parameterized probability box variables. Struct. Multidiscip. Optim. 2022, 65, 32211. [Google Scholar] [CrossRef]
- Zhang, T. An improved high-moment method for reliability analysis. Struct. Multidiscip. Optim. 2017, 56, 1225–1232. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Ono, T. Moment methods for structural reliability. Struct. Saf. 2001, 23, 47–75. [Google Scholar] [CrossRef]
- E, S.; Wang, Y.; Xie, B.; Lu, F. An Adaptive Kriging-Based Fourth-Moment Reliability Analysis Method for Engineering Structures. Appl. Sci. 2024, 14, 3247. [Google Scholar] [CrossRef]
- Chen, W.; Gong, C.; Wang, Z.; Frangopol, D.M. Application of first-order reliability method with orthogonal plane sampling for high-dimensional series system reliability analysis. Eng. Struct. 2023, 282, 115778. [Google Scholar] [CrossRef]
- Dong, M.; Cheng, Y.; Wan, L. A Novel Adaptive Bayesian Model Averaging-Based Multiple Kriging Method for Structural Reliability Analysis. Ieee Trans. Reliab. 2025, 74, 2185–2199. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. Graph Neural Network Surrogate for Seismic Reliability Analysis of Highway Bridge Systems. J. Infrastruct. Syst. 2024, 30, 050240044. [Google Scholar] [CrossRef]
- Li, C.; Wen, J.-R.; Wan, J.; Taylan, O.; Fei, C.-W. Adaptive directed support vector machine method for the reliability evaluation of aeroengine structure. Reliab. Eng. Syst. Saf. 2024, 246, 110064. [Google Scholar] [CrossRef]
- Zakian, P. Stochastic finite cell method for structural mechanics. Comput. Mech. 2021, 68, 185–210. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Jospin, L.V.; Laga, H.; Boussaid, F.; Buntine, W.; Bennamoun, M. Hands-On Bayesian Neural Networks—A Tutorial for Deep Learning Users. IEEE Comput. Intell. Mag. 2022, 17, 29–48. [Google Scholar] [CrossRef]
- Fu, Z.; Xu, W.; Liu, S. Physics-informed kernel function neural networks for solving partial differential equations. Neural Netw. 2024, 172, 106098. [Google Scholar] [CrossRef]
- Zafar, A.; Aamir, M.; Nawi, N.M.; Arshad, A.; Riaz, S.; Alruban, A.; Dutta, A.K.; Almotairi, S. A Comparison of Pooling Methods for Convolutional Neural Networks. Appl. Sci. 2022, 12, 8643. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.-H.; Wang, D.; Chai, M. A reliability calculation method based on ISSA-BP neural network. Int. J. Struct. Integr. 2024, 15, 1249–1267. [Google Scholar] [CrossRef]
- Dong, Z.; Sheng, Z.; Zhao, Y.; Zhi, P. Robust optimization design method for structural reliability based on active-learning MPA-BP neural network. Int. J. Struct. Integr. 2023, 14, 248–266. [Google Scholar] [CrossRef]
- Xie, B.; Wang, Y.; Zhu, Y.; Lu, F. A novel reliability analysis method combining adaptive relevance vector machine and subset simulation for small failure probability. Struct. Multidiscip. Optim. 2023, 66, 473. [Google Scholar] [CrossRef]
- Zhang, T.; He, D. A Reliability-Based Robust Design Method for the Sealing of Slipper-Swash Plate Friction Pair in Hydraulic Piston Pump. IEEE Trans. Reliab. 2018, 67, 459–469. [Google Scholar] [CrossRef]
- Zhang, T. Matrix description of differential relations of moment functions in structural reliability sensitivity analysis. Appl. Math. Mech.-Engl. Ed. 2017, 38, 57–72. [Google Scholar] [CrossRef]
- Ma, L.; Tian, F. Pneumonia Incidence Rate Predictive Model of Nonlinear Time Series Based on Dynamic Learning Rate BP Neural Network. Fuzzy Inf. Eng. 2010, 1, 739–749. [Google Scholar]
- Xie, B.; Peng, C.; Wang, Y. Combined relevance vector machine technique and subset simulation importance sampling for structural reliability. Appl. Math. Model. 2023, 113, 129–143. [Google Scholar] [CrossRef]
- Xie, B.; Wang, Y.; Zhu, Y.; E, S.; Wu, Y. Vibration response-based time-variant reliability and sensitivity analysis of rolling bearings using the first-passage method. Reliab. Eng. Syst. Saf. 2025, 256, 110706. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y. An active learning reliability analysis method using adaptive Bayesian compressive sensing and Monte Carlo simulation (ABCS-MCS). Reliab. Eng. Syst. Saf. 2022, 221, 108377. [Google Scholar] [CrossRef]
- E, S.; Wang, Y.; Xie, B.; Lu, F. A Reliability-Based Robust Design Optimization Method for Rolling Bearing Fatigue under Cyclic Load Spectrum. Mathematics 2023, 11, 2843. [Google Scholar] [CrossRef]
- Xie, B.; Wang, Y.; Zhu, Y.; Liu, P.; Wu, Y.; Lu, F. Time-variant reliability analysis of angular contact ball bearing considering the coupled effect of rolling contact fatigue damage and wear. Reliab. Eng. Syst. Saf. 2024, 241, 109667. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Z.; Li, G.; He, J.; Shi, R.; Liu, C. Adaptive Kriging-based probabilistic subset simulation method for structural reliability problems with small failure probabilities. Structures 2024, 70, 107726. [Google Scholar] [CrossRef]


| Size Parameters | Mean | Variance |
|---|---|---|
| Center circle diameter (mm) | 102.4874 | 2.6 × 10−5 |
| Ball diameter (mm) | 13.4940 | 3.9 × 10−6 |
| Inner ring groove radius (mm) | 7.1010 | 1.2 × 10−6 |
| Outer ring groove radius (mm) | 6.9960 | 1.3 × 10−6 |
| Method | Initial Training Sample Size | Number of Predictions | Running Time s | Reliability /% | Relative Error/% |
|---|---|---|---|---|---|
| BP-FM | 20 | 1000 | 2.66 | 83.53 | 0.1438 |
| BP-MCS | 20 | 8.49 | 83.41 | / |
| Point of Time | Method | Initial Training Sample Size | Number of Predictions for the State Function | Reliability/% | Error Value |
|---|---|---|---|---|---|
| = 2800 h | BP-FM | 20 | 1000 | 94.8427 | 0.1836 |
| BP-MSC | 20 | 94.6591 | |||
| = 2850 h | BP-FM | 20 | 1000 | 76.0754 | −0.1592 |
| BP-MSC | 20 | 76.2346 | |||
| = 2900 h | BP-FM | 20 | 1000 | 43.8098 | −0.2703 |
| BP-MSC | 20 | 44.0801 | |||
| = 2950 h | BP-FM | 20 | 1000 | 16.6548 | 0.2491 |
| BP-MSC | 20 | 16.4057 | |||
| = 2992 h | BP-FM | 20 | 1000 | 5.3447 | 0.4121 |
| BP-MSC | 20 | 4.9326 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Li, W.; Xun, J.; Yang, X.; Wang, Y.; E, S. A Fourth-Order Moment Method Based on Back Propagation Neural Network for High-Dimensional Nonlinear Reliability Analysis. Appl. Sci. 2025, 15, 9046. https://doi.org/10.3390/app15169046
Yang K, Li W, Xun J, Yang X, Wang Y, E S. A Fourth-Order Moment Method Based on Back Propagation Neural Network for High-Dimensional Nonlinear Reliability Analysis. Applied Sciences. 2025; 15(16):9046. https://doi.org/10.3390/app15169046
Chicago/Turabian StyleYang, Kai, Weiye Li, Jiaqi Xun, Xiaotao Yang, Yanzhong Wang, and Shiyuan E. 2025. "A Fourth-Order Moment Method Based on Back Propagation Neural Network for High-Dimensional Nonlinear Reliability Analysis" Applied Sciences 15, no. 16: 9046. https://doi.org/10.3390/app15169046
APA StyleYang, K., Li, W., Xun, J., Yang, X., Wang, Y., & E, S. (2025). A Fourth-Order Moment Method Based on Back Propagation Neural Network for High-Dimensional Nonlinear Reliability Analysis. Applied Sciences, 15(16), 9046. https://doi.org/10.3390/app15169046







