Classification of Rockburst Intensity Grades: A Method Integrating k-Medoids-SMOTE and BSLO-RF
Abstract
1. Introduction
2. Rockburst Case Acquisition and Data Cleaning
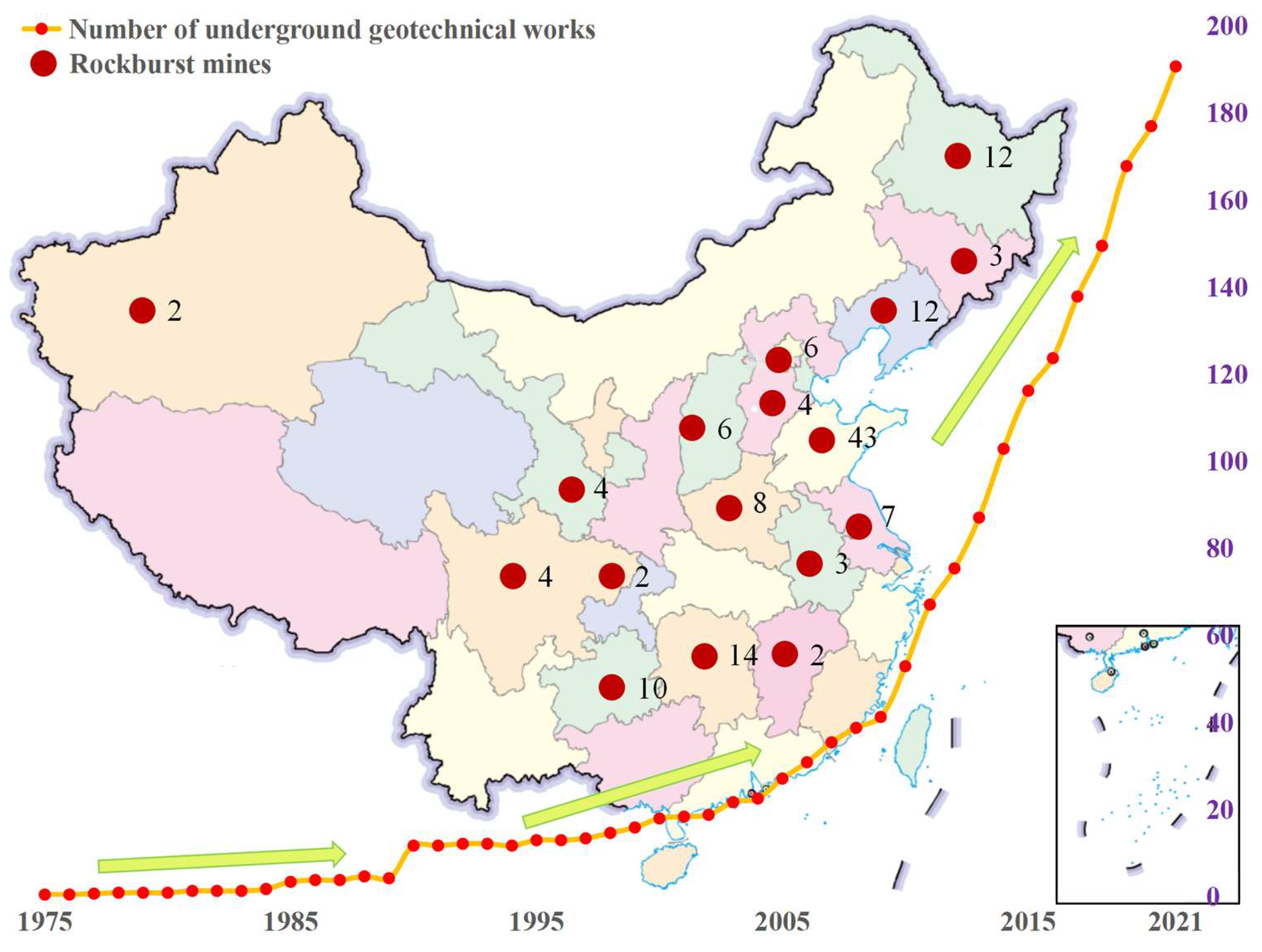
2.1. Database Establishment and Analysis
- Literature-driven preliminary selection: A systematic review of key rockburst prediction studies [11,22,31] confirmed these parameters as consistently critical. For example, Xue (2020) [30] demonstrated that , , and / are core indicators in 344 case studies, while Gong (2023) [31] identified as a robust energy-related predictor in 1114 rockburst instances.
- Correlation analysis validation: Pearson correlation analysis was performed between candidate features and rockburst intensity grades, revealing that the six parameters exhibit significant correlations (|r| > 0.6, p < 0.01). This statistical relevance confirms their ability to reflect rockburst characteristics.
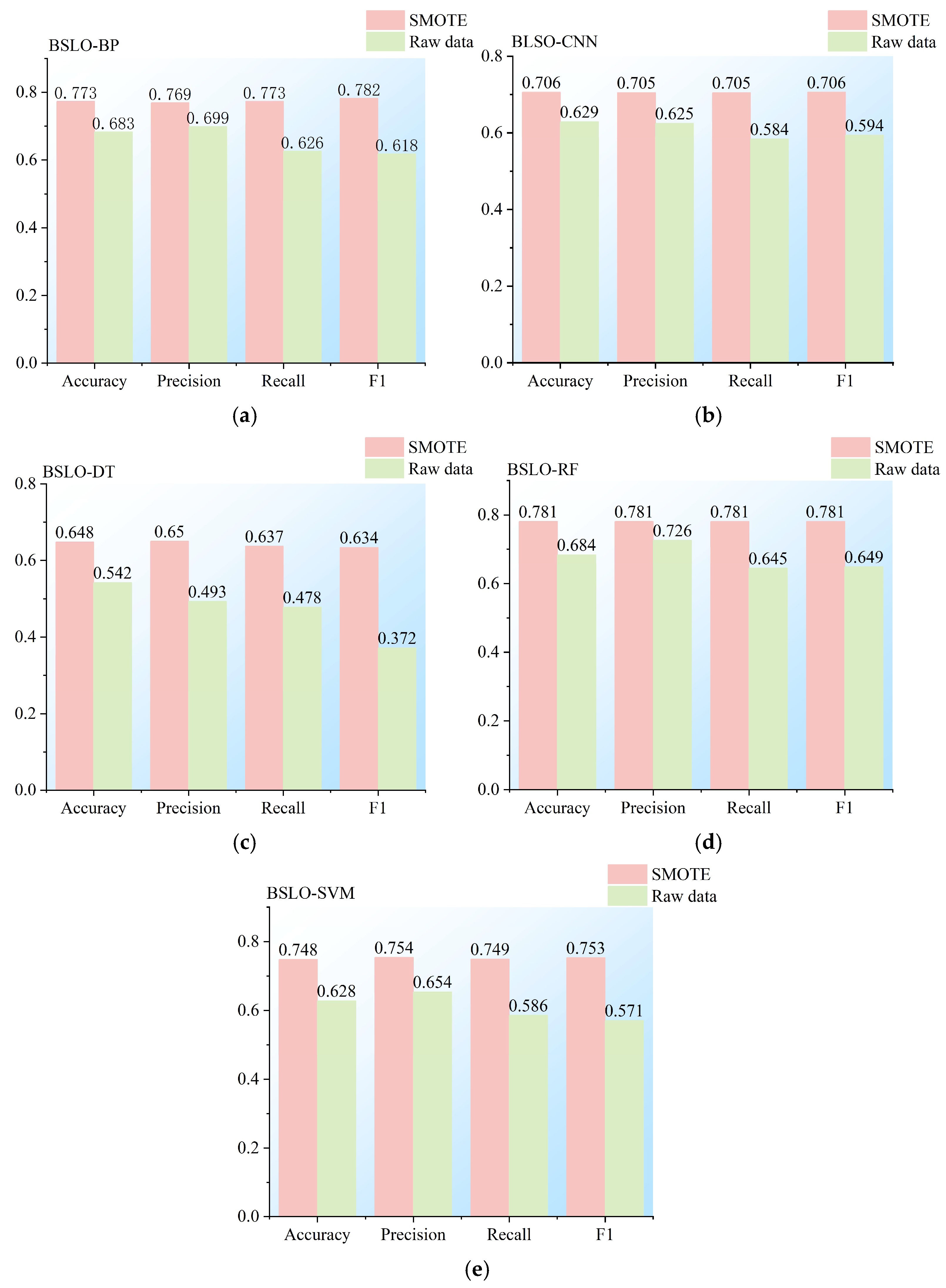
2.2. Data Preprocessing
3. Construction of the BSLO-RF Algorithm
3.1. BSLO Algorithm
3.2. BSLO-RF Model Construction
- (1)
- The dataset is divided into a training set (480 samples, 80%) and a testing set (120 samples, 20%) using stratified sampling to maintain the original proportional distribution of rockburst intensity grades (Level I:Level II:Level III:Level IV ≈ 1.5:2.5:4.3:1.7). This ensures that each grade’s representation in the training and testing sets is consistent with the overall dataset, avoiding bias caused by uneven class distribution. Both subsets undergo dimensionless preprocessing using the Robust normalization method.
- (2)
- The BSLO algorithm parameters are configured, including population size, maximum number of iterations, the ratio between directional and directionless leech individuals, the threshold for exploration and exploitation switching, and the execution conditions for the re-tracking strategy.
- (3)
- The initial leech population is randomly generated to form the initial solution space.
- (4)
- The perception distance (PD) is used to determine the leech’s search status, allowing for adaptive switching between exploration and exploitation strategies, and updating individual positions accordingly.
- (5)
- A re-tracking strategy is implemented to prevent individuals from being trapped in local optima, thereby enhancing global search capability and continuously optimizing the location of the optimal solution.
- (6)
- The hyperparameters optimized by BSLO are applied to the Random Forest (RF) model. The RF model is then trained, and predictions are performed on the validation set. Prediction accuracy metrics such as mean absolute error (MAE), root mean square error (RMSE), and the coefficient of determination (R2) are calculated.
- (7)
- The optimal parameter combination of the BSLO-RF model is output, completing the construction of the rockburst intensity level prediction model.
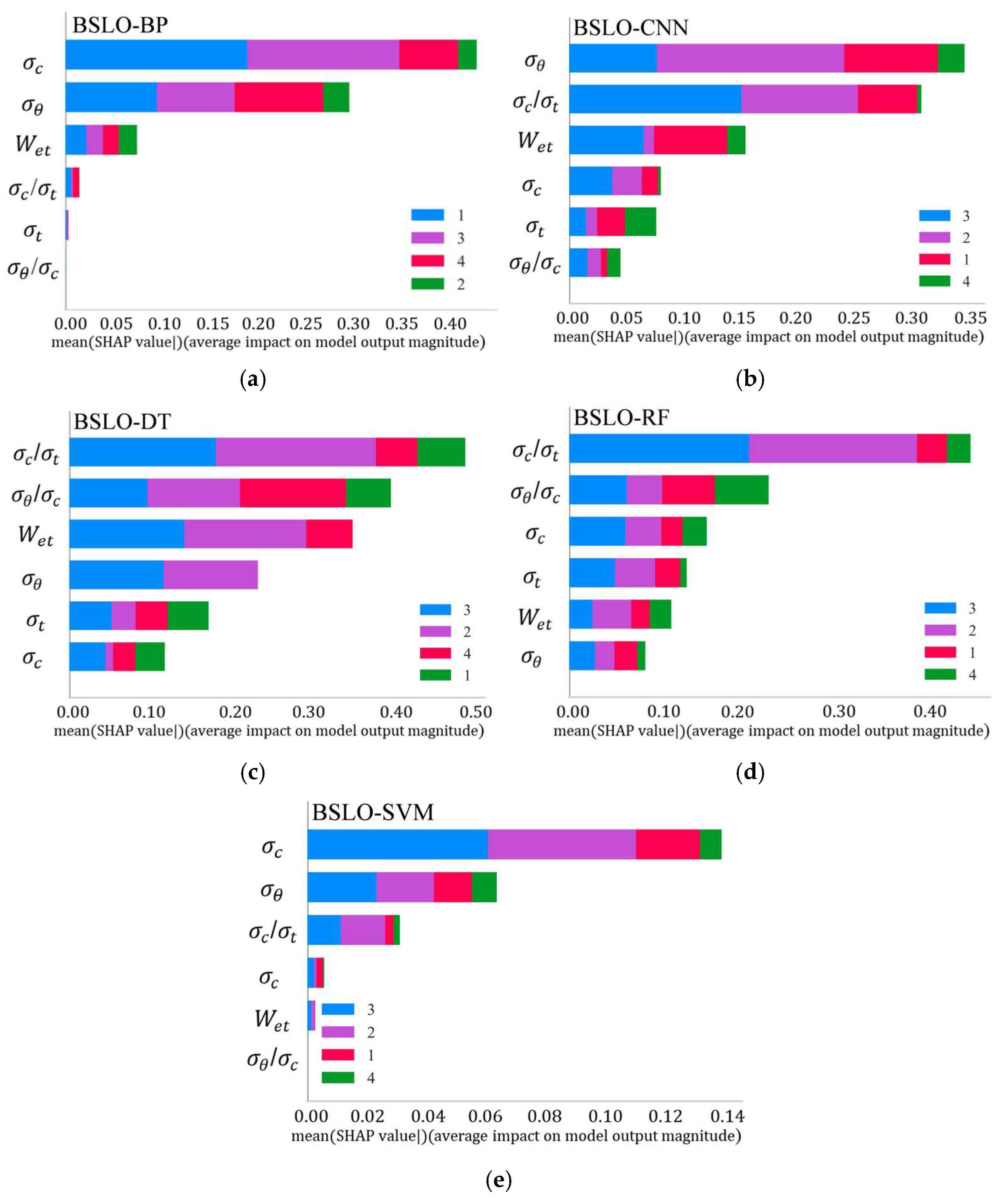
3.3. Parameter Optimization of BSLO-RF Model
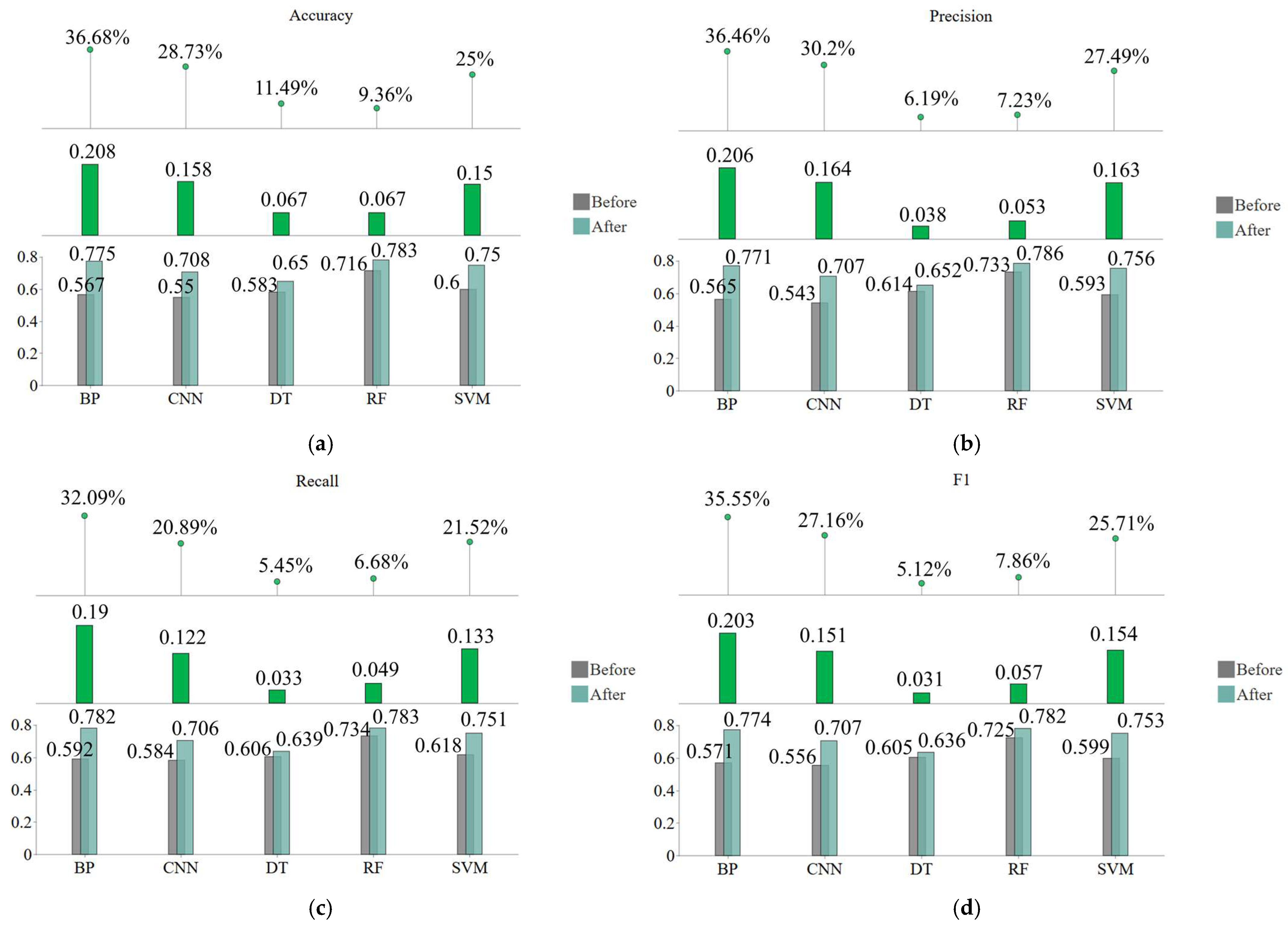
3.4. Comparison of Prediction Results
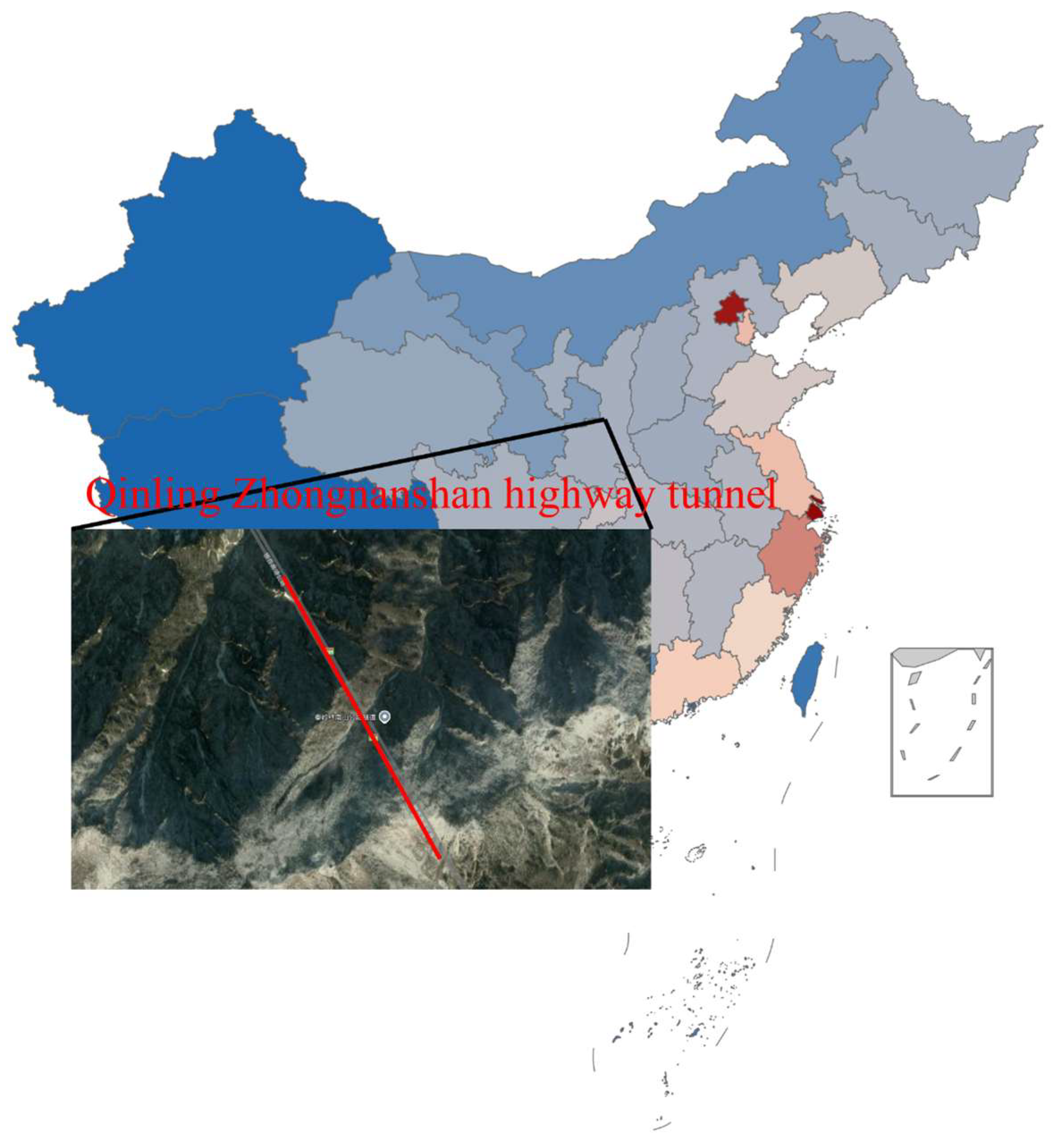
4. Engineering Verification
5. Conclusions
- (1)
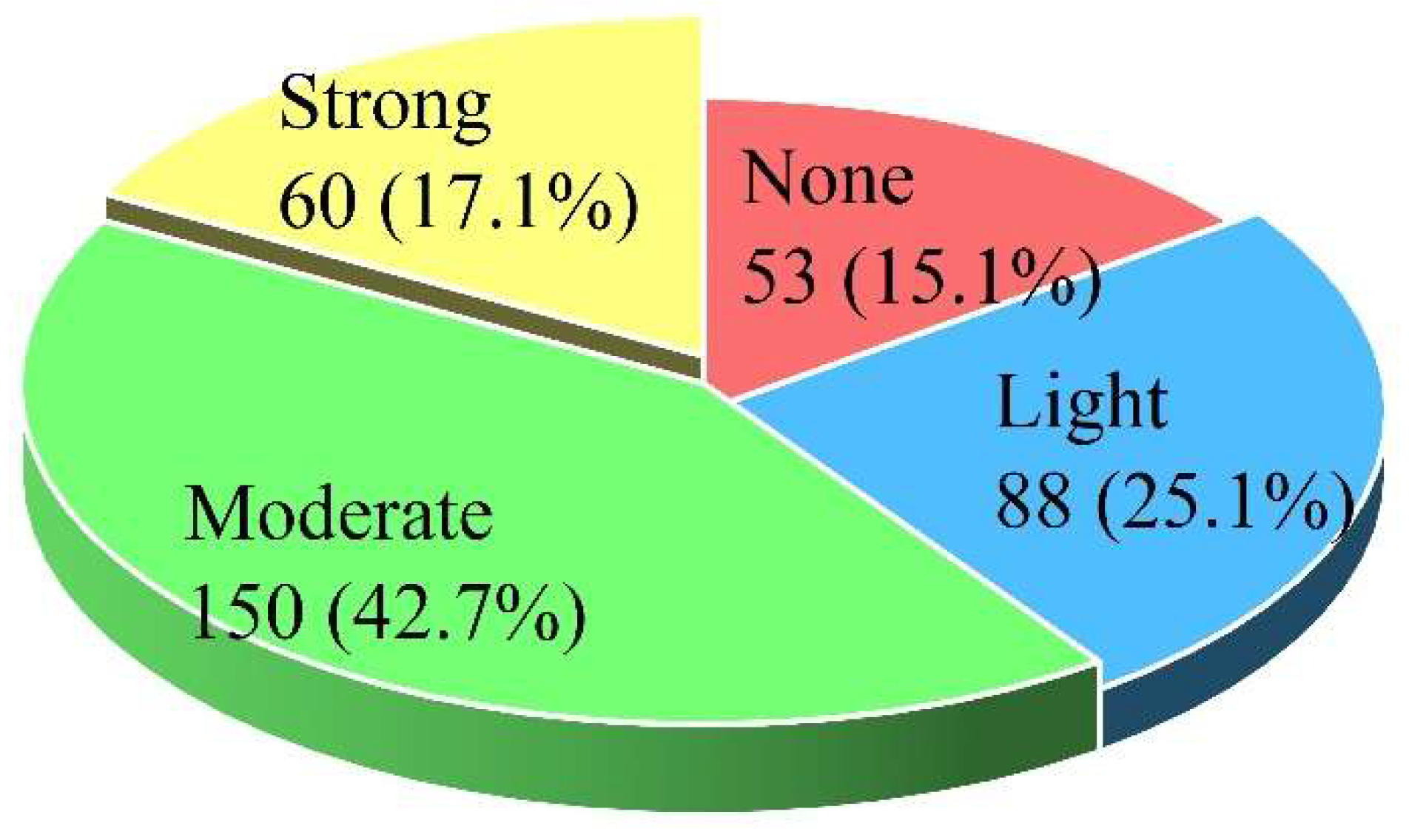
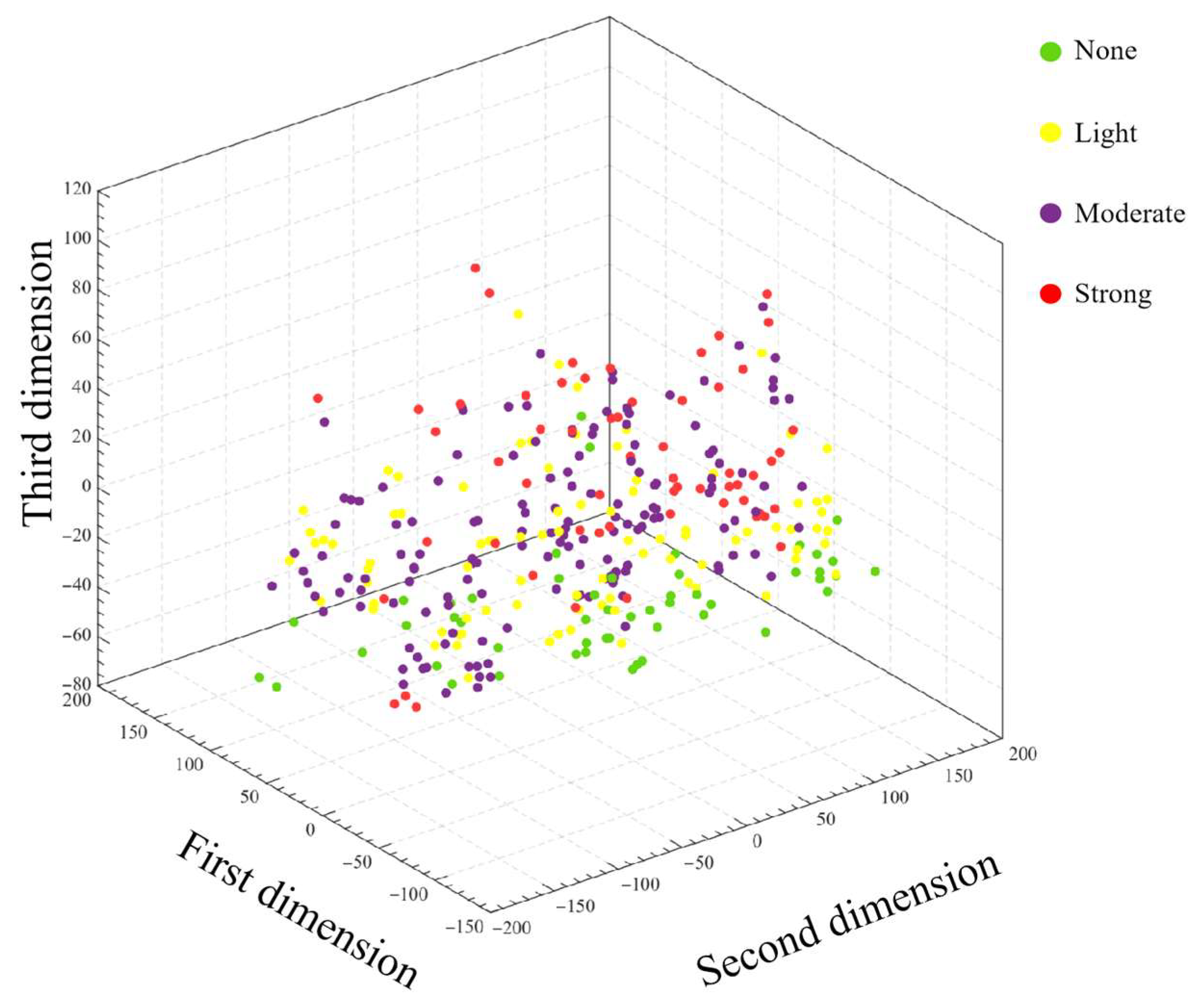
- A dataset of 351 documented rockburst cases was compiled and classified into four intensity levels. Data imbalance and outlier effects were mitigated using z-score normalization and k-medoids-SMOTE, improving inter-class separability.
- (2)
- The BSLO algorithm effectively tuned Random Forest hyperparameters, enhancing classification accuracy, recall, and F1-score compared with conventional methods. On the balanced dataset, the BSLO-RF model achieved an average accuracy of 89.16%, with notable improvements in extreme-grade prediction.
- (3)
- Application to the Zhongnanshan Tunnel project achieved 80% prediction accuracy, verifying the model’s robustness and adaptability in complex geological conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, W.; Zhao, G.; Wu, H.; Dai, B. Risk Assessment of Rockburst via an Extended MABAC Method under Fuzzy Environment. Tunn. Undergr. Space Technol. 2019, 83, 533–544. [Google Scholar] [CrossRef]
- Zhai, S.; Su, G.; Yin, S.; Zhao, B.; Yan, L. Rockburst Characteristics of Several Hard Brittle Rocks: A True Triaxial Experimental Study. J. Rock. Mech. Geotech. Eng. 2020, 12, 279–296. [Google Scholar] [CrossRef]
- Ma, C.S.; Chen, W.Z.; Tan, X.J.; Tian, H.M.; Yang, J.P.; Yu, J.X. Novel Rockburst Criterion Based on the TBM Tunnel Construction of the Neelum–Jhelum (NJ) Hydroelectric Project in Pakistan. Tunn. Undergr. Space Technol. 2018, 81, 391–402. [Google Scholar] [CrossRef]
- Barton, N. Some New Q-Value Correlations to Assist in Site Characterisation and Tunnel Design. Int. J. Rock. Mech. Min. Sci. 2002, 39, 185–216. [Google Scholar] [CrossRef]
- Malan, D.F.; Napier, J.A.L. Rockburst Support in Shallow-Dipping Tabular Stopes at Great Depth. Int. J. Rock. Mech. Min. Sci. 2018, 112, 302–312. [Google Scholar] [CrossRef]
- Gong, F.; Wang, Y.; Luo, S. Rockburst Proneness Criteria for Rock Materials: Review and New Insights. J. Cent. South. Univ. Technol. 2020, 27, 2793–2821. [Google Scholar] [CrossRef]
- Ghasemi, E.; Gholizadeh, H.; Adoko, A.C. Evaluation of Rockburst Occurrence and Intensity in Underground Structures Using Decision Tree Approach. Eng. Comput. 2020, 36, 213–225. [Google Scholar] [CrossRef]
- Li, N.; Feng, X.; Jimenez, R. Predicting Rock Burst Hazard with Incomplete Data Using Bayesian Networks. Tunn. Undergr. Space Technol. 2017, 61, 61–70. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-Term Rockburst Damage Assessment in Burst-Prone Mines: An Explainable XGBOOST Hybrid Model with SCSO Algorithm. Rock Mech. Rock Eng. 2023, 56, 8745–8770. [Google Scholar] [CrossRef]
- Sun, L.; Hu, N.; Ye, Y.; Tan, W.; Wu, M.; Wang, X.; Huang, Z. Ensemble Stacking Rockburst Prediction Model Based on Yeo–Johnson, K-Means SMOTE, and Optimal Rockburst Feature Dimension Determination. Sci. Rep. 2022, 12, 15352. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, P.; Peng, P.; Khandelwal, M.; Qiu, Y. Performance Evaluation of Rockburst Prediction Based on PSO-SVM, HHO-SVM, and MFO-SVM Hybrid Models. Min. Met. Explor. 2023, 40, 617–635. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel Ensemble Tree Solution for Rockburst Prediction Using Deep Forest. Mathematics 2022, 10, 787. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, J.; Wang, S.; Wang, S. Analysis of Rock Cuttability Based on Excavation Parameters of TBM. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 93. [Google Scholar] [CrossRef]
- Cook, N.G.W.; Hoek, E.; Pretorius, J.P.G.; Ortlepp, W.D.; Salamon, H.D.G. Rock Mechanics Applied to the Study of Rockbursts. J. South. Afr. Inst. Min. Metallurgy. 1966, 66, 435–528. [Google Scholar]
- Aubertin, M.; Gill, D.; Simon, R. On the Use of the Brittleness Index Modified (BIM) to Estimate the Post-Peak Behavior of Rocks. 1994. Available online: https://scispace.com/papers/on-the-use-of-the-brittleness-index-modified-bim-to-estimate-3ckb47y2cn (accessed on 5 August 2025).
- Brown, E.T.; Hoek, E. Underground Excavations in Rock; CRC Press: Boca Raton, FL, USA, 1980; ISBN 1-4822-8892-3. [Google Scholar]
- Tao, Z.Y. Rockburst in High Ground Stress Area and Its Identification. People’s Yangtze River 1987, 4, 25–32. [Google Scholar]
- Li, D.; Chen, Y.; Dai, B.; Wang, Z.; Liang, H. Numerical Study of Dig Sequence Effects during Large-Scale Excavation. Appl. Sci. 2023, 13, 11342. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Liu, V.; Mitri, H. Machine Learning Methods for Rockburst Prediction-State-of-the-Art Review. Int. J. Min. Sci. Technol. 2019, 29, 565–570. [Google Scholar] [CrossRef]
- Xue, Y.; Bai, C.; Qiu, D.; Kong, F.; Li, Z. Predicting Rockburst with Database Using Particle Swarm Optimization and Extreme Learning Machine. Tunn. Undergr. Space Technol. 2020, 98, 103287. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Q.; Huang, X.; Pan, Y. Real-Time Prediction of Rockburst Intensity Using an Integrated CNN-Adam-BO Algorithm Based on Microseismic Data and Its Engineering Application. Tunn. Undergr. Space Technol. 2021, 117, 104133. [Google Scholar] [CrossRef]
- Ullah, B.; Kamran, M.; Rui, Y. Predictive Modeling of Short-Term Rockburst for the Stability of Subsurface Structures Using Machine Learning Approaches: T-SNE, K-Means Clustering and XGBoost. Mathematics 2022, 10, 449. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, S. Rockburst Prediction Based on Particle Swarm Optimization and Machine Learning Algorithm. In Proceedings of the 3rd International Conference on Information Technology in Geo-Engineering, Guimarães, Portugal, 29 September–2 October 2019; Springer Nature: Berlin/Heidelberg, Germany, 2020; pp. 292–303. [Google Scholar] [CrossRef]
- Qiu, D.; Li, X.; Xue, Y.; Fu, K.; Zhang, W.; Shao, T.; Fu, Y. Analysis and Prediction of Rockburst Intensity Using Improved DS Evidence Theory Based on Multiple Machine Learning Algorithms. Tunn. Undergr. Space Technol. 2023, 140, 105331. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Yang, S. Rockburst Interpretation by a Data-Driven Approach: A Comparative Study. Mathematics 2021, 9, 2965. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, H.; Koopialipoor, M.; Jahed Armaghani, D.; Tahir, M.M. Investigating the Effective Parameters on the Risk Levels of Rockburst Phenomena by Developing a Hybrid Heuristic Algorithm. Eng. Comput. 2021, 37, 1679–1694. [Google Scholar] [CrossRef]
- Ma, K.; Shen, Q.-q.; Sun, X.-y.; Ma, T.-h.; Hu, J.; Tang, C.-a. Rockburst prediction model using machine learning based on microseismic parameters of Qinling water conveyance tunnel. J. Cent. South. Univ. 2023, 30, 289–305. [Google Scholar] [CrossRef]
- Liu, R.; Ye, Y.; Hu, N.; Chen, H.; Wang, X. Classified Prediction Model of Rockburst Using Rough Sets-Normal Cloud. Neural Comput. Appl. 2019, 31, 8185–8193. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Xu, H. Rockburst Prediction in Kimberlite with Unsupervised Learning Method and Support Vector Classifier. Tunn. Undergr. Space Technol. 2019, 90, 12–18. [Google Scholar] [CrossRef]
- Xue, Y.; Bai, C.; Kong, F.; Qiu, D.; Li, L.; Su, M.; Zhao, Y. A Two-Step Comprehensive Evaluation Model for Rockburst Prediction Based on Multiple Empirical Criteria. Eng. Geol. 2020, 268, 105515. [Google Scholar] [CrossRef]
- Gong, F.; Dai, J.; Xu, L. A Strength-Stress Coupling Criterion for Rockburst: Inspirations from 1114 Rockburst Cases in 197 Underground Rock Projects. Tunn. Undergr. Space Technol. 2023, 142, 105396. [Google Scholar] [CrossRef]
- Wang, J.; Ma, H.; Yan, X. Rockburst Intensity Classification Prediction Based on Multi-Model Ensemble Learning Algorithms. Mathematics 2023, 11, 838. [Google Scholar] [CrossRef]
- Bai, J.; Nguyen-Xuan, H.; Atroshchenko, E.; Kosec, G.; Wang, L.; Abdel Wahab, M. Blood-Sucking Leech Optimizer. Adv. Eng. Softw. 2024, 195, 103696. [Google Scholar] [CrossRef]
- Yu, W.; Xu, Q. Rock Burst Prediction in Deep Shaft Based on RBF-AR Model. J. Jilin Univ. 2013, 43, 1943–1949. [Google Scholar]

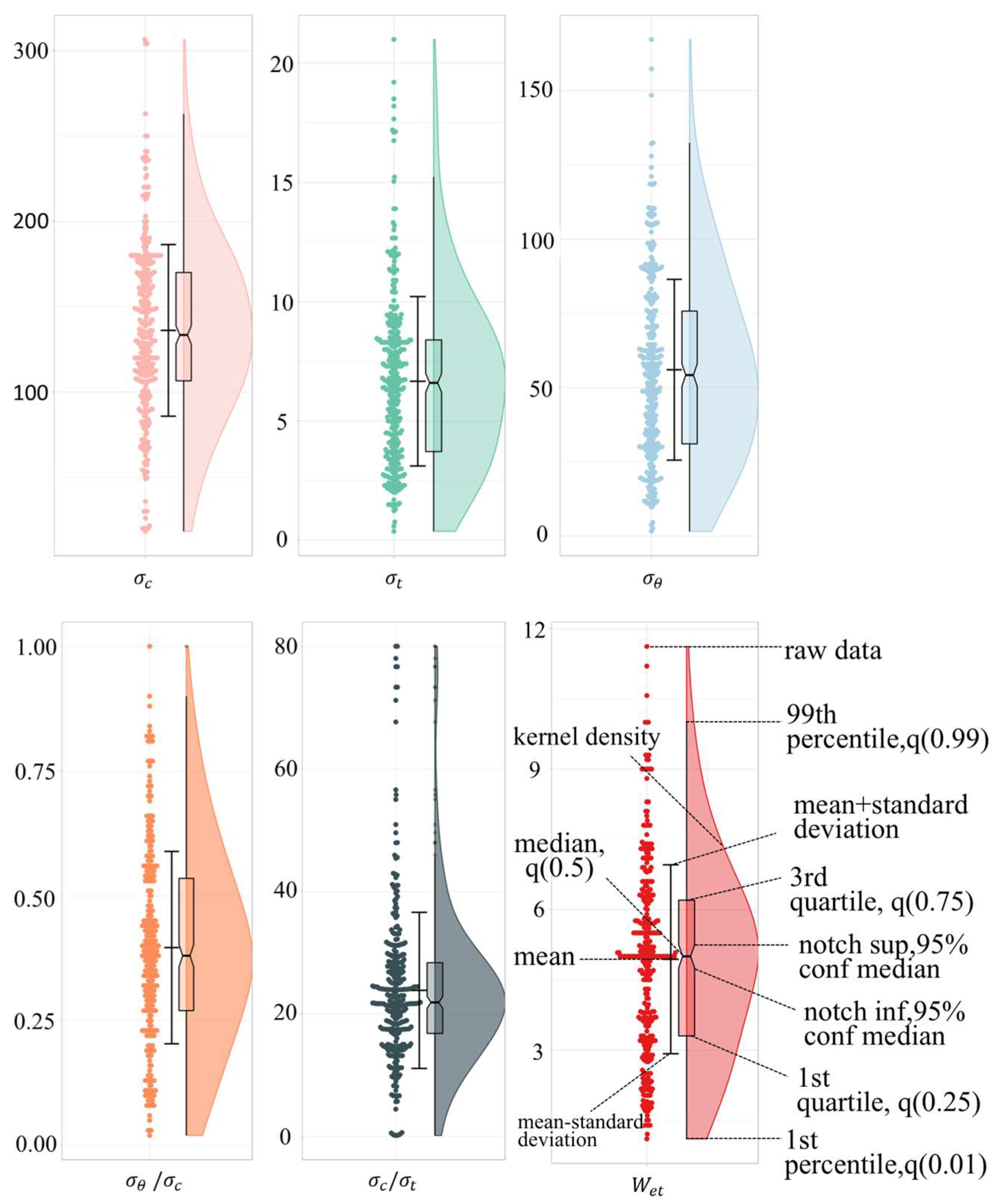
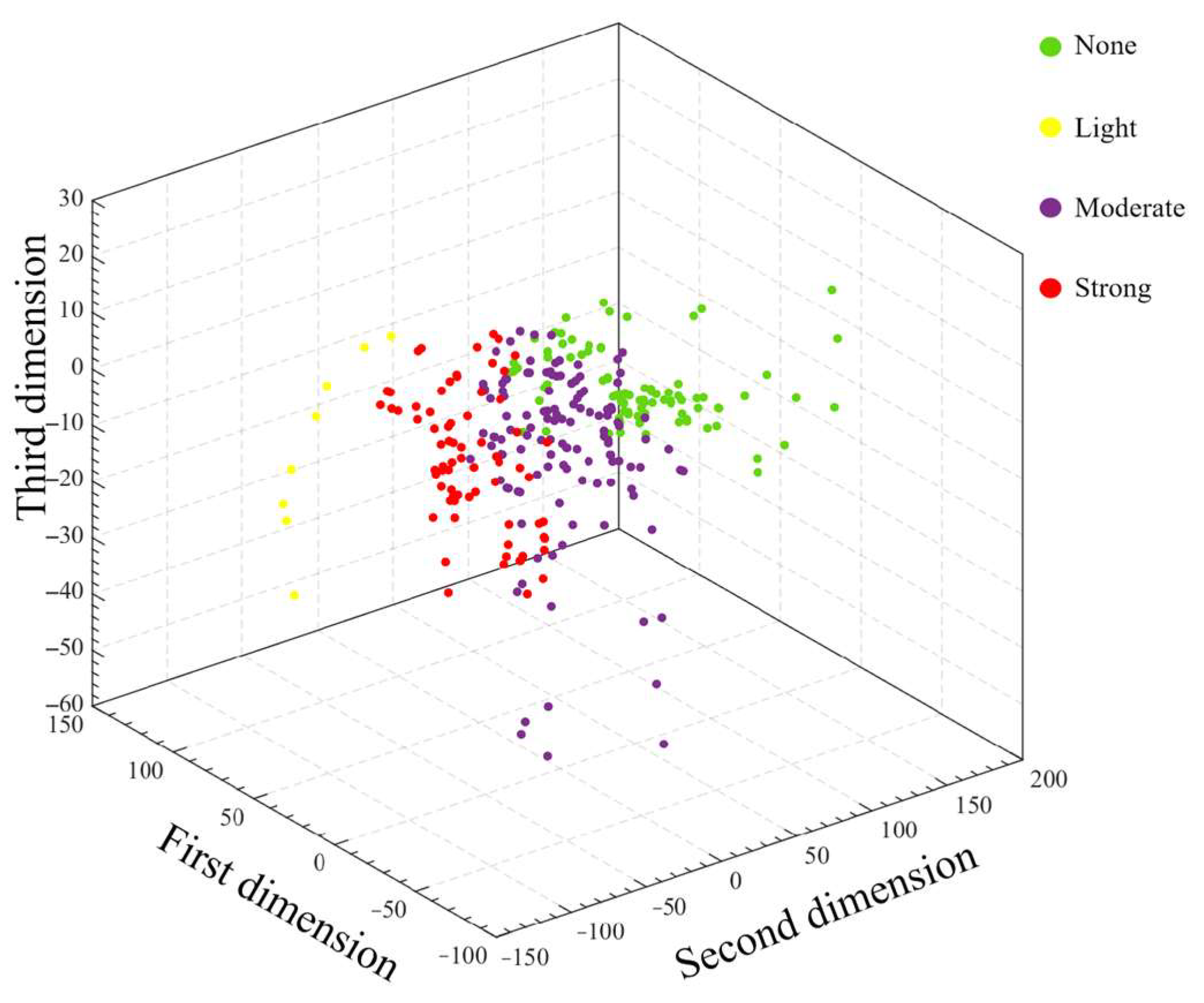

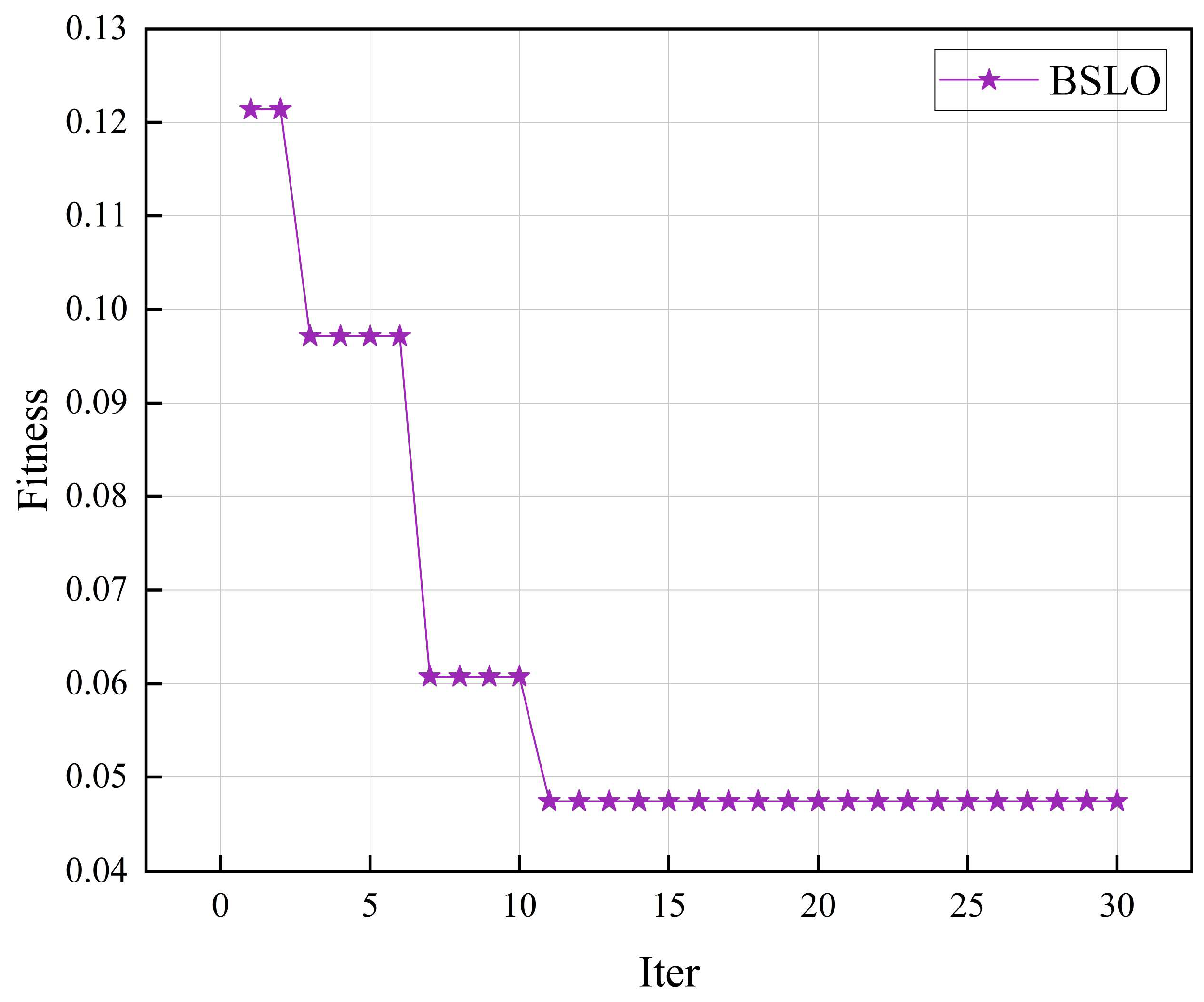
| Rockburst Grade | Rockburst Characteristic Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Statistical Parameter | (MPa) | (MPa) | (MPa) | Wet (MJ/m3) | |||
| None | Maximum value | 241.00 | 18.50 | 107.50 | 5.26 | 48.21 | 7.90 |
| Minimum value | 18.32 | 0.38 | 1.60 | 0.08 | 5.70 | 1.10 | |
| Mean value | 115.55 | 5.37 | 26.13 | 0.40 | 27.01 | 3.74 | |
| Coefficient of variation | 0.49 | 0.72 | 0.75 | 2.42 | 0.47 | 0.62 | |
| Light | Maximum value | 263.00 | 18.20 | 148.40 | 4.55 | 42.96 | 10.00 |
| Minimum value | 26.06 | 0.77 | 10.90 | 0.09 | 4.48 | 1.80 | |
| Mean value | 130.18 | 6.07 | 53.07 | 0.50 | 24.68 | 4.39 | |
| Coefficient of variation | 0.38 | 0.52 | 0.52 | 1.22 | 0.36 | 0.43 | |
| Moderate | Maximum value | 304.00 | 19.20 | 132.10 | 2.57 | 80.00 | 10.00 |
| Minimum value | 30.00 | 1.43 | 10.36 | 0.08 | 9.74 | 1.20 | |
| Mean value | 141.00 | 6.96 | 60.41 | 0.45 | 23.26 | 5.17 | |
| Coefficient of variation | 0.33 | 0.46 | 0.43 | 0.52 | 0.47 | 0.34 | |
| Strong | Maximum value | 306.58 | 20.99 | 167.20 | 1.72 | 80.00 | 11.62 |
| Minimum value | 30.00 | 1.50 | 12.36 | 0.08 | 10.76 | 2.03 | |
| Mean value | 150.59 | 7.96 | 75.63 | 0.54 | 24.84 | 6.22 | |
| Coefficient of variation | 0.34 | 0.52 | 0.44 | 0.52 | 0.73 | 0.28 | |
| Step | Key Operation | Biological Analogy | Purpose |
|---|---|---|---|
| 1 | Initialize population with two types of individuals: directional leeches (sensitive to environmental cues) and directionless leeches (limited perception). | Leeches scatter across the rice field to maximize coverage. | Cover the entire solution space to avoid missing potential optima. |
| 2 | Update positions of directional leeches based on the current optimal solution. | Leeches move toward detected hosts using sensory signals. | Rapidly converge toward promising regions in the search space. |
| 3 | Update positions of directionless leeches via random walks (Lévy flight). | Leeches wander randomly after being disturbed by the host. | Refine local search to exploit details around potential optima. |
| 4 | Calculate Perceived Distance (PD) to switch between exploration (PD > 1) and exploitation (PD ≤ 1) modes. | Leeches adjust behavior based on proximity to the host (far: explore broadly; near: focus locally). | Dynamically balance global and local search to prevent premature convergence. |
| 5 | Trigger re-tracking strategy: Re-initialize positions of leeches that stagnate (no improvement after t1 iterations compared to t2 prior steps). | Leeches relocate to new areas if they fail to find prey for too long. | Escape local optima and maintain search diversity. |
| 6 | Repeat steps 2–5 until maximum iterations (T) are reached. | Sustained foraging cycles to ensure thorough exploration. | Output the globally optimal solution. |
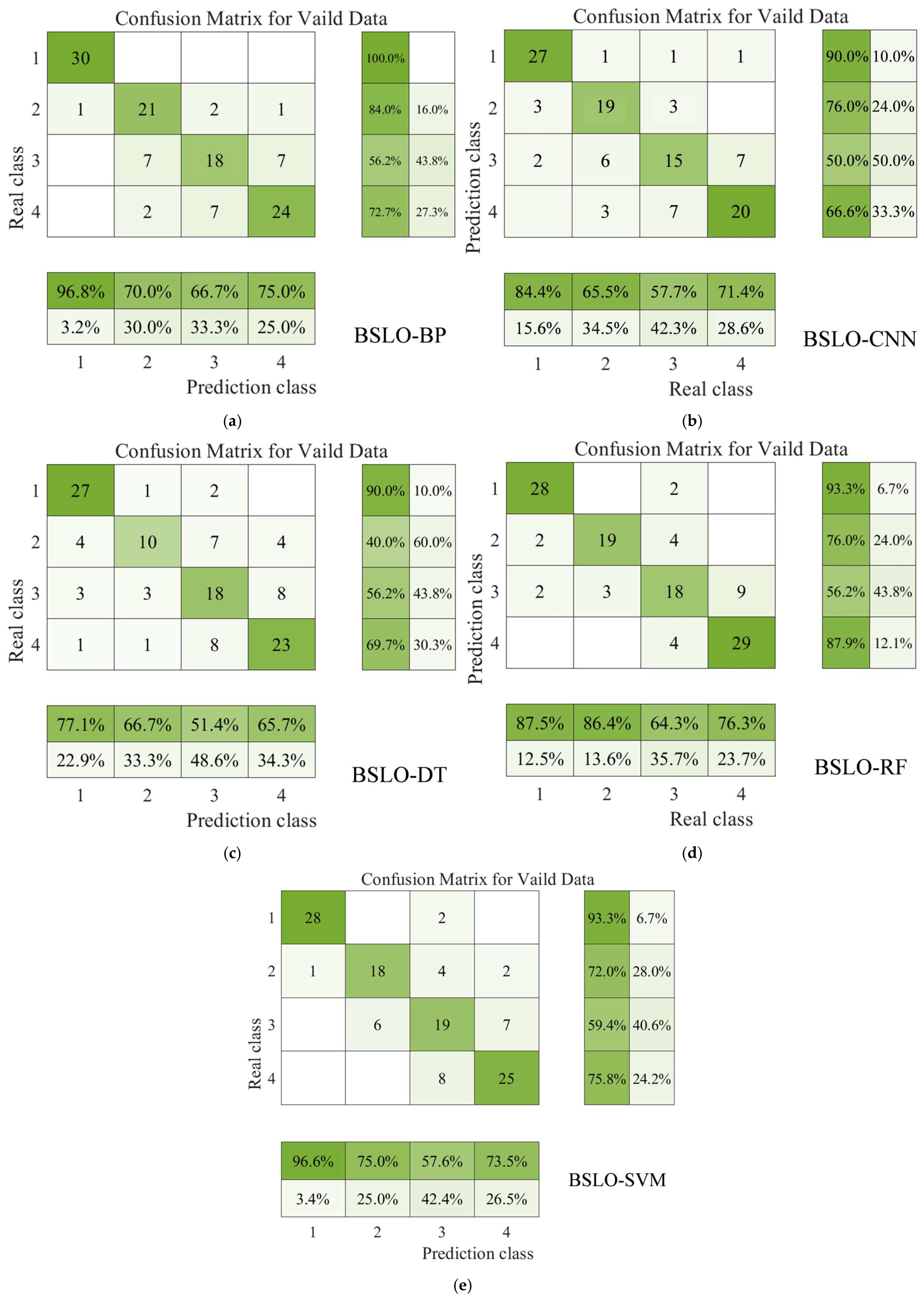
| Model | Accuracy | Recall | F1-Score | Accuracy (Class I) | Accuracy (Class IV) |
|---|---|---|---|---|---|
| BSLO-RF | (89.16 ± 1.23)% | (87.5 ± 1.56)% | 0.88 ± 0.02 | 93.3% | 87.9% |
| BSLO-SVM | (82.45 ± 1.89)% | (80.1 ± 2.11)% | 0.81 ± 0.03 | 93.3% | 75.8% |
| BSLO-BP | (77.50 ± 2.34)% | (75. ± 2.56)% | 0.76 ± 0.04 | 100% | 72.7% |
| BSLO-CNN | (72.33 ± 2.67)% | (70.58 ± 2.89)% | 0.71 ± 0.05 | 90% | 66.6% |
| BSLO-DT | (65.21 ± 3.12)% | (63.15 ± 3.22)% | 0.64 ± 0.06 | 90% | 69.7% |
| NO. | Provenance | UCS (MPa) | UTS (MPa) | MTS (MPa) | MTS/UCS | UCS/ UTS | (MJ/m3) | Rockburst Hazard | |
|---|---|---|---|---|---|---|---|---|---|
| Engineering Records | BSLO-RF | ||||||||
| 1 | Zhongnanshan Tunnel | 122 | 5.38 | 43.1 | 0.35 | 22.68 | 3.31 | Ⅱ | Ⅲ * |
| 2 | Zhongnanshan Tunnel | 121 | 8.73 | 87.5 | 0.72 | 13.86 | 9.05 | Ⅳ | Ⅳ |
| 3 | Zhongnanshan Tunnel | 124 | 8.64 | 79.1 | 0.64 | 14.35 | 7.74 | Ⅳ | Ⅳ |
| 4 | Zhongnanshan Tunnel | 119 | 7.21 | 56.2 | 0.47 | 16.5 | 5.52 | Ⅲ | Ⅲ |
| 5 | Zhongnanshan Tunnel | 120 | 6.45 | 62.8 | 0.52 | 18.6 | 4.16 | Ⅲ | Ⅲ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Dai, B.; Li, D.; Jia, H.; Li, P. Classification of Rockburst Intensity Grades: A Method Integrating k-Medoids-SMOTE and BSLO-RF. Appl. Sci. 2025, 15, 9045. https://doi.org/10.3390/app15169045
Wu Q, Dai B, Li D, Jia H, Li P. Classification of Rockburst Intensity Grades: A Method Integrating k-Medoids-SMOTE and BSLO-RF. Applied Sciences. 2025; 15(16):9045. https://doi.org/10.3390/app15169045
Chicago/Turabian StyleWu, Qinzheng, Bing Dai, Danli Li, Hanwen Jia, and Penggang Li. 2025. "Classification of Rockburst Intensity Grades: A Method Integrating k-Medoids-SMOTE and BSLO-RF" Applied Sciences 15, no. 16: 9045. https://doi.org/10.3390/app15169045
APA StyleWu, Q., Dai, B., Li, D., Jia, H., & Li, P. (2025). Classification of Rockburst Intensity Grades: A Method Integrating k-Medoids-SMOTE and BSLO-RF. Applied Sciences, 15(16), 9045. https://doi.org/10.3390/app15169045