A Possible Tram–Train System Covering Bratislava Old Bridge—Petrzalka Railway Station
Abstract
1. Introduction
- The complexity of servicing the built-up area and its agglomeration via urban rail;
- The possibilities of linking a combined double-gauge system comprising 1000 and 1435 mm gauges—in this case, we examine the urban tramway and the railway infrastructure from a technical point of view;
- The comprehensive traffic modeling of the city’s PT system to support the proposal, considering a change in the modal split, diverting the use of automobile transport towards PT.
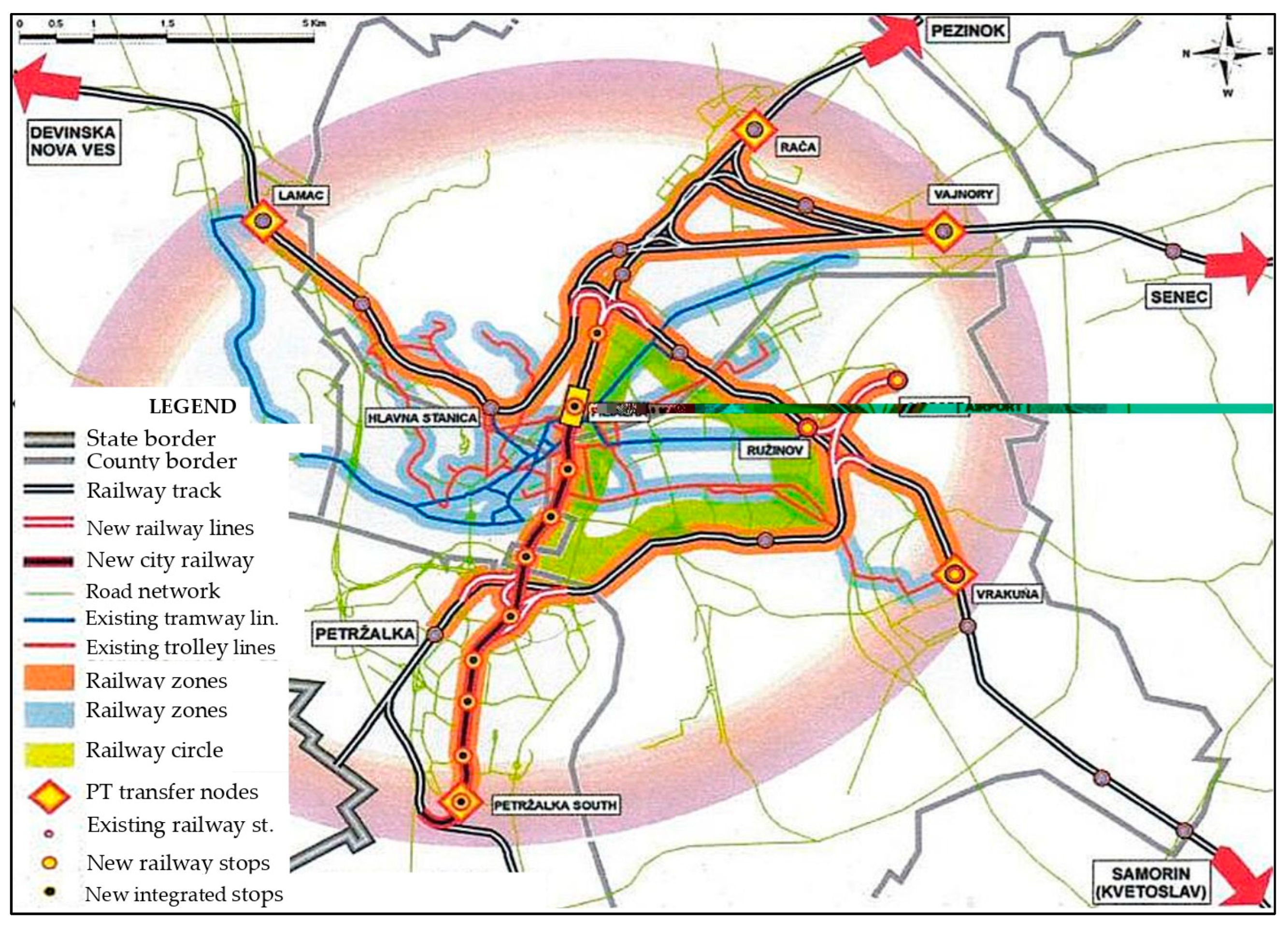
2. Bratislavan Tram–Train Network Development Strategy
- The design and implementation of parallel-operated railway and tram transport infrastructure;
- A suitable “designed vehicle” type;
- The risks and uncertainty resulting from the design, implementation, and operation of transport infrastructure considering the common operation of rail and tramway vehicles;
- An estimate of the investment and operating costs;
- An assessment of the economic parameters of the construction.
- A permanent railway vehicle (tram–train) will be built within a construction with “linking corridors” with train lines from Petrzalka:
- ▪
- A railway station from Bratislava to Filiálka (the subject of the current study) to the Bratislava–Predmestie railway station, possibly followed by continuing movement through the region (Raca borough, Pezinok, Trnava);
- ▪
- A railway station running from Bratislava to the Nove Mesto borough, Podunajske Biskupice borough, and Dunajska Streda;
- ▪
- Movement from the Vajnory borough towards Galanta and Nove Zamky (this is a complete review of the Bratislava agglomeration).
- Locomotion in the opposite direction, from Petrzalka railway station, with possible extension to Austria and Hungary.
- Gauge: 1000 mm;
- Maximum boarding edge height: 300 mm above the railhead;
- Traction power system: 750 V DC (at current lines 600 V DC);
- In common (railway) infrastructure sections, the direction and high-rise route (rail track) design must comply with ON 73 6412 [Geometric position and track arrangement of 1000 mm gauge tracks];
- In sections outside the common (railway) infrastructure, Standard STN 73 6405 [11] [Designing of tramway tracks] can be used.
- Gauge: 1435 mm;
- Traction power system: single-phase 25 kV/50 Hz AC;
- Maximum boarding edge height: 550 mm above the railhead, with sliding steps at floor level for railway platforms; at the tram stops inside the city, the coach will have a 300 mm step;
- Maximum axle pressure: 18 t (after testing, that of the TT was defined as 12.5 t);
- Minimum arc radius: 300 m;
- Platform length: 80 m (120 m for selected stations); for tram stops inside the city, a maximum platform length of 70 m;
- Track speed: 80 km.h−1;
- Cross-section UIC-C;
- Lightweight station and track security devices;
- Track equipped with ERTMS (ETCS LEVEL 2, GSM-R);
- The direction and high-rise route design must comply with STN 73 6360 [12].
Modal Split Problem: Personal Dynamic Car Traffic and Modal Split
- The creation of multiple individual radial connections of railway lines entering the city;
- The ability to link integrated rail transport on the tram track network using the tram–train double-feed vehicle, as well as operating them on the railway infrastructure;
- The necessity of requirements for the implementation of the subsurface north–south interconnection at the future Filiálka railway station.
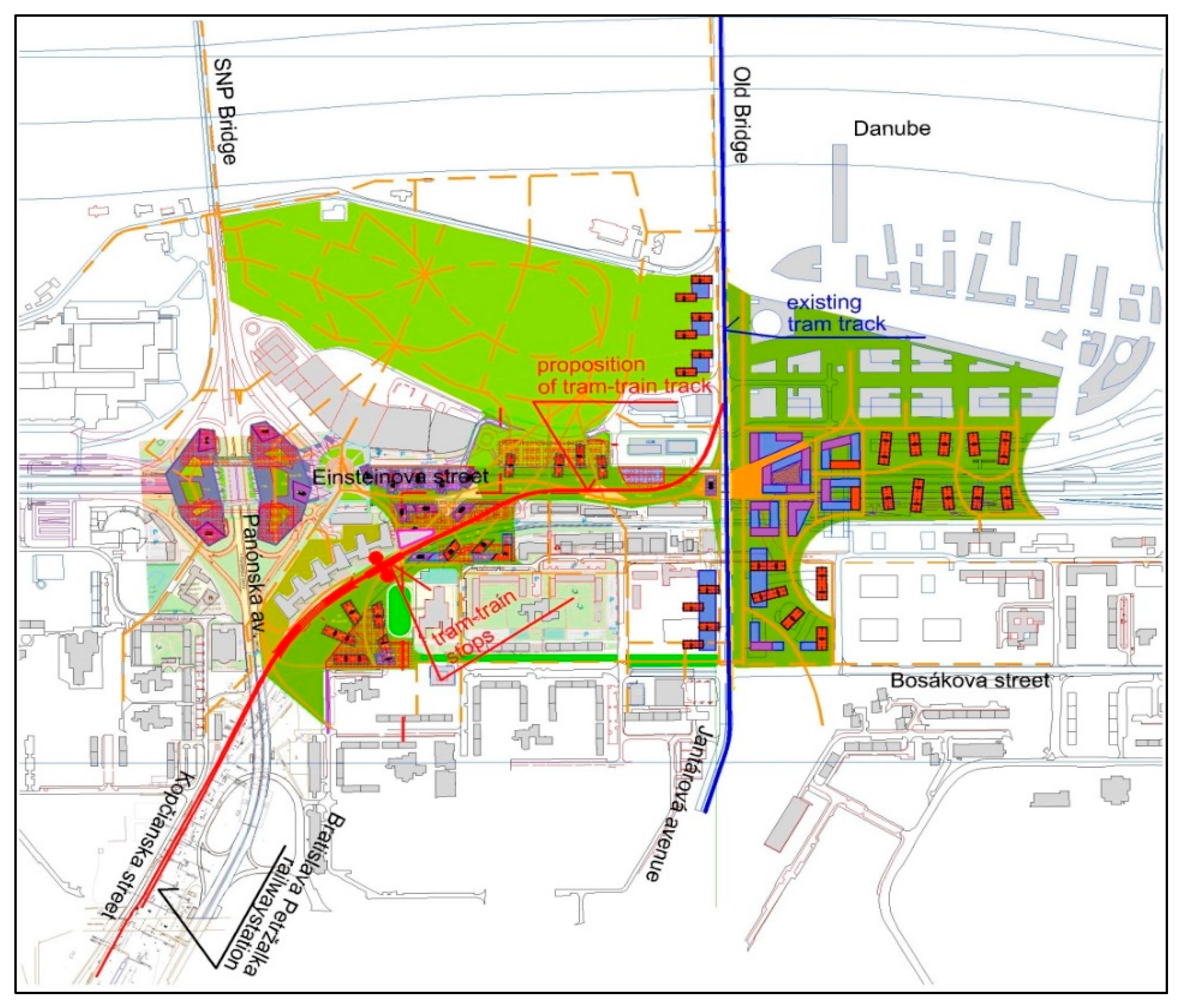
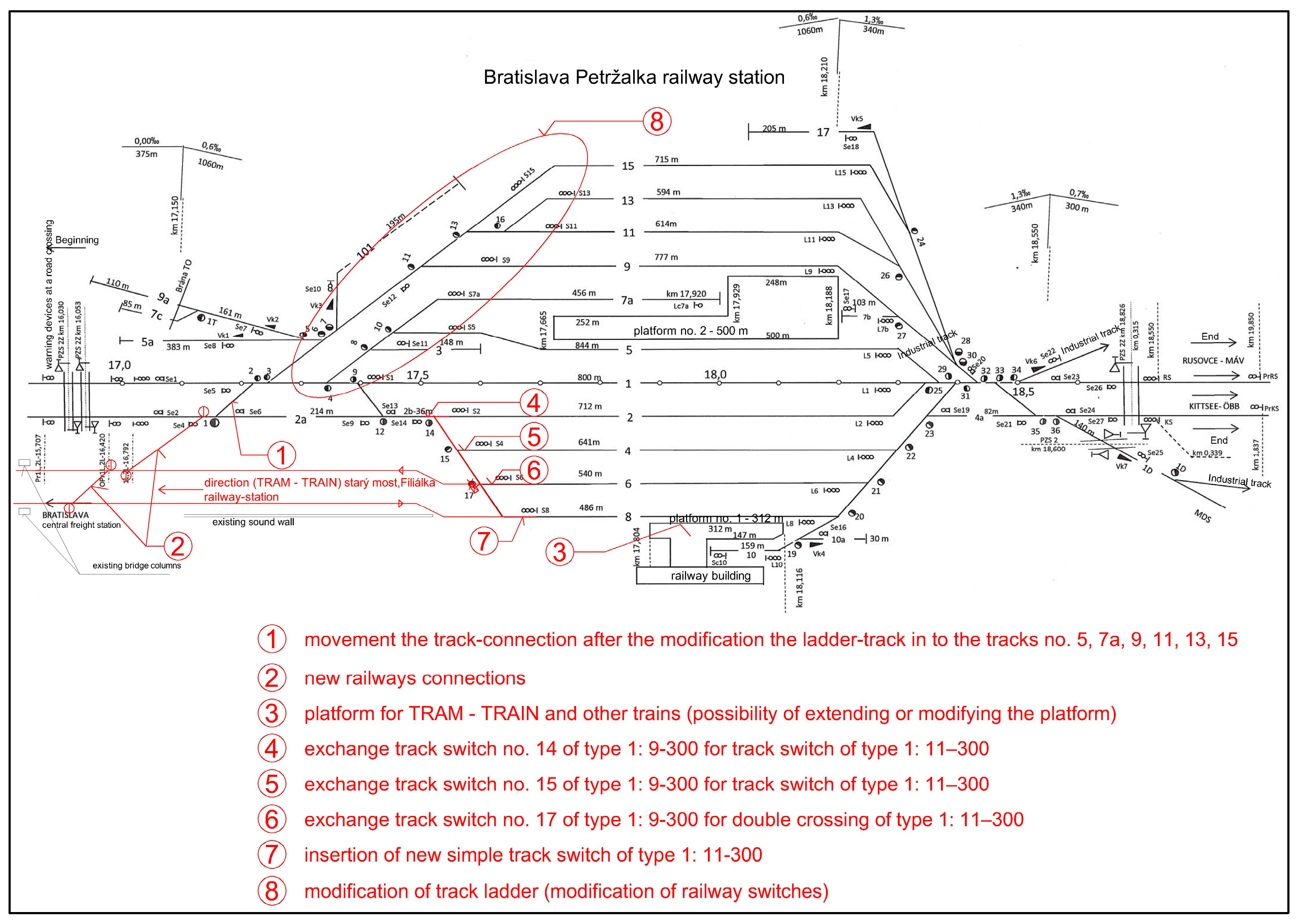
3. Proposed Tram–Train Route for the Filiálka–Petrzalka Project
4. Transport Model Scenario of Modal Split for New Tram–Train Line
- Automatic traffic counter (ATC) traffic survey;
- Static traffic survey;
- Directional traffic survey;
- Urban public transport traffic survey;
- Data on demography;
- Data on land use;
- Traffic demand survey data.
- Validation of the number of people transported by public transport
Design of Traffic Model—Standard Four-Step Model
- Trip generation
- Trip distribution
- Mode choice
- Those referring directly to a demand matrix allocated to a single demand segment or several demand segments;
- Those whose demand matrix is not related to any demand segment.
- Gravity model calculation
- General form of the distribution formula
- Uij—a value for the utility between zones—for example, the distance or travel time from zone i to zone j;
- Qi—the origin zone i;
- Zj—the destination zone j;
- kij—a scaling factor (attractiveness factor) for OD pair zone i to zone j;
- n—the number of zones.
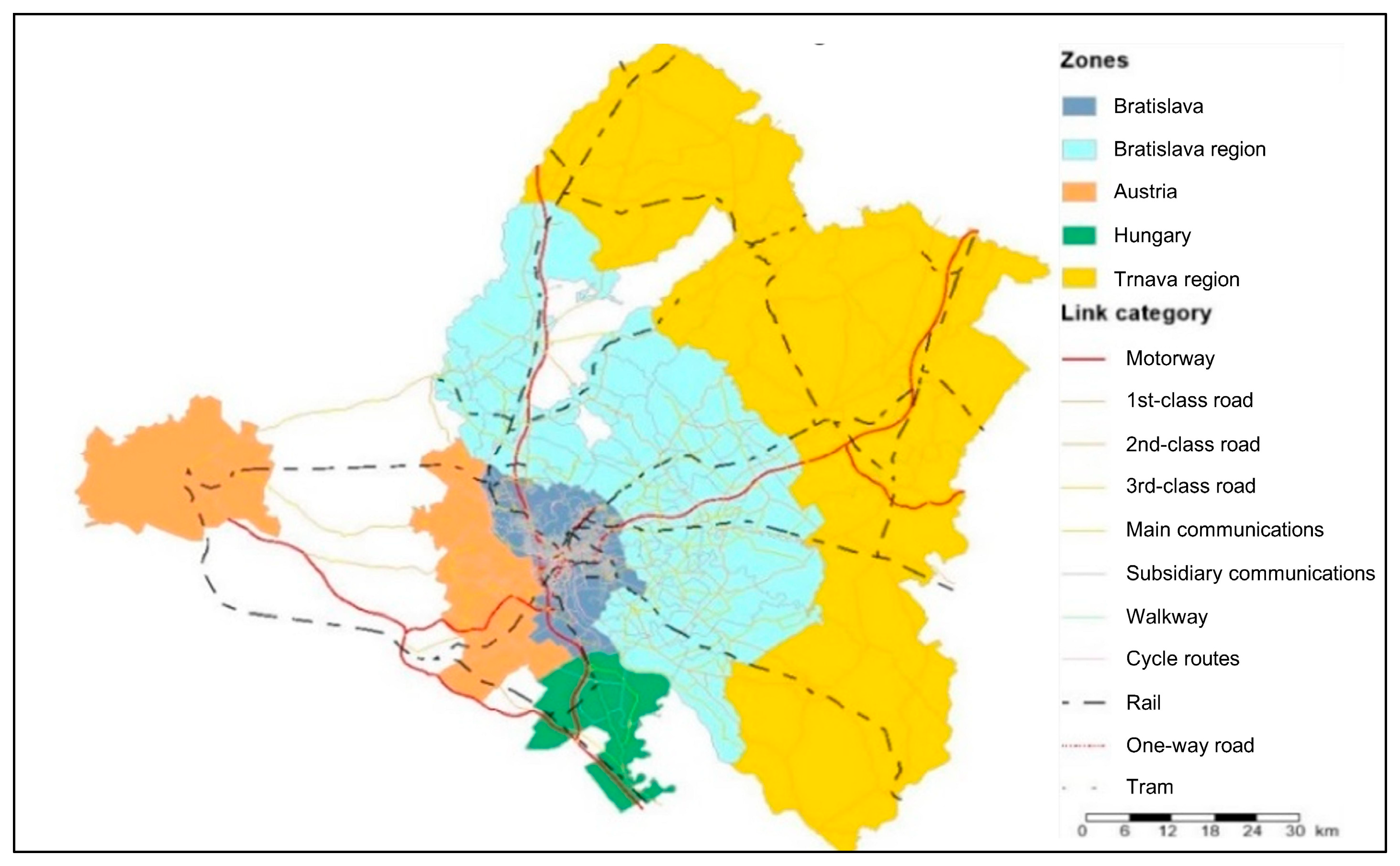
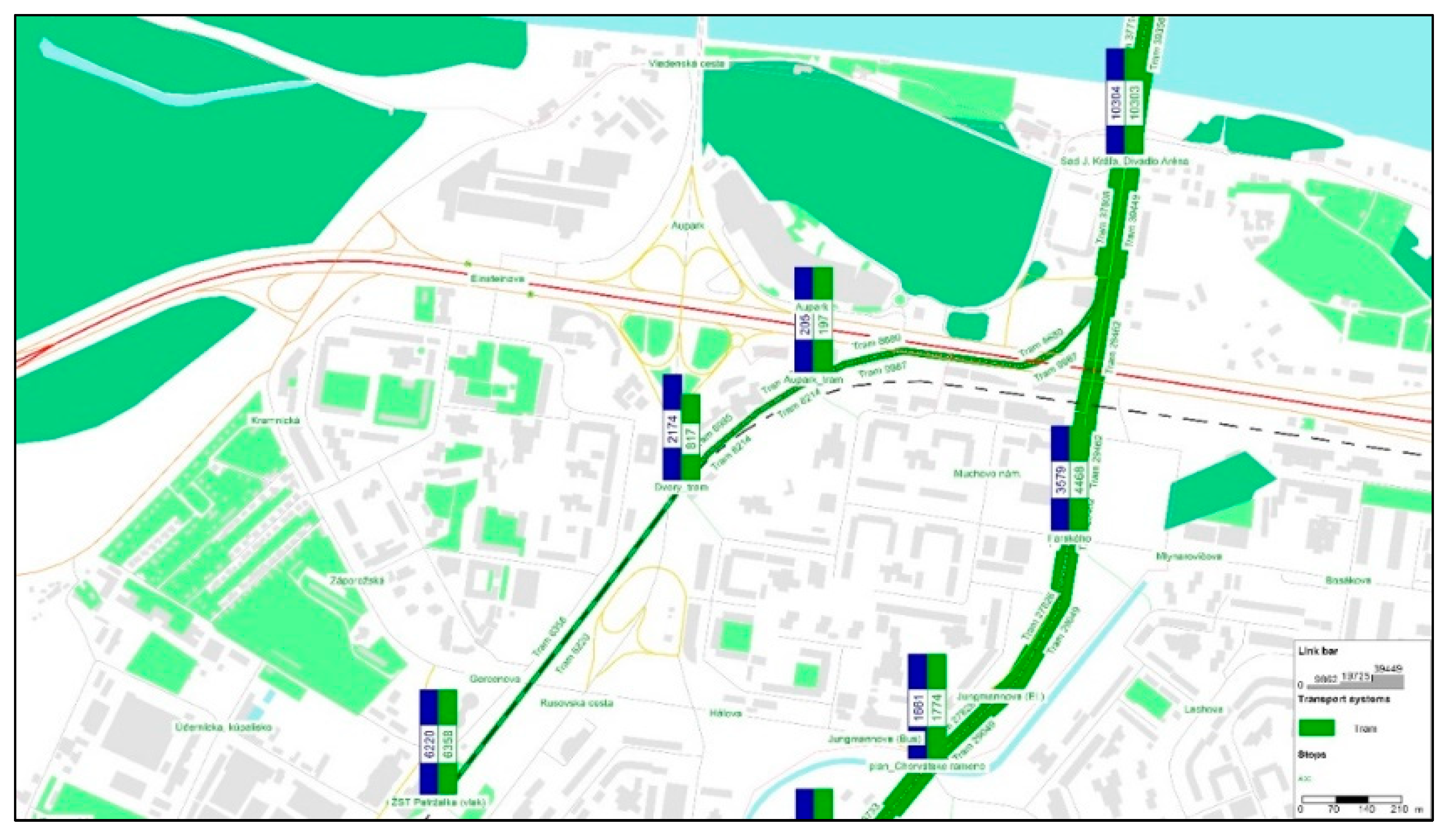
5. Results
- Sad J. Krala–Aupark (tram)—990 m;
- Aupark (tram)–Dvory (tram)—370 m;
- Dvory (tram)–Petrzalka railway station—860 m.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADT | Average Daily traffic |
| CPTS | Carrying Public Transport System |
| EU DG | European Union Directorate General |
| MoT | Ministry of Transport |
| PT | Public Transport |
| TT | Tram–Train |
References
- Novales, M.; Orro, A.; Bugarin, M.R. The tram-train: State of the art. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2002, 216, 1–13. [Google Scholar] [CrossRef]
- Nuhamin, G.A.; Carra, M.; Ventura, R.; Richiedei, A.; Barabino, B. Assessing Tram-Train feasibility via multicriteria approach: The case of Brescia (Italy). Res. Transp. Bus. Manag. 2024, 56, 101178. [Google Scholar] [CrossRef]
- Kačo, I. Koľajová Trať Na Území Mestskej Časti Bratislava Petrzalka, Technicko-Ekonomická Štúdia (Rail Track in the Area of Bratislava Petrzalka, Technical and Economic Study); Dopravoprojekt, a.s.: Bratislava, Slovakia, 2009. (In Slovak) [Google Scholar]
- Podolec, O. Implementácia Integrovaného Dopravného Systému Na Území Bratislavy S Dosahom Na Priľahlé Regióny, Technicko-Ekonomická Štúdia (Implementation of the Integrated Transport System in Bratislava with Connection of Adjacent Regions, Technical and Economic Study); Reming Consult, a.s.: Bratislava, Slovakia, 2010. (In Slovak) [Google Scholar]
- Schlosser, T. Rozvoj Elektrickej Trakcie Na Území Hlavného Mesta SR Bratislavy–Príspevok K Rozvoju Bratislavskej Integrovanej Dopravy a Plánu Dopravnej Obslužnosti Bratislavského Samosprávneho Kraja (Development of Electrical Traction in the Capital City of the Slovak Republic Bratislava-Contribution to the Development of Bratislava Integrated Transport and the Plan of Transport Service of the Bratislava Self-Governing Region); Magistrát Mesta Bratislavy: Bratislava, Slovakia, 2012. (In Slovak) [Google Scholar]
- Schlosser, T.; Schlosser, P. Suburban public transport network optimization and operation strategy of the new bus station in Bratislava. J. Adv. Eng. 2017, 1, 1–10. [Google Scholar] [CrossRef]
- Novales, M.; Orro, A.; Bugarin, M.R. Tram-train: New public transport system. Transp. Res. Rec. 2002, 1793, 80–90. [Google Scholar] [CrossRef]
- Novales, M.; Orro, A.; Bugarín, M.R. Use of a genetic algorithm to optimize wheel profile geometry. Proc. Inst. Mech. Eng. Part F. J. Rail Rapid Transit. 2007, 221, 467–476. [Google Scholar] [CrossRef]
- Schlosser, T.; Schlosser, P. New Tramway Infrastructure in Bratislava-How Can Influence the Well Prepared Traffic Engineering Analysis and Planning Tools the Decision Making. Procedia Eng. 2016, 161, 247–252. [Google Scholar] [CrossRef]
- Novales, M.; Orro, A.; Bugarin, M.R. Madrid tram-train feasibility study conclusions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2003, 217, 1–10. [Google Scholar]
- STN 73 6405; Projektovanie Električkových Tratí (Designing of Tramway Tracks). UNMS: Bratislava, Slovakia, 1975.
- STN 73 6360; Železnice Koľaj Časť 1: Geometrická Poloha a Usporiadanie Koľaje Železničných Dráh Rozchodu 1 435 mm (Railways Track Part 1: Geometric Position and Arrangement of 1 435 mm Gauge Railway Tracks). UNMS: Bratislava, Slovakia, 2015.
- Schlosser, P.; Mališová, D.; Schlosser, T. Nosný Systém MHD-Dopravno-Inžinierske Prieskumy Dopravy V Mestskej Časti Petrzalka, I. Etapa, (Carrying Public Transport System–Traffic Engineering Surveys in Petrzalka Borough); Dotis Consult, s.r.o.: Bratislava, Slovakia, 2010. (In Slovak) [Google Scholar]
- Schlosser, P.; Mališová, D.; Schlosser, T.; Schlosser, M. Nosný Systém MHD-Prevádzkový Úsek Janíkov Dvor–Šafárikovo Nám. V Bratislave, Časť II. (Carrying Public Transport System—Operational Section Janikov Dvor–Safarikovo Nám., Part II); Dotis Consult, s.r.o.: Bratislava, Slovakia, 2010; 133p. (In Slovak) [Google Scholar]
- City of Bratislava. LMP (2007–2021). Územný Plán Mesta Bratislavy (Land Use Master Plan of Bratislava). Available online: https://bratislava.sk/sk/uzemny-plan (accessed on 15 May 2025). (In Slovak).
- Šebo, T.; Lichý, I.; Mihálik, J.; Zatlukaj, E.; Matúšová, M. Nová Einsteinova-Mesto Na Úrovni, Urbanistická Štúdia (New Einstein Street-City at Level, Urban Study); Architekti Šebo–Lichý: Bratislava, Slovakia, 2012. (In Slovak) [Google Scholar]
- ZZ ŽSR. Jednotná Železničná Mapa Žst. Petrzalka (Unified Railway Map of the Railway Station Petrzalka); Stredisko Železničnej Geodézie: Bratislava, Slovakia, 1992. (In Slovak) [Google Scholar]
- Plišková, J. Dopravný Uzol Bratislava–Štúdia Realizovateľnosti (Transport Node Bratislava—Feasibility Study); Združenie Uzol Bratislava: Bratislava, Slovakia, 2019. (In Slovak) [Google Scholar]
- Schlosser, T.; Schlosser, P.; Schlosser, M. Traffic model as a tool for changing of modal split in Bratislava new city centre. In Proceedings of the Conference of Transport Science-Technology in Service of Sustainable Transport; Universitas-Győr Nonprofit Kft.: Győr, Hungary, 2018; ISBN 1757-899X. [Google Scholar]
- Bálint, G. Modelovanie Dopravného Zaťaženia V Integrovanom Systéme Dopravy (Modelling of Passenger Traffic Flows in Integrated Public Transport System). Ph.D. Thesis, Slovak University of Technology, Bratislava, Slovakia, 2019. (In Slovak). [Google Scholar]
- Galkin, A.; Davidich, Y.; Kush, Y.; Davidich, N.; Tkachenko, I. Improving of urban public transportation quality via operator schedule optimization. J. Urban Environ. Eng. 2019, 13, 23–33. [Google Scholar] [CrossRef]
- PTV VISUM Manual, Version 15; PTV AG: Karlsruhe, Germany, 2015.
- Šenk, P.; Pípa, N.; Lazor, M. Územný Generel Dopravy Hl. M. SR Bratislavy (Transport Master Plan of Capital of Slovakia-Bratislava); Centrum Dopravního Dýskumu: Brno, Czech Republic, 2015. (In Slovak) [Google Scholar]
- Ventura, R.; Bonera, M.; Carra, M.; Barabino, B.; Maternini, G. Evaluating the viability of a tram-train system: A case study from Salento (Italy). Case Stud. Transp. Policy 2022, 10, 1945–1963. [Google Scholar] [CrossRef]
- De Aloe, M.; Ventura, R.; Bonera, M.; Barabino, B.; Maternini, G. Applying cost-benefit analysis to the economic evaluation of a tram-train system: Evidence from Brescia (Italy). Res. Transp. Bus. Manag. 2023, 47, 100916. [Google Scholar] [CrossRef]

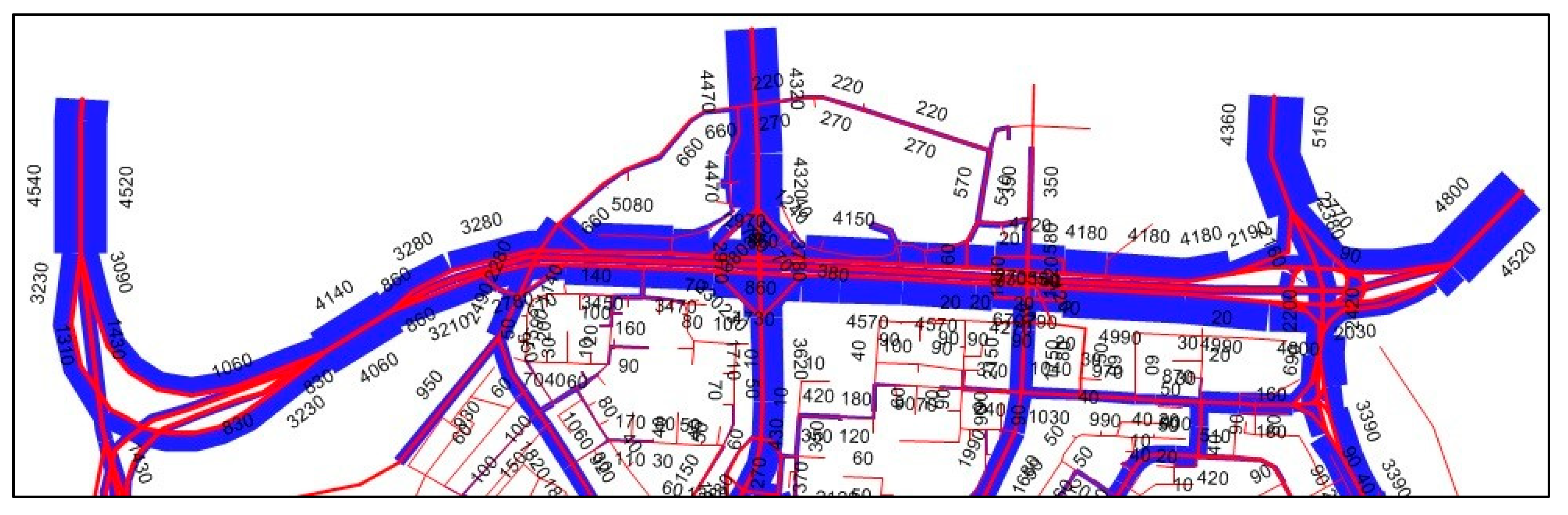


| 2020 (ADT veh./24 h) | Peak HT—Maximum (veh./h) | Peak HT—50th h (veh./h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Danube Bridge | Direction 1 | Direction 3 | Profile | Direction 1 | Direction 3 | Profile | Direction 1 | Direction 3 | Profile |
| Lafranconi | 34.980 | 34.670 | 69.650 | 4.520 | 4.520 | 9.040 | 3.680 | 3.670 | 7.350 |
| SNP | 35.220 | 35.280 | 70.500 | 4.320 | 4.470 | 8.790 | 3.700 | 3.550 | 7.250 |
| Apollo | 26.580 | 26.470 | 53.050 | 5.150 | 4.360 | 9.510 | 4.220 | 3.780 | 8.000 |
| Port | 45.830 | 45.270 | 91.100 | 4.520 | 4.800 | 9.320 | 3.830 | 4.280 | 8.110 |
| Sum | 142.610 | 141.690 | 284.300 | 18.510 | 18.150 | 36.660 | 15.430 | 15.280 | 30.710 |
| 2020 (ADT veh./24 h) | Peak HT—Maximum (veh./h) | Peak HT—50th h (veh./h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Danube Bridge | Direction 1 | Direction 3 | Profile | Direction 1 | Direction 3 | Profile | Direction 1 | Direction 3 | Profile |
| Lafranconi | 25.900 | 28.770 | 54.670 | 3.770 | 3.350 | 7.120 | 3.020 | 2.700 | 5.720 |
| SNP | 27.280 | 28.880 | 56.160 | 3.380 | 3.690 | 7.070 | 2.880 | 2.910 | 5.790 |
| Apollo | 20.500 | 22.360 | 42.860 | 3.960 | 3.720 | 7.680 | 3.240 | 3.240 | 6.480 |
| Port | 35.700 | 38.010 | 73.710 | 3.540 | 4.010 | 7.550 | 2.990 | 3.590 | 6.580 |
| Sum | 109.380 | 118.020 | 227.400 | 14.650 | 14.770 | 29.420 | 12.130 | 12.440 | 24.570 |
| 2020 (ADT veh./24 h) | Peak HT—Maximum (veh./h) | Peak HT—50th h (veh./h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Difference | 33.230 | 23.670 | 56.900 | 3.860 | 3.380 | 7.240 | 3.300 | 2.840 | 6.140 |
| Public Transport Stop | Volume of Passengers (pass./24 h) | Boarding (pass./24 h) | Alighting (pass./24 h) | Volume to (pass./24 h) | Volume from (pass./24 h) | Cross-Section Volume (pass./24 h) |
|---|---|---|---|---|---|---|
| Petrzalka Railway Station | 12,578 | 6220 | 6358 | 6220 | 6358 | 12,578 |
| Dvory (tram) | 2991 | 2174 | 817 | |||
| 8214 | 6995 | 15,209 | ||||
| Aupark (tram) | 4028 | 2058 | 1970 | |||
| 9987 | 8680 | 18,667 | ||||
| Sad Janka Krala (Stary Most profile) | 20,607 | 10,304 | 10,303 | |||
| 39,356 | 37,714 | 77,070 | ||||
| SND (Olejkarska profile) | 13,314 | 6675 | 6639 | |||
| 14,873 | 10,375 | 25,248 | ||||
| Twin City | 9390 | 3918 | 5472 | |||
| 14,857 | 11,913 | 26,770 | ||||
| Mlynske Nivy | 5532 | 2482 | 3050 | |||
| 14,234 | 11,858 | 26,092 | ||||
| Soltesovej | 3353 | 1578 | 1775 | |||
| 13,785 | 11,606 | 25,391 | ||||
| Krizna (tram) | 7563 | 3716 | 3847 | |||
| 12,337 | 10,289 | 22,626 | ||||
| Bratislava–Filiálka | 3829 | 1847 | 1982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlosser, T.; Bálint, G.; Korfant, M.; Schlosser, P. A Possible Tram–Train System Covering Bratislava Old Bridge—Petrzalka Railway Station. Appl. Sci. 2025, 15, 9042. https://doi.org/10.3390/app15169042
Schlosser T, Bálint G, Korfant M, Schlosser P. A Possible Tram–Train System Covering Bratislava Old Bridge—Petrzalka Railway Station. Applied Sciences. 2025; 15(16):9042. https://doi.org/10.3390/app15169042
Chicago/Turabian StyleSchlosser, Tibor, Gabriel Bálint, Matúš Korfant, and Peter Schlosser. 2025. "A Possible Tram–Train System Covering Bratislava Old Bridge—Petrzalka Railway Station" Applied Sciences 15, no. 16: 9042. https://doi.org/10.3390/app15169042
APA StyleSchlosser, T., Bálint, G., Korfant, M., & Schlosser, P. (2025). A Possible Tram–Train System Covering Bratislava Old Bridge—Petrzalka Railway Station. Applied Sciences, 15(16), 9042. https://doi.org/10.3390/app15169042






