Abstract
Generative model-assisted design has become a trend, providing a new paradigm for knitted fabric image generation. The FLUX diffusion model was chosen to generate images in this study and was compared to other generative models. In order to effectively apply the large model to specialized verticals, an efficient fine-tuning method, low-rank adaptation, was used. Experiments showed that the method allows a pre-trained model to stably generate knitted fabric images in batches through easily understandable text prompts. The generated images have clear textures and correct structures, and can display the surface characteristics of knitted fabrics generated by using different yarn specifications and yarn bristles. Moreover, the unit tissue structural similarity index measure (SSIM) is 0.6528, which is very similar to real fabrics. This research expands the application of fabric generation in the field of deep learning. This method is highly efficient, low-cost, and capable of stably simulating knitted fabrics, which can be used to rapidly expand the image design materials of knitted fabrics.
1. Introduction
Computer model-assisted design generation in professional fields is gradually becoming a trend [1]. Classical generative models [2] mainly include Variational Auto-Encoder (VAE), Generative Adversarial Networks (GANs) and Stable Diffusion.
VAE [3] is composed of an encoder and a decoder. The training process involves encoding the input data to obtain a low-dimensional vector and using a decoder to reduce the output data, which leads to low fidelity and high diversity in the training results. With the development of deep learning, VAE is often combined with other generative models [4,5] for apparel generation, blemish detection in textile images [6,7] and yarn recognition and classification [8]. During the training process, VAE is more responsible for the compression and reconstruction of high-resolution images into the low-dimensional potential space, thus enabling other generative models to train and reason more efficiently in the potential space.
In recent years, diffusion models beat GAN [9] to generate high-resolution images from natural language inputs with strong graph generation and generalization capabilities [10]. However, due to its iterative nature, high computational cost, and the problem of there being a long sampling time during inference, many studies have explored the optimization of model performance to improve the sampling efficiency with enhanced training effectiveness [11,12,13]. The stable diffusion model 3 (SD3) [14] innovatively employs the Flow Matching [15] framework to directly accomplish noise-to-data mapping by constructing a continuous-time probabilistic flow, compressing the generation step to 10–20 steps. The model further incorporates the Multimodal Diffusion Transformer Backbone (MM-DiT) [16] and introduces rotational position coding [17] to improve the model performance and enable hardware utilization [18].
Based on this, the FLUX.1 Dev (FLUX) [19] integrates the MM-DiT architecture with Single Transformer Blocks (Single-DiT), which employs parallel attention layers [20], effectively increasing the model’s parameter count to 12 billion and further enhancing the overall performance.
Although the diffusion model already has a strong generalization ability for generating simple and clear fabric textures, it is not able to generate information on microscopic details such as the specific loop structure of yarns in the fabric. This makes it necessary for the design generation of knitted fabrics to integrate process constraints to meet actual design requirements. Parameter-efficient fine-tuning (PEFT) aims to customize diffusion models by training a small number of parameters. After an experimental comparison of 15 different PEFT methods in terms of performance and efficiency [21], low-rank adaptation [22] requires only 0.1% parameter updates to complete the fine-tuning, which significantly reduces the number of parameters and the computational cost, and can provide near-full fine-tuning in resource-constrained environments. The method has achieved better results in clothing style fine-tuning [23], blue print pattern style [24] learning, and woven fabric generation [25].
In summary, the application of diffusion modeling in the textile field focuses on the design generation of styles and patterns [26], repair migration [27] and virtual fitting [28], and less on the research and application of fabric simulation generation. As the curved coils are strung together to form knitted fabrics, the organizational structure is more complex compared to woven fabrics, so the research in the field of fabrics is more focused on the identification and generation of woven fabrics [29]. However, the image generation of knitted fabrics has important application value in many fields such as the digital design of clothing and textile industry applications, but lacks research in the field of intelligent generation. Based on this, this study applies a low-rank adaptation of the FLUX model to generate knitted fabric simulation by means of text-generated image. The contributions of this paper are as follows:
The low-rank adaptation of the FLUX model supports the fast batch generation of knitted fabric images with easy-to-understand textual prompts, and the generated images have clear textures and correct structural features.
We conducted a comparative analysis of the model before and after fine-tuning, as well as between the FLUX and SD1.5 diffusion models. Structural similarity evaluation at the unit organization level demonstrates that the results generated by Knit-FLUX (Low-Rank Adaptation of FLUX model) closely approximate real knitted fabrics compared to Knit-Diff (Low-Rank Adaptation of SD1.5 model).
This study extends the application of knitted fabric image generation in the field of deep learning, and the method is efficient, low-cost, and capable of stably simulating knitted fabrics, which can be used to rapidly expand knitted fabric design materials.
The following are the remaining four sections of this paper. Section 2 provides a detailed theoretical overview of diffusion model concepts and flow-matching diffusion concepts. Section 3 introduces the flow-matching diffusion model architecture and low-rank adaptive fine-tuning methods. Section 4 introduces the dataset, experimental environment, parameter settings, experimental results, and evaluation metrics, and analyzes the experimental results. Section 5 summarizes the entire paper and proposes plans for further research in this field.
2. Theory
Diffusion models are generative probabilistic models that learn to reconstruct data through iterative denoising steps. Recently, Flow Matching has emerged as an efficient training paradigm that constructs a continuous-time probabilistic flow to directly learn the data-to-noise mapping, significantly reducing the number of inference steps. In this section, we provide the theoretical foundation of diffusion modeling, followed by an explanation of the Flow Matching framework used in the FLUX model, which forms the basis of our proposed approach.
2.1. Diffusion Model
The diffusion model [30] is based on the denoising probabilistic framework, which is realized through step-by-step iterations from Gaussian noise to target image generation. As shown in Figure 1, the diffusion model structure realizes the diffusion process through U-Net structure and temporal coding. The diffusion process includes forward diffusion and backward denoising.
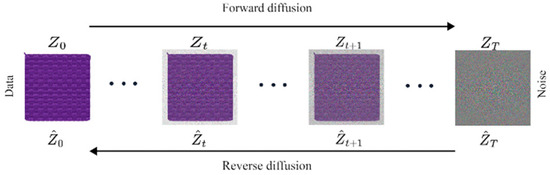
Figure 1.
Diffusion process.
During the forward diffusion process, the model gradually adds Gaussian noise to the original data , which satisfies the initial distribution , . For , and satisfy the following equation [31]:
is the noise variance added at each step of the forward process, which is usually a predefined incremental sequence controlling the rate at which the data is corrupted. is the proportionality coefficient for retaining the original signal, defined as , which represents the proportion of the original data retained at each step. The noise intensity at each time step is controlled by the noise attenuation coefficient and the noise variance . Changing the scheduling rule of can control the rhythm of noise addition and balance the efficiency of signal retention and noise addition. The recursive derivation is obtained from the initial data at step :
where is the cumulative attenuation coefficient, which is the cumulative product of .
In the reverse denoising process, the diffusion model needs to predict the previous moment’s picture based on the current moment’s picture . This prediction process uses the probabilistic Bayesian formula to calculate the posterior probability:
The denoising process [30] is obtained after derivation:
During the training process, the final optimization goal is to make the network-predicted noise consistent with the real noise, so the loss function [30] needs to be as small as possible; this is given by the following:
2.2. Conditional Flow Matching
The FLUX diffusion model is based on the diffusion model and uses Conditional Flow Matching [32] (CFM) theory to improve the denoising sampling process. It transforms the sampling process of data distribution into a trajectory solution problem of Ordinary Differential Equation (ODE) by constructing a continuous time probabilistic flow field. As shown in Figure 2, conditional flow matching constructs a conditional probabilistic path from the source distribution to each target data point as , which satisfies and . The Gaussian distribution is chosen as the conditional path [15]:
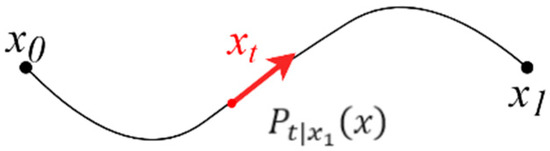
Figure 2.
Single-point conditional probability path. is the point of the path at time
.
In the expression of probability distributions, semi-colons “;” are used to separate random variables and distribution parameters. Here, the semicolon indicates that the random variable x follows a normal distribution with a mean of and a variance of . is the mean path as , which transitions linearly from the source distribution to the target point . The standard deviation is the variance path as , which decays from to . When , the path degenerates to a deterministic linear interpolation .
According to the continuity equation of the probabilistic flow, the corresponding conditional velocity field [15] can be derived as follows:
Substituting and , we obtain the following:
When ,
This means that the velocity field points to the target , and moves toward the target with a uniform velocity.
Averaging the above conditional path over all target data points yields the global marginal velocity field , which is the velocity of the overall flow when the conditional variables are not considered, and is the expectation of the conditional velocity field over the target distribution :
where is the posterior distribution of the conditional variable , given the current state . is the target distribution, and is the marginal distribution at moment .
can be expressed by the integral formula [15]:
is an explicit but implicitly defined reference velocity field defined by the easily sampled conditional path while guaranteeing the transportation of to .
The training objective of the conditional flow matching technique can be formulated as predicting the regression of the marginal velocity field . The loss function [15] adopts the mean square error between the model predicted flow field and the true probabilistic flow field . The loss objective is for the model predicted flow field to be close to the true probabilistic flow field that we obtained analytically.
are the sampling points along the conditional path , where denotes the probability distribution of state xt at time step t given target point x1.
When the loss convergence tends to zero, it is said that agrees with the reference almost everywhere through implicit learning, at which point the model has learned how to transform the initial distribution of the flow into the target distribution.
3. Methods
3.1. Text-to-Image Architecture
The diffusion process only requires its denoising network to be an image-to-image model with equal dimensions of inputs and outputs, and the convolutional neural network-based U-Net can realize the same dimensions of outputs and inputs, so a basic diffusion model such as SD1.5 uses U-Net for diffusion, which contains a residual-based convolutional module, and at the same time adopts self-attention to enhance the perception of key features. The FLUX model architecture uses a transformer architecture to model the diffusion model to complete the diffusion process compared to U-Net, as shown in Figure 3 below.
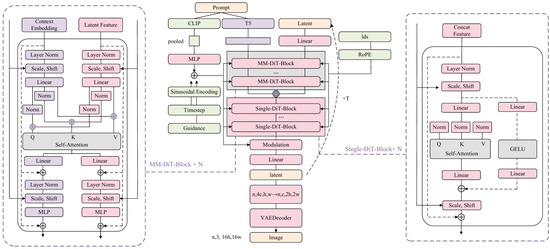
Figure 3.
FLUX Architecture.
The feature extraction module converts the input data into feature vectors that can be learned by the model. The inputs include image and location encoded inputs, text inputs, and guidance scale and timestep.
Text inputs mainly rely on pre-trained Contrastive Language-Image Pre-training (CLIP) [33] and Text-to-Text Transfer Transformer encoders (T5) [34]. While CLIP embeddings provide a global semantic representation of the input text, T5 embeddings extract fine-grained contextual hierarchical information from the text through their sequence-to-sequence pre-training capability, enabling the model to accurately capture the detailed elements of the conditional text.
Firstly, CLIP text encoder is usually based on the Transformer architecture, which first tokenizes the input text to obtain the token sequence , which is transformed into the sequence of embedding vectors , where each embedding vector has the dimension of . Then, position coding is added to the sequence of embedding vectors and fed it into the Transformer encoder to obtain the text feature vector , where represents the real number space, and d represents the dimension of the vector; the T5 text encoder performs the deep contextual modeling of the text through the encoder–decoder architecture to generate the fine-grained feature sequence , which preserves the word-level semantic relations.
The image input is first patched using a patch embedding to obtain a series of tokens; after tokenization RoPE (Rotary Position Embedding) is added to obtain the image feature vector , which can be accessed for transformer blocks.
are projection matrices, and are bias terms.
The information extracted through CLIP is computed with the Timestep and Guidance scale as conditional inputs, which accept the conditional information and compute the parameters through the Adaptive Layer Normalization (adaLN) method, and the generated parameters are controlled through in modulation.
and are input into the transformer block as image features and text features, and the transformer block includes MM-DiT and Single-DiT. Firstly, and are fed into MM-DiT, and are processed separately in the block in the form of double streams, but together they are computed by the attention mechanism. Take the text feature , which is symmetric with , as an example; in each block, it firstly passes through a layer norm, and is then modulated according to the calculated parameter ; after passing through a linear layer, it is spliced with the corresponding to compute the Query, Key, Value projection matrices (Q,K,V) in the attention layer. After that, it passes through the linear layer, residual network, layer norm, modulation and Multi-Layer Perceptron (MLP) to complete the calculation of a block.
After completing the computation of MM-DiT, the text and images are spliced together and fed into Single-DiT for processing, which completes the computation of a block in the form of a single stream, which is able to reduce the number of parameters in a single layer and increase the depth of the network. Unlike MM-DiT, Single-DiT performs attention and MLP computations in parallel within a single stream, where MLP consists of a Linear layer, a Gaussian Error Linear Unit activation function (GELU), and another Linear layer.
denotes that the text and images are spliced together.
The iterative computation continues at MM-DiT and Single-DiT as the timestep continues; when , the obtained final latent variable is mapped back to the pixel space by the VAE decoder, and the final desired knitwear design image is output.
where C represents the number of channels in an image, H represents the number of pixels in the vertical dimension of the image, and W represents the number of pixels in the horizontal dimension of the image.
With the above formulae and steps, the FLUX diffusion model is able to efficiently transform the source distribution into a target distribution and supports batch generation.
3.2. Training Low-Rank Adaption of Model
LoRA (Low-Rank Adaptation) fine-tuning is the core part of this module. The LoRA fine-tuning pre-training model works by introducing low-rank matrices A and B into the Transformer model while the original weight matrix parameters are kept fixed, and then learning task-specific feature representations through low-rank decomposition.
The fine-tuning process is shown below in Figure 4, loading the pre-trained FLUX model with the velocity field network and the multimodal encoders T5, CLIP. The original weight matrices are frozen and do not participate in the training. Two low-rank matrices A and B are introduced into the attention layer (Query, Value projection matrices) and the modulation parameter generation layer of the velocity field network for operations, and their product approximates the update of the weight matrix. For the original forward propagation , this equation [22] becomes the following:
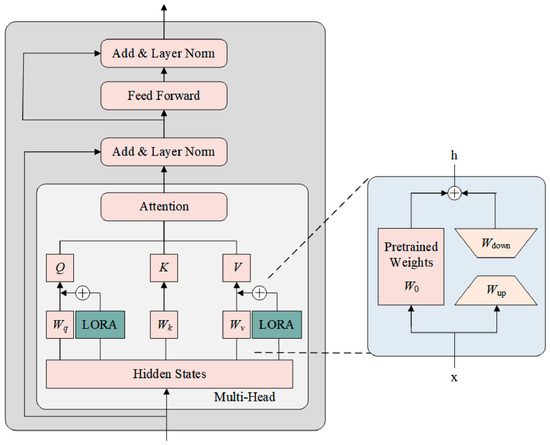
Figure 4.
Low-rank adaptation of transformer.
in the initial state. initialized as a stochastic Gaussian distribution. is initialized as the null matrix, where With this decomposition, the number of fine-tuned parameters is reduced from the original to , which significantly reduces the number of parameters and the computational cost.
After training to obtain the low-rank adaptation weights file, load the FLUX diffusion model weight file and LoRA weight file, and dynamically superimpose the updated parameter weights from the LoRA fine-tuning process onto the original model weights , with the formula . Then, apply it to the query and projection matrix in the Spatial Transformer layer of the Attention Mechanism; then the formula of the Attention Mechanism [35] is updated as follows:
The updated , changes the projection matrix of the query and , and the scale is adjusted; generation is shifted to make the fine-tuned model pay more attention to the key features in the textual conditions such as double ribbing, and hairless feather yarns, and to make sure that the generated content conforms to the textual constraints.
4. Experiment and Result Analysis
4.1. Dataset Preparation
The low-rank adaptation aims to fine-tune the diffusion model with small batches of data, so each type of feature image is greater than or equal to 20, and the dataset contains a total of 288 image–text pairs of real fabrics. The data requires complete content features, and in order for the model to learn different weave piece length and width ratios, all images are processed as squares with a resolution of .
During the construction of the dataset, the following two types of key parameters affecting fabric texture features are selected: fabric tissue structure and yarn surface features. In this study, six types of commonly used weft knitted fabrics, weft flat knit, two types of ribbed, three types of double reverse, three different yarn surfaces without hairiness, short hairiness and long hairiness, and two different yarn diameters of 4 mm and 2 mm for real fabrics were selected for the experiment. To control the study variables, the knitted fabrics had the same warp and weft densities and the same yarn count and other elements. A schematic diagram of the knitted fabric structure is shown in Figure 5. Weft flat stitch organization plain stitch consists of continuous unit coils in one direction; the front side presents a continuous “V”-shaped appearance along the longitudinal direction formed by the coil columns, and the reverse side presents a continuous corrugated appearance along the transverse direction formed by the coil arcs; ribbed fabrics are configured from the front coil vertical rows and the reverse coil vertical rows in a certain combination, so the front side of the ribbed fabric will have a continuous “V”-shaped appearance and corrugated appearance in the vertical direction. Double reverse is made by alternating one front coil row and one reverse coil row, so the front of double reverse has a continuous corrugated and “V”-shaped appearance in the horizontal direction.
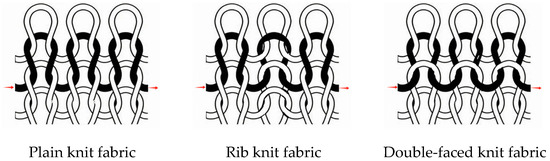
Figure 5.
Schematic diagram of knitted fabric structure.
The tags are manually labelled according to image features: set the image data as I1, then the corresponding text features are the three types of feature tags t1, t2, t3 and trigger word tag t4: knitwear, respectively. Its dataset is shown in Figure 6:

Figure 6.
Dataset.
4.2. Experimental Setup
In the experimental setup, this study sets the rank dimension to r = 32 for the LoRA fine-tuning approach to balance the model representation capability and parameter efficiency, and adopts the adaptive momentum optimizer Adam with Weight Decay (AdamW) for the parameter updating, with the learning rate fixed at to avoid gradient oscillation. In the model training process, the sample size of a single batch is set to 4, and 100 training rounds are used to ensure parameter convergence. In the inference generation stage, 30 iteration steps are set to realize the balance between generation quality and computational efficiency, while the cue word correlation coefficient is adjusted to 7.0 to enhance the control strength of text conditions on image generation.
4.3. Generation Parameters
This experiment takes hairless feather double rib tight fabric as an example, and uses the same labels as the conditions in the denoising stage to test the effect of fine-tuning the weights on the generated results. The image generation effect of the low-rank adaptation model with weights of 0.1~1.0 is shown in Figure 7: with the increase in the weights of the low-rank adaptation model, the bulging stripes in the generated image of the double ribbed knitted fabric gradually change from yarns to string-set coils from 0.4, and the string-set law gradually becomes correct from splicing with errors. The loop structure gradually becomes correct from the splicing error; from 0.7, raising the weight of image generation seems to confuse the generated features, and double ribbed fabrics change single ribbed fabrics, making the generated weight of 0.4 to 0.7 better.

Figure 7.
LORA model weight 0.1~1.
4.4. Generation Results
The fabrics with different organizational structures are generated by hairless roving for example, as shown in Figure 8 below, and the prompts for the knitted fabric organizational structure design include plain fabric, 1-1-ribbed fabric, 2-2-ribbed fabric, 1-over-1-double-faced fabric, 5-over-5-double-faced fabric, and 5-5-checkered-double-faced fabric. The low-rank adaptation of the FLUX model can be used to design knitted fabrics with different organizational structures according to the cue word, and better simulate the real fabric coil string set structure.
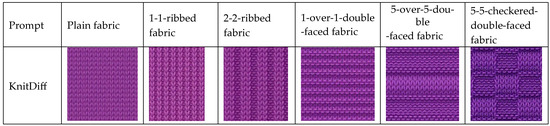
Figure 8.
Fabric generation with different organizational structures.
Take 1 × 1 double reverse knitted fabric is an example of fabric generation with different characteristic yarns, as shown in Figure 9.

Figure 9.
Fabric generation with different characteristic yarns.
The prompts for yarn thickness are tight knitting and loose knitting, respectively, and the FLUX model can generate the corresponding knitted fabric images accordingly. As shown in Figure 9, from “fine yarn without hair” and “coarse yarn without hair” in the fourth column of the image, it can be clearly seen that the fine yarn fabrics are looser and the coarse yarn fabrics are tighter and thicker.
The prompt words for the characteristics of yarn hairiness are smooth fiber, short hairy feather fiber and long hairy feather fiber. As shown in the picture, the fabric structure of smooth fiber is the most clear, and the organizational structure of the coil can be seen; in the short feather fabric, the basic outline can be clearly seen, and there are short hairs at the edges. The long feathered fabric, on the other hand, has a plush texture like the shaggy-feathered fabric, presenting a fluffier surface.
Based on the above generation results, the low-rank adaptation of the FLUX diffusion model allows the use of easy-to-understand textual prompts to modulate the image generation results, which can be reflected in the generation of the effect of the fabric organizational structure, the hairiness of the yarn, and changes in the realization of the text-generated graphs from the yarn to the fabric shown at two levels.
In order to further prove the correctness of the generated results, a qualitative and quantitative assessment is performed using the fabric organizational structure as an example.
4.5. Evaluation
4.5.1. Qualitative Assessment
In this paper, real fabrics are used as the basis to compare the generation effects. The comparison data include the SD1.5 Model and FLUX Model in group A and Knit-Diff and Knit-FLUX in group B; the results are shown in Figure 10.

Figure 10.
Qualitative assessment.
Group A FLUX models are able to generate plain knit fabrics but not other types of fabrics, such as double ribbed fabrics with a woolen bulge; Group B models are all enhanced in the fine-tuning process to predict the noise of knitting semantics, and their microstructures are more similar to the real fabrics. The Knit-Diff of Group B is not clear enough compared to the FLUX models of Group A, but the picture quality is not clear enough. The Knit-Diff in group B is more similar to the real fabric than the FLUX model in group A. The Knit-FLUX performs stably in high-resolution generation, surpasses the previous diffusion model in details such as fabric organization, and has the highest similarity to real fabrics among the four groups of data.
4.5.2. Quantitative Assessment
This paper selected two quantitative evaluation indicators, including the Structural Similarity Index (SSIM) and Human Perceptual (HP), to evaluate the structural consistency of the fabric generated. The SSIM and HP values were normalized to the [0, 1] range, where higher values indicate greater similarity between the two images, and a value of 1 denotes identical images. SSIM calculates the brightness, contrast, and structure to quantify the topological consistency between the generated image and the target image. The formula [36] is as follows:
is the mean value of x; is the variance of x; is the mean value of y; is the variance of y; is the covariance of x and y; and and are constants.
Although SSIM evaluation is an important reference, it also has certain limitations. Therefore, based on the above objective indicators, this study introduced human perception score (HP) as a supplementary evaluation method to supplement the shortcomings of objective indicators and obtain more comprehensive and reliable evaluation results. The HP score was obtained through evaluations conducted by six textile engineering experts.
Under the same parameter settings, the structural similarity comparison indices are presented in Table 1. The upward arrows indicate that larger values represent better results, the more similar the two images are. The images generated by Knit-FLUX achieve a Structural Similarity Index Measure (SSIM) of 0.6528 with respect to real fabrics, and a Human Perceptual (HP) score of 0.883. Compared with Knit-Diff, the proposed method yields the highest similarity to real knitted fabrics, demonstrating superior performance in both structural fidelity and human perceptual alignment. These results collectively indicate that the generated knitted fabric images accurately reflect the textile structures.

Table 1.
Results comparison.
In this study, fabric pixel coverage was selected as a quantitative evaluation metric to assess the effectiveness of yarn thickness representation in the generated fabric images.
Fabric pixel coverage refers to the proportion of pixels occupied by yarn regions within the entire fabric image. A higher coverage value indicates coarser yarns, denser surface fuzz, and fewer inter-yarn gaps, whereas a lower value suggests finer yarns, less fuzz, and a looser structural arrangement.
To ensure consistency in the evaluation of structural representations, the experiments were conducted on five distinct groups of fabric data. The selected fabric categories cover a range of yarn types and surface textures, including loose knit with smooth fiber, tight knit with smooth fiber, tight knit with smooth fiber, tight knit with short feather fiber, and tight knit with long feather fiber. For each fabric category, both original (real) samples and generated images were included for comparative analysis.
As shown in Figure 11, The results demonstrate that for most fabric types, the generated images closely approximate the structural features of the originals. Comparing the two groups of loose and tight knitting, the coverage of the fine yarn fabrics was significantly lower than that of the coarse yarn fabrics. Specifically, the coverage of the fine yarn fabrics was concentrated between 0.4 and 0.5, while the coverage of the coarse yarn fabrics was concentrated at 0.7. This comparison of performance metrics suggests that the coverage of the fine yarn fabrics was lower. Comparing the three groups of smooth and short feather fibers and long feather fibers, the coverage of long feather fibers is concentrated at 0.8 with the highest value. In addition, the fabric coverage of the two groups of training data and generated data are similar, with an average difference of less than 0.15, indicating that the model is able to effectively learn the fabric size information while maintaining the category learning; however, for the coarse yarn fabrics, the average difference in the coverage between the original data and the generated data is slightly larger, suggesting that there is still room for the optimization of knit-FLUX in terms of the size control during the generation process.
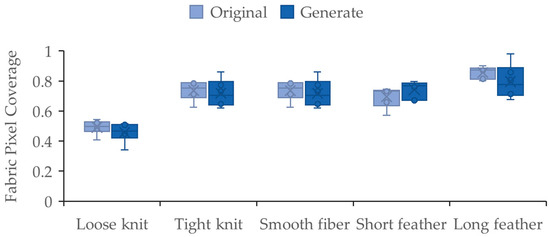
Figure 11.
Fabric pixel coverage distribution image.
4.5.3. Generation Efficiency
In addition, this study tested and analyzed the model’s image generation time to evaluate the computational efficiency and scalability of Knit-FLUX in practical application scenarios. The generation time directly affects the model’s response speed and user experience, which in turn affects the model’s practicality and market competitiveness. By generating 100 images in batch and calculating the average generation time per image, the average inference speed of the three diffusion models can be quantitatively analyzed. This provides an objective basis for performance evaluation and offers data support for further model optimization.
As shown in Table 2, KNIT-SD1.5 demonstrates significant advantages in terms of time consumption, with an average running time of only 1.9 s. KNIT-FLUX has an average runtime of 16.8 s. Despite a relatively higher average generation time than KNIT-SD1.5, KNIT-FLUX delivers superior visual fidelity and supports fast batch generation, proving its effectiveness for real-time design support and scalable fabric material production. Therefore, it remains the preferred solution when both quality and usability are prioritized.

Table 2.
Image generation efficiency comparison.
5. Conclusions
This paper is based on the low-rank adaptation of the FLUX model (Knit-FLUX) for knitted fabric image generation, which supports the stable, batch and fast generation of knitted fabric images through easy-to-understand text prompts, and the generated images have clear texture and correct structural features, which are close to the real fabric.
In the typical workflow of fashion design, designers often begin by sketching garment illustrations, yet the representation of fabric textures usually relies on hand-drawn patterns or collage materials, which lack accuracy in reflecting the true structural characteristics of the intended textile. With the integration of the proposed knitted texture generation model, designers can input specific pattern parameters to rapidly generate structurally consistent and visually realistic knitted textures. These generated textures can then be applied to garment illustrations as high-fidelity replacements, thereby enhancing the visual expressiveness and material authenticity of the design renderings. Moreover, in educational settings, this method can assist students in understanding the mapping between knitted structures and surface textures, thus improving the visualization and interactivity of textile pattern design.
Although Knit-FLUX significantly enhances the controllability of image generation with domain-specific feature prompts, when the input prompt contains multiple conceptually or visually similar descriptors, the model may conflate distinct attributes, resulting in inaccurate or ambiguous feature representations in the generated image. This limitation can be attributed to the inherent overlap in the learned latent space and the insufficient disentanglement of features during fine-tuning. Future improvements may involve prompt refinement strategies and feature-space regularization to mitigate such ambiguities.
Author Contributions
Conceptualization, X.L. and Z.L.; formal analysis, X.L.; methodology, X.L.; software, X.L.; validation, F.L., Y.W. and Z.L.; writing—original draft, X.L.; writing—review and editing, J.P., Z.L. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Exploration of Graduate Student Talent Cultivation Mode in Textile and Garment Direction of “Civic and Political Leadership + Digital Intelligence Empowerment” in Shanxi Province (No. 2024JG042), Research on the Protection Strategy of Mural Painting Cultural Relics in Shanxi under the Background of Digital Intelligence Technology of Shanxi Province (No. 202404030401110).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the editors and anonymous reviewers for their helpful suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SSIM | Structural similarity index measure |
| VAE | Variational auto-encoder |
| GAN | Generative Adversarial Networks |
| SD3 | Stable Diffusion model 3 |
| MM-DiT | Multimodal Diffusion Transformer Backbone |
| FLUX | FLUX.1 Dev |
| Single-DiT | Single Transformer Block |
| PEFT | Parameter efficient fine-tuning |
| Knit-FLUX | Low-Rank Adaptation of FLUX model |
| Knit-Diff | Low-Rank Adaptation of SD1.5 model |
| CFM | Conditional Flow Matching |
| ODE | Ordinary Differential Equation |
| CLIP | Contrastive Language-Image Pre-training |
| T5 | Text-to-Text Transfer Transformer encoders |
| RoPE | Rotary Position Embedding |
| adaLN | Adaptive Layer Normalization |
| MLP | Multi-Layer Perceptron |
| GELU | Gaussian Error Linear Unit activation function |
| LoRA | Low-Rank Adaptation |
| AdamW | Adam with Weight Decay |
References
- Alcaide-Marzal, J.; Diego-Mas, J.A. Computers as Co-Creative Assistants. A Comparative Study on the Use of Text-to-Image AI Models for Computer Aided Conceptual Design. Comput. Ind. 2025, 164, 104168. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Chen, J.; Tian, Z.; Liu, H.; Chi, X.; Liu, R.; Yuan, R.; Xing, Y.; Wang, W.; et al. LLMs Meet Multimodal Generation and Editing: A Survey. arXiv 2024, arXiv:2405.19334. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2022, arXiv:1312.6114. [Google Scholar]
- Chen, J.; Song, W. GAN-VAE: Elevate Generative Ineffective Image through Variational Autoencoder. In Proceedings of the 2022 5th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), Chengdu, China, 19–21 August 2022; pp. 765–770. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–22 June 2022; pp. 10674–10685. [Google Scholar]
- Zhang, H.; Qiao, G.; Liu, S.; Lyu, Y.; Yao, L.; Ge, Z. Attention-bassed Vector Quantisation Variational Autoencoder for Colour-patterned Fabrics Defect Detection. Color. Technol. 2023, 139, 223–238. [Google Scholar] [CrossRef]
- Lu, G.; Xiong, T.; Wu, G. YOLO-BGS Optimizes Textile Production Processes: Enhancing YOLOv8n with Bi-Directional Feature Pyramid Network and Global and Shuffle Attention Mechanisms for Efficient Fabric Defect Detection. Sustainability 2024, 16, 7922. [Google Scholar] [CrossRef]
- Wang, S.; Yu, J.; Li, Z.; Chai, T. Semisupervised Classification with Sequence Gaussian Mixture Variational Autoencoder. IEEE Trans. Ind. Electron. 2024, 71, 11540–11548. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion Models Beat GANs on Image Synthesis. In Proceedings of the Advances in Neural Information Processing Systems, Virtual Event, 6–14 December 2021; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 8780–8794. [Google Scholar]
- Sengar, S.S.; Hasan, A.B.; Kumar, S.; Carroll, F. Generative Artificial Intelligence: A Systematic Review and Applications. Multimed. Tools Appl. 2024, 84, 23661–23700. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Li, Y.; Yan, Z.; Gao, C.; Chen, R.; Yuan, Z.; Huang, Y.; Sun, H.; Gao, J.; et al. Sora: A Review on Background, Technology, Limitations, and Opportunities of Large Vision Models. arXiv 2024, arXiv:2402.17177. [Google Scholar] [CrossRef]
- Liu, X.; Gong, C.; Liu, Q. Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow. arXiv 2022, arXiv:2209.03003. [Google Scholar] [CrossRef]
- Podell, D.; English, Z.; Lacey, K.; Blattmann, A.; Dockhorn, T.; Müller, J.; Penna, J.; Rombach, R. SDXL: Improving Latent Diffusion Models for High-Resolution Image Synthesis. arXiv 2023, arXiv:2307.01952. [Google Scholar] [CrossRef]
- Esser, P.; Kulal, S.; Blattmann, A.; Entezari, R.; Müller, J.; Saini, H.; Levi, Y.; Lorenz, D.; Sauer, A.; Boesel, F.; et al. Scaling Rectified Flow Transformers for High-Resolution Image Synthesis. In Proceedings of the Forty-first International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Lipman, Y.; Chen, R.T.Q.; Ben-Hamu, H.; Nickel, M.; Le, M. Flow Matching for Generative Modeling. arXiv 2022, arXiv:2210.02747. [Google Scholar]
- Peebles, W.; Xie, S. Scalable Diffusion Models with Transformers 2023. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 4–6 October 2023; pp. 4195–4205. [Google Scholar]
- Su, J.; Ahmed, M.; Lu, Y.; Pan, S.; Bo, W.; Liu, Y. RoFormer: Enhanced Transformer with Rotary Position Embedding. Neurocomputing 2024, 568, 127063. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Q.; Chen, D.; Yuan, L.; Fu, Y. AnimeDiff: Customized Image Generation of Anime Characters Using Diffusion Model. IEEE Trans. Multimed. 2024, 26, 10559–10572. [Google Scholar] [CrossRef]
- Black Forest Labs—Frontier AI Lab. Available online: https://blackforestlabs.ai/ (accessed on 30 May 2025).
- Dehghani, M.; Djolonga, J.; Mustafa, B.; Padlewski, P.; Heek, J.; Gilmer, J.; Steiner, A.; Caron, M.; Geirhos, R.; Alabdulmohsin, I.; et al. Scaling Vision Transformers to 22 Billion Parameters. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 7480–7512, PMLR. [Google Scholar]
- Lialin, V.; Deshpande, V.; Yao, X.; Rumshisky, A. Scaling down to Scale up: A Guide to Parameter-Efficient Fine-Tuning. arXiv 2024, arXiv:2303.15647. [Google Scholar]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Guo, Y.; Sun, L. Designer-style Clothing Generation Method Based on LoRA Model Fine-tuning Stable Diffusion 2024. J. Beijing Inst. Fash. Technol. 2024, 44, 58–69. [Google Scholar] [CrossRef]
- Fei, R.; Jun, J.; Xiang, W.; Hao, X.; Yuan, X. Automatic generation of blue calico’s single pattern based on Stable Diffusion. Adv. Text. Technol. 2024, 32, 48–57. [Google Scholar] [CrossRef]
- Huang, H.; Li, C.; Zhang, X. Research on the appearance simulation of fabrics by generative artificial intelligence. J. Donghua Univ. 2024, 24, 46–55+64. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, H.; Liu, L.; Zhou, D.; Xu, X.; Zhang, Z.; Yan, S. Toward Intelligent Design: An AI-Based Fashion Designer Using Generative Adversarial Networks Aided by Sketch and Rendering Generators. IEEE Trans. Multimed. 2023, 25, 2323–2338. [Google Scholar] [CrossRef]
- Cao, S.; Chai, W.; Hao, S.; Zhang, Y.; Chen, H.; Wang, G. DiffFashion: Reference-Based Fashion Design with Structure-Aware Transfer by Diffusion Models. IEEE Trans. Multimed. 2024, 26, 3962–3975. [Google Scholar] [CrossRef]
- Zhang, S.; Ni, M.; Chen, S.; Wang, L.; Ding, W.; Liu, Y. A Two-Stage Personalized Virtual Try-on Framework with Shape Control and Texture Guidance. IEEE Trans. Multimed. 2024, 26, 10225–10236. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, H.; Zhang, Z. Learning to Disentangle the Colors, Textures, and Shapes of Fashion Items: A Unified Framework. IEEE Trans. Multimed. 2024, 26, 5615–5629. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-Based Generative Modeling through Stochastic Differential Equations. arXiv 2021, arXiv:2011.13456. [Google Scholar] [CrossRef]
- Tong, A.; Malkin, N.; Huguet, G.; Zhang, Y.; Rector-Brooks, J.; Fatras, K.; Wolf, G.; Bengio, Y. Improving and Generalizing Flow-Based Generative Models with Minibatch Optimal Transport. arXiv 2023, arXiv:2302.00482. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models from Natural Language Supervision. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021. [Google Scholar]
- Ni, J.; Ábrego, G.H.; Constant, N.; Ma, J.; Hall, K.B.; Cer, D.; Yang, Y. Sentence-T5: Scalable Sentence Encoders from Pre-Trained Text-to-Text Models. arXiv 2021, arXiv:2108.08877. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).