Abstract
This study introduces an amphibious spherical robot equipped with a dual-propulsion system (ASR-DPS) and investigates its water-surface motion characteristics. Due to its distinctive spherical geometry, the robot exhibits markedly different hydrodynamic behavior compared to conventional vessels. A comparative analysis of the frontal wetted area is performed, followed by computational fluid dynamics (CFD) simulations to assess water-surface performance. The results indicate that the hemispherical bow increases hydrodynamic resistance and generates large-scale vortex structures as a consequence of intensified flow separation. Although the resistance is higher than that of traditional hulls, the robot’s greater draft and dual-propulsion configuration enhance stability and maneuverability during surface operations. To validate real-world performance, standard maneuvering tests, including circle and zig-zag maneuvers, are conducted to evaluate the effectiveness of the propeller-based propulsion system. The robot achieves a maximum surface speed of 1.2 m/s and a zero turning radius, with a peak yaw rate of 0.54 rad/s under differential thrust. Additionally, experiments on the pendulum-based propulsion system demonstrate a maximum speed of 0.239 m/s with significantly lower energy consumption (220.6 Wh at 60% throttle). A four-degree-of-freedom kinematic and dynamic model is formulated to describe the water-surface motion. To address model uncertainties and external disturbances, two control strategies are proposed: one employing model simplification and the other adaptive control. Simulation results confirm that the adaptive sliding mode controller provides precise surge speed tracking and smooth yaw regulation with near-zero steady-state error, exhibiting superior robustness and reduced chattering compared to the baseline controller.
1. Introduction
Amphibious robots have garnered widespread attention due to their unique advantages in operating across diverse terrains. Depending on their intended application scenarios, amphibious robots exhibit considerable differences in structural design, functional configuration, and propulsion mechanisms. For instance, Bong-Huan Jun et al. [1] developed a legged amphibious robot named CR200 for shipwreck inspection and erosion monitoring, capable of operating in turbid, fast-flowing underwater environments for seabed imaging missions. CR200 adopts a hexapod locomotion system that enables seamless transition between land and seabed operation, and is equipped with onboard sensors for underwater data acquisition. To reduce its overall weight, the frame is constructed from carbon fiber reinforced plastic (CFRP), and the streamlined body design minimizes hydrodynamic drag. In another example, Sandeep Dhull et al. [2] proposed a compact amphibious robot called Aquapod, designed for in situ water sampling and toxicity analysis. It utilizes an environment-driven rolling locomotion mechanism and features a detachable sampling unit for collecting liquid samples. The outer shell is made of transparent polycarbonate, providing both pressure resistance and chemical compatibility. In the domain of amphibious operations, several robotic systems have been developed to autonomously perform tasks in surf zones, including mine clearance in shallow waters and mapping of potential underwater threats [3,4,5,6]. Spherical structures offer notable advantages during locomotion, such as low energy consumption and high mobility. Moreover, spherical geometry provides the maximum internal volume for a given surface area, making it particularly attractive for robotic applications. These benefits have fueled growing interest in spherical amphibious robots. For example, Guo et al. [7,8,9,10] proposed a turtle-inspired spherical robot powered by water-jet propulsion for underwater navigation, which transforms into a legged robot for land-based locomotion. This multifunctional propulsion mechanism enables amphibious operation via structural reconfiguration. The upper hemisphere contains sealed compartments housing electronics, while the lower half integrates the propulsion system. With a compact form factor (diameter of only 250 mm, the robot is densely packed internally, and its maximum speed is relatively low at 0.248 m/s. Zhan et al. [11] developed a spherical robot equipped with auxiliary fins that enable locomotion both on land and in water through rotational motion. The robot incorporates 16 triangular fins arranged across its spherical surface. These fins generate additional thrust during underwater movement by interacting with the surrounding fluid. Importantly, their geometric design ensures that they do not hinder the robot’s rolling motion on land. Experimental results demonstrated that the robot can achieve a maximum speed of 0.4 m/s within 5 s in water. Li et al. [12] introduced a spherical robot featuring a triple-mode propulsion system consisting of flywheels, a pendulum, and propellers. The propellers enable underwater propulsion, the pendulum facilitates rolling motion on land or seabed, and the flywheel assists with attitude stabilization. The design includes a central tunnel through the shell, with the pendulum suspended across its midsection. The robot has a shell diameter of 0.4 m, a maximum underwater speed of 1.4 m/s, and a total weight of 25 kg. Jia et al. [13] proposed a conceptual amphibious spherical robot with two extendable arms equipped with propellers. During underwater operations, the arms rotate horizontally to provide thrust, while for land locomotion, the arms rotate vertically to enable rolling. By adjusting the arm positions, the robot’s center of mass is manipulated, enabling rolling motion under gravity. Muhammad Affan Arif et al. [14] developed an amphibious spherical robot equipped with dual eccentric pendulums and a flywheel. The eccentric pendulums generate rolling motion, while the flywheel delivers high instantaneous torque for overcoming obstacles. The design emphasizes high torque, multiple locomotion modes, and a compact, lightweight structure. Experiments on both land and water validate the robot’s functionality. Despite these advancements, most spherical robots remain at the conceptual or prototype stage. To advance their practical application, this work proposes a novel all-terrain, multi-environment amphibious spherical robot featuring dual propulsion systems—a pendulum-driven mechanism and a propeller-based system. Both propulsion modes are operable during water-surface motion, providing redundancy in case of failure. For instance, if the propeller becomes entangled and loses effectiveness, the pendulum-driven system can generate internal torques to rotate the shell and induce a rolling motion, akin to a wheel. This internal actuation is less susceptible to external interference and effectively mitigates issues such as stranding or propulsion failure. The hybrid propulsion concept significantly enhances the robot’s adaptability in complex amphibious scenarios. Given these advantages, the proposed robot is especially suited for autonomous patrol, search-and-rescue, and environmental monitoring in water-surface, shoreline, and intertidal zones.
Compared to land locomotion, surface navigation is more susceptible to environmental disturbances such as wind and currents. Sliding mode control (SMC), known for its robustness against system uncertainties and disturbances, has been widely applied in surface vehicle control. For instance, Wang et al. [15] integrated fuzzy logic with SMC to develop an adaptive fuzzy sliding mode controller for dynamic positioning. Gandikota et al. [16] proposed an adaptive super-twisting sliding mode controller with a disturbance observer for uncertainty compensation. Inspired by these works, this study also employs SMC to design a robust control system for the proposed robot. While surface vehicle dynamics are often modeled using three degrees of freedom (surge, sway, yaw), such simplifications may be inadequate for spherical robots with significant rolling motion. Hence, some studies have incorporated roll dynamics into 4-DOF models (surge, sway, yaw, roll) [17,18,19]. Since the proposed robot can actively control its roll motion via the pendulum, a 4-DOF dynamic model is developed to accurately describe its behavior.
The main contributions of this paper are as follows:
- (1)
- A novel amphibious spherical robot platform with dual propulsion systems is presented. The hydrodynamic characteristics of the robot on the water-surface are investigated, including stability analysis and a comparative study of the wetted surface area. Computational fluid dynamics (CFD) simulations are conducted to analyze the water-surface motion, and the results are compared with those of conventional ships. To the best of our knowledge, this is the first detailed comparative analysis between a spherical amphibious robot and traditional vessels in terms of water-surface dynamics.
- (2)
- The water-surface locomotion characteristics of the robot under propeller propulsion are experimentally evaluated using standard marine maneuvering tests, including the circle test and zig-zag test. Additionally, the performance of the pendulum propulsion system is also examined through controlled experiments.
- (3)
- A four-degree-of-freedom (4-DOF) kinematic and dynamic model of the robot’s water-surface motion is established to describe its behavior more precisely.
- (4)
- Based on the derived dynamic model, a control system is developed using sliding mode control (SMC). To address model uncertainties and environmental disturbances, two control strategies are proposed: a simplified model-based controller and an adaptive controller. Their performances are compared and analyzed through simulations.
The remainder of this paper is organized as follows: Section 2 introduces the overall design of the amphibious spherical robot and analyzes its hydrodynamic behavior on the water surface. Section 3 establishes a four-degree-of-freedom (4-DOF) kinematic and dynamic model for its water-surface motion. In Section 4, experimental analyses are conducted to evaluate the motion characteristics of the robot under different propulsion systems. Section 5 presents the design of a sliding mode controller and compares two control strategies for addressing model uncertainties. Simulation results validating the control performance are also provided. Finally, Section 6 discusses the conclusions and draws key insights.
2. Overall Design and Water Surface Locomotion Characteristics
2.1. Overall Design
The proposed amphibious spherical robot consists of three primary structural components: the spherical shell, the main internal frame, and the mounting platforms, as illustrated in Figure 1. The shell adopts a truncated-sphere geometry, providing a relatively large internal volume. The main frame is rotatably connected to the shell via a rotating shaft, enabling internal actuation. The control units, electrical modules, and various sensing components are housed within the main frame. A pendulum propulsion system is mounted on the lower part of the main frame, which allows the pendulum to swing in both pitch and roll directions, thereby changing the orientation and motion of the robot. The detailed mechanical design of this system can be found in our previous work [20,21]. The robot includes two external mounting platforms symmetrically located on both sides of the spherical shell. These platforms are rigidly connected to the internal main frame and serve as carriers for external sensors and actuators. The proposed amphibious spherical robot is equipped with two independent propulsion systems: a propeller propulsion system and a pendulum propulsion system. The propellers are mounted on the external mounting platforms, with one located on each side. Together with the internal electrical and control modules housed in the main frame, these two thrusters constitute the propeller propulsion system. This system serves as the primary means of locomotion on the water-surface and is capable of achieving zero-radius turning via differential thrust. In addition to the propeller propulsion system, a pendulum propulsion system is also integrated. This system comprises an internal pendulum and its associated components. By adjusting the pendulum’s position, an eccentric torque is generated, which induces rotational motion of the outer shell, thereby enabling the robot to move. The basic parameters are presented in Table 1.
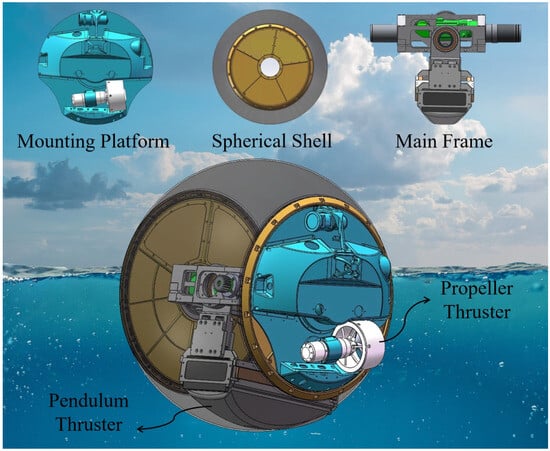
Figure 1.
Schematic diagram of the amphibious spherical robot. (Source: own elaboration).

Table 1.
Parameter list of ASR-DPS. (Source: own elaboration).
2.2. Water Surface Locomotion Characteristics
2.2.1. Water Surface Locomotion Stability
Unlike conventional unmanned surface vehicles (USVs), the amphibious spherical robot features its propeller thrusters mounted laterally beneath its hull. Additionally, it incorporates an internal two-degrees-of-freedom pendulum propulsion system, enabling active adjustment of the robot’s attitude. The lateral placement of the propellers facilitates differential thrust, allowing for zero-radius turning. The key advantage of the internal pendulum propulsion lies in its capability for continuous, real-time attitude control, preventing the robot from being passively subjected to environmental disturbances that could lead to uncontrollable attitude changes. Another significant advantage is the ability to overcome stranding through spherical rolling locomotion—a critical challenge typically insurmountable for traditional USVs.
However, a drawback arises during water-surface locomotion: a stable and reliable controller is essential to regulate the pendulum’s position. Without such control, the amphibious spherical robot is highly prone to capsizing to the left or right during water-surface motion, as illustrated in Figure 2a,b. Our team has previously designed a robust controller to stabilize the robot’s attitude via the pendulum propulsion system and eliminate roll motion, as detailed in our prior work [20,21].

Figure 2.
Schematic illustration of the amphibious spherical robot tipping in water. (a) Tilting to the left. (b) Tilting to the right. (c) In a stable state. (Source: own elaboration).
However, following the elimination of roll motion, the amphibious spherical robot behaves akin to a self-righting roly-poly toy when in water. Its center of gravity is located below the waterline. Furthermore, the inherent structural characteristics of the spherical robot result in a significantly larger wetted surface area compared to conventional USVs and a draft exceeding 60% of its overall height. This structure also exhibits greater symmetry relative to typical USVs. Consequently, the robot demonstrates superior stability when encountering wind and waves, as illustrated in Figure 2c.
2.2.2. Water-Facing Surface and Hydrodynamic Resistance
As Figure 3 shows, during water-surface locomotion, the spherical robot exhibits a substantially different hydrodynamic profile compared to conventional vessels or unmanned surface vehicles (USVs). Its forward-facing geometry is characterized by a bluff, hemispherical leading surface rather than a streamlined pointed bow, resulting in a relatively large frontal cross-sectional area in the direction of motion. This non-streamlined shape induces greater form and pressure drag, which dominate the total resistance, particularly at moderate-to-high speeds, contrasting with the friction-dominated resistance observed in slender hull designs. The resistance formula is [22]
where is the hydrodynamic damping coefficient, denotes the fluid density, A denotes the submerged cross-sectional area, and u is the surge velocity.
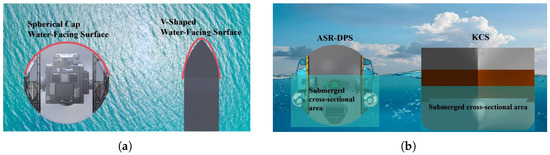
Figure 3.
Hydrodynamic structure features. (a) Contrasting water-facing surface designs (spherical cap vs. V-shaped). (b) Submerged body geometries (ASR-DPS vs. KCS). (Source: own elaboration).
According to this formula, under identical conditions, a larger submerged cross-sectional area A leads to greater hydrodynamic resistance. The amphibious spherical robot exhibits significantly higher hydrodynamic resistance during water-surface locomotion compared with conventional vessels, primarily due to two structural factors: its circular cross-section and a draft-to-height ratio exceeding 60%.
2.2.3. CFD Simulation Analysis of Water-Surface Motion
During water-surface locomotion, the amphibious spherical robot exhibits distinct hydrodynamic characteristics compared to conventional marine vessels. This difference stems primarily from its forward wetted surface, which features a spherical cap structure with significant curvature. This geometry results in a larger cross-sectional area in the direction of water ingress (flow direction). Consequently, the robot demonstrates marked differences in fluid flow characteristics around the body, hydrodynamic resistance distribution, and lift generation mechanisms relative to traditional vessels. To quantitatively assess and visually represent these disparities, we performed computational fluid dynamics (CFD) simulations of the amphibious spherical robot’s water-surface motion using the commercial software STAR-CCM+ version 2410 (Siemens Digital Industries Software, Plano, TX, USA) [23,24]. The computational setup mirrored that employed in a published STAR-CCM+ benchmark case study for a conventional vessel navigating at comparable speeds [25]. A comparative analysis of the simulation results, highlighting the key hydrodynamic differences, is presented in Figure 4.
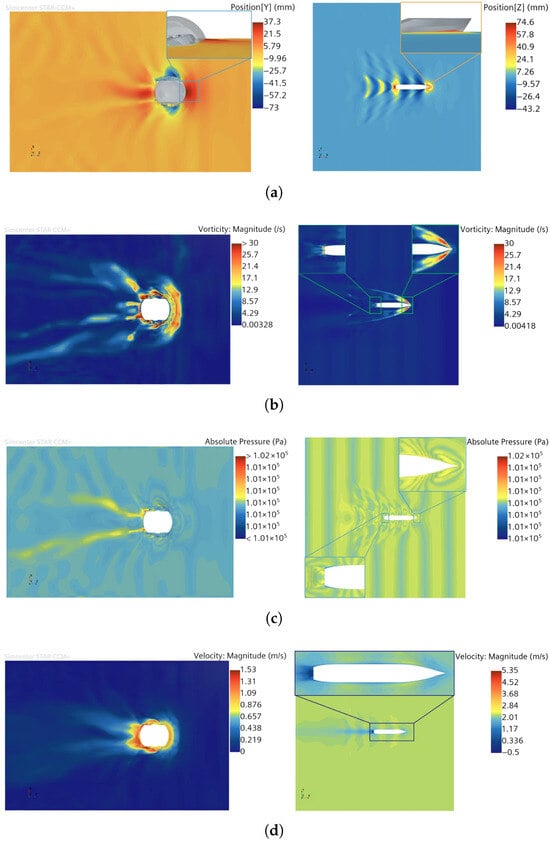
Figure 4.
Comparison of surface motion characteristics of spherical robots. (a) Position. (b) Vorticity. (c) Pressure. (d) Velocity. (Source: simulation conducted by authors).
As shown in Figure 4a, the simulated free surface profiles indicate the formation of distinct bow and stern wave crests for both the amphibious spherical robot and the conventional ship. However, it is evident that the wave crest generated at the bow of the spherical robot exhibits a significantly wider spread compared to that of the ship. Moreover, the highest point of the bow wave in the case of the spherical robot is located directly in front of the robot, whereas for the ship, the wave crests reach their maximum height along the port and starboard sides near the bow. This discrepancy arises from the difference in hull geometry: the spherical robot features a dome-shaped frontal surface that causes oncoming flow to accumulate at the front, whereas the V-shaped bow of the ship facilitates lateral flow separation, diverting water to both sides. Furthermore, the free surface displacement pattern induced by the spherical robot appears more irregular and lacks a well-defined structure, in contrast to the triangular and more orderly wave pattern observed in the ship’s case.
In Figure 4b, the vorticity plot clearly illustrates the motion of the spherical robot, with significant vortex formation surrounding the entire surface, particularly at the robot’s bow. A large C-shaped high-vorticity vortex forms along the leading edge, adhering closely to the wetted surface. The highest vorticity is observed on both sides and at the stern, where large-scale flow separation occurs, generating a persistent, high-intensity vortex structure encircling the central region. This is likely due to the sharp curvature and symmetry of the spherical robot, which causes the fluid to separate violently almost immediately upon encountering the sphere, forming a strong vortex ring around the rear. These turbulent vortices increase the hydrodynamic drag and energy dissipation of the spherical robot during its movement on the water-surface. In contrast, the vorticity plot of the ship hull shows that vortex structures are mainly concentrated around the bow, with the streamlined design of the hull delaying flow separation. This allows the fluid to stay attached to the surface for a longer distance, guiding the separation to a more controlled region. Consequently, vortices primarily form and shed at the bow and shoulders, resulting in smaller, more organized vortex structures with reduced intensity and influence. This design minimizes the turbulence in the wake, thus reducing energy loss and drag.
Similarly, the pressure distribution results in Figure 4c reveal that the spherical robot exhibits a region of locally elevated pressure in its near-wake region, aligning with characteristic bluff body drag behavior. Furthermore, the pressure distribution downstream appears highly disordered, indicative of significant turbulence and vortex shedding within the robot’s wake. In contrast, the vessel’s pressure distribution displays a gradual pressure decay radiating outwards from the hull, resulting in a relatively smooth distribution consistent with its streamlined form. The most striking feature is a distinct, organized striated pattern of high- and low-pressure regions extending orthogonally from the hull surface, perpendicular to its direction of travel.
Figure 4d presents the corresponding velocity distributions. It can be clearly seen that a distinct annular region of high-speed flow forms around the spherical robot, resulting from rapid flow separation from its surface. A wide and irregular wake region is also observed at the rear, characterized by varying flow velocities, indicating significant flow separation and turbulence in the wake of the spherical robot. Conversely, the velocity field around the vessel is overall smoother with lower localized gradients, reflecting the attached flow characteristic of a streamlined body.
In summary, the comparative flow field analyses presented in Figure 4 clearly demonstrate the distinct hydrodynamic characteristics of the amphibious spherical robot relative to a conventional streamlined ship hull. The spherical robot exhibits broader and more irregular bow wave patterns, stronger and more chaotic vortex structures, and larger near-wake pressure and velocity fluctuations—hallmarks of pronounced flow separation and bluff-body behavior. These features are primarily attributed to the robot’s dome-shaped frontal geometry and omnidirectional symmetry, which inherently promote early boundary layer detachment and unsteady wake development. In contrast, the ship’s streamlined hull guides the flow more effectively along its surface, producing narrower and more coherent wave patterns, delayed separation, and diminished wake turbulence. Importantly, these simulated flow features align well with established hydrodynamic theory. The observed characteristics of the spherical robot are consistent with canonical bluff-body flow behavior described in classical fluid mechanics literature [22], while the ship’s flow responses resemble those documented in standard hull benchmark studies, such as the KCS model reported in ITTC CFD validation guidelines. This agreement supports the reliability of our simulation results. Despite the inherent hydrodynamic drawbacks associated with bluff-body effects—such as elevated drag and energy dissipation—the spherical robot design offers several unique advantages. These include omnidirectional geometric symmetry, excellent stability across varied terrains, integrated multi-modal locomotion capabilities (e.g., rolling, pendulum swinging, and hybrid propulsion), and strong adaptability in unstructured or amphibious environments. Such attributes make the spherical robot particularly well-suited for operations in shallow water zones, obstacle-dense areas, and aquatic-terrestrial transition regions where traditional hull designs may encounter limitations.
3. Modeling of 4-DOF Kinematics and Dynamics
Generally, the amphibious spherical robot exhibits motion characterized by six degrees of freedom (6-DOF) during water-surface locomotion [26]. These DOFs comprise:
- 1.
- Translational motion along three orthogonal axes (X, Y, Z).
- 2.
- Rotational motion about these same axes, denoted by the Euler angles: roll (), pitch (), and yaw ().
The specific definitions of these motions are illustrated in the Figure 5 Within the robot’s body-fixed coordinate frame, the origin is defined at the center of mass of the ASR-DPR. Symbol definitions are provided in Table 2
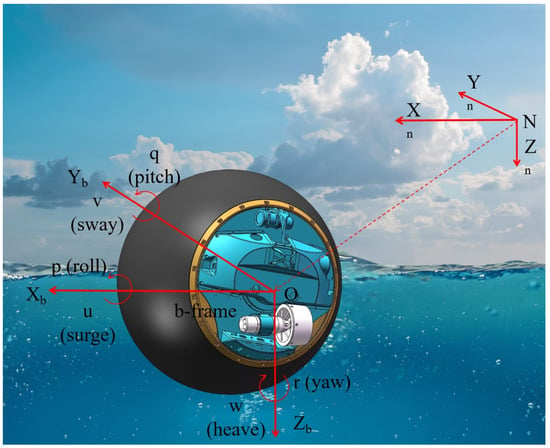
Figure 5.
Reference frames associated with the robot (Source: own elaboration).

Table 2.
The notation of SNAMME (1950) for marine vessels. (Source: [26]).
Most USV studies employ a three-degrees-of-freedom (3-DOF) dynamic model, justified by typical operating environments in calm inland waters or sheltered coastal areas where motion in the heave (z), roll (), and pitch () degrees of freedom is negligible. However, research addressing vessels operating in high sea states with significant wind and wave action often incorporates roll motion (), adopting a 4-DOF model to mitigate the critical risk of capsizing due to destabilizing roll moments. As previously established, the center of gravity (CG) of the amphibious spherical robot is dynamically coupled to its pendulum position. The pendulum’s capability for bi-directional actuation (surge-sway plane) renders the robot highly susceptible to roll excitation (). Consequently, this study develops a 4-DOF kinematic model encompassing surge (x), sway (y), roll (), and yaw () to capture the robot’s unique dynamics. The robot features two distinct propulsion systems: 1. Propeller propulsion system: Fixed thrusters provide surge force (X) and yaw moment (N). 2. Pendulum propulsion system: Generates surge force (X), roll moment (K), and yaw moment (N). In general, most USVs are modeled with 3 DOFs, namely surge, sway, and yaw. However, considering that the ASR-DPS’s pendulum propulsion system enables active control of the roll motion, a four-DOF kinematic and dynamic model is developed in this study.
3.1. Kinematic Model Derivation
The kinematic model of the ASR-DPS can be formulated as [26]:
where , is the generalized velocity vector decomposed in the b-frame.
Thus, the kinematic model can be written as:
3.2. Dynamics Model Derivation
The dynamics equations for surface navigation can be expressed as follows [26]:
The mass matrix is defined as , which includes both the rigid-body mass matrix of the robot () and the added mass matrix due to fluid interaction (). The Coriolis-centripetal matrix is given by , comprising the rigid-body Coriolis matrix () and the Coriolis matrix associated with the added mass (). The damping matrix is expressed as , where represents the linear damping component and represents the nonlinear damping. The vector denotes the restoring forces. The generalized force input is defined as , where refers to the thrust forces and moments generated by the propulsion system, and denotes the external environmental forces and moments. The 4-DOF model necessitates control inputs in surge, sway, roll, and yaw. However, the available actuators only provide three independent control channels, resulting in an underactuated control problem. The generalized control input vector is defined as:
It is also common to assume that the craft has homogeneous mass distribution and xz-plane symmetry so that . Let . Based on these definitions, the model can be further simplified and written in the following form:
3.3. Model Preprocessing
The dynamic model described above contains several uncertain components and external disturbances. To facilitate controller design, the known and unknown (uncertain and disturbance) terms are separated. The total uncertainty and disturbance terms are denoted by , where represent the total uncertainties associated with the surge, sway, roll, and yaw degrees of freedom, respectively. These terms include unmodeled dynamics, parameter uncertainties, and external disturbances. Some key hydrodynamic parameters are less affected by disturbances and can be estimated using empirical formulas available in the literature [20,27,28,29]. The retained parameters include . The calculation formula is as shown in Table 3:

Table 3.
Hydrodynamic parameter calculation formulas. (Source: own elaboration and [27]).
It is worth noting that, due to the highly symmetrical geometry of the spherical robot, it is reasonable to assume that . By defining the following mass and damping terms: , , , the system dynamics can be rewritten as the following equation:
4. Experimental Analysis of Motion Characteristics Under Different Propulsion Systems
Based on the methodologies proposed in literature [12,30,31,32], this subsection presents an experimental analysis of the water-surface motion characteristics of the amphibious spherical robot. The water-surface mobility tests were conducted in Qizhen Lake on the Zijingang Campus of Zhejiang University. During the experiments, the wind and water current speeds were relatively low, and there were no disturbances from other vessels, indicating that the environmental interference in the lake was minimal. Figure 6 shows images of the field test.

Figure 6.
The amphibious spherical robot during water-based testing. (It is worth noting that the waterline appears to be slightly above the midpoint of the robot, indicating that more than half of the robot’s body is submerged.) (Source: own elaboration).
4.1. Motion Characteristic Analysis Under Propeller Propulsion System
To evaluate the maneuverability and dynamic response characteristics of the ASR-DPS, zig-zag and circle tests were selected as standard experimental protocols. These tests are widely adopted in both academic research and practical guidelines [30] (e.g., IMO standards [33]) for assessing the hydrodynamic behavior and control performance of marine vehicles. The zig-zag test provides insights into the yaw response, time delay, overshoot, and damping characteristics of the USV under abrupt steering inputs, making it particularly valuable for tuning and validating heading control algorithms. Meanwhile, the circle test assesses the turning stability and steady-state turning behavior under constant rudder input, which is essential for identifying the system’s nonlinear maneuvering tendencies and verifying the existence of stable spiral motion. By combining these two complementary tests, a comprehensive understanding of the USV’s maneuvering behavior can be achieved, enabling robust controller design and reliable path-following performance in real-world conditions.
4.1.1. Circle Test
The circle test was conducted through two sets of experiments, as outlined in Table 4. Each experiment consisted of three sequential stages: an initial straight-line acceleration phase, followed by a constant-speed cruising phase, and finally a turning maneuver to assess the robot’s circular motion performance. In the course of the circle test, key dynamic parameters including the rotational speed, roll, pitch, and yaw angles, as well as the turning radius of the amphibious spherical robot, were recorded for analysis.

Table 4.
Circle test settings. (Source: own elaboration).
As shown in Figure 7a,b, when the propeller thrusters reach their maximum rotational speed, the amphibious spherical robot achieves a peak surge velocity of approximately 1.2 m/s. Notably, as soon as a differential in rotational speed is introduced between the left and right thrusters at the beginning of the circle test, the surge velocity drops rapidly to near zero. This indicates that the robot experiences significant hydrodynamic resistance during water-surface navigation—once propulsion support is lost, the velocity decays quickly (first test: 0.21 m/s2;; second test: 0.147 m/s2;). Meanwhile, the yaw rate increases sharply, reaching 0.43 rad/s in the first test and 0.33 rad/s in the second test. Figure 7c,d illustrate the evolution of roll and pitch angles during the circle test. A key observation is that the roll angle remains within 5° during both the acceleration and steady-state motion phases, with fluctuations constrained within ±2°. This suggests that the amphibious spherical robot maintains satisfactory roll stability during straight-line motion, validating the effectiveness of the implemented PID controller. However, during the circular maneuver phase, the roll angle suddenly increases from approximately 2° to 12°, resulting in a visibly tilted posture of the robot—a phenomenon also evident in the experimental photographs. This indicates a significant risk of lateral instability during sharp rotational maneuvers. One plausible explanation lies in the robot’s unique internal pendulum propulsion system, which allows motion in multiple directions. Despite having a dedicated roll control loop, the large differential torque generated by the side-mounted propellers during the turn can exceed the control authority of the system, leading to a temporary loss of roll stability. Once the propeller torque is removed, the roll angle quickly drops back to around 5°. Regarding the pitch angle, a sharp decrease is observed during the acceleration phase. This is attributed to the sudden thrust causing the pendulum mechanism to swing backward. Since the IMU is mounted on the central structural frame, it captures this backward motion, resulting in a rapid drop in pitch angle before it stabilizes. During the turning phase, the tilted motion of the spherical shell causes both the internal frame and the pendulum to incline, leading to an increase in pitch angle. The trajectory plot indicates that the thrusts generated by the left and right propellers are well balanced, enabling the robot to maintain a stable straight-line motion. The amphibious spherical robot demonstrates a zero turning radius, allowing for rapid in-place rotations. This highlights the high maneuverability and flexibility achieved by mounting propeller thrusters symmetrically on both sides of the robot. As shown in Figure 7h, under the influence of environmental factors alone, the velocity fluctuates around 0.01 m/s. Compared to the tested velocity of 1.2 m/s, the effect is negligible.
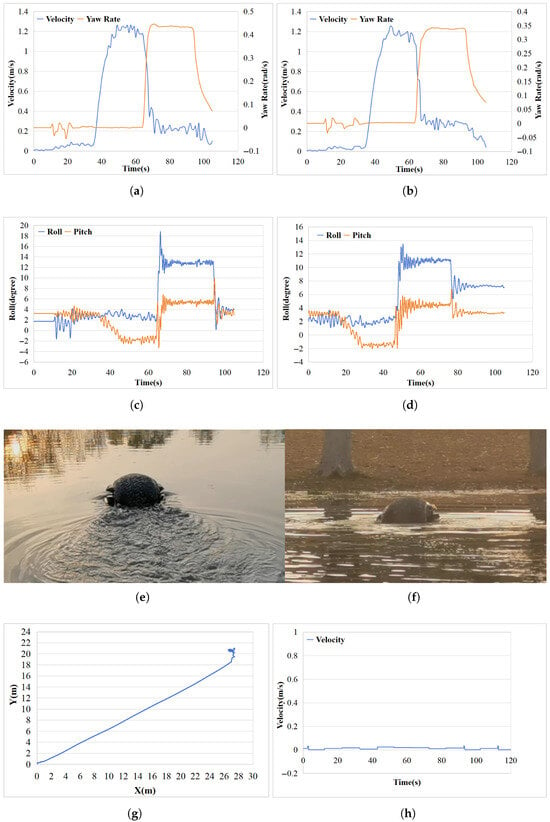
Figure 7.
Circle test data plots. (a) Surge velocity and yaw rate in the first test. (b) Surge velocity and yaw rate in the second test. (c) Roll and pitch angle variations in the first test. (d) Roll and pitch angle variations in the second test. (e,f) Images of the robot during real-world circle tests. (g) Trajectory plot. (h) Velocity caused by environmental factors. (Source: own elaboration).
4.1.2. Zig-Zag Test
The experimental setup for the zig-zag test is detailed in Table 5.

Table 5.
Zig-zag test settings. (Source: own elaboration).
Figure 8 presents the experimental data from the zig-zag test. Similarly, the zig-zag test reveals the motion characteristics of the amphibious spherical robot (ASR). In Figure 8a, the maximum surge speed is approximately 1.2 m/s, and the yaw rate at the half-maximum moment is 0.54 rad/s. The yaw rate curve clearly shows four sawtooth patterns, consistent with the standard zig-zag test variations. In Figure 8b, the variation in roll indicates that during the acceleration phase, the roll change is minimal, meaning the ASR maintained a flat locomotion. However, as the zig-zag test commenced, four cusp-like catastrophes occurred (as shown in the ellipse), indicating that the posture of the ASR tilted, which aligns with the observations from the circle test. The pitch angle variation is also consistent with the circle test results. Figure 8c shows the change in yaw during the test, where four rapid yaw variations are evident, indicating that the ASR-DPS performed quick rotations. From the results of the circle and zig-zag tests, it is clear that the ASR-DPS, due to its secondary power system (the pendulum propulsion system), experiences a disruption in posture stability under large rotational torques. However, once the large torque is removed, the ASR-DPS can quickly regain its stable posture. This also validates, from another perspective, that the pendulum propulsion system can flexibly alter the posture of the ASR-DPS to adapt to complex external environments—an advantage that conventional USVs lack. In Figure 8d, the shape of the trajectory matches the standard zig-zag test pattern. Both experiments further demonstrate that the ASR-DPS has agile movement capabilities on the water-surface, can rapidly respond to controller commands, and has the ability to actively adjust the roll angle.
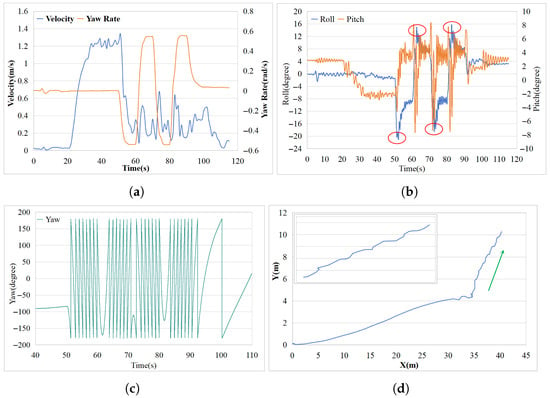
Figure 8.
Zig-zag test data plots. (a) Surge velocity and yaw rate. (b) Roll and pitch angle variations. (c) Yaw variations. (d) Trajectory plot. (Source: own elaboration).
4.2. Analysis of Motion Characteristics Under the Pendulum Propulsion System
The pendulum propulsion system provides thrust by changing the position of the pendulum to generate an internal eccentric torque, which causes the spherical shell to roll. The rolling motion is naturally suitable for terrestrial locomotion. However, in fact, this rolling motion can also enable movement on the water-surface. Due to its inherent limitations, the motion speed on water is relatively low. In order to investigate the actual effect of using the pendulum propulsion system for water-surface movement in the proposed amphibious spherical robot, we conducted field tests.
To analyze the water-surface locomotion characteristics of the pendulum propulsion system, we conducted five sets of experiments. As shown in Table 6, the motion speed of the amphibious spherical robot gradually increases with throttle input. However, even at 60% throttle, the maximum speed only reaches 0.239 m/s, which is significantly lower than the speed achieved using the propeller-based propulsion system. On the other hand, this propulsion method exhibits relatively low power consumption. This is primarily due to the reduced friction during rolling on the water-surface, resulting in lower energy usage. At the same time, this low-friction condition also contributes to the limited speed performance of the robot under this mode of operation.

Table 6.
Test results of the pendulum propulsion system performance. (Source: own elaboration).
As shown in Figure 9a, during water-surface locomotion powered by the pendulum propulsion system, a large volume of water is lifted off the surface by the rotation of the spherical shell. The resulting wake is notably different from the triangular track observed under propeller-based propulsion. Figure 9b illustrates the swinging motion of the internal pendulum during this mode of propulsion. Furthermore, by simultaneously actuating the pendulum to swing both forward-backward and left-right, the amphibious spherical robot is capable of executing a zero-radius turn on the water-surface. Unlike the differential-thrust-based zero-radius turn achieved by the twin propellers, the pendulum-driven zero-radius turn arises from the pendulum tilting to one side, which creates an asymmetry in the submerged surface area of the shell. This, combined with the eccentric torque generated by the pendulum, causes uneven hydrodynamic forces on either side of the sphere, resulting in a pivot-like rotation with essentially zero turning radius.
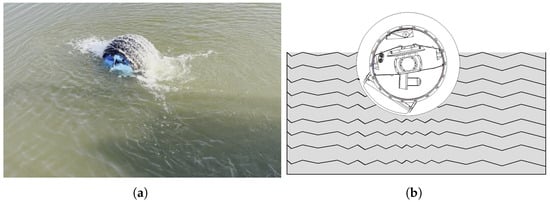
Figure 9.
Surface motion of the water ball robot under the pendulum propulsion system. (a) Photograph. (b) Schematic Diagram (Source: own elaboration).
5. Controller Design
In Section 3, we established the kinematic and dynamic models of the amphibious spherical robot, and performed preliminary model preprocessing. In this section, we will design controllers for the amphibious spherical robot based on the established dynamic model. Regarding the four unknown disturbance terms in the model, and , current research mainly addresses them in two ways. The first approach is to directly ignore these terms, since their effects are relatively small during normal motion in still water; thus, many scholars have neglected them [34,35,36]. Another approach is to design adaptive methods to compensate for these four terms [27,37,38]. Sliding mode control, known for its strong robustness against disturbances and time delays, has been widely used in water-surface motion control of USVs [27,32,35,36]. Therefore, this work implements both approaches for the design of sliding mode controllers and provides a comparative simulation analysis of their performance. Prior to controller design, several assumptions are made to ensure the validity of the control strategy:
- Assumption 1: The disturbances and are bounded but unknown.
- Assumption 2: The ASR-DPS is modeled as a rigid body with symmetric geometry about both the longitudinal and lateral axes.
- Assumption 3: During controller design, the pendulum propulsion system is considered locked and inactive; thus, the center of mass of the ASR remains fixed.
- Assumption 4: The body-fixed coordinate system is established at the center of mass.
The primary control objective is to ensure that the surge velocity and the yaw rate accurately track their respective desired values and . Mathematically, this can be expressed as:
The control system also aims to ensure the global asymptotic stability of the closed-loop tracking errors.
5.1. Sliding Mode Controller with Neglected Uncertainties and Disturbances (SMC-NUD)
When the robot operates at low speeds on calm, flat water, the model can be further simplified by omitting factors with negligible influence and disregarding environmental disturbances (i.e., ). The resulting simplified model is therefore given by:
Due to the weak coupling between the surge dynamics and the other degrees of freedom, the surge-direction dynamics can be decoupled from the overall model, yielding the following expression:
The sliding surface is defined as follows:
where the surge speed error is denoted as and stands the desired speed, parameter . The reaching law of the sliding mode controller is
By differentiating Equation (12), we can obtain
According to the transformation, we can obtain the surge speed sliding controller :
Similarly, a sliding mode controller for yaw rate can be obtained:
5.2. Adaptive Sliding Mode Controller(ASMC)
Note that in both SMC and ASMC, the sliding surface follows the same structure but is denoted differently for convenience. During the design of the adaptive sliding mode controller, we set the sliding surface as
Adaptive convergence laws can be designed based on the literature [26,27].
where denotes the self-adaptive gain coefficient, while signifies the constant gain coefficient. The specific self-adaptive gain coefficient is illustrated below:
where the adjustment of enables the establishment of a work range for a specific model, designated as . This is accomplished by employing the tanh continuous law, which facilitates the realization of through the implementation of the double-sided curve at the specified boundary value, denoted as . This process ensures a seamless transition at the specified boundary value, .
After substituting into the dynamic Equation (8) and simplifying, the adaptive surge speed sliding mode controller can be obtained as
The same method can lead to the adaptive sliding mode control law for yaw rate as follows:
5.3. Stability Analysis of Controller
5.3.1. Stability Analysis of SMC-NUD
To analyze the stability of the surge tracking controller, we define the sliding surface:
We choose the following Lyapunov candidate function:
which is positive definite. Differentiating along the system trajectory:
Since for all , the sliding surface asymptotically, ensuring that the tracking error . Hence, the closed-loop surge subsystem is globally asymptotically stable under the proposed control law.
A similar Lyapunov-based stability proof can be derived for the yaw-direction controller , using an equivalent sliding surface and the same reaching law. The analysis leads to a negative definite derivative of the Lyapunov function, thereby ensuring global asymptotic stability of the yaw tracking dynamics.
5.3.2. Stability Analysis of ASMC
To analyze the closed-loop stability of the adaptive sliding mode controller in the presence of bounded disturbances, we consider the surge tracking error dynamics derived as:
where , and is a bounded external disturbance satisfying:
We construct the following Lyapunov candidate function:
Differentiating V with respect to time:
Using the inequality , we obtain:
To ensure , a sufficient condition is:
That is,
This implies that the adaptive gain must increase proportionally to dominate the disturbance. Since is governed by the continuous update law:
it can grow automatically when tracking errors rise, thus guaranteeing closed-loop stability even under bounded disturbances. This shows the robustness of the proposed ASMC scheme.
Similarly, for the yaw-direction controller , the same structure and Lyapunov-based stability analysis apply. By defining a corresponding sliding surface and considering the bounded disturbance in yaw dynamics, the same conclusion on asymptotic stability and robustness can be drawn.
5.4. Simulation Results of the SMC-NUD
As shown in Figure 10, during surge speed tracking, the actual velocity exhibits minor fluctuations around the desired value. In contrast, the yaw angle tracking performance is excellent, with the actual trajectory closely matching the desired trajectory. Notably, while the yaw rate tracking curve generally coincides with its desired counterpart, two distinct transient spikes appear in the yaw rate response during abrupt reversals in turning direction (e.g., switching instantly from clockwise to counterclockwise, corresponding to sign changes in the torque command from positive to negative or vice versa). Concurrently, the torque command also undergoes abrupt step changes. Analysis of the control inputs and reveals a significant reduction in chattering. This demonstrates that the designed SMC-NUD performs robustly and effectively mitigates the inherent chattering issue associated with sliding mode control method.
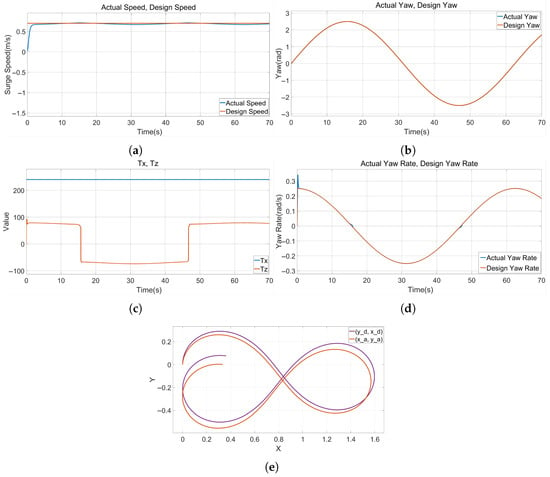
Figure 10.
Simulation results of the SMC−NUD. (a) Surge speed. (b) Yaw angle. (c) Yaw rate. (d) Control inputs. (e) Trajectory tracking.
5.5. Simulation Results of the ASMC
As illustrated in the Figure 11, the tracking performance for surge speed, yaw angle, and yaw rate is consistently excellent, with both the desired and actual trajectories exhibiting close agreement. Concurrently, the control inputs and remain smooth, exhibiting significantly reduced chattering. Notably, the simulation results for the adaptive sliding mode control approach show no recurrence of the transient spikes in the yaw rate response. This indicates that the ASMC effectively handles transient yaw maneuvers without inducing abrupt changes in the torque command. Furthermore, a comparison of the trajectory tracking performance clearly demonstrates superior accuracy under ASMC compared to the SMC-NUD scheme. These results collectively validate the enhanced overall control performance achieved by ASMC.
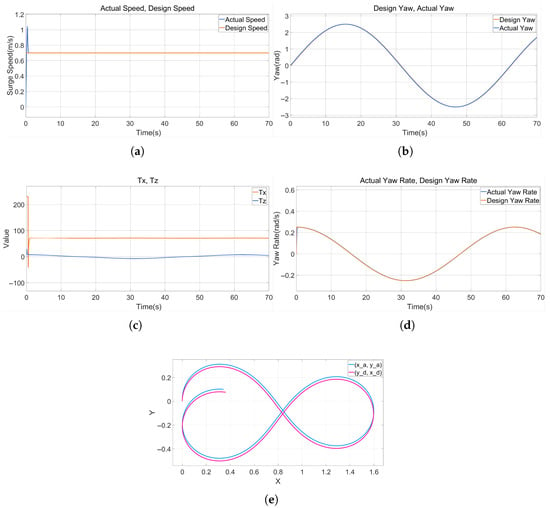
Figure 11.
Simulation results of the ASMC. (a) Surge speed. (b) Yaw angle. (c) Yaw rate. (d) Control inputs. (e) Trajectory tracking.
6. Discussion and Conclusions
Compared to the amphibious spherical robots reported in the literature, the proposed ASR-DPS demonstrates several distinctive features and advantages.
Firstly, in terms of size, most existing amphibious spherical robots are considerably smaller. For instance, Guo’s [7] team developed a robot with a diameter of 250 mm, Zhan’s [11] design measures 350 mm, and Sun’s [12] design is 400 mm in diameter. A smaller size limits the integration of multiple sensors or actuators, reducing adaptability in complex environments. By contrast, ASR-DPS provides sufficient internal volume for additional functional modules, enabling enhanced perception and control capabilities. Secondly, as shown in Table 7, ASR-DPS outperforms other designs in terms of endurance and speed. While most reported robots exhibit relatively low speeds suitable only for still water conditions, ASR-DPS achieves higher locomotion efficiency, thereby improving operational effectiveness in mildly dynamic aquatic environments. Weight is another critical factor. Robots that are too light suffer from low resistance to external disturbances, whereas excessive weight results in significantly higher energy consumption. For example, Bong-Huan Jun’s [1] robot is extremely heavy, limiting its endurance, while ASR-DPS maintains an optimized weight-to-size ratio that balances stability and energy efficiency. These characteristics collectively highlight the superior environmental adaptability of ASR-DPS for short-range amphibious missions.

Table 7.
Comparison of amphibious spherical robots (Source: own elaboration).
Despite these advantages, the study also reveals technical limitations. Hydrodynamic evaluations based on naval architecture principles and CFD simulations identified distinct flow separation patterns, vortex shedding, and elevated wave resistance, which collectively contribute to increased drag during surface motion. Experimental results further indicate roll instability under high-torque conditions, often leading to capsizing in extreme cases. Additionally, while the pendulum propulsion system is energy-efficient, it produces insufficient thrust for high-speed aquatic motion, making it unsuitable for large-wave or velocity-critical scenarios. These limitations underscore the need for structural optimization and advanced stability enhancement strategies.
To address control challenges under dynamic uncertainties and environmental disturbances, two control strategies were introduced: model simplification and adaptive sliding mode control (ASMC). Simulation results confirmed that ASMC achieves accurate surge speed tracking, robust yaw regulation, and chatter-free torque output, demonstrating its feasibility for hydrodynamic stabilization of unconventional amphibious platforms. However, these strategies were validated only in simulation, and real-world experimental verification remains an essential future step.
From a theoretical perspective, this study contributes to the field of multi-modal locomotion by integrating internal and external propulsion systems under a unified dynamic control framework, while practically enabling compact, energy-efficient amphibious operations such as near-shore environmental monitoring, shallow-water sampling, and transition-zone exploration in lakes and marshlands.
Future work will focus on enhancing mechanical stability, potentially through gyroscopic stabilization mechanisms, passive hydrodynamic fins, or internal mass redistribution strategies. In addition, further refinement of hybrid propulsion coordination using energy-aware control logic, real-time wave prediction integration, and improvements in waterproofing and buoyancy control are planned. Finally, extensive field trials under diverse environmental conditions will be conducted to validate system robustness and long-term operational reliability.
Author Contributions
Conceptualization, Y.W., H.Z. and G.L.; methodology, Y.W. and H.Z.; software, F.Z., M.W. and H.Z.; validation, F.Z., M.W. and H.Z.; data curation, H.Z.; writing—original draft preparation, H.Z.; writing—review and editing, Y.W. and H.Z.; funding acquisition, Y.W. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the State Key Laboratory of Industrial Control Technology, China (Grant No. ICT2024A21) and the Rotunbot (Hangzhou) Technology Co., Ltd. fund.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
Author Meng Wang was employed by the company Rotunbot (Hangzhou) Technology Co., Ltd., Hangzhou. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASR-DPS | Amphibious Spherical Robot equipped with a Dual-Propulsion System |
| CFD | Computational Fluid Dynamics |
| USVs | Unmanned Surface Vehicles |
| SMC-NUD | Sliding Mode Controller with Neglected Uncertainties and Disturbance |
| ASMC | Adaptive Sliding Mode controller |
References
- Jun, B.-H.; Shim, H.; Kim, B.; Park, J.-Y.; Baek, H.; Yoo, S.; Lee, P.-M. Development of seabed walking robot CR200. In Proceedings of the 2013 MTS/IEEE OCEANS—Bergen, Bergen, Norway, 10–14 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Dhull, S.; Canelon, D.; Kottas, A.; Dancs, J.; Carlson, A.; Papanikolopoulos, N. Aquapod: A small amphibious robot with sampling capabilities. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 100–105. [Google Scholar]
- Bernstein, C.; Connolly, M.; Gavrilash, M.; Kucik, D.; Threatt, S. Demonstration of surf zone crawlers: Results from auv fest 01. In Proceedings of the International Symposium on Technology and Mine Problem (5th), Monterey, CA, USA, 22–25 April 2002. [Google Scholar]
- Prahacs, C.; Saudners, A.; Smith, M.K.; McMordie, D.; Buehler, M. Towards legged amphibious mobile robotics. In Proceedings of the Canadian Design Engineering Network Conference, Montreal, QC, Canada, 29–30 July 2004. [Google Scholar]
- Harkins, R.; Ward, J.; Vaidyanathan, R.; Boxerbaum, A.; Quinn, R.D. Design of an autonomous amphibious robot for surf zone operations: Part II—Hardware, control implementation and simulation. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; IEEE: Piscataway, NJ, USA, 2015; pp. 1465–1470. [Google Scholar]
- Boxerbaum, A.S.; Werk, P.; Quinn, R.D.; Vaidyanathan, R. Design of an autonomous amphibious robot for surf zone operation: Part I—Mechanical design for multi-mode mobility. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Li, M.; Guo, S.; Hirata, H.; Ishihara, H. Design and performance evaluation of an amphibious spherical robot. Robot. Auton. Syst. 2015, 64, 21–34. [Google Scholar] [CrossRef]
- Guo, S.; Mao, S.; Shi, L.; Li, M. Design and kinematic analysis of an amphibious spherical robot. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2214–2219. [Google Scholar]
- Xing, H.; Shi, L.; Hou, X.; Liu, Y.; Hu, Y.; Xia, D.; Li, Z.; Guo, S. Design, modeling and control of a miniature bio-inspired amphibious spherical robot. Mechatronics 2021, 77, 102574. [Google Scholar] [CrossRef]
- Xing, H.; Guo, S.; Shi, L.; He, Y.; Su, S.; Chen, Z.; Hou, X. Hybrid locomotion evaluation for a novel amphibious spherical robot. Appl. Sci. 2018, 8, 156. [Google Scholar] [CrossRef]
- Chi, X.; Zhan, Q. Design and modelling of an amphibious spherical robot attached with assistant fins. Appl. Sci. 2021, 11, 3739. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Sun, H.; Liu, Z.; Zhang, Y. A novel amphibious spherical robot equipped with flywheel, pendulum, and propeller. J. Intell. Robot. Syst. 2018, 89, 485–501. [Google Scholar] [CrossRef]
- Jia, L.; Hu, Z.; Geng, L.; Yang, Y.; Wang, C. The concept design of a mobile amphibious spherical robot for underwater operation. In Proceedings of the 2016 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Chengdu, China, 19–22 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 411–415. [Google Scholar]
- Arif, M.A.; Zhu, A.; Mao, H.; Zhou, X.; Song, J.; Tu, Y.; Ma, P. Design of an amphibious spherical robot driven by twin eccentric pendulums with flywheel-based inertial stabilization. ISA Trans. 2023, 28, 2690–2702. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, B.; Wu, Z.G.; Xie, S.; Peng, Y. Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6691–6700. [Google Scholar] [CrossRef]
- Gurumurthy, G.; Das, D.K. Terminal sliding mode disturbance observer based adaptive super twisting sliding mode controller design for a class of nonlinear systems. Eur. J. Control 2021, 57, 232–241. [Google Scholar] [CrossRef]
- Liu, C.; Wang, D.; Zhang, Y.; Meng, X. Model predictive control for path following and roll stabilization of marine vessels based on neurodynamic optimization. Ocean. Eng. 2020, 217, 107524. [Google Scholar] [CrossRef]
- Jeon, M.; Yoon, H.K.; Park, J.; Rhee, S.H.; Seo, J. Identification of 4-DoF maneuvering mathematical models for a combatant in intact and damaged conditions. Int. J. Nav. Archit. Ocean. Eng. 2022, 14, 100480. [Google Scholar] [CrossRef]
- Li, J.; Zhu, G.; Lu, J.; Chen, C. FTILOS-based self-triggered adaptive neural path following control for 4DOF underactuated unmanned surface vehicles. Ocean. Eng. 2024, 295, 116947. [Google Scholar] [CrossRef]
- Zou, H.; Wang, M.; Zhang, F.; Guan, X.; Liu, Y.; Wang, Y.; Luo, Z.; Li, G. Design of an amphibious spherical robot with roll auto-stabilisation and propulsion system auto-switching. Ships Offshore Struct. 2025, 1–13. [Google Scholar] [CrossRef]
- Zou, H.; Lin, B.; Cao, X.; Zhang, F.; Zhang, Z.; Wang, Y. Research on Amphibious Spherical Robot with Water Surface Posture Self-Stabilization. In Proceedings of the 2023 China Automation Congress, Chongqing, China, 17–19 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 6183–6187. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R.; Capecelatro, J. Fluid Mechanics; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Zou, H.; Hu, D.; Zhang, B.; Wang, Y.; Li, G. Analysis and Evaluation of a Multi-Modal Propulsion System for Aquatic Locomotion in Amphibious Spherical Robots. SSRN Electron. J. 2024, 5166970. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. STAR-CCM+ Marine Resistance Prediction for KCS Hull with Rudder. STAR-CCM+ Case Study. 2023. Available online: https://docs.sw.siemens.com/documentation/external/PL20221128664127487/en-US/userManual/starccmp_userguide_html/STARCCMP/GUID-79564ACE-BD7B-4F18-929F-DA6B92A2AE1F.html (accessed on 6 August 2025).
- Khan, O.U.; Riaz, Z.; Mansoor, A.; Zai, B.A.; us Saqib, N. Numerical Estimation and Validation of Drag Force for KCS Hull using STAR CCM+. J. Marit. Res. 2023, 20, 46–50. [Google Scholar]
- IMO. Standards for Ship Manoeuvrability; Resolution MSC.137(76); International Maritime Organization: London, UK, 2002; Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/MSCResolutions/MSC.137(76).pdf (accessed on 6 August 2025).
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Gonzalez-Garcia, A.; Castañeda, H. Guidance and control based on adaptive sliding mode strategy for a USV subject to uncertainties. Int. J. Offshore Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Klinger, W.B.; Bertaska, I.R.; von Ellenrieder, K.D.; Dhanak, M.R. Control of an unmanned surface vehicle with uncertain displacement and drag. Int. J. Offshore Eng. 2016, 42, 458–476. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge at the University Press: London, UK, 1945. [Google Scholar]
- Marquardt, J.G.; Alvarez, J.; von Ellenrieder, K.D. Characterization and system identification of an unmanned amphibious tracked vehicle. Int. J. Offshore Eng. 2013, 39, 641–661. [Google Scholar] [CrossRef]
- Woo, J.; Park, J.; Yu, C.; Kim, N. Dynamic model identification of unmanned surface vehicles using deep learning network. Appl. Ocean Res. 2018, 78, 123–133. [Google Scholar] [CrossRef]
- Gokarn, R. Ship Manoeuvring Standards and Guidelines. In A Study of Ship Manoeuvrability; Springer: Cham, Switzerland, 2024; pp. 199–205. [Google Scholar]
- Liao, Y.; Pang, Y.; Wan, L. Combined speed and yaw control of underactuated unmanned surface vehicles. In Proceedings of the 2010 2nd International Asia Conference on Informatics in Control, Automation and Robotics, Wuhan, China, 6–7 March 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 157–161. [Google Scholar]
- Khooban, M.H.; Vafam, N.; Dragičević, T.; Blaabjerg, F. Polynomial fuzzy model-based approach for underactuated surface vessels. IET Control Theory Appl. 2018, 12, 914–921. [Google Scholar] [CrossRef]
- Ghommam, J.; Mnif, F.; Benali, A.; Derbel, N. Asymptotic backstepping stabilization of an underactuated surface vessel. IEEE Trans. Control Syst. Technol. 2006, 14, 1150–1157. [Google Scholar] [CrossRef]
- Castañeda, H.; Rodriguez, J.; Gordillo, J.L. Continuous and smooth differentiator based on adaptive sliding mode control for a quad-rotor MAV. Asian J. Control 2021, 23, 661–672. [Google Scholar] [CrossRef]
- Cantu, R.; Castañeda, H. Smooth differentiator based on adaptive sliding mode control for a quadrotor Micro Air Vehicle. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems, Dallas, TX, USA, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1150–1156. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).