A Novel Hyperbolic Unsaturated Bistable Stochastic Resonance System and Its Application in Weak Signal Detection
Abstract
1. Introduction
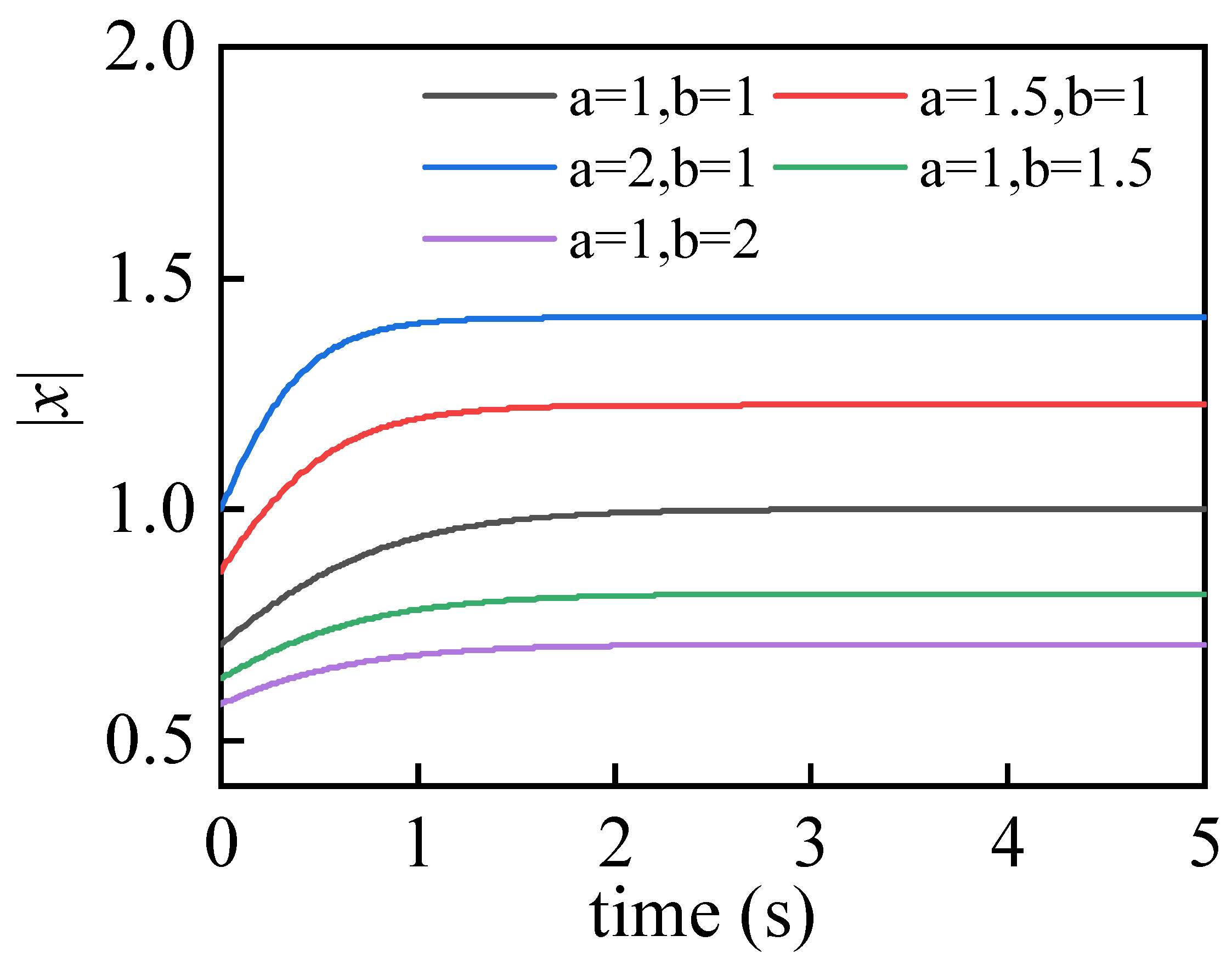
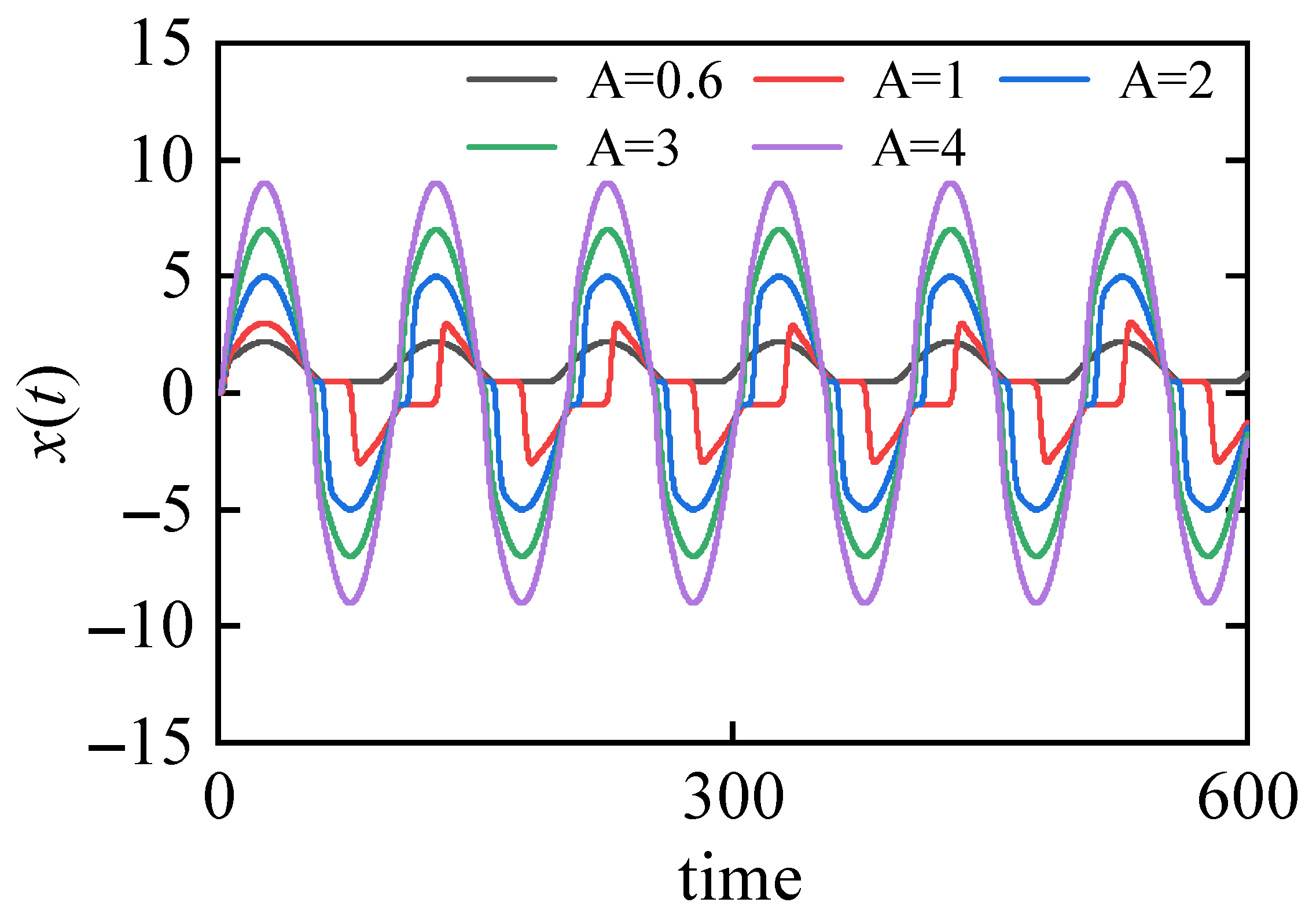
2. The Output Saturation of the CBSR
3. The Analysis of the Proposed UDHQSR System
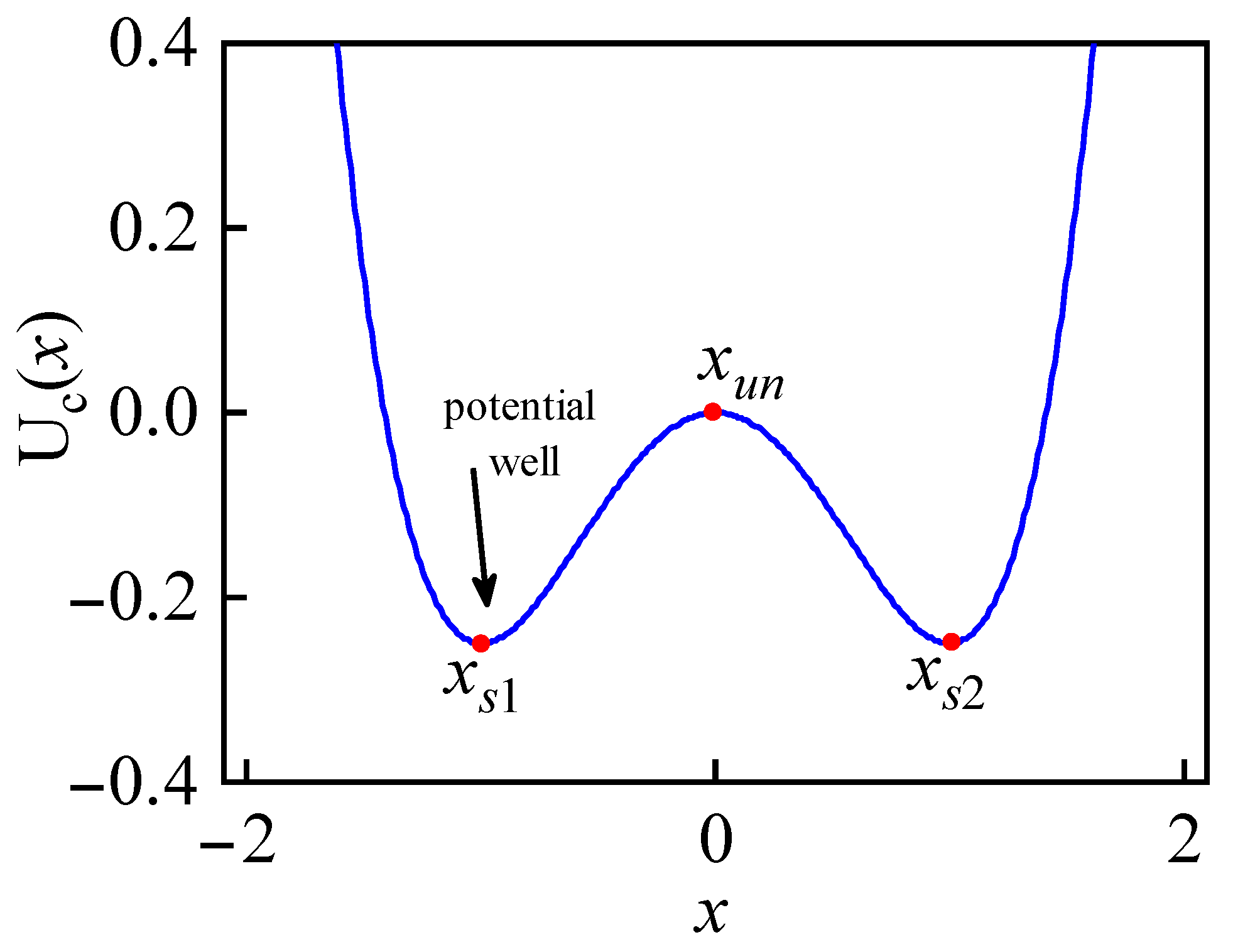
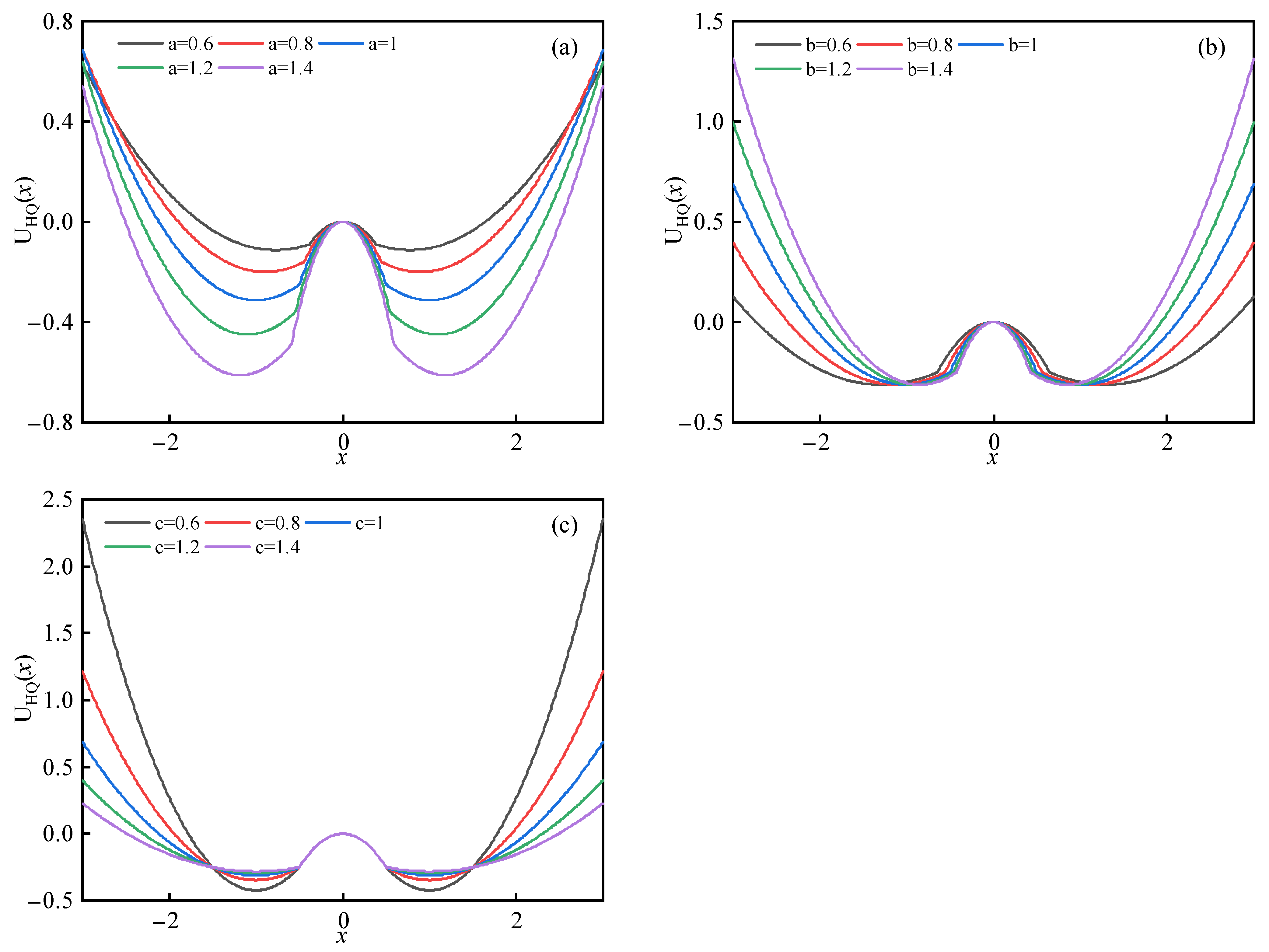
3.1. The Unsaturated Piecewise Bistable Potential Function
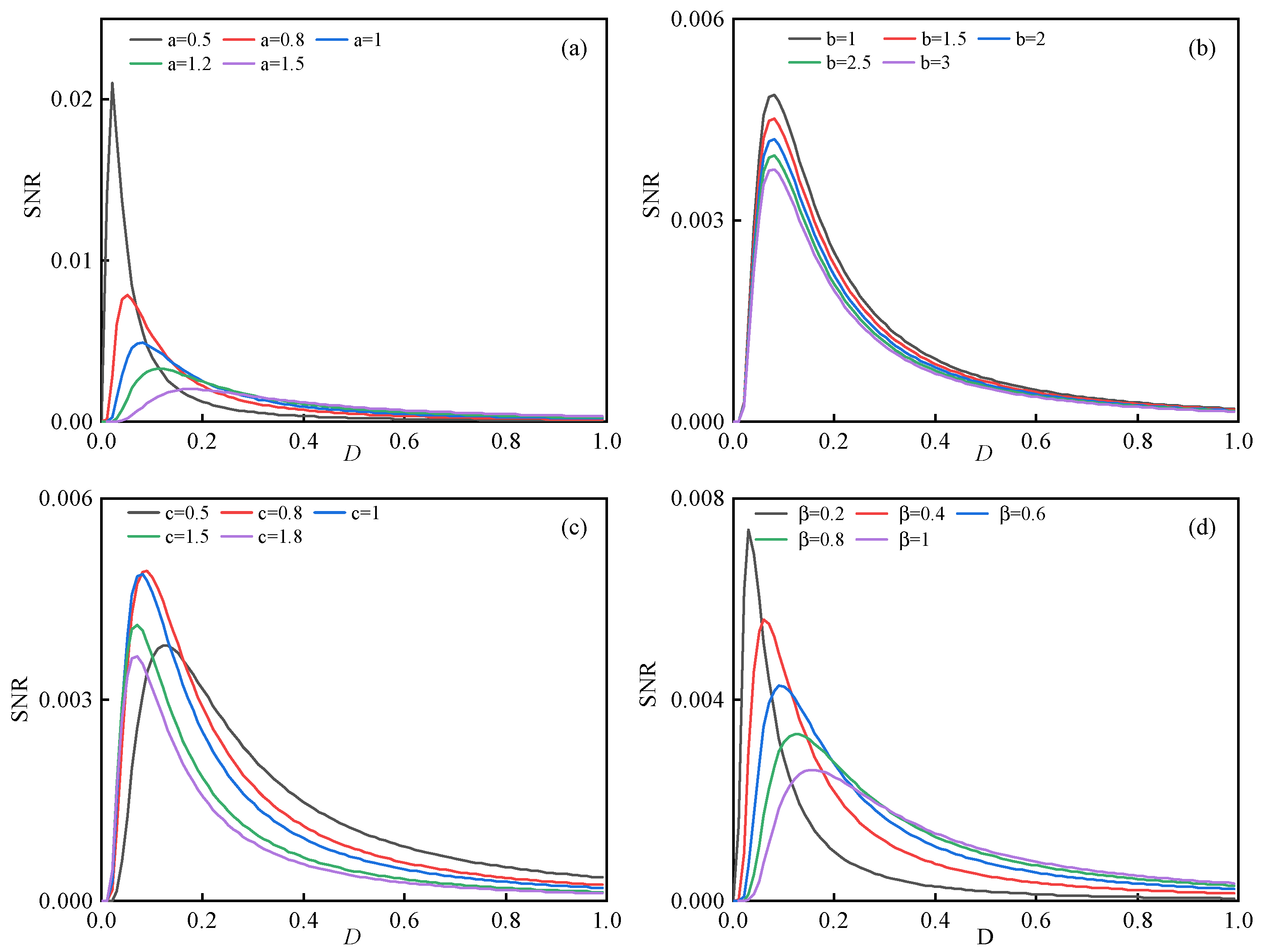
3.2. Derivation of the Theoretical Output SNR
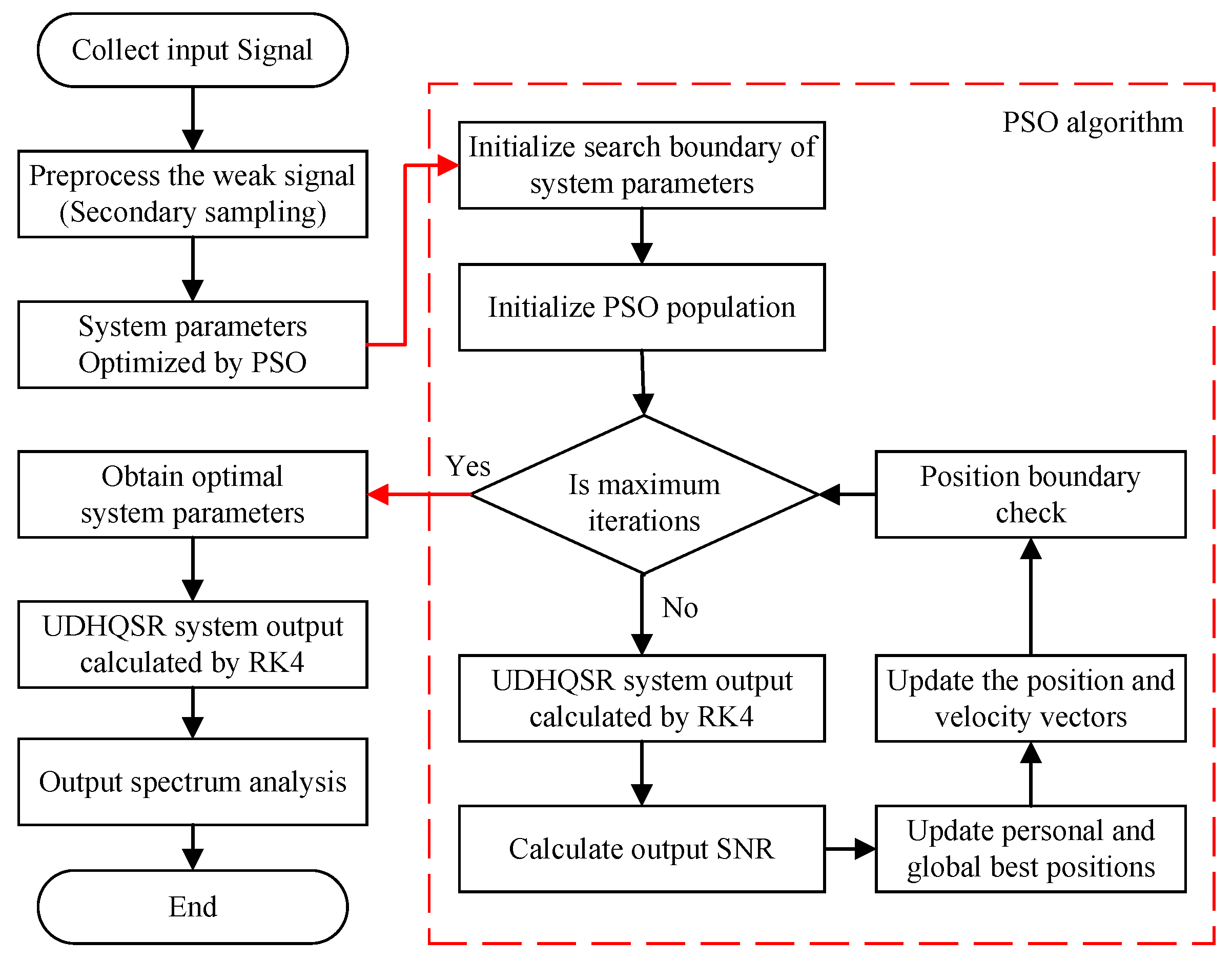
4. Weak Signal Detection Algorithm Based on the UDHQSR System
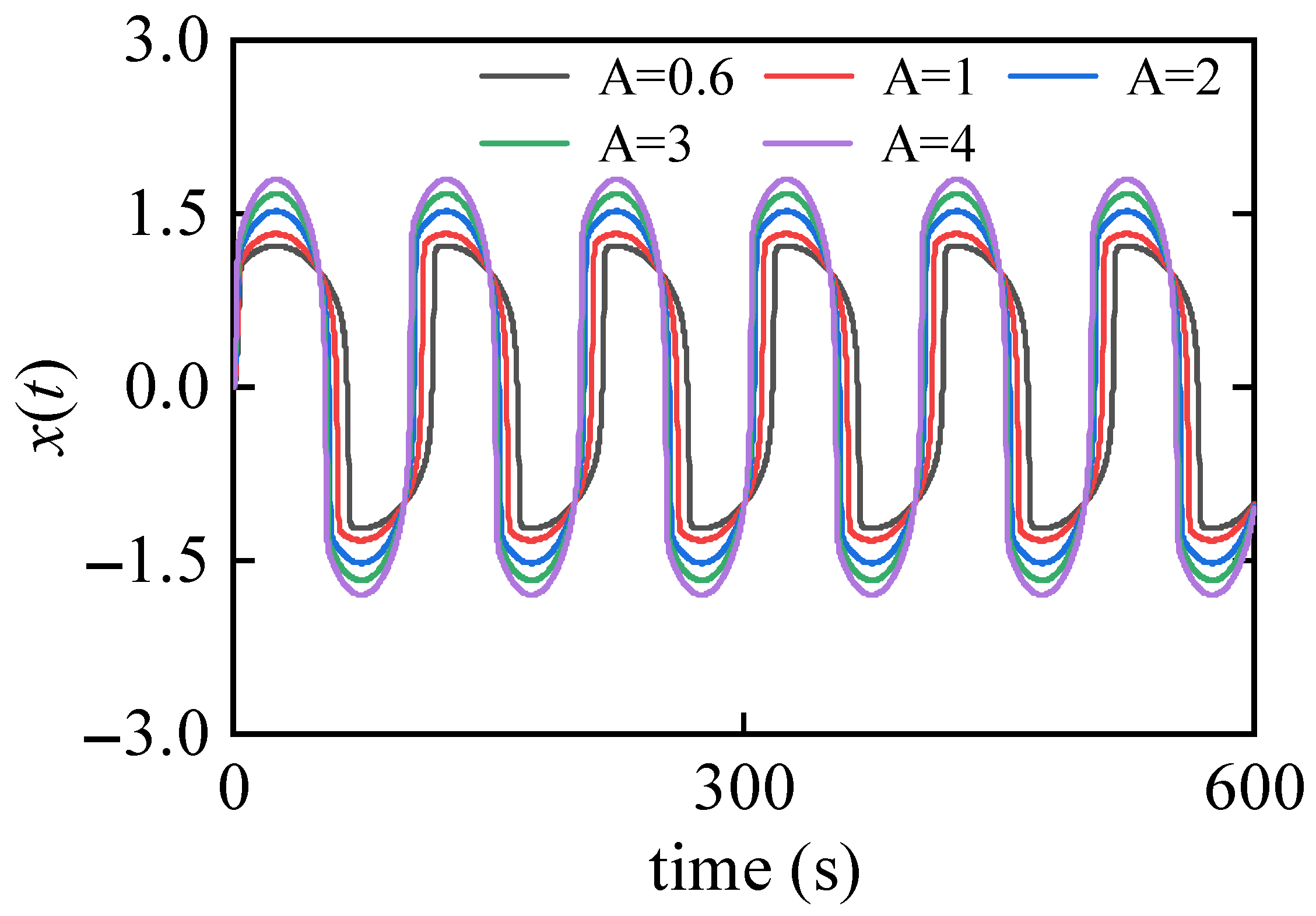
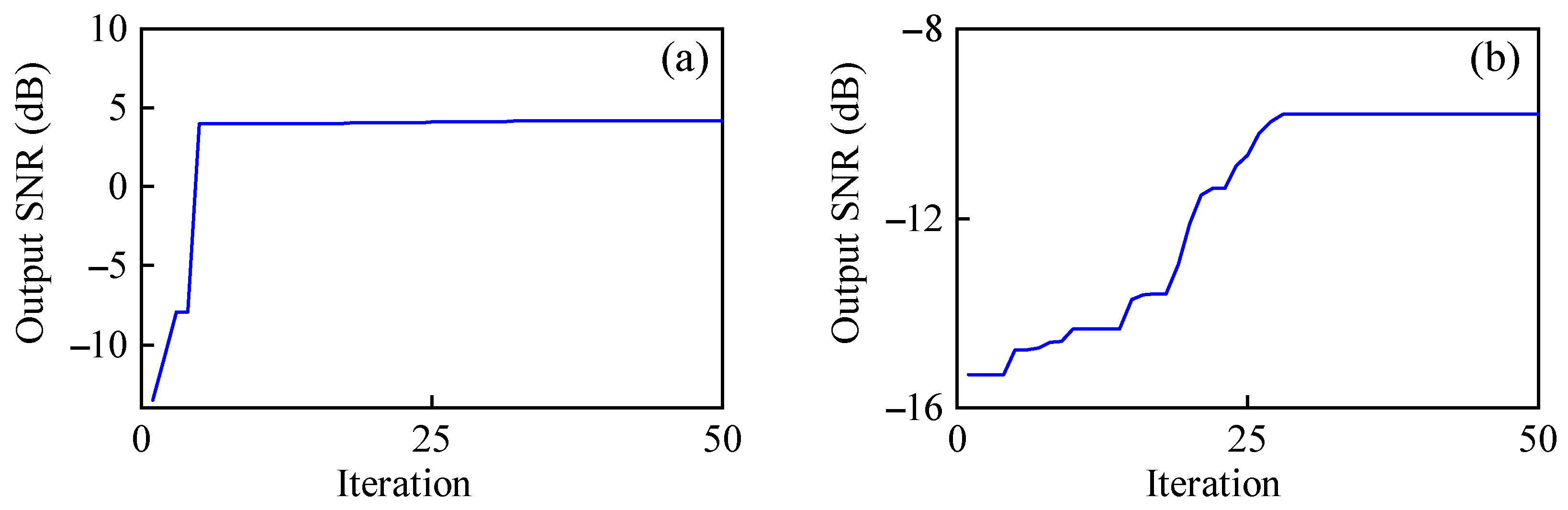
5. Simulation Verification
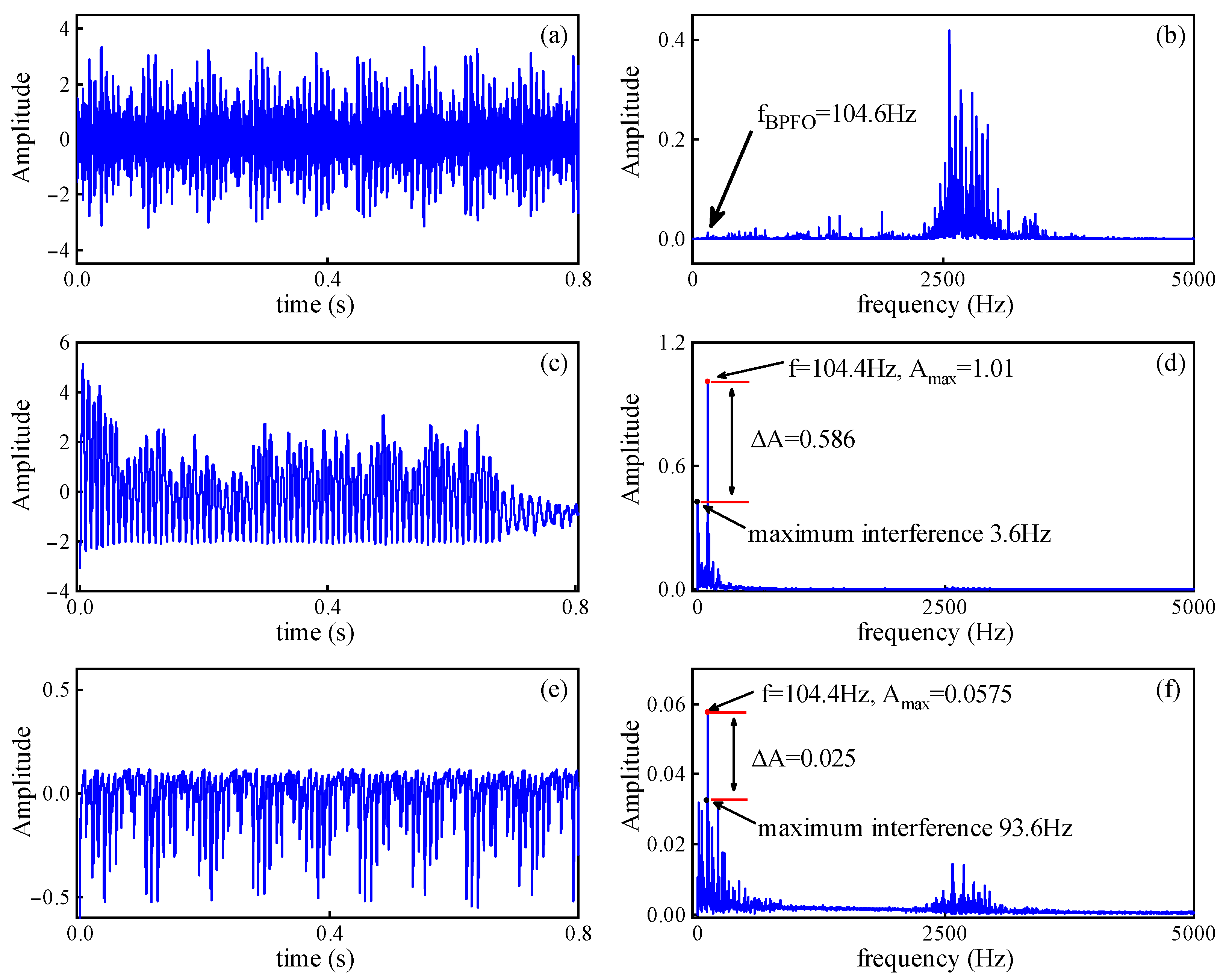
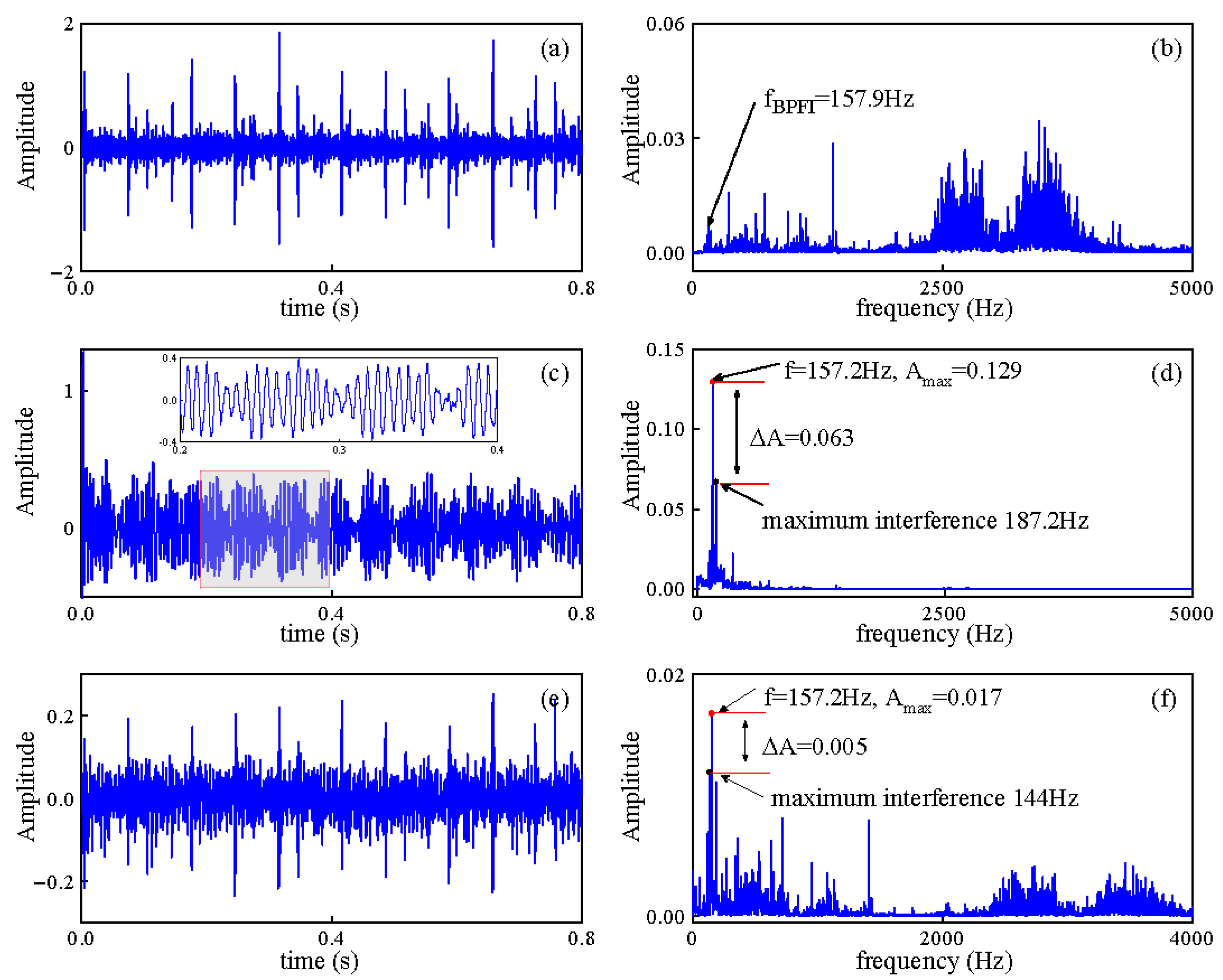
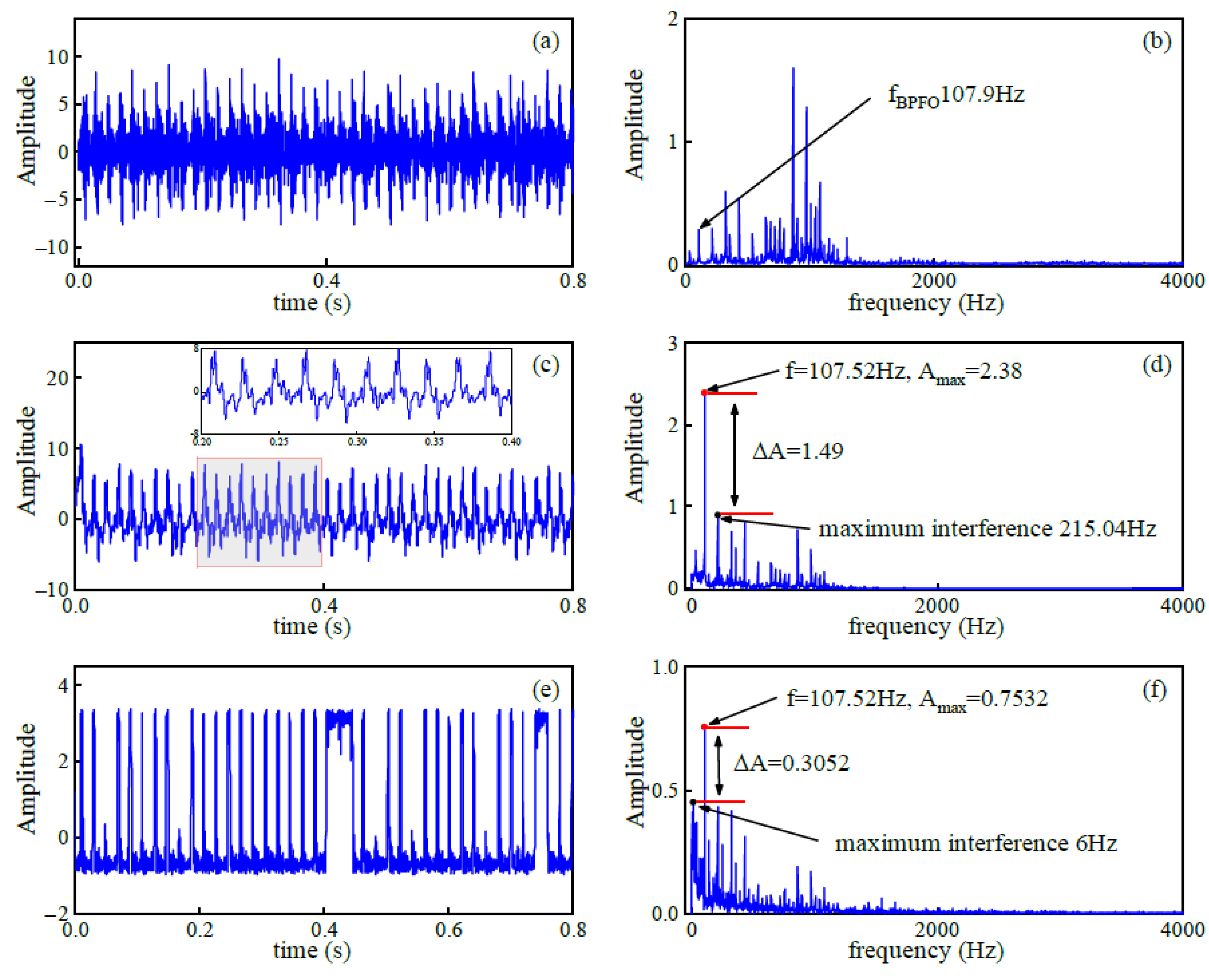
6. Bearing Fault Signal Verification
6.1. Fault Diagnosis Verification via the CWRU Dataset
6.2. Fault Diagnosis Verification via the XJTU-SY Dataset
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, Y.; Piao, S.; Guo, J. Line Spectrum Detection and Motion Parameters Estimation for Underwater Moving Target. J. Phys. Conf. Ser. 2024, 2718, 012090. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, G.; Du, C.; Wu, Y.; Zheng, X.; Zhang, S.; Han, C.; Liang, R.; Chen, R. Weak Feature Extraction and Strong Noise Suppression for SSVEP-EEG Based on Chaotic Detection Technology. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 862–871. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Ding, W.; Zhang, B.; Liu, C.; Han, J.; Doermann, D. Learning Modulation Filter Networks for Weak Signal Detection in Noise. Pattern Recognit. 2021, 109, 107590. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Pan, Z.; Wang, G. A Novel Stochastic Resonance Based Deep Residual Network for Fault Diagnosis of Rolling Bearing System. ISA Trans. 2024, 148, 279–284. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Tang, C.; Hu, B.; Guo, J.; Qiao, Z.; Liao, Z. A Novel Exponential Unsaturated Bistable Stochastic Resonance-Boosted Incipient Fault Identification in Rotating Machineries. Meas. Sci. Technol. 2024, 35, 116140. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, X.; Jiang, Z. Research and Application of a Novel Combined Asymmetric Tristable Stochastic Resonance System. Fluct. Noise Lett. 2022, 21, 2250050. [Google Scholar] [CrossRef]
- Benzi, R.; Parisi, G.; Sutera, A.; Vulpiani, A. Stochastic Resonance in Climatic Change. Tellus 1982, 34, 10–16. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Li, J.; Meng, Z. Stochastic Resonance in an Underdamped Duffing Bistable System Embedded with Overdamped Feedback Control for Rolling Bearing Fault Detection. Meas. Sci. Technol. 2025, 36, 036128. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, X.; Wang, B.; Cheng, X. Bearing Fault Feature Extraction Method: Stochastic Resonance-Based Negative Entropy of Square Envelope Spectrum. Meas. Sci. Technol. 2024, 35, 045102. [Google Scholar] [CrossRef]
- Ma, Q.; Cao, S.; Gong, T.; Yang, J. Stochastic Resonance in Strong Poisson White Noise Excited System and Its Application in Multi-Features Identification. Pramana 2024, 98, 41. [Google Scholar] [CrossRef]
- Shi, P.; Li, M.; Zhang, W.; Han, D. Weak Signal Enhancement for Machinery Fault Diagnosis Based on a Novel Adaptive Multi-Parameter Unsaturated Stochastic Resonance. Appl. Acoust. 2022, 189, 108609. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, S.; Yang, H.; Liu, H.; Song, N.; Li, Q. Adaptive Two-Dimensional Coupled Bistable Stochastic Resonance and Its Application in Bearing Fault Diagnosis. Chaos Solitons Fractals 2025, 194, 116245. [Google Scholar] [CrossRef]
- Yang, C.; Yang, J.; Zhou, D.; Zhang, S.; Litak, G. Adaptive Stochastic Resonance in Bistable System Driven by Noisy NLFM Signal: Phenomenon and Application. Philos. Trans. R. Soc. A 2021, 379, 20200239. [Google Scholar] [CrossRef]
- Gong, S.; Li, S.; Wang, H.; Ma, H.; Yu, T. Multi-Frequency Weak Signal Detection Based on Wavelet Transform and Parameter Selection of Bistable Stochastic Resonance Model. J. Vib. Eng. Technol. 2021, 9, 887–906. [Google Scholar] [CrossRef]
- Zhao, D.; Luo, M. A Novel Weak Signal Detection Method for Linear Frequency Modulation Signal Based on Bistable System and Fractional Fourier Transform. Optik 2016, 127, 4405–4412. [Google Scholar] [CrossRef]
- Cheng, W.; Xu, X.; Ding, Y.; Sun, K.; Li, Q.; Dong, L. An Adaptive Smooth Unsaturated Bistable Stochastic Resonance System and Its Application in Rolling Bearing Fault Diagnosis. Chin. J. Phys. 2020, 65, 629–641. [Google Scholar] [CrossRef]
- Che, L.; Ao, K.; Jiang, L. AEEFCSR: An Adaptive Ensemble Empirical Feed-Forward Cascade Stochastic Resonance System for Weak Signal Detection. Meas. Sci. Technol. 2024, 35, 126108. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Han, S.; Wang, J.; Ren, X. Fault Diagnosis Method and Application Based on Unsaturated Piecewise Linear Stochastic Resonance. Rev. Sci. Instruments 2019, 90, 065112. [Google Scholar] [CrossRef] [PubMed]
- Xia, P.; Xu, H.; Lei, M.; Zhang, S. An Improved Underdamped Asymmetric Bistable Stochastic Resonance Method and Its Application for Spindle Bearing Fault Diagnosis. IEEE Access 2020, 8, 46824–46836. [Google Scholar] [CrossRef]
- Zhang, G.; Tan, C.; He, L. Piecewise Unsaturated Under-Damped Tri-Stable Stochastic Resonance System and Its Application in Bearing Fault Diagnosis. J. Vib. Eng. Technol. 2021, 9, 1869–1884. [Google Scholar] [CrossRef]
- Cui, W.; Jiao, S.; Gao, R.; Zhang, Q.; Wang, C.; Li, Y.; Zhang, Y. Continuous Unsaturated Second-Order Hybrid Multi-Stable Stochastic Energy Resonance and Its Application in Rolling Bearing Fault Diagnosis. Appl. Acoust. 2025, 228, 110298. [Google Scholar] [CrossRef]
- Zhang, G.; Tan, C.; He, L. Piecewise Asymmetric Exponential Potential Under-Damped Bi-Stable Stochastic Resonance and Its Application in Bearing Fault Diagnosis. Mod. Phys. Lett. B 2021, 35, 2150280. [Google Scholar] [CrossRef]
- Li, Z.; Shi, B. An Adaptive Stochastic Resonance Method for Weak Fault Characteristic Extraction in Planetary Gearbox. J. Vibroeng. 2017, 19, 1782–1792. [Google Scholar] [CrossRef]
- Xu, P.; Jin, Y.; Zhang, Y. Stochastic Resonance in an Underdamped Triple-Well Potential System. Appl. Math. Comput. 2019, 346, 352–362. [Google Scholar] [CrossRef]
- Cui, L.; Yang, J.; Wang, L.; Liu, H.; Xiao, Y. An Adaptive Improved Unsaturated Bistable Stochastic Resonance Method Based on Weak Signal Detection. Int. J. Adapt. Control. Signal Process. 2021, 35, 2314–2327. [Google Scholar] [CrossRef]
- Casado-Pascual, J.; Gómez-Ordóñez, J.; Morillo, M. Stochastic Resonance: Theory and Numerics. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 026115. [Google Scholar] [CrossRef]
- Tang, J.; Shi, B. Asymmetric Second-Order Stochastic Resonance Weak Fault Feature Extraction Method. Meas. Control 2020, 53, 788–795. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the MHS’95 Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Du, Y.; Xu, F. A Hybrid Multi-Step Probability Selection Particle Swarm Optimization with Dynamic Chaotic Inertial Weight and Acceleration Coefficients for Numerical Function Optimization. Symmetry 2020, 12, 922. [Google Scholar] [CrossRef]
- Zhao, S.; Shi, P.; Han, D. A Novel Mechanical Fault Signal Feature Extraction Method Based on Unsaturated Piecewise Tri-Stable Stochastic Resonance. Measurement 2021, 168, 108374. [Google Scholar] [CrossRef]
- CWRU. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 2 November 2024).
- Wang, B.; Lei, Y.; Li, N.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]





| Description | Symbol | Value | |
|---|---|---|---|
| PSO settings | population size | M | 50 |
| iteration times | T | 50 | |
| self-learning factor | 1.2 | ||
| group-learning factor | 1.2 | ||
| inertial weight | |||
| UDHQSR parameter setting | a | a | |
| b | b | ||
| c | c | ||
| damping factor |
| Parameter | Value |
|---|---|
| Inner ring diameter | 25.001 mm |
| Outer ring diameter | 51.999 mm |
| Thickness | 15.001 mm |
| Rolling element diameter | 7.940 mm |
| Pitch diameter diameter | 39.04 mm |
| Number of bearing balls | 9 |
| Rotation speed | 1750 r/min |
| Sampling frequency | 12 kHz |
| Parameter | Value |
|---|---|
| Inner ring diameter | 29.30 mm |
| Outer ring diameter | 39.80 mm |
| Rolling element diameter | 7.92 mm |
| Pitch diameter | 34.55 mm |
| Number of bearing balls | 8 |
| Rotation speed | 2100 r/min |
| Sampling frequency | 25.6 kHz |
| Fault Type | Method | PDR | (dB) | ||
|---|---|---|---|---|---|
| CWRU Outer ring | UDHQSR system | 1.01 | 0.586 | 0.58 | −3.8 |
| CBSR system | 0.0575 | 0.025 | 0.435 | −8.82 | |
| ASUBSR system | 0.0387 | 0.021 | 0.543 | −7.8 | |
| CWRU Inner ring | UDHQSR system | 0.129 | 0.063 | 0.488 | −2.51 |
| CBSR system | 0.017 | 0.005 | 0.294 | −10.18 | |
| ASUBSR system | 0.021 | 0.0075 | 0.357 | −7.95 | |
| XJTU-SY Outer ring | UDHQSR system | 2.38 | 1.49 | 0.626 | −1.487 |
| CBSR system | 0.7532 | 0.3052 | 0.405 | −7.98 | |
| ASUBSR system | 0.355 | 0.207 | 0.583 | −5.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Y.; Wang, L.; Lu, Y.; Zhou, Z. A Novel Hyperbolic Unsaturated Bistable Stochastic Resonance System and Its Application in Weak Signal Detection. Appl. Sci. 2025, 15, 8970. https://doi.org/10.3390/app15168970
Wang Y, Li Y, Wang L, Lu Y, Zhou Z. A Novel Hyperbolic Unsaturated Bistable Stochastic Resonance System and Its Application in Weak Signal Detection. Applied Sciences. 2025; 15(16):8970. https://doi.org/10.3390/app15168970
Chicago/Turabian StyleWang, Yifan, Yao Li, Li Wang, Yiting Lu, and Zheng Zhou. 2025. "A Novel Hyperbolic Unsaturated Bistable Stochastic Resonance System and Its Application in Weak Signal Detection" Applied Sciences 15, no. 16: 8970. https://doi.org/10.3390/app15168970
APA StyleWang, Y., Li, Y., Wang, L., Lu, Y., & Zhou, Z. (2025). A Novel Hyperbolic Unsaturated Bistable Stochastic Resonance System and Its Application in Weak Signal Detection. Applied Sciences, 15(16), 8970. https://doi.org/10.3390/app15168970





