The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland
Abstract
1. Introduction
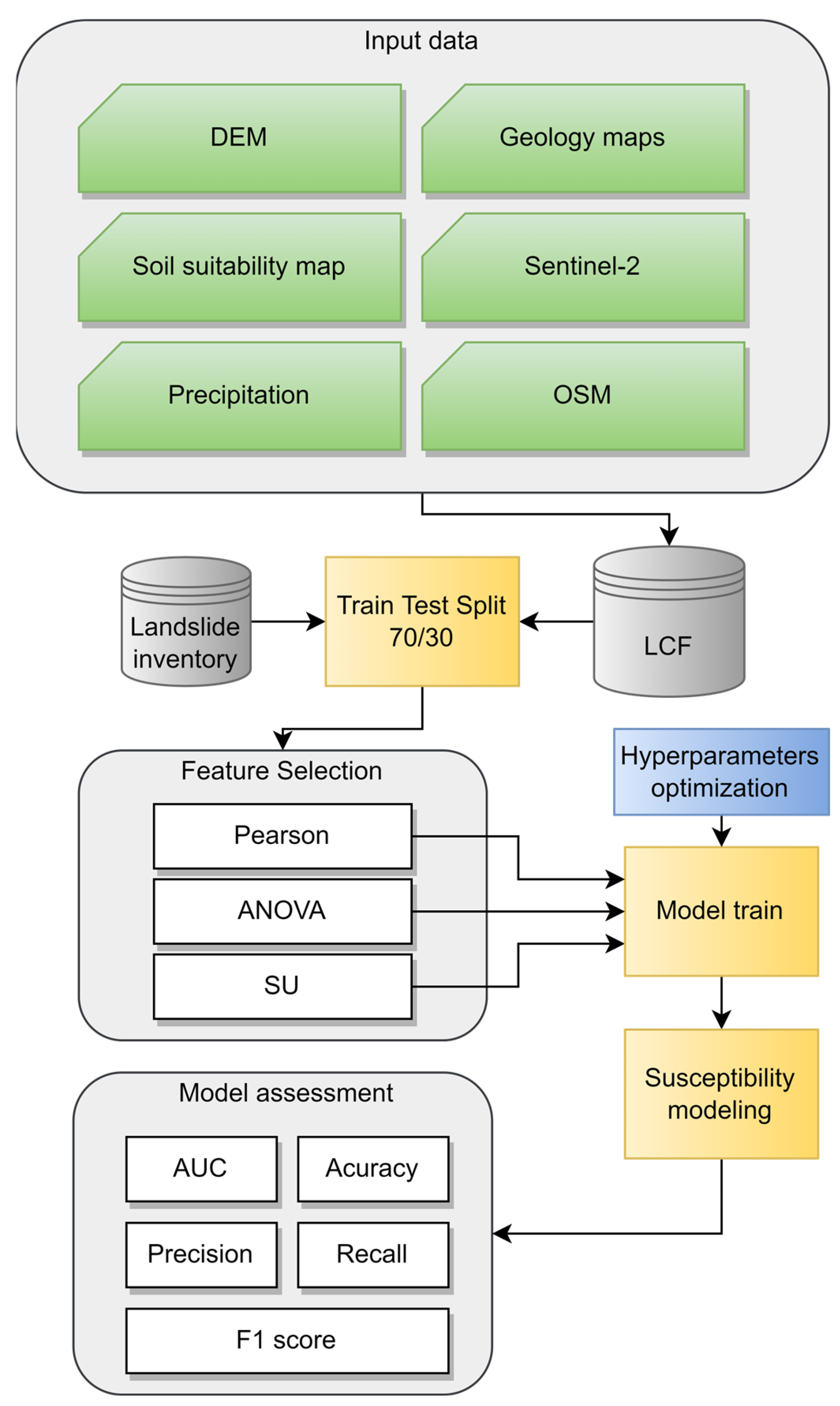
2. Materials and Methods
2.1. Case Studies
2.2. Input Data
2.3. Methodology
2.3.1. Generation of Landslide Conditioning Factors
| LCF | Method | Data | Data Source | Application Example | |
|---|---|---|---|---|---|
| 1. | DEM | - | DEM | ISOK data, https://www.geoportal.gov.pl (accessed on 8 August 2025) | [35,85] |
| 2. | Aspect | ArcGIS | [41,86,87] | ||
| 3. | Slope | ArcGIS | [86,88] | ||
| 4. | Flow direction | ArGIS | [12,75] | ||
| 5. | Curvature | ArcGIS | [3,41] | ||
| 6. | Plan curvature | ArcGIS | [10,86] | ||
| 7. | Profile curvature | ArcGIS | [86,87] | ||
| 8. | CTI | ArcGIS—Geomorphometry and Gradient Metrics | [10,12] | ||
| 9. | IMI | ArcGIS—Geomorphometry and Gradient Metrics | [12,89] | ||
| 10. | TPI | ArcGIS—Topography Toolbox | [33,34] | ||
| 11. | SEI | ArcGIS—Geomorphometry and Gradient Metrics | [12,75] | ||
| 12. | Stream proximity | Euclidean distance | [10,90] | ||
| 13. | Precipitation | IDW interpolation | Precipitation points | IMGW data https://danepubliczne.imgw.pl (accessed on 8 August 2025) | [13,35,91] |
| 14. | Tectonics | Vectorization | Geology maps | PGI data https://geolog.pgi.gov.pl (accessed on 8 August 2025) | [13,88] |
| 15. | Fault proximity | Euclidean distance | [92,93] | ||
| 16. | Thrust proximity | Euclidean distance | [12,64,94] | ||
| 17. | Roads proximity | Euclidean distance | Road network | OSM data | [95,96] |
| 18. | River proximity | Euclidean distance | River network | [13,88] | |
| 19. | Soil suitability | Vectorization | Soil suitability maps | MIIP data https://miip.geomalopolska.pl (accessed on 8 August 2025) | [12,95] |
| 20. | Soil texture | Vectorization | [12] | ||
| 21. | Soil type | Vectorization | [35,82] | ||
| 22. | NDVI | , NIR is near-infrared band and red is red band | Satellite image | Sentinel-2 | [33,93] |
| 23. | Land cover | Supervised classification | Sentinel-2 | [12,35] |
2.3.2. Feature Selection Methods
- Pearson correlation
- 1 indicates a perfect positive correlation;
- 0 indicates no linear relationship;
- −1 indicates a perfect negative correlation.
- ANOVA
- Grand mean (GM): the average of all observations across all groups;
- Sum of squares (SS): is the sum of the squared deviations of data points from a specific mean, measuring the variability of the data around that mean.
- Mean squares (MS): This is calculated as the ratio of the corresponding sum of squares to their degrees of freedom (df):
- SSbetween is the sum of squared differences between each group mean and the grand mean, weighted by the group size.
- SSwithin is the sum of squared differences between individual observations and their respective group means.
- represents the average variability between groups (e.g., landslide vs. non-landslide), measuring how much the group means differ from the grand mean;
- reflects the average variability within each group, indicating the internal dispersion of values around each group’s mean.
- Symmetrical Uncertainty (SU)
2.3.3. Landslide Susceptibility Mapping Using XGBoost
2.3.4. Accuracy Assessment
3. Results
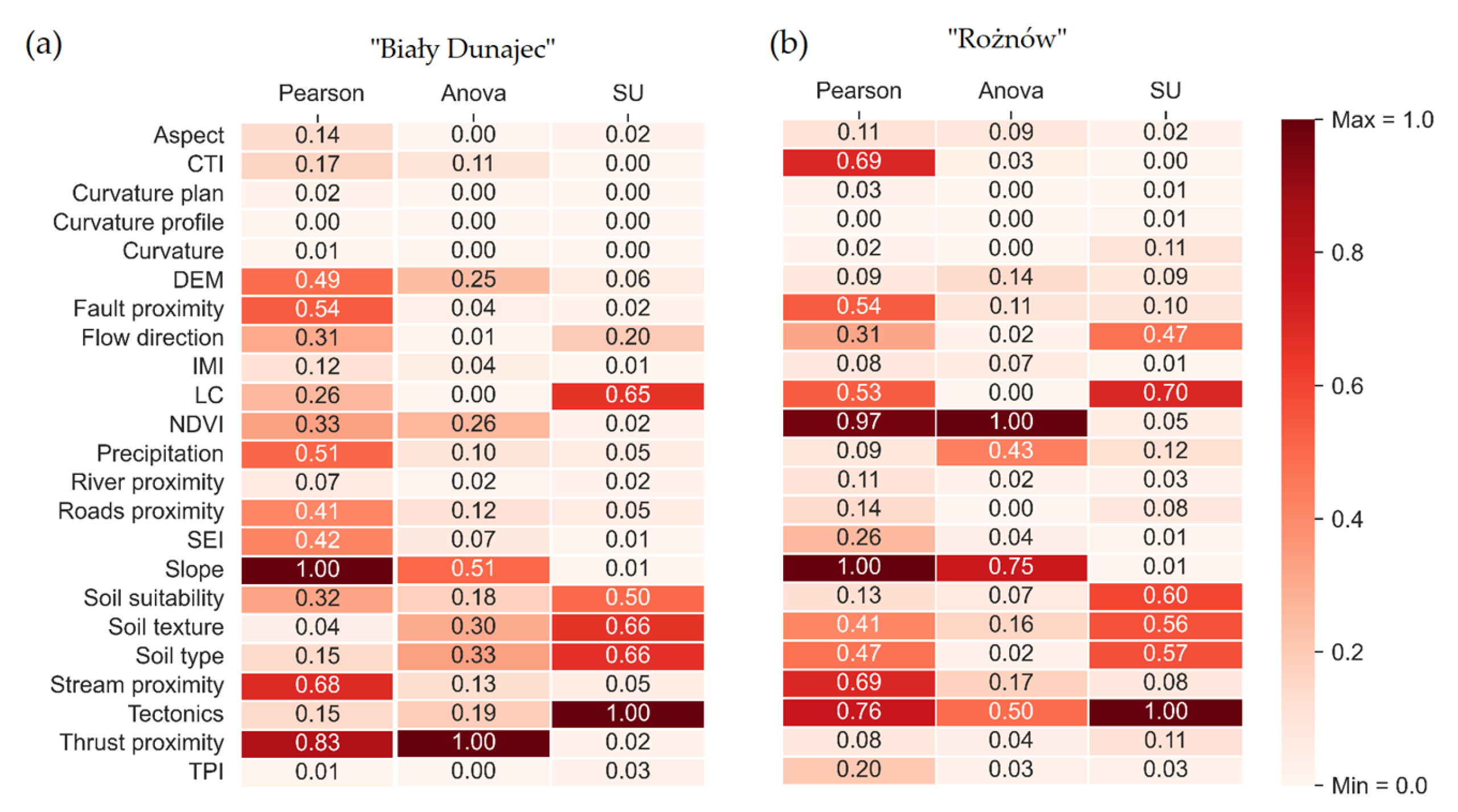
3.1. Feature Correlation
3.2. Feature Importance Analysis
3.3. Various Strategies of LSM—Selected Features
3.4. Landslide Susceptibility Maps and Accuracy Measures
4. Discussion
4.1. Correlations Between LCFs
4.2. Feature Selection
4.3. Accuracy Assessment of Various Models
4.4. Comparison with Other Related Studies
4.5. Potential Applicability and Future Perspectives of Feature Selection Methods in Diverse Geological Settings
4.6. Beyond Accuracy Measures: A Funcional Perspective on LSM Validity Assessment—Metrics, Challenges, and Temporal Relevance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Landslide Conditioning Factors for the Biały Dunajec Case Study
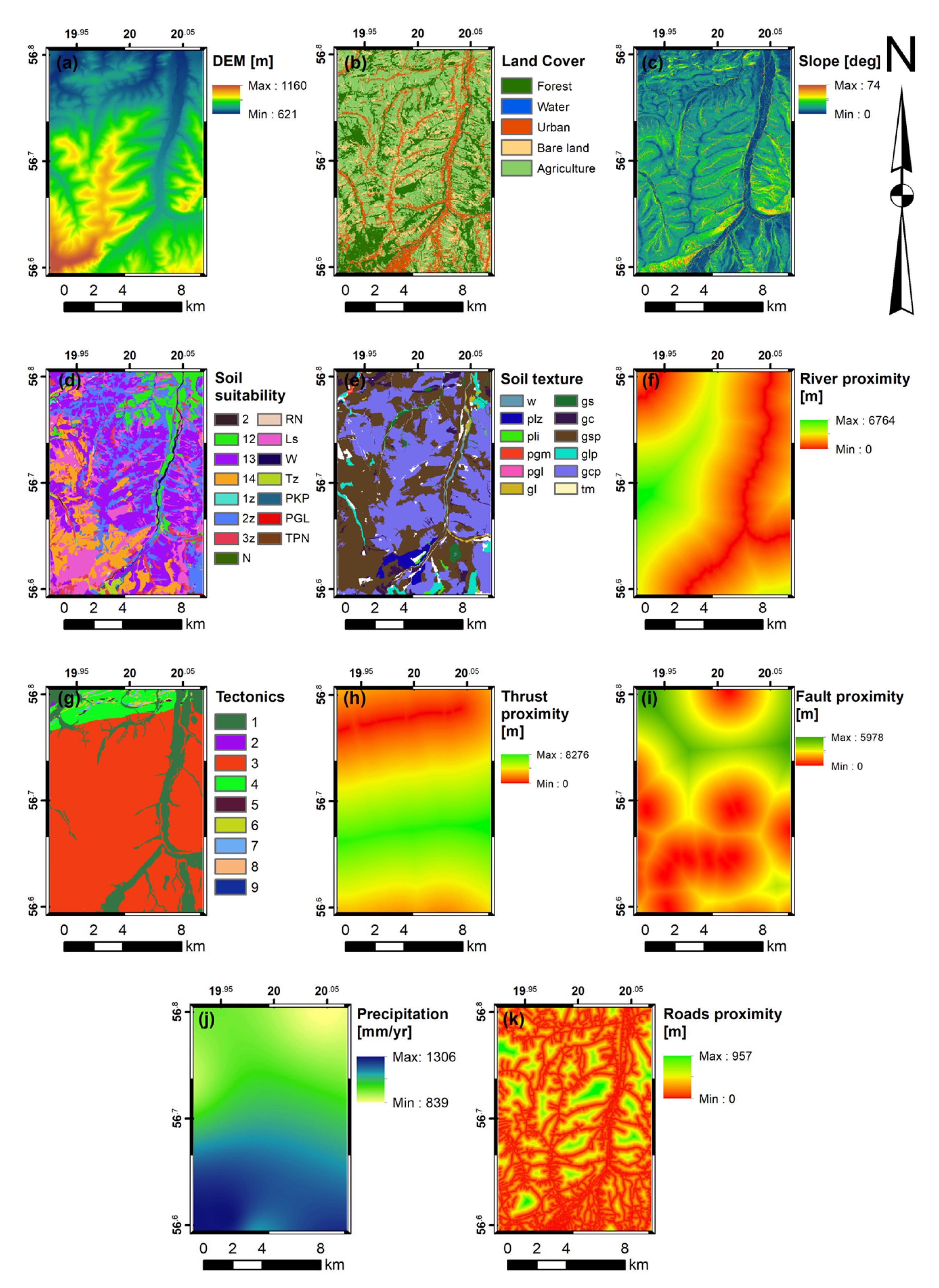
Appendix A.2. Landslide Conditioning Factors for the Rożnów Case Study
Appendix A.3. Description of Symbols Used for Categorical Landslide Conditioning Factors
| LCF | Symbol | Description |
|---|---|---|
| Soil suitability | 2 | good wheat |
| 3 | defective wheat | |
| 8 | strong grain and fodder | |
| 10 | highland wheat | |
| 11 | highland grain | |
| 12 | weak rye | |
| 13 | highland oat–potato | |
| 14 | arable soils intended for grassland | |
| 1z | very good and good grassland | |
| 2z | medium grassland | |
| 3z | weak and very weak grassland | |
| N | wasteland | |
| RN | agriculturally unsuitable soil | |
| Ls | forests | |
| W | water | |
| Tz | urban areas | |
| PKP | Polish State Railway areas | |
| PGL | State Forests National Forest Holding areas | |
| TPN | Tatra National Park | |
| Soil texture | w | water |
| plz | silt | |
| pli | silt clay | |
| pgm | strong clay sands | |
| pgl | light clay sands | |
| gl | light clay | |
| gs | medium clays | |
| gc | heavy clays | |
| lp | silty loams | |
| ls | loess and loess formation | |
| zg | clay gravel | |
| pl | loose sands | |
| gsp | medium silty clays | |
| glp | light silty clays | |
| gcp | heavy silty clays | |
| tm | peat and silt | |
| Tectonics | 1 | Quaternary |
| 2 | Neogen | |
| 3 | Paleogene | |
| 4 | Upper Cretaceous | |
| 5 | Upper Jurassic | |
| 6 | malm–neakon | |
| 7 | Upper Jurassic | |
| 8 | Middle Jurassic | |
| 9 | Triassic |
References
- Schuster, R.L.; Fleming, R.W. Economic losses and fatalities due to landslides. Bull. Assoc. Eng. Geol. 1986, 23, 11–28. [Google Scholar] [CrossRef]
- Schuster, R.L.; Highland, L.M. Socioeconomic and Environmental Impacts of Landslides in the Western Hemisphere; Open-File Report 2001-276; USGS: Reston, VA, USA, 2001. [CrossRef]
- Prakash, N.; Manconi, A.; Loew, S. Mapping landslides on EO data: Performance of deep learning models vs. Traditional machine learning models. Remote Sens. 2020, 2, 346. [Google Scholar] [CrossRef]
- Haque, U.; Blum, P.; Da Silva, P.F.; Andersen, P.; Pilz, J.; Chalov, S.R.; Malet, J.P.; Auflič, M.J.; Andres, N.; Poyiadji, E.; et al. Fatal landslides in Europe. Landslides 2016, 13, 1545–1554. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Fidan, S.; Tanyaş, H.; Akbaş, A.; Lombardo, L.; Petley, D.N.; Görüm, T. Understanding fatal landslides at global scales: A summary of topographic, climatic, and anthropogenic perspectives. Nat. Hazards 2024, 120, 6437–6455. [Google Scholar] [CrossRef]
- Varnes, D.J. Landslide types and processes. In Landslides and Engineering Practice; Literary Licensing, LLC.: Whitefish, MT, USA, 1958; Volume 24, pp. 20–47. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Pawłuszek, K.; Borkowski, A. Automatic landslides mapping in the principal component domain. In Advancing Culture of Living with Landslides: Volume 5 Landslides in Different Environments; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 421–428. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Oreńczak, N.; Pasternak, M. Investigating the effect of cross-modeling in landslide susceptibility mapping. Appl. Sci. 2020, 10, 6335. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Schuster, R.L.; Wieczorek, G.F. Landslide triggers and types. In Landslides; Routledge: Abingdon, UK, 2018; pp. 59–78. [Google Scholar]
- McColl, S.T. Landslide causes and triggers. In Landslide Hazards, Risks, and Disasters; Elsevier: Amsterdam, The Netherlands, 2002; pp. 13–41. [Google Scholar] [CrossRef]
- Wojciechowski, T.; Laskowicz, I.; Kos, J.; Marciniec, P.; Uścinowicz, G.; Karkowska, K.; Przyłucka, M.; Wódka, M. Geohazards in Poland in 2021. Przegląd Geol. 2021, 70, 617–626. (In Polish) [Google Scholar]
- Brabb, E.E. Innovative approaches to landslide hazard and risk mapping. In Proceedings of the IV International Symposium on Landslides [Canadian Geotechnical Society], Toronto, ON, Canada, 16–21 September 1984. [Google Scholar]
- Dahal, A.; Huser, R.; Lombardo, L. At the junction between deep learning and statistics of extremes: Formalizing the landslide hazard definition. J. Geophys. Res. Mach. Learn. Comput. 2024, 1, e2024JH000164. [Google Scholar] [CrossRef]
- Caleca, F.; Lombardo, L.; Steger, S.; Tanyas, H.; Raspini, F.; Dahal, A.; Nefros, C.; Mărgărint, M.C.; Drouin, V.; Jemec-Auflič, M.; et al. Pan-European landslide risk assessment: From theory to practice. Rev. Geophys. 2025, 63, e2023RG000825. [Google Scholar] [CrossRef]
- Roccati, A.; Paliaga, G.; Luino, F.; Faccini, F.; Turconi, L. GIS-based landslide susceptibility mapping for land use planning and risk assessment. Land 2021, 10, 162. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Kıncal, C.; Akgun, A.; Koca, M.Y. Landslide susceptibility assessment in the Izmir (West Anatolia, Turkey) city center and its near vicinity by the logistic regression method. Environ. Earth Sci. 2009, 59, 745–756. [Google Scholar] [CrossRef]
- Mashari, S.; Solaimani, K.; Omidvar, E. Landslide susceptibility mapping using multiple regression and GIS tools in Tajan Basin, North of Iran. Environ. Nat. Resour. Res. 2012, 2, 43. [Google Scholar] [CrossRef]
- Mezughi, T.H.; Akhir, J.M.; Rafek, A.G.; Abdullah, I. Landslide susceptibility assessment using frequency ratio model applied to an area along the EW highway (Gerik-Jeli). Am. J. Environ. Sci. 2011, 7, 43. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Moradi, H.R.; Fatemi Aghda, S.M.; Gokceoglu, C.; Pradhan, B. GIS-based landslide susceptibility mapping with probabilistic likelihood ratio and spatial multi-criteria evaluation models (North of Tehran, Iran). Arab. J. Geosci. 2014, 7, 1857–1878. [Google Scholar] [CrossRef]
- Mohammady, M.; Pourghasemi, H.R.; Pradhan, B. Landslide susceptibility mapping at Golestan Province, Iran: A comparison between frequency ratio, Dempster–Shafer, and weights-of-evidence models. J. Asian Earth Sci. 2012, 61, 221–236. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- Yilmaz, I.; Keskin, I. GIS based statistical and physical approaches to landslide susceptibility mapping (Sebinkarahisar, Turkey). Bull. Eng. Geol. Environ. 2009, 68, 459–471. [Google Scholar] [CrossRef]
- Ado, M.; Amitab, K.; Maji, A.K.; Jasińska, E.; Gono, R.; Leonowicz, Z.; Jasiński, M. Landslide susceptibility mapping using machine learning: A literature survey. Remote Sens. 2022, 14, 3029. [Google Scholar] [CrossRef]
- Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef]
- Liu, Z.; L’Heureux, J.S.; Glimsdal, S.; Lacasse, S. Modelling of mobility of Rissa landslide and following tsunami. Comput. Geotech. 2021, 140, 104388. [Google Scholar] [CrossRef]
- Sahin, E.K. Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2020, 37, 2441–2465. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Maghsoudi Moud, F. Landslide susceptibility mapping using hybridized block modular intelligence model. Bull. Eng. Geol. Environ. 2021, 80, 267–284. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, J.; Zheng, J.; Fan, H.; Kong, J.; Zhan, J. Application of Bayesian hyperparameter optimized random forest and XGBoost model for landslide susceptibility mapping. Front. Earth Sci. 2021, 9, 712240. [Google Scholar] [CrossRef]
- Tanyaş, H.; van Westen, C.J.; Allstadt, K.E.; Jessee, M.A.N.; Görüm, T.; Jibson, R.W.; Godt, J.W.; Sato, H.P.; Schmitt, R.G.; Marc, O.; et al. Presentation and analysis of a worldwide database of earthquake-induced landslide inventories. J. Geophys. Res. Earth Surf. 2017, 122, 1991–2015. [Google Scholar] [CrossRef]
- Chen, M.; Tang, C.; Xiong, J.; Chang, M.; Li, N. Spatio-temporal mapping and long-term evolution of debris flow activity after a high magnitude earthquake. Catena 2024, 236, 107716. [Google Scholar] [CrossRef]
- Zhao, B.; Yuan, L.; Geng, X.; Su, L.; Qian, J.; Wu, H.; Liu, M.; Li, J. Deformation characteristics of a large landslide reactivated by human activity in Wanyuan city, Sichuan Province, China. Landslides 2022, 19, 1131–1141. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, C.; Li, M.; Tan, J.; Wang, Y. Landslide susceptibility prediction considering land use change and human activity: A case study under rapid urban expansion and afforestation in China. Sci. Total Environ. 2023, 866, 161430. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.W.; Chun, K.W.; Kim, M.; Catani, F.; Choi, B.; Seo, J.I. Effect of antecedent rainfall conditions and their variations on shallow landslide-triggering rainfall thresholds in South Korea. Landslides 2021, 18, 569–582. [Google Scholar] [CrossRef]
- Johnston, E.C.; Davenport, F.V.; Wang, L.; Caers, J.K.; Muthukrishnan, S.; Burke, M.; Diffenbaugh, N.S. Quantifying the effect of precipitation on landslide hazard in urbanized and non-urbanized areas. Geophys. Res. Lett. 2021, 48, e2021GL094038. [Google Scholar] [CrossRef]
- Pilecka, E.; Moskal, M. The influence of foundation for the initiation and growth of the landslide in the Carpathian Flysch. Tech. Trans. 2017, 114, 113–121. [Google Scholar] [CrossRef]
- Holcombe, E.A.; Beesley, M.E.; Vardanega, P.J.; Sorbie, R. Urbanisation and landslides: Hazard drivers and better practices. Proc. Inst. Civ. Eng. Civ. Eng. 2016, 169, 137–144. [Google Scholar] [CrossRef]
- Ren, Z.; Liu, H.; Li, L.; Wang, Y.; Sun, Q. On the effects of rheological behavior on landslide motion and tsunami hazard for the Baiyun Slide in the South China Sea. Landslides 2023, 20, 1599–1616. [Google Scholar] [CrossRef]
- Abbas, F.; Zhang, F.; Abbas, F.; Ismail, M.; Iqbal, J.; Hussain, D.; Khan, G.; Alrefaei, A.F.; Albeshr, M.F. Landslide susceptibility mapping: Analysis of different feature selection techniques with artificial neural network tuned by bayesian and metaheuristic algorithms. Remote Sens. 2023, 15, 4330. [Google Scholar] [CrossRef]
- Pham, Q.B.; Achour, Y.; Ali, S.A.; Parvin, F.; Vojtek, M.; Vojteková, J.; Al-Ansari, N.; Achu, A.L.; Costache, R.; Khedher, K.M.; et al. A comparison among fuzzy multi-criteria decision making, bivariate, multivariate and machine learning models in landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2021, 12, 1741–1777. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.T. Rainfall-induced shallow landslide susceptibility mapping at two adjacent catchments using advanced machine learning algorithms. ISPRS Int. J. Geo-Inf. 2020, 9, 569. [Google Scholar] [CrossRef]
- Singh, B.; Kushwaha, N.; Vyas, O.P. A feature subset selection technique for high dimensional data using symmetric uncertainty. J. Data Anal. Inf. Process. 2014, 2, 95–105. [Google Scholar] [CrossRef]
- Yu, L.; Cao, Y.; Zhou, C.; Wang, Y.; Huo, Z. Landslide susceptibility mapping combining information gain ratio and support vector machines: A case study from Wushan segment in the three gorges reservoir area, China. Appl. Sci. 2019, 9, 4756. [Google Scholar] [CrossRef]
- Chen, C.; Fan, L. Selection of contributing factors for predicting landslide susceptibility using machine learning and deep learning models. Stoch. Environ. Res. Risk Assess. 2023, 1–26. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, C. Assessment of Landslide Susceptibility Based on ReliefF Feature Weight Fusion: A Case Study of Wenxian County, Longnan City. Sustainability 2025, 17, 3536. [Google Scholar] [CrossRef]
- Dung, N.V.; Hieu, N.; Phong, T.V.; Amiri, M.; Costache, R.; Al-Ansari, N.; Prakash, I.; Le, H.V.; Nguyen, H.B.; Pham, B.T. Exploring novel hybrid soft computing models for landslide susceptibility mapping in Son La hydropower reservoir basin. Geomat. Nat. Hazards Risk 2021, 12, 1688–1714. [Google Scholar] [CrossRef]
- Pawluszek, K.; Borkowski, A. Landslides identification using airborne laser scanning data derived topographic terrain attributes and support vector machine classification. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; The ISPRS Foundation: Baton Rouge, LA, USA, 2016; Volume 41, pp. 145–149. [Google Scholar] [CrossRef]
- Camilo, D.C.; Lombardo, L.; Mai, P.M.; Dou, J.; Huser, R. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through LASSO-penalized Generalized Linear Model. Environ. Model. Softw. 2017, 97, 145–156. [Google Scholar] [CrossRef]
- Lombardo, L.; Mai, P.M. Presenting logistic regression-based landslide susceptibility results. Eng. Geol. 2018, 244, 14–24. [Google Scholar] [CrossRef]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine learning feature selection methods for landslide susceptibility mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef]
- Caleca, F.; Confuorto, P.; Raspini, F.; Segoni, S.; Tofani, V.; Casagli, N.; Moretti, S. Shifting from traditional landslide occurrence modeling to scenario estimation with a “glass-box” machine learning. Sci. Total Environ. 2024, 950, 175277. [Google Scholar] [CrossRef]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Kumar, C.; Walton, G.; Santi, P.; Luza, C. An ensemble approach of feature selection and machine learning models for regional landslide susceptibility mapping in the arid mountainous terrain of Southern Peru. Remote Sens. 2023, 15, 1376. [Google Scholar] [CrossRef]
- Meena, S.R.; Hussain, M.A.; Ullah, H.; Ullah, I. Landslide susceptibility mapping using hybrid machine learning classifiers: A case study of Neelum Valley, Pakistan. Bull. Eng. Geol. Environ. 2025, 84, 242. [Google Scholar] [CrossRef]
- Nirbhav; Malik, A.; Maheshwar; Jan, T.; Prasad, M. Landslide susceptibility prediction based on decision tree and feature selection methods. J. Indian Soc. Remote Sens. 2023, 51, 771–786. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A comprehensive assessment of XGBoost algorithm for landslide susceptibility mapping in the upper basin of Ataturk dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Wójcik, A.; Wojciechowski, T.; Wódka, M.; Krzysiek, U. Mapa Osuwisk i Terenów Zagrożonych Ruchami Masowymi. Gmina Gródek nad Dunajcem, Skala 1:10,000; Państwowy Instytut Geologiczny: Warszawa, Poland, 2015. (In Polish)
- Gałdyn, P.; Balon, J.; Maciejowski, W. Zagrożenie osuwiskami a planowanie przestrzenne w wybranych gminach podhalańskich. Pr. Geogr. 2024, 176, 61–75. (In Polish) [Google Scholar] [CrossRef]
- Varnes, D.J. Slope movement types and processes. In Landslides, Analysis and Control; Transportation Research Board, Special Report; National Academy of Science: Washington, DC, USA, 1978; Volume 176, pp. 11–33. [Google Scholar]
- Cruden, D.M.; Varnes, D.J. Landslides Types and Processes; Transportation Research Board, Special Report; NRC: Washington, DC, USA, 1996; Volume 247, pp. 36–75. [Google Scholar]
- Dikau, R.; Brunsden, D.; Schrott, L.; Ibsen, M.L. (Eds.) Landslide Recognition. Identification, Movement and Causes; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Wódka, M. Conditions of landslide development during the last decade in the Rożnów Dam-Lake region (Southern Poland) based on Airborne Laser Scanning (ALS) data analysis. Geol. Q. 2022, 66, 4. [Google Scholar] [CrossRef]
- Chowaniec, J.; Wójcik, A.; Mrozek, T.; Rączkowski, W.; Nescieruk, P.; Perski, Z.; Wojciechowski, T.; Marciniec, P.; Zimnal, Z.; Granoszewski, W. Osuwiska w województwie małopolskim. In Atlas-Przewodnik; Chowaniec, J., Wójcik, A., Eds.; Departament Środowiska, Rolnictwa i Geodezji Urzędu Marszałkowskiego Województwa Małopolskiego, Zespół Geologii: Kraków, Poland, 2012. (In Polish) [Google Scholar]
- Zabuski, L.; Thiel, K.; Bober, L. Osuwiska we Fliszu Polskich Karpat: Geologia, Modelowanie, Obliczenia Stateczności; Institute of Hydro-Engineering of Polish Academy of Sciences: Gdańsk, Poland, 1999. (In Polish) [Google Scholar]
- Cieszkowski, M.; Koszarski, A.; Leszczyñski, S.; Michalik, M.; Radomski, A.; Szulc, J. Szczegółowa Mapa Geologiczna Polski w Skali 1:50,000, Arkusz Ciężkowice; Państwowy Instytut Geologiczny: Warszawa, Poland, 1987. (In Polish)
- Cieszkowski, M. Michalczowa Zone–A new unit of the Fore-Magura Zone, West Carpathians, South Poland. Geologia 1992, 18, 1–125, (In Polish with English Summary). [Google Scholar]
- Kurczyński, Z.; Bakuła, K. Generowanie referencyjnego numerycznego modelu terenu o zasięgu krajowym w oparciu o lotnicze skanowanie laserowe w projekcie ISOK. In Arch Fotogram Kartogr i Teledetekcji; Zarząd Główny Stowarzyszenia Geodetów Polskich: Warszawa, Poland, 2013; pp. 59–68. (In Polish) [Google Scholar]
- Pawłuszek, K.; Borkowski, A.; Tarolli, P. Towards the optimal Pixel size of dem for automatic mapping of landslide areas. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; The ISPRS Foundation: Baton Rouge, LA, USA, 2017; Volume 42, pp. 83–90. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- ESRI. Curvature Function—Help|ArcGIS for Desktop. ArcGIS Help Page. 2016. Available online: https://desktop.arcgis.com/en/arcmap/latest/manage-data/raster-and-images/curvature-function.htm (accessed on 8 August 2025).
- Yang, X.; Chapman, G.A.; Gray, J.M.; Young, M.A. Delineating soil landscape facets from digital elevation models using compound topographic index in a geographic information system. Soil Res. 2007, 45, 569–576. [Google Scholar] [CrossRef]
- Iverson, L.R.; Scott, C.T.; Dale, M.E.; Prasad, A. Development of an Integrated Moisture Index for Predicting Species Composition; USDA Forest Service: Washington, DC, USA, 1995.
- Iverson, L.R.; Prasad, A.M. A GIS-derived integrated moisture index. In Characteristics of Mixed Oak Forest Ecosystems in Southern Ohio Prior to the Reintroduction of Fire; Sutherland, E.K., Hutchinson, T.F., Eds.; Gen. Technical Report NE-299; US Department of Agriculture, Forest Service, Northeastern Research Station: Newtown Square, PA, USA, 2003; pp. 29–41, 299. [Google Scholar]
- Balice, R.G.; Miller, J.D.; Oswald, B.P.; Edminster, C.; Yool, S.R. Forest Surveys and Wildfire Assessment in the Los Alamos Region; 1998–1999 (No. LA-13714-MS); Los Alamos National Lab: Los Alamos, NM, USA, 2000. [CrossRef]
- Evans, J.; Oakleaf, J.; Cushman, S.; Theobald, D. An ArcGIS Toolbox for Surface Gradient and Geomorphometric Modeling, Version 2.0-0, 2014, Laramie, WY. Available online: https://evansmurphy.wixsite.com/evansspatial/arcgis-gradient-metrics-toolbox (accessed on 8 August 2025).
- Dilts, T. Topography Tools for ArcGIS 10.1. 2015. Available online: http://www.arcgis.com/home/item.html?id=b13b3b40fa3c43d4a23a1a09c5fe96b9 (accessed on 8 August 2025).
- Gudiyangada Nachappa, T.; Kienberger, S.; Meena, S.R.; Hölbling, D.; Blaschke, T. Comparison and validation of per-pixel and object-based approaches for landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2020, 11, 572–600. [Google Scholar] [CrossRef]
- Di Napoli, M.; Carotenuto, F.; Cevasco, A.; Confuorto, P.; Di Martire, D.; Firpo, M.; Pepe, G.; Raso, E.; Calcaterra, D. Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 2020, 17, 1897–1914. [Google Scholar] [CrossRef]
- Xiao, T.; Segoni, S.; Chen, L.; Yin, K.; Casagli, N. A step beyond landslide susceptibility maps: A simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 2020, 17, 627–640. [Google Scholar] [CrossRef]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall induced landslide susceptibility mapping based on Bayesian optimized random forest and gradient boosting decision tree models—A case study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Ahmed, B.; Rahman, M.S.; Sammonds, P.; Islam, R.; Uddin, K. Application of geospatial technologies in developing a dynamic landslide early warning system in a humanitarian context: The Rohingya refugee crisis in Cox’s Bazar, Bangladesh. Geomat. Nat. Hazards Risk 2020, 11, 446–468. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Tien Bui, D. Landslide susceptibility evaluation and management using different machine learning methods in the Gallicash River Watershed, Iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef]
- Arab Amiri, M.; Conoscenti, C. Landslide susceptibility mapping using precipitation data, Mazandaran Province, north of Iran. Nat. Hazards 2017, 89, 255–273. [Google Scholar] [CrossRef]
- Yao, J.; Qin, S.; Qiao, S.; Che, W.; Chen, Y.; Su, G.; Miao, Q. Assessment of landslide susceptibility combining deep learning with semi-supervised learning in Jiaohe County, Jilin Province, China. Appl. Sci. 2020, 10, 5640. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2021, 35, 321–347. [Google Scholar] [CrossRef]
- Pokharel, B.; Thapa, P.B. Landslide susceptibility in Rasuwa District of central Nepal after the 2015 Gorkha Earthquake. J. Nepal Geol. Soc. 2019, 59, 79–88. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. A comparative study of landslide susceptibility maps produced using support vector machine with different kernel functions and entropy data mining models in China. Bull. Eng. Geol. Environ. 2018, 77, 647–664. [Google Scholar] [CrossRef]
- Javier, D.N.; Kumar, L. Frequency ratio landslide susceptibility estimation in a tropical mountain region. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; The ISPRS Foundation: Baton Rouge, LA, USA, 2019; Volume 42, pp. 173–179. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical methods for research workers. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 66–70. [Google Scholar]
- Sawyer, S.F. Analysis of Variance: The Fundamental Concepts. J. Man. Manip. Ther. 2009, 17, 27E–38E. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Nogueira, F. Bayesian Optimization: Open Source Constrained Global Optimization Tool for Python. 2014. Available online: https://bayesian-optimization.github.io/BayesianOptimization/master/ (accessed on 8 August 2025).
- Ayalew, L.; Yamagishi, H.; Ugawa, N. Landslide susceptibility mapping using GIS-based weighted linear combination, the case in Tsugawa area of Agano River, Niigata Prefecture, Japan. Landslides 2004, 1, 73–81. [Google Scholar] [CrossRef]
- Chen, J.; Yang, S.T.; Li, H.W.; Zhang, B.; Lv, J.R. Research on geographical environment unit division based on the method of natural breaks (Jenks). In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; The ISPRS Foundation: Baton Rouge, LA, USA, 2013; Volume 40, pp. 47–50. [Google Scholar] [CrossRef]
- Li, J. Area under the ROC Curve has the most consistent evaluation for binary classification. PLoS ONE 2024, 19, e0316019. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical Relationships between Topography and Precipitation Patterns. J. Clim. 1994, 7, 1305–1315. [Google Scholar] [CrossRef]
- Gouvas, M.; Sakellariou, N.; Xystrakis, F. The relationship between altitude of meteorological stations and average monthly and annual precipitation. Stud. Geophys. Geod. 2009, 53, 557–570. [Google Scholar] [CrossRef]
- Pawluszek, K.; Borkowski, A.; Tarolli, P. Sensitivity analysis of automatic landslide mapping: Numerical experiments towards the best solution. Landslides 2018, 15, 1851–1865. [Google Scholar] [CrossRef]

| Data | Data Type | Source | Link | |
|---|---|---|---|---|
| 1. | DEM | Raster | ISOK | https://www.geoportal.gov.pl (accessed on 8 August 2025) |
| 2. | Geology maps | Raster | PGI | https://geolog.pgi.gov.pl/ (accessed on 8 August 2025) |
| 3. | Soil suitability maps | Raster | MIIP | https://mapymalopolski.pl/app/mapa/miip/1f402b8a-47c0-6894-4ed2-d4ef71d84ede/ (accessed on 8 August 2025) |
| 4. | Satellite images | Raster | Sentinel-2 | https://browser.dataspace.copernicus.eu/ (accessed on 8 August 2025) |
| 5. | Road network | Shapefile | OSM | https://download.geofabrik.de/ (accessed on 8 August 2025) |
| 6. | River network | Shapefile | OSM | https://download.geofabrik.de/ (accessed on 8 August 2025) |
| 7. | Precipitation | Points | IMGW | https://danepubliczne.imgw.pl/ (accessed on 8 August 2025) |
| Biały Dunajec Case Study | Rożnów Case Study | |||||
|---|---|---|---|---|---|---|
| Method | No. of Rejected Features | No. of Preserved Features | Rejected Features | No. of Rejected Features | No. of Preserved Features | Rejected Features |
| PCC | 6 | 17 | Curvature, curvature planar, curvature profile, river proximity, soil texture, TPI | 3 | 20 | Curvature, curvature planar, curvature profile |
| ANOVA | 10 | 13 | Aspect, curvature, curvature planar, curvature profile, flow direction, LC, main geological units, river proximity, TPI | 6 | 17 | Curvature profile, DEM, curvature, curvature planar, precipitation, road proximity |
| SU | 9 | 14 | CTI, curvature, curvature planar, DEM, fault proximity, IMI, river proximity, thrust proximity, TPI | 3 | 20 | River proximity, CTI, IMI |
| Feature Selection Method | ||||||
|---|---|---|---|---|---|---|
| Measure | PearsonBD | ANOVABD | SUBD | PearsonR | ANOVAR | SUR |
| Accuracy | 0.93 | 0.93 | 0.90 | 0.93 | 0.91 | 0.93 |
| Precision | 0.66 | 0.65 | 0.57 | 0.69 | 0.62 | 0.67 |
| Recall | 0.93 | 0.93 | 0.89 | 0.94 | 0.92 | 0.93 |
| F1 | 0.77 | 0.76 | 0.69 | 0.79 | 0.74 | 0.78 |
| AUC | 0.985 | 0.981 | 0.981 | 0.983 | 0.972 | 0.980 |
| Method | Training–Testing Ratio | Feature List | Feature Selection | Overall Accuracy | Precision | Recall | F1-Score | AUC | |
|---|---|---|---|---|---|---|---|---|---|
| Wang et al., 2021 [36] | XGBoost | 70–30% | Slope, aspect, altitude, lithology, average annual rainfall, distance to rivers, HI, TWI, NDVI, distance to roads, distance to villages, curvature | Pearson correlation coefficient | 0.784 | 0.802 | 0.758 | 0.779 | 0.860 |
| Sahin, 2020 [33] | XGBoost | 70–30% | Slope, elevation, TWI, STI, drainage density, lithology, NDVI, LULC, SPI, aspect, distance to rivers, TRI, TPI, plan curvature, profile curvature | SU | 0.875 | - | - | - | 0.957 |
| Pradhan and Kim, 2020 [48] | XGBoost | Two areas for training and testing | Aspect, elevation, slope, curvature, drainage proximity (horizontal), drainage proximity (vertical), SPI, STI, TWI, forest, soil, geology | Variance inflation | 0.74 | 0.60 | 0.70 | 0.657 | 0.740 |
| Can et al., 2021 [63] | XGBoost | 80–20% | Lithology, altitude, TWI, slope orientation, slope gradient, drainage density, plan curvature, SPI, profile curvature | - | 0.90 | 0.86 | 0.91 | 0.88 | 0.96 |
| This work, Biały Dunajec case study | XGBoost | 70–30% | DEM, aspect, slope, flow direction, CTI, IMI, SEI, stream proximity, precipitation, tectonics, fault proximity, thrust proximity, road proximity, soil suitability, soil type, NDVI, land cover | PCC | 0.93 | 0.65 | 0.93 | 0.77 | 0.985 |
| This work, Roźnów case study | XGBoost | 70–30% | DEM, aspect, slope, flow direction, CTI, IMI, TPI, SEI, stream proximity, precipitation, tectonics, fault proximity, thrust proximity, road proximity, river proximity, soil suitability, soil texture, soil type, NDVI, land cover | PCC | 0.93 | 0.69 | 0.94 | 0.79 | 0.980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawłuszek-Filipiak, K.; Lewandowski, T. The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland. Appl. Sci. 2025, 15, 8955. https://doi.org/10.3390/app15168955
Pawłuszek-Filipiak K, Lewandowski T. The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland. Applied Sciences. 2025; 15(16):8955. https://doi.org/10.3390/app15168955
Chicago/Turabian StylePawłuszek-Filipiak, Kamila, and Tymon Lewandowski. 2025. "The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland" Applied Sciences 15, no. 16: 8955. https://doi.org/10.3390/app15168955
APA StylePawłuszek-Filipiak, K., & Lewandowski, T. (2025). The Impact of Feature Selection on XGBoost Performance in Landslide Susceptibility Mapping Using an Extended Set of Features: A Case Study from Southern Poland. Applied Sciences, 15(16), 8955. https://doi.org/10.3390/app15168955







