Hand Kinematic Model Construction Based on Tracking Landmarks
Abstract
1. Introduction
1.1. Literature Review
1.1.1. Non-Invasive Hand-Tracking Systems
1.1.2. Depth-Based and Anatomically Constrained Models
1.1.3. Kinematic Modeling from Anatomical Landmarks
1.1.4. Recent Advances in Adaptive and Probabilistic Modeling
1.1.5. MediaPipe-Based Tracking and Limitations
2. Background Material
2.1. Sensor Specifications
2.2. MediaPipe
3. Hand Kinematic Model Definitions
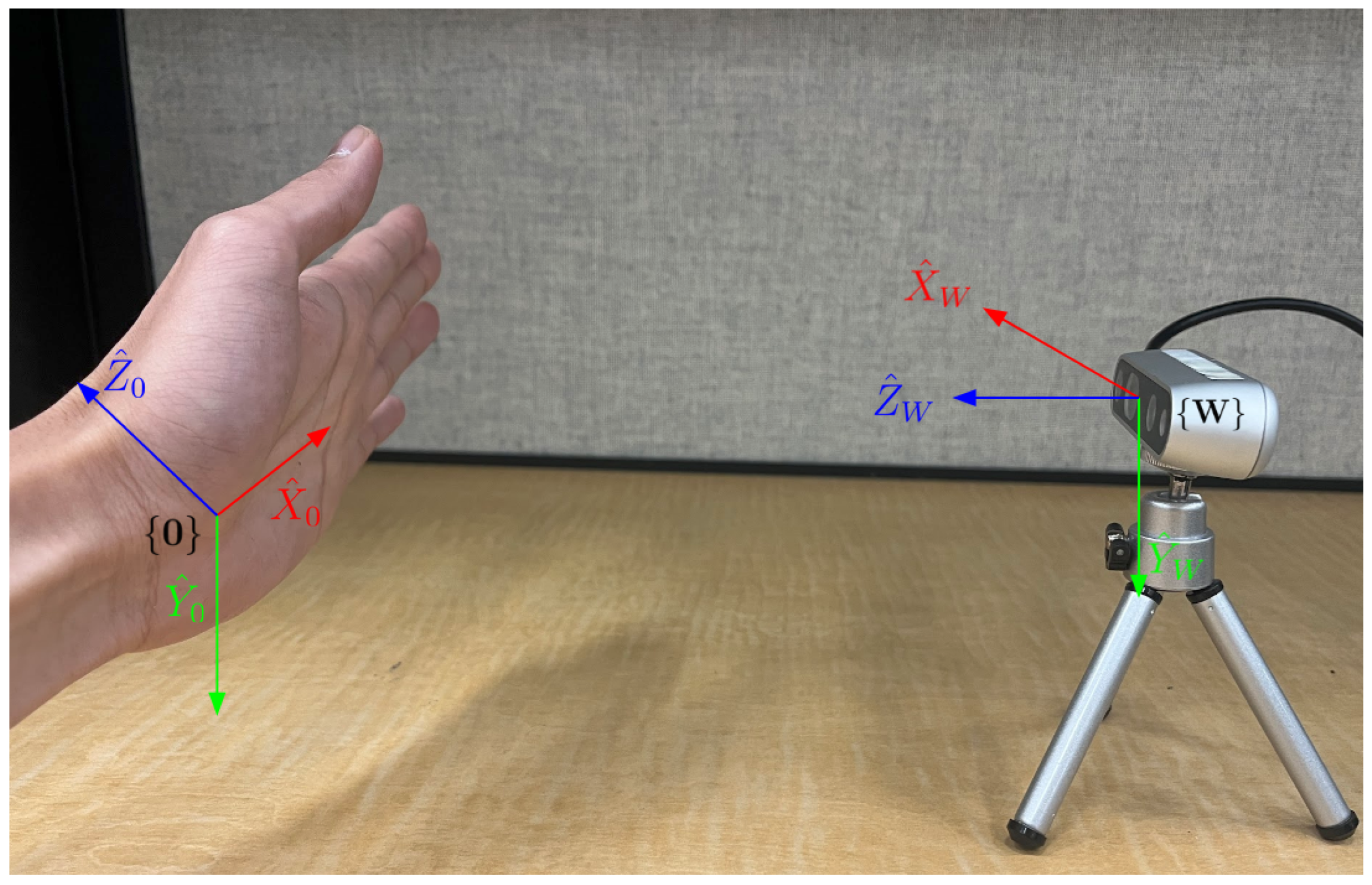
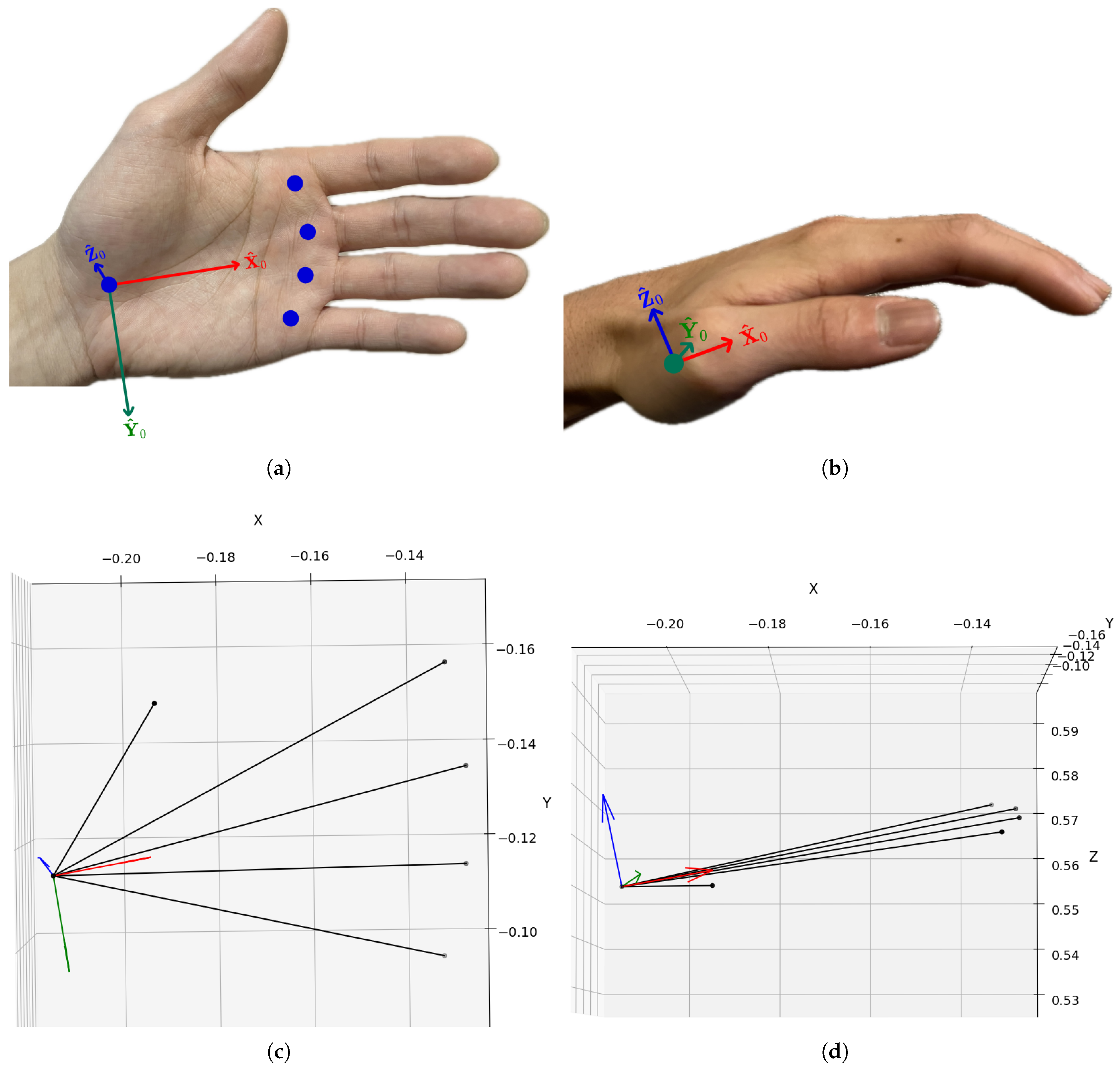
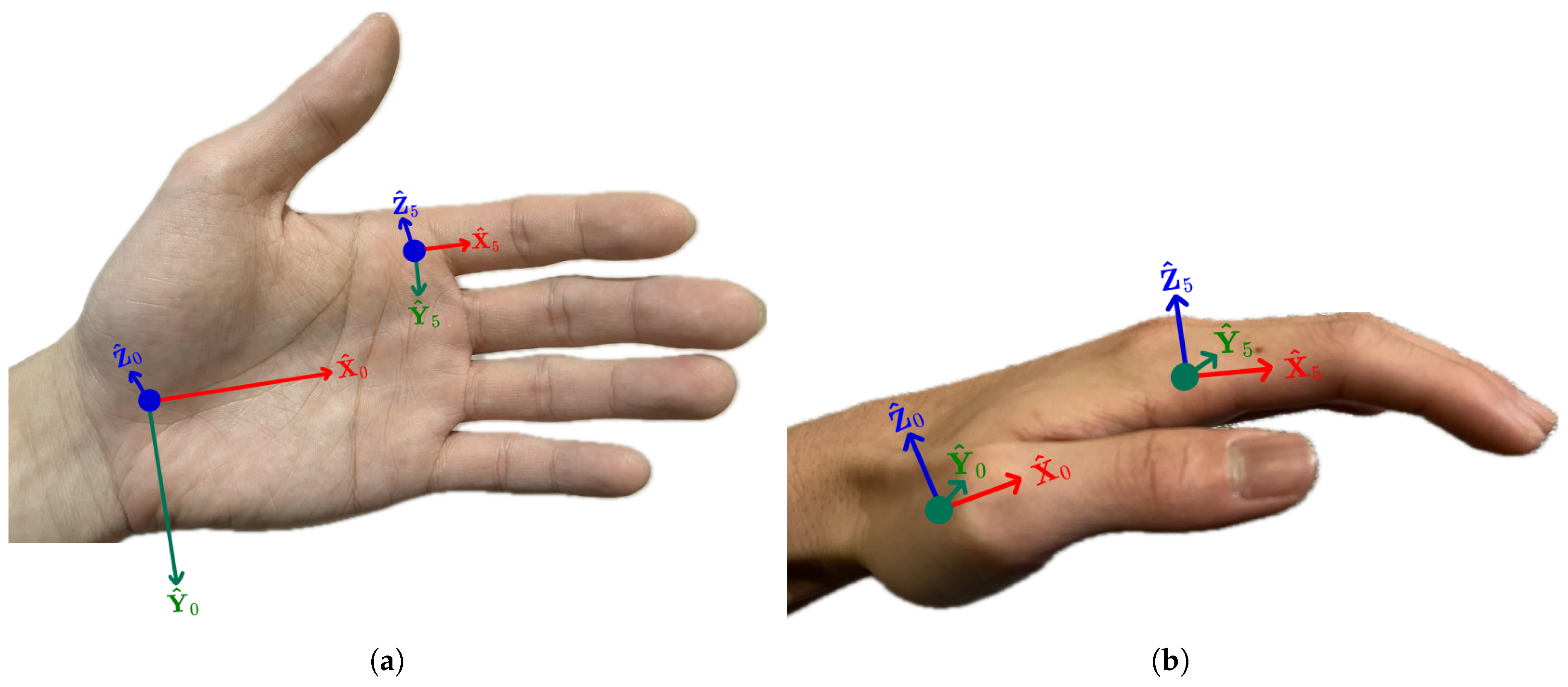
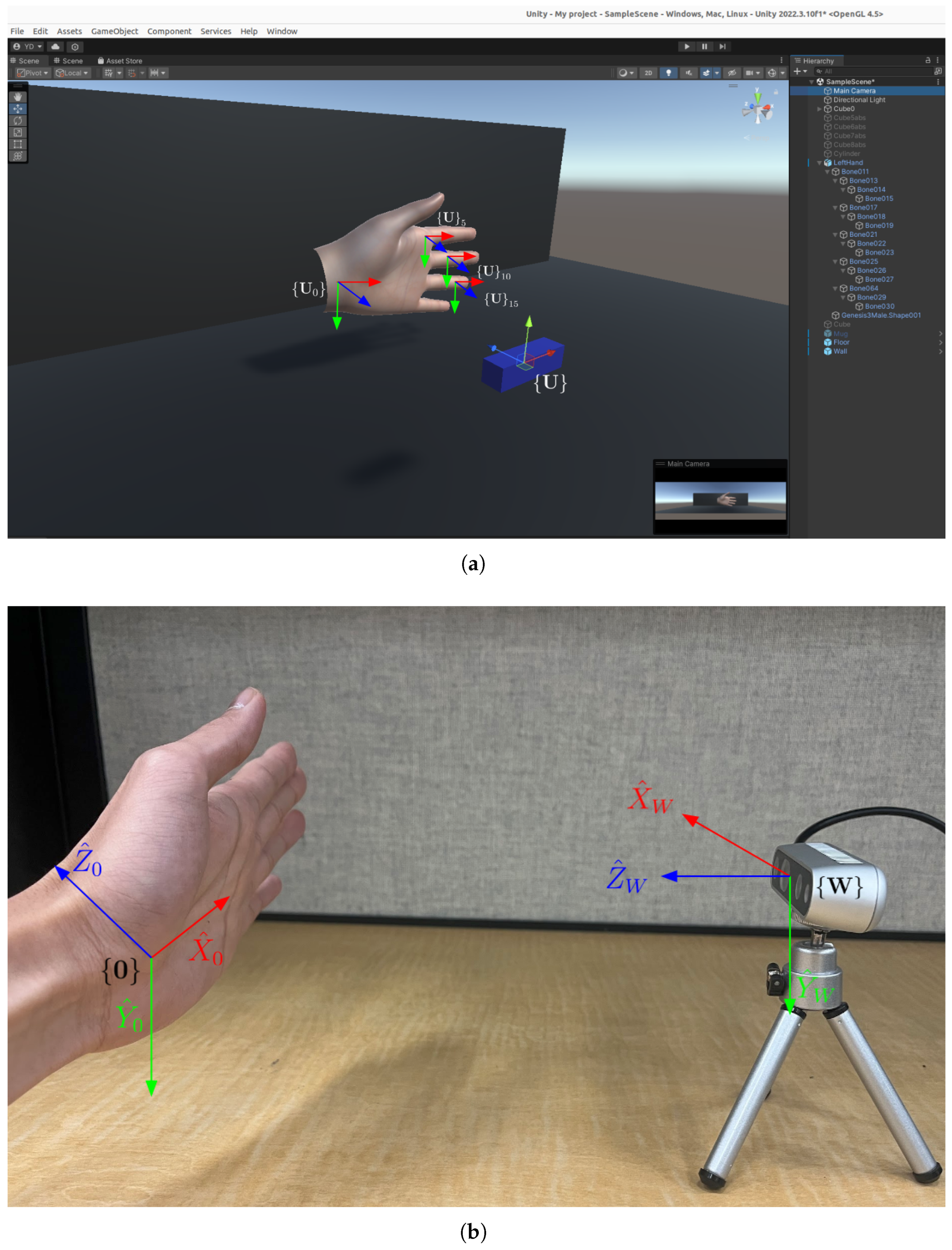
3.1. The World-Frame Definition
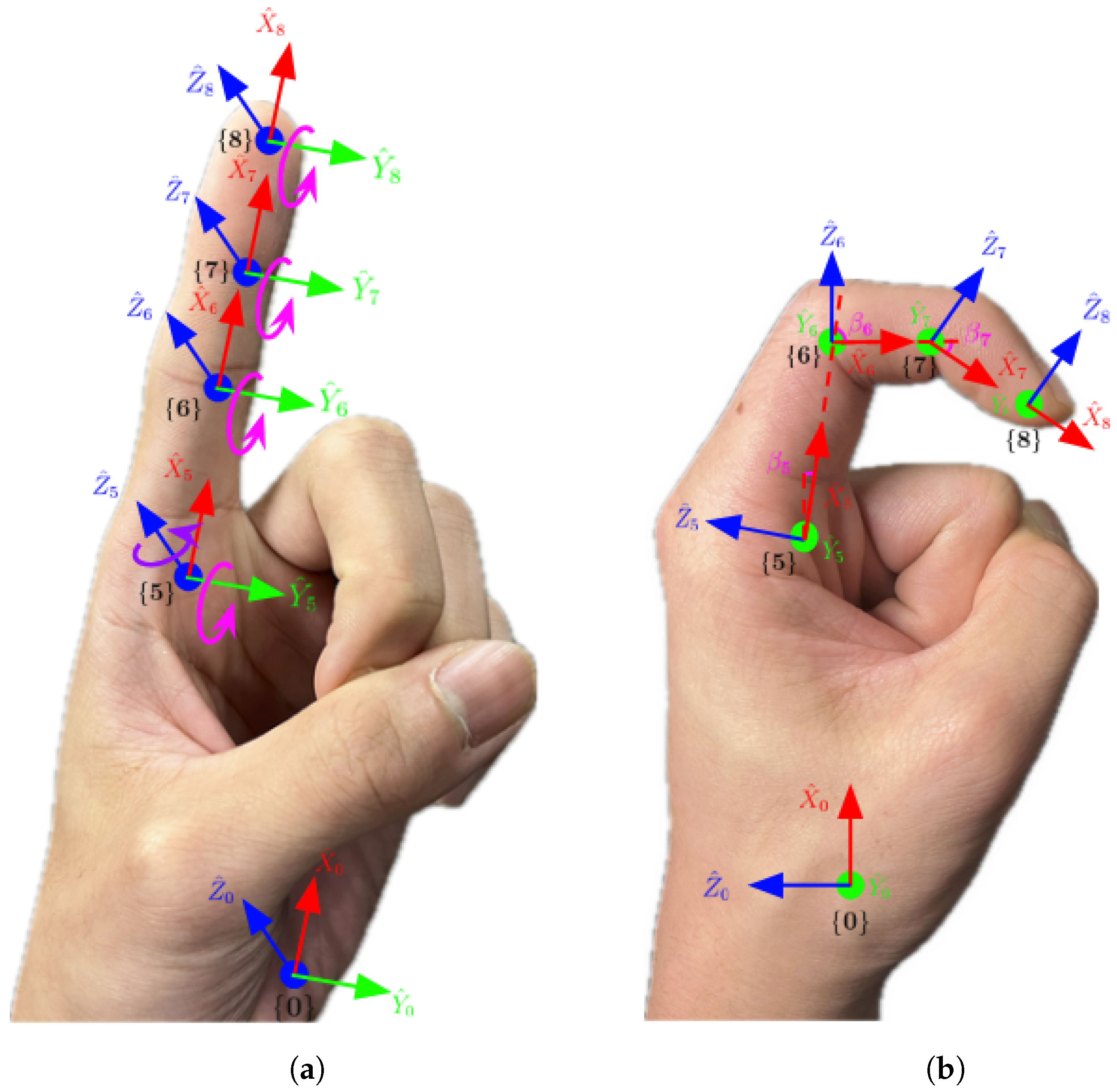
3.2. Definitions of Hand Hierarchical Coordinate Frames
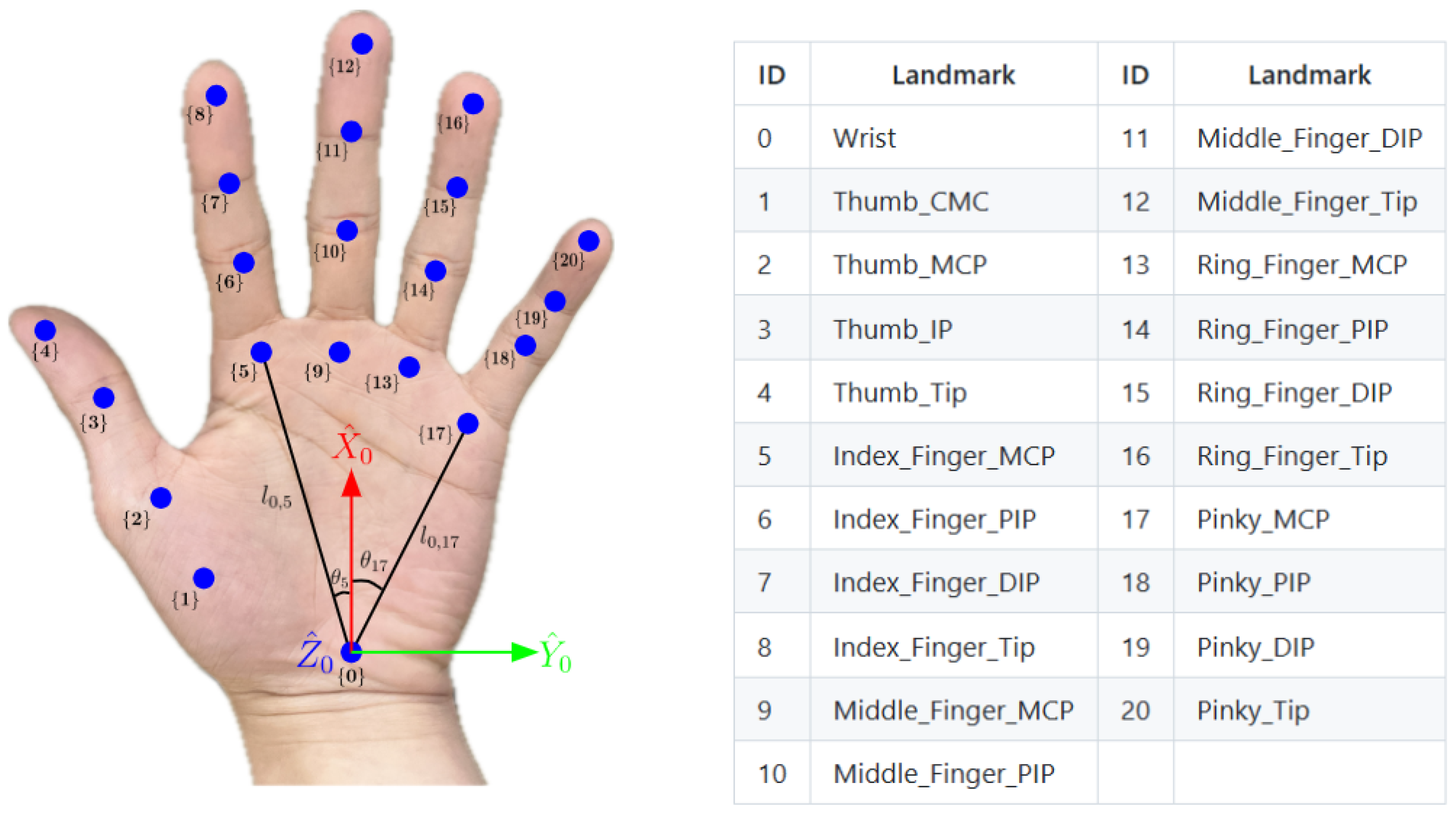
3.3. Hand Kinematic Parameters
- Position Parameters: The position vector specifies the distance of translation between the origins of the wrist frame and the world frame along , and , respectively.
- Orientation Parameters: The orientation of the local frame is defined by the Euler angles ; these angles describe the sequential rotations around axes , , and .
- Base Length Parameters: The lengths represent the fixed distances between the origin of the local frame and the origins of local frames , , , , and . These measurements, in centimeters, are spatial relationships between the wrist and finger roots.
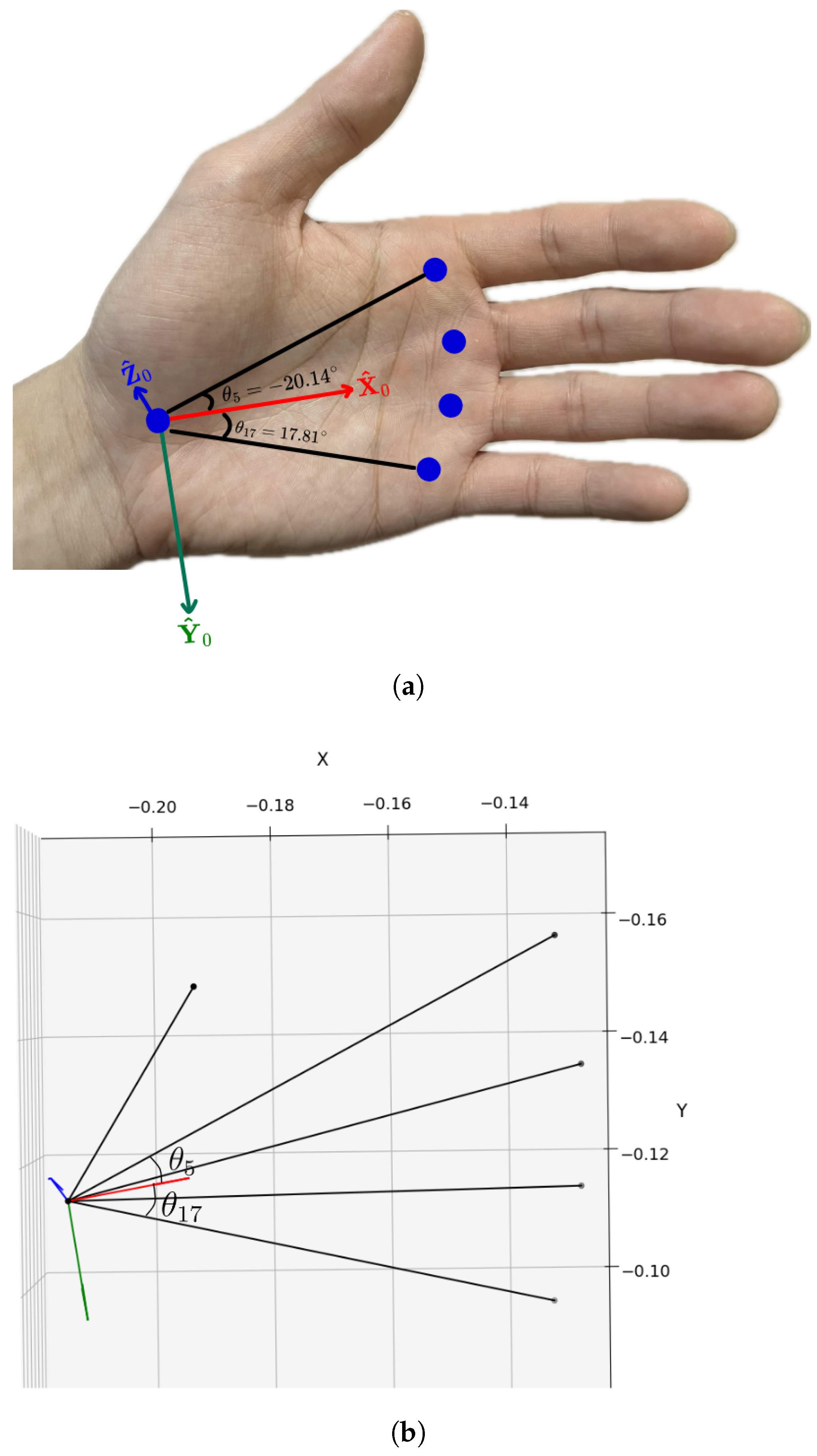
- Angle Parameters: The angles describe the rotational offset between the axis and the axes , , , , and , respectively. These angles, measured in radians, are pivotal for capturing the hand’s natural articulation around the axis.
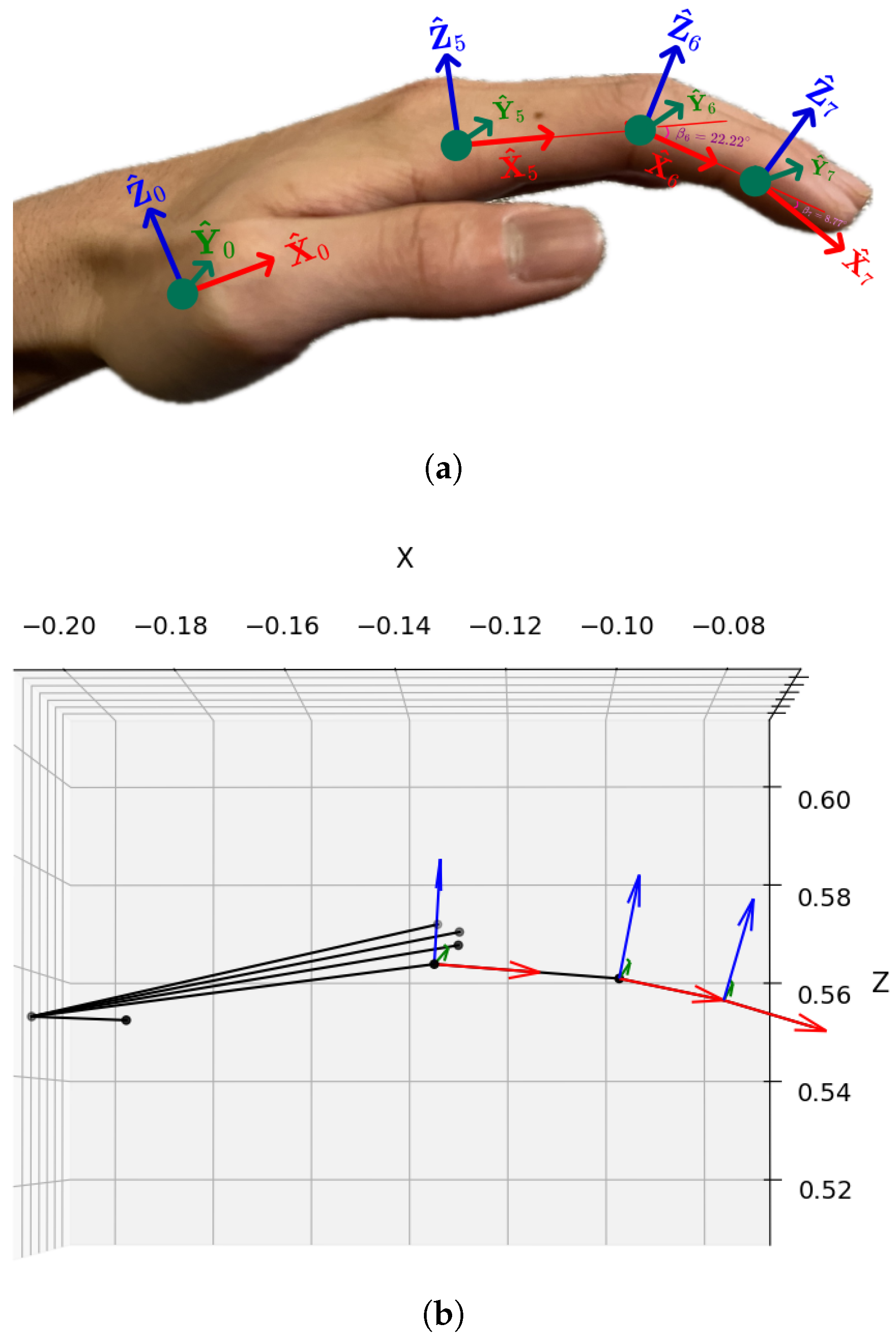
- Base-Length Parameters: A set of 15 parameters determines the fixed lengths of the three links , and , within each finger, where :
- Angle Parameters for Finger Roots: A set of 10 parameters describes five pairs of rotation angles and around axes and for the root joints of each finger, where :
- Angle Parameters for Other Joints: A set of 10 parameters describes five pairs of rotation angles and for the PIP and DIP joints around corresponding of each finger, :
4. Hand Hierarchical Transformations
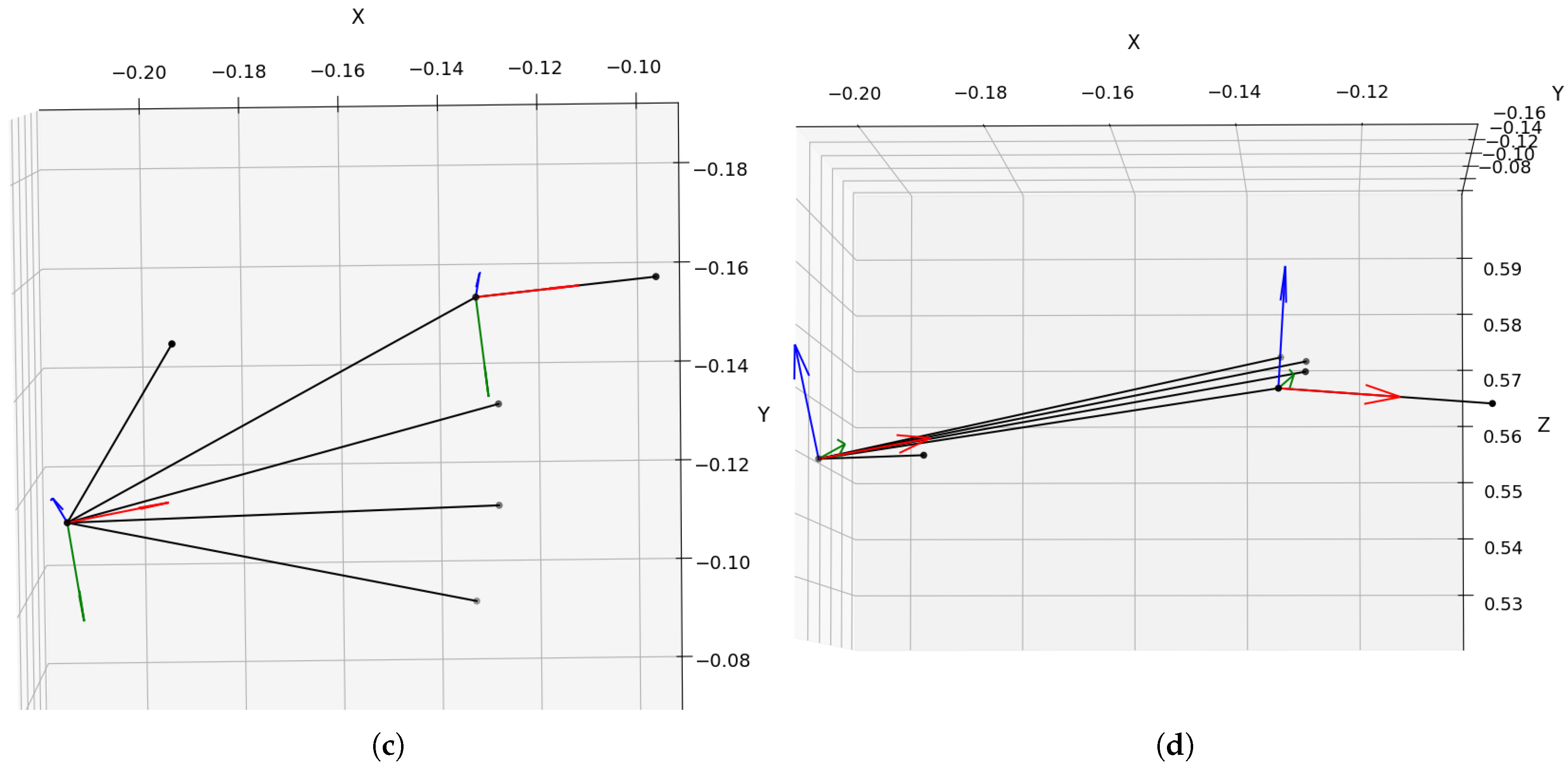
4.1. Resolution of Palm-Coordinate Frame
4.2. Resolving Layered Parameters of Fingers in Hierarchical Transformations
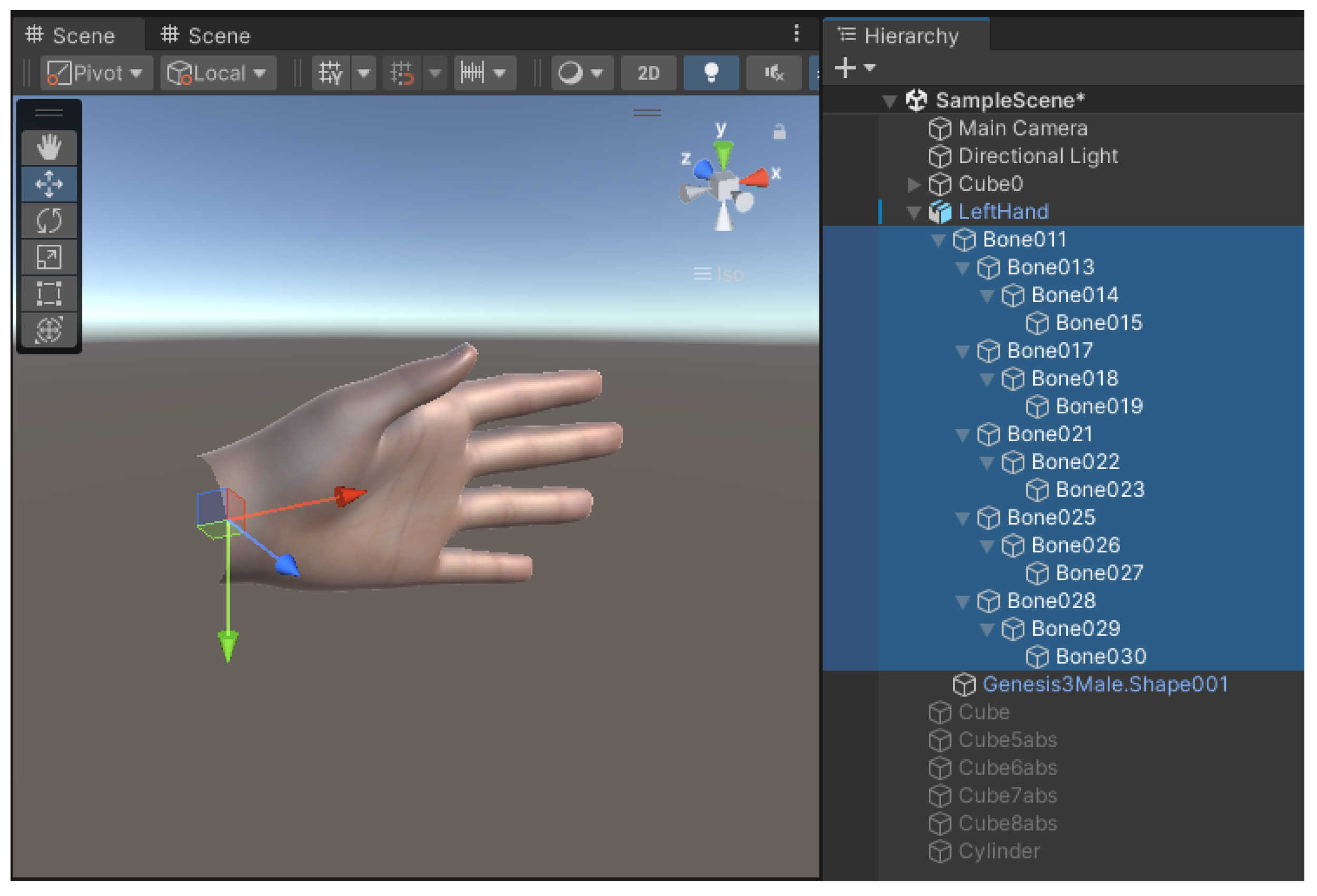
5. Kinematic of Hand for Graphical Reconstruction in Unity
5.1. Unity Environment and Rigged Hand Model
5.2. Left-Handed Frame in Unity
5.3. Transformation from Hand Kinematic Model to Rigged Hand
5.4. Quaternions Representation for Joint Rotations
6. Discussions and Conclusions
6.1. Discussions
6.2. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Camera Calibration and RGB-Depth Pixel Association
Appendix A.1. Intrinsic and Extrinsic Calibration
- RGB camera intrinsics:
- Depth camera intrinsics:
Appendix A.2. Aligning Depth to RGB Stream of the Sensor
- Image resolution: pixels.
- Focal length: , .
- Principal point: , .
References
- Rahman, M.M.; Uzzaman, A.; Khatun, F.; Aktaruzzaman, M.; Siddique, M. A comparative study of advanced technologies and methods in hand gesture analysis and recognition systems. Expert Syst. Appl. 2025, 266, 125929. [Google Scholar] [CrossRef]
- Amprimo, G.; Masi, G.; Pettiti, G.; Olmo, G.; Priano, L.; Ferraris, C. Hand tracking for clinical applications: Validation of the Google MediaPipe Hand (GMH) and the depth-enhanced GMH-D frameworks. Biomed. Signal Process. Control 2024, 96 Pt A, 106508. [Google Scholar] [CrossRef]
- Diaz, C.; Payandeh, S. Preliminary Experimental Study of Marker-based Hand Gesture Recognition System. J. Autom. Control Eng. 2014, 2, 242–249. [Google Scholar] [CrossRef]
- Wang, J.; Payandeh, S. Hand Motion and Posture Recognition in a Network of Calibrated Cameras. Adv. Multimed. 2017, 1, 1–25. [Google Scholar] [CrossRef]
- Rehg, J.M.; Kanade, T. DigitEyes: Vision-based hand tracking for human-computer interaction. In Proceedings of the 1994 IEEE Workshop on Motion of Non-Rigid and Articulated Objects, Austin, TX, USA, 11–12 November 1994; pp. 16–22. [Google Scholar] [CrossRef]
- Rehg, J.M.; Kanade, T. Visual tracking of high DOF articulated structures: An application to human hand tracking. In Computer Vision — ECCV’94, Lecture Notes in Computer Science; Eklundh, J.O., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; Volume 801, pp. 35–46. [Google Scholar] [CrossRef]
- Isaac, J.H.; Manivannan, M.; Ravindran, B. Corrective Filter Based on Kinematics of Human Hand for Pose Estimation. Front. Virtual Real. 2021, 2, 663618. [Google Scholar] [CrossRef]
- Li, T.; Xiong, X.; Xie, Y.; Hito, G.; Yang, X.; Zhou, X. Reconstructing Hand Poses Using Visible Light. Proc. Acm Interactive Mobile Wearable Ubiquitous Technol. 2017, 1, 71. [Google Scholar] [CrossRef]
- Cerveri, P.; De Momi, E.; Lopomo, N.; Baud-Bovy, G.; Barros, R.M.L.; Ferrigno, G. Finger Kinematic Modeling and Real-Time Hand Motion Estimation. Ann. Biomed. Eng. 2007, 35, 1989–2002. [Google Scholar] [CrossRef] [PubMed]
- Haustein, M.; Blanke, A.; Bockemühl, T.; Bockemühl, A. A leg model based on anatomical landmarks to study 3D joint kinematics of walking in Drosophila melanogaster. Front. Bioeng. Biotechnol. Sec. Biomech. 2024, 12, 1357598. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Li, H.; Yang, Y.; Li, S. Hierarchical topology based hand pose estimation from a single depth image. Multimed. Tools Appl. 2018, 77, 10553–10568. [Google Scholar] [CrossRef]
- Peña-Pitarch, E.; Falguera, N.T.; Yang, J. Virtual human hand: Model and kinematics. Comput. Methods Biomech. Biomed. Eng. 2012, 17, 568–579. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, C.; Brox, T. A Hybrid Model for Real-Time 3D Hand Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Lapresa, M.; Zollo, L.; Cordella, F. A user-friendly automatic toolbox for hand kinematic analysis, clinical assessment and postural synergies extraction. Front. Bioeng. Biotechnol. 2022, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Lee, G.H. Probabilistic Modeling of Hand Pose Under Occlusions with Anatomical Constraints. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023. [Google Scholar]
- Pfisterer, A.; Li, X.; Mengers, V.; Brock, O. A Helping (Human) Hand in Kinematic Structure Estimation. arXiv 2025, arXiv:2503.05301. [Google Scholar] [CrossRef]
- Zhang, F.; Bazarevsky, V.; Vakunov, A.; Tkachenka, A.; Sung, G.; Chang, C.L.; Grundmann, M. MediaPipe Hands: On-device Real-time Hand Tracking. arXiv 2020, arXiv:2006.10214. [Google Scholar] [CrossRef]
- Shoemake, K. Animating rotation with quaternion curves. ACM SIGGRAPH Comput. Graph. 1985, 19, 245–254. [Google Scholar] [CrossRef]
- Ahmad, A.; Migniot, C.; Dipanda, A. Tracking Hands in Interaction with Objects: A Review. In Proceedings of the 13th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Jaipur, India, 4–7 December 2017; pp. 360–369. [Google Scholar] [CrossRef]
- Cheng, W.; Kim, E.; Ko, J.H. HandDAGT: A Denoising Adaptive Graph Transformer for 3D Hand Pose Estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024. in press. [Google Scholar]
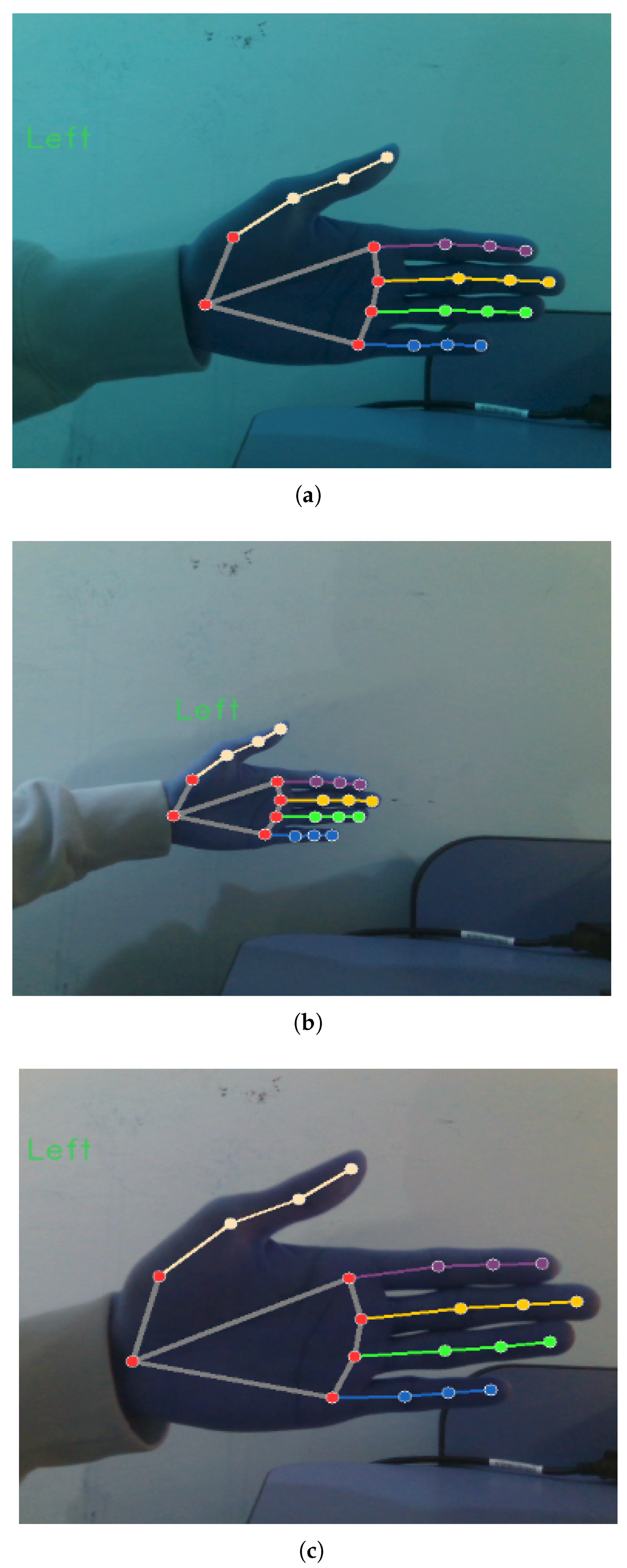
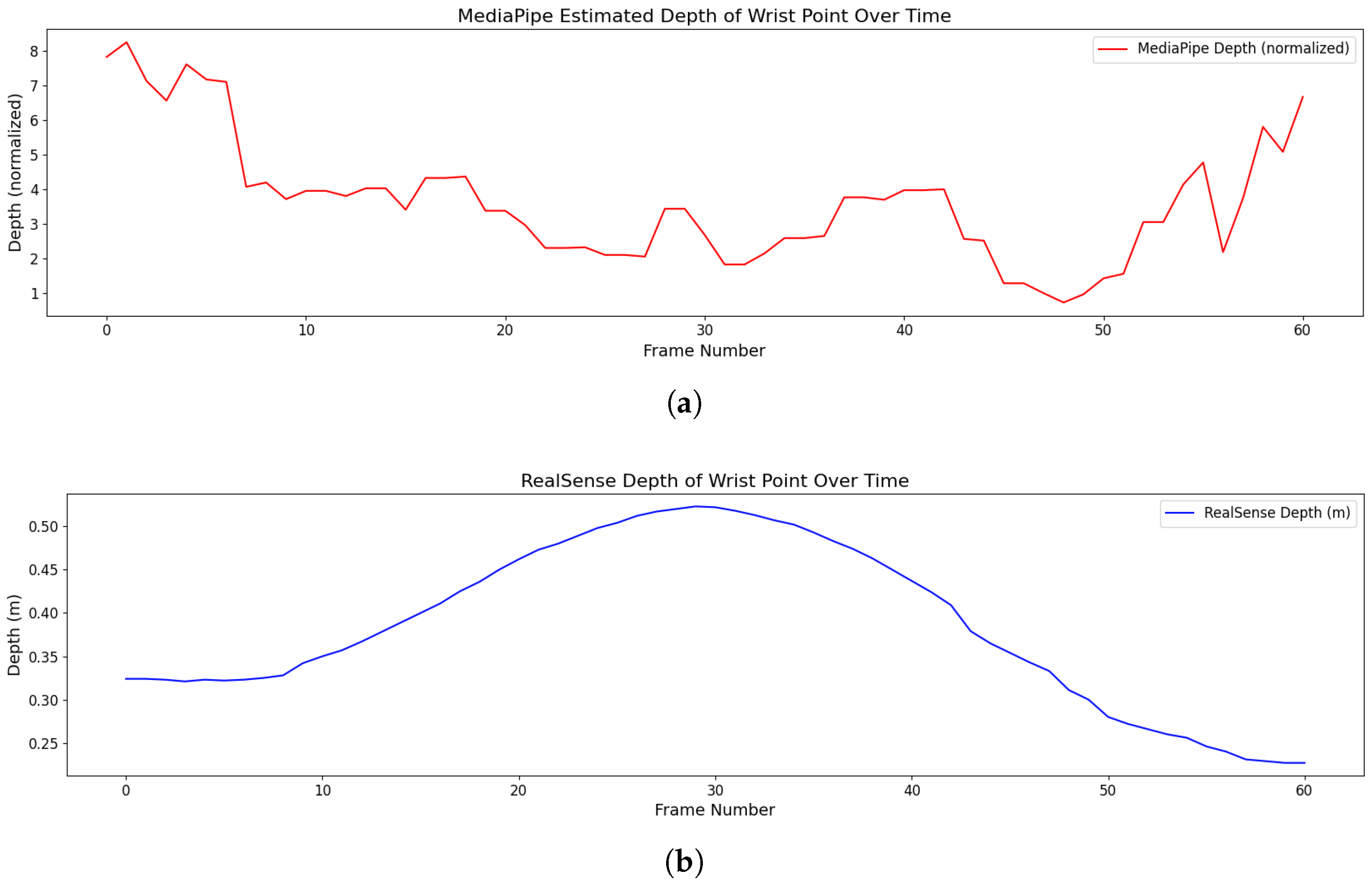
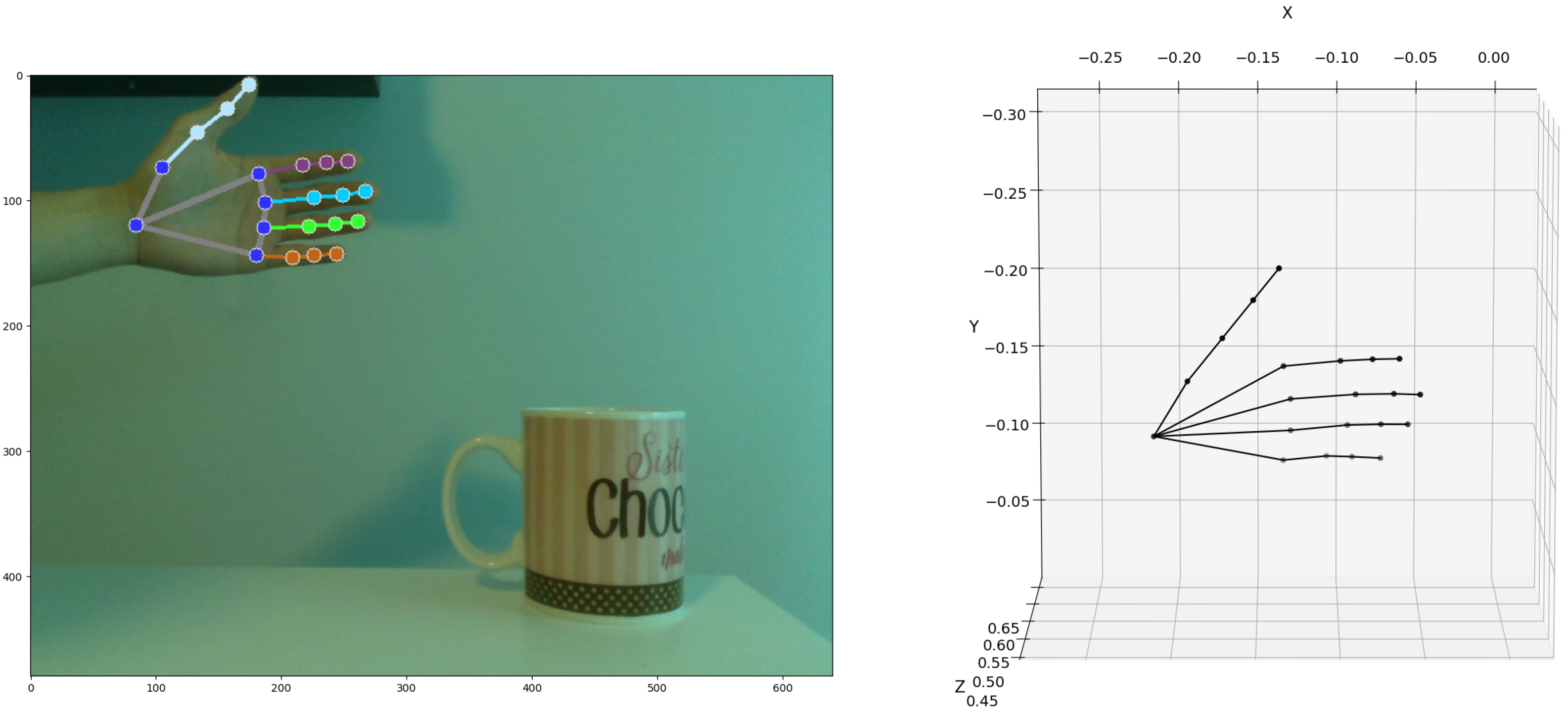


| Joints | MCP (1st Layer) | PIP (2nd Layer) | DIP (3rd Layer) | Tip (4th Layer) | |
|---|---|---|---|---|---|
| Finger | |||||
| Wrist | |||||
| Thumb | |||||
| Index | |||||
| Middle | |||||
| Ring | |||||
| Little | |||||
| Joints | MCP (1st Layer) | PIP (2nd Layer) | DIP (3rd Layer) | Tip (4th Layer) | |
|---|---|---|---|---|---|
| Finger | |||||
| Wrist | (−0.21, −0.11, 0.54) | ||||
| Thumb | (−0.19, −0.15, 0.53 ) | (−0.17, −0.18, 0.54) | (−0.15, −0.20, 0.55) | (−0.14, −0.22, 0.56) | |
| Index | (−0.13, −0.16, 0.56) | (−0.10, −0.16, 0.56) | (−0.08, −0.16, 0.55) | (−0.06, −0.16, 0.55) | |
| Middle | (−0.13, −0.14, 0.57) | (−0.09, −0.14, 0.57) | (−0.07, −0.14, 0.56) | (−0.05, −0.14, 0.55) | |
| Ring | (−0.13, −0.12, 0.57) | (−0.10, −0.12, 0.57) | (−0.07, −0.12, 0.56) | (−0.06, −0.12, 0.56) | |
| Little | (−0.14, −0.10, 0.57) | (−0.11, −0.10, 0.57) | (−0.09, −0.10, 0.57) | (−0.07, −0.10, 0.57) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Payandeh, S. Hand Kinematic Model Construction Based on Tracking Landmarks. Appl. Sci. 2025, 15, 8921. https://doi.org/10.3390/app15168921
Dong Y, Payandeh S. Hand Kinematic Model Construction Based on Tracking Landmarks. Applied Sciences. 2025; 15(16):8921. https://doi.org/10.3390/app15168921
Chicago/Turabian StyleDong, Yiyang, and Shahram Payandeh. 2025. "Hand Kinematic Model Construction Based on Tracking Landmarks" Applied Sciences 15, no. 16: 8921. https://doi.org/10.3390/app15168921
APA StyleDong, Y., & Payandeh, S. (2025). Hand Kinematic Model Construction Based on Tracking Landmarks. Applied Sciences, 15(16), 8921. https://doi.org/10.3390/app15168921








