Optimal Hole Shapes in Composite Structural Elements Considering Their Mechanical and Strength Anisotropy

Abstract

A method for selecting the optimal shape of holes, taking into account the strength anisotropy of composites, is proposed. The methodology includes the following: an algorithm for stress determination based on singular integral equations and Green’s solutions; a strength criterion for the boundary of unloaded holes, which takes into account the anisotropic mechanical and strength properties of composites; an algorithm for determining hole shapes by a formulated nonlinear programming problem. The results of the research are presented for holes of various shapes, including single- and double-periodic hole systems. It is established that the calculated allowable loads for composite plates with holes based on stress concentration factors can be significantly overestimated. At the same time, by designing holes of optimal shape, the allowable loads can be many times greater than those for circular holes.

1. Introduction

Structural elements in various industries are manufactured out of composite materials, which, in terms of strength, specific weight, and other performance properties, surpass traditional metal materials. It is well known that ensuring the reliability of composite structures with holes is a complex problem. This is due to the fact that near the holes, there is a high concentration of stresses, which is generally higher in composites than in isotropic materials.

Cracks often initiate near holes with high stress levels and may grow to critical sizes during operation. In this regard, the problem of reducing stress concentrations near the created holes is relevant.

For isotropic materials, a method based on determining the optimal shape of holes is widely used. Methods for determining the shape of equal-strength holes, in which the stresses at the hole boundary are uniform, have been developed for a wide range of problems. It has been demonstrated that it is at such holes that there are minimum stress levels.

Analytical methods based on the conformal mapping method [1,2,3,4,5] have proven to be effective in obtaining equally strong holes. A system of two holes of optimal shape was considered in [6,7]. In [8], using the method of singular integral equations, a numerical method for obtaining the shapes of holes has been developed. A generalization of methods for determining optimal holes was proposed in [9].

Equal-strength holes are widely used in various industries. In particular, in certain types of aircraft, the windows had the shape of elongated ellipses (elliptical holes are of equal strength for plates that are in biaxial tension).

Composite materials are anisotropic, which significantly complicates the stress analysis in them and, accordingly, makes it difficult to assess their strength. When considering composite materials, it is necessary to take into account that the strength of the region near the boundary of the hole depends not only on the stress distribution, but also on the orientation of the reinforcing elements in them. In particular, as reported in the literature, experimental studies indicate that the failure of composite plates with holes often initiates in zones that are displaced relative to the region of maximum stress concentration.

Only a few works are devoted to determining the optimal shape of holes in composite materials [10]. For composite materials, there are no analytical methods for determining equal-strength holes.

The strength of composites is calculated based on the study of stresses near the holes. The boundary element method (BEM) has become widely used for stress analysis in composite plates with holes [11,12]. Anisotropic plates using BEM were considered in [13,14,15,16]. When applying BEM, as a rule, an integral Somiliano identity in real form, on the basis of which hypersingular integral equations, are further constructed. In this work, we used singular integral equations, as presented in [17] and are based on the Lekhnitskii method [18]. For plates weakened by periodic hole systems, Green’s solutions are additionally used.

Other modern approaches to optimizing structures and analyzing their strength were considered in [19,20].

The aim of this work is to develop a computational method for determining holes of optimal shape using additional experimental data on the mechanical and strength properties of composites. To achieve this aim, the following tasks were performed: the strength conditions for the hole boundary were formulated, accounting for the anisotropy of the mechanical and strength properties of composites; the nonlinear programming problem of determining the optimal hole shape was formulated so as to maximize the allowable loads on the structures; the effectiveness of the proposed approach was demonstrated.

2. Materials and Methods

2.1. Materials

Let us take a closer look at graphite-epoxy and boron-epoxy plates under their uniaxial tension by loads p in the direction of Oy, in which the stiffness of the material is maximum. Strength properties for them are given in

Table 1. Values concerning Formula (1).

Magnitudes	Boron-Epoxy	Graphite-Epoxy
$X_t$, MPa	1380	1035
$Y_t$, MPa	83	41
S, MPa	124	69
$X_c$, MPa	2380	689
$Y_c$, MPa	276	117

and in Figure 1 [21].

Elasticity constants for these materials are given in [21]. In particular, the ratio of Young’s moduli for these materials $W_E=E_{\max }/E_{\min }$ are 41.4 and 9.86, respectively.

2.2. Methods

2.2.1. Strength Criteria for Composite Plates with Holes

We will consider the case of a load-free hole. Consider an arbitrary point M on the boundary of the hole (Figure 2) and denote the hoop stresses in it by σ_θ. Consider a quadrilateral element of small dimensions ABCD, which is adjacent to the boundary and contains the point M.

It can be seen from Figure 2 that the determination of the strength of plates with holes is significantly simplified, since it is reduced to the consideration of elements ABCD, which are under conditions of uniaxial tension by stresses σ_θ (Figure 2).

The literature provides experimental data on the permissible stress values for rectangular specimens made of composite materials that are under uniaxial tension–compression conditions by the loads of p. Limit stress values for glass-epoxy and graphite-epoxy specimens, in which reinforcing elements are placed at an angle θ to the direction of the applied load, are shown in Figure 1. Experimental data for tension is shown here in circles, and for compression in squares [22].

Similar data are given in the literature for other classes of materials [21,23].

Such experimental data are for samples in which reinforcing elements are placed at an angle θ to the direction of action of loads of p, where it is possible to write down the condition of strength in the following form:

$$P_c(\theta )<p<P_t(\theta )$$

(1)

where P_t(θ) and P_c(θ) are limit stresses, which are determined experimentally based on one-sided tension and compression of samples.

To implement the methodology developed in the work, the limiting stresses must be determined for the angles $0<\theta <\pi /2$.

Values of P_t(θ) and P_c(θ) can also be determined by a simpler method, using a smaller amount of experimental data. To do this, consider the Hoffman strength criterion, which is widely used to estimate the strength of composite plates [22] for the general case of loading as

$$-{\displaystyle \frac{{\sigma }_1^2}{X_c{X}_t}}+{\displaystyle \frac{{\sigma }_1{\sigma }_2}{X_c{X}_t}}-{\displaystyle \frac{{\sigma }_2^2}{Y_c{Y}_t}}+{\displaystyle \frac{X_c+X_t}{X_c{X}_t}}{\sigma }_1+{\displaystyle \frac{Y_c+Y_t}{Y_c{Y}_t}}{\sigma }_2+{\displaystyle \frac{{\tau }_{12}^2}{S_{12}^2}}=1$$

(2)

where X_t and Y_t are the limit values of the stresses under uniaxial stretching of the specimen along the first and second axes, respectively; X_c and Y_c are the corresponding values under compression, which are negative; S₁₂ is the limit value of the tangential stresses for the specimen that is under simple shear.

It is assumed here that the plate is referenced to the coordinate system Ox₁x₂, in which the rigidity of the material is maximal in the direction of the axis Ox₁; σ₁, σ₂, and τ₁₂ are the stresses in this coordinate system.

With uniaxial stretching of the plate by loads p at an angle θ to the axis Ox₁, stresses are written in the form [24].

$${\sigma }_1=p {\cos }^2\theta ,{\sigma }_2=p {\sin }^2\theta ,{\tau }_{12}=-p\cos \theta \sin \theta$$

(3)

By substituting stress (3) into condition (2), we obtained the permissible values of load p from the equation.

$$A{p}^2+Bp-1=0$$

where

$$A=-{\displaystyle \frac{{\cos }^4\theta }{X_c{X}_t}}+{\cos }^2\theta {\sin }^2\theta \left({\displaystyle \frac{1}{X_c{X}_t}}+{\displaystyle \frac{1}{S_{12}^2}}\right)-{\displaystyle \frac{{\sin }^4\theta }{Y_c{Y}_t}},B={\displaystyle \frac{X_c+X_t}{X_c{X}_t}}{\cos }^2\theta +{\displaystyle \frac{Y_c+Y_t}{Y_c{Y}_t}}{\sin }^2\theta$$

The root equations have the following form:

$$p_1=-{\displaystyle \frac{B}{2A}}-\sqrt{{\displaystyle \frac{B^2}{4A^2}}+{\displaystyle \frac{1}{A}}}, p_2=-{\displaystyle \frac{B}{2A}}+\sqrt{{\displaystyle \frac{B^2}{4A^2}}+{\displaystyle \frac{1}{A}}}$$

(4)

Thus, in this case, the limit stresses under tension and compression will be $P_t=P_t(\theta )=p_2, P_c=P_c(\theta )=p_1$; $P_c(\theta )=p_{\min }$.

It is shown in [22] that the limit values for stress (1), depending on the angle θ, are obtained in this way for glass-epoxy, graphite-epoxy, and other materials in good agreement with the experimental data (in Figure 1, the calculated values are represented by solid lines). The advantage of using the Hoffmann criterion is that its application requires experimentally determining only five quantities—$X_t, Y_t$, $X_c, Y_c$, and $S_{12}$—while the relationship for the limiting stresses can be obtained in analytical form.

We will use the presented results to record the criterion condition of the strength of the boundary of the load-free hole. Let us denote the obtained hoop stresses at an arbitrary point M of the hole by σ_θ (M).

The angle between the tangent to the hole boundary at this point and the direction (the Oy axis in Figure 2) with the maximum rigidity of the material is denoted by γ = γ(M). The angle between the tangent to the hole boundary at this point and the direction (the Oy axis in Figure 2) with the maximum rigidity of the material is denoted by $P_c(\gamma )<{\sigma }_{\theta }(M)<P_t(\gamma )$

Let us introduce the quantity as follows:

$$S_{\theta }(M)={\displaystyle \frac{{\sigma }_{\theta }(M)}{S_T(M)}},$$

(5)

where $S_T(M)=P_t(\gamma (M))/P_t(0), P_t(0)=X_t$.

The strength of the plate boundary is checked by the condition $S_{\theta }<X_t$ in all its points where ${\sigma }_{\theta }$ is positive. Thus, when calculating the strength, it is necessary, besides the stress distribution over the whole boundary of the hole, to determine the criterion value of $S_{\theta }$, on the basis of which we can estimate permissible loads. When calculating the strength of isotropic materials, the calculations are limited to calculating the maximum stress values (SCF). When calculating the strength of composite materials, a similar quantity is the maximum value of the quantity $S_{\theta }$, which will be denoted as SCFA (the first letter indicates that this coefficient takes into account the strength anisotropy of the material).

2.2.2. Calculation of Stresses in Anisotropic Plates with Holes

The boundary element method (BEM) was widely used to determine the stresses in plates with holes [13,14,15,16]. Anisotropic plates, according to BEM, were considered in [15,16,17,18]. When using BEM, the Somiliano integral representation is, as a rule, used in real form, on the basis of which the hypersingular integral equations are then written. To determine the stresses near the holes, the method of integral equations, which is based on the Lekhnitskii method [18], was used. To make the equations, we will use the approach developed in [25]. Let us consider an anisotropic plate that occupies region D and is weakened by holes with boundaries $L_j, j=1,\dots ,J$. Next, let us express the solution in terms of Lekhnitskii’s potentials $\Phi (z_1), \Psi (z_2)$, where $z_j=x+s_{j}y$, $s_j$ are roots with a positive imaginary part of the characteristic equation [18]. Then we can write the integral equations for such a plate with holes in such a way that the conditions on the boundary of region D are satisfied automatically. For this purpose, it is necessary [25] to write Lekhnitskii’s complex potentials ${\Phi }_j^D, {\Psi }_j^D$ (j = 1, 2), which are the solution of the problem of elasticity for domain D with selected homogeneous conditions on the boundary. This is true, provided that these functions have the following features at an arbitrary point $(x_0,y_0) \in D$:

$${\Phi }_j^D~-{\displaystyle \frac{A_j}{z_1-z_{10}}}, {\Psi }_j^D~-{\displaystyle \frac{B_j}{z_2-z_{20}}}, j=1,2$$

(6)

where $z_{10}=x_0+s_1{y}_0, z_{20} =x_0+s_2{y}_0$,

$$\begin{gathered} A_1=-{\displaystyle \frac{i{s}_1}{2\pi {\Delta }_1}}, A_2={\displaystyle \frac{i}{2\pi {\Delta }_1}}, B_1=-{\displaystyle \frac{i{s}_2}{2\pi {\Delta }_2}}, B_2={\displaystyle \frac{i}{2\pi {\Delta }_2}} \\ {\Delta }_1={\alpha }_{11}(s_1-s_2)(s_1-\overline{s_1})(s_1-\overline{s_2}), {\Delta }_2={\alpha }_{11}(s_2-s_1)(s_2-\overline{s_1})(s_2-\overline{s_2}) \end{gathered}$$

(7)

Let us denote these potentials as ${\Phi }_j^D(z_1,T), {\Psi }_j^D(z_2, T)$, where T is a point with coordinates $( x_0,y_0)$. The general solution to the problem of elasticity (Lekhnitskii potentials) for region D with holes with load-free boundaries has the following form [25]:

$$\begin{gathered} \Phi (z_1)={\displaystyle \underset{L}{\int }[{\Phi }_1^D(z_1,T)u^{\prime }(s)+{\Phi }_2^D(z_1,T)v^{\prime }(s)]ds}+{\Phi }_D(z_1), \\ \Psi (z_2)={\displaystyle \underset{L}{\int }[{\Psi }_1^D(z_2,T)u^{\prime }(s)+{\Psi }_2^D(z_2,T)v^{\prime }(s)]ds}+{\Psi }_D(z_2), \end{gathered}$$

(8)

where ${\Phi }_D(z_1)={\Phi }_D^P(z_1)+{\Phi }_D^{\infty }(z_1), {\Psi }_D(z_2)={\Psi }_D^P(z_2)+{\Psi }_D^{\infty }(z_2)$, T is a point with which integration is performed, and $L=L_1+\dots ,L_J$.

There is potential that ${\Phi }_D^P, {\Psi }_D^P$ are solutions to elasticity problems for area D with homogeneous boundary conditions under the action of infinite forces and (or) concentrated forces applied to the plate.

By construction, the potentials (8) identically satisfy the given conditions on the boundary of domain D for arbitrary functions $u^{\prime }, v^{\prime }$.

Integral equations for obtaining $u^{\prime }, v^{\prime }$ are achieved after substituting (8) into the boundary conditions [17]. The algorithm for solving integral equations that are singular is given in [17]. In its construction, quadrature formulas for regular and singular integrals from work [26,27] were used.

3. Results and Discussion

Calculation of the Strength of Composite Plates with Specified Hole Shapes

Let us take a closer look at graphite-epoxy and boron-epoxy plates under uniaxial tension by loads p in the direction of Oy, in which the stiffness of the material is maximum. Their strength properties are given in Table 1 and in Figure 1 [22].

Calculated for graphite-epoxy and boron-epoxy plates with a circular hole, the maximum values of stresses, divided into p (SCF), and the maximum values of $S_{\theta }$, divided into p (SCF), are given in

Table 2. SCF and ultimate loads for holes of different shapes.

Hole	SCF		${\mathit{S}}_{\mathit{\theta } \mathbf{max}}/\mathit{p}$		${\mathit{p}}_{\mathit{K}}$ (MPa), on the Basis of SCF		${\mathit{p}}_{\mathit{S}} \left(\mathbf{MPa}\right), \mathbf{Based} \mathbf{on} {\mathit{S}}_{\mathit{\theta }}$
	Graphite-Epoxy	Boron-Epoxy	Graphite-Epoxy	Boron-Epoxy	Graphite-Epoxy	Boron-Epoxy	Graphite-Epoxy	Boron-Epoxy
Circle	10.59	6.94	10.59	6.94	97.7	198.8	97.7	198.8
Ellipse	20.18	12.87	25.24	18.85	51.29	107.2	41	73.3
Square	5.91	4.54	16.32	9,13	175.1	304.0	63.4	151.1
Optimal	5.52	5.42	5.01	4.06	187.5	254.6	206.6	339.9

. The table also presents the values of the limit loads calculated on the basis of the SCF (value of $p_K$) and based on $S_{\theta }$ (value of $p_S$). Thus, for a circular hole, it turned out that $p_S=p_K$, i.e., the calculation in this case can be performed on the basis of the SCF.

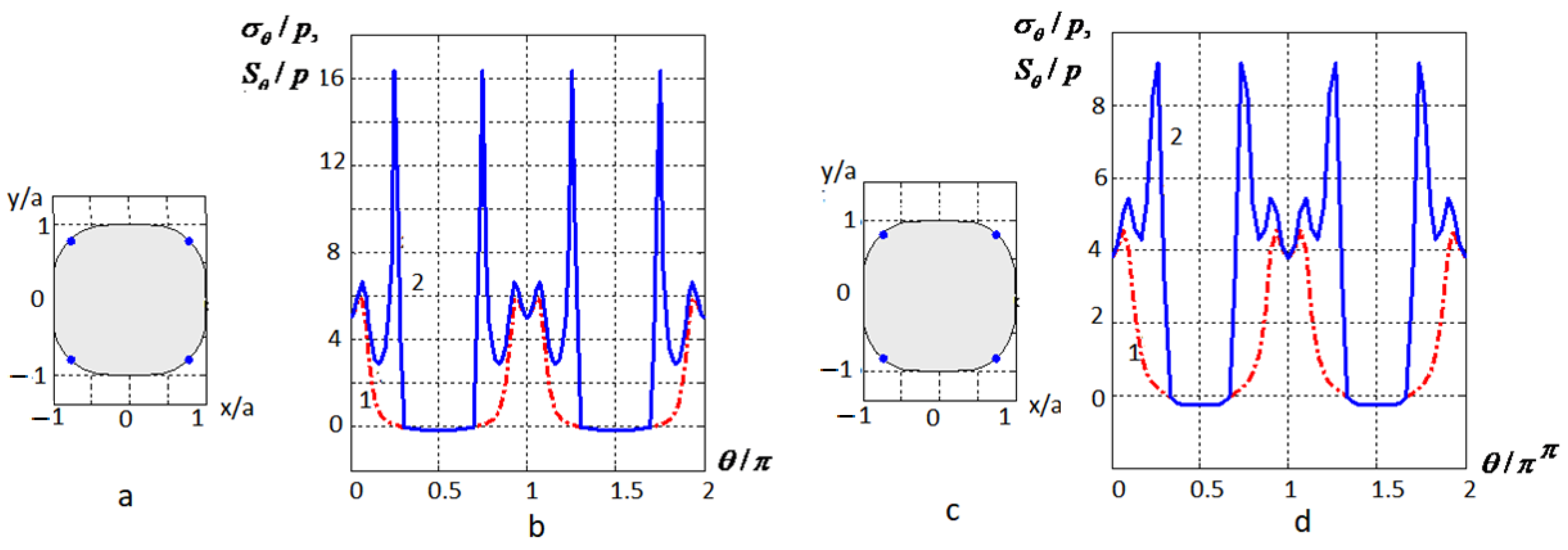
In Figure 3 curves 1 (dashed lines) represent the hoop stresses divided into p at the boundary of an elliptical hole with a ratio of semi-axes of 0.5 for graphite-epoxy (Figure 3b), as well as for boron-epoxy (Figure 3d) plates when the reinforcing elements are parallel to the Oy-axis. Solid curves 2 represent the value of $S_{\theta }/p$, which is the starting point for strength calculation. Figure 3a,c are the shape of the hole in the plate. The dots indicate the points on the boundary where fracturing will begin (the values $S_{\theta }$ are much greater than the maximum stresses). In Figure 3, on the left, there are the points of the ellipse at which the value $S_{\theta }$ is maximum, and therefore it predicts the beginning of the initiation of fracture.

From Figure 3, it can be seen that the fracture will begin at the four points on the boundary in which the value of the quantity $S_{\theta }$ is significantly greater than the maximum stresses that are reached at $x=\pm a$. The values of the maximum stresses and permissible values of loads p for this case are given in Table 2.

Let us consider a square-shaped hole with its half sides and vertices rounded by arcs of a circle with radius a/2 (Figure 4a,c). Calculated relative stress and the value $S_{\theta }$/p are shown in Figure 4.

The SCF calculated for this case is equal to 5.913 for graphite-epoxy and 4.542 for boron-epoxy plates. That is, these values are significantly smaller than those for the case of a circular hole (see Table 2). At the same time, (Figure 4a,c) it can be seen that the fracture will begin at the four points on the boundary in which the value of $S_{\theta }$ is significantly greater than the maximum stresses. These points for the two materials are on the rounded boundary arcs (shown in dots). The value of the permissible loads for these two plates will be 63.4 MPa and 151.1 MPa, i.e., much less than those for a circular hole.

Therefore, for composite plates with holes of a typical shape (round, square with rounded vertices), the permissible loads are much lower than that for solid plates.

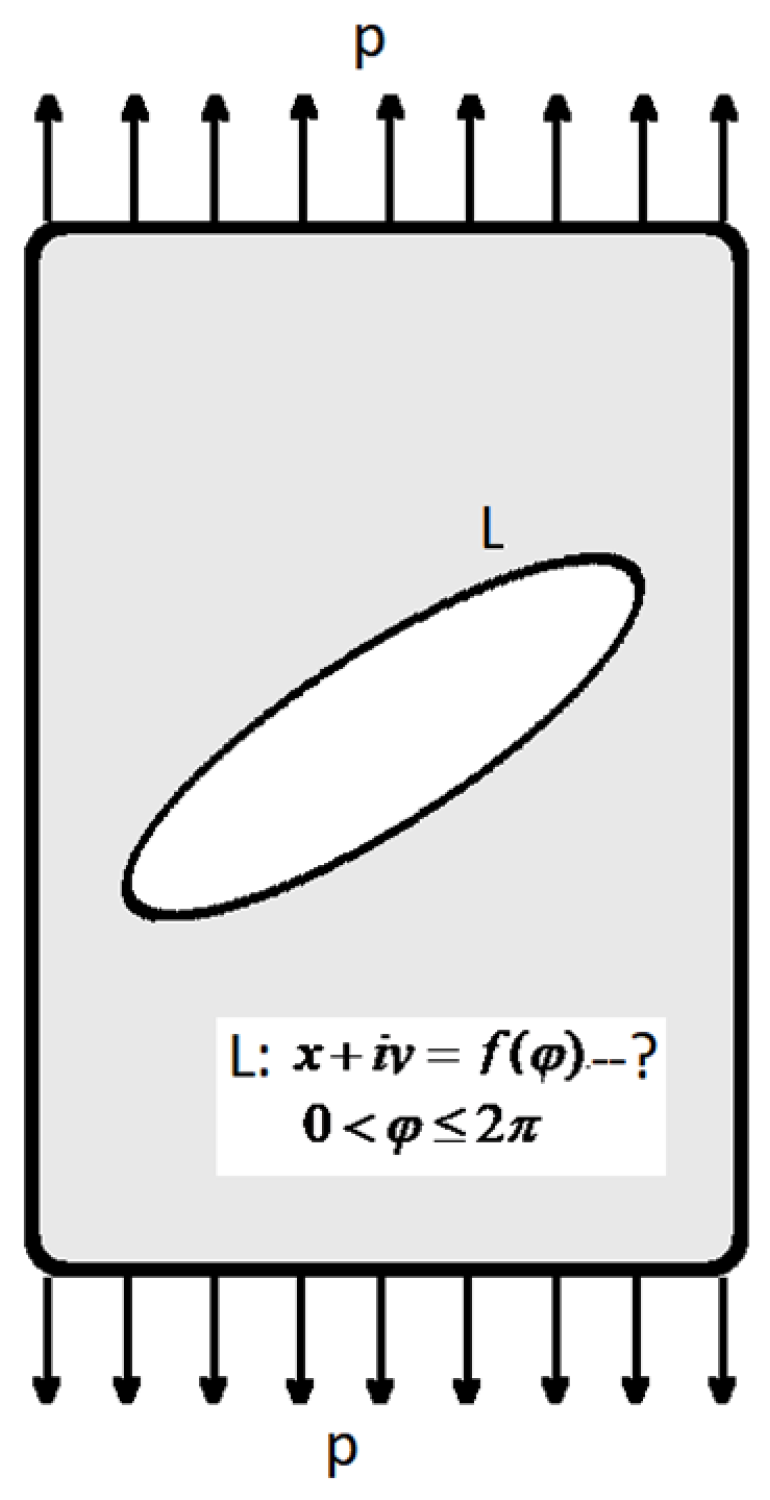
4. Holes of Optimal Shape

The results obtained above show that stress concentration significantly reduces the strength of composite materials. Therefore, the task of choosing the shape of the hole (Figure 5) in such a way as to reduce the stress level and the level of $S_{\theta }$ is relevant. Consider a plate with a hole that is under the action of uniaxial tension by load p, and starting from the following statement of the problem, we will write the equation of the boundary of the searched hole shape in the form of $x+iy=\omega (\zeta )$, where

$$\omega \left(\zeta \right)=a\zeta +{\displaystyle \sum _{j=1}^J\frac{a_j}{{\zeta }^j}}$$

(9)

where $\zeta =\cos \phi +i\sin \phi$, $0\le \phi \le 2\pi$, $a, a_j$ are unknown constants that satisfy certain equations that follow on the conditions imposed on the contour.

The chosen functional dependence (9) for describing the contour is used in the conformal mapping of the exterior of the hole onto the exterior of a circle of unit radius. It is known that for an arbitrary region, there exists a mapping function of the form (9) when $J\to \infty$. That is, by choosing a sufficiently great J here, any hole profile can be obtained. The coefficients must be such that the condition $\left|{\omega }^{\prime }(\zeta )\right|>0$ is satisfied [28]. For this problem, there is an optimal hole near which there is no stress concentration—a rectilinear section parallel to the Oy-axis. However, this case has no practical value. Let us narrow down the class of holes among which we will search for the optimal hole.

Next, we will consider holes that have symmetry relative to the center of the optimal hole. Then the coefficients $a, a_j$ will be real numbers, while $a_2=a_4=a_6\dots =0$. We will also put restraints in the sought after coefficients in the form of the inequalities

$${\alpha }_j<a_j<{\beta }_j, j=1,3,\dots ,J$$

(10)

where ${\alpha }_j,{\beta }_j$ are the given numbers ${\alpha }_j<{\beta }_j, \left|{\alpha }_j\right|<1/j,\left|{\beta }_j\right|<1/j$.

The algorithm for solving the problem of elasticity concerning holes [17,21] allows us to determine the stresses and, accordingly, the values of $S_{\theta }$ on the boundary contour at selected nodal points $M_n, n=1,\dots ,N$ with arbitrarily set coefficients $a, a_j$ in Equation (9). Let us denote the value of the function $S_{\theta }$ at these points by $S_n$, as well as consider the fact that $S_n=S_n(a,a_1,\dots ,a_J)$. We obtained the unknown coefficients from the problem, as well as the minimum value of the quantity

$$I={\displaystyle \sum _{n=1}^N{S}_n^m}$$

if conditions (10) are satisfied.

It should be noted that equal-strength holes for isotropic materials are determined using this approach.

The formulated problem belongs to the well-studied problem of nonlinear programming, for which effective solution methods have been developed in the literature [29]. When solving the problem of nonlinear programming, we limited the quantities J and m to the values J = 7, m = 4. As an initial approximation, we took $a=1, a_1=a_3=a_5=a_7=0$ (that is, the minimization began with consideration of a circular hole).

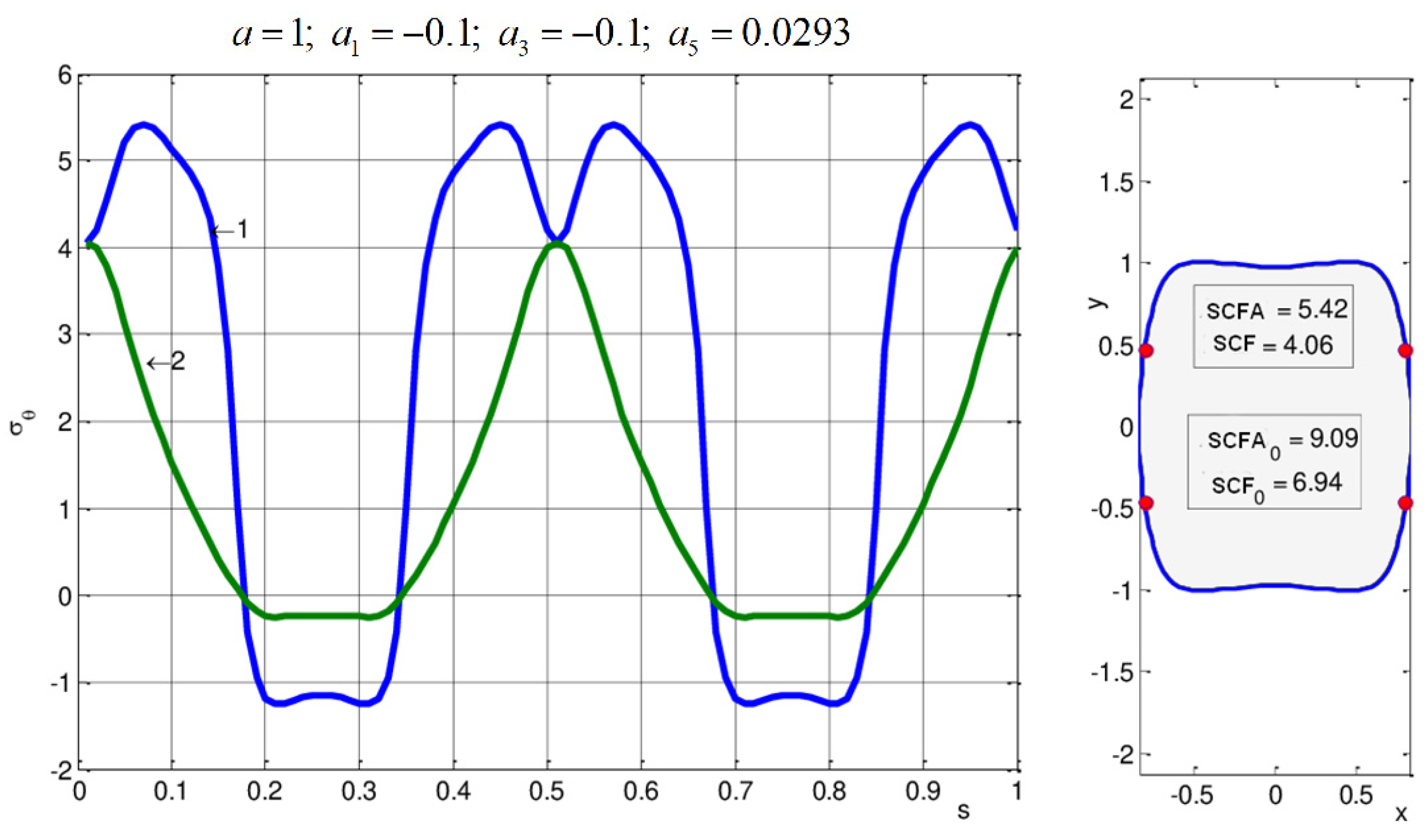
The calculated shapes of the holes and the distribution of relative stresses on them for a graphite-epoxy plate are shown in Figure 6 and for a boron-epoxy plate in Figure 6. Values of $S_{\theta }(\theta )/p$ calculated here are given by lines 1, while the hoop stresses divided into p are given by lines 2. The values of the coefficients in Formula (6) are given above. The shape of the hole is shown on the right. Here, the values of SCF for the optimal hole are (SCF = 5.01) and the maximum value of the quantity $S_{\theta }(\theta )/p$ is (SCF = 5.22). Similar values for a circular hole are given below for comparison. That is, the values of SCF and SCF decreased by more than half at the obtained hole. Accordingly, the permissible loads for a plate with an optimal hole turned out to be twice as large as those for a circular hole.

Analogous results for the boron-epoxy plate are shown in Figure 7.

Calculated SCF, as well as maximum values of the criterion quantity of $S_{\theta }(\theta )/p$ and limit loads, are given in Table 2.

From the data given in Table 2, it is found that:

(1)

Calculations of the strength of structural elements made of composite materials must be performed with complete consideration of the mechanical and strength properties of the material. At the same time, a comparative estimation of the strength of plates with holes of various shapes, based only on SCF, can lead to erroneous conclusions.

(2)

Fractures in plates with sufficiently close strength and mechanical properties can differ significantly not only in value, but also in character.

(3)

By creating holes of optimal shape (Figure 6 and Figure 7), the limit loads for the considered composite plates can be increased by approximately two times compared to the case of a circular hole.

(4)

From the point of view of strength, the least favorable hole was a square-shaped hole with rounded vertices, although its SCF turned out to be much smaller than for a circular hole. The shape of the optimal hole is close to a rounded square, but the limit loads for the former are more than twice as large as that for the latter.

(5)

Limit loads can reach 353.8 MPa for boron-epoxy plate and 213.8 MPa for graphite-epoxy plates. These loads are quite large compared to the corresponding values for most conventional materials.

5. Taking into Account the Mutual Influence of Holes

Let us consider two symmetrically placed holes, the centers of which are located at the points $(\pm x_c,0)$, and each of the holes can be located in the ring mentioned above and drawn from the aforesaid centers; the plate is stretched by the load p in the direction of the Oy-axis. The results of calculations at $x_c=1.5$ R for a graphite-epoxy plate, with (solid lines) and without considering strength anisotropy, are shown in Figure 8.

It can be seen that, when taking into account the strength anisotropy at the optimal hole, the permissible stresses decrease by more than 3 times.

6. One-Period System of Holes

Consider a boron-epoxy plate, which has a system of periodically placed holes on the axis Ox with centers at $0,\pm d,\pm 2d,\dots$, the plate is stretched in the direction of the Oy-axis (Figure 9). Green’s solution (potentials ${\Phi }_j^D(z_1,T), {\Psi }_j^D(z_2, T)$) is given in [29].

Calculated values of $S_{\theta }$/p and hoop stresses on the central hole are shown in Figure 10 by curves 1 and 2. Solid lines correspond to d = 2.5, dashed lines to d = 3, and dotted lines to d = 4.

The shape of the optimal hole and that of circular hole of equal size at d = 2.5 are shown in Figure 10 on the right.

Table 3. Coefficients of (9) and values of SCFA and SCF for a periodic system of holes; transverse tension.

d	A	a1	a3	a5	a7	S	SCFA	SCF	SCFA0	SCF0
2.5	1.000	−0.167	−0.083	0.030	−0.008	2.973	7.042	4.812	14.177	10.737
3	1.000	−0.167	−0.083	0.031	−0.008	2.972	6.383	4.365	11.491	8.655
4	1.000	−0.167	−0.083	0.031	−0.007	2.973	5.815	4.080	10.036	7.608

shows the values of the coefficients of (6), the area occupied by the hole, the maximum values of $S_{\theta }$/p (SCFA), and stress concentration factors (SCFs) for the case of optimal holes. For comparison, similar data is presented for a circular hole of the same area, which is marked by SCFA₀ and SCF₀ (with the subscript 0) as given below.

Similar results are obtained for the case when the plate is stretched along the axis Ox (longitudinal tension), as well as when the rigidity of the material is maximal in the horizontal direction. The results of the calculations are shown in Figure 11 and in

Table 4. Coefficients of (9) and values of SCFA and SCF for a periodic system of holes; longitudinal stretching.

d	A	a1	a3	a5	a7	S	SCFA	SCF	SCFA0	SCF0
2.5	1	0.167	−0.083	0.007	0.010	2.986	1.753	1.488	3.391	2.685
3	1	0.167	−0.083	0.001	0.008	2.987	1.972	1.642	3.682	2.893
4	1	0.167	−0.083	−0.007	0.004	2.988	2.308	1.890	4.196	3.265

.

It can be seen from Table 3 and Table 4 that on holes of optimal shape, the limit values of loads are approximately twice as large as those for plates with a circular hole. At the same time, the concentration of stresses when the holes converge increases with transverse stretching and decreases with longitudinal stretching.

Two-period problem. Perforated plates with a large number of holes are often used. In this case, consider a two-period system of holes. Green’s junction (potentials ${\Phi }_j^D(z_1,T), {\Psi }_j^D(z_2, T)$) is given in [30,31]. Let us assume that the main period has the shape of a square with side d, and the plate is stretched by loads p in the direction of the Oy-axis (Figure 12).

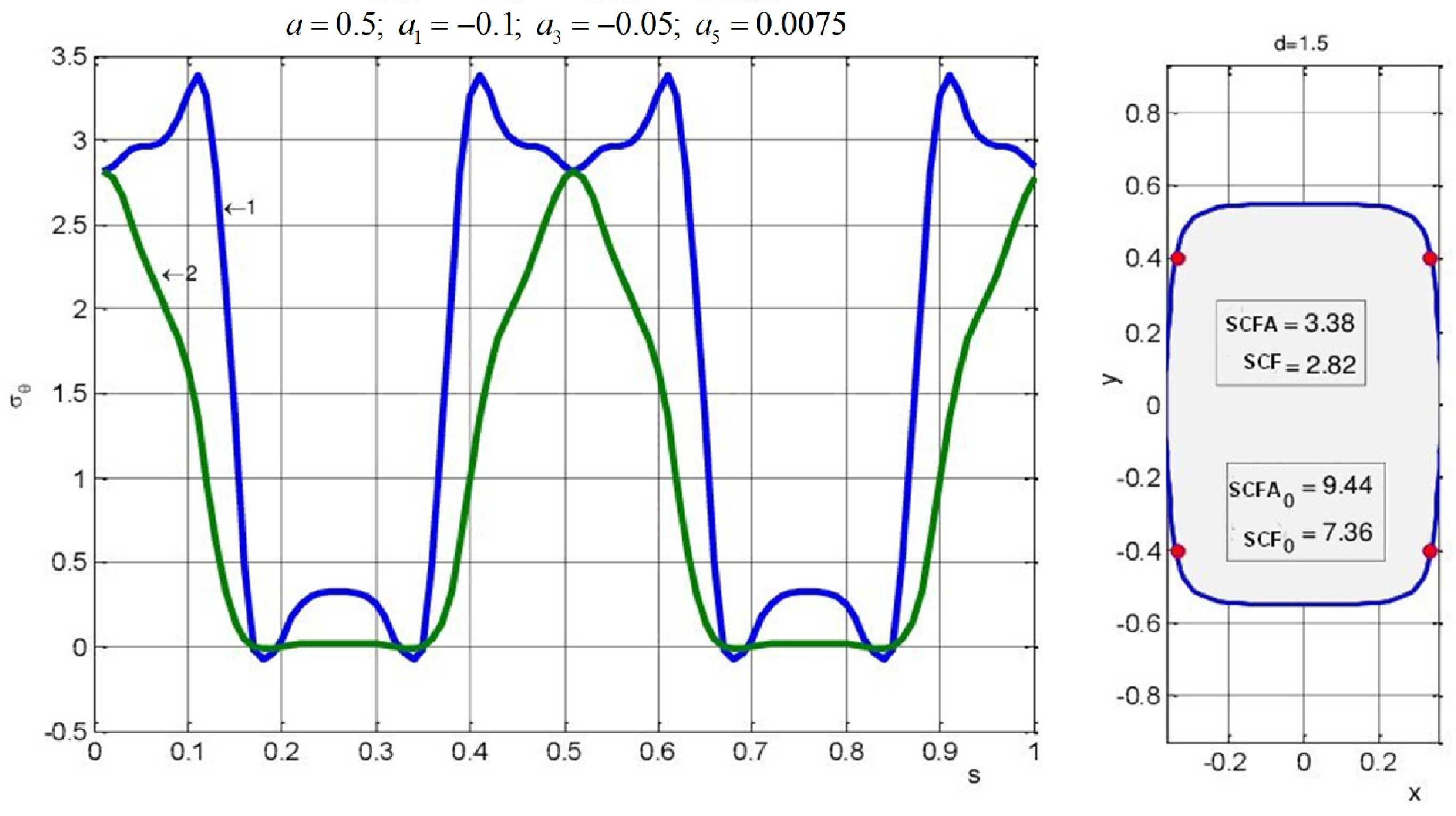
Calculations were made for a boron-epoxy plate at d = 1.25, d = 1.5, d = 2, the results of which are shown in Figure 13, Figure 14 and Figure 15. In the figure below, the values of the coefficients for (6) are presented. The value of the first coefficient a was assumed equal to 1, due to which the sought hole was located in a circle with a radius of ~0.5.

From the given data, it shows that the limit loads in a plate with an optimal hole of 3.57, 2.8, and 2.36 are greater in comparison with those of a plate with circular holes of equal size at d = 1.25, d = 1.5, and d = 2.

Above, the stresses in a plate with a two-periodic system of holes arranged in a square lattice were determined. To assess the accuracy of the algorithm used, the stresses in an isotropic plate with a two-periodic system of circular holes of radius a and a distance between the holes, given as d, were determined.

The calculated SCF for different ratios of the radius and distances between the holes are given in

Table 5. Comparison of SCF for a two-period problem.

d/a	0.1	0.2	0.5	0.8
SCF	21.682 (21.581)	11.701 (11.712)	5.773 (5.773)	4.3803 (4.364)

. Here, for comparison, the results of calculations for an isotropic plate from [32] are also given in parentheses.

It can be seen that the relative deviation between the data obtained by different methods does not exceed 0.5% for d/a > 0.2.

7. Conclusions

A method for increasing the strength of composite plates has been developed, based on the optimal selection of the hole shapes. The method takes into account the anisotropy of the strength properties of composites.

The study of stresses in composite plates was performed by the method of singular integral equations, the kernels of which are constructed on the basis of Green’s solutions.

The calculation of strength was performed using the generalized stress concentration coefficient (SCFA), which incorporates both stresses, while the anisotropic strength of the materials is taken into account.

The incorrectness of calculations of the strength of composite materials based on SCF was established. In particular, for a square hole with rounded vertices in a graphite-epoxy plate, SCF turned out to be almost twice as small as that for a circular hole. At the same time, the calculated allowable forces accounting for strength anisotropy were 1.5 times greater for a plate with a circular hole.

An approach to determining the hole shapes is proposed, at which the permissible loads on the composite were maximized. The coefficients of the equations describing the hole shape were determined by solving the nonlinear programming problem. Based on the performed calculations, the following was established:

(a) For the considered composite plates with holes of optimal shape, the limiting loads are approximately twice as high as those for a circular hole;

(b) The limiting loads for boron-epoxy and graphite-epoxy plates with optimally shaped holes were higher compared to the corresponding values for traditional materials.

Optimal hole shapes were also determined for the following configurations: two closely spaced holes; a single-periodic system of holes; and a two-periodic system of holes arranged in a square lattice.

The effectiveness of the proposed approach is demonstrated for cases where the hole sizes are small compared to the overall sizes of the plate. The same approach can be used for plates of limited sizes. The stress determination algorithm required for its implementation can be based on the method of integral equations or the finite element method.