Abstract
Radar jamming resource allocation is crucial for maximizing jamming effectiveness and ensuring operational superiority in complex electromagnetic environments. However, the existing approaches still sufferfrom inefficiency, instability, and suboptimal global solutions. To address these issues, this work proposes addressing effective jamming resource allocation in dynamic radar countermeasures with multiple jamming types. A deep reinforcement learning framework is designed to jointly optimize transceiver strategies for adaptive jamming under state-switching scenarios. In this framework, a hybrid policy network is proposed to coordinate beam selection and power allocation, while a dynamic fusion metric is integrated to evaluate jamming effectiveness. Then the non-convex optimization is resolved via a proximal policy optimization version 2 (PPO2)-driven iterative algorithm. Experiments demonstrate that the proposed method achieves superior convergence speed and reduced power consumption compared to baseline methods, ensuring robust jamming performance against eavesdroppers under stringent resource constraints.
1. Introduction
Radar jamming is an electronic countermeasure where a transmitter emits signals to disrupt a radar’s ability of detecting and tracking targets. By suppressing or deceiving the radar receiver, the jammer degrades situational awareness and protects assets in modern warfare. Radar jamming resource allocation is crucial for maximizing jamming effectiveness and ensuring operational superiority in complex electromagnetic environments, which has widely adopted heuristic algorithms due to their scalability and adaptability to large-scale optimization [1]. Previous studies optimized jamming allocation using detection probability models and cooperative strategies [2,3,4] or combinatorial algorithms [5,6], while radar-side resource allocation employed modified PSO [7]. Distinctly, this work [8] introduces a game-theoretic framework, formulating the radar–jammer interaction via a novel utility function and the CPAG algorithm to find the strategic Nash Equilibrium—moving beyond single-sided optimization. These optimization-based approaches primarily employ frame-by-frame optimization, which suffers from inefficiency, instability, and suboptimal global solutions. As deep reinforcement learning (DRL) offers dynamic resource allocation through agent–environment interactions, some approaches [9,10,11] have begun to employ DRL algorithms for jamming policy optimization in radar countermeasure scenarios. Among them, to quickly find a jamming policy for multifunctional radar, an advantage actor–critic (A2C)-driven jamming policy generation scheme [12] was introduced, utilizing heuristic reward functions and Markov decision process-based interactive learning. In [13], to address the joint optimization issue of jamming task and power allocation within the netted radars anti-jamming fusion game, a hierarchical reinforcement learning-based jamming resource allocation scheme was established, neglecting the dynamic action switching of the jammer based on radar operating state. These DRL-based approaches could optimally adjust the jamming policy to the limited states of radars.
However, these existing approaches fail to comprehensively model the intricate game-theoretic interplay between jammers and netted radars, particularly in mixed discrete-continuous action spaces of jammers. It does not address adaptive jamming policy optimization under dynamic radar state-switching constraints using DRL-based joint transceiver design. The efficient collaborative exploration is absent in heterogeneous action spaces. Meanwhile, the difficulty in adapting to non-stationary environmental disturbances caused by real-time radar state switching is increased. Consequently, the policy network in DRL framework needs to be adaptive to the dynamic variation of jammers, which has not been explored sufficiently.
In this work, to address the challenge of previous works, we design a multi-stage game optimization framework with a hybrid policy network (HPN)-based DRL. The game process between the jammer agent and the netted radars is shown in Figure 1. In the framework, jammers are modeled as intelligent agents with rigorously defined state transition rules under composite jamming environments. For various jamming types, the framework aims to maximize penetration distance, ensuring the successful accomplishment of the mission, while minimizing jamming power consumption. The resulting non-convex optimization problem is then addressed via a PPO2-driven [14] iterative algorithm, enabling adaptive policy generation under dynamic radar state-switching constraints. The main contributions are summarized as follows.

Figure 1.
The game process of the jammer agent and the netted radar.
- A hybrid policy network is designed to simultaneously generate coordinated beam selection and power allocation actions across the decomposed action space, enabling the jammer to efficiently handle mixed actions in complex confrontation scenarios.
- A dynamic weighted fusion metric is introduced to comprehensively assess the jamming effectiveness, with weights dynamically adjusted based on the radar’s various operational stages.
- The PPO2 algorithm is employed to train the reinforcement network, preventing policy collapse due to improper power allocation through importance sampling ratio clipping, and balancing task success and energy efficiency.
2. Jamming Model of Netted Radars
In this context, we aim to address a one-to-many electronic warfare scenario where an adaptive jammer, escorting a penetration target, allocates jamming resources against an N-node netted radar system. The jammer employs multi-beam coverage to engage all radars simultaneously, optimizing type-power coordination under full radar-state observability.
2.1. Active Jamming Type
Research on active jamming techniques for netted radar systems must be systematically designed based on their netted characteristics. Netted radars enhance detection capabilities through multi-node collaboration, yet significant differences in parameters such as frequency band configuration, signal structure, and deployment locations among nodes render a single jamming strategy ineffective in synchronously suppressing all network nodes. Radar jamming can be categorized by energy source into two primary types as follows: passive jamming and active jamming [15,16]. Passive jamming, which employs media such as chaff to reflect or absorb radar waves, exhibits strong concealment but suffers from poor controllability. Active jamming, which actively transmits electromagnetic signals to disrupt radar operations, has become the preferred solution in contemporary netted radars confrontation scenarios due to its high adaptability and precise control advantages.
The engineering implementation of active jamming encompasses two distinct paradigms—suppression jamming and deception jamming—whose operational principles and application scenarios exhibit complementary relationships. Suppression jamming transmits high-power noise signals to saturate the target frequency band, significantly degrading the signal-to-noise ratio (SNR) of the radar receiver and thus reducing its target detection probability and operational range. Such jamming directly disrupts radar signal processing systems, particularly demonstrating efficacy against modern radars employing complex signal modulation techniques. Deception jamming replicates radar signal waveforms while introducing artificial error parameters, generating false echoes with characteristics similar to genuine targets to mislead radar perception.
2.2. Radar Echo Signal Model Under Jamming Condition
The composite signal received by radar node n at time k consists of target reflections and jamming components as follows:
where t is a continuous-time variable, represents the transmission path loss, denotes the transmitted power of the radar, stands for the reflection coefficient of the target, represents the normalized complex envelope of radar transmitted signal, indicates the transmission delay, is the Doppler shift, and is the zero-mean white Gaussian noise. and can be calculated by the following formulas:
where c denotes the speed of light, represents the wavelength of the radar-transmitted signal, , and correspond to the velocity components of the penetrating target, , and denote the target’s 3D Cartesian coordinates at time k, , and denote the radar’s 3D Cartesian coordinates at time k, and quantifies the instantaneous range between radar n and the target at the time k as follows:
The radar detects penetrating target by transmitting pulsed signals and receiving target echoes. Assuming identical operational parameters across all radars, the received echo-signal power at radar n from the target is given by the following [3,17]:
where denotes the transmit power of the radar n, represents the antenna gain, is the radar cross-section (RCS) of the target relative to radar n at time k, and quantifies the instantaneous distance between radar n and the target at time k.
The received signal at radar n contains both target echoes and jamming components, and the received jamming power is as follows [3,17]:
where denotes the power of the jamming signal transmitted by the jammer to radar n, is a binary variable indicating whether radar n is being jammed at discrete time k, indicates the jammer transmit antenna gain, corresponds to polarization mismatch loss, defines the distance between the jammer and radar n at time k. As shown in Figure 2, represents the angular separation within the target–jammer–radar geometric configuration, and describes the radar antenna gain pattern as a function of , typically modeled by the following [13]:
where represents the 3-dB beamwidth of the radar antenna, and denotes the antenna gain coefficient.
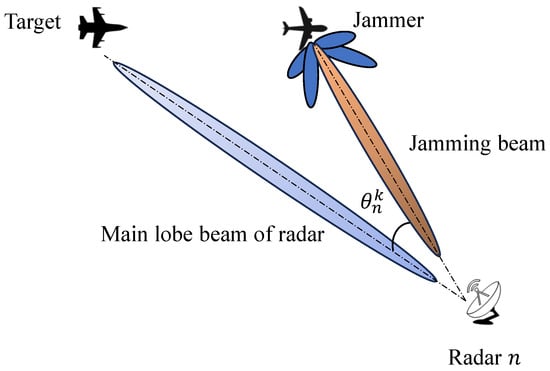
Figure 2.
Schematic diagram of relative positions among the jammer, radar, and target.
2.3. Jamming Effect Evaluation Index
2.3.1. Detection Probability
When subjected to active suppression jamming, the radar receiver acquires not only target echo signals and inherent system noise but also suppression jamming signals. Considering a radar n detecting the target under such conditions, the SNR is defined as follows:
where represents the receiver’s thermal noise power.
The fundamental principles of radar detection indicate that when the target fluctuation type is known, the detection probability for a specific target can be calculated by combining the SNR [18]. We assume that the target fluctuation follows the Swerling I detection model, and the single-pulse detection probability of radar n for target at time k is expressed as:
where represents the detection threshold determined by the false alarm probability requirement, denotes the number of non-coherent pulse integrations.
In netted radar systems, each radar generates local detection criteria, which will be aggregated at the fusion center via the fusion rule [19] to achieve robust decision-making. This framework ensures efficient information fusion while maintaining operational resilience against jamming threats. We assume that each radar n makes a local binary decision , where indicates target detection and indicates no detection. The fusion center collects these decisions into a global decision vector . Since each can take one of two values, there are possible distinct combinations for D. The fusion rule for the netted radar system is then defined as follows: A target is declared detected () if at least K radars confirm its presence; otherwise, it is declared undetected ().
According to the fusion rule, the joint detection probability of the netted radar system is defined as follows:
where is the set of radars that have detected a target, is the set of radars that have not detected a target, and is the detection probability of the individual radar.
2.3.2. Positioning Accuracy
Deception jamming operates through a fundamentally distinct mechanism. Unlike the suppression technique, it exploits radar signal triggering to autonomously generate modulated pulses synchronized with the target radar’s frequency. These pulses embed falsified target parameters into the victim radar’s processing chain, inducing systematic biases in its detection outputs.
Under deception jamming and noise environments, the range measurement error , azimuth angle error , and elevation angle error of radar systems follow Gaussian distributions with variances given by the following [20]:
where and denote the elevation angle and azimuth angle of the target relative to the radar, respectively. c is the speed of light, denotes the pulse width, represents the pulse repetition frequency, is the antenna servo bandwidth, B indicates the radar receiver bandwidth, and , are system-dependent calibration constants.
The resulting degradation in positioning accuracy can be quantified using the geometric dilution of precision (GDOP), which is defined as follows:
where is the GDOP of a single radar. By employing the dynamic weighted fusion rule [21] and Equation (15), it can be obtained that the GDOP of the netted radar system for the target position measurement under jamming is formulated as follows:
2.3.3. Weighted Model for Evaluation Indicators
The netted radar system exhibits varying threat priorities across operational phases [22,23]. During long-range target search, the primary objective is detection confirmation, necessitating jamming strategies that suppress radar detection probability. As target proximity increases and detection confidence surpasses a defined threshold, the system transmits to the positioning phase. In this stage, resource allocation shifts toward optimizing geometric positioning accuracy, guiding adaptive countermeasure deployment aligned with real-time mission demands. In view of the differences in the characteristics of netted radars in different operational states, we use the dynamic weighted fusion metric F to comprehensively and accurately evaluate the jamming effectiveness and improve the overall countermeasure ability and task execution effect as follows:
where and represent the dynamic weights of the metrics, and the two jamming metrics are dimensionless normalized. In the search state, and , while in the tracking state, and . The indicators of max, min, and tilde denote the maximum value, minimum value, and the value without any jamming for the detection probability and GDOP of netted radars. The metric F quantifies the enhancement of jamming effectiveness relative to the non-jamming baseline, and the netted radar system can be identified as capable of detecting the jammer under current operational states when F exceeds the predefined threshold range.
3. HPN Based DRL for Jamming
To establish the theoretical foundation for our hybrid policy network, we first formalize the core reinforcement learning paradigms enabling adaptive jamming control, including policy gradient methods and the actor–critic framework. These fundamentals underpin the proximal policy optimization and its extension to hybrid action spaces for coordinated jamming.
3.1. Policy Gradient Methods
DRL aims to maximize cumulative rewards through two primary approaches: value-based methods and policy gradient methods. Value-based methods (e.g., Q-learning, DQN) derive optimal policies indirectly by constructing value functions for states or state–action pairs, demonstrating notable advantages in discrete action spaces. In contrast, policy gradient methods directly optimize policy parameters through iterative policy evaluation and improvement phases.
Let the parameterized policy , a stochastic mapping from states to action probability distributions, interact with the environment to generate trajectories through sequential sampling. The optimization objective of policy gradient methods is to maximize the expected return , where denotes the discounted cumulative reward over a trajectory of length T. By leveraging the policy gradient theorem, this optimization problem is addressed through parameter updates along the direction . denotes the gradient with respect to policy parameters , thereby specifying the gradient direction for optimizing .
Due to the intractability of direct expectation computation, Monte Carlo approximation is typically employed. A set of Q samples of trajectories are sampled, and the gradient is estimated as follows:
Policy optimization increases the selection probability of actions associated with positively rewarded trajectories and decreases it otherwise.
Traditional policy gradient methods require repeated trajectory sampling for updates, which severely limits their data efficiency. Importance sampling techniques address this by reusing historical data from policy , constructing importance weight ratios for gradient correction as follows:
Policy gradient methods demonstrate significant advantages, particularly in their capacity to effectively address high-dimensional continuous action spaces, circumvent the need for explicit environment dynamics modeling, and achieve robustness to environmental noise via direct policy optimization.
3.2. Advantage Actor-Critic
Traditional policy gradient methods assign uniform reward weighting across entire trajectories, resulting in high variance. The actor–critic framework mitigates this by introducing a state-value function as a baseline, with the advantage function quantifying the relative merit of action compared to the policy average. The improved gradient estimate becomes as follows:
Practical implementation must address distribution shift between old and new policies. Gradient updates incorporate the following importance ratio:
3.3. Proximal Policy Optimization
To stabilize policy updates, Proximal Policy Optimization (PPO) constrains the Kullback–Leibler (KL) divergence between successive policies [14]. The following two principal variants exist:
(1) PPO-Penalty: Augments the objective with KL divergence penalty
where denotes importance ratio and is an adaptive coefficient.
(2) PPO-Clip (PPO2): Implicitly constrains policy updates via a clipping mechanism
where controls maximum update deviation. By eliminating KL divergence computation, this variant achieves superior computational efficiency, establishing itself as the dominant approach in deep reinforcement learning.
3.4. Jammer Agent Model
In the complex confrontation between the jammer and netted radars, a hybrid DRL based resource allocation network is designed to generate jamming policies, selecting jamming types and allocating power. The jammer applies jamming to the chosen radar, collects feedback, and updates its state information. Key data such as states, actions, and rewards are stored in the experience pool, allowing the hybrid policy network (HPN) to learn from these samples and optimize its parameters, improving decision-making and jamming effectiveness.
3.4.1. States of Jammer Agent
The distance between the jammer and radar nodes is a key factor in resource allocation and serves as the jammer agent’s raw observation data. During the penetration process, the radar switches dynamically between search, track, and guidance states [24]. The operational state transition mechanism of the multi-functional netted radar system is modeled through a state machine framework, as illustrated in Figure 3. The system state variable quantifies the operational state for netted radar system, corresponding to search state (), track state (), and guidance state (). The search state serves as the initial state, while the guidance state functions as the terminal state, with the operational mission terminating if either the target successfully executes penetration (i.e., exceeds the maximum penetration distance) or the netted radar system transitions into guidance state prior to the target exceeding the maximum penetration distance, and the state transition protocol is defined as follows:

Figure 3.
Schematic diagram of the netted radar system working state conversion.
(1) Search-to-Track Transition Criterion: The netted radars transition from search state () to track state () when three successful target acquisition confirmations are achieved within four consecutive detection cycles. Failure to meet this empirical threshold maintains the system in its current search operational state.
(2) Track State Management Criterion: The tracking state executes adaptive state evaluation through:
- State Promotion Condition: Activation of transition to the guidance state () occurs when at least two valid target locks are confirmed across three sequential detection intervals.
- State Regression Condition: Return to search state () is triggered if zero valid target detections are recorded during three consecutive detection windows.
- State Retention Policy: Detection outcomes sustain the track state if just one successful confirmation occurs in three consecutive detections.
This state representation framework establishes quantitative mapping between observational data and state transition probabilities, enabling dynamic resource allocation optimization in contested electromagnetic environments. The threshold parameters incorporate both statistical characteristics of target detection processes and weapon system reaction latency considerations, while maintaining strict adherence to the original operational specifications without introducing extraneous interpretations.
The raw observations are normalized and combined with the operational state of the netted radar system to construct the input state of the jammer agent as follows:
where represents the distance between the jammer and the i-th radar, and the greater the value of the state variable corresponding to the operational state of the netted radar system, the higher the associated threat level.
3.4.2. Action of the Jammer Agent
Jamming actions are divided into continuous jamming power action and discrete jamming type action , which are defined as follows:
where and are the jamming power and jamming type for i-th radar, respectively.
The jammer agent faces two decision tasks: selecting discrete jamming beams and allocating continuous power. We present a new HPN, where a discrete Actor network in DRL framework determines beam selection, and a continuous Actor network based on Gaussian distribution handles power allocation. This design enables efficient and coordinated handling of both discrete and continuous actions, enhancing the jammer’s performance in complex confrontation scenarios.
3.4.3. Rewards for Jammer Agent
Reasonable reward value setting can accelerate the agent’s learning and convergence in the interaction with the environment. Therefore, we set rewards from radar state transition reward and jamming power reward as follows:
where is the attenuation coefficient that controls the rate of exponential decay, T represents the total frame of the task, and denotes the cumulative jamming power allocated to all jammed radars. Thus, the per-step total reward is obtained as .
In typical electronic countermeasure scenarios, combat processes exhibit distinct phased characteristics as follows: the initial search phase prioritizes suppression of target detection probability, while the subsequent tracking phase emphasizes positioning accuracy assurance. To address this, we established a state transition model based on operating states of the netted radar system, enabling multi-scale quantitative evaluation of jamming effects. The proposed dual-dimensional reward system integrates radar state evolution information with power consumption constraints, constructing an environmentally aware dynamic value assessment framework. The core innovation lies in introducing phase-aware weight allocation mechanisms and exponentially decaying power penalty terms, with design principles stemming from the following two engineering considerations:
- Mitigation of the Sparse Reward Problem: Traditional reward mechanisms often suffer from sparsity in complex confrontation scenarios, leading to unstable policy updates. We designed the following three-tier reward scheme: a phased reward upon radar state escalation, a penalty for state degradation due to electronic countermeasures, and terminal rewards for task success or failure. This event-driven reward injection increases effective reward density during training while reducing policy gradient estimation variance.
- The Balance Between Energy Efficiency and Task Performance Efficacy: enforces hard energy constraints via reciprocal power accumulation, while the exponential term introduces temporal decay. This forces agents to prioritize jamming intensity during early mission phases while shifting to refined power allocation near mission deadlines, as the marginal benefit of power consumption decays exponentially over time.
3.4.4. HPN Optimization
The DRL framework with HPN shown in Figure 4 is optimized according to the PPO2 algorithm [14] described in Algorithm 1. The core objective of the DRL framework with HPN jamming resource allocation is to enable intelligent agents to simultaneously execute two heterogeneous action types in complex electromagnetic environments as follows: discrete jamming pattern selection and continuous beam power allocation. The traditional PPO2 algorithm inherently supports only single-action spaces (either discrete or continuous), making them unsuitable for such hybrid action scenarios. To address this, the framework extends PPO2 through a dual-branch HPN. The discrete branch employs a Softmax activation function to generate categorical distributions for jamming beam type selection, while the continuous branch utilizes Tanh activation to output mean and variance parameters for Gaussian-distributed power allocation sampling. Two parallel branches share a unified state encoder, followed by an intermediate fully connected network with a 128-unit hidden layer employing the ReLU activation function, ensuring feature extraction consistency when decoupling action spaces.
| Algorithm 1 Optimized jamming strategy allocation-based HPN-enhanced PPO2 |
| Require: Maximum episodes M, discount factor , clip threshold , learning rates |
| Ensure: Optimized policy network and value network |
|
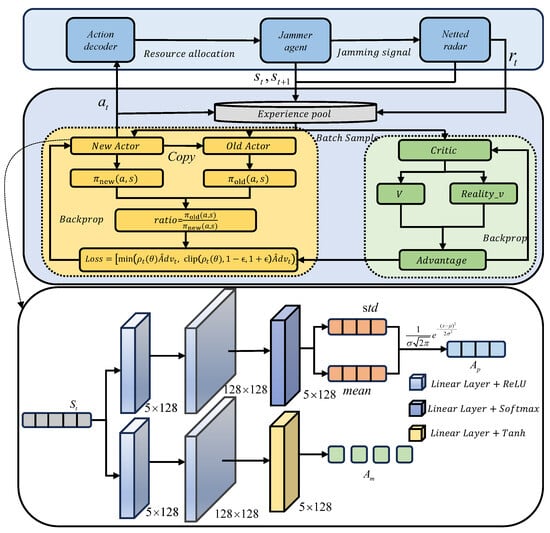
Figure 4.
Schematic diagram of hybrid policy network (HPN)-based DRL.
The proposed algorithm workflow consists of data interaction and policy update. In the interaction phase, the agent generates hybrid actions and based on the current state . The jammer executes these actions, and the environment returns the next state and reward . These trajectory data are stored in the replay buffer until task termination or reaching the maximum step limit. In the update phase, the algorithm samples batches of data from the replay buffer, and optimizes both the policy network and the value network through a combination of Generalized Advantage Estimation (GAE) [25] and a clipped surrogate objective. A detailed elucidation of the core architectural components and algorithmic update procedures is provided below.
- GAE advantage calculation: The GAE method balances bias and variance in advantage estimation by aggregating multi-step temporal difference (TD) errors. The advantage function is computed as follows:where represents the TD error at time step t, is the discount factor, and controls the trade-off between bias and variance. The term is the state-value predicted by the critic network.
- Actor Update: The policy network is updated using a clipped surrogate objective to ensure stable policy improvement. For hybrid action spaces, the importance ratios for both action types are computed separately as follows:According to Equation (23), the overall policy loss integrates both ratios with the advantage function and applies a clipping mechanism:where (typically ) is the clipping threshold. The gradients are computed via backpropagation, and gradient clipping is applied to prevent exploding gradients. The final loss is a weighted sum of discrete and continuous action losses.
- Critic Update: The value network minimizes the mean squared error (MSE) between predicted state-values and target values derived from discounted cumulative rewards. The Critic loss function is calculated as follows:where is the target value. The value network undergoes multiple optimization steps per batch to enhance value estimation accuracy.
4. Experiment and Simulation
4.1. Scene Description and Parameter Settings
In the experiments, we investigate a complex electromagnetic countermeasure scenario involving coordinated jamming against a widely distributed networked radar system during target penetration. A simulation environment is constructed, consisting of multiple spatially dispersed monostatic radars and a multi-beam jammer. As illustrated in Figure 5, the system comprises radar nodes, with the fusion center adopting the fusion role (). Based on the data provided in [3,26], all radar nodes share identical parameters, with detailed configurations for both the jammer and radars provided in Table 1 and Table 2, respectively. The initial motion states of the jammer and the target are shown in Table 3. The netted radars are deployed in a fan-shaped spatial configuration with overlapping detection ranges, while the jammer—equipped with a phased array and multi-beam system—maneuvers synchronously with the penetrating target. These configurations are denoted as Config A. The most of the following experiments are conducted using the aforementioned parameter configuration (denoted as Config A) unless specifically indicated. To further evaluate the effectiveness of our proposed method, we also perform two experiments on extended configurations, namely Config B and Config C, which are discussed in Section 4.4. By dynamically allocating jamming beam patterns and transmission power, the jammer implements coordinated suppression.
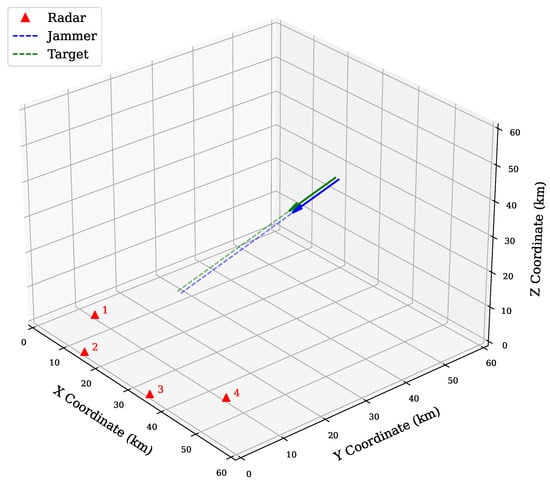
Figure 5.
Penetration scenario simulation diagram.

Table 1.
Operating parameters of jammer.

Table 2.
Operating parameters of radar.

Table 3.
Initial motion states of jammer and target.
In the design and implementation of algorithms, the rational configuration of hyper-parameters is a critical factor in ensuring model performance and training stability. For the dynamic characteristics of jamming resource allocation in complex electromagnetic countermeasure scenarios, parameter settings must balance task requirements, the heterogeneity of network architectures, and practical computational resource constraints. The multi-dimensional action space inherent in such tasks demands a careful equilibrium between exploration in strategy optimization and accurate value estimation, while the dual-branch network architecture introduces additional complexity by coupling discrete and continuous action representations. To address these challenges, we conducted extensive comparative experiments and comprehensive evaluations of algorithm convergence trends and generalization capabilities. Ultimately, we identified a set of hyper-parameters tailored to the task’s characteristics (as shown in Table 4), whose design rationale reflects a judicious trade-off among dynamic environment adaptability, policy update stability, and computational efficiency.

Table 4.
Parameters of PPO2 algorithm based on HPN.
4.2. Comparison Strategies
To validate the effectiveness of the proposed method, the HPN with PPO2 algorithm is compared with the following two baseline strategies: (1) Distribution policy based on real digital action key encoding (AKE) of jamming type and jamming power [27]: This method encodes discrete jamming type selection as the integer part and maps continuous power allocation to the decimal part. By leveraging prior knowledge, it simplifies the action space and performs hybrid decision-making through a fixed encoding coupling mechanism. (2) Discrete action space deep Q-network (DQN) algorithm with interval division of power [11]: Although this method simplifies the action space, the coarse-grained power quantization degrades jamming effectiveness and introduces suboptimal solutions.
4.3. Training Process
Based on the parameter settings in Section 4.1 and the training framework in Section 3.4.4, we conduct hybrid action strategy training for the jammer agent. After every policy-update steps, the target’s motion state is re-initialized, and a new training episode is initiated. The total number of training episodes is set to 1000 to balance exploration and convergence requirements. As shown in Figure 6, the reward function converges across different training episodes, with the average reward gradually increasing to a steady-state value as the number of episodes grows. This indicates that the policy network effectively learns the joint optimization pattern of beamforming and power allocation.
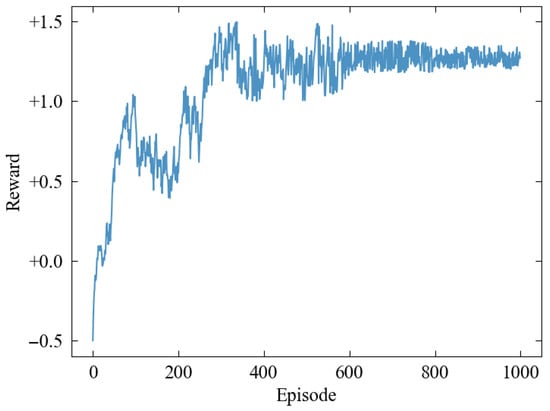
Figure 6.
Reward variation curve of the jammer.
4.4. Experimental Results
Maximum penetration distance is defined as the farthest distance the penetrating target achieves before the netted radar system transitions to the guidance state across all training episodes. Figure 7 shows the change in the maximum penetration distance with increasing simulation times. Results show that after about 440 training runs (), the maximum penetration distance under the HPN stabilizes. In comparison, the AKE and DQN algorithms need around 600 and 800 runs to finish the penetration task. Figure 8 shows total power consumption of different strategies at each penetration time step. The figure reveals that the HPN with PPO2 algorithm generally has a lower proportion of jamming power consumption than the AKE and DQN approaches, and it utilizes jamming power more efficiently while fulfilling the penetration task.
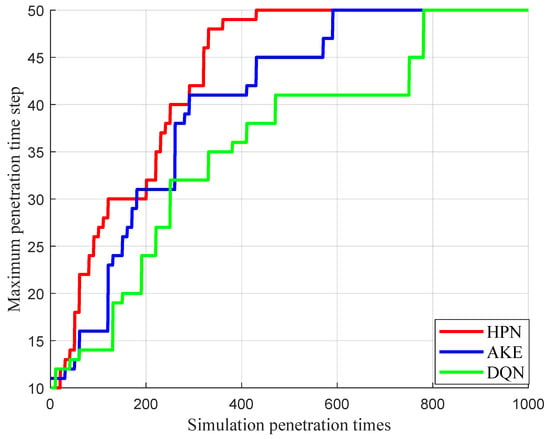
Figure 7.
Maximum penetration distance change.
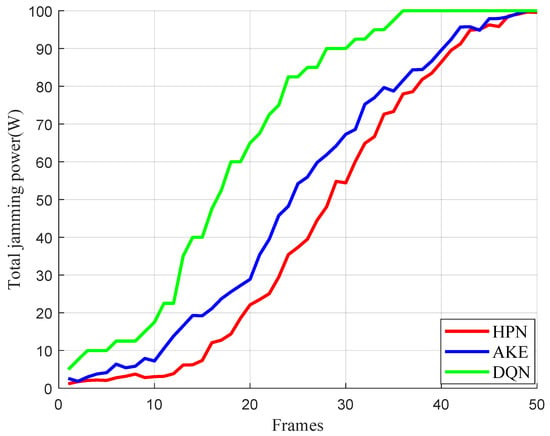
Figure 8.
Total power consumption of jamming.
In addition, to observe the effectiveness of our proposed method in more scenarios, we have also added several experiments on various configurations (i.e., Config B and Config C). The results are illustrated in Figure 9 and Figure 10, which depict the jamming resource consumption curves under different operational settings. In Figure 9, we have evaluated a 3-node radar network with fusion role (); the method maintains effective jamming while strategically concentrating power on critical nodes to prevent detection confirmation (Config B). Figure 10 examines the modified penetration geometry, where the z-coordinates of both radars and jammer are adjusted to 35 km, with their velocity vectors set to (0, −0.4, −0.2) km/s. In this scenario, power distribution dynamically adjusts throughout the mission according to real-time positional changes (Config C).
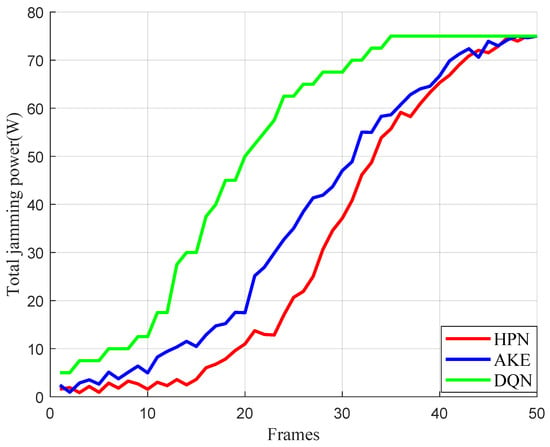
Figure 9.
Total power consumption of jamming in Config B.
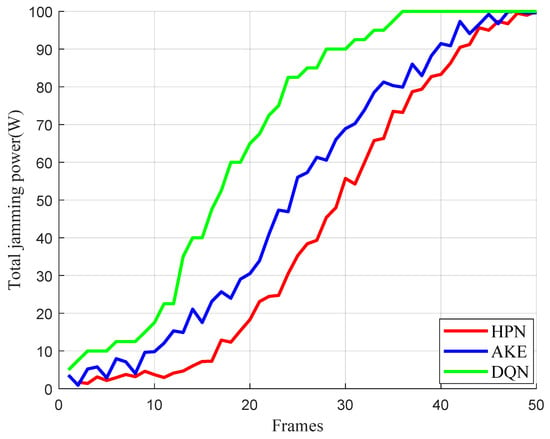
Figure 10.
Total power consumption of jamming in Config C.
To validate the stability of the proposed algorithm, Figure 11 and Figure 12 illustrate the dynamic evolution of jamming beam power distribution and beam type allocation. The analysis reveals that during the initial phase (Frames 1–24), Radars 1 and 4 exhibited significantly higher received jamming power due to their geometric configuration, as follows: the angle between the jammer–radar line-of-sight and the target-radar line-of-sight remained within the mainlobe beamwidth of the radar, allowing energy penetration through the main lobe. Jamming power demonstrated a strong inverse correlation with jammer-to-radar distance, resulting in higher received power at Radars 1 and 4. As the jammer accompanied the target into the intermediate phase (Frames 25–28), Radars 2 and 3 experienced shorter distances to the jammer, while Radars 1 and 4 became relatively distant. At this stage, the angle between the jammer–radar and target-radar lines-of-sight exceeded the mainlobe beamwidth, causing significant received power reduction due to sidelobe attenuation effects and leading to power equalization across radars. In the final penetration phase, Radars 2 and 3 further approached the jammer, where near-field jamming gain surpassed the path loss advantage of mainlobe-directed energy, becoming the dominant factor in jamming power. Consequently, jamming power was redistributed primarily towards Radars 2 and 3.
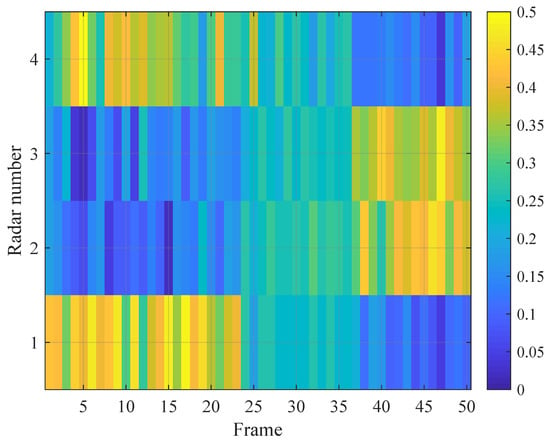
Figure 11.
Jamming power allocation result.
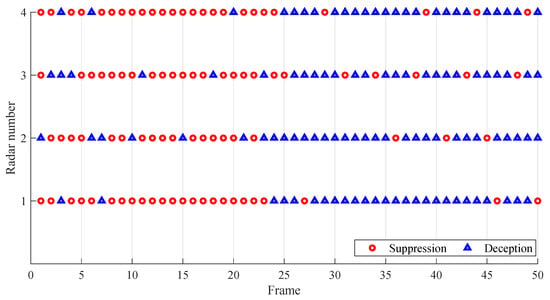
Figure 12.
Jamming type allocation result.
Additionally, concurrent analysis of beam type allocation indicates that the netted radar system operated in search state during the initial phase (1–23 frames), employing suppression jamming to overwhelm radar search beams. After radar transitioned to track state, the jamming strategy adaptively shifted to deception jamming to counter the dynamically enhanced radar signal processing capabilities.
Furthermore, based on the computational efficiency analysis, we have conducted rigorous timing experiments to evaluate the three methods. The results in Table 5 demonstrate significant differences in algorithm efficiency. HPN and AKE exhibit significantly shorter training times compared to DQN, primarily because DQN must handle a high-dimensional discrete action space (with 20 optional actions per radar, resulting in a total of 80-dimensional outputs), which increases the computational overhead of both forward and backward propagation in the network. In terms of inference efficiency, HPN and AKE require approximately 15 milliseconds per step for decision-making, whereas DQN needs 32.5 milliseconds. This discrepancy arises because DQN must evaluate all possible actions at each step to select the optimal one. Notably, although HPN has a slightly longer training time than AKE (3560 s vs. 3200 s), its superior jamming performance justifies this minor computational overhead. Overall, HPN achieves the best balance between effectiveness and efficiency.

Table 5.
Differences in algorithm efficiency and complexity.
These results demonstrate the robustness and timeliness of the proposed algorithm in multi-target cooperative jamming under complex electromagnetic environments. Our proposed method preserves the physical independence of actions by separately modeling them through a discrete actor and a continuous actor, and its HPN achieves cross-action-space parameter sharing through a shared feature extraction layer. In contrast, the AKE method forcibly couples discrete beam selection with continuous power allocation through real-number coding, which forces two action dimensions with distinct physical meanings to share the same coding space and introduces spurious correlations; DQN suffers from quantization errors when discretizing power into discrete levels. Meanwhile, compared with DQN’s greedy exploration policy, HPN’s exploration policy employs importance sampling ratio clipping to prevent policy collapse caused by improper power allocation during early exploration phases.
5. Discussion
The proposed HPN-PPO2 framework demonstrates superior convergence and energy efficiency compared to conventional AKE and DQN approaches. This stems from the following three key innovations: (1) The hybrid action space decomposition eliminates spurious correlations between beam selection and power allocation, mitigating the dimensional coupling inherent in AKE’s real-number encoding. (2) The dynamic fusion metric aligns jamming objectives with radar operational states, enabling phase-aware resource allocation—critical for countering adaptive radar state transitions. (3) PPO2’s clipped surrogate objective ensures stable policy updates in hybrid action spaces, overcoming DQN’s quantization errors and exploration inefficiency.
However, three limitations require further investigation. First, the assumption of perfect radar state observability may not hold in practical scenarios with signal occlusion. In the future, we may develop recurrent neural networks with attention mechanism to reconstruct hidden states from partial observations, enabling robust decision-making under uncertainty. Second, mobile radar networks may create coverage gaps that exceed beam steering rates. This might be addressed by integrating Kalman filtering with graph neural networks to predict radar trajectories, combined with threat-prioritized beam-sweeping protocols that dynamically adjust sector coverage. Third, scenarios with more radars than available beams () or multiple penetration targets require architectural extensions. For radar-beam imbalance, we propose adaptive beam-sharing via multi-beam waveforms and time-division hopping. Multiple targets will be handled through distributed multi-agent coordination using shared critic networks.
These findings highlight the potential of hybrid policy architectures in electromagnetic countermeasure optimization. Our framework’s modular design permits straightforward integration of additional jamming modalities, suggesting promising directions for cognitive electronic warfare systems.
6. Conclusions
In this work, we proposed a DRL-based collaborative jamming resource allocation method. A hybrid policy network (HPN) coordinated beam selection and power allocation simultaneously, and a dynamic metric quantified the jamming effectiveness. Using the HPN with PPO2 algorithm, it enabled adaptive policy optimization for the DRL framework. Experiments show it outperformed the existing approaches (AKE and DQN) in terms of the following: 30% faster convergence in penetration, 18.7% less power consumption, 95.2% utilization, and enhancing jamming adaptability and resource efficiency. The framework’s modular design supports seamless integration of emerging jamming techniques while maintaining adaptability in complex electromagnetic environments. Future work will extend this architecture to multi-agent collaborative jamming scenarios and incorporate partial observability modeling for enhanced battlefield realism.
Author Contributions
Conceptualization, W.H. and Z.X.; Data curation, W.H.; Funding acquisition, X.F.; Methodology, W.H. and W.K.; Project administration, Z.X.; Supervision, Z.X.; Validation, W.K.; Writing—original draft, W.H. and W.K.; Writing—review and editing, X.F. and Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly supported by the Key Research & Development Program of Shaanxi (Nos. 2023-ZDLGY-12 and 2023-ZDLGY-16.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, B.; Tian, L.; Chen, D.; Liang, S. An adaptive dwell time scheduling model for phased array radar based on three-way decision. J. Syst. Eng. Electron. 2020, 31, 500–509. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Xu, H. Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm. IET Radar Sonar Navig. 2017, 11, 185–192. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, J.; Yang, C.; Yi, W. Joint jamming beam and power scheduling for suppressing netted radar system. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar]
- Yao, Z.; Tang, C.; Wang, C.; Shi, Q.; Yuan, N. Cooperative jamming resource allocation model and algorithm for netted radar. Electron. Lett. 2022, 58, 834–836. [Google Scholar] [CrossRef]
- You, S.; Diao, M.; Gao, L. Implementation of a combinatorial-optimisation-based threat evaluation and jamming allocation system. IET Radar Sonar Navig. 2019, 13, 1636–1645. [Google Scholar] [CrossRef]
- Zou, W.; Niu, C.; Liu, W.; Wang, Y.; Zhan, J. Combination search strategy-based improved particle swarm optimisation for resource allocation of multiple jammers for jamming netted radar system. IET Signal Process. 2023, 17, e12198. [Google Scholar] [CrossRef]
- Tian, L.; Liu, F.; Miao, Y.; Li, K.; Liu, Q. Resource allocation of radar network based on particle swarm optimisation. J. Eng. 2019, 2019, 6568–6572. [Google Scholar] [CrossRef]
- He, B.; Yang, N. Power allocation between radar and jammer using conflict game theory. Electron. Lett. 2024, 60, e13311. [Google Scholar] [CrossRef]
- Zhang, S.; Tian, H. Design and implementation of reinforcement learning-based intelligent jamming system. IET Commun. 2020, 14, 3231–3238. [Google Scholar] [CrossRef]
- Li, S.; Liu, G.; Zhang, K.; Qian, Z.; Ding, S. DRL-Based joint path planning and jamming power allocation optimization for suppressing netted radar system. IEEE Signal Process. Lett. 2023, 30, 548–552. [Google Scholar] [CrossRef]
- Feng, L.; Liu, S.; Xu, H. Multifunctional radar cognitive jamming decision based on dueling double deep Q-network. IEEE Access 2021, 10, 112150–112157. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, B.; Ji, W.; Hu, J.; Xu, S.; Xiao, Y. Cognitive jamming policy generation based on A2C algorithm. In Proceedings of the 2024 International Radar Symposium (IRS), Wroclaw, Poland, 2–4 July 2024; pp. 33–38. [Google Scholar]
- Wang, Y.; Liang, Y.; Wang, Z. Hierarchical reinforcement learning-based joint allocation of jamming task and power for countering netted radar. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 2149–2167. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Wang, B.; Cui, G.; Zhang, B.; Sheng, B.; Kong, L.; Ran, D. Deceptive jamming suppression based on coherent cancelling in multistatic radar system. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Wang, Y.; Dong, Q.; Jin, Q.; Mao, X. A deception jamming detection and suppression method for multichannel SAR. In Proceedings of the 2022 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 20–22 July 2022; pp. 29–34. [Google Scholar]
- Li, J.; Shen, X.; Xiao, S. Robust jamming resource allocation for cooperatively suppressing multi-station radar systems in multi-jammer systems. In Proceedings of the 2022 25th International Conference on Information Fusion (FUSION), Linköping, Sweden, 4–7 July 2022; pp. 1–8. [Google Scholar]
- Liu, W.; Wang, Y.; Liu, J.; Huang, L.; Jao, C. Performance analysis of adaptive detectors for point targets in subspace interference and Gaussian noise. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 429–441. [Google Scholar] [CrossRef]
- Pham, V.; Nguyen, T.; Nguyen, D.; Morishita, H. A new method based on copula theory for evaluating detection performance of distributed-processing multistatic radar system. IEICE Trans. Commun. 2022, 105, 67–75. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, X.; Hong, S.; Gong, Y. Receiver placement in passive radar through GDOP coverage ratio with TDOA-AOA hybrid localization. In Proceedings of the IET International Radar Conference, Chongqing, China, 4–6 November 2020; pp. 476–480. [Google Scholar]
- Xia, J.; Ma, J.; Li, Y.; Song, M. Cooperative jamming resource allocation based on integer-encoded directed mutation artificial bee colony algorithm. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 695–700. [Google Scholar]
- Bachamann, D.; Evans, R.; Moran, B. Game theoretic analysis of adaptive radar jamming. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1081–1100. [Google Scholar] [CrossRef]
- Nichlors, R.; Warren, P. Threat evaluation and jamming allocation. IET Radar Sonar Navig. 2017, 11, 459–465. [Google Scholar]
- Tang, Z.; Gong, Y.; Tao, M.; Su, J.; Fan, Y.; Li, T. Recognition of working mode for multifunctional phased array radar Uunder small sample condition. In Proceedings of the 2023 IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT), Qingdao, China, 21–24 July 2023; pp. 1157–1160. [Google Scholar]
- Schulman, S.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Wu, Z.; Hu, S.; Luo, Y.; Li, X. Optimal distributed cooperative jamming resource allocation for multi-missile threat scenario. IET Radar Sonar Navig. 2022, 16, 113–128. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Xiao, S. Dynamic weighted fusion algorithm and its accuracy analysis for multi-radar localization. Electron. Opt. Control 2010, 5, 35–37. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).