The Influence Mechanism and Identification Method of the First Four Harmonics of the Mass Defect of Hemispherical Resonators
Abstract
1. Introduction
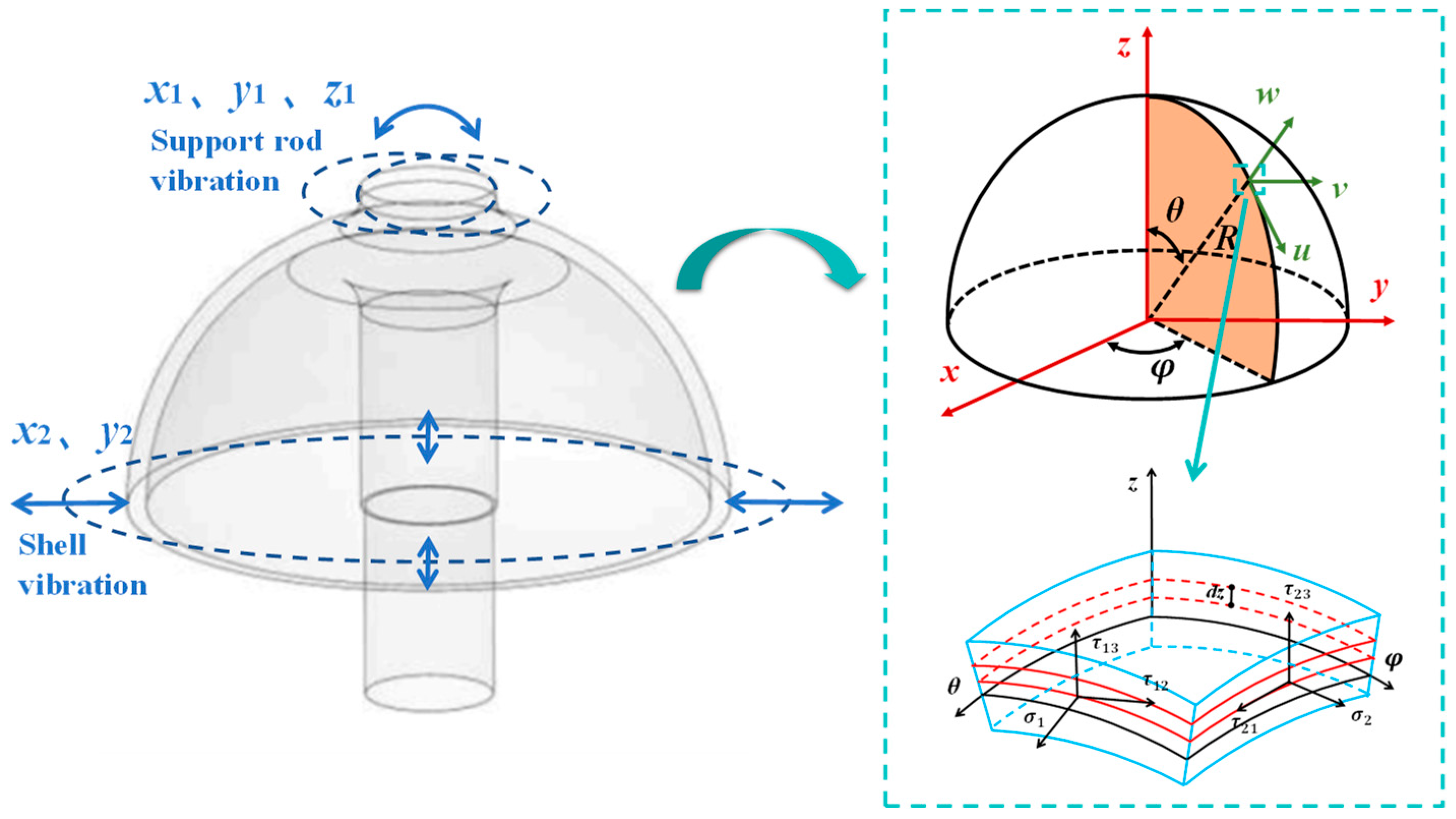
2. Hemispherical Resonator Mass Defects Characterization System
2.1. Hemispherical Resonator Shell–Rod Coupling Vibration Model
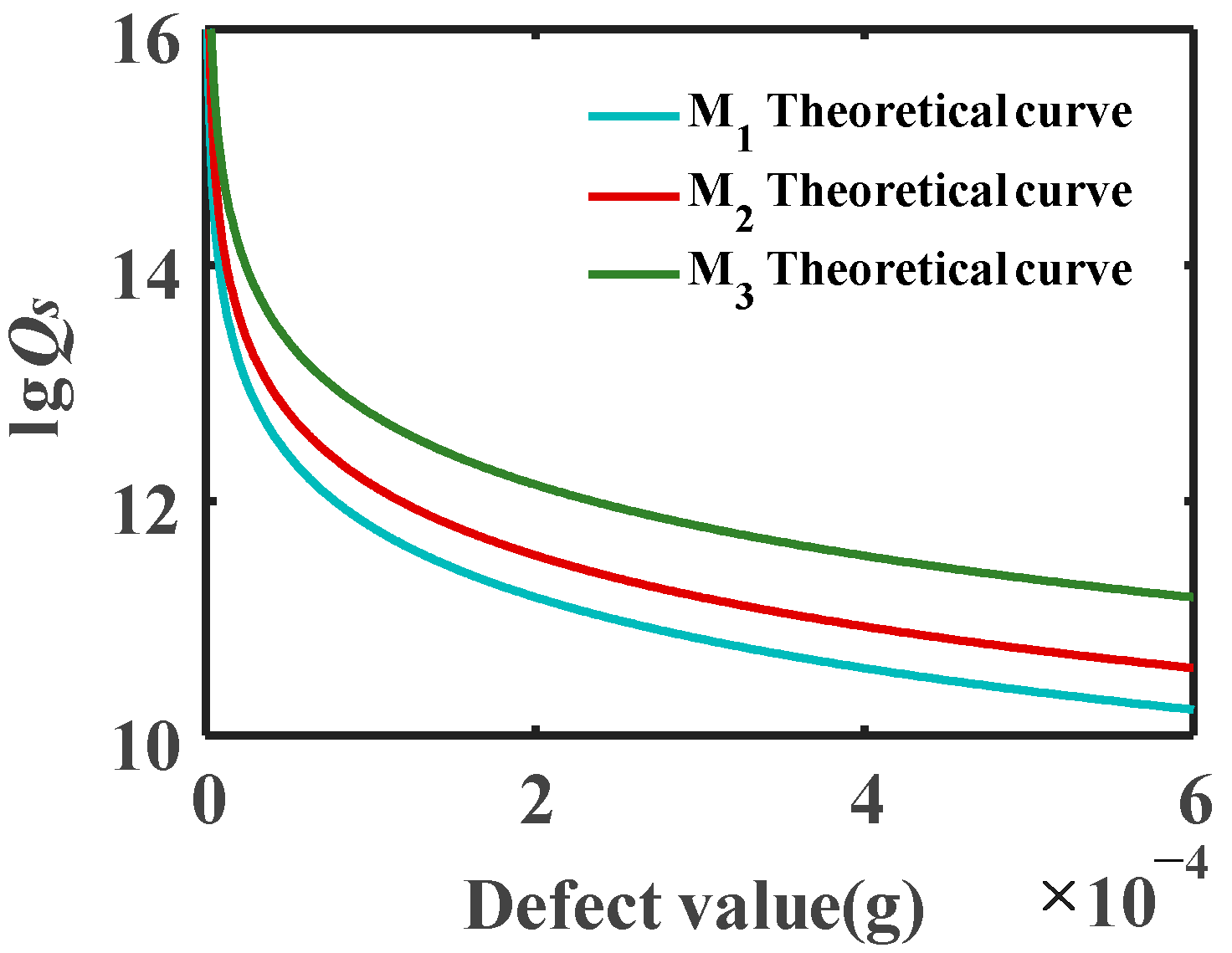
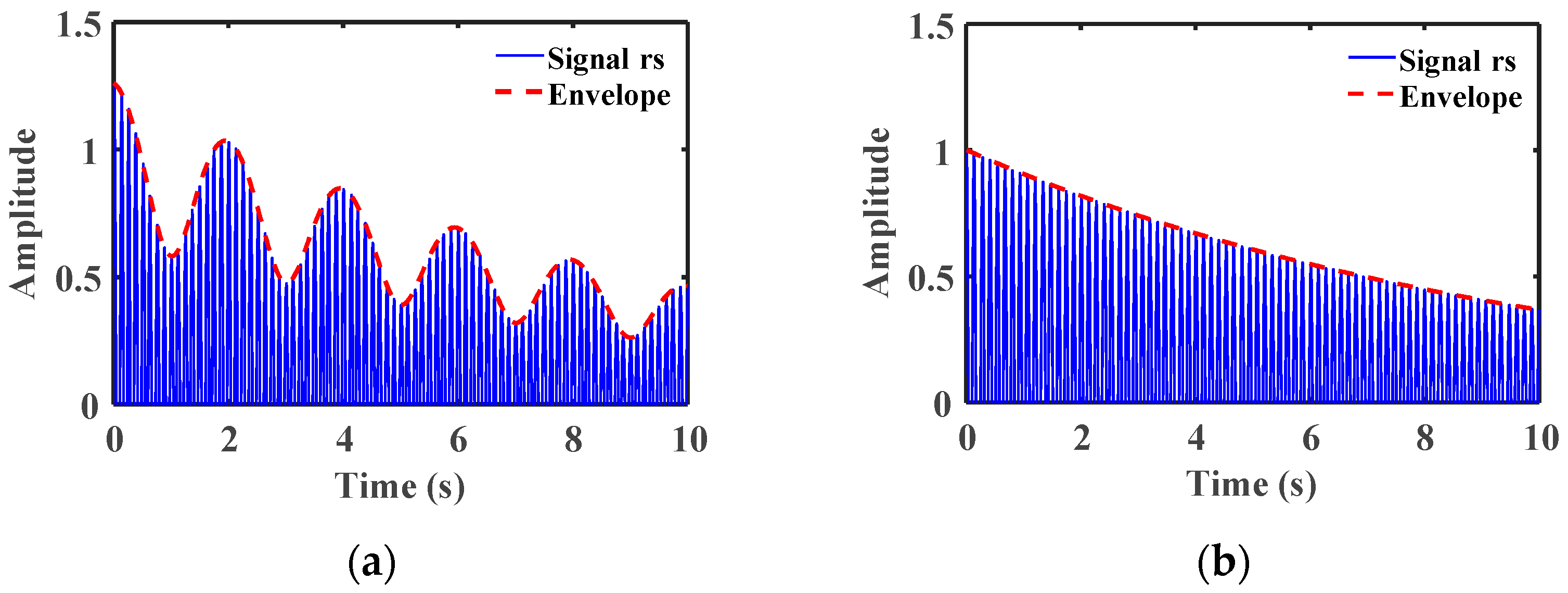
2.2. Characterization of the Influence of Mass Defects on Quality Factors
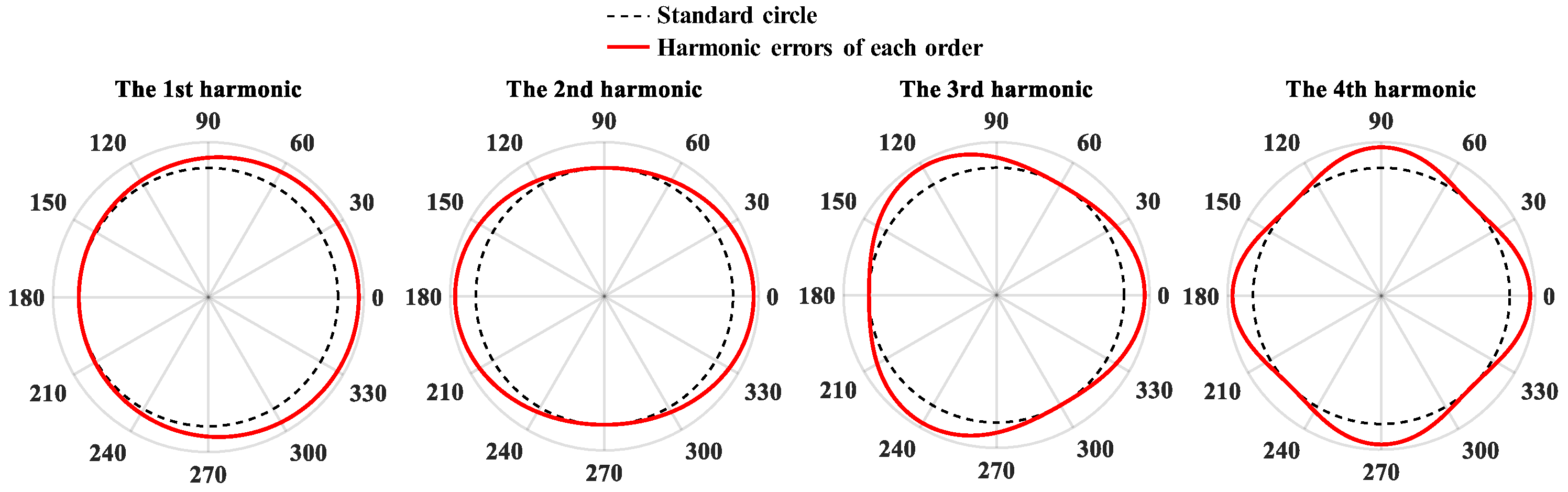
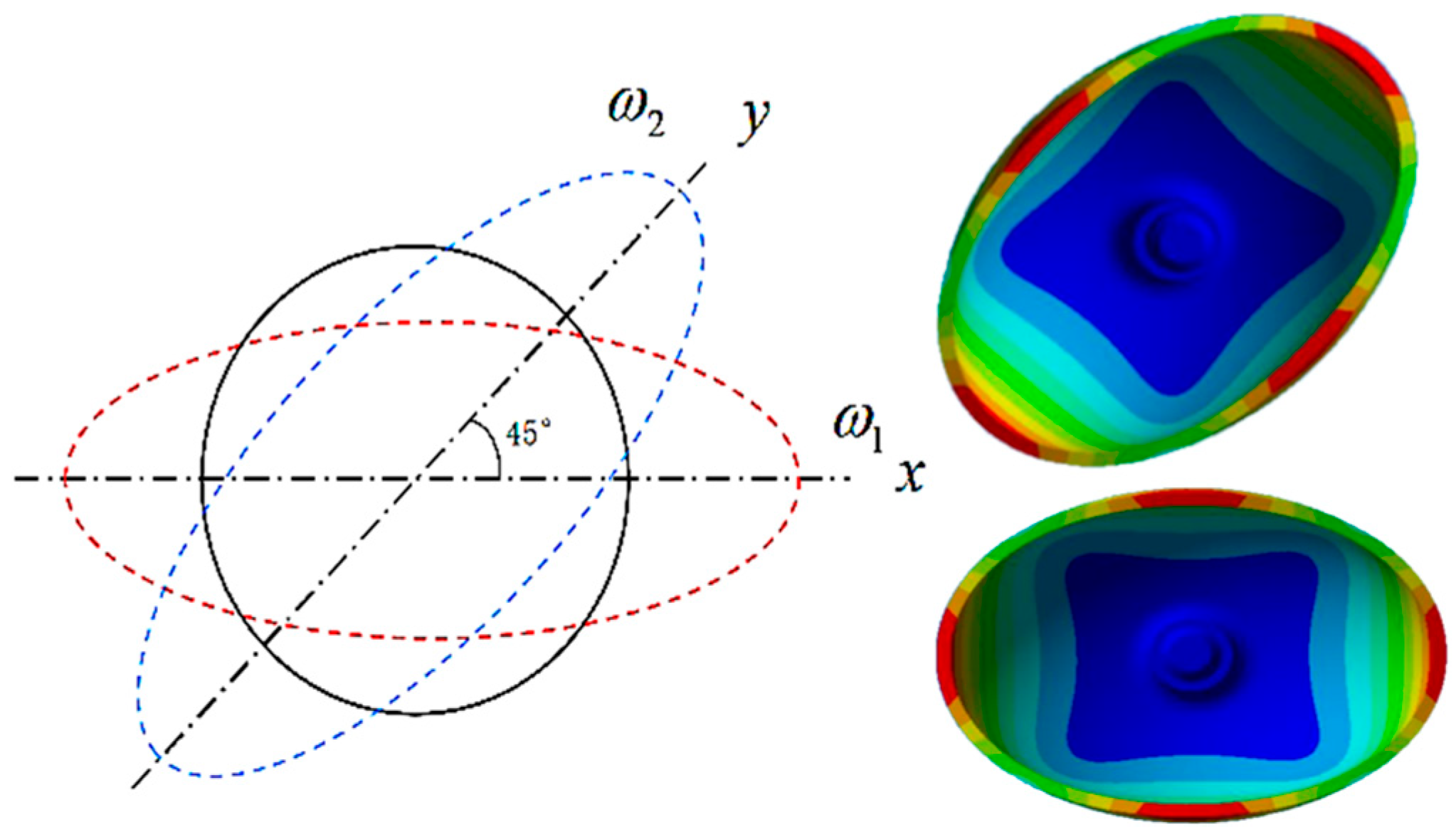
2.3. Characterization of the Influence of Mass Defects on Frequency Split
3. Simulation Analysis
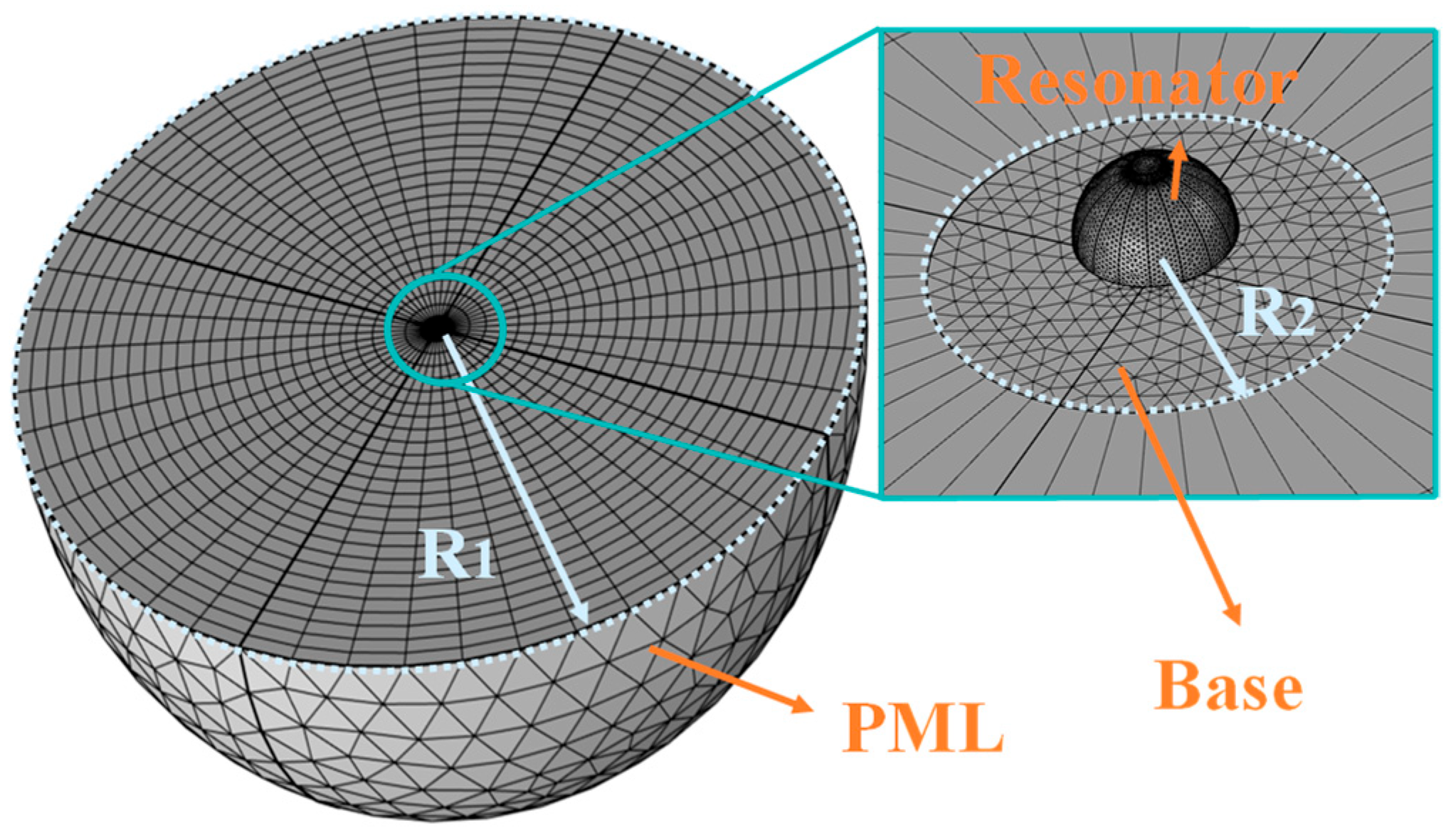
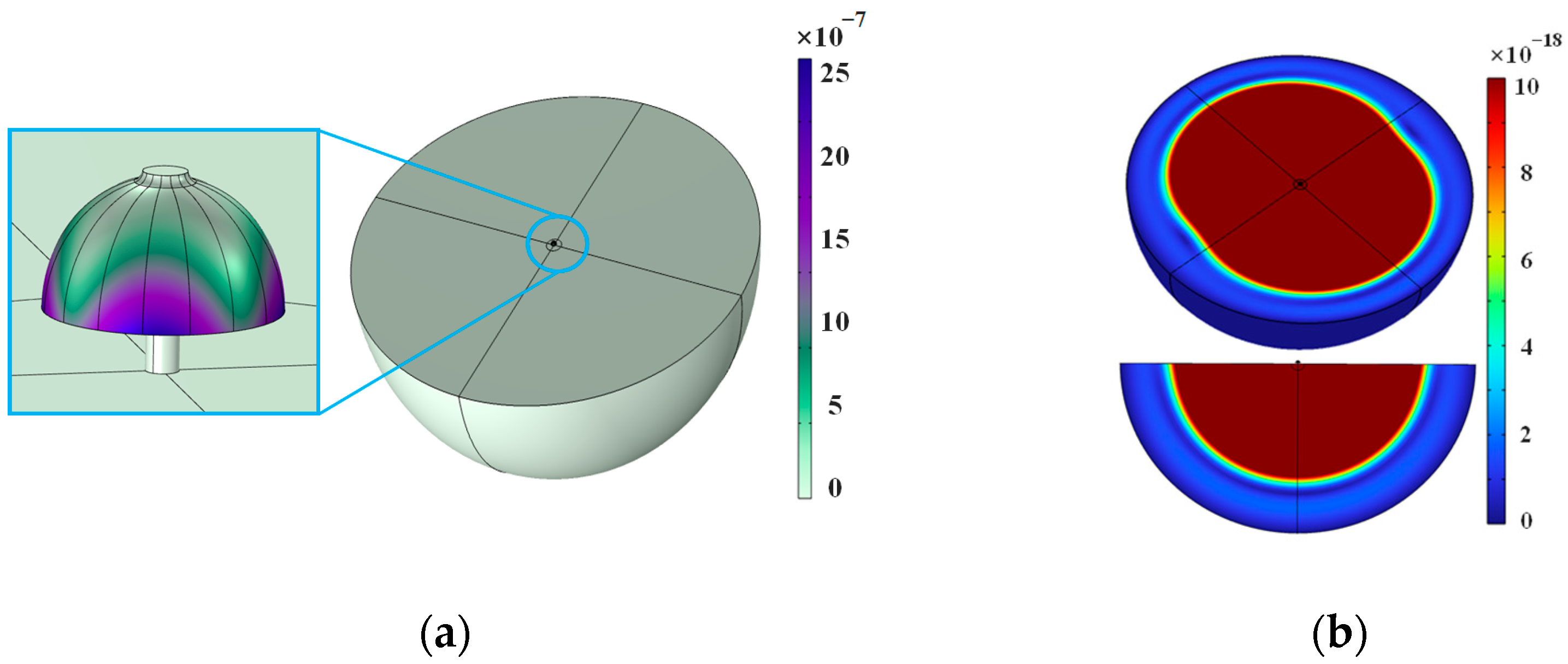
3.1. Support Loss Simulation
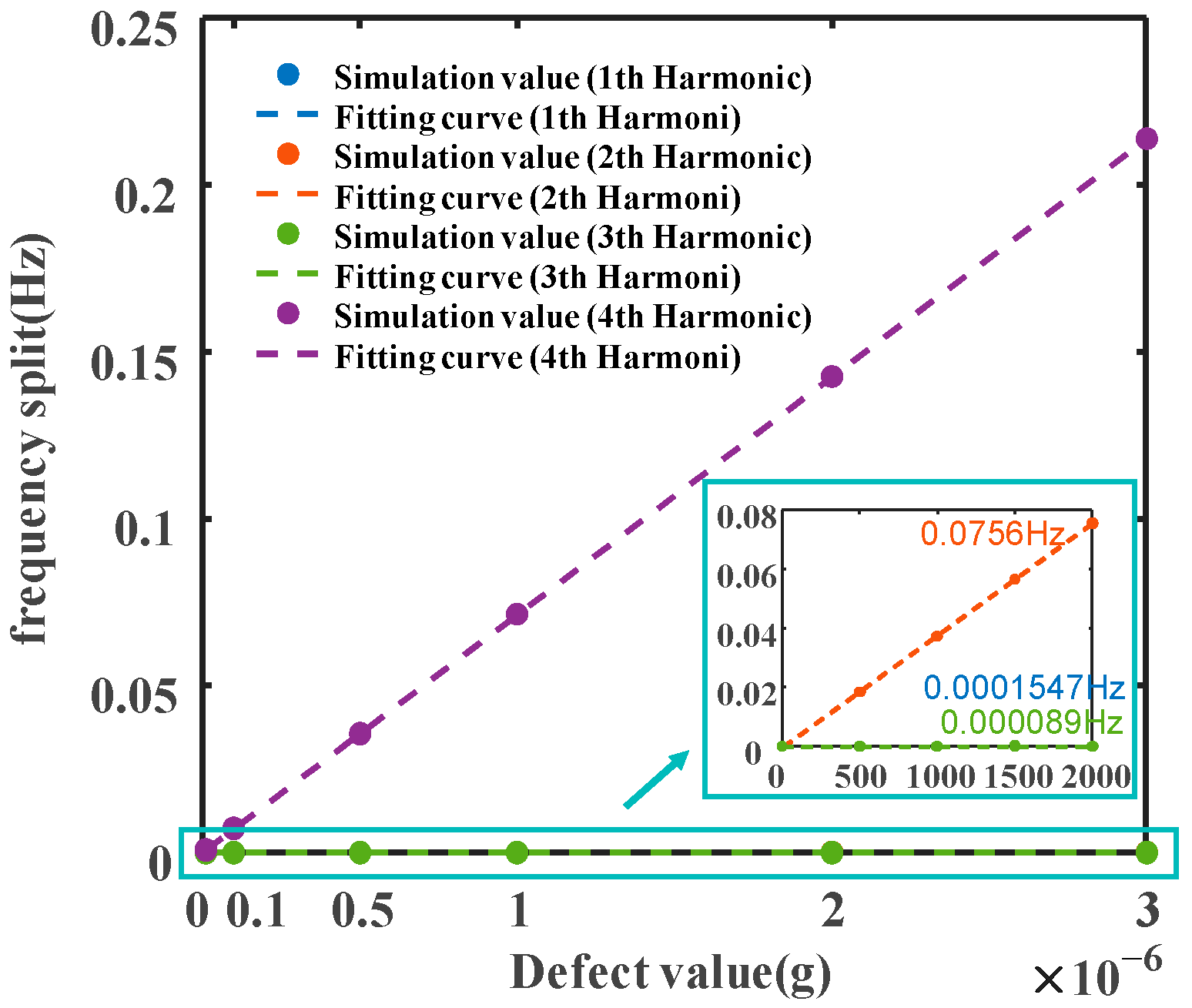
3.2. Frequency Split Simulation
4. Identification of Mass Defects
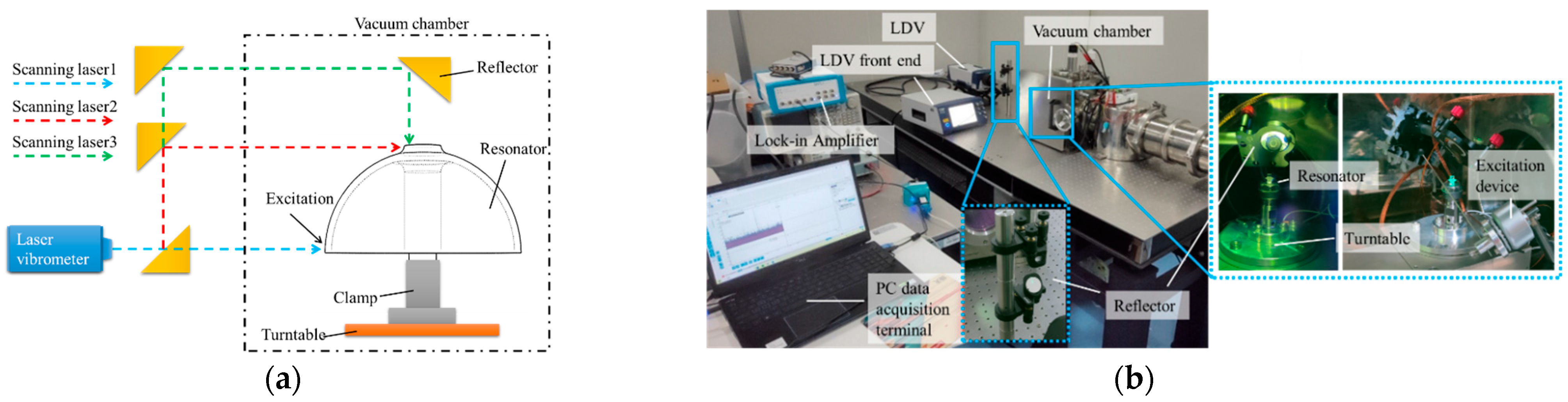
4.1. Identification Methods and Devices
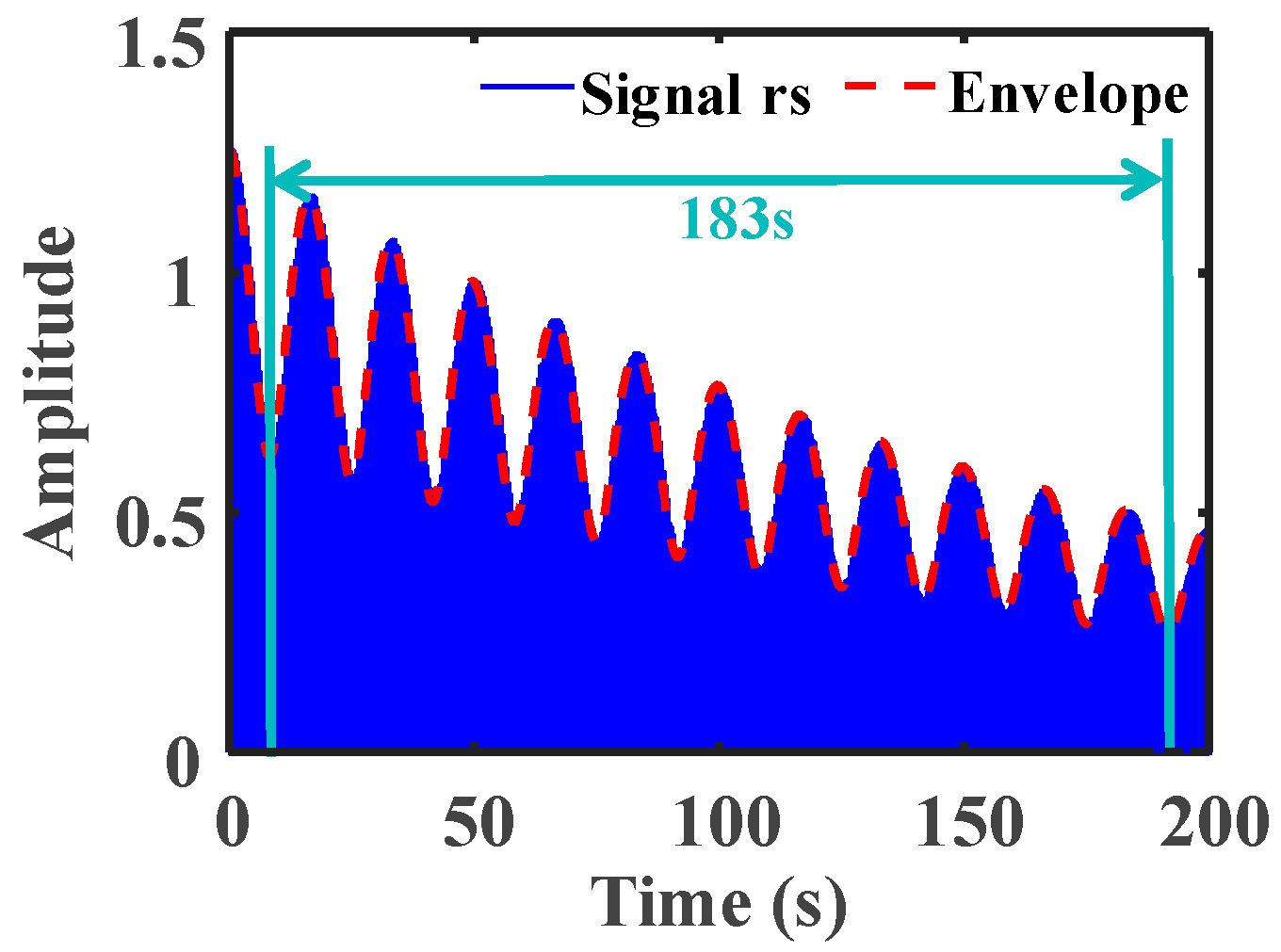
4.2. Identification Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Delhaye, F. HRG by Safran: The Game-Changing Technology. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems, Moltrasio, Italy, 26–29 March 2018. [Google Scholar]
- Jeanroy, A.; Grosset, G.; Goudon, J.C.; Delhaye, F. HRG by Sagem from Laboratory to Mass Production. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems, Hawaii, HI, USA, 22–25 February 2016; pp. 1–4. [Google Scholar]
- Xia, D.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef]
- Deng, K.; Pan, Y.; Jia, Y.; Li, J.; Tang, X.; Wu, W.; Yuan, J. Separation of mass and gap errors of hemispherical resonator gyroscopes by varying bias voltage. Meas. J. Int. Meas. Confed. 2024, 228, 114308. [Google Scholar] [CrossRef]
- Xu, Z.; Yi, G.; Zhu, W. An accurate thermoelastic model and thermal output error analysis of a hemispherical resonator gyroscope under varying temperatures. Mech. Syst. Signal Process. 2022, 170, 108760. [Google Scholar] [CrossRef]
- Wang, C.; Ning, Y.; Zhao, W.; Yi, G.; Huo, Y. Surface Evolution of Fused Silica Hemispherical Resonators and Its Influence on the Quality Factor. Sens. Actuators A Phys. 2023, 359, 114456. [Google Scholar] [CrossRef]
- Xu, Z.; Li, J.; Wang, Z.; Chen, X.L.; Chen, X.Z. Discussion on Precision Machining Technology of Quartz Hemispherical Harmonic Oscillator. Navig. Control 2019, 18, 69–76. [Google Scholar]
- Ma, Z.K.; Zhao, H.B.; Zhao, W.; Song, X.; Chen, X. Precision Forming Technology of Quartz Hemispherical Harmonic Oscillator. Navig. Control 2019, 18, 77–83. [Google Scholar]
- Liu, J.; Xiong, C.; Qu, T.; Che, C. External Sphere Grinding Principle Error Analysis and Experimental Study of Hemispherical Resonator. Opt. Tech. 2022, 48, 295–300. [Google Scholar]
- Zha, X.; Jiang, F.; Xu, X. Investigation of Modelling and Stress Distribution of a Coating/Substrate System after an Indentation Test. Int. J. Mech. Sci. 2017, 134, 1–14. [Google Scholar] [CrossRef]
- Liu, H.; Chen, M.; Yu, B.; Fang, Z. Configuration Design and Accuracy Analysis of a Novel Magnetorheological Finishing Machine Tool for Concave Surfaces with Small Radius of Curvature. J. Mech. Sci. Technol. 2016, 30, 3301–3311. [Google Scholar] [CrossRef]
- Ma, C.; Liu, H.; Chen, M.; Cheng, J.; Tian, J.; Zhou, Z. Research on the Effect of Geometric Parameters of Hemispherical Resonator on Thermoelastic Dissipation. J. Mech. Eng. 2024, 60, 75–84. [Google Scholar]
- Khooshehmehri, A.; Eslami Majd, A.; Arabsheybani, E. Thermo-Elastic Damping and Anchor Loss in the Operational Modes of a Hemispherical Shell Resonator. J. Comput. Appl. Res. Mech. Eng. 2023, 12, 211–224. [Google Scholar]
- Remillieux, G.; Delhaye, F. Sagem Coriolis vibrating gyros: A vision realized. In Proceedings of the 2014 DGON Inertial Sensors and Systems (ISS), Karlsruhe, Germany, 16–17 September 2014. [Google Scholar]
- Shi, Y.; Xi, X.; Li, B.; Chen, Y.; Wu, Y.; Xiao, D.; Wu, X.; Lu, K. Micro Hemispherical Resonator Gyroscope With Teeth-Like Tines. IEEE Sens. J. 2021, 21, 13098–13106. [Google Scholar] [CrossRef]
- Lu, K.; Xi, X.; Xiao, D.; Shi, Y.; Zhuo, M.; Wu, X.; Wu, Y. A Study on the Trimming Effects on the Quality Factor of Micro-Shell Resonators Vibrating in Wineglass Modes. Micromachines 2019, 10, 695. [Google Scholar] [CrossRef]
- Luo, H.; Tao, Y.; Zeng, L.; Tang, X.; Yang, K.; Luo, H. Investigation on the optimal fixation condition of cylindrical resonators. In Proceedings of the 28th Saint Petersburg International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 31 May–2 June 2021. [Google Scholar]
- Fan, S.; Liu, G. Analysis of Bending Vibration of Hemispherical Shells. Appl. Math. Mech. 1991, 12, 957–964. [Google Scholar]
- Sharma, G.N.; Sundararajan, T.; Gautam, S.S. Effect of Geometric Imperfections on Anchor Loss and Characterisation of a Gyroscope Resonator with High Quality Factor. Gyroscopy Navig. 2020, 11, 206–213. [Google Scholar] [CrossRef]
- Darvishian, A.; Nagourney, T.; Cho, J.Y.; Shiari, B.; Najafi, K. Thermoelastic Dissipation in Micromachined Birdbath Shell Resonators. J. Microelectromech. Syst. 2017, 26, 758–772. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, G.; Cheng, R. Mechanism of Frequency Splitting in Micro Hemispherical Resonator with T-Shape Masses: Study on the Harmonic Error Order Characteristics. Meas. Sci. Technol. 2025, 36, 085105. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, N.; Xie, R.; Wei, Z.; Zeng, Q.; Wang, C. Study on the Mechanism of Energy Dissipation in Hemispherical Resonator Gyroscope. Sensors 2025, 25, 74. [Google Scholar] [CrossRef]
- Basarab, M.A.; Matveev, V.A.; Lunin, B.S.; Fetisov, S.V. Influence of nonuniform thickness of hemispherical resonator gyro shell on its unbalance parameters. Gyroscopy Navig. 2017, 8, 97–103. [Google Scholar] [CrossRef]
- Basarab, M.A.; Chumankin, E.A.; Lunin, B.S. Application of a magnetic sensor for determining the mass imbalance of the Coriolis vibratory gyroscope with cylindrical metallic resonator. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—SPRING (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 2975–2979. [Google Scholar]
- Tao, Y.; Pan, Y.; Liu, J.; Jia, Y.; Yang, K.; Luo, H. A novel method for estimating and balancing the second harmonic error of cylindrical fused silica resonators. Micromachines 2021, 12, 380. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.; Xi, B.; Ren, S.; Ning, Y.; Tian, Z. Defects Identification and Mass Trimming in Hemispherical Resonators. Int. J. Mech. Sci. 2025, 294, 110242. [Google Scholar] [CrossRef]
- Ning, Y.; Wang, C.; Cheng, W.; Tian, Z. Anchor Loss Improvement in Hemispherical Resonators with Ion Beams. Int. J. Mech. Sci. 2024, 277, 109413. [Google Scholar] [CrossRef]
- Chen, Y.; Kong, F.; Zeng, K.; Xi, X.; Shi, Y.; Xiao, D.; Wu, X. A Trimming Strategy for Mass Defects in Hemispherical Resonators Based on Multi-Harmonic Analysis. Micromachines 2025, 16, 480. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.; Liu, G.; Wang, Z. On flexural vibration of hemispherical shell. Appl. Math. Mech. 1991, 12, 1023–1030. [Google Scholar] [CrossRef]








| Symbol | Parameters | Value |
|---|---|---|
| E | Young’s modulus | 76.7 GPa |
| ρ | Average density | 2200 kg/m3 |
| μ | Poisson’s ratio | 0.17 |
| ω1 | Frequency of first-order modes | 5528 × 2pi rad/s |
| ω2 | Frequency of second-order modes | 7919 × 2pi rad/s |
| Symbol | Parameters | Value |
|---|---|---|
| c | Elastic wave propagation speed | 6.12 km/s |
| λ | Elastic wave length | 0.773 m |
| d | The radius of the bottom of the support beam | 1.5 mm |
| R1 | PML radius | 803 mm |
| R2 | Base radius | 30 mm |
| Item | Existing Methods | Proposed Method |
|---|---|---|
| System complexity | Require multiple laser vibrometers, resulting in complex setups | A mirror-based beam-splitting optical configuration enables a single sensor to measure multiple shell–rod positions simultaneously, significantly simplifying the system |
| Error control | Sensor repositioning introduces alignment errors and environmental interference | Synchronous measurement eliminates these errors entirely |
| Efficiency | Sequential identification required for each harmonic order | Simultaneously identifies the first four harmonic errors in a single excitation cycle, improving efficiency |
| Symbol | Parameters | Value |
|---|---|---|
| ra | Maximum amplitude in xy-plane under 0° excitation | 320 pm |
| β | Included angle of maximum amplitude in xy-plane under 0° excitation | 0°3 |
| rz | Maximum amplitude in z-direction under 0° excitation | 148 pm |
| A | Four-node antinode amplitude under 0° excitation | 990 nm |
| ra′ | Maximum amplitude in xy-plane under 45° excitation | 420 pm |
| β′ | Included angle of maximum amplitude in xy-plane under 45° excitation | 45° |
| rz′ | Maximum amplitude in z-direction under 45° excitation | 140 pm |
| A′ | Four-node antinode amplitude under 45° excitation | 990 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Chen, W.; Li, Y.; Zhou, Y.; Liu, J. The Influence Mechanism and Identification Method of the First Four Harmonics of the Mass Defect of Hemispherical Resonators. Appl. Sci. 2025, 15, 8851. https://doi.org/10.3390/app15168851
Liu Q, Chen W, Li Y, Zhou Y, Liu J. The Influence Mechanism and Identification Method of the First Four Harmonics of the Mass Defect of Hemispherical Resonators. Applied Sciences. 2025; 15(16):8851. https://doi.org/10.3390/app15168851
Chicago/Turabian StyleLiu, Qingheng, Wenhui Chen, Yuhang Li, Yufang Zhou, and Junfeng Liu. 2025. "The Influence Mechanism and Identification Method of the First Four Harmonics of the Mass Defect of Hemispherical Resonators" Applied Sciences 15, no. 16: 8851. https://doi.org/10.3390/app15168851
APA StyleLiu, Q., Chen, W., Li, Y., Zhou, Y., & Liu, J. (2025). The Influence Mechanism and Identification Method of the First Four Harmonics of the Mass Defect of Hemispherical Resonators. Applied Sciences, 15(16), 8851. https://doi.org/10.3390/app15168851







