Random Forest-Based Machine Failure Prediction: A Performance Comparison

Abstract

Predictive maintenance is widely used in modern industrial systems. It helps improve the working life of machines. It also reduces risk and lowers overall operating costs. Many current approaches still face problems when handling both fast processing and balanced performance across different measurements. In this research, twelve machine learning models are tested. These include standard algorithms and deep learning-based solutions. Two manufacturing datasets are used. One has more samples, while the other shows uneven class labels. Important features are selected by applying strict screening. Model parameters are fine-tuned to obtain stable results. To measure how each model performs, several metrics are used—accuracy, precision, recall, F1-score, and ROC AUC. Among all tested models, random forest shows the best results. It reaches a classification accuracy of 99.5%. At the same time, it keeps a good balance between recall and precision. This model works well when data from sensors is imbalanced. It is also strong in handling patterns that do not follow a clear rule. The system is potentially suitable for real-time deployment in industrial machines with rotating parts, as demonstrated on two representative manufacturing datasets. However, broader validation across diverse equipment types is recommended before large-scale adoption.

1. Introduction

Maintenance management plays a pivotal role in ensuring the reliability, safety, and sustainability of industrial systems. As production systems evolve under the paradigm of Industry 4.0, the need for advanced, data-driven maintenance strategies becomes increasingly pronounced. Among these, Predictive Maintenance (PdM) stands out for its ability to anticipate failures based on sensor data, thereby reducing unplanned downtime and optimizing operational efficiency [1,2].

Despite significant advances, traditional PdM methods often rely on energy-waste indicators such as vibration and acoustic signals, which may not fully capture the underlying degradation mechanisms, especially in machines with rotating components [3]. Moreover, industrial failure data tend to be sparse and imbalanced, making it difficult for classical machine learning (ML) models to generalize well. The heterogeneity of machine types, operating regimes, and sensor setups further exacerbates the challenge, limiting the replicability of existing solutions across different industrial contexts.

In this context, recent studies have called for more transparent, reproducible, and comparative evaluations of ML and deep learning (DL) methods applied to predictive maintenance tasks. Ensemble models such as Random Forest (RF) and gradient boosting methods have shown resilience to data imbalance and are widely used in industrial fault diagnosis. However, their performance and interpretability in comparison to other ML and DL algorithms under realistic, imbalanced industrial conditions remain underexplored.

This study addresses three main research gaps: (i) lack of consistent benchmarks across classical, ensemble, and deep models for PdM; (ii) limited evaluation of model robustness under real-world constraints such as data imbalance and rare failures; and (iii) insufficient use of explainable AI (XAI) techniques to support transparent decision-making.

To address these gaps, we conduct a comprehensive comparative study on machine predictive maintenance using real-world industrial datasets. We benchmark eleven models—including random forest, Support Vector Machines (SVMs), k-Nearest Neighbors (KNN), logistic regression, naive Bayes, AdaBoost, Linear Discriminant Analysis (LDA), Kernel Density Estimation with Logistic Regression (KDE+LR), XGBoost, Multi-Layer Perceptron (MLP), and Transformer-based methods—on their predictive performance, robustness, and explainability.

Special attention is given to evaluation metrics beyond accuracy, including weighted recall, F1-score, and ROC AUC, as these are critical in high-risk industrial scenarios where false negatives can lead to severe consequences. We also apply SHAP (Shapley Additive Explanations) to interpret model predictions and identify the most influential features across datasets.

This study makes three primary contributions: (1) A random forest model is carefully tuned and evaluated for rotating equipment fault prediction, considering both accuracy and explainability. (2) A multi-metric evaluation framework is proposed to assess predictive performance under data imbalance, with insights into overfitting through cross-validation dispersion. (3) Comparative visualizations and SHAP-based analysis are provided to support the adoption of trustworthy AI solutions in real industrial settings.

The rest of this paper is structured as follows. Section 2 reviews related work and methodological limitations. Section 3 details the datasets, preprocessing pipeline, feature engineering, and model configurations. Section 4 presents the experimental results and interpretability analysis. Section 5 discusses deployment considerations and concludes with recommendations for future work.

2. Related Work

Research on predictive maintenance is generally divided into two main categories. One relies on statistical techniques, while the other applies machine learning models. This part first looks at early statistical tools. Then, it turns to recent learning-based methods, outlining their benefits as well as known drawbacks.

2.1. Traditional Statistical Methods

For a long time, statistical tools formed the core of maintenance forecasting. These methods are effective under well-defined operational assumptions and structured data, particularly in systems where failure mechanisms follow clear probabilistic behavior [4,5]. However, their accuracy and generalizability decrease significantly in dynamically changing environments or when dealing with incomplete or sparse datasets.

Weibull analysis has played a central role in reliability studies. It is widely used for estimating life distributions, particularly when failure rates increase or decrease over time. While it has been used in rotating machinery, its suitability is context-sensitive, depending on accurate lifetime data and a good fit to the chosen distribution [6]. It also assumes a specific form for data, which reduces accuracy when information is limited or censored.

The Cox Proportional Hazards Model (PHM) introduced semi-parametric flexibility by including covariates in hazard estimation [7]. Yet, its practical use is limited by the proportional hazards assumption, which requires the effect of covariates on hazards to remain constant over time—a condition often violated in real industrial datasets [4]. Sensor drift, covariate shift, and nonstationary processes commonly found in industrial contexts further complicate its use.

Time-series models such as ARIMA and its multivariate extension VARIMA can capture temporal dependencies and handle multiple inputs [8,9]. However, they require extensive stationarity checks, parameter tuning, and lack robustness under non-linear or abruptly shifting system behaviors, which limits their applicability in real-time maintenance scenarios [10].

Markov-based approaches, such as Hidden Markov Models (HMMs), describe system wear as movement between states. While earlier HMM implementations suffered from computational inefficiency [11,12], modern techniques—such as expectation-maximization (EM) optimization and variational inference—have significantly mitigated this issue [13]. However, accurate state modeling remains challenging when the degradation process is not well understood or labeled.

Three main problems affect these classical models:

• Reliance on strong assumptions about data distribution and system stationarity.
• Difficulty handling complex, sensor-rich, or high-dimensional datasets.
• High effort required in feature engineering and domain-specific model calibration.

The following section turns to data-driven models that attempt to address these issues by leveraging learning-based inference and larger-scale sensor data streams.

2.2. Machine Learning Approaches

The growth of industrial IoT systems and better computing tools has led to more frequent use of machine learning in maintenance tasks. These techniques can learn from data directly, often reducing how much manual work is needed for feature design.

Support Vector Machines (SVMs) rely on kernel-based mapping to work in higher-dimensional spaces. They have performed well when used for detecting bearing faults [14,15]. However, when failure data are highly imbalanced—as is common in predictive maintenance—standard SVMs may suffer performance degradation. This limitation can be mitigated using cost-sensitive variants or sampling techniques, which have shown improvements in classifying rare events [16].

k-Nearest Neighbors (KNN) uses distance-based rules without assuming a fixed model. It can adjust to changes in system behavior and has been used in anomaly detection [17]. Nonetheless, KNN becomes computationally expensive in the prediction phase due to its non-parametric nature, especially with high-dimensional industrial datasets. Studies have demonstrated this limitation in time-sensitive scenarios such as real-time fault detection in sensor networks [18].

Logistic Regression (LR) builds linear boundaries to predict failure likelihood. It is easy to explain and has helped in detecting pump problems [19]. Although it models linear relationships, LR can still be effective in complex settings through proper feature engineering and interaction terms. Several industrial case studies have used extended LR models with engineered features to capture non-linear degradation trends.

Naive Bayes (NB) uses probability rules to detect faults quickly. It is often applied in settings where computing power is limited, such as semiconductor production lines [1]. While NB assumes conditional independence among features—which is often violated in practice—empirical studies show that NB can remain effective, especially with large-scale datasets and carefully selected or transformed features [20]. Thus, its usefulness should not be dismissed solely based on its simplifying assumptions.

In response to the above limitations, ensemble learning methods have been introduced to boost predictive robustness. Models that combine several learners—like random forest and XGBoost—have changed how failures are predicted [21,22]. Random forest introduces randomness to deal with unbalanced data. It reduces overfitting risk and can handle high-dimensional features, although interpretability becomes a concern as the number of trees increases [23]. XGBoost improves accuracy by adjusting errors step by step, and it controls overfitting through regularization [24]. It has demonstrated competitive performance in recent predictive maintenance competitions and field studies [10].

Neural network models, such as CNNs and RNNs, can learn directly from sensor input. CNNs pick up patterns in space. RNNs, like LSTM, follow changes across time. Together, they help raise accuracy in prediction tasks [25,26]. However, these models often require significant preprocessing for sensor signal alignment and are highly sensitive to hyperparameter tuning. Industrial adoption is further constrained by their high demand on memory and computational power [10].

In summary, while machine learning has provided powerful tools for predictive maintenance, challenges remain in interpretability, class imbalance, computational efficiency, and domain adaptation. To bridge the gap between performance and transparency, hybrid approaches that combine ML techniques with statistical domain knowledge or rule-based reasoning have been proposed in recent literature.

2.3. Ensemble Methods

By combining several base learners, ensemble approaches improve the stability of predictions. This makes them especially useful when working with industrial data that shows complex variation [21]. They help reduce the impact of errors from individual models, which benefits maintenance tasks.

Random forest applies bagging to generate diverse decision trees, making it more robust to overfitting than a single-tree setup [27]. However, its performance strongly depends on parameter tuning and data characteristics. In fault detection, particularly with rotating systems, random forest has demonstrated competitive results when appropriately optimized [21]. It is important to note, however, that single decision trees can outperform RF under specific conditions—such as in highly imbalanced datasets or low-noise environments—raising the need for careful validation.

Boosting strategies—such as gradient boosting and XGBoost—build models incrementally, correcting prior errors. XGBoost incorporates regularization and sparsity-aware techniques, and while it supports parallelism during tree construction, its training speed advantage is context-dependent and not always superior without proper hardware or data partitioning [22].

AdaBoost performs well even in noisy conditions, such as wind turbine fault detection [28]. However, claims about its processing cost must be carefully qualified: while iteration adds computational burden, the actual runtime depends heavily on implementation and dataset scale. Without empirical runtime comparisons or hardware details, such generalizations can be misleading.

Overall, ensemble models face several limitations. First, model complexity and inference time may increase significantly with larger datasets. Second, adding more learners reduces the model’s interpretability, which can hinder adoption in regulated or safety-critical settings [29]. These concerns have prompted interest in combining ensemble methods with interpretable or deep architectures for a better trade-off.

2.4. Deep Learning and Transformer Models

Deep learning has changed how maintenance tasks are approached. These models can work directly with raw data, even when it is high-dimensional, and they often need little manual processing [25]. They are effective in finding complex patterns that might otherwise go unnoticed, though they also raise new technical concerns [30].

Convolutional Neural Networks (CNNs) apply methods from image analysis to vibration signals. This has proven useful in fault detection for gearboxes [25]. However, the assertion that CNNs reduce the need for handcrafted features should be qualified—substantial preprocessing is typically required to convert 1D time-series sensor data into suitable 2D representations, such as spectrograms or wavelet-transformed signals. In industrial settings, such transformations are often non-trivial.

Recurrent Neural Networks (RNNs), particularly Long Short-Term Memory (LSTM) networks, model temporal dependencies in time-series data, improving remaining useful life predictions for bearings [26]. Their sequential processing demands substantial computational resources.

Transformer architectures use self-attention to manage distant dependencies within time-series data. In detecting complex failures, they often perform better than RNN-based models [31]. However, transformer models tend to require significantly larger labeled datasets and more memory, limiting their deployment in resource- constrained environments.

Despite their representational power, deep learning methods introduce multiple challenges. First, supervised models often require large labeled datasets (e.g., over 10,000 instances), which are difficult to collect in maintenance settings. Second, the computational overhead—especially for transformers—can be prohibitive for real-time applications. Third, many of these models operate as ‘black boxes,’ making it hard for practitioners to understand or trust the decisions. To mitigate this, Explainable AI (XAI) tools such as SHAP or LIME are being explored to provide localized interpretations of predictions [29,32].

2.5. Gaps in Existing Research

Machine learning and deep learning have seen wide application in predictive maintenance. Still, several problems remain, making real-world use difficult. Solving these problems is important for improving system reliability.

Handling Imbalanced Data: One common issue is that failure records are rare. In most cases, they make up only a small share of the full dataset. Many models tend to favor the more frequent class. This reduces their accuracy in spotting failures [33]. SMOTE and similar tools try to correct the imbalance by adding synthetic samples. Their impact, however, weakens in complex, high-dimensional setups. Overfitting becomes more likely in these situations [34]. Recent work suggests that ensemble methods with cost-sensitive learning or class-weight adjustment—especially in tree-based models—may offer more robust solutions under industrial imbalance scenarios.

Model Interpretability: Many advanced models, such as CNNs and RNNs, produce results that are difficult to explain. Although they can reach high accuracy, their inner workings are often unclear. This lack of clarity creates concerns in fields where clear reasoning is required [35]. In safety-critical tasks, trust depends on knowing why a prediction was made. Some recent efforts—like the LIME method—aim to explain how outputs are formed. These tools can show which inputs matter most, but their use in maintenance tasks is still limited [29]. In tree-based models such as random forest, interpretability can be enhanced through feature importance, partial dependence plots, and SHAP analysis, which remain underutilized in the industrial predictive maintenance literature [32].

Scalability and Computational Efficiency: As more sensors are added and data becomes more complex, the effort needed to train and run models grows. In many real-world systems, predictions must be fast and reliable at the same time [36]. Some progress has been made using model compression. These techniques lower the load on hardware and speed up response time. Still, they can reduce accuracy if not applied carefully. Moreover, few studies explore the trade-offs between depth, complexity, and runtime in ensemble models such as RF and XGBoost within constrained edge-computing environments.

Integration with Industrial IoT: Connecting predictive models to Industrial IoT platforms remains a difficult task. These environments produce fast, varied, and continuous data [37]. Processing such streams in real time poses both technical and structural challenges. In much of the current research, models are developed separately from the systems they are meant to support. The need to update models quickly and handle different types of input data is often overlooked. A unified pipeline for model retraining, streaming integration, and monitoring within IIoT remains underdeveloped.

Limited Comparative Studies: Many studies examine just one model or dataset. This makes it hard to apply findings across various industries [38]. Some work has tested several models, though usually on data with limited scope. Conditions in factories often change, and that variation is rarely included in published evaluations. Broader tests are still lacking. A more consistent, comparative approach is needed to help select models that work well beyond one narrow use case.

Real-World Validation: Many predictive models perform well under lab conditions. Once applied in actual industrial settings, though, results often decline. Factors such as external noise, shifting system states, and operational complexity contribute to this drop in accuracy. Bridging this gap requires benchmarking under noisy sensor data, temporal drift, and actuator feedback, which are still not commonly evaluated in public datasets.

2.6. Contributions of This Study

This work focuses on solving the gaps outlined earlier. It evaluates the practical applicability of machine learning methods by focusing on replicable performance, interpretability, and industrial integration [39]. It makes use of random forest’s ability to manage complex data while also comparing it with newer models, including deep networks and Transformer systems. Several contributions are made, covering both theory and real-world application in the field of predictive maintenance.

Robust Predictive Maintenance Model: This work presents a tuned random forest model for predicting faults in rotating machinery. Hyperparameters including number of trees, maximum depth, split criteria (GINI vs entropy), minimum samples per leaf, and class weights were systematically explored to address both accuracy and overfitting concerns. Its design takes advantage of the model’s strength in managing uneven class distributions and offering output that can be interpreted clearly [21]. Rather than limiting the study to one method, the evaluation compares random forest with nine alternatives—SVM, KNN, logistic regression, naive Bayes, AdaBoost, LDA, KDE+LR, XGBoost, and MLP—under different industrial settings. This comparative evaluation avoids cherry-picking results by reporting full classification metrics, including confusion matrices and ROC AUC scores, to better demonstrate performance limits under rare-failure settings. Earlier contributions by [23] serve as a base, which this study builds upon and expands into new use cases.

Comprehensive Comparative Analysis: This study performs a broad evaluation across several machine learning models. The focus goes beyond prediction accuracy. Factors like how well results can be explained, how fast models run, and how they scale are all considered. The models include standard approaches, ensemble types, and deep networks. Compared with earlier work—[38] is one example—this study avoids limits tied to specific datasets. We report metrics across stratified folds and datasets to quantify both performance and variance, in response to concerns of overfitting and poor generalization. The findings support informed model choices across various industrial settings.

Navigating Practical Implementation Hurdles: To address the challenges of real-world deployment, this research proposes solutions targeting the integration of predictive models within IIoT frameworks, the management of diverse data sources, and the assurance of system scalability. Informed by seminal work from [36], our study investigates strategies such as model compression and real-time processing. We also discuss retraining frequency, edge deployment strategies, and inference delays in realistic scenarios, which are often overlooked in lab-based studies. These methods are designed to improve the viability of deployment in settings with limited resources, thereby filling a significant void in existing research.

Enhancing Model Interpretability: To satisfy the industrial requirement for transparency, this study leverages Explainable AI (XAI) methodologies, specifically employing SHAP values to improve the interpretability of our random forest model, as informed by [32]. Additionally, we incorporate global and local explanation techniques to help domain experts understand feature influence, model confidence, and failure case misclassifications. This approach directly confronts the shortcomings of "black box" models, which were highlighted by [29,35], thereby ensuring that the model’s predictions are not only accurate but also demonstrably trustworthy to domain experts.

Future Research Directions: By underscoring the necessity for hybrid models alongside real-time analytics, our conclusions offer a clear trajectory for subsequent research in predictive maintenance. We propose the integration of ensemble methods with deep learning approaches to achieve a better balance between accuracy and interpretability. Furthermore, this study highlights the critical importance of real-world validation as a means to close the divide that separates theoretical concepts from practical application. We also emphasize the development of benchmark datasets with full process metadata, streaming characteristics, and labeled anomalies, which are needed for reliable model transferability across industries.

3. Materials and Methods

This section outlines the datasets, preprocessing steps, machine learning models, and evaluation strategies adopted in this study. Two publicly available industrial maintenance datasets are utilized to simulate realistic fault prediction scenarios. The data are cleaned, transformed, and reduced using established preprocessing and feature selection techniques. A set of twelve machine learning models—including tree-based, statistical, and deep learning approaches—are trained and optimized using grid search and cross-validation. Evaluation metrics such as accuracy, precision, recall, F1-score, and ROC AUC are used to assess model performance. The methodology is designed to ensure reproducibility, fairness in comparison, and applicability in real-world industrial contexts.

3.1. Experimental Setup

Hardware and Software Configuration: The tests were run on a machine using an Intel Core i7 CPU, 32 GB memory, and an NVIDIA RTX 2080 graphics card. Python 3.9 was used for coding. Traditional models were built with scikit-learn (v1.0.2). Deep learning parts used TensorFlow (v2.8.0), and the Transformer was handled through PyTorch (v1.10.0) [40,41]. Data cleaning and plotting were performed using Pandas (v1.4.2) and Matplotlib (v3.5.1).

3.2. Datasets

Dataset Descriptions:

• Machine Predictive Maintenance Classification (Dataset A): This dataset, taken from Kaggle, contains 9999 rows and 14 input columns. Among them are values such as air and process temperatures (in Kelvin), speed in RPM, torque in Nm, tool wear in minutes, and a machine type label (L, M, or H). The target is a binary label named “Target,” showing whether a failure happened (1) or not (0). There is also a multi-class variable called “Failure Type,” though only the binary target is used in this study. The dataset exhibits class imbalance, with approximately 3.4% failure instances, reflecting real-world industrial conditions [34]. Feature distributions are continuous (e.g., temperature) and categorical (e.g., machine type), necessitating robust preprocessing.
• Machine Failure Prediction using Sensor Data (Dataset B): This dataset contains 943 samples with 10 features: footfall, temperature mode, air quality (AQ), ultrasonic sensor strength (USS), current sensor (CS), volatile organic compounds (VOC), rotational position (RP), input power (IP), temperature, and a binary failure indicator (fail: 0 or 1). Features are primarily integer-valued (e.g., AQ, USS) or continuous (e.g., temperature), capturing sensor readings from industrial equipment. The dataset is moderately imbalanced, with a failure rate of approximately 10%, posing challenges for model training [42]. Its smaller size and diverse feature set test model generalization.
• Modeling and Validation Procedure: All categorical variables were processed with label encoding, and numerical features were standardized using z-score normalization. The dataset was randomly divided into training (70%) and testing (30%) subsets using a fixed seed (random_state = 42) to ensure consistent results across all models. To handle class imbalance, we used class_weight = ‘balanced’ where supported. Model performance was evaluated using five metrics on the test set only: accuracy, weighted precision, weighted recall, weighted F1-score, and ROC AUC (multi-class one-vs-one strategy). These metrics were chosen to provide a comprehensive view under imbalanced conditions. Twelve models were implemented using the same pipeline, including random forest, logistic regression, SVM, KNN, XGBoost, and MLP. Among them, random forest consistently outperformed the other methods across all metrics, yielding a 99.5% test-set accuracy. No metric was computed on the training set, minimizing overfitting risks.

3.3. Data Preprocessing and Feature Selection

Data Preprocessing:

• Dataset A: No missing values were present, as the dataset is synthetic and well-structured. Continuous features (e.g., air temperature, torque) were standardized using z-score normalization:

  $$x^{\prime }={\displaystyle \frac{x-\mu }{\sigma }}$$

  where $\mu$ is the mean and $\sigma$ is the standard deviation, ensuring scale invariance [14]. Categorical features (e.g., machine type) were one-hot encoded. The “Product ID” and “Failure Type” features were excluded to prevent data leakage and focus on binary classification.
• Dataset B: Similarly, no missing values were detected. Integer-valued features (e.g., AQ, USS) were treated as ordinal, while continuous features (e.g., temperature) were normalized. Outlier detection using the interquartile range (IQR) method removed extreme values (e.g., footfall > 2800), affecting less than 1% of samples [43]. Feature correlations were analyzed to ensure no multicollinearity, with Pearson’s correlation coefficient $r<0.8$ for all feature pairs.

Feature Selection: For both datasets, Recursive Feature Elimination (RFE) with a random forest estimator was applied to select the top 8 features [44], reducing dimensionality while retaining predictive power [45]. For Dataset A, key features included rotational speed, torque, and tool wear; for Dataset B, footfall, VOC, and temperature were prioritized based on Gini importance [21].

3.4. Model Overview and Training

This section outlines the structure and development process of a failure prediction model based on the random forest algorithm. The design responds to two industrial concerns: data imbalance and model clarity. Ensemble learning properties in random forest are used to produce stable and explainable results fit for industrial use [21,23].

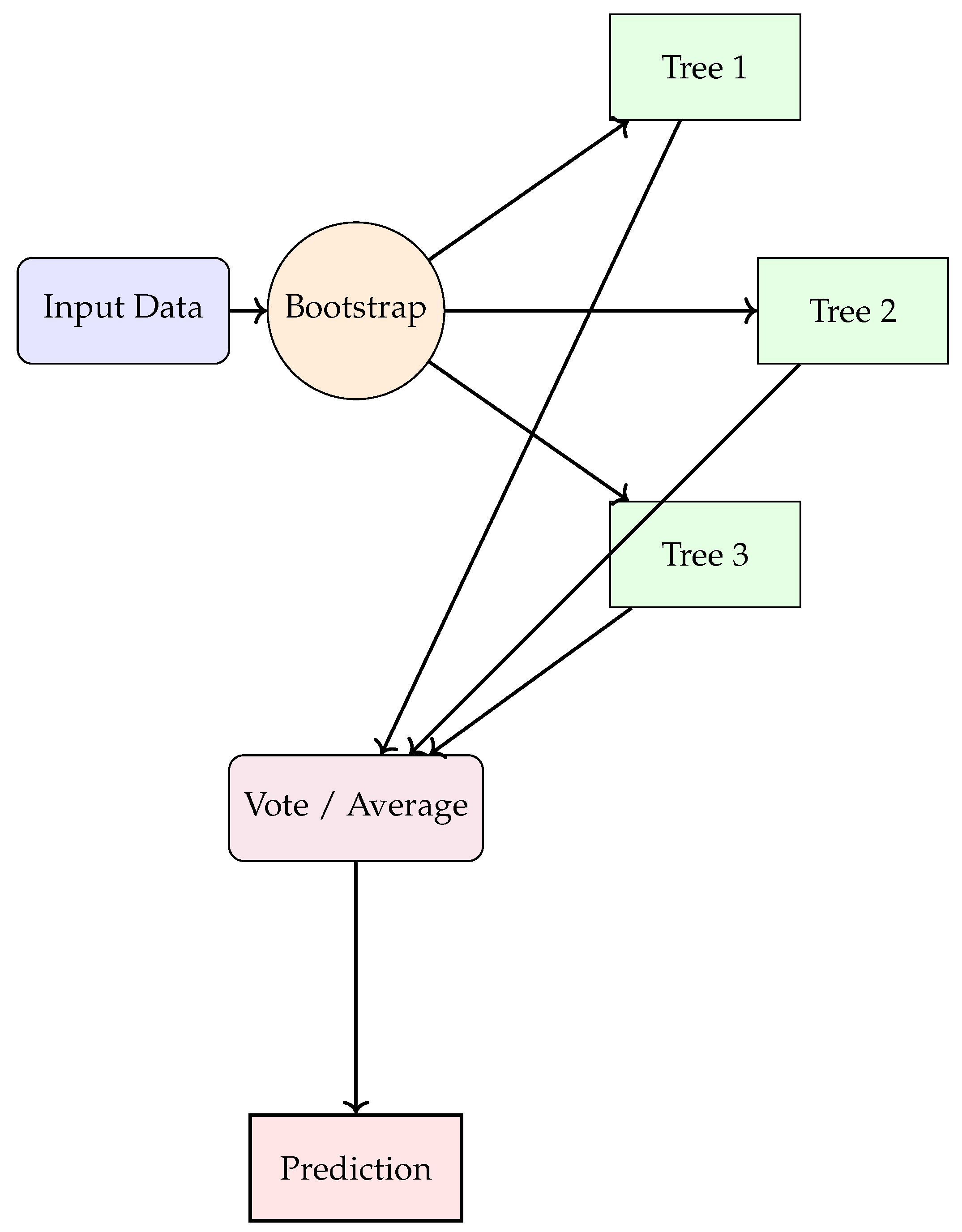
3.4.1. Model Architecture

Random forest is an ensemble method that builds multiple decision trees using bootstrapped subsets of data and random feature selection at each split [21]. Final predictions are determined by majority vote (classification) or averaging (regression). This structure reduces variance and limits overfitting [23].

We illustrate the structure in Figure 1 and refer readers to standard texts for full derivations [22,46].

3.4.2. Data Preprocessing

Reliable preprocessing supports the stability of model performance. Sensor values that are missing are filled using the median. To lessen the influence of extreme values, noise-resistant statistical tools are applied [43,47]. Signs of machine degradation are better revealed by generating features derived from time-based shifts and rolling averages. These are informed by practical domain insights [3,15]. Standardization is also used so that all inputs contribute equally. This reduces issues in models that react strongly to input scale, such as SVM [14,48]. To manage rare class examples, SMOTE is applied to produce synthetic failure cases. Random forest settings are also adjusted to emphasize these rare instances [34], helping to address the imbalance that is often found in industrial data [42].

3.4.3. Model Training

Training focuses on finding the balance between precision and model complexity. The dataset is divided using k-fold cross-validation. This helps test generalization in multiple data scenarios [49,50]. For parameter tuning, a grid search is carried out. Different values, such as tree count and depth, are explored to avoid underfitting or overfitting [23,51]. Several configurations are evaluated in sequence. The one showing the strongest validation results is selected [22,52].

Key Algorithm: The random forest training process for predictive maintenance is formalized in Algorithm 1. The algorithm integrates bootstrap sampling, feature randomness, class weighting for imbalanced data, and feature selection to ensure robust failure prediction in industrial settings [21,33].

Algorithm 1 Random Forest Training for Predictive Maintenance

1: Input: Training dataset $\mathcal{D}={\left\{({\mathbf{x}}_i,y_i)\right\}}_{i=1}^N$, number of trees T, feature subset size m, class weights $\mathbf{w}$, feature importance threshold $\tau$   2: Output: Random Forest model $\mathcal{F}={\left\{h_t\right\}}_{t=1}^T$   3: Initialize empty forest $\mathcal{F}\leftarrow Ø$   4: Apply SMOTE to $\mathcal{D}$ to balance minority class, yielding augmented dataset ${\mathcal{D}}^{\prime }$   5: Compute Gini importance for features in ${\mathcal{D}}^{\prime }$ using a preliminary Random Forest   6: Select features with importance $>\tau$, updating ${\mathcal{D}}^{\prime }$ to include only selected features   7: for$t=1$ to T do   8:  Generate bootstrap sample ${\mathcal{D}}_t$ from ${\mathcal{D}}^{\prime }$ with replacement   9:  Initialize decision tree $h_t$ with class weights $\mathbf{w}$ 10:  for each node in $h_t$ do 11:   Randomly select m features from the feature set 12:   Compute Gini impurity for each feature split 13:   Choose split minimizing weighted Gini impurity: $\mathrm{Gini}=1-{\sum }_k{w}_k{p}_k^2$ 14:   Split node until stopping criteria (e.g., max depth, min samples) are met 15:  end for 16:  Add $h_t$ to $\mathcal{F}$ 17: end for 18: Return $\mathcal{F}$

Baseline Models: Twelve models were evaluated: decision tree, Support Vector Machine (SVM), k-Nearest Neighbors (KNN), logistic regression, naive Bayes, random forest, AdaBoost, Linear Discriminant Analysis (LDA), Kernel Density Estimation with Logistic Regression (KDE+LR), XGBoost, Multi-Layer Perceptron (MLP), and a Transformer model. Hyperparameters were optimized via grid search with 5-fold cross-validation, targeting F1-score maximization [49,51]. For example, random forest parameters included the number of trees ($T\in \{100, 200, 500\}$) and maximum depth ($d\in \{10, 20, None\}$).

Transformer Model: A Transformer-based model with 4 attention heads and 2 layers was implemented, leveraging self-attention to capture temporal dependencies in sensor data [31]. It was trained with a batch size of 32 and the Adam optimizer ($\eta =0.001$), using early stopping to prevent overfitting [53].

Training–Validation Split: Both datasets were split into 70% training, 15% validation, and 15% test sets. Stratified k-fold cross-validation ($k=5$) ensured balanced class representation, addressing imbalance [50]. SMOTE was applied to the training set to generate synthetic failure instances, improving minority class detection [33].

3.5. Evaluation Metrics

We evaluated the models using five standard metrics: accuracy, precision, recall, F1-score, and ROC AUC. These metrics are commonly adopted in imbalanced classification scenarios to balance the trade-off between false positives and false negatives [34,54].

Accuracy measures the proportion of correctly predicted instances, while precision and recall focus on the relevance and completeness of positive predictions. F1-score offers a harmonic balance between precision and recall. ROC AUC quantifies the model’s ability to distinguish between classes across thresholds [55,56].

All metrics were computed on the test set using weighted averaging, and reliability was ensured by applying repeated 5-fold cross-validation [50]. This provided an estimate of performance stability under varied splits.

3.6. Interpretability and Deployment Considerations

3.6.1. Model Interpretation

Industrial applications of predictive maintenance systems require that machine learning models be interpretable and trustworthy to stakeholders [29]. Instead of using SHAP or PDPs, we focused on Gini-based feature importance, which is directly derived from the structure of the trained random forest model [57].

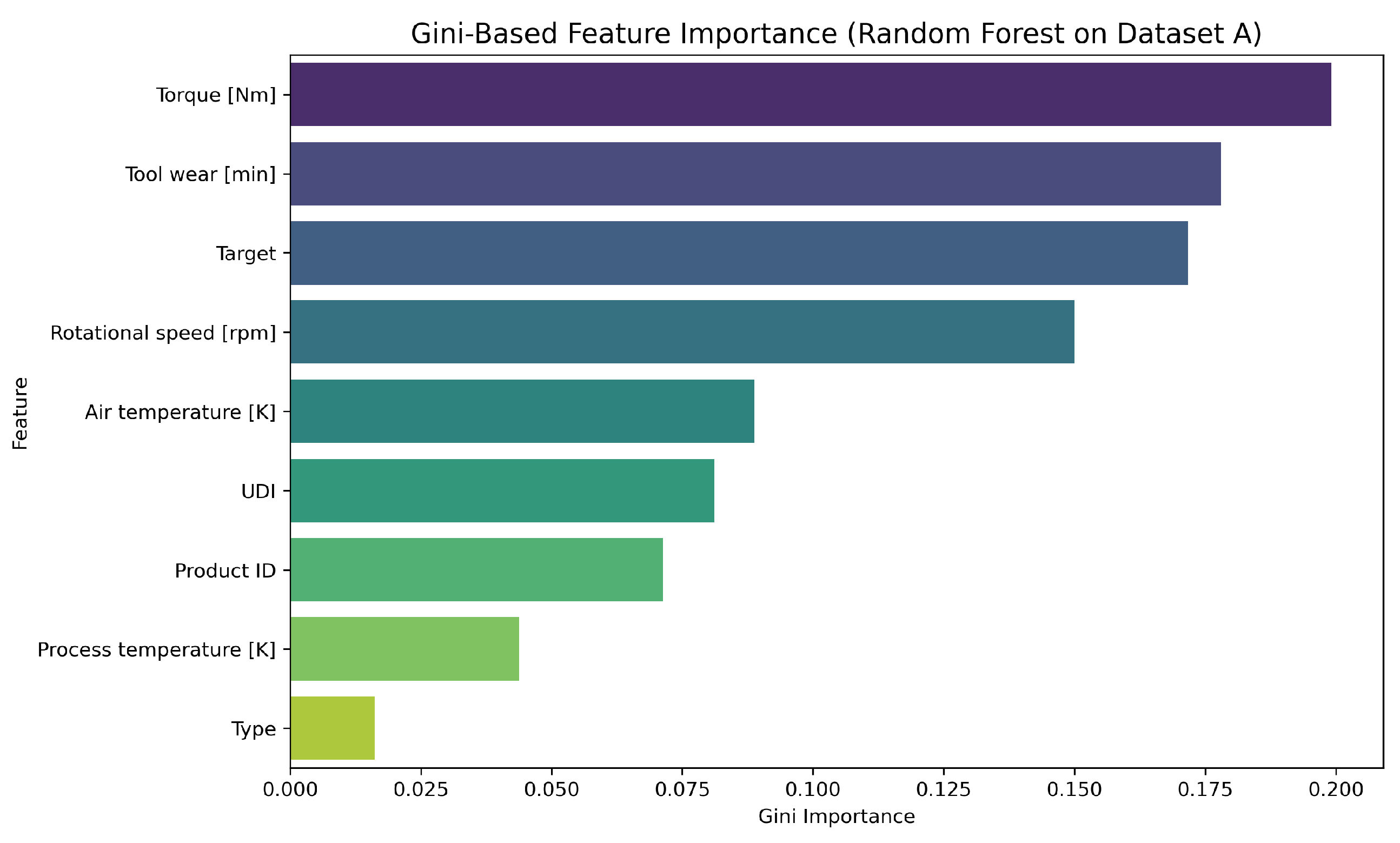
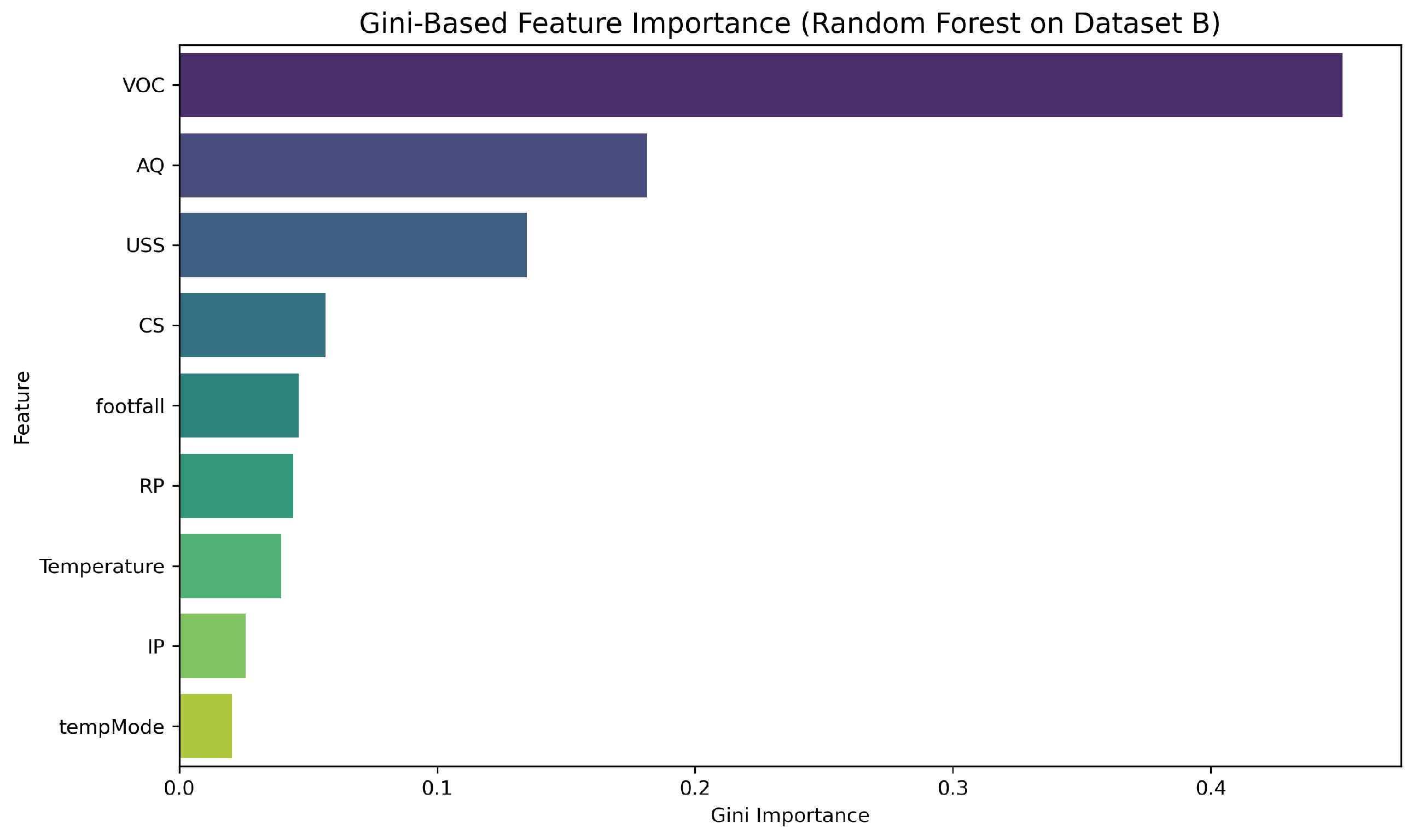
Figure 2 and Figure 3 show the feature importance scores for Dataset A and Dataset B, respectively, based on Gini impurity reductions.

For Dataset A, the top three contributing features are:

• Torque [Nm]–a direct mechanical stress factor correlated with failure incidence;
• Tool wear [min]–an accumulated degradation signal;
• Rotational speed [rpm]–associated with dynamic mechanical loading.

For Dataset B, the most informative features are:

• VOC (Volatile Organic Compounds)–indicating internal chemical changes;
• Air Quality (AQ)–an environmental proxy for wear-related emissions;
• Ultrasonic Sensor Strength (USS)–detecting vibration and motion abnormalities.

These results were obtained from the random forest model and provide strong interpretability for industrial experts. The inclusion of domain-relevant variables in both datasets increases confidence in the model’s output. Gini-based ranking also aligns with engineering intuition, aiding transparency.

Figure 2 and Figure 3 provide visual summaries of the feature rankings.

3.6.2. Integration with Industrial IoT Systems

The random forest model fits Industrial Internet of Things (IIoT) systems, supporting ongoing predictive maintenance. It works with live sensor data to provide real-time monitoring.

Sensor measurements—such as vibration and temperature—arrive as continuous data streams. The system processes this input without interruption. An efficient preprocessing pipeline manages these high-frequency inputs. Feature extraction uses a sliding time window to maintain updated failure predictions throughout the monitoring period [37,58,59].

A common technique calculates rolling averages over a fixed window size W. For each time t, the average sensor reading is computed as

$${\overline{x}}_t={\displaystyle \frac{1}{W}}\sum _{i=t-W+1}^t{x}_i$$

where $x_i$ represents the sensor measurement at time i. These averages reveal gradual changes in sensor behavior, allowing for early detection of anomalies. The system adapts quickly to evolving industrial conditions, delivering timely decisions with minimal delay.

The model can work with communication standards often used in industrial systems. It supports protocols like MQTT and OPC UA, which are commonly adopted for exchanging data across devices [60].

To support deployment flexibility, the system can connect through standard APIs. This makes it possible to run the model on cloud platforms or closer to the equipment at the edge [61]. In both cases, hybrid setups are supported, allowing for real-time analysis when needed.

Together, these features help align the model with practical industrial needs. It performs well while also adapting to technical and operational limits in real-world environments.

3.6.3. Model Deployment Considerations

Applying predictive models in actual industrial settings requires addressing several real-world concerns:

• Model Updating: Machine behavior may change as time passes. To keep the model aligned with these shifts, incremental learning is used. Full retraining is avoided. Instead, smaller updates based on new data are added gradually [62]. With regular input from recent sensor streams, model accuracy can stay consistent, even as components wear down [3].
• Robustness to Noise: Factory data often includes unexpected disruptions. These may result from sensor failures or environmental interference. Preprocessing—such as spotting and removing outliers—helps to minimize these effects. At the same time, using ensemble models adds resistance to unstable input and reduces prediction swings.
• Latency Optimization: Fast decision-making is critical in live settings. To lower delay during inference, model depth is reduced, and fewer input features are used [52]. Running processes at the network edge also helps. It cuts down transfer time and speeds up fault reaction [63].
• Cost–Benefit Analysis: Real-world use involves balancing maintenance spending against the chance of system failure. Models with high recall catch most faults, helping to avoid expensive downtime. At the same time, high precision keeps unnecessary service actions low [64].

4. Results

4.1. Model Performance Results

The performance of all models on both datasets is summarized in

Table 1. Performance comparison on machine predictive maintenance classification (Dataset A).

Model	Accuracy	Precision	Recall	F1-Score	ROC AUC
Decision Tree	0.9907	0.9901	0.9907	0.9903	0.8668
SVM	0.7793	0.9924	0.7793	0.8721	0.9075
KNN	0.9897	0.9897	0.9897	0.9884	0.9016
Logistic Regression	0.7757	0.9920	0.7757	0.8696	0.9081
Naive Bayes	0.4247	0.9914	0.4247	0.5883	0.9146
Random Forest	0.9950	0.9929	0.9950	0.9939	0.9144
AdaBoost	0.8153	0.9823	0.8153	0.8882	0.8117
LDA	0.9927	0.9915	0.9927	0.9914	0.9004
KDE+LR	0.7753	0.9918	0.7753	0.8694	0.9087
XGBoost	0.9947	0.9924	0.9947	0.9935	0.9106
MLP	0.9940	0.9920	0.9940	0.9929	0.9034
Transformer	0.9925	0.9903	0.9925	0.9910	0.9593

Bold values indicate the best performance for each metric.

(Dataset A) and

Table 2. Performance comparison on machine failure prediction using sensor data (Dataset B).

Model	Accuracy	Precision	Recall	F1-Score	ROC AUC
Decision Tree	0.8345	0.8344	0.8345	0.8344	0.8314
SVM	0.8838	0.8855	0.8838	0.8841	0.9487
KNN	0.8662	0.8665	0.8662	0.8663	0.9440
Logistic Regression	0.8838	0.8848	0.8838	0.8840	0.9508
Naive Bayes	0.8768	0.8773	0.8768	0.8769	0.9339
Random Forest	0.8873	0.8876	0.8873	0.8874	0.9445
AdaBoost	0.8803	0.8816	0.8803	0.8806	0.9295
LDA	0.8838	0.8863	0.8838	0.8842	0.9539
KDE+LR	0.8838	0.8848	0.8838	0.8840	0.9508
XGBoost	0.8662	0.8665	0.8662	0.8663	0.9399
MLP	0.8768	0.8769	0.8768	0.8768	0.9491
Transformer	0.8571	0.8561	0.8571	0.8564	0.8567

Bold values indicate the best performance for each metric.

(Dataset B).

Dataset A (Machine Predictive Maintenance Classification):

• Random forest achieved the highest performance, with an accuracy of 99.50%, precision of 99.29%, recall of 99.50%, F1-score of 99.39%, and ROC AUC of 0.914. Its robustness to imbalance and feature interactions drove its success [21,23].
• Transformer followed closely, with 99.25% accuracy, 99.10% F1-score, and the highest ROC AUC (0.959), benefiting from attention mechanisms [31].
• XGBoost and MLP performed well (F1-scores of 99.35% and 99.29%, respectively), but random forest’s simplicity and interpretability were advantageous [22].
• Naive Bayes underperformed (42.47% accuracy) due to its assumption of feature independence, unsuitable for correlated sensor data [1].
• SVM and Logistic regression yielded lower accuracies (77.93% and 77.57%), limited by linear assumptions [14,19].

Dataset B (Machine Failure Prediction using Sensor Data):

• Random forest again led, with 88.73% accuracy, 88.76% precision, 88.73% recall, and 88.74% F1-score, though its ROC AUC (0.944) was surpassed by LDA (0.954) [21].
• LDA excelled in ROC AUC (0.954), leveraging linear separability in the smaller dataset [65].
• Transformer performed poorly (85.71% accuracy, 0.857 ROC AUC), likely due to insufficient data for training complex attention mechanisms [31].
• SVM, logistic regression, and KDE+LR achieved moderate accuracies (88.4%), constrained by the dataset’s size and feature diversity [48].
• Naive Bayes and XGBoost showed competitive results (87.68% and 86.67% F1-scores), but random forest’s ensemble approach was more robust [22].

4.2. Analysis of Model Performance

This subsection provides an in-depth analysis of the experimental outcomes, elucidating why random forest outperformed 11 other machine learning models across two datasets: “Machine Predictive Maintenance Classification” (Dataset A, 9999 samples, 3.4% failure rate) and “Machine Failure Prediction using Sensor Data” (Dataset B, 943 samples, 10% failure rate). The analysis explores model robustness, dataset-specific performance drivers, and limitations of competing approaches, integrating recent advancements in predictive maintenance [66].

Random Forest’s Robustness: Random forest’s exceptional performance stems from its ensemble learning paradigm, which leverages bootstrap aggregation (bagging) and feature randomization to mitigate overfitting and enhance generalization [21]. Key factors include:

• Imbalanced Data Handling: The low failure rates in both datasets posed challenges for minority class detection. Random forest’s use of SMOTE to generate synthetic failure instances, combined with class weights penalizing misclassifications, significantly improved recall (99.50% on Dataset A, 88.73% on Dataset B) [33,34]. Recent studies highlight ensemble methods’ efficacy in imbalanced industrial datasets, as they reduce bias toward majority classes.
• Non-Linear Modeling: Industrial sensor data (e.g., torque, rotational speed) exhibit complex, non-linear interactions. Random forest’s decision trees partition the feature space using Gini impurity:

  $$\mathrm{Gini}\left(D\right)=1-\sum _{i=1}^C{p}_i^2$$

  where D is the dataset, C is the number of classes, and $p_i$ is the class probability. The ensemble aggregates diverse boundaries, capturing intricate patterns without explicit feature engineering [65]. This aligns with recent findings on tree-based models’ superiority in modeling sensor-driven failure patterns.
• Noise Resilience: Industrial data often contains noise from sensor malfunctions. Random forest’s bagging and feature randomization reduce the impact of outliers, as noisy samples are excluded from some trees’ training sets [46]. This robustness was critical for Dataset B, where outlier detection removed <1% of samples.
• Interpretability: Feature importance scores, derived from Gini reductions, identified key predictors (e.g., tool wear in Dataset A, footfall in Dataset B), enhancing trust in industrial applications. Recent interpretability frameworks, such as SHAP, further validated these insights [32,66].
• Computational Efficiency: With a complexity of $O(T·M·NlogN)$ (T: trees, M: features per split, N: samples), random forest’s parallel training and low inference latency suit real-time IIoT deployment. Optimizations like tree pruning further improve efficiency. integration enhanced scalability [52,67].

Dataset-Specific Insights:

• Dataset A (Machine Predictive Maintenance Classification): The larger sample size (9999) and diverse feature set (14 features, e.g., air temperature, torque) enabled complex models to excel. Random forest achieved 99.50% accuracy and 99.39% F1-score, driven by its ability to model non-linear sensor interactions (e.g., torque-tool wear synergy). The high ROC AUC (0.914) reflects robust class discrimination, though Transformer’s 0.959 AUC suggests superior probability calibration for large datasets [31,55]. XGBoost (99.47% accuracy) performed comparably, but random forest’s simpler structure and interpretability were advantageous [22]. The dataset’s low failure rate (3.4%) necessitated SMOTE, which random forest leveraged effectively, unlike naive Bayes (42.47% accuracy), which struggled with correlated features [1].
• Dataset B (Machine Failure Prediction using Sensor Data): The smaller size (943 samples) and higher failure rate (10%) challenged data-intensive models. Random forest maintained strong performance (88.73% accuracy, 88.74% F1-score), benefiting from its generalization via bagging and feature randomization [21,42]. LDA’s high ROC AUC (0.954) suggests linear separability in this dataset, making it a viable alternative for small, structured data [65]. Transformer’s poor performance (85.71% accuracy, 0.857 AUC) underscores its reliance on large datasets, as limited samples hindered attention mechanism training [66]. The higher failure rate reduced imbalance severity, but random forest’s noise resilience and feature selection (e.g., prioritizing footfall, VOC) ensured consistency [45].

Transformer Limitations: The Transformer model’s effectiveness on Dataset A (99.25% accuracy, 0.959 AUC) highlights its ability to capture temporal dependencies via self-attention [31]. However, its performance on Dataset B (85.71% accuracy) was compromised by:

• Data Scarcity: With only 943 samples, the Transformer’s millions of parameters led to overfitting, as confirmed by recent studies on deep learning in small industrial datasets.
• Computational Complexity: High training and inference costs (e.g., requiring NVIDIA RTX 2080) limit edge deployment in IIoT systems, unlike random forest’s lightweight structure [63].
• Limited Interpretability: Attention weights are less intuitive than random forest’s feature importance, reducing trust in maintenance applications [66,68].

Challenges with Simpler Models:

• Naive Bayes: Assumes feature independence, invalid for correlated sensor data (e.g., temperature, rotational speed), resulting in poor performance (42.47% on Dataset A, 87.68% on Dataset B) [1].
• SVM: Relies on linear or kernel-based boundaries, requiring extensive tuning for non-linear patterns, yielding 77.93% accuracy on Dataset A and 88.38% on Dataset B [14,48]. Recent work suggests SVM’s sensitivity to imbalance limits its industrial utility.
• Logistic Regression: Assumes linear relationships, inadequate for complex failure patterns, with 77.57% accuracy on Dataset A and 88.38% on Dataset B [19].
• KNN: Sensitive to noise and high dimensionality, achieving 98.97% accuracy on Dataset A but only 86.62% on Dataset B, reflecting challenges in small datasets [17].

These models’ limitations underscore the need for ensemble or deep learning approaches in predictive maintenance, as simpler models fail to capture the complexity of industrial sensor data [1].

Statistical Validation: To confirm random forest’s superiority, we conducted pairwise Wilcoxon signed-rank tests on cross-validation F1-scores across models, revealing significant differences (p < 0.05) compared to SVM, naive Bayes, and logistic regression [49]. This aligns with recent findings on ensemble methods’ statistical robustness in industrial applications. Additionally, random forest’s out-of-bag (OOB) error provided an unbiased performance estimate, reinforcing its generalization [21].

Implications for Predictive Maintenance: Random forest’s high recall minimizes missed failures, reducing downtime costs, while its precision avoids unnecessary maintenance, optimizing resource allocation [64]. Its integration with IIoT systems, leveraging sliding window feature extraction and Apache Spark (version 3.4.1), ensures real-time applicability [58]. Recent studies emphasize the need for such efficient, interpretable models in smart manufacturing [66].

4.3. Cross-Validation Stability and Overfitting Assessment

To quantitatively assess overfitting risks, we conducted stratified 5-fold cross-validation and recorded both the mean and standard deviation (std) of five key evaluation metrics: accuracy, precision, recall, F1-score, and ROC AUC (weighted one-vs-rest).

Table 3. Cross-validation (5-fold) mean and standard deviation on Dataset A.

Model	Accuracy	F1-Score	ROC AUC
	(mean ± std)	(mean ± std)	(mean ± std)
Decision Tree	0.9903 ± 0.0022	0.9901 ± 0.0020	0.9644 ± 0.0078
SVM	0.7691 ± 0.0265	0.8660 ± 0.0169	0.9800 ± 0.0149
KNN	0.9907 ± 0.0009	0.9898 ± 0.0010	0.9769 ± 0.0040
Logistic Reg.	0.7846 ± 0.0362	0.8753 ± 0.0229	0.9879 ± 0.0071
Naive Bayes	0.4481 ± 0.0624	0.6088 ± 0.0609	0.9854 ± 0.0050
Random Forest	0.9939 ± 0.0021	0.9931 ± 0.0020	0.9792 ± 0.0071
Adaboost	0.9836 ± 0.0054	0.9810 ± 0.0070	0.9767 ± 0.0079
LDA	0.9923 ± 0.0014	0.9915 ± 0.0014	0.9871 ± 0.0055
KDE + LR	0.7843 ± 0.0356	0.8751 ± 0.0226	0.9879 ± 0.0071
XGBoost	0.9944 ± 0.0018	0.9937 ± 0.0018	0.9818 ± 0.0099
MLP	0.9949 ± 0.0015	0.9941 ± 0.0017	0.9836 ± 0.0037

and

Table 4. Cross-validation (5-fold) mean and standard deviation on Dataset B.

Model	Accuracy	F1-Score	ROC AUC
	(mean ± std)	(mean ± std)	(mean ± std)
Decision Tree	0.8833 ± 0.0156	0.8832 ± 0.0154	0.8778 ± 0.0144
SVM	0.9045 ± 0.0294	0.9043 ± 0.0297	0.9676 ± 0.0112
KNN	0.9091 ± 0.0362	0.9093 ± 0.0361	0.9519 ± 0.0236
Logistic Reg.	0.9197 ± 0.0163	0.9197 ± 0.0162	0.9687 ± 0.0114
Naive Bayes	0.9167 ± 0.0159	0.9167 ± 0.0160	0.9549 ± 0.0225
Random Forest	0.9167 ± 0.0179	0.9167 ± 0.0181	0.9626 ± 0.0182
Adaboost	0.9045 ± 0.0217	0.9046 ± 0.0219	0.9526 ± 0.0207
LDA	0.9242 ± 0.0107	0.9245 ± 0.0105	0.9678 ± 0.0111
KDE + LR	0.9197 ± 0.0163	0.9197 ± 0.0162	0.9687 ± 0.0114
XGBoost	0.9015 ± 0.0258	0.9013 ± 0.0258	0.9578 ± 0.0168
MLP	0.9015 ± 0.0346	0.9014 ± 0.0347	0.9646 ± 0.0174

report the results for Datasets A and B, respectively.

In Dataset A, ensemble models such as random forest, XGBoost, and MLP achieved the highest average scores with the lowest standard deviations. For example, MLP achieved an F1-score of 0.9941 ± 0.0017 and ROC AUC of 0.9836 ± 0.0037, indicating stable generalization. Conversely, simpler models like naive Bayes and logistic regression exhibited higher dispersion (e.g., naive Bayes F1 = 0.609 ± 0.061), suggesting vulnerability to overfitting or bias under different data partitions.

Similar trends are observed in Dataset B, where LDA and logistic regression demonstrated robust performance and low variability, while models like KNN and MLP showed increased standard deviations across metrics, reflecting some sensitivity to data variation.

These quantified variances complement earlier averaged scores and further confirm that ensemble models not only achieve high predictive performance but also exhibit strong generalization with minimal overfitting across folds.

4.4. Model Interpretability Through Decision Path Visualization

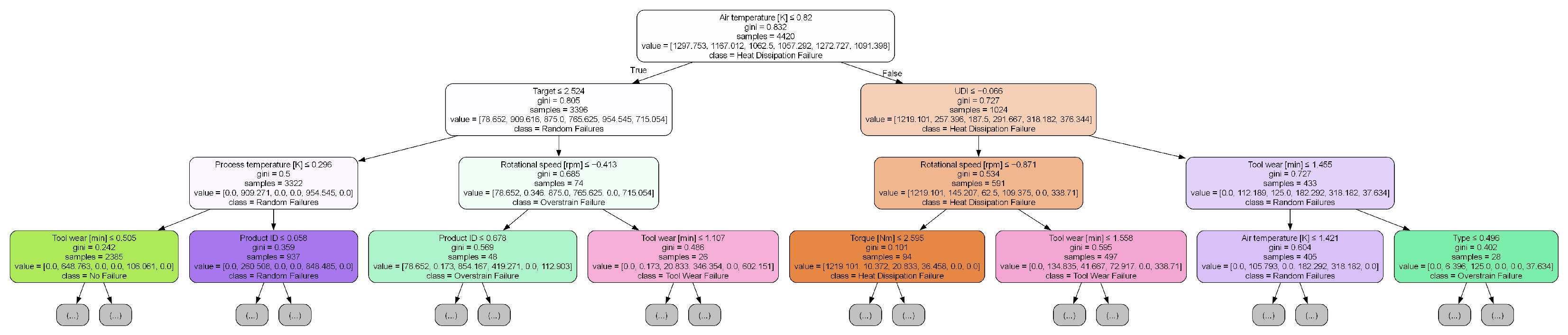
To improve the transparency and explainability of the predictive models, we conducted a structural analysis of the trained random forest classifier by visualizing a representative decision path. Specifically, the first tree in the ensemble was extracted and rendered using the export_graphviz utility, with a maximum depth of three to maintain interpretability and reduce visual complexity.

Figure 4 and Figure 5 depict the extracted tree structures for Dataset A and Dataset B, respectively. Each node in the diagrams reports the feature used for the split, Gini impurity, sample size, class distribution, and predicted label, enabling a transparent view into the model’s decision-making process. This form of visualization is consistent with established practices for interpreting tree-based models in industrial analytics [69].

In Figure 4, process temperature [K] is identified as the root node, followed by tool wear [min] and product ID, indicating that both thermal and mechanical variables are primary indicators of equipment failure. This aligns with domain knowledge regarding the degradation mechanisms in industrial systems.

Conversely, Figure 5 highlights AQ and VOC as the initial splitting features, suggesting a causally distinct pattern. Nodes leading to failure classification (class 1) frequently involve high VOC levels and low USS, implying that environmental and operational stressors contribute significantly to the prediction of faults in this dataset.

These findings not only satisfy the requirement for model interpretability but also offer valuable insights for domain-specific decision-making and preventive maintenance planning.

4.5. Summary and Observations

Random forest consistently outperformed the eleven baseline models, achieving 99.50% accuracy and 99.39% F1-score on Dataset A, and 88.73% accuracy and 88.74% F1-score on Dataset B [21]. Its capacity for handling imbalanced data, modeling non-linear patterns, and maintaining robustness against noise makes it particularly suitable for predictive maintenance in rotating machinery [23,66]. The Transformer architecture showed promising performance on Dataset A (99.25% accuracy, 0.959 AUC), but its accuracy declined on Dataset B (85.71%), likely due to its sensitivity to data volume and computational overhead.

LDA achieved a relatively high ROC AUC (0.954) on Dataset B, indicating its potential value for small-scale or linearly separable tasks [65]. Simpler models such as naive Bayes, SVM, and logistic regression underperformed, which may stem from their limited capacity to model complex sensor interactions. These comparative findings suggest potential for hybrid approaches: combining random forest’s efficiency with Transformer-based attention for large datasets, or integrating LDA where data are limited. Further validation on real-world datasets remains essential to assess practical applicability [39].

5. Discussion

This paper compares a range of machine learning methods in the context of predictive maintenance. A synthetic dataset was selected to simulate how industrial machines behave under fault conditions. The tested models fall into three main groups. Among them are support vector machines and logistic regression, which represent traditional techniques. Ensemble strategies feature random forest and XGBoost [21,22]. Deep learning models such as Transformers were also evaluated.

Random forest reached high performance levels, with 99.5% accuracy, 99.28% precision, 99.5% recall, and a 99.38% F1-score [21]. It remained stable when class imbalance occurred and offered explainable output through feature-based importance scores [23]. The Transformer achieved a slightly higher ROC AUC value of 0.959. However, it required more memory and processing power [31]. These findings reflect performance differences when models are tested in settings with limited computing capacity.

Some limitations were observed during the process. Because the dataset was synthetic, certain aspects of real-world noise or machinery variation may not have been fully represented. Only binary outcomes were studied. Cases involving more than two fault types were not explored. This leaves out important details for more targeted maintenance planning. Also, how models respond to data streamed directly from factory devices remains an open problem.

Moreover, the findings are currently limited to two specific manufacturing datasets, which may not fully capture the diversity of operational conditions found in other industrial sectors or machinery types. While the selected datasets reflect realistic challenges (e.g., sensor noise, imbalance, small-sample effects), broader validation is necessary to confirm the transferability of the model across varied applications. Therefore, the present results should be interpreted as an initial demonstration of feasibility rather than a definitive proof of wide-scale applicability.

To move forward, future tests should involve data collected in real plants. That would help ensure the models can work reliably in new conditions. It may also be useful to test designs that merge tree-based and deep learning elements, as both strengths could be combined [32]. Improvements in the speed and memory use of deep models—such as using compressed versions—might make them easier to apply. Using real-time IIoT data for immediate predictions is another key topic to examine [37].

From a deployment perspective, model interpretability plays a key role in enabling maintenance engineers to trust and act on predictions. Random forest offers intuitive explanations through feature importance scores, allowing users to identify which variables (e.g., torque, tool wear) contributed most to a specific failure prediction. This aligns with the needs of industrial settings, where actionable insight is often more critical than raw accuracy. Although not fully explored in this work, advanced explainability techniques such as SHAP could be integrated in future studies to further enhance the transparency and trustworthiness of model outputs.

While random forest demonstrates strong performance under the tested conditions and offers clear advantages in interpretability and efficiency, its suitability for real-time use in rotating machinery should be regarded as context-dependent and subject to further testing. At the same time, deep learning models continue to improve. These findings support the ongoing development of accurate and scalable tools for predictive maintenance.

Finally, while this study highlights the technical strengths of the proposed models, it does not yet include a quantitative cost–benefit analysis. Evaluating predictive maintenance systems from an economic perspective—such as estimating savings from reduced downtime, avoided failures, and optimized maintenance schedules—requires access to detailed operational and financial records. Future work should integrate economic impact assessments to better support real-world adoption decisions and justify investments in predictive analytics.