Effects of Perforation Location in Gas Diffusion Layers on Electrochemical Characteristics of Proton Exchange Membrane Fuel Cells
Abstract
1. Introduction
2. Numerical Process
2.1. Analysis Model
- The flow is regarded as incompressible and laminar.
- All gas species are treated as ideal gases.
- As the membrane is impermeable, crossover does not occur.
- Effects of thermal and electrical contact resistance are neglected.
2.2. Governing Equations
2.3. Analysis Conditions
3. Results and Discussion
3.1. Model Validation
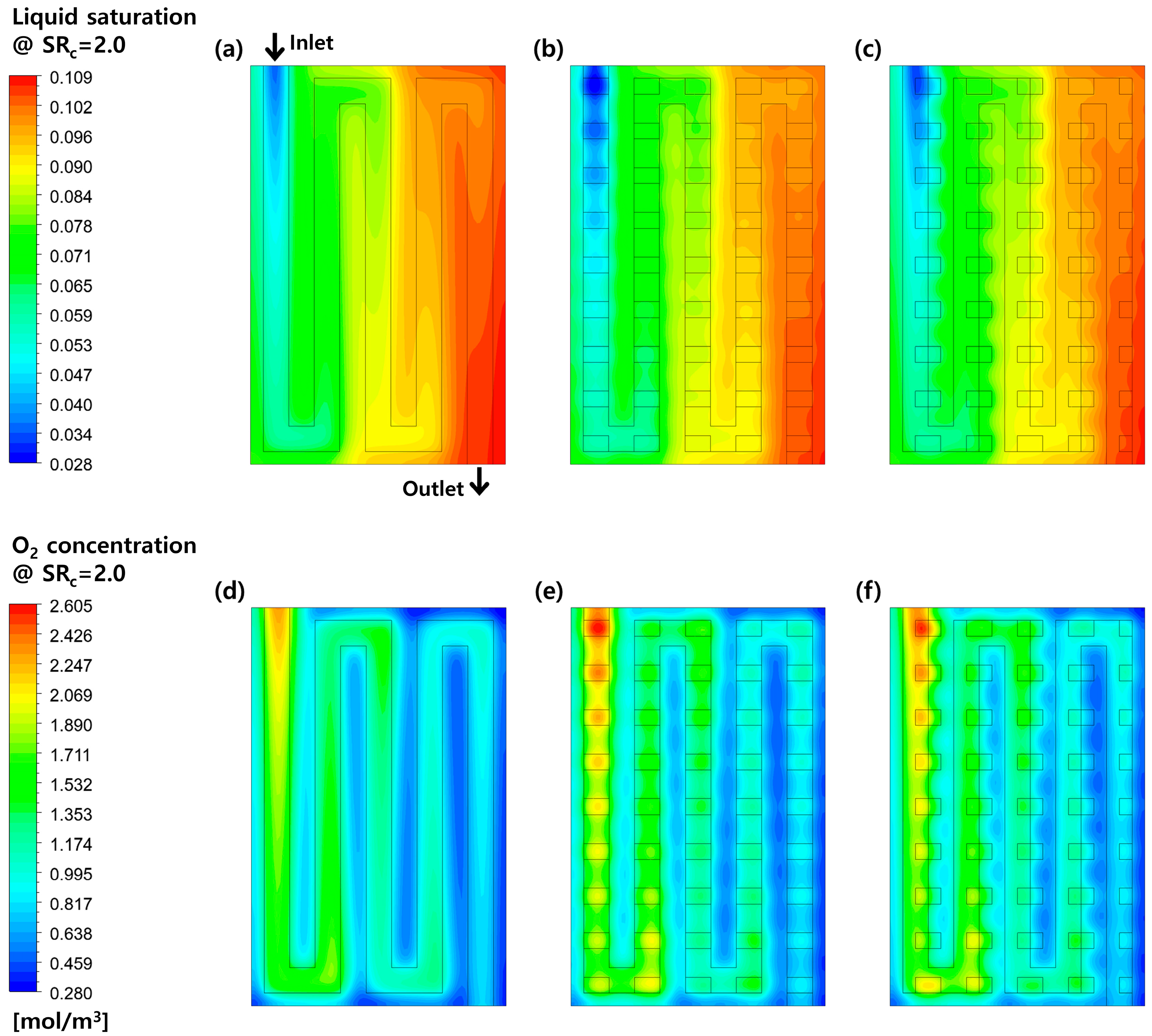
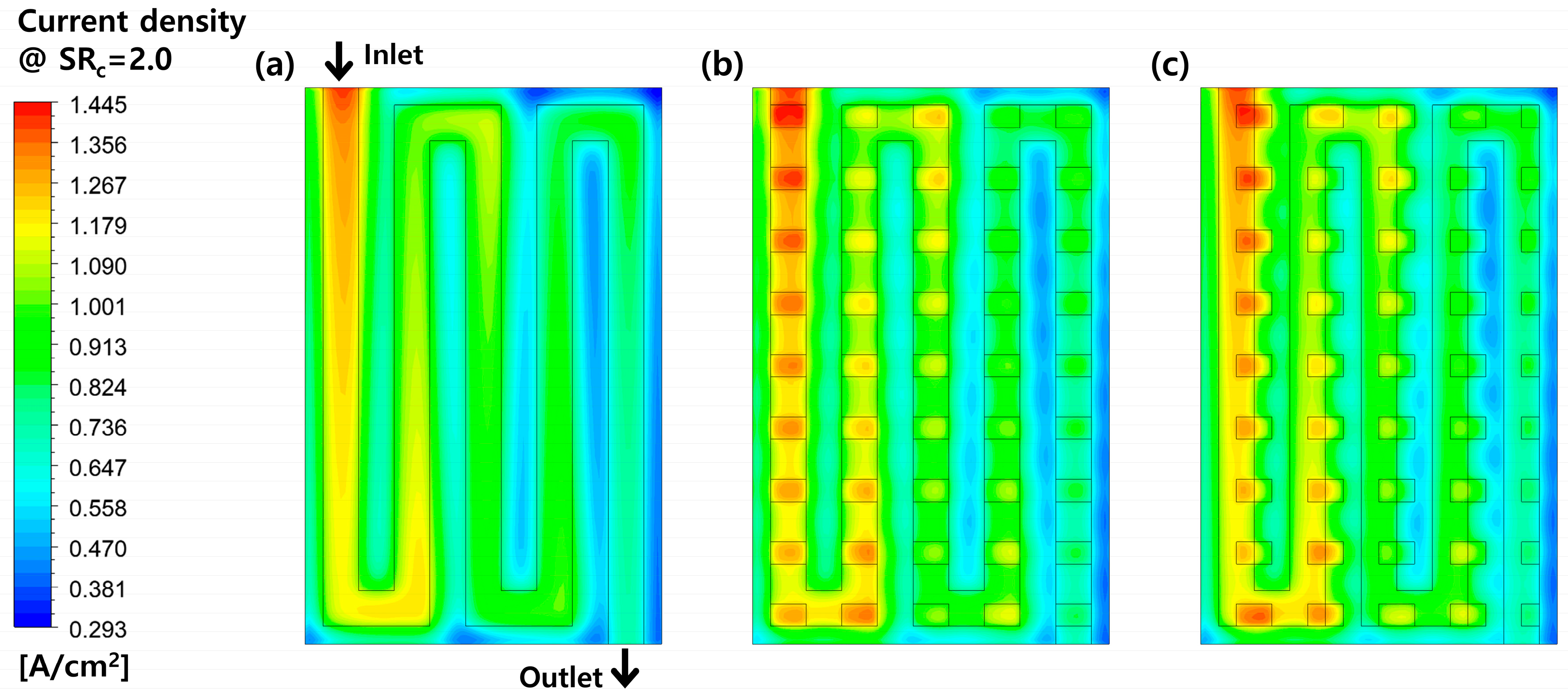
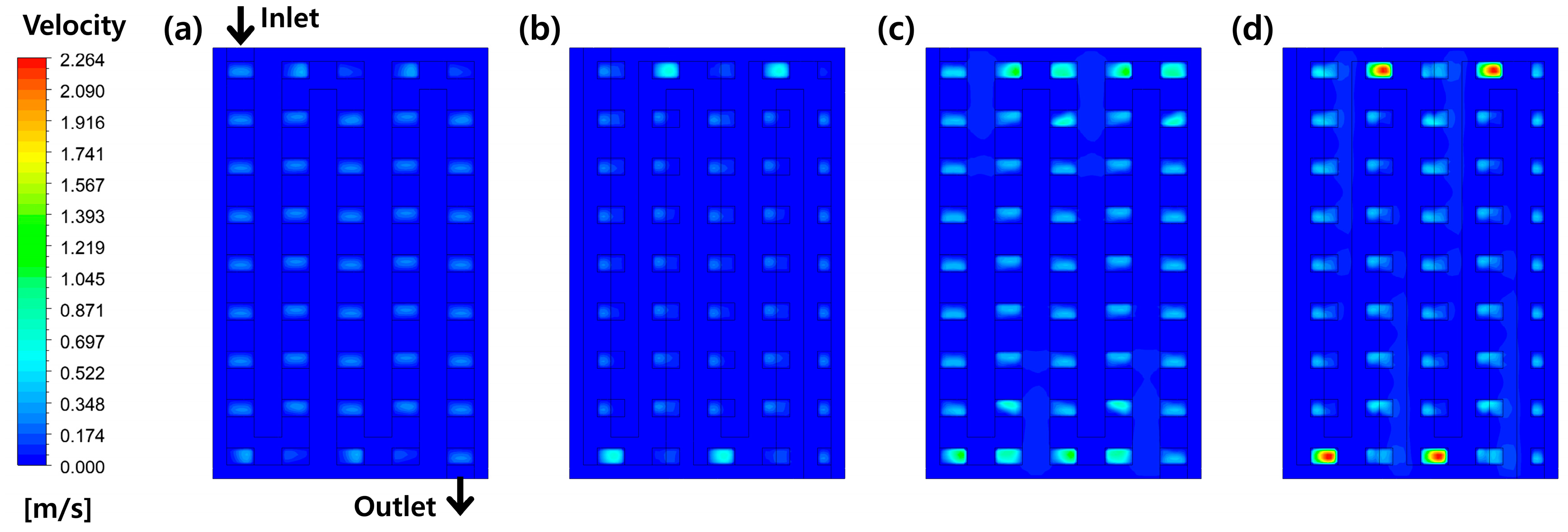
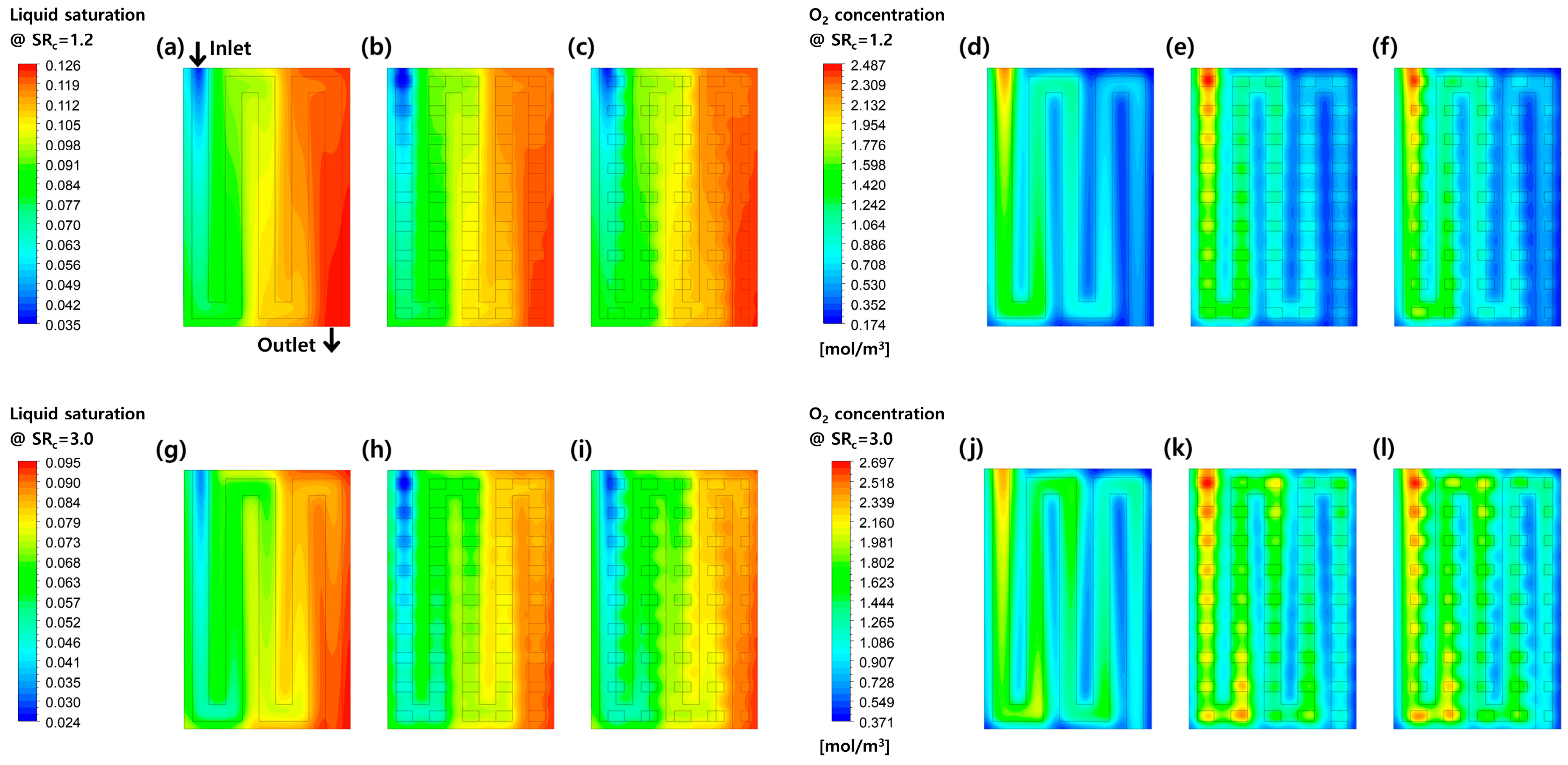
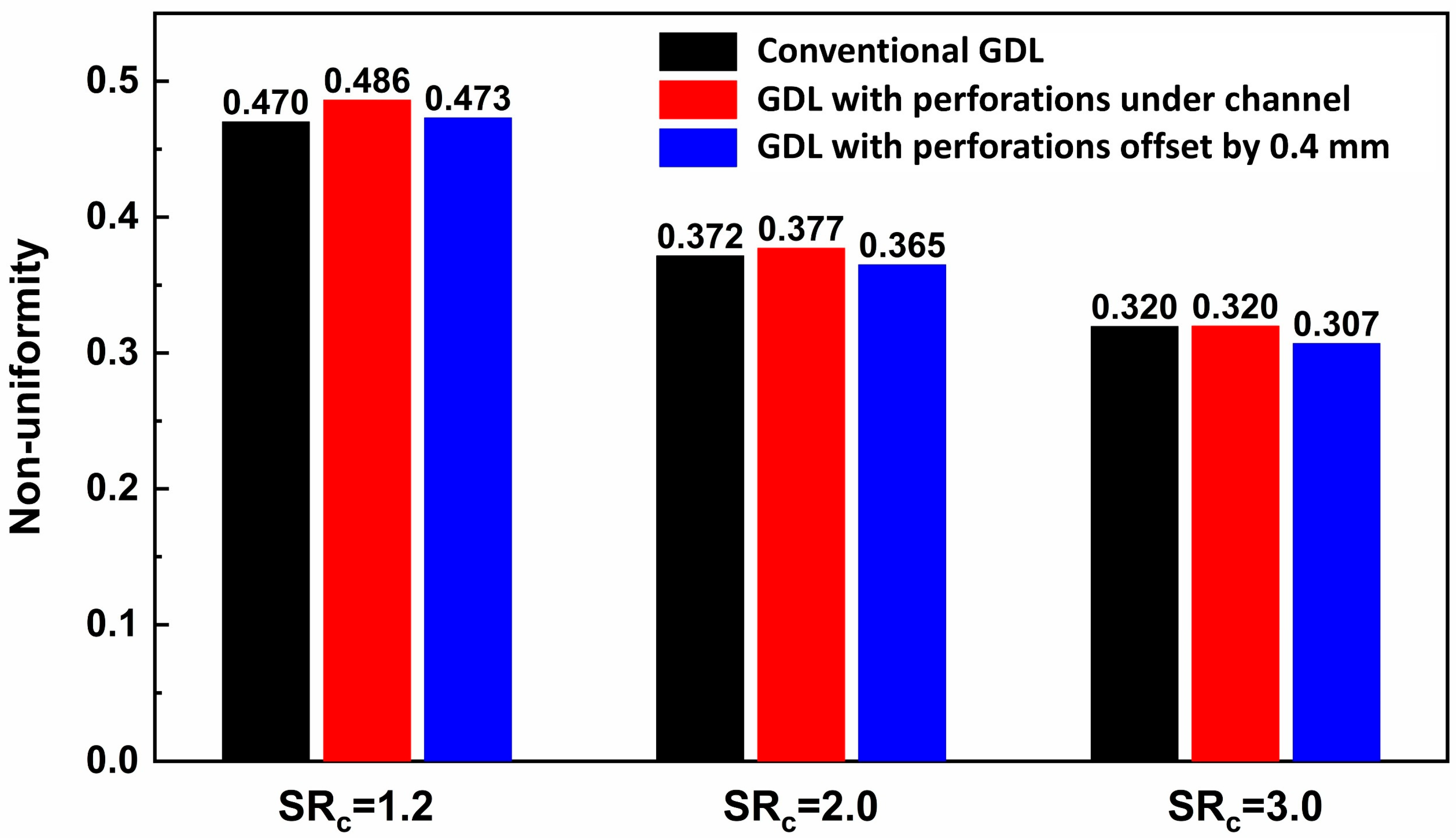
3.2. Effects of Perforation Locations
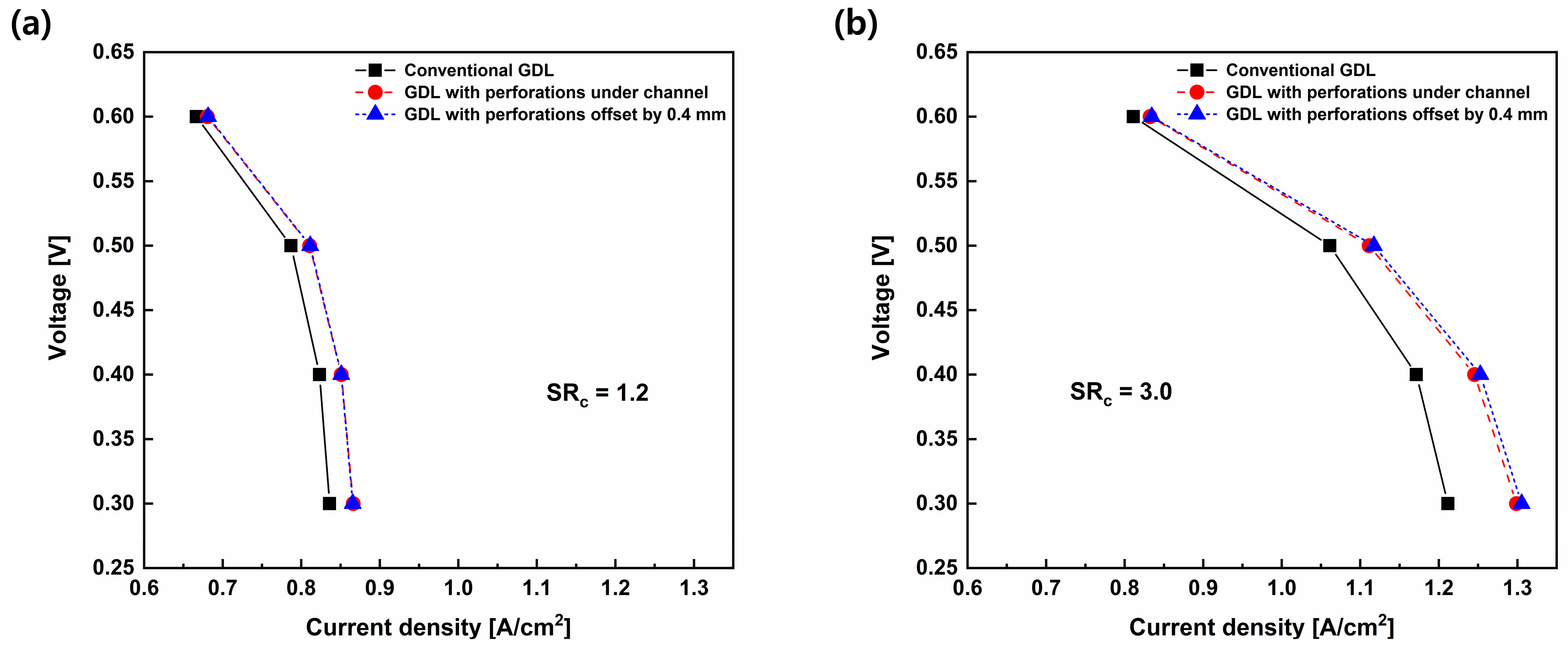
3.3. Effects of Stoichiometric Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CL | Catalyst layer |
| GDL | Gas diffusion layer |
| MPL | Microporous layer |
| PEMFC | Proton exchange membrane fuel cell |
| SRc | Stoichiometric ratio on the cathode side |
References
- O’Hayre, R.; Cha, S.-W.; Colella, W.; Prinz, F.B. Fuel Cell Fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Jang, G.-E.; Cho, G.-Y. Effects of Ag Current Collecting Layer Fabricated by Sputter for 3D-Printed Polymer Bipolar Plate of Ultra-Light Polymer Electrolyte Membrane Fuel Cells. Sustainability 2022, 14, 2997. [Google Scholar] [CrossRef]
- Yoo, H.J.; Cho, G.Y. Influences of Flow Channel on Electrochemical Characteristics of Polymer Electrolyte Fuel Cells Humidified with NaCl Contained H2O. Sustainability 2023, 15, 2415. [Google Scholar] [CrossRef]
- Hong, K.W.; Kwon, Y.R.; Song, D.K.; Jung, D.Y.; Kang, B.K.; Kwon, S.K.; Ryu, S.; Cho, G.Y. Fabrication and Characterization of Pt-Pr6O11 Nano Cathode Electrode for Polymer Electrolyte Membrane Fuel Cells via Co-Sputtering Method. Sustainability 2024, 17, 198. [Google Scholar] [CrossRef]
- Jung, D.Y.; Song, D.K.; Kim, J.S.; Lee, S.H.; Min, G.W.; Son, J.H.; Cho, G.Y. Numerical Investigation of Effects of Obstacles in Flow Channels and Depth of Flow Channels for PEMFCs. Sustainability 2024, 16, 10144. [Google Scholar] [CrossRef]
- Kang, B.G.; Kwon, Y.R.; Hong, K.W.; Kwon, S.K.; Lee, H.M.; Song, D.K.; Jeon, J.W.; Jung, D.Y.; Go, D.; Cho, G.Y. Performance Improvement of Proton Exchange Membrane Fuel Cells with a TiO2 Sputtered Gas Diffusion Layer Under Low-Humidity Conditions. Energies 2025, 18, 1525. [Google Scholar] [CrossRef]
- Jing, S.-Y.; Sun, Z.Y.; Yang, L.; Wang, Y. Effects of porosity and porosity distribution in gas diffusion layer on the performances of proton exchange membrane fuel cell. J. Power Sources 2024, 613, 234957. [Google Scholar] [CrossRef]
- Kahveci, E.E.; Taymaz, I. An Investigation of GDL Porosity on PEM Fuel Cell Performance. Chem. Eng. Trans. 2014, 42, 37–42. [Google Scholar] [CrossRef]
- Feser, J.P.; Prasad, A.K.; Advani, S.G. Experimental characterization of in-plane permeability of gas diffusion layers. J. Power Sources 2006, 162, 1226–1231. [Google Scholar] [CrossRef]
- Zhang, J.; Xuan, D.; Liu, S.; Chen, C. Influence and Optimization of Gas Diffusion Layer Porosity Distribution along the Flow Direction on the Performance of Proton Exchange Membrane Fuel Cells. ACS Omega 2024, 9, 239–251. [Google Scholar] [CrossRef]
- Son, J.; Um, S.; Kim, Y.-B. Numerical analysis of the effect of anisotropic gas diffusion layer permeability on polymer electrolyte membrane fuel cell performance with various channel types. Fuel 2021, 289, 119888. [Google Scholar] [CrossRef]
- Kakaee, A.H.; Molaeimanesh, G.R.; Garmaroudi, M.H.E. Impact of PTFE distribution across the GDL on the water droplet removal from a PEM fuel cell electrode containing binder. Int. J. Hydrogen Energy 2018, 43, 15481–15491. [Google Scholar] [CrossRef]
- Calili-Cankir, F.; Can, E.M.; Ingham, D.B.; Hughes, K.J.; Ma, L.; Pourkashanian, M.; Lyth, S.M.; Ismail, M.S. Patterned hydrophobic gas diffusion layers for enhanced water management in polymer electrolyte fuel cells. Chem. Eng. J. 2024, 484, 149711. [Google Scholar] [CrossRef]
- Sim, J.; Kang, M.; Min, K. Effects of porosity gradient and average pore size in the in-plane direction and disposition of perforations in the gas diffusion layer on the performance of proton exchange membrane fuel cells. J. Power Sources 2022, 544, 231912. [Google Scholar] [CrossRef]
- Lin, P.; Sun, J.; He, C.; Wu, M.; Zhao, T. Quadrilateral-Patterned Perforated Gas Diffusion Layers Boost the Performance of Fuel Cells. ACS Energy Lett. 2024, 9, 1710–1716. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Zhang, Y.; Hou, Z.; Liu, J. Effect of Gas Diffusion Layer Notch Arrangement and Gradient Depth on the Performance of Proton Exchange Membrane Fuel Cells in the Serpentine Flow Field. ACS Omega 2023, 8, 10191–10201. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, S.; Fan, Z.; Li, W.; Wang, S.; Li, X.; Zhao, Y.; Zhu, T.; Xie, X. Laser-perforated gas diffusion layer for promoting liquid water transport in a proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2017, 42, 29995–30003. [Google Scholar] [CrossRef]
- Fang, W.-Z.; Tang, Y.-Q.; Chen, L.; Kang, Q.-J.; Tao, W.-Q. Influences of the perforation on effective transport properties of gas diffusion layers. Int. J. Heat Mass Transf. 2018, 126, 243–255. [Google Scholar] [CrossRef]
- Yin, B.; Xu, S.; Yang, S.; Dong, F. Influence of Microelliptical Groove Gas Diffusion Layer (GDL) on Transport Behavior of Proton Exchange Membrane Fuel Cell (PEMFC). Int. J. Heat Mass Transf. 2021, 180, 121793. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, P.; Gao, Y.; He, W.; Zhao, Y.; Wang, X. Optimal design of cathode gas diffusion layer with arrayed grooves for performance enhancement of a PEM fuel cell. Renew. Energy 2022, 199, 697–709. [Google Scholar] [CrossRef]
- Sun, S.-F.; Sun, Z.Y. Water distribution and transmission within perforated gas diffusion layer and layered gas diffusion layer of a proton exchange membrane fuel cell. J. Power Sources 2025, 643, 237024. [Google Scholar] [CrossRef]
- Fluent, A. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011; Volume 15317. [Google Scholar]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Son, J.; Um, S.; Kim, Y.-B. Relationship between number of turns of serpentine structure with metal foam flow field and polymer electrolyte membrane fuel cell performance. Renew. Energy 2022, 188, 372–383. [Google Scholar] [CrossRef]
- Xing, L.; Mamlouk, M.; Kumar, R.; Scott, K. Numerical investigation of the optimal Nafion® ionomer content in cathode catalyst layer: An agglomerate two-phase flow modelling. Int. J. Hydrogen Energy 2014, 39, 9087–9104. [Google Scholar] [CrossRef]
- Li, S.; Yuan, J.; Xie, G.; Sundén, B. Effects of agglomerate model parameters on transport characterization and performance of PEM fuel cells. Int. J. Hydrogen Energy 2018, 43, 8451–8463. [Google Scholar] [CrossRef]
- Wang, B.; Xie, B.; Xuan, J.; Jiao, K. AI-based optimization of PEM fuel cell catalyst layers for maximum power density via data-driven surrogate modeling. Energy Convers. Manag. 2020, 205, 112460. [Google Scholar] [CrossRef]
- Yoo, B.; Lim, K.; Salihi, H.; Ju, H. A parametric study on the performance requirements of key fuel cell components for the realization of high-power automotive fuel cells. Int. J. Heat Mass Transf. 2022, 186, 122477. [Google Scholar] [CrossRef]
- Lampinen, M.J.; Fomino, M. Analysis of Free Energy and Entropy Changes for Half-Cell Reactions. J. Electrochem. Soc. 1993, 140, 3537–3546. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Convers. Manag. 2018, 176, 409–421. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, M.; Hu, H.; Hou, Y.; Vesztergom, S.; Gálvez-Vázquez, M.d.J.; Montiel, I.Z.; Kolivoška, V.; Broekmann, P. Cracks as Efficient Tools to Mitigate Flooding in Gas Diffusion Electrodes Used for the Electrochemical Reduction of Carbon Dioxide. Small Methods 2022, 6, 2200369. [Google Scholar] [CrossRef]
- Son, J.; Lee, D.; Um, S.; Kim, Y.-B. Effect of stacking pressure on the performance of polymer electrolyte membrane fuel cell with various channel types. Energy Convers. Manag. 2021, 232, 113803. [Google Scholar] [CrossRef]
- Chen, C.; Wang, C.; Zhang, Z. Numerical investigation of the water transport and performance of proton exchange membrane fuel cell with an imitating river flow field. Energy Convers. Manag. 2023, 276, 116532. [Google Scholar] [CrossRef]
- Peron, J.; Mani, A.; Zhao, X.; Edwards, D.; Adachi, M.; Soboleva, T.; Shi, Z.; Xie, Z.; Navessin, T.; Holdcroft, S. Properties of Nafion® NR-211 membranes for PEMFCs. J. Membr. Sci. 2010, 356, 44–51. [Google Scholar] [CrossRef]
- Gostick, J.T.; Fowler, M.W.; Pritzker, M.D.; Ioannidis, M.A.; Behra, L.M. In-plane and through-plane gas permeability of carbon fiber electrode backing layers. J. Power Sources 2006, 162, 228–238. [Google Scholar] [CrossRef]
- Xing, L.; Das, P.K.; Song, X.; Mamlouk, M.; Scott, K. Numerical analysis of the optimum membrane/ionomer water content of PEMFCs: The interaction of Nafion® ionomer content and cathode relative humidity. Appl. Energy 2015, 138, 242–257. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Ye, Q.; Nguyen, T.V. Three-Dimensional Simulation of Liquid Water Distribution in a PEMFC with Experimentally Measured Capillary Functions. J. Electrochem. Soc. 2007, 154, B1242. [Google Scholar] [CrossRef]
- Mann, R.F.; Amphlett, J.C.; Peppley, B.A.; Thurgood, C.P. Henry’s Law and the solubilities of reactant gases in the modelling of PEM fuel cells. J. Power Sources 2006, 161, 768–774. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, G.; Jiao, K. Characteristics of PEMFC operating at high current density with low external humidification. Energy Convers. Manag. 2017, 150, 763–774. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Z.Y.; Yang, L. Enhancement effects of the obstacle arrangement and gradient height distribution in serpentine flow-field on the performances of a PEMFC. Energy Convers. Manag. 2022, 252, 115077. [Google Scholar] [CrossRef]
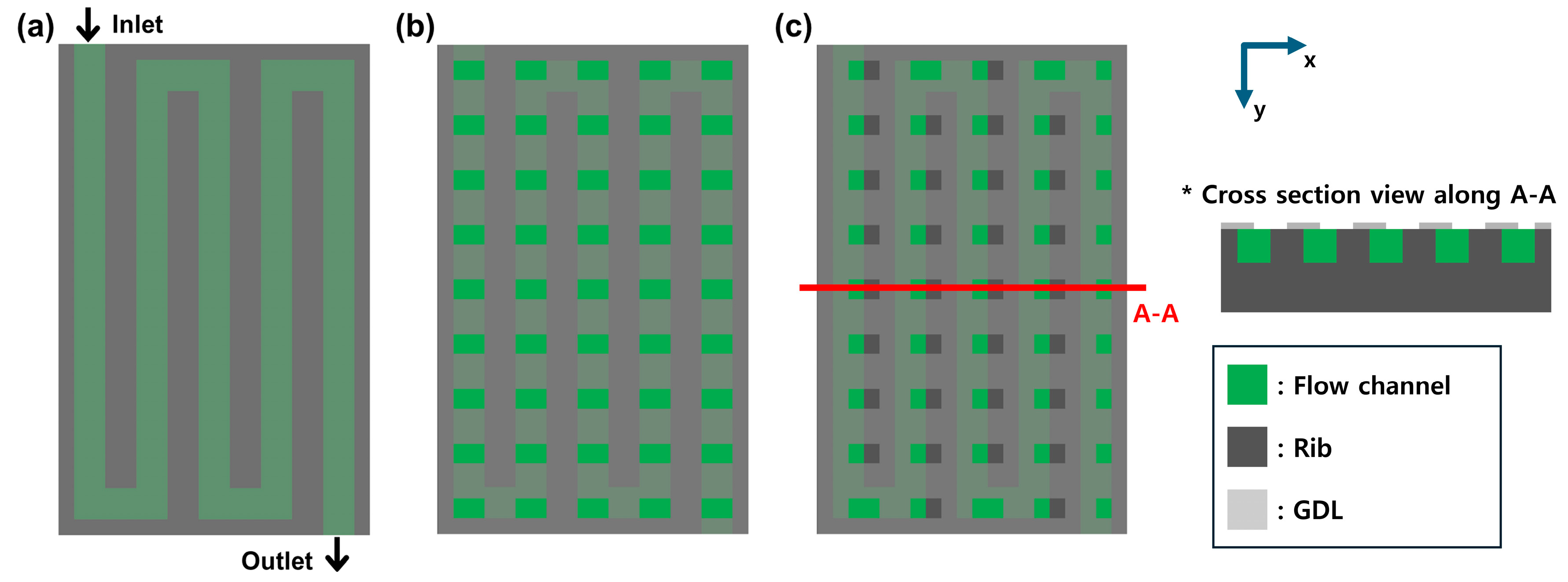
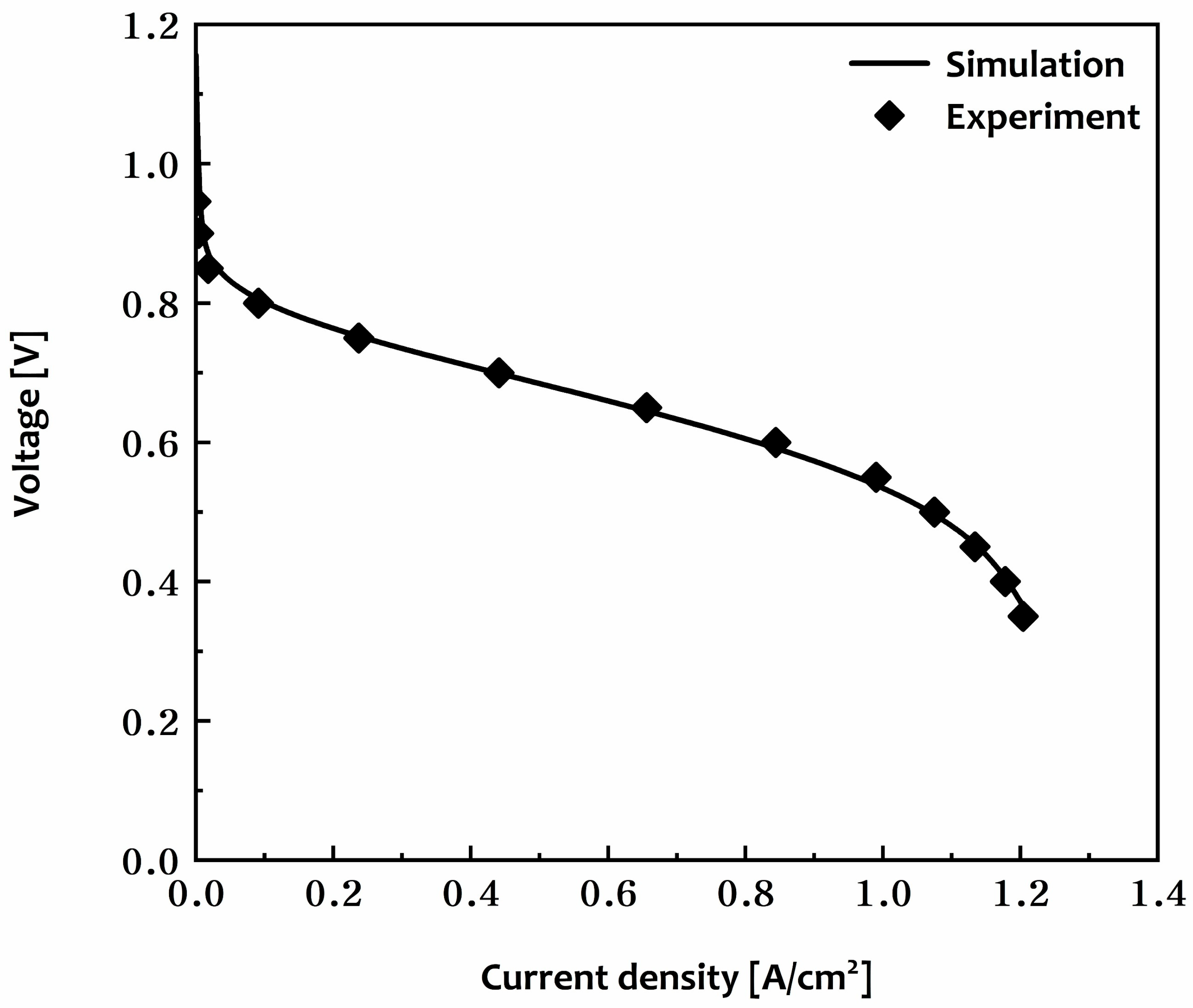
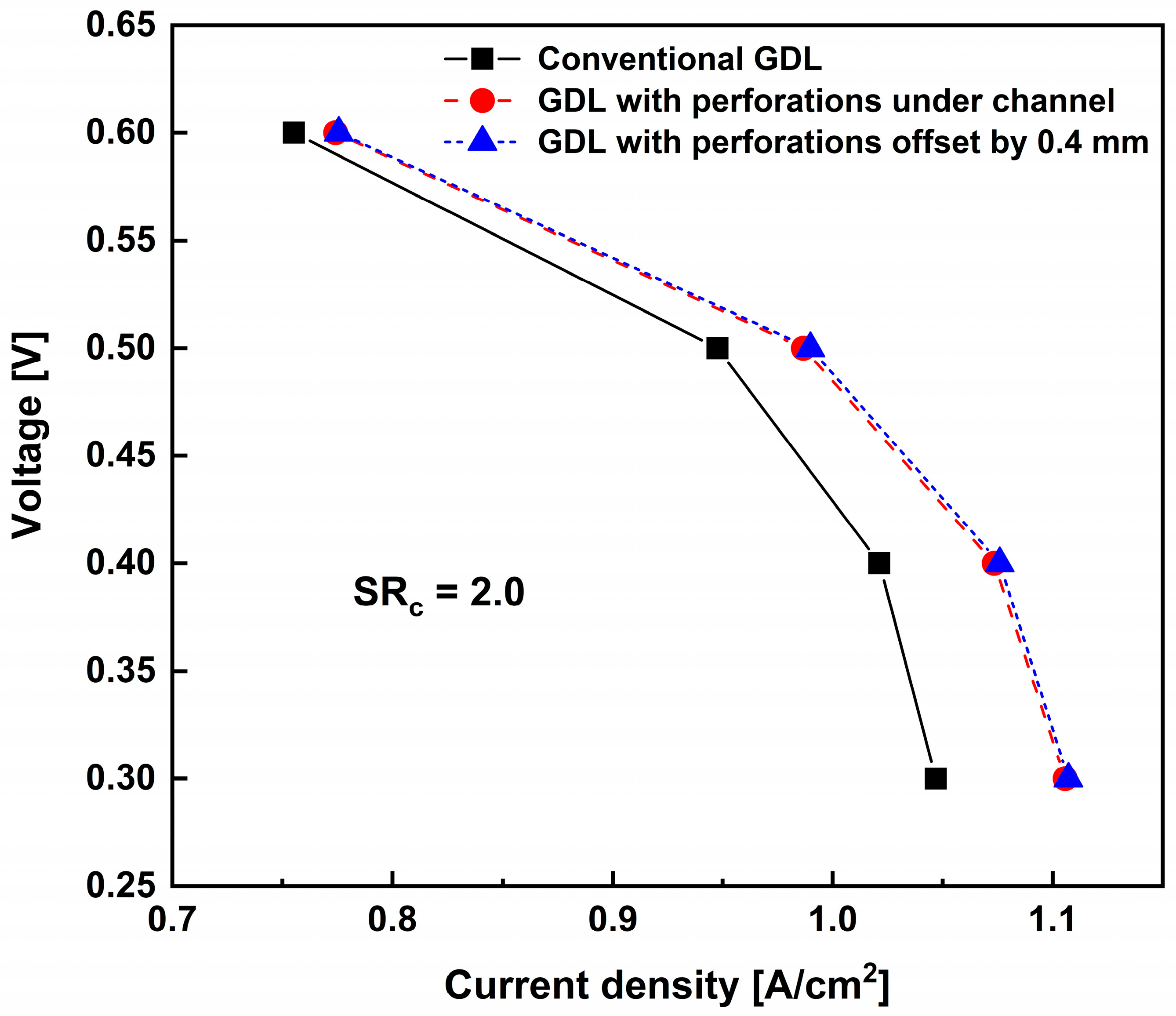
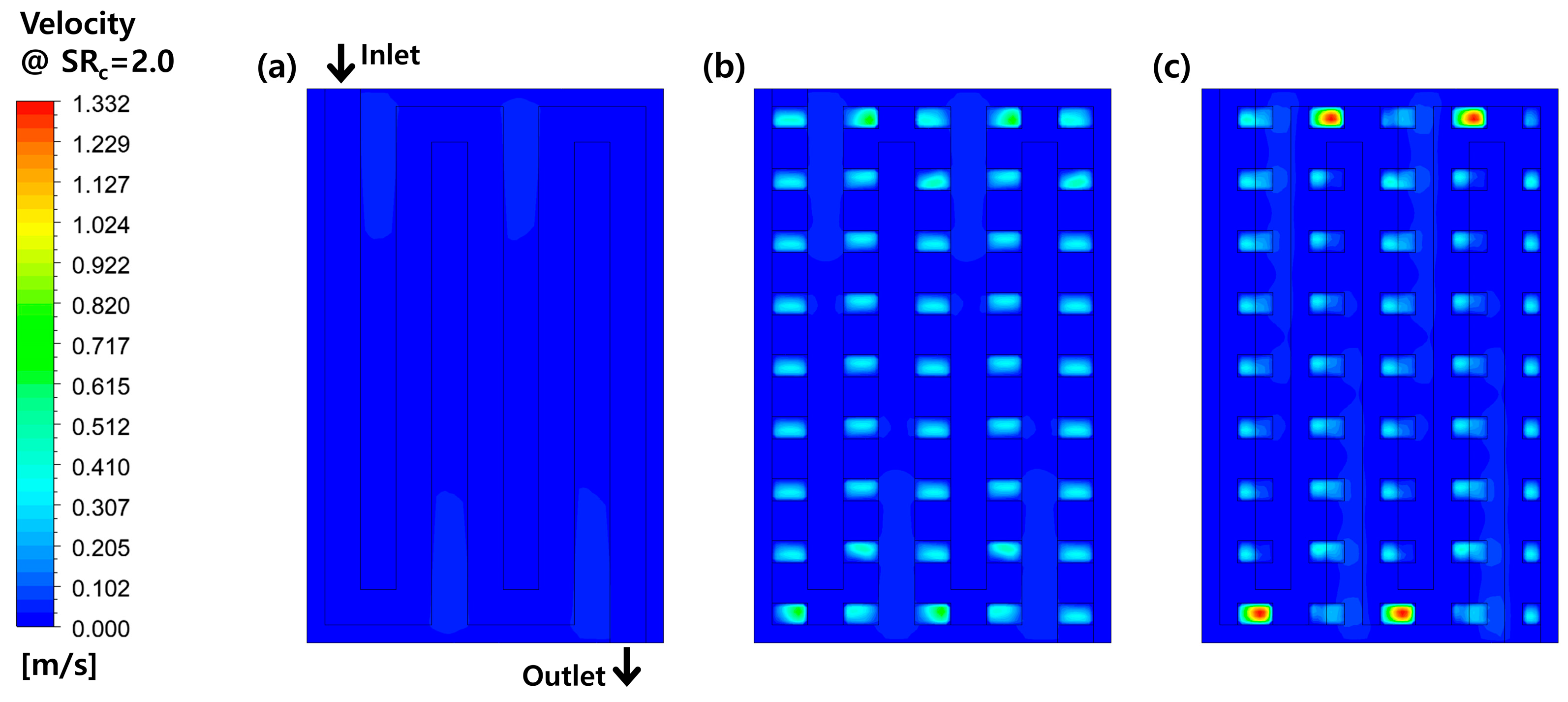
| Main Author | Scope | Methodology | Main Findings |
|---|---|---|---|
| Wang (2017) [17] | Enhancing liquid water transport with laser-perforated GDL designs. | Experiment and 3D level set simulation. | Optimal perforation size improves drainage and avoids flooding. |
| Fang (2018) [18] | Transport properties evaluation of perforated GDL. | Multiple-relaxation time lattice Boltzmann based on stochastic reconstructed microstructures. | Perforations increase permeability and diffusivity but decrease thermal conductivity. |
| Yin (2021) [19] | Transport properties improvement with microelliptical groove GDLs. | 3D numerical modeling with parametric variation. | Elliptical grooves improve water removal and oxygen supply within the GDL. |
| Wang (2022) [20] | Grooved GDL design optimization. | 3D multiphase CFD simulation with various parameters. | Nonuniformly arrayed grooves facilitates drainage and uniform distribution. |
| Zhang (2023) [16] | Influence of notch arrangement and gradient on water transport. | 3D simulations under steady and transient conditions. | Optimal notch gradient and arrangement improve drainage and reduce local flooding. |
| Lin (2024) [15] | Analysis of quadrilaterally patterned perforations on GDLs. | Experiment and multiscale simulations. | Vertically arranged perforations reduce liquid saturation and boost performance. |
| Sun (2025) [21] | Investigation of water transport behavior within the GDLs. | 3D multiphase simulation validated with experiment. | Smaller holes with proper pitch improve drainage under various conditions. |
| Geometrical Dimensions | Value | Unit |
|---|---|---|
| Reaction area | 1 | cm2 |
| Sizes of perforations | 0.8 × 0.5 | mm2 |
| Gaps between perforations | 0.9 | mm |
| Width of channel | 0.8 | mm |
| Width of rib | 0.8 | mm |
| Thickness of bipolar plate | 2 | mm |
| Thickness of GDL | 160 | µm |
| Thickness of MPL | 90 | µm |
| Thickness of CL | 5 | µm |
| Thickness of membrane | 25.4 | µm |
| Source Term | Description | Unit |
|---|---|---|
| Mass | kg m−3 s−1 | |
| Momentum | kg m−2 s−2 | |
| Hydrogen | kg m−3 s−1 | |
| Oxygen | kg m−3 s−1 | |
| Vapor | kg m−3 s−1 | |
| Energy | W m−3 | |
| Electron | A m−3 | |
| Proton | A m−3 | |
| Liquid water | kg m−3 s−1 | |
| Dissolved water | mol m−3 | |
| Water condensation and evaporation | kg m−3 s−1 | |
| Dissolved water adsorption and desorption | mol m−3 |
| Parameter | Value | Unit |
|---|---|---|
| Anode transfer coefficient [26,27], | 0.5 | - |
| Cathode transfer coefficient [26,27], | 1.0 | - |
| Reference H2 concentration [26,27], | 56.4 | mol m−3 |
| Reference O2 concentration [26,27], | 3.39 | mol m−3 |
| Activation energy of hydrogen oxidation [28], | 10,000 | J mol−1 |
| Activation energy of oxygen reduction [28], | 70,000 | J mol−1 |
| Entropy change by hydrogen oxidation [29], | 0.104 | J mol−1 K−1 |
| Entropy change by oxygen reduction [29], | −326.36 | J mol−1 K−1 |
| Electrical conductivity of BPP, GDL, MPL, CL [30], | 20,000, 8000, 5000, 5000 | S m−1 |
| Thermal conductivity of BPP, MPL, CL, membrane [30], | 120, 1, 1, 0.16 | W m−1 K−1 |
| Through-plane thermal conductivity of GDL [30], | 1.7 | W m−1 K−1 |
| In-plane thermal conductivity of GDL [30], | 21 | W m−1 K−1 |
| Porosity of GDL, MPL [31,32], | 0.8, 0.7 | - |
| Permeability of GDL, MPL, CL [30], | 110−11, 110−12, 110−13 | m2 |
| Contact angle of GDL, MPL, CL [30], | 110, 130, 95 | deg |
| Surface tension [33], | 0.0625 | N m−1 |
| Latent heat of water phase change [24], | 2.36106 | J kg−1 |
| Dry membrane density [34], | 1970 | kg m−3 |
| Membrane equivalent weight [34], | 1.050 | kg mol−1 |
| Condensation rate [23], | 100 | s−1 |
| Evaporation rate [23], | 100 | s−1 |
| Inertial coefficient [35], | 2.8810−6 | m−1 |
| Platinum loading [26], | 0.4 | mg cm−2 |
| Platinum density [26], | 21,450 | kg m−3 |
| Carbon loading, | 0.27 | mg cm−2 |
| Carbon density [26], | 1800 | kg m−3 |
| Agglomerate radius [26], | 0.2 | µm |
| Ionomer volume fraction of catalyst layer [26], | 0.4 | - |
| Ionomer volume fraction of agglomerate [26], | 0.5 | - |
| Description | Equation | Unit |
|---|---|---|
| Open circuit voltage [24] | V | |
| Overpotential [24] | V | |
| Anode volumetric current density [11,36] | A m−3 | |
| Cathode reaction rate [11,36] | A m−3 | |
| Anode exchange current density [11,28] | A m−2 | |
| Cathode exchange current density [11,28] | A m−2 | |
| Proton conductivity [37] | S m−1 | |
| Effective proton conductivity [26] | S m−1 | |
| Effective electrical conductivity [26] | S m−1 | |
| H2 and H2O diffusivity in the anode side [38] | m2 s−1 | |
| O2 diffusivity in the cathode side [38] | m2 s−1 | |
| H2O diffusivity in the cathode side [38] | m2 s−1 | |
| Effective gas diffusivity [11] | m2 s−1 | |
| Henry’s constant for H2 in ionomer [39] | Pa m3 mol−1 | |
| Henry’s constant for O2 in ionomer [39] | Pa m3 mol−1 | |
| Saturation pressure [23] | Pa | |
| water activity [23] | - | |
| Liquid velocity [38] | m s−1 | |
| Relative permeability [38] | m2 | |
| Capillary pressure [40] | Pa | |
| Liquid water diffusivity [38] | m2 s−1 | |
| Equilibrium water content [23,37] | - | |
| Electro-osmotic drag coefficient [37] | - | |
| Dissolved water diffusivity [23,37] | m2 s−1 | |
| Adsorption rate [25] | s−1 | |
| Desorption rate [25] | s−1 |
| Description | Equation | Unit |
|---|---|---|
| Cathode volumetric current density | A m−3 | |
| Pt mass ratio of Pt/C particles | - | |
| Pt/C volume fraction of catalyst layer | - | |
| Active surface area | m−1 | |
| CL porosity | - | |
| Number of agglomerate particles per CL volume | - | |
| Ionomer film thickness | m | |
| Water film thickness | m | |
| Effective agglomerate surface area of ionomer film | m−1 | |
| Effective agglomerate surface area of water film | m−1 | |
| Dissolved O2 diffusivity in ionomer film [39] | m2 s−1 | |
| Dissolved O2 diffusivity in water film [39] | m2 s−1 | |
| Thiele modulus | - | |
| Effectiveness factor | - |
| Conventional GDL | GDL with Perforations Under Channel | GDL with Perforations Offset by 0.4 mm | Unit | |
|---|---|---|---|---|
| Average oxygen concentration in the cathode CL | 0.9559 | 1.027 | 1.032 | mol/m3 |
| Current density | 0.9477 | 0.9867 | 0.9898 | A/cm2 |
| Improvement | - | 4.12 | 4.44 | % |
| Conventional GDL | GDL with Perforations Under Channel | GDL with Perforations Offset by 0.4 mm | Unit | |
|---|---|---|---|---|
| Average oxygen concentration in the cathode CL at SRc = 1.2 | 0.7460 | 0.7857 | 0.7852 | mol/m3 |
| Current density at SRc = 1.2 | 0.7869 | 0.8107 | 0.8114 | A/cm2 |
| Improvement at SRc = 1.2 | - | 3.02 | 3.11 | % |
| Average oxygen concentration in the cathode CL at SRc = 3.0 | 1.1299 | 1.2331 | 1.2441 | mol/m3 |
| Current density at SRc = 3.0 | 1.0612 | 1.1113 | 1.1173 | A/cm2 |
| Improvement at SRc = 3.0 | - | 4.72 | 5.29 | % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, D.K.; Kim, G.H.; Son, J.; Bai, S.J.; Cho, G.Y. Effects of Perforation Location in Gas Diffusion Layers on Electrochemical Characteristics of Proton Exchange Membrane Fuel Cells. Appl. Sci. 2025, 15, 8804. https://doi.org/10.3390/app15168804
Song DK, Kim GH, Son J, Bai SJ, Cho GY. Effects of Perforation Location in Gas Diffusion Layers on Electrochemical Characteristics of Proton Exchange Membrane Fuel Cells. Applied Sciences. 2025; 15(16):8804. https://doi.org/10.3390/app15168804
Chicago/Turabian StyleSong, Dong Kun, Geon Hyeop Kim, Jonghyun Son, Seoung Jai Bai, and Gu Young Cho. 2025. "Effects of Perforation Location in Gas Diffusion Layers on Electrochemical Characteristics of Proton Exchange Membrane Fuel Cells" Applied Sciences 15, no. 16: 8804. https://doi.org/10.3390/app15168804
APA StyleSong, D. K., Kim, G. H., Son, J., Bai, S. J., & Cho, G. Y. (2025). Effects of Perforation Location in Gas Diffusion Layers on Electrochemical Characteristics of Proton Exchange Membrane Fuel Cells. Applied Sciences, 15(16), 8804. https://doi.org/10.3390/app15168804




