Theoretical Estimation of Wheat Straw Sound Absorption Coefficient Using Computed Tomography Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Wheat Straw Incident Sound Absorption Coefficient Testing
2.2. Tortuosity
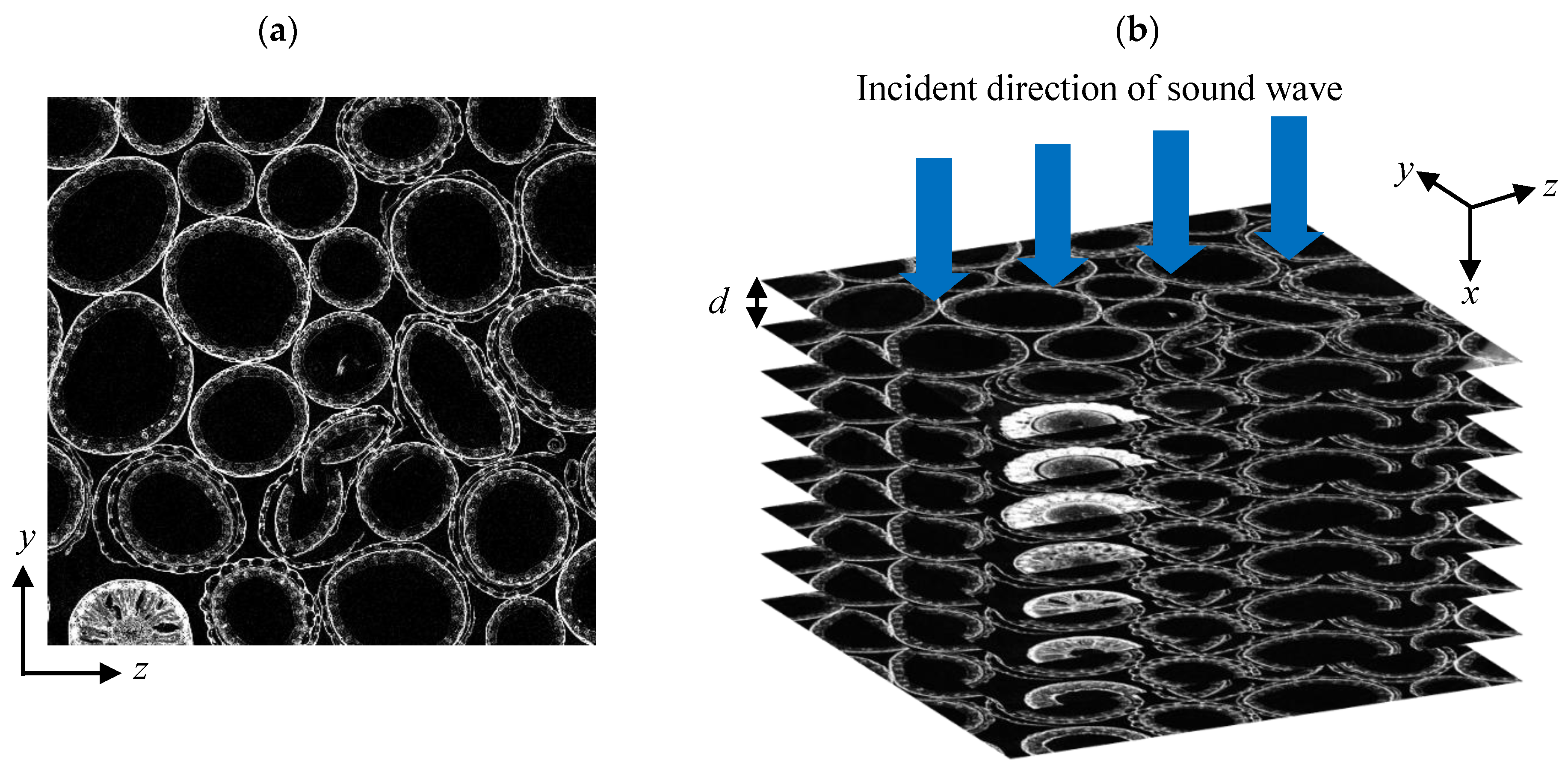
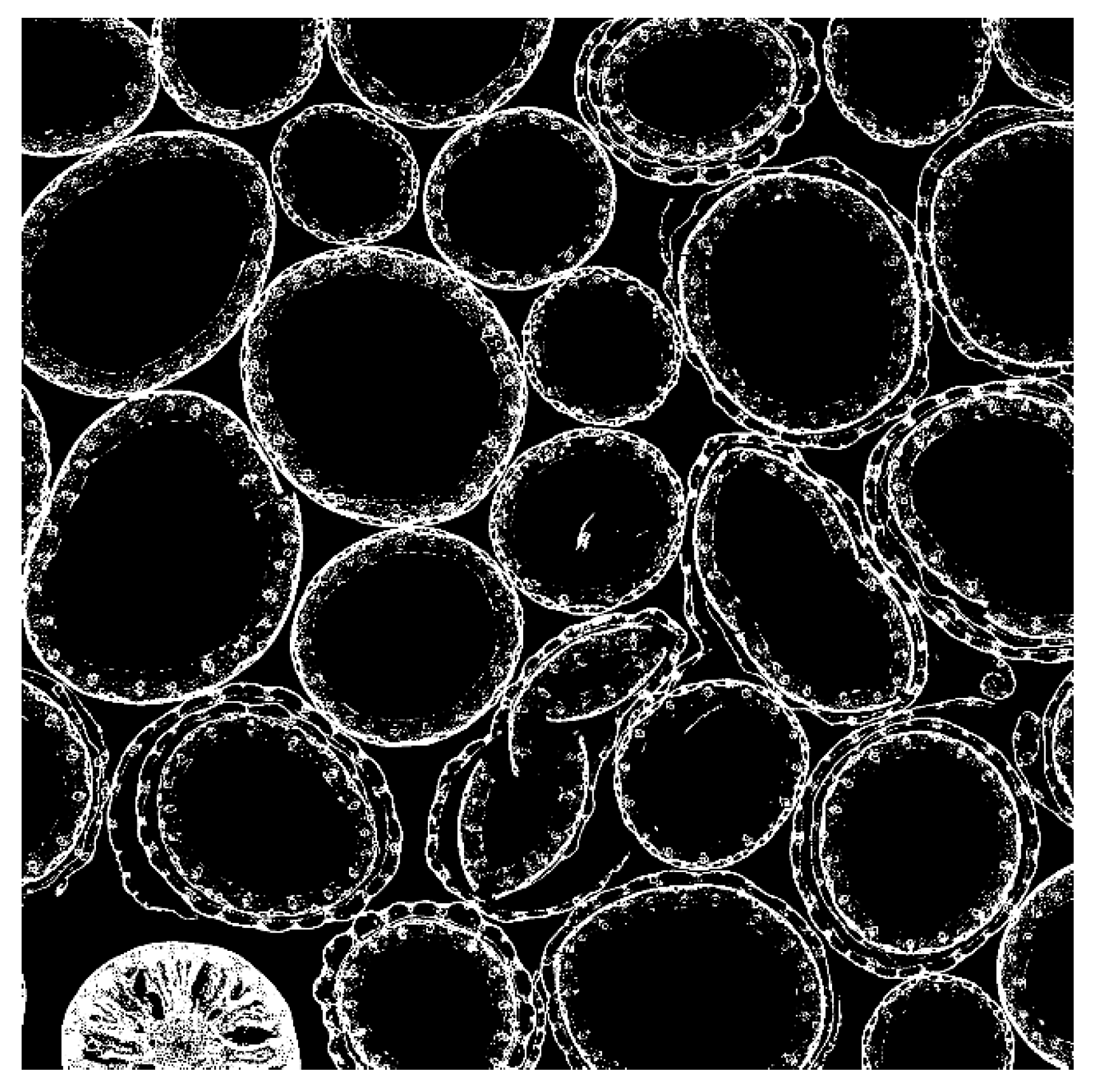
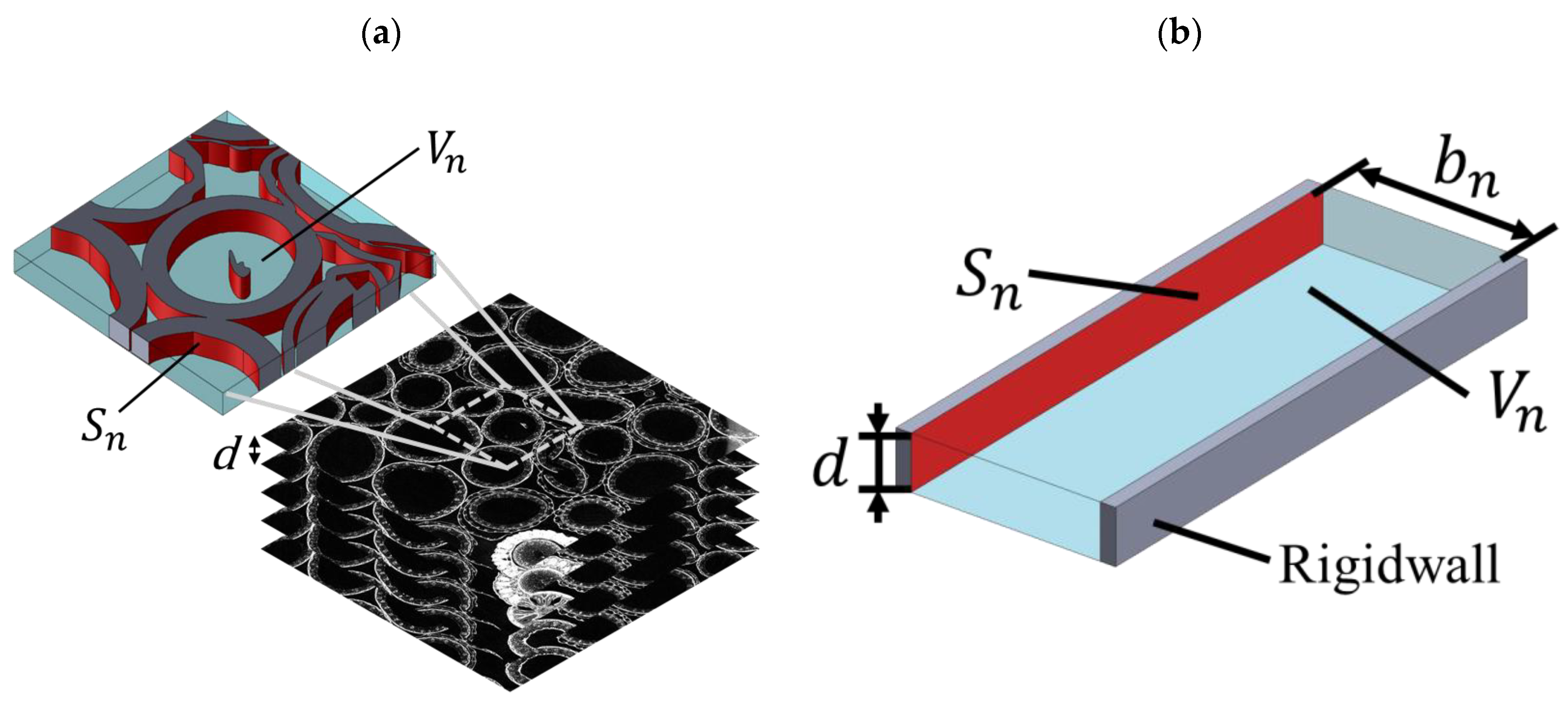
2.3. CT Images
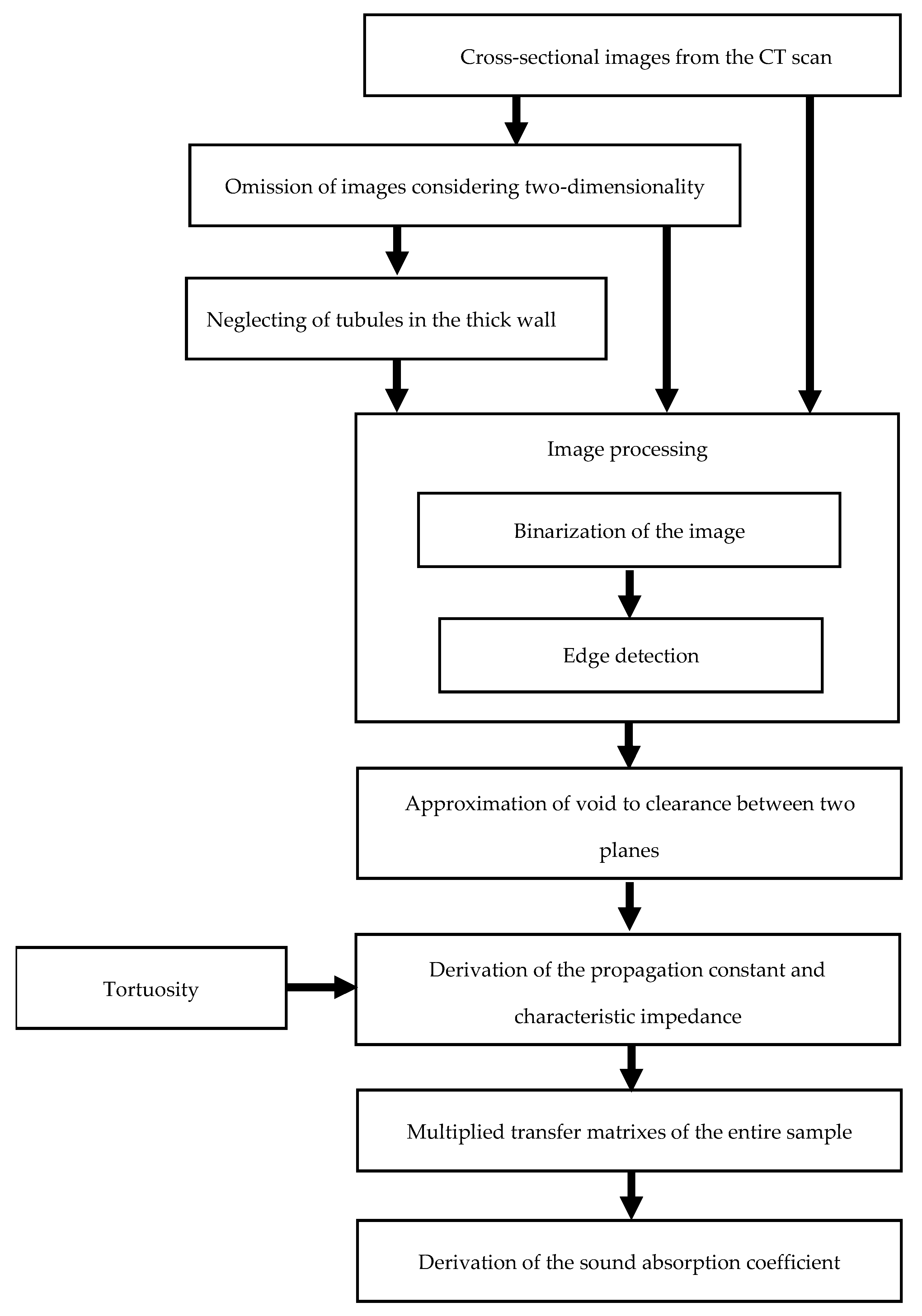
2.4. Derivation of Sound Absorption Coefficient
2.4.1. Image Processing
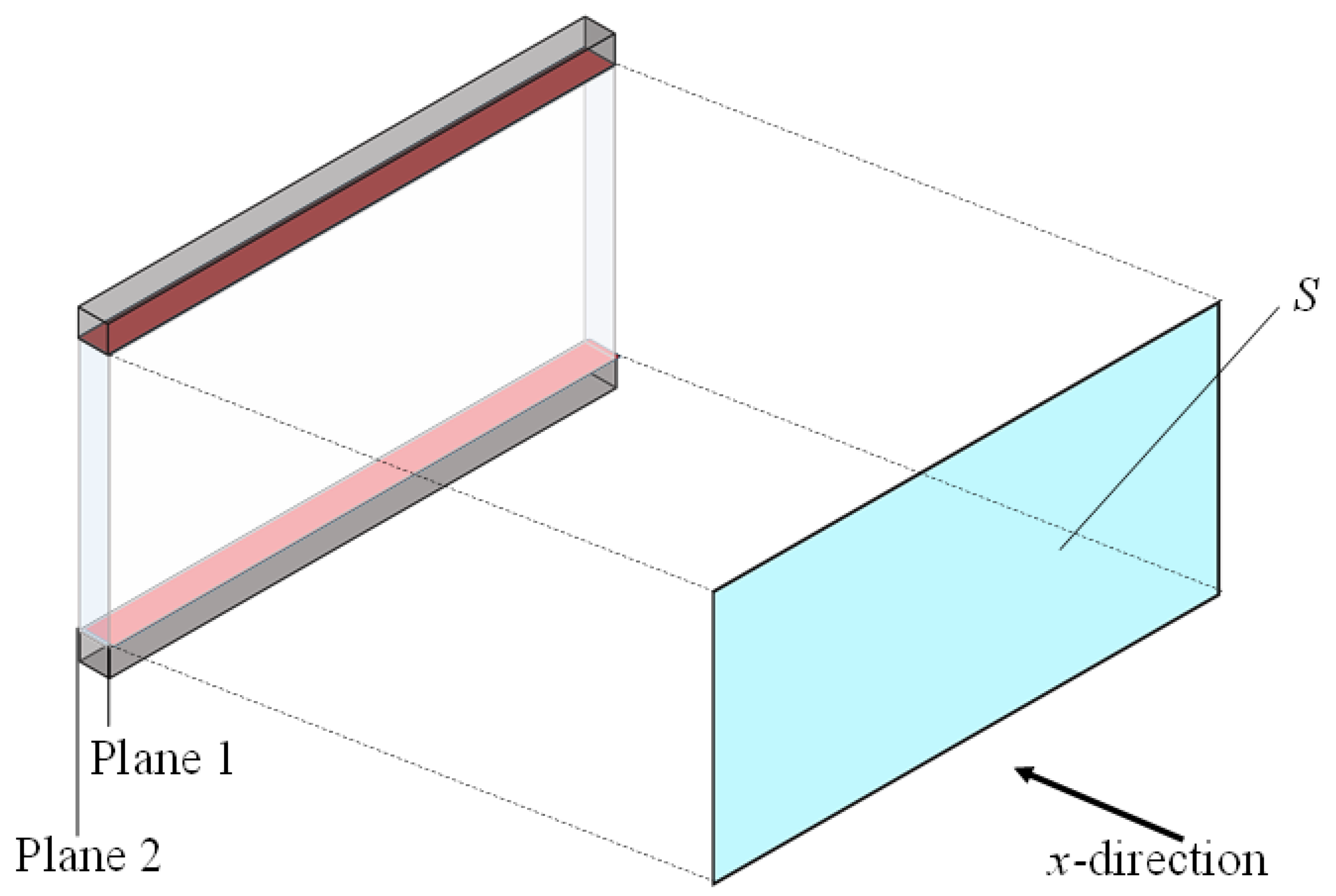
2.4.2. Approximation of Clearance Between Two Planes
2.4.3. Propagation Constant and Characteristic Impedance
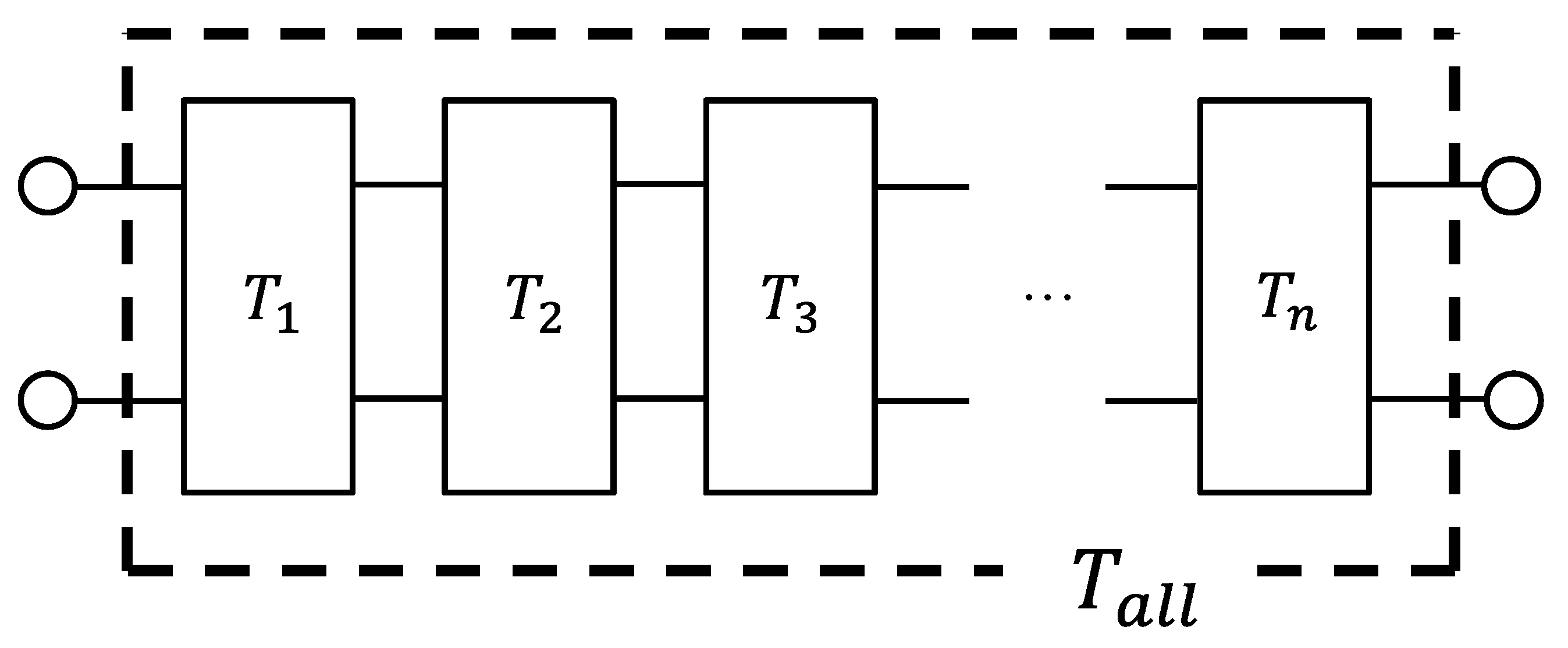
2.4.4. Transfer Matrix
2.4.5. Normal Incident Sound Absorption Coefficient
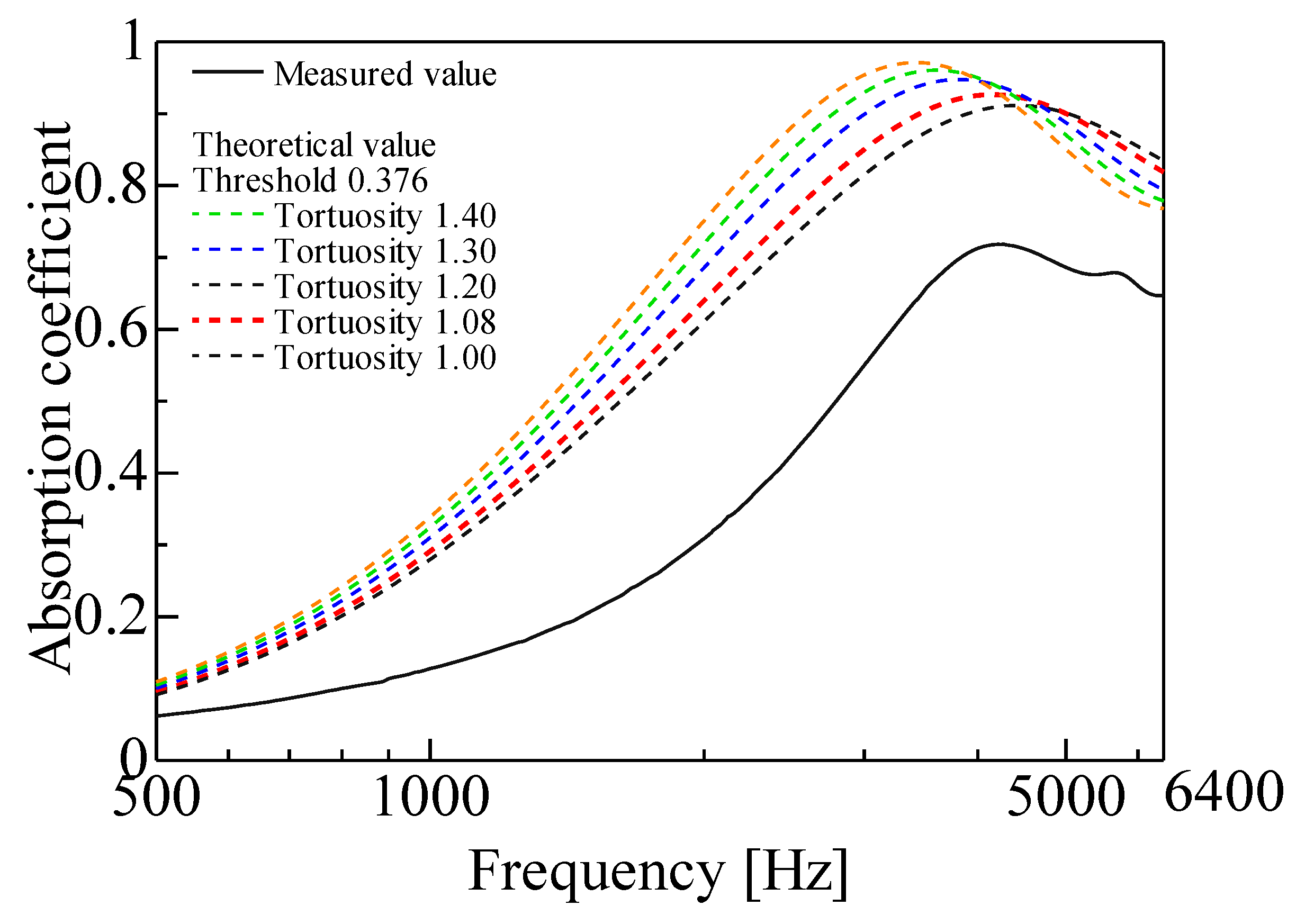
3. Comparison of Measured and Theoretical Incident Sound Absorption Coefficients
3.1. Theoretical Incident Sound Absorption Coefficient
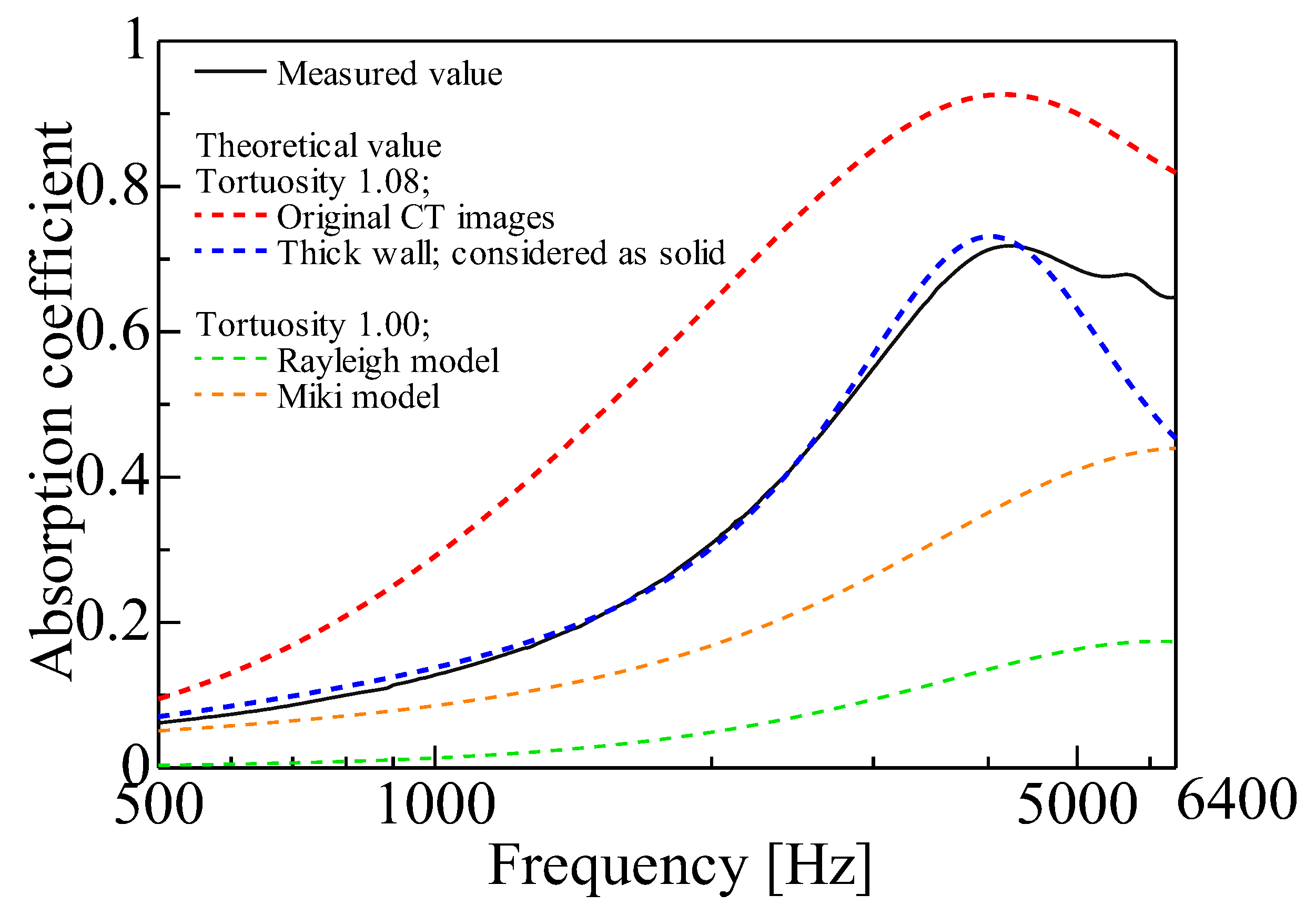
3.2. Theoretical Absorption Coefficient Considering Tortuosity
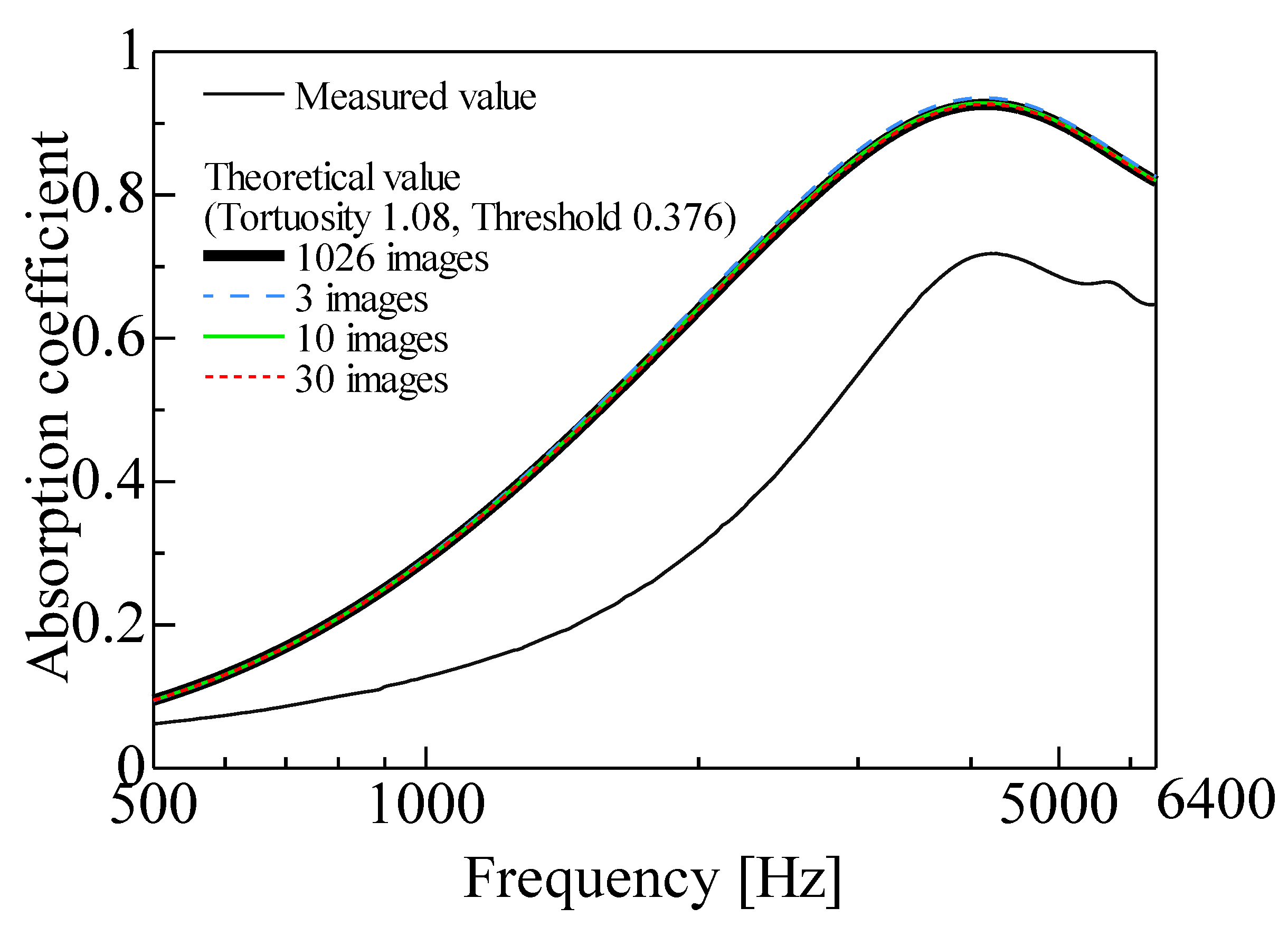
3.3. Changes in Theoretical Absorption Coefficient When Approaching a Two-Dimensional Model
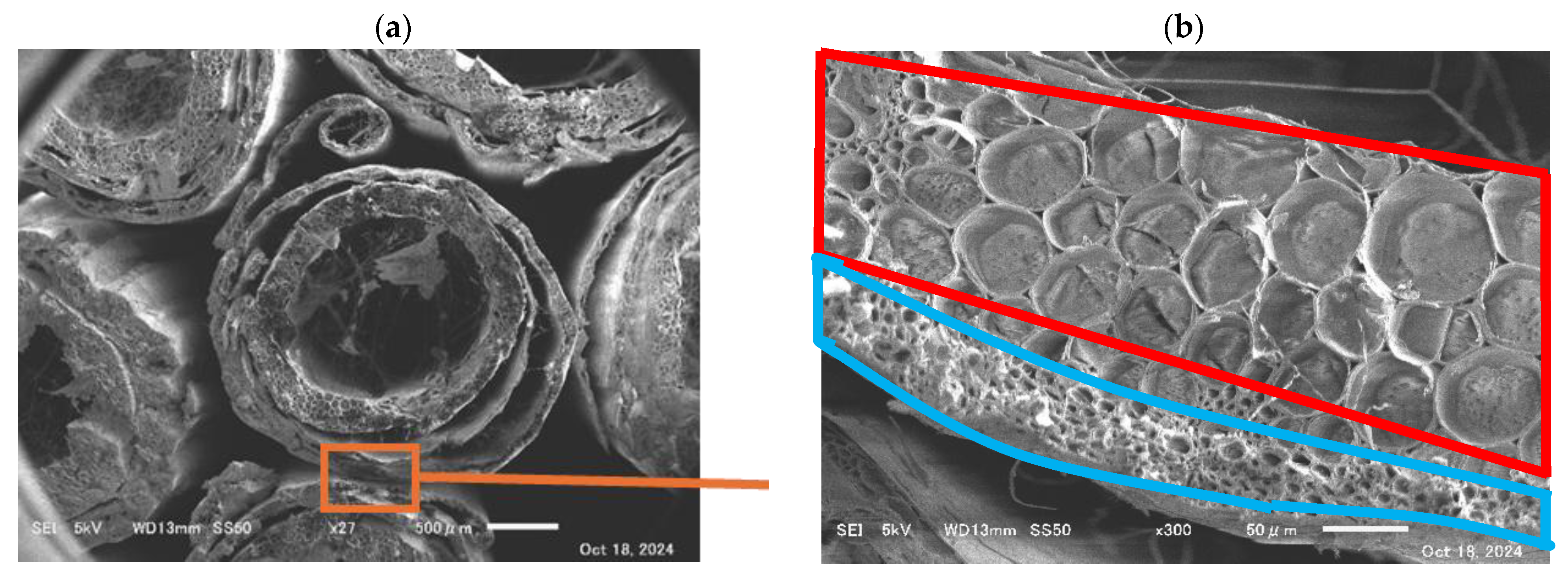
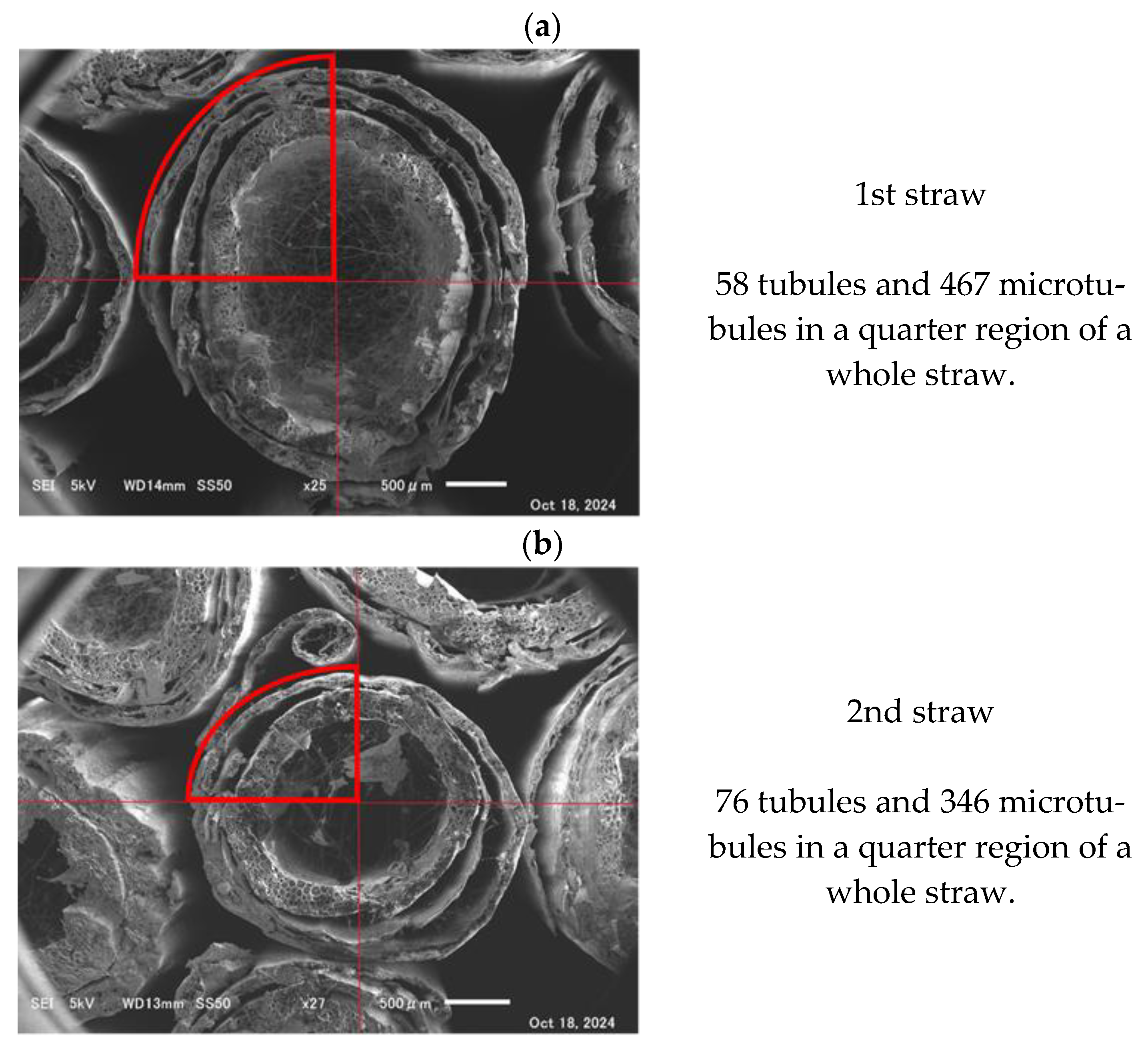
3.4. Observation of Wheat Straw Cut Surface Using SEM
3.5. Estimation of Sound Absorption Coefficient of Thick-Walled Portion of Wheat Straw
3.6. Treatment of Thick-Walled Portion of Wheat Straw as a Solid in CT Images
4. Conclusions
- (1)
- The circumference of the skeletal outlines and the cross-sectional area of the voids in the wheat straw CT images were calculated to obtain the propagation constant and characteristic acoustic impedance. The measured tortuosity was considered when calculating the normal incidence sound absorption coefficient.
- (2)
- The CT images were binarized to clarify the grayscale boundaries between the skeletal outlines and void areas of the wheat straw. Otsu’s binarization was used to determine the binarization threshold value. This threshold value uniquely determines the porosity, which is closely related to the sound absorption coefficient. Future research should include experiments using various porosities and straw diameters.
- (3)
- The two-dimensionality of the bundled wheat straw as a sound-absorbing structure was confirmed. As a result, when 10 or more CT scan images were used for a 20 mm-thick sample, the theoretical results were similar to those obtained when using the entire sample (1026 images).
- (4)
- Based on the cross-sectional SEM images, the sound absorption coefficient of the porous part of the thick-walled portion of the wheat straw was calculated using Tidgeman’s cylindrical model. It was found that the contribution of the porous part to the sound absorption of the entire sample was negligible.
- (5)
- The CT images were corrected to reflect the lack of sound absorption by the porous part of the thick-walled portion by considering it as a solid structure. The theoretical sound absorption coefficients calculated from the corrected images were in good agreement with the measured sound absorption coefficients.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A-D | Four-terminal constants of transfer matrix |
| bn | Thickness of the clearance in two-plane approximation [m] |
| c0 | Speed of sound in air [m/s] |
| C | Speed of sound in sample [m/s] |
| Cs | Compression ratio |
| D | The pitch of the slice of the CT scan image [m] |
| J | Imaginary unit |
| L | Sample thickness [m] |
| N | The number of CT scan images |
| Npr | Prandtl number |
| P0 | Atmospheric pressure [Pa] |
| p0 | Sound pressure just outside and in front of Plane 1 [m/s] |
| p1, p2 | Sound pressure at each plane [Pa] |
| R | Reflection coefficient |
| S | Cross-sectional area [m2] |
| Sn | Surface area of the skeletal section [m2] |
| T | Transfer matrix |
| Tall | Transfer matrix for the entire sample |
| u0 | Particle velocity just outside and in front of Plane 1 [Pa] |
| u1, u2 | Particle velocity at each plane [m/s] |
| Vn | Volume of the void [m3] |
| X | x coordinate [m] |
| Y | y coordinate [m] |
| Z | z coordinate [m] |
| Zc | Characteristic acoustic impedance [Ns/m3] |
| Z0 | Specific acoustic impedance [Ns/m3] |
| A | Sound absorption coefficient |
| α∞ | Tortuosity |
| γ | Propagation constant [1/m] |
| κ | Specific heat ratio of air |
| λs | Mediating variable |
| ρ0 | Density of air [kg/m3] |
| ρs | Effective density [kg/m3] |
| Viscosity of air [Pa·S] | |
| ω | Angular frequency [rad/s] |
Abbreviations
| CT | Computed tomography |
| SEM | Scanning electron microscope |
References
- Yang, T.; Hu, L.; Xiong, X.; Petru, M.; Noman, M.T.; Mishra, R.; Militky, J. Sound Absorption Properties of Natural Fibers: A Review. Sustainability 2020, 12, 8477. [Google Scholar] [CrossRef]
- Berardi, U.; Iannace, G. Acoustic characterization of natural fibers for sound absorption applications. Build. Environ. 2015, 94, 840–852. [Google Scholar] [CrossRef]
- Sakamoto, S.; Seino, S.; Hoshiyama, K.; Kojima, Y. Estimation and experiment of acoustic properties of rice straw (estimation of sound absorption coefficient using CT images). Noise Control Eng. J. 2025, 73, 12. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, X.; Gao, Y.; Lyu, L. Structural Characteristics and Sound Absorption Properties of Waste Hemp Fiber. Coatings 2022, 12, 1907. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, S.; Tang, X. Sound Absorption of Hemp Fibers (Cannabis Sativa L.) Based Nonwoven Fabrics and Composites: A Review. J. Nat. Fibers 2020, 19, 1297–1309. [Google Scholar] [CrossRef]
- Bastos, L.P.; de Melo, G.D.; Soeiro, N.S. Panels Manufactured from Vegetable Fibers: An Alternative Approach for Controlling Noises in Indoor Environments. Adv. Acoust. Vib. 2012, 2012, 698737. [Google Scholar] [CrossRef]
- Buot, P.G.C.; Cueto, R.M.; Esguerra, A.A.; Pascua, R.I.C.; Magon, E.S.S. Design and Development of Sound Absorbing Panels using Biomass Materials. In Proceedings of the 2nd African International Conference on Industrial Engineering and Operations Management Harare, Harare, Zimbabwe, 7–10 December 2020; Available online: https://www.ieomsociety.org/harare2020/papers/489.pdf (accessed on 12 June 2025).
- Or, K.H.; Putra, A.; Selamat, M.Z. Oil palm empty fruit bunch fibres as sustainable acoustic absorber. Appl. Acoust. 2017, 119, 9–16. [Google Scholar] [CrossRef]
- Ersoy, S.; Küçük, H. Investigation of industrial tea-leaf-fibre waste material for its sound absorption properties. Appl. Acoust. 2009, 70, 215–220. [Google Scholar] [CrossRef]
- Maderuelo-Sanz, R.; Morillas, J.M.B.; Escobar, V.G. Acoustical performance of loose cork granulates. Eur. J. Wood Wood Prod. 2012, 72, 321–330. [Google Scholar] [CrossRef]
- Alhijazi, M.; Safaei, B.; Zeeshan, Q.; Asmael, M.; Eyvazian, A.; Qin, Z. Recent Developments in Luffa Natural Fiber Composites: Review. Sustainability 2020, 12, 7683. [Google Scholar] [CrossRef]
- Thilagavathi, G.; Pradeep, E.; Kannaian, T.; Sasikala, L. Development of Natural Fiber Nonwovens for Application as Car Interiors for Noise Control. J. Ind. Text. 2010, 39, 267–278. [Google Scholar] [CrossRef]
- Sakamoto, S.; Tsurumaki, T.; Fujisawa, K.; Yamamiya, K. Study for sound-absorbing materials of biomass tubule (Oblique incident sound-absorption coefficient of oblique arrangement of rice straws). Trans. JSME 2016, 83, 16–00344. [Google Scholar] [CrossRef]
- Sakamoto, S.; Tanikawa, H.; Maruyama, Y.; Yamaguchi, K.; Ii, K. Estimation and experiment for sound absorption coefficient of three clearance types using a bundle of nested tubes. J. Acoust. Soc. Am. 2018, 144, 2281–2293. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Mathematical Models and Experiments on the Acoustic Properties of Granular Packing Structures (Measurement of Tortuosity in Hexagonal Close-Packed and Face-Centered Cubic Lattices). Materials 2022, 15, 7393. [Google Scholar] [CrossRef]
- Sakamoto, S.; Suzuki, K.; Toda, K.; Seino, S. Estimation of the Acoustic Properties of the Random Packing Structures of Granular Materials: Estimation of the Sound Absorption Coefficient Based on Micro-CT Scan Data. Materials 2023, 16, 337. [Google Scholar] [CrossRef]
- Hideshima, Y.; Arima, S.; Suzuki, A. Effects of the Method of Processing Wheat or Barly Straw in the Double Cropping System on Weed Incidence and Growth of Paddy Rice. Jpn. J. Crop Sci. 2016, 85, 122–129. [Google Scholar] [CrossRef][Green Version]
- Ministry of the Environment (Waste & Recycling), Report for FY2021 Nationwide Survey Regarding Measures for Wide-Area Waste Transportation and the Actual Utilization of Recyclable Waste Materials (Survey on the Actual Utilization of Recyclable Waste Materials). 2022. Available online: https://www.env.go.jp/recycle/report/post_20.html (accessed on 5 August 2025).
- Ye, F.; Wei, H.; Xiao, Y.; Berardi, U.; Quaranta, G. Bio-based insulation materials in sustainable constructions: A review of environmental, thermal and acoustic insulation, durability, and mechanical performances. Renew. Sustain. Energy Rev. 2025, 223, 115872. [Google Scholar] [CrossRef]
- Food and Agriculture Organization. World Food and Agriculture—Statistical Yearbook 2023; Food and Agriculture Organization of the United Nations: Rome, Italy, 2023; p. 14. [CrossRef]
- Ministry of Agriculture, Forestry and Fisheries. FY2023 Food Supply and Demand Chart. 2025. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00500300&tstat=000001017950&cycle=8&tclass1=000001032890&tclass2=000001226685&cycle_facet=tclass1%3Atclass2&tclass3val=0 (accessed on 5 August 2025).
- ISO 10534-2:2023; Acoustics—Determination of Acoustic Properties in Impedance Tubes—Part 2: Two-Microphone Technique for Normal Sound Absorption Coefficient and Normal Surface Impedance. ISO: Geneva, Switzerland, 2023. [CrossRef]
- Allard, J.F.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, 2nd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, S.; Toda, K.; Seino, S.; Hoshiyama, K.; Satoh, T. Theoretical and Experimental Analyses on the Acoustic Properties of Rice and Buckwheat Husks Based on Micro-CT Scan Data. Materials 2023, 16, 5671. [Google Scholar] [CrossRef]
- Tijdeman, H. On the propagation of sound waves in cylindrical tubes. J. Sound Vib. 1975, 39, 1–33. [Google Scholar] [CrossRef]
- Stinson, M.R. The propagation of plane sound waves in narrow and wide circular tubes and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am. 1991, 89, 550–558. [Google Scholar] [CrossRef]
- Stinson, M.R.; Champou, Y. Propagation of sound and the assignment of shape factors in model porous materials having simple pore geometries. J. Acoust. Soc. Am. 1992, 91, 685–695. [Google Scholar] [CrossRef]
- Beltman, W.M.; van der Hoogt, P.J.M.; Spiering, R.M.E.J.; Tijdeman, H. Implementation and experimental validation of a new viscothermal acoustic finite element for acousto-elastic problems. J. Sound Vib. 1998, 216, 159–185. [Google Scholar] [CrossRef]
- Sakamoto, S.; Hoshino, A.; Sutou, K.; Sato, T. Estimating Sound-Absorption Coefficient and Transmission Loss by the Dimensions of Bundle of Narrow Holes (Comparison between Theoretical Analysis and Experiments). Trans. Jpn. Soc. Mech. Eng Ser. C 2013, 79, 4164–4176. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. The Theory of Sound, 2nd ed.; Dover Publications: Garden City, NY, USA, 1945. [Google Scholar]
- Miki, Y. Acoustical properties of porous materials-modifications of Delany-Bazley models. J. Acoust. Soc. Jpn 1990, 11, 19–24. [Google Scholar] [CrossRef]
- Kuttruff, H. Room Acoustics, 5th ed.; Spon Press: New London, NY, USA, 2009. [Google Scholar]
- Suzuki, H.; Omoto, A.; Fujiwara, K. Treatment of boundary conditions by finite difference time domain method. J. Acoust. Soc. Jpn. 2007, 28, 16–26. [Google Scholar] [CrossRef][Green Version]
- Ferreira, N.; Hopkins, C. Using finite-difference time-domain methods with a Rayleigh approach to model low-frequency sound fields in small spaces subdivided by porous materials. J. Acoust. Soc. Jpn. 2013, 34, 332–341. [Google Scholar] [CrossRef]

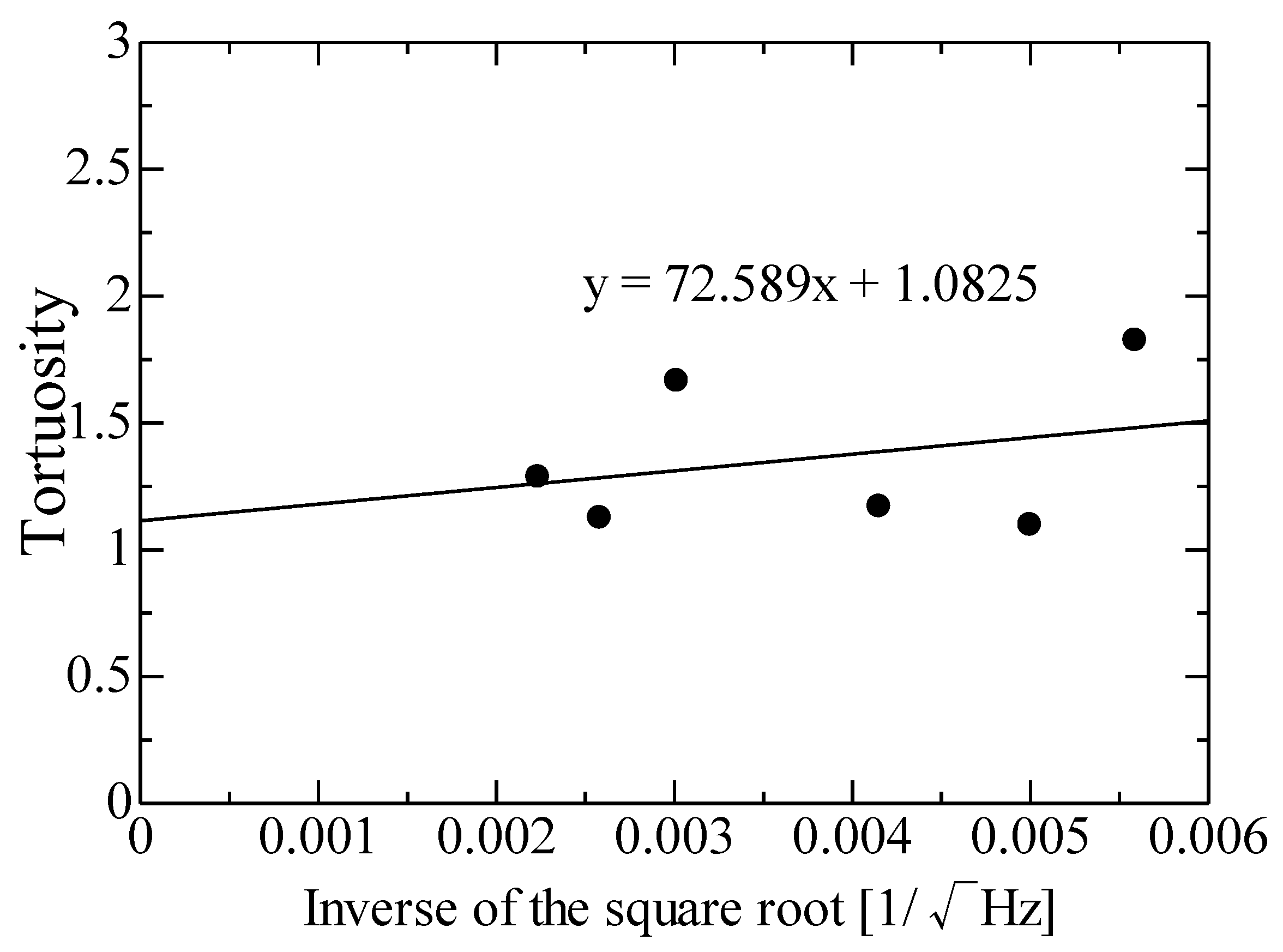






| Equipment | Manufacturer | Product Name |
|---|---|---|
| Impedance measurement tube | Brüel & Kjær | Type 4206 two-microphone impedance measurement tube |
| Microphone | Brüel & Kjær | Type 4187 |
| Pre-amplifier | Brüel & Kjær | Type 2670 |
| Microphone amplifier | Brüel & Kjær | Type 2690 |
| Power amplifier | Yamaha (Hamamatsu, Japan) | Natural sound integrated amplifier A-S301 |
| FFT analyzer with signal generator | Ono Sokki (Yokohama, Japan) | DS-3000 |
| Software | Ono Sokki | DS-0320 |
| Components and Software | Details |
|---|---|
| Processor | Intel Core i5 8400 |
| Motherboard | ASUS PRIME H370M-PLUS |
| RAM | 16 GB |
| GPU | Intel UHD Graphics 630 |
| Operating system | Microsoft Windows 11 |
| Numerical computation software | Dassault Systems Scilab 6.6.1 |
| Microtubule Group (Depth = 20 mm) | Tubule Group (Depth = 0.03 mm) | ||
|---|---|---|---|
| Diameter [mm] | Number of microtubules | Diameter [mm] | Number of tubules |
| 0.003 | 8600 | 0.02 | 1560 |
| 0.006 | 8600 | 0.04 | 1560 |
| 0.010 | 8600 | 0.06 | 1560 |
| 0.015 | 8600 | 0.08 | 1560 |
| 0.020 | 8600 | 0.10 | 1560 |
| Total number of microtubules = 43,000 | Total number of tubules = 7800 | ||
| Frequency | 500 Hz (304–707 Hz) | 1 kHz (707–1414 Hz) | 2 kHz (1414–2828 Hz) | 4 kHz (2828–5657 Hz) | |||
|---|---|---|---|---|---|---|---|
| Tortuosity | |||||||
| Average sound absorption coefficient at octave band frequencies | Measured | - - - | 0.066 | 0.138 | 0.342 | 0.669 | |
| Theoretical (blue line) | 1.08 | 0.075 | 0.147 | 0.341 | 0.652 | ||
| Theoretical (Rayleigh) | N/A (1.00) | 0.015 | 0.026 | 0.067 | 0.139 | ||
| Theoretical (Miki) | N/A (1.00) | 0.058 | 0.091 | 0.181 | 0.358 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, S.; Hoshiyama, K.; Kojima, Y.; Saito, K.; Roslan, Z.S.B. Theoretical Estimation of Wheat Straw Sound Absorption Coefficient Using Computed Tomography Images. Appl. Sci. 2025, 15, 8803. https://doi.org/10.3390/app15168803
Sakamoto S, Hoshiyama K, Kojima Y, Saito K, Roslan ZSB. Theoretical Estimation of Wheat Straw Sound Absorption Coefficient Using Computed Tomography Images. Applied Sciences. 2025; 15(16):8803. https://doi.org/10.3390/app15168803
Chicago/Turabian StyleSakamoto, Shuichi, Kohta Hoshiyama, Yoshiaki Kojima, Kenta Saito, and Zulhafiz Syazmi Bin Roslan. 2025. "Theoretical Estimation of Wheat Straw Sound Absorption Coefficient Using Computed Tomography Images" Applied Sciences 15, no. 16: 8803. https://doi.org/10.3390/app15168803
APA StyleSakamoto, S., Hoshiyama, K., Kojima, Y., Saito, K., & Roslan, Z. S. B. (2025). Theoretical Estimation of Wheat Straw Sound Absorption Coefficient Using Computed Tomography Images. Applied Sciences, 15(16), 8803. https://doi.org/10.3390/app15168803






