Physics-Informed Surrogate Modelling in Fire Safety Engineering: A Systematic Review

Abstract

Surrogate modelling is increasingly used in engineering to improve computational efficiency in complex simulations. However, traditional data-driven surrogate models often face limitations in generalizability, physical consistency, and extrapolation—issues that are especially critical in safety-sensitive fields such as fire safety engineering (FSE). To address these concerns, physics-informed surrogate modelling (PISM) integrates physical laws into machine learning models, enhancing their accuracy, robustness, and interpretability. This systematic review synthesises existing applications of PISM in FSE, classifies the strategies used to embed physical knowledge, and outlines key research challenges. A comprehensive search was conducted across Google Scholar, ResearchGate, ScienceDirect, and arXiv up to May 2025, supported by backward and forward snowballing. Studies were screened against predefined criteria, and relevant data were analysed through narrative synthesis. A total of 100 studies were included, covering five core FSE domains: fire dynamics, wildfire behaviour, structural fire engineering, material response, and heat transfer. Four main strategies for embedding physics into machine learning were identified: feature engineering techniques (FETs), loss-constrained techniques (LCTs), architecture-constrained techniques (ACTs), and offline-constrained techniques (OCTs). While LCT and ACT offer strict enforcement of physical laws, hybrid approaches combining multiple strategies often produce better results. A stepwise framework is proposed to guide the development of PISM in FSE, aiming to balance computational efficiency with physical realism. Common challenges include handling nonlinear behaviour, improving data efficiency, quantifying uncertainty, and supporting multi-physics integration. Still, PISM shows strong potential to improve the reliability and transparency of machine learning in fire safety applications.

1. Introduction: Addressing Challenges in Fire Safety Engineering with Surrogate Modelling

1.1. Surrogate Modelling Definition and Motivation

Fire safety engineering faces several challenges that hinder the development of accurate and efficient predictive models. Experimental testing is often expensive, and results can be highly variable due to differing procedures, making direct comparisons difficult [1]. Additionally, certain fire phenomena, such as spalling in concrete, remain not fully understood, adding uncertainty to fire performance assessments [2]. Where the underlying physics are sufficiently understood, numerical simulations can complement experiments; however, such simulations are often computationally demanding. These limitations highlight the need for efficient modelling approaches that can capture the complexity of fire behaviour while reducing computational costs.

In surrogate modelling, the results of a computationally expensive model are used as training data for a computationally efficient “surrogate”. Such surrogate models have become a fundamental tool in engineering thanks to their ability to approximate the complex physical phenomena governing behaviour while significantly reducing computational effort [3,4,5]. This substantial decrease in computational time makes surrogate modelling particularly valuable for high-dimensional and nonlinear systems [3,6,7]. Additionally, surrogate models facilitate optimisation [8,9], uncertainty quantification [10,11,12], risk assessment [10,11,12], and real-time decision-making [13,14,15]. As a result, their use has expanded across various engineering disciplines, including aerodynamics [16,17], thermodynamics [18,19], and materials science [20,21,22]. Considering the above, surrogate modelling has particular promise for fire safety engineering (FSE), as conceptually elaborated in Figure 1. Establishing the state-of-the-art in FSE, with a particular focus on physics-informed surrogate modelling approaches, will be the focus of Section 1.3 further in this paper.

1.2. Surrogate Modelling Algorithms

Surrogate modelling algorithms can be broadly categorised into regression-based, neural network-based and partition-based categories (see Figure 2) [23]. Regression-based approaches are widely used due to their interpretability [24,25]. These methods establish explicit mathematical relationships between input variables and outputs, with the simplest form being polynomial regression. Linear regression (first-order polynomial) is particularly popular due to its simplicity and minimal computational cost. However, for highly nonlinear systems, higher-order polynomial models may be necessary to capture complex input–output relationships. While increasing the polynomial order can enhance accuracy, it also raises the risk of overfitting, where the model performs well on training data but fails to generalise to other data points within the intended parameter space. Regularisation techniques, by adding a penalty for model complexity, can mitigate this issue [26]. Additionally, support vector machines (SVMs), though originally developed for classification, can be employed in surrogate modelling through support vector regression (SVR), offering robustness and flexibility in capturing nonlinear relationships [27].

For systems with highly complex and nonlinear behaviours, neural network-based models provide a more flexible alternative [28]. A neural network consists of a single or multiple layers of interconnected neurons, each applying an activation function to transform inputs into outputs [29]. The neural network’s reported flexibility then results from the use of nonlinear activation functions in a system with multiple interconnected layers. This allows them to learn intricate mappings between inputs and outputs, and approximate a wider range of complex functional forms compared to traditional regression models with fixed basis functions. However, the complex interactions within the multiple layers and the large number of learnable parameters limit interpretability, resulting in the neural network’s ‘black-box’ nature. Furthermore, large datasets are required to effectively train the high number of parameters within a multi-layer model and avoid overfitting, especially when dealing with complex, high-dimensional problems [30]. The most widely used neural-network-based surrogate modelling approaches are artificial neural networks (ANNs), convolutional neural networks (CNNs), and long short-term memory (LSTM) networks. ANNs are general-purpose models composed of layers of neurons that process information through weighted connections and activation functions, enabling them to approximate complex relationships in data. CNNs, a specialised type of ANN, are particularly effective for spatially structured data, utilising convolutional layers to extract hierarchical features, making them widely used in image and pattern recognition tasks. LSTMs, a class of recurrent neural networks (RNNs), are designed to handle sequential data by maintaining memory over time through specialised gating mechanisms, making them well-suited for time-series forecasting and dynamic system modelling.

Decision-tree-based models are another main category of surrogate modelling. This category relies on the identification of separated subcategories for the data [31]. They are effective when the data can be separated into subcategories, each with a different behaviour and thus a different model. The basic model uses a tree-like structure to categorise based on input features [32]. Example approaches within this category are random forest (RF) [33], gradient boosting machines (GBMs) [34], and extreme gradient boosting algorithm (XGBoost) [35].

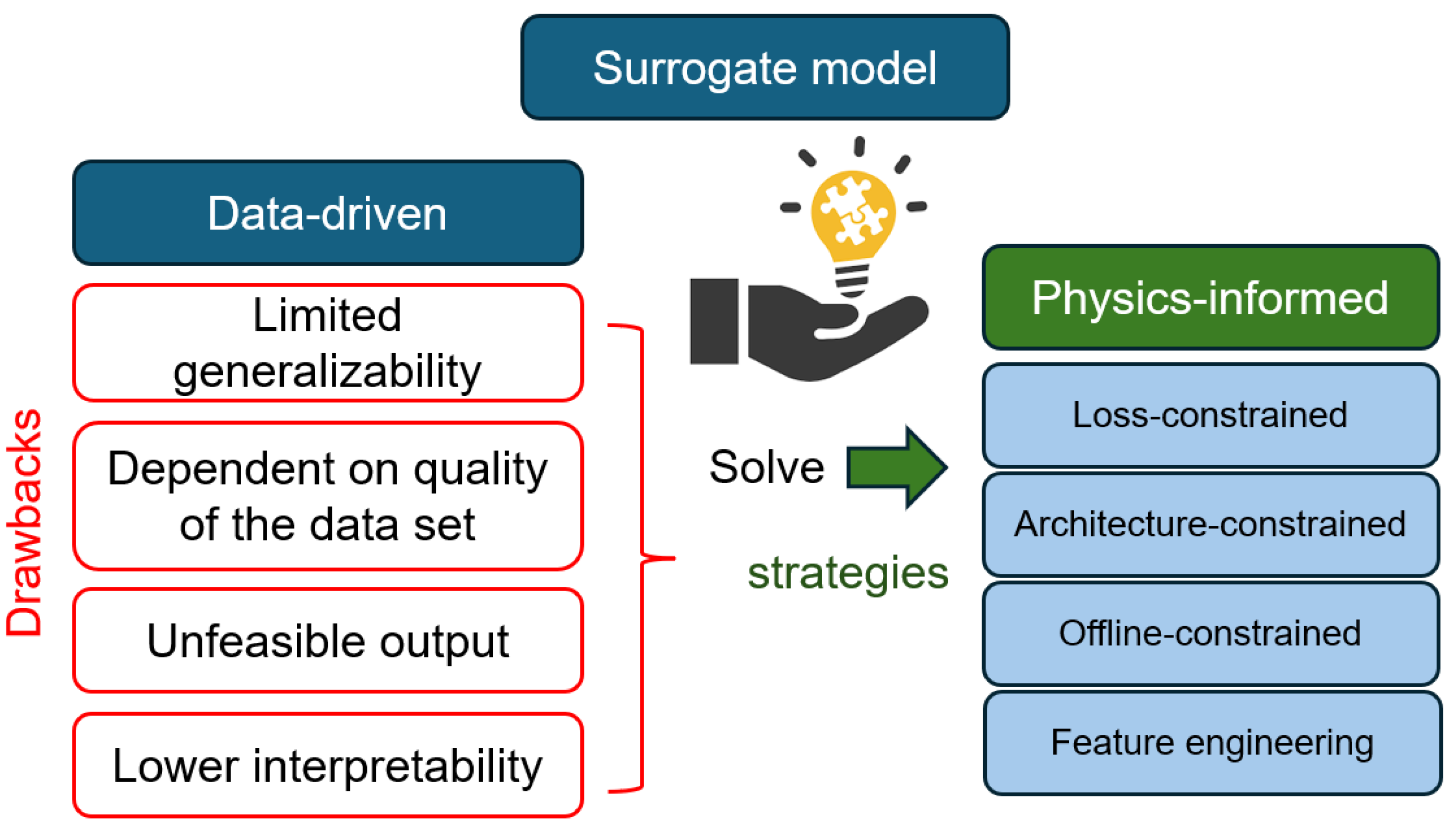
1.3. Data-Driven vs. Physics-Informed Surrogate Models

Traditional surrogate models are fundamentally data-driven, meaning they rely solely on the available training data. The resulting trained model thus provides an empirical correlation without explicitly incorporating physical principles. Such purely data-driven approaches have a long history in FSE. Heskestad’s correlation, for example, is widely used to estimate flame height based on heat release rate and source diameter but is fully empirical [36,37]. While empirical models offer computational efficiency, they often lack the ability to accurately represent complex fire phenomena across a wide range of conditions.

Due to the absence of physical constraints, several critical drawbacks can manifest. Firstly, such models are prone to generating physically implausible predictions, especially when extrapolating beyond the bounds of the training data or when encountering novel scenarios not well-represented in the training set. Secondly, they typically suffer from poor extrapolation capabilities, meaning their accuracy degrades significantly when applied to conditions outside the range of the data they were trained on. This is a major limitation in fire safety engineering, where predicting behaviour in extreme or unforeseen circumstances is crucial. Thirdly, achieving and maintaining accuracy often necessitates extensive and high-quality datasets that adequately cover the relevant parameter space. Acquiring such comprehensive data can be expensive, time-consuming, or even practically infeasible for certain fire scenarios [24,38,39].

A fourth significant challenge for more complex data-driven models, particularly neural networks, is their limited interpretability; without a clear connection to the underlying physical laws, it becomes difficult to assess the reliability and trustworthiness of a model’s predictions, especially in safety-critical scenarios where being sure of the reasonable nature of the prediction is paramount [40].

To tackle the problems faced by conventional data-driven models, physics-informed machine learning (PIML) has been introduced. The architecture and training of these models are specifically designed to encourage or even strictly enforce adherence to the underlying physics governing the problem [23,41]. This integration of physical prior knowledge with available data can lead to improved accuracy, enhanced generalizability, better interpretability, and the potential to work effectively with smaller datasets compared to purely data-driven methods [42,43,44,45,46,47].

Physics-informed surrogate modelling (PISM) is a direct application of PIML whereby the training data is generated by a numerical model [48], as conceptually shown in Figure 3. Within this framework, physics-informed surrogate modelling (PISM) is thus defined as a specific subclass of PIML, based on the source of its training data.

1.4. Strategies for Implementing Physics in Surrogate Models

Different strategies exist for making physics-informed models, and a classification system for physics-integration strategies for PIML has been presented in [49,50]. The following strategies have been identified (visually represented in Figure 4):

• Loss-constrained technique (LCT): These models integrate physical knowledge by introducing physical constraints directly into the training process through the loss function. This is typically achieved by incorporating penalty terms that quantify the violation of known physical laws (e.g., conservation of mass, momentum, and energy, or governing partial differential equations). During training, the model is penalised for making predictions that do not satisfy these constraints. While this approach encourages the model to learn physically consistent solutions, it does not entirely prevent the possibility of non-physical predictions, especially in regions with limited data or complex physics. The strength of the penalty term influences the degree to which the model adheres to the physical constraints.
• Architecture-constrained technique (ACT): This strategy involves embedding physical laws directly into the architecture of the surrogate model. This can be done by designing specific activation functions, network layers, or even entire model structures that inherently respect or align with fundamental physical properties or concepts. As an example, suppose we are modelling the cooling of a steel section at uniform temperature after fire exposure. To ensure that the model respects the basic physics of cooling (i.e., the temperature must decay over time and never increase after the heat source is removed), we could design the model architecture to enforce this by using exponentially decaying functions (e.g., $T\left(t\right)=Tambient+\left(T_{initial}-Tambient\right)·e^{-\lambda t})$ as part of the output layer. This guarantees that predicted temperatures always decay monotonically over time, reflecting the natural cooling behaviour of materials post-fire. This approach offers a strong form of physics integration, as it makes predictions that violate the implemented physical laws mathematically impossible. However, designing such architectures can be complex.
• Offline-constrained technique (OCT): These models apply physical constraints after the surrogate model has been trained, refining predictions during the inference phase. One approach is to perform a “sanity check” to ensure the model’s output falls within physically plausible ranges or adheres to basic physical principles. Another effective strategy involves using the initial output from the trained model as an input to a separate, well-established physical correlation or a set of physical equations. This allows for the imposition of more complex physical relationships on the model’s predictions, generating a new, physically refined output. This, in other words, introduces a physically informed refinement as an additional final step in the predictions by the trained model. This latter approach closely links with the ACT approach to PISM: the architecture of the global surrogate model is split into a data-driven model and a physical model, whereby the former provides input to the latter.
• Feature engineering technique (FET): The variables describing the training data are engineered to align with physical insights, such as non-dimensional parameters. This avoids, for example, non-physical combined effects of parameters within the trained model. This is thus a strategy for incorporating physics in the preprocessing stage.

Figure 5. PRISMA 2020 flow diagram summarising the identification, screening, eligibility assessment, and inclusion of studies in the systematic review on PISM applications in SFE.

Figure 5. PRISMA 2020 flow diagram summarising the identification, screening, eligibility assessment, and inclusion of studies in the systematic review on PISM applications in SFE.

It is necessary to highlight that using a combination of strategies is possible. These strategies and their combinations offer varying balances between flexibility and physical consistency in surrogate modelling.

1.5. Research Scope and Objectives

Despite the growing recognition of PISM in FSE, a comprehensive and systematic synthesis of its diverse applications, methodological approaches to physics integration, and inherent challenges is currently lacking. To address this gap and guide future research and implementation, this systematic review aims to answer the following research questions:

• What are the reported applications of PISM across various domains within FSE?
• What distinct strategies for integrating fundamental physical principles into machine learning models (i.e., feature engineering techniques, loss-constrained techniques, architecture-constrained techniques, and offline-constrained techniques) are employed in PISM studies within FSE?
• What are the current challenges and limitations associated with the development and application of PISM in FSE?
• Based on the synthesis of existing literature, what best practices can be identified, and what stepwise framework can be proposed for the systematic creation of PISMs in FSE?

By systematically addressing these questions, this work seeks to enhance both computational efficiency and physical fidelity in predictive models for FSE, ultimately advancing the field.

2. Materials and Methods

This systematic review was conducted in accordance with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 guidelines [51]. An a priori protocol was developed prior to the review to ensure methodological transparency and consistency throughout the process. The aim of the review was to identify and synthesise current applications of machine learning-based modelling within the domain of FSE, with a particular focus on PISM. The review also sought to categorise the various strategies employed to integrate physical knowledge into machine learning models, and to identify key challenges and best practices observed in the literature.

Studies were eligible for inclusion if they were (i) peer-reviewed primary research articles published in English that (ii) directly applied PISM or physics-informed machine learning (PIML) (iii) within any subdomain of FSE, and (iv) for which full-text articles could be obtained using the Ghent University academic licenses. No publication date restrictions were applied in order to capture the full breadth of the available literature. In the initial screening phase, review articles and purely data-driven modelling approaches without explicit physics integration were also retained in order to obtain a comprehensive view of the state-of-the-art in machine learning applications in FSE.

A comprehensive literature search was carried out from 1 December 2024 to 15 May 2025, across Scopus, ScienceDirect, ResearchGate, Google Scholar, and aRxiv. The search strategy was done considering keyword combinations related to physics-informed modelling, surrogate models, machine learning, and fire safety engineering. The specific search variations of “physics-informed,” “physics-based,” “PIML,” “explainable machine learning”, “Physics-enhanced”, “Scientific machine learning”, and “PISM,” in combination with “surrogate model,” “reduced-order model,” “machine learning,” and “fire safety.” Approximately 220 records were retrieved in total. All references were imported into Mendeley for management, and duplicate entries were removed prior to screening.

In addition to the database search, a snowballing approach was employed to ensure more comprehensive coverage of the literature. This involved both backward snowballing—screening the reference lists of included articles for additional relevant studies—and forward snowballing by reviewing newer publications that cited the included papers using Google Scholar and ResearchGate. This iterative process helped identify studies that may not have been captured through keyword searches alone, particularly those using less standardised terminology or published in interdisciplinary venues.

The screening process was conducted in two stages. First, one reviewer (the first author) screened the titles and abstracts of all retrieved articles against the predefined eligibility criteria. Full-text articles were then reviewed to determine final inclusion (i.e., confirming that the article meets eligibility criteria (ii) and (iii)). In this stage, some of the papers were excluded [52,53]. Studies were organised according to five subcategories of fire safety engineering, as defined in Section 2.1. Any disagreements regarding the inclusion of specific studies were resolved through discussion and consensus with the co-authors.

The study selection process is summarised in the PRISMA 2020 flow diagram (Figure 5), which outlines the number of records retrieved, screened, excluded, and, ultimately, included in the final review. For each included study, detailed information was systematically extracted using a pre-designed data collection form. Extracted data consisted of the fire safety engineering sub-discipline addressed, the specific physics-informed modelling strategy used (including feature engineering, loss-constrained, architecture-constrained, and offline-constrained approaches), the type of machine learning algorithm employed, the underlying physics principles integrated into the model, and the key findings reported. Additional notes were taken on each study’s stated strengths and limitations. Data extraction was carried out by the first author and cross-verified for accuracy by the co-authors.

To assess the methodological quality and reporting transparency of the included studies, a bespoke evaluation checklist was developed and applied independently by two authors. This checklist focused on several core aspects, in particular the clarity with which the physics-informed methodology was described, the robustness of the validation strategy (such as whether physical consistency or cross-validation was performed), and the overall transparency of the modelling process.

As the included studies exhibited considerable heterogeneity in modelling objectives, algorithms, and validation strategies, a narrative synthesis approach was adopted. Consequently, no standardised quantitative effect measures (e.g., risk ratios, mean differences) were used. Instead, outcomes were compared and summarised descriptively based on reported model performance, validation methods, and the nature of physics integration. Studies were grouped according to their corresponding FSE sub-discipline, and further examined based on the physics integration strategy employed. The synthesis aimed to identify recurring application patterns, common benefits and limitations of different approaches, and key methodological considerations. These findings were then used to inform the development of a proposed stepwise framework for constructing physics-informed surrogate models in fire safety engineering, presented in Section 2.1 below.

2.1. Literature Review

2.1.1. Fire Dynamics

Fire dynamics simulations require solving physical equations specifying the conservation of mass, momentum, and energy. High-fidelity approaches, such as computational fluid dynamics (CFD), offer detailed predictions but demand significant computing power and long simulation times [54,55].

Several data-driven machine learning models in the sub-discipline of fire dynamics were identified, most of which make predictions based purely on training data without explicit integration of physical laws. Zhang et al., for example, developed an ML model trained on CFD-generated fire simulations, making it a fully data-driven approach [56]. Other studies developed flashover prediction models, relying on sensor data for learning temporal patterns, without embedding governing fire dynamics. Applied methodologies included long short-term memory (LSTM) networks [57], support vector regression (SVR) [58], and conditional generative adversarial networks (GANs) [59].

As part of the review in the subfield of fire dynamics, PIML studies were identified. FlashNet and xFlashNet are considered as FET [60,61]. The use of maximum operating temperatures of heat detectors is a form of a physical constraint, based on physical limitations, and was considered in this research on the data in the preprocessing phase. To have a more physical model, they used the operational limit of the detectors to cut the data. The integration of this soft constraint can be considered part of the FET strategy [61]. Subsequently, they utilise graph neural networks (GNNs) to capture spatial-temporal fire dynamics [61] to predict flashover within the next 30 s, using data from the CFAST simulator for temperature history at the location of heat detectors.

Lattimer et al.’s reduced-order modelling (ROM) approach projects governing CFD equations into a reduced-dimensional space, preserving fire physics while significantly improving computational efficiency [62]. The results of 220 FDS simulations were used to extract dominant spatial features using proper orthogonal decomposition to replace the full-order model with a small system of ordinary differential equations (ODEs) that can effectively reduce the computational cost while maintaining physics. Subsequently, a fully data-driven neural network-based model (in this case, a full field spatial distribution CNN) was trained to capture the relationship between input (geometry and fire size) and output fire dynamics (temperature and velocity fields). Since the physical link is laid before the model and is not included within the ML; this method is categorised as FET.

Similarly, surrogate modelling with ANN and multiple linear regression (MLR) has been used to specify fire source properties for CFD simulations [63]. Where this combination of a data-driven surrogate and a physical model together acts as a surrogate for a more expensive physical model, the joint surrogate modelling approach can be classified as offline-constrained. In other words, the final calculation step applying a physical model effectively constrains the surrogate model output to physically relevant solutions (as controlled by the physics of the physical model).

Despite these developments, several methodological limitations are apparent. While [61] presents some performance comparisons, they are restricted to accuracy metrics and omit evaluations of physical constraint violations. No standard criteria exist to assess whether predictions adhere to conservation laws or boundary conditions.

Table 1. Physics-informed models in fire simulation.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Fan et al. [61]	Flashover time	Neural network-based	FET	Using a soft constraint on the data by introducing a temperature cut-off to take into consideration the working temperature limit for detectors.
Lattimer et al. [62]	Temperature, velocity fields	Neural network based on CNN	FET	Using ROM as a physical link before on data to reduce the complexity of the problem and keeping the physics at the same time.
Nguyen et al. [63]	Temperature fields, flow fields… (CFD output)	ANN	OCT	A two-step calculation is performed whereby fire source properties generated by a data-driven model are implemented in a physical (CFD) calculation.
Tam et al. [60]	Flashover time	Neural network-based	FET	Using a soft constraint on the data by introducing a temperature cut-off to take into consideration the working temperature limit for detectors.

summarises the identified PISM applications in fire dynamics, listing their model algorithm and the physics-informed techniques used. PIML remains relatively underexplored in this domain, with only a few studies using feature engineering or offline constraints. No studies applying loss-constrained techniques were found, and none explicitly incorporate architectural constraints—both of which offer promising directions for improving model reliability.

2.1.2. Wildfire

Wildfire behaviour is a highly complex phenomenon influenced by multiple interrelated factors, including ignition sources, fuel composition, weather conditions, and topography [64,65]. While physics-based models offer detailed simulations, their high computational costs often limit real-time applications. In contrast, advances in remote sensing and ML have enabled the development of data-driven approaches for wildfire monitoring, detection, and prediction [66,67,68].

One key application of ML in wildfire research is fuel characterisation, where large datasets from satellite imagery are analysed to classify vegetation types and assess fire risk [69,70]. These models predominantly rely on partition-based models, which are well-suited for classification tasks. Similarly, for wildfire detection, ML algorithms process vast amounts of satellite and sensor data to identify active fires in near real-time [71,72]. Neural network-based and decision partition-based models are widely used in this domain [73,74,75,76]. Techniques such as learning without forgetting allow models to retain previously learned features while adapting to new datasets. However, these methods operate purely within a statistical learning framework and do not explicitly incorporate fire physics [77,78].

Another critical application is wildfire spread prediction, where ML models aim to forecast fire progression over time. Data-driven models, such as CNNs, have been used to predict fire spread dynamics through autoregressive processes that stream data from live satellite feeds [79,80,81,82]. These models learn spatio-temporal patterns from past wildfire simulations but do not enforce physical constraints in their architecture or training. Recent research has explored integrating constraints in preprocessing. Shaddy et al. introduced a neural network-based model trained on WRF-SFIRE simulations [83]. A preprocessing step transforms simulated fire arrival time data to mimic satellite measurements; however, this does not constitute FET, as no physical considerations underlie the feature specification. Building on this trajectory, a recent study proposed embedding a physics-based entropy formulation from statistical mechanics directly into the architecture of a neural network, enabling interpretable wildfire risk predictions grounded in physical principles [84]. By designing a custom entropy layer as part of the model’s structure, the authors adopted an architecture-constrained technique that aligns model outputs with theoretical understandings of landscape complexity and fire susceptibility.

In contrast to the above data-driven approaches, physics-informed studies have been gaining some traction.

Table 2. Physics-informed models in the wildfire field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Bottero et al. [85]	Fire spread map	Neural-network based	LCT	Loss terms for residual PDE and initial condition, and boundary condition were included in the total loss calculation for model training.
Latimer et al. [87,88]	Spatiotemporal evolution of fire	Regression-based (ROM, DEIM)	ACT	Mathematically reduced form for solving a complex system
Vogiatzoglou et al. [86]	Spatiotemporal evolution of fire, wind velocity and heat transfer coefficient	Neural-network-based	LCT	A loss function was adopted that penalises deviations from the governing PDEs
Jadouli et al. [84]	Wildfire risk score	Neural-network-based	ACT	The physics-embedded entropy layer uses the Boltzmann–Gibbs entropy equation from statistical mechanics, enabling the architecture to inherently compute a physically meaningful quantity

provides an overview of the identified studies. In this regard, Bottero et al. developed a PINN that couples an atmospheric model with a fire spread model. Extra loss terms were added to the total loss function to guide the neural network towards obeying the physics of the phenomenon (initial condition, boundary conditions and partial differential equation) [85], thus adopting LCT. Their study furthermore replaces relatively slow traditional numerical solvers within the WRF-SFIRE simulation environment with ML models that adhere to physics. This approach is also classified as LCT, considering Section 1.3. However, the model struggles with large domains and multiple ignition points, and numerical instabilities have been reported depending on the training setup. Another LCT study in which physical constraints were embedded directly into the loss function for a PINN has been presented by Vogiatzoglou et al. [86], where a physics-informed neural network (PINN) framework was developed to infer unknown parameters controlling fire propagation, which are typically challenging to quantify in practical scenarios. The model was trained using a hybrid optimisation approach—employing the Adam algorithm in the initial phase, followed by L-BFGS—to address stiffness introduced by additional loss terms. Prior to application to real wildfire data from California, the framework was validated using synthetically generated noisy data.

Lattimer et al. applied their reduced order approach (see Section 2.1.1, [62]) also to wildfire fire spread modelling [87,88]. By deriving reduced-order models from the underlying physical PDEs, they retain physics-based models. The adopted methods introduce a form of architecture constraint technique by defining the model’s structure based on dominant physical modes, thereby improving computational efficiency.

2.1.3. Structural Fire Engineering

In the field of structural fire engineering, several studies have used the data-driven approach. These include models trained to predict the thermo-structural response of timber elements, the fire resistance of compressed steel members, composite shallow floor systems, timber columns, gypsum plasterboard walls, cold-formed steel walls, concrete-filled steel tube columns, and concrete beams and columns [89,90,91,92,93,94].

In addition, several PISM/PIML studies were identified as part of the literature review, as presented in Table 3. Esteghamati et al. [95] used a combination of engineering knowledge, understanding of fire behaviour, and data availability to select the most relevant input features, thus adopting a FET approach to predict the fire resistance of timber columns. Similarly, Wang et al. used FET to predict reinforced concrete column fire resistance [96]. Prior to training the ML model, the authors performed frequency and correlation analyses, identifying influential features based on correlation strength. They also compared their findings to existing formulas. This multi-faceted approach narrowed the feature space to parameters with the strongest statistical relationship to fire resistance. Shan Li et al. developed a model to predict the fire resistance of concrete-encased steel columns [97], adopting both FET and OCT. First, an ANN predicts the equivalent temperatures of the column’s components (steel, concrete, rebar). Features were selected based on a parametric study, a form of FET. Subsequently, to translate these predicted temperatures into fire resistance capacity, they used established engineering relationships between temperature and material strength, i.e., OCT. This offline step acts as a physical link, incorporating domain knowledge without directly influencing the ANN’s training. Thus, while the ANN itself is purely data-driven, the overall surrogate model integrates physics through feature engineering and an offline physical constraint, effectively separating the thermal and mechanical aspects of the problem.

A similar approach to OCT was presented by Li et al., who trained an ANN to predict the equivalent temperature of the steel section for concrete-encased steel composite columns [97]. By implementing the obtained steel temperature in a physical (finite element) model, the final result for the column capacity can be considered an application of OCT.

LCT has also gained significant attention in this field. Bazmara et al. embedded the Euler–Bernoulli beam theory and Hamilton’s principle in the loss function when training a model to predict the structural response of functionally graded beams [98], and Raj et al. proposed a neural network to solve coupled thermo-mechanical problems of functionally graded materials [99]. These authors use the governing PDEs to construct a loss function that guides the neural network’s training, effectively guiding the surrogate model towards complying with the physical constraints of the system. Similarly, Giu et al. introduced an adaptive approach to tackle dynamic coupled problems in functionally graded materials with large-size ratios [100]. They adopted the standard LCT method of embedding PDEs into the loss function and extended this with an adaptive loss balancing algorithm, which dynamically adjusts loss weights during training, enhancing performance for complex geometries. Furthermore, their model employs separate neural networks to represent distinct physical fields (displacement and temperature), effectively incorporating ACT aligned with the system’s structure.

Another application of ACT was presented by Naser et al., who employed causal discovery and inference to evaluate the fire resistance of reinforced concrete columns, moving beyond traditional predictive modelling by focusing on uncovering causal relationships and interventional effects [101]. Notably, the authors incorporated domain knowledge to refine the causal structure generated by the algorithm. By manually adjusting the links between variables based on an established understanding of the fire resistance phenomenon, they effectively introduce an architecture constraint. Harandi et al. [102] also used ACT and LCT as part of their PIML approach. To improve how physics is included in neural networks for complex problems, they used a “mixed formulation” technique, which predicts not only the absolute value of variables of interest (like temperature or movement) but also their rates of change (like heat flow or stress). To achieve this, they designed their network in such a way that separate parts of the network result in each prediction. They also created a special loss function, combining regular and more advanced forms of the physics equations, i.e., adopting LCT. By carefully choosing how the network is built and what physics it learns, they made a system that can solve tough problems without needing a lot of real-world data.

Table 3. Physics-informed models in the structural behaviour field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Esteghamati et al. [95]	Fire resistance of timber columns	Regression-based, partition-based, neural-network-based	FET	Features were selected through data processing and prior knowledge
Giu et al. [100]	Thermo-mechanical response	Neural-network based	LCT, ACT	Embedded physics in loss functions with different networks for different physics.
Harandi et al. [102]	Thermo-mechanical response	Neural-network based	LCT, ACT	A mixed PINN architecture for coupled thermo-mechanical analysis, together with physical loss functions, is used.
Li et al. [97]	Fire resistance of the composite column	Neural-network based	FET OCT	Frequency analysis used for feature selection A physical link for mechanical evaluation is also used
Naser et al. [101]	Fire resistance of the reinforced concrete column	Regression-based (Causal analysis)	ACT	Modifying links between parameters based on prior knowledge and causal analysis
Raj et al. [99]	Thermo-mechanical response	Neural-network based	LCT	Loss functions created to incorporate the thermo-elastic partial differential equation with the degradation of the material
Wang et al. [96]	Fire resistance of the concrete column	Regression-based	FET	Frequency analysis, correlation analysis

Table 3. Physics-informed models in the structural behaviour field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Esteghamati et al. [95]	Fire resistance of timber columns	Regression-based, partition-based, neural-network-based	FET	Features were selected through data processing and prior knowledge
Giu et al. [100]	Thermo-mechanical response	Neural-network based	LCT, ACT	Embedded physics in loss functions with different networks for different physics.
Harandi et al. [102]	Thermo-mechanical response	Neural-network based	LCT, ACT	A mixed PINN architecture for coupled thermo-mechanical analysis, together with physical loss functions, is used.
Li et al. [97]	Fire resistance of the composite column	Neural-network based	FET OCT	Frequency analysis used for feature selection A physical link for mechanical evaluation is also used
Naser et al. [101]	Fire resistance of the reinforced concrete column	Regression-based (Causal analysis)	ACT	Modifying links between parameters based on prior knowledge and causal analysis
Raj et al. [99]	Thermo-mechanical response	Neural-network based	LCT	Loss functions created to incorporate the thermo-elastic partial differential equation with the degradation of the material
Wang et al. [96]	Fire resistance of the concrete column	Regression-based	FET	Frequency analysis, correlation analysis

2.1.4. Material Behaviour

Data-driven ML techniques have been widely used to estimate material behaviour under ambient conditions [103,104,105,106,107]. However, at elevated temperatures, additional degradation mechanisms come into play, complicating predictive modelling due to the nonlinear and irreversible nature of material degradation. Therefore, machine learning has also been extensively applied to assess the performance of materials subjected to high temperatures. Data-driven approaches have been used to evaluate ceramics [108], stainless steel [109,110,111], concrete [112,113,114,115,116,117,118], and fibre-reinforced concrete [119,120,121,122,123].

A subfield of material behaviour at high temperatures that has used ML extensively is fire-induced spalling, which refers to the detachment and ejection of concrete fragments when exposed to extreme heat [124]. This phenomenon results from a highly complex interaction of thermal, mechanical, hygral, and chemical processes, making it challenging to develop a unified predictive framework. Despite extensive research, no single dominant mechanism has been universally identified, largely due to the interdependencies among these processes [125]. Data-driven models for predicting fire-induced spalling have been proposed leveraging large experimental datasets to identify correlations among key factors such as concrete composition, moisture content, heating rate, and applied stress. The adopted approaches include ANN, SVM, and DT [24,126,127,128,129]. Naser et al. demonstrated that specimen size significantly influences pore pressure buildup and stress distribution, leading to inconsistencies when scaling results across datasets [128]. As a result, purely data-driven ML models may struggle to generalise across varying conditions.

The application of physics-informed strategies in high-temperature material modelling remains limited. All identified cases [130,131,132] adopt FET, see

Table 4. Physics-informed paper in the material behaviour field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Liu et al. [131]	Splitting tensile strength of recycled aggregate concrete	Partition-based and regression-based	FET	Using known fracture models (prior knowledge) for feature selection
Onyelowe et al. [132]	Tensile strength of recycled aggregate concrete	Partition-based and regression-based	FET	Key features were determined through prior domain knowledge, and sensitivity analyses were used to reduce features.
Peng et al. [130]	Yield strength of alloys	Regression-based and partition-based	FET	Correlation analysis, maximal information coefficient, and synthetic physically linked features were used

. Specifically, Peng et al. proposed a model capable of predicting the properties of alloys at high temperatures [130]. They translated the raw data taken from the experiment into “synthetic alloy features”. This involved computing crucial microstructure-related properties, such as the volume fractions of key phases and phase transformation temperatures, which directly influence alloy strength. These calculated features, grounded in thermodynamic principles, provided the models with a more physically relevant representation of the material’s behaviour. This was complemented with a correlation analysis to identify the most influential features, using Pearson’s and maximal information coefficients. In the case of [131], prior knowledge of fracture mechanics in concrete—including concepts like fictitious cracks and size effect formulae—was leveraged to identify influential features. Similarly, [132] adopted sensitivity analysis as a crucial preliminary step before model training, ensuring that the most effective features are selected in addition to those identified through prior domain knowledge.

Despite these advances, the use of physics-informed machine learning in high-temperature material degradation remains underdeveloped compared to fields such as fire resistance prediction. The primary challenge presumably lies in the complexity of high-temperature behaviour, which involves irreversible phase transitions, chemical reactions, and microstructural evolution that are difficult to represent through explicit physical constraints. As a result, most existing models continue to rely on data-driven methodologies, which, while effective for pattern recognition, cannot enforce fundamental physical laws within their predictive frameworks.

2.1.5. Heat Transfer

The calculation of heat transfer in FSE is governed by three modes: conduction, convection, and radiation, each described by well-established laws that can be directly incorporated into physics-informed models. The review reveals a strong focus on LCT. By directly embedding fundamental heat transfer equations into the learning process, these approaches demonstrate significant potential to overcome the computational bottlenecks and limitations associated with traditional finite element simulations in fire safety engineering. The identified models are discussed below. A summary is provided in Table 5.

In 2018, Raissi [133] presented an LCT neural network-based model, trained considering a loss function defined by the residuals of different governing equations (initial condition, boundary condition and partial differential equation). Similarly, Sirignano et al. [134] presented another LCT neural network to approximate PDE solutions. Unlike traditional numerical methods, these solvers employ a mesh-free strategy, making them particularly suitable for high-dimensional heat transfer problems (many independent variables—spatial dimensions, time, and possibly other parameters like material properties). Another notable study is the one by Cai et al. [135], which explores a deep learning-based approach to solving heat transfer equations involving forced and mixed convection, as well as radiation. The methodology employs a composite loss function that minimises the residuals of governing PDEs, boundary conditions, and sparse experimental temperature data. As an additional step, they also propose a method to adaptively select the location of sensors to minimise the number of temperature measurements. By leveraging automatic differentiation, the model eliminates discretisation errors, facilitating the resolution of ill-posed inverse problems, such as inferring unknown thermal boundary conditions and tracking dynamic phase interfaces. The direct incorporation of conservation laws within the loss function classifies this approach as LCT. Likewise, a temperature field solver has been proposed by Gao et al., which embeds governing equations directly into the loss term definitions (i.e., LCT) [136].

A more advanced model is presented by Zobeiry et al. [14], combining LCT, ACT, and FET strategies. The loss function was constructed from the heat transfer partial differential equation (PDE) and boundary conditions. In addition, a specific configuration was adopted for the model architecture such that the grouping of neurons aligns with a well-known analytical solution. The activation functions were selected to have second-order derivatives (exponential linear unit, ELU) so that second-order derivatives would remain meaningful. Lastly, feature engineering was employed by introducing input parameters based on heat transfer principles. The integration of these components allowed the model to achieve superior predictive accuracy, outperforming conventional data-driven methods, particularly when extrapolating beyond the training region.

A new way to solve the heat transfer problem has been explored in Koric’s research using a special type of neural network called a Deep Operator Network (DeepONet) [137]. Instead of teaching the network to determine the heat distribution for a single specific heat source, the network was trained to learn the general rule that connects any heat source to its corresponding heat distribution. Koric tested two approaches to training DeepONet. The data-driven approach involved feeding the network a large set of pre-calculated examples of heat sources and their solutions, generated by traditional numerical solvers. In the second approach, the heat equation and thermal boundary conditions were directly embedded into the network’s learning process through LCT. This eliminated the need for a large dataset of pre-calculated solutions.

Table 5. Examples of physics-informed models in the heat transfer field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Cai et al. [135]	Temperature field	Neural network-based	LCT	Using loss terms from physics (from PDE) in combination with a data-driven loss term.
Gao et al. [136]	Pore pressure in the heated porous medium	Neural network-based	ACT LCT	Two coupled networks with loss terms defined by PDEs.
Koric et al. [137]	Temperature field solver	Neural network-based	LCT	Loss terms evaluated divergence from PDEs.
Niaki et al. [138]	Temperature field	Neural network-based	LCT	Loss terms evaluated divergence from PDEs (just convection at the boundary).
Raissi [133]	PDE solver	Neural network-based	LCT	Creating loss terms linked to the residual of the physical equation.
Sirignano et al. [134]	PDE solver	Neural network-based	LCT	Creating loss terms linked to the residual of the physical equation.
Zobeiry et al. [14]	Temperature field	Neural network-based	LCT ACT	Loss terms from PDE. Selecting activation functions and the configuration of the network.

Table 5. Examples of physics-informed models in the heat transfer field.

Article	Output of the Model	Model Algorithm	Physics-Informed Strategy	Implementation of the Physics-Informed Strategy
Cai et al. [135]	Temperature field	Neural network-based	LCT	Using loss terms from physics (from PDE) in combination with a data-driven loss term.
Gao et al. [136]	Pore pressure in the heated porous medium	Neural network-based	ACT LCT	Two coupled networks with loss terms defined by PDEs.
Koric et al. [137]	Temperature field solver	Neural network-based	LCT	Loss terms evaluated divergence from PDEs.
Niaki et al. [138]	Temperature field	Neural network-based	LCT	Loss terms evaluated divergence from PDEs (just convection at the boundary).
Raissi [133]	PDE solver	Neural network-based	LCT	Creating loss terms linked to the residual of the physical equation.
Sirignano et al. [134]	PDE solver	Neural network-based	LCT	Creating loss terms linked to the residual of the physical equation.
Zobeiry et al. [14]	Temperature field	Neural network-based	LCT ACT	Loss terms from PDE. Selecting activation functions and the configuration of the network.

2.2. Discussion and Conclusions

The preceding literature review has explored the expanding field of PISM within fire safety engineering, showcasing its diverse applications across fire dynamics, wildfire behaviour, structural fire engineering, material degradation, and heat transfer. Notably, although there are multiple PISM applications across most fire safety domains, researchers predominantly favour data-driven models, employing them as purely mathematical tools for prediction without explicit incorporation of physical principles. The heat transfer field stands as a notable exception, where physics-informed approaches are increasingly prevalent, thanks to the clearly defined mathematical formulations (PDEs) in this sub-domain, allowing for direct implementation through LCT.

Our observations indicate that the practical application of PISM varies significantly. This highlights the importance of tailoring modelling strategies to the specific characteristics of each problem. We have learned that effective integration of physical principles can enhance model accuracy (as in [97]), but also that challenges persist. This is especially the case in areas where specifying the underlying physics is hard, such as in the field of concrete spalling, where all identified studies so far remain data-driven. Furthermore, the review highlights that adopting a single strategy, particularly feature engineering (FET) and offline-constrained techniques (OCT), does not guarantee a fully physics-compliant model. Combining multiple strategies [14,97,100,136] is therefore recommended. Additionally, PISM models often exhibit more challenging convergence during training compared to purely data-driven models, especially under severe and realistic fire conditions.

A final critical observation is that model limitations, such as physical constraint violations or poor generalisation under extrapolative conditions, are rarely addressed in reported studies. This hampers the ability to identify best practices. Future research should prioritise addressing critical gaps, including uncertainty quantification, data efficiency, multi-physics integration, and explainable AI [40]. The development of standardised validation metrics and open-source libraries will also be crucial. By acknowledging these challenges and building upon the strengths of PISM, the promise of surrogate modelling techniques in FSE can be achieved, creating more reliable and insightful predictive tools with limited computational cost.

3. Implementing Physics-Informed Surrogate Model

Taking into account the taxonomy of Section 1.4 and the literature review of Section 2.1, a framework is presented in this chapter for the creation of PISMs. This stepwise framework is intended to help researchers identify and integrate physical considerations in the different stages of the model creation. The framework builds upon Naser’s general framework for data-driven modelling [23] and the stepwise physics integration approach proposed by Hao et al. [42]. The resulting stepwise strategies align with the four physics-integration strategies (ACT, LCT, FET, OCT) introduced in Section 1.4.

3.1. Framework

A framework for data-driven modelling has been established by Naser [23], outlining essential steps from problem understanding to model tuning. Building upon this framework and the stepwise physics integration approach of [42], a general framework for developing a physics-informed surrogate model (PISM) is presented in Figure 6. The framework recognises that the opportunities for physics integration in ML models vary based on data availability, incorporation strategy, and prior knowledge, resulting in a continuum of physics integration [139].

3.2. Integrating Physics with Surrogate Models

According to Hao et al. [42], physics can be integrated into surrogate models at different levels. These five layers of physics integration (Figure 6) define where and how physics can be embedded in ML models:

• Understanding physics

Before developing a model, a thorough understanding of the physical system is crucial. This involves identifying (i) sub-models and their interaction (series, parallel, coupled), (ii) the relevant physical and engineering constraints (conservation laws, domain-specific rules), as well as (iii) known solution types. Aspect (iii) relates, for example, to situations where analytical results are known for specific cases. This then provides information for consideration in the development of the more general surrogate model. This step establishes the foundation for integrating physics into the model.

2.

Database development (Feature Engineering technique—FET)

Physical principles can be embedded into the training dataset by selecting and refining input features. This can be done based on the problem understanding of Level 1, and can also involve leveraging numerical simulations and sensitivity analysis to identify key parameters that capture physical correlations. This step ensures that only (combinations of) parameters that are known to be physically relevant are taken into account for the model training. Feature engineering furthermore allows to constrain the model output to physically relevant ranges, e.g., by scaling the training data so that all physically relevant results are known to fall within a certain range (such as the range from 0 to 1).

3.

Model selection (Architecture-Constrained technique—ACT)

This level relates to selecting and designing a model architecture that inherently reflects physical considerations. This includes choosing appropriate model types (regression, neural networks) and potentially using multiple networks for different sub-models identified in the problem-understanding stage. This level also includes selecting activation functions that are compatible with the physical constraints (i.e., derivatives).

4.

Objective level (Loss-Constrained technique—LCT)

This level includes designing physics-informed loss functions that incorporate conservation laws and domain-specific constraints. This can involve adding penalty terms to the loss function to enforce adherence to governing equations, ensuring the model’s predictions align with physical principles. The case-specific loss function can also be defined in such a way that bias is purposefully introduced in the surrogate model, pushing the trained model away from errors which are deemed especially unwanted.

5.

Optimiser level

Special attention is required to employ optimisation techniques that can handle the complex loss landscapes introduced by physics-based constraints. This can include using adaptive weighting strategies to balance loss terms and support convergence, preventing any single loss component from dominating the training process.

6.

Inference level (Offline-Constrained technique—OCT)

Post-processing constraints can be applied to maintain physical consistency in predictions (e.g., ensuring non-negative mass loss rates and bounded temperature values). Inference can also leverage precomputed numerical or experimental constraints, refining outputs to align with validated physical models. A different OCT approach is to divide the model architecture into a machine-learning-inspired sub-model that provides input to a physical model. The total model architecture then results in a surrogate model output that is constrained by the physical model.

3.3. Understanding Physics

As illustrated in Figure 7, developing a physics-informed model requires a structured understanding of the underlying physical processes. This involves three key steps: (i) identifying sub-models, (ii) identifying physical and engineering constraints, and (iii) identifying known solution types. The following subsections explain these steps in sequence.

3.3.1. Identifying Sub-Models

A complex physical system can often be decomposed into smaller sub-models, which can be categorised as series models, parallel models, and coupled models, depending on their interactions and dependencies, as elaborated below. Decomposing a system into sub-models provides several advantages. It simplifies complex problems into manageable components, enables targeted physics integration within each sub-model, improves the modularity and interpretability of the overall PISM, and allows for the application of different modelling techniques best suited to each sub-problem. By systematically identifying sub-models, it becomes easier to ensure physical consistency, enhance computational efficiency, and improve predictive accuracy.

Series models consist of sequentially dependent components, where the output of one model serves as the input for the next (see Figure 8). In fire safety engineering, for instance, multiple sub-models describe the progression from ignition to structural performance, including ignition, fire development, heat transfer, material degradation, and structural response. Each of these processes directly influences the next in a chain of dependencies, and this chain of dependencies can be adopted as part of the overall model architecture when developing the surrogate model. Thus, in fire safety assessments, thermal models are often used to inform mechanical models that evaluate structural integrity under fire conditions, as in [97].

Parallel models describe distinct behaviours within the same system (see Figure 8). These distinct behaviours imply that a single model may struggle to generalise across both behaviours. Both behaviours may also be distinct with regard to their influencing parameters (which is important for the feature selection discussed below). Thus, the use of separate surrogate models for each behavioural region may be beneficial. This approach has been applied, for example, by Giu et al., whose model for the thermo-mechanical behaviour of functionally graded materials employs separate neural networks to represent distinct physical fields (displacement and temperature) [100] into their model.

Coupled models interact dynamically rather than operating strictly in series or parallel. Recognising these interactions is crucial for integrating physics into machine learning models. One notable example is atmospheric-wildfire coupled models, where capturing the interaction between atmospheric dynamics and wildfire progression was essential for accurate modelling [85]. Similarly, coupled structural failure mechanisms may require joint modelling to account for interdependencies. Integrating such physical interactions can be done as part of the model architecture, as is explained further in Section 3.4.2.

3.3.2. Identifying Physical Constraints

Before incorporating physical constraints into a model, they must first be systematically identified. Fundamental conservation laws—mass, energy, and momentum—are universally applicable and serve as the foundation for numerous physical principles. Therefore, an initial step in defining constraints is to assess whether conservation laws can effectively regulate the model. Other physical constraints can be identified from governing laws, such as the fundamental equations within heat transfer (conduction, convection and radiation), fluid mechanics considerations (e.g., Navier–Stokes equations), and structural engineering concepts such as thermal expansion.

Although such physical laws do not always provide direct parametric correlations, they can provide constraints for the data-driven models. For instance, when predicting temperature distribution in a concrete wall exposed to fire, enforcing the conservation of energy through a heat conduction PDE-based loss function ensures that the predicted temperature field adheres to fundamental thermodynamic laws [102].

Beyond fundamental laws, domain-specific constraints can also play a critical role. These arise from expert knowledge and physical expectations of system behaviour. For example, in a fire protection scenario, the maximum temperature of a protected steel element must not exceed the maximum temperature of the fire itself. Such constraints introduce explicit parameter relationships that can be integrated into machine learning models through different approaches. They may be enforced via penalty terms in the loss function (LCT) as in [99], incorporated as a verification step in offline model validation (OCT) as in [97], or directly embedded within the model architecture to enforce predefined correlations (ACT) as in [101].

3.3.3. Identifying Known Solution Types

In certain cases, analytical or semi-analytical solutions are available for specific scenarios within the broader problem domain. Identifying these known solution types is critical, as they can provide valuable benchmarks or guide the development of the surrogate model. For instance, closed-form solutions derived from simplified assumptions, such as steady-state heat conduction in one dimension, offer exact reference points that any predictive model should reproduce under equivalent conditions. Incorporating such solutions during training, validation, or loss function design can significantly enhance the model.

3.4. Injecting Physics into Models

A comprehensive physics-integrated model incorporates multiple physics-informed techniques at various stages of development. The conceptual framework, illustrated in Figure 9, outlines a structured approach where physics is injected at different levels to enhance model reliability and interpretability. The process begins with feature engineering (FET), where data are refined and preprocessed to incorporate meaningful physical relationships. Subsequently, the model architecture is designed to inherently respect fundamental physical constraints (i.e., ACT). The loss function is then formulated to enforce governing physical laws, providing incentives for the trained model to align with these physical considerations, i.e., LCT. Finally, a post-processing physical link is introduced to validate the outputs (OCT), either through additional verification steps or by correlating predictions with physically constrained quantities.

The effectiveness of integrating multiple physics-based techniques depends on the specific problem and the governing physical principles. The techniques can be classified into two broad categories: core model integration and external physical links [139,140]. The first category embeds physics directly within the model, and includes LCT and ACT. The second category consists of pre- and post-processing techniques that establish external physics-based connections, and includes FET and OCT. The following sections provide a detailed exploration of each method, adopting the framework structure of Figure 6 and Section 3.2.

3.4.1. Database Development (Feature Engineering Technique—FET)

The first step in developing a physics-informed surrogate model (PISM) is the construction of a database and the identification of relevant input features. This process begins by identifying a broad set of potential influencing factors, which are then refined to retain only the most significant ones. A thorough understanding of the governing physics, as established in previous sections, is essential in selecting these parameters. In cases where multiple interdependent parameters influence the response, dimensionality reduction techniques, such as principal component analysis (PCA), can help isolate dominant parameter combinations governing the output, as adopted in [130]. Where combinations of parameters are known to act together, they can be implemented as a single feature for model training, as in [132].

To identify meaningful features from high-fidelity numerical models, parameter studies can be conducted. This involves individually varying selected features and assessing their correlation with the predicted outcomes. The strength and nature of these relationships—whether positive, negative, or nonlinear—can be evaluated using a combination of visual, statistical, and expert-driven approaches.

• Visual Analysis: Plotting output values as a function of each input parameter allows for an intuitive assessment of trends (for example, in [96]).
• Statistical Analysis: Quantitative measures, such as Pearson correlation coefficients (PCCs) [141] for linear dependencies and maximal information coefficient (MIC) [142] for nonlinear correlations, can help determine parameter significance. Advanced techniques, such as partial dependence plots or feature importance rankings from tree-based models, provide additional insight.
• Expert Judgment: Domain expertise is incorporated to assess the practical significance of observed sensitivities.

For example, Peng et al. [130] applied a combination of PCC and MIC to rank input features for predicting the tensile strength of alloys. Similarly, Onyelowe et al. [132] employed Hoffman and Gardner’s sensitivity index to evaluate key features for developing their PIML model for the tensile strength of recycled concrete. Zaker Esteghamati et al. used simplified structural mechanics models for their sensitivity analysis to reveal that section dimensions and fire exposure time are among the most critical parameters, guiding their inclusion in the final surrogate model [95]. Wang et al. [96] followed a similar methodology, selecting features based on governing physics and empirical equations before performing frequency-based and single-parameter analysis to detect both linear and higher-order correlations.

3.4.2. Model Selection (Architecture-Constrained Technique—ACT)

As mentioned in Section 1.2, the surrogate model is a mathematical tool which relates features to the outputs. This algorithm can be as simple as linear regression or as complex as a network of complex functions. Selecting an appropriate model or algorithm is a crucial step in developing a PISM and should be done taking into account the identified sub-models and constraints (see Section 3.3). Where distinct series models have been identified, implementing a series architecture as part of the surrogate model setup is recommended, as it greatly supports interpretability and quality control. The same applies to other types of identified sub-models and constraints.

The choice of model algorithm (e.g., regression, neural network, …) depends on the system’s complexity, available data, and the necessary balance between interpretability and predictive accuracy. In fire safety engineering, interpretability, transparency, and feasibility are highly valued. White-box models, such as regression-based approaches, offer explicit mathematical formulations, making them preferable when the underlying physics is relatively well understood and can be represented with simpler functional relationships. In the following, different model algorithms are discussed to help readers choose the ones which are more suited to their application, with examples.

Regression-Based Models

When using a regression-based approach, different functional forms can be employed based on the nature of the relationship between inputs and outputs. Exponential functions are well-suited for modelling growth or decay processes, while harmonic functions capture periodic phenomena, such as vibrational responses in mechanical systems. Choosing a function aligned with known physical behaviour ensures more realistic and physically consistent predictions [101].

It is also possible to inherently enforce physical constraints through the choice of regression functions, such as the sigmoid function, which is particularly useful when outputs must remain within a bounded range (see Equation (1)). In applications like temperature prediction, where physical laws define permissible output limits, the basic sigmoid function—naturally restricting values between 0 and 1—can be applied to constrain predictions within realistic temperature ranges [143].

Equation (1). Sigmoid function

$$0<f(h\left(x\right))={\displaystyle \frac{1}{1+e^{-h\left(x\right)}}}<1$$

(1)

with

• x: the feature vector
• h(.): the regression function

Neural Networks-Based Models

Different neural network-based models have been combined with physical considerations, as highlighted in the literature review in Section 2.1. Physics-informed neural networks (PINNs) are well-suited for problems governed by known PDEs, integrating PDE residuals into the loss function to enforce physical constraints. Using standard feed-forward architectures, they minimise both data mismatch and PDE violations, making them effective in heat transfer, fluid dynamics, and structural mechanics. Convolutional neural networks (CNNs) excel in processing image-based data, including thermal and satellite imagery for fire detection. They enhance feature extraction and pattern recognition [79]. Example applications are in Section 2.1.2. Graph neural networks (GNNs) are ideal for fire safety problems involving graph-structured data, such as fire spread modelling in buildings or wildfire propagation across spatial grids [82]. GNNs capture spatial dependencies through graph convolution operations that respect physical principles.

Irrespective of the type of neural network, the architecture of the network significantly impacts its performance and ability to capture physical behaviour. Several key factors must be considered when designing a neural network for a physics-informed surrogate model, the most important of which are (i) sub-models (i.e., number of networks); (ii) number of neurons and hidden layers; and (iii) activation functions.

Firstly, the number of networks is important when multiple sub-models have been identified as part of the problem understanding (see Section 3.3.1). In such a case, it is recommended to train a different network for each of these sub-models. This has been done, for example, in [100,136], where parallel models were used for thermo-mechanical modelling and concrete spalling evaluations, and in [85], where coupled models were used for wildfire modelling (see Section 3.3.1). Secondly, the number of neurons per layer and the number of hidden layers determine the network’s capacity to learn complex relationships. A deeper network (more layers) with more neurons can capture highly nonlinear interactions but may require careful regularisation to prevent overfitting. This does not directly contribute to integrating physics into the model; however, it is nevertheless also from a PISM perspective recommendable to align the complexity of the neural network with the complexity of the underlying physical model. Lastly, the choice of activation functions plays a particularly important role in PINNs. In cases where the loss function depends on higher-order derivatives of the output, the activation function should be capable of producing meaningful higher-order derivatives. For example, in heat transfer analysis using PINNs, a linear activation function is not recommended because it would fail to generate the required derivatives for additional loss terms associated with PDE constraints for conduction [14]. On the other hand, using simpler activation functions in neural networks improves computational efficiency, prevents vanishing/exploding gradients, and ensures better gradient flow for stable training. Functions like ReLU are preferred as they enable faster optimisation and reduce the risk of overfitting compared to complex, saturating functions like sigmoid or hyperbolic tangent [144].

Another way to embed physical constraints in neural networks is through the network architecture itself. A recent study implemented an architecture-constrained technique by introducing a custom entropy-based layer derived from principles of statistical mechanics into the neural network structure [84]. Specifically, the authors designed a differentiable entropy layer that computes Shannon entropy over spatial vegetation patterns, capturing landscape complexity associated with wildfire risk. This entropy measure was not used as a post-processing tool or loss term, but rather as an internal part of the model’s forward pass, influencing subsequent predictions.

3.4.3. Objective Level (Loss-Constrained Techniques—LCT)

The objective layer defines the optimisation criteria of a model. This section first describes the formulation of a purely data-driven objective and then introduces physics-informed loss functions to highlight the distinction.

Data-Driven Objective

In a conventional data-driven model, the objective is to minimise the error between predicted and actual values for the training dataset. The most common loss functions include Mean Squared Error (MSE) and Mean Absolute Error (MAE). MSE penalises large deviations more heavily, making it suitable for cases where significant errors must be minimised. In contrast, MAE is more robust to noise and outliers, making it advantageous for models incorporating experimental data [26]. A hybrid alternative, referred to as Huber loss, combines MSE for large deviations and MAE for small deviations, offering a balance between robustness and precision [145].

Beyond standard loss functions, regularisation techniques enhance model stability and generalizability. L1 regularisation (Lasso) [146] promotes sparsity by reducing the impact of less significant coefficients, while L2 regularisation (Ridge) [147] discourages large parameter values, mitigating overfitting. These techniques are particularly valuable in physics-based surrogate models, where model interpretability and generalisation to unseen data are crucial.

Physics-Informed Objective (Loss-Constrained Technique—LCT)

Physics-informed objectives integrate known physical relationships into the loss function, ensuring model predictions adhere to fundamental laws. This is achieved by introducing penalty terms that constrain deviations from governing equations, such as partial differential equations (PDEs), boundary conditions, and initial conditions.

For instance, in heat conduction analysis, the governing equation is given by Equation (2). To enforce adherence to this equation, the model’s predicted temperature field T(x,t) can be substituted into the equation, and the obtained residual (i.e., the resulting deviation from the theoretical equation) can be added to the loss function, as in Equation (3). Similarly, separate loss functions can be designed to explicitly handle boundary and initial conditions, ensuring physically meaningful outputs throughout the domain. This approach pushes the model to remain physically consistent while being trained. Similar approaches can be applied in fluid dynamics and structural mechanics, where higher-order derivatives of solutions are used to enforce smoothness and stability [41,134]. Physics-informed neural networks (PINNs) leverage such constraints, incorporating conservation laws within the learning process [14,44,134,135,137,138,148,149]. For more complex problems, additional constraints such as pore pressure buildup within concrete under high temperatures can be modelled by enforcing the conservation of mass and energy within a porous medium [136].

Equation (2). Heat conduction equation

$${\displaystyle \frac{\mathit{\partial }T}{\mathit{\partial }t}}=\alpha ·{\nabla }^{2}T$$

(2)

Equation (3). Loss term for heat conduction

$${Loss}_{PDE}=\left|{\displaystyle \frac{\mathit{\partial }T}{\mathit{\partial }t}}-\alpha ·{\nabla }^{2}T\right|$$

(3)

In cases where enforcing strict PDE constraints is not a primary objective, soft constraints can be applied. Instead of directly penalising deviations from physical equations, a weighted combination of data-driven and physics-based loss terms can be used. A penalty multiplier adjusts the relative importance of each term, allowing flexibility in how strictly physical laws are enforced [14].

3.4.4. Optimiser Level

Integrating physical constraints into machine learning models presents significant optimisation challenges [150,151]. In PISMs, the total loss function is typically a weighted sum of multiple physics-informed loss components, i.e., Equation (4), where ${\omega }_i$ represents the weight assigned to each loss term. The presence of physics-based loss terms often leads to highly complex loss landscapes, affecting convergence efficiency. As a result, optimisation becomes the primary bottleneck in training PISM models. One of the primary difficulties in physics-informed optimisation is the imbalance in loss magnitudes.

Equation (4). Total loss

$${Loss}_{total}={\omega }_1·{Loss}_1+\cdots +{\omega }_n·{Loss}_n$$

(4)

with:

• ${Loss}_{total}:$ Loss function on which model is trained.
• ${\omega }_i·{Loss}_i:$ Weighted loss function for each physics-informed loss component.

A naive approach for the loss function of Equation (4) is to set fixed weights; however, different loss components often have vastly different magnitudes. For example, PDE residuals may be orders of magnitude smaller than data loss, causing the optimiser to focus disproportionately on minimising data error while neglecting physical constraints. This imbalance can result in overfitting to data while violating fundamental physics. To address this issue, adaptive weighting techniques dynamically adjust loss term weights during training. Several approaches have been proposed [152]:

• Gradient-Based Reweighting: The model rescales loss weights based on the magnitude of their gradients, ensuring that all terms contribute equally to optimisation [153].
• Uncertainty-Based Weighting: Weights are adjusted according to the confidence or uncertainty in each term, giving lower weights to noisier loss components [100,154].
• Multi-Objective Optimisation: Reformulating training as a multi-objective problem allows for an automatic trade-off between competing loss components [155,156].
• Gradient Normalisation: Rescales gradients to balance optimisation across all terms, preventing any single loss component from dominating [157].
• Hybrid training scheme: It is based on an initial first-order optimisation like ADAM, followed by a second-order optimisation [86].

3.4.5. Inference Level (Offline-Constrained Techniques—OCT)

Post-processing techniques play a crucial role in refining model outputs after training, allowing to ensure adherence to established scientific principles and maintaining physical consistency. The effectiveness of this approach depends on an initial understanding of the underlying physics, as discussed in Section 3.3. In certain cases, particularly for identified series models, a final physics-based computation can remain external to the model, provided that its computational cost is not prohibitive.

A well-documented example of offline-constrained techniques can be found in weather forecasting. Researchers have employed machine learning models, such as neural networks, to predict meteorological variables like temperature and humidity. However, to maintain physical realism, additional post-processing adjustments using established physical laws—such as the ideal gas law and the Clausius–Clapeyron equation—are applied. These corrections, performed separately from the training phase, ensure that predictions remain consistent with fundamental scientific principles [49].

The utility of offline-constrained techniques is particularly evident in fields where multiple modelling approaches need to be integrated, such as fire safety engineering. A basic application involves predicting the structural performance of simply supported fire-exposed beams, as in [12]. Here, a machine learning model first estimates the peak temperature of embedded steel reinforcement bars. This output is then used as an input for a physics-based calculation, such as a sectional analysis, to determine the beam’s moment capacity under fire conditions. This two-stage process guarantees that the final structural performance assessment aligns with established physical laws, even if the initial machine learning model does not explicitly incorporate physical constraints. Similarly, Li et al. [97] proposed an approach where the temperature of a steel column, predicted by a machine learning model, is linked to its load-bearing capacity through a physical equation. Nguyen et al. [63] presented a model that predicts fire source properties, which can then be used in a physics-based model to estimate fire-induced temperature distributions.

There are, however, limits to what can be achieved with OCT. Since corrections occur after training, the model may still learn non-physical relationships. The post-processing can only provide superficial adjustments rather than fundamentally improving model behaviour. Moreover, post-processing cannot practically be used to enforce complex physical principles, particularly PDEs and multi-physics interactions. Without embedding these physical constraints as part of the model training, the model lacks inherent physics awareness, which cannot be resolved through OCT. For problems requiring strict adherence to governing laws, integrating physics directly into the learning process is thus essential.

4. Challenges and Future Directions

The literature review of Section 2 has shown that PISM is gaining traction within FSE, but that large unexplored areas remain. Crucially, the currently best approach to incorporating physics into surrogate modelling tools is a multi-level approach whereby physical considerations are implemented from the level of the data, through the levels of the model architecture and objective functions, up to the level of inference (see Figure 9). It is strongly recommended that future studies in FSE adopt this multi-level approach from the get-go.

Even when adopting a structured approach, however, PISMs frequently encounter challenges such as slow convergence rates and suboptimal minima (incomplete convergence) [41]. These difficulties stem from the added complexity of incorporating physics-based constraints into the loss function, which can create an intricate optimisation landscape. Given that one of the key advantages of surrogate modelling is computational efficiency, the added cost of physics-informed constraints must be carefully weighed against the benefits. The choice between a purely data-driven approach and a physics-informed surrogate thus depends on several factors, including the availability of training data, computational efficiency, and the necessity of enforcing physical constraints. If large, high-quality datasets are available, a data-driven model may be sufficient [29], possibly extended with cheap offline constraints for the model predictions. Conversely, when adherence to physical laws is critical, a physics-informed model remains the more reliable choice despite its computational demands.

PINNs, in particular, struggle with imbalanced loss terms, as different constraints may exhibit varying convergence speeds. To address this, researchers have implemented learning rate annealing methods inspired by traditional multi-task learning [158]. Additionally, optimising the placement of collocation points—by concentrating them in regions with high residual errors—has been found to significantly improve training performance [159]. Loss reweighting strategies have also been explored, including inverse Dirichlet weighting [160], characteristic quantity-based weighting [52,153], and meta-learning approaches that dynamically update loss functions during training [161]. Lastly, gradient-enhanced methods have shown promise in stabilising training by incorporating derivative information, particularly in high-order systems [162].

Engineering applications often involve high-dimensional and multi-scale problems, which present unique challenges for surrogate modelling [41,163]. As the number of input parameters increases, traditional models struggle with the “curse of dimensionality”, leading to reduced generalisation capabilities and computational inefficiencies. Additionally, in multi-scale problems, fine-scale variations can significantly influence large-scale behaviour, making accurate modelling more complex.

To enhance training efficiency and overcome optimisation challenges, researchers have proposed various strategies. Adaptive activation functions offer a promising solution by aligning activation function behaviour with the underlying physics of the problem. For instance, in harmonic motion modelling, sinusoidal activation functions facilitate faster convergence by naturally capturing the system’s behaviour [164]. Importance sampling techniques further improve computational efficiency by prioritising regions of the solution space where accuracy is most crucial [165]. Another key approach to improving learning efficiency is data resampling, where collocation points are adaptively sampled to correct imbalances in training data. Representative methods include the Sobol sequence [166] and Latin hypercube sampling [53]. Multi-view transfer learning has also been introduced as a technique to enhance generalisation by leveraging insights from related problems [167,168,169].

Recent studies have demonstrated that second-order optimisation strategies significantly improve both convergence speed and generalisation accuracy in PINNs, particularly for solving complex partial differential equations (PDEs) [170,171]. Compared to widely used first-order optimisers such as ADAM, these methods are reported to improve performance by orders of magnitude. Among second-order methods, quasi-Newton approaches have shown particular effectiveness in accelerating training by reducing the number of iterations required for convergence and enhancing numerical stability, especially when dealing with stiff PDEs and multiple loss terms [171]. Use of a hybrid training scheme ([86]) is stated to help both in computational cost and in solving the rigidity of loss terms.

Implementing these and other novel techniques within FSE presents major challenges and may complicate the peer review process within the discipline. To build trust in newly proposed tools and ensure their physical consistency, a discipline-level approach to quality control is essential. Although a wide range of performance and error metrics exist in ML [172], traditional statistical metrics alone are insufficient for physics-informed surrogate models [173]. Model evaluation must also explicitly assess violations of physical constraints, such as residuals of governing equations and boundary condition errors, to confirm that predictions align with underlying physics. One promising strategy involves establishing discipline-level reference models and standardised lists of recognised physical constraints, enabling objective validation—and potentially certification—of surrogate models. Concurrently, the development of standardised validation metrics and open-source frameworks will be crucial to enhance model credibility and support broader adoption and iterative refinement of PIML techniques.

5. Conclusions

This study systematically reviewed the state-of-the-art of PISMs in FSE. By embedding fundamental physical principles—such as conservation laws, heat transfer equations, and material degradation mechanisms—into machine learning frameworks, PISMs improve predictive accuracy, interpretability, and reliability. Case studies spanning fire dynamics, wildfire, structural fire engineering, material behaviour, and heat transfer illustrate the diverse applications and advantages of this methodology.

Four distinct strategies for integrating physics into machine learning models have been identified:

• Feature Engineering Technique (FET): Incorporates physics-based variables and transformations into the dataset before training.
• Loss-Constrained Technique (LCT): Embeds physics-based constraints directly into the loss function to guide optimisation.
• Architecture-Constrained Technique (ACT): Modifies the neural network structure to enforce physical constraints (e.g., sub-models, and activation functions for bounded outputs).
• Offline-Constrained Technique (OCT): Applies physics-based corrections in post-processing, refining model predictions after training.

Each approach presents trade-offs between accuracy, computational cost, and physical fidelity. It is important to recognise that different techniques incorporate physics to varying degrees. When carefully designed, architectural constrained techniques (ACTs) and loss-constrained techniques (LCTs) can strictly enforce certain physical laws, ensuring that model outputs remain consistent with the governing physics. Combining multiple strategies often leads to better performance and greater efficiency than relying on a single method. To systematically integrate these techniques, a stepwise framework for building PISM is proposed. This framework outlines how and when each method can be introduced during the modelling process to enhance both physical realism and computational performance.

Despite these advancements, challenges remain. PISMs often face convergence difficulties, particularly under highly nonlinear conditions (such as fire), and many studies overlook critical aspects such as uncertainty quantification, data efficiency, and multi-physics integration. Future research should focus on addressing these limitations and developing standardised validation metrics to enhance model credibility. Open-source frameworks will also be crucial in promoting wider adoption and refinement of PIML techniques.

Ultimately, the choice between purely data-driven and physics-informed approaches depends on data availability, computational constraints, and the risks associated with unphysical predictions. In safety-critical applications such as fire engineering, where physically inconsistent predictions can have severe consequences, physics-informed models are indispensable. By refining physics integration techniques and expanding their application, researchers and engineers can develop more reliable and actionable predictive tools for fire safety optimisation, risk assessment, and design.