A Logarithmic Transfer Function for Binary Swarm Intelligence Algorithms: Enhanced Feature Selection with White Shark Optimizer

Abstract

With the increasing size of datasets in data mining applications, feature selection has become critical for enhancing classification accuracy and reducing computational complexity. In this study, a novel binary feature selection algorithm, called bWSO-log, is proposed based on the White Shark Optimizer (WSO). Unlike the commonly used S-shaped and V-shaped transfer functions in the literature, the WSO algorithm is converted into a binary form for the first time using a logarithmic transfer function. The performance of the proposed method was tested on nineteen benchmark datasets and compared with eight widely used metaheuristic algorithms. The results show that the bWSO-log algorithm demonstrates superior or competitive performance in terms of classification accuracy and the number of selected features. These findings reveal the effectiveness of the proposed logarithmic function and highlight the potential of WSO-based binary optimization in feature selection problems.

1. Introduction

With the widespread use of the internet today, there has been a significant increase in the size of emerging datasets. The rapid growth of datasets leads to challenges such as difficulties in extracting relevant information from real-world applications, increased processing time, hardware limitations, and higher computational complexity. Therefore, feature selection methods, which hold an important place in data mining, are gaining importance [1]. Feature selection methods aim to identify relevant features prior to training models on real-world datasets containing many features. Relevant features are those directly related to the target concept and are neither irrelevant nor redundant; irrelevant features do not affect the target concept, whereas redundant features contain duplicate or unnecessary information [2]. Given a dataset with N features, there exist possible subsets. As the number of features increases, the search space grows exponentially, making it increasingly challenging to find the optimal subset. Therefore, removing unnecessary features reduces both training time and memory requirements during model training [2]. Moreover, reducing the dataset size facilitates simpler representation, visualization, and interpretation of the data [3]. In line with the advantages offered by feature selection methods, various techniques have been developed in the literature. These methods are generally classified into three main categories: filter methods, wrapper methods, and hybrid methods [4].

Filter methods operate independently of the learning algorithm; data are scored based on statistical criteria, and feature selection is performed according to these scores [5]. These methods are generally faster than wrapper methods. However, due to uncertainties in determining the threshold that distinguishes between relevant and irrelevant features, filter methods are often considered less effective and less successful compared to wrapper methods [3].

Wrapper methods comprise feature evaluation criterion, a search strategy, and a stopping criterion. Unlike filter methods, wrapper models use the performance of the learning algorithm as the evaluation metric and select the subset of features that achieves the best performance [6]. Wrapper methods can be categorized into three main groups based on their feature search strategies: sequential, bio-inspired, and iterative methods. Sequential search methods are easy to implement and fast. Bio-inspired methods incorporate randomness into the search process to avoid getting trapped in local minima, while iterative methods aim to avoid combinatorial search [4].

Hybrid methods have been developed to overcome the disadvantages of filter and wrapper methods. These approaches incorporate both a feature selection algorithm and a classification algorithm, and perform both processes simultaneously [7].

Feature selection methods aim to determine which features should be selected from a dataset. The resulting solutions take binary values of 0 or 1, indicating whether each feature is excluded or included. In order to obtain an exact solution, all possible subsets must be evaluated; however, this significantly increases the computational cost. As the size of datasets increases, the use of heuristic methods to achieve an optimal solution has become increasingly common [8]. Continuous versions of optimization algorithms need to be discretized in order to be applied to decision problems. Numerous discretization methods have been proposed in the literature for this purpose. By developing a reupdate rule as in discrete Jaya algorithm (DJAYA) [9] algorithm, using XOR method as in Jaya-based binary optimization algorithm (JAYAX) [10] or using transfer functions [11,12], discrete versions of these algorithms have been developed. Although these algorithms do not always guarantee the best solution, they can produce acceptable solutions within a reasonable time. Despite the existence of many optimization methods in the literature, researchers continue to develop new approaches specifically for feature selection problems due to unresolved issues such as getting stuck in local minima and premature convergence [11].

The WSO is an optimization method inspired by the hunting behavior of white sharks [13]. Developed in 2022, the WSO algorithm is designed for solving continuous optimization problems. It is recommended for further development due to its applicability to high-dimensional engineering problems and its ability to produce fast and accurate solutions [13].

Motivation and Contribution of the Study

The increasing size and complexity of real-world data have made feature selection a critical step in data mining and machine learning processes. As the number of features grows, the search space required to identify the optimal subset expands exponentially; this situation increases computational complexity and adversely affects model performance. Therefore, developing efficient and scalable feature selection methods is of great importance.

Although many metaheuristic algorithms have been proposed for feature selection, most of these algorithms face challenges such as premature convergence, imbalance between exploration and exploitation, or insufficient adaptation to binary search spaces. The WSO, originally developed for continuous problem domains, has strong exploration capabilities and, inspired by the predatory behavior of sharks, provides a promising foundation for binary optimization problems.

In this study, to overcome the aforementioned limitations and leverage WSO’s potential in binary problem domains, a binary version of WSO (bWSO) specifically adapted for feature selection tasks is proposed. The contributions of this study to the literature can be summarized as follows:

• A novel logarithmic transfer function offering a flexible and adaptive mechanism for converting continuous values into binary decisions is proposed.
• The original WSO algorithm is adapted to binary problem solving by incorporating the proposed logarithmic transfer function along with eight other commonly used transfer functions, resulting in the bWSO algorithm.
• The performance of the bWSO-log algorithm is evaluated on nineteen benchmark datasets, and it is observed to outperform other well-known metaheuristic algorithms in the context of feature selection.
• In terms of classification accuracy, the algorithm is comprehensively compared with Artificial Algae Algorithm (AAA) [11], Bat Optimization Algorithm (BAT) [14], Firefly Algorithm (FA) [15], Grey Wolf Optimizer (GWO) [16], Moth Flame Optimizer (MFO) [17], Multi-Verse Optimizer (MVO) [18], Particle Swarm Optimization (PSO) [19], and Whale Optimization Algorithm (WOA) [20]
• A simple yet effective feature selection framework combining WSO’s powerful search mechanism with adaptive discretization techniques is presented.

The remaining sections of the paper are organized as follows: Section 2 provides a brief overview of related work. Section 3 introduces the original WSO algorithm. The details of the proposed bWSO approach are presented in Section 4. Section 5 describes the experimental setup. Section 6 presents the results along with a discussion, while Section 7 offers conclusions and suggestions for future work.

2. Related Works

Swarm intelligence-based metaheuristic optimization algorithms have recently been widely used not only for solving continuous-valued problems but also for addressing feature selection problems effectively [21]. This section examines feature selection approaches based on swarm intelligence optimization algorithms.

Various methods have been employed to discretize swarm intelligence-based optimization algorithms. These methods include [8,10], threshold-based transformation approaches [22], transfer functions [9,23,24], entropy-based methods [25], similarity-based approaches [26,27], and hybrid methods [28].

In most metaheuristic algorithms, an initial set of solutions—i.e., a population—is generated randomly, and these solutions are evaluated using a fitness function [26]. New generations are iteratively produced until a termination criterion is met, and at each step, the solutions are re-evaluated according to the fitness function [29,30].

The WSO algorithm is a bio-inspired optimization method based on swarm intelligence. Therefore, this study focuses on the effects of swarm intelligence-based optimization algorithms on feature selection within the context of the literature.

Table 1. Overview of swarm intelligence techniques employed in feature selection.

Year	Algorithm	Instruction
2014	BBA [31]	A feature selection method based on the BAT algorithm and the Optimum-Path Forest classifier has been proposed.
2015	DisABC [23]	The ABC algorithm has been discretized using bitwise operators, transfer functions, and a Jaccard similarity-based mutation strategy.
2016	MFO [32]	The MFO algorithm, developed by drawing inspiration from the nocturnal flight strategy of moths, has been employed in the feature selection process.
2017	WOASA [33]	To achieve optimal feature selection, a hybrid binary whale optimization algorithm (WOASA) was proposed by integrating Simulated Annealing (SA) with the WOA.
2017	Rc-BBFA [34]	A return-cost-based binary Firefly Algorithm (Rc-BBFA) has been proposed for feature selection. The method incorporates a mechanism specifically designed to prevent premature convergence.
2018	MCSRS [35]	A modified cuckoo search-based RS (MCSRS) method with coarse clusters has been developed for feature selection.
2020	TMGWO [36]	A novel GWO algorithm incorporating a two-stage mutation mechanism has been proposed for feature selection.
2020	BMVO [24]	For feature selection, the MVO algorithm was discretized using transfer functions, and the BMVO algorithm was introduced.
2020	BinSSA [28]	In this study, a binary version of the Social Spider Algorithm, called the Binary Social Spider Algorithm (BinSSA), was proposed. Additionally, transfer functions (S-Shape, V-Shape) and a crossover operator were utilized.
2021	MPPSO [37]	A novel multi-population-based Particle Swarm Optimization (MPPSO) algorithm has been proposed for feature selection.
2021	IDPSO-FS [25]	Using an entropy-based cut-point method, predefined cut-points were selected and optimized by PSO to discretize the features.
2022	BAAA [11]	For feature selection, a binary version of the AAA was developed using transfer functions (S-Shape, V-Shape).
2023	BIWSO [38]	A binary version of the WSO using transfer functions (S-shape, V-shape) has been developed for feature selection.
2023	IBGJO [39]	An improved Binary Golden Jackal Optimization (IBGJO) was proposed for feature selection, using Chaotic Tent Map and Cosine Similarity to enhance solution quality and diversity.
2024	HFPSO [40]	A hybrid metaheuristic algorithm combining PSO and FA methods is proposed for feature selection

presents some of the methods used for this purpose.

3. Original White Shark Optimizer (WSO)

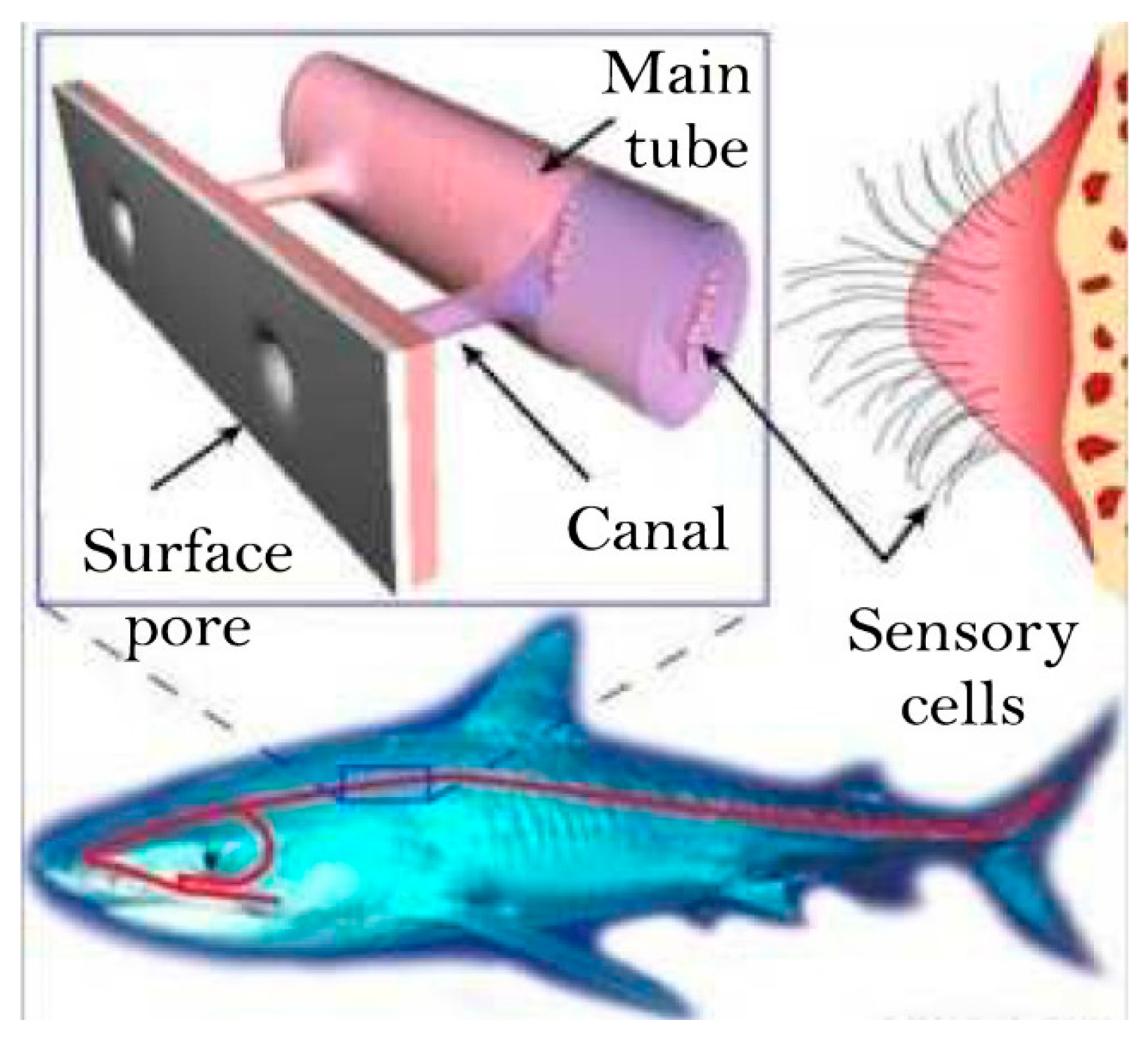
The WSO is a nature-inspired metaheuristic optimization algorithm developed by Braik et al. in 2022 [13]. The fundamental principle of the algorithm is based on the dynamic and directional movements of white sharks during the hunting process. These creatures prefer to detect their prey using their sense of smell and hearing rather than directly chasing it. Their advanced hearing abilities enable them to explore the search space effectively. As illustrated in Figure 1, white sharks can detect changes in water pressure, electromagnetic waves, and wave frequencies through the lateral lines extending along both sides of their bodies, allowing them to locate the prey.

The structure of the algorithm is designed to model exploration and exploitation behaviors in the solution space based on these biological features. WSO begins with a randomly generated initial population, where each individual is represented by a d-dimensional solution vector corresponding to the problem’s dimensionality. The initial positions of individuals are randomly selected within predefined lower and upper bounds. The quality of each solution is evaluated using a fitness function.

The WSO algorithm operates based on three main behavioral models:

• Moving towards prey: White sharks estimate the approximate position of their prey by sensing wave trails and odor signals. This orientation is modeled through velocity and position updates, allowing individuals to explore better regions in the solution space.
• Moving towards optimal prey: Similarly to fish swarms, white sharks perform random exploratory behaviors to locate their prey. This mechanism enables a broader coverage of the solution space and reduces the risk of premature convergence.
• Movement towards the best white shark: Individuals move toward the position of the best-performing shark (closest to the prey) and tend to cluster around it. This behavior simulates collective movement and enhances information sharing, leading to faster convergence to better solutions.

In each iteration, the population is updated according to these three strategies, and the best-found solution is preserved. Additionally, the tendency of individuals to move closer to one another reinforces dense convergence within the solution space. The overall functioning of the algorithm is summarized in the pseudo-code presented in Algorithm 1.

Algorithm 1 Pseudo-code WSO [13]
1:	Initialize the parameters of the problem
2:	Initialize the parameters of WSO
3:	Randomly generate the initial positions of WSO
4:	Initialize the velocity of the initial population
5:	Evaluate the positions of the initial population
6:	while $(k<K)$do
7:	Update the parameters, $p_1$, $p_2$, $\mu$, $a$, $b$, $w_0$, $f$, $mv$, and $s_s$, using their corresponding update rules defined in the algorithm.
8:	for $i = 1$ to $n$ to do
9:	$v_{k+1}^i=\mu [v_k^i+p_1\left(w_{{gbest}_k}-w_k^i\right)\times c_1+p_2 \left(w_{best}^{v_k^i}-w_k^i\right)\times c_2]$
10:	end for
11:	for $i = 1$ to $n$ to do
12:	if $rand<mv$ then
13:	$w_{k+1}^i=w_k^i .\neg \oplus w_o+u.a+l.b$
14:	else
15:	${w_{k+1}^i=w}_k^i+v_k^i/f$
16:	end if
17:	end for
18:	for $i = 1$ to$n$ to do
19:	if$rand<s_{s }$then
20:	${\overrightarrow{D}}_w=|rand \times \left(w_{{gbest}_k}-w_k^i\right)|$
21:	if$i==1$then
22:	$w_{k+1}^i=w_{{gbest}_k}+r_1{\overrightarrow{D}}_{w}sgn\left(r_2-0.5\right)$
23:	else
24:	${\stackrel{\prime }{w}}_{k+1}^i=w_{{gbest}_k}+r_1{\overrightarrow{D}}_{w}sgn\left(r_2-0.5\right)$
25:	$w_{k+1}^i={\displaystyle \frac{w_k^i+{\grave{w}}_{k+1}^i}{2\times rand}}$
26:	end if
27:	end if
28:	end for
29:	Adjust the position of the white sharks that proceed beyod the boundary
30:	Evaluate and update the news positions
31:	$k=k+1$
32:	end while
33:	Return the optimal solution obtained so far

Beyond the biological and behavioral modeling of the algorithm’s structure, there are also methodological reasons that support the preference for WSO in the context of the feature selection problem. Although numerous optimization algorithms have been proposed in the literature, there are several reasons why WSO was chosen in this study. First, WSO provides an effective balance between exploration and exploitation phases, which is particularly beneficial for solving complex and multimodal problems such as feature selection. Second, WSO has a low computational cost and has demonstrated competitive performance on various high-dimensional benchmark problems. Finally, the biologically inspired search mechanism based on the predatory behavior of white sharks offers flexible adaptation capabilities that align well with the structure of binary search spaces. All these characteristics make WSO a suitable and potentially powerful candidate for the feature selection problem addressed in this study.

4. The Proposed Binary White Shark Optimizer

The WSO algorithm is designed to provide optimal solutions in continuous search spaces. However, to apply WSO to feature selection problems, a discretization process is required. This section presents the details of the bWSO_log algorithm, which has been developed specifically for solving feature selection problems. In this context, the details of the bWSO_log algorithm developed for feature selection are presented, and its variants obtained using different discretization strategies are also included.

• bWSO_log: In each position update step of the original WSO algorithm, the logarithmic transfer function described in Section 4.2 is used.
• bWSO-0: In this version, discretization is performed using a direct thresholding method without employing any transfer function. The obtained continuous value is compared with a randomly selected threshold; if it is greater, it is assigned 1, otherwise 0.
• bWSO_s: Instead of the logarithmic function, the S-Shape transfer function is used.
• bWSO_v: Instead of the logarithmic function, the V-Shape transfer function is used.

To rigorously assess the performance contribution of the proposed logarithmic transfer function, a baseline variant without any transfer function, denoted as bWSO-0, was also included in the evaluation. Accordingly, the effectiveness of the logarithmic function was empirically analyzed by comparing its optimization performance against the S-Shape, V-Shape, and transfer-function-free (bWSO-0) counterparts.

This section is organized as follows: Section 4.1 explains the Problem Formulation and Solution Representation. Section 4.2 discusses the binarization strategy applied to the original WSO algorithm.

4.1. Problem Formulation and Solution Representation

In this study, the feature selection problem is addressed as a binary optimization task. The primary objective is to identify the optimal subset of features that maximizes classification accuracy while minimizing the number of selected features.

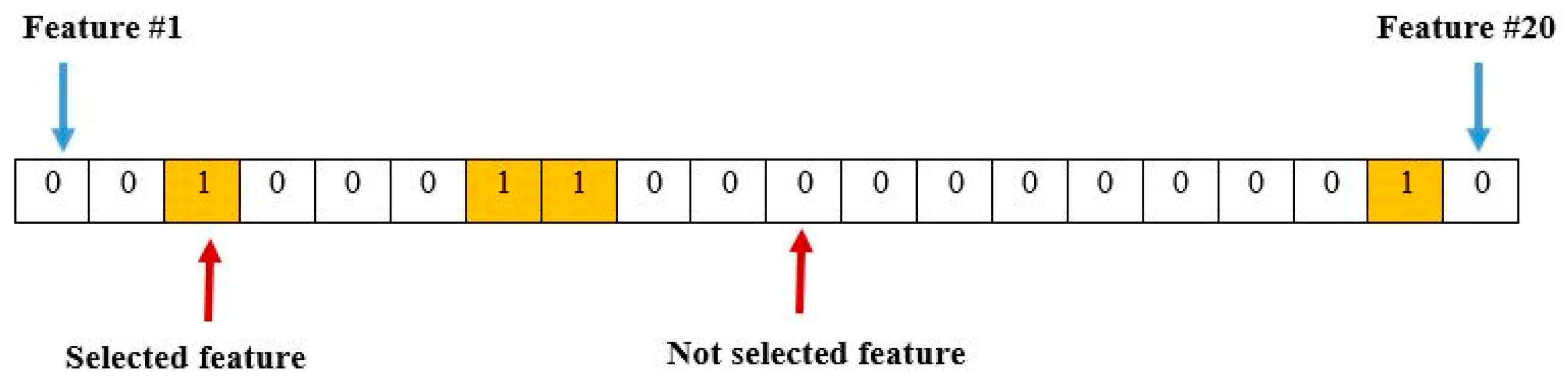
Each candidate solution is represented as a binary vector with a length equal to the number of features in the dataset, as shown in Equation (1).

$$X=\left[x_1, x_2, ..,x_n\right], x_i \in \left\{\mathrm{0,1}\right\}$$

(1)

where $n$ represents the total number of features; a value of $x_i=1$ indicates that the $i$th feature is selected, while $x_i=0$ indicates that the th feature is not selected. An example of the solution representation is shown in Figure 2. Figure 2 illustrates the binary vector representation of a candidate solution, where each element corresponds to a feature in the dataset. A value of 1 indicates that the corresponding feature is selected, whereas a value of 0 means the feature is not selected. For example, in the given illustration, features 3, 7, 8 and 19 are included in the selected subset.

Fitness Function: In feature selection problems, the goal is to identify an ideal subset by minimizing the number of selected features while maximizing classification performance. The features selected by each search agent in the algorithm are evaluated using a fitness function based on the K-nearest neighbor (KNN) classifier to estimate classification accuracy. The fitness function is used by optimization algorithms to measure the performance of solution vectors. The fitness function used in this study is shown in Equation (2).

$$\downarrow Fitness=\mathsf{\alpha }{\gamma }_{R }\left(D\right)+\beta {\displaystyle \frac{\left|M\right|}{\left|N\right|}}$$

(2)

The fitness function represents the fitness value of the White Shark; ${\gamma }_{R }\left(D\right)$ denotes the classification error rate; $\left|M\right|$ is the number of selected features; and $\left|N\right|$ is the total number of features. The parameters α and β correspond to the importance of the number of selected features and classification accuracy, respectively. In the literature, they are commonly used as $\alpha \in \left[\mathrm{0,1}\right],\beta =(1-\alpha )$ [11,28,33,38]. In this study, alpha was selected as 0.99 and beta as 0.01.

Classification Process: The K-nearest neighbor (K-NN) classifier is a commonly used method in feature selection problems [11,28,33]. The Euclidean distance is used in the K-NN classifier, as shown in Equation (3). The value of K was set to 5 to obtain the optimal feature subset.

$$distance\left(x_a-x_b\right)={({\sum }_{i=1}^N{(x_{ai}-x_{bi})}^2)}^{0.5}$$

(3)

where $x_a$ and $x_b$ denote two instances represented as $N$-dimensional feature vectors, where $N$ corresponds to the total number of features. The term $x_{ai}$ refers to the value of the $ith$ feature of instance $x_a$, and similarly $x_{bi}$ corresponds to the $ith$ feature of instance.

4.2. Discretization Strategy

In the literature, discretization is performed using various transfer functions. To convert the outputs of these transfer functions into binary values (0 or 1), different thresholding approaches are employed. The thresholding method used in this study is presented in Equation (4).

$$w_{k+1}^i=\left\{\begin{array}{l}1, if rand<w_k^i\\ 0, if otherwise\end{array}\right.$$

(4)

where $w_k^i$ represents white sharks. The rand is a random value in the range. In the WSO algorithm, if the position update value can exceed the randomly generated value, it is equalized to take the value of 1, in other cases it will be zero.

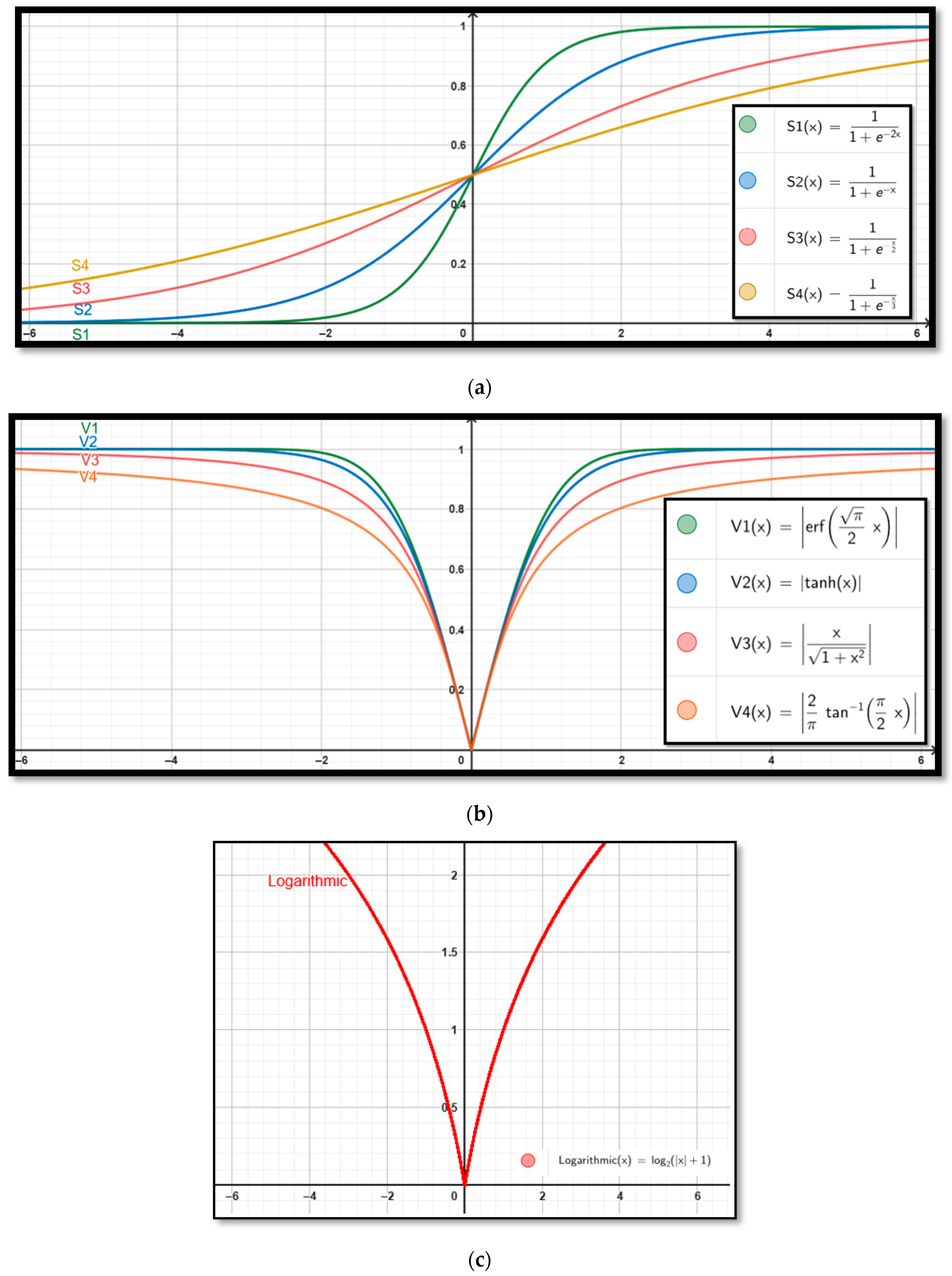
In this study, to evaluate the impact of discretization functions, the bWSO-0 algorithm was first implemented without employing any transfer function. Subsequently, experiments were conducted using S-Shape, V-Shape, and the proposed logarithmic transfer function. The transfer functions used in all proposed bWSO variants are presented in

Table 2. Definition of the transfer functions (S-shaped, V-shaped and proposed function).

Proposed bWSO		Transfer Functions	Proposed bWSO		Transfer Functions
bWSO-log		Logarithmic = ${\log }_2(\left|x\right|+1)$	bWSO-v1		${\mathit{V}}_{\mathbf{1}}\mathbf{=}\left|\mathit{e}\mathit{r}\mathit{f}\mathbf{(}{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathbf{2}}}\left(\mathit{x}\right)\mathbf{)}\right|$
bWSO-s1		${\mathit{S}}_{\mathbf{1}}\mathbf{=}{\displaystyle \frac{\mathbf{1}}{\mathbf{1}\mathbf{+}{\mathit{e}}^{\mathbf{-}\mathbf{2}\mathit{x}}}}$	bWSO-v2		${\mathit{V}}_{\mathbf{2}}\mathbf{=}\left|\mathit{t}\mathit{a}\mathit{n}\mathit{h}\left(\mathit{x}\right)\right|$
bWSO-s2		${\mathit{S}}_{\mathbf{2}}\mathbf{=}{\displaystyle \frac{\mathbf{1}}{\mathbf{1}\mathbf{+}{\mathit{e}}^{\mathbf{-}\mathit{x}}}}$	bWSO-v3		${\mathit{V}}_{\mathbf{3}}\mathbf{=}\left|\mathit{x}\mathbf{/}\sqrt{\mathbf{1}\mathbf{+}{\left(\mathit{x}\right)}^{\mathbf{2}}}\right|$
bWSO-s3		${\mathit{S}}_{\mathbf{3}}\mathbf{=}{\displaystyle \frac{\mathbf{1}}{\mathbf{1}\mathbf{+}{\mathit{e}}^{\mathbf{(}\mathbf{-}\mathit{x}\mathbf{/}\mathbf{2}\mathbf{)}}}}$	bWSO-v4		${\mathit{V}}_{\mathbf{4}}\mathbf{=}\left|{\displaystyle \frac{\mathbf{2}}{\mathit{\pi }}}\mathit{a}\mathit{r}\mathit{c}\mathit{tan}\mathbf{\left(}{\displaystyle \frac{\mathit{\pi }}{\mathbf{2}}}\mathit{x}\right)\right|$
bWSO-s4		${\mathit{S}}_{\mathbf{4}}\mathbf{=}{\displaystyle \frac{\mathbf{1}}{\mathbf{1}\mathbf{+}{\mathit{e}}^{\mathbf{(}\mathbf{-}\mathit{x}\mathbf{/}\mathbf{3}\mathbf{)}}}}$	bWSO-0		Transfer function not used.

and the corresponding Figure 3. Figure 3 presents the graphical representation of the transfer functions used in the bWSO variants, including S-shaped, V-shaped, and the proposed logarithmic transfer function. These curves illustrate how the continuous values generated by the optimization algorithm are converted into binary values (0 or 1) during the discretization process.

The logarithmic transfer function provides a more flexible and gradual probability distribution on the transformation curve compared to traditional S-shaped and V-shaped functions. This characteristic enables the algorithm to maintain a better balance between exploration and exploitation during the search process, thereby preventing entrapment in local minima and improving solution quality. In addition, the natural monotonic structure of the logarithmic function offers a more controlled binary conversion mechanism in the solution space.

The pseudocode of the proposed bWSO algorithm is provided in Algorithm 2.

Algorithm 2 Pseudo-code of binary WSO
1:	Initialize the parameters of the problem
2:	Initialize the parameters of WSO
3:	Randomly generate the initial positions of WSO
4:	Initialize the velocity of the initial population
5:	Evaluate the positions of the initial population
6:	while$(k<K)$do
7:	Update the parameters, $p_1$, $p_2$, $\mu$, $a$, $b$, $w_0$, $f$, $mv$, and $s_s$, using their corresponding update rules defined in the algorithm.
8:	for $i = 1$ to$n$ to do
9:	$v_{k+1}^i=\mu [v_k^i+p_1\left(w_{{gbest}_k}-w_k^i\right)\times c_1+p_2 \left(w_{best}^{v_k^i}-w_k^i\right)\times c_2]$
10:	end for
11:	for $i = 1$ to$n$ to do
12:	if$rand<mv$then
13:	$w_{k+1}^i=w_k^i .\neg \oplus w_o+u.a+l.b$
14:	$w_{k+1}^i=transferFunction (w_{k+1}^i )$
15:	else
16:	${w_{k+1}^i=w}_k^i+v_k^i/f$
17:	$w_{k+1}^i=transferFunction (w_{k+1}^i )$
18:	end if
19:	end for
20:	for $i = 1$ to$n$ to do
21:	if$rand<s_s$then
22:	${\overrightarrow{D}}_w=|rand \times \left(w_{{gbest}_k}-w_k^i\right)|$
23:	if$i==1$ then
24:	$w_{k+1}^i=w_{{gbest}_k}+r_1{\overrightarrow{D}}_{w}sgn\left(r_2-0.5\right)$
25:	$w_{k+1}^i=transferFunction (w_{k+1}^i )$
26:	else
27:	${\stackrel{\prime }{w}}_{k+1}^i=w_{{gbest}_k}+r_1{\overrightarrow{D}}_{w}sgn\left(r_2-0.5\right)$
28:	$w_{k+1}^i={\displaystyle \frac{w_k^i+{\grave{w}}_{k+1}^i}{2\times rand}}$
29:	$w_{k+1}^i=transferFunction (w_{k+1}^i )$
30:	end if
31:	end if
32:	end for
33:	Adjust the position of the white sharks that proceed beyod the boundary
34:	Evaluate and update the news positions
35:	$k=k+1$
36:	end while
37:	Return the optimal solution obtained so far

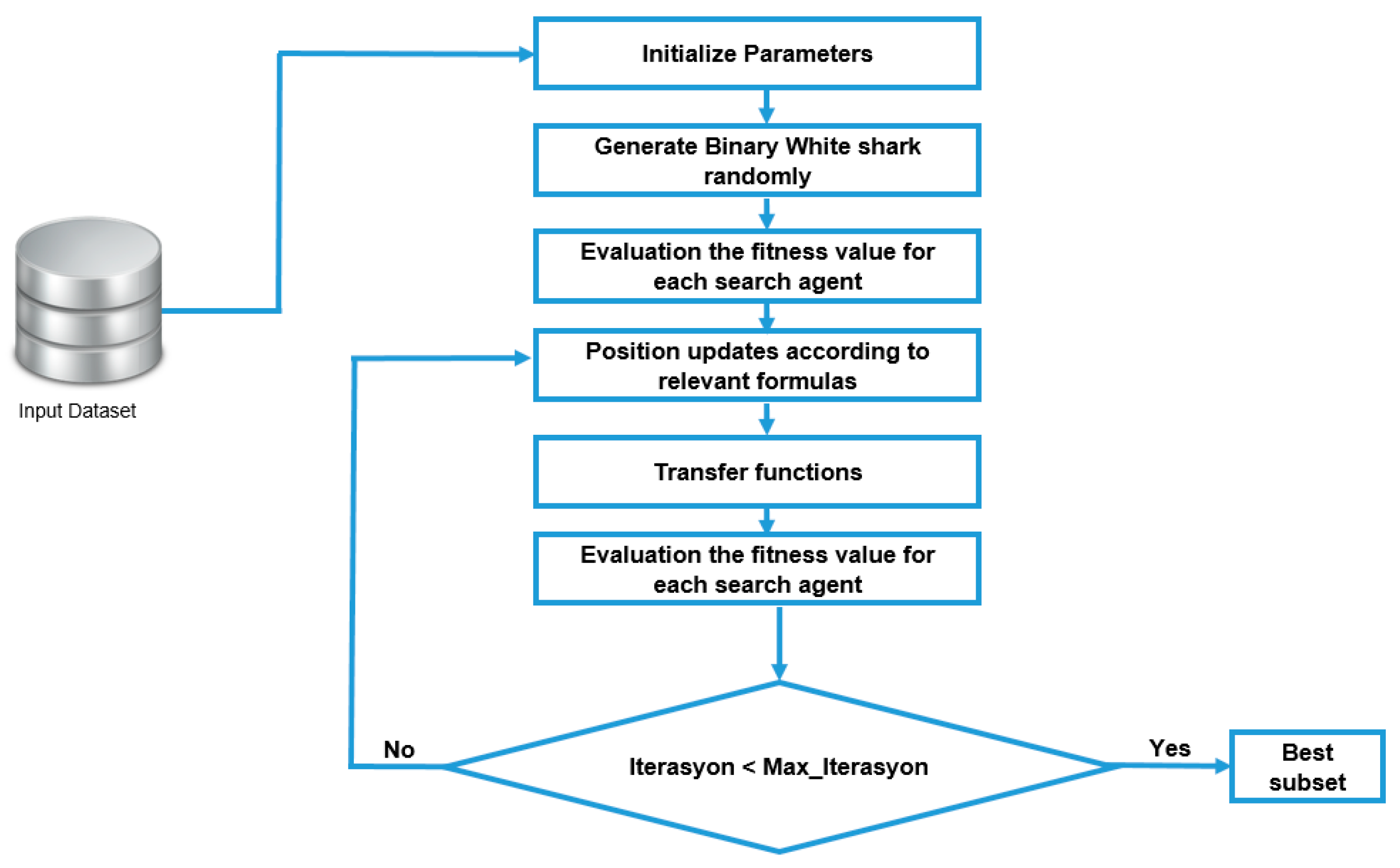
Figure 4 presents a block diagram illustrating the step-by-step workflow of the proposed bWSO algorithm. The process begins with the input of the dataset into the algorithm. Next, the algorithm parameters are initialized, and binary white sharks are generated randomly. Each search agent (white shark) is evaluated using a fitness function. The positions of the agents are then updated based on the relevant formulas, followed by the application of transfer functions for the discretization process. The fitness values are recalculated according to the new positions. This loop continues until the maximum number of iterations is reached. Once the iteration limit is exceeded, the best feature subset is returned as the output. This diagram aims to visualize how each component of the algorithm operates systematically.

5. Experiments

This section describes the experimental details. The datasets used in the study were selected due to their open access availability [42], varying levels of difficulty [28], and their usage in other studies in the literature [11,28,31,37]. Detailed information about the datasets is provided in

Table 3. Dataset description.

	Dataset Name	Features	Samples	Classes	Missing Value	Subject Area
N1	Breast cancer Wisconsin (original)	9	699	2	Yes	Health and Medicine
N2	Planning relax	12	182	2	No	Computer Science
N3	Heart failure clinical records	12	299	2	No	Health and Medicine
N4	Wine	13	178	3	No	Physics and Chemistry
N5	Zoo	16	101	7	No	Biology
N6	Lymphography	18	148	4	No	Health and Medicine
N7	Climate Model Simulation Crashes	18	540	2	No	Climate and Environment
N8	Hepatitis	19	155	2	Yes	Health and Medicine
N9	Waveform (Version 1)	21	5000	3	No	Physics and Chemistry
N10	Parkinsons	22	195	2	No	Health and Medicine
N11	Breast Cancer Wisconsin (Diagnostic)	30	569	2	No	Health and Medicine
N12	Ionosphere	34	351	2	No	Physics and Chemistry
N13	Dermatology	34	366	6	Yes	Health and Medicine
N14	Soybean Small	35	47	4	No	Biology
N15	Qsar Biodegradation	41	1055	2	No	Other
N16	Lung Cancer	56	32	3	Yes	Health and Medicine
N17	Spambase	57	4601	2	No	Computer Science
N18	Sonar	60	208	2	No	Physics and Chemistry
N19	CNAE-9	856	1080	9	No	Business

. All datasets listed in Table 3 were obtained from the UC Irvine Machine Learning Repository [42]. The datasets used in this study were divided into two groups: training and testing sets. The training and testing data ratios were set to 80% and 20%, respectively.

In the experimental study, the proposed bWSO algorithm was compared with eight widely preferred population-based algorithms from the literature [11,24,28,31,37]. The algorithms used in this comparison include AAA [11], BAT [14], FA [15], GWO [16], MFO [17], MVO [18], PSO [19], WOA [20]. To ensure a fair comparison, AAA, BAT, FA, GWO, MFO, MVO, PSO, WOA, and bWSO algorithms were executed on the same platform. The experiments were conducted on a Windows 10 operating system equipped with an Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz (6 cores, 12 logical processors) and 16 GB of RAM. Coding was performed using Python (version 3.7.3 64bit) programming language within the Visual Studio Code (Version 1.92.2) editor. The EvolopyFS library was utilized in the experimental studies [43]. EvolopyFS is a Python-based library containing frequently used metaheuristic optimization methods. The experiments were carried out with a population size of 30, 500 iterations, and 30 runs.

The hyperparameter values of all algorithms used in the experiments were determined based on default settings that are commonly used in the relevant literature and have been proven effective in previous studies. In particular, the parameters chosen for the WSO algorithm are those recommended in the original study [13] and selected after comprehensive parameter analyses. This approach was adopted to reduce the need for additional optimization of parameter settings and to ensure a fair comparison among different algorithms. Thus, the focus of the experiments was on comparing the fundamental performance of the algorithms. The hyperparameter values of all algorithms are presented in

Table 4. Hyperparameters values used in all algorithms.

Algorithm	Hyperparameters	Values
WSO	$f_{max}$	0.75
	$f_{min}$	0.07
	$p_{max}$	1.5
	$p_{min}$	0.5
	$tau$	4.11
	$a_0$	6.25
	$a_1$	100
	$a_2$	0.0005
AAA	$∆ Share force$	2
	$e Energy loss$	0.3
	$A_p \mathrm{A}\mathrm{d}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$	0.2
BAT	$A \left(Loudness\right)$	0.5
	$r (Pulse rate)$	0.5
	$Q$	[0, 2]
FA	$alpha \left(Randomness\right)$	0.5
	${Beta}_{min } (minimum value of beta)$	0.2
	$\mathrm{G}\mathrm{a}\mathrm{m}\mathrm{a}(absorption coefficient)$	1
GWO	$alpha$	2
MFO	$b$	1
MVO	${wep}_{max}$	1
	${wep}_{min}$	0.2
PSO	$c1,$	2
	$c2$	2
	$w_{max}$	0.9
	$w_{min}$	0.2
WOA	$alpha$	2

.

Evaluation Criteria

The performance of the proposed method was analyzed and compared using various evaluation metrics. In this context, the obtained results were evaluated in terms of accuracy, recall, and F1-Score.

Accuracy: Indicates the ratio of correctly predicted to all predictions. A value close to 1 indicates that the classification is a model that is highly accurate. It is shown in Equation (5)

$$\uparrow Accuracy={\displaystyle \frac{ TP+TN}{TP+TN+FP+FN}}$$

(5)

where $TP$ (True Positive): What is actually true (actual positive) and what is predicted correctly (predicted positive). $TN$ (True Negative): It is not actually true (actual negative) and not predicted correctly (predicted negative). $FP$ (False Positive): Actually incorrect (actual negative) and correctly predicted (predicted positive). $FN$ (False Negative): What is actually correct (actual positive) and not correctly predicted (predicted negative).

Recall: Shows the ratio of correctly predicted to true positives. A value close to 1 indicates that the classification is a model that is highly recalled. It is shown in Equation (6).

$$Recall={\displaystyle \frac{TP}{TP+FN }}$$

(6)

F1-Score: Recall and Precision harmonic average. A value close to 1 indicates that the classification is a model that has a high F1-Score. It is shown in Equation (7).

$$\uparrow F1\text{-}Score={\displaystyle \frac{2 \times Precision \times Recall}{(Precision+Recall)}}$$

(7)

Wilcoxon signed-rank test: It is a test frequently used in the literature to test whether the results obtained by the algorithms are significant or not if they are remarkably close to each other. If the obtained value is greater than the significance level, H0 (Null Hypothesis) is accepted. Accepting the H0 hypothesis indicates that there is no significant difference between the two methods. If the obtained value is less than the significance level, H1 (Alternative Hypothesis) is accepted. H1 Hypothesis is the opposite of H0 Hypothesis. In other words, the H1 hypothesis states that there is a significant difference. In this study, the significance level was determined as p-Value 0.05 [44].

6. Results and Discussion

In this section, the proposed bWSO-log algorithm and the other algorithms were executed on the relevant datasets, and the experimental results were comprehensively analyzed. Initially, ten different versions of the bWSO algorithm were evaluated. During the analysis, the results obtained using 19 different datasets, as listed in Table 3, were compared. Performance comparisons between the different versions of bWSO and the other algorithms were conducted based on the mean and standard deviation values obtained from 30 independent runs for each algorithm.

6.1. Comparison Between Versions of bWSO

In

Table 5. The test accuracy and detailed results of the bWSO-Log and other versions.

ID		bWSO-log	bWSO-0	bWSO-s1	bWSO-s2	bWSO-s3	bWSO-s4	bWSO-v1	bWSO-v2	bWSO-v3	bWSO-v4
N1	↑mean	0.960	0.959	0.952	0.955	0.946	0.954	0.950	0.952	0.946	0.940
	±std	0.017	0.019	0.022	0.016	0.025	0.017	0.024	0.018	0.023	0.028
	↑best	0.986	1.000	0.993	0.986	0.986	0.986	0.986	0.979	0.986	0.986
	↑worst	0.921	0.914	0.914	0.929	0.886	0.907	0.886	0.929	0.879	0.850
N2	↑mean	0.661	0.645	0.627	0.612	0.638	0.622	0.610	0.638	0.632	0.634
	±std	0.056	0.071	0.067	0.079	0.068	0.067	0.079	0.051	0.087	0.073
	↑best	0.757	0.838	0.784	0.757	0.784	0.757	0.757	0.730	0.757	0.784
	↑worst	0.541	0.514	0.486	0.459	0.459	0.486	0.432	0.541	0.378	0.514
N3	↑mean	0.841	0.826	0.819	0.809	0.817	0.835	0.799	0.800	0.821	0.798
	±std	0.050	0.069	0.064	0.076	0.061	0.063	0.077	0.074	0.065	0.087
	↑best	0.917	0.950	0.933	0.900	0.933	0.933	0.933	0.883	0.917	0.900
	↑worst	0.733	0.633	0.667	0.600	0.683	0.667	0.617	0.583	0.700	0.533
N4	↑mean	0.912	0.905	0.903	0.889	0.908	0.896	0.897	0.912	0.895	0.882
	±std	0.057	0.052	0.072	0.074	0.057	0.069	0.054	0.051	0.053	0.079
	↑best	1.000	1.000	1.000	1.000	0.972	1.000	0.972	0.972	1.000	1.000
	↑worst	0.750	0.778	0.694	0.667	0.694	0.694	0.750	0.750	0.778	0.722
N5	↑mean	0.856	0.806	0.829	0.813	0.830	0.852	0.824	0.835	0.794	0.830
	±std	0.085	0.115	0.093	0.101	0.099	0.103	0.081	0.092	0.120	0.105
	↑best	1.000	1.000	0.952	1.000	1.000	1.000	0.952	0.952	1.000	0.952
	↑worst	0.619	0.476	0.524	0.571	0.619	0.571	0.667	0.619	0.429	0.524
N6	↑mean	0.768	0.761	0.749	0.722	0.740	0.764	0.727	0.731	0.746	0.753
	±std	0.062	0.073	0.073	0.095	0.103	0.087	0.084	0.091	0.089	0.088
	↑best	0.933	0.900	0.900	0.900	0.933	0.900	0.900	0.900	0.900	0.900
	↑worst	0.667	0.600	0.600	0.500	0.467	0.533	0.533	0.500	0.600	0.500
N7	↑mean	0.940	0.935	0.926	0.930	0.925	0.925	0.927	0.923	0.926	0.923
	±std	0.020	0.021	0.023	0.028	0.026	0.026	0.027	0.031	0.030	0.026
	↑best	0.972	0.963	0.981	0.972	0.972	0.972	0.972	0.972	0.981	0.981
	↑worst	0.907	0.880	0.861	0.880	0.870	0.880	0.870	0.852	0.852	0.880
N8	↑mean	0.822	0.813	0.804	0.782	0.805	0.814	0.805	0.790	0.789	0.799
	±std	0.057	0.043	0.066	0.055	0.067	0.059	0.066	0.064	0.085	0.082
	↑best	0.935	0.903	0.968	0.903	0.935	0.903	0.935	0.903	0.935	0.935
	↑worst	0.742	0.742	0.677	0.677	0.645	0.645	0.613	0.645	0.581	0.613
N9	↑mean	0.820	0.817	0.817	0.815	0.818	0.812	0.814	0.817	0.812	0.808
	±std	0.010	0.011	0.014	0.014	0.014	0.011	0.016	0.011	0.011	0.013
	↑best	0.845	0.843	0.848	0.841	0.842	0.832	0.840	0.836	0.835	0.827
	↑worst	0.802	0.790	0.798	0.789	0.785	0.792	0.776	0.793	0.787	0.778
N10	↑mean	0.817	0.858	0.854	0.858	0.850	0.865	0.840	0.855	0.837	0.814
	±std	0.013	0.053	0.066	0.061	0.076	0.063	0.076	0.066	0.048	0.077
	↑best	0.844	0.974	0.974	0.949	0.974	0.974	0.949	0.949	0.923	0.949
	↑worst	0.780	0.744	0.744	0.692	0.667	0.692	0.590	0.641	0.744	0.641
N11	↑mean	0.936	0.927	0.933	0.928	0.934	0.930	0.928	0.919	0.923	0.924
	±std	0.024	0.039	0.020	0.025	0.024	0.027	0.027	0.024	0.025	0.021
	↑best	0.991	0.974	0.982	0.974	0.974	0.982	0.974	0.965	0.965	0.965
	↑worst	0.860	0.763	0.895	0.860	0.868	0.851	0.868	0.886	0.868	0.895
N12	↑mean	0.855	0.864	0.823	0.838	0.846	0.849	0.866	0.880	0.884	0.860
	±std	0.036	0.044	0.043	0.061	0.042	0.051	0.045	0.047	0.037	0.052
	↑best	0.930	0.986	0.901	0.944	0.930	0.944	0.944	0.958	0.944	0.944
	↑worst	0.789	0.789	0.704	0.634	0.732	0.761	0.789	0.789	0.817	0.732
N13	↑mean	0.933	0.932	0.957	0.948	0.945	0.932	0.916	0.899	0.923	0.918
	±std	0.047	0.038	0.035	0.033	0.031	0.037	0.038	0.039	0.042	0.035
	↑best	0.986	1.000	1.000	1.000	0.986	0.986	0.973	0.973	1.000	0.986
	↑worst	0.811	0.838	0.851	0.865	0.851	0.824	0.838	0.824	0.838	0.838
N14	↑mean	0.933	0.837	0.937	0.953	0.950	0.943	0.880	0.873	0.923	0.873
	±std	0.096	0.190	0.110	0.090	0.114	0.101	0.124	0.134	0.114	0.178
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	↑worst	0.700	0.400	0.600	0.700	0.500	0.700	0.600	0.600	0.600	0.100
N15	↑mean	0.830	0.834	0.841	0.839	0.836	0.829	0.837	0.828	0.826	0.834
	±std	0.020	0.029	0.022	0.022	0.018	0.025	0.021	0.023	0.028	0.025
	↑best	0.858	0.896	0.877	0.882	0.872	0.905	0.877	0.872	0.891	0.867
	↑worst	0.777	0.777	0.801	0.796	0.801	0.787	0.782	0.782	0.763	0.768
N16	↑mean	0.557	0.367	0.471	0.524	0.467	0.443	0.429	0.419	0.438	0.395
	±std	0.189	0.179	0.188	0.152	0.240	0.217	0.188	0.154	0.187	0.218
	↑best	0.857	0.857	0.857	0.857	1.000	0.857	0.714	0.714	0.714	0.857
	↑worst	0.143	0.143	0.000	0.286	0.000	0.000	0.143	0.143	0.143	0.000
N17	↑mean	0.918	0.915	0.918	0.913	0.912	0.913	0.914	0.916	0.914	0.914
	±std	0.008	0.010	0.010	0.010	0.012	0.008	0.012	0.007	0.009	0.011
	↑best	0.933	0.936	0.940	0.937	0.935	0.932	0.931	0.929	0.933	0.935
	↑worst	0.907	0.897	0.902	0.895	0.871	0.900	0.873	0.903	0.895	0.893
N18	↑mean	0.797	0.767	0.781	0.796	0.781	0.790	0.771	0.764	0.771	0.775
	±std	0.065	0.074	0.063	0.067	0.055	0.055	0.075	0.068	0.060	0.069
	↑best	0.905	0.905	0.905	0.929	0.881	0.881	0.905	0.881	0.929	0.881
	↑worst	0.667	0.571	0.643	0.667	0.690	0.643	0.643	0.619	0.643	0.619
N19	↑mean	0.888	0.877	0.864	0.852	0.816	0.818	0.838	0.836	0.799	0.803
	±std	0.021	0.026	0.029	0.026	0.034	0.028	0.036	0.027	0.029	0.037
	↑best	0.931	0.944	0.903	0.921	0.880	0.856	0.903	0.907	0.866	0.875
	↑worst	0.829	0.782	0.778	0.801	0.718	0.741	0.745	0.787	0.722	0.722
	↑Best Count	14.000	0.000	3.000	1.000	0.000	1.000	0.000	1.000	1.000	0.000
	↓Average Sort	2.368	4.789	4.474	5.474	5.053	4.947	6.579	6.263	7.158	7.579
	↓Ranking	1.000	3.000	2.000	6.000	5.000	4.000	8.000	7.000	9.000	10.000

, the average accuracy value, the best standard deviation, and the worst result of the binary bWSO algorithm are given as a result of 30 independent runs. The best results are highlighted in bold font. Considering the average success value, it was seen that using the appropriate transfer function increased the success rate when comparing the bWSO-0 version with the value bWSO versions. It has been seen that the bWSO versions proposed using the V-shape transfer function are more successful than the bWSO versions proposed with the S-shape transfer functions. Considering the average ranking value in total, it is seen that the proposed logarithmic transfer function is in the first place. In the bWSO versions whose Recall values are given in

Table 6. The test recall and detailed results of the bWSO-log and other versions.

ID		bWSO-log	bWSO-0	bWSO-s1	bWSO-s2	bWSO-s3	bWSO-s4	bWSO-v1	bWSO-v2	bWSO-v3	bWSO-v4
N1	↑mean	0.958	0.957	0.946	0.952	0.942	0.950	0.946	0.946	0.940	0.935
	±std	0.022	0.022	0.025	0.017	0.027	0.020	0.032	0.020	0.027	0.037
	↑best	0.991	1.000	0.995	0.984	0.990	0.989	0.989	0.979	0.984	0.990
	↑worst	0.913	0.900	0.894	0.915	0.886	0.903	0.854	0.914	0.875	0.808
N2	↑mean	0.497	0.488	0.474	0.465	0.481	0.478	0.471	0.469	0.480	0.482
	±std	0.049	0.067	0.052	0.073	0.076	0.064	0.059	0.055	0.076	0.067
	↑best	0.613	0.670	0.631	0.613	0.669	0.615	0.587	0.598	0.633	0.669
	↑worst	0.411	0.420	0.397	0.315	0.293	0.362	0.353	0.379	0.304	0.339
N3	↑mean	0.797	0.778	0.762	0.756	0.759	0.786	0.755	0.749	0.769	0.743
	±std	0.057	0.083	0.079	0.090	0.082	0.073	0.093	0.075	0.086	0.104
	↑best	0.889	0.912	0.946	0.889	0.870	0.911	0.913	0.838	0.870	0.877
	↑worst	0.675	0.579	0.601	0.481	0.520	0.550	0.550	0.529	0.542	0.447
N4	↑mean	0.925	0.913	0.910	0.902	0.914	0.907	0.902	0.917	0.905	0.895
	±std	0.046	0.050	0.073	0.068	0.058	0.064	0.052	0.057	0.048	0.077
	↑best	1.000	1.000	1.000	1.000	0.982	1.000	0.981	0.978	1.000	1.000
	↑worst	0.806	0.778	0.706	0.675	0.712	0.712	0.750	0.715	0.790	0.694
N5	↑mean	0.721	0.676	0.704	0.669	0.685	0.737	0.673	0.667	0.654	0.693
	±std	0.144	0.139	0.121	0.170	0.149	0.166	0.132	0.156	0.139	0.165
	↑best	1.000	1.000	0.979	1.000	1.000	1.000	0.944	0.982	1.000	0.983
	↑worst	0.429	0.343	0.500	0.333	0.381	0.408	0.429	0.333	0.472	0.408
N6	↑mean	0.573	0.550	0.599	0.541	0.511	0.565	0.563	0.548	0.533	0.556
	±std	0.152	0.145	0.168	0.166	0.148	0.167	0.152	0.141	0.130	0.156
	↑best	0.915	0.906	0.852	0.897	0.938	0.892	0.935	0.900	0.871	0.906
	↑worst	0.376	0.375	0.326	0.297	0.321	0.292	0.318	0.333	0.347	0.338
N7	↑mean	0.677	0.692	0.649	0.677	0.652	0.644	0.680	0.662	0.662	0.640
	±std	0.124	0.101	0.083	0.088	0.077	0.096	0.094	0.088	0.082	0.093
	↑best	0.870	0.881	0.895	0.890	0.833	0.833	0.823	0.841	0.800	0.828
	↑worst	0.481	0.495	0.495	0.542	0.490	0.475	0.490	0.519	0.485	0.485
N8	↑mean	0.644	0.653	0.654	0.643	0.666	0.686	0.685	0.649	0.653	0.650
	±std	0.120	0.102	0.120	0.094	0.119	0.090	0.120	0.086	0.111	0.120
	↑best	0.964	0.877	0.981	0.798	0.950	0.836	0.929	0.838	0.819	0.946
	↑worst	0.466	0.414	0.480	0.462	0.397	0.500	0.446	0.500	0.442	0.432
N9	↑mean	0.819	0.817	0.817	0.815	0.818	0.812	0.814	0.818	0.812	0.808
	±std	0.010	0.011	0.014	0.014	0.014	0.011	0.016	0.011	0.011	0.014
	↑best	0.846	0.841	0.847	0.841	0.841	0.832	0.840	0.836	0.838	0.827
	↑worst	0.802	0.790	0.800	0.790	0.788	0.794	0.777	0.795	0.787	0.774
N10	↑mean	0.775	0.775	0.778	0.782	0.777	0.782	0.755	0.770	0.760	0.736
	±std	0.092	0.100	0.102	0.086	0.101	0.102	0.102	0.090	0.073	0.112
	↑best	0.933	0.985	0.952	0.937	0.958	0.985	0.911	0.916	0.955	0.969
	↑worst	0.600	0.585	0.594	0.593	0.492	0.554	0.528	0.500	0.600	0.538
N11	↑mean	0.926	0.917	0.922	0.920	0.925	0.922	0.919	0.906	0.911	0.914
	±std	0.027	0.046	0.022	0.027	0.026	0.031	0.030	0.030	0.031	0.024
	↑best	0.987	0.974	0.981	0.969	0.974	0.977	0.974	0.963	0.962	0.953
	↑worst	0.849	0.720	0.881	0.847	0.854	0.831	0.848	0.868	0.830	0.877
N12	↑mean	0.798	0.830	0.771	0.787	0.799	0.793	0.833	0.846	0.855	0.828
	±std	0.041	0.058	0.048	0.060	0.044	0.062	0.053	0.057	0.042	0.058
	↑best	0.903	0.979	0.859	0.915	0.886	0.933	0.937	0.953	0.939	0.909
	↑worst	0.717	0.720	0.667	0.618	0.722	0.688	0.729	0.728	0.778	0.677
N13	↑mean	0.917	0.921	0.948	0.936	0.944	0.927	0.901	0.870	0.906	0.892
	±std	0.064	0.042	0.044	0.046	0.031	0.035	0.052	0.059	0.061	0.052
	↑best	0.990	1.000	1.000	1.000	0.989	0.985	0.969	0.978	1.000	0.986
	↑worst	0.741	0.828	0.821	0.807	0.854	0.846	0.782	0.753	0.774	0.775
N14	↑mean	0.921	0.873	0.949	0.953	0.948	0.938	0.872	0.870	0.929	0.856
	±std	0.110	0.152	0.082	0.095	0.109	0.113	0.126	0.147	0.101	0.173
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	↑worst	0.667	0.425	0.688	0.625	0.625	0.583	0.542	0.500	0.700	0.250
N15	↑mean	0.817	0.823	0.828	0.825	0.822	0.817	0.824	0.811	0.810	0.818
	±std	0.024	0.030	0.029	0.025	0.020	0.027	0.029	0.030	0.030	0.031
	↑best	0.848	0.896	0.879	0.867	0.863	0.896	0.869	0.861	0.877	0.869
	↑worst	0.763	0.754	0.766	0.779	0.782	0.765	0.752	0.761	0.751	0.745
N16	↑mean	0.601	0.387	0.512	0.603	0.494	0.491	0.460	0.484	0.446	0.414
	±std	0.195	0.180	0.193	0.172	0.248	0.243	0.207	0.165	0.204	0.218
	↑best	0.889	0.889	0.833	0.917	1.000	0.833	0.778	0.833	0.867	0.833
	↑worst	0.222	0.067	0.000	0.222	0.000	0.000	0.083	0.167	0.056	0.000
N17	↑mean	0.914	0.911	0.914	0.908	0.906	0.907	0.909	0.911	0.909	0.909
	±std	0.009	0.011	0.011	0.012	0.014	0.009	0.010	0.008	0.009	0.011
	↑best	0.929	0.933	0.938	0.939	0.931	0.927	0.926	0.927	0.929	0.930
	↑worst	0.899	0.888	0.893	0.884	0.856	0.889	0.879	0.899	0.890	0.887
N18	↑mean	0.794	0.766	0.777	0.792	0.779	0.789	0.770	0.763	0.769	0.776
	±std	0.065	0.073	0.062	0.066	0.059	0.057	0.071	0.068	0.060	0.065
	↑best	0.904	0.904	0.899	0.931	0.884	0.893	0.887	0.882	0.924	0.880
	↑worst	0.655	0.606	0.619	0.667	0.660	0.665	0.645	0.643	0.646	0.625
N19	↑mean	0.890	0.878	0.867	0.853	0.816	0.820	0.839	0.836	0.803	0.802
	±std	0.019	0.028	0.027	0.025	0.033	0.028	0.036	0.028	0.028	0.037
	↑best	0.930	0.945	0.902	0.912	0.878	0.862	0.903	0.908	0.867	0.869
	↑worst	0.836	0.773	0.796	0.803	0.735	0.755	0.745	0.778	0.735	0.711
	↑Best Count	9.000	1.000	3.000	3.000	0.000	2.000	0.000	0.000	1.000	0.000
	↓Average Sort	3.053	4.842	3.947	5.316	5.053	4.947	6.105	6.895	7.105	7.737
	↓Ranking	1.000	3.000	2.000	6.000	5.000	4.000	7.000	8.000	9.000	10.000

, the recommended bWSO-log method achieved successful results in nine of the nineteen datasets. In the bWSO versions with the F1-Score values in

Table 7. The test F1-Score and detailed results of the bWSO-log and other versions.

ID		bWSO-log	bWSO-0	bWSO-s1	bWSO-s2	bWSO-s3	bWSO-s4	bWSO-v1	bWSO-v2	bWSO-v3	bWSO-v4
N1	↑mean	0.955	0.954	0.946	0.950	0.940	0.949	0.944	0.947	0.940	0.932
	±std	0.019	0.021	0.025	0.018	0.027	0.019	0.027	0.020	0.026	0.033
	↑best	0.984	1.000	0.992	0.985	0.985	0.984	0.984	0.977	0.984	0.984
	↑worst	0.916	0.904	0.890	0.915	0.872	0.904	0.866	0.919	0.870	0.820
N2	↑mean	0.474	0.466	0.447	0.442	0.461	0.450	0.441	0.445	0.465	0.457
	±std	0.061	0.082	0.061	0.086	0.079	0.076	0.070	0.062	0.085	0.074
	↑best	0.624	0.702	0.648	0.624	0.648	0.611	0.589	0.580	0.633	0.681
	↑worst	0.373	0.339	0.351	0.315	0.315	0.327	0.339	0.362	0.275	0.339
N3	↑mean	0.807	0.787	0.773	0.763	0.768	0.797	0.761	0.757	0.777	0.752
	±std	0.059	0.085	0.079	0.094	0.088	0.080	0.098	0.086	0.091	0.107
	↑best	0.899	0.935	0.921	0.872	0.888	0.911	0.923	0.854	0.881	0.877
	↑worst	0.683	0.576	0.603	0.467	0.489	0.520	0.551	0.496	0.531	0.444
N4	↑mean	0.913	0.903	0.903	0.888	0.908	0.897	0.897	0.909	0.896	0.882
	±std	0.056	0.053	0.073	0.076	0.057	0.068	0.053	0.057	0.049	0.082
	↑best	1.000	1.000	1.000	1.000	0.976	1.000	0.974	0.974	1.000	1.000
	↑worst	0.756	0.771	0.691	0.665	0.704	0.705	0.754	0.723	0.774	0.679
N5	↑mean	0.680	0.626	0.661	0.627	0.634	0.710	0.617	0.621	0.605	0.638
	±std	0.158	0.147	0.122	0.183	0.169	0.170	0.145	0.156	0.153	0.172
	↑best	1.000	1.000	0.933	1.000	1.000	1.000	0.943	0.970	1.000	0.925
	↑worst	0.288	0.289	0.429	0.256	0.330	0.343	0.364	0.295	0.406	0.334
N6	↑mean	0.563	0.535	0.591	0.528	0.497	0.556	0.547	0.530	0.522	0.547
	±std	0.158	0.146	0.171	0.172	0.152	0.172	0.155	0.150	0.135	0.159
	↑best	0.915	0.900	0.867	0.899	0.933	0.898	0.877	0.890	0.867	0.900
	↑worst	0.348	0.361	0.326	0.263	0.310	0.276	0.291	0.227	0.342	0.338
N7	↑mean	0.709	0.719	0.686	0.713	0.693	0.671	0.705	0.690	0.694	0.668
	±std	0.134	0.094	0.088	0.088	0.094	0.116	0.103	0.091	0.095	0.113
	↑best	0.893	0.847	0.895	0.877	0.893	0.893	0.877	0.852	0.870	0.856
	↑worst	0.476	0.478	0.481	0.550	0.468	0.468	0.465	0.521	0.481	0.471
N8	↑mean	0.637	0.655	0.651	0.639	0.657	0.688	0.661	0.643	0.643	0.639
	±std	0.117	0.102	0.119	0.101	0.106	0.104	0.115	0.090	0.126	0.122
	↑best	0.856	0.854	0.935	0.793	0.897	0.854	0.856	0.805	0.834	0.897
	↑worst	0.426	0.436	0.415	0.436	0.426	0.436	0.380	0.436	0.415	0.380
N9	↑mean	0.819	0.816	0.816	0.814	0.818	0.811	0.814	0.817	0.811	0.807
	±std	0.010	0.011	0.014	0.014	0.014	0.011	0.016	0.011	0.011	0.014
	↑best	0.845	0.842	0.847	0.841	0.841	0.831	0.839	0.836	0.835	0.827
	↑worst	0.801	0.790	0.798	0.789	0.786	0.792	0.776	0.793	0.787	0.774
N10	↑mean	0.785	0.780	0.782	0.794	0.785	0.791	0.753	0.782	0.757	0.734
	±std	0.088	0.092	0.097	0.080	0.107	0.102	0.096	0.099	0.063	0.113
	↑best	0.933	0.954	0.947	0.937	0.969	0.954	0.902	0.913	0.876	0.933
	↑worst	0.607	0.607	0.606	0.606	0.463	0.541	0.519	0.450	0.606	0.478
N11	↑mean	0.930	0.920	0.928	0.923	0.927	0.924	0.923	0.911	0.916	0.918
	±std	0.026	0.045	0.021	0.027	0.025	0.029	0.028	0.027	0.027	0.022
	↑best	0.990	0.971	0.981	0.973	0.972	0.981	0.973	0.963	0.962	0.962
	↑worst	0.853	0.728	0.887	0.842	0.862	0.841	0.861	0.870	0.847	0.884
N12	↑mean	0.820	0.843	0.787	0.803	0.816	0.812	0.846	0.859	0.868	0.840
	±std	0.041	0.055	0.052	0.070	0.047	0.064	0.052	0.056	0.041	0.059
	↑best	0.917	0.984	0.880	0.928	0.912	0.939	0.937	0.955	0.939	0.930
	↑worst	0.743	0.735	0.658	0.602	0.709	0.700	0.743	0.743	0.797	0.683
N13	↑mean	0.917	0.921	0.949	0.937	0.937	0.922	0.902	0.866	0.904	0.895
	±std	0.068	0.043	0.043	0.042	0.032	0.037	0.047	0.061	0.063	0.050
	↑best	0.986	1.000	1.000	1.000	0.989	0.985	0.969	0.978	1.000	0.980
	↑worst	0.730	0.820	0.815	0.819	0.851	0.846	0.801	0.747	0.737	0.771
N14	↑mean	0.903	0.831	0.937	0.947	0.941	0.931	0.844	0.839	0.910	0.822
	±std	0.139	0.193	0.111	0.105	0.126	0.126	0.151	0.171	0.132	0.209
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	↑worst	0.546	0.321	0.583	0.631	0.567	0.593	0.600	0.500	0.622	0.050
N15	↑mean	0.813	0.818	0.822	0.820	0.817	0.812	0.819	0.807	0.807	0.817
	±std	0.024	0.030	0.027	0.023	0.020	0.029	0.027	0.026	0.030	0.030
	↑best	0.844	0.883	0.866	0.866	0.860	0.898	0.867	0.857	0.876	0.860
	↑worst	0.751	0.758	0.765	0.773	0.780	0.762	0.750	0.766	0.754	0.744
N16	↑mean	0.536	0.323	0.443	0.514	0.442	0.424	0.385	0.373	0.381	0.335
	±std	0.195	0.179	0.202	0.175	0.250	0.219	0.189	0.177	0.192	0.204
	↑best	0.867	0.867	0.822	0.886	1.000	0.778	0.722	0.722	0.750	0.822
	↑worst	0.111	0.083	0.000	0.148	0.000	0.000	0.083	0.095	0.083	0.000
N17	↑mean	0.914	0.911	0.914	0.909	0.907	0.908	0.909	0.912	0.910	0.910
	±std	0.008	0.011	0.010	0.010	0.013	0.009	0.012	0.008	0.009	0.011
	↑best	0.928	0.934	0.938	0.934	0.931	0.928	0.928	0.926	0.930	0.931
	↑worst	0.902	0.892	0.897	0.888	0.862	0.894	0.869	0.898	0.889	0.885
N18	↑mean	0.790	0.761	0.772	0.790	0.774	0.783	0.766	0.757	0.766	0.770
	±std	0.067	0.076	0.066	0.068	0.060	0.057	0.075	0.072	0.061	0.069
	↑best	0.904	0.904	0.903	0.928	0.881	0.880	0.896	0.880	0.927	0.880
	↑worst	0.658	0.571	0.605	0.660	0.658	0.633	0.637	0.596	0.641	0.619
N19	↑mean	0.888	0.877	0.863	0.851	0.815	0.820	0.838	0.836	0.806	0.804
	±std	0.020	0.027	0.029	0.025	0.032	0.029	0.035	0.028	0.026	0.035
	↑best	0.929	0.943	0.905	0.911	0.872	0.865	0.907	0.908	0.862	0.864
	↑worst	0.832	0.776	0.780	0.805	0.730	0.752	0.739	0.774	0.741	0.726
	↑Best Count	10.00	1.000	4.000	2.000	0.000	2.000	0.000	0.000	1.000	0.000
	↓Average Sort	2.947	5.000	4.105	5.000	5.000	5.000	6.316	6.789	6.842	7.947
	↓Ranking	1.000	3.000	2.000	3.000	3.000	3.000	7.000	8.000	9.000	10.00

, the proposed bWSO-log method was found to be better in ten of the nineteen datasets.

6.2. Comparison with the State of the Art Approaches

In the second part of the experimental study, the proposed binary bWSO-log method was compared with algorithms widely used in the literature. All other algorithms included in the comparison were discretized using the S1 transfer function, which is frequently preferred in the literature. These algorithms are as follows: bAAA, bBAT, bFA, bGWO, bMFO, bMVO, bPSO, and bWOA.

Table 8. Average of classification accuracy for the proposed bWSO-log algorithm in comparison to other algorithms.

ID		bWSO-log	bAAA	bBAT	bFA	bGWO	bMFO	bMVO	bPSO	bWOA
N1	↑mean	0.960	0.950	0.948	0.954	0.959	0.958	0.952	0.958	0.952
	±std	0.017	0.023	0.023	0.018	0.018	0.020	0.020	0.016	0.019
	↑best	0.986	0.993	0.979	0.986	0.993	0.993	0.986	0.986	0.986
	↑worst	0.921	0.900	0.886	0.907	0.914	0.921	0.914	0.929	0.893
N2	↑mean	0.661	0.628	0.648	0.633	0.635	0.637	0.630	0.627	0.633
	±std	0.056	0.073	0.069	0.056	0.069	0.066	0.054	0.079	0.073
	↑best	0.757	0.784	0.757	0.757	0.757	0.757	0.730	0.784	0.757
	↑worst	0.541	0.459	0.486	0.514	0.514	0.514	0.514	0.486	0.486
N3	↑mean	0.841	0.833	0.636	0.785	0.831	0.829	0.821	0.691	0.818
	±std	0.050	0.051	0.056	0.079	0.046	0.064	0.081	0.111	0.085
	↑best	0.917	0.917	0.717	0.900	0.917	0.950	0.933	0.883	0.950
	↑worst	0.733	0.700	0.467	0.550	0.750	0.717	0.583	0.500	0.633
N4	↑mean	0.912	0.924	0.705	0.908	0.869	0.924	0.902	0.767	0.879
	±std	0.057	0.042	0.100	0.064	0.102	0.048	0.052	0.109	0.048
	↑best	1.000	1.000	0.972	1.000	0.972	0.972	1.000	0.972	0.972
	↑worst	0.750	0.806	0.472	0.694	0.528	0.806	0.750	0.556	0.778
N5	↑mean	0.856	0.860	0.851	0.843	0.889	0.844	0.832	0.856	0.846
	±std	0.085	0.094	0.069	0.135	0.078	0.093	0.104	0.082	0.088
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.952	0.952
	↑worst	0.619	0.571	0.667	0.429	0.619	0.619	0.571	0.667	0.571
N6	↑mean	0.780	0.762	0.704	0.738	0.749	0.773	0.758	0.748	0.752
	±std	0.062	0.078	0.077	0.077	0.065	0.080	0.081	0.097	0.087
	↑best	0.867	0.933	0.867	0.867	0.900	1.000	0.933	0.900	0.900
	↑worst	0.600	0.633	0.500	0.533	0.600	0.633	0.567	0.467	0.500
N7	↑mean	0.940	0.931	0.915	0.920	0.923	0.926	0.927	0.919	0.920
	±std	0.020	0.019	0.023	0.027	0.027	0.028	0.017	0.028	0.032
	↑best	0.972	0.963	0.954	0.963	0.963	0.991	0.954	0.981	0.963
	↑worst	0.907	0.889	0.870	0.852	0.861	0.870	0.889	0.861	0.815
N8	↑mean	0.822	0.795	0.760	0.804	0.783	0.815	0.780	0.790	0.792
	±std	0.057	0.070	0.059	0.057	0.070	0.083	0.061	0.069	0.068
	↑best	0.935	0.903	0.839	0.935	0.935	0.968	0.903	0.903	0.935
	↑worst	0.742	0.613	0.645	0.677	0.677	0.645	0.645	0.645	0.677
N9	↑mean	0.820	0.815	0.668	0.817	0.798	0.816	0.812	0.809	0.815
	±std	0.010	0.011	0.055	0.011	0.014	0.014	0.014	0.016	0.013
	↑best	0.845	0.840	0.770	0.846	0.835	0.842	0.837	0.841	0.838
	↑worst	0.802	0.794	0.503	0.792	0.770	0.790	0.790	0.778	0.789
N10	↑mean	0.817	0.861	0.842	0.847	0.844	0.848	0.854	0.852	0.852
	±std	0.013	0.041	0.045	0.053	0.064	0.067	0.067	0.040	0.047
	↑best	0.844	0.923	0.949	0.949	0.923	0.949	0.974	0.923	0.949
	↑worst	0.780	0.769	0.769	0.769	0.667	0.692	0.718	0.769	0.769
N11	↑mean	0.936	0.932	0.918	0.934	0.937	0.930	0.934	0.925	0.920
	±std	0.024	0.020	0.023	0.023	0.019	0.020	0.020	0.021	0.028
	↑best	0.991	0.974	0.956	0.982	0.982	0.974	0.974	0.965	0.965
	↑worst	0.860	0.886	0.860	0.904	0.895	0.886	0.895	0.886	0.868
N12	↑mean	0.855	0.840	0.838	0.838	0.853	0.843	0.853	0.838	0.854
	±std	0.036	0.044	0.049	0.048	0.038	0.053	0.046	0.048	0.049
	↑best	0.930	0.944	0.901	0.944	0.915	0.901	0.930	0.958	0.972
	↑worst	0.789	0.761	0.746	0.732	0.775	0.676	0.746	0.761	0.732
N13	↑mean	0.933	0.947	0.722	0.941	0.954	0.951	0.941	0.896	0.939
	±std	0.047	0.029	0.064	0.038	0.028	0.023	0.030	0.076	0.036
	↑best	0.986	1.000	0.824	0.986	1.000	1.000	1.000	0.986	1.000
	↑worst	0.811	0.865	0.581	0.824	0.878	0.892	0.865	0.757	0.838
N14	↑mean	0.933	0.923	0.907	0.897	0.930	0.927	0.940	0.927	0.963
	±std	0.096	0.097	0.120	0.150	0.115	0.091	0.097	0.126	0.061
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	↑worst	0.700	0.600	0.600	0.400	0.500	0.700	0.700	0.400	0.800
N15	↑mean	0.830	0.844	0.799	0.838	0.834	0.840	0.835	0.816	0.835
	±std	0.020	0.022	0.040	0.018	0.032	0.029	0.027	0.029	0.028
	↑best	0.858	0.882	0.877	0.867	0.891	0.882	0.882	0.863	0.886
	↑worst	0.777	0.806	0.701	0.796	0.768	0.758	0.768	0.749	0.777
N16	↑mean	0.557	0.448	0.414	0.471	0.386	0.448	0.429	0.471	0.433
	±std	0.189	0.175	0.132	0.164	0.188	0.190	0.212	0.209	0.223
	↑best	0.857	0.857	0.571	0.857	0.714	0.714	1.000	1.000	1.000
	↑worst	0.143	0.143	0.143	0.286	0.000	0.143	0.000	0.143	0.000
N17	↑mean	0.918	0.918	0.777	0.909	0.899	0.912	0.912	0.856	0.915
	±std	0.008	0.008	0.017	0.012	0.012	0.010	0.013	0.052	0.009
	↑best	0.933	0.937	0.815	0.933	0.932	0.944	0.931	0.926	0.935
	↑worst	0.907	0.895	0.747	0.874	0.881	0.897	0.887	0.776	0.893
N18	↑mean	0.797	0.796	0.792	0.770	0.788	0.788	0.771	0.790	0.767
	±std	0.065	0.051	0.071	0.058	0.050	0.047	0.070	0.064	0.071
	↑best	0.905	0.881	0.905	0.857	0.905	0.857	0.929	0.929	0.881
	↑worst	0.667	0.714	0.667	0.667	0.714	0.667	0.619	0.690	0.595
N19	↑mean	0.888	0.865	0.566	0.816	0.761	0.862	0.850	0.816	0.869
	±std	0.021	0.022	0.087	0.031	0.044	0.031	0.037	0.050	0.025
	↑best	0.931	0.903	0.736	0.884	0.833	0.903	0.907	0.903	0.931
	↑worst	0.829	0.810	0.380	0.745	0.630	0.755	0.782	0.722	0.819
	↑Best Count	11.000	4.000	0.000	0.000	3.000	1.000	0.000	0.000	1.000
	↓Average Sort	2.474	3.526	7.947	5.579	5.000	3.947	5.053	6.263	5.000
	↓Ranking	1.000	2.000	9.000	7.000	4.000	3.000	6.000	8.000	4.000

presents the performance of the bWSO-log and the other algorithms in terms of classification accuracy. According to the results obtained, the bWSO-log algorithm demonstrated superior performance in eleven out of nineteen datasets. In other words, the bWSO-log method achieved approximately 58% superior performance across the datasets.

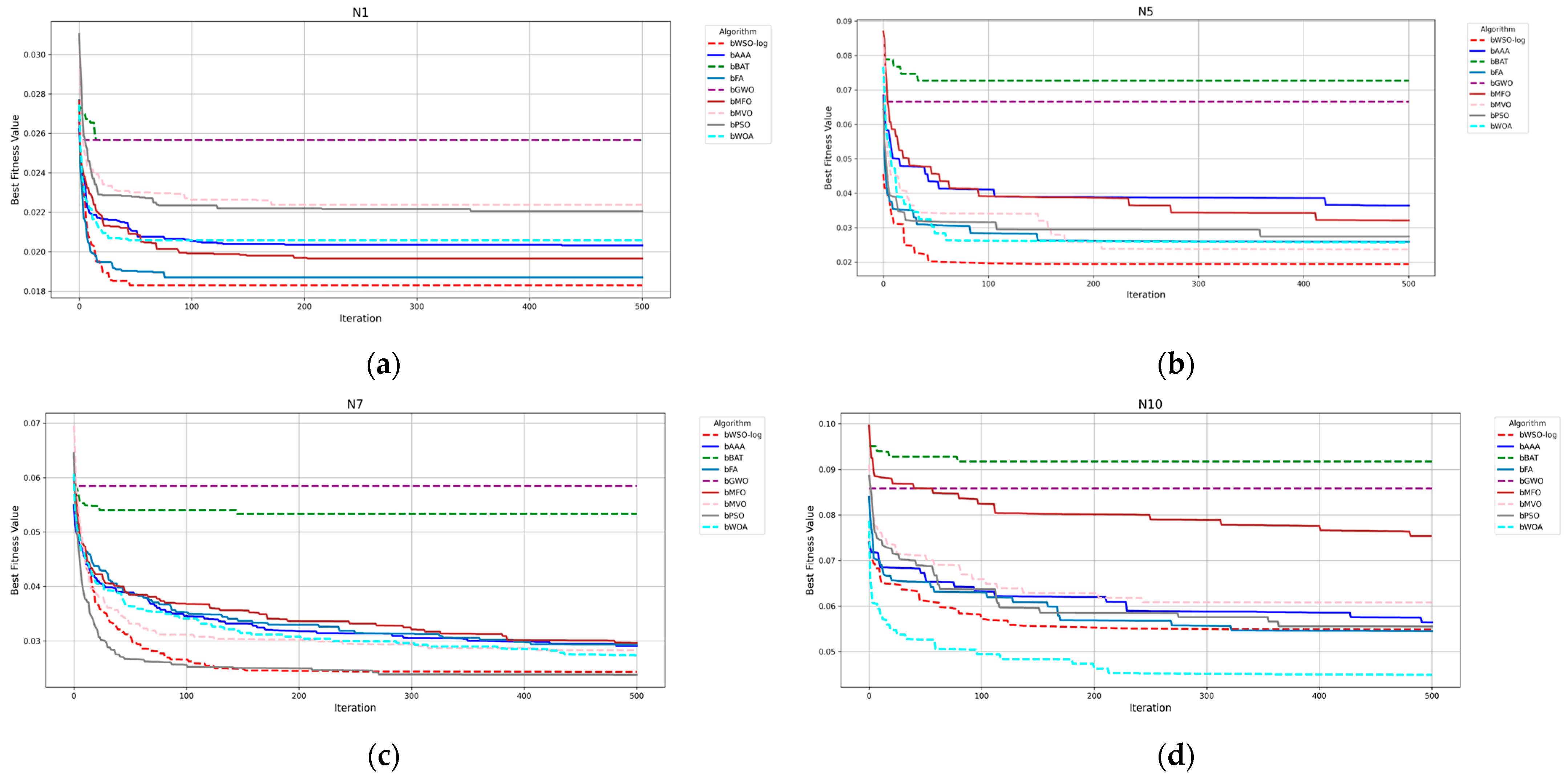
Figure 5 presents a comparative analysis of the convergence performance of the proposed bWSO-log algorithm against other algorithms for the N1, N5, N7, and N10 datasets. Only these four datasets are included as examples to avoid visual clutter and maintain clarity in the figure. Including all datasets would have made the diagram overly complex and difficult to interpret. However, the algorithm applies the same processing steps to the entire feature set of each dataset. As seen in the convergence curves, the proposed algorithm achieves the best results for the N1 and N5 datasets and produces results close to the best for the N7 and N10 datasets.

Table 9. p-values of Wilcoxon signed rank test comparing bWSO-log fitness results with other algorithms (p < 0.05 in bold).

	bAAA	bBAT	bFA	bGWO	bMFO	bMVO	bPSO	bWOA
N1	2.52 × 10−2	6.02 × 10−2	1.96 × 10−1	8.28 × 10−1	4.83 × 10−1	8.32 × 10−2	4.83 × 10−1	7.59 × 10−2
N2	1.04 × 10−1	3.86 × 10−1	5.87 × 10−2	1.55 × 10−1	6.10 × 10−2	1.38 × 10−2	3.06 × 10−2	1.28 × 10−1
N3	4.75 × 10−1	1.86 × 10−9	5.17 × 10−3	3.30 × 10−1	5.01 × 10−1	5.69 × 10−1	2.99 × 10−5	3.41 × 10−1
N4	5.73 × 10−1	2.83 × 10−6	8.39 × 10−1	8.47 × 10−2	5.22 × 10−1	4.73 × 10−1	6.41 × 10−6	2.40 × 10−2
N5	7.77 × 10−1	8.54 × 10−1	7.60 × 10−1	4.04 × 10−2	5.29 × 10−1	3.90 × 10−1	9.90 × 10−1	5.53 × 10−1
N6	1.73 × 10−1	7.24 × 10−4	2.38 × 10−2	1.71 × 10−1	8.29 × 10−1	2.03 × 10−1	2.22 × 10−1	1.07 × 10−1
N7	5.15 × 10−2	6.29 × 10−4	8.25 × 10−3	7.72 × 10−3	8.71 × 10−2	2.66 × 10−2	2.91 × 10−3	3.13 × 10−3
N8	1.25 × 10−1	1.94 × 10−3	3.43 × 10−1	3.41 × 10−2	7.92 × 10−1	1.72 × 10−2	1.06 × 10−1	1.24 × 10−1
N9	1.68 × 10−1	1.73 × 10−6	5.93 × 10−1	2.59 × 10−5	3.49 × 10−1	4.83 × 10−2	7.26 × 10−3	1.50 × 10−1
N10	8.29 × 10−1	3.36 × 10−1	5.23 × 10−1	4.04 × 10−1	5.52 × 10−1	8.08 × 10−1	7.21 × 10−1	6.19 × 10−1
N11	4.74 × 10−1	1.06 × 10−2	5.47 × 10−1	7.77 × 10−1	1.99 × 10−1	7.09 × 10−1	5.39 × 10−2	3.70 × 10−2
N12	2.44 × 10−1	1.13 × 10−1	1.44 × 10−1	9.09 × 10−1	5.30 × 10−1	8.39 × 10−1	1.51 × 10−1	8.29 × 10−1
N13	1.74 × 10−1	1.73 × 10−6	5.50 × 10−1	7.00 × 10−2	1.00 × 10−1	4.93 × 10−1	1.43 × 10−2	6.14 × 10−1
N14	9.86 × 10−1	4.01 × 10−1	3.61 × 10−1	7.34 × 10−1	8.77 × 10−1	8.12 × 10−1	1.00 × 100	1.24 × 10−1
N15	1.02 × 10−2	1.67 × 10−3	2.55 × 10−2	3.93 × 10−1	4.58 × 10−2	2.03 × 10−1	6.91 × 10−2	4.71 × 10−1
N16	5.26 × 10−2	4.30 × 10−3	3.10 × 10−2	2.31 × 10−3	3.13 × 10−2	4.03 × 10−2	1.08 × 10−1	7.69 × 10−2
N17	8.29 × 10−1	1.72 × 10−6	1.38 × 10−3	8.81 × 10−6	1.84 × 10−2	2.97 × 10−2	3.88 × 10−6	2.99 × 10−1
N18	9.80 × 10−1	8.03 × 10−1	1.35 × 10−1	4.94 × 10−1	4.83 × 10−1	2.55 × 10−1	5.72 × 10−1	8.50 × 10−2
N19	7.18 × 10−4	1.73 × 10−6	3.15 × 10−6	1.73 × 10−6	1.90 × 10−4	2.50 × 10−4	3.50 × 10−6	7.16 × 10−3

presents the comparison of the accuracy rates of the proposed bWSO-log method with other algorithms based on the p-value results of the Wilcoxon signed-rank test. In

Table 10. Average of F1-Score for the proposed bWSO-log algorithm in comparison to other algorithms.

ID		bWSO-log	bAAA	bBAT	bFA	bGWO	bMFO	bMVO	bPSO	bWOA
N1	↑mean	0.955	0.945	0.941	0.949	0.955	0.953	0.946	0.954	0.946
	±std	0.019	0.025	0.026	0.021	0.020	0.022	0.021	0.018	0.022
	↑best	0.984	0.992	0.976	0.985	0.992	0.992	0.984	0.985	0.985
	↑worst	0.916	0.891	0.866	0.896	0.910	0.914	0.904	0.923	0.881
N2	↑mean	0.474	0.451	0.465	0.464	0.446	0.474	0.466	0.462	0.474
	±std	0.061	0.075	0.080	0.061	0.070	0.088	0.062	0.073	0.082
	↑best	0.624	0.612	0.624	0.656	0.624	0.656	0.580	0.624	0.624
	↑worst	0.373	0.315	0.327	0.383	0.339	0.351	0.362	0.327	0.327
N3	↑mean	0.807	0.795	0.503	0.740	0.792	0.790	0.779	0.606	0.768
	±std	0.059	0.068	0.061	0.086	0.054	0.082	0.097	0.144	0.108
	↑best	0.899	0.909	0.630	0.878	0.881	0.924	0.921	0.848	0.928
	↑worst	0.683	0.621	0.384	0.500	0.666	0.607	0.496	0.394	0.549
N4	↑mean	0.913	0.923	0.671	0.910	0.866	0.922	0.903	0.747	0.880
	±std	0.056	0.043	0.106	0.065	0.105	0.051	0.052	0.126	0.050
	↑best	1.000	1.000	0.973	1.000	0.977	0.978	1.000	0.976	0.968
	↑worst	0.756	0.800	0.444	0.685	0.531	0.783	0.758	0.489	0.759
N5	↑mean	0.680	0.726	0.662	0.667	0.748	0.680	0.646	0.697	0.643
	±std	0.158	0.156	0.133	0.205	0.123	0.169	0.161	0.138	0.139
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.967	0.959
	↑worst	0.288	0.396	0.383	0.321	0.516	0.231	0.386	0.473	0.400
N6	↑mean	0.599	0.550	0.504	0.513	0.547	0.598	0.566	0.551	0.551
	±std	0.162	0.179	0.142	0.128	0.142	0.187	0.152	0.173	0.157
	↑best	0.867	0.933	0.792	0.796	0.814	1.000	0.890	0.890	0.877
	↑worst	0.354	0.289	0.261	0.263	0.310	0.317	0.362	0.245	0.307
N7	↑mean	0.709	0.677	0.519	0.666	0.606	0.693	0.679	0.613	0.672
	±std	0.134	0.091	0.061	0.092	0.100	0.100	0.088	0.093	0.099
	↑best	0.893	0.821	0.665	0.865	0.821	0.926	0.818	0.798	0.821
	↑worst	0.476	0.473	0.465	0.515	0.473	0.471	0.478	0.463	0.468
N8	↑mean	0.637	0.642	0.501	0.669	0.597	0.670	0.646	0.547	0.623
	±std	0.117	0.124	0.102	0.090	0.114	0.122	0.103	0.114	0.130
	↑best	0.856	0.868	0.765	0.832	0.834	0.897	0.815	0.805	0.881
	↑worst	0.426	0.380	0.392	0.446	0.415	0.465	0.426	0.392	0.426
N9	↑mean	0.819	0.814	0.666	0.817	0.798	0.815	0.811	0.808	0.814
	±std	0.010	0.011	0.055	0.011	0.015	0.014	0.013	0.016	0.012
	↑best	0.845	0.840	0.769	0.845	0.835	0.842	0.837	0.840	0.837
	↑worst	0.801	0.793	0.502	0.792	0.769	0.790	0.789	0.777	0.789
N10	↑mean	0.785	0.796	0.752	0.785	0.771	0.784	0.777	0.773	0.797
	±std	0.088	0.059	0.067	0.071	0.089	0.081	0.100	0.065	0.065
	↑best	0.933	0.887	0.861	0.933	0.887	0.933	0.962	0.902	0.933
	↑worst	0.607	0.662	0.606	0.662	0.511	0.597	0.586	0.677	0.686
N11	↑mean	0.930	0.927	0.911	0.928	0.931	0.924	0.928	0.918	0.913
	±std	0.026	0.021	0.026	0.025	0.022	0.021	0.023	0.023	0.028
	↑best	0.990	0.971	0.955	0.981	0.981	0.969	0.969	0.960	0.959
	↑worst	0.853	0.876	0.854	0.889	0.872	0.881	0.882	0.874	0.859
N12	↑mean	0.820	0.804	0.805	0.797	0.818	0.809	0.826	0.801	0.828
	±std	0.041	0.051	0.059	0.060	0.048	0.059	0.052	0.054	0.059
	↑best	0.917	0.930	0.891	0.915	0.904	0.889	0.917	0.949	0.965
	↑worst	0.743	0.716	0.689	0.640	0.722	0.634	0.696	0.718	0.674
N13	↑mean	0.917	0.939	0.682	0.933	0.948	0.947	0.933	0.875	0.928
	±std	0.068	0.036	0.064	0.042	0.030	0.031	0.034	0.096	0.045
	↑best	0.986	1.000	0.791	0.985	1.000	1.000	1.000	0.984	1.000
	↑worst	0.730	0.843	0.576	0.803	0.876	0.838	0.862	0.688	0.776
N14	↑mean	0.903	0.902	0.895	0.895	0.932	0.915	0.930	0.920	0.941
	±std	0.139	0.125	0.132	0.148	0.101	0.109	0.122	0.127	0.112
	↑best	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	↑worst	0.546	0.533	0.602	0.389	0.636	0.652	0.544	0.467	0.625
N15	↑mean	0.813	0.826	0.776	0.821	0.817	0.824	0.816	0.800	0.816
	±std	0.024	0.025	0.046	0.022	0.036	0.029	0.031	0.030	0.032
	↑best	0.844	0.863	0.861	0.859	0.879	0.876	0.864	0.846	0.875
	↑worst	0.751	0.777	0.651	0.771	0.744	0.746	0.742	0.727	0.742
N16	↑mean	0.536	0.404	0.380	0.422	0.374	0.415	0.395	0.433	0.377
	±std	0.195	0.188	0.139	0.187	0.198	0.209	0.211	0.228	0.217
	↑best	0.867	0.841	0.657	0.886	0.778	0.778	1.000	1.000	1.000
	↑worst	0.111	0.111	0.083	0.167	0.000	0.095	0.000	0.083	0.000
N17	↑mean	0.914	0.914	0.766	0.904	0.893	0.907	0.908	0.849	0.911
	±std	0.008	0.008	0.017	0.012	0.013	0.010	0.013	0.055	0.010
	↑best	0.928	0.933	0.807	0.930	0.927	0.942	0.928	0.921	0.932
	↑worst	0.902	0.889	0.736	0.871	0.874	0.892	0.881	0.764	0.889
N18	↑mean	0.790	0.789	0.783	0.759	0.782	0.782	0.766	0.784	0.762
	±std	0.067	0.051	0.075	0.062	0.051	0.048	0.070	0.066	0.072
	↑best	0.904	0.879	0.905	0.857	0.893	0.857	0.927	0.929	0.879
	↑worst	0.658	0.708	0.637	0.647	0.697	0.660	0.619	0.676	0.595
N19	↑mean	0.888	0.863	0.565	0.816	0.764	0.861	0.848	0.814	0.866
	±std	0.020	0.020	0.085	0.028	0.042	0.029	0.035	0.048	0.025
	↑best	0.929	0.907	0.738	0.878	0.826	0.904	0.907	0.901	0.931
	↑worst	0.832	0.814	0.395	0.759	0.644	0.770	0.788	0.718	0.832
	↑Best Count	8.000	2.000	0.000	0.000	3.000	2.000	0.000	0.000	3.000
	↓Average Sort	2.737	4.000	8.105	5.421	5.368	3.526	4.684	6.158	5.000
	↓Ranking	1.000	3.000	9.000	7.000	6.000	2.000	4.000	8.000	5.000

, p-values less than 0.05 are highlighted in bold. Values highlighted in bold indicate that the null hypothesis (H₀) is rejected and the alternative hypothesis (H₁) is accepted. In other words, a statistically significant difference is assumed. Upon examination of Table 10, it is observed that the proposed bWSO-log method achieves a significant difference in terms of fitness values compared to the other algorithms.

Mean value, standard deviation, best and worst values of F1-Score values are given in Table 10. It has been seen that the proposed bWSO-log value has better values than other algorithms.

7. Conclusions and Future Works

In this study, a novel approach called bWSO-log was proposed for addressing feature selection problems. The WSO, one of the swarm intelligence-based optimization algorithms, was adapted into a binary form using various discretization strategies, and the resulting bWSO-log method was evaluated on nineteen datasets with varying levels of complexity. In addition to commonly used algorithms in the literature (bAAA, bBAT, bFA, bGWO, bMFO, bMVO, bPSO, and bWOA), comparative analyses were conducted with bWSO variants employing S-Shape and V-Shape transfer functions.

To more clearly assess the contribution of the proposed logarithmic transfer function, a version of the algorithm without any transfer function, referred to as bWSO-0, was also included in the experiments. The results demonstrated that the logarithmic function not only significantly enhanced optimization performance but also offered a strong alternative to the widely used S-Shape and V-Shape transfer functions.

The findings indicate that the bWSO-log method is an effective and competitive solution for feature selection problems. However, this study also has certain limitations. First, the proposed algorithm was tested on a limited number of datasets; applying the method to a broader range of datasets from diverse domains would allow for a more comprehensive assessment of its generalizability. Furthermore, the performance of the algorithm is highly dependent on the structure of the logarithmic transfer function and the proper tuning of algorithm parameters, making parameter selection a critical factor.

For future research, different variants or parametric versions of the logarithmic function can be explored to examine their impact on performance, and the proposed algorithm can be compared with recently developed optimization algorithms. Additionally, the bWSO algorithm can be integrated with other feature selection strategies or deep learning-based models to develop more robust and comprehensive hybrid approaches.