Machine-Learning Insights from the Framingham Heart Study: Enhancing Cardiovascular Risk Prediction and Monitoring
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design and Population
2.2. Data Collection
2.3. Machine-Learning Analysis
- XGBoostGradient boosting algorithm known for its high predictive accuracy and ability to handle complex interactions between variables.
- Random ForestEnsemble learning method that constructs multiple decision trees and outputs the mode of the classes (classification) or mean prediction (regression).
- Logistic RegressionTraditional statistical model used as a baseline for binary classification tasks.
- Weighted EnsembleCombines multiple model predictions by assigning different weights based on each model’s performance.
- LightGBMA fast, efficient gradient boosting framework that uses histogram-based algorithms and is optimized for speed and memory usage.
- Neural NetworkA machine-learning model inspired by the human brain, capable of capturing complex non-linear relationships in the data.
- Gradient BoostingAn ensemble technique that builds models sequentially, where each new model corrects the errors of the previous ones.
- k-Nearest Neighbors (kNN)A non-parametric method that classifies instances based on the majority label of their k closest neighbors in the feature space.
- Support Vector Machine (SVM)A supervised learning algorithm that finds the optimal hyperplane to separate classes with maximum margin.
2.4. Train Test Split and Value of k in the Cross Fold Validation
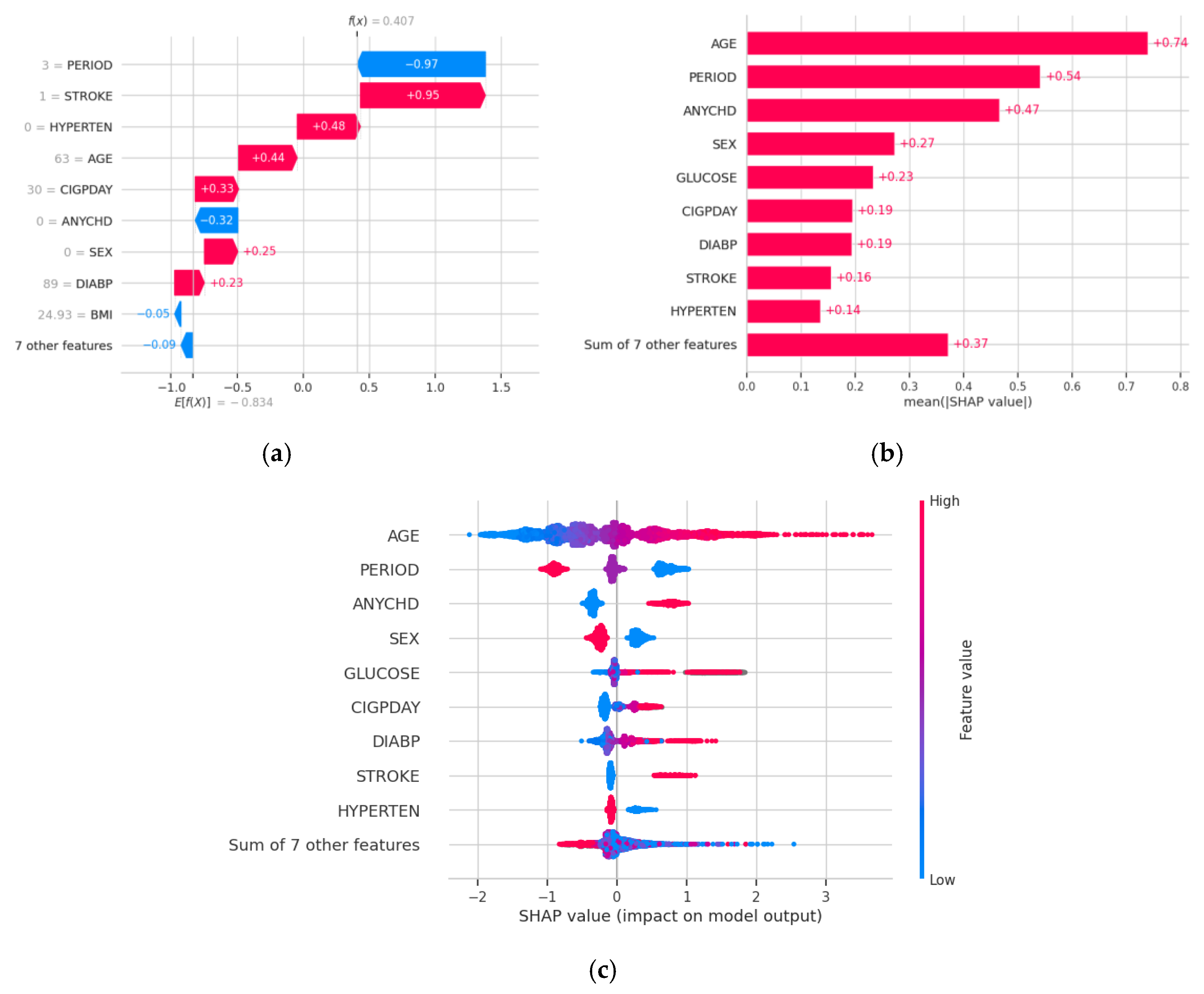
3. Results
- n_estimators (number of trees): [50, 100, 200]
- max_depth (maximum depth of trees): [3, 5, 7]
- learning_rate (step size shrinkage): [0.01, 0.1, 0.2]
- subsample (subsampling ratio of training instances): [0.7, 0.8, 0.9]
- colsample_bytree (subsampling ratio of features): [0.7, 0.8, 0.9]
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Teo, K.K.; Rafiq, T. Cardiovascular Risk Factors and Prevention: A Perspective from Developing Countries. Can. J. Cardiol. 2021, 37, 733–743. [Google Scholar] [CrossRef]
- Lopez-Jaramillo, P.; Lopez-Lopez, J.P.; Tole, M.C.; Cohen, D.D. Muscular Strength in Risk Factors for Cardiovascular Disease and Mortality: A Narrative Review. Anatol. J. Cardiol. 2022, 26, 598–607. [Google Scholar] [CrossRef] [PubMed]
- Artola Arita, V.; Beigrezaei, S.; Franco, O.H. Risk Factors for Cardiovascular Disease: The Known Unknown. Eur. J. Prev. Cardiol. 2024, 31, e106–e107. [Google Scholar] [CrossRef]
- Miller, D.V.; Watson, K.E.; Wang, H.; Fyfe-Kirschner, B.; Heide, R.S.V. Racially Related Risk Factors for Cardiovascular Disease: Society for Cardiovascular Pathology Symposium 2022. Cardiovasc. Pathol. 2022, 61, 107470. [Google Scholar] [CrossRef]
- Saba, P.S.; Parodi, G.; Ganau, A. From Risk Factors to Clinical Disease: New Opportunities and Challenges for Cardiovascular Risk Prediction. J. Am. Coll. Cardiol. 2021, 77, 1436–1438. [Google Scholar] [CrossRef]
- Whelton, S.P.; Post, W.S. Importance of Traditional Cardiovascular Risk Factors for Identifying High-Risk Persons in Early Adulthood. Eur. Heart J. 2022, 43, 2901–2903. [Google Scholar] [CrossRef]
- Pirzada, A.; Cai, J.; Cordero, C.; Gallo, L.C.; Isasi, C.R.; Kunz, J.; Thyagaragan, B.; Wassertheil-Smoller, S.; Daviglus, M.L. Risk Factors for Cardiovascular Disease: Knowledge Gained from the Hispanic Community Health Study/Study of Latinos. Curr. Atheroscler. Rep. 2023, 25, 785–793. [Google Scholar] [CrossRef]
- Godijk, N.G.; Vos, A.G.; Jongen, V.W.; Moraba, R.; Tempelman, H.; Grobbee, D.E.; Coutinho, R.A.; Devillé, W.; Klipstein-Grobusch, K. Heart Rate Variability, HIV and the Risk of Cardiovascular Diseases in Rural South Africa. Glob. Heart 2020, 15, 17. [Google Scholar] [CrossRef]
- Rosenthal, T.; Touyz, R.M.; Oparil, S. Migrating Populations and Health: Risk Factors for Cardiovascular Disease and Metabolic Syndrome. Curr. Hypertens. Rep. 2022, 24, 325–340. [Google Scholar] [CrossRef] [PubMed]
- Quesada, O. Reproductive Risk Factors for Cardiovascular Disease in Women. Menopause 2023, 30, 1058–1060. [Google Scholar] [CrossRef] [PubMed]
- Hauer, R.N.W. The Fractionated QRS Complex for Cardiovascular Risk Assessment. Eur. Heart J. 2022, 43, 4192–4194. [Google Scholar] [CrossRef]
- Thayer, J.F.; Yamamoto, S.S.; Brosschot, J.F. The Relationship of Autonomic Imbalance, Heart Rate Variability and Cardio-vascular Disease Risk Factors. Int. J. Cardiol. 2010, 141, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Wekenborg, M.K.; Künzel, R.G.; Rothe, N.; Penz, M.; Walther, A.; Kirschbaum, C.; Thayer, J.F.; Hill, L.K. Exhaustion and Car-diovascular Risk Factors: The Role of Vagally-Mediated Heart Rate Variability. Ann. Epidemiol. 2023, 87, S1047–S2797. [Google Scholar] [CrossRef] [PubMed]
- Malik, M. Heart Rate Variability. Curr. Opin. Cardiol. 1998, 13, 36–44. [Google Scholar] [CrossRef]
- Hutchesson, M.; Campbell, L.; Leonard, A.; Vincze, L.; Shrewsbury, V.; Collins, C.; Taylor, R. Disorders of Pregnancy and Cardiovascular Health Outcomes? A Systematic Review of Observational Studies. Pregnancy Hypertens. 2022, 27, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Freak-Poli, R.; Phyo, A.Z.Z.; Hu, J.; Barker, S.F. Are Social Isolation, Lack of Social Support or Loneliness Risk Factors for Cardiovascular Disease in Australia and New Zealand? A Systematic Review and Meta-Analysis. Health Promot. J. Aust. 2022, 33, 278–315. [Google Scholar] [CrossRef]
- Bergami, M.; Scarpone, M.; Bugiardini, R.; Cenko, E.; Manfrini, O. Sex Beyond Cardiovascular Risk Factors and Clinical Biomarkers of Cardiovascular Disease. Rev. Cardiovasc. Med. 2022, 23, 19. [Google Scholar] [CrossRef]
- Kato, M. Diet- and Sleep-Based Approach for Cardiovascular Risk/Diseases. Nutrients 2023, 15, 3668. [Google Scholar] [CrossRef]
- Greiser, K.H.; Kluttig, A.; Schumann, B.; Kors, J.A.; Swenne, C.A.; Kuss, O.; Werdan, K.; Haerting, J. Cardiovascular Disease, Risk Factors and Heart Rate Variability in the Elderly General Population: De-sign and Objectives of the CARLA Study. BMC Cardiovasc. Disord. 2005, 5, 36. [Google Scholar] [CrossRef]
- Nakayama, N.; Miyachi, M.; Tamakoshi, K.; Morikawa, S.; Negi, K.; Watanabe, K.; Moriwaki, Y.; Hirai, M. Increased After-noon Step Count Increases Heart Rate Variability in Patients with Cardiovascular Risk Factors. J. Clin. Nurs. 2022, 31, 1636–1642. [Google Scholar] [CrossRef]
- Møller, A.L.; Andersson, C. Importance of Smoking Cessation for Cardiovascular Risk Reduction. Eur. Heart J. 2021, 42, 4154–4156. [Google Scholar] [CrossRef] [PubMed]
- Yuda, E.; Ueda, N.; Kisohara, M.; Hayano, J. Redundancy among risk predictors derived from heart rate variability and dynamics: ALLSTAR big data analysis. Ann. Noninvasive Electrocardiol. 2021, 26, e12790. [Google Scholar] [CrossRef] [PubMed]
- Carney, R.M.; Blumenthal, J.A.; Freedland, K.E.; Stein, P.K.; Howells, W.B.; Berkman, L.F.; Watkins, L.L.; Czajkowski, S.M.; Hayano, J.; Domitrovich, P.P.; et al. Low heart rate variability and the effect of depression on post-myocardial infarction mortality. Arch. Intern. Med. 2005, 165, 1486–1491. [Google Scholar] [CrossRef]
- Blumenthal, J.A.; Sherwood, A.; Babyak, M.A.; Watkins, L.L.; Waugh, R.; Georgiades, A.; Bacon, S.L.; Hayano, J.; Coleman, R.E.; Hinderliter, A. Effects of exercise and stress management training on markers of cardiovascular risk in patients with ischemic heart disease: A randomized controlled trial. JAMA 2005, 293, 1626–1634. [Google Scholar] [CrossRef] [PubMed]
- Kiyono, K.; Hayano, J.; Watanabe, E.; Struzik, Z.R.; Yamamoto, Y. Non-Gaussian heart rate as an independent predictor of mortality in patients with chronic heart failure. Heart Rhythm 2008, 5, 261–268. [Google Scholar] [CrossRef]
- Kojima, M.; Hayano, J.; Fukuta, H.; Sakata, S.; Mukai, S.; Ohte, N.; Seno, H.; Toriyama, T.; Kawahara, H.; Furukawa, T.A.; et al. Loss of fractal heart rate dynamics in depressive hemodialysis patients. Psychosom. Med. 2008, 70, 177–185. [Google Scholar] [CrossRef]
- Vu, T.; Kokubo, Y.; Inoue, M.; Yamamoto, M.; Mohsen, A.; Martin-Morales, A.; Dawadi, R.; Inoue, T.; Ting, T.J.; Yoshizaki, M.; et al. Unveiling Coronary Heart Disease Prediction through Machine Learning Techniques: Insights from the Suita Population-Based Cohort Study. Res. Sq. 2024, 2024, 1–10. [Google Scholar] [CrossRef]
- Mahmood, S.S.; Levy, D.; Vasan, R.S.; Wang, T.J. The Framingham Heart Study and the Epidemiology of Cardiovascular Disease: A Historical Perspective. Lancet 2014, 383, 999–1008. [Google Scholar] [CrossRef]
- Andersson, C.; Johnson, A.D.; Benjamin, E.J.; Levy, D.; Vasan, R.S. 70-Year Legacy of the Framingham Heart Study. Nat. Rev. Cardiol. 2019, 16, 687–698. [Google Scholar] [CrossRef]
- D’Agostino, R.B., Sr.; Vasan, R.S.; Pencina, M.J.; Wolf, P.A.; Cobain, M.; Massaro, J.M.; Kannel, W.B. General Cardiovascular Risk Profile for Use in Primary Care: The Framingham Heart Study. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef]
- Andersson, C.; Nayor, M.; Tsao, C.W.; Levy, D.; Vasan, R.S. Framingham Heart Study: JACC Focus Seminar, 1/8. J. Am. Coll. Cardiol. 2021, 77, 2680–2692. [Google Scholar] [CrossRef]
- Cooper, L.L.; Mitchell, G.F. Incorporation of Novel Vascular Measures into Clinical Management: Recent Insights from the Framingham Heart Study. Curr. Hypertens. Rep. 2019, 21, 19. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Mandapati, A.; Hamel, A.P.; Karjadi, C.; Ang, T.F.A.; Xia, W.; Au, R.; Lin, H. Multimodal Machine Learning for 10-Year Dementia Risk Prediction: The Framingham Heart Study. J. Alzheimers Dis. 2023, 96, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Graf, G.H.J.; Aiello, A.E.; Caspi, A.; Kothari, M.; Liu, H.; Moffitt, T.E.; Muennig, P.A.; Ryan, C.P.; Sugden, K.; Belsky, D.W. Educational Mobility, Pace of Aging, and Lifespan Among Participants in the Framingham Heart Study. JAMA Netw. Open 2024, 7, e240655. [Google Scholar] [CrossRef]
- Murabito, J.M. Women and Cardiovascular Disease: Contributions from the Framingham Heart Study. J. Am. Med. Womens Assoc. 1995, 50, 35–39, 55. [Google Scholar] [PubMed]
- Rempakos, A.; Prescott, B.; Mitchell, G.F.; Vasan, R.S.; Xanthakis, V. Association of Life’s Essential 8 with Cardiovascular Disease and Mortality: The Framingham Heart Study. J. Am. Heart Assoc. 2023, 12, e030764. [Google Scholar] [CrossRef]
- Cybulska, B.; Kłosiewicz-Latoszek, L. Landmark Studies in Coronary Heart Disease Epidemiology: The Framingham Heart Study after 70 Years and the Seven Countries Study after 60 Years. Kardiol. Pol. 2019, 77, 173–180. [Google Scholar] [CrossRef]
- Kahouadji, N. Comparison of Machine Learning Classification Algorithms and Application to the Framingham Heart Study. arXiv 2024, arXiv:2402.15005. [Google Scholar] [CrossRef]
- Keizer, S.; Zhan, Z.; Ramachandran, V.S.; van den Heuvel, E.R. Joint Modeling with Time-Dependent Treatment and Heteroskedasticity: Bayesian Analysis with Application to the Framingham Heart Study. arXiv 2019, arXiv:1912.06398. [Google Scholar]
- Psychogyios, K.; Ilias, L.; Askounis, D. Comparison of Missing Data Imputation Methods Using the Framingham Heart Study Dataset. In Proceedings of the Institute of Electrical and Electronics Engineers Conference, Seoul, Republic of Korea, 16–20 May 2022. [Google Scholar]
- Priyanka, H.U.; Vivek, R. Multi Model Data Mining Approach for Heart Failure Prediction. Int. J. Data Min. Knowl. Manag. Process 2016, 6, 31–39. [Google Scholar] [CrossRef]
- Rao, A.R.; Wang, H.; Gupta, C. Predictive Analysis for Optimizing Port Operations. Appl. Sci. 2025, 15, 2877. [Google Scholar] [CrossRef]
- Hayano, J.; Yamada, A.; Yoshida, Y.; Ueda, N.; Yuda, E. Spectral Structure and Nonlinear Dynamics Properties of Long-Term Interstitial Fluid Glucose. Int. J. Biosci. Biochem. Bioinform. 2020, 10, 137–143. [Google Scholar] [CrossRef]
- Schutte, A.E.; Kollias, A.; Stergiou, G.S. Blood Pressure and Its Variability: Classic and Novel Measurement Techniques. Nat. Rev. Cardiol. 2022, 19, 643–654. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.K.; Shimbo, D.; Colburn, D.A.; Pugliese, D.N.; Padwal, R.; Sia, S.K.; Anstey, D.E. Cuffless Blood Pressure Devices. Am. J. Hypertens. 2022, 35, 380–387. [Google Scholar] [CrossRef]
- Sagirova, Z.; Kuznetsova, N.; Gogiberidze, N.; Gognieva, D.; Suvorov, A.; Chomakhidze, P.; Omboni, S.; Saner, H.; Kopylov, P. Cuffless Blood Pressure Measurement Using a Smartphone-Case Based ECG Monitor with Photoplethysmography in Hypertensive Patients. Sensors 2021, 21, 3525. [Google Scholar] [CrossRef]
- Tamura, T.; Huang, M. Cuffless Blood Pressure Monitor for Home and Hospital Use. Sensors 2025, 25, 640. [Google Scholar] [CrossRef]
- Tamura, T.; Shimizu, S.; Nishimura, N.; Takeuchi, M. Long-Term Stability of Over-the-Counter Cuffless Blood Pressure Monitors: A Proposal. Health Technol. 2023, 13, 53–63. [Google Scholar] [CrossRef]
- Pandit, J.A.; Lores, E.; Batlle, D. Cuffless Blood Pressure Monitoring: Promises and Challenges. Clin. J. Am. Soc. Nephrol. 2020, 15, 1531–1538. [Google Scholar] [CrossRef]
- Gogiberidze, N.; Suvorov, A.; Sultygova, E.; Sagirova, Z.; Kuznetsova, N.; Gognieva, D.; Chomakhidze, P.; Frolov, V.; Bykova, A.; Mesitskaya, D.; et al. Practical Application of a New Cuffless Blood Pressure Measurement Method. Pathophysiology 2023, 30, 586–598. [Google Scholar] [CrossRef]
- Rajendran, A.; Minhas, A.S.; Kazzi, B.; Varma, B.; Choi, E.; Thakkar, A.; Michos, E.D. Sex-Specific Differences in Cardiovascular Risk Factors and Implications for Cardiovascular Disease Prevention in Women. Atherosclerosis 2023, 384, 117269. [Google Scholar] [CrossRef] [PubMed]
- Faulkner, J.L. Obesity-Associated Cardiovascular Risk in Women: Hypertension and Heart Failure. Clin. Sci. 2021, 135, 1523–1544. [Google Scholar] [CrossRef] [PubMed]
- Mehta, L.S.; Velarde, G.P.; Lewey, J.; Sharma, G.; Bond, R.M.; Navas-Acien, A.; Fretts, A.M.; Magwood, G.S.; Yang, E.; Blumenthal, R.S.; et al. Cardiovascular Disease Risk Factors in Women: The Impact of Race and Ethnicity: A Scientific Statement from the American Heart Association. Circulation 2023, 147, 1471–1487. [Google Scholar] [CrossRef]
- Kim, C. Management of Cardiovascular Risk in Perimenopausal Women with Diabetes. Diabetes Metab. J. 2021, 45, 492–501. [Google Scholar] [CrossRef]
- Brown, R.M.; Tamazi, S.; Weinberg, C.R.; Dwivedi, A.; Mieres, J.H. Racial Disparities in Cardiovascular Risk and Cardiovascular Care in Women. Curr. Cardiol. Rep. 2022, 24, 1197–1208. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez de Morales, Y.A.; Abramson, B.L. Cardiovascular and Physiological Risk Factors in Women at Mid-Life and Beyond. Can. J. Physiol. Pharmacol. 2024, 102, 442–451. [Google Scholar] [CrossRef] [PubMed]

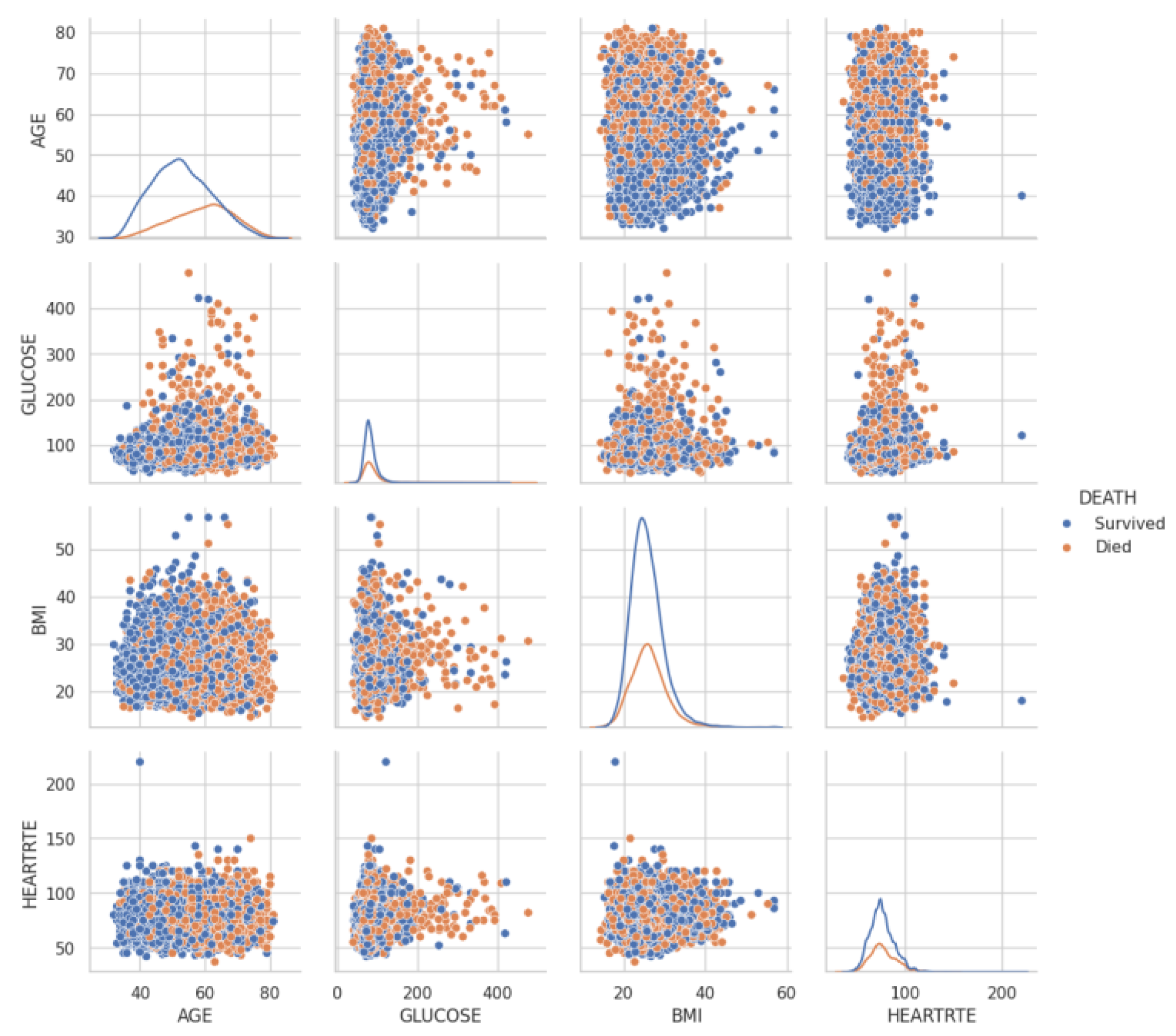
| Category | Variable Name | English Description |
|---|---|---|
| Basic Information | RANDID | Random ID for individual identification |
| SEX | Sex (1 = Male, 2 = Female) | |
| AGE | Age (years) | |
| Health Status and Risk Factors | TOTCHOL | Total cholesterol (mg/dL) |
| SYSBP | Systolic blood pressure (mmHg) | |
| DIABP | Diastolic blood pressure (mmHg) | |
| CURSMOKE | Current smoking status (1 = Yes, 0 = No) | |
| CIGPDAY | Cigarettes per day | |
| BMI | Body mass index (BMI, kg/m2) | |
| DIABETES | Diabetes (1 = Yes, 0 = No) | |
| BPMEDS | Antihypertensive medication (1 = Yes, 0 = No) | |
| HEARTRTE | Heart rate (bpm) | |
| GLUCOSE | Glucose level (mg/dL) | |
| HDLC | High-density lipoprotein cholesterol (mg/dL) | |
| LDLC | Low-density lipoprotein cholesterol (mg/dL) | |
| Medical History | educ | Education level |
| PREVCHD | Previous coronary heart disease (1 = Yes, 0 = No) | |
| PREVAP | Previous angina pectoris (1 = Yes, 0 = No) | |
| PREVMI | Previous myocardial infarction (1 = Yes, 0 = No) | |
| PREVSTRK | Previous stroke (1 = Yes, 0 = No) | |
| PREVHYP | Previous hypertension (1 = Yes, 0 = No) | |
| Event Occurrence | DEATH | Death (1 = Yes, 0 = No) |
| ANGINA | Angina occurrence (1 = Yes, 0 = No) | |
| HOSPMI | Hospitalization for myocardial infarction (1 = Yes, 0 = No) | |
| MI_FCHD | Myocardial infarction or coronary heart disease occurrence (1 = Yes, 0 = No) | |
| ANYCHD | Any coronary heart disease occurrence (1 = Yes, 0 = No) | |
| STROKE | Stroke occurrence (1 = Yes, 0 = No) | |
| CVD | Cardiovascular disease occurrence (1 = Yes, 0 = No) | |
| HYPERTEN | Hypertension occurrence (1 = Yes, 0 = No) | |
| Follow-Up Period | TIME | Follow-up period (months or years) |
| PERIOD | Study period or phase | |
| TIMEAP | Time to angina occurrence | |
| TIMEMI | Time to myocardial infarction occurrence | |
| TIMEMIFC | Time to myocardial infarction or coronary heart disease occurrence | |
| TIMECHD | Time to coronary heart disease occurrence | |
| TIMESTRK | Time to stroke occurrence | |
| TIMECVD | Time to cardiovascular disease occurrence | |
| TIMEDTH | Time to death | |
| TIMEHYP | Time to hypertension occurrence |
| Item | Value | ||
|---|---|---|---|
| Total missing cells | 20,075 | ||
| Total number of cells | 453,453 | ||
| Overall missing rate | 4.43% | ||
| Variable | Missing Rate (%) | Number of Missing Entries | |
| GLUCOSE | 12.38 | 1440 | |
| BPMEDS | 5.10 | 593 | |
| TOTCHOL | 3.52 | 409 | |
| educ | 2.54 | 295 | |
| CIGPDAY | 0.68 | 79 | |
| BMI | 0.45 | 52 | |
| HEARTRTE | 0.05 | 6 | |
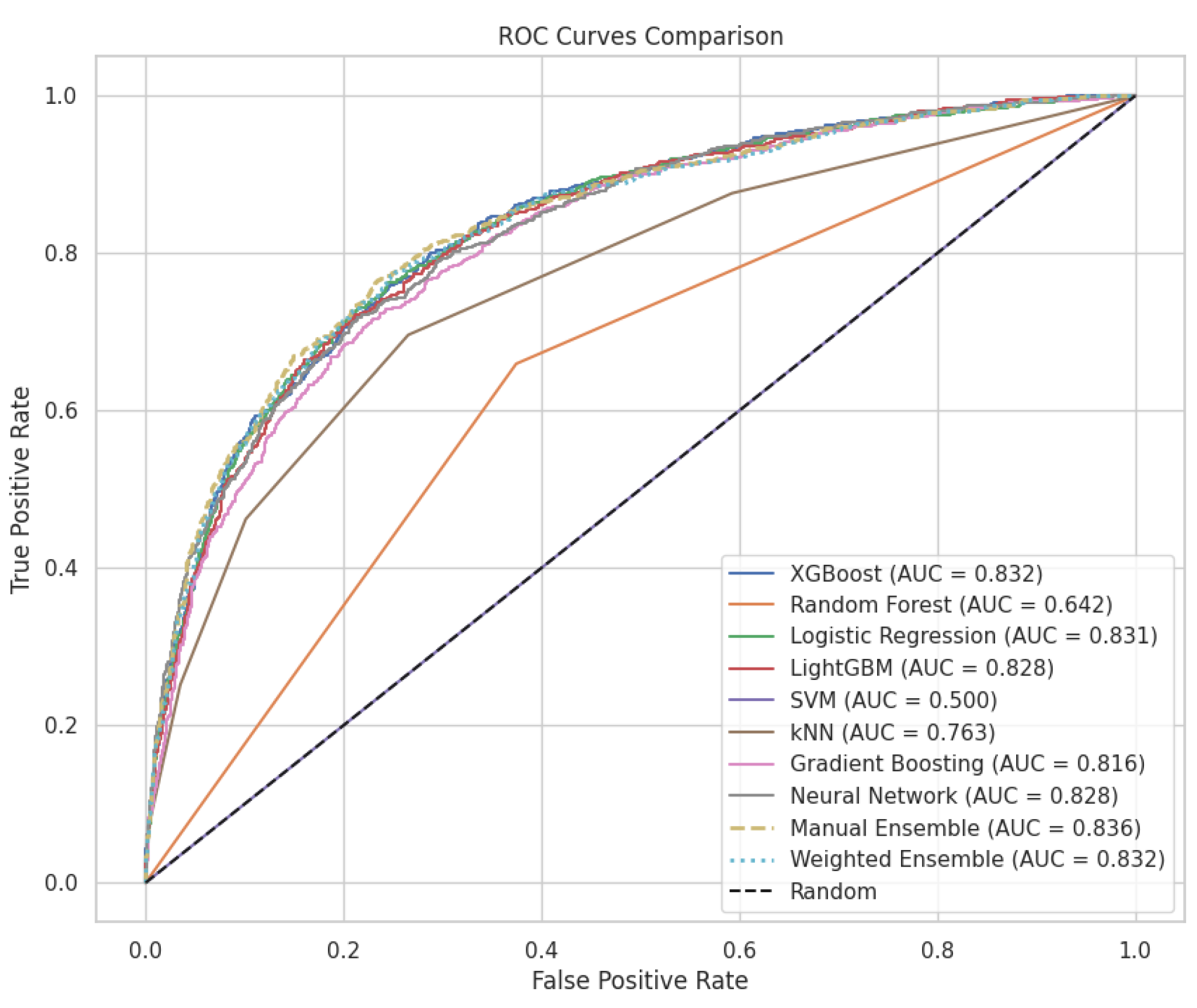
| Model | Accuracy | Precision | Recall | F1 Score | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|---|
| Manual Ensemble | 0.799106 | 0.781250 | 0.458716 | 0.578035 | 0.458716 | 0.944963 | 0.835598 |
| XGBoost | 0.800826 | 0.732171 | 0.529817 | 0.614770 | 0.529817 | 0.916953 | 0.832301 |
| Weighted Ensemble | 0.796354 | 0.778884 | 0.448394 | 0.569141 | 0.448394 | 0.945455 | 0.832050 |
| Logistic Regression | 0.798074 | 0.725118 | 0.526376 | 0.609967 | 0.526376 | 0.914496 | 0.830773 |
| LightGBM | 0.791882 | 0.710236 | 0.517202 | 0.598540 | 0.517202 | 0.909582 | 0.827951 |
| Neural Network | 0.790506 | 0.697151 | 0.533257 | 0.604288 | 0.533257 | 0.900737 | 0.827666 |
| Gradient Boosting | 0.782938 | 0.708117 | 0.470183 | 0.565127 | 0.470183 | 0.916953 | 0.815959 |
| kNN | 0.767802 | 0.661741 | 0.462156 | 0.544227 | 0.462156 | 0.898771 | 0.763361 |
| Random Forest | 0.700034 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.642478 |
| SVM | 0.700034 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.500000 |
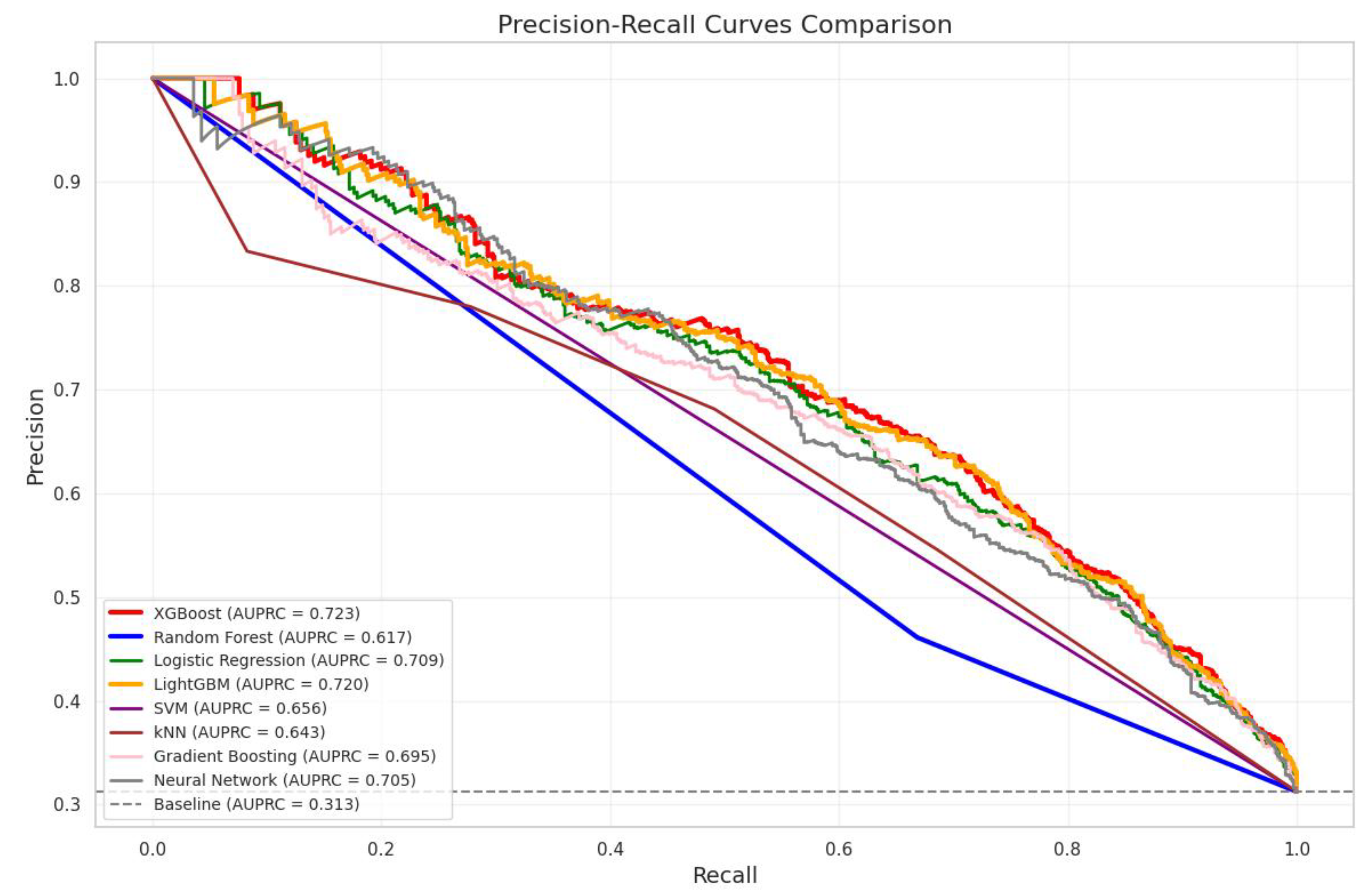
| Model | AUPRC | Improvement Over Baseline (%) |
|---|---|---|
| Baseline (Random Classifier) | 0.3126 | – |
| XGBoost | 0.7232 | 131.37% |
| LightGBM | 0.7202 | 130.44% |
| Logistic Regression | 0.7093 | 126.95% |
| Neural Network | 0.7054 | 125.69% |
| Gradient Boosting | 0.6950 | 122.36% |
| SVM | 0.6563 | 109.97% |
| kNN | 0.6433 | 105.83% |
| Random Forest | 0.6166 | 97.28% |
| Model Comparison | AUC1 (95% CI) | AUC2 (95% CI) | Δ AUC | Z | p-Value | Adj. P | Effect Size |
|---|---|---|---|---|---|---|---|
| XGBoost vs. Random Forest | 0.834 (0.814–0.854) | 0.500 (0.480–0.520) | 0.3341 | 36.96 | <0.001 *** | <0.001 *** | 0.758 |
| XGBoost vs. kNN | 0.834 (0.814–0.854) | 0.766 (0.746–0.786) | 0.0683 | 8.45 | <0.001 *** | <0.001 *** | 0.171 |
| XGBoost vs. Neural Network | 0.834 (0.814–0.854) | 0.797 (0.777–0.817) | 0.0375 | 5.08 | <0.001 *** | <0.001 *** | 0.097 |
| XGBoost vs. SVM | 0.834 (0.814–0.854) | 0.815 (0.795–0.835) | 0.0191 | 3.36 | <0.001 *** | 0.018 * | 0.050 |
| XGBoost vs. Logistic Regression | 0.834 (0.814–0.854) | 0.822 (0.802–0.842) | 0.0119 | 4.35 | <0.001 *** | <0.001 *** | 0.032 |
| XGBoost vs. LightGBM | 0.834 (0.814–0.854) | 0.831 (0.811–0.851) | 0.0032 | 1.77 | 0.077 | 1.000 | 0.009 |
| XGBoost vs. Gradient Boosting | 0.834 (0.814–0.854) | 0.832 (0.812–0.852) | 0.0019 | 0.93 | 0.352 | 1.000 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuda, E.; Kaneko, I.; Hirahara, D. Machine-Learning Insights from the Framingham Heart Study: Enhancing Cardiovascular Risk Prediction and Monitoring. Appl. Sci. 2025, 15, 8671. https://doi.org/10.3390/app15158671
Yuda E, Kaneko I, Hirahara D. Machine-Learning Insights from the Framingham Heart Study: Enhancing Cardiovascular Risk Prediction and Monitoring. Applied Sciences. 2025; 15(15):8671. https://doi.org/10.3390/app15158671
Chicago/Turabian StyleYuda, Emi, Itaru Kaneko, and Daisuke Hirahara. 2025. "Machine-Learning Insights from the Framingham Heart Study: Enhancing Cardiovascular Risk Prediction and Monitoring" Applied Sciences 15, no. 15: 8671. https://doi.org/10.3390/app15158671
APA StyleYuda, E., Kaneko, I., & Hirahara, D. (2025). Machine-Learning Insights from the Framingham Heart Study: Enhancing Cardiovascular Risk Prediction and Monitoring. Applied Sciences, 15(15), 8671. https://doi.org/10.3390/app15158671








