A Drilling Debris Tracking and Velocity Measurement Method Based on Fine Target Feature Fusion Optimization

Abstract

During unmanned drilling operations, the velocity of drill cuttings serves as an important indicator of drilling conditions, which necessitates real-time and accurate measurements. To address challenges such as the small size of cuttings, weak feature representations, and complex motion trajectories, we propose a novel velocity measurement method integrating small-object detection and tracking. Specifically, we enhance the multi-scale feature fusion capability of the YOLOv11 detection head by incorporating a lightweight feature extraction module, Ghost Conv, and a feature-aligned fusion module, FA-Concat, resulting in an improved model named YOLOv11-Dd (drilling debris). Furthermore, considering the robustness of the ByteTrack algorithm in retaining low-confidence targets and handling occlusions, we integrate ByteTrack into the tracking phase to enhance tracking stability. A velocity estimation module is introduced to achieve high-precision measurement by mapping the pixel displacement of detection box centers across consecutive frames to physical space. To facilitate model training and performance evaluation, we establish a drill-cutting splash simulation dataset comprising 3787 images, covering a diverse range of ejection angles, velocities, and material types. The experimental results show that the YOLOv11-Dd model achieves a 4.65% improvement in mAP@80 over YOLOv11, reaching 76.04%. For mAP@75–95, it improves by 0.79%, reaching 41.73%. The proposed velocity estimation method achieves an average accuracy of 92.12% in speed measurement tasks, representing a 0.42% improvement compared to the original YOLOv11.

1. Introduction

Unmanned drilling rigs are widely adopted because they integrate real-time monitoring systems that enable environmental awareness and dynamic risk alerts during drilling. In risk prediction, the motion characteristics of drill cuttings serve as key indicators of the drill bit’s working condition, the bottom-hole flow field, and other drilling dynamics. Accurate detection and tracking of drill cuttings can thus provide valuable insights into borehole conditions, offering significant engineering benefits.

With the rapid advancement of unmanned drilling technology over the past decade, numerous industrial methods for drill-cutting detection have emerged. Ref. [1] proposed an acoustic detection approach, analyzing the sound signals generated by drill cuttings impacting the pipe wall or moving through drilling fluids to infer their velocity and distribution. While suitable for downhole environments without requiring optical equipment, this method is highly susceptible to environmental noise and fluid property variations, limiting its measurement accuracy. With the increasing adoption of radar and laser technologies, some systems utilize Laser Doppler Velocimetry (LDV) to measure the velocity and particle size distribution of drill cuttings [2], while systems requiring high-precision real-time monitoring have employed millimeter-wave (MMW) radar for flow velocity and distribution measurements [3]. Although these methods offer high detection accuracy, they suffer from high costs and vulnerability to dust and electromagnetic noise under harsh conditions. Pressure sensors, due to their low cost and simple installation [4], are widely favored. By installing pressure sensors near the drill string or drill bit, the flow behavior of drill cuttings can be inferred from fluctuations in drilling fluid pressure. However, pressure-based methods cannot directly measure particle size or velocity, and downhole conditions such as high temperature, high pressure, and severe vibrations often lead to sensor zero drift or signal distortion, thereby compromising measurement stability.

Leveraging computer vision, drill-cutting monitoring can achieve low-cost, highly stable, all-weather, non-contact, real-time perception by simply addressing the issue of insufficient downhole illumination. As numerous solutions to the illumination challenge already exist, this study focuses on two core technologies critical for drill-cutting velocity measurement: object detection [5] and multi-object tracking (MOT) [6]. Object detection is employed to identify drill cuttings and provide precise localization, while the MOT algorithm ensures consistent target association across frames, thereby supporting accurate velocity computation.

The current object detection techniques can be broadly categorized into one-stage [7] and two-stage approaches [8]. The YOLO series [9], representing one-stage methods, excels in high real-time requirements due to its end-to-end training and rapid inference capabilities. In contrast, two-stage methods—such as the Region-Based Convolutional Neural Network (R-CNN), Fast R-CNN, and Faster R-CNN proposed by [10,11,12]—enhance detection accuracy by generating candidate regions followed by classification and regression. However, their high computational complexity limits their applicability in real-time industrial monitoring.

Effective detection of flying drill cuttings requires the deployment of multi-object tracking (MOT) algorithms. Based on the independence of detection and tracking stages, MOT approaches can be divided into Detection-Based Tracking (DBT) [13] and Joint Detection and Tracking (JDT) [14]. JDT methods require manual initialization, involve high computational overhead, struggle to recover from target loss, and exhibit limited adaptability to the appearance variations in drill cuttings, rendering them unsuitable for the harsh operational environments of unmanned drilling rigs. In contrast, DBT methods automatically detect drill cuttings, exhibit superior robustness and computational efficiency, adapt more effectively to target appearance changes, and can leverage deep learning detection advances to enhance tracking performance and stability. ByteTrack [15], a representative DBT method, improves target trajectory consistency and reduces ID switching by optimizing data association and refining the matching of low-confidence detections, thus achieving high accuracy and robustness in real-world scenarios. Consequently, this study adopts ByteTrack as the tracking framework and introduces a velocity estimation module tailored to the motion characteristics of drill cuttings, achieving high-precision velocity measurement by mapping pixel displacement to physical displacement.

The primary contributions of this study are as follows:

1.

Enhancement of the YOLOv11 detection head. We optimize the multi-scale feature fusion capability of the YOLOv11 detection head by integrating the lightweight feature extraction module Ghost Conv and the feature-aligned fusion module FA-Concat, resulting in an improved model named YOLOv11-Dd (drilling debris).

2.

Development of a speed detection module. Leveraging the robust tracking capabilities of ByteTrack, we design a high-precision speed detection module that calculates the real-time movement speed of drilling debris by mapping the pixel displacement of detection box centers between consecutive frames to physical space.

3.

Construction of a custom dataset and comprehensive experimental validation. We build a drilling debris splashing simulation dataset comprising 3787 images, covering various ejection angles, speeds, and material conditions. The experimental results demonstrate that our YOLOv11-Dd detection head achieves a 4.65% improvement in detection performance compared to YOLOv11, with an mAP@80 of 76.04%. The proposed drilling debris speed measurement method achieves an accuracy of 92.12% in the speed detection task.

The remainder of this paper is organized as follows: Section 2 reviews the related work; Section 3 discusses the optimization of the detection head and the design of the speed detection module; Section 4 presents the experimental validation and analysis based on the custom drilling debris splashing simulation dataset; and Section 5 concludes the paper.

2. Related Work

This literature review covers studies published between 2017 and 2024, focusing on object detection, multi-object tracking, and velocity estimation. Relevant sources were retrieved from academic databases including IEEE Xplore, ScienceDirect, and SpringerLink. The main keywords used in the search included “object detection”, “small-object detection”, “multi-object tracking”, and “cutting recognition”. Priority was given to works with strong relevance to industrial applications, fine-grained target detection, and real-time processing techniques. Studies focused solely on static 2D images or tasks unrelated to our problem domain were excluded.

2.1. Object Detection

In recent years, single-stage object detectors have emerged as the mainstream choice for real-time applications, owing to their simple architectures and fast inference speeds. The SSD (Single Shot MultiBox Detector), proposed by [16], utilizes multi-scale feature maps for bounding box regression and classification. Several improved versions have subsequently been developed, such as DSSD [17], which incorporates a deconvolution module to enhance contextual information and improve small-object detection performance; FSSD [18], which adds a feature fusion module to generate richer pyramid features; and PSSD [19], which introduces an efficient feature enhancement module to strengthen local detection capabilities and semantic expressiveness. RetinaNet [20] uses Focal Loss to address the imbalance between foreground and background classes, reaching accuracy close to two-stage methods while retaining high inference speed. RTMDet [21] enhances detection accuracy through the integration of an efficient Transformer module, demonstrating superior performance particularly in small-object detection and under complex background conditions.

The YOLO series, as a hallmark of single-stage detectors, started with anchor-free detection in YOLOv1 and has undergone multiple structural evolutions. YOLOv3 [22] integrates ResNet and FPN to improve multi-scale perception; YOLOv4 [23] enhances feature reuse and path aggregation efficiency through CSPNet and PANet; YOLOv5 [24] optimizes the network with lightweight designs, achieving simultaneous improvements in both accuracy and speed, making it ideal for resource-constrained environments; YOLOv8 [25] introduces the C2f module to optimize semantic feature extraction, further enhancing detection performance. The latest YOLOv11 [26] builds upon YOLOv8 by introducing the more efficient C3k2 module and the SPPF (Spatial Pyramid Pooling—Fast) structure, along with the C2PSA module that integrates spatial attention mechanisms, significantly strengthening the model’s multi-scale perception and directional robustness. However, although YOLOv5 performs well in speed and model size, its simplistic feature fusion limits its precision on fast and small targets. YOLOv8 improves semantic features but struggles in multi-scale detection accuracy. YOLOv11 further enhances backbone extraction, yet coarse concatenation of multi-level features hinders edge precision for small objects. In contrast, YOLOv11-Dd maintains efficiency while incorporating Ghost Conv to reduce complexity and FA-Concat to align cross-level features. These enhancements improve detection precision and robustness for small fast-moving objects in challenging environments.

2.2. Multi-Object Tracking

The current multi-object tracking (MOT) methods predominantly follow the Tracking-By-Detection (TbD) paradigm, wherein targets are first localized using an object detector and subsequently associated across frames via a tracking algorithm [27,28]. Within this framework, two mainstream strategies have emerged: Joint Detection and Embedding (JDE) and Separate Detection and Embedding (SDE). JDE methods [29,30] simultaneously perform object detection and feature extraction within a single deep network, offering improved computational efficiency. However, because detection and embedding share the same feature extraction backbone, JDE methods are prone to feature confusion in high-density scenes—particularly in unmanned drilling operations, where debris particles are densely packed, small in size, and weak in texture—leading to frequent mismatches and ID switches. Additionally, JDE methods face accuracy bottlenecks when handling small objects, compromising tracking stability.

In contrast, SDE methods utilize separate object detectors and re-identification (Re-ID) models, allowing independent optimization of detection and feature extraction. This significantly enhances detection precision and tracking robustness. ByteTrack, an SDE-based approach, further improves tracking stability by retaining low-confidence detections and employing an IoU-based matching strategy; however, the model does not natively support velocity estimation.

In summary, YOLOv11-Dd as the detection head and ByteTrack as the tracker form an effective solution for unmanned drilling environments, yet challenges remain in further improving detection accuracy and enabling real-time velocity measurement.

3. Research Methods

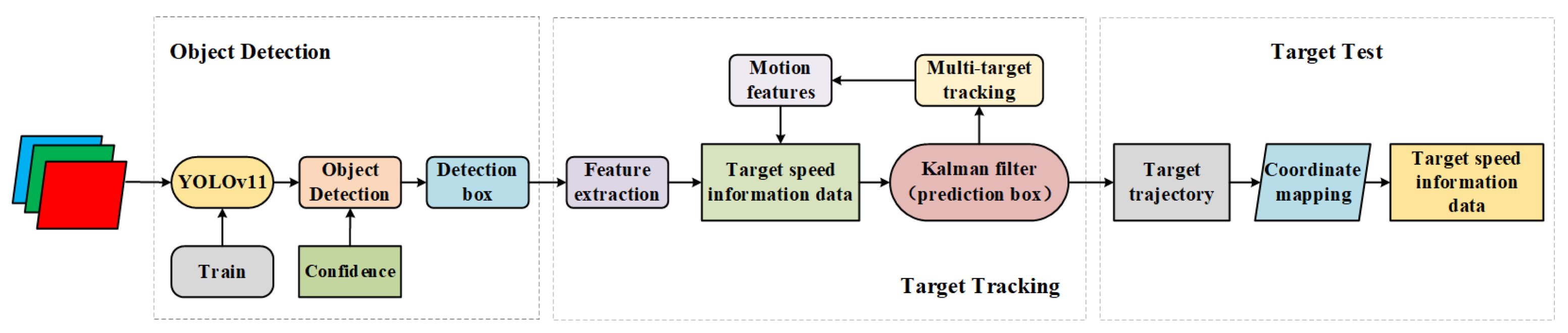
Compared to earlier versions, the YOLOv11 algorithm demonstrates superior performance in detecting small and overlapping objects. However, there is still room for improvement in the fusion methods of different extracted features. Additionally, the ByteTrack algorithm currently lacks direct velocity detection capabilities for drilling debris tracking and speed measurement. Therefore, this paper seeks to enhance these two algorithms to better meet the performance demands of practical applications.The specific workflow for tracking and speed estimation is shown in Figure 1.

3.1. YOLOv11-Dd Model

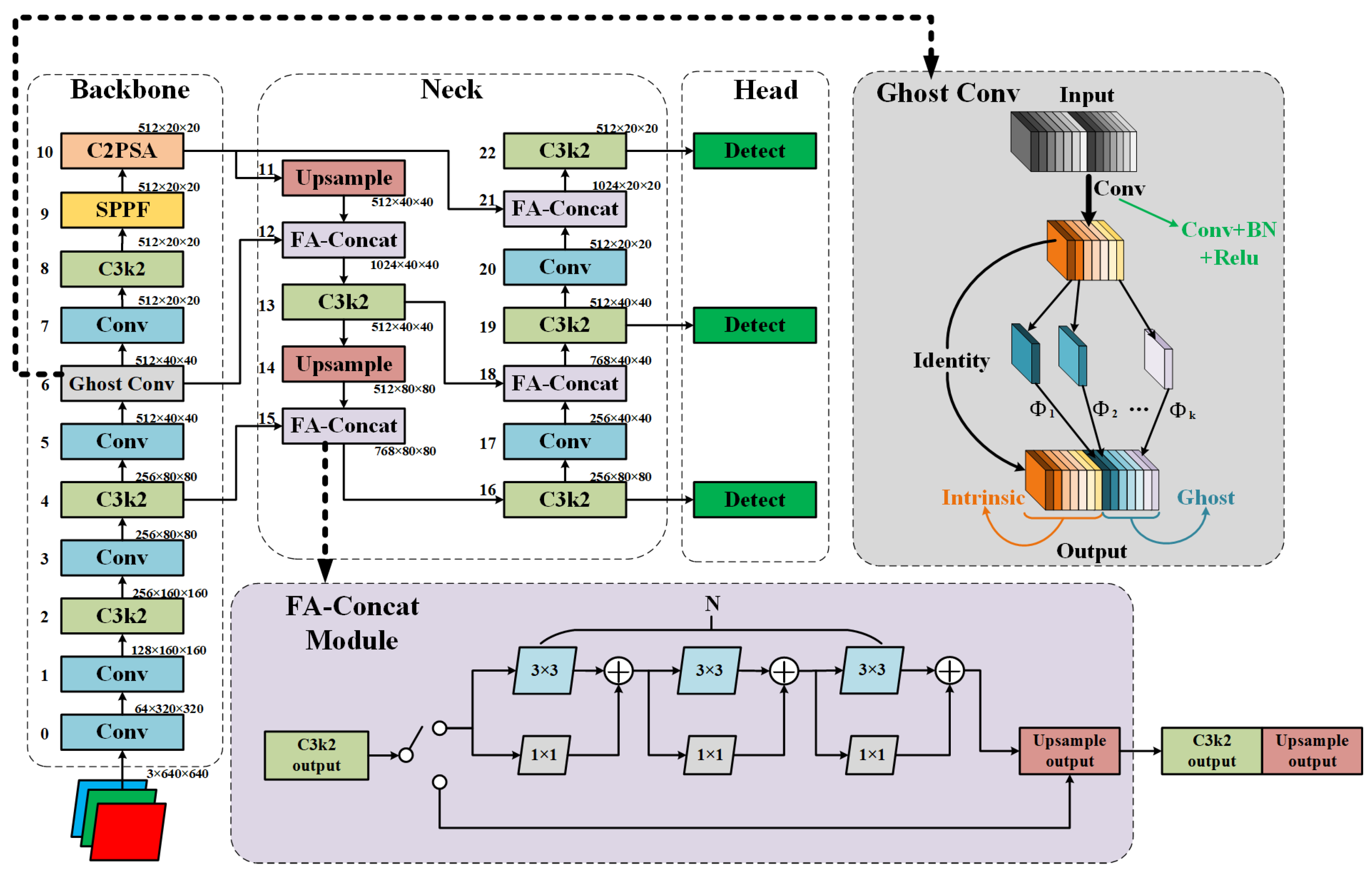
To further improve the accuracy and small-object detection capabilities of YOLOv11, we propose an enhanced detection model, YOLOv11-Dd, based on the original YOLOv11 architecture. This model optimizes the network structure in two key areas: first by replacing certain modules in the backbone network to reduce computational costs while enhancing feature representation and second by refining the feature fusion strategy to improve the synergy among multi-scale features.

First, in the sixth layer of the YOLOv11 backbone network, we replace the original C3f2 structure with the Ghost Conv module. Ghost Conv is a lightweight convolution technique that significantly reduces computation while preserving the model’s expressive power. It extracts a small number of primary features via standard convolution, applies linear transformations to generate Ghost features, and merges them into the final output map. The Ghost Conv module is illustrated in Figure 2.

Second, we introduce an improved feature concatenation method through the FA-Concat (Feature Alignment Concat) module. The original Concat module in YOLOv11 simply concatenates feature vectors. However, due to significant differences in features across layers, such straightforward concatenation can lead to performance degradation. To address this, we connect the feature map from the C3k2 layer to the Unsample layer through a residual convolutional layer chain, as shown in Figure 2, rather than directly concatenating them. By assessing the feature differences between layers, we adjust the number of convolution layers in the chain, which helps to minimize the feature discrepancies and enhances the model’s ability to fuse features effectively.

3.2. Tracking and Speed Measurement Central-ByteTrack Module

ByteTrack is an efficient multi-object tracking (MOT) algorithm. Its core concept is to generate candidate targets through an accurate detector and then use a Kalman filter to predict each target’s state, such as position and velocity. By combining appearance features and motion information, the algorithm evaluates the matching degree between detection boxes and existing trajectories. The greedy algorithm is then used to achieve optimal frame-to-frame association. This method significantly enhances both tracking stability and target association accuracy, making it highly effective for multi-target tracking in complex dynamic environments.

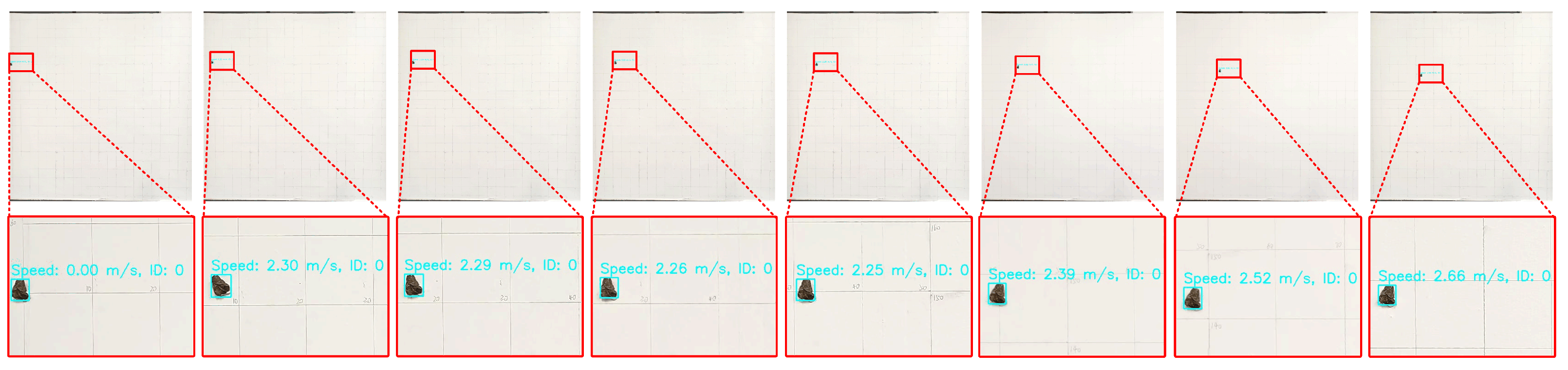
In this research, to accurately measure the speed of fast-moving targets such as splashing drilling debris, we propose a speed measurement module based on the center point displacement of the detection box, built upon the ByteTrack framework. This module extracts the center point coordinates of the detection box for each target across consecutive frames, calculates its displacement in pixel space, and uses camera parameters along with the calibration distance between the target’s movement plane and the camera. The pixel displacement is then converted into a real-world speed value, enabling precise estimation of the target’s instantaneous velocity. The design principles, calculation methods, and related equations of this module are elaborated below.

3.2.1. Transformation Between the World Coordinate System and the Image Coordinate System

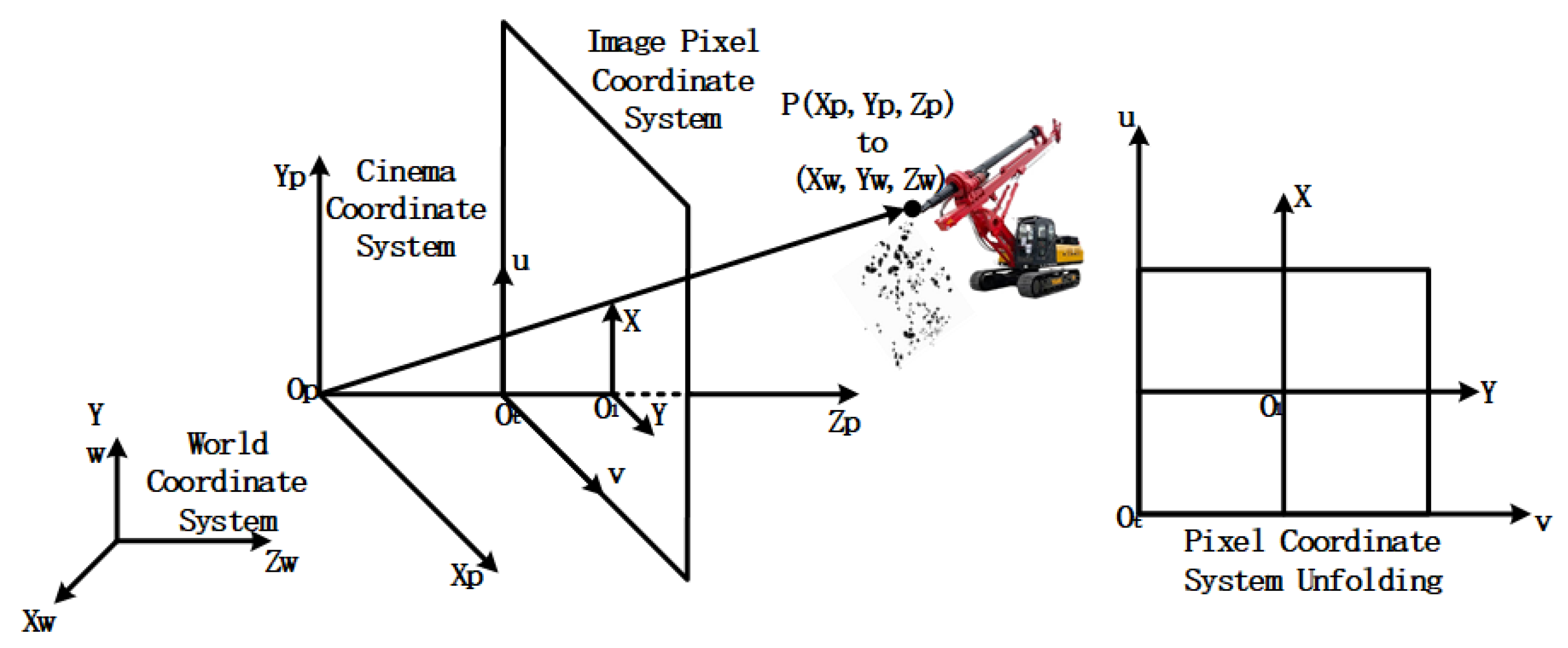
In the task of detecting the velocity of drilling debris, it is essential to accurately map the motion trajectory of the debris presented in the image to the physical space in order to achieve precise estimation of its true velocity. To address this, this paper establishes a mapping relationship between the image coordinate system and the real-world (world) coordinate system. The image coordinate system represents the two-dimensional pixel position of the target on the camera’s sensing plane, while the world coordinate system describes the physical position of the target in the actual three-dimensional space. Considering the stability of the unmanned drilling machine operation environment and the controllability of camera parameters, this paper utilizes fixed industrial cameras, along with parameters such as field of view, camera height, lens focal length, and image resolution, to map pixel points in the image to physical space. Specifically, by calibrating the size and position of a reference object, a conversion relationship between pixels and real-world distance is established, allowing for accurate conversion of debris displacement in the image to real-world physical displacement. Figure 3 illustrates the process of transforming between different coordinate systems, visually demonstrating how a three-dimensional spatial point is mapped to a two-dimensional image plane through various coordinate systems.

As shown in Figure 4, during the actual camera calibration process, the range of the drilling machine’s working surface is relatively limited, and the vertical height difference can be considered negligible. As a result, the drilling debris ejection surface can be approximated as a plane, with minimal error introduced by this approximation. Therefore, the core task primarily focuses on the two-dimensional coordinate transformation between the image pixel coordinate system and the working surface coordinate system.

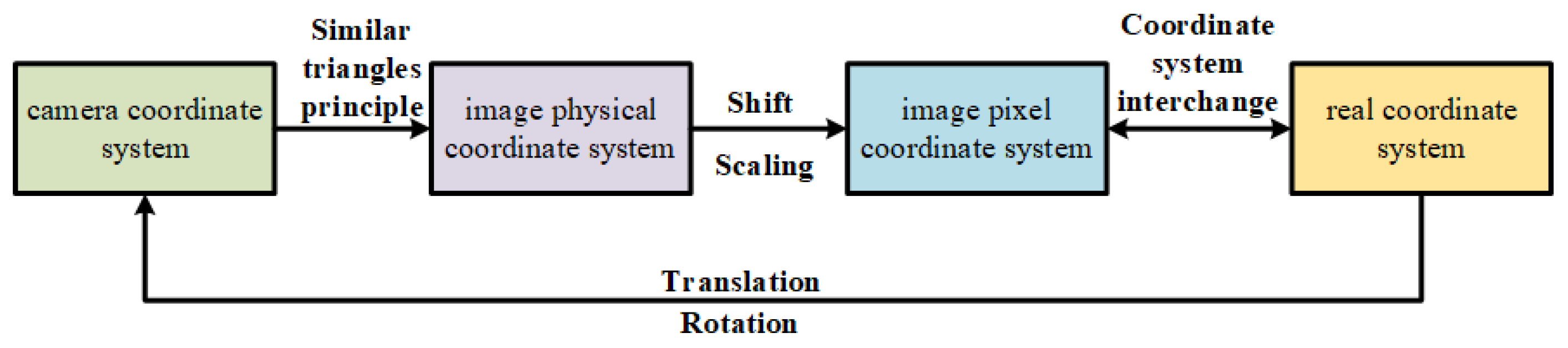
As shown in Figure 5, this paper systematically outlines the transformation relationships between the four coordinate systems and rigorously derives the transformation process using mathematical equations, ultimately establishing the mapping relationship between the image pixel coordinate system and the world coordinate system. The specific transformation equations are as follows:

(1) The translation relationship between the physical image coordinate system and the image pixel coordinate system.

$$u={\displaystyle \frac{X}{d_x}}+u_0$$

(1)

$$v={\displaystyle \frac{X}{d_y}}+v_0$$

(2)

In the equations, $(u_0,v_0)$ denotes the origin of the image pixel coordinate system, while $d_x$ and $d_y$ represent the size of each pixel along the x and y axes in the pixel plane, and X and Y correspond to the values of the point in the image physical coordinate system.

(2) The relationship between the image physical coordinate system, the camera coordinate system, and the world coordinate system.

$$Z_p\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{\displaystyle \frac{f}{dx}}& 0& u_0\\ 0& {\displaystyle \frac{f}{dy}}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_p\\ Y_p\\ Z_p\end{array}\right]=K\left[\begin{array}{c}{X}_p\\ Y_p\\ Z_p\end{array}\right]$$

(3)

$$\left[\begin{array}{c}{X}_p\\ Y_p\\ Z_p\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+t$$

(4)

In the equations, the coordinates of point p in the camera coordinate system are ${(X_p,Y_p,Z_p)}^T$, in the image physical coordinate system ${(X,Y)}^T$, with the focal length being f. The point ${(X_w,Y_w,Z_w)}^T$ represents the origin of the world coordinate system, with R and t being the rotation matrix and translation vector between the two, and K is a constant.

(3) The transformation relationship between the image pixel coordinate system and the world coordinate system.

$$Z_p\left[\begin{array}{c}u\\ \nu \\ 1\end{array}\right]=\left[\begin{array}{ccc}{\displaystyle \frac{1}{dx}}& 0& u_0\\ 0& {\displaystyle \frac{1}{dy}}& {\nu }_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

(5)

This equation is obtained by combining Equations (1)–(4).

This conversion mechanism serves as a crucial foundation for drilling debris speed detection, enabling the reconstruction of debris trajectories, obtained using the ByteTrack algorithm, in the real-world space. By incorporating time information, it calculates the actual movement speed of the debris, thereby significantly enhancing the accuracy and practicality of the unmanned drilling rig’s intelligent monitoring system.

3.2.2. Speed Estimation Based on Pixel Displacement

First, the pixel displacement of the object’s center point is computed based on the detection boxes across consecutive frames. Let the center coordinates of the target in frame t and frame $t+1$ be $(x_t,y_t)$ and $(x_{t+1},y_{t+1})$, respectively. The center point’s pixel displacement $\Delta d_p$ can then be calculated using the following equation:

$$\Delta d_p=\sqrt{{(x_{t+1}-x_t)}^2+{(y_{t+1}-y_t)}^2}$$

(6)

where $(x_t,y_t)$ and $(x_{t+1},y_{t+1})$ denote the center coordinates of the target in frames t and $t+1$, respectively, and $\Delta d_p$ indicates the pixel-level displacement between two consecutive frames.

The pixel displacement is subsequently mapped to real-world displacement. Assuming that the actual distance from the camera to the object is $D_r$, the real-world displacement corresponding to the pixel shift can be derived using the camera’s focal length f and the principle of similar triangles. Accordingly, the physical displacement $\Delta d_d$ can be calculated using the following equation:

$$\Delta d_d={\displaystyle \frac{\Delta d_p·D_r}{f}}$$

(7)

In this equation, $\Delta d_d$ denotes the real-world displacement of the object between two consecutive frames, $D_r$ refers to the actual distance between the camera and the object, and f represents the focal length of the camera.

Once the actual displacement of the object is obtained, the subsequent step involves calculating the object’s real-world velocity based on the time interval between frames. Assuming a frame rate of $f_r$ frames per second, the time interval $\Delta t$ between two consecutive frames can be determined by

$$\Delta t={\displaystyle \frac{1}{f_r}}$$

(8)

Based on the displacement–time relationship, the object’s real-world velocity $v_r$ can be computed using the following equation:

$$v_d={\displaystyle \frac{\Delta d_c}{\Delta t}}$$

(9)

In the equation, $v_d$ denotes the estimated real-world velocity of the object.

By following the above procedure, the velocity estimation based on the displacement of the detection box center is accomplished. This method determines the target’s motion speed by calculating its displacement across consecutive frames and translating it into real-world velocity according to the frame interval.

4. Experiments

4.1. Dataset Construction and Evaluation Metrics

4.1.1. Dataset Construction

Given the absence of suitable existing datasets, we constructed an idealized simulated cutting ejection dataset to train the detection head and validate the effectiveness of the proposed integrated detection–tracking–speed measurement framework.

To simulate realistic operational conditions, the ejection parameters were selected based on typical cutting trajectories observed in drilling environments. Ejection angles were set between 30° and 75° to reflect cases ranging from vertical free-fall to strong oblique projection. Initial velocities included both gravity-driven free-fall (0 m/s) and impact-driven ejection (2–6 m/s), corresponding to common release modes of debris. During image acquisition, the camera model is defined with fixed intrinsic parameters, including field of view (FOV), focal length, and pixel size, which are all known a priori. No additional calibration is required. Pixel coordinates in rendered images can be directly mapped to physical coordinates, and projection accuracy has been verified to ensure precise pixel-to-space displacement correspondence for velocity estimation.

The dataset comprises two parts:

The first part simulates the ejection of cuttings when a drilling rig operates on a horizontal top rock layer, covering free-fall trajectories and trajectories with varying initial velocities. All samples were generated based on free-fall motion models, assuming camera frame rates of 30 fps and 60 fps to simulate detection under different temporal resolutions. To enrich the dataset’s diversity, six types of stones with different materials and particle sizes were used, resulting in 1402 images.

The second part simulates the cutting ejection when drilling against a vertical rock wall. For simplification, the ejection trajectories were constrained within a single plane, and lateral displacement effects were neglected. The camera’s field of view was set to a 2 × 2 m area, with frame rates similarly set at 30 fps and 60 fps. This part contributed 2418 images.

In total, the dataset consists of 3787 images, all annotated following the COCO standard format. Each label is expressed in the form “stone;speed:4.5”, where “stone” indicates the category and “speed:4.5” represents the real-time velocity, separated by a semicolon “;” to facilitate decoupled processing for detection and speed regression tasks. The overall situation is shown in

Table 1. Ratio of training group, value group, and test group.

Dataset Classification	Quantity
Training Set	2535
Value Set	568
Test Set	684

.

This dataset underpins the training and evaluation of the improved detection head, the integration of the ByteTrack tracking algorithm, and the velocity estimation module, ensuring the robustness and generalization capability of the proposed method in small-object and high-speed motion scenarios.

The experimental environment configuration is summarized in

Table 2. Experimental environment configuration.

Operating System	Windows 10
Deep learning framework	Pytorch:(version=2.3.0)
CPU	AMD Ryzen 5 5600 (3.50 GHz)
GPU	NVIDIA GeForce RTX 4060 Ti
CUDA	12.6

. During the training of the YOLOv11-Dd model, the number of training epochs was set to 300, with a batch size of 16 images per epoch, and the input image resolution was fixed at 640 × 640 pixels.

4.1.2. Evaluation Metrics

In this study, precision (P), recall (R), average precision (AP), mean average precision (mAP), frames per second (fps), and the number of parameters are utilized as evaluation metrics to assess the object detection performance of the model. The corresponding calculation equations are provided as follows:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(10)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(11)

$$AP={\int }_0^{1}P\left(R\right)dR$$

(12)

$$mAP={\displaystyle \frac{1}{N}}\sum _{k=1}^N{R}_n{P}_n$$

(13)

$$fps={\displaystyle \frac{F_i}{T_n}}$$

(14)

In these equations, precision (P) measures the proportion of correctly predicted positive samples among all predicted positives; recall (R) measures the proportion of actual positive samples that are correctly identified; average precision (AP) evaluates the detection accuracy for a single class; mean average precision (mAP) indicates the mean detection accuracy across all classes; and frames per second (fps) reflects the average inference speed on the drilling cutting test dataset.

To quantitatively assess the accuracy of velocity measurements in drilling cutting detection, this paper introduces two evaluation metrics: Velocity Accuracy (A) and Variance of Error (V), which are used to evaluate the model’s performance in target velocity estimation.

The equation for calculating Velocity Accuracy (A) is given as follows:

$$Accuracy=1-{\displaystyle \frac{|v_d-v_r|}{v_r}}\in (0,1)$$

(15)

In the equation, $v_d$ represents the measured velocity of the object, while $v_r$ denotes the true velocity of the object.

The Variance of Error (V) metric is used to assess the stability of the discrepancy between the measured velocity and the true velocity. A smaller value indicates greater measurement accuracy. The calculation equation is as follows:

$${\epsilon }_i=V_{d,i}-V_{r,i}$$

(16)

$$\overline{\epsilon }={\displaystyle \frac{1}{M}}\sum _{i=1}^M{\epsilon }_i$$

(17)

$${\sigma }_{\epsilon }^2={\displaystyle \frac{1}{M}}\sum _{i=1}^M{({\epsilon }_i-\overline{\epsilon })}^2$$

(18)

In the equation, ${\epsilon }_i$ denotes the measurement error of the i-th target; $v_{r,i}$ indicates the true velocity of the i-th target; $v_{d,i}$ represents the measured velocity of the i-th target; M stands for the number of times the target has been measured; and $\overline{\epsilon }$ represents the average measurement error of the target.

4.2. Experiment and Analysis

4.2.1. Object Detection

In the evaluation of object detection performance, this paper shifts from the commonly used mean average precision (mAP@50) and mAP@50–95 metrics to mAP@80 and mAP@75–95 at higher confidence thresholds as the primary evaluation metrics. The reason for this change is that the core goal of this method is to accurately localize the target and calculate pixel displacement, which is then used to infer the real-world speed. Therefore, rather than focusing on the generalization of detection results, the ability to precisely localize the target has a greater influence on the subsequent speed calculation. Relying solely on the lower-threshold mAP@50 might obscure issues related to the inaccurate prediction of boundary boxes, which could lead to misalignments between the detection box and the actual target, thus introducing significant errors during the speed estimation phase. In addition, we found that mAP@80 shows a stronger Pearson correlation (R = 0.91) with velocity estimation accuracy compared to mAP@50 (R = 0.67). This indicates that, from a statistical perspective, using mAP@80 and mAP@75–95 provides a more reliable reflection of the model’s actual effectiveness in this task scenario. By contrast, using stricter mAP@80 and mAP@75–95 provides a more accurate reflection of the detection head’s ability to precisely capture target positions, thereby enhancing the stability and accuracy of speed measurement. To validate the effectiveness of the proposed YOLOv11-Dd detection head, we compared it with the current mainstream models YOLOv5, YOLOv8, and the base version YOLOv11. Performance evaluation experiments were conducted on a unified test set, with results including mAP@80, mAP@75–95, fps (frame rate), and model parameter count (Params/e6), as shown in

Table 3. Test results of different models.

Model	mAP@80/(%)	mAP@75–95/(%)	fps	Params/M
YOLOv5	72.48	39.93	78	50.70
YOLOv8	72.15	41.24	93	41.61
YOLOv11	71.39	40.94	111	24.20
YOLOv11-Dd	76.04	41.73	76	43.51

Boldface denotes the best result for each evaluation metric.

. A comparison of detection results between YOLOv11 and YOLOv11-Dd is presented in Figure 6.

As shown in Table 3, the proposed improved model YOLOv11-Dd demonstrates outstanding performance in the debris detection task. Specifically, under the mAP@80 metric, it achieves improvements of 3.56%, 3.89%, and 4.65% compared to YOLOv5, YOLOv7, and the original YOLOv11 models, respectively. In the mAP@[75:95] metric, the increases are 1.8%, 0.49%, and 0.79%. This indicates that YOLOv11-Dd offers a significant advantage in detection accuracy under high-confidence requirements. As shown in Figure 6, YOLOv11-Dd shows greater accuracy in the localization of target bounding boxes compared to the original YOLOv11 model. The detection boxes fit the target edges more precisely, enabling a more complete enclosure of the target. This improvement is attributed to the optimization of the feature fusion method in the Concat module of the original YOLOv11 structure. The original model uses a direct feature concatenation approach, which overlooks the feature scale and semantic differences between layers, potentially leading to the loss of critical information. The FA-Concat (Feature Alignment Concat) module introduced in this paper effectively addresses the semantic difference issue in multi-layer feature fusion, enhancing the model’s ability to capture key target regions and improving overall detection accuracy. It is important to note that, with the introduction of the residual connection convolution structure, the model complexity of YOLOv11-Dd has increased, leading to a decrease in frame rate (fps) compared to the original YOLOv11 model. However, when compared to the YOLOv8 model, YOLOv11-Dd significantly improves detection accuracy while maintaining a similar parameter count, demonstrating the effectiveness and adaptability of the proposed structure in small-target detection scenarios. In summary, YOLOv11-Dd shows excellent overall performance in high-precision debris detection tasks, making it well-suited for deployment in real-world unmanned drilling machine environments.

4.2.2. Target Speed Measurement

In this paper, the motion of the detected debris is categorized into two types: one for angled splashing debris with initial velocity and another for free-falling debris without initial velocity. Multiple sets of samples are collected for each category to measure the speed, and the average value is taken to enhance measurement accuracy. The results of the speed measurements are shown in

Table 4. Speed measurement results.

Motion Type	Frame Rate	Variance/(m/s)2	Average Variance/(m/s)2	Accuracy/(%)	Average Accuracy/(%)
Free-fall	30	0.0128	0.0122	92.05	94.83
With initial velocity	30	0.0115		97.61
Free-fall	60	0.0360	0.0392	84.32	89.40
With initial velocity	60	0.0424		94.47

Boldface denotes the best result for each evaluation metric.

.

Figure 7 illustrates a sequence of images of simulated debris splashing diagonally upward with initial velocity. From the figure, it is clearly observed that the speed of the target decreases during the upward motion and increases after reaching the peak, which is consistent with the basic laws of projectile motion. Moreover, the measured speed variation curve aligns closely with physical reality, thus validating the effectiveness and reliability of the pixel displacement-based speed measurement method for dynamic target tracking.

The comparison in Table 4 shows that the proposed debris speed measurement model performs well across different testing scenarios. Notably, the 30 fps data outperforms the 60 fps data in terms of speed measurement accuracy. This is because, with a lower frame rate, the pixel displacement of the debris per unit time is larger, reducing errors caused by small offsets between the detected center of the bounding box and the true centroid position. Debris with initial velocity shows higher measurement accuracy due to larger displacement in a given time, which reduces the relative error. In contrast, the displacement of free-falling motion in the initial phase is very small, and even minor prediction errors by the detector can result in large speed measurement inaccuracies, thereby lowering overall accuracy.

Based on the above analysis, future research will focus on improving the detection of low-speed small-displacement targets. This could involve introducing higher-resolution image perception modules or guiding the model to emphasize target contour features, which would further enhance speed measurement accuracy during the initial stages.

4.2.3. Real-World Scenario Experiment

To further assess the adaptability and robustness of the proposed model in complex real-world environments, we captured a video sequence at 30 fps, where debris splashes were generated by a handheld portable impact drill striking a wall. A portion of the speed measurement process is presented in Figure 8.

From Figure 8, it is clear that, despite the complex texture of the wall and the presence of background distractions, such as weeds, the model successfully detects, tracks, and computes the speed of the target. The entire processing pipeline takes an average of 15 ms per frame, including 13 ms for object detection, 1 ms for tracking and matching, and 1 ms for speed estimation and label rendering. The resulting average frame rate is 67 fps, which fully supports real-time monitoring of video streams at 60 fps or lower. This demonstrates that the method proposed in this paper is robust and adaptable even in real-world conditions with high background noise and uncertainty. These results further validate the practical utility of the proposed algorithm, showcasing its potential application for debris motion analysis and speed monitoring in engineering environments.

4.3. Ablation Experiment

To evaluate the impact of the newly added Ghost Conv module and the enhanced FA-Concat feature fusion module on model performance, this paper designs an ablation experiment, analyzing the influence of each module on detection accuracy (mAP@80 and mAP@75–95), speed measurement accuracy, and inference speed (fps). The experimental results are presented in

Table 5. Target detection ablation experiments (“✓” indicates that the corresponding module is enabled).

YOLOv11	Ghost Conv	Concat	mAP@80/(%)	mAP@75–95/(%)	fps	Params/M
✓			71.36	40.94	111	24.20
✓	✓		71.75	39.70	114	22.24
✓		✓	74.18	42.25	75	45.39
✓	✓	✓	76.04	41.73	76	43.51

Boldface denotes the best result for each evaluation metric.

and

Table 6. Target-tracking ablation experiments (“✓” indicates that the corresponding module is enabled).

YOLOv11	Ghost Conv	Concat	Variance (30 Frames) ((m/s)2)	Variance (60 Frames) ((m/s)2)	Accuracy (30 Frames)/(%)	Accuracy (60 Frames)/(%)
✓			0.0177	0.0411	94.44	88.97
✓	✓		0.0184	0.0427	94.51	89.65
✓		✓	0.0148	0.0393	94.44	89.41
✓	✓	✓	0.0122	0.0392	94.83	89.40

Boldface denotes the best result for each evaluation metric.

, with “✓” indicating that the corresponding module is enabled.

4.3.1. Replacing the C3k2 Module with the Ghost Conv Module

As shown in Table 5, after incorporating the Ghost Conv module, the model improved by 1.56% in the mAP@80 metric but decreased by 1.24% in the stricter mAP@75–95 metric. Additionally, as shown in Table 6, the model achieved a speed detection accuracy of 89.65% in 60-frame videos, the best performance across all the experimental settings, although its speed measurement results fluctuated significantly across different scenarios, indicating poor stability.

This indicates that, while the Ghost Conv module effectively reduces model complexity and improves inference speed (fps), it still has limitations in feature representation. Ghost Conv generates redundant features by applying linear transformations to a small number of primary features. Although this approach maintains high accuracy in static or low-complexity scenes, it struggles to capture key visual cues—such as object boundaries, shape deformations, and motion blur—in scenarios involving fast motion or complex appearances. As a result, despite its strong performance on the mAP@80 metric, its accuracy drops under the stricter mAP@75–95 evaluation due to insufficient modeling of subtle displacements and fine structural details. In summary, while Ghost Conv provides computational benefits, it also challenges the robustness of object detection and requires complementary modules to enhance feature expressiveness.

4.3.2. Replacement of the Original Concat Module with the FA-Concat Module Only

As indicated in Table 5, incorporating the FA-Concat module improved the model’s mAP@80 by 4.99% and mAP@75–95 by 4.27%, demonstrating that the enhanced feature fusion strategy substantially strengthened the model’s object recognition capability, particularly under high-precision matching conditions. However, this improvement came at the cost of a significant increase in computational complexity, resulting in a marked reduction in inference speed (fps).

Further evidence from Table 6 shows that, in the speed measurement task, the FA-Concat module outperformed the original YOLOv11 model in both speed estimation accuracy and stability, indicating that its enhanced feature representation capacity contributes to better capturing subtle variations in the target’s motion trajectory, thereby improving the consistency and reliability of velocity estimation.

These findings confirm that the improved FA-Concat module significantly enhances detection accuracy by employing an aligned feature fusion strategy. Unlike the original simple concatenation approach, the FA-Concat module effectively aligns features from different network layers to better capture fine-grained target details. Nevertheless, this enhancement also increases network complexity, substantially impacting computational efficiency. Specifically, the FA-Concat module introduces convolutional chains with residual connections to mitigate differences between hierarchical features, optimizing feature integrity, especially when fusing low-resolution semantic features with high-resolution detail features. Furthermore, the module customizes the number of convolutional layers based on the receptive field variations across feature levels to further strengthen the fusion effect. Despite achieving notable improvements in feature fusion, the considerable increase in computational overhead leads to a significant drop in fps.

4.3.3. Simultaneous Replacement of the C3k2 and Concat Modules with the Ghost Conv and FA-Concat Modules

As illustrated in Table 6, when both the Ghost Conv and FA-Concat modules are integrated, a significant improvement in the stability of speed estimation can be observed. Compared to the original YOLOv11 model, the error variance decreased by 31.07% under the 30-frame video setting and by 4.62% under the 60-frame setting, indicating that the proposed architectural combination plays a positive role in enhancing model robustness. Nevertheless, it is important to note that the overall speed estimation accuracy under the 60-frame condition dropped by 0.25%. This phenomenon suggests that the increased model complexity results in reduced inference efficiency at higher frame rates, thereby impairing the model’s responsiveness to subtle displacements in rapid successive frames and exposing a certain performance bottleneck.

From the detection performance results in Table 5, compared to introducing only the FA-Concat module, the mAP@80 increased by 1.86%, whereas the mAP@75–95 dropped by 0.52%. This outcome further verifies that, under stricter detection accuracy requirements, the Ghost Conv module exhibits limitations in feature extraction depth and richness. Although the FA-Concat module enhances feature representation consistency and completeness through cross-layer alignment, the semantic information loss introduced by the Ghost Conv module at the low-level feature extraction stage constrains the overall detection network’s performance ceiling.

Hence, in high-precision object detection tasks, the trade-off undertaken by the Ghost Conv module between computational efficiency and representational power may no longer be optimal. Meanwhile, the FA-Concat module still presents opportunities for further improvement in feature alignment and fusion strategies. In future work, we intend to incorporate attention-guided mechanisms or design more sophisticated residual-guided structures for cross-layer features with dynamic scales and larger semantic gaps, aiming to further enhance the semantic consistency and discriminative power of the fused features.

5. Conclusions

In response to the need for cutting-motion monitoring in unmanned drilling operations, this paper proposes a high-precision detection approach that integrates small-object detection with speed estimation. The method is built upon an improved YOLOv11 detection algorithm and establishes an end-to-end solution for cutting-speed measurement by leveraging the mapping relationship between image pixel displacement and actual physical displacement. Firstly, to address challenges such as the small size and weak features of cuttings, we optimize the YOLOv11 detection head by introducing a multi-scale feature alignment and fusion strategy, significantly enhancing the small-object detection capabilities. The experimental results demonstrate that the proposed improvements boost detection performance by 4.65% compared to the original model, achieving a final mAP@80 of 76.04%. Secondly, during the object tracking phase, the ByteTrack ensures stable tracking, while the speed estimation module maps pixel displacement to real-world coordinates using camera calibration, enabling precise velocity measurement. The proposed model was trained and evaluated on a custom-built dataset. The experimental results show that, while detection accuracy decreases under low-speed motion with high frame rates compared to high-speed motion with low frame rates, the method still achieves an average speed estimation accuracy of 92.12%. It also outperforms the baseline model in detection accuracy, tracking stability, and computational efficiency. However, the dataset used in this study was generated under idealized conditions and does not fully represent the complexity of real-world environments. Future research will focus on expanding and enriching the dataset to cover more realistic and challenging working conditions, enabling more targeted validation. In addition, we plan to further optimize the YOLOv11-Dd detection architecture by reducing model complexity while maintaining detection accuracy. Special improvements will also be made for low-speed target scenarios to enhance the system’s overall robustness and adaptability.