Abstract
Container liner shipping companies operate within a complex environment where they must balance profitability and service reliability. Meanwhile, evolving regulatory policies, such as surcharges imposed on ships of a particular origin or type on specific trade lanes, introduce new operational challenges. This study addresses the heterogeneous ship routing and demand acceptance problem, aiming to maximize two conflicting objectives: weekly profit and total transport volume. We formulate the problem as a bi-objective mixed-integer programming model and prove that the ship chartering constraint matrix is totally unimodular, enabling the reformulation of the model into a partially relaxed MIP that preserves optimality while improving computational efficiency. We further analyze key mathematical properties showing that the Pareto frontier consists of a finite union of continuous, piecewise linear segments but is generally non-convex with discontinuities. A case study based on a realistic liner shipping network confirms the model’s effectiveness in capturing the trade-off between profit and transport volume. Sensitivity analyses show that increasing freight rates enables higher profits without large losses in volume. Notably, this paper provides a practical risk management framework for shipping companies to enhance their adaptability under shifting regulatory landscapes.
1. Introduction
Container liner shipping is a cornerstone of global trade, enabling the efficient transport of goods across continents and supporting much of the world’s economic activity [1]. In 2025, however, the transpacific shipping market and the broader containerized ocean transport system are experiencing significant disruptions due to new U.S. Section 301 actions targeting ships built in China or operated by Chinese companies [2,3,4]. These measures impose phased port surcharges, effective after a 180-day grace period starting 17 April 2025, with fees for Chinese ship owners/operators beginning at $50 per net ton per U.S. voyage and escalating to $140 per net ton by 17 April 2028 [5]. For China-built ships operated by non-China entities, fees start at $18 per net ton (or $120 per container unloaded) and rise to $33 per net ton (or $250 per container) by the same date, applied up to five times annually per ship [5]. Additionally, the policy mandates that a growing share of U.S. exports, such as liquefied natural gas (LNG), be carried on U.S.-operated ships, starting at 1% in 2028 and increasing to 15% by 2047 [2]. These measures have already caused significant disruptions across key sectors. In the coal sector, ship owners are refusing U.S. coal shipment contracts due to the cost increases, halting $130 billion in exports within 60 days, as the fees have raised delivered coal costs by up to 35% [6]. Agricultural exporters of corn, soybeans, and wheat are struggling to secure ocean freight since May 2025, incurring additional transportation costs of $372 million to $930 million annually [6]. Energy exports, including LNG and oil, are being curtailed due to the absence of non-China-built ships, significantly impacting shipments [6]. Operationally, carriers are suspending routes to smaller ports like Oakland in favor of larger hubs like Los Angeles, causing congestion and equipment misallocation [7]. Industry estimates indicate the fees are adding $600–$800 per container, costing the shipping sector $20 billion annually and increasing consumer prices [7]. These disruptions highlight the urgency and scale of the policy shock, underscoring the need for stakeholders to adapt swiftly to mitigate economic fallout.
Liner operators, already navigating a highly competitive and volatile market [8], must now grapple with these profound regulatory changes in addition to existing challenges such as fluctuating demand, rising operating costs, and increasing ship heterogeneity stemming from fleet expansion and alliance strategies [8,9]. This significantly complicates key decisions in operational management [9], including ship routing, fleet deployment, and transport demand acceptance, which must be carefully balanced to maintain competitiveness [10]. The introduction of such significant port surcharges based on ship origin and ownership fundamentally alters ship routing and deployment decisions. Prior studies on ship routing and scheduling emphasize that changes in cost structures, such as the imposition of new regional fees, directly affect optimal fleet routing, port call patterns, and service frequency [4,11,12]. When operational costs increase on specific routes or port calls, liner operators have strong incentives to adjust their deployment, potentially discontinuing routes that include high-fee ports to minimize surcharge exposure [4]. Empirical research and optimization models show that fleet deployment decisions are highly sensitive to regulatory and cost-driven shocks [13], with dynamic re-routing occurring not only in response to fuel price shifts and emission control area (ECA) regulations, but also as shippers and carriers seek least-cost pathways under new port or trade restrictions [14]. Consequently, shipping lines have begun reviewing fleet composition, revisiting newbuilding strategies, and considering detaching beneficial ownership links to avoid U.S. surcharges, potentially transferring China-built ships to non-U.S. trades or substituting other nations’ builds into U.S. lanes [2,4].
Against this backdrop of specific and evolving regulatory challenges, including changing cost structures, environmental rules, and geopolitical pressures, existing research has extensively studied a wide range of operational decisions in liner shipping, particularly in areas such as multi-route scheduling, fleet deployment under cost variability, ship speed optimization, and port time windows. Numerous studies develop optimization models for ship routing and scheduling, addressing both industrial and tramp segments as well as liner shipping, and often tackle multi-ship, multi-route scenarios, variable ship speeds, and constraints arising from port schedules and ship heterogeneity [11,12,15,16,17]. These frequently employ mathematical programming techniques like mixed-integer linear programming (MILP), mixed-integer nonlinear programming (MINLP), and advanced heuristic methods to handle large-scale, realistic instances [12]. Given the inherent trade-offs in liner shipping operations between economic performance, service quality, energy consumption, and environmental regulations, multi-objective optimization frameworks have gained prominence for addressing these complex decisions [18]. These frameworks aim to identify effective operational strategies by considering divergent objectives like cost minimization, profit maximization, service coverage, and on-time delivery, with much research dedicated to finding robust solutions in these multifaceted decision environments [18,19,20]. Separately, the critical role of demand acceptance in revenue management is also well established, with numerous studies addressing its optimization, particularly for scenarios involving transit-time-sensitive demand [21]. These studies highlight effective strategies for maximizing revenue based on demand characteristics. While both multi-objective optimization and demand acceptance are individually well explored, their integration within comprehensive models for optimizing ship routing, fleet deployment, and service design, particularly for models that must also account for dynamic slot allocation alongside periodic demand structures or heterogeneous fleet operations, represents an area with ongoing research opportunities [22]. In tackling such comprehensive models, they must incorporate complexities like ship heterogeneity, multi-objective trade-offs, and general regulatory constraints [12,17].
In addition, the latest U.S. measures underscore a more profound research gap: while operational decision making under general regulatory and cost constraints has been widely examined, most existing research on fleet deployment and ship routing does not fully account for the specific impacts of regulatory measures like Section 301 surcharges, which are based on a ship’s country of build or ownership [23]. Most prior studies on ship routing and fleet deployment assume homogeneous fleets or do not explicitly model the bi-objective trade-offs, indicating a clear lack of integrated models that simultaneously optimize heterogeneous ship routing in the context of specific and impactful regulatory shocks such as the Section 301 surcharges. Even when general regulatory constraints are considered, analyses rarely examine the specific operational impacts of surcharges differentiated by ship build country on route selection, ship assignment with particular attention to China-built ships compared to others, and transport demand acceptance strategies within a unified bi-objective optimization framework. Such a framework should incorporate both operational heterogeneity and policy-driven risks. There is a clear need for new models to investigate the consequences of these policies, especially regarding global fleet renewal, cross-border cargo flows, and the resilience and adaptability of international shipping networks amid shifting regulatory landscapes.
To address these gaps comprehensively, this study formulates a heterogeneous ship routing and demand acceptance (HSR-DA) problem under the influence of U.S. regulatory surcharges on China-built ships. The HSR-DA problem jointly optimizes route operation, heterogeneous ship assignments, transport demand acceptance, and chartering decisions with the dual objectives of maximizing weekly profit and total transport volume. A bi-objective mixed-integer programming (MIP) model is developed to support integrated decision making, incorporating practical constraints such as ship requirements, fleet availability considering chartering, accepted transport volume, and transport capacity limits. To enhance computational efficiency, this study further introduces a partially relaxed mixed-integer programming (PRMIP) model by leveraging the TU properties of the chartering constraint matrices, which significantly reduces computational complexity without compromising optimality. Overall, the proposed bi-objective MIP model provides a practical and implementable optimization framework for shipping companies seeking to adapt their operations optimally in response to challenging regulatory landscapes.
In particular, the multifaceted contributions of this paper are outlined as follows:
- We establish a bi-objective MIP model for jointly optimizing the heterogeneous ship routing and transport demand acceptance, subject to ship requirement constraints, fleet availability and demand acceptance limits. This formulation enables shipping companies to effectively evaluate and strategically balance the often competing objectives of maximizing weekly profit and maximizing total transport volume, thereby facilitating more informed decision making in their operational planning and resource allocation under the new regulatory pressures.
- We prove the necessity of maintaining integrality for route operation variables and ship assignment variables and develop a computationally efficient PRMIP model by leveraging the totally unimodular (TU) property of the chartering constraint matrices, allowing for continuous relaxation of the ship chartering variables without compromising optimality. The model is validated through a real-world case study, which shows that the PRMIP model achieves identical optimal solutions to the MIP model with significantly reduced computational time.
- We analyze the structural properties of the Pareto frontier for the bi-objective MIP model and find that it consists of a finite union of continuous, piecewise linear segments. We also show that the global frontier is generally non-convex and can exhibit discontinuities due to the discrete nature of ship assignment and route operation decisions. This structural insight provides a precise characterization of the optimal trade-offs between profit maximization and transport volume, illuminating the set of efficient solutions.
- Sensitivity analyses demonstrate that as freight rates increase, the Pareto frontier shifts to offer simultaneously improved profitability and transport volume potential. This shift shows diminished marginal trade-offs between the two objectives, enhancing operational flexibility.
- A case study based on a global liner network, considering the impact of U.S. surcharges, yields three major managerial insights: (i) optimal fleet deployment under the surcharges consistently involves avoiding the assignment of China-built ships to routes serving U.S. ports to minimize regulatory cost impacts; (ii) strategic selection of an operating point on the profit-volume Pareto frontier is crucial, as an extreme focus on one objective leads to disproportionate sacrifices in the other, underscoring the practical value of balanced operational strategies; and (iii) prioritizing profitability naturally drives route network rationalization and selective acceptance of higher-value cargo, which in turn reduces overall operational costs and optimizes fleet utilization.
The remainder of this paper is structured as follows. Section 2 provides an overview of the relevant literature on liner shipping optimization, fleet deployment, demand acceptance, and the impact of regulatory policies. Section 3 formulates the research problem as a bi-objective MIP model and presents its theoretical properties. Section 4 details the augmented -constraint method adopted to solve the bi-objective optimization model. Section 5 reports the numerical results and sensitivity experiments. Finally, Section 6 concludes the paper and outlines directions for future research.
2. Literature Review
To comprehensively understand the methodologies for ship routing, fleet deployment, and transport demand acceptance under regulatory pressures, this review examines the literature focusing on optimization models and algorithms for HSR-DA within liner shipping operational frameworks.
2.1. Ship Routing, Fleet Deployment, and Demand Acceptance
Several studies investigate the optimization of ship routing and fleet deployment under complex operational constraints. Christiansen et al. provide a comprehensive overview, addressing network design, ship routing, and speed optimization, emphasizing the necessity of integrated decision making to enhance operational efficiency [1]. Tran and Haasis review network optimization, highlighting that routing decisions must carefully account for port capacity constraints, vessel types, and market demand characteristics, typically employing mathematical programming to minimize total operational costs [24].
To minimize costs or maximize profits, Gu et al. develop a model for fleet deployment and speed optimization, explicitly considering fuel consumption heterogeneity, through integrated decisions on node selection, ship assignment, and speed setting [25]. Jiang et al. construct a MILP model to optimize route and schedule design within port time window constraints [26]. Zheng et al. propose a MILP model combined with global optimization algorithms to handle heterogeneous fleets and reduce total operational costs [18]. Multi-objective approaches are also proposed in response to environmental and regulatory pressures. Pasha et al. introduce a tactical-level joint optimization model for heterogeneous fleets, balancing CO2 emissions reduction and profit maximization [27]. Zhao et al. incorporate low-carbon operations and fuel bunkering into a cost-minimization model for greener shipping [28]. Tran and Haasis survey various multi-objective strategies addressing multiple performance indicators including customer satisfaction and carbon emissions [24]. To solve large-scale container liner shipping optimization problems, researchers formulate MILP or MINLP models and employ exact algorithms, heuristics, and matheuristics [25,27,28,29].
Demand acceptance optimization is also receiving increasing attention. Cheaitou et al. model time-sensitive demand using integer nonlinear programming and heuristics to maximize profit [30]. Pasha et al. propose a holistic MILP model that integrates demand elasticity with fleet deployment and speed optimization [10]. Xia et al. consider joint planning of cargo allocation, speed, and fleet deployment to minimize fuel and operational costs [31]. Lai et al. adopt a two-stage robust optimization framework under demand uncertainty [32], while Zhao et al. summarize multi-objective planning approaches for demand acceptance, focusing on tonnage limits and route capacity [33].
2.2. Impact of Regulatory Policies and External Disruptions
Regulatory policies profoundly influence container liner shipping by imposing constraints that reshape routing, fleet deployment, and demand acceptance strategies, compelling operators to balance compliance with cost efficiency. Environmental regulations, such as sulfur emission caps and carbon reduction targets, promote sustainable practices. Psaraftis and Kontovas demonstrate through speed optimization models how minimizing fuel costs and emissions via measures like low sulfur fuel or speed reductions can increase operational costs by up to 20% [34]. Pasha et al. optimize tactical planning using a model that incorporates carbon taxes and varied ship efficiencies, achieving considerable emission reductions alongside cost minimization [27]. Zhao et al. propose a model for green liner shipping that balances costs and emissions through fleet deployment and fuel bunkering, resulting in significant emission reductions [28]. Trade policies, such as proposed U.S. surcharges on certain foreign built ships involving substantial fees per port call, necessitate rerouting or fleet reconfiguration [3]. Bertho et al. use regression-based econometric analysis to show that foreign investment restrictions raise shipping costs by 24–50% and reduce trade flows, necessitating adaptive routing models [35]. Notteboom et al. and Fan et al. apply descriptive statistics and network modeling to highlight how U.S.–China trade tensions increase operating costs by 5–10% and transit times by up to 12% on Asia–North America routes [36]. Safety regulations, for instance the International Ship and Port Facility Security Code, extend port turnaround times by 10–20%, indirectly increasing costs, as Bichou’s qualitative analysis indicates [37]. These studies underscore the need for optimization models that incorporate specific regulatory constraints.
External disruptions, including pandemics, geopolitical events, and natural disasters, exacerbate operational challenges in liner shipping, requiring resilient strategies to mitigate delays and costs. The COVID-19 pandemic, as Jin et al. show through AIS-driven data analysis, reduced China’s port network connectivity by 15% due to congestion, while Notteboom’s descriptive analysis reports a 20% rise in schedule disruptions, prompting network reconfiguration [38]. Ksciuk et al. propose a simulation-based optimization model, integrating simulation and optimization techniques to manage pandemic induced congestion, reducing delays and costs by up to 25% through optimized ship assignments [39]. Zhu et al. develop exact branch and bound and metaheuristic algorithms to optimize vessel deployment and routing under congestion, achieving 8–12% cost savings [40]. The 2021 Suez Canal blockage, which caused substantial daily trade losses according to Verschuur et al.’s economic modeling, necessitated rerouting via the Cape of Good Hope, increasing transit times by 10–14 days [41]. Elmi et al. advocate port skipping, which their review shows can reduce delays by up to 20% [42]. Natural disasters, addressed by Zheng et al.’s distributed predictive control model, require rapid rerouting to minimize response times [43].
2.3. Recent Trends in Multi-Objective Optimization
Recent advancements in multi-objective optimization provide methodologies that can inspire solutions for ship routing, fleet deployment, and demand acceptance in liner shipping. For instance, skip-stop strategies in urban rail transit optimize total travel time and equity in service distribution. Han et al. [44] formulate a multi-objective mixed integer nonlinear programming model to minimize both inequity and total travel time through train stop planning and scheduling, with a case study on Seoul’s urban railways. Rajabighamchi et al. [45] propose a robust multi-objective model for skip-stop scheduling, minimizing travel and waiting times while ensuring equitable service through robust scheduling under demand uncertainty. Shang et al. [46] address passenger crowding risks and revenue losses in oversaturated networks, offering insights for port call sequence optimization in liner shipping under congestion or regulatory constraints. Similarly, accessible routing strategies provide inspiration for customized routing; Lee et al. [47] develop an accessible taxi routing model based on the travel behavior of people with disabilities, using a Gaussian mixture model to optimize routes, which can guide prioritization of ports with specialized cargo needs. Additionally, Lee and Kim [48] develop a multi-objective model for submerged floating tunnel routing, balancing structural safety and travel time using Non-dominated Sorting Genetic Algorithm II (NSGA-II), achieving 9.9% to 10.5% time savings on the Mokpo–Jeju route. These techniques can inform ship routing under complex constraints like safety regulations or emission control areas.
Recent progress in liner shipping has focused on integrating multi-objective optimization with heterogeneous fleet assignment under regulatory constraints. Pasha et al. [27] propose a multi-objective MILP model for tactical-level planning in liner shipping, optimizing ship deployment and routing for heterogeneous fleets while balancing costs and CO2 emissions under carbon tax regulations, achieving up to 15% cost savings and 20% emission reductions on a transatlantic route. Wang et al. [9] investigate co-management of heterogeneous ship fleets in liner alliances, optimizing profit-sharing, fleet utilization, and service reliability under emission caps, improving profit by 10% and reducing delays by 12% on an Asia–Europe route. Wen et al. [49] develop a multi-objective MILP model for ship scheduling, addressing port congestion and environmental regulations using queuing theory, optimizing costs, emissions, and service unreliability with improvements of 4%, 6%, and 44% over NSGA-II, applied to Maersk’s Trans-Pacific route with nine ports and five ships of 10,000 TEU. These studies highlight the potential of multi-objective MILP frameworks to balance economic, environmental, and operational objectives in liner shipping under stringent regulatory environments.
2.4. Research Gap
Despite the significant advancements in optimization models for ship routing, fleet deployment, and demand acceptance, several key gaps remain in the existing literature:
- The lack of comprehensive frameworks for coordinating ship fleet management and surging regulatory policies: While some studies have explored fleet deployment in the context of heterogeneous fleets, few models address the origin-based cost differences arising from regulatory policies, such as surcharges on certain foreign-built ships. Regulatory impacts, such as the penalties imposed on China-built ships, are often overlooked in operational models despite their significant effects on route viability and fleet deployment decisions. Christiansen et al. [1], Gu et al. [25], and Jiang et al. [26] investigate fleet deployment, but they do not consider regulatory policies like U.S. surcharges on China-built ships that directly influence fleet deployment strategies and routing decisions. Pasha et al. [27], Zhao et al. [28], and Bertho et al. [35] explore regulatory constraints like carbon taxes or fuel efficiency but do not explicitly incorporate surcharges based on ship origin or other regulatory policies into fleet deployment and routing frameworks. In contrast, our work integrates these origin-based cost differences into the optimization framework, providing a more realistic model for ship routing and fleet deployment under such regulatory pressures.
- The limited availability of integrated optimization models that jointly consider routing, fleet assignment, and demand acceptance decisions: A recurring issue in the literature is the treatment of routing, fleet assignment, and demand acceptance as separate or loosely coupled problems. This approach limits the ability to model the intricate trade-offs between short-term cost efficiency and long-term network viability, especially in markets affected by volatile demand and regulatory shocks. Song et al. [18], Jiang et al. [26], and Zhao et al. [28] develop MILP models for routing and scheduling under specific constraints but often treat fleet deployment and demand acceptance separately, missing the dynamic interactions between these components. Tran and Haasis [24] review network optimization but fail to provide a unified framework that integrates fleet deployment, routing, and demand acceptance within a single optimization model. Wang et al. [9], Pasha et al. [10], and Cheaitou et al. [30] also examine these components separately, limiting the scope of their models. Our model addresses this gap by unifying routing, fleet assignment, and demand acceptance within a single framework, enabling the consideration of trade-offs between cost, fleet utilization, regulatory constraints, and demand acceptance in an integrated manner.
- The challenge of balancing profitability and service scale under regulatory constraints: A key challenge in liner shipping optimization is the trade-off between maximizing profitability and meeting service volume targets, particularly in light of regulatory changes such as surcharges on foreign-built ships. While multi-objective optimization has been increasingly employed in shipping optimization, few models effectively address the balance between cost efficiency and service scale, especially in the context of specific regulatory pressures. Pasha et al. [27], Zhao et al. [28], and Wang et al. [9] propose multi-objective models for fleet deployment and route optimization but fail to fully address the conflict between profitability and service volume. Their models typically consider cost minimization and emission reduction without taking into account the penalties and increased costs imposed by regulatory policies. Cheaitou et al. [30], Pasha et al. [10], and Lai et al. [32] also address demand acceptance and fleet deployment but do not fully integrate the operational impact of regulatory changes on the profitability–service scale balance. Wen et al. [49] optimize ship scheduling under port congestion and environmental regulations, but their work focuses more on service reliability and emission reduction, not on explicitly balancing profitability with service volume. Our research bridges this gap by explicitly modeling the bi-objective conflict between profitability and service scale in the context of regulatory surcharges, which significantly affect route-specific costs and margins. By incorporating regulatory costs into our multi-objective optimization model, we allow liner shipping companies to make more informed decisions on how to balance profitability and service commitments.
To bridge these gaps, we propose a bi-objective MIP model designed for the HSR-DA problem, which integrates route operation, ship assignment, and transport demand acceptance. This MIP model uniquely incorporates real-world cost structures, especially surcharges such as those imposed on China-built ships. These surcharges are embedded in the objective function and play a critical role in shaping routing and deployment decisions across a heterogeneous fleet. The model formulation incorporates several practical constraints, including ship assignment limitations, fleet availability, demand-related transport volume constraints, and transport capacity requirements. This model provides a comprehensive decision-support tool for operational planning under real-world regulatory and market conditions. In particular, it provides guidance for ship routing and demand acceptance decisions under the influence of recent policy proposals to impose substantial surcharges on China-built ships calling at U.S. ports.
3. Problem Formulation
In this section, we first introduce the problem background and describe the challenges in route deployment, ship assignment, and transport demand acceptance in Section 3.1. Following that, we formulate the problem using a bi-objective MIP model in Section 3.2. Finally, Section 3.3 provides a detailed description of model analysis.
3.1. Problem Description
Container liner operators are under constant pressure to balance network coverage, asset utilization, and profitability. They must decide which cyclic routes to operate, how to deploy heterogeneous ships, and how much freight demand to accept, all while facing volatile fuel prices, charter rates, and regulatory surcharges. Recent policy proposals to levy additional port fees on China-built ships calling at U.S. ports have further complicated fleet planning. These surcharges specifically apply only to China-built ships above a certain capacity threshold, while ships constructed in other countries or smaller China-built ships are exempt [50]. As a result, carriers with mixed fleets must now carefully account for route-dependent surcharges in their cost structure. Against this backdrop, a strategic yet tractable planning framework is indispensable for maximizing profit without jeopardizing service reliability.
For the shipping company, three interdependent planning tasks are of primary importance: selecting a subset of candidate routes to operate, assigning a suitable mix of ship types to each operated route to meet the required ship count, and determining how much of the origin–destination (OD) demand to accept and how to allocate the accepted demand across the selected network. If route deployment and fleet composition are poorly matched to demand geography, high-yield OD pairs may be rejected, deployed ships may be underutilized, or routes may involve China-built ships incurring avoidable penalties at U.S. ports. In light of these considerations, it is crucial to precisely choose operating routes based on transport demand and associated costs, including fuel cost, berthing cost, and route-specific surcharges for certain ship types, and to allocate the fleet accordingly. Making informed decisions on ship deployment and chartering actions, including when to charter in and charter out ships, is vital to maintaining the cost-effectiveness and competitiveness of the operator’s network.
Consider the route–ship–demand allocation problem in a liner-shipping network that provides stable containerized services over a set of predefined cyclic routes. The set of all candidate routes is denoted by (indexed by ). Each route represents a predefined closed-loop trajectory involving a sequence of ports and is a candidate for service deployment with a fixed weekly schedule. The set of OD pairs is denoted by , where each element indicates an origin port and a destination port . For each OD pair, the subset of feasible routes that connect the two ports is denoted by . The set of all legs between consecutive ports of call on route is denoted by (indexed by ). For each leg , we denote the set of OD pairs routing passes through the leg by . The set of available ship types is denoted by , where ships built in China are represented by the subset . The available fleet includes both ships owned by the shipping company and charterable ships.
To ensure a weekly departure frequency on any operated route, a sufficient number of ships must be deployed to maintain the required frequency, given the time needed to complete a full loop. We assume that all ships sail at a uniform speed when deployed on the same route, and the total number of ships required on route , denoted by , is numerically equal to the round-trip time (in weeks) for route , as one ship must depart each week while another completes the full loop.
The weekly transport demand for each OD pair is denoted by , and the corresponding revenue earned per TEU transported is denoted by . The total volume of accepted demand for each OD pair cannot exceed , and the shipping company is allowed to reject part of the demand if full acceptance leads to unprofitable operations. Each ship type has a capacity of twenty-foot equivalent units (TEUs). The transportation cost of one ship of type completing a full round trip on route includes fuel costs (), berthing costs (), and any extra penalties specifically incurred by China-built ships when deployed on routes calling at U.S. ports (). The company’s owned fleet includes ships of type . To reduce operating costs, such as avoiding penalty fees associated with deploying China-built ships on routes that call at U.S. ports, the company may choose to charter in additional ships of alternative types and charter out idle ships that are not required. The weekly cost of chartering in a ship of type is given by , and the revenue obtained from chartering out an idle ship of type is denoted by .
A route represents a complete, cyclical sequence of port calls that a ship follows. A leg is the segment of a route connecting two adjacent ports. An OD pair represents a specific transport demand from a port of origin to a port of destination, both of which lie on the same route. The path for fulfilling an OD pair’s demand consists of one or more sequential legs along the route. To visually illustrate these relationships, Figure 1 presents an illustrative diagram.
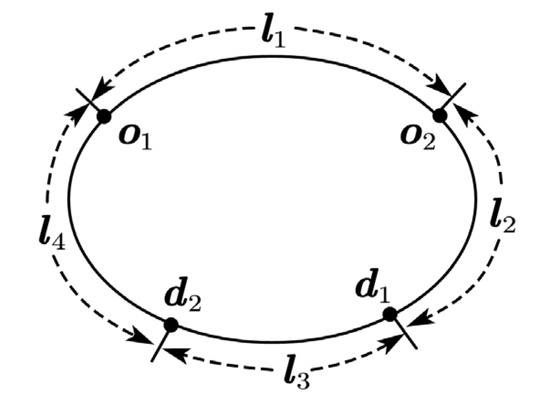
Figure 1.
OD pairs and legs on a route .
Figure 1 shows an example circle route that consists of four ports. The segments connecting adjacent ports form the four legs of the route: , , , and . The figure also illustrates two distinct OD pairs. The first is a transport demand from origin port to destination port , with its path covering legs and . The second is a transport demand from origin port to destination port , which is fulfilled by traversing legs and . This structure highlights how multiple OD demands can share capacity on common legs within a single shipping route.
The objective of this study is formulated as a bi-objective optimization that simultaneously maximizes the weekly profit and maximizes the total weekly transport volume across all OD pairs. The weekly profit consists of the total revenue from accepted transport demand, minus the total transportation costs of deployed ships, minus the cost of chartering in ships, plus the revenue generated from chartering out idle ships. To this end, we need to decide which candidate routes to operate. This decision is represented by the binary variable , which equals 1 if route is operated, and 0 otherwise. We also determine the fleet composition on each operated route by assigning specific ship types. This is described by the integer decision variable , which indicates the number of ships of type assigned to route . In addition, we consider whether ships are rented in or chartered out. The integer decision variable denotes the number of ships of type chartered in during the planning horizon, while represents the number of ships of type chartered out. For each OD pair and each route , the transport volume is determined by the continuous decision variable , which specifies the amount of accepted demand (TEUs/week) allocated to route .
3.2. Model Formulation
In this subsection, we present a bi-objective MIP model based on the problem setting described above. The model captures the integrated planning decisions required for route selection, ship assignment, and demand acceptance in a container liner shipping network. It focuses on strategic decisions for which routes to operate, the type and quantity of ships assigned to each operated route, the amount of weekly transport demand for each OD pair to accept, the allocation of accepted demand across the operated routes, and the number of ships to charter in and charter out. The objective is to maximize the weekly total profit and the total weekly transport volume across all OD pairs while adhering to practical constraints such as ship assignment limitations, fleet availability, demand-related transport volume constraints, and transport capacity requirements. Table 1 summarizes the notations used in the model.

Table 1.
Notations used in the model formulation.
The MIP model, formulated as Model (1), is developed to optimize route selection, ship assignment, weekly transport allocation, and chartering decisions, and can be written as follows:
| max | (1-1) | ||
| max | (1-2) | ||
| s.t. | (1-3) | ||
| (1-4) | |||
| (1-5) | |||
| (1-6) | |||
| (1-7) | |||
| (1-8) | |||
| (1-9) | |||
| (1-10) | |||
| (1-11) | |||
The objective function (1-1) maximizes the total weekly profit, which consists of four major components: the total revenue generated from accepted OD transport demand, the transportation cost (including fuel, berthing, and extra penalty costs) associated with route operation and ship assignment, the chartering cost for ships chartered in, and the revenue earned from chartering out surplus owned ships. The objective function (1-2) maximizes the total weekly transport volume across all OD pairs. Constraints (1-3) ensure that the quantity of ships assigned to each operated route equals the total number of ships required to operate that route. Constraints (1-4) ensure that the total number of ships of each type assigned to all routes does not exceed the available fleet after chartering in and chartering out. Constraints (1-5) require that the number of ships chartered out for each ship type does not exceed the company’s owned fleet. Constraints (1-6) ensure that, for each OD pair, the total accepted transport volume allocated to all routes does not exceed the total market demand for that OD pair. Constraints (1-7) denote that, for each leg on each operated route, the total transport volume assigned across all relevant OD pairs does not exceed the transport capacity of that route. Constraints (1-8)–(1-11) are the domains of the decision variables.
Figure 2 illustrates the decision-making flow of our MIP model.
Figure 2.
Illustration of Pareto frontier segments and gaps.
3.3. Model Analysis
In this section, we introduce some theoretical properties regarding the MIP model presented in Section 3.2.
3.3.1. Integrality Necessity of Binary and Integer Variables
To improve the solving efficiency of the MIP model, we first investigate whether the binary variables and integer variables can be relaxed. Through meticulous analysis, we establish Theorems 1 and 2.
Theorem 1.
The binary variables
cannot be relaxed to continuous ones as non-integer solutions will emerge and violate practical feasibility.
Theorem 2.
The integer variables
cannot be relaxed to continuous ones, as this would lead to impractical fractional ship assignment.
The proofs of Theorems 1 and 2 are presented in Appendix A.1.
3.3.2. Totally Unimodular Property of the Coefficient Matrix for and
A key strategy for efficiently solving large-scale optimization problems involves relaxing binary or integer variables into continuous ones without compromising the integrity of the solution. Within our proposed framework, the structure of constraints related to vessel chartering is of particular interest. By examining the mathematical properties of the corresponding coefficient matrix, we can identify conditions that permit such a relaxation, thereby enhancing the model’s tractability while preserving solution validity.
The TU property holds considerable significance in Integer Linear Programming (ILP). It enables the dropping of integer constraints without compromising optimality, thereby simplifying the solution process [51]. In practical scenarios, an ILP problem, which is generally NP-hard, can be solved efficiently through simpler LP techniques that work in polynomial time. This makes the TU property highly valuable in applications like network flows, scheduling, and resource allocation, where the underlying matrices often naturally possess this characteristic.
We introduce the following theorem to formalize this property for the variables and .
Theorem 3.
For all
in, the coefficient matrices of
and are TU.
The proof of Theorem 3 is presented in Appendix A.2. Combining Theorem 3 with the fact that the right-hand-side terms of constraints (1-4) and (1-5) are always integral allows for the relaxation of the integer variables and to be continuous. The integrality of the right-hand side is assured, as these terms are constructed solely from the integer variables and the integer parameters . The direct consequence of this relaxation is a significant reduction in the model’s computational burden, achieved without compromising the optimality of the solution.
3.3.3. Structural Properties of the Pareto Frontier
To understand the structure of trade-offs between weekly profit and transport volume, it is essential to analyze the mathematical characteristics of the Pareto frontier generated by the bi-objective MIP model. Unlike single-objective models, bi-objective optimization yields a set of non-dominated solutions rather than a unique optimum. The following theorem characterizes the geometric and continuity properties of the Pareto frontier, providing foundational understanding for both theoretical analysis and algorithmic development.
Theorem 4.
The Pareto frontier consists of a finite union of line segments, and within each segment, the Pareto frontier is continuous and piecewise linear.
Theorem 5.
The Pareto frontier is generally non-convex and exhibits discontinuities.
The proofs of Theorems 4 and 5 are presented in Appendix A.3. This structure, which is non-convex and exhibits discontinuities due to distinct integer configurations, is illustrated in Figure 3, which provides a visual representation of the disconnected Pareto frontier. Each colored segment corresponds to the subset of solutions in the Pareto frontier under a fixed-integer configuration.
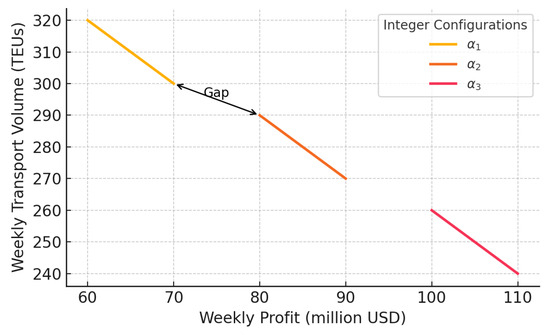
Figure 3.
Decision flow of the MIP model for HSR-DA problem.
3.3.4. Diminishing Returns Within Local Pareto Segments
While the global Pareto frontier of the bi-objective model is composed of disconnected, non-convex segments arising from distinct integer configurations (as shown in Theorems 4 and 5), each individual segment associated with a fixed configuration exhibits a more regular structure. In particular, when integer decisions are held constant, the remaining problem reduces to a linear program over continuous variables, whose Pareto-efficient outcomes form a convex and piecewise-linear frontier. Within such a local segment, the trade-off between the two objectives intensifies progressively: improving one objective further requires increasingly larger sacrifices in the other. This structural property is formally characterized below.
Theorem 6.
The local Pareto frontier under a fixed-integer configuration becomes progressively steeper, indicating an increasing marginal rate of substitution between the two objectives.
The proof of Theorem 6 is presented in Appendix A.4.
4. Solving Method
4.1. Bi-Objective Optimization
Consider a bi-objective maximization problem formulated as follows:
where the solution belongs to a non-empty, compact set . The two objective functions, and , are upper semi-continuous functions to be maximized over this set. These objectives can be represented by a single objective vector . Any such vector generated by a solution is termed a feasible objective vector. The universe of all such achievable outcomes is the set . Within this framework, the goal is to identify Pareto-optimal solutions. A feasible solution is designated as Pareto optimal if it generates a non-dominated objective vector. A vector is defined as non-dominated if no other feasible vector in offers a superior outcome. Specifically, there exists no other vector that is at least as good in all objectives (i.e., for ) and strictly better in at least one objective (i.e., for some ). This definition aligns with the principle that a Pareto-optimal solution cannot be improved with respect to one objective without a simultaneous degradation in at least one of the others [52]. The locus of all such Pareto-optimal solutions, formally described by the set , is designated as the Pareto frontier.
In previous research, the weighted sum method has been one of the most extensively applied approaches for addressing the multi-objective optimization problem of marine shipping route planning and ship allocation (e.g., [53,54,55]). This method aggregates multiple objectives, such as navigation risk, fuel consumption, travel time, and operational costs, into a single objective function by assigning specific weights to each objective. These weights reflect the relative importance of each objective and are typically determined through expert judgment, as exemplified by standardized allocations of 0.4 for risk, 0.3 for fuel consumption, and 0.3 for travel time in one study [53]. Alternatively, weights may be derived using systematic techniques such as the Analytic Hierarchy Process (AHP) combined with entropy-based methods to ensure robustness in complex scenarios like Arctic rescue operations [54]. In some cases, weights are dynamically adjusted during algorithm execution, accompanied by sensitivity analysis to assess their impact on the solution, as seen in hub-and-spoke network optimization for short sea shipping [55].
The weighted sum method is advantageous due to its simplicity, as it allows for an easy assessment of the trade-offs between different objectives based on assigned weights. It also facilitates the interaction between decision makers’ subjective preferences and the system’s objective information through the adjustment of the weight combinations for various objective functions. Nevertheless, this approach has certain limitations when applied to multi-objective optimization problems. As an a priori technique, it necessitates predetermined weights for each objective function, meaning that the optimal result obtained is heavily dependent on these assigned weights. Therefore, when the relative importance of each objective is uncertain or cannot be established beforehand, which is common in hazardous waste management system planning due to the complexity of balancing environmental risks, economic costs, and social impacts, the weighted sum method becomes less effective. In the context of a posteriori decision making, Das and Dennis [56] noted that it cannot produce a well-distributed set of Pareto solutions or a comprehensive array of points along the Pareto frontier. An example shown in Figure 4 of this study demonstrates that the weighted sum method is unable to identify the Pareto frontier within a non-convex feasible region, with their work providing further details about the method’s limitations.
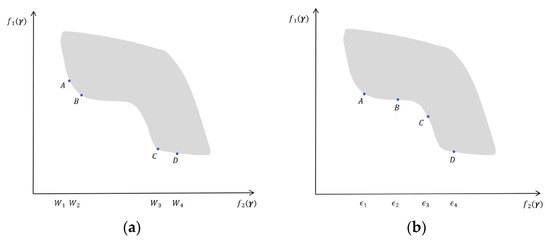
Figure 4.
Graphical comparison of the Pareto frontier for an example: (a) weighted sum method with evenly distributed weight combinations. (b) -constraint method with evenly distributed .
4.2. The Augmented -Constraint Method
Given the limitations of the weighted sum method, especially in scenarios where objective importance is unclear or in a posteriori decision making, it becomes necessary to explore alternative approaches. As an a posteriori method, the -constraint method has been extensively employed in the literature for approximating the Pareto frontier in multi-objective problems [52]. In this approach, one objective is selected as the primary goal, with the remaining objectives reformulated as constraints. However, identifying extreme value points typically requires sorting, expansion, and compression steps, which are time-consuming and make it difficult to estimate the maximum attainable value of the objective to be maximized. To address the bi-objective MIP model, we utilize the augmented -constraint approach, which enhances the standard method by adding a penalty term to the objective function. This innovation brings multiple key advancements over classical -constraint techniques. In contrast to the basic -constraint method, which often generates weakly efficient solutions that allow one objective function to be improved while keeping the other objective functions unaffected, the augmented -constraint method effectively eliminates such weak solutions by integrating both objectives into a single penalized objective function. Specifically, non-Pareto-optimal solutions require manual removal through pairwise comparisons. The augmented approach integrates both objectives into a single optimized function, inherently filtering out non-Pareto-optimal candidates during computation and eliminating the need for post-processing steps. Additionally, the penalty term’s design allows dynamic adjustment of the tolerance level , enabling more flexible and precise control over solution density. For instance, when objective functions take integer values, setting ensures the augmented method captures the full set of non-dominated objective vectors, making it particularly suitable for complex scenarios like transportation route optimization where fine-grained management of trade-offs between objectives (such as time and risk) is critical [57]. This improvement not only helps to better manage infeasible solutions but also accelerates convergence toward the Pareto frontier. Moreover, compared with traditional -constraint variants (such as the revised or improved revised methods) that require solving two separate single-objective models for each iteration, the augmented method achieves equivalent results with only one model, significantly reducing redundant calculations and boosting computational efficiency. Overall, this approach effectively balances solution quality and computational efficiency while maintaining the theoretical rigor of Pareto optimality. The augmented -constraint method is elaborated as follows.
Based on the bi-objective optimization model (2), let and . Let subject to , . Let be a small positive number such that is an integer multiple of . Define a multiset , where represents a multiset composed of obtained solutions by the augmented -constraint method. Define as the parameter that determines the maximum number of iterations in the subsequent iterative process. It essentially quantifies how many discrete steps can be taken based on the chosen . . Set where is an iteration counter initializing to the value of . In each iteration of the algorithm, the value of will be updated based on the results of the optimization in that iteration. We solve the following single-objective optimization model:
subject to
Then, we let be an optimal solution obtained by (2) and in each iteration. Let be the largest integer satisfying . If , return and stop. Conversely, if , we update the value of by . Then, the procedure of solving (2) is repeated. This iterative process continues until , gradually refining and expanding the set of optimal solutions stored in . Through this iterative mechanism, the algorithm systematically explores the solution space of the bi-objective optimization problem, aiming to converge at the Pareto-optimal set. Compared to classical scalarization techniques, this method provides a balance between exploration and efficiency by embedding trade-off control directly into the objective function and requiring only one model to be solved per iteration, making it especially suitable for large-scale or computation-intensive bi-objective optimization problems.
The pseudocode for the augmented -constraint method is shown in Algorithm 1.
| Algorithm 1 Augmented -constraint method |
| 1: Calculate 2: Calculate 3: Calculate subject to , 4: a small positive number such that is an integer multiple of 5: 6: 7: 8: 9: while do 10: Solve the model , and obtain an optimal solution . 11: 12: Calculate the largest integer satisfying . 13: 14: end while 15: Return . |
5. Experiments
To validate the performance of our proposed model, this section presents a series of computational experiments. All numerical tests were conducted on a desktop equipped with a 13th Generation Intel Core i7 CPU and 32 GB of RAM. All codes are computed in Python (version 3.11.5) and the mathematical models are solved by Gurobi (version 10.0.1). The experiment section contains mainly two parts: a case study based on the real shipping network, where we established a baseline of results by assigning initial values to the model’s parameters, and detailed sensitivity analyses on critical parameters, through which we systematically investigate how variations in these parameters influence the outcomes.
5.1. Experiment Settings
The parameters are divided into three categories as follows:
- Ship-Type-Related Parameters. Three ship capacities (12,000-TEU, 15,000-TEU, and 20,000-TEU) and two types of countries of construction (China and other countries) are considered, resulting in six distinct ship types. The weekly charter-in prices for the 12,000-TEU, 15,000-TEU, and 20,000-TEU ships are set at 0.6 million USD, 0.7 million USD, and 1 million USD, respectively. The corresponding charter-out prices are fixed at 80% of the charter-in prices, i.e., . Based on operational data detailing the CMA CGM‘s owned fleet deployed in Asia, Europe, and North America [58,59,60,61], and in line with reports indicating that and 64% of its newbuilding capacity was on order at Chinese yards [62], we consider 15 China-built 12,000-TEU ships, 25 China-built 15,000-TEU ships, 41 China-built 20,000-TEU ships, 10 non-China-built 12,000-TEU ships, 13 non-China-built 15,000-TEU ships, and 23 non-China-built 20,000-TEU ships. The specific technical parameters corresponding to these six categories are presented in Table 2.
 Table 2. The parameters for the six types of ships.
Table 2. The parameters for the six types of ships. - Rout-Related Parameters. In this study, we select 20 candidate routes, including their ports of call and the corresponding number of ships required to ensure a weekly departure frequency on each operated route [62,63,64,65,66,67,68]. The routes and their weekly departure frequencies are detailed in Table 3.
 Table 3. The parameters for the 20 routes.
Table 3. The parameters for the 20 routes. - Transport-Related Parameters. We select a set of OD pairs and estimate the pairs’ weekly transport demand for each OD pair. To ensure these estimations are grounded in realistic market conditions, they are carefully calibrated. This calibration is based on aggregated containerized cargo flow data from [69] and insights into global shipping trends from [70], ensuring that the demand volumes and their distribution are representative of actual trade patterns. The weekly transport demand of these OD pairs are detailed in Table 4. The involved ports are classified into three geographic regions: East Asia and Southeast Asia, Europe and the Mediterranean, and North America. Based on [71,72,73] we further estimate the freight rate per transported TEU for each OD pair, which is detailed in Table 5.
 Table 4. The weekly transport demands of the OD pairs.
Table 4. The weekly transport demands of the OD pairs. Table 5. Profit parameters of OD pairs.
Table 5. Profit parameters of OD pairs.
All ships use very low-sulfur fuel oil (VLSFO). Referring to [74], the daily consumption (ton/day) of ships of type sailing on route at speed is expressed as follows:
where and are parameters related to ship types and sea conditions on the route. The fuel cost parameters for ships with different capacities are presented in Table 6, with and derived from the median of the value ranges provided in [74].

Table 6.
The fuel cost parameters for ships of different capacities.
The sailing speed is uniformly set to knots. The round-trip time required for one ship to complete the full loop at speed is denoted by (weeks), which is numerically equal to . Thus, the fuel cost of one ship of type completing one full trip on route is calculated by , where is the unit fuel price, set as 574 USD/ton based on global bunker prices [75].
The berthing cost for one ship of type per port visit is denoted by , specifically 0.3 million USD, 0.4 million USD, and 0.5 million USD for the 12,000-TEU, 15,000-TEU, and 20,000-TEU ships, respectively. Given the number of ports visited on route (denoted by ), the berthing cost for a ship of type for a full round trip on route is calculated as .
The extra penalties specifically incurred by China-built ships when deployed on routes calling at U.S. ports are based on [50]. Specifically, only China-built ships with capacities above 4000 TEUs incur an extra fee of 120 USD/TEU per rotation or per string of U.S. port calls. China-built ships below 4000 TEUs and ships built in other countries are exempt from this fee when calling at U.S. ports. As all China-built ship types considered in this study have capacities exceeding 4000 TEUs; they are all subject to this extra fee when sailing on routes which include U.S. port calls.
After establishing the parameter settings, we use these values to derive the basic results, and then we conduct a sensitivity analysis on a key parameter.
5.2. Basic Results
This section presents the detailed basic results derived from the proposed bi-objective MIP model using the augmented -constraint method, with . Section 5.2.1 provides a comprehensive bi-objective optimization analysis, during which three representative Pareto-optimal solutions were identified along the Pareto frontier. Section 5.2.2 analyzes these three Pareto-optimal solutions in terms of route operation strategy, ship charter strategy, and route assignment, as well as transport demand assignment.
5.2.1. Bi-Objective Optimization Results Analysis
Figure 5 shows the optimal results of the bi-objective MIP model. Figure 5a shows the Pareto frontier, with the x-axis representing the total weekly profit (Obj 1) and the y-axis representing the total weekly transport volume (Obj 2). In Figure 5b–d, the x-axis represents , tracking increasing values of Obj 1. The y-axis of Figure 5b–d corresponds to the values of indicators, including the number of operated routes (ORN) and the average freight rate (AFR) of accepted transport demand, the total fuel cost (TFC) and the total berthing cost (TBC) of all ships, and the revenue from chartering out idle ships minus the cost of chartering in ships (COIR).
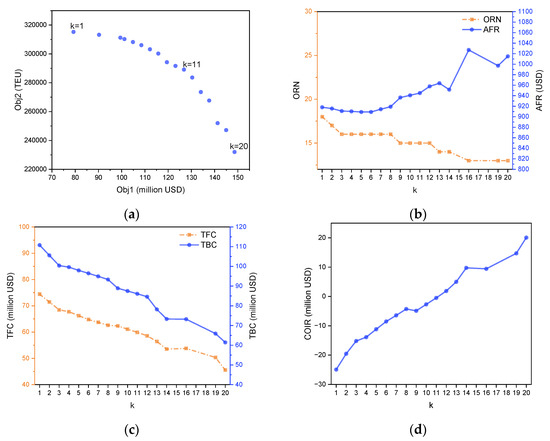
Figure 5.
Pareto-optimal solutions of the bi-objective MIP model. (a) Obj 1 and Obj 2 of instance. (b) ORN and AFR of instance. (c) TFC and TBC of instance. (d) COIR of instance.
The Pareto frontier depicted in Figure 5a demonstrates the inherent trade-off between Obj 1 and Obj 2. The Pareto frontier provides a powerful decision-making reference for shipping managers by revealing two distinct layers of choice. The first layer concerns major strategic decisions. For a shipping company, these correspond to discrete, high-impact actions, for example, activating an entire service route or reallocating a specific ship type. This structure indicates that when the company wants to pursue one objective significantly, such as substantially increasing profit, it must make these major adjustments to its route operations and fleet deployment. This is fundamentally different from making small-scale adjustments to accepted cargo while the network structure remains fixed. In situations where only minor fine-tuning between profit and transport volume is desired, keeping the activated routes and deployed ships constant while adjusting cargo acceptance is the more effective strategy. This clear distinction between major structural changes and minor operational adjustments provides a practical validation of Theorem 5, which establishes that the frontier’s overall structure is fundamentally determined by the integer decision variables governing the network design. At the operational level, within each of these fixed strategic configurations, the convex shape of the frontier illustrates the law of diminishing returns. For a shipping manager, this signifies that pushing for an extreme on one objective comes at a disproportionately high cost to the other. This phenomenon of a progressively steepening trade-off is formally established in Theorem 6. Therefore, the frontier serves as a practical guide for finding the optimal trade-off based on current corporate priorities. For instance, if the primary goal is to expand market share, a decision maker would select a solution from the frontier that prioritizes higher transport demand acceptance. Conversely, if the immediate need is to improve profitability and strengthen cash flow, a solution yielding higher profit would be chosen, even at the expense of some volume. The frontier quantifies these choices, enabling managers to make informed decisions that align their network strategy with their most pressing business objectives.
Figure 5b shows that ORN decreases as Obj 1 increases. This reduction in ORN enables the company to concentrate resources on the most profitable transport services rather than dispersing them across marginally profitable ones. The strategic elimination of less profitable routes directly contributes to cost reduction and operational efficiency. This cost reduction is clearly demonstrated in Figure 5c, where both TFC and TBC decrease as Obj 1 increases. Simultaneously, AFR rises from approximately 900 USD/TEU to 1000 USD/TEU as Obj 1 increases, demonstrating that the company prioritizes transport demand with high (such as from Asia to North America) while rejecting lower-value shipments (such as from Europe to Asia). This selective approach to transport demand acceptance significantly reduces transport cost and increases the total profit.
Figure 5d illustrates the COIR increases as Obj 1 increases, indicating that the fleet size required diminishes as ORN decreases. As accepted transport demand decreases, more ships become available for chartering out. The combination of reduced charter-in costs and increased charter-out revenue creates a substantial positive impact on profitability. Table 7 shows the optimal results of the model.

Table 7.
Pareto-optimal solutions of the bi-objective MIP model.
Notably, the extra penalty cost specifically incurred by China-built ships when deployed on routes calling at U.S. ports is equal to 0 in every Pareto-optimal solution, indicating that the model effectively avoids the extra penalty cost. The extra fee, amounting to 120 USD/TEU per rotation or per string of U.S. port calls for China-built ships with capacities above 4000 TEUs [50], is evidently substantial. Consequently, the model strategically assigns these China-built ships to routes excludes U.S. ports.
5.2.2. Representative Solutions Analysis
Based on the analysis of the Pareto frontier, three representative Pareto-optimal solutions are strategically selected for analysis in terms of route operation strategy, ship charter strategy, and route assignment, as well as transport demand assignment. These solutions, corresponding to = 1, = 11, and = 20, were chosen to capture distinct positions along the trade-off curve between maximizing Obj 1 and Obj 2. Specifically, the solution at = 1 represents a strategy characterized by the highest accepted transport demand among the non-dominated set. Conversely, the solution at = 20 corresponds to the highest total weekly profit. The solution at = 11 serves as an intermediate point, reflecting a balanced compromise between the competing objectives. The route operation strategy of the three selected optimal solutions is detailed in Table 8.

Table 8.
Route operation strategy of the selected Pareto-optimal solutions.
Table 8 shows that the 13 routes selected for operation when are also part of the operational set for and , indicating these routes are economically attractive, as the OD pairs on these routes offer higher freight rates or the ships deployed on these routes incur relatively lower transport costs.
Table 9 details the ship charter and route assignment strategy for the three selected Pareto-optimal solutions. When , the strategy prioritizes maximizing Obj 2. This is reflected in significant charter-in activity, particularly charting in 28 20,000-TEU ships, suggesting an effort to expand the average transport capacity of available fleet. Conversely, when , the strategy prioritizes maximizing Obj 1. For this instance, 17 units of owned China-built 20,000-TEU ships (Type 3), 8 units of owned China-built 12,000-TEU ships (Type 1), and 7 units of owned China-built 15,000-TEU ships (Type 2) are chartered out. This indicates a smaller operational scale consistent with a profit-maximization approach.

Table 9.
Ship charter and route assignment strategy.
A noteworthy pattern observed across all three Pareto-optimal solutions (, 11, and 20) is the simultaneous chartering out of owned China-built 12,000-TEU ships (Type 1) and the chartering in of non-China-built ships of the same 12,000-TEU capacity (Type 4). For example, even at , while pursuing maximum volume, 4 owned Type 1 ships are chartered out, and 13 Type 4 ships are chartered in. This consistent swap suggests a deliberate operational tactic to manage the fleet composition, likely to avoid the extra penalty cost associated with deploying specific ship types (China-built) on certain routes, by substituting them with exempt alternatives.
Table 10 presents the total volume of accepted transport demand and the average freight rate of the transported cargo.

Table 10.
Total volume of accepted transport demand and the average freight rate of the transported cargo.
5.3. Sensitivity Analysis
By conducting sensitivity analysis experiments, we further analyze the sensitivity of our model to the changes in input parameters, including the freight rate, the surcharge intensity, the charter-in cost and charter-out revenue of ships, and the transport demand.
5.3.1. Sensitivity Analysis on the Freight Rate Ratio
In this section, we further analyze the sensitivity of our bi-objective MIP model to the changes in the freight rate per transported TEU. Generally, we conduct 6 experiments, aiming to illustrate the performance of the bi-objective MIP model in solving instances with different freight rate ratio. The ratio is denoted as , where the original freight rate is , the actual freight rate is , and . To investigate the impact of varying the freight rate ratio of all OD pairs on the model’s effectiveness, we design instances by altering the freight rate ratio from 0.7 to 1.2 with a step size of 0.1 while keeping other parameters unchanged. Figure 6 shows the Pareto frontiers of all instances.
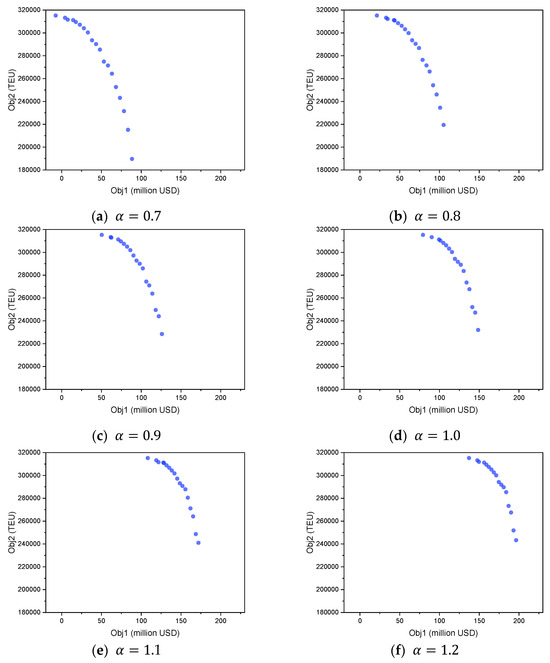
Figure 6.
The Pareto frontiers with different freight rate ratios.
The results of our bi-objective optimization model are presented as a series of Pareto frontiers. The concept of Pareto frontiers is derived from the work of economist Vilfredo Pareto and is a powerful tool for visualizing the trade-offs between two or more conflicting objectives [76]. A solution is considered to be Pareto optimal if it is not possible to improve one objective without making at least one other objective worse. The Pareto frontier is a graph that plots all these optimal, non-dominated solutions. In the context of our study, as shown in Figure 6a, the Pareto frontier illustrates the inherent trade-off between maximizing profit and maximizing transport volume. Here is how to interpret the graph:
- Each point is an optimal strategy: every blue point on the curve represents a complete, viable, and optimal operational plan (i.e., a specific set of decisions about which routes to open, which ships to deploy, and which transport demands to accept).
- The curve shows the trade-off: The downward slope of the frontier demonstrates the conflict. To make more profit (moving to the right along the curve), the shipping company must accept less transport volume (moving down). Conversely, to increase market share by accepting more volume (moving up), the company must sacrifice some profit (moving to the left).
- The “frontier” is the limit of achievable performance: Any point below and to the left of the curve represents a suboptimal, inefficient strategy. Any point above and to the right of the curve is an unattainable goal given the current model constraints and resources. The frontier itself represents the best possible outcomes.
As the freight rate ratio increases from 0.7 to 1.2, reflecting higher revenue per transported TEU, the Pareto frontier consistently moves upwards and towards the right, indicating improved profitability for the same or greater transport volumes. At lower freight rates (), the Pareto frontier indicates limited profitability, constraining operators to accept relatively lower transport volumes as many OD pairs become economically unviable. As the freight rate ratio rises, higher profitability allows operators greater flexibility, enabling them to accept more transport demand selectively, thereby significantly increasing total profit and volume simultaneously.
The progressive outward shift of the Pareto frontier as the freight rate ratio α increases illustrates a critical change in the operational landscape: diminishing marginal trade-offs between profit and transport volume. At lower freight rates, increasing Obj 1 often necessitated significant reductions in Obj 2, as lower freight rates for specific OD pairs frequently failed to cover transport costs along particular routes. Consequently, enhancing Obj 1 requires selectively shedding these less profitable services, leading to a pronounced trade-off. However, as α rises, the revenue per TEU increases, transforming previously unprofitable transport demands into financially viable options. This improved baseline profitability means that operators can now pursue higher profit levels with smaller sacrifices in total transported volume or expand transport volume with less detriment to their profit. The frontier, therefore, not only moves to a more favorable position but its slope, representing the rate of substitution between the two objectives, becomes less steep, indicating that higher freight rates grant operators greater flexibility to enhance profitability with smaller volume compromises.
To compare computational efficiency, Table 11 presents the required solution time across different for two key comparisons: the MIP model against the PRMIP model, and the augmented -constraint method against the basic -constraint method.

Table 11.
Comparison of computational efficiency for MIP and PRMIP models using two different -constraint methods.
Table 11 details the computational performance of the proposed models. Using the augmented -constraint method, the average CPU time for the full MIP model is 9.2 s, whereas the PRMIP model, with its relaxed ship chartering variables, significantly reduces this computation time to an average of just 3.7 s. This efficiency is benchmarked against the standard basic -constraint method, which required substantially more time on average: 155.4 s for the MIP and 58.6 s for the PRMIP on average. Consequently, the average solution time of the augmented method is merely 5.9% of the basic method’s time for the MIP model, and 6.3% for the PRMIP model. This highlights a critical gain in computational performance by selecting the more advanced solution technique. In summary, these results confirm that the PRMIP model is significantly more computationally efficient than the MIP model without surrendering solution quality, which aligns with Theorem 3. Furthermore, the dramatic performance gain from using the augmented -constraint method validates its suitability for solving large-scale, practical problems efficiently.
Computational experiments conducted with real-world-inspired scenarios highlight the practical effectiveness of the proposed PRMIP model compared to the MIP model, as well as our augmented -constraint method compared to the basic -constraint method.
5.3.2. Sensitivity Analysis on the Surcharge Intensity
In this section, we conduct 6 experiments, aiming to illustrate the performance of our proposed model in solving instances with different surcharge intensities. We design instances by altering the unit penalty surcharge from 0 to 100 with a step size of 20 while keeping other parameters unchanged. Figure 7 shows the Pareto frontiers of all instances.
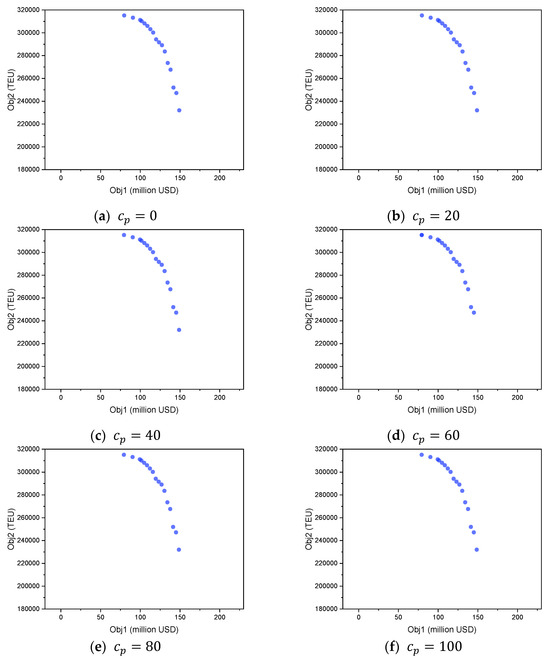
Figure 7.
The Pareto frontiers with different freight surcharge intensities.
As the unit penalty surcharge increases from 0 to 100, the Pareto frontier remains largely consistent, indicating that the shipping line can maintain a similar level of performance in terms of both profit and transport volume. This stability indicates that the model is effective at finding potent mitigation strategies. The model achieves this by effectively navigating the complex trade-off between maximizing profit, increasing transport volume, and mitigating the extra penalty. It strategically reconfigures the fleet, for instance by systematically chartering out penalized China-built ships from U.S. routes and chartering in compliant ships to take their place, thereby preserving the core trade-off between Obj 1 and Obj 2.
To quantitatively dissect this mitigation strategy and reveal the underlying economic trade-offs, we analyze the total penalty paid across all Pareto-optimal solutions for each surcharge level. The results are summarized in Table 12.

Table 12.
Analysis of total penalty cost incurred under different surcharge intensities.
It is observed that as rises from 20 to 60, the total penalty incurred generally increases. This indicates that at these lower levels, it is often optimal to accept the surcharge for certain highly profitable routes where the additional cost of chartering ships to avoid using a penalized ship would exceed the penalty itself. A significant strategic shift becomes evident at . At this level, some of the Pareto-optimal solutions show a total penalty of zero, indicating that for a wide range of strategies, complete avoidance has become the more profitable choice. This trend culminates at , a level at which the unit penalty cost becomes so high that the total penalty across all Pareto-optimal solutions drops to zero. This illustrates the model’s sophisticated decision making, which involves calculating the most profitable strategy: paying a manageable fee on certain routes or altering fleet and route assignments to completely avoid the penalty once the cost becomes prohibitive.
5.3.3. Sensitivity Analysis on the Charter Ratio
In this section, we conduct 6 experiments, aiming to illustrate the performance of the bi-objective MIP model in solving instances with different charter ratios. The ratio is denoted as , where the original weekly charter-in cost and charter-out revenue for a ship of type is and , respectively. The actual charter-in cost and chareter-out revenue is and , respectively. Then, . To investigate the impact of varying the charter ratio of all ship types on the model’s effectiveness, we design instances by altering from 0.6 to 1.6 with a step size of 0.2 while keeping other parameters unchanged. Figure 8 shows the Pareto frontiers of all instances.
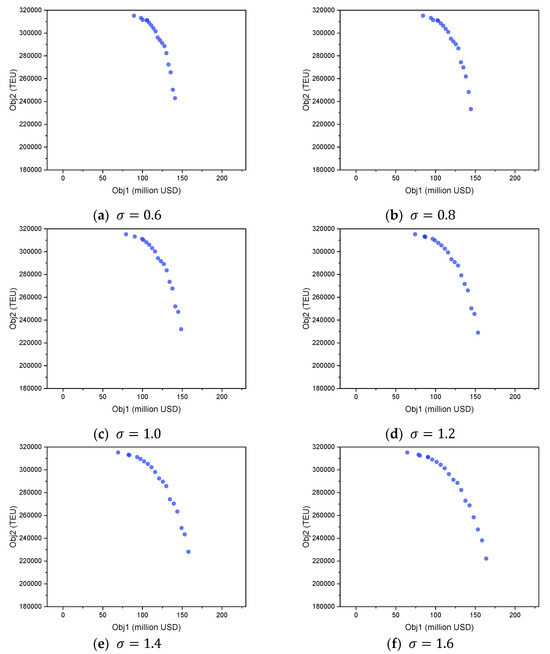
Figure 8.
The Pareto frontiers with different charter ratios.
The sensitivity analysis on the charter ratio reveals a distinct transformation in the shape of the Pareto frontier. As the charter ratio increases, the frontier becomes progressively flatter. When the charter ratio is low (e.g., ), the frontier is steep, meaning that achieving a higher profit requires giving up a large amount of transport volume. In contrast, when the charter ratio is high (e.g., ), the frontier is much flatter, allowing the company to improve its profit with a smaller reduction in volume. This change is driven by the direct link between charter-in costs and charter-out revenues. In a low charter ratio environment, chartering out yields less revenue. Therefore, the company’s strategy focuses on deploying its fleet to serve a broad range of transport demands, resulting in higher transport volume. To improve profit from this state, the company must forgo large quantities of accepted demand, which explains the steep trade-off. In contrast, in a high charter ratio environment, chartering out a ship becomes a very attractive alternative. As a result, the company’s optimal strategy shifts: it serves only the demand that generates more profit than simply chartering out a ship. This reveals that a high charter ratio fundamentally changes the business priority from focusing on transport volume to strategically managing the fleet as a portfolio of assets, where chartering ships out can be a more profitable decision than using them to serve all but the most sufficiently valuable transport demands.
5.3.4. Sensitivity Analysis on the Transport Demand Ratio
In this section, we conduct 6 experiments, aiming to illustrate the performance of the bi-objective MIP model in solving instances with different transport demand ratios. The ratio is denoted as , where the original weekly transport demand for an OD pair is , the actual transport demand is , and . To investigate the impact of varying the transport demand of all OD pairs on the model’s effectiveness, we design instances by altering from 0.6 to 1.6 with a step size of 0.2 while keeping other parameters unchanged. Figure 9 shows the Pareto frontiers of all instances.
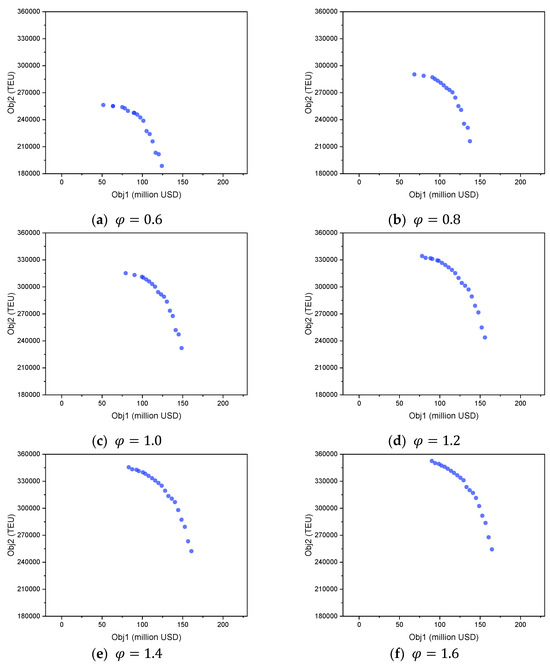
Figure 9.
The Pareto frontiers with different transport demand ratios.
The sensitivity analysis with respect to the transport demand ratio demonstrates the profound impact of market size on the shipping line’s operational scale and profitability. As the transport demand ratio increases from 0.6 to 1.6, representing a market shift from low to high demand, the Pareto frontier exhibits a significant and consistent outward expansion. The entire set of non-dominated solutions moves upwards and to the right, indicating that a high-demand market environment enables the simultaneous achievement of both higher total profits and greater transport volumes. At low demand levels (e.g., ), the frontier is tightly constrained, positioned close to the origin, reflecting a market where limited cargo availability severely caps the potential for both revenue and service scale. Conversely, as demand grows, the frontier expands dramatically, unlocking a much larger space of high-performance strategic options.
This outward expansion is driven by a fundamental shift in the company’s core challenge, which necessitates a corresponding shift in management strategy. In a low-demand scenario, the primary challenge of the shipping company is to find enough cargo to fill its ships, often forcing it to accept less profitable OD pairs to maintain fleet utilization. In a high-demand scenario, the market offers more cargo than the fleet can physically transport. This surplus of demand grants the shipping company a powerful strategic advantage by enabling it to prioritize more profitable OD pairs.
Given that the PRMIP model yields optimal solutions identical to those of the full MIP model (as established in Section 3.3), the detailed numerical results for the two most extreme scenarios of each of the four sensitivity analyses are presented for the PRMIP model in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 in Appendix B.
6. Conclusions
Container liner shipping companies operate within a complex environment where they must balance profitability and service reliability, all while navigating evolving regulatory policies such as surcharges imposed on China-built ships calling at U.S. ports. These challenges complicate strategic planning related to route deployment, ship assignment, and demand acceptance, requiring integrated decision-making frameworks.
To address these challenges, this study develops a bi-objective MIP model for the HSR-DA problem. We establish a series of theorems to analyze the mathematical structure of the model. Specifically, we prove that the route operation decision variables and ship assignment variables must remain integers due to the practical infeasibility of fractional route operation and ship assignment, while the chartering constraints form a TU matrix, which allows the corresponding variables to be relaxed to continuous values without loss of integrality. Additionally, we demonstrate that the Pareto frontier consists of a finite union of line segments. Within each segment, it is continuous and piecewise linear, while generally being non-convex and exhibiting discontinuities. Based on these theorems, we reformulate the original MIP into a PRMIP model. We demonstrate that the PRMIP model can generate the same optimal objective value as the one obtained by the MIP model when solving the same instance, while significantly improving computational efficiency. Furthermore, we can always find an optimal solution to the PRMIP model such that it is equivalent to an optimal solution to the MIP model. These theoretical insights provide a solid foundation for enhancing solution efficiency and understanding the structural characteristics of the Pareto frontier.
Computational experiments conducted with real-world-inspired scenarios highlight the practical effectiveness of the proposed model. The results demonstrate a clear trade-off between maximizing profitability and maximizing transport volumes, represented through an explicitly characterized Pareto frontier. Notably, the model consistently avoids costly surcharges for China-built ships through strategic fleet assignment and chartering decisions, underscoring its ability to inform operational strategies under complex regulatory constraints. In scenarios prioritizing profit maximization, the accepted transport volume decreases while the average freight rate increases, confirming the necessity of targeted and strategic route selection and demand acceptance. Sensitivity analysis further reveals that variations in freight rates significantly affect the structure of optimal decisions. Higher freight rates provide greater flexibility, allowing operators to selectively expand transport volumes while enhancing profitability simultaneously. Conversely, lower freight rates necessitate stringent selectivity in demand acceptance, reinforcing the importance of adaptive decision making in response to market fluctuations.
Future work can extend our model by addressing several key areas to enhance its robustness and practical applicability:
- Incorporating transshipment and empty container repositioning: The current model excludes transshipment and empty container repositioning, which are critical for operational efficiency. Future work can optimize cargo routing and empty container flows, potentially using foldable containers or leasing strategies to reduce costs and improve container utilization [77,78,79].
- Incorporating variable sailing speeds: Allowing speed to be a decision variable can build a more comprehensive framework. This extension can capture the critical trade-off between fuel costs and service efficiency by directly linking sailing speed to operational fuel expenses and strategic ship allocation. Higher speeds increase fuel consumption, while lower speeds extend voyage times, which may require additional ships to maintain fixed service frequencies. Recent studies provide valuable insights in this field. For example, a holistic optimization model was developed [10] that integrates sailing speed optimization with port service frequency, fleet deployment, and ship schedule design, demonstrating the benefits of joint tactical planning. Similarly, a multi-objective mixed-integer linear programming model was proposed [27] to optimize sailing speed, as well as fleet deployment and routing under carbon tax regulations, achieving cost savings of up to 15% and emission reductions of 20% on a transatlantic route. A hybrid dynamic model with receding horizon speed optimization was introduced [80], emphasizing schedule reliability and energy efficiency when port handling times are uncertain. In addition, the focus was on sailing speed optimization for near-sea shipping services, integrating container routes to improve operational efficiency [81]. With these advancements, future work can co-optimize shipping networks, fleet deployment, and sailing speeds, providing in-depth insights into how shipping companies can balance strategic and operational strategies while adapting to external policies to maintain economic and environmental sustainability.
- The challenge of expanding models to accommodate multinational regulatory compliance and carbon pricing mechanisms: The current fleet deployment model can be extended to incorporate either multinational regulatory compliance or carbon pricing mechanisms to enhance its applicability in a globalized market. Dynamic fleet reallocation can further support these extensions by enabling real-time adjustments to ship assignments in response to varying regulatory requirements or carbon pricing impacts [82]. Multi-objective optimization models have been proposed to incorporate the EU Emissions Trading System (EU ETS) into China–Europe liner shipping, optimizing speed to balance emissions and costs [83]. Frameworks for carbon and cost accounting under EU ETS focus on operational adjustments like fuel choice and speed optimization to ensure compliance [84]. Bi-level programming models incorporate carbon taxes into network design, addressing route planning and fleet deployment under environmental constraints [85]. Compliance with diverse international standards, such as those for sustainable maritime operations, has also been explored to ensure operational feasibility across jurisdictions [86]. Future work could extend the current fleet deployment model to incorporate either compliance with multinational regulations, such as EU ETS and other global standards, or carbon pricing mechanisms into strategies like speed optimization, fuel choice, and route planning. These models could explore collaborative agreements or standardized practices to address regulatory variations across jurisdictions, ensuring cost-effective compliance and sustainability in a globalized market.
Author Contributions
Conceptualization, S.W.; methodology, Y.T., Y.Y. and S.W.; software, Y.T.; validation, Y.T.; formal analysis, Y.T.; investigation, Y.T., Y.Y. and S.W.; resources, S.W.; data curation, Y.T. and Y.Y.; writing—original draft preparation, Y.T., Y.Y. and S.W.; writing—review and editing, Y.T., Y.Y. and S.W.; visualization, Y.T.; supervision, S.W.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. Proofs of Theorems 1 and 2
Proof of Theorem 1.
We demonstrate this via a synthetic counterexample. Assume that there is only one candidate route , which excludes U.S. ports and needs three ships for operation, i.e., . There is only one OD pair , and its weekly transport demand is 2000 TEUs, i.e., TEUs. The revenue earned per TEU for this OD pair is set as USD. Consider that the company owns three ships of the same type, (), i.e., . The transport capacity of each ship is 6000 TEUs, i.e., TEUs. The transportation cost incurred by each ship deployed on route consists of the following components: the fuel cost million USD, the berthing cost million USD, and the extra penalty cost of , since the route does not include any U.S. ports. The weekly cost for chartering in a ship of type is set as million USD, and the weekly revenue from chartering out one idle ship is set as million USD. Then, for the original model, there will be two possible route operation and ship assignment solutions: (1) Operating no route, i.e., . This solution is feasible, and the company can charter out all three ships to earn revenue. The weekly profit in this case is million USD, which is the first objective of the model. The total weekly transport volume for the second objective in this case is . (2) Operating route , i.e., . In this case, the company deploys all three owned ships on the route, i.e., , and no ship is chartered in or out, i.e., . Since the demand is 2000 TEUs and each ship has a capacity of 6000 TEUs, the demand is fully satisfied. Then, the weekly profit in this case can be calculated as follows:
The total weekly transport volume in this case is 2000 TEUs. It is notable that strategy (1) yields a higher weekly profit (1.2 million USD), but the transport volume is zero. In contrast, strategy (2) results in a lower weekly profit (0.4 million USD), yet it fully satisfies the demand, achieving a transport volume of 2000 TEUs. These two solutions represent trade-offs between the two conflicting objectives of the model. Therefore, both solutions constitute a set of Pareto-optimal solutions under the original MIP model.
However, if we relax the binary variable to be continuous, will also satisfy the weekly operation requirement, as the number of required ships becomes . The company can assign one owned ship to route , i.e., , and charter out the remaining two idle ships, i.e., . Since the ship capacity is 6000 TEUs and the weekly transport demand is 2000 TEUs, . Therefore, the demand of the OD pair can be fully transported, i.e., TEUs, and thus constraint (1-7) can be satisfied. The first objective function value, then, can be calculated as follows:
The second objective is 2000 TEUs. This relaxed linear programming (LP) solution improves both objectives compared to strategy (1) with the integer solution , and achieves a higher value in the first objective while keeping the second objective unchanged compared to strategy (2). Critically, is practically invalid as we cannot operate only one-third of the route. Hence, the LP relaxation of inherently produces non-integer solutions conflicting with the real-world integer operation requirement, proving cannot be freely relaxed. □
Proof of Theorem 2.
We demonstrate this via a synthetic counterexample. Assume that there is only one candidate route , which excludes U.S. ports and needs three ships for operation, i.e., . There is only one OD pair , and its weekly transport demand is 3500 TEUs, i.e., TEUs. The revenue earned per TEU for this OD pair is set as USD. Consider there are two ship types, and . The company now owns one ship of type and two ships of type , i.e., , . Ship type has a capacity of TEUs, a charter-in cost million USD, a charter-out revenue 4 million USD, and a transport cost of million USD. Ship type has a capacity of TEUs, a charter-in cost million USD, a charter-out revenue million USD, and a transport cost of million USD. Since the route does not include any U.S. ports, the extra penalty costs are zero. Then, for the original model, there will be multiple possible route operation and ship assignment solutions. Through calculation, the two solutions that maximize the first objective and the second objective, respectively, are in the Pareto-optimal solutions as follows: (1) Operating route , i.e., . In this case, the company deploys three ships of type , i.e., , ; then, one ship of type is chartered out and one ship of type is chartered in, i.e., , . Since TEUs, the weekly accepted transport demand is TEUs. Then, the weekly profit in this case can be calculated as follows:
The total weekly transport volume in this case is 3000 TEUs. (2) Operating route , i.e., . In this case, the company deploys one ship of type and two ships of type , i.e., , , and no ship is chartered in or chartered out, i.e., . Since , the demand is fully satisfied. Then, the weekly profit in this case can be calculated as follows:
The total weekly transport volume in this case is 3500 TEUs. It is notable that strategy (1) yields a higher weekly profit (1.65 million USD), but its transport volume is lower (3000 TEUs). In contrast, strategy (2) results in a lower weekly profit (1.3 million USD), yet it fully satisfies the demand, achieving a transport volume of 3500 TEUs. These two solutions represent trade-offs between the two conflicting objectives of the model.
However, if we relax the integer variable to be continuous, as in , then will also satisfy the weekly operation requirement. Since , the demand is fully satisfied, i.e., TEUs. In this case, the company needs to charter in one ship of type , i.e., , . Then, the weekly profit in this case can be calculated as follows:
This relaxed LP solution achieves a higher value in the first objective while keeping the second objective unchanged compared to strategy (2). Critically, , is practically invalid as we cannot assign a ship by half. Hence, the LP relaxation of inherently produces non-integer solutions conflicting with the real-world integer operation requirement, proving cannot be freely relaxed. □
Appendix A.2. Proof of Theorem 3
Proof of Theorem 3. 
For ease of explanation, we denote as the coefficient matrix of variables , which includes associating with constraints (1-4), and associating with constraints (1-5). The structure of can be presented as follows:

Firstly, according to [51], a sufficient condition for a matrix to be TU is that row indices of matrix can be partitioned into two sets such that the following four conditions are all satisfied: (i) each entry of satisfies ; (ii) each column of contains at most two nonzero entries; (iii) if a column has two entries of the same sign, their row indices are in different sets; and (iv) if a column has two entries of different signs, their row indices are in the same set.
For our matrix , we consider dividing it naturally into two sets, and . For and , each column contains at most one 1. This implies that there are no more than two nonzero entries per column in the matrix , and all coefficients belong to . Therefore, conditions (i) and (ii) are satisfied immediately. Then, we can partition all rows of into one set and those of into another, meeting criteria (iii) and (iv). Thus, we conclude that matrix is TU.
The coefficient matrix of variables is only associated with constraints (1-4), and each of its columns contain at most one . Therefore, conditions (i) and (ii) are satisfied immediately. Moreover, since no column has two nonzero entries, criteria (iii) and (iv), which involve pairs of entries with the same or different signs, do not need to be considered. Therefore, the coefficient matrix corresponding to is TU. Then, we can conclude that the coefficient matrices of the variables and are TU. □
Appendix A.3. Proofs of Theorems 4 and 5
Proof of Theorem 4.
Let be the set of feasible objective values produced by the bi-objective MIP model, and denote the Pareto-optimal set. Let the integer decision tuple be , where each component is bounded, resulting in a finite set . For a fixed , the optimization problem reduces to a linear program (LP) in continuous variables , under constraints (1-6) and (1-7), with linear objectives which denote the weekly profit, and which denote the total weekly transport volume. Let denote the feasible region for , given a fixed-integer configuration . We stick to this notation in the remainder of this paper. The feasible region is defined by linear constraints and bounds. It is a closed, convex, and bounded polyhedron, since each and each is upper bounded by demand and transport capacity. Let denote the set of non-dominated points in the objective space given a fixed-integer decision tuple , i.e., such that , , with at least one strict point. This captures all points for which no other feasible can improve both the weekly profit and the transport volume simultaneously. The image of under the linear objective mapping is a convex polygon in , whose Pareto-efficient boundary consists of one or more line segments. Since is finite, the union of such segments over all gives , where each is continuous and piecewise linear. Thus, is composed of finitely many such segments. □
Proof of Theorem 5.
Consider two distinct integer configurations and . Let and be two feasible continuous decisions such that their objective vectors and lie in and , respectively. Define their convex combination in the objective space as , . Since the integer configuration cannot take fractional values, there generally does not exist any feasible pair satisfying constraints (1-3)–(1-11) such that the resulting objective vector equals . Thus, , which implies that , and therefore , are not convex.
Furthermore, since is finite and each is compact in , define the minimal gap between efficient frontiers:
By the compactness and separation of distinct integer supports, this infimum is bounded by [87]. Therefore, the Pareto frontier is not only non-convex, but also globally disconnected, with finite-length gaps between segments. □
Appendix A.4. Proof of Theorem 6
Proof of Theorem 6.
Fix an integer configuration , which defines a convex and bounded feasible region in the space of continuous variables. The Pareto-efficient frontier under bi-objective linear mapping is a convex polygonal chain composed of finite segments. For notation convenience, we denote . Let the extreme efficient points be ordered by increasing values of : , , …, . Then, the slope of each segment is defined as follows:
Let weight the two objectives and consider the scalarised LP:
Since is a bounded polyhedron, the optima occur at basic feasible solutions and vary only at finitely many breakpoints of . Standard LP duality shows that the supporting hyperplane to with normal vector touches at an efficient extreme point whose frontier slope equals . As increases, the supporting hyperplanes generate efficient points with higher values of objective 1 and lower values of objective 2. Since , it follows that
which confirms that the marginal rate of substitution between the two objectives increases in magnitude along the local Pareto frontier. □
Appendix B

Table A1.
Pareto-optimal solutions of the PRMIP model ().
Table A1.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | −7.56 | 315,250 | 18 | 643 | 74.44 | 110.79 | 0 | −24.92 |
| 2 | 4.21 | 313,250 | 17 | 641 | 71.45 | 105.59 | 0 | −19.52 |
| 3 | 7.65 | 311,583 | 17 | 640 | 70.23 | 104.29 | 0 | −17.32 |
| 4 | 14.39 | 311,250 | 16 | 638 | 68.46 | 100.39 | 0 | −15.20 |
| 5 | 17.83 | 309,583 | 16 | 637 | 67.24 | 99.09 | 0 | −13.00 |
| 6 | 22.85 | 307,217 | 16 | 636 | 65.50 | 97.17 | 0 | −9.84 |
| 7 | 27.83 | 304,098 | 16 | 638 | 63.96 | 95.35 | 0 | −6.96 |
| 8 | 32.90 | 300,439 | 16 | 643 | 62.59 | 93.37 | 0 | −4.28 |
| 9 | 38.18 | 293,564 | 15 | 655 | 61.83 | 88.37 | 0 | −4.00 |
| 10 | 43.16 | 290,231 | 15 | 660 | 60.36 | 86.67 | 0 | −1.36 |
| 11 | 48.04 | 285,392 | 15 | 664 | 58.58 | 84.81 | 0 | 1.96 |
| 12 | 53.09 | 274,903 | 14 | 654 | 55.99 | 76.10 | 0 | 5.28 |
| 13 | 58.14 | 271,500 | 14 | 659 | 54.53 | 74.29 | 0 | 7.92 |
| 14 | 63.17 | 264,342 | 14 | 665 | 52.05 | 72.10 | 0 | 11.60 |
| 15 | 68.26 | 252,633 | 14 | 671 | 48.46 | 68.39 | 0 | 15.52 |
| 16 | 73.27 | 243,175 | 13 | 697 | 48.60 | 64.45 | 0 | 16.88 |
| 17 | 78.31 | 231,496 | 13 | 707 | 44.91 | 61.02 | 0 | 20.56 |
| 19 | 83.38 | 215,175 | 12 | 743 | 42.79 | 56.96 | 0 | 23.36 |
| 20 | 88.42 | 189,667 | 11 | 741 | 35.82 | 48.71 | 0 | 32.32 |

Table A2.
Pareto-optimal solutions of the PRMIP model (2).
Table A2.
Pareto-optimal solutions of the PRMIP model (2).
| Obj 1 (Million USD) | Obj 2 (TEUs) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 137.15 | 315,250 | 18 | 1102 | 74.44 | 110.79 | 0 | −24.92 |
| 2 | 147.63 | 313,250 | 17 | 1099 | 71.45 | 105.59 | 0 | −19.52 |
| 3 | 149.64 | 311,917 | 17 | 1098 | 70.47 | 104.55 | 0 | −17.76 |
| 4 | 156.14 | 311,250 | 16 | 1093 | 68.46 | 100.39 | 0 | −15.20 |
| 5 | 159.07 | 309,398 | 16 | 1093 | 67.22 | 99.08 | 0 | −12.92 |
| 6 | 162.10 | 307,398 | 16 | 1092 | 65.75 | 97.52 | 0 | −10.28 |
| 7 | 165.35 | 305,175 | 16 | 1092 | 64.28 | 95.93 | 0 | −7.64 |
| 8 | 168.34 | 302,648 | 16 | 1098 | 63.45 | 94.65 | 0 | −6.00 |
| 9 | 171.37 | 300,050 | 16 | 1104 | 62.40 | 93.36 | 0 | −4.00 |
| 10 | 174.58 | 294,231 | 15 | 1124 | 62.32 | 88.89 | 0 | −4.88 |
| 11 | 177.79 | 291,898 | 15 | 1127 | 61.10 | 87.52 | 0 | −2.68 |
| 12 | 180.72 | 289,675 | 15 | 1133 | 60.12 | 86.39 | 0 | −0.92 |
| 13 | 183.90 | 285,350 | 15 | 1145 | 58.89 | 85.05 | 0 | 1.14 |
| 15 | 186.89 | 273,355 | 14 | 1158 | 56.42 | 78.17 | 0 | 5.00 |
| 16 | 190.00 | 267,581 | 14 | 1176 | 55.20 | 76.80 | 0 | 7.20 |
| 19 | 193.11 | 251,858 | 13 | 1233 | 53.77 | 73.20 | 0 | 9.44 |
| 20 | 196.39 | 243,300 | 13 | 1216 | 49.85 | 65.10 | 0 | 15.60 |

Table A3.
Pareto-optimal solutions of the PRMIP model ().
Table A3.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 149.06 | 232,016 | 13 | 1014 | 45.57 | 61.42 | 0.00 | 20.56 |
| 2 | 145.44 | 247,188 | 13 | 997 | 50.34 | 65.90 | 0.00 | 15.20 |
| 3 | 141.76 | 251,997 | 13 | 1027 | 53.77 | 73.20 | 0.00 | 9.92 |
| 4 | 138.12 | 267,675 | 14 | 951 | 53.52 | 73.30 | 0.00 | 10.24 |
| 5 | 134.54 | 273,564 | 14 | 963 | 56.42 | 78.17 | 0.00 | 5.48 |
| 6 | 130.84 | 283,641 | 15 | 957 | 58.6 | 84.61 | 0.00 | 2.36 |
| 7 | 127.28 | 289,119 | 15 | 945 | 59.87 | 86.10 | 0.00 | 0.00 |
| 8 | 123.61 | 291,675 | 15 | 940 | 61.10 | 87.50 | 0.00 | −2.20 |
| 9 | 119.95 | 294,230 | 15 | 936 | 62.32 | 88.89 | 0.00 | −4.40 |
| 10 | 116.26 | 300,208 | 16 | 917 | 62.40 | 93.33 | 0.00 | −3.52 |
| 11 | 112.64 | 303,203 | 16 | 914 | 63.69 | 94.94 | 0.00 | −5.96 |
| 12 | 108.95 | 306,064 | 16 | 909 | 64.77 | 96.48 | 0.00 | −8.04 |
| 13 | 105.32 | 308,216 | 16 | 909 | 66.24 | 97.95 | 0.00 | −10.68 |
| 14 | 101.66 | 310,250 | 16 | 910 | 67.73 | 99.61 | 0.00 | −13.40 |
| 15 | 99.92 | 311,250 | 16 | 910 | 68.46 | 100.39 | 0.00 | −14.72 |
| 17 | 90.74 | 313,250 | 17 | 915 | 71.45 | 105.59 | 0.00 | −19.04 |
| 20 | 79.74 | 315,250 | 18 | 918 | 74.44 | 110.79 | 0.00 | −24.44 |

Table A4.
Pareto-optimal solutions of the PRMIP model ().
Table A4.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (TEUs) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 148.58 | 232,016 | 13 | 1014 | 45.57 | 61.42 | 0 | 20.08 |
| 2 | 144.96 | 247,188 | 13 | 997 | 50.34 | 65.9 | 0 | 14.72 |
| 3 | 141.28 | 251,997 | 13 | 1027 | 53.77 | 73.2 | 0 | 9.44 |
| 4 | 137.64 | 267,675 | 14 | 951 | 53.52 | 73.3 | 0 | 9.76 |
| 5 | 134.06 | 273,564 | 14 | 963 | 56.42 | 78.17 | 0 | 5.00 |
| 6 | 130.36 | 283,641 | 15 | 957 | 58.6 | 84.61 | 0 | 1.88 |
| 7 | 126.80 | 289,119 | 15 | 945 | 59.87 | 86.1 | 0 | −0.48 |
| 8 | 123.13 | 291,675 | 15 | 940 | 61.1 | 87.5 | 0 | −2.68 |
| 9 | 119.47 | 294,230 | 15 | 936 | 62.32 | 88.89 | 0 | −4.88 |
| 10 | 115.74 | 300,230 | 16 | 919 | 62.59 | 93.33 | 0 | −4.28 |
| 11 | 112.16 | 303,203 | 16 | 914 | 63.69 | 94.94 | 0 | −6.44 |
| 12 | 108.47 | 306,064 | 16 | 909 | 64.77 | 96.48 | 0 | −8.52 |
| 13 | 104.84 | 308,216 | 16 | 909 | 66.24 | 97.95 | 0 | −11.16 |
| 14 | 101.18 | 310,250 | 16 | 910 | 67.73 | 99.61 | 0 | −13.88 |
| 15 | 99.44 | 311,250 | 16 | 910 | 68.46 | 100.39 | 0 | −15.20 |
| 17 | 90.26 | 313,250 | 17 | 915 | 71.45 | 105.59 | 0 | −19.52 |
| 20 | 79.26 | 315,250 | 18 | 918 | 74.44 | 110.79 | 0 | −24.92 |

Table A5.
Pareto-optimal solutions of the PRMIP model ().
Table A5.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 140.88 | 242,871 | 13 | 1014 | 49.82 | 65.04 | 0 | 9.41 |
| 2 | 138.16 | 250,335 | 13 | 1036 | 53.77 | 73.2 | 0 | 5.66 |
| 3 | 135.44 | 265,583 | 14 | 990 | 55.2 | 76.8 | 0 | 4.32 |
| 4 | 132.72 | 272,440 | 14 | 967 | 56.17 | 78 | 0 | 3.26 |
| 5 | 130.02 | 282,391 | 15 | 960 | 58.36 | 84.31 | 0 | 1.31 |
| 6 | 127.59 | 288,564 | 15 | 946 | 59.63 | 85.82 | 0 | −0.02 |
| 7 | 124.61 | 291,342 | 15 | 940 | 60.85 | 87.24 | 0 | −1.34 |
| 8 | 121.86 | 293,827 | 15 | 936 | 62.08 | 88.52 | 0 | −2.66 |
| 9 | 119.14 | 296,108 | 16 | 927 | 61.61 | 92.32 | 0 | −1.60 |
| 10 | 116.44 | 301,536 | 16 | 917 | 62.96 | 94.09 | 0 | −3.16 |
| 11 | 113.77 | 304,175 | 16 | 913 | 64.04 | 95.6 | 0 | −4.40 |
| 12 | 111.07 | 306,730 | 16 | 909 | 65.26 | 97 | 0 | −5.64 |
| 13 | 108.26 | 309,064 | 16 | 910 | 66.97 | 98.82 | 0 | −7.49 |
| 14 | 105.69 | 311,216 | 16 | 910 | 68.44 | 100.29 | 0 | −9.07 |
| 15 | 105.52 | 311,250 | 16 | 910 | 68.46 | 100.39 | 0 | −9.12 |
| 16 | 100.25 | 311,550 | 17 | 914 | 70.2 | 104.19 | 0 | −10.34 |
| 17 | 98.07 | 313,250 | 17 | 915 | 71.45 | 105.59 | 0 | −11.71 |
| 20 | 89.23 | 315,250 | 18 | 918 | 74.44 | 110.79 | 0 | −14.95 |

Table A6.
Pareto-optimal solutions of the PRMIP model ().
Table A6.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 163.76 | 222,188 | 12 | 1062 | 45.73 | 59.3 | 0.72 | 33.54 |
| 2 | 158.53 | 238,175 | 13 | 1011 | 47.62 | 63.25 | 0.72 | 29.31 |
| 3 | 153.30 | 247,744 | 13 | 997 | 50.58 | 66.1 | 0.72 | 23.62 |
| 4 | 148.04 | 258,411 | 14 | 958 | 50.51 | 70.37 | 0.72 | 22.02 |
| 5 | 142.81 | 268,855 | 14 | 945 | 53.52 | 73.46 | 0.72 | 16.38 |
| 6 | 137.64 | 273,008 | 14 | 963 | 56.17 | 77.97 | 0.72 | 9.47 |
| 7 | 132.38 | 282,325 | 15 | 960 | 58.33 | 84.23 | 0.72 | 4.61 |
| 8 | 127.59 | 288,564 | 15 | 946 | 59.63 | 85.82 | 0.72 | 0.70 |
| 9 | 122.41 | 291,342 | 15 | 940 | 60.85 | 87.24 | 0.72 | −2.82 |
| 10 | 116.76 | 296,275 | 16 | 922 | 61.32 | 92.12 | 0.18 | −2.88 |
| 11 | 111.52 | 301,411 | 16 | 917 | 62.93 | 94.04 | 0.72 | −7.30 |
| 12 | 106.38 | 304,494 | 16 | 910 | 64.01 | 95.6 | 0.72 | −10.62 |
| 13 | 101.31 | 306,916 | 16 | 908 | 65.28 | 97.01 | 0.72 | −14.40 |
| 14 | 95.83 | 309,064 | 16 | 910 | 66.97 | 98.82 | 0.72 | −19.20 |
| 15 | 90.62 | 311,216 | 16 | 910 | 68.44 | 100.29 | 0.72 | −23.42 |
| 16 | 90.37 | 311,250 | 16 | 910 | 68.46 | 100.39 | 0.72 | −23.55 |
| 17 | 80.28 | 312,583 | 17 | 915 | 70.96 | 105.07 | 0.72 | −29.06 |
| 18 | 78.60 | 313,250 | 17 | 915 | 71.45 | 105.59 | 0.72 | −30.46 |
| 20 | 64.44 | 315,250 | 18 | 918 | 74.44 | 110.79 | 0.64 | −39.10 |

Table A7.
Pareto-optimal solutions of the PRMIP model ().
Table A7.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 124.10 | 188,653 | 12 | 1069 | 43.62 | 57.08 | 0 | 23.08 |
| 2 | 120.25 | 201,673 | 13 | 1016 | 45 | 60.48 | 0 | 20.76 |
| 3 | 116.41 | 203,291 | 13 | 1062 | 47.72 | 67.72 | 0 | 15.84 |
| 4 | 112.59 | 215,907 | 13 | 980 | 47.91 | 67.98 | 0 | 16.88 |
| 5 | 108.99 | 224,070 | 14 | 994 | 51.57 | 73.47 | 0 | 11.16 |
| 6 | 105.21 | 227,403 | 14 | 996 | 54.02 | 76.08 | 0 | 8.76 |
| 7 | 101.22 | 238,847 | 15 | 961 | 54.29 | 80.65 | 0 | 6.60 |
| 8 | 97.41 | 242,514 | 15 | 952 | 56 | 82.61 | 0 | 4.92 |
| 9 | 93.62 | 245,736 | 15 | 953 | 58.21 | 84.98 | 0 | 2.56 |
| 10 | 90.08 | 247,536 | 15 | 954 | 59.65 | 86.42 | 0 | −0.12 |
| 11 | 89.39 | 247,670 | 15 | 954 | 59.87 | 86.55 | 0 | −0.60 |
| 12 | 82.06 | 249,794 | 16 | 935 | 59.65 | 90.73 | 0 | −1.32 |
| 13 | 78.24 | 252,683 | 16 | 936 | 61.61 | 92.84 | 0 | −3.84 |
| 14 | 75.15 | 253,970 | 16 | 937 | 62.81 | 93.95 | 0 | −6.08 |
| 17 | 63.56 | 255,170 | 17 | 940 | 65.79 | 99.15 | 0 | −11.48 |
| 19 | 63.58 | 255,150 | 17 | 940 | 65.77 | 99.09 | 0 | −11.52 |
| 20 | 51.52 | 256,370 | 18 | 942 | 68.78 | 104.35 | 0 | −16.88 |

Table A8.
Pareto-optimal solutions of the PRMIP model ().
Table A8.
Pareto-optimal solutions of the PRMIP model ().
| Obj 1 (Million USD) | Obj 2 (Million USD) | ORN | AFR (USD) | TFC (Million USD) | TBC (Million USD) | The Extra Penalty Cost | COIR (Million USD) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 164.54 | 254,346 | 13 | 1035 | 50.14 | 63.88 | 0 | 15.12 |
| 2 | 160.51 | 267,788 | 13 | 1018 | 52.88 | 70.07 | 0 | 10.64 |
| 3 | 156.71 | 283,746 | 14 | 977 | 54.58 | 73.91 | 0 | 7.88 |
| 4 | 152.70 | 291,746 | 14 | 981 | 58.22 | 76.82 | 0 | 1.36 |
| 5 | 148.75 | 302,493 | 15 | 979 | 60.51 | 85.65 | 0 | −1.50 |
| 6 | 144.87 | 311,437 | 15 | 971 | 63.11 | 88.41 | 0 | −6.24 |
| 7 | 141.09 | 317,048 | 15 | 966 | 65.06 | 90.36 | 0 | −9.76 |
| 8 | 137.03 | 320,048 | 15 | 959 | 66.29 | 91.8 | 0 | −11.96 |
| 9 | 133.11 | 323,604 | 16 | 948 | 66.41 | 96.33 | 0 | −11.24 |
| 10 | 129.39 | 331,160 | 16 | 934 | 67.78 | 98.36 | 0 | −13.92 |
| 11 | 125.53 | 333,937 | 16 | 929 | 69.01 | 99.78 | 0 | −16.12 |
| 12 | 121.58 | 336,715 | 16 | 924 | 70.23 | 101.23 | 0 | −18.32 |
| 13 | 117.55 | 339,271 | 16 | 920 | 71.45 | 102.76 | 0 | −20.52 |
| 14 | 113.81 | 341,604 | 16 | 917 | 72.68 | 104.23 | 0 | −22.72 |
| 15 | 109.77 | 343,937 | 16 | 918 | 74.39 | 106.05 | 0 | −25.80 |
| 16 | 106.01 | 346,160 | 16 | 918 | 75.86 | 107.66 | 0 | −28.44 |
| 17 | 102.00 | 347,471 | 17 | 925 | 77.62 | 111.51 | 0 | −30.56 |
| 18 | 98.83 | 349,360 | 17 | 925 | 78.84 | 112.86 | 0 | −32.76 |
| 19 | 94.15 | 350,226 | 18 | 927 | 80.12 | 116.24 | 0 | −34.36 |
| 20 | 90.10 | 352,560 | 18 | 928 | 81.83 | 118.06 | 0 | −37.44 |
References
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Optimization in liner shipping. 4OR A Q. J. Oper. Res. 2017, 15, 327–341. [Google Scholar]
- Notice of Action and Proposed Action in Section 301 Investigation of China’s Targeting the Maritime, Logistics, and Shipbuilding Sectors for Dominance, Request for Comments. Available online: https://www.federalregister.gov/documents/2025/04/23/2025-06927/notice-of-action-and-proposed-action-in-section-301-investigation-of-chinas-targeting-the-maritime (accessed on 5 May 2025).
- U.S. Proposes Port Fees on Chinese-Built Ships and Operators to Counter China’s Shipping Dominance. Available online: https://www.hklaw.com/en/insights/publications/2025/03/us-proposes-port-fees-on-chinese-built-ships (accessed on 5 May 2025).
- U.S. Revises Section 301 Tariffs on Chinese Vessels Amid Industry Pushback. Available online: https://www.shipuniverse.com/news/u-s-revises-section-301-tariffs-on-chinese-vessels-amid-industry-pushback/ (accessed on 5 May 2025).
- USTR Section 301 Action on China’s Targeting of the Maritime, Logistics, and Shipbuilding Sectors for Dominance. Available online: https://ustr.gov/about/policy-offices/press-office/press-releases/2025/april/ustr-section-301-action-chinas-targeting-maritime-logistics-and-shipbuilding-sectors-dominance (accessed on 16 July 2025).
- Proposed U.S. Port Fees on China-Built Ships Begins Choking Coal, Agriculture Exports. Available online: https://www.reuters.com/world/us/proposed-us-port-fees-china-built-ships-begins-choking-coal-agriculture-exports-2025-03-19/ (accessed on 16 July 2025).
- Trump Is Targeting China-Made Containerships in New Flank of Global Economic War on the Oceans. Available online: https://www.cnbc.com/2025/03/11/trump-pursues-new-trade-war-on-seas-targeting-china-containerships.html (accessed on 16 July 2025).
- Launch of the Review of Maritime Transport 2024. Available online: https://unctad.org/meeting/launch-review-maritime-transport-2024 (accessed on 5 May 2025).
- Wang, Y.; Zhang, H.; Wang, T.; Liu, J. Heterogeneous vessel fleet co-management for liner alliances under profit-sharing agreement and weekly-dependent demand. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103494. [Google Scholar] [CrossRef]
- Pasha, J.; Dulebenets, M.A.; Kavoosi, M.; Abioye, O.F.; Theophilus, O.; Wang, H.; Kampmann, R.; Guo, W. Holistic tactical-level planning in liner shipping: An exact optimization approach. J. Shipp. Trade 2020, 5, 8. [Google Scholar] [CrossRef]
- Meng, L.; Ge, H.; Wang, X.; Yan, W.; Han, C. Optimization of ship routing and allocation in a container transport network considering port congestion: A variational inequality model. Ocean Coast. Manag. 2023, 244, 106798. [Google Scholar] [CrossRef]
- Ting, S.C.; Tzeng, G.H. Ship scheduling and cost analysis for route planning in liner shipping. Marit. Econ. Logist. 2003, 5, 378–392. [Google Scholar] [CrossRef]
- Cariou, P.; Cheaitou, A.; Larbi, R.; Hamdan, S. Liner shipping network design with emission control areas: A genetic algorithm-based approach. Transp. Res. Part D Transp. Environ. 2018, 63, 604–621. [Google Scholar] [CrossRef]
- Fagerholt, K.; Gausel, O.B.; Rakke, J.G.; Psaraftis, H.N. Maritime routing and speed optimization with emission control areas. Transp. Res. Part C Emerg. Technol. 2015, 55, 419–430. [Google Scholar] [CrossRef]
- Wen, M.; Ropke, S.; Petersen, H.L.; Larsen, R.; Madsen, O.B. Full-shipload tramp ship routing and scheduling with variable speeds. Comput. Oper. Res. 2016, 70, 1–8. [Google Scholar] [CrossRef]
- Mahmoodjanloo, M.; Chen, G.; Asian, S.; Iranmanesh, S.H.; Tavakkoli-Moghaddam, R. In-port multi-ship routing and scheduling problem with draft limits. Marit. Policy Manag. 2021, 48, 966–987. [Google Scholar] [CrossRef]
- Venturini, G.; Iris, Ç.; Kontovas, C.A.; Larsen, A. The multi-port berth allocation problem with speed optimization and emission considerations. Transp. Res. Part D Transp. Environ. 2017, 54, 142–159. [Google Scholar] [CrossRef]
- Song, D.P.; Li, D.; Drake, P. Multi-objective optimization for a liner shipping service from different perspectives. Transp. Res. Procedia 2017, 25, 1441–1452. [Google Scholar] [CrossRef]
- Xiao, P.; Wang, H. Ship type selection and cost optimization of marine container ships based on genetic algorithm. Appl. Sci. 2024, 14, 9816. [Google Scholar] [CrossRef]
- Liu, T.; Liu, J.; Xu, H. A multi-population multi-objective maritime inventory routing optimization algorithm with three-level dynamic encoding. Sci. Rep. 2025, 15, 5701. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Meng, Q.; Lee, C.Y. Liner container assignment model with transit-time-sensitive container shipment demand and its applications. Transp. Res. Part B Methodol. 2016, 85, 97–119. [Google Scholar] [CrossRef]
- Wang, T.; Liu, J.; Wang, Y.; Jin, Y.; Wang, S. Dynamic flexible allocation of slots in container line transport. Sustainability 2024, 16, 9146. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.; Lee, S. Regulatory compliance and operational efficiency in maritime transport: Strategies and insights. Transp. Policy 2024, 146, 130–140. [Google Scholar] [CrossRef]
- Tran, N.K.; Haasis, H.D. Literature survey of network optimization in container liner shipping. Flex. Serv. Manuf. J. 2015, 27, 139–179. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Y.; Zhang, J. Fleet deployment and speed optimization of container ships considering bunker fuel consumption heterogeneity. Manag. Syst. Eng. 2022, 1, 3. [Google Scholar] [CrossRef]
- Jiang, X.; Mao, H.; Zhang, H. Simultaneous optimization of the liner shipping route and ship schedule designs with time windows. Math. Probl. Eng. 2020, 2020, 3287973. [Google Scholar] [CrossRef]
- Pasha, J.; Dulebenets, M.A.; Fathollahi-Fard, A.M.; Tian, G.; Lau, Y.Y.; Singh, P.; Liang, B. An integrated optimization method for tactical-level planning in liner shipping with heterogeneous ship fleet and environmental considerations. Adv. Eng. Inform. 2021, 48, 101299. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, Z.; Zhou, J.; Notteboom, T.; Ma, Y. Toward green container liner shipping: Joint optimization of heterogeneous fleet deployment, speed optimization, and fuel bunkering. Int. Trans. Oper. Res. 2024, 32, 863–887. [Google Scholar] [CrossRef]
- Brouer, B.D.; Desaulniers, G.; Pisinger, D. A matheuristic for the liner shipping network design problem. Transp. Res. Part E Logist. Transp. Rev. 2014, 72, 42–59. [Google Scholar] [CrossRef]
- Cheaitou, A.; Hamdan, S.; Larbi, R. Liner shipping network design with sensitive demand. Marit. Bus. Rev. 2021, 6, 293–313. [Google Scholar] [CrossRef]
- Xia, J.; Li, K.X.; Ma, H.; Xu, Z. Joint planning of fleet deployment, speed optimization, and cargo allocation for liner shipping. Transp. Sci. 2015, 49, 922–938. [Google Scholar] [CrossRef]
- Lai, X.; Wu, L.; Wang, K.; Wang, F. Robust ship fleet deployment with shipping revenue management. Transp. Res. Part B Methodol. 2022, 161, 169–196. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Wang, H.; Cheng, S.; Liu, W. Fleet deployment optimization for LNG shipping vessels considering the influence of mixed factors. J. Mar. Sci. Eng. 2022, 10, 2034. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Kontovas, C.A. Speed models for energy-efficient maritime transportation: A taxonomy and survey. Transp. Res. Part C Emerg. Technol. 2013, 26, 331–351. [Google Scholar] [CrossRef]
- Bertho, F.; Borchert, I.; Mattoo, A. The trade-reducing effects of restrictions on liner shipping. J. Comp. Econ. 2016, 44, 231–242. [Google Scholar] [CrossRef]
- Notteboom, T.; Pallis, T.; Rodrigue, J.P. Disruptions and resilience in global container shipping and ports: The COVID-19 pandemic versus the 2008–2009 financial crisis. Marit. Econ. Logist. 2021, 23, 179. [Google Scholar] [CrossRef]
- Bichou, K. Port Operations, Planning and Logistics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Jin, L.; Chen, J.; Chen, Z.; Sun, X.; Yu, B. Impact of COVID-19 on China’s international liner shipping network based on AIS data. Transp. Policy 2022, 121, 90–99. [Google Scholar] [CrossRef]
- Ksciuk, J.; Kuhlemann, S.; Tierney, K.; Koberstein, A. Uncertainty in maritime ship routing and scheduling: A Literature review. Eur. J. Oper. Res. 2023, 308, 499–524. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, S.; Cao, Z. Exact and heuristic methods for the integrated optimisation of vessel deployment and liner shipping routing schedule. Int. J. Syst. Sci. Oper. Logist. 2025, 12, 2505920. [Google Scholar] [CrossRef]
- Verschuur, J.; Koks, E.E.; Hall, J.W. Port disruptions due to natural disasters: Insights into port and logistics resilience. Transp. Res. Part D Transp. Environ. 2020, 85, 102393. [Google Scholar] [CrossRef]
- Elmi, Z.; Singh, P.; Meriga, V.K.; Goniewicz, K.; Borowska-Stefańska, M.; Wiśniewski, S.; Dulebenets, M.A. Uncertainties in liner shipping and ship schedule recovery: A state-of-the-art review. J. Mar. Sci. Eng. 2022, 10, 563. [Google Scholar] [CrossRef]
- Zheng, H.; Negenborn, R.R.; Lodewijks, G. Robust distributed predictive control of waterborne AGVs—A cooperative and cost-effective approach. IEEE Trans. Cybern. 2017, 48, 2449–2461. [Google Scholar] [CrossRef] [PubMed]
- Han, S.W.; Lee, E.H.; Kim, D.K. Multi-objective optimization for skip-stop strategy based on smartcard data considering total travel time and equity. Transp. Res. Rec. 2021, 2675, 841–852. [Google Scholar] [CrossRef]
- Rajabighamchi, F.; Hajlou, E.M.H.; Hassannayebi, E. A multi-objective optimization model for robust skip-stop scheduling with earliness and tardiness penalties. Urban Rail Transit 2019, 5, 172–185. [Google Scholar] [CrossRef]
- Shang, P.; Li, R.; Liu, Z.; Yang, L.; Wang, Y. Equity-oriented skip-stopping schedule optimization in an oversaturated urban rail transit network. Transp. Res. Part C Emerg. Technol. 2018, 89, 321–343. [Google Scholar] [CrossRef]
- Lee, E.H.; Jeong, J. Accessible taxi routing strategy based on travel behavior of people with disabilities incorporating vehicle routing problem and Gaussian mixture model. Travel Behav. Soc. 2024, 34, 100687. [Google Scholar] [CrossRef]
- Lee, E.H.; Kim, G.J. Multi-objective optimization of submerged floating tunnel route considering structural safety and total travel time. Struct. Eng. Mech. Int. J. 2023, 88, 323–334. [Google Scholar]
- Wen, X.; Chen, Q.; Yin, Y.Q.; Lau, Y.Y.; Dulebenets, M.A. Multi-objective optimization for ship scheduling with port congestion and environmental considerations. J. Mar. Sci. Eng. 2024, 12, 114. [Google Scholar] [CrossRef]
- Revised US Port Fee Plan Leaves Important Questions Unanswered, Lawyers Argue. Available online: https://www.lloydslist.com/LL1153244/Revised-US-port-fee-plan-leaves-important-questions-unanswered-lawyers-argue (accessed on 5 May 2025).
- Hoffman, A.J.; Kruskal, J.B. Integral boundary points of convex polyhedra. In 50 Years of Integer Programming 1958–2008: From the Early Years to the State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2010; pp. 49–76. [Google Scholar]
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Zhang, Z.; Wang, H. Multicriteria ship route planning method based on improved particle swarm optimization–genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 357. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Hao, X.; Zhao, Y.; Gong, Y. Dispatch optimization of maritime rescue forces in Arctic shipping based on the comparison of TOPSIS and the weighted scoring method. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Sapporo, Japan, 19–24 June 2022; p. ISOPE-I. [Google Scholar]
- Farmakis, P.; Chassiakos, A.; Karatzas, S. A Multi-Objective Tri-Level Algorithm for Hub-and-Spoke Network in Short Sea Shipping Transportation. Algorithms 2023, 16, 379. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. A closer look at drawbacks of minimizing weighted sums of objectives for Pareto set generation in multicriteria optimization problems. Struct. Optim. 1997, 14, 63–69. [Google Scholar] [CrossRef]
- Deb, K.; Sindhya, K.; Hakanen, J. Multi-objective optimization. In Decision Sciences, 1st ed.; Ravindran, A.R., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 161–200. [Google Scholar]
- CMA CGM, Maersk, and COSCO Compete for the Market Lead in the Asia–North America Trade. Available online: https://globalmaritimehub.com/cma-cgm-maersk-and-cosco-compete-for-the-market-lead-in-the-asia-north-america-trade.html (accessed on 5 May 2025).
- Better Ways, Making Supply Chains More Sustainable Every Day. Available online: https://www.cma-cgm.com/about/the-group (accessed on 5 May 2025).
- Evolution of Vessel Size on the Asia-Europe Route. Available online: https://www.porttechnology.org/news/evolution-of-vessel-size-on-the-asia-europe-route/ (accessed on 5 May 2025).
- Alphaliner Top 100. Available online: https://alphaliner.axsmarine.com/PublicTop100/ (accessed on 5 May 2025).
- Most Shipping Lines Can Avoid US Port Fees but Cosco Faces Major Challenge. Available online: https://www.lloydslist.com/LL1153279/Most-shipping-lines-can-avoid-US-port-fees-but-Cosco-faces-major-challenge (accessed on 5 May 2025).
- Ocean Alliance Day9 Route Products. Available online: https://www.cargoespi.com/blogs/news/ocean-alliance-day9-routes (accessed on 5 May 2025).
- MSC China-North Europe Sea Route. Available online: https://www.shiphub.co/msc-china-north-europe-sea-route/ (accessed on 5 May 2025).
- The Future Standalone MSC East/West Network. Available online: https://www.msc.com/en/solutions/our-trade-services/east-west-network (accessed on 5 May 2025).
- Maersk and MSC Switch to Liverpool Port Permanently. Available online: https://www.logisticsmanager.com/maersk-and-msc-switch-to-liverpool-port-permanently/ (accessed on 5 May 2025).
- MSC Revises Its Asia to North America West Coast Network. Available online: https://www.msc.com/en/newsroom/customer-advisories/2025/february/msc-revises-its-asia-to-north-america-west-coast-network (accessed on 5 May 2025).
- THE Alliance Announces Updated Service Network for 2024. Available online: https://container-news.com/the-alliance-announces-updated-service-network-for-2024/ (accessed on 5 May 2025).
- Containerized Cargo Flows on Major Container Trade Routes in 2024, by Trade Route. Available online: https://www.statista.com/statistics/253988/estimated-containerized-cargo-flows-on-major-container-trade-routes/ (accessed on 5 May 2025).
- Review of Maritime Transport 2024. Available online: https://unctad.org/publication/review-maritime-transport-2024 (accessed on 5 May 2025).
- Drewry World Container Index. Available online: https://www.drewry.co.uk/supply-chain-advisors/supply-chain-expertise/world-container-index-assessed-by-drewry (accessed on 5 May 2025).
- Freightos Container Shipping Cost Calculator. Available online: https://www.freightos.com/freight-resources/container-shipping-cost-calculator-free-tool/ (accessed on 5 May 2025).
- Drewry Intra-Asia Container Index. Available online: https://www.drewry.co.uk/supply-chain-advisors/supply-chain-expertise/intra-asia-container-index (accessed on 5 May 2025).
- Wang, S.; Meng, Q. Sailing speed optimization for container ships in a liner shipping network. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 701–714. [Google Scholar] [CrossRef]
- Ship & Bunker. Global 20 Ports Average Bunker Prices. Available online: https://shipandbunker.com/prices/av/global/av-g20-global-20-ports-average (accessed on 5 May 2025).
- Wilkinson, L. Revising the Pareto Chart. Am. Stat. 2006, 60, 332–334. [Google Scholar] [CrossRef]
- Wang, S.; Meng, Q. Liner ship fleet deployment with container transshipment operations. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 470–484. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Z.; Liu, R.; Sun, L. Distribution-free approaches for an integrated cargo routing and empty container repositioning problem with repacking operations in liner shipping networks. Sustainability 2022, 14, 14773. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, J.; Lu, B. Liner shipping hub location and empty container repositioning: Use of foldable containers and container leasing. Expert Syst. Appl. 2024, 237, 121592. [Google Scholar] [CrossRef]
- Zheng, J.; Mao, C.; Zhang, Q. Hybrid dynamic modeling and receding horizon speed optimization for liner shipping operations from schedule reliability and energy efficiency perspectives. Front. Mar. Sci. 2023, 10, 1095283. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, Y. Sailing speed optimization for near-sea shipping services considering container routing. In Proceedings of the 2024 International Conference on Cloud Computing and Big Data, Dali, China, 26–28 July 2024; pp. 616–620. [Google Scholar]
- Li, C.; Qi, X.; Song, D. Real-time schedule recovery in liner shipping service with regular uncertainties and disruption events. Transp. Res. Part B Methodol. 2016, 93, 762–788. [Google Scholar] [CrossRef]
- Sun, M.; Vortia, M.P.; Xiao, G.; Yang, J. Carbon policies and liner speed optimization: Comparisons of carbon trading and carbon tax combined with the European Union Emissions Trading Scheme. J. Mar. Sci. Eng. 2025, 13, 204. [Google Scholar] [CrossRef]
- Sun, L.; Wang, X.; Hu, Z.; Ning, Z. Carbon and cost accounting for liner shipping under the European Union Emission Trading System. Front. Mar. Sci. 2024, 11, 1291968. [Google Scholar] [CrossRef]
- Chen, K.; Yi, X.; Xin, X.; Zhang, T. Liner shipping network design model with carbon tax, seasonal freight rate fluctuations and empty container relocation. Sustain. Horiz. 2023, 8, 100073. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Li, F.; Wang, S. Sustainable maritime transportation operations with emission trading. J. Mar. Sci. Eng. 2023, 11, 1647. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization, 2nd ed.; Springer: Berlin, Germany, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).