Research on Oriented Object Detection in Aerial Images Based on Architecture Search with Decoupled Detection Heads
Abstract
1. Introduction
- Feature fusion network design based on automated structure searchThe FAS module is incorporated into the Inception-ResNet feature extraction network for general object detection. This module enables automatic identification of optimal feature fusion paths, mitigating content loss in large-scale, dense rotated targets during multi-layer feature extraction and overcoming the limitations of manually designed fusion paths. Additionally, by designing the search space and search strategy, the proposed method resolves the issue of wide-ranging architecture search methods being infeasible on a single GPU.
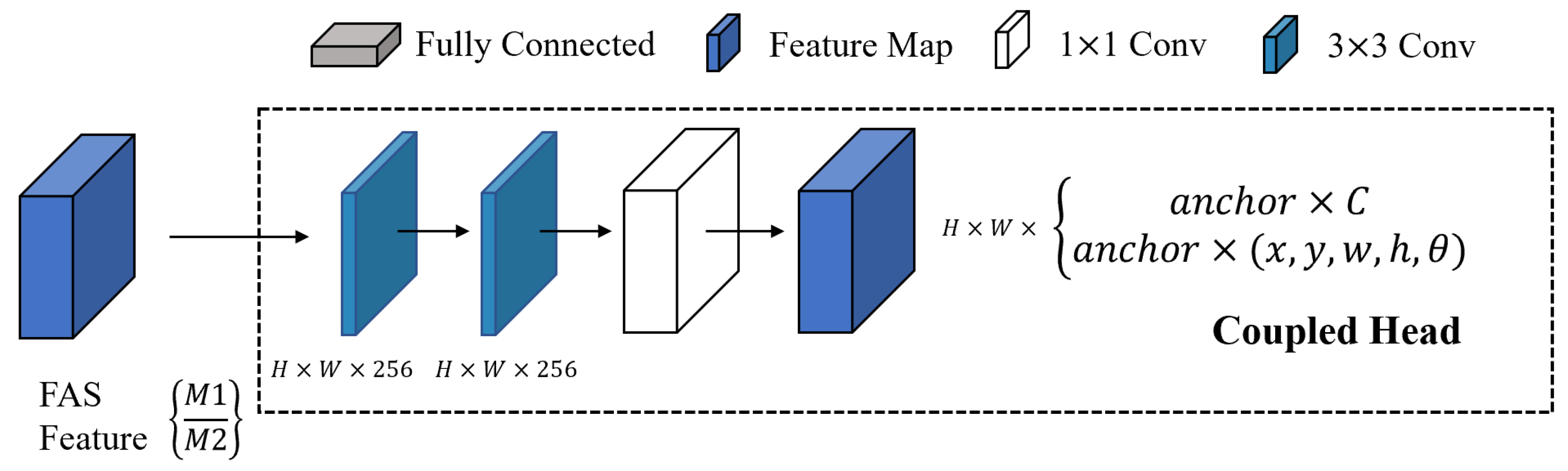
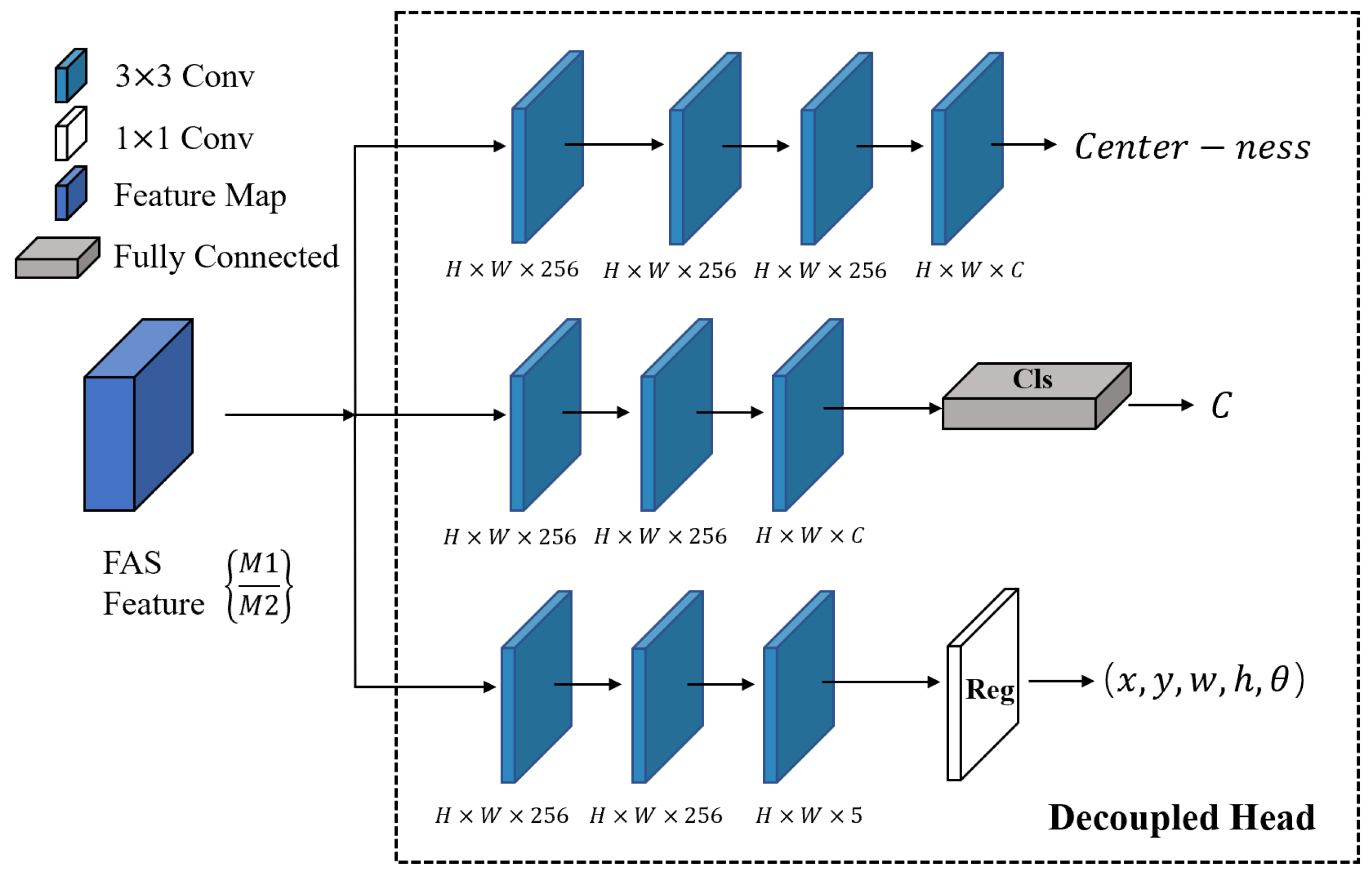
- Design of an anchor-free decoupled detection head for oriented object detectionFor dense rotated targets, which are often non-horizontally arranged, traditional Region Proposal Network (RPN) approaches exhibit low detection efficiency and often include multiple targets within a single candidate box, resulting in poor performance. This paper proposes a decoupled detection head (DDH) without anchors, which decouples the processes of target bounding box regression and target classification. This allows different convolutional branches to learn distinct feature emphases. Furthermore, a centrality branch is introduced on top of the decoupling mechanism to enhance the precision of bounding box regression and improve recognition speed.
- Ellipse center sampling methodTo address the issue of low sampling rates in horizontal center sampling for detecting rotated targets with large aspect ratios, this study proposes an improved ellipse center sampling (ECS) method. The ECS method increases the sampling area of rotated detection boxes, reducing the difficulty of network training and improving object detection accuracy. Additionally, it converts rotated rectangles into a distance representation based on an elliptical Gaussian distribution, resolving the challenge of computing gradients for intersection over union (IoU) loss at arbitrary angles. Experiments on the DOTA [3] and HRSC2016 [4] datasets validate the feasibility of the proposed method. Compared to improved second-order methods [5,6,7,8], the proposed approach not only employs an anchor-free detection head but also requires only convolutional layers due to internal decoupling, making it more easily deployable on most edge computing platforms.
2. Related Work
3. Design of FAS Structures
3.1. FAS Search Strategy
3.2. Design of the FAS Search Space
3.3. FAS Search Results
3.4. Ablation Experiments and Analysis of Results
4. Design of Decoupled Detection Head for Elliptical Center Sampling
4.1. Implementation Method of the Oriented Object Detection Head
- Panning the box:
- Scaling the box:
4.2. Decoupled Detection Branch Design
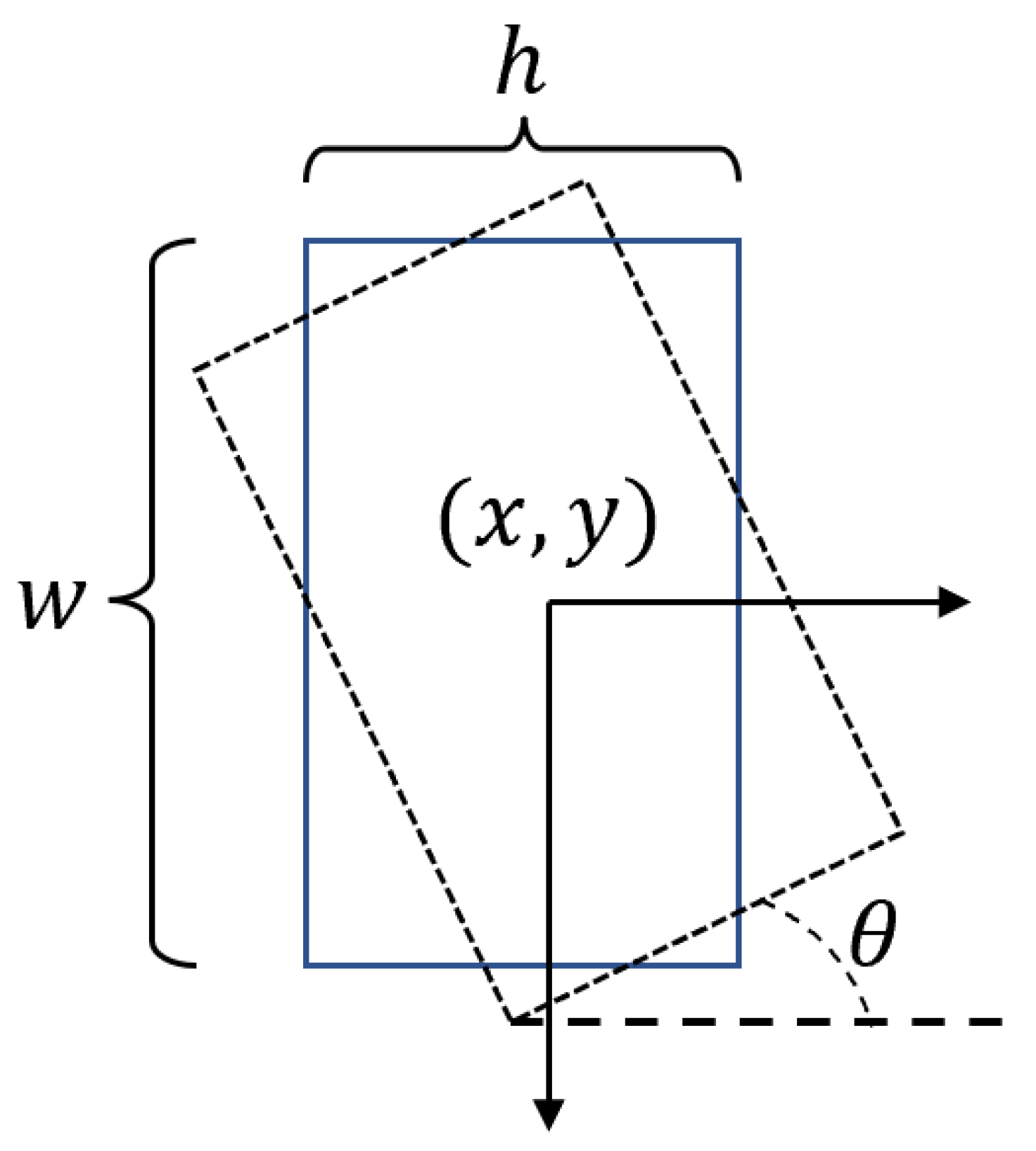
4.3. Ellipse Center Sampling and Anchor-Free Implementation Approach
4.4. Loss Function Design
5. Experiments
5.1. Datasets
5.2. Experiment Environment
- CPU: Intel(R) Silver Xeon 2140B, 3.8 GHz(Intel, Shanghai, China): 8 cores 16 threads;
- Memory: 32 GB DDR4 REG ECC 2400 MHz(Dell, Shantou, China);
- GPU: NVIDIA TESLA V100×2 16 GB GBBR5(GIGABYTE, Shenzhen, China);
- Operating system: Ubuntu 20.04 distribution.The software environment for this study’s comparison experiments was as follows:
- CUDA 11.2 cuDNN 7.6.5;
- Python 3.8;
- Pytorch 1.12.0;
- OpenCV 3.4.1.
5.3. Assessment of Indicators
5.4. Hyperparameter Selection
5.4.1. Model Architecture
5.4.2. Training Settings
5.4.3. Loss Function Weights
5.4.4. Learning Rate Scheduling
5.4.5. All Hyperparameters
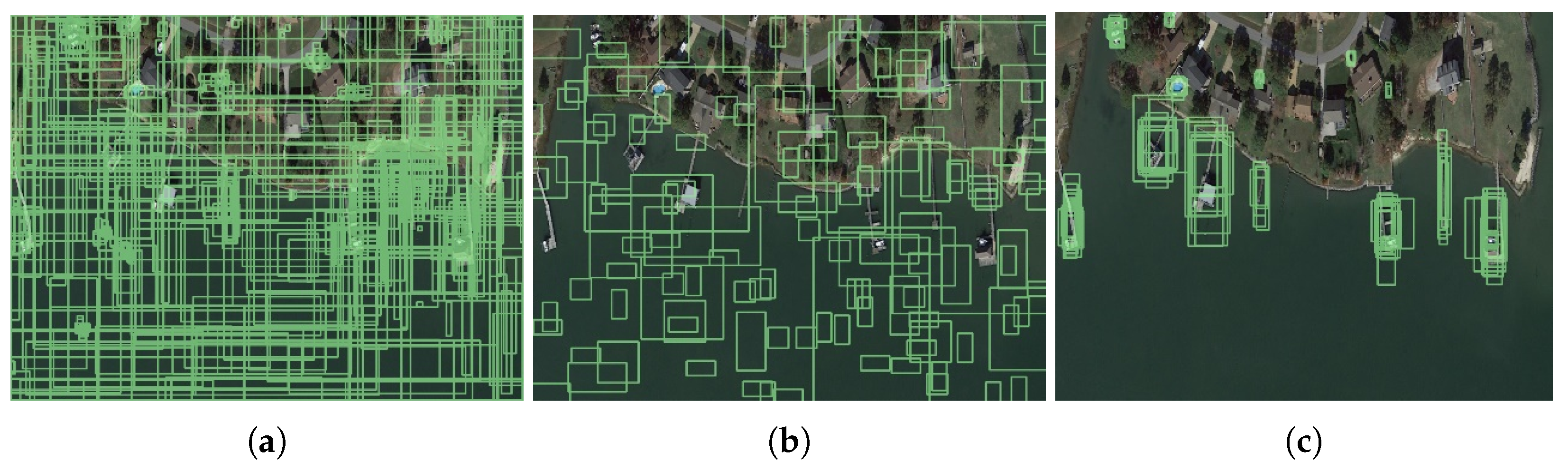
5.5. Ablation Experiments
5.6. Generalization Experiments with Different Backbone Networks Using the Proposed Method
5.7. Experiments on Speed and Accuracy of the Proposed Method Compared to Other Networks
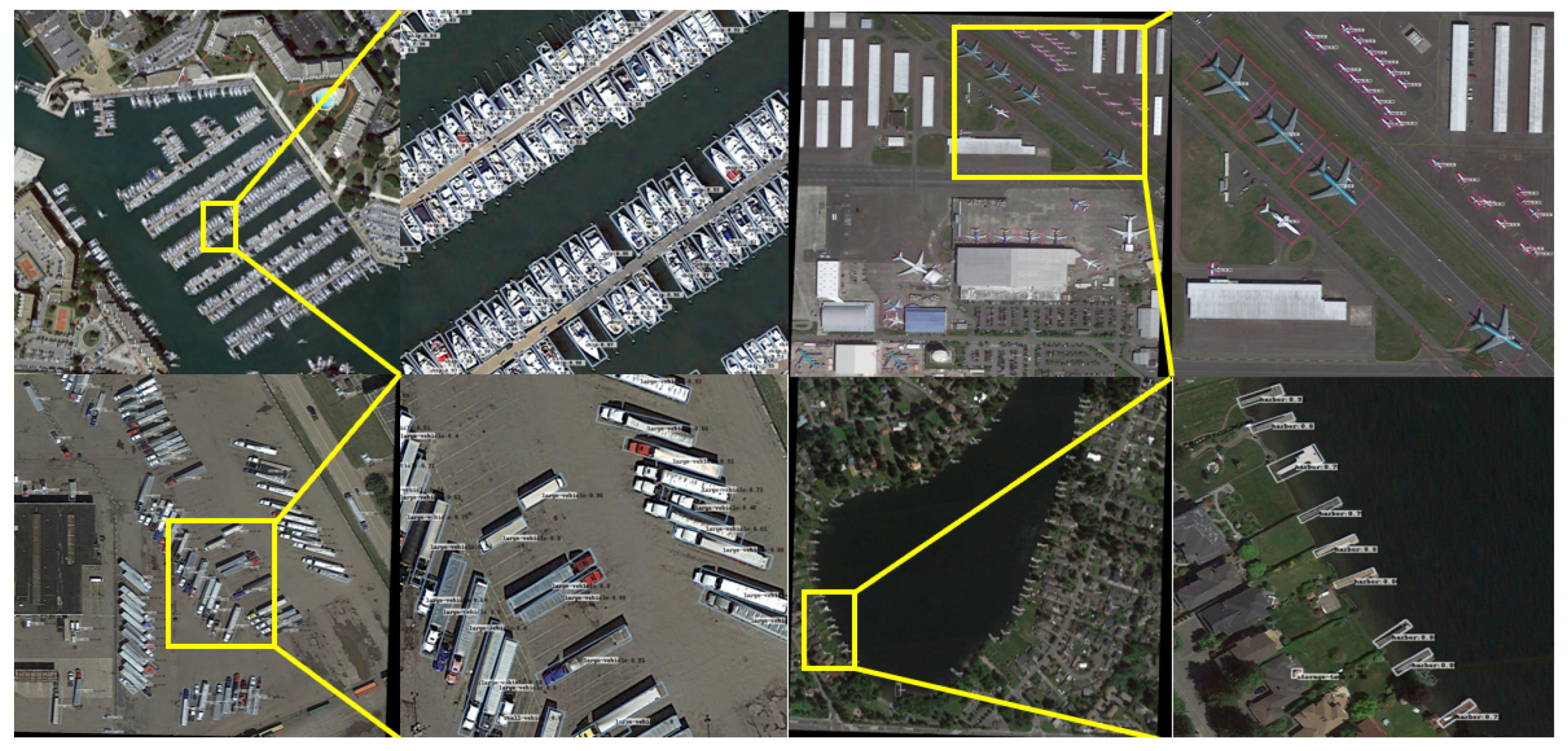
5.8. Experimental Effect
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2015, arXiv:1506.02640. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef]
- Ding, J.; Xue, N.; Xia, G.S.; Bai, X.; Yang, W.; Yang, M.Y.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; et al. Object detection in aerial images: A large-scale benchmark and challenges. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7778–7796. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A high resolution optical satellite image dataset for ship recognition and some new baselines. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Porto, Portugal, 24–26 February 2017; SciTePress: Setubal, Portugal, 2017; Volume 2, pp. 324–331. [Google Scholar]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. YOLOX: Exceeding YOLO Series in 2021. arXiv 2021. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), ICCV ’15, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, L.; Liang, X.; He, K. Is faster R-CNN doing well for pedestrian detection? In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Amsterdam, The Netherlands, 2016; pp. 443–457. [Google Scholar]
- Cheng, B.; Wei, Y.; Shi, H.; Feris, R.; Xiong, J.; Huang, T. Revisiting rcnn: On awakening the classification power of faster rcnn. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 453–468. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. Fcos: Fully convolutional one-stage object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9627–9636. [Google Scholar]
- Zhang, R.; Hang, S.; Sun, Z.; Nie, F.; Wang, R.; Li, X. Anchor-based fast spectral ensemble clustering. Inf. Fusion 2025, 113, 102587. [Google Scholar] [CrossRef]
- Chu, Q.; Li, S.; Chen, G.; Li, K.; Li, X. Adversarial alignment for source free object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 452–460. [Google Scholar]
- Xu, X.; Jiang, Y.; Chen, W.; Huang, Y.; Zhang, Y.; Sun, X. Damo-yolo: A report on real-time object detection design. arXiv 2022, arXiv:2211.15444. [Google Scholar]
- Jing, W.; Lin, J.; Wang, H. Building NAS: Automatic designation of efficient neural architectures for building extraction in high-resolution aerial images. Image Vis. Comput. 2020, 103, 104025. [Google Scholar] [CrossRef]
- Aharon, S.; Louis-Dupont; Masad, O.; Yurkova, K.; Fridman, L.; Lkdci; Khvedchenya, E.; Rubin, R.; Bagrov, N.; Tymchenko, B.; et al. Super-Gradients. 2021. Available online: https://zenodo.org/records/7789328 (accessed on 26 July 2025).
- Pan, M.; Xia, W.; Yu, H.; Hu, X.; Cai, W.; Shi, J. Vehicle Detection in UAV Images via Background Suppression Pyramid Network and Multi-Scale Task Adaptive Decoupled Head. Remote Sens. 2023, 15, 5698. [Google Scholar] [CrossRef]
- Ren, Z.; Yao, K.; Sheng, S.; Wang, B.; Lang, X.; Wan, D.; Fu, W. YOLO-SDH: Improved YOLOv5 using scaled decoupled head for object detection. Int. J. Mach. Learn. Cybern. 2024, 16, 1643–1660. [Google Scholar] [CrossRef]
- Ma, J.; Fu, D.; Wang, D.; Li, Y. A Decoupled Head and Multiscale Coordinate Convolution Detection Method for Ship Targets in Optical Remote Sensing Images. IEEE Access 2024, 12, 59831–59841. [Google Scholar] [CrossRef]
- Katz, M.L.; Karnesis, N.; Korsakova, N.; Gair, J.R.; Stergioulas, N. Efficient GPU-accelerated multisource global fit pipeline for LISA data analysis. Phys. Rev. D 2025, 111, 024060. [Google Scholar] [CrossRef]
- Li, P.; Chen, J.; Lin, B.; Xu, X. Residual spatial fusion network for RGB-thermal semantic segmentation. Neurocomputing 2024, 595, 127913. [Google Scholar] [CrossRef]
- Shit, S.; Roy, B.; Das, D.K.; Ray, D.N. Single Encoder and Decoder-Based Transformer Fusion with Deep Residual Attention for Restoration of Degraded Images and Clear Visualization in Adverse Weather Conditions. Arab. J. Sci. Eng. 2024, 49, 4229–4242. [Google Scholar] [CrossRef]
- Savaştaer, E.F.; Çelik, B.; Çelik, M.E. Automatic detection of developmental stages of molar teeth with deep learning. BMC Oral Health 2025, 25, 465. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, X.; Wang, J.; Wu, R.; Li, X.; Hou, Q.; Cheng, M.M. YOLO-MS: Rethinking multi-scale representation learning for real-time object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 4240–4252. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, Y.; Guo, X.; Ling, X.; Geng, Q. Metal surface defect detection using SLF-YOLO enhanced YOLOv8 model. Sci. Rep. 2025, 15, 11105. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.Y.; Han, J.M. Deep learning (Fast R-CNN)-based evaluation of rail surface defects. Appl. Sci. 2024, 14, 1874. [Google Scholar] [CrossRef]
- Chaudhuri, A. Smart traffic management of vehicles using faster R-CNN based deep learning method. Sci. Rep. 2024, 14, 10357. [Google Scholar] [CrossRef]
- Li, W.; Liu, D.; Li, Y.; Hou, M.; Liu, J.; Zhao, Z.; Guo, A.; Zhao, H.; Deng, W. Fault diagnosis using variational autoencoder GAN and focal loss CNN under unbalanced data. Struct. Health Monit. 2025, 24, 1859–1872. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, W.; Hou, R. Mfil-fcos: A multi-scale fusion and interactive learning method for 2d object detection and remote sensing image detection. Remote Sens. 2024, 16, 936. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, K.; Li, Y.; Liu, Z. Generalized out-of-distribution detection: A survey. Int. J. Comput. Vis. 2024, 132, 5635–5662. [Google Scholar] [CrossRef]
- Liu, C.; Gao, G.; Huang, Z.; Hu, Z.; Liu, Q.; Wang, Y. Yolc: You only look clusters for tiny object detection in aerial images. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13863–13875. [Google Scholar] [CrossRef]
- Hao, M.; Zhang, Z.; Li, L.; Dong, K.; Cheng, L.; Tiwari, P.; Ning, X. Coarse to fine-based image–point cloud fusion network for 3D object detection. Inf. Fusion 2024, 112, 102551. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, Y. KLDet: Detecting tiny objects in remote sensing images via kullback-leibler divergence. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4703316. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, P.; Yan, S.; Wang, X. Inceptionnext: When inception meets convnext. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 5672–5683. [Google Scholar]
- Chen, X.; Li, H.; Wu, Q.; Meng, F.; Qiu, H. Bal-R 2 CNN: High quality recurrent object detection with balance optimization. IEEE Trans. Multimed. 2021, 24, 1558–1569. [Google Scholar] [CrossRef]
- Han, J.; Ding, J.; Xue, N.; Xia, G.S. Redet: A rotation-equivariant detector for aerial object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2786–2795. [Google Scholar]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3det: Refined single-stage detector with feature refinement for rotating object. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 3163–3171. [Google Scholar]
- Guo, J.; Hao, J.; Mou, L.; Hao, H.; Zhang, J.; Zhao, Y. S2A-Net: Retinal structure segmentation in OCTA images through a spatially self-aware multitask network. Biomed. Signal Process. Control 2025, 110, 108003. [Google Scholar] [CrossRef]
- Das, A.; Singh, A.; Nishant; Prakash, S. CapsuleNet: A Deep Learning Model To Classify GI Diseases Using EfficientNet-b7. arXiv 2024. [Google Scholar] [CrossRef]








| m | Operation |
|---|---|
| 0 | Separable convolution |
| 1 | Separable convolution dilation rate = 3 |
| 2 | Separable convolution dilation rate = 6 |
| 3 | Crosslink |
| 4 | Transformable convolution |
| Model | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| AP@IOU = 0.7 (%) | ||||
| Inception | √ | √ | √ | √ |
| ResNet101 | - | √ | √ | √ |
| SPP | - | - | √ | √ |
| FAS | - | - | - | √ |
| Plane | 88.6 | 89.6 | 89.7 | 90.5 |
| Baseball diamond | 76.8 | 85.2 | 85.3 | 87.1 |
| Bridge | 54.6 | 57.5 | 62.4 | 62.5 |
| Ground track field | 69.2 | 70.5 | 74.2 | 82.1 |
| Small vehicle | 78.1 | 71.7 | 77.6 | 78.5 |
| Large vehicle | 77.7 | 77.6 | 81.1 | 82.7 |
| Ship | 87 | 78.1 | 88.3 | 87.2 |
| Tennis court | 91 | 91 | 91.5 | 91 |
| Basketball court | 84 | 85.1 | 83.6 | 88.7 |
| Storage tank | 83.6 | 85.5 | 86.1 | 87.2 |
| Soccer ball field | 58.7 | 67.5 | 68.8 | 69.6 |
| Roundabout | 65.7 | 61.6 | 67.6 | 68.9 |
| Harbor | 75.8 | 76.1 | 82.6 | 85.6 |
| Swimming pool | 70.7 | 79 | 81.1 | 82 |
| Helicopter | 59.4 | 62.9 | 66.1 | 73.2 |
| mAP (%) | 74.8 | 76.2 | 78 | 81 |
| Training Phase | Iteration Range | Description | Learning Rate |
|---|---|---|---|
| Warm-up | 0–20,000 | Warm-up phase | Linearly increases to 0.01 |
| Main Training | 20,000–960,000 | Initial learning rate | 0.01 |
| First Decay | 960,000–1,280,000 | First decay phase | (0.001) |
| Second Decay | 1,280,000–1,600,000 | Second decay phase | (0.0001) |
| Parameter | Value |
|---|---|
| Maximum Iterations | 1,600,000 (20 epochs, 80,000 per epoch) |
| Images per Epoch | 118,000 |
| Batch Size | 8 |
| GPU Count | 2 |
| Optimizer | SGD Momentum (momentum=0.9, epsilon=) |
| Initial Learning Rate | 0.01 () |
| Warmup Iterations | 20,000 (0.25 epochs) |
| Learning Rate Decay Steps | 960,000, 1,280,000, 1,600,000 |
| Learning Rate Decay Factor | 0.1 (0.01 → 0.001 → 0.0001) |
| RPN Classification Loss Weight | 1.0 |
| RPN Regression Loss Weight | 1.0 |
| RPN Balancing Factor | 3.0 |
| SHARE_HEADS | True |
| GRADIENT_CLIPPING_BY_NORM | None |
| MUTILPY_BIAS_GRADIENT | None |
| FAS-FPN Layers | 7 |
| FAS-FPN Channels | 384 |
| FAS-FPN Activation | ReLU |
| Gradient Clipping | Not enabled |
| FAS | DDH | ECS | mAP/% | FPS/Frame |
|---|---|---|---|---|
| - | - | - | 73.2 | 26.2 |
| √ | - | - | 78.6 | 25.8 |
| √ | √ | - | 80.1 | 24.5 |
| √ | - | √ | 79.8 | 25.5 |
| √ | √ | √ | 82.6 | 24.4 |
| Model | BFLOPS/s | DOTA1.0 mAP/% | DOTA1.5 mAP/% | HRSC2016 mAP/% | FPS/Frame |
|---|---|---|---|---|---|
| ResNet-50 | 197.1 | 65.5 | 63.6 | 52.1 | 23.6 |
| ResNet-152 | 243.0 | 67.8 | 68.9 | 58.2 | 17.1 |
| ConvNext-XL [34] | 249.0 | 83.9 | 72.9 | 89.3 | 17.5 |
| Inception-ResNet101 | 204.0 | 82.6 | 79.5 | 89.1 | 24.4 |
| Model | Backbone | DOTA1.0 mAP/% | DOTA1.5 mAP/% | HRSC2016 mAP/% | FPS/Frames Change |
|---|---|---|---|---|---|
| R2CNN [35] | ResNet101 | 72.3 | 67.5 | 79.5 | 5.5 |
| RetinaNet | ResNet101 | 77.4 | 68.7 | 86.3 | 22.4 |
| ReDet [36] | Darknet53 | 78.6 | 72.7 | 82.1 | 24.5 |
| R3Det [37] | ResNet101 | 79.8 | 73.4 | 83.5 | 12.0 |
| FCOS | ResNet101 | 80.3 | 74.1 | 90.3 | 17.5 |
| S2A-Net [38] | ResNet101 | 81.4 | 76.3 | 81.2 | 2.0 |
| EfficientNet-B7 [39] | ResNet101 | 62.1 | 53.2 | 80.7 | 12.8 |
| Oriented R-CNN | ResNet101 | 81.8 | 78.4 | 86.2 | 21.1 |
| Ours | FAS-Inception-ResNet101 | 82.6 | 79.5 | 89.1 | 24.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Zheng, B.; Shen, W. Research on Oriented Object Detection in Aerial Images Based on Architecture Search with Decoupled Detection Heads. Appl. Sci. 2025, 15, 8370. https://doi.org/10.3390/app15158370
Kang Y, Zheng B, Shen W. Research on Oriented Object Detection in Aerial Images Based on Architecture Search with Decoupled Detection Heads. Applied Sciences. 2025; 15(15):8370. https://doi.org/10.3390/app15158370
Chicago/Turabian StyleKang, Yuzhe, Bohao Zheng, and Wei Shen. 2025. "Research on Oriented Object Detection in Aerial Images Based on Architecture Search with Decoupled Detection Heads" Applied Sciences 15, no. 15: 8370. https://doi.org/10.3390/app15158370
APA StyleKang, Y., Zheng, B., & Shen, W. (2025). Research on Oriented Object Detection in Aerial Images Based on Architecture Search with Decoupled Detection Heads. Applied Sciences, 15(15), 8370. https://doi.org/10.3390/app15158370






