Comparative Analysis of Fracture Mechanics Parameters for Wrought and SLM-Produced Ti-6Al-7Nb Alloy
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
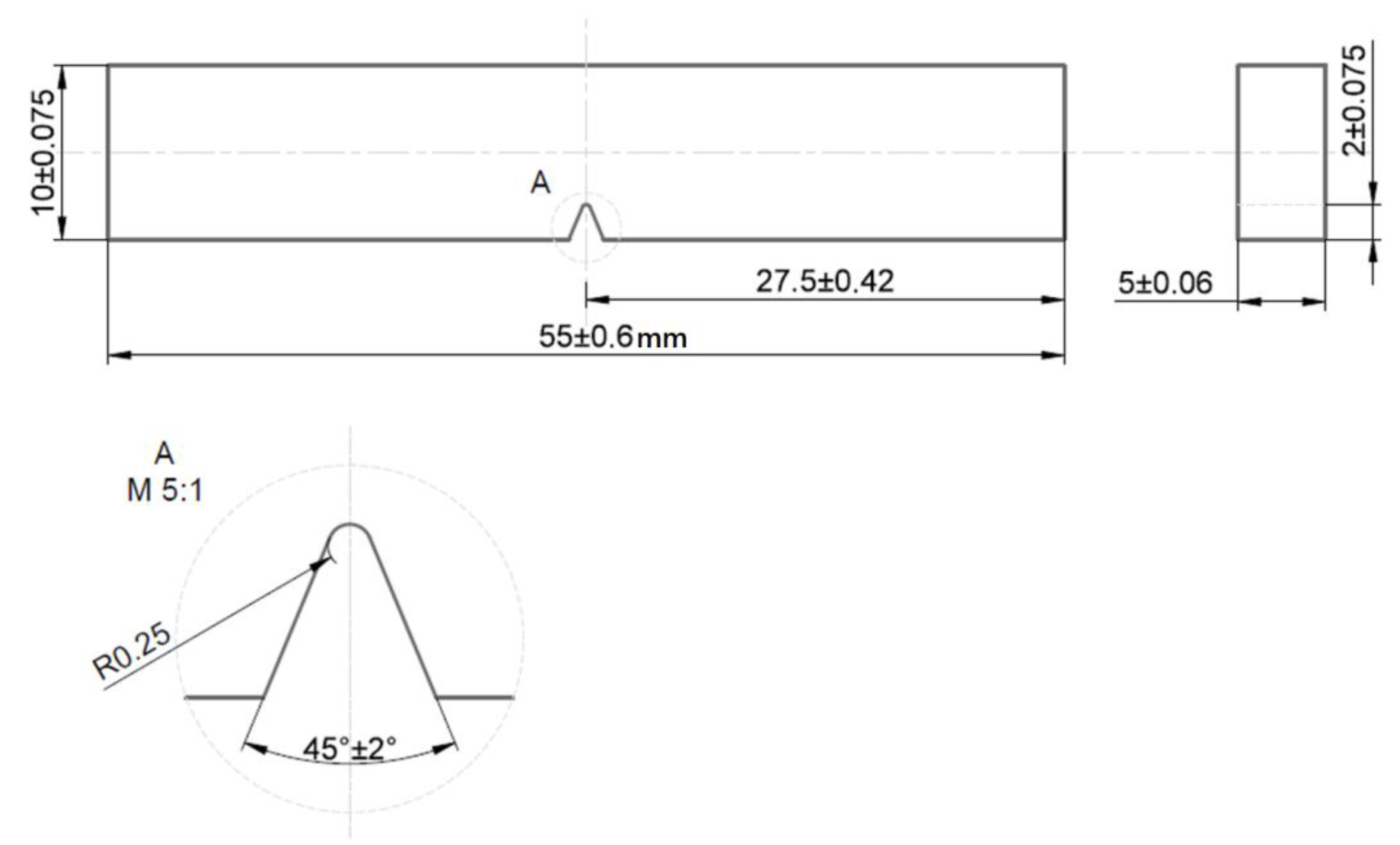
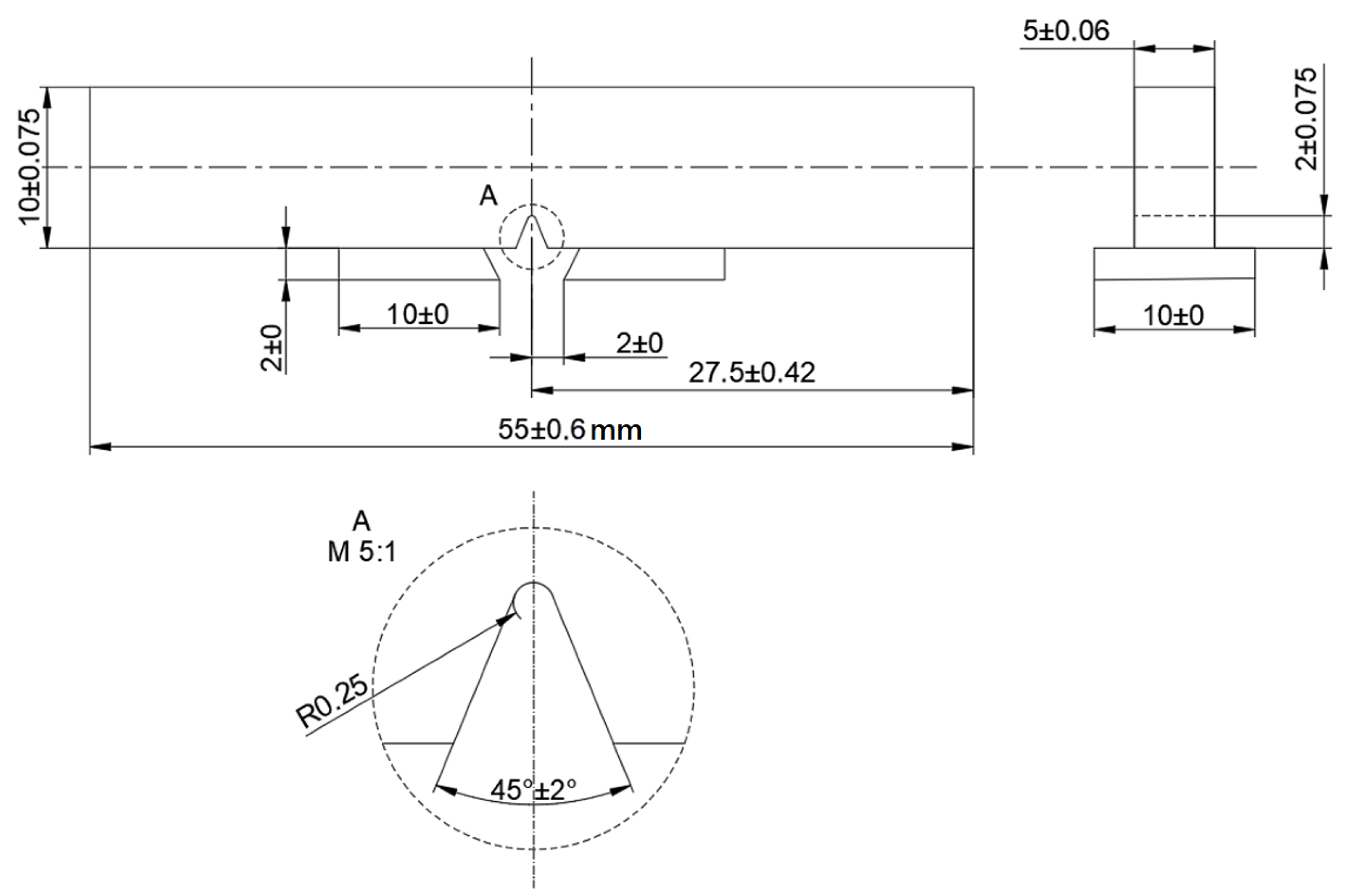
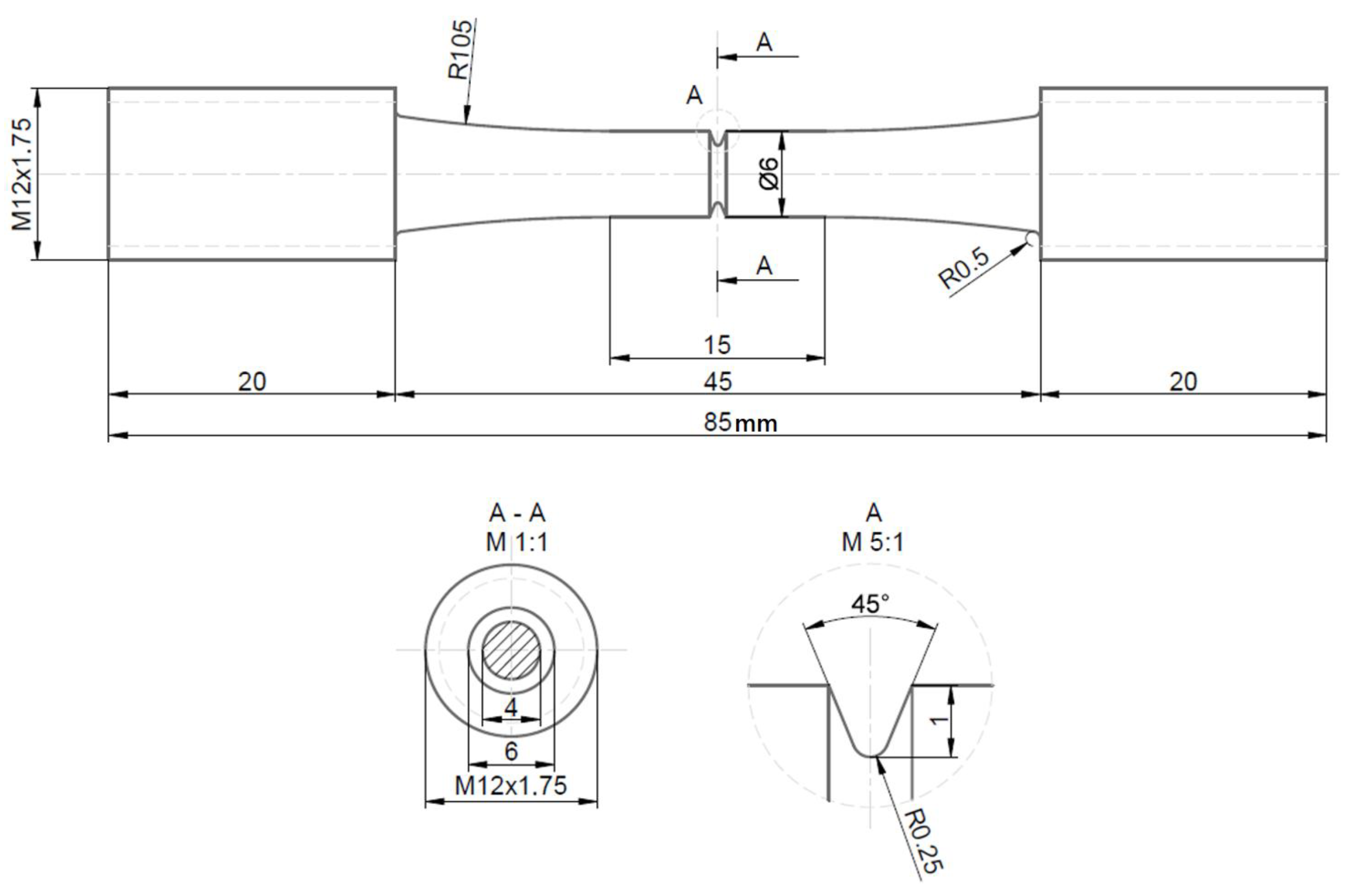
2.1. Test Specimen Geometry Determination
2.2. Crack Growth Curve Determination Procedure
2.3. Fracture Toughness and Resistance Curves Determination Procedure
- KI—stress intensity factor, MPam0.5
- D—test specimen outer diameter, m
- d—diameter of the test specimen notch root after failure, mm
- F—tensile force applied to test specimen, N,
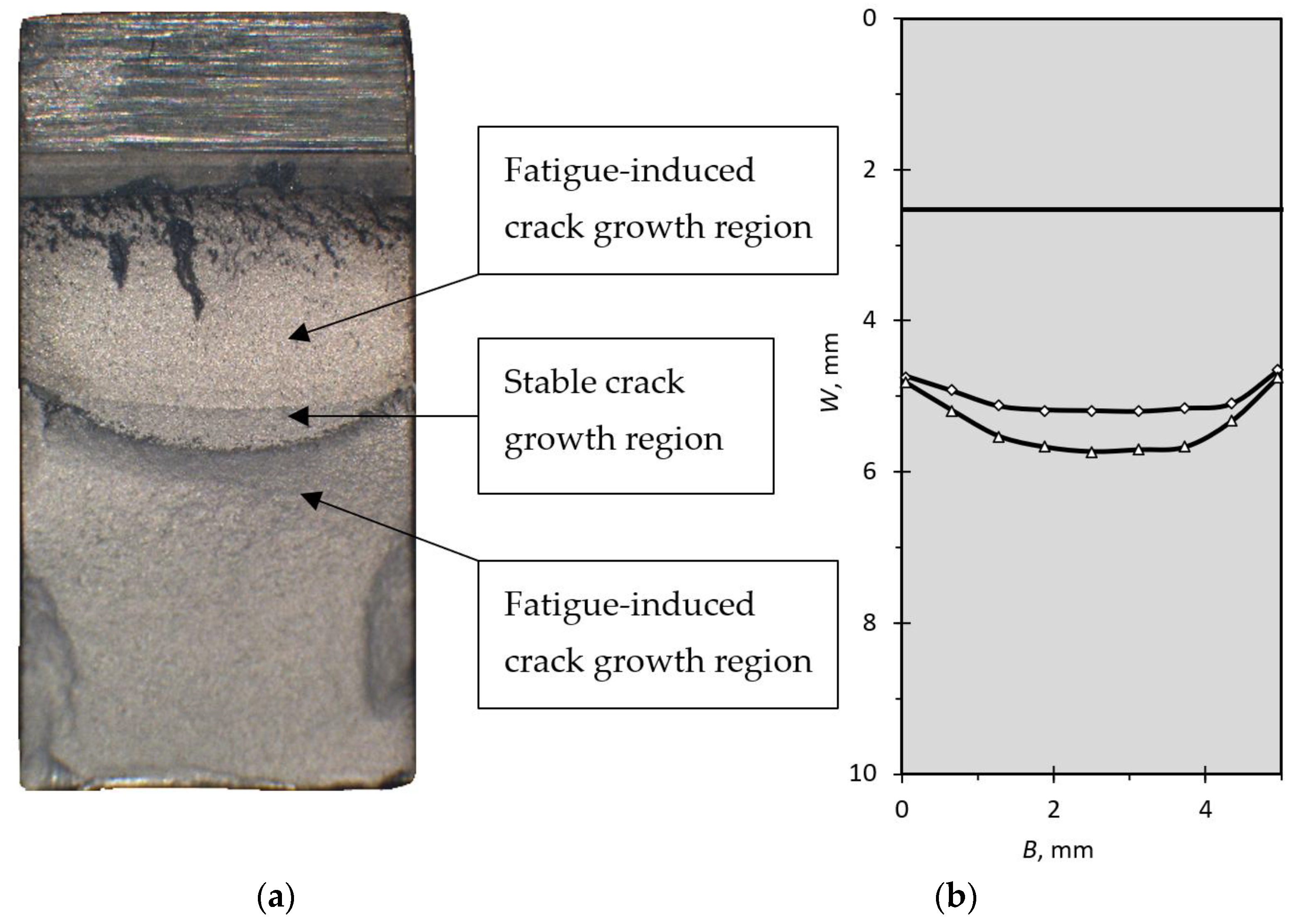
- using the maximum force applied to the test specimen, it is possible to calculate the fracture toughness value of the material, i.e., for F = Fmax, KI = Kc. This experiment was performed on Instron 1255 universal testing machine. The fracture surfaces of the specimens were observed using a microscope at 20× magnification, and the notch root diameters were measured after fracture, as presented in the Results section.
2.4. Experimental Limitations
3. Results
3.1. Threshold Stress Intensity Factor
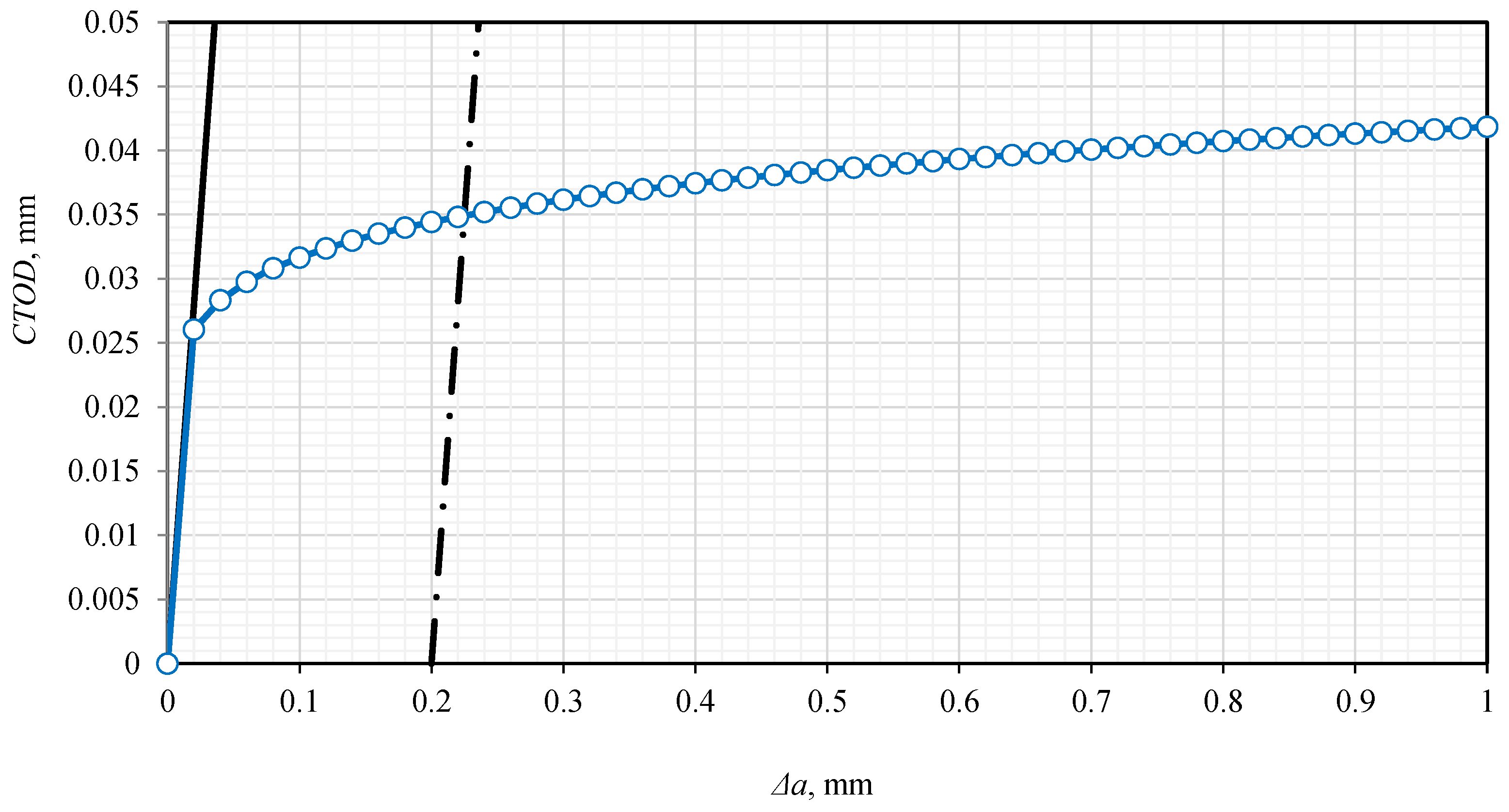
3.2. Fracture Toughness and Resistance Curves According to ASTM E1820
3.3. Fracture Toughness Determination Using Cylindrical Test Specimen
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SLM | Selective Laser Melting |
| AM | Additive Manufacturing |
| ISO | International Organization for Standardization |
| ASTM | American Society for Testing and Materials |
| CMOD | Crack Mouth Opening Displacement |
| LLD | Load Line Displacement |
| SEN | Scanning Electron Microscopy |
References
- Cosma, C.; Drstvensek, I.; Berce, P.; Prunean, S.; Legutko, S.; Popa, C.; Balc, N. Physical–Mechanical Characteristics and Microstructure of Ti6Al7Nb Lattice Structures Manufactured by Selective Laser Melting. Materials 2020, 13, 4123. [Google Scholar] [CrossRef] [PubMed]
- Delshadmanesh, M. Fatigue Investigations of Metallic Biomaterials Based on Ti-Nb and Co-Cr. 01 11 2018. Available online: https://repositum.tuwien.at/handle/20.500.12708/7333 (accessed on 2 June 2025).
- Hein, M.; Kokalj, D.; Dias, N.F.L.; Stangier, D.; Oltmanns, H.; Pramanik, S.; Kietzmann, M.; Hoyer, K.-P.; Meißner, J.; Tillman, W.; et al. Low Cycle Fatigue Performance of Additively Processed and Heat-Treated Ti-6Al-7Nb Alloy for Biomedical Applications. Metals 2022, 12, 122. [Google Scholar] [CrossRef]
- Laskowska, D.; Bałasz, B.; Zawadka, W. Microstructure and Mechanical Properties of As-Built Ti-6Al-4V and Ti-6Al-7Nb Alloys Produced by Selective Laser Melting Technology. Materials 2024, 17, 4604. [Google Scholar] [CrossRef] [PubMed]
- Gür, Y. Deformation Behaviour and Energy Absorption of 3D Printed Polymeric Gyroid Structures. Teh. Vjesn.—Tech. Gaz. 2024, 31, 1582–1588. [Google Scholar] [CrossRef]
- Pinheiro, T.S.; Gallego, J.; Bolfarini, C.; Kiminami, C.S.; Junior, A.M.J.; Botta, W.J. Microstructural Evolution of Ti-6Al-7Nb Alloy During High Pressure Torsion. Mater. Res. 2012, 15, 792–795. [Google Scholar] [CrossRef]
- Fellah, M.; Labaïz, M.; Assala, O.; Dekhil, L.; Taleb, A.; Rezag, H.; Iost, A. Tribological behavior of Ti-6Al-4V and Ti-6Al-7Nb Alloys for Total Hip Prosthesis. Adv. Tribol. 2014, 2014, 451387. [Google Scholar] [CrossRef]
- Tuninetti, V.; Fuentes, G.; Oñate, A.; Narayan, S.; Celentano, D.; García-Herrera, C.; Menacer, B.; Pincheira, G.; Garrido, C.; Valle, R. Computational Shape Design Optimization of Femoral Implants: Towards Efficient Forging Manufacturing. Appl. Sci. 2024, 18, 8289. [Google Scholar] [CrossRef]
- Hijazi, K.; Dixon, J.; Armstrong, J.; Rizkalla, A. Titanium Alloy Implants with Lattice Structures for Mandibular Reconstruction. Materials 2023, 17, 140. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhao, Q.; Fu, J.; Hu, Y.; Liang, J.; Li, J.; Xu, W. The design of oxidation resistant Ni superalloys for additive manufacturing. Addit. Manuf. 2025, 97, 104616. [Google Scholar] [CrossRef]
- Squillaci, L.; Neikter, M.; Hansson, T.; Pederson, R.; Moverare, J. Microstructure and mechanical properties of Ti-6Al-4V alloy fabricated using powder bed fusion—Laser beam additive manufacturing process: Effect of hot isostatic pressing. Mater. Sci. Eng. A 2025, 931, 148226. [Google Scholar] [CrossRef]
- Sidambe, A.T. Biocompatibility of Advanced Manufactured Titanium Implants—A Review. Materials 2014, 7, 8168–8188. [Google Scholar] [CrossRef] [PubMed]
- Novak, R.; Valjak, F.; Bojčetić, N.; Šercer, M. Design Principle for Additive Manufacturing: Direct Metal Sintering. Teh. Vjesn.—Tech. Gaz. 2023, 30, 937–944. [Google Scholar] [CrossRef]
- Taherzadeh, P.; Kelleci, K.; Özer, S. Biomechanical Effects of the Implant Designed for Posterior Dynamic Stabilization of the Lumbar Spine (L4–L5): A Finite Element Analysis Study. Teh. Vjesn.—Tech. Gaz. 2024, 31, 193–199. [Google Scholar] [CrossRef]
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H. Effects of Heat Accumulation on Microstructure and Mechanical Properties of Ti6Al4V Alloy Deposited by Wire Arc Additive Manufacturing. Addit. Manuf. 2018, 23, 151–160. [Google Scholar] [CrossRef]
- Cao, L.; Lu, R.; Dou, Z.; Zheng, M.; Han, X.; Hau, Y.; Zhang, L.; Zhang, J.; Liu, B.; Li, X. Understanding the influence of high-strength submicron precipitate on the fracture performance of additively-manufactured aluminum alloy. Int. J. Plast. 2025, 188, 104306. [Google Scholar] [CrossRef]
- ISO 148-1:2009; Metallic Materials—Charpy Pendulum Impact Test—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2009.
- ASTM E466-96; Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2021.
- Jelaska, D. Fundamentals of Fracture Mechanics, Part 2: Crack Propagation. Available online: https://bib.irb.hr/datoteka/121375.Cl-MehLoma2.pdf (accessed on 2 June 2025).
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 6. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Broek, D. Elementary Engineering Fracture Mechanics; Martinus Nijhoff Publishers: Dodrecht, The Netherlands, 1986. [Google Scholar]
- ASTM E1820; Standard Test Method for Measurement of Fracture Toughness. ASTM International: West Conshohocken, PA, USA, 2019.
- Schwalbe, K.; Neal, B.; Heerens, J. The GKSS Test Procedure for Determining the Fracture Behaviour of Materials; GKSS Forschungszentrum Geesthacht GmbH: Geesthacht, Germany, 1994. [Google Scholar]
- Gubeljak, N. Fracture Mechanics. University of Maribor, Faculty of Mechanical Engineering: Maribor, Slovenia, 2008. [Google Scholar]
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Sci. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Tuninetti, V.; Sepúlveda, H.; Betaieb, E.; Pincheira, G.; Gilles, G.; Duchêne, L.; Habraken, A.M. Accurate numerical prediction of ductile fracture and micromechanical damage evolution for Ti6Al4V alloy. Comput. Mech. 2024, 73, 177–198. [Google Scholar] [CrossRef]
- Riemer, A.; Leuders, S.; Thöne, M.; Richard, H.A.; Tröster, T.; Niendorf, T. On the fatigue crack growth behavior in 316L stainless steel manufactured by selective laser melting. Eng. Fract. Mech. 2014, 120, 15–25. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Q.; Zhou, Y.; Wang, D.; Wang, L.; Wahab, M.A. Fretting fatigue crack initiation and propagation behaviours of Ti6Al4V alloy coated by functionally graded material. Compos. Struct. 2024, 343, 118285. [Google Scholar] [CrossRef]








| ΔK, MPam0.5 | da/dN, nm/Cycle | a, mm | N, - | R, - | ΔM, Nm | Mm, Nm |
|---|---|---|---|---|---|---|
| 20 | 0 | 2.12 | 367,294 | 0.1 | 20.61 | 12.60 |
| 18.99 | 130.517 | 2.171 | 404,365 | 0.1 | 19.31 | 11.80 |
| 18.76 | 122.77 | 2.184 | 404,466 | 0.1 | 19.01 | 11.62 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 15 | 150.081 | 2.407 | 405,952 | 0.1 | 14.35 | 8.77 |
| 14.84 | 155.135 | 2.418 | 406,025 | 0.1 | 14.14 | 8.64 |
| 14.68 | 129.771 | 2.429 | 406,108 | 0.1 | 13.95 | 8.53 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 10.02 | 87.253 | 2.811 | 411,791 | 0.1 | 8.64 | 5.28 |
| 9.91 | 31.133 | 2.822 | 412,137 | 0.1 | 8.52 | 5.21 |
| 9.81 | 42.583 | 2.832 | 412,388 | 0.1 | 8.41 | 5.14 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 6.6 | 1.235 | 3.228 | 517,276 | 0.1 | 5.11 | 3.12 |
| 6.53 | 0.901 | 3.238 | 528,412 | 0.1 | 5.05 | 3.09 |
| 6.47 | 0.919 | 3.248 | 539,289 | 0.1 | 4.99 | 3.05 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 4.55 | 0.205 | 3.599 | 1,528,913 | 0.1 | 3.2 | 1.96 |
| 4.51 | 0.194 | 3.609 | 1,580,407 | 0.1 | 3.16 | 1.93 |
| 4.46 | 0.16 | 3.619 | 1,642,995 | 0.1 | 3.12 | 1.91 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 3.88 | 0.038 | 3.762 | 3,202,639 | 0.1 | 2.61 | 1.60 |
| 3.84 | 0.029 | 3.772 | 3,547,316 | 0.1 | 2.58 | 1.58 |
| 3.84 | 0.001 | 3.774 | 6,106,690 | 0.1 | 2.58 | 1.58 |
| ΔK, MPam0.5 | da/dN, nm/Cycle | a, mm | N, - | R, - | ΔM, Nm | Mm, Nm |
|---|---|---|---|---|---|---|
| 13 | 0 | 2.011 | 12,542 | 0.1 | 13.79 | 8.43 |
| 12.54 | 804.794 | 2.047 | 27,878 | 0.1 | 13.17 | 8.05 |
| 12.34 | 618.045 | 2.063 | 27,904 | 0.1 | 12.9 | 7.88 |
| 12.05 | 418.945 | 2.087 | 27,949 | 0.1 | 12.53 | 7.66 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 9.34 | 93.277 | 2.267 | 30,997 | 0.1 | 9.26 | 5.66 |
| 9.24 | 73.037 | 2.278 | 31,148 | 0.1 | 9.13 | 5.58 |
| 9.14 | 47.136 | 2.289 | 31,375 | 0.1 | 9.01 | 5.51 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 7.38 | 10.214 | 2.382 | 44,671 | 0.1 | 7.1 | 4.34 |
| 7.3 | 14.362 | 2.392 | 45,372 | 0.1 | 7.01 | 4.28 |
| 7.23 | 8.162 | 2.402 | 46,611 | 0.1 | 6.92 | 4.23 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 5.42 | 1.392 | 2.691 | 185,318 | 0.1 | 4.82 | 2.95 |
| 5.36 | 0.907 | 2.702 | 197,320 | 0.1 | 4.75 | 2.9 |
| 5.31 | 0.801 | 2.712 | 209,809 | 0.1 | 4.7 | 2.87 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 4.63 | 0.064 | 2.852 | 866,415 | 0.1 | 3.95 | 2.41 |
| 4.58 | 0.045 | 2.862 | 1,089,085 | 0.1 | 3.9 | 2.38 |
| 4.53 | 0.001 | 2.872 | 2,460,570 | 0.1 | 3.85 | 2.35 |
| Production Process | Kc, MPam0.5 |
|---|---|
| Drawing (Specimen 1) | 84 |
| Drawing (Specimen 2) | 83.5 |
| Selective Laser Melting | 21.9 |
| Production Process | F, N | D, mm | D, mm | Kc, MPam0.5 |
|---|---|---|---|---|
| Drawing | 23,114 | 5.95 | 3.91 | 61.34 |
| Selective laser melting | 9468 | 5.78 | 3.92 | 24.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gelo, I.; Kozak, D.; Gubeljak, N.; Vuherer, T.; Konjatić, P.; Katinić, M. Comparative Analysis of Fracture Mechanics Parameters for Wrought and SLM-Produced Ti-6Al-7Nb Alloy. Appl. Sci. 2025, 15, 8308. https://doi.org/10.3390/app15158308
Gelo I, Kozak D, Gubeljak N, Vuherer T, Konjatić P, Katinić M. Comparative Analysis of Fracture Mechanics Parameters for Wrought and SLM-Produced Ti-6Al-7Nb Alloy. Applied Sciences. 2025; 15(15):8308. https://doi.org/10.3390/app15158308
Chicago/Turabian StyleGelo, Ivan, Dražan Kozak, Nenad Gubeljak, Tomaž Vuherer, Pejo Konjatić, and Marko Katinić. 2025. "Comparative Analysis of Fracture Mechanics Parameters for Wrought and SLM-Produced Ti-6Al-7Nb Alloy" Applied Sciences 15, no. 15: 8308. https://doi.org/10.3390/app15158308
APA StyleGelo, I., Kozak, D., Gubeljak, N., Vuherer, T., Konjatić, P., & Katinić, M. (2025). Comparative Analysis of Fracture Mechanics Parameters for Wrought and SLM-Produced Ti-6Al-7Nb Alloy. Applied Sciences, 15(15), 8308. https://doi.org/10.3390/app15158308











