Accelerated Tensor Robust Principal Component Analysis via Factorized Tensor Norm Minimization
Abstract
1. Introduction
2. Notations and Preliminaries
3. Related Works
4. Proposed Algorithm
4.1. Optimization Model
4.2. Solution Algorithm
- (1)
- Computation of .Finding the optimal at iteration k, while keeping the other variables fixed, involves solving the following sub-problem derived from (17) such thatwhere . By taking the derivative of (19) with respect to , and rearranging terms, we obtain the closed-form solution for as follows:where denotes the identity tensor.
- (2)
- Computation of .Similar to (19), we fix and , and then formulate the sub-problem for updating such thatBy taking the derivative of (21) with respect to , and rearranging terms, we obtain the closed-form solution for such that
- (3)
- Computation of .The optimal sub-problem for updating , while keeping the other terms in (17) fixed, is defined as follows:where . Since the second term in (23) is convex and differentiable, the closed-form solution of (23) can be obtained using the soft-thresholding operator defined as [24]where denotes the th element of . Thus, the update for is obtained by applying soft-thresholding as .
| Algorithm 1 |
4.3. Computational Complexity
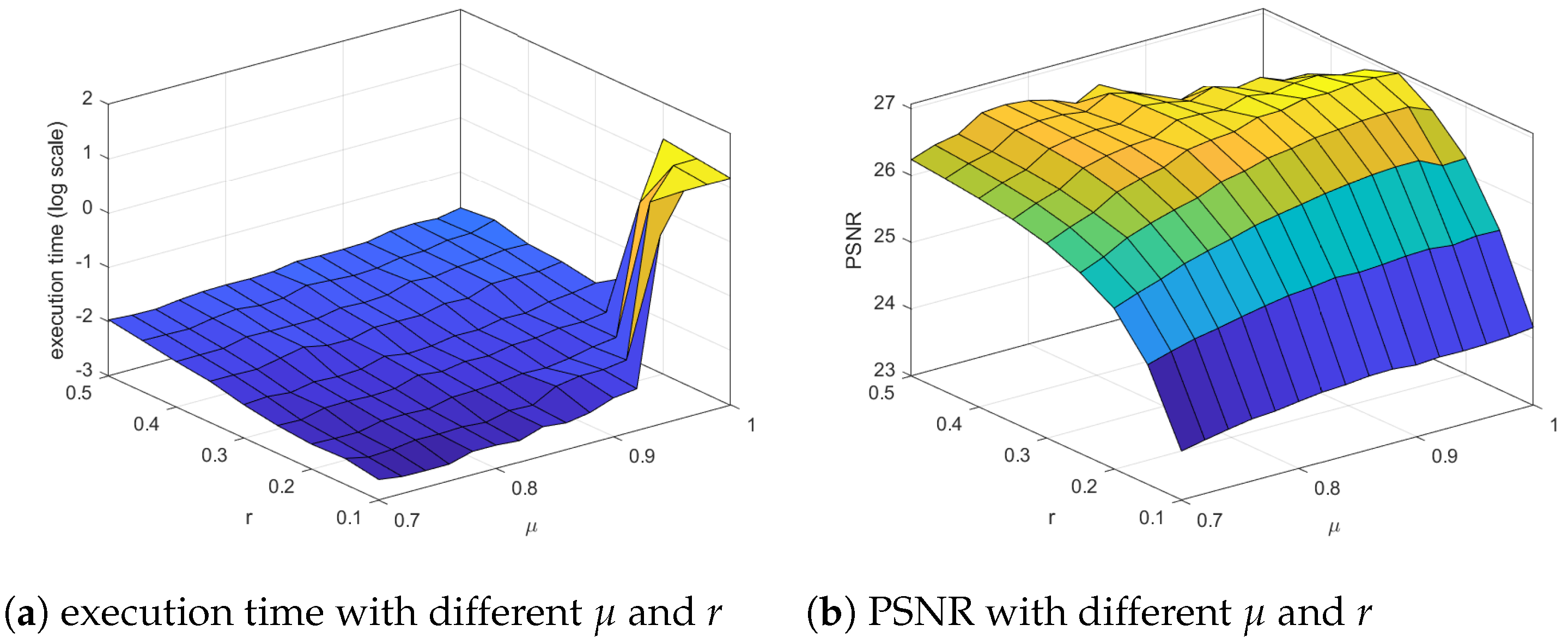
5. Experimental Results
5.1. Color Image Recovery
5.2. Background Subtraction
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TRPCA | tensor robust principal component analysis |
| T-SVD | tensor singular value decomposition |
| T-product | tensor–tensor product |
References
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust Principal Component Analysis? J. ACM 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Bouwmans, T.; Javed, S.; Zhang, H.; Lin, Z.; Otazo, R. On the Applications of Robust PCA in image and Video Processing. Proc. IEEE 2018, 160, 1427–1457. [Google Scholar] [CrossRef]
- Cao, W.; Wang, Y.; Sun, J.; Meng, D.; Yan, C.; Cichocki, A.; Xu, Z. Total Variation Regularized Tensor RPCA for Background Subtraction from Compressive Measurement. IEEE Trans. Image Proc. 2016, 25, 4075–4090. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Liu, J.; Gao, Y.; Shang, J. DSTPCA: Double-Sparse Constrained Tensor Principal Component Analysis Method for Feature Selection. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 1481–1491. [Google Scholar] [CrossRef]
- Markowitz, S.; Snyder, C.; Eldar, Y.C.; Do, M.N. Mutilmodal unrolled robust RPCA for background foreground separation. IEEE Trans. Image Proc. 2022, 31, 3553–3564. [Google Scholar] [CrossRef]
- Zhong, G.; Pun, C.M. RPCA-induced self-representation for subspace clustering. Neurocomputing 2021, 437, 249–260. [Google Scholar] [CrossRef]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decomposition and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Hillar, J.C.; Lim, L.H. Most tensor problems are NP-Hard. J. ACM 2013, 60, 1–39. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Horesh, L.; Avron, H.; Newman, E. Tensor-tensor algebra for optimal representation and compression of multiway data. Proc. Natl. Acad. Sci. USA 2021, 118, e205851118. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis with a New Tensor Nuclear Norm. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 925–938. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M.E. Novel methods for multilinear data completion and de-noising based on tensor-SVD. IEEE Conf. Comput. Vis. Pattern Recognit. 2014, 3842–3849. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, P.; Xia, W.; Xie, D.; Gao, X.; Tao, D. Enhanced Tensor RPCA and its Application. IEEE Trans. Pattern Anal. Machine Intell. 2021, 43, 2133–2140. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Tong, T.; Ma, C.; Chi, Y. Fast and provable tensor robust principal component analysis via scaled gradient descent. Inform. Inference J. IMA 2023, 12, iaad019. [Google Scholar] [CrossRef]
- Qui, H.; Wang, Y.; Tang, S.; Meng, D.; Yao, Q. Fast and Provable Nonconvex Tensor RPCA. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MI, USA, 17–23 July 2022. [Google Scholar]
- Geng, X.; Guo, Q.; Hui, S.; Yang, M.; Zhang, C. Tensor robust PCA with nonconvex and nonlocal regularization. Comput. Vision Image Understand 2024, 243, 104007. [Google Scholar] [CrossRef]
- Qui, Y.; Zhou, G.; Huang, Z.; Zhao, Q.; Xie, S. Efficient Tensor Robust PCA Under Hybrid Model of Tucker and Tensor Train. IEEE Sig. Proc. Lett. 2022, 29, 627–631. [Google Scholar]
- Cai, H.; Chao, Z.; Huang, L.; Needell, D. Fast Robust Tensor Principal Component Analysis via Fiber CUR Decomposition. IEEE/CVF Int. Conf. Comput. Vision Work. 2021, 189–197. [Google Scholar] [CrossRef]
- Salut, M.M.; Anderson, D.V. Online Tensor Robust Principal Component Analysis. IEEE Access 2022, 10, 69354–69363. [Google Scholar] [CrossRef]
- Hastie, T.; Mazumder, R.; Lee, J.D.; Zadeh, R. Matrix Completion and Low-Rank SVD via Fast Alternating Least Squares. J. Machin. Learn. Res. 2015, 16, 3367–3402. [Google Scholar]
- Mazumder, R.; Hastie, T.; Tibshirani, R. Spectral Regularization Algorithms for Learning Large Incomplete Matrices. J. Machine Learn. Res. 2010, 11, 2287–2322. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, C.; Qian, J.; Zhang, B.; Xu, C.; Yang, J. Efficient recovery of low-rank via double nonconvex nonsmooth rank minimization. IEEE Trans. Neural Net. Learn. Syst. 2019, 30, 2916–2925. [Google Scholar] [CrossRef]
- Bouwmans, T.; Zahzah, E.H. Robust PCA via Principal Component Pursuit: A review for a comparative evaluation in video surveillance. Comput. Vision Image Understand 2014, 122, 22–34. [Google Scholar] [CrossRef]




| Noise | Iterations | Execution Time | PSNR (dB) | FSIM | |
|---|---|---|---|---|---|
| 10% | noisy image | - | - | 18.0072 | 0.8318 |
| TRPCAAL | 9.00 | 0.0404 | 25.6008 | 0.9305 | |
| FTTNN | 27.00 | 0.1343 | 23.8266 | 0.8816 | |
| IRCUR | 5.95 | 1.1376 | 22.9337 | 0.8581 | |
| TRPCA_TNN | 59.45 | 0.2261 | 23.5337 | 0.9051 | |
| N-TRPCA | - | 1.1046 | 25.4216 | 0.9369 | |
| EATP-DCT | 12.30 | 0.0494 | 22.6369 | 0.8710 | |
| 20% | noisy image | - | - | 14.9630 | 0.7333 |
| TRPCAAL | 11.00 | 0.0426 | 22.0561 | 0.8594 | |
| FTTNN | 27.00 | 0.1376 | 20.7689 | 0.8095 | |
| IRCUR | 5.95 | 1.1420 | 19.8246 | 0.7855 | |
| TRPCA_TNN | 58.75 | 0.2232 | 21.9983 | 0.8615 | |
| N-TRPCA | - | 1.3306 | 23.2304 | 0.8950 | |
| EATP-DCT | 11.70 | 0.0484 | 20.5974 | 0.8285 | |
| 40% | noisy image | - | - | 11.9594 | 0.6209 |
| TRPCAAL | 12.90 | 0.0240 | 17.3287 | 0.7286 | |
| FTTNN | 25.00 | 0.1144 | 17.5832 | 0.7196 | |
| IRCUR | 5.85 | 1.1113 | 16.5159 | 0.6955 | |
| TRPCA_TNN | 58.55 | 0.2312 | 16.9219 | 0.7254 | |
| N-TRPCA | - | 1.1406 | 18.8762 | 0.7780 | |
| EATP-DCT | 11.45 | 0.0442 | 16.0244 | 0.7030 |
| Noise | Iterations | Execution Time | PSNR (dB) | FSIM | |
|---|---|---|---|---|---|
| 10% | noisy image | - | - | 17.4030 | 0.7873 |
| TRPCAAL | 7.00 | 0.1922 | 30.8806 | 0.9564 | |
| FTTNN | 26.00 | 0.3211 | 26.5445 | 0.8668 | |
| IRCUR | 5.95 | 3.2608 | 26.0213 | 0.8629 | |
| TRPCA_TNN | 58.10 | 1.0414 | 28.1301 | 0.9327 | |
| N-TRPCA | - | 5.0506 | 32.2581 | 0.9691 | |
| EATP-DCT | 19.70 | 0.3506 | 26.8569 | 0.8964 | |
| 20% | noisy image | - | - | 14.3960 | 0.6763 |
| TRPCAAL | 12.00 | 0.1444 | 27.0307 | 0.9083 | |
| FTTNN | 26.00 | 0.3311 | 24.6861 | 0.8249 | |
| IRCUR | 5.90 | 3.2266 | 23.1291 | 0.7837 | |
| TRPCA_TNN | 58.10 | 1.0400 | 26.4528 | 0.9040 | |
| N-TRPCA | - | 5.0613 | 29.3179 | 0.9409 | |
| EATP-DCT | 19.05 | 0.3411 | 23.8989 | 0.8517 | |
| 40% | noisy image | - | - | 11.4025 | 0.5574 |
| TRPCAAL | 14.00 | 0.1090 | 21.4635 | 0.7780 | |
| FTTNN | 24.00 | 0.2807 | 19.4878 | 0.6968 | |
| IRCUR | 5.85 | 2.3384 | 17.9545 | 0.6502 | |
| TRPCA_TNN | 57.60 | 1.0468 | 20.0816 | 0.7619 | |
| N-TRPCA | - | 5.0344 | 23.6163 | 0.8286 | |
| EATP-DCT | 14.45 | 0.2787 | 15.3644 | 0.6345 |
| Noise | Iterations | Execution Time | PSNR (dB) | FSIM | |
|---|---|---|---|---|---|
| 10% | noisy image | - | - | 18.6444 | 0.8690 |
| TRPCAAL | 8.00 | 0.3435 | 37.7254 | 0.9915 | |
| FTTNN | 26.00 | 1.0196 | 33.9594 | 0.9725 | |
| IRCUR | 6.80 | 16.1834 | 33.5131 | 0.9698 | |
| TRPCA_TNN | 58.05 | 4.3278 | 35.6128 | 0.9838 | |
| N-TRPCA | - | 19.4259 | 42.1522 | 0.9976 | |
| EATP-DCT | 24.10 | 1.4197 | 35.2786 | 0.9740 | |
| 20% | noisy image | - | - | 15.6322 | 0.7935 |
| TRPCAAL | 13.15 | 0.5223 | 34.3571 | 0.9830 | |
| FTTNN | 25.00 | 0.8425 | 29.5879 | 0.9186 | |
| IRCUR | 5.90 | 10.6101 | 28.1123 | 0.9047 | |
| TRPCA_TNN | 57.25 | 4.2798 | 33.0207 | 0.9730 | |
| N-TRPCA | - | 19.4864 | 38.8358 | 0.9940 | |
| EATP-DCT | 27.35 | 1.5598 | 33.9489 | 0.9716 | |
| 40% | noisy image | - | - | 12.6272 | 0.6913 |
| TRPCAAL | 17.10 | 0.5034 | 27.0085 | 0.9195 | |
| FTTNN | 24.00 | 0.7682 | 23.6106 | 0.8241 | |
| IRCUR | 19.20 | 18.1779 | 24.3123 | 0.8327 | |
| TRPCA_TNN | 56.60 | 4.3993 | 24.7224 | 0.9139 | |
| N-TRPCA | - | 20.2492 | 31.5374 | 0.9640 | |
| EATP-DCT | 44.80 | 2.3762 | 20.3844 | 0.8389 |
| Noise | Iterations | Execution Time | PSNR (dB) | FSIM | |
|---|---|---|---|---|---|
| 10% | noisy image | - | - | 14.5079 | 0.0965 |
| TRPCAAL | 65.95 | 0.6039 | 29.6132 | 0.9305 | |
| FTTNN | 20.00 | 0.2796 | 4.7797 | 0.0898 | |
| IRCUR | 22.25 | 10.0694 | 15.5529 | 0.6053 | |
| TRPCA_TNN | 63.00 | 1.2621 | 12.9168 | 0.6503 | |
| N-TRPCA | - | 6.2646 | 32.3481 | 0.9704 | |
| EATP-DCT | 24.25 | 0.3680 | 12.9846 | 0.3860 | |
| 20% | noisy image | - | - | 11.5019 | 0.0263 |
| TRPCAAL | 67.45 | 0.6158 | 27.1214 | 0.9012 | |
| FTTNN | 20.00 | 0.2926 | 4.5666 | 0.0615 | |
| IRCUR | 21.35 | 9.6075 | 15.0562 | 0.5743 | |
| TRPCA_TNN | 62.15 | 1.2326 | 10.6987 | 0.5592 | |
| N-TRPCA | - | 6.2572 | 29.5371 | 0.9449 | |
| EATP-DCT | 23.15 | 0.3483 | 8.9972 | 0.1999 | |
| 40% | noisy image | - | - | 8.4811 | 0.0135 |
| TRPCAAL | 87.85 | 0.6828 | 21.9168 | 0.7935 | |
| FTTNN | 20.00 | 0.2797 | 4.5093 | 0.0427 | |
| IRCUR | 20.20 | 9.1873 | 13.8373 | 0.4780 | |
| TRPCA_TNN | 62.00 | 1.2249 | 8.1658 | 0.4618 | |
| N-TRPCA | - | 6.2689 | 24.1166 | 0.8463 | |
| EATP-DCT | 24.00 | 0.3597 | 4.6647 | 0.0194 |
| Noise | Iterations | Execution Time | Precision | Recall | F-Score | |
|---|---|---|---|---|---|---|
| TRPCAAL | 4 | 3.7391 | 0.5295 | 0.5672 | 0.5407 | |
| FTTNN | 25 | 32.6119 | 0.4749 | 0.1468 | 0.2041 | |
| IRCUR | 24 | 513.9714 | 0.4855 | 0.5898 | 0.5269 | |
| TRPCA_TNN | 43 | 82.7404 | 0.0244 | 0.4375 | 0.0456 | |
| N-TRPCA | - | 249.2075 | 0.0954 | 0.3753 | 0.1474 | |
| EATP-DCT | 25 | 32.9607 | 0.4377 | 0.5587 | 0.4826 |
| Noise | Iterations | Execution Time | Precision | Recall | F-Score | |
|---|---|---|---|---|---|---|
| TRPCAAL | 4 | 4.2106 | 0.3719 | 0.5477 | 0.4356 | |
| FTTNN | 25 | 36.8798 | 0.3322 | 0.1521 | 0.2047 | |
| IRCUR | 24 | 585.0544 | 0.1704 | 0.6491 | 0.2565 | |
| TRPCA_TNN | 43 | 93.0426 | 0.1195 | 0.1549 | 0.1310 | |
| N-TRPCA | - | 287.7277 | 0.7393 | 0.0243 | 0.0470 | |
| EATP-DCT | 26 | 38.5858 | 0.1635 | 0.5586 | 0.2455 |
| Noise | Iterations | Execution Time | Precision | Recall | F-Score | |
|---|---|---|---|---|---|---|
| TRPCAAL | 4 | 4.9572 | 0.2727 | 0.4436 | 0.3294 | |
| FTTNN | 24 | 35.0960 | 0.3105 | 0.0738 | 0.1157 | |
| IRCUR | 23 | 658.9767 | 0.2541 | 0.5875 | 0.3475 | |
| TRPCA_TNN | 40 | 112.5505 | 0.6425 | 0.0201 | 0.0387 | |
| N-TRPCA | - | 346.1222 | 0.0583 | 0.0329 | 0.0396 | |
| EATP-DCT | 26 | 45.2597 | 0.1281 | 0.5621 | 0.2040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G. Accelerated Tensor Robust Principal Component Analysis via Factorized Tensor Norm Minimization. Appl. Sci. 2025, 15, 8114. https://doi.org/10.3390/app15148114
Lee G. Accelerated Tensor Robust Principal Component Analysis via Factorized Tensor Norm Minimization. Applied Sciences. 2025; 15(14):8114. https://doi.org/10.3390/app15148114
Chicago/Turabian StyleLee, Geunseop. 2025. "Accelerated Tensor Robust Principal Component Analysis via Factorized Tensor Norm Minimization" Applied Sciences 15, no. 14: 8114. https://doi.org/10.3390/app15148114
APA StyleLee, G. (2025). Accelerated Tensor Robust Principal Component Analysis via Factorized Tensor Norm Minimization. Applied Sciences, 15(14), 8114. https://doi.org/10.3390/app15148114





