The Estimation of the Remaining Useful Life of Ceramic Plates Used in Iron Ore Filtration Through a Reliability Model and Machine Learning Methods Applied to Industrial Process Variables of a Pims
Abstract
1. Introduction
2. Theoretical Framework
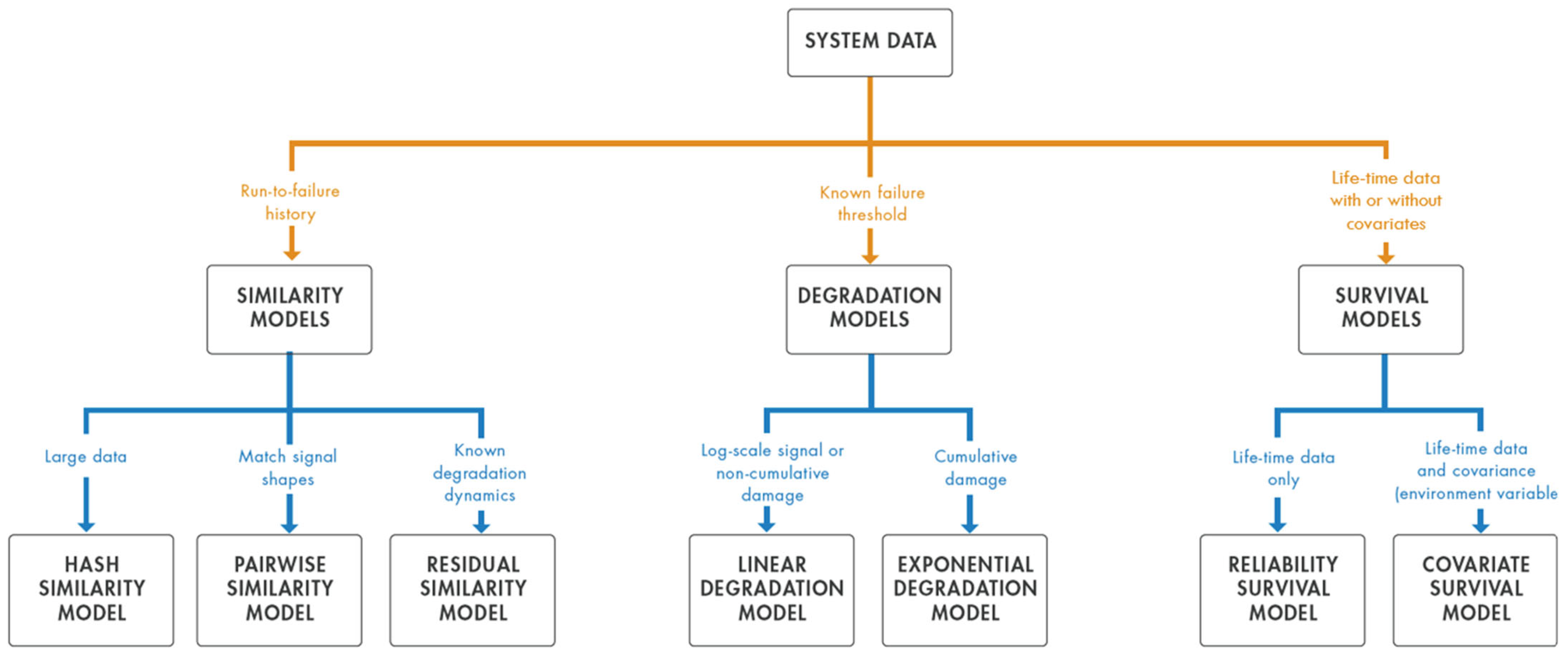
2.1. RUL: Reliability and Predictive Maintenance
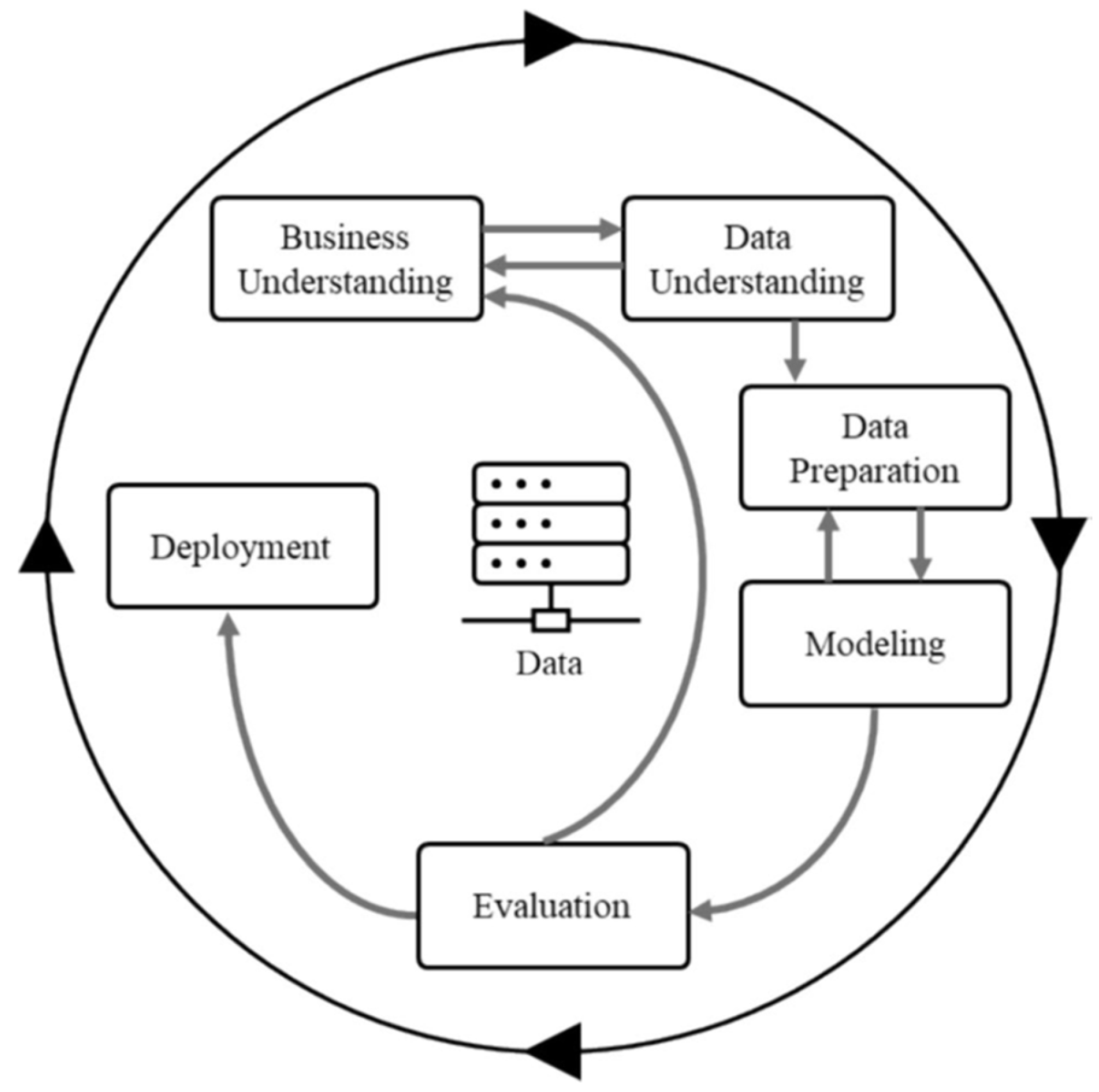
2.2. CRISP-DM: Framework for Data Analysis
2.3. Machine Learning: Prediction via Linear Regression
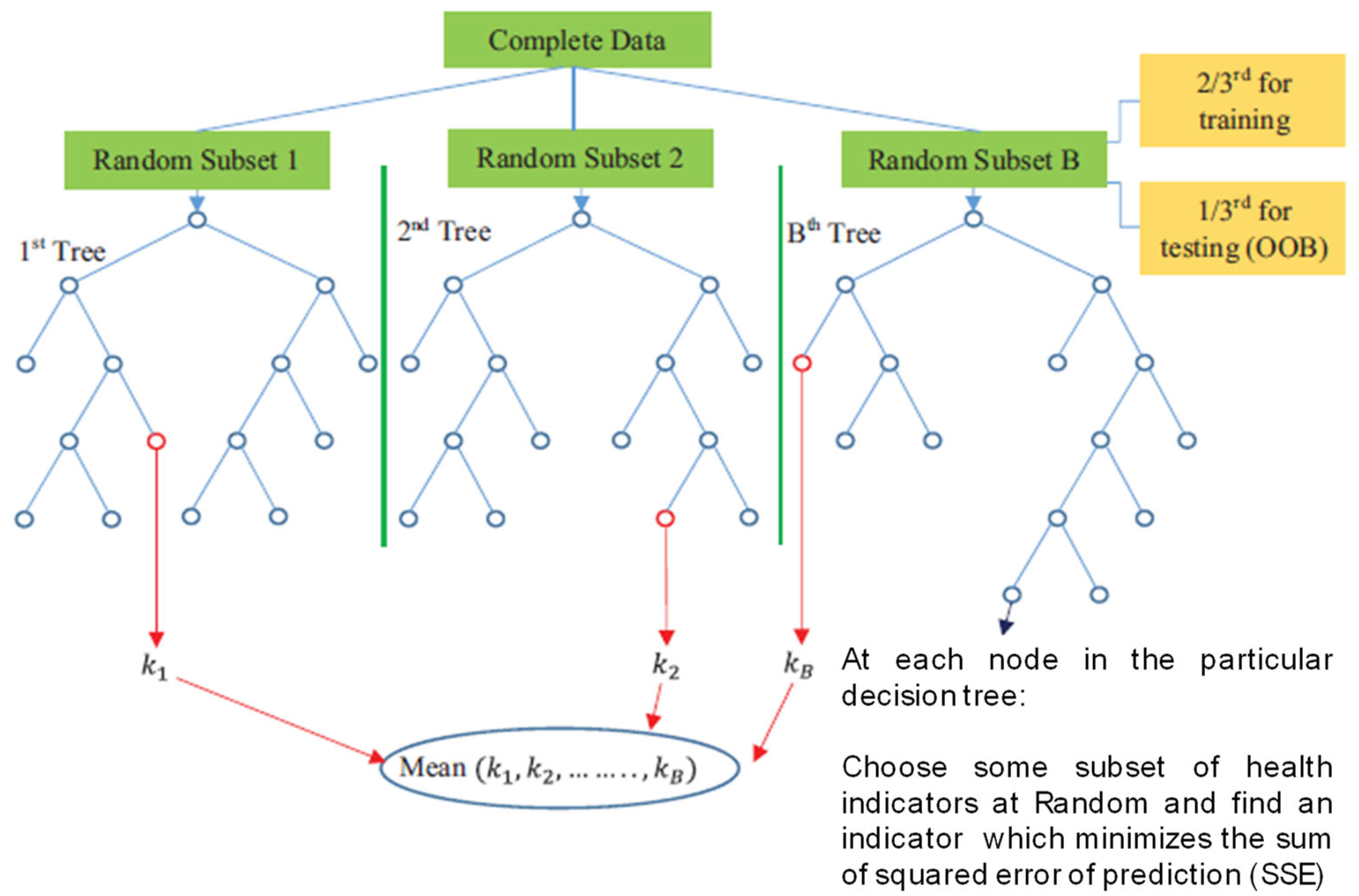
2.4. Machine Learning: Random Forest Regression Algorithm
- For nodes b = 1 through B:
- A size n × p bootstrap sample is used for size N × p training data, where N is the number of observations, p is the number of variables and n is a sample of N.
- A decision tree is created based on the sampled data via the minimization criterion of , where represents the observed values and represents the mean fitted values. The sampled data is divided recursively according to the following steps:
- For each node, select m variables (out of the total p variables) and split points;
- Among the variables, select the best variable and its best division points;
- Split each parent node between two child nodes.
- 2.
- B decision trees are developed via the procedure applied in step 1, as shown in .
- 3.
- For a given x, the prediction will be the average of the predictions made by the individual decision trees B.
3. Methodological Procedures
Case Study: Ceramic Plates in Vacuum Filters
4. Results and Discussion
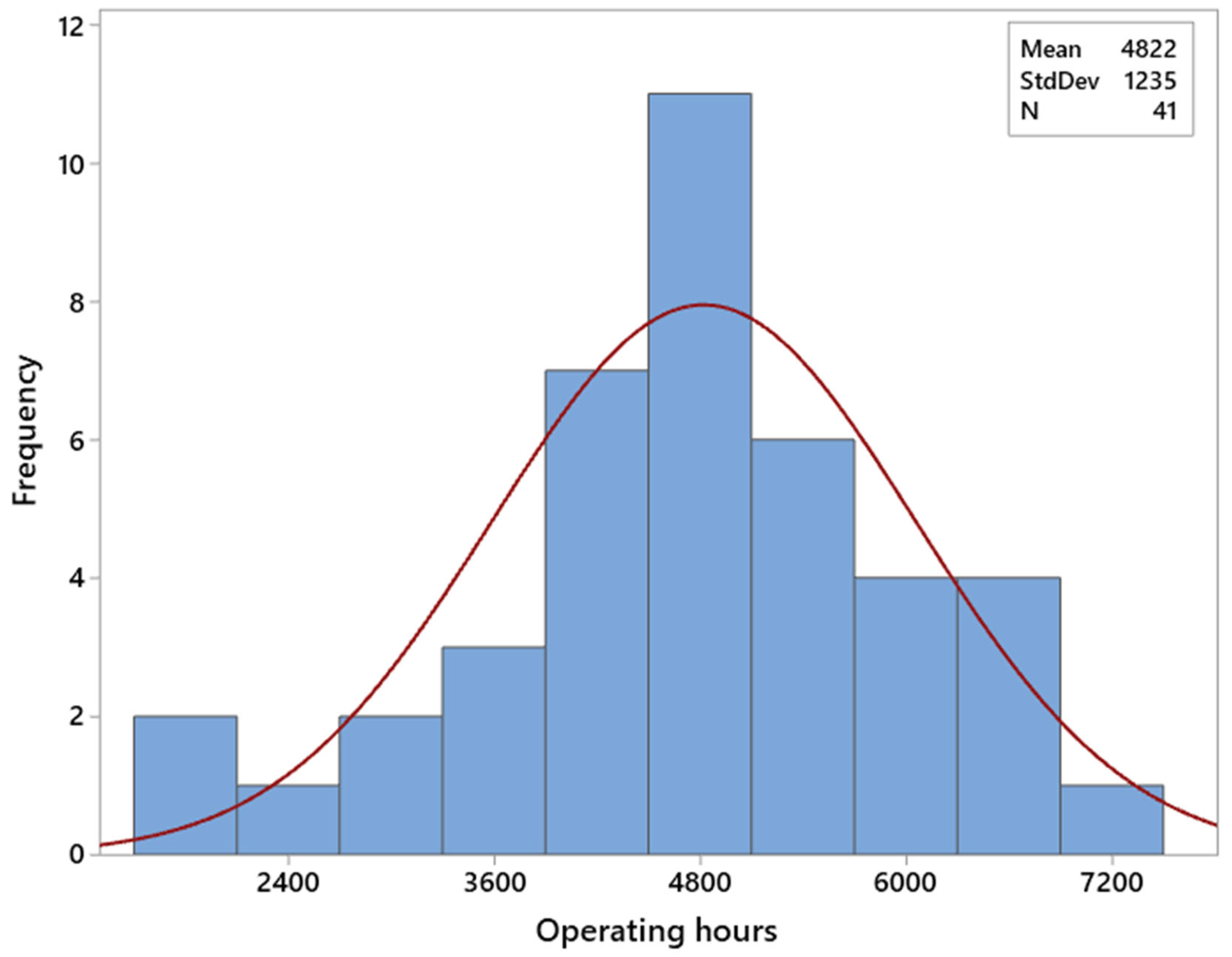
4.1. Descriptive Analysis
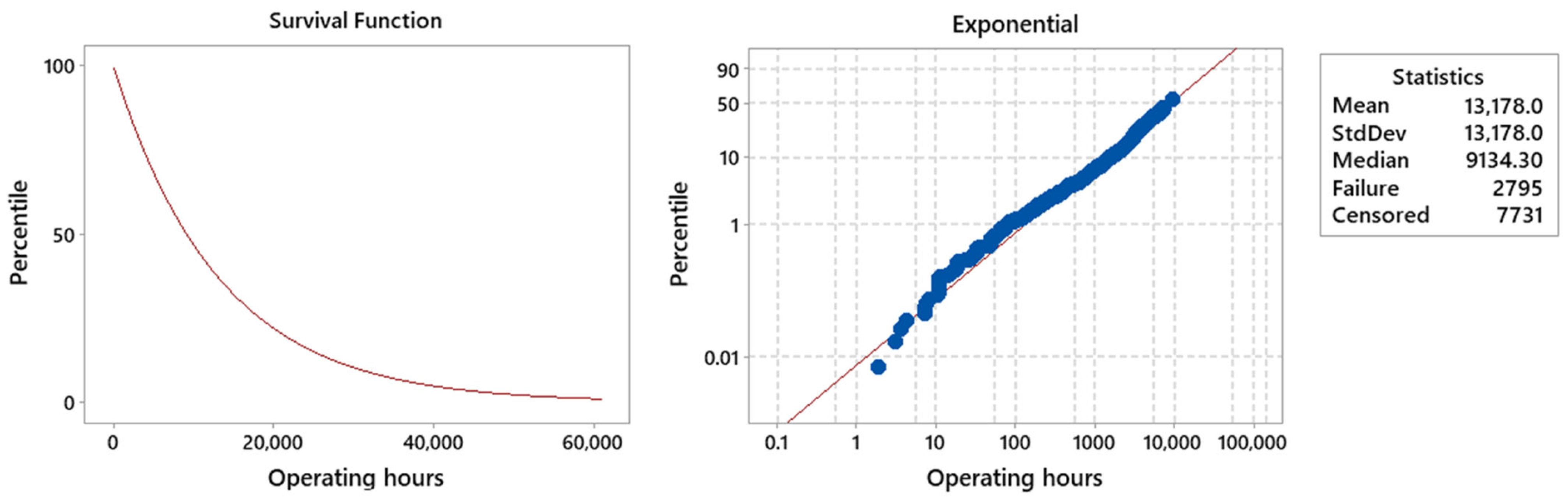
4.2. Reliability Model
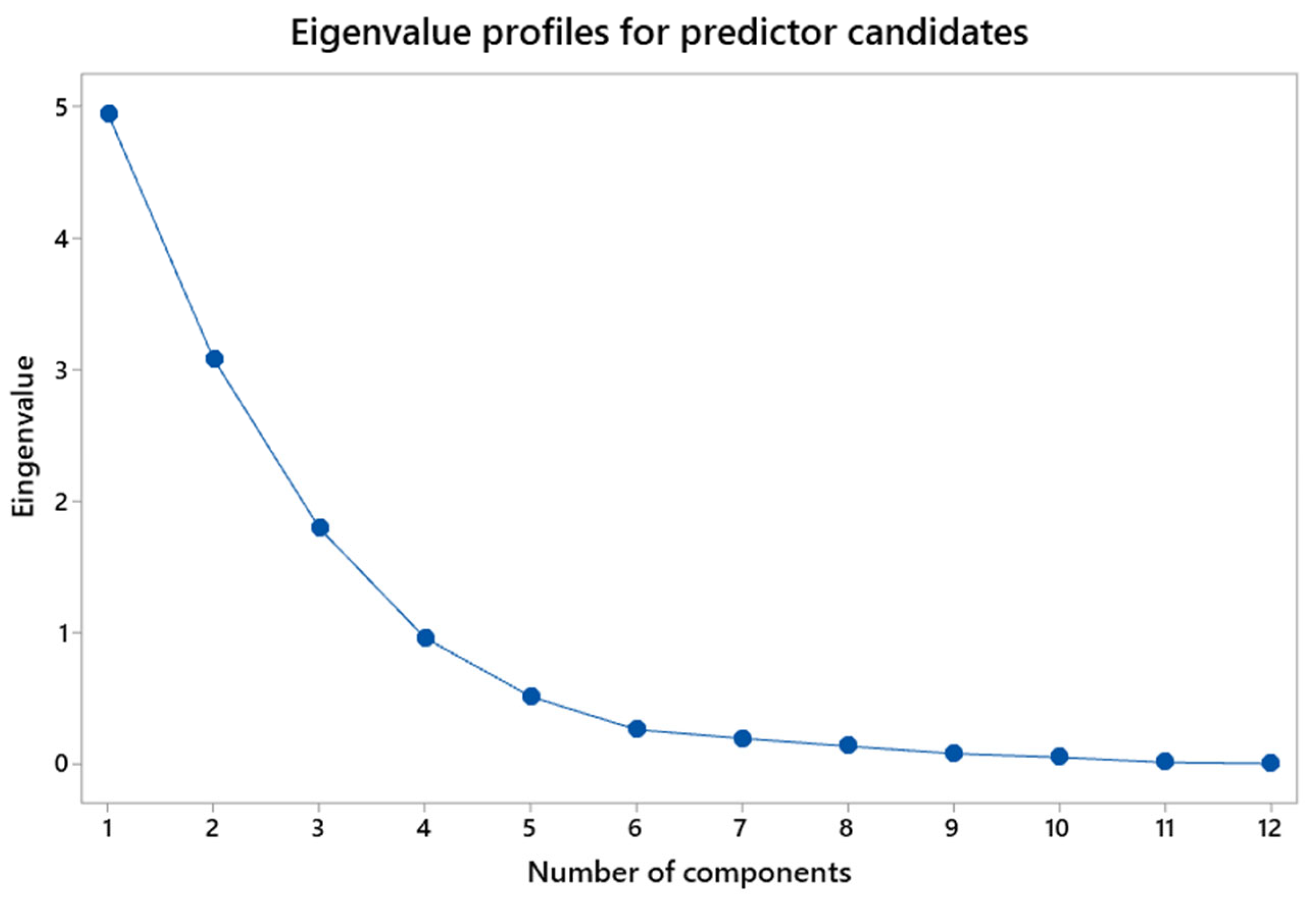
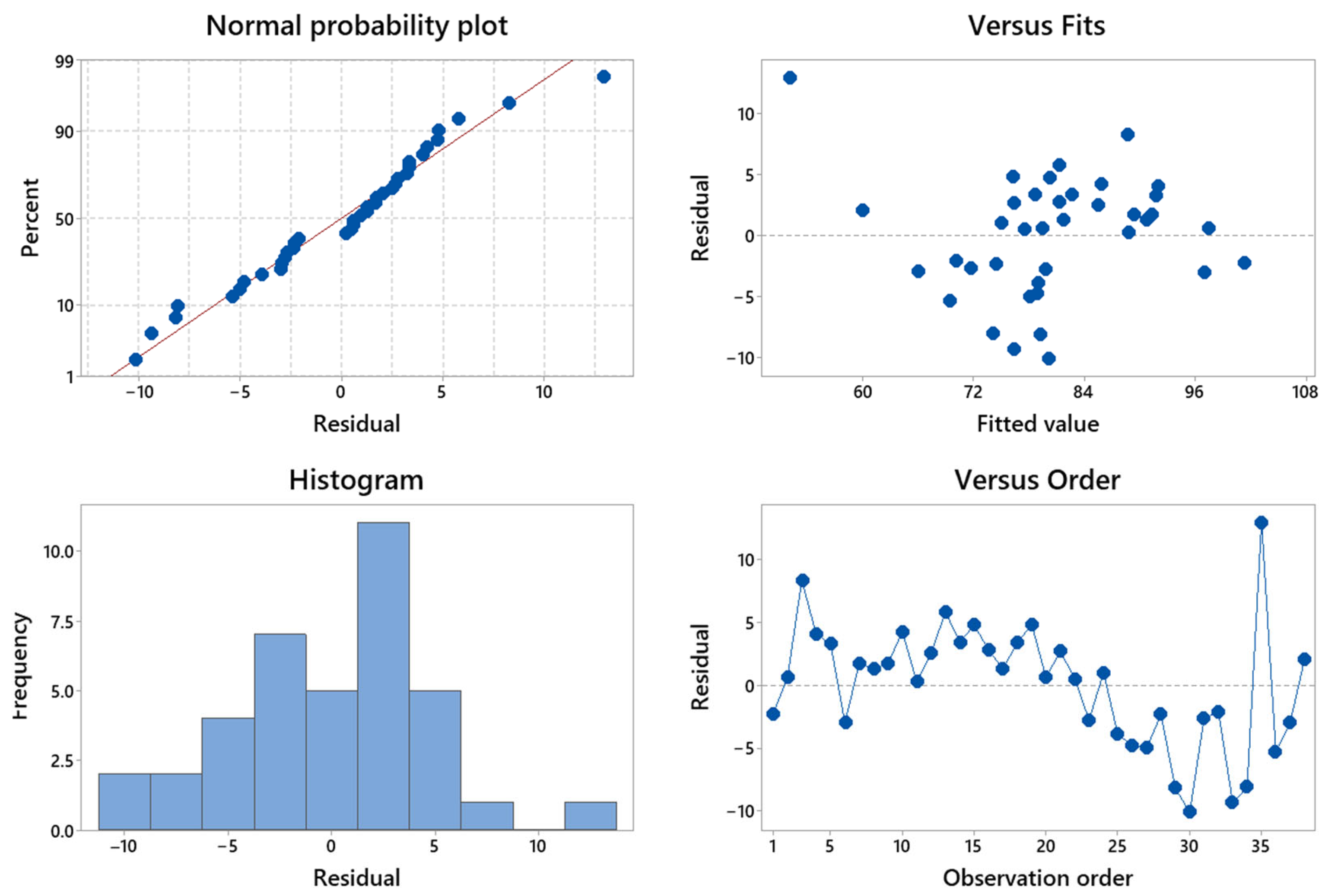
4.3. Linear Regression Model for Reliability Prediction
- R(t) is the exponential model for the reliability of ceramic plates;
- U129_IIT is the electrical current in the drive motor of the backwash pump;
- U129 is the frequency inverter control of the backwash pump motor;
- U009_IIT is the electrical current in the motor of the drum drive;
- PT325 is the vacuum pressure in the second cake-formation section;
- PT225 is the vacuum pressure in the first cake-formation section;
- PT125 is the vacuum pressure in the cake-drying section;
- PT101 is the vacuum pressure in the vacuum pump;
- KPV325 is the percentage of valve opening in the second cake-formation section;
- PT329 is the pressure in the backwash pipeline before bag filtration;
- PT129 is the pressure in the backwash pipeline after the bag is filtered;
- FT129 is the backwash flow rate;
- Delta P is the pressure variation in bag filters.
- PT101(t)—The loss of vacuum pressure in a vacuum pump. Lower negative vacuum pressures are related to the lower reliability of ceramic plates. The average vacuum pressure loss of 0.1 bar is related to 0.8% lower reliability or, alternatively, a 0.8% increase in the probability of failure.
- KPV325(t)—The higher average second-cake-formation valve opening readings are related to lower reliability values of the ceramic plates. An increase in the average percentage of valve openings by 10% is related to a reliability reduction of approximately 16% or, alternatively, an increase in the probability of failure by 16%.
- PT329(t)—Regarding the variables related to backwash pressure, the higher the average value measured before the bag filter, the lower the reliability of the ceramic plates. A 0.1-bar increase in backwash pressure before the use of the bag filter leads to a reliability reduction of 8.2% or, similarly, an increase in the probability of failure of 8.2%.
- PT129(t)—For the backwash pressure after bag filtration, higher values are associated with higher reliability. The 0.01-bar reduction in the average value of this pressure is related to 10.7% lower reliability or, alternatively, a 10.7% increase in the probability of failure.
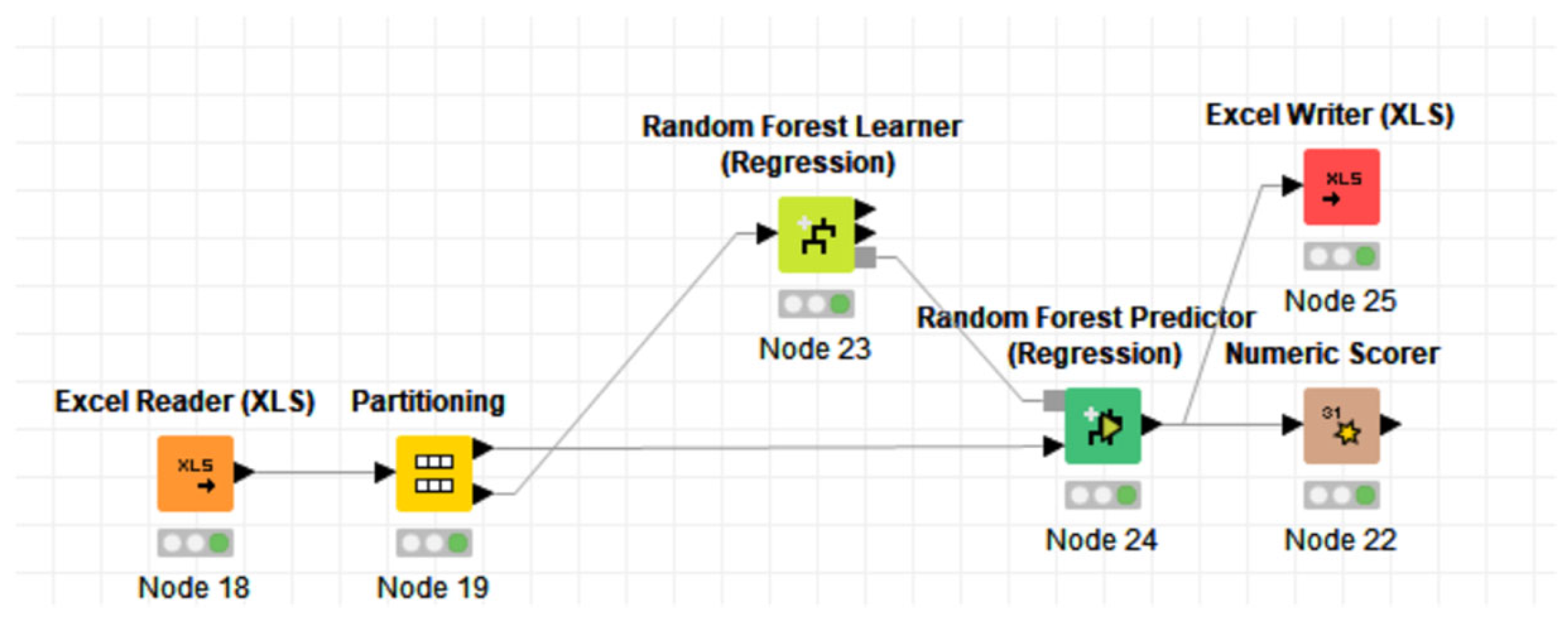
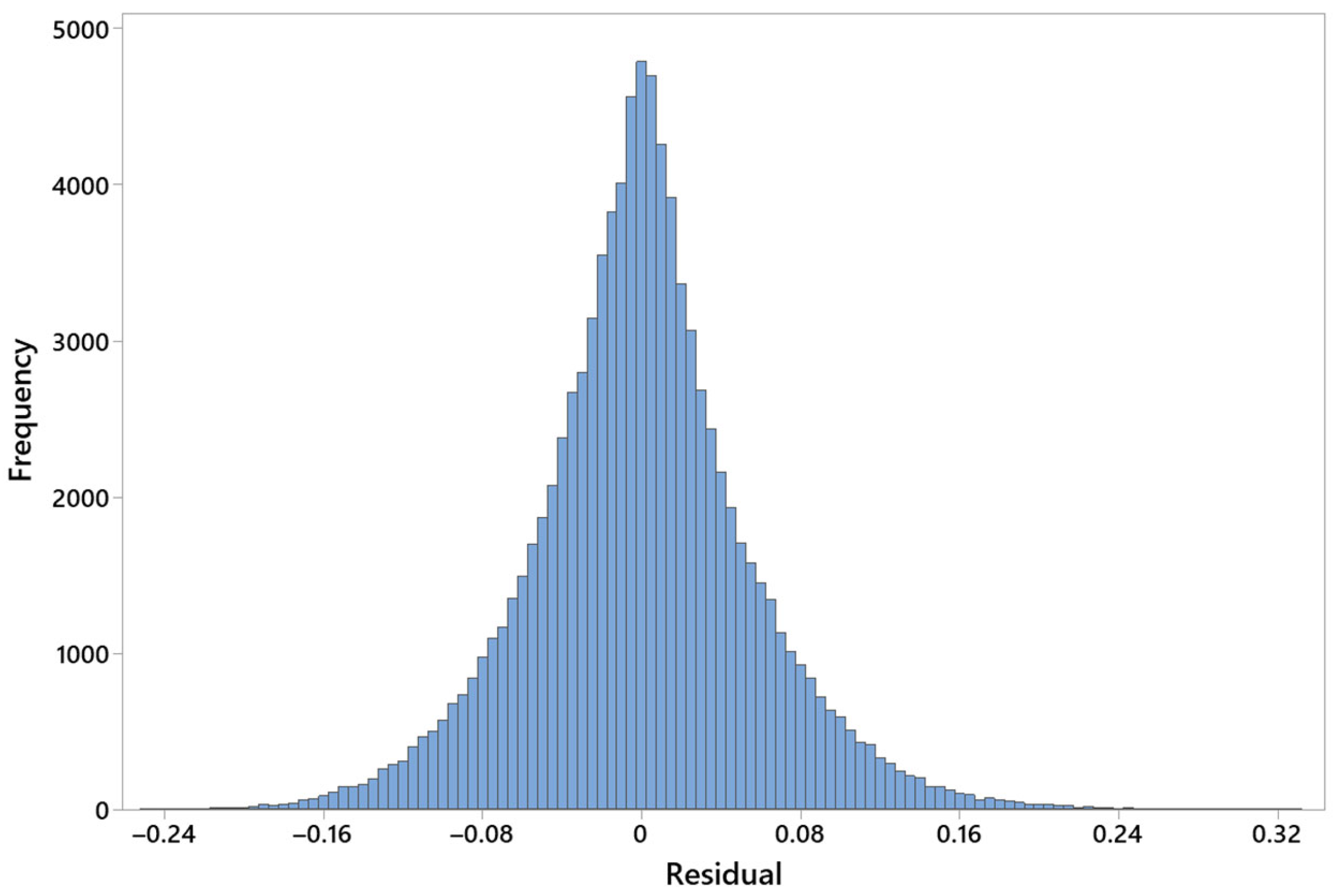
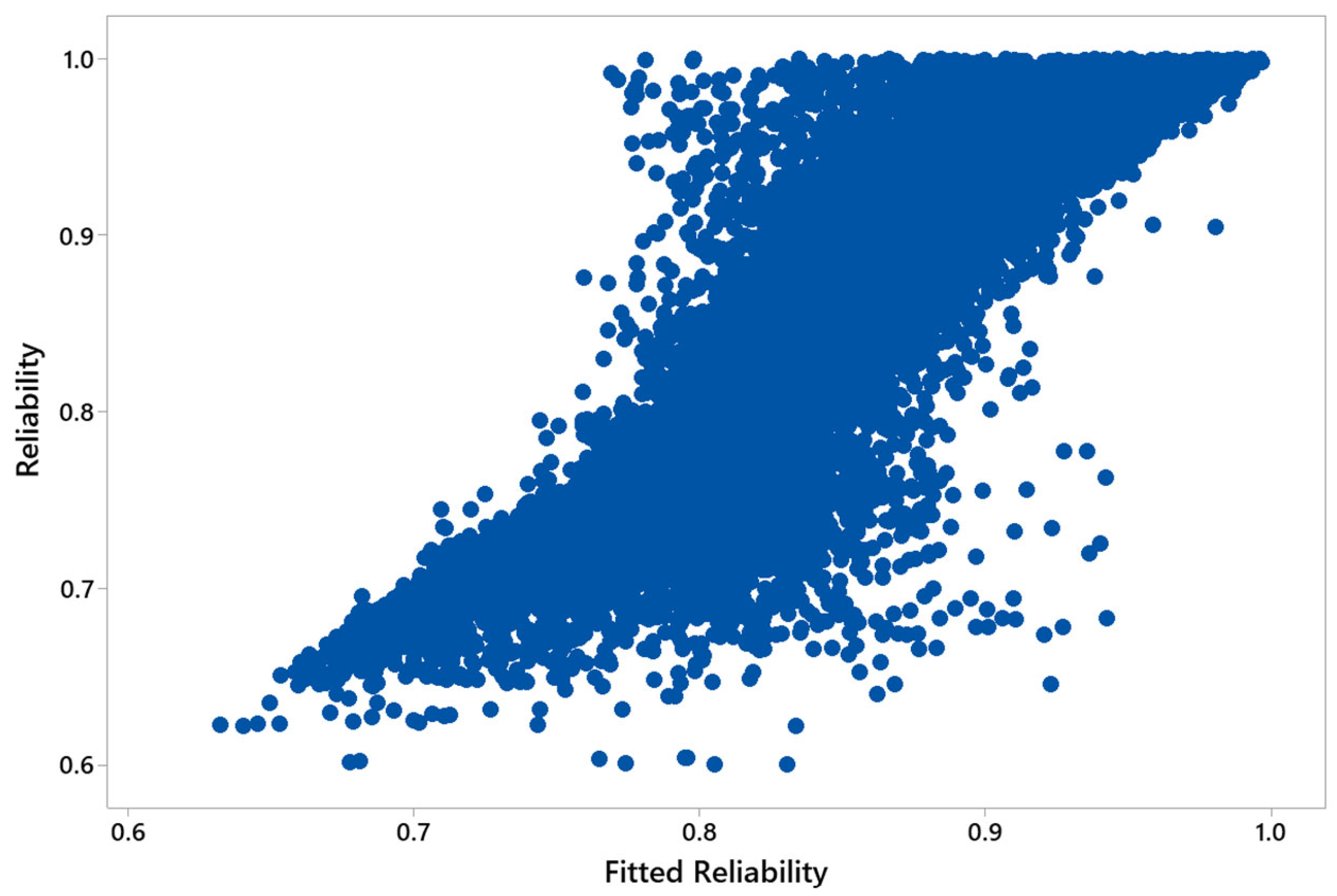
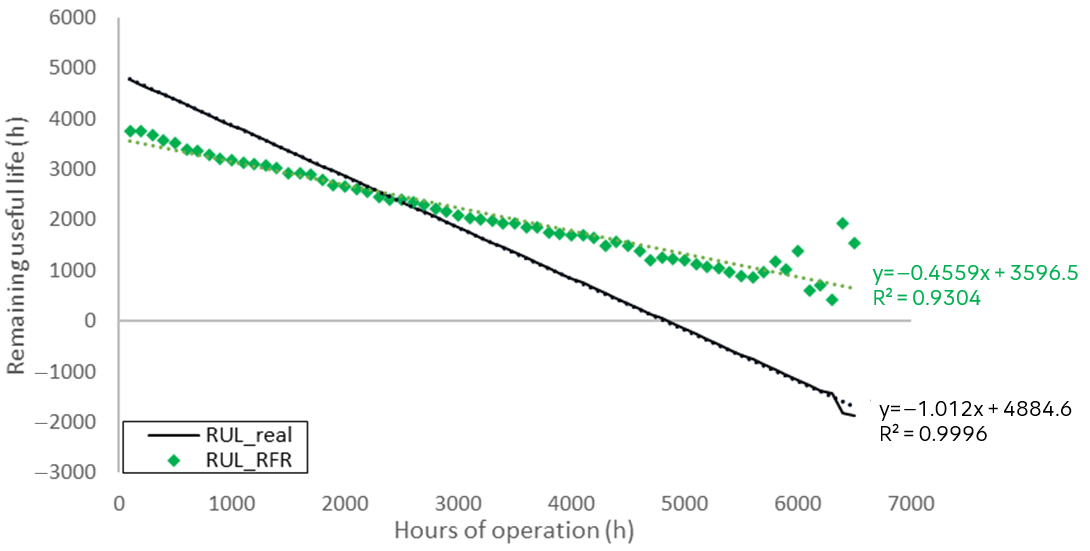
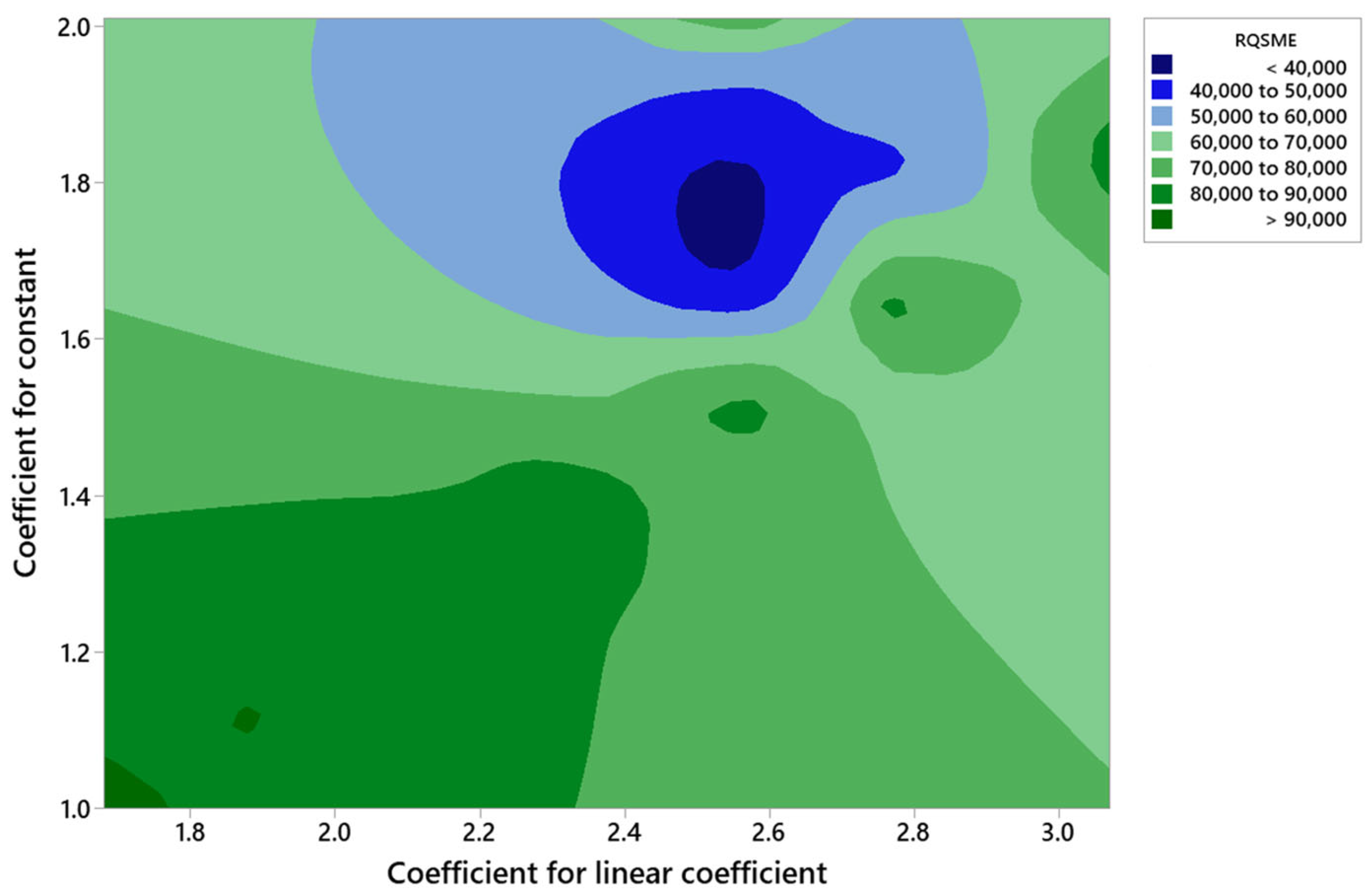
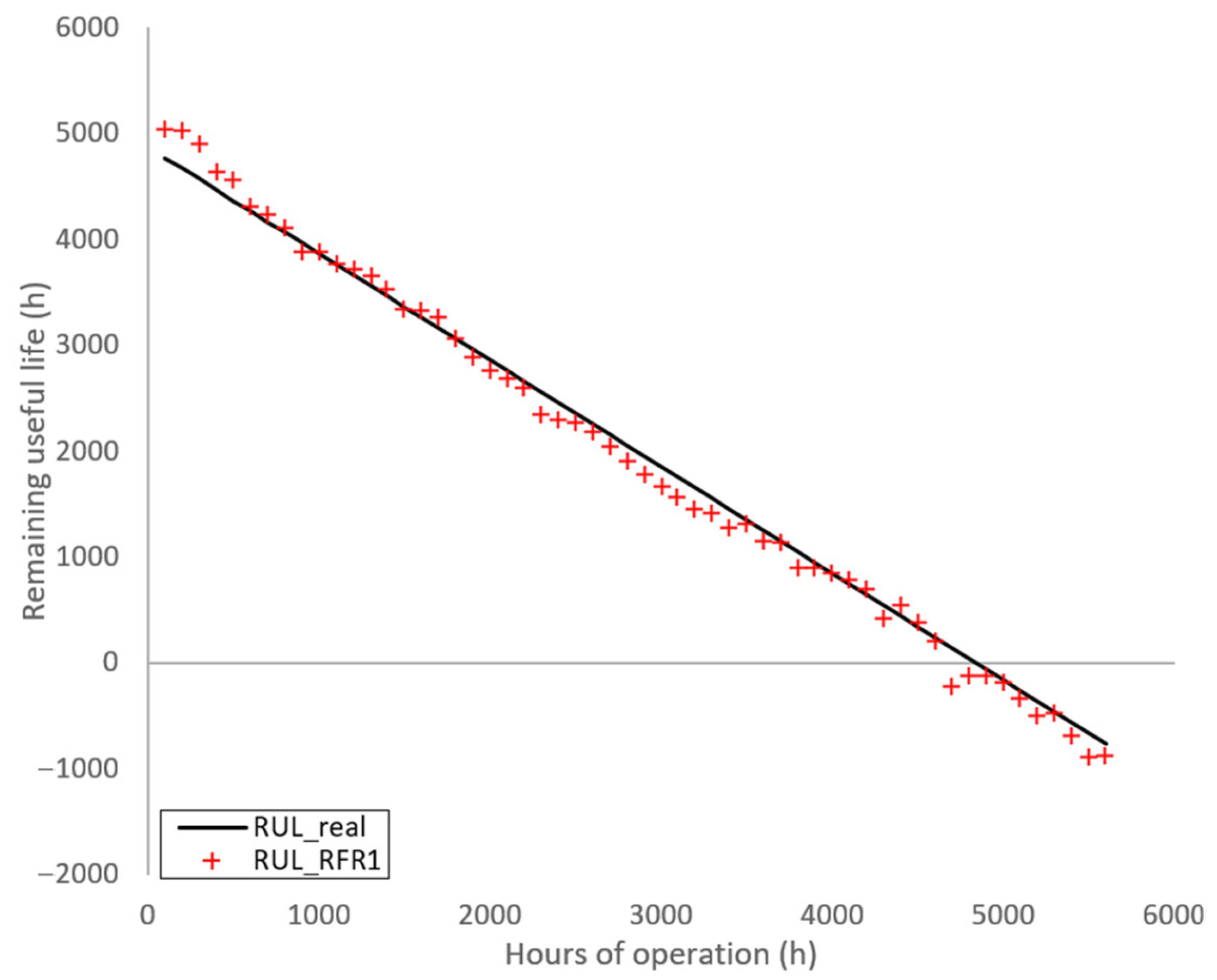
4.4. Random Forest Regression Model for Reliability Prediction
5. Conclusions
- The proposed methodology innovates in establishing a link between the CRISP-DM methodology and a methodology for determining the remaining useful life of equipment and components;
- The methodology presented here can be applied to other industrial problems with similar objectives where investment in traditional predictive maintenance sensors (vibration and temperature) is not readily achievable or technically feasible;
- The concept of embedding reliability estimates in PIMSs is not widely applied, even with its high potential. This manuscript can motivate further works considering similar methodologies and environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kundu, P.; Darpe, A.K.; Kulkarni, M.S. An ensemble decision tree methodology for remaining useful life prediction of spur gears under natural pitting progression. Struct. Health Monit. 2020, 19, 854–872. Available online: https://journals.sagepub.com/doi/10.1177/1475921719865718 (accessed on 7 March 2025). [CrossRef]
- MATLAB. Predictive Maintenance with MATLAB Ebook Documentation; The MathWorks Inc.: Natick, MA, USA, 2020; Available online: https://www.mathworks.com/content/dam/mathworks/ebook/gated/predictive-maintenance-ebook-all-chapters.pdf (accessed on 18 January 2025).
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0888327017305988 (accessed on 7 March 2025). [CrossRef]
- Qin, A.; Zhang, Q.; Hu, Q.; Sun, G.; He, J.; Lin, S. Remaining Useful Life Prediction for Rotating Machinery Based on Optimal Degradation Indicator. Shock Vib. 2017, 2017, 1–12. Available online: https://www.hindawi.com/journals/sv/2017/6754968/ (accessed on 7 March 2025). [CrossRef]
- Wang, Q.; Zheng, S.; Farahat, A.; Serita, S.; Gupta, C. Remaining Useful Life Estimation Using Functional Data Analysis. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 17–20 June 2019; IEEE: San Francisco, CA, USA, 2019; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/8819420/ (accessed on 7 March 2025).
- Liu, G.; Fan, W.; Li, F.; Wang, G.; You, D.; Kastanya, D. Remaining Useful Life Prediction of Nuclear Power Machinery Based on an Exponential Degradation Model. Sci. Technol. Nucl. Install. 2022, 2022, 1–9. Available online: https://www.hindawi.com/journals/stni/2022/9895907/ (accessed on 7 March 2025). [CrossRef]
- Chu, C.M.; Moon, J.F.; Lee, H.T.; Kim, J. Extraction of Time-varying Failure Rates on power distribution system equipment considering failure modes and regional effects. Int. J. Electr. Power Energy Syst. 2010, 32, 721–727. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0142061510000165 (accessed on 7 March 2025). [CrossRef]
- Djonglibet, W.-D.; Bianzeube, T.; Ouinra, K. Reliability of Life Calculation Laws for Materials under Variable Amplitude Loading. Open J. Appl. Sci. 2022, 12, 1922–1930. Available online: https://www.scirp.org/journal/doi.aspx?doi=10.4236/ojapps.2022.1211133 (accessed on 7 March 2025). [CrossRef]
- Santos, L.S.; Pinotti, F.; Luis Duarte Ribeiro, J.; Botelho, H.C. Reliability of Redundant Systems with Repair in an Oil Refinery. Ind. Manag. Mag. 2015, 11, 3. Available online: https://periodicos.utfpr.edu.br/revistagi/article/view/2759 (accessed on 7 March 2025).
- Hasanain, W.S.; Elaibi, W.M. Reliability Estimation for the Exponential-Pareto Hybrid System. Iraqi J. Sci. 2023, 64, 4622–4633. Available online: https://ijs.uobaghdad.edu.iq/index.php/eijs/article/view/4354 (accessed on 7 March 2025). [CrossRef]
- Xuegang, L. A Reliability Prediction Method Based on Simulation Analysis. Procedia Eng. 2015, 99, 219–223. Available online: https://linkinghub.elsevier.com/retrieve/pii/S1877705814036431 (accessed on 7 March 2025). [CrossRef][Green Version]
- Zhang, C.W.; Zhang, T.; Xu, D.; Xie, M. Analyzing Highly Censored Reliability Data without Exact Failure Times: An Efficient Tool for Practitioners. Qual. Eng. 2013, 25, 392–400. Available online: http://www.tandfonline.com/doi/abs/10.1080/08982112.2013.783598 (accessed on 7 March 2025). [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 6th ed.; Technical and Scientific Books: Rio de Janeiro, Brazil, 2016. [Google Scholar]
- Bokrantz, J.; Subramaniyan, M.; Skoogh, A. Realizing the promises of artificial intelligence in manufacturing by enhancing CRISP-DM. Prod. Plan. Control 2024, 35, 2234–2254. Available online: https://www.tandfonline.com/doi/full/10.1080/09537287.2023.2234882 (accessed on 7 March 2025). [CrossRef]
- Doede, N.; Merkel, P.; Kriwall, M.; Stonis, M.; Behrens, B.-A. Implementation of an intelligent process monitoring system for screw presses using the CRISP-DM standard. Prod. Eng. 2025, 19, 77–88. Available online: https://link.springer.com/10.1007/s11740-024-01298-8 (accessed on 7 March 2025). [CrossRef]
- Wiemer, H.; Drowatzky, L.; Ihlenfeldt, S. Data Mining Methodology for Engineering Applications (DMME)A Holistic Extension to the CRISP-DM Model. Appl. Sci. 2019, 9, 2407. Available online: https://www.mdpi.com/2076-3417/9/12/2407 (accessed on 7 March 2025). [CrossRef]
- Gayathri, R.; Rani, S.U.; Čepová, L.; Rajesh, M.; Kalita, K. A Comparative Analysis of Machine Learning Models in Prediction of Mortar Compressive Strength. Processes 2022, 10, 1387. Available online: https://www.mdpi.com/2227-9717/10/7/1387 (accessed on 7 March 2025). [CrossRef]
- Tayade, A.; Patil, S.; Phalle, V.; Kazi, F.; Powar, S. Remaining useful life (RUL) prediction of bearing by using regression model and principal component analysis (PCA) technique. Vibroeng. Procedia 2019, 23, 30–36. Available online: https://www.extrica.com/article/20617 (accessed on 7 March 2025). [CrossRef]








| Stage | Description |
|---|---|
| Business Understanding | Ceramic plates are the main components of a ceramic filter and correspond to approximately 40% of the operating cost of an industrial filtration plant, in addition to having a direct effect on the production capacity and quality of the final product (moisture content). These are the reasons to optimize the useful life of these components, accurately identifying the optimal time to carry out plate set renewals. |
| Data Acquisition and Data Understanding | Based on the business understanding phase and facility’s database, a selection of 12 sensors is made. According to process specialists, these variables can influence or be influenced by the change in the performance of ceramic plates, and this, alongside reliability models obtained by the failure and replacement data, can be combined to predict the remaining useful life of these components. The sensor reading data are obtained from the PIMS—Plant Information Management System (Osisoft AVEVA PI Vision/PI Datalink ®, ver. 2023 SP1)—and the ceramic plate failure and replacement data are exported from the MES—Manufacturing Enterprise System (Osisoft AVEVA Production Management ®, ver. 2020 U1). |
| Data Preparation | After identifying the main process variables and obtaining the failure data records, they undergo treatment to remove outliers and missing data. In addition, different data sources are combined into one, making it possible to relate the useful life to the process variables. To prepare the data, electronic spreadsheets in Microsoft Excel® (MS Office 365 version) are used. |
| Identification of Health Condition Indicators | In this stage, statistical descriptive analyses are carried out to achieve a correct and broad understanding of data that characterizes normal operation, and to determine which are the best indicators for anomalies in these readings over time. With a condition indicator, a time trigger is established in which the reliability of the plate sets reaches 70%. Statistical analysis and modeling are performed using Minitab® software (version 19). |
| Modeling | Modeling consists of identifying the best models of survival/the reliability of failure and plate replacement data and identifying the best machine learning models that may be able to use sensor readings as predictors of reliability and, ultimately, the remaining useful life of these components. Model creation uses only a fraction of the partitioned data, called the training set. |
| In the evaluation of the models, the main statistical metrics are used to evaluate the significance and predictive capacity. In this step, partitioned validation data is used as input into the model for evaluation. | |
| Model Deployment and Integration | After being tested and validated, the model can be released in a production environment in software/systems, being fed back whenever new data becomes available. |
| Hours Operated | Data Operation | Failures |
|---|---|---|
| 0–1000 | 29,119 | 120 |
| 1000–2000 | 29,068 | 226 |
| 2000–3000 | 27,761 | 504 |
| 3000–4000 | 25,219 | 644 |
| 4000–5000 | 18,058 | 457 |
| 5000–6000 | 4549 | 97 |
| 6000–7000 | 288 | 6 |
| Total | 134,062 | 2054 |
| U129_IIT | U129 | U009_IIT | PT325 | PT225 | PT125 | PT101 | KPV325 | PT329 | PT129 | FT129 | Delta P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U129 | 0.114 | |||||||||||
| U009_IIT | 0.355 | 0.073 | ||||||||||
| PT325 | 0.061 | 0.09 | 0.039 | |||||||||
| PT225 | 0.015 | 0.009 | 0.021 | 0.351 | ||||||||
| PT125 | −0.036 | −0.026 | 0.057 | 0.021 | 0.489 | |||||||
| PT101 | −0.045 | −0.093 | 0.022 | −0.055 | 0.454 | 0.794 | ||||||
| KPV325 | −0.037 | −0.068 | −0.02 | −0.901 | −0.383 | −0.028 | 0.038 | |||||
| PT329 | 0.132 | 0.526 | 0.031 | −0.01 | −0.018 | −0.013 | −0.004 | −0.001 | ||||
| PT129 | −0.011 | 0.014 | −0.02 | 0.039 | −0.267 | −0.429 | −0.465 | −0.019 | 0.029 | |||
| FT129 | 0.158 | 0.212 | 0.13 | 0.137 | −0.098 | −0.391 | −0.447 | −0.1 | 0.122 | 0.329 | ||
| Delta P | 0.133 | 0.52 | 0.033 | −0.015 | 0.021 | 0.05 | 0.064 | 0.002 | 0.989 | −0.119 | 0.072 | |
| R(t) | 0.046 | 0.002 | −0.007 | 0.197 | 0.186 | −0.008 | −0.008 | −0.149 | −0.045 | 0.005 | 0.044 | −0.045 |
| Term | Coef | Coef SE | T Value | p Value | VIF |
|---|---|---|---|---|---|
| Constant | −558 | 533 | −1.05 | 0.303 | |
| PT101 | 8.01 | 2.21 | 3.62 | 0.001 | 1.42 |
| KPV325 | −1.61 | 0.187 | −8.60 | 0.000 | 1.22 |
| PT329 | −82.0 | 13.8 | −5.96 | 0.000 | 1.22 |
| PT129 | 1073 | 409 | 2.63 | 0.013 | 1.53 |
| Vars | R2 | R2 (aj) | R2 (pred) | Mallow’s Cp | S | U129_IIT | U009_IIT | PT225 | PT101 | KPV325 | PT329 | PT129 | FT129 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 80.7 | 78.3 | 71.4 | 3.9 | 5.1743 | X | X | X | X | ||||
| 6 | 82 | 78.6 | 57.3 | 5.7 | 5.1454 | X | X | X | X | X | X | ||
| 8 | 82.4 | 77.6 | 31.4 | 9 | 5.2588 | X | X | X | X | X | X | X | X |
| Metric | Result |
|---|---|
| R2 | 0.637 |
| Mean Absolute Error | 0.042 |
| Mean Square Error | 0.003 |
| Square Root of Mean Square Error | 0.056 |
| Average Difference | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florentino, R.B.; Moura, L.G.L. The Estimation of the Remaining Useful Life of Ceramic Plates Used in Iron Ore Filtration Through a Reliability Model and Machine Learning Methods Applied to Industrial Process Variables of a Pims. Appl. Sci. 2025, 15, 8081. https://doi.org/10.3390/app15148081
Florentino RB, Moura LGL. The Estimation of the Remaining Useful Life of Ceramic Plates Used in Iron Ore Filtration Through a Reliability Model and Machine Learning Methods Applied to Industrial Process Variables of a Pims. Applied Sciences. 2025; 15(14):8081. https://doi.org/10.3390/app15148081
Chicago/Turabian StyleFlorentino, Robert Bento, and Luiz Gustavo Lourenço Moura. 2025. "The Estimation of the Remaining Useful Life of Ceramic Plates Used in Iron Ore Filtration Through a Reliability Model and Machine Learning Methods Applied to Industrial Process Variables of a Pims" Applied Sciences 15, no. 14: 8081. https://doi.org/10.3390/app15148081
APA StyleFlorentino, R. B., & Moura, L. G. L. (2025). The Estimation of the Remaining Useful Life of Ceramic Plates Used in Iron Ore Filtration Through a Reliability Model and Machine Learning Methods Applied to Industrial Process Variables of a Pims. Applied Sciences, 15(14), 8081. https://doi.org/10.3390/app15148081






