Abstract
Gait analysis is a valuable tool for aiding in the diagnosis of neurological diseases, providing objective measurements of human gait kinematics and kinetics. These data enable the quantitative estimation of movement abnormalities, which helps to diagnose disorders and assess their severity. In this regard, machine learning techniques and explainability methods offer an opportunity to enhance anomaly detection in gait measurements and support a more objective assessment of neurodegenerative disease, providing insights into the most relevant gait parameters used for disease identification. This study employs several classifiers and explainability methods to analyze gait data from a public dataset composed of patients affected by degenerative neurological diseases and healthy controls. The work investigates the relevance of spatial, temporal, and kinematic gait parameters in distinguishing such diseases. The findings are consistent among the classifiers employed and in agreement with known clinical findings about the major gait impairments for each disease. This work promotes the use of data-driven assessments in clinical settings, helping reduce subjectivity in gait evaluation and enabling broader deployment in healthcare environments.
1. Introduction
Gait analysis provides a quantitative framework for assessing human movement through measurements of spatial and temporal data, kinematics, and kinetics [1,2]. By analyzing gait patterns, researchers can identify abnormalities possibly related to conditions ranging from traumatic injuries to neurodegenerative disorders. In fact, several neurodegenerative diseases are associated with gait dysfunctions, such as Parkinson’s disease and cerebellar ataxia [3,4,5,6].
Traditionally, the diagnosis and severity assessments of these disorders relied on expert observation, which can be time-consuming and may be influenced by the subjective judgment of a limited group of specialists. On the other hand, machine learning (ML) applications for healthcare are on the rise, with the possibility of assisting experts in the diagnosis of diseases or in evaluating rehabilitation progress. In this framework, gait analysis is no exception [7]: many strategies have been proposed for the identification of neurodegenerative diseases through gait analysis, from the analysis of spatial and temporal to the kinematic and kinetic features [2].
Moreover, these approaches can be supported by explainable AI (XAI) methods that make the classification process of the models understandable by humans. This aspect can be relevant in fields such as healthcare, since it can shed light on non-trivial relations between different measures, providing more insights for diagnosing or assessing a disease.
Public datasets of gait analysis are fundamental to advancing research and developing innovative methodologies for analyzing such data. For instance, they can enable reproducibility and serve as a benchmark for comparing different analysis approaches. Indeed, several datasets are available for studying gait dysfunction in neurodegenerative diseases [2]. Some of them record floor sensor data, which measure ground reaction forces and provide insights into the center of pressure of the body [8,9], whereas others record spatial, temporal, and kinematic features through motion analysis systems [10,11]. In particular, the dataset [10] has been made available and employed in [12] to identify gait patterns in patients affected by neurodegenerative diseases through cluster analysis. The work underlined the importance of a subset of parameters able to distinguish healthy subjects from people affected by one of the neurological diseases considered (i.e., cerebellar ataxia, Parkinson’s disease, and hereditary spastic paraplegia). Also, it gave insights into the parameters that better distinguish a neurological disease from the others.
Similar considerations can be made using XAI techniques. For instance, in [13], these techniques were employed to evaluate the importance of several gait parameters, many of them being extracted from the gait profiles, in the identification of foot conditions. Other interesting applications of XAI methods in gait analysis can be found in [14], where the authors used wearable sensors to identify patients with osteopenia and sarcopenia.
This work aims to identify the most relevant gait parameters for detecting neurodegenerative diseases by using a public dataset [10], which employed an established optoelectronic motion analysis system.
To increase the robustness of the results and minimize model-specific biases, this work analyzed the spatial, temporal, and kinematic data obtained by the system using diverse supervised classifiers, such as Random Forest, gradient-boosted trees (i.e., XGBoost), Support Vector Machine (SVM), and Multi-Layer Perceptron (MLP), and explainability techniques such as permutation importance [15] and SHapley Additive exPlanations (SHAP) [16] were applied to interpret the output of the classification.
2. Materials and Methods
Here, the methodology adopted to select the most important parameters for classification is presented. After a brief introduction of the dataset, the training protocol used for training the classifiers is described. Finally, the classifiers and the explainability methods employed are illustrated.
2.1. Dataset
The publicly available data of [10] collected gait spatiotemporal parameters and joint kinematics of the lower limbs of 142 subjects. A list of demographic and anthropometric data (such as age, gender, weight, and height) is available for each subject, and additional clinical data are provided for patients affected by each neurodegenerative disease. The composition of the dataset is illustrated in Table 1.

Table 1.
Composition of the dataset, with age and gender information. Age range is expressed as min–max, whereas the average age indicates mean ± std.dev.
The gait parameters measured are cadence (in steps per minute), speed (in meters per second), step width (in meters), stance and swing time, double support time (provided as a percentage of the gait cycle), step length (in meters), and the sagittal plane range of motion (ROM) of hip, knee, and ankle joints. All of the listed measures above are provided for the right and left limbs (except for cadence and step width by definition). For more information about data acquisition and processing, please refer to the work by [10].
Since spatial and temporal parameters, such as speed, are influenced by body size, the data needed to be normalized to achieve a better comparison. We used the Froude number [17] to normalize the speed, which is defined as follows:
where g is the gravitational acceleration, and h is the height of the subject.
Moreover, spatial and temporal parameters were used to compute indexes for evaluating walking patterns. We used the walk ratio [18], given by the ratio between step length and cadence. This parameter reflects the degree of gait coordination between spatial and temporal walking aspects (i.e., step length and cadence, respectively). It has been shown that it is reproducible and does not vary over a wide range of speeds [18,19]. Since the subjects involved in the study were asked to walk at a self-selected speed, this parameter represents a useful yet simple parameter to describe the rhythm and amplitude of walking. Also, the walk ratio was normalized with subjects’ height, since the step length is related to body size. This normalization can be relevant for avoiding erroneous correlation, as shown in [20]. Figures S1 and S2 of the Supplementary Materials show that the application of the Froude number for the speed and the normalization of the step length made these metrics not correlated to subjects’ height and age. To avoid redundancies in the gait features provided to the classifiers, the walk ratio replaced the step length and cadence parameters.
Another parameter considered consistent for comfortable walking speed is the ratio between stance and swing times, which typically occupy around and of the gait cycle, respectively. A change in this ratio is usually associated with pathological gait [21]. We thus used the ratio between stance and swing time for left and right limbs, removing the stance and swing from the set of features to avoid redundancies.
Among the gait parameters provided by the dataset, we decided not to use the ankle ranges of motion in our study. This choice was related to an anomalous asymmetry reported in the values of the left-side ankle range of motion among the healthy subjects, which resulted in significantly higher values than the right-limb ones. An in-depth statistical analysis is reported in Appendix A.
In this work, we focused only on gait parameters for classification, intentionally excluding anthropometric and clinical data (except for subjects’ height measurements, which were used for normalization purposes). This approach was intended to capture the most relevant gait-related features for classification.
Additionally, since some of the employed classifiers, particularly those based on distance metrics or gradient-based optimization, are sensitive to differences in the scale of input features, we standardized each gait parameter individually using the z-score. For each parameter, given the mean and standard deviation of the values computed across all subjects, the value of the parameter for the i-th subject was standardized according to the following formula:
where is the standardized value.
2.2. Training Protocol and Hyperparameters Optimization
Since the numerosity of the dataset is limited, we performed repeated stratified cross-validation (CV). In particular, we repeated the CV five times, with the test set size constituting of the dataset, so that the test sets in each repetition would be independent. The test set was employed for final evaluation, whereas the rest of the dataset was used for a 10-fold CV, according to which we further divided the data into training and validation sets. These splits were performed in a stratified fashion so that the class balance would be preserved. At this point, some of the classifier’s hyperparameters were optimized using the software Optuna (version 4.2.0) [22], with classification accuracy being the metric to be optimized. This was achieved by performing multiple trials. We performed 100 trials per fold to ensure that the optimization method would converge to the best set of hyperparameters.
The optimized classifier was then trained, and the final evaluation was performed using the test set. The metrics employed to evaluate the performance of the model were accuracy, precision, recall, f1-score, and the Area Under the Receiver Operating Characteristic Curve (AUC). Figure 1 depicts a diagram of the training protocol.
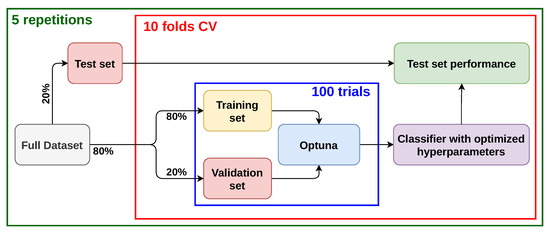
Figure 1.
Representation of the training protocol. The full dataset is split so that of it is used as test set, and the remaining is used for the cross-validation. Inside, the cross-validation (red rectangle) is further split with the same ratio into validation and training sets. The classifier hyperparameters are then optimized with Optuna (blue rectangle).
To better highlight the differences between healthy controls and patients affected by one of the diseases, we performed multiple classification tasks that included the following:
- Multi-class classification;
- Binary classification between healthy and affected by any disease. In this case, the class labels PD, CA, and HSP were replaced with a common label, and we labeled this case as HC vs. rest;
- Binary classification between healthy and affected by disease. In this case, only the data belonging to the class HC and one of the other classes were provided to the model. We performed all the possible binary classifications, i.e., HC vs. PD, HC vs. CA, and HC vs. HSP.
Since the dataset includes subjects of age ranging from 21 to 79 years, we decided to use this information to improve the robustness of our results. Indeed, even the healthy older population shows differences in spatial, temporal, and kinematic gait parameters with respect to the younger population [23,24]. Considering the classification tasks only involving a neurodegenerative disease, since the age range differed for every disease, we performed the classification using the subset of the controls whose age was inside the age range of the subjects affected by the disease. In this way, we avoided introducing additional variability to the gait parameters that could be predominantly age-related.
2.3. Classifiers
In this study, we used several classifiers to ensure the robustness of both classification performance and interpretability outcomes. Indeed, each classifier has different learning mechanisms and decision boundaries; by exploiting diverse methods, we could better assess the consistency and generalizability of the results. In particular, we employed the following classifiers:
- Random Forest (i.e., the RandomForestClassifier of scikit-learn (version 1.6.1) [25]);
- XGBoost (i.e., the XGBClassifier of the xgboost Python package, version 3.0.0);
- Multi-Layer Perceptron (i.e., the MLPClassifier of scikit-learn);
- Support Vector Machines (i.e., the SVC of scikit-learn), both with linear and Radial Basis Function (RBF) kernels.
XGBoost [26] is a tree-based classifier proven particularly effective for tabular data processing and classification. Furthermore, this classifier has better generalization capability and is less susceptible to overfitting than other classifiers. MLP consists of a feedforward network with fully connected layers, where every node of each adjacent layer is connected. Given the relatively small dataset employed and to limit model complexity, the MLP classifier employed in this work included a single hidden layer. It is a fast and easy-to-implement classifier and, despite its relative simplicity, can outperform other classifiers under certain conditions [27,28].
We optimized most of the parameters for each classifier, and we evaluated their importance for performance optimization using the optuna.importance.get_param_importances function of Optuna. For each fold, we recorded the optimal hyperparameter values and their importance. We collected the optimized values for the hyperparameters to better adjust the range of values and the granularity of the search during optimization, particularly focusing on those that have greater importance. The list of hyperparameters tuned for every classifier and the range chosen for optimization can be found in Appendix B.
2.4. Explainable AI
The quest for transparent and human-interpretable ML models has led to the development of several techniques, which are generally referred to as Explainable Artificial Intelligence (XAI). These techniques also opened the possibility of evaluating the contribution of individual input features to a model’s predictions, thus increasing the interpretability of the model output. Unlike classical feature selection methods, which are used before model training to identify the most predictive input variables, XAI methods are applied post hoc to assess feature contributions after model training, reflecting how the trained model uses the input features to make the prediction. This opens to the identification of context-specific effects, feature interactions, potential biases, or clinically relevant patterns. In this work, we applied these methods to enlighten the most relevant gait parameters using model-agnostic XAI methods. In this way, despite the different nature of the classifiers employed, the importance of the gait parameters can be compared.
In this regard, we applied permutation importance [15] and SHAP [16] for all the classifiers. Permutation importance is considered one of the global XAI methods. The permutation importance estimates the relevance of a feature by evaluating the change of a reference metric (e.g., the accuracy) of the classifier when the feature values are replaced with shuffled ones. A high score indicates that the shuffling of the feature values has a great impact on the classification, and vice versa, a negative score indicates that the performance of the classifier increased when the feature values were shuffled, meaning that the feature was not relevant for classification. In this work, we used the permutation_importance function of scikit-learn, with classification accuracy as the scoring metric. This method was applied to the model’s predictions on the test set, allowing us to evaluate the most relevant features for classifying previously unseen data.
SHAP [16] is a local, model-agnostic explanation method based on Shapley values computation, which uses only the input and output of a classifier. It is a game-theoretic approach that returns a value for each feature and for each prediction made by a classifier. The importance of each feature is based on averaging its marginal contribution to the classifier output conditioned on all possible subsets of other features. This method is not related to the correctness of the prediction; however, it can detect even a small contribution a feature has in the internal decision making of a classifier, even if its removal has no significant effect on the reference metric—differently from permutation importance, which estimates the impact of a feature on model performance [29]. As for the permutation importance, we computed the so-called SHAP values for each feature based on the model’s predictions on the test set (i.e., an array of dimension ). For each fold, we then took the absolute SHAP values and averaged them across data points, obtaining a single importance value for each feature (i.e., an array of dimension ). For tree-based models, a specific version of the SHAP explainer function was used, i.e., the TreeExplainer [30].
We computed the Shapley values only for the binary classification tasks. In fact, when a multi-class problem is studied with SHAP, the method returns, for each gait parameter, an array of size , with the Shapley value derived by treating the output for each class as the result of a binary classification (in a One-vs-Rest fashion). Moreover, SHAP values can change significantly among the classifiers. To better compare the values obtained for different classifiers, we first computed the average of the absolute SHAP values for every classification task and then normalized this quantity.
3. Results
This section presents the performance of the classifiers employed in the different classification tasks, followed by the results of the importance of the gait parameters. As discussed in Section 2.2, we extracted the performance evaluation metrics for every cross-validation fold. The results shown from now on have been averaged over the folds, and the standard deviation of the metrics is also shown to give insights on the fluctuation of the values.
By using only the gait parameters as input, the classifiers achieved optimal performance in distinguishing healthy subjects from people affected by a specific neurodegenerative disease, particularly in the case of Parkinson’s disease (PD) and hereditary spastic paraplegia (HSP), as shown in Figure 2.
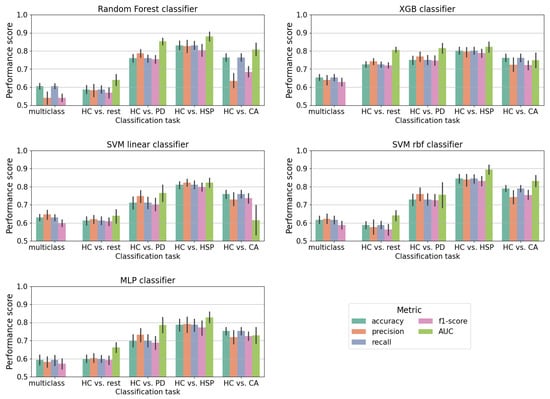
Figure 2.
Performance scores (i.e., accuracy, precision, recall, f1-score, and AUC metrics) from every classifier in each classification task. The scores are averaged over the folds and evaluated on the test set. The error bars represent the standard deviation of the metric values obtained from every fold.
To avoid age-related classification bias, the classifiers were trained using a population of healthy controls matched in age with the diseased groups. This was particularly important in the HC vs. PD task, where the average age of participants with Parkinson’s disease was notably higher than that of the healthy controls.
As expected, the binary classification tasks outperformed the multi-class setting across all classifiers. In the multi-class case, the accuracy results ranged from for the MLP to for the XGB. Similar trends were observed across the other evaluation metrics. The binary classification tasks reached accuracy values up to , particularly in the ones when only one disease was considered. Indeed this was expected, as each disease is characterized by specific gait alterations. In contrast, grouping all diseases into a broader class (i.e., in the HC vs. rest task) reduced discriminability, which was likely due to overlapping gait features among the conditions. Consequently, the relative importance of gait parameters is expected to vary depending on the disease considered.
In this regard, XAI methods were used here to enhance the model interpretability by identifying the most influential gait parameters in classification. Figure 3 shows the permutation importance for all the classifiers in different classification tasks.
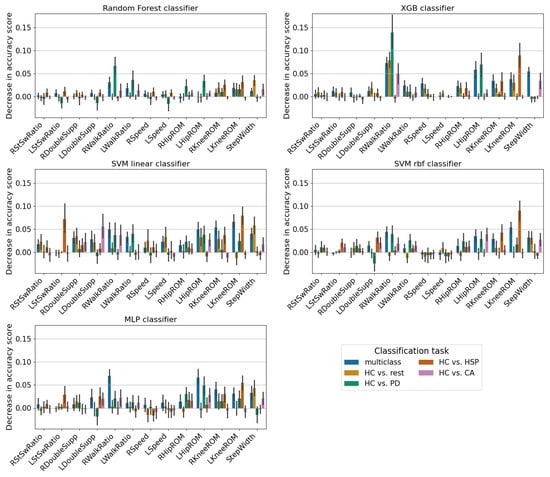
Figure 3.
Permutation importance of every gait parameter for every classifier and classification task. The values are collected for every fold so that the bin height is the average, and the black vertical bar is the standard deviation of the permutation importance over the folds. Higher values of the score indicate higher relevance of the feature analyzed.
As can be seen, many parameters had importance values within , with standard deviations that made the values consistent with zero, meaning that the importance of these gait parameters was not statistically significant. However, the walk ratio and knee ROM emerged as the most important gait parameters for all the classifiers. Figure 4 depicts the importance of the gait parameters estimated with the SHAP explainability method. In line with the permutation importance results, walk ratio and knee ROM were among the most relevant gait parameters, together with step width, which was significantly important for every classifier in the HC vs. CA classification task.
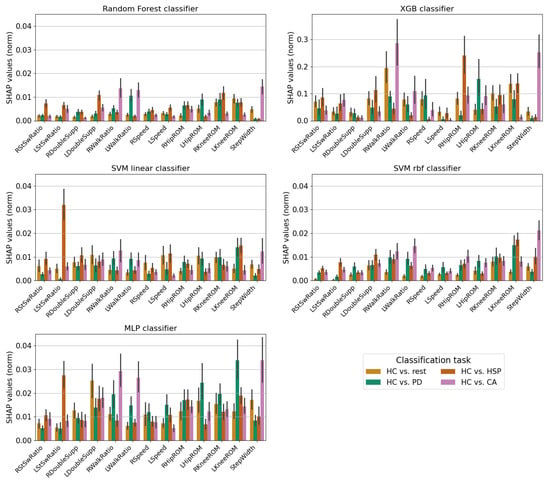
Figure 4.
Normalized SHAP importance of every gait parameter for every classifier and binary classification task. The bins represent the absolute SHAP values averaged over the folds, and the black vertical lines represent their standard deviation. Higher values of the score indicate higher relevance of the feature analyzed. Please note the different extent of the ordinate for the XGBoost classifier.
4. Discussion
Neurodegenerative diseases exhibit distinct gait characteristics, as revealed by the explainability methods used in this study. Compared to healthy gait, cerebellar ataxia shows reduced step and stride length, swing time, speed, and cadence and increased step width, stance time, and double support time. Moreover, many of these parameters show significant variability across different gait cycles [31]. This is consistent with our analysis: step width emerged as the most relevant gait parameter by SHAP for all the classifiers used, along with walk ratio, which is expected to decrease in ataxic gait due to reduced cadence and step length.
For Parkinson’s disease, the most important gait parameters for the classification, according to the explainability methods used, are the knee and hip ROMs and walk ratio. Indeed, as reported in [32,33,34], reduced ranges of motion are common gait impairments for PD patients, as well as an increased cadence and decreased step length, resulting in a lower walk ratio compared to healthy subjects.
In the classification of hereditary spastic paraplegia (HSP), both SHAP and permutation importance highlighted the knee ROM and the stance-to-swing time ratio as key features, and these are consistent with known gait impairments in HSP [35].
Ankle ROM, although known to decrease in pathological gait [35,36,37,38], was not used in our analysis. This decision was based on a systematic asymmetry observed in the left-limb data of healthy controls, which may have resulted in bias outcomes in our analysis. Further details are provided in Appendix A.
In general, we can notice that some gait characteristics, such as reduced ROM in lower-limb joints, are similar among different diseases. This effect may explain the lower performance on the multi-class classification task. To provide more insights into the multi-class classification task and the classification errors for each class, we also computed the confusion matrices for every classifier, which are shown in Figure A4, and their results are discussed in Appendix C. It can be noticed that the greater source of confusion is related to misclassification of subjects affected by a disease, which were classified as healthy (which was the class with more subjects), and to misclassification between HSP and PD subjects. Other methods have been adopted to improve the performance for this task, including a hierarchical approach, which classifies first healthy subjects from subjects affected by any disease, with a second classifier dedicated to the classification of the specific disease. Additionally, oversampling techniques such as SMOTE [39] have been adopted to achieve class balance during training. However, the results obtained were compatible with the ones achieved through the classification approach described in Section 2.2 and Section 2.3. More details on these methods can be found in Figures S3 and S4 in Supplementary Materials. The classification error between PD and HSP can be due to the overlap of gait parameters such as knee ROM (see Figure A1), which are considered relevant for classification and, at the same time, show a similar behavior between PD and HSP patients. In this regard, an in-depth analysis of the gait profiles may be beneficial for better distinguishing between different diseases. Moreover, a dataset with several gait cycles for each subject could also enable the evaluation of the relevance of the variability in certain gait parameters in different diseases.
As illustrated in Figure 3 and Figure 4, the features show different importance values, and gait parameters relevant for an XAI method cannot be as relevant for the other. This difference stems from the different approaches used by the methods to assess feature relevance. By combining permutation importance and SHAP, we aimed to capture both global and local patterns in feature relevance. Indeed, unlike the permutation importance, which assesses model sensitivity by measuring the decrease in performance when a feature’s values are randomly shuffled, SHAP extracts the Shapley values for each feature based on their contribution to the classifier prediction. In particular, different importance estimations from the two methods suggest that the feature contribution to the model’s predictions may arise primarily through interactions with other features (which are captured by SHAP) rather than through a strong marginal effect on predictive accuracy when considered in isolation.
An example is the step width in the HC vs. rest task, which was not among the most important parameters for permutation importance but was relevant according to SHAP. Moreover, parameter inter-relationships are common for gait analysis data; thus, shuffling the values of a gait parameter can have a limited impact on the model output, since related information may be retrieved from another gait parameter. In Figure S5 of the Supplementary Materials, we investigated the relation between gait parameters, revealing a high correlation between the same parameters for left and right limbs and an inverse relationship between speed and double support phases, which is expected from a biomechanical perspective. On the contrary, SHAP can assign similar importance values when features are dependent. For instance, we observed that when stance and swing time were provided separately to the model, rather than the stance-to-swing ratio, they yielded comparable SHAP values.
The results obtained in this work yielded lower classification performance than the ones obtained by [12], who used non-hierarchical clustering and presented accuracies spanning from to depending on the gait parameters employed. However, their study included a larger number of patients and parameters such as ankle ROM, which were excluded from our analysis for the reasons previously discussed.
Studies such as [40] showed higher performance outcomes using different machine learning models (including Random Forest classifiers) by providing the classifiers with both the gait parameters and some anthropometric data, which in this case were not considered for classification. Indeed, we aimed to provide insights only on the gait parameters’ role in the classification, using anthropometric data only for normalizing the parameters or for selecting the healthy controls within the same age range.
Other studies applied ML techniques and explainability methods in gait analysis for neurodegenerative diseases. For instance, reference [41] used ground reaction forces to train a deep learning classifier for the recognition of Parkinson’s disease and assessment of its severity. In particular, the model identifies specific frequency bands in the gait cycle associated with PD severity, which improves model interpretability. Similarly, reference [42] analyzed videos of patients to assess Parkinson’s severity. In that work, SHAP and other methods were used to improve the interpretability of the results. Given the dataset employed, both these studies focused on spatial and temporal gait parameters.
Many public gait analysis datasets, while valuable, present limitations for ML applications, which are mainly related to size and limited variability in participants. These limitations restrict the generalizability of models trained on such data. Additionally, differences in data acquisition protocols, sensor setups, and marker placements across datasets introduce biases that complicate cross-dataset comparisons and model transferability.
Despite being relatively small, the dataset employed in this work is one of the largest public collections providing both spatial, temporal, and kinematic data of patients affected by different neurodegenerative diseases, and it also comprises a dataset of healthy controls. This constrains the possibility of conducting a fully stratified analysis; nevertheless, this study can serve as a preliminary step toward achieving such an objective. In future work, a more granular examination of subgroups may be possible with larger and more diverse datasets.
Although we acknowledge that, from a purely clinical point of view, distinguishing among pathological gait patterns may not always be necessary once a diagnosis is established, our work is not intended to replace standard diagnostic procedures. Rather, it seeks to complement them by leveraging ML models and XAI techniques to uncover objective, discriminative gait features across different neurodegenerative diseases. In this regard, the classification of pathologies based on gait patterns holds promising potential for practical applications. For instance, this approach could be used as an auxiliary tool in screening programs aimed at identifying individuals at risk for specific neurodegenerative conditions, aiding early clinical decision making. Moreover, the use of standardized, data-driven gait analysis opens possibilities for remote patient monitoring and integration into telemedicine platforms, supporting longitudinal assessments and follow-up in a home setting, which are particularly relevant for patients with limited mobility or living in remote areas. This framework may offer valuable support in complex (e.g., patients showing low engagement) or ambiguous cases where the clinical presentation may not point clearly to a specific condition, and it can also assist in tracking disease progression or evaluating treatment efficacy over time.
5. Conclusions
This study presented the analysis of a public dataset of optoelectronic gait measurements for studying neurological diseases using an ML framework equipped with explainability methods. By employing multiple classifiers and techniques such as SHAP and permutation importance, we identified key gait features contributing to classification, showing strong agreement with known impairments associated with different neurodegenerative diseases.
Future improvements of the study can also shed light on the relevance of specific gait parameters with disease progression to see which gait parameter anomalies become more or less evident at a late disease stage. However, to have a more detailed description, additional data, such as kinetics data and joint angles time series data would be desirable, together with a larger dataset with multiple measures per subject to estimate the intra-subject gait variability.
In conclusion, this study highlights the potential of explainable machine learning to not only classify gait patterns but also to identify clinically meaningful gait parameters, paving the way for more interpretable and personalized diagnostic tools. In the future, such an approach could be applied at early stages of clinical assessment and integrated into screening programs for populations at risk for neurodegenerative diseases. Its capacity for fast analysis of large-scale gait data makes it particularly well suited for supporting timely and scalable decision making in both traditional and remote healthcare settings.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app15148078/s1. Figure S1: Speed and step length as a function of subjects’ height; Figure S2: Speed and step length as a function of subjects’ age; Figure S3: Confusion matrices of the multiclass classification tasks with hierarchical classification; Figure S4: Confusion matrices of the multiclass classification tasks using SMOTE for oversampling; Figure S5: Pearson correlation matrix for the gait parameters employed in the study.
Author Contributions
Conceptualization, investigation, methodology, writing—original draft: G.T., F.M., A.R. and P.O. Data curation, formal analysis, software, validation, visualization: G.T. and F.M. Funding acquisition, project administration, resources, supervision: A.R. and P.O. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Italian Ministry of Health, project TELE-NEURART, PSC Ministero Salute-FSC 2014-2020-Traiettoria 2 “E-Health, diagnostica avanzata, medical devices e mini invasività”-Linea di Azione 2.1 “Creazione di una rete nazionale per le malattie ad alto impatto”—CUP I53C22001040008. It was also partially supported by the following projects: Artificial Intelligence in Medicine (AIM), funded by INFN-CSN5; PNRR-M4C2-I1.3 PE00000013 “FAIR—Future Artificial Intelligence Research”, and PNRR-M4C2-I1.4 CN00000013-“ICSC—Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing”. Both of these are funded by the European Commission under the NextGeneration EU programme.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data used for this study can be found in [10].
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Exclusion of the Ankle ROM Data
As discussed in the main body of the work, the range of motion of the ankle (both from the left and right limb) is not used in our analysis. This choice is related to the fact that we identified this gait parameter as biased. This section provides insights into this matter.
Figure A1 shows the gait parameters of all the subjects grouped by their class (i.e., HC, PC, CA, or HSP) to qualitatively distinguish the variability of the parameters for different neurodegenerative diseases and healthy subjects. To better represent the extent of the data distributions, we z-scored them before grouping the data by their class.
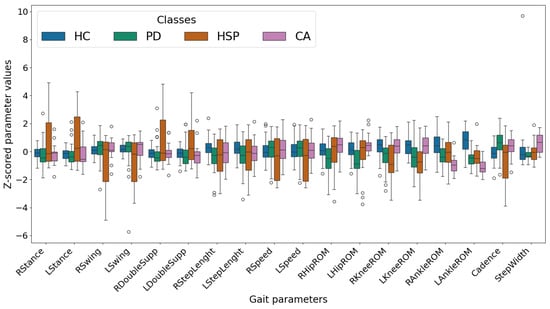
Figure A1.
Z-scored gait parameters of all the subjects of the dataset grouped by their class. The middle horizontal line in each box represents the average, with the boxplot extending to the quartiles of the data. The whiskers extend to the rest of the data distribution, and dots represent the outliers.
As expected, the different classes revealed different distributions. A visible example is represented by most of the distributions of the gait parameters of patients affected by hereditary spastic paraplegia, which are significantly broader than the values collected from healthy controls. Additionally, one of the parameters showing a significant difference in the distributions of controls and neurodegenerative disease is the ROM of the ankle. On the one hand, this is expected, since many studies indicate a decrease in the ankle ranges of motion in patients affected by neurodegenerative diseases [35,36,37,38]. On the other hand, it is also possible to notice a significant difference between the behaviors of HC distribution and the rest of the data when considering the left and right values of ankle ROM: when the distribution of right-ankle ROM (i.e., RAnkleROM) has a higher average but also presents a partial overlap with the distribution of other classes, as in the case of the left-ankle ROM (i.e., LAnkleROM), the HC distribution shows a different extent, with no overlap with other distributions of the same parameter.
To better visualize and estimate the difference in the ankle range of motion across the different classes, Figure A2 shows a scatter plot of the values collected for each patient and the relative distribution for every class.
The figure above clearly shows a different behavior of healthy controls and neurodegenerative diseases. Considering the distributions, when compared to the diseases, healthy controls showed higher values, and the difference in the distributions was more pronounced for the LAnkleROM than for the RAnkleROM. Additionally, subjects affected by neurodegenerative diseases showed similar values for the right and left limbs: Indeed, most of the points of the scatter plot were distributed along the bisector, with deviations in agreement with the expected degree of fluctuations between the left and right limbs. Nevertheless, healthy subjects showed values predominantly higher for the left limb, with in-subject differences that reached up to 20°, in contrast with what is reported in the literature for healthy subjects [43].
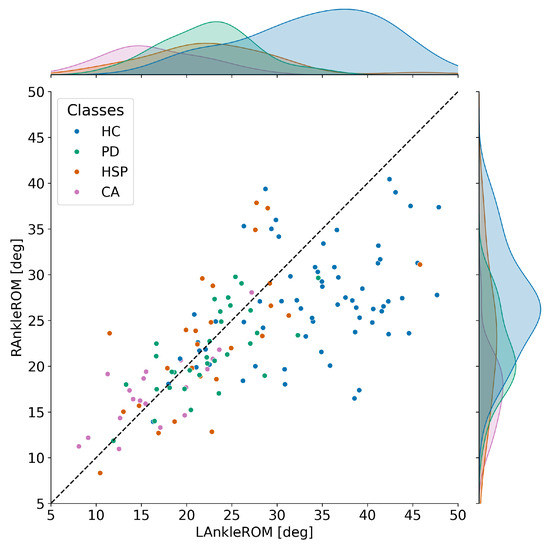
Figure A2.
Scatter plot with the values of ankle range of motion for left and right limbs. Each dot represents the values collected for a subject of the study, and the color represents his class. A dotted line indicates the line across which the left and right values of the angle are identical. On the top and on the right of the plot, the distributions of the values of LAnkleROM and RAnkleROM are shown for each class.
To statistically estimate the difference between left and right values of ankle ranges of motion between healthy controls and the subjects affected by neurodegenerative diseases, we performed the Welch’s t-test, which was supported by effect size estimations such as the Cohen’s d [44] and Hedges’ g [45] that are used to estimate the effect size in the case of small samples. The results are summarized in Table A1.

Table A1.
Effect sizes and t-test results for comparisons between healthy controls (HC) and neurodegenerative groups for left- and right-ankle ROM distributions.
Table A1.
Effect sizes and t-test results for comparisons between healthy controls (HC) and neurodegenerative groups for left- and right-ankle ROM distributions.
| Comparison | Cohen’s d | Hedges’ g | t-Statistic | p-Value | df | |
|---|---|---|---|---|---|---|
| LAnkleROM | HC vs. PD | 1.64 | 1.63 | 8.79 | 88.19 | |
| HC vs. CA | 2.37 | 2.35 | 11.41 | 45.17 | ||
| HC vs. HSP | 1.45 | 1.43 | 6.42 | 49.18 | ||
| RAnkleROM | HC vs. PD | 0.95 | 0.95 | 4.84 | 78.58 | |
| HC vs. CA | 1.70 | 1.68 | 7.92 | 42.02 | ||
| HC vs. HSP | 0.59 | 0.58 | 2.29 | 38.06 |
It can be noticed that the effect size was large both for the left and right limbs; however, the largest differences were consistently on the left ankle distributions. Similar conclusions can be driven considering the t-test results, which were statistically significant in all cases, but the left-limb comparisons produced p-values lower than the right-limb ones by several orders of magnitude. Additionally, a paired-samples t-test comparing the left- and right-ankle ROM distributions of healthy controls revealed a statistically significant difference, with , where .
Indeed, these parameters, when included in the analysis, led to an increase in classification performance by around 10% across all the classification tasks. Furthermore, XAI methods consistently identified left-ankle ROM as the most influential feature for classification.
Given the results obtained, we decided to exclude ankle range of motion values from the analyses presented in this work to minimize the risk of introducing biased data. The causes behind this unexpected difference are not known; however, we posit that a systematic marker misplacement during the acquisition of the healthy control data can be related to this behavior. Indeed, even a small marker misplacement can result in a significant difference in the kinematic measurements, with this effect being one of the most impactful for their variability [46].
Appendix B. Hyperparameter Tuning
In the following, we provide the list of the hyperparameters optimized through Optuna with the possible range of values for every classifier.
- Random Forest:
- –
- n_estimators—ranging from 100 to 1000, with a step of 100;
- –
- criterion—to be chosen between gini, entropy and log_loss;
- –
- max_depth—ranging from 2 to 8;
- –
- min_samples_split—ranging from 2 to 5;
- –
- min_samples_leaf—ranging from 1 to 5;
- –
- min_weight_fraction_leaf—ranging from 0 to , with a step of . In our case, all the data have the same weight;
- –
- max_features—to be chosen between sqrt and log2;
- –
- max_leaf_nodes—ranging between 4 and 16, with step of 1.
- XGBoost:
- –
- n_estimators—ranging from 100 to 1000, with a step of 100;
- –
- max_depth—ranging from 2 to 8;
- –
- max_leaves—ranging from 0 to 16, with step of 1;
- –
- learning_rate—ranging from to , with step of ;
- –
- booster—to be chosen between gbtree and dart;
- –
- gamma—ranging from 0 to , with step of ;
- –
- min_child_weight—ranging from 0 to 5, with step of 1;
- –
- max_delta_step—ranging from 0 to 10, with step of 1.
- MLP:
- –
- hidden_layer_sizes—ranging from 10 to 200, with a step of 10. This size refers to the number of nodes of the single hidden layer added to the model;
- –
- solver—to be chosen between sgd and adam;
- –
- alpha—ranging from to , with a step of ;
- –
- batch_size—ranging from 4 to 32, with a step of 4;
- –
- learning_rate—to be chosen between constant, invscaling, and adaptive;
- –
- learning_rate_init—ranging from to , with step of ;
- –
- power_t—ranging from to , with a step of ;
- –
- max_iter—ranging from 100 to 1000, with a step of 100;
- –
- tol—ranging from to , with step of ;
- –
- momentum—ranging from to , with step of .
- SVM: In this case, the kernel is treated separately from the other hyperparameters because of the kernel’s impact on the decision boundaries of the classifier. The hyperparameters optimized are the following:
- –
- C—ranging from to , with step of ;
- –
- gamma—to be chosen between scale and auto;
- –
- tol—ranging from to , with a step of ;
- –
- max_iter—ranging from 10 to , with a step of 100;
During hyperparameter optimization, the importance of each hyperparameter was computed by the Optuna function optuna.importance.get_param_importances. We used the importance estimation and the optimized hyperparameter value collected for each fold to adjust the ranges shown. Figure A3 shows the values of hyperparameter importance averaged over the folds for every classifier.
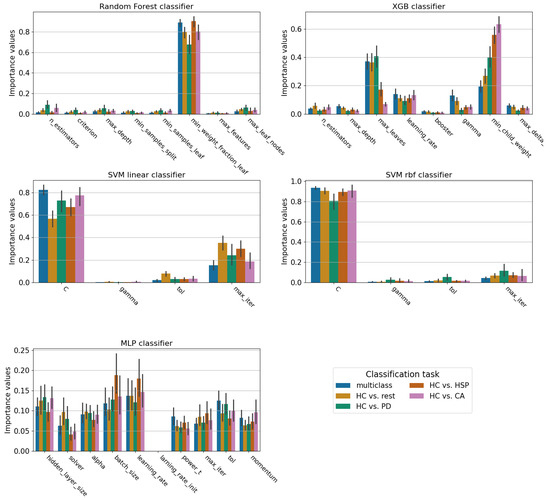
Figure A3.
Hyperparameter importance averaged over the folds for every classifier employed. Different bins represent the values of importance obtained when optimizing different classification tasks.
Appendix C. Confusion Matrices of the Multi-Class Classification Task
Figure 2 shows the classification performance metrics of the classifier employed in this study. As a support for investigating the performance of the multi-class classification task, we also computed the confusion matrices, which are shown in Figure A4.
As can be seen, the most relevant off-diagonal elements indicate misclassification of healthy subjects distributed across the three diseases, together with misclassification of subjects affected by a disease as healthy. This is mainly related to the class imbalance. Indeed, when the number of subjects does not vary significantly, e.g., in the case of the three neurodegenerative diseases, the off-diagonal elements show relatively low values. The most relevant misclassification in this case is the one between the PD and HSP patients. Indeed, as can be seen in Figure A1, some of the gait parameters with large importance for both the cases, such as knee range of motion, showed some similarities between the two classes of neurodegenerative diseases, with CA patients showing different distributions of such a parameter.
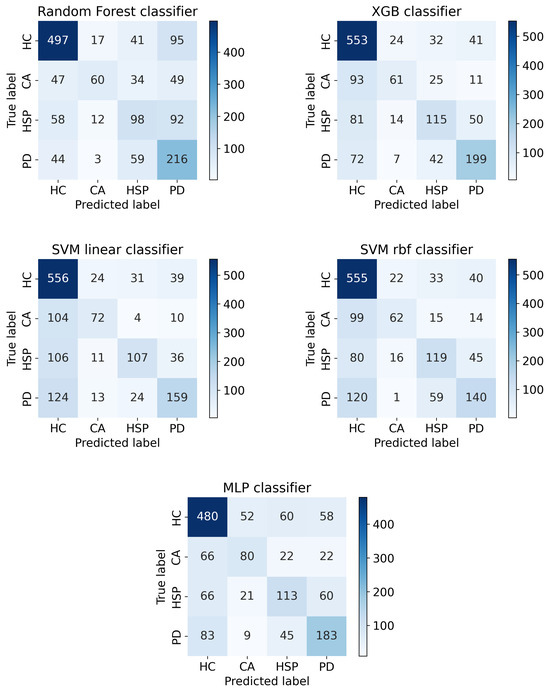
Figure A4.
Confusion matrices of the multi-class classification tasks for the classifiers employed in this study. The entries of the confusion matrices are summed over the folds.
References
- Hausdorff, J.M.; Rios, D.A.; Edelberg, H.K. Gait variability and fall risk in community-living older adults: A 1-year prospective study. Arch. Phys. Med. Rehabil. 2001, 82, 1050–1056. [Google Scholar] [CrossRef] [PubMed]
- Cicirelli, G.; Impedovo, D.; Dentamaro, V.; Marani, R.; Pirlo, G.; D’Orazio, T.R. Human Gait Analysis in Neurodegenerative Diseases: A Review. IEEE J. Biomed. Health Inform. 2022, 26, 229–242. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.M. Gait Disorders. Am. J. Med. 2018, 131, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Bodranghien, F.; Bastian, A.; Casali, C.; Hallett, M.; Louis, E.D.; Manto, M.; Mariën, P.; Nowak, D.A.; Schmahmann, J.D.; Serrao, M.; et al. Consensus Paper: Revisiting the Symptoms and Signs of Cerebellar Syndrome. Cerebellum 2015, 15, 369–391. [Google Scholar] [CrossRef] [PubMed]
- Comber, L.; Galvin, R.; Coote, S. Gait deficits in people with multiple sclerosis: A systematic review and meta-analysis. Gait Posture 2017, 51, 25–35. [Google Scholar] [CrossRef] [PubMed]
- Creaby, M.W.; Cole, M.H. Gait characteristics and falls in Parkinson’s disease: A systematic review and meta-analysis. Park. Relat. Disord. 2018, 57, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Khera, P.; Kumar, N. Role of machine learning in gait analysis: A review. J. Med. Eng. Technol. 2020, 44, 441–467. [Google Scholar] [CrossRef] [PubMed]
- Horsak, B.; Slijepcevic, D.; Raberger, A.M.; Schwab, C.; Worisch, M.; Zeppelzauer, M. GaitRec, a large-scale ground reaction force dataset of healthy and impaired gait. Sci. Data 2020, 7, 143. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M. Gait in Parkinson’s Disease. 2008. Available online: https://physionet.org/content/gaitpdb/1.0.0/ (accessed on 11 July 2025).
- Serrao, M.; Chini, G.; Bergantino, M.; Sarnari, D.; Casali, C.; Conte, C.; Ranavolo, A.; Marcotulli, C.; Rinaldi, M.; Coppola, G.; et al. Dataset on gait patterns in degenerative neurological diseases. Data Brief 2018, 16, 806–816. [Google Scholar] [CrossRef] [PubMed]
- Schülein, S.; Barth, J.; Rampp, A.; Rupprecht, R.; Eskofier, B.M.; Winkler, J.; Gaßmann, K.G.; Klucken, J. Instrumented gait analysis: A measure of gait improvement by a wheeled walker in hospitalized geriatric patients. J. Neuroeng. Rehabil. 2017, 14, 18. [Google Scholar] [CrossRef] [PubMed]
- Serrao, M.; Chini, G.; Bergantino, M.; Sarnari, D.; Casali, C.; Conte, C.; Ranavolo, A.; Marcotulli, C.; Rinaldi, M.; Coppola, G.; et al. Identification of specific gait patterns in patients with cerebellar ataxia, spastic paraplegia, and Parkinson’s disease: A non-hierarchical cluster analysis. Hum. Mov. Sci. 2018, 57, 267–279. [Google Scholar] [CrossRef] [PubMed]
- Özateş, M.E.; Yaman, A.; Salami, F.; Campos, S.; Wolf, S.I.; Schneider, U. Identification and interpretation of gait analysis features and foot conditions by explainable AI. Sci. Rep. 2024, 14, 5998. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.K.; Bae, M.N.; Lee, K.; Kim, J.C.; Hong, S.G. Explainable Artificial Intelligence and Wearable Sensor-Based Gait Analysis to Identify Patients with Osteopenia and Sarcopenia in Daily Life. Biosensors 2022, 12, 167. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification And Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Hof, A.L. Scaling gait data to body size. Gait Posture 1996, 4, 222–223. [Google Scholar] [CrossRef]
- Nagasaki, H.; Itoh, H.; Hashizume, K.; Furuna, T.; Maruyama, H.; Kinugasa, T. Walking Patterns and Finger Rhythm of Older Adults. Percept. Mot. Skills 1996, 82, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Sekiya, N.; Nagasaki, H. Reproducibility of the walking patterns of normal young adults: Test-retest reliability of the walk ratio(step-length/step-rate). Gait Posture 1998, 7, 225–227. [Google Scholar] [CrossRef] [PubMed]
- Bogen, B.; Moe-Nilssen, R.; Kristin Aaslund, M. O27: The Walk Ratio: Gender differences or height differences? Gait Posture 2017, 57, 49. [Google Scholar] [CrossRef]
- Perry, J. Gait Analysis: Normal and Pathological Function; SLACK: Thorofare, NJ, USA, 1992. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Rössler, R.; Wagner, J.; Knaier, R.; Rommers, N.; Kressig, R.W.; Schmidt-Trucksäss, A.; Hinrichs, T. Spatiotemporal gait characteristics across the adult lifespan: Reference values from a healthy population—Analysis of the COmPLETE cohort study. Gait Posture 2024, 109, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Schloemer, S.A.; Thompson, J.A.; Silder, A.; Thelen, D.G.; Siston, R.A. Age-Related Differences in Gait Kinematics, Kinetics, and Muscle Function: A Principal Component Analysis. Ann. Biomed. Eng. 2016, 45, 695–710. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular Data: Deep Learning is Not All You Need. arXiv 2021, arXiv:2106.03253. [Google Scholar] [CrossRef]
- Hossain, M.; Kabir, M.; Anwar, A.; Islam, M.Z. Detecting autism spectrum disorder using machine learning techniques. Health Inf. Sci. Syst. 2021, 9, 17. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ma, Y. Application of supervised machine learning algorithms in the classification of sagittal gait patterns of cerebral palsy children with spastic diplegia. Comput. Biol. Med. 2019, 106, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Molnar, C. Interpretable Machine Learning, 3rd ed.; Christoph Molnar. 2025. Available online: https://christophm.github.io/interpretable-ml-book (accessed on 11 July 2025).
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 2522–5839. [Google Scholar] [CrossRef] [PubMed]
- Buckley, E.; Mazzà, C.; McNeill, A. A systematic review of the gait characteristics associated with Cerebellar Ataxia. Gait Posture 2018, 60, 154–163. [Google Scholar] [CrossRef] [PubMed]
- Zanardi, A.P.J.; da Silva, E.S.; Costa, R.R.; Passos-Monteiro, E.; dos Santos, I.O.; Kruel, L.F.M.; Peyré-Tartaruga, L.A. Gait parameters of Parkinson’s disease compared with healthy controls: A systematic review and meta-analysis. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef] [PubMed]
- Pistacchi, M. Gait analysis and clinical correlations in early Parkinson’s disease. Funct. Neurol. 2017, 32, 28. [Google Scholar] [CrossRef] [PubMed]
- Russo, M.; Amboni, M.; Pisani, N.; Volzone, A.; Calderone, D.; Barone, P.; Amato, F.; Ricciardi, C.; Romano, M. Biomechanics Parameters of Gait Analysis to Characterize Parkinson’s Disease: A Scoping Review. Sensors 2025, 25, 338. [Google Scholar] [CrossRef] [PubMed]
- Faccioli, S.; Cavalagli, A.; Falocci, N.; Mangano, G.; Sanfilippo, I.; Sassi, S. Gait analysis patterns and rehabilitative interventions to improve gait in persons with hereditary spastic paraplegia: A systematic review and meta-analysis. Front. Neurol. 2023, 14, 1256392. [Google Scholar] [CrossRef] [PubMed]
- Serrao, M.; Chini, G.; Casali, C.; Conte, C.; Rinaldi, M.; Ranavolo, A.; Marcotulli, C.; Leonardi, L.; Fragiotta, G.; Bini, F.; et al. Progression of Gait Ataxia in Patients with Degenerative Cerebellar Disorders: A 4-Year Follow-Up Study. Cerebellum 2016, 16, 629–637. [Google Scholar] [CrossRef] [PubMed]
- Palliyath, S.; Hallett, M.; Thomas, S.L.; Lebiedowska, M.K. Gait in patients with cerebellar ataxia. Mov. Disord. 1998, 13, 958–964. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.I.; Braatz, F.; Metaxiotis, D.; Armbrust, P.; Dreher, T.; Döderlein, L.; Mikut, R. Gait analysis may help to distinguish hereditary spastic paraplegia from cerebral palsy. Gait Posture 2011, 33, 556–561. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Loya, A.; Deshpande, S.; Purwar, A. Machine Learning Driven Individualized Gait Rehabilitation: Classification, Prediction, and Mechanism Design. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 5A: 43rd Mechanisms and Robotics Conference; Anaheim, CA, USA, 18–21 August 2019, American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Salimi-Badr, A.; Veisi, M.; Berangi, S. SincPD: An Explainable Method based on Sinc Filters to Diagnose Parkinson’s Disease Severity by Gait Cycle Analysis. arXiv 2025, arXiv:2502.17463. [Google Scholar]
- Rupprechter, S.; Morinan, G.; Peng, Y.; Foltynie, T.; Sibley, K.; Weil, R.S.; Leyland, L.A.; Baig, F.; Morgante, F.; Gilron, R.; et al. A Clinically Interpretable Computer-Vision Based Method for Quantifying Gait in Parkinson’s Disease. Sensors 2021, 21, 5437. [Google Scholar] [CrossRef] [PubMed]
- Ugbolue, U.C.; Robson, C.; Donald, E.; Speirs, K.L.; Dutheil, F.; Baker, J.S.; Dias, T.; Gu, Y. Joint Angle, Range of Motion, Force, and Moment Assessment: Responses of the Lower Limb to Ankle Plantarflexion and Dorsiflexion. Appl. Bionics Biomech. 2021, 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: Abingdon, UK, 2013. [Google Scholar] [CrossRef]
- Hedges, L.V. Distribution Theory for Glass’s Estimator of Effect size and Related Estimators. J. Educ. Stat. 1981, 6, 107–128. [Google Scholar] [CrossRef]
- Gorton, G.E.; Hebert, D.A.; Gannotti, M.E. Assessment of the kinematic variability among 12 motion analysis laboratories. Gait Posture 2009, 29, 398–402. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).