Reaction Forces and Apparent Thrust in Dual Oscillating Control Moment Gyroscopes
Abstract
1. Introduction
- When the intended thrust was upward, the average reaction force at two (front end) out of the four cart wheels was also directed upward (thus claiming net thrust, in violation of Newton’s third law), consistent with the behavior shown in Figure 1.
- When the intended thrust was horizontal, the oscillation of the eccentricity resulted in smooth, continuous rolling of the cart along the ground (video-recorded in [25]). This effect was attributed to frictional forces similar to those involved in human locomotion.
2. Materials and Methods
2.1. General
2.2. Presentation of the Mechanical Set-Up
2.3. Description of Mechanical Model
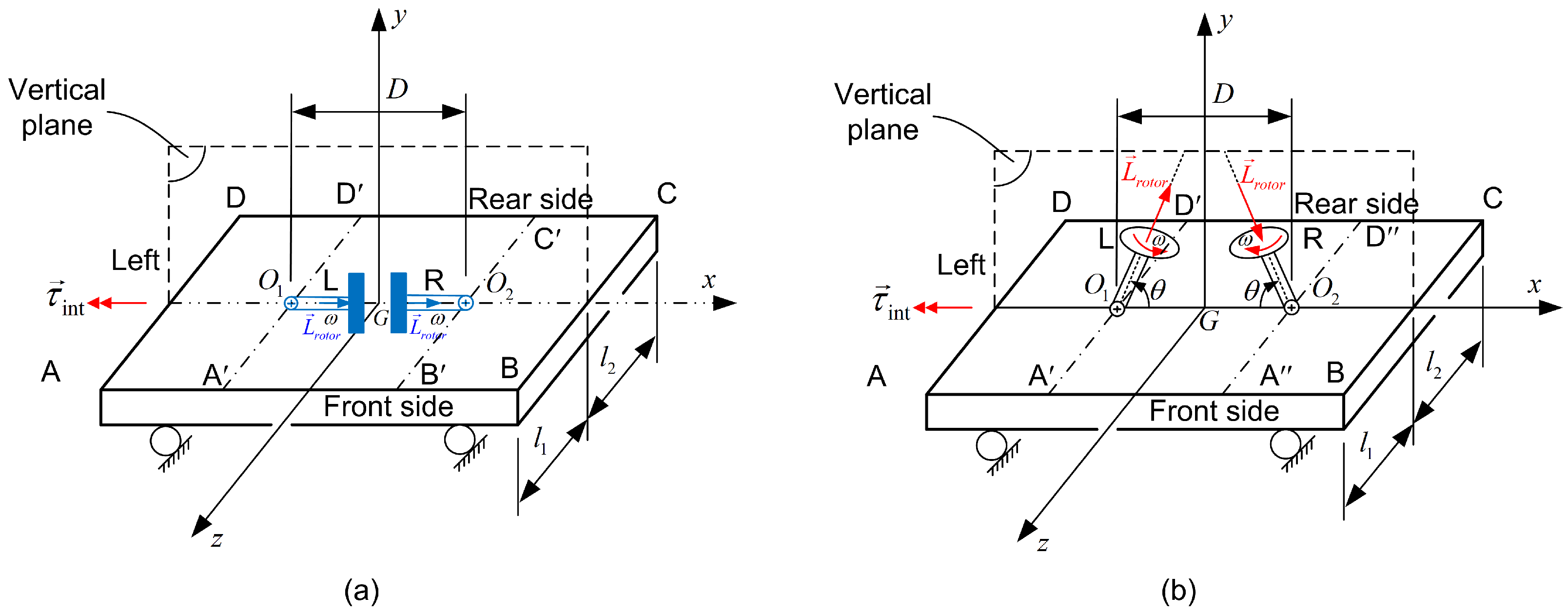
- The propulsion system consists of two identical gyroscopes that undergo controlled rotation (forced precession) about parallel spindles, positioned at the same height above the horizontal ground. The ideal geometric axis of each spindle is fixed relative to the cart. As is customary, each spinning wheel is housed within a circular ring, with its spin axis mounted on a gimbal (Figure 3). These two frames are mutually perpendicular and behave as a rigid body with one degree of freedom (see the third bullet below for further details).
- Each gyroscope is spun by an electric motor (driver) mounted on the gimbal (Figure 3), maintaining a nearly constant spin rate .
- The single degree of freedom for each gyroscope (illustrated in Figure 2b), along with the associated spindle rotation, is actuated by a servomotor (torquer).
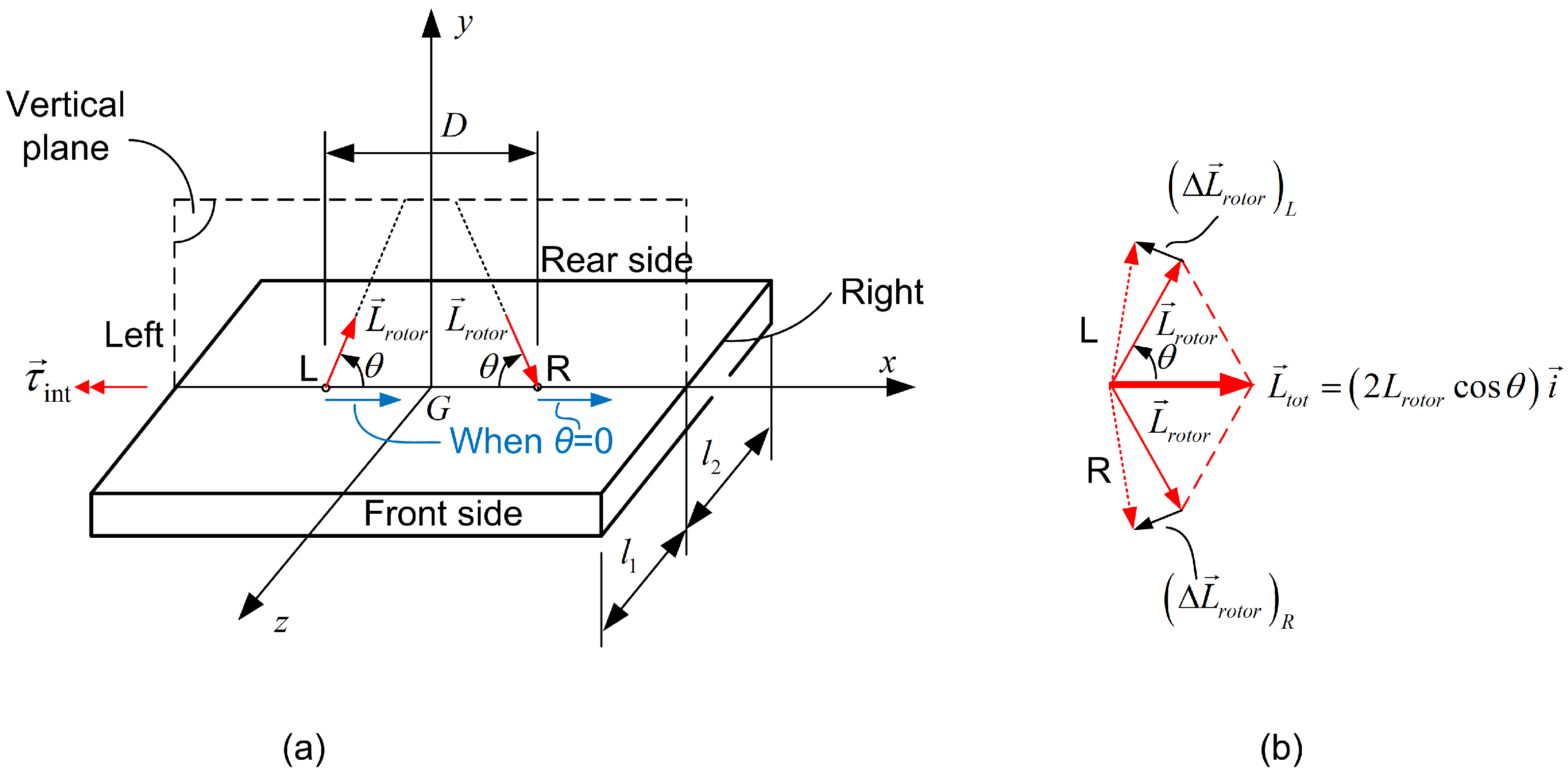
- When the axes of the synchronized gyroscopes are coaligned, they share the same magnitude and direction of angular velocity (see Figure 2a). This means that on the left gyrocope (L), the vector of angular momentum is directed from the pivot toward the spinning wheel, whereas on the right gyroscope (R), it is directed from the spinning wheel to the pivot .
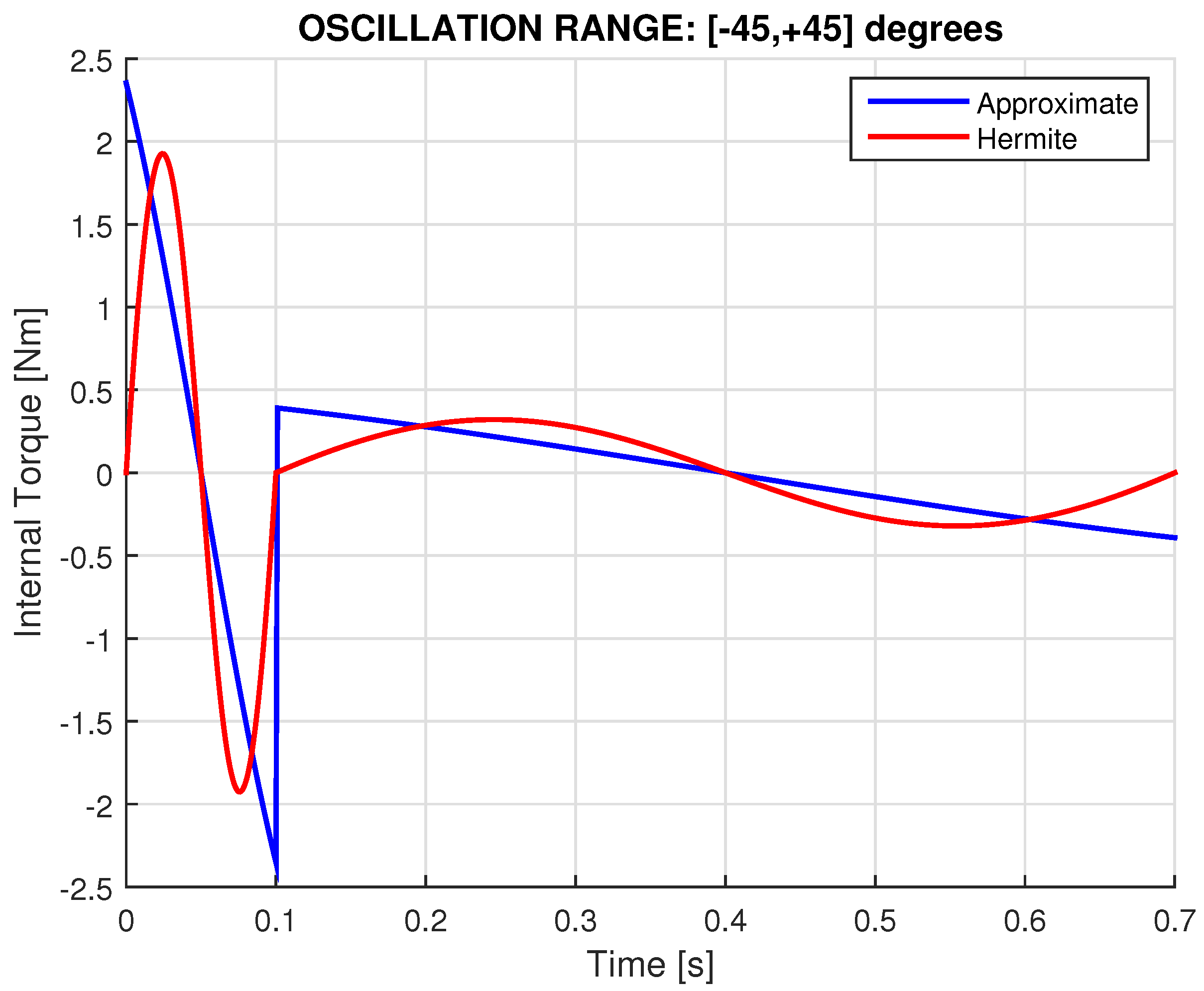
2.4. Differential Torques
2.5. Modeling the Inertial Forces
- Due to rotating masses (Dean-drive term): This kind will be discussed below in the current subsection.
- Due to gyroscopic motion: This kind was covered above in Section 2.2.
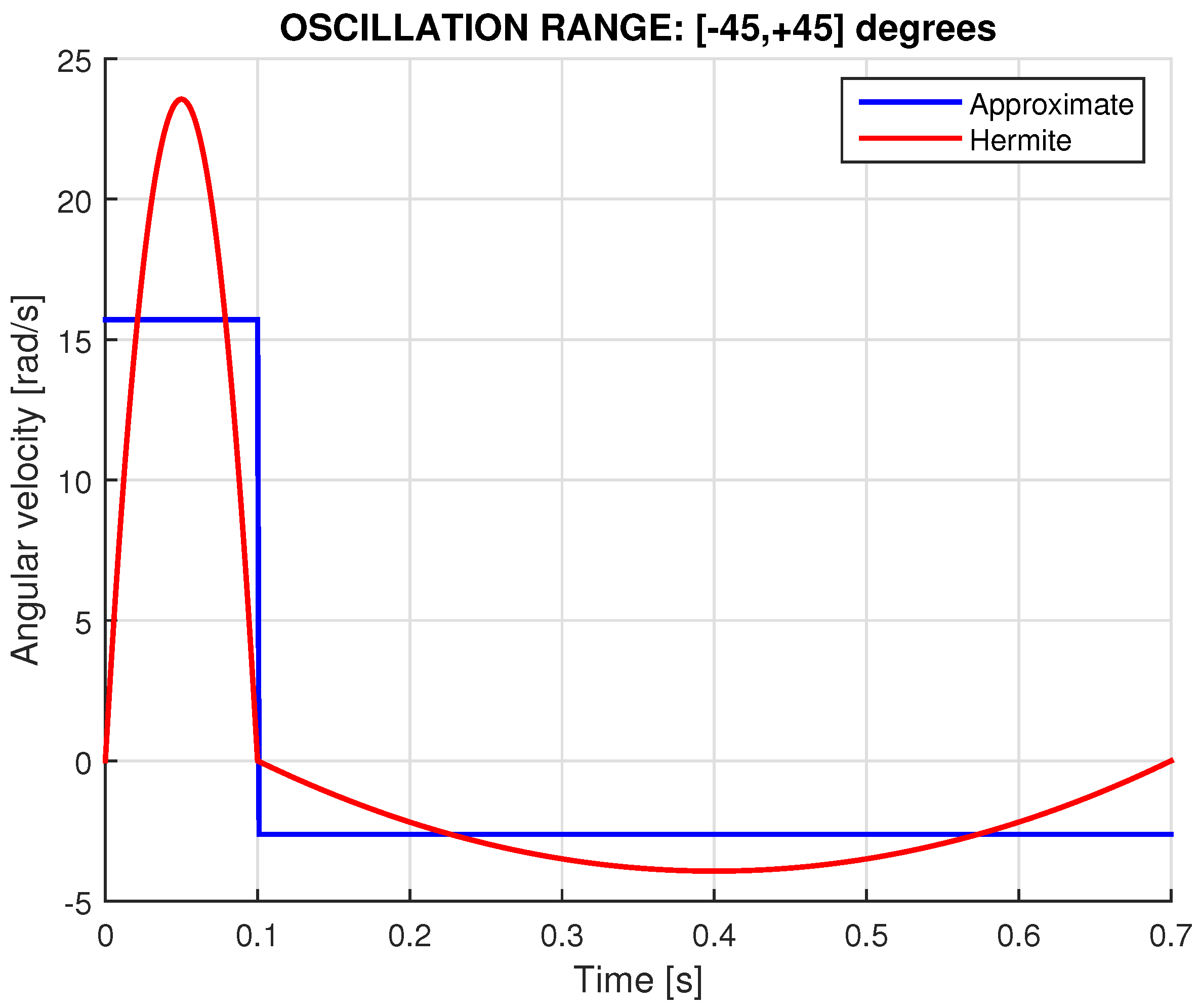
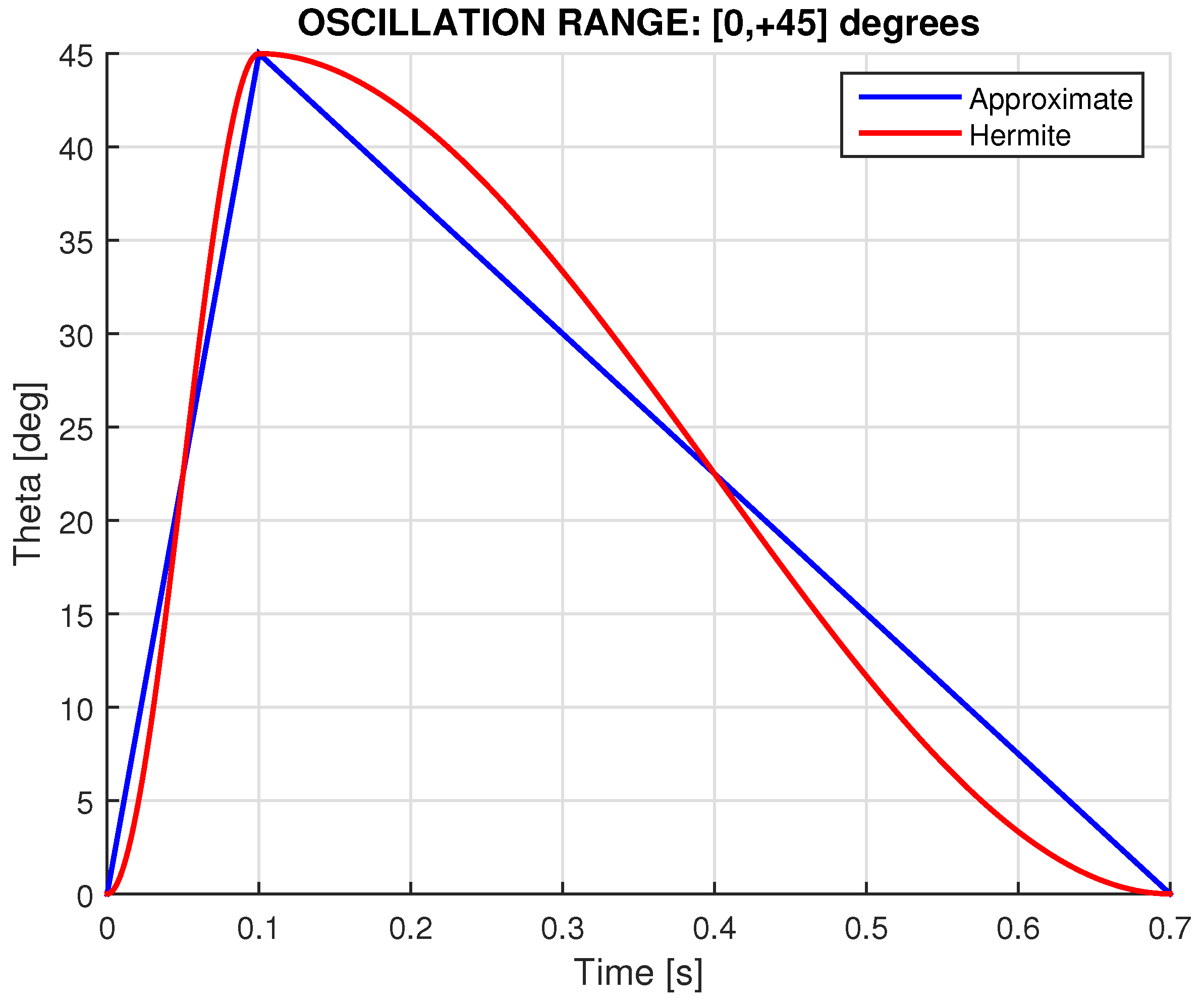
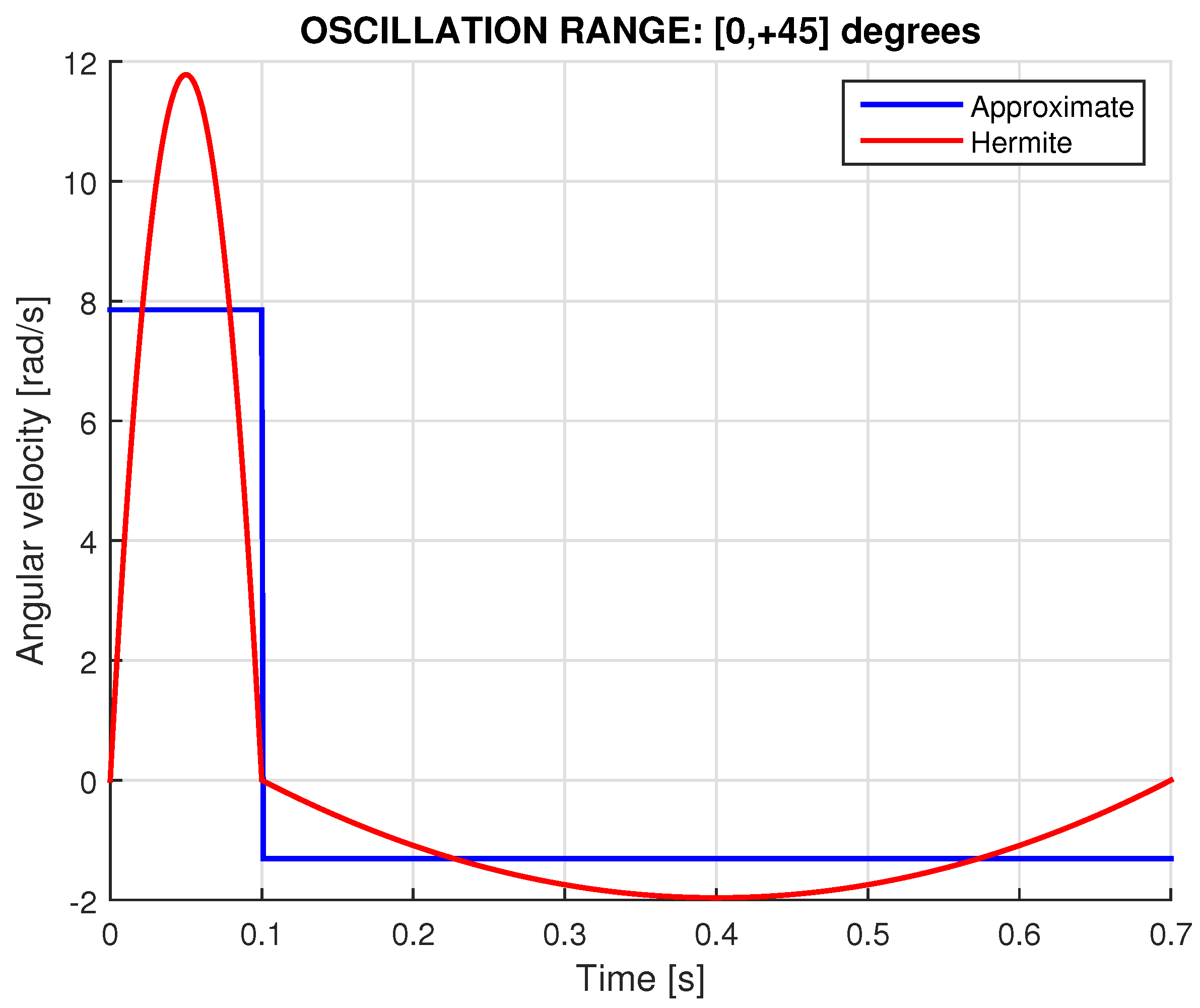
- Approximate Model: A constant angular velocity per phase, with one high for “rise” and another low for “reset”.
- Exact Model: A variable angular velocity which vanishes at the ends of the angular oscillation (), where the polar angle corresponds to the transition from “rise” to “reset”.
2.6. Dynamic Equilibrium: Newton’s Laws
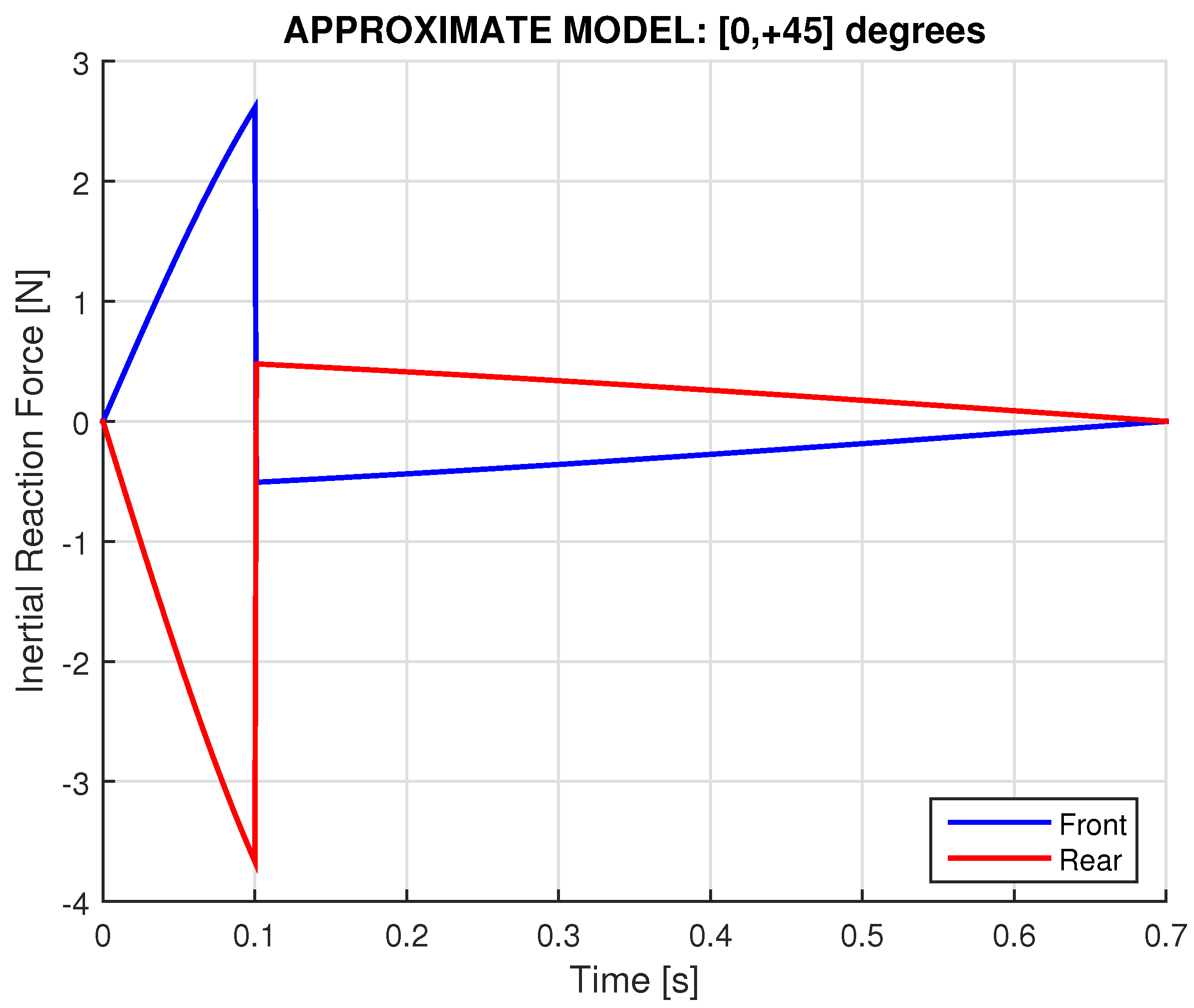
2.6.1. Approximate Model: Piecewise-Constant Angular Velocity
- Both reaction (ground) forces at the front and rear ends of the cart are influenced by the inertial forces () as well as the gyroscopic term ().
- While in the Dean drive the excitation force is distributed proportionally to the lever lengths ( and ), as shown by the second terms inside the square brackets, the asymmetry due to the internal torque (directed to the negative side of the x axis)—imposed by the operation of the dual gyroscopes—results in an equal differentiation of the reaction forces at the front (with the + sign) and rear (with the − sign) supports. In other words, what is lost at the front support is gained at the rear support, and vice versa.
- When (i.e., the axles are beyond the horizontal level), if we isolate the out-of-balance mass (Dean drive term), then it relieves both the front and rear reaction forces. Nevertheless, the additional gyroscopic term operates as follows. The front reaction force further decreases while the (previously decreased by the Dean-drive term) rear force increases. The latter finding is in accordance with the experimental results reported by the creators of the prototypes [22,23,24,25], and thus the above discussion demystifies them.
- Given , the difference between the Dean drive effect and the gyroscopic effect highly depends on the spin () and thus the associated angular momentum .
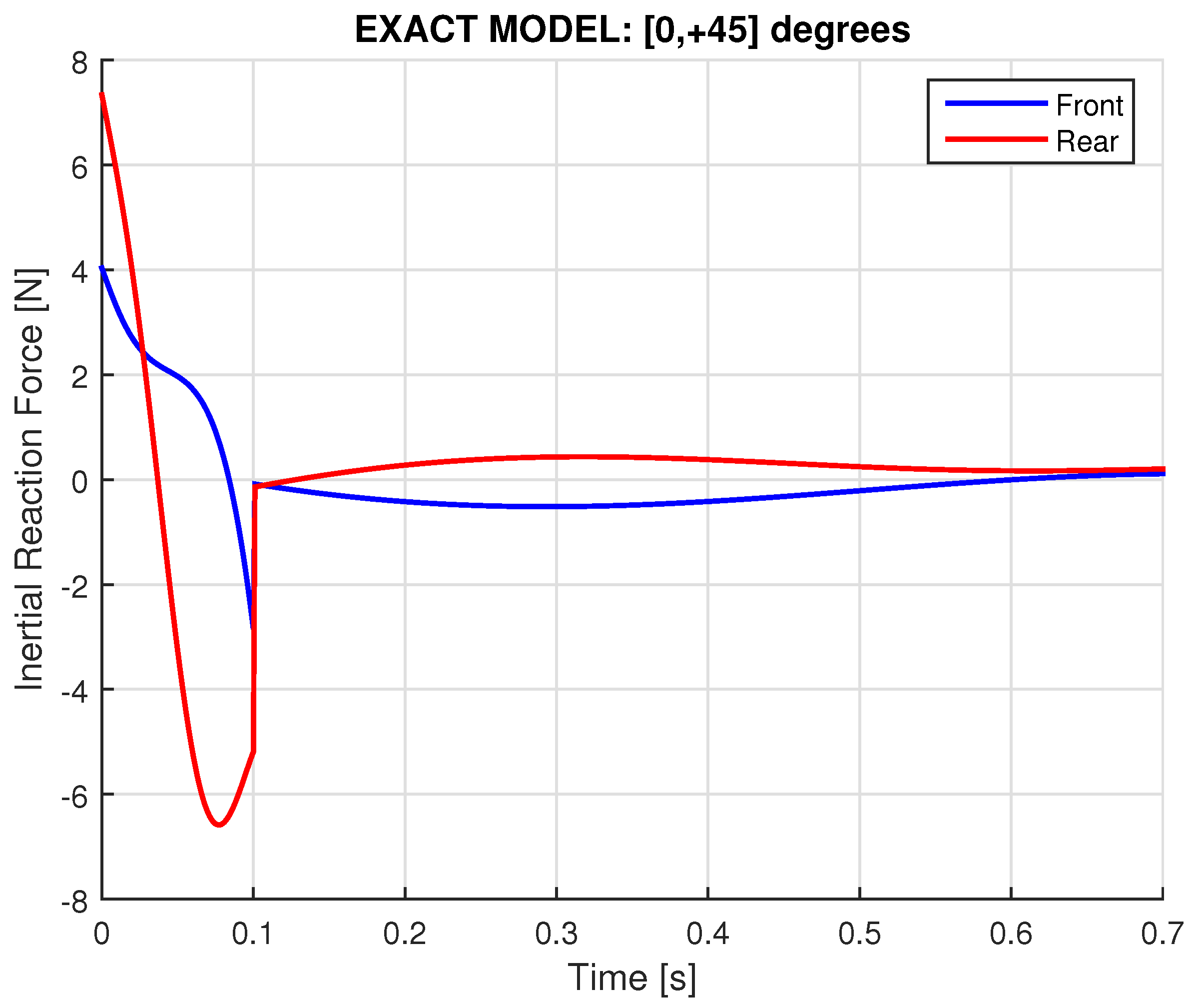
2.6.2. Exact Model: Variable Angular Velocity
2.7. Operation
2.8. Impulse of Reaction Forces
2.8.1. Approximate Model
2.8.2. Variable Angular Velocity
2.8.3. The Most General Case
3. Numerical Simulation
- Axle oscillation in the interval ;
- Axle oscillation in the interval .
3.1. General Data
- Mass of the gyroscope’s frame: g;
- Mass of the gyroscope’s rotor: g;
- Mass of the motor driver: g;
- Length of the motor driver: mm;
- Rotor’s outer diameter: mm;
- Rotor’s inner diameter: mm;
- Rotor speed: 16,000 RPM;
- Frame’s outer diameter: mm;
- Length from the front end to the centroid: m;
- Length from the rear end to the centroid: m (i.e., );
- Time for the rising phase: s;
- Time for the reset phase: s.
3.2. Elementary Calculations
3.3. Numerical Implementation of the Approximate Model
- Split the rising interval (100 ms) into 100 equal segments, thus using a time step of .
- At the end of the ith time step, calculate the current time instant as .
- Find the current polar angle with .
- Find the inertial force of the Dean drive with .
- Find the differential gyroscopic torque with .
- Find the total vertical reaction force of the cart with .
- Find the vertical reaction force at the rear support with .
- Find the vertical reaction force at the front support with .
- Continue with the reset phase of the first cycle, in which is replaced by and the updated initial polar angle is with the final , while the new interval is divided into 600 equal time steps.
3.4. Servo Oscillation for
3.5. Servo Oscillation for
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robertson, G.A.; Murad, P.A.; Davis, E. New frontiers in space propulsion sciences. Energy Convers. Manag. 2008, 49, 436–452. [Google Scholar] [CrossRef]
- Robertson, G.A.; Webb, D.W. The death of rocket science in the 21st century. Phys. Procedia 2011, 20, 319–330. [Google Scholar] [CrossRef]
- Allen, J.E. Quest for a novel force: A possible revolution in aerospace. Prog. Aerosp. Sci. 2003, 39, 1–60. [Google Scholar] [CrossRef]
- Meek, J. Bae’s Anti-Gravity Research Braves X-Files Ridicule. The Guardian. 27 March 2000. Available online: https://www.theguardian.com/science/2000/mar/27/uknews (accessed on 22 June 2025).
- Anonymous. Project Greenglow and the Battle with Gravity. News. 23 March 2016. Available online: https://www.bbc.com/news/magazine-35861334 (accessed on 22 June 2025).
- Interview from Ron Evans. Available online: https://www.youtube.com/watch?v=BwI7Ij-5cMA&ab_channel=TimVentura (accessed on 22 June 2025).
- Wilson, J. Science Does the Impossible: February 2003 Cover Story. Pop. Mech. 2003, 180. Available online: https://books.google.gr/books?id=UtMDAAAAMBAJ&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false (accessed on 22 June 2025).
- Millis, M.G. Breakthrough Propulsion Physics Research Program. AIP Conf. Proc. 1997, 387, 1297–1302. [Google Scholar] [CrossRef]
- Millis, M.G. NASA breakthrough propulsion physics program. Acta Astronaut. 1999, 44, 175–182. [Google Scholar] [CrossRef]
- Millis, M.G. Assessing potential propulsion breakthroughs. Annu. N. Y. Acad. Sci. 2005, 1065, 441–461. [Google Scholar] [CrossRef]
- Millis, M.G. Progress in revolutionary propulsion physics, Paper IAC-10-C4.8.7. In Proceedings of the 61st International Astronautical Congress, Prague, Czech Republic, 27 September–1 October 2010. [Google Scholar]
- Millis, M.G.; Davis, E.W. Frontiers of Propulsion Science; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2009. [Google Scholar]
- Dean, N.L. System for Converting Rotary Motion into Unidirectional Motion. U.S. Patent 2,886,976, 19 May 1959. [Google Scholar]
- Dean, N.L. Variable Oscillator System. U.S. Patent 3,182,517, 11 May 1965. [Google Scholar]
- Laithwaite, E.R. Propulsion Without Wheels, 2nd ed.; English Universities Press: London, UK, 1970. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Eric_Laithwaite (accessed on 23 January 2024).
- Laithwaite, E.R. The Engineer through the Looking Glass|The Royal Institution: Science Lives Here. Available online: https://www.rigb.org/explore-science/explore/video/engineer-through-looking-glass-looking-glass-house-1974 (accessed on 7 January 2024).
- Provatidis, C.G. Inertial Propulsion Devices: A Review. Eng 2024, 5, 851–880. [Google Scholar] [CrossRef]
- Provatidis, C.G. On the incapability of inertial forces as a means of repeated self-propulsion of an object in a vacuum. Proc. Eur. Acad. Sci. Arts 2025, 4, 45. [Google Scholar] [CrossRef]
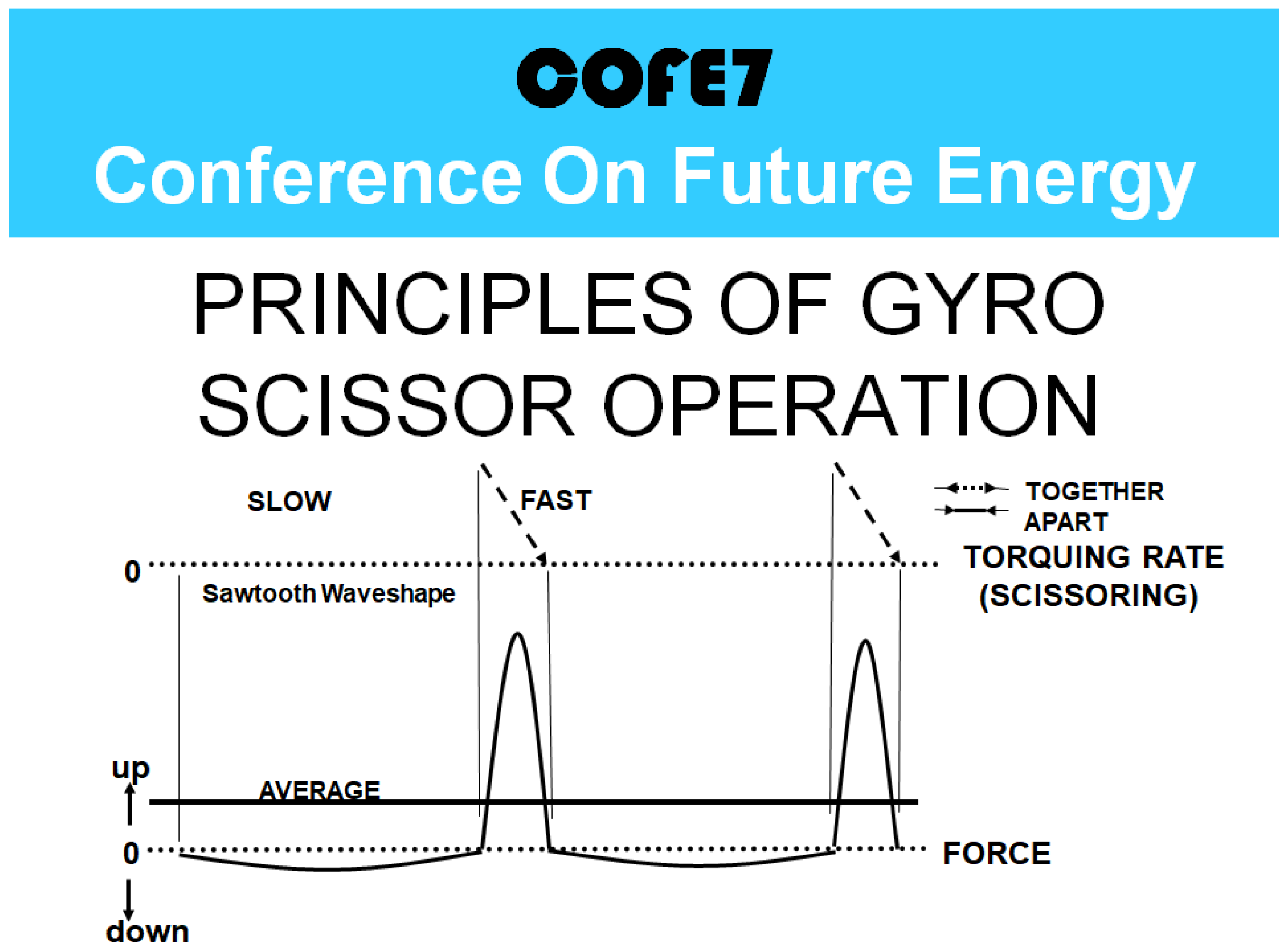
- Gamble, M. History of Boeing control moment gyros (CMG). Presented at the Seventh International Conference on Future Energy (COFE7), Embassy Suites, (Boeing 15-00051-EOT), Albuquerque, NM, USA, 30 July–1 August 2015. [Google Scholar]
- Gamble, M. Linear propulsion. Presented at the Seventh International Conference on Future Energy (COFE7), Embassy Suites, Albuquerque, NM, USA, 30 July–1 August 2015. [Google Scholar]
- Gamble, M. Dual CMG Gyroscopic Operation. In Proceedings of the COFE9, Albuquerque, NM, USA, 30 July 2017. [Google Scholar]
- Gamble, M.; Valone, T. Differential CMG (Part II). In Proceedings of the COFE10, Albuquerque, NM, USA, 10 August 2018. [Google Scholar]
- Gamble, M.; Valone, T. Control Moment Gyro Experiment (Part III). In Proceedings of the COFE11, Albuquerque, NM, USA, 9–10 August 2019. [Google Scholar]
- Gamble, M.; Valone, T. Differential CMG (Part IV). In Proceedings of the COFE12, Online, 14 August 2020; Available online: https://www.youtube.com/watch?v=n1CH9_0Fs0E&ab_channel=ThomasValone (accessed on 17 July 2025).
- Leve, F.A.; Hamilton, B.J.; Peck, M.A. Spacecraft Momentum Control Systems; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Gurrisi, C.; Seidel, R.; Dickerson, S.; Didziulis, S.; Frantz, P.; Ferguson, K. Space Station Control Moment Gyroscope Lessons Learned. In Proceedings of the 40th Aerospace Mechanisms Symposium, NASA Kennedy Space Center, Cocoa Beach, FL, USA, 12–14 May 2010; pp. 161–175. [Google Scholar]
- Russell, S.P.; Spencer, V.; Metrocavage, K.; Swanson, R.A.; Kamath, U.P. On-Orbit Propulsion and Methods of Momentum Management for the International Space Station. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008. AIAA 2008-4855 (6 pages). [Google Scholar] [CrossRef]
- Brennan, L. Means for Imparting Stability to Unstable Bodies. U.S. Patent 796893, 8 August 1905. [Google Scholar]
- Murtagh, T.B.; Whitsett, C.E.; Goodwin, M.A. Automatic Control of the Skylab Astronaut Maneuvering Research Vehicle. J. Spacecr. Rocket. 1974, 11, 321–326. [Google Scholar] [CrossRef]
- Aubrun, J.N.; Margulies, G. Gyrodampers for Large Space Structures; NASA: Washington, DC, USA, 1979; p. 159171. Available online: https://ntrs.nasa.gov/citations/19800019916 (accessed on 17 July 2025).
- Carpenter, M.D.; Peck, M.A. Dynamics of a High-Agility, Low-Power Imaging Payload. IEEE Trans. Robot. 2008, 24, 666–675. [Google Scholar] [CrossRef]
- Brown, D.; Peck, M.A. Scissored-Pair Control-Moment Gyros: A Mechanical Constraint Saves Power. J. Guid. Control Dyn. 2008, 31, 1823–1826. [Google Scholar] [CrossRef]
- Brown, D.; Peck, M. Energetics of Control Moment Gyroscopes as Joint Actuators. J. Guid. Control Dyn. 2009, 32, 1871–1883. [Google Scholar] [CrossRef]
- National Geographic, Uncovering the Secrets of the International Space Station (Full Episode)|Superstructures, 11 February 2024. Available online: https://www.youtube.com/watch?v=Ei-TcECJVXU&ab_channel=NationalGeographic (accessed on 17 July 2025).
- Zeledon, R.A. Electrolysis Propulsion for Small-Scale Spacecraft. Doctoral Dissertation, Faculty of the Graduate School, Cornell University, Ithaca, NY, USA, 2015. Available online: https://ecommons.cornell.edu/items/f1617ab5-ce70-4829-88dd-142fba33844b (accessed on 17 July 2025).
- Zeledon, R.A.; Peck, M.A. Attitude Dynamics and Control of a 3U CubeSat with Electrolysis Propulsion. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Paper AIAA 2013-4943, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef]
- Yoon, H.; Tsiotras, P. Singularity Analysis and Avoidance of Variable-Speed Control Moment Gyros. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Guidance, Navigation, and Control and Co-Located Conferences, AIAA 2004-5207 Paper, American Institute of Aeronautics and Astronautics, Providence, RI, USA, 16–19 August 2004. Part I: No Power Constraint Case. [Google Scholar] [CrossRef]
- Yoon, H.; Tsiotras, P. Singularity Analysis and Avoidance of Variable-Speed Control Moment Gyros. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Guidance, Navigation, and Control and Co-Located Conferences, AIAA 2004-5208 Paper, American Institute of Aeronautics and Astronautics, Providence, RI, USA, 16–19 August 2004. Part II: Power Constraint Case. [Google Scholar] [CrossRef]
- Jung, D.; Tsiotras, P. An Experimental Comparison of CMG Steering Control Laws. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Guidance, Navigation, and Control and Co-Located Conferences, AIAA 2004-5294 Paper, American Institute of Aeronautics and Astronautics, Providence, RI, USA, 16–19 August 2004. [Google Scholar] [CrossRef]
- Yoon, H.; Tsiotras, P. Spacecraft Adaptive Attitude and Power Tracking with Variable Speed Control Moment Gyroscopes. J. Guid. Control Dyn. 2002, 25, 1081–1090. [Google Scholar] [CrossRef]
- Yoon, H.; Tsiotras, P. Singularity Analysis of Variable-Speed Control Moment Gyros. J. Guid. Control Dyn. 2004, 27, 374–386. [Google Scholar] [CrossRef]
- Lappas, V.J. A control Moment Gyro (CMG) Based Attitude Control System (ACS) for Agile Small Satellites. Ph.D. Thesis, Surrey Space Centre School of Electronics and Physical Sciences, University of Surrey, Guildford, Surrey, UK, 2002. Available online: https://openresearch.surrey.ac.uk/esploro/outputs/doctoral/A-Control-Moment-Gyro-CMG-Based/99516248502346 (accessed on 17 July 2025).
- Lappas, V.; Steyn, W.H.; Underwood, C. Design and Testing of a Control Moment Gyroscope Cluster for Small Satellites. J. Spacecr. Rocket. 2005, 42, 729–739. [Google Scholar] [CrossRef]
- Lappas, V.J.; Steyn, W.I.-I.; Underwood, C.I. Attitude control for small satellites using control moment gyros. Acta Astronaut. 2002, 51, 101–111. [Google Scholar] [CrossRef]
- Yang, Y.; Kim, S.; Lee, K.; Leeghim, H. Disturbance Robust Attitude Stabilization of Multirotors with Control Moment Gyros. Sensors 2024, 24, 8212. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.; Li, L.; Liao, Y. An Attitude Determination and Sliding Mode Control Method for Agile Whiskbroom Scanning Maneuvers of Microsatellites. Aerospace 2024, 11, 778. [Google Scholar] [CrossRef]
- Aranovskiy, S.; Ryadchikov, I.; Nikulchev, E.; Wang, J.; Sokolov, D. Experimental Comparison of Velocity Observers: A Scissored Pair Control Moment Gyroscope Case Study. IEEE Access 2020, 8, 21694–21702. [Google Scholar] [CrossRef]
- Ünker, F.; Çuvalci, O. Gyroscopic inertial thruster (GIT). In Proceedings of the 9th International Automotive Technologies Congress, Bursa, Turkey, 7–8 May 2018; pp. 686–695. [Google Scholar]
- Ünker, F. Gyroscopic suspension for a heavy vehicle. Int. J. Heavy Veh. Syst. 2023, 30, 201–210. [Google Scholar] [CrossRef]
- Ünker, F. Proportional control moment gyroscope for two-wheeled self-balancing robot. J. Vib. Control 2022, 28, 2310–2318. [Google Scholar] [CrossRef]
- Cao, C.A.; Lieu, D.K.; Stuart, H.S. Dynamic Analysis of Gyroscopic Force Redistribution for a Wheeled Rover. In Proceedings of the 17th Biennial International Conference on Engineering, Science, Construction, and Operations in Challenging Environments: Earth and Space, Virtually, 19–23 April 2021; pp. 318–327. [Google Scholar] [CrossRef]
- Ouyang, X.; Cao, S.; Hou, Y.; Li, G.; Huang, X. Nonlinear dynamics of a dual-rotor system with active elastic support / dry friction dampers based on complex nonlinear modes. Int. J. Non-Linear Mech. 2024, 166, 104856. [Google Scholar] [CrossRef]
- Peng, X.; Li, J.; Wang, P.; Lv, Y. Leaderless consensus-based formation stabilization control for nonholonomic vehicles in the GPS-denied environment. IEEE/ASME Trans. Mechatron. 2024, 1–11. [Google Scholar] [CrossRef]
- Starosta, R.; Fritzkowski, P. Inertial Forces and Friction in Propulsion of a Rigid Body. Appl. Sci. 2025, 15, 517. [Google Scholar] [CrossRef]
- Melchiorre, M.; Colamartino, T.; Ferrauto, M.; Troise, M.; Salamina, L.; Mauro, S. Design of a Spherical Rover Driven by Pendulum and Control Moment Gyroscope for Planetary Exploration. Robotics 2024, 13, 87. [Google Scholar] [CrossRef]
- YouTube: #AntiGravity Part 3: Eric Laithwaite’s Reality-Defying 1974 Lecture on Gyroscopes #HiddenScience. Available online: https://www.youtube.com/watch?v=0L2YAU-jmcE&ab_channel=MathEasySolutions (accessed on 22 June 2025).






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Provatidis, C. Reaction Forces and Apparent Thrust in Dual Oscillating Control Moment Gyroscopes. Appl. Sci. 2025, 15, 8074. https://doi.org/10.3390/app15148074
Provatidis C. Reaction Forces and Apparent Thrust in Dual Oscillating Control Moment Gyroscopes. Applied Sciences. 2025; 15(14):8074. https://doi.org/10.3390/app15148074
Chicago/Turabian StyleProvatidis, Christopher. 2025. "Reaction Forces and Apparent Thrust in Dual Oscillating Control Moment Gyroscopes" Applied Sciences 15, no. 14: 8074. https://doi.org/10.3390/app15148074
APA StyleProvatidis, C. (2025). Reaction Forces and Apparent Thrust in Dual Oscillating Control Moment Gyroscopes. Applied Sciences, 15(14), 8074. https://doi.org/10.3390/app15148074





