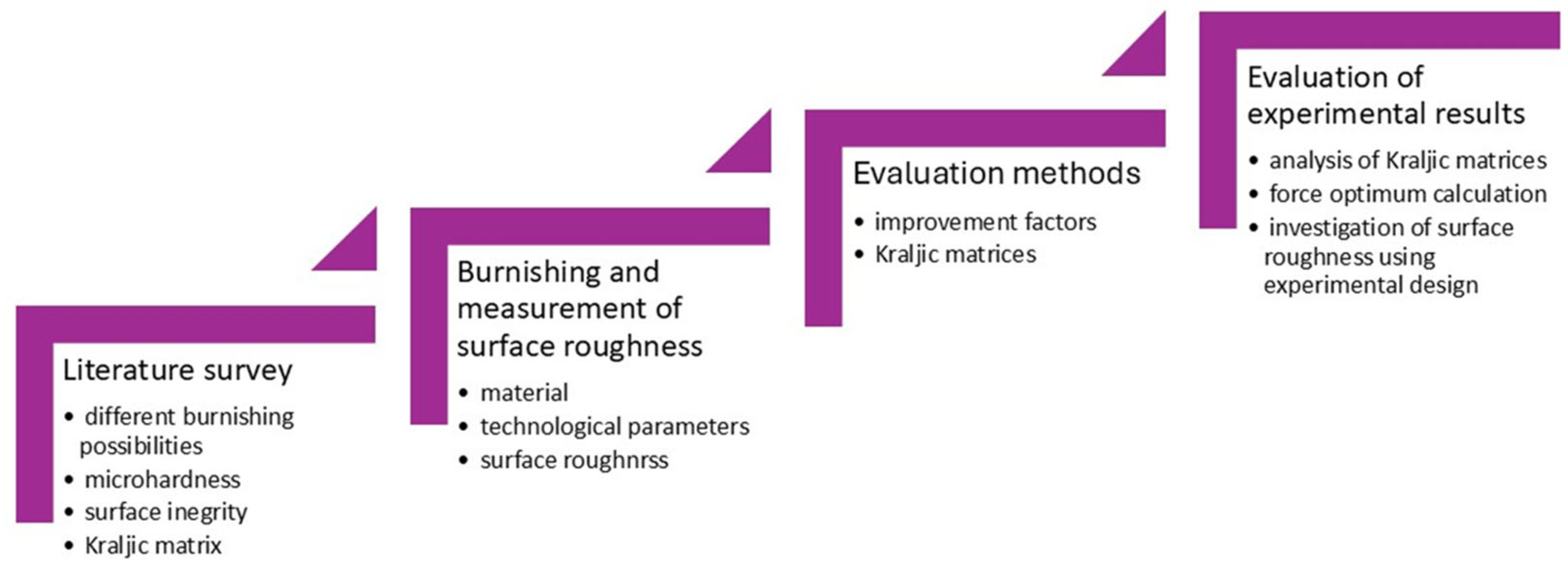
Analysis of Surface Roughness of Diamond-Burnished Surfaces Using Kraljic Matrices and Experimental Design
Abstract
1. Literature Review
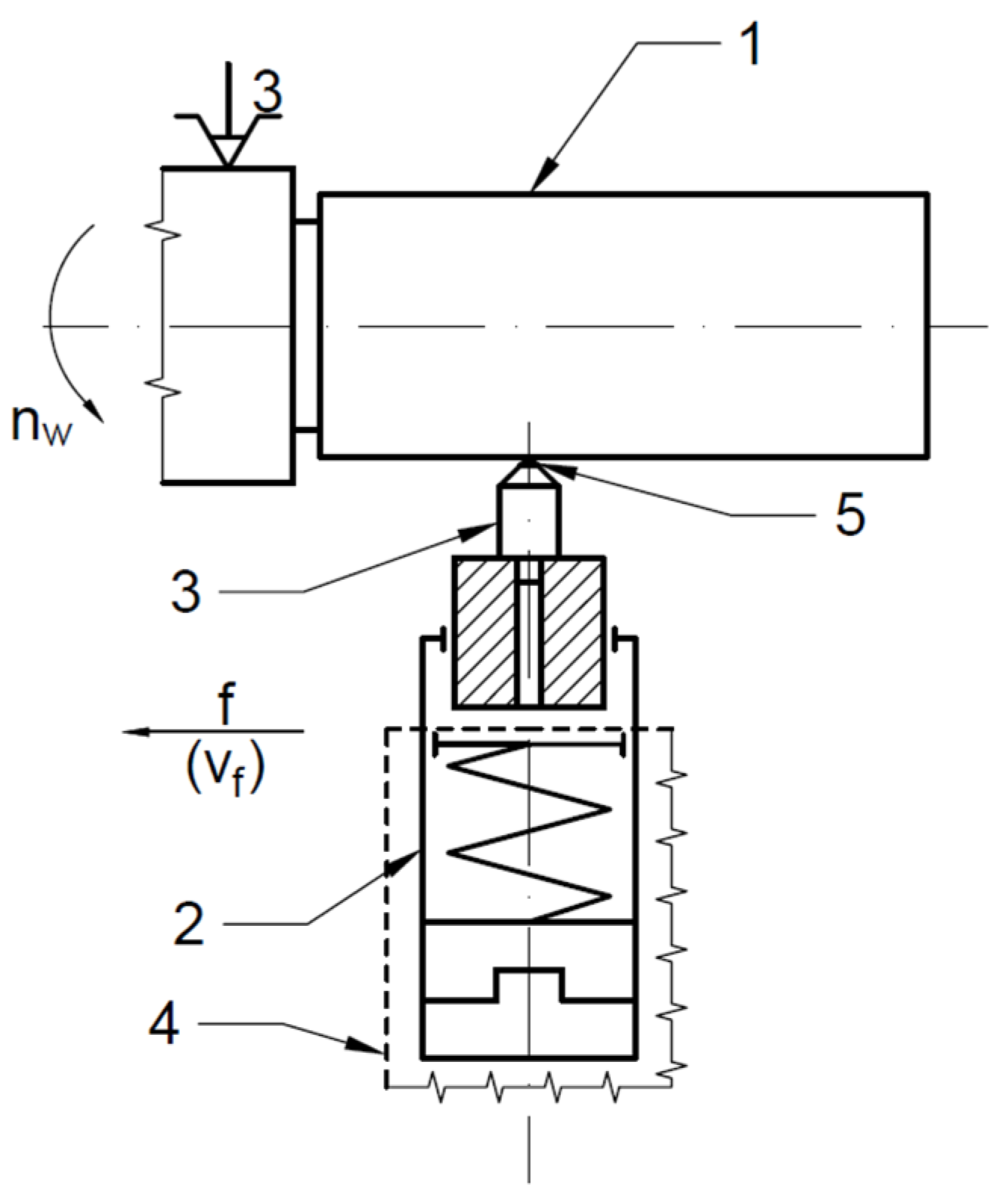
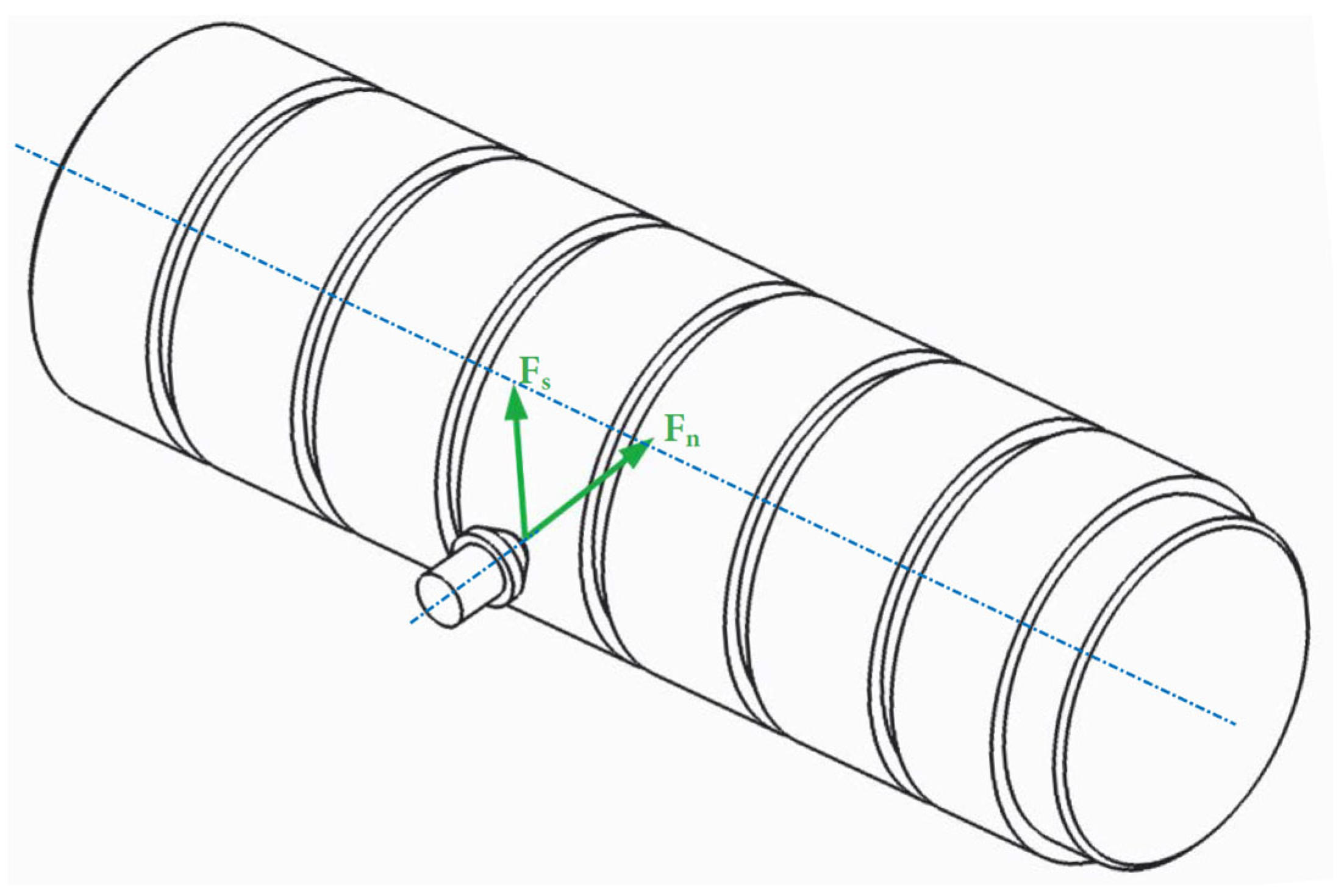
2. Surface Machining and Roughness Measurement
3. Evaluation Methods
4. Evaluation of Experimental Results
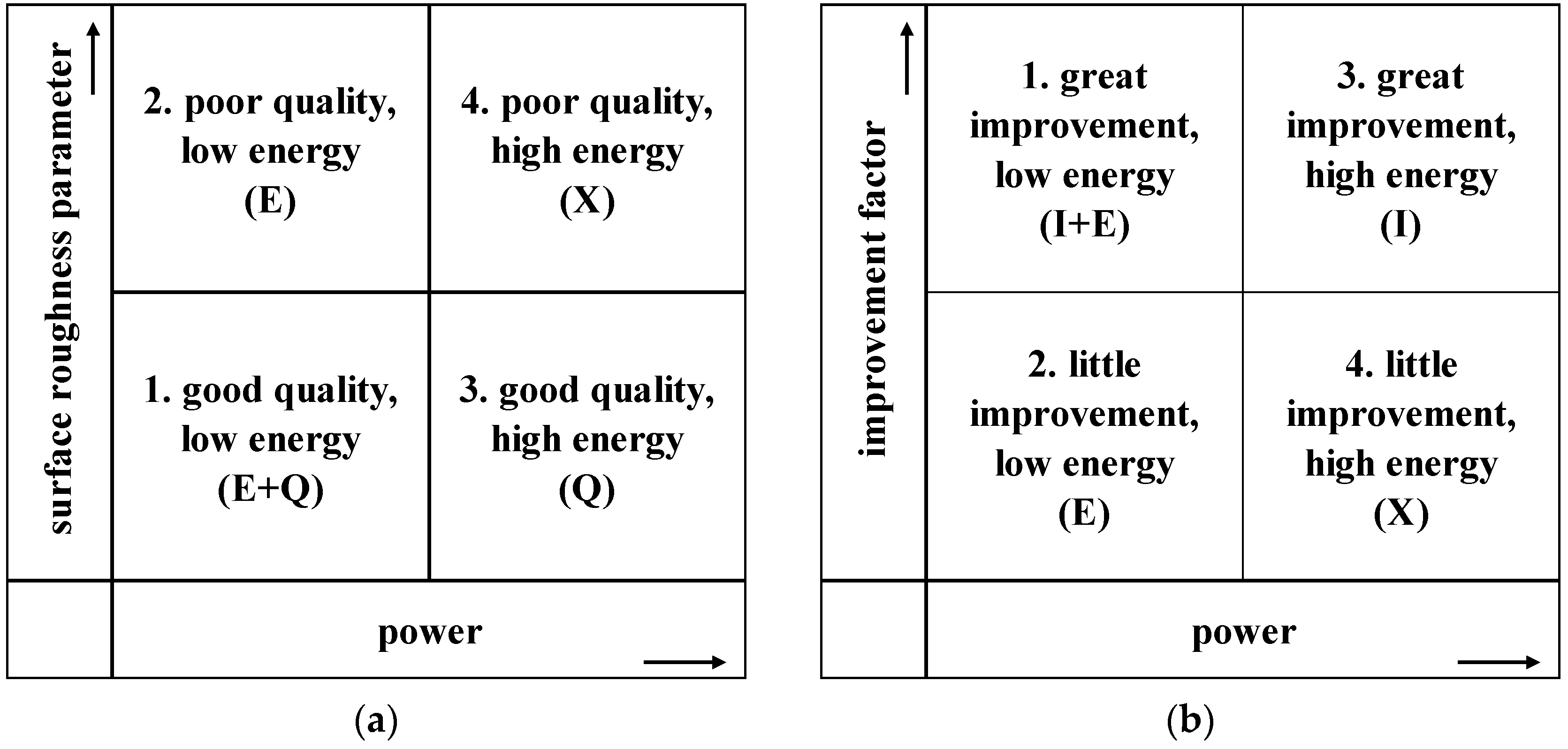
4.1. Analysis of the Kraljic Matrices
4.2. Optimum Force Calculation for Surface Roughness Optimisation
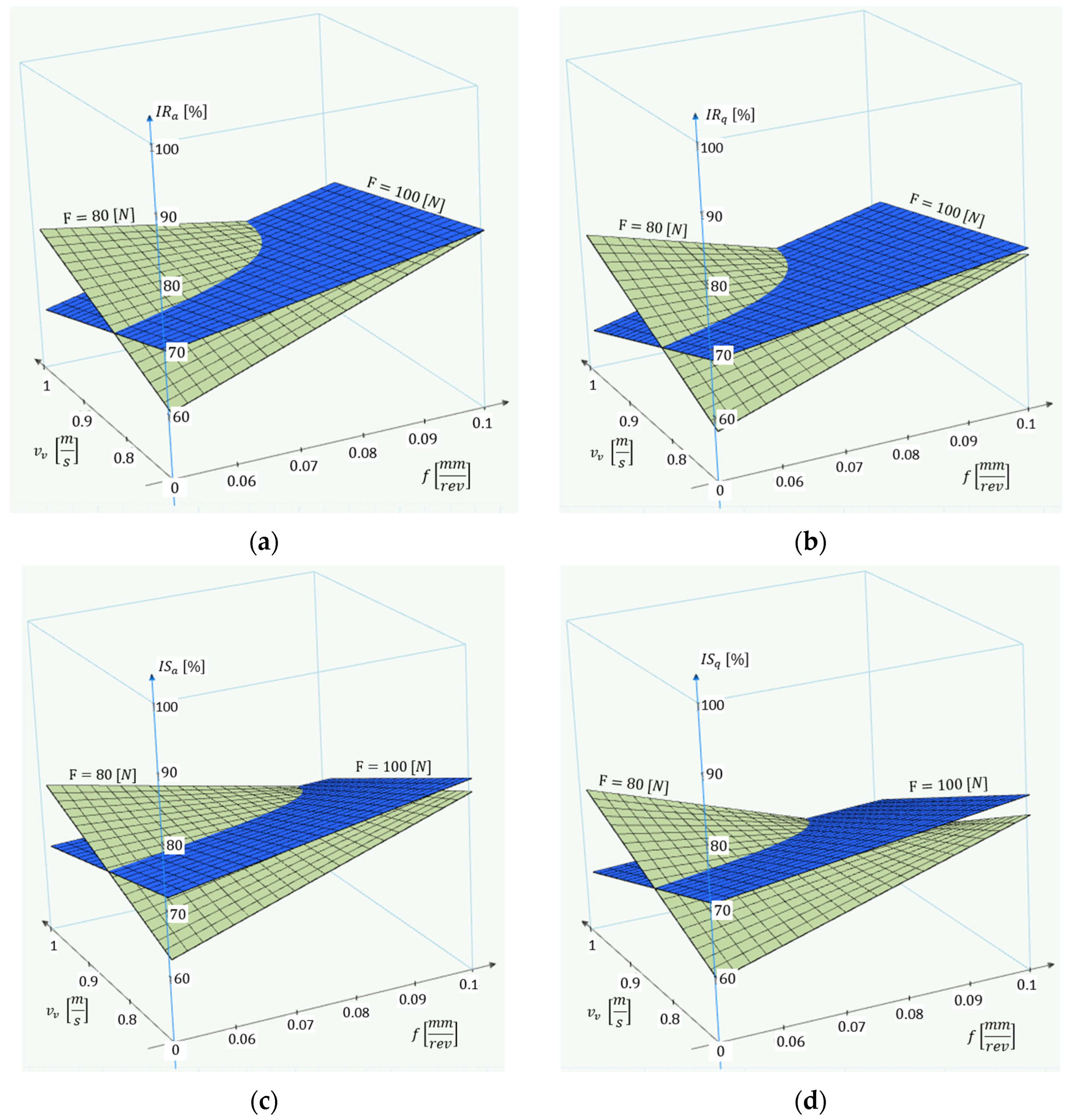
4.3. Investigation of Surface Roughness by Experimental Design for Different Process Parameters
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kovács, G. Combination of Lean value-oriented conception and facility layout design for even more significant efficiency improvement and cost reduction. Int. J. Prod. Res. 2020, 58, 2916–2936. [Google Scholar] [CrossRef]
- Sztankovics, I. Preliminary Study on the Function-Defining 3D Surface Roughness Parameters in Tangential Turning. Int. J. Integr. Eng. 2023, 15, 72–81. [Google Scholar] [CrossRef]
- Kundrák, J.; Felhő, C.; Nagy, A. Analysis and Prediction of Roughness of Face Milled Surfaces using CAD Model. Manuf. Technol. 2022, 22, 558–572. [Google Scholar] [CrossRef]
- Ferencsik, V. Analytical analysis of the theoretical surface roughness in the case of burnishing of cylindrical workpiece. Cut. Tool Technol. Syst. 2023, 99, 101–109. [Google Scholar] [CrossRef]
- Tesfom, K.F.; Felho, C. Examining the impact of slide burnishing parameters on the 3D surface features of medium carbon steel. J. Prod. Eng. 2024, 27, 30–35. [Google Scholar] [CrossRef]
- Dix, M.; Posdzich, M. Force-controlled burnishing process for high surface integrity on additive manufactured parts. Procedia CIRP 2022, 108, 642–647. [Google Scholar] [CrossRef]
- Ulhe, P.N.; Patil, U.D.; Patil, C.R. Optimization of Roller Burnishing Process Parameters on Surface Roughness Using Response Surface Methodology. Mater. Today Proc. 2019, 18, 3632–3637. [Google Scholar] [CrossRef]
- Varga, G.; Smolnicki, S.; Babič, M.; Caesarendra, W. Energy Efficiency Analysis When Grinding and Diamond Burnishing of Components. In Towards Industry 5.0: Selected Papers from ISPR2022; Güneş, G.M., Durakbasa, N.M., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 378–396. [Google Scholar] [CrossRef]
- Keymanesh, M.; Ji, H.; Zhang, X.; Wang, J.; Feng, P.; Zhang, J. Multi-roller taper burnishing of internal chamfers and its enhancement mechanism on 7050 aluminum alloy. Int. J. Fatigue 2024, 189, 108571. [Google Scholar] [CrossRef]
- Zhou, Z.-Y.; Shi, H.-H.; Zheng, Q.-Y.; Li, Y.; Jiang, Z.-G.; Yuan, Z.-P.; Piao, Z.-P. Research on fabricating gradient nanostructure and enhancing wear resistance in aluminum alloy via two-dimensional ultrasonic surface burnishing. Surf. Coat. Technol. 2024, 494, 131302. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, Z.; Jiang, Z.; Zhao, Z.; Ding, C.; Piao, Z. Evaluation of Surface Roughness of Aluminum Alloy in Burnishing Process Based on Chaos Theory. Chin. J. Mech. Eng. 2023, 36, 2. [Google Scholar] [CrossRef]
- Maximov, J.T.; Anchev, A.P.; Duncheva, G.V.; Ganev, N.; Selimov, K.F. Influence of the process parameters on the surface roughness, micro-hardness, and residual stresses in slide burnishing of high-strength aluminum alloys. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3067–3078. [Google Scholar] [CrossRef]
- Cai, Y.; Tang, K.; Zhang, H.; Xue, J.; Aslam, J.; Liang, X.; Song, Q.; Liu, Z. Fatigue performance of Ti6Al4V alloy treated with laser-assisted burnishing. Int. J. Fatigue 2025, 193, 108788. [Google Scholar] [CrossRef]
- Saffioti, M.R.; Rotella, G.; Cosco, F.; Umbrello, D. Surface changes and fretting fatigue evaluation of Ti6Al4V burnished hip necks. Procedia CIRP 2024, 123, 352–356. [Google Scholar] [CrossRef]
- Shen, X.; Ma, S.; Wang, Z.; Yu, Z.; Zhang, J.; Ma, X.; Zhu, J.; Yin, Y.; Pan, S.; Wei, F. Multiscale mechanical performance evaluation of L-DED Ti6Al4V by novel ultrasonic burnishing (UB). J. Manuf. Process. 2024, 124, 708–719. [Google Scholar] [CrossRef]
- Jagadeesh, G.V.; Setti, S.G. Biodegradation performance of ball burnished magnesium alloy in stimulated body fluids for bioresorbable implant applications. Mater. Today Commun. 2024, 38, 108525. [Google Scholar] [CrossRef]
- Buldum, B.B.; Cagan, S.C. Study of Ball Burnishing Process on the Surface Roughness and Microhardness of AZ91D Alloy. Exp. Tech. 2018, 42, 233–241. [Google Scholar] [CrossRef]
- Teimouri, R. A framework toward fatigue life modeling of machining process verified in burnishing. Mech. Syst. Signal Process. 2025, 223, 111923. [Google Scholar] [CrossRef]
- Alharbi, N. Interaction of electric current with burnishing parameters in surface integrity assessment of additively manufactured Inconel 718. Measurement 2024, 230, 114474. [Google Scholar] [CrossRef]
- Qi, B.; Chai, Z.; Huang, X.; Guo, W.; Ren, X.; Chen, H.; Chen, X. Surface integrity improvement of the ground surface of Inconel 718 fabricated by forging and additive manufacturing using a robotic rotational burnishing method. J. Manuf. Process. 2024, 125, 566–579. [Google Scholar] [CrossRef]
- Brocka, G.; Saelzera, J.; Biermann, D. Finite element analysis of the surface finishing of additively manufactured 316L stainless steel by ball burnishing. Procedia CIRP 2023, 117, 287–292. [Google Scholar] [CrossRef]
- Teimouri, R.; Sohrabpoor, H.; Grabowski, M.; Wyszynski, D.; Skoczypiec, S.; Raghavendra, R. Simulation of surface roughness evolution of additively manufactured material fabricated by laser powder bed fusion and post-processed by burnishing. J. Manuf. Process. 2022, 84, 10–27. [Google Scholar] [CrossRef]
- Attabi, S.; Himour, A.; Laouar, L.; Motallebzadeh, A. Effect of Ball Burnishing on Surface Roughness and Wear of AISI 316L SS. J. Bio-Tribo-Corros. 2021, 7, 7. [Google Scholar] [CrossRef]
- Argirov, Y.; Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Mechkarova, T. Evolution of Surface Integrity Characteristics and Mechanical Behavior of Diamond Burnished and Turned AISI 304 Steel Specimens After Prolonged Exposure to Natural Seawater. Coatings 2025, 15, 31. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y. Improvement in Fatigue Strength of Chromium–Nickel Austenitic Stainless Steels via Diamond Burnishing and Subsequent Low-Temperature Gas Nitriding. Appl. Sci. 2024, 14, 1020. [Google Scholar] [CrossRef]
- de Oliveira, D.A.; Brito, P.P.; de Castro Magalhaes, F.; Azzi, P.C.; Ardisson, J.D.; Abrao, A.M. Influence of low plasticity burnishing on the formation of strain induced martensite in the surface layer. J. Mater. Res. Technol. 2023, 27, 4573–4594. [Google Scholar] [CrossRef]
- Kluz, R.; Antosz, K.; Trzepiecinski, T.; Bucior, M. Modelling the Influence of Slide Burnishing Parameters on the Surface Roughness of Shafts Made of 42CrMo4 Heat-Treatable Steel. Materials 2021, 14, 1175. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Shen, X.; Xu, C.; He, J.; Wang, B.; Su, G. Surface characteristics and corrosion behavior of TC11 titanium alloy strengthened by ultrasonic roller burnishing at room and medium temperature. J. Mater. Res. Technol. 2020, 9, 8172–8185. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Ichkova, M.; Anastasov, K. Optimal Diamond Burnishing of Chromium–Nickel Austenitic Stainless Steels Based on the Finishing Process–Surface Integrity–Operating Behavior Correlations. Metals 2025, 15, 574. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Anastasov, K.; Argirov, Y. Sustainable Diamond Burnishing of Chromium–Nickel Austenitic Stainless Steels: Effects on Surface Integrity and Fatigue Limit. Appl. Sci. 2024, 14, 9031. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Anchev, A.P.; Dunchev, V.P. Explicit correlation between surface integrity and fatigue limit of surface cold worked chromium nickel austenitic stainless steels. Int. J. Adv. Manuf. Technol. 2024, 133, 6041–6058. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y.; Nikolova, M. Effects of Heat Treatment and Diamond Burnishing on Fatigue Behaviour and Corrosion Resistance of AISI 304 Austenitic Stainless Steel. Appl. Sci. 2023, 13, 2570. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y. Effect of Diamond Burnishing on Fatigue Behaviour of AISI 304 Chromium-Nickel Austenitic Stainless Steel. Materials 2022, 15, 4768. [Google Scholar] [CrossRef] [PubMed]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y.; Todorov, V.; Mechkarova, T. Effects of Heat Treatment and Severe Surface Plastic Deformation on Mechanical Characteristics, Fatigue, and Wear of Cu-10Al-5Fe Bronze. Materials 2022, 15, 8905. [Google Scholar] [CrossRef] [PubMed]
- Varga, G.; Dezső, G.; Szigeti, F. Surface Roughness Improvement by Sliding Friction Burnishing of Parts Produced by Selective Laser Melting of Ti6Al4V Titanium Alloy. Machines 2022, 10, 400. [Google Scholar] [CrossRef]
- Ferencsik, V.; Varga, G. The Influence of Diamond Burnishing Process Parameters on Surface Roughness of Low-Alloyed Aluminium Workpieces. Machines 2022, 10, 564. [Google Scholar] [CrossRef]
- Duncheva, G.; Maximov, J.; Anchev, A.; Dunchev, V.; Argirov, Y.; Velkov, S. Modelling and Optimization of Surface Integrity and Sliding Wear Resistance of Diamond-Burnished Holes in Austenitic Stainless Steel Cylinder Lines. Machines 2023, 11, 872. [Google Scholar] [CrossRef]
- Duncheva, G.V.; Maximov, J.T.; Anchev, A.P.; Dunchev, V.P.; Argirov, Y.B.; Kandeva-Ivanova, M. Enhancement of the wear resistance of CuAl9Fe4 sliding bearing bushings via diamond burnishing. Wear 2022, 510–511, 204491. [Google Scholar] [CrossRef]
- Maximov, J.T.; Anchev, A.P.; Dunchev, V.P.; Argirov, Y.B.; Ganev, N.; Drumeva, D.K. Improvement in surface integrity of CuAl8Fe3 bronze via diamond burnishing. Int. J. Adv. Manuf. Technol. 2022, 119, 5885–5902. [Google Scholar] [CrossRef]
- Patel, K.A.; Brahmbhatt, P.K. A comparative study of the RSM and ANN models for predicting surface roughness in roller burnishing. Procedia Technol. 2016, 23, 391–397. [Google Scholar] [CrossRef]
- Kanovic, Z.; Vukelic, D.; Simunovic, K.; Prica, M.; Saric, T.; Tadic, B.; Simunovic, G. The Modelling of Surface Roughness after the Ball Burnishing Process with a High-Stiffness Tool by Using Regression Analysis, Artificial Neural Networks, and Support Vector Regression. Metals 2022, 12, 320. [Google Scholar] [CrossRef]
- Marquez-Herrera, A.; Diosdado-De la Peña, J.A. Influence of ball-burnishing on roughness, hardness and corrosion resistance of AISI 1045 steel. Procedia Manuf. 2019, 34, 287–292. [Google Scholar] [CrossRef]
- Patel, K.A.; Brahmbhatt, P.K. Burnishing of aerospace alloy: A theoretical–experimental approach. J. Manuf. Syst. 2015, 37, 472–478. [Google Scholar] [CrossRef]
- Babu, P.R.; Ankamma, K.; Prasad, T.S.; Raju, A.V.S.; Prasad, N.E. Optimization of Burnishing Parameters by DOE and Surface Roughness, Microstructure and Micro Hardness Characteristics of AA6061 Aluminium Alloy in T6 Condition. J. Eng. Res. Appl. (IJERA) 2012, 2, 1139–1146. [Google Scholar]
- Thorat, S.R.; Thakur, A.G. Analysis of surface roughness and wear resistance in low plasticity burnishing process using multi-objective optimization technique. Mater. Today Proc. 2021, 41, 1082–1088. [Google Scholar] [CrossRef]
- Kovács, Z.F.; Viharos, Z.J.; Kodácsy, J. Surface flatness and roughness evolution after magnetic assisted ball burnishing of magnetizable and non-magnetizable materials. Measurement 2020, 158, 107750. [Google Scholar] [CrossRef]
- Swirad, S.; Wdowik, R. Determining the effect of ball burnishing parameters on surface roughness using the Taguchi method. Procedia Manuf. 2019, 34, 287–292. [Google Scholar] [CrossRef]
- Sachin, B.; Narendranath, S.; Chakradhar, D. Analysis of surface hardness and surface roughness in diamond burnishing of 17-4 PH stainless steel. IOP Conf. Ser. Mater. Sci. Eng. 2019, 577, 012075. [Google Scholar] [CrossRef]
- Shirsat, U.; Ahuja, B.; Dhuttargaon, M. Effect of Burnishing Parameters on Surface Finish. J. Inst. Eng. India Ser. C 2017, 98, 431–436. [Google Scholar] [CrossRef]
- Borysenko, D.; Welzel, F.; Karpuschewski, B.; Kundrák, J.; Voropai, V. Simulation of the burnishing process on real surface structures. Precis. Eng. 2021, 68, 166–173. [Google Scholar] [CrossRef]
- Ferencsik, V. FEM Investigation of the Roughness and Residual Stress of Diamond Burnished Surface. J. Exp. Theor. Anal. 2024, 2, 80–90. [Google Scholar] [CrossRef]
- Duncheva, G.V.; Maximov, J.T.; Anchev, A.P.; Dunchev, V.P.; Atanasov, T.P.; Capek, J. Finite element and experimental study of the residual stresses in 2024-T3 Al alloy treated via single toroidal roller burnishing. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 55. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Dunchev, V.P.; Anchev, A.P. Different strategies for finite element simulations of static mechanical surface treatment processes—A comparative analysis. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 371. [Google Scholar] [CrossRef]
- Yamana, N.; Sunay, N.; Kaya, M.; Kaynak, Y. Enhancing Surface Integrity of Additively Manufactured Inconel 718 by Roller Burnishing Process. Procedia CIRP 2022, 108, 681–686. [Google Scholar] [CrossRef]
- Duncheva, G.V.; Maximov, J.T.; Dunchev, V.P.; Anchev, A.P.; Atanasov, T.P. Improvement in Fatigue Performance of 2024-T3 Al Alloy Via Single Toroidal Roller Burnishing. J. Mater. Eng. Perform. 2021, 30, 2256–2266. [Google Scholar] [CrossRef]
- Thit, M.; Rocissano, A.; Hatem, A.; Uddin, M.; Hall, C.; Schlaefer, T. Surface integrity and high-cycle fatigue life of direct laser metal deposited AISI 431 alloys modified by plasticity ball burnishing. Int. J. Fatigue 2025, 190, 108614. [Google Scholar] [CrossRef]
- Li, T.; Uddin, M.; Stevens, G. Effect of ball burnishing on surface roughness, wettability, mechanical integrity and antifouling resistance of UHMWPE. Surf. Coat. Technol. 2024, 476, 130237. [Google Scholar] [CrossRef]
- Han, K.; Tan, L.; Yao, C.; Zhang, D. Evolution and anti-fatigue mechanism of surface characteristics of Ti60 alloy induced by ball burnishing and shot peening during tensile-compression fatigue. Eng. Fail. Anal. 2024, 159, 108136. [Google Scholar] [CrossRef]
- Jiménez-García, J.I.; Capilla-González, G.; Balvantín-García, A.de.J.; Travieso-Rodriguez, J.A.; Ruíz-López, I.; Saldana-Robles, A. A numerical investigation into the influence of the slide burnishing process on the real surface roughness and residual stress profiles of AHSS. J. Mater. Res. Technol. 2024, 33, 1406–1419. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, H.; Li, Y.; Yang, C.; Xue, H. Combining turning with slide burnishing to improve surface integrity and stress corrosion resistance. J. Manuf. Process. 2023, 107, 16–33. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. Effects of Cryogenic- and Cool-Assisted Burnishing on the Surface Integrity and Operating Behavior of Metal Components: A Review and Perspectives. Machines 2024, 12, 312. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. The Correlation between Surface Integrity and Operating Behaviour of Slide Burnished Components—A Review and Prospects. Appl. Sci. 2023, 13, 3313. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Anchev, A.P.; Dunchev, V.P.; Capek, J. A cost effective optimization approach for improving the fatigue strength of diamond burnished steel components. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 33. [Google Scholar] [CrossRef]
- Kraljic, P. Purchasing Must Become Supply Management. Harv. Bus. Rev. 1983, 61, 109–117. [Google Scholar]
- Saputro, T.E.; Figueira, G.; Almada-Lobo, B. A comprehensive framework and literature review of supplier selection under different purchasing strategies. Comput. Ind. Eng. 2022, 167, 108010. [Google Scholar] [CrossRef]
- Chen, X.; He, Y.; Pakdel, G.H.; Liu, X.; Wang, S. A comprehensive multi-stage decision-making model for supplier selection and order allocation approach in the digital economy. Adv. Eng. Inform. 2025, 63, 102961. [Google Scholar] [CrossRef]
- Corsini, F.; Bernardi, C.D.; Gusmerotti, N.M.; Frey, M. Introducing the circular assessment of suppliers (CAoS) tool: A Kraljic matrix-based tool to facilitate circular procurement in private organizations. J. Clean. Prod. 2024, 452, 142085. [Google Scholar] [CrossRef]
- Pulicharla, R.; Brar, S.K.; Rouissi, T.; Auger, S.; Drogui, P.; Verma, M.; Surampalli, R.Y. Degradation of chlortetracycline in wastewater sludge by ultrasonication, Fenton oxidation, and ferro-sonication. Ultrason. Sonochem. 2017, 34, 332–342. [Google Scholar] [CrossRef] [PubMed]
- Skarohlíd, R.; Kraljic, D.; Suchan, J.; Kühnl, K.; Hanzlová, B.; Tesínská, P.; Kholomyeva, M.; Martinec, M.; Michalcová, A.; McGachy, L. Overlooked effects of chlorides and bicarbonates on the intensity of peroxydisulfate activation in Fe(II)/citric acid-S2O82− process. Environ. Technol. Innov. 2024, 35, 103687. [Google Scholar] [CrossRef]
- Karabulut, G.; Subasi, B.G.; Ivanova, P.; Goksen, G.; Chalova, V.; Capanoglu, E. Towards sustainable and nutritional-based plant protein sources: A review on the role of rapeseed. Food Res. Int. 2025, 202, 115553. [Google Scholar] [CrossRef] [PubMed]
- Felhő, C.; Tesfom, F.; Varga, G. ANOVA Analysis and L9 Taguchi Design for Examination of Flat Slide Burnishing of Unalloyed Structural Carbon Steel. J. Manuf. Mater. Process. 2023, 7, 136. [Google Scholar] [CrossRef]
- Varga, G. Effect of burnishing technological parameters on the surface roughness and hardness of stainless steel test pieces (A vasalástechnológiai paraméterek hatása a rozsdamentes acél próbadarabok felületi érdességére és keménységére). Multidiszcip. Tudományok Miskolci Egy. Közleménye 2022, 12, 151–163. (In Hungarian) [Google Scholar] [CrossRef]
- Maximov, J.T.; Anchev, A.P.; Duncheva, G.V. Modeling of the friction in the tool-workpiece system in diamond burnishing process. Coupled Syst. Mech. 2015, 4, 279–295. [Google Scholar] [CrossRef]
- Available online: https://www.imeco-th.cz/files/tinymce/AltiSurf%E2%84%A2%20520.pdf (accessed on 13 July 2025).
- ISO 21920-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- ISO 25178-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Areal. Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Fridrik, L. Selected Chapters on the Topic of Designing Engineering Technology Experiments; Tankönyvkiadó: Budapest, Hungary, 1993. (In Hungarian) [Google Scholar]

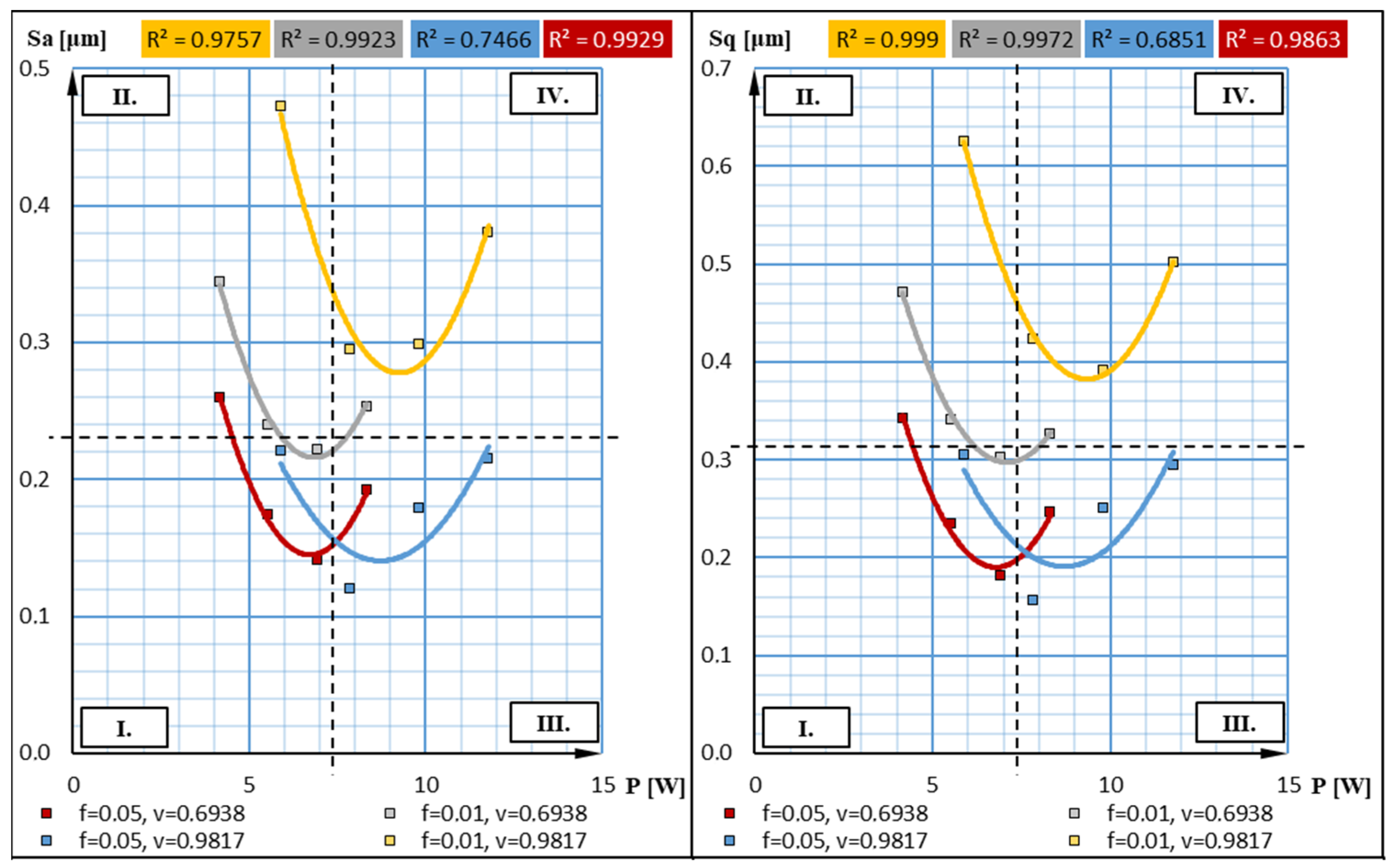

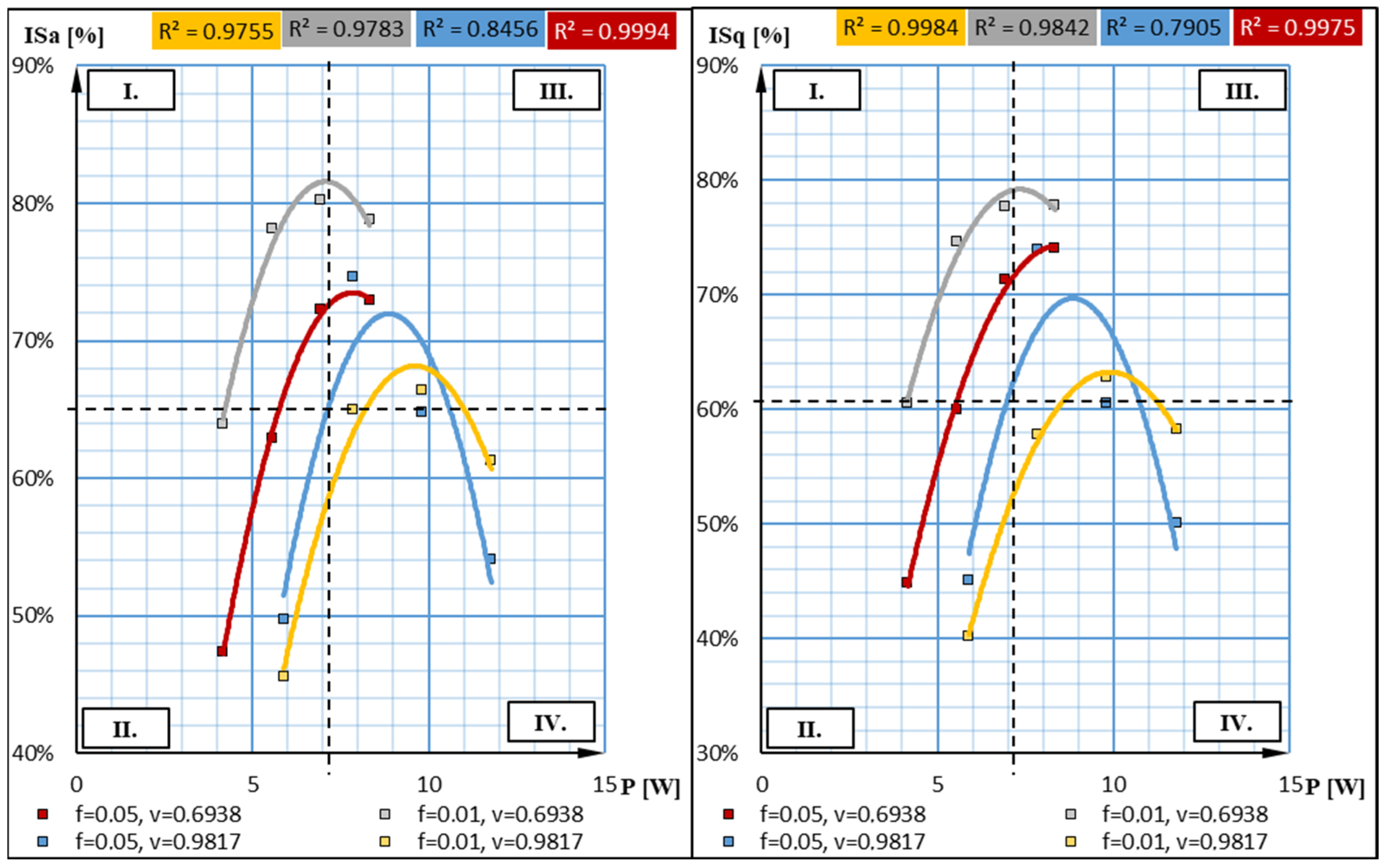

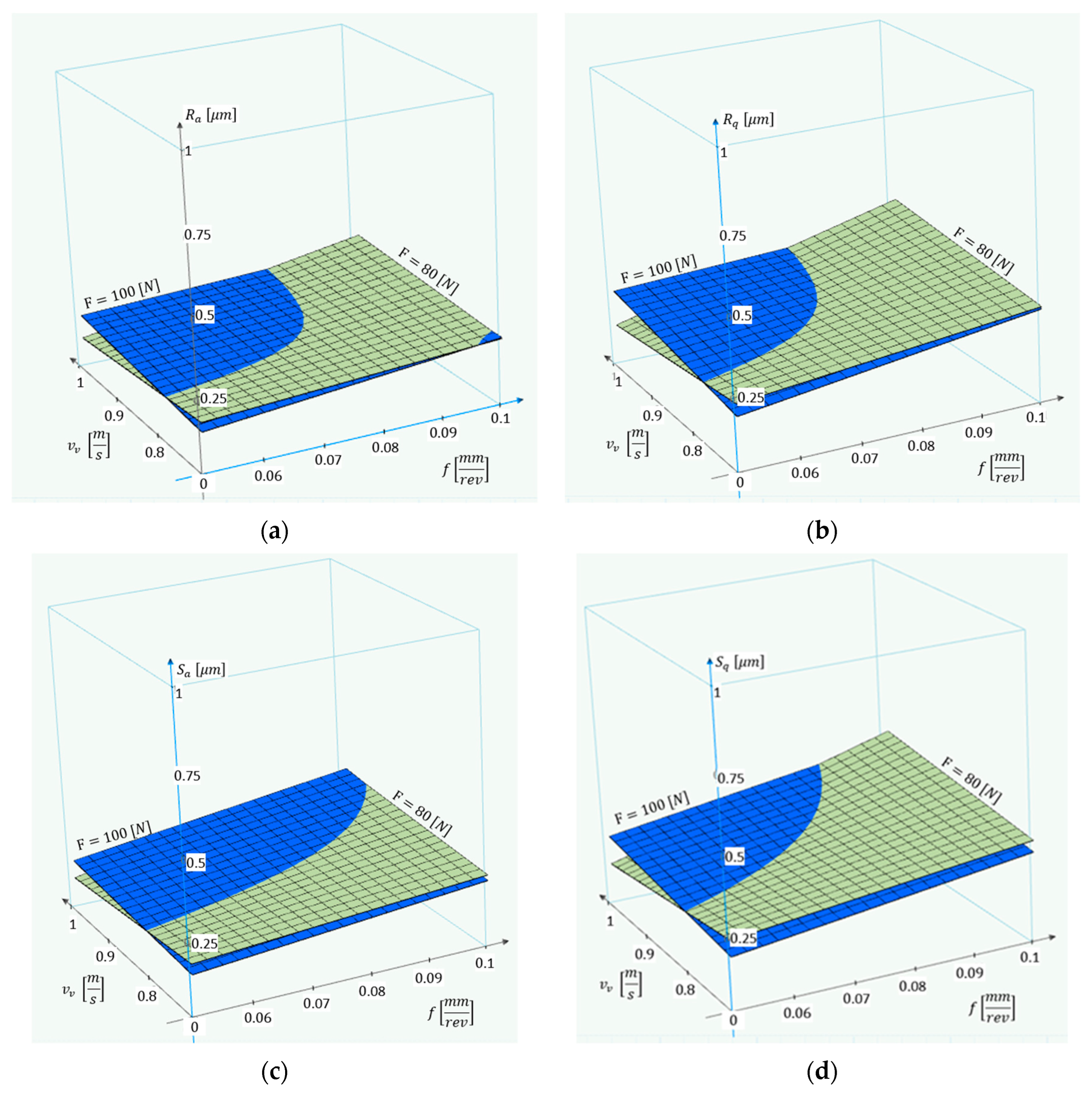
| No. | |||
|---|---|---|---|
| 1-1 | 0.05 | 265 | 120 |
| 1-2 | 0.05 | 265 | 100 |
| 1-3 | 0.05 | 265 | 80 |
| 1-4 | 0.05 | 265 | 60 |
| 2-1 | 0.1 | 265 | 120 |
| 2-2 | 0.1 | 265 | 100 |
| 2-3 | 0.1 | 265 | 80 |
| 2-4 | 0.1 | 265 | 60 |
| 3-1 | 0.05 | 375 | 120 |
| 3-2 | 0.05 | 375 | 100 |
| 3-3 | 0.05 | 375 | 80 |
| 3-4 | 0.05 | 375 | 60 |
| 4-1 | 0.1 | 375 | 120 |
| 4-2 | 0.1 | 375 | 100 |
| 4-3 | 0.1 | 375 | 80 |
| 4-4 | 0.1 | 375 | 60 |
| No. | |||||||
|---|---|---|---|---|---|---|---|
| 1-1 | 0.05 | 0.6938 | 120 | 0.1613 | 0.2047 | 0.1918 | 0.2465 |
| 1-2 | 0.05 | 0.6938 | 100 | 0.1425 | 0.1856 | 0.1408 | 0.1816 |
| 1-3 | 0.05 | 0.6938 | 80 | 0.1729 | 0.2254 | 0.1743 | 0.2338 |
| 1-4 | 0.05 | 0.6938 | 60 | 0.2365 | 0.3036 | 0.2597 | 0.3423 |
| 2-1 | 0.1 | 0.6938 | 120 | 0.2097 | 0.2715 | 0.4295 | 0.5365 |
| 2-2 | 0.1 | 0.6938 | 100 | 0.2297 | 0.3151 | 0.5779 | 0.6953 |
| 2-3 | 0.1 | 0.6938 | 80 | 0.2269 | 0.3225 | 0.2534 | 0.3262 |
| 2-4 | 0.1 | 0.6938 | 60 | 0.3263 | 0.4285 | 0.2217 | 0.3026 |
| 3-1 | 0.05 | 0.9817 | 120 | 0.2148 | 0.2614 | 0.2152 | 0.2940 |
| 3-2 | 0.05 | 0.9817 | 100 | 0.1955 | 0.2705 | 0.1784 | 0.2505 |
| 3-3 | 0.05 | 0.9817 | 80 | 0.1180 | 0.1545 | 0.1201 | 0.1559 |
| 3-4 | 0.05 | 0.9817 | 60 | 0.1910 | 0.2507 | 0.2208 | 0.3047 |
| 4-1 | 0.1 | 0.9817 | 120 | 0.3081 | 0.3865 | 0.3805 | 0.5016 |
| 4-2 | 0.1 | 0.9817 | 100 | 0.2404 | 0.3206 | 0.2983 | 0.3909 |
| 4-3 | 0.1 | 0.9817 | 80 | 0.2800 | 0.3960 | 0.2951 | 0.4235 |
| 4-4 | 0.1 | 0.9817 | 60 | 0.4026 | 0.5435 | 0.4719 | 0.6252 |
| No. | |||||||
|---|---|---|---|---|---|---|---|
| 1-1 | 0.05 | 0.6938 | 120 | 75.40% | 74.82% | 72.94% | 74.00% |
| 1-2 | 0.05 | 0.6938 | 100 | 69.94% | 68.73% | 72.24% | 71.37% |
| 1-3 | 0.05 | 0.6938 | 80 | 60.65% | 58.07% | 62.95% | 59.94% |
| 1-4 | 0.05 | 0.6938 | 60 | 50.73% | 48.33% | 47.32% | 44.88% |
| 2-1 | 0.1 | 0.6938 | 120 | 82.00% | 80.96% | 78.82% | 77.80% |
| 2-2 | 0.1 | 0.6938 | 100 | 78.35% | 75.53% | 80.23% | 77.70% |
| 2-3 | 0.1 | 0.6938 | 80 | 78.37% | 74.55% | 78.18% | 74.61% |
| 2-4 | 0.1 | 0.6938 | 60 | 64.96% | 63.08% | 63.97% | 60.53% |
| 3-1 | 0.05 | 0.9817 | 120 | 50.94% | 52.37% | 54.10% | 50.10% |
| 3-2 | 0.05 | 0.9817 | 100 | 60.71% | 57.33% | 64.79% | 60.53% |
| 3-3 | 0.05 | 0.9817 | 80 | 73.96% | 72.92% | 74.69% | 73.92% |
| 3-4 | 0.05 | 0.9817 | 60 | 55.62% | 53.90% | 49.78% | 45.12% |
| 4-1 | 0.1 | 0.9817 | 120 | 66.49% | 64.44% | 61.25% | 58.31% |
| 4-2 | 0.1 | 0.9817 | 100 | 72.49% | 69.02% | 66.36% | 62.77% |
| 4-3 | 0.1 | 0.9817 | 80 | 66.45% | 59.85% | 65.00% | 57.75% |
| 4-4 | 0.1 | 0.9817 | 60 | 53.25% | 47.12% | 45.56% | 40.18% |
| R/S | Equation | ||||
|---|---|---|---|---|---|
| 0.05 | 0.6938 | y = 0.0107x2 − 0.1519x + 0.6844 | 7.10 | 102 | |
| y = 0.0126x2 − 0.1821x + 0.8436 | 7.23 | 104 | |||
| y = 0.0177x2 − 0.2382x + 0.946 | 6.73 | 97 | |||
| y = 0.0225x2 − 0.3057x + 1.2277 | 6.79 | 98 | |||
| 0.05 | 0.9817 | y = 0.006x2 − 0.0982x + 0.5512 | 8.18 | 83 | |
| y = 0.0057x2 − 0.0924x + 0.5819 | 8.11 | 83 | |||
| y = 0.0089x2 − 0.1554x + 0.818 | 8.73 | 89 | |||
| y = 0.0125x2 − 0.2172x + 1.1365 | 8.69 | 88 | |||
| 0.1 | 0.6938 | y = 0.0103x2 − 0.1538x + 0.7815 | 7.47 | 108 | |
| y = 0.0081x2 − 0.1356x + 0.846 | 8.37 | 121 | |||
| y = 0.0177x2 − 0.2417x + 1.0418 | 6.83 | 98 | |||
| y = 0.02x2 − 0.2843x + 1.306 | 7.11 | 102 | |||
| 0.1 | 0.9817 | y = 0.0123x2 − 0.2346x + 1.3576 | 9.54 | 97 | |
| y = 0.0138x2 − 0.2724x + 1.6716 | 9.87 | 101 | |||
| y = 0.0168x2 − 0.3107x + 1.7141 | 9.25 | 94 | |||
| y = 0.0203x2 − 0.3785x + 2.1508 | 9.32 | 95 |
| R/S | Equation | ||||
|---|---|---|---|---|---|
| 0.05 | 0.6938 | y = −0.0058x2 + 0.1324x + 0.055 | 11.41 | 165 | |
| y = −0.0047x2 + 0.1241x + 0.046 | 13.20 | 190 | |||
| y = −0.0194x2 + 0.3041x − 0.4581 | 7.84 | 113 | |||
| y = −0.0161x2 + 0.2728x − 0.4096 | 8.47 | 122 | |||
| 0.05 | 0.9817 | y = −0.0182x2 + 0.3083x − 0.6095 | 8.47 | 86 | |
| y = −0.0155x2 + 0.2645x − 0.457 | 8.53 | 87 | |||
| y = −0.0231x2 + 0.4094x − 1.096 | 8.86 | 90 | |||
| y = −0.0254x2 + 0.4502x − 1.2957 | 8.86 | 90 | |||
| 0.1 | 0.6938 | y = −0.0127x2 + 0.1952x + 0.0654 | 7.69 | 111 | |
| y = −0.0078x2 + 0.1373x + 0.2027 | 8.80 | 127 | |||
| y = −0.0203x2 + 0.287x − 0.1991 | 7.07 | 102 | |||
| y = −0.0181x2 + 0.2662x − 0.1842 | 7.35 | 106 | |||
| 0.1 | 0.9817 | y = −0.0125x2 + 0.2434x − 0.4714 | 9.74 | 99 | |
| y = −0.0112x2 + 0.2295x − 0.4964 | 10.25 | 104 | |||
| y = −0.0159x2 + 0.306x − 0.7887 | 9.62 | 98 | |||
| y = −0.0143x2 + 0.2828x − 0.7667 | 9.89 | 101 |
| No. | |||
|---|---|---|---|
| 1-3 | 0.05 | 0.6938 | 80 |
| 2-3 | 0.1 | 0.6938 | 80 |
| 3-3 | 0.05 | 0.9817 | 80 |
| 4-3 | 0.1 | 0.9817 | 80 |
| 1-2 | 0.05 | 0.6938 | 100 |
| 2-2 | 0.1 | 0.6938 | 100 |
| 3-2 | 0.05 | 0.9817 | 100 |
| 4-2 | 0.1 | 0.9817 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smolnicki, S.; Varga, G. Analysis of Surface Roughness of Diamond-Burnished Surfaces Using Kraljic Matrices and Experimental Design. Appl. Sci. 2025, 15, 8025. https://doi.org/10.3390/app15148025
Smolnicki S, Varga G. Analysis of Surface Roughness of Diamond-Burnished Surfaces Using Kraljic Matrices and Experimental Design. Applied Sciences. 2025; 15(14):8025. https://doi.org/10.3390/app15148025
Chicago/Turabian StyleSmolnicki, Szilárd, and Gyula Varga. 2025. "Analysis of Surface Roughness of Diamond-Burnished Surfaces Using Kraljic Matrices and Experimental Design" Applied Sciences 15, no. 14: 8025. https://doi.org/10.3390/app15148025
APA StyleSmolnicki, S., & Varga, G. (2025). Analysis of Surface Roughness of Diamond-Burnished Surfaces Using Kraljic Matrices and Experimental Design. Applied Sciences, 15(14), 8025. https://doi.org/10.3390/app15148025







