Hybrid Methods for Selecting Precast Concrete Suppliers Based on Factory Capacity
Abstract
1. Introduction
2. Literature Review
2.1. Methods Utilized for Selecting a Supplier
2.2. Previous Studies on the Relationship Between Factory Supplier Capacity and Its Quality
2.3. Overview of Integrated Decision-Making Methodologies
2.4. Gap in Knowledge
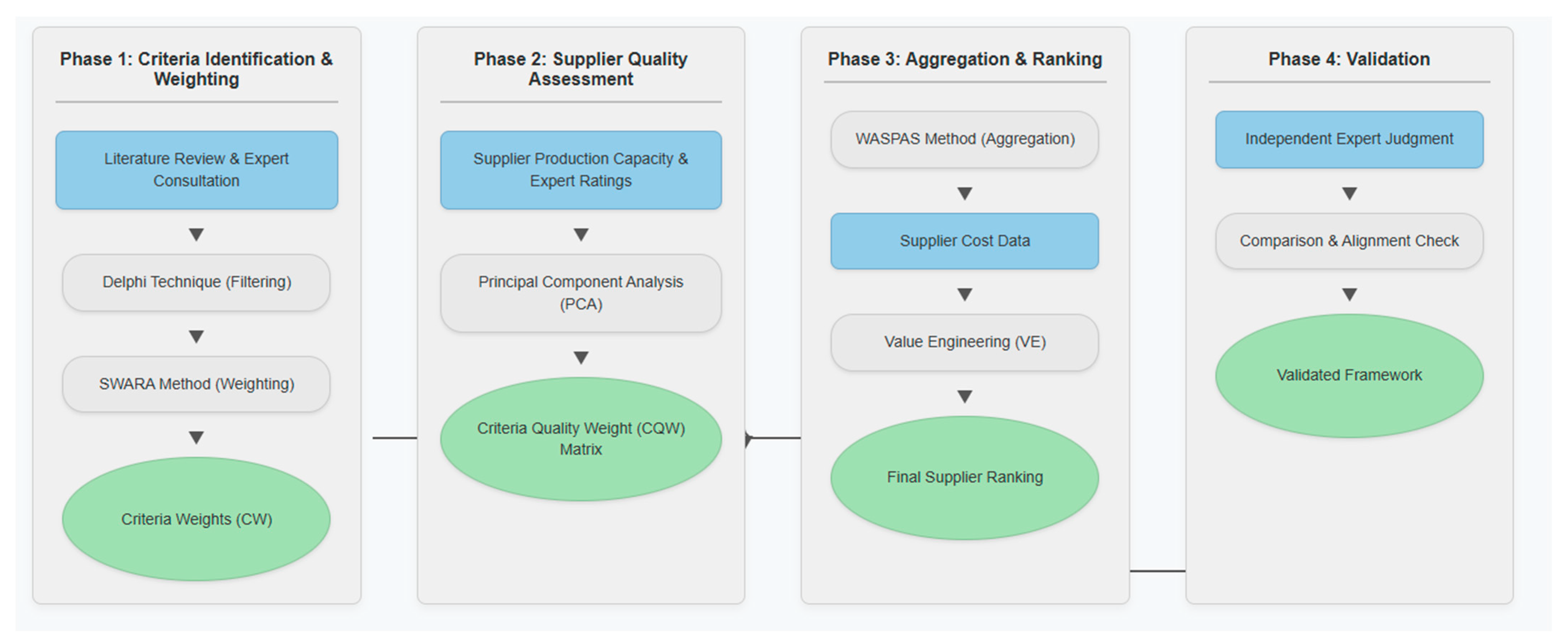
3. Methodology
3.1. Collect Data
3.2. Identify the Significant Criteria
3.3. Determine Quality Weight
3.4. Estimate the CQW of the Alternative Based on Its Capacity
Determining the CQW by PCA
3.5. Estimate Each Supplier’s Qi Score Using the WASPAS Method
3.6. Compute VE and Ranking
4. Sensitivity Analysis
4.1. Sensitivity to Changes in Criteria Weights
4.2. Sensitivity to the Lambda (λ) Parameter
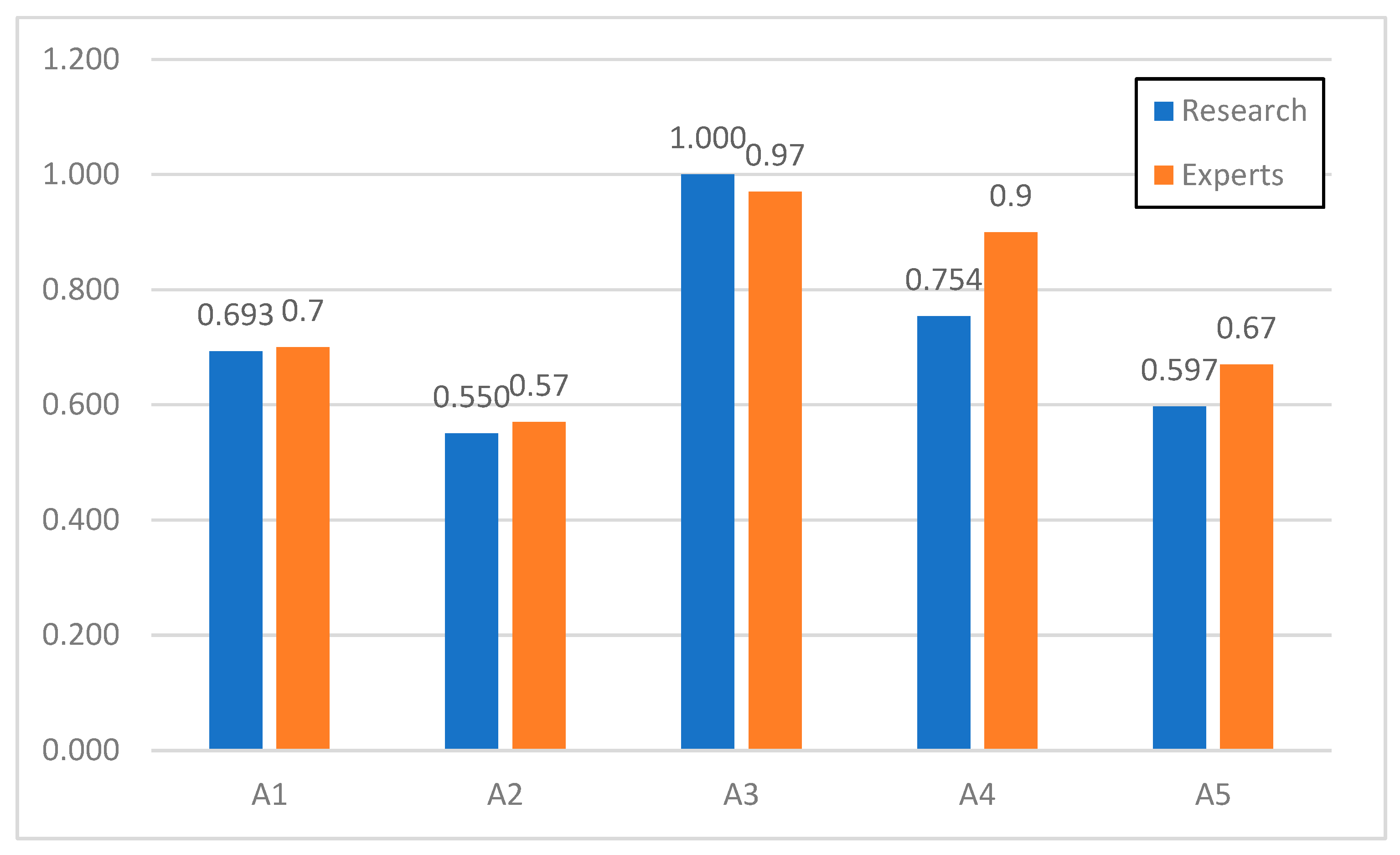
5. Validation
6. Discussion
6.1. Practies and Implementation
6.2. Comparative Advantages of the Proposed Framework
7. Conclusions
- The framework’s ability to rank suppliers in a manner perfectly consistent with expert judgment (Spearman’s coefficient = 1.0) validates its core premise: that a supplier’s production capacity is a robust indicator of its overall quality and reliability. The top-ranked supplier (A3) demonstrated a superior capacity, which translated into a higher Value Engineering (VE) score, confirming that in capital-intensive projects, capacity is a critical differentiator.
- The SWARA revealed that “Method of payment” was the most heavily weighted criterion by the expert panel. This indicates that in the Saudi Arabian construction context, a supplier’s financial terms and their impact on a contractor’s cash flow are considered paramount, often outweighing purely technical specifications in the final decision-making calculus.
- The novel use of PCA to systematically link an objective metric (factory capacity) to the subjective quality criteria (the CQW matrix) proved highly effective. This automated approach reduces the subjective burden on decision-makers, enhances consistency, and provides a transparent, data-driven foundation for the evaluation, addressing a common limitation in many traditional MCDM models.
- The framework demonstrated high stability in the sensitivity analysis, with rankings remaining consistent despite significant variations in criteria weights and aggregation parameters. This robustness, combined with the strong validation against expert opinion, establishes the proposed hybrid model as an unprecedentedly effective and reliable tool for strategic supplier selection in the precast concrete industry.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Customer satisfactory survey | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Company Name: | Location: | ||||||||
| ATTN: | Project(s) date/duration: | ||||||||
| P.O. Box: | Tel: | ||||||||
| E-Mail: | Fax: | Survey date: | |||||||
| Inspection/Project: | |||||||||
| Please mark √ against the boxes below based on your assessment of our services to your esteemed organization. | |||||||||
| You need not write your name on this sheet if you feel so. We would appreciate your sincere comments and valid suggestions for improvement. | |||||||||
| SL | Description | Poor | Satisfactory | Good | Very good | Excellent | |||
| 1 | Material suitability with the required specification | 3 | |||||||
| 2 | Guarantee conditions | 3 | |||||||
| 3 | Method of payments | 2 | 1 | ||||||
| 4 | Accuracy of the quantity sent | 3 | |||||||
| 5 | On-time delivery | 2 | 1 | ||||||
| 6 | Easy to communicate | 3 | |||||||
| 7 | Quick response regarding the quality problem | 1 | 2 | ||||||
| 8 | Quick response regarding urgent order | 1 | 2 | ||||||
| 9 | Technical expertise | 3 | |||||||
| General remarks/Comments/Suggestions: | |||||||||
| Name: | Signature: | ||||||||
| Denoted | Criteria | Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| C1 | Material suitability with the required specification | ||||||||||
| C2 | Guarantee conditions | ||||||||||
| C3 | Method of payments | ||||||||||
| C4 | Accuracy of the quantity sent | ||||||||||
| C5 | On-time delivery | ||||||||||
| C6 | Easy to communicate | ||||||||||
| C7 | Quick response regarding the quality problem | ||||||||||
| C8 | Quick response regarding urgent order | ||||||||||
| C9 | Technical expertise | ||||||||||
References
- GCC Statistical Yearbook 2023. Gulf Cooperation Council (GCC) Secretariat. 2023. Available online: https://www.gcc-sg.org/en-us/Statistics/Pages/default.aspx (accessed on 23 June 2025).
- Mulliner, E.; Algrnas, M. Preferences for housing attributes in Saudi Arabia: A comparison between consumers’ and property practitioners’ views. Cities 2018, 83, 152–164. [Google Scholar] [CrossRef]
- Grand, S.R.; Wolff, K. Assessing Saudi Vision 2030: A 2020 Review; Atlantic Council: Washington, DC, USA, 2022. [Google Scholar]
- Henderson, J.C. Religious Tourism and Its Management: The Hajj in Saudi Arabia. Int. J. Tour. Res. 2010, 13, 541–552. [Google Scholar] [CrossRef]
- Shash, A.A.; Alawad, M. Modern Construction Methods (MMC) in Saudi Arabia: Evaluation Aspects and Barriers. J. Eng. Arch. 2020, 8, 50–65. [Google Scholar] [CrossRef]
- Mohammed, H.A. Precast Concrete Cost Solution. 2018. Available online: https://www.researchgate.net/publication/329391473 (accessed on 14 June 2023).
- Priya, P.K.; Neamitha, M. A review on precast concrete. Int. Res. J. Eng. Technol. 2018, 5, 967–971. Available online: www.irjet.net (accessed on 5 April 2023).
- Abdellatif, H.; Alshibani, A. Major factors causing delay in the delivery of manufacturing and building projects in Saudi Arabia. Buildings 2019, 9, 93. [Google Scholar] [CrossRef]
- Alshakhrit, A.K.; Supeni, E.E.; Zahari, N.I. Causes and effects of delays in Saudi arAabian construction projects. J. Glob. Econ. Manag. Bus. Res. 2019, 11, 165–174. [Google Scholar]
- Alsuliman, A.K. Causes of delay in Saudi public construction projects. Alex. Eng. J. 2019, 58, 801–808. [Google Scholar] [CrossRef]
- Singh, R.K.; Modgil, S. Supplier selection using SWARA and WASPAS—A case study of Indian cement industry. Meas. Bus. Excell. 2020, 24, 243–265. [Google Scholar] [CrossRef]
- Rahmiati, F.; Syafei, H.Y.; Purwanto, P.; Andianto, J. Ceramic supplier selection using analytical hierarchy process method. Int. J. Ind. Optim. 2021, 2, 113–124. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Hashemi-Tabatabaei, M.; Zavadskas, E.K.; Kaklauskas, A. A new decision-making approach based on fermatean fuzzy sets and WASPAS for green construction supplier evaluation. Mathematics 2020, 8, 2202. [Google Scholar] [CrossRef]
- El Bettioui, W.; Zaim, M.; Sbihil, M. A combined fuzzy multicriteria decision making approach for green supplier selection in building material industry. J. Theor. Appl. Inf. Technol. 2022, 15, 6913–6933. Available online: www.jatit.org (accessed on 23 March 2023).
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Mardani, A.; Cavallaro, F.; Ravichandran, K.S.; Balasubramanian, K. Hesitant fuzzy SWARA-complex proportional assessment approach for sustainable supplier selection (HF-SWARA-COPRAS). Symmetry 2020, 12, 1152. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Kubek, D. Multicriteria Selection of the Building Material Supplier Using AHP and Fuzzy AHP. J. Constr. Eng. Manag. 2016, 142, 04015057. [Google Scholar] [CrossRef]
- Al-Ghamdi, M.A.; Al-Gahtani, K.S. Integrated Value Engineering and Life Cycle Cost Modeling for HVAC System Selection. Sustainability 2022, 14, 2126. [Google Scholar] [CrossRef]
- Bayazit, O.; Karpak, B.; Yagci, A. A purchasing decision: Selecting a supplier for a construction company. J. Syst. Sci. Syst. Eng. 2006, 15, 217–231. [Google Scholar] [CrossRef]
- Abdolshah, M. A Review of Quality Criteria Supporting Supplier Selection. J. Qual. Reliab. Eng. 2013, 2013, 621073. [Google Scholar] [CrossRef]
- Cagnin, F.; Oliveira, M.C.; Simon, A.T.; Helleno, A.L.; Vendramini, M.P.; Sampaio, M.S. Proposal of a method for selecting suppliers considering risk management. Int. J. Qual. Reliab. Manag. 2016, 33, 488–498. [Google Scholar] [CrossRef]
- Biruk, S.; Jaskowski, P.; Czarnigowska, A. Fuzzy AHP for selecting suppliers of construction materials. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; p. 032093. [Google Scholar] [CrossRef]
- Tushar, Z.N.; Bari, A.B.M.M.; Khan, M.A. Circular supplier selection in the construction industry: A sustainability perspective for the emerging economies. Sustain. Manuf. Serv. Econ. 2022, 1, 100005. [Google Scholar] [CrossRef]
- Ulutaş, A. Supplier Selection by Using a Fuzzy Integrated Model for a Textile Company. Eng. Econ. 2019, 30, 579–590. [Google Scholar] [CrossRef]
- Lopes, A.P.; Rodriguez-Lopez, N. A Decision Support Tool for Supplier Evaluation and Selection. Sustainability 2021, 13, 12387. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Yazdani, M.; Zavadskas, E.K. An extended stepwise weight assessment ratio analysis (SWARA) method for improving criteria prioritization process. Soft Comput. 2018, 22, 7399–7405. [Google Scholar] [CrossRef]
- Nurprihatin, F.; Antonius, R.; Rembulan, G.D.; Djajasoepena, R.; Sulistyo, E. Analytical hierarchy process and TOPSIS approach to perform supplier selection in construction industry. J. Ind. Eng. Manag. Syst. 2022, 15, 130–138. Available online: http://journal.ubm.ac.id/index.php/jiems (accessed on 23 June 2025). [CrossRef]
- Su, Y. Selection and Application of Building Material Suppliers Based on Intuitionistic Fuzzy Analytic Hierarchy Process (IFAHP) Model. IEEE Access 2020, 8, 136966–136977. [Google Scholar] [CrossRef]
- Qambrani, F.U.R.; Yousfani, A.M. Quality Attributes for Supplier Selection in the Construction Industry of Pakistan: The Contractors’ Perspective. Eng. Conf. 2022, 22, 10. [Google Scholar] [CrossRef]
- Majd, E.; Balakrishnan, V.; Godazgar, V. Selecting the reliable supplier by using the advisor agents. J. Bus. Ind. Mark. 2017, 32, 238–250. [Google Scholar] [CrossRef]
- Alsanabani, N.M.; Al-Gahtani, K.S.; Bin Mahmoud, A.A.; Aljadhai, S.I. Integrated Methods for Selecting Construction Foundation Type Based on Using a Value Engineering Principle. Sustainability 2023, 15, 8547. [Google Scholar] [CrossRef]
- Jiang, B.; Tian, L. Effects of Reactive Capacity on Product Quality and Firm Profitability in an Uncertain Market. Oper. Res. 2022, 70, 2619–2636. [Google Scholar] [CrossRef]
- Elshafei, B.; Mo, F.; Chaplin, J.C.; Arellano, G.M.; Ratchev, S. Capacity Modelling and Measurement for Smart Elastic Manufacturing Systems. In Proceedings of the 2023 AeroTech, Fort Worth, TX, USA, 14–16 March 2023. SAE Technical Paper. [Google Scholar]
- Ahmad, N.; Kasim, M.M.; Rajoo, S.S.K. Evaluating supplier quality performance using fuzzy analytical hierarchy process. AIP Conf. Proc. 2014, 1635, 35–40. [Google Scholar] [CrossRef]
- Ding, F.-Y.; Raghavan, B.; Pollard, S. Supplier capacity analysis for a manufacturing firm with a case study. Prod. Plan. Control. 2007, 18, 514–525. [Google Scholar] [CrossRef]
- Bradford, P.; Koenig, T.; Cordonnier, K.; Buckmaster, J.; Ballinger, J.; Ladd, D.; Gale, J.; Gilstorf, A.; Honda Motor Co., Ltd. Computerized Dynamic Capacity Management System and Method. U.S. Patent Application 13/205, 9 February 2012. [Google Scholar]
- Tu, J.F.; Liu, K. Order Allocation Based on Supplier Capacity-Load Balance. In 2011 International Conference on Computer Science and Service System (CSSS); IEEE: New York, NY, USA, 2011. [Google Scholar]
- Zolfani, S.H.; Zavadskas, E.K.; Turskis, Z. Design of products with both international and local perspectives based on Yin-Yang balance theory and SWARA method. Ekon. Istraz. 2013, 26, 153–166. [Google Scholar] [CrossRef]
- Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K. A framework for the selection of a packaging design based on the SWARA method. Eng. Econ. 2015, 26, 181–187. [Google Scholar] [CrossRef]
- Alinezhad, A.; Khalili, J. International Series in Operations Research & Management Science New Methods and Applications in Multiple Attribute Decision Making (MADM). 2019. Available online: http://www.springer.com/series/6161 (accessed on 15 May 2023).
- Chakraborty, D.; Elhegazy, H.; Elzarka, H.; Gutierrez, L. A novel construction cost prediction model using hybrid natural and light gradient boosting. Adv. Eng. Inform. 2020, 46, 101201. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Ravichandran, K.; Kar, S. Multi-criteria food waste treatment method selection using single-valued neutrosophic-CRITIC-MULTIMOORA framework. Appl. Soft Comput. 2021, 111, 107657. [Google Scholar] [CrossRef]
- Polat, G.; Eray, E.; Bingol, B.N. An integrated fuzzy MCGDM approach for supplier selection problem. J. Civ. Eng. Manag. 2017, 23, 926–942. [Google Scholar] [CrossRef]
- Tomczak, M.; Biruk, S.; Jaskowski, P. Selection of Construction Products Suppliers According to the Condorcet Criterion. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar] [CrossRef]
- Azadeh, A.; Zarrin, M.; Salehi, N. Supplier selection in closed loop supply chain by an integrated simulation-Taguchi-DEA approach. J. Enterp. Inf. Manag. 2016, 29, 302–326. [Google Scholar] [CrossRef]
- de Santis, R.B.; Golliat, L.; de Aguiar, E.P. Multi-criteria supplier selection using fuzzy analytic hierarchy process: Case study from a Brazilian railway operator. Braz. J. Oper. Prod. Manag. 2017, 14, 428–437. [Google Scholar] [CrossRef]
- Shrestha, N. Factor Analysis as a Tool for Survey Analysis. Am. J. Appl. Math. Stat. 2021, 9, 4–11. [Google Scholar] [CrossRef]
- Akintoye, A. Analysis of factors influencing project cost estimating practice. Constr. Manag. Econ. 2000, 18, 77–89. [Google Scholar] [CrossRef]
- Mamavi, O.; Nagati, H.; Pache, G.; Wehrle, F.T. How does performance history impact supplier selection in public sector? Ind. Manag. Data Syst. 2015, 115, 107–128. [Google Scholar] [CrossRef]
- Ebrahimipour, V.; Shoja, B.M.; Li, S.; Madu, C. Supplier selection considering product structure and product life cycle cost. Int. J. Qual. Reliab. Manag. 2016, 33, 654–675. [Google Scholar] [CrossRef]
- de Araújo, M.C.B.; Alencar, L.H.; Viana, J.C. Structuring a model for supplier selection. Manag. Res. Rev. 2015, 38, 1213–1232. [Google Scholar] [CrossRef]



| S. No | Author(s) and Year | Research Intentions | Unit of Analysis | Tool of Analysis | Approach |
|---|---|---|---|---|---|
| 1 | [16] | building materials | Industry | Analytical Hierarchy Process (AHP) and Fuzzy Analytic Hierarchical Process (FAHP) | Findings are available in the literature, as well as the authors’ own experience |
| 2 | [11] | cement | Industry | Stepwise Weight Assessment Ratio Analysis (SWARA) and Weighted Aggregated Sum Product Assessment (WASPAS) | Brainstorming sessions for SWARA and WASPS with a set of experts |
| 3 | [18] | lime | Firm | Analytic Hierarchical Process (AHP) and sensitivity analysis | Meetings with a team of AKG decision-makers |
| 4 | [24] | fresh fruit | Firm | Preference Ranking Organization Method for Enrichment of Evaluations—Geometrical Analysis for Interactive Assistance (PROMETHEE-GAIA) | Use of expert knowledge from specialists |
| 5 | [25] | high-tech industries | Industry | Stepwise Weight Assessment Ratio Analysis (SWARA) | Integrating the reliability evaluation of experts’ ideas into the first step of SWARA |
| 6 | [12] | feldspar | Firm | Analytical Hierarchy Process (AHP) | Questionnaires and an interview |
| 7 | [23] | textile supplier | Firm | Fuzzy Analytic Hierarchy Process (FAHP) and fuzzy extension of Operational Competitiveness Rating (Fuzzy OCRA) | Questionnaires |
| 8 | [17] | an HVAC system | Industry | AHP, pairwise, Function Analysis System (FAST), and Monte Carlo techniques | Interviews and case study |
| 9 | [19] | the quality evaluation of suppliers | Industry | AHP and Modified Likelihood Ratio (MLR) selection rule | Review of the existing literature |
| 10 | [20] | material suppliers’ systematic selection in the automotive industry | Firm | AHP, Failure Mode and Effect Analysis (FMEA) | Case study |
| 11 | [13] | evaluation of green construction suppliers | Firm | Fuzzy sets: simple multi-attribute rating technique (SMART) and WASPAS | A group of decision-makers, including three experts |
| 12 | [15] | to evaluate and select a desirable sustainable supplier within the HFS context | Firm | COPRAS (Complex Proportional Assessment) and SWARA (Stepwise Weight Assessment Ratio Analysis) | Use of expert knowledge from a team of managers |
| 13 | [21] | construction material | Firm | Fuzzy AHP | Case study |
| 14 | [26] | financial and non-financial losses | Firm | Analytical Hierarchy Process (AHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) | Qualitative opinions based on pairwise comparisons |
| 15 | [27] | building material | Firm | Intuitionistic Fuzzy Analytic Hierarchy Process (IFAHP) Model | Knowledgeable and experienced experts |
| 16 | [14] | ceramic tile company | Firm | Fuzzy Analytic Hierarchical Process (Fuzzy AHP) and Fuzzy Technique for Order Preference by Similarity to Ideal Solution (Fuzzy TOPSIS) | A real-world case study |
| 17 | [28] | quality attributes | Industry | Weighted Sum Model (WSM) | A survey targeting renowned contractors in Pakistan |
| 18 | [22] | building and construction industry suppliers | Industry | Fuzzy Analytical Hierarchy Process (FAHP) and a Preference Ranking Organization Method for Enrichment of Evaluations II (PROMETHEE II) | Literature reviews and expert feedback |
| 19 | [29] | intelligent agents | Industry | Trust-based recommender system for the peer production services (TREPPS) model, Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) | Case study |
| 20 | [30] | to develop a framework for selecting appropriate foundation types | Firm | Function Analysis System Technique (FAST), SWARA, WASPAS, and Value Engineering (VE) methods | Reviewing international standards, expert interviews, and the literature |
| # | Criterion | Author(s) |
|---|---|---|
| C1 | Material suitability with the required specification | [12] |
| C2 | Guarantee conditions | [43] |
| C3 | Method of payment | [12] |
| C4 | Accuracy of the quantity sent | [12] |
| C5 | On-time delivery | [12] |
| C6 | Easy communication | [43] |
| C7 | Quick response regarding quality problems | [12] |
| C8 | Quick response regarding an urgent order | [12] |
| C9 | Technical expertise | [43] |
| C10 | Cost | [14] |
| C11 | Production capacity | [44] |
| C12 | Experience and track record | [22] |
| C13 | Sustainability practices | [15] |
| C14 | Supply chain management | [11] |
| C15 | Safety standards | [45] |
| Expert | Sector | Position | Years of Experience |
|---|---|---|---|
| Exp. 1 | Governmental | Supplier relationship manager | 13 |
| Exp. 2 | Private | Construction manager | 23 |
| Exp. 3 | Private | Procurement manager | 18 |
| Exp. 4 | Governmental | Supplier relationship specialist | 9 |
| Exp. 5 | Governmental | Supply chain supervisor | 12 |
| Exp. 6 | Private | Project manager | 12 |
| Exp. 7 | Private | Project manager | 10 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| Exp. 1 | 2 | 3 | 1 | 7 | 4 | 6 | 8 | 9 | 5 |
| Exp. 2 | 1 | 4 | 2 | 8 | 3 | 9 | 5 | 6 | 7 |
| Exp. 3 | 3 | 2 | 4 | 5 | 1 | 7 | 9 | 8 | 6 |
| Exp. 4 | 3 | 4 | 2 | 7 | 1 | 8 | 9 | 5 | 6 |
| Exp. 5 | 3 | 4 | 1 | 8 | 2 | 9 | 7 | 6 | 5 |
| Exp. 6 | 2 | 4 | 1 | 9 | 3 | 8 | 5 | 7 | 6 |
| Exp. 7 | 2 | 3 | 1 | 8 | 5 | 7 | 6 | 9 | 4 |
| RII | S | K | q | W | |
|---|---|---|---|---|---|
| C6 | 0.857143 | 1.000 | 1.000 | 0.171 | |
| C4 | 0.825397 | 0.038 | 1.038 | 0.963 | 0.165 |
| C8 | 0.793651 | 0.040 | 1.040 | 0.926 | 0.159 |
| C7 | 0.777778 | 0.020 | 1.020 | 0.907 | 0.156 |
| C9 | 0.619048 | 0.256 | 1.256 | 0.722 | 0.124 |
| C2 | 0.380952 | 0.625 | 1.625 | 0.444 | 0.076 |
| C5 | 0.301587 | 0.263 | 1.263 | 0.352 | 0.060 |
| C1 | 0.253968 | 0.188 | 1.188 | 0.296 | 0.051 |
| C3 | 0.190476 | 0.333 | 1.333 | 0.222 | 0.038 |
| No | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 |
|---|---|---|---|---|---|---|---|---|---|
| Exp. 1 | 4 | 3 | 5 | 5 | 5 | 5 | 5 | 5 | 4 |
| Exp. 2 | 4 | 4 | 1 | 3 | 4 | 3 | 3 | 1 | 4 |
| Exp. 3 | 0 | 0 | 2 | 0 | 5 | 0 | 0 | 5 | 3 |
| Exp. 4 | −1 | −2 | −4 | −4 | −5 | −4 | −4 | −4 | −4 |
| Exp. 5 | 0 | 0 | 0 | −5 | −5 | 0 | 0 | −5 | 0 |
| Exp. 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Exp. 7 | −1 | −2 | −3 | −2 | −2 | −4 | 0 | 0 | 5 |
| Exp. 8 | 5 | 5 | 0 | 5 | 5 | 4 | 3 | 5 | 5 |
| Exp. 9 | 4 | 4 | 4 | 4 | 5 | 4 | 4 | 4 | 4 |
| Exp. 10 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
| Exp. 11 | 3 | 4 | 0 | 0 | 5 | −3 | −2 | 3 | 4 |
| Exp. 12 | 5 | 4 | 4 | 4 | −2 | 4 | −2 | −3 | 5 |
| Exp. 13 | 3 | 4 | 0 | 4 | 4 | 0 | 1 | 2 | 3 |
| Exp. 14 | 0 | 0 | 3 | 2 | 5 | 5 | 5 | 5 | 1 |
| Exp. 15 | 3 | 0 | 5 | 0 | 0 | 0 | 4 | 5 | 5 |
| Exp. 16 | 0 | 3 | 0 | 0 | 3 | 0 | 4 | 5 | 4 |
| Exp. 17 | 5 | 5 | 3 | 2 | 5 | 5 | 5 | 3 | 5 |
| Exp. 18 | −5 | 3 | 1 | −1 | 1 | 1 | −5 | −4 | −5 |
| Exp. 19 | 4 | 4 | 4 | 5 | 3 | 2 | 3 | 4 | 5 |
| Exp. 20 | 1 | 2 | 3 | 2 | 5 | 3 | 2 | 4 | 4 |
| Kaiser–Meyer–Olkin Measure of Sampling Adequacy | 0.708 | |
|---|---|---|
| Bartlett’s Test of Sphericity | Approx. Chi-Square | 142.271 |
| df | 36 | |
| Sig. | 0.000 | |
| Component | Initial Eigenvalues | |||
|---|---|---|---|---|
| Total | % of Variance | Cumulative % | ||
| Raw | 1 | 49.117 | 63.179 | 63.179 |
| 2 | 9.345 | 12.020 | 75.199 | |
| 3 | 7.474 | 9.613 | 84.813 | |
| 4 | 5.823 | 7.490 | 92.302 | |
| 5 | 2.405 | 3.094 | 95.396 | |
| 6 | 1.479 | 1.903 | 97.299 | |
| 7 | 1.059 | 1.362 | 98.660 | |
| 8 | 0.732 | 0.941 | 99.602 | |
| 9 | 0.310 | 0.398 | 100.000 | |
| Component | ||
|---|---|---|
| 1 | 2 | |
| C1 | 1.865 | 1.010 |
| C2 | 1.827 | 0.436 |
| C3 | 1.760 | 0.893 |
| C4 | 2.383 | 1.350 |
| C5 | 1.371 | 2.611 |
| C6 | 2.484 | 0.717 |
| C7 | 1.130 | 2.330 |
| C8 | 0.568 | 3.355 |
| C9 | 1.170 | 2.002 |
| RML | ||
|---|---|---|
| C1 | 1.865 | 0.128 |
| C2 | 1.827 | 0.125 |
| C3 | 1.760 | 0.121 |
| C4 | 2.383 | 0.164 |
| C5 | 1.371 | 0.094 |
| C6 | 2.484 | 0.171 |
| C7 | 1.130 | 0.078 |
| C8 | 0.568 | 0.039 |
| C9 | 1.170 | 0.080 |
| ∑ | 1.000 | |
| Alternative Supplier | Capacity per Year (m3) | ) (m3) | |
|---|---|---|---|
| A1 | 360,000 | 986 | 0.72 |
| A2 | 300,000 | 822 | 0.6 |
| A3 | 500,000 | 1370 | 1 |
| A4 | 300,000 | 822 | 0.6 |
| A5 | 250,000 | 685 | 0.5 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.092 | 0.09 | 0.087 | 0.118 | 0.118 | 0.068 | 0.123 | 0.056 | 0.028 |
| A2 | 0.077 | 0.075 | 0.073 | 0.098 | 0.098 | 0.056 | 0.103 | 0.047 | 0.023 |
| A3 | 0.128 | 0.125 | 0.121 | 0.164 | 0.164 | 0.094 | 0.171 | 0.078 | 0.039 |
| A4 | 0.077 | 0.075 | 0.073 | 0.098 | 0.098 | 0.056 | 0.103 | 0.047 | 0.023 |
| A5 | 0.064 | 0.063 | 0.061 | 0.082 | 0.082 | 0.047 | 0.086 | 0.039 | 0.02 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | WSM | |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.005 | 0.007 | 0.003 | 0.019 | 0.007 | 0.012 | 0.019 | 0.009 | 0.003 | 0.085 |
| A2 | 0.004 | 0.006 | 0.003 | 0.016 | 0.006 | 0.010 | 0.016 | 0.007 | 0.003 | 0.070 |
| A3 | 0.007 | 0.010 | 0.005 | 0.027 | 0.010 | 0.016 | 0.027 | 0.012 | 0.005 | 0.118 |
| A4 | 0.004 | 0.006 | 0.003 | 0.016 | 0.006 | 0.010 | 0.016 | 0.007 | 0.003 | 0.070 |
| A5 | 0.003 | 0.005 | 0.002 | 0.014 | 0.005 | 0.008 | 0.013 | 0.006 | 0.002 | 0.059 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | WPM | |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.885 | 0.833 | 0.911 | 0.703 | 0.880 | 0.631 | 0.721 | 0.632 | 0.642 | 0.077 |
| A2 | 0.877 | 0.821 | 0.905 | 0.682 | 0.870 | 0.611 | 0.701 | 0.615 | 0.626 | 0.064 |
| A3 | 0.900 | 0.854 | 0.923 | 0.742 | 0.897 | 0.667 | 0.759 | 0.667 | 0.669 | 0.107 |
| A4 | 0.877 | 0.821 | 0.905 | 0.682 | 0.870 | 0.611 | 0.701 | 0.615 | 0.626 | 0.064 |
| A5 | 0.869 | 0.810 | 0.899 | 0.662 | 0.861 | 0.593 | 0.682 | 0.597 | 0.616 | 0.054 |
| WSM | WPM | WASPAS | |
|---|---|---|---|
| A1 | 0.085 | 0.077 | 0.081 |
| A2 | 0.070 | 0.064 | 0.067 |
| A3 | 0.118 | 0.107 | 0.112 |
| A4 | 0.070 | 0.064 | 0.067 |
| A5 | 0.059 | 0.054 | 0.056 |
| Alternatives to the Supplier | WASPAS | Cost (SAR/m2) | Normalization of Cost (Cost/Max Cost) | VE | Normalized VE = VEi/Max(VEi) | Rank |
|---|---|---|---|---|---|---|
| A1 | 0.081 | 125 | 0.96 | 0.084 | 0.693 | 3 |
| A2 | 0.067 | 130 | 1 | 0.067 | 0.550 | 5 |
| A3 | 0.112 | 120 | 0.92 | 0.122 | 1.000 | 1 |
| A4 | 0.067 | 95 | 0.73 | 0.092 | 0.754 | 2 |
| A5 | 0.056 | 100 | 0.77 | 0.073 | 0.597 | 4 |
| Scenario | Weight of C6 (w6) | A1 Rank | A2 Rank | A3 Rank | A4 Rank | A5 Rank | Final Ranking (A3 > A4 > A1 > A5 > A2) |
|---|---|---|---|---|---|---|---|
| Base Case | 0.171 | 3 | 5 | 1 | 2 | 4 | A3 > A4 > A1 > A5 > A2 |
| Scenario 1 (+10%) | 0.188 | 3 | 5 | 1 | 2 | 4 | A3 > A4 > A1 > A5 > A2 |
| Scenario 2 (+20%) | 0.205 | 3 | 5 | 1 | 2 | 4 | A3 > A4 > A1 > A5 > A2 |
| Scenario 3 (+30%) | 0.222 | 3 | 5 | 1 | 2 | 4 | A3 > A4 > A1 > A5 > A2 |
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| Exp. 1 | 8 | 6 | 10 | 9 | 7 |
| Exp. 2 | 7 | 5 | 10 | 8 | 6 |
| Exp. 3 | 6 | 6 | 9 | 7 | 7 |
| Average | 7.00 | 5.67 | 9.67 | 8.00 | 6.67 |
| RII | 0.70 | 0.57 | 0.97 | 0.80 | 0.67 |
| Rank | 3 | 5 | 1 | 2 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldokhi, M.I.; Al-Gahtani, K.S.; Alsanabani, N.M.; Aljadhai, S.I. Hybrid Methods for Selecting Precast Concrete Suppliers Based on Factory Capacity. Appl. Sci. 2025, 15, 8027. https://doi.org/10.3390/app15148027
Aldokhi MI, Al-Gahtani KS, Alsanabani NM, Aljadhai SI. Hybrid Methods for Selecting Precast Concrete Suppliers Based on Factory Capacity. Applied Sciences. 2025; 15(14):8027. https://doi.org/10.3390/app15148027
Chicago/Turabian StyleAldokhi, Mohammed I., Khalid S. Al-Gahtani, Naif M. Alsanabani, and Saad I. Aljadhai. 2025. "Hybrid Methods for Selecting Precast Concrete Suppliers Based on Factory Capacity" Applied Sciences 15, no. 14: 8027. https://doi.org/10.3390/app15148027
APA StyleAldokhi, M. I., Al-Gahtani, K. S., Alsanabani, N. M., & Aljadhai, S. I. (2025). Hybrid Methods for Selecting Precast Concrete Suppliers Based on Factory Capacity. Applied Sciences, 15(14), 8027. https://doi.org/10.3390/app15148027







