Abstract
Precisely predicting photovoltaic (PV) output is crucial for reliable grid integration; so far, most models rely on site-specific sensor data or treat large meteorological datasets as black boxes. This study proposes an explainable machine-learning framework that simultaneously ranks the most informative weather parameters and reveals their physical relevance to PV generation. Starting from 27 local and plant-level variables recorded at 15 min resolution for a 1 MW array in Çanakkale region, Türkiye (1 August 2022–3 August 2024), we apply a three-stage feature-selection pipeline: (i) variance filtering, (ii) hierarchical correlation clustering with Ward linkage, and (iii) a meta-heuristic optimizer that maximizes a neural-network R2 while penalizing poor or redundant inputs. The resulting subset, dominated by apparent temperature and diffuse, direct, global-tilted, and terrestrial irradiance, reduces dimensionality without significantly degrading accuracy. Feature importance is then quantified through two complementary aspects: (a) tree-based permutation scores extracted from a set of ensemble models and (b) information gain computed over random feature combinations. Both views converge on shortwave, direct, and global-tilted irradiance as the primary drivers of active power. Using only the selected features, the best model attains an average R2 ≅ 0.91 on unseen data. By utilizing transparent feature-reduction techniques and explainable importance metrics, the proposed approach delivers compact, more generalized, and reliable PV forecasts that generalize to sites lacking embedded sensor networks, and it provides actionable insights for plant siting, sensor prioritization, and grid-operation strategies.
1. Introduction
Renewable energy (RE) will play a significant role in the future energy structure as one of the ways that humanity may address the issue of fossil fuels [1]. Because it is widely available and sustainable, solar energy is regarded as one of the most promising RE sources [2]. A significant portion of RE power generation comes from solar power generation, particularly photovoltaic (PV) power generation. The great potential for energy productivity of PV energy systems makes them one of the most popular and desired RE technologies [3]. Therefore, as the use of PV power-generating systems increases, so does the importance of ensuring reliability in PV power systems [4]. As the capacity of PV systems increases, the risks associated with controlling the power generated also increase [5]. Therefore, studies to evaluate and improve the performance of solar energy systems are crucial. The power output evaluation studies of PV modules can be performed by obtaining the I-V (current–voltage) curve with solar simulators that provide the Standard Test Conditions specified in American Society for Testing and Materials (ASTM) 927-10 (a standard radiation spectrum of 1000 W/m2, a cell temperature of 25 °C, and an air mass of AM1.5) [6]. However, forecasting studies have emerged since this method cannot be applied in PV power plants, where meteorological conditions vary significantly. Numerous studies have demonstrated that local climate zones and meteorological conditions significantly impact the amount of solar energy [7]. The fluctuation in PV power generation is determined by meteorological conditions, including temperature, wind speed and direction, relative humidity, cloud cover, and solar radiation [4,8].
Regarding PV power system operation, planning, and marketing, the unpredictability and fluctuation of these weather variables pose significant challenges to stability, dependability, and integration [9]. Therefore, PV power forecasting has become essential for economic load allocation and system functioning [10]. A highly accurate forecast can lower operating costs, increase system operational efficiency, and enhance the performance of the system’s contingency analysis [11]. Integrating PV power into modern energy systems requires accurate forecasting to ensure grid stability and efficient energy management. However, irrelevant data in meteorological datasets for PV power estimation poses significant challenges, including model inefficiency, computational burden, and reduced forecasting accuracy. Many meteorological variables, although readily available, do not significantly contribute to PV power prediction, resulting in data redundancy and noise in forecasting models [12]. Unfiltered and excessive data inputs can obscure the relationships between key meteorological factors, such as solar irradiance, temperature, and wind speed, and PV power output, thereby complicating the development of robust predictive models.
One of the primary issues caused by unnecessary data is the increased dimensionality of datasets. When irrelevant or weakly correlated meteorological parameters are included in forecasting models, they increase computational complexity without improving prediction accuracy. High-dimensional data can slow down model training, resulting in longer processing times and requiring more computational resources [13]. Additionally, deep learning (DL) models trained on excessive features may suffer from overfitting, where the model learns noise and irrelevant fluctuations instead of meaningful trends, ultimately reducing generalization performance when applied to new data [14]. Another major concern is the introduction of collinearity between meteorological variables, which can distort the estimation of their respective impacts on PV power generation. For example, multiple atmospheric parameters, such as humidity, cloud cover, and air pressure, may exhibit strong correlations, leading to redundancy and reducing the interpretability of machine-learning (ML) models [15]. This redundancy can lead to unstable coefficient estimates in regression-based models and suboptimal performance in data-driven methods. Effective feature selection and dimensionality reduction techniques are necessary to mitigate these challenges. By refining data inputs, these methods enhance forecasting accuracy and reduce computational costs, making PV power estimation models more efficient and scalable. In conclusion, the inclusion of unnecessary and irrelevant data in meteorology can negatively impact PV power estimation by increasing computational demands, leading to overfitting and reducing interpretability. Addressing this issue through advanced data preprocessing techniques is crucial to enhance forecasting accuracy, ensure energy grid stability, and facilitate the reliable integration of solar energy into power networks [16].
This study examines the relationship between weather parameters and the generation of PV power. As the measurements obtained from PV sensors of power-generating modules are only available in previously installed plants, they may not be generalizable. While most studies focus on exact measurements of modules, we tend to study a wide range of areal weather parameters and explain their contribution to predicting the PV power in ML tasks.
1.1. Motivation and Context
This study is driven by the need to address key challenges in PV power forecasting, including weather dependency, short-term and spatial variability, data limitations, and scaling difficulties. Tackling these issues requires advanced modeling techniques, high-quality data, and robust computational approaches. Achieving high-accuracy PV power forecasts is essential for grid stability, effective energy management, and seamless integration of RE into the power grid. Moreover, accurate forecasting enables a balanced electricity supply and demand, minimizes grid disruptions caused by fluctuations in solar energy, and enhances the efficiency of energy storage systems. It also optimizes the planning of various power sources, improves market operations by providing reliable data for energy trading, lowers operational costs, ensures regulatory compliance, and maximizes the utilization of RE resources. Besides the accurate prediction power of the trained models, the generalization ability is crucial. Using more general features, such as areal meteorological parameters, may increase training loss. However, it can assist researchers in conducting a robust and generalizable evaluation of repeating the experiment in unseen locations, which can lead to reducing bias. Therefore, we preferred to utilize local weather parameters instead of information from module-embedded sensors.
1.2. Problem Statement and Research Objectives
PV power forecasting is crucial for power networks to include solar energy, increase energy efficiency, and ensure grid stability. However, the availability of redundant and plentiful meteorological data poses a significant challenge to PV power forecasting, which could negatively impact forecast precision and computational efficiency. Temperature, humidity, solar radiation, air pressure, and many other interrelated climatic characteristics can introduce noise, raise processing costs, and complicate the interpretation of models. Furthermore, redundant data may lead to model overfitting, a phenomenon in which predictive algorithms find patterns that do not translate well to fresh inputs. Additionally, PV forecasting models often require extensive preprocessing to filter out irrelevant variables while retaining the most relevant predictors. The inclusion of unnecessary meteorological variables increases computational time without necessarily improving accuracy.
This study aims to investigate the impact of weather parameters on PV power estimation by employing feature selection and ranking methods.
With feature selection, irrelevant or ineffective input data are eliminated without compromising the model’s prediction accuracy. This process is useful for determining the fewest features that provide the best performance. Therefore, efficiency can be increased, and interpretability can be achieved easily. Separating unnecessary features from the data with feature selection simplifies the model and reduces the risk of overfitting. Finding each feature’s degree of influence in predicting the target variable is the main goal of feature ranking. By elucidating the relative significance of various inputs, ranking techniques offer insights into the reasons behind the model’s specific behavior. Because it identifies the factors that influence decisions, this level of explanation is particularly helpful in avoiding training problems, such as overfitting or bias. Ultimately, these two strategies provide more reliable and intelligible models by facilitating the feature set while maintaining the most useful predictors.
PV power forecasting and removing useless data can increase forecast accuracy, reduce computational complexity, and improve energy management. Predictive models become more effective by eliminating unnecessary climate factors, which enhances the integration of solar power into power grids. This optimization promotes the efficient use of renewable resources, reduces energy waste, and increases grid stability. Therefore, improved PV forecasting supports a more resilient and environmentally friendly power system by promoting efficiency, reducing dependence on fossil fuels, and enabling a cleaner energy transition, all of which contribute to the larger goal of sustainable energy.
The main contributions of this study are as follows:
- We propose a three-stage feature selection pipeline combining variance filtering, hierarchical correlation clustering, and a meta-heuristic wrapper, specifically tailored for photovoltaic power forecasting.
- We perform a dual-perspective feature-importance analysis using tree-based permutation scores and information-theory metrics, providing a robust and explainable understanding of the key weather parameters.
- We use areal meteorological data instead of module-embedded sensors, enabling generalizable and sensor-free forecasting solutions suitable for locations without detailed instrumentation.
- We identify that irradiance-related variables dominate predictive power, while many commonly used variables (e.g., humidity, wind speed, wind direction) contribute minimally or even negatively, which is critical for model simplification and deployment.
- We release a high-resolution, real-world dataset (covering 15 min intervals over two years) and provide open access to the data for reproducibility and further research.
2. Literature Review
2.1. Overview of PV Power Prediction
These days, there are three primary types of PV power forecasting techniques. Physical approaches based on the PV power model are the first. Techniques like time series analysis, ML, and DL fall under the second group, statistical approaches. Lastly, hybrid approaches that combine statistical and physical methods have been created to improve prediction accuracy [17].
2.1.1. Physical Models
Physical models for PV power estimation predict energy production by modeling the interaction of meteorological variables, such as solar radiation, temperature, wind speed, etc., with PV panels using mathematical and physical principles. These models are based on fundamental laws of physics to predict the performance of PV systems and often include numerical weather prediction, sky imaging, and satellite imaging techniques [18]. In their study, Zhao et al. developed a physical model that incorporated tilted radiation, diffuse radiation, PV cell models, and inverter models for estimating PV power. Validated on a 250 kW PV plant, the model demonstrated high accuracy, with a monthly error rate of 5% and a daily error rate of 10%, while offering flexibility. Mayer and Grof [19] comprehensively compare different physical PV power forecasting models. Using one year of data from 16 PV plants, the analysis found that radiation separation and transposition modeling are the most critical factors in forecasting accuracy. A difference of 13% Mean Absolute Error (MAE) and 12% Root Mean Square Error (RMSE) was found between the best and worst models. Li et al. [20] evaluated the performance of the physical method PVPro in day-ahead power estimation on four different PV systems and reported that the mean normalized absolute error (nMAE) rate was 1.4%, indicating a 17.6% reduction in error compared to other techniques. It was also emphasized that PVPro demonstrated robust performance across different seasons and weather conditions and could operate effectively with limited historical production data (3 days). Physical models of the processes involved in producing electrical energy in PV systems can be used to estimate the daily power output based on the expected weather on a specific day. However, complex nonlinear interactions and unpredictability may not be sufficiently taken into account by the empirical formulas and assumptions that this approach frequently employs. Moreover, physical models are often challenging to apply due to the need for numerous costly variables and equipment that are not always readily available in many parts of the world.
2.1.2. Statistical and AI Methods
Statistical methods stand out in solar energy estimation because they are fast, are efficient, and have low computational costs for short and medium-term estimations [21,22]. Future PV power output is estimated using a statistical method, which utilizes historical time series data measurements as input data [23,24]. There are many benefits to using statistical approaches. Even if there are gaps in the data, they can still function after being trained using examples from the data. They can generate and generalize predictions after being trained [25]. Time series analysis, ML, and DL are the categories into which statistical techniques can be separated [22]. The statistical methods are explained as follows:
Time series analysis methods: These methods include statistical techniques for predicting future energy production using historical production data. These methods analyze historical data from PV systems to reveal specific patterns and trends and create mathematical models to predict future production. Since PV power is variable and influenced by weather conditions, solar irradiation, and system configurations, time series analysis techniques are crucial for modeling and predicting PV power. These approaches, ranging from complex ML models to traditional statistical techniques, allow for efficient PV power estimation [3,26,27].
The primary time series analysis methods employed for PV power estimation are Autoregressive (AR) and Moving Average (MA) models as well as ARMA, which combines AR and MA models, and ARIMA, which incorporates the difference process (integrated) to render the time series stationary. Sharadga et al. [3] performed PV power forecasting using time series analysis in large-scale PV plants, which showed that ARIMA is effective in short-term forecasting. Sumorek and Idzkowski [28] compared the ARIMA model with other ML techniques in solar energy forecasting and stated that ARIMA is a competitive method in certain scenarios. Time series data with periodic characteristics can be predicted using the Seasonal Autoregressive Integrated Moving Average (SARIMA) model, which is based on the ARIMA model and considers periodic components [29]. As a generalization of the ARIMA model, the Autoregressive Moving Average with Exogenous Variables (ARMAX) offers greater practical flexibility. Unlike ARIMA, the ARMAX model allows for the inclusion of external data; however, its application in PV power prediction has been relatively limited so far [30].
ML models: The foundation of ML models is a more intricate collection of algorithms that enable the model to identify patterns and connections in the data independently. ML outperforms conventional techniques in many situations due to its ability to manage nonlinearities, integrate multiple data sources, and adapt to changing circumstances. To fully realize their potential, however, issues such as weather fluctuations and data quality must be addressed [31,32]. The leading ML models for PV power prediction are Artificial Neural Networks (ANNs), random forests (RFs), Support Vector Machines (SVMs), Gaussian Process Regression (GPR), and Extreme Learning Machines (ELMs) [31,33,34].
Nespoli et al. [35] proposed an innovative selective ensemble method to increase the PV power prediction accuracy and reduce the computational burden using ANNs. Multiple independently trained ANN models were created, and the prediction performance of each model was evaluated. An ensemble was formed by selecting models performing above a certain threshold value. The proposed selective ensemble method significantly increased the accuracy of PV power prediction. In 2024, Amiri et al. [36] identified RF as the best-performing model for predicting power output from PV plants through rigorous data preprocessing, feature selection, and model evaluation in their forecasting study on a PV plant in Algeria. Abdulai et al. employed random forest and gradient-boosting regressor techniques to produce both deterministic and probabilistic estimates of solar energy output based on data collected over an eleven-month period. Some of their results showed that the RF model outperformed the other models they examined in terms of producing probabilistic estimations [37]. Tripathi et al. [38] compared different ML models in PV panel power estimation. Support Vector Machine Regression (SVMR) provided the highest accuracy with R2 = 0.99, MSE = 0.038, and MAE = 0.17. They stated that SVMR can better model environmental factors such as solar radiation, temperature, and humidity. Tahir et al. [39] analyzed a one-year dataset in hourly intervals collected from a 10 MW PV plant (Masdar) using regression tree ensemble, an SVM, GPR, and an ANN. Based on their results, they stated that GPR showed the best performance with the lowest prediction errors.
Ganesh et al. [40] propose short-term forecasting of PV power generation using an optimized Extreme Learning Machine (ELM) model to reduce the impact of solar energy variability on grid instability. The ELM model is optimized to forecast PV generation online in the short term. They stated that the proposed method provides stable energy management in the microgrid system despite the changes in irradiance, temperature, and Alternating Current (AC) load demand. Tercha et al. compared DT, RF, XBoost, and SVM regression models with 7-month meteorological data from NASA/POWER CERES/MERRA2 for estimating irradiance and temperature, two important parameters for energy production in PV systems, highlighting the importance of accurate weather forecasts for PV system operation and the difficulties associated with traditional meteorological models [41]. Alsharabi et al. employed SWM and Gaussian Process (GP) in their predictions for various time horizons, ranging from one day to fifteen days, in a study conducted in Riyadh, Saudi Arabia, in 2025. They stated that the SVM is an efficient algorithm for processing high-dimensional data [42]. In recent years, explainable AI (XAI) techniques have been developed to increase the interpretability of ML models and make the obtained outputs more understandable. The primary goal of XAI is to enable users of ML models to better understand their behavior without compromising the model’s performance [43].
DL models: DL is an extension of ML created to address a challenging issue with large amounts of data. Since it has been noted that ML models in PV forecast the research plateau as the quantity of training data increases, DL is employed in forecasting studies using large datasets. The more input data, the better DL models perform [44]. Since PV power forecasting is mostly conducted with sequential data, the main DL methods recommended are Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), and Convolutional Neural Networks–LSTM (CNN–LSTM) [5].
RNN’s recurrent architecture and memory units allow it to remember power changes over time. Consequently, RNN is a very short-term PV power forecasting model that takes intraday and interday PV power into account [45]. In the literature, some studies use only RNN in PV power forecasting [46,47]. However, recently, RNN has been proposed more as a hybrid with other models. For example, Narayanan et al. propose a hybrid prediction model that integrates traditional electrical components with RNN-LSTM in their 2024 study. The model has shown higher accuracy, adaptability, and robustness to data quality than existing methods, with 3.21% Mean Absolute Percentage Error (MAPE) and 0.0423 RMSE values [48]. LSTM is a unique type of RNN that can learn both short-term and long-term dependencies and is designed to avoid long-term dependencies [49]. Dhaked et al. [50] applied the LSTM to predict the production of a solar power plant in Brazil. They studied the effect of the number of hidden layers on the prediction accuracy and found that the 4-layer LSTM model provided the lowest error rate. To allow each iterative unit in RNN to capture dependencies at various time scales adaptively, GRU was first proposed in 2014 [51]. Similar to LSTM, GRU features gate units that control the information flow within the unit, eliminating the need for independent memory cells. Compared to LSTM, GRU is more robust, requires fewer parameters, and trains more quickly [52]. Articles from recent years that combine LSTM and GRU in PV power estimation stand out when the literature is reviewed [53,54,55]. CNN, a feed-forward neural network, increases the scalability and training efficiency of the model by reducing the number of parameters that need to be optimized with the parameter-sharing feature [56]. It is observed in the literature that CNN is preferred as a hybrid with other approaches, especially LSTM [57,58].
2.1.3. Hybrid Methods
To cope with the inherent complexity of solar energy and the unpredictability of meteorological conditions, hybrid methods that combine the capabilities of different approaches are becoming increasingly popular for PV power forecasting. With hybrid methods, projections become more reliable and accurate, facilitating better operational planning and integration of PV power into power grids [59,60]. Preprocessing data, building forecast models, and fine-tuning model parameters are just a few of the stages involved in solving the forecasting problem addressed by hybrid approaches [61]. The hybrid approach combines physical and statistical methods, utilizing optimization algorithms to leverage the strengths of each method while mitigating their limitations [62].
Asiedu et al. employed a hybrid RF and XGBoost model, combined with a single ANN and RF, in their forecasting studies using operational data from a grid-connected solar power plant with a capacity of 180 kWp. They stated that ANNs provided the best accuracy for one-day-ahead forecasts, RFs for two-week-ahead and one-month-ahead forecasts, and the hybrid model consisting of XGBoost and RF for one-week-ahead forecasts [63]. Tercha et al. aimed to combine the nonlinear data processing capability of ANNs with the capacity of LSTM to capture long-term dependencies in time series data, thereby increasing the accuracy of PV power estimates. As a result of the study, they stated that the model showed superior performance by achieving lower error rates (MAE, RMSE, etc.) in terms of error metrics and provided higher estimation accuracy compared to ANN or LSTM models [64]. Yang and Luo performed feature selection and optimization processes using the RF method for short-term PV power prediction, thereby increasing prediction accuracy by eliminating unnecessary features. They employed the Symplectic Geometry Model Decomposition (SGMD) technique to enhance input features and opted for the Bi-directional Long Short-Term Memory (BiLSTM) model in the prediction process. They also increased the prediction’s stability by optimizing the BiLSTM model’s hyperparameter settings with the Gray Wolf Optimization Algorithm (GWO). The study showed that the developed hybrid model is scalable and robust in different climate conditions and PV technologies and verified its applicability to real-world scenarios [65]. Hou et al. PV power forecasting is performed with a hybrid model based on Variational Mode Decomposition (VMD)–Whale Optimization Algorithm (WOA)–LSTM. The model tested for a 1.8 MW system in Yulara, Australia, achieved high accuracy with MAE: 15.247 kW, RMSE: 19.753 kW, MAPE: 4.405%, and R2: 0.997. The results show that the model successfully predicts PV generation fluctuations [61]. Al-Dahidi et al. investigated five different ML models (Multiple Linear Regression (MLR), Decision Tree Regression (DTR), random forest regression (RFR), Support Vector Regression (SVR), Multi-Layer Perceptron (MLP)) to improve solar energy production forecasting. They optimized their hyperparameters with the Chimpanzee Optimization Algorithm (ChOA). Among the models tested with data from a 264 kWp PV system in Jordan, the MLP model showed the best performance (RMSE: 0.503, MAE: 0.397, R2: 0.99). They emphasized that the results proved that ChOA effectively improves forecasting accuracy [66].
Du et al. proposed the Enhanced and Improved Beluga Whale Optimization (EIBWO) to optimize the internal parameters of ELM. The R2 of their proposed EIBWO-ELM exceeded 0.99, highlighting its efficient ability to adapt to PV power generation [67]. Radhi et al. utilized real data obtained from the experimental PV generation system installed at the Faculty of Engineering, Misan University, Iraq, to propose a short-term power forecast model. In a study where various forecast models were used, it was stated that the ANN model based on the genetic algorithm created the most accurate PV generation model in three different climatic condition tests [68]. Li et al. applied a Particle Swarm Optimization-based XGBoost model (PSO-XGBoost) for PV power prediction. They introduced the PSO algorithm to optimize the hyperparameters in the XGBoost model. They demonstrated that the prediction accuracy and stability of PV power prediction by the PSO-XGBoost model, based on meteorological data, are higher compared to the XGBoost model [69]. Similarly, a wide range of optimizers has been used to solve models or tune hyperparameters in various studies [70,71,72].Haupt et al. proposed a new methodology to forecast the power production of a 48 kWp PV system located at Campus Feuchtwangen in 2025. Their proposed methodology incorporates hybrid time series techniques, including state-space models, supported by artificial intelligence tools to generate forecasts. Their results show an accuracy of about 3% for the forecast in nRMSE [73]. Guo et al. presented a hybrid Attention-Temporal Convolutional Network (TCN)-LSTM model for short-term PV power forecasting. They utilized the PSO algorithm to determine the optimal hyperparameters, ensuring that these parameters did not impact the forecasting results. They obtained an RMSE value of 0.363, an MAE value of 0.161, and an R2 value of 0.98 with their proposed algorithm [74].
2.2. Feature Selection and Feature Importance
It is obvious in the literature that a wide range of ML and DL models are used for PV power prediction in single and hybrid models. Among these models, the LSTM model has shown superior performance. However, in this context, managing the data, especially the feature selection process, is as critical a factor as model selection in increasing the accuracy of the prediction models [75]. Feature selection enhances the accuracy and efficiency of the model by identifying the most significant variables within the dataset. This process enables more reliable predictions by reducing the data size, eliminating unnecessary or repetitive information, and enhancing the model’s interpretability. An effective feature selection method reduces computational time and improves overall performance by allowing the model to focus only on the most important variables [76].
In classification and regression tasks, feature importance is carefully considered. This process involves evaluating the impact of each feature on the target variable. One commonly used method to determine feature importance is to remove a feature from the dataset and analyze how the model’s prediction error changes. This process is repeated for each feature separately, allowing the system to understand which variables are more informative in predicting the target value. As a result of this analysis, unimportant features can be dropped, and only the most critical variables can be selected, thus reducing system complexity and optimizing computational time. In the final stage, the impact of the features determined by the cross-validation method on the model accuracy is evaluated. This step is critical in terms of increasing the prediction model’s reliability and strengthening the model’s generalization ability by eliminating unnecessary variables. This comprehensive analysis allows for selecting only the parameters that significantly contribute to the prediction performance and provides an effective strategy for increasing model accuracy [77,78].
3. Data Collection and Preprocessing
3.1. Description of Data Sources
The dataset for this experiment was obtained from a PV power plant with a 1 MW installed capacity located in Çanakkale, Turkey. Çanakkale is situated in the northwest of Turkey, and most of its land lies within the borders of the Marmara Region. It is between 25°40′–27°30′ east longitudes and 39°27′–40°45′ north latitudes. The weather station integrated into the power plant provides real and reliable meteorological data. Many PV power generation systems have been installed in the region. Among the PV systems, the system located between 26°41′ longitude and 40°12′ latitude was selected as the one that best meets the ideal standards for data collection. The collected data, which contains records between 1 August 2022 and 3 August 2024 in 15 min intervals, is published for the first time in the literature and is publicly available in Supplementary Materials. Besides the active power data of the PV panels, the dataset includes meteorological data on total radiation, wind speed, PV module temperature, and ambient temperature, obtained from the meteorological measurement station of the power plant where the panels are located. Other data that could not be measured at the PV power plant meteorological station (such as relative humidity, wind direction, and dew point) were obtained from source [79] for the same dates and within the same time range. The satellite image of the PV power plant from which the data were taken is given in Figure 1 [80].

Figure 1.
The satellite image of the PV power plant in Çanakkale, Türkiye (reference: Google Earth).
3.1.1. Module-Level Measurements
At the meteorological station of the PV power plant used for this study, the following parameters can be measured: total irradiance, ambient temperature of the power plant, surface temperature (module temperature) of the PV panels, and wind speed. These data were taken directly from the power plant’s meteorological station. The active power obtained from the PV output can be calculated from the measured current and voltage values and recorded directly with a wattmeter. It is well known that temperature negatively impacts PV module performance; this effect can be roughly expressed as a linear relationship. An increase in ambient temperature and module temperature will cause a decrease in open-circuit voltage and a slight increase in short-circuit current, thereby reducing the PV module’s efficiency and power output [81]. When the total irradiance (W/m2) increases at a constant temperature, the output current of the PV module will increase, which will lead to an increase in output power [82].
Wind speed is a positive factor in PV panel efficiency and power output, ensuring PV modules work well in energy conversion thanks to their strong cooling effects [83]. The effect of temperature change on the current–voltage (I–V) curve of the PV module and its efficiency is shown in Figure 2. The effect of radiation on the I–V curve of the PV module can be seen in Figure 3.
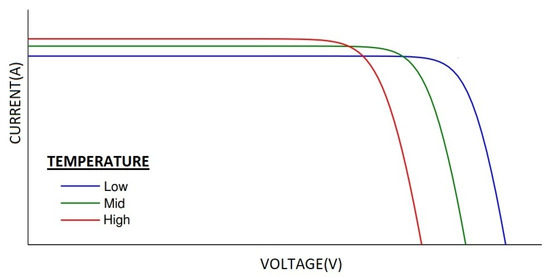
Figure 2.
Influence of temperature on I–V curve [84].
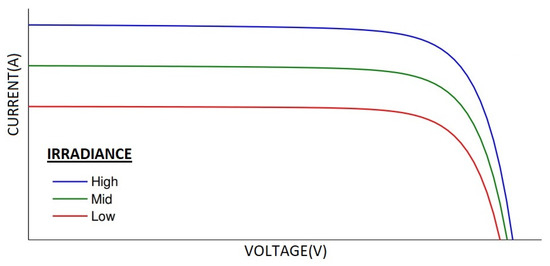
Figure 3.
Influence of irradiance on I–V curve [84].
3.1.2. Local Weather Parameters
Other meteorological data that could not be obtained from the meteorological station of the PV power plant in question were obtained from source [79]. Unlike the data taken from the PV station, these data are not obtained from the point where the power plant is located. They are obtained from general measurements of the region where the power plant is located. These data include temperature, relative humidity, and dew point measurements two meters above sea level. Wind speed and direction were measured at 10 m and 80 m above ground level. The wind gust value was measured at 10 m. Visibility, precipitation, and apparent temperature are also among these data. Radiation is categorized into four types: shortwave, direct, diffuse, and terrestrial. Direct normal irradiance, with its instantaneous value, and finally global tilted irradiance instant are other local data used.
As the relative humidity increases, dew can form on the surface of PV modules. Dew droplets will reflect incoming solar radiation in different directions, reducing the amount of incoming energy. This is a negative effect of relative humidity; however, it can have a positive impact on power generation, as the evaporation of dew can provide additional cooling to the PV modules [85]. Another local datum used in the study is the dew point. If a humid air mass is cooled at constant pressure, it reaches saturation, and liquid water forms in the form of dew or fog. The temperature at which this occurs is defined as the dew point of the air [86]. In PV studies, precipitation is generally considered to be the accumulation of water in the form of wetness. Precipitation reduces temperature, especially in spring and summer, cleans the surface of dust, and can reduce reflection losses in cases where a thin water layer forms. With these features, its contribution to power generation can be considered positive. Its effect in autumn and winter is not fully evident [87,88]. Visibility measures the distance at which an object or light can be clearly distinguished. This parameter affects the efficiency of PV modules due to the negative effects of light absorption and scattering by gases, water vapor, and dust particles in the air [89]. Large fluctuations in atmospheric winds at small scales are defined as wind gusts [90]. This parameter is also among the data considered in the study. Wind direction is a frequently used data point, along with wind speed, in PV forecasting studies. The effect of wind direction on PV power generation varies depending on the hemisphere in which the plant is located. A PV plant in the northern hemisphere positively affects production when it receives strong and frequent winds from the south. A PV plant in the southern hemisphere benefits from its performance when it receives strong and frequent winds from the north [91].
Local parameters related to the sun are as follows:
Shortwave radiation is the total solar radiation with wavelengths ranging from 300 to 3000 nm [92]. Sunlight that is not scattered is called direct beam radiation. Direct beam, when sunlight illuminates a plane perpendicular to the direction of the sun, is referred to as direct normal radiation. Therefore, any shortwave radiation consists of two basic components: direct and diffuse. Direct and diffuse radiation are collectively referred to as global radiation [93]. Global tilted irradiance expresses the total solar energy received per unit area of a sloped surface. It includes direct radiation and diffuse components. It provides an approximate value for calculating the energy yield of PV panels positioned permanently at a certain inclination [94]. The longwave, low-energy radiation that the Earth emits, corresponding to the emission spectrum of a mixture of blackbody spectra with temperatures ranging from 220 to 320 K, is called terrestrial radiation. Greenhouse gases in the atmosphere absorb this radiation, storing the energy and releasing it as heat [95].
4. Methodology
This section is divided into two main segments: feature selection and feature ranking. In feature selection, the goal is to remove irrelevant or unhelpful inputs while maintaining the model’s predictive accuracy. This process is particularly useful when the objective is to spot the fewest features yielding strong performance, thus improving efficiency and interpretability. Discarding unnecessary features makes the model less prone to complexity and potential overfitting.
In feature ranking, the emphasis is on identifying the influence of each feature in predicting the target variable. Ranking methods help clarify the relative importance of different inputs, offering insights into why the model behaves a certain way. This level of explanation is especially beneficial in avoiding training pitfalls such as overfitting or bias since it reveals which features drive decisions. These two approaches facilitate the feature set while ensuring the most informative predictors remain, ultimately leading to more robust and understandable models.
Both the PV output data and meteorological variables were collected at 15 min intervals over 2 years (August 2022–August 2024). To preserve the temporal integrity of the time series, we used a chronological split: the first 90% of the dataset was used for training, and the remaining 10% was reserved as unseen test data. This block-based split prevents data leakage and better reflects real-world deployment, where future forecasts are made based on past observations.
4.1. Feature Selection Methods
Feature selection is crucial because it focuses on the information that truly matters when predicting solar power output. By narrowing the features to genuinely relevant ones, we ensure that trained models capture the most important factors without diving into unnecessary details. This approach improves model accuracy and makes the results more interpretable and computationally efficient. The first feature selection step in this study involves a variance-based method that filters out weather parameters showing little to no variation. Such low-variance parameters contribute minimal predictive value and can add noise to the model. Next, a hierarchical clustering based on correlation is performed to group parameters with redundant information. From each cluster, only one representative parameter is chosen, minimizing duplication. Finally, a meta-heuristic algorithm is applied to further refine the set of selected features by simultaneously aiming to reduce their number while maximizing the score.
4.1.1. Variance-Based Feature Selection
First-order feature selection refers to basic techniques that use straightforward statistics to identify the most important features in a dataset. Instead of diving deep into complex models, it relies on metrics such as variance and correlation to quickly gauge which features stand out. These methods can remove less relevant or redundant information early, making subsequent analyses more focused and efficient. Variance analysis examines the extent to which a feature’s values vary within the dataset. If a feature shows almost no change, it is unlikely to help predict the outcome. By removing features with extremely low variance, inputs that do not add meaningful information to the model are eliminated. This simple step helps streamline the data, reduce the noise risk, and make the model training process more efficient. Equation (1) denotes the variance. In this study, a parameter-wise variance function calculates a variance matrix containing scalar values. Finally, parameters with low variance are removed from the feature list. The remaining features will be passed on to the next analysis.
where n is the number of measurements, x is the observed parameter, and is the mean of all observations’ mean.
4.1.2. Hierarchical Correlation Clustering
Correlation analysis measures how strongly each feature is related to the target variable and other features. A high correlation with the target indicates that the feature may be useful for predictions. However, if two features strongly overlap, keeping both can be redundant. By calculating correlation values, we can identify pairs of features that convey nearly the same information and determine which ones are more valuable or relevant to the outcome. This method helps us maintain a balanced feature set, reducing unnecessary complexity and focusing our model on the variables that influence predictions. This study utilizes the Pearson correlation coefficient, as defined in Equation (2), to identify the weather parameters that exhibit the most similar behaviors.
where is the Pearson correlation coefficient between features and . This value lies between −1 and +1.
We first computed the correlation matrix for the remaining features to address highly correlated features. After obtaining these values, hierarchical clustering was performed using Ward’s method, which merges features into clusters based on their similarity (or distance), as in Equation (3). We obtained distance-based clusters by applying a specific distance threshold to the resulting linkage matrix. The feature with the highest absolute correlation value was selected within each cluster, while the others, typically offering redundant or nearly duplicated information, were removed. This step ensured that only the most representative features from each correlation group remained in the dataset.
A grid search systematically examined distances ranging from 0 to the maximum possible distance in increments of 0.1 to determine the optimal distance threshold for Ward’s linkage. Finding an intersection between the chosen Ward’s linkage distance and the desired correlation threshold removed duplicated features whose absolute correlation exceeded 0.7. Assigning the significance level to flag correlations less than −0.7 or greater than 0.7 guaranteed that only truly redundant features were excluded. This procedure not only streamlined the feature set but also safeguarded the model from issues arising from multicollinearity.
Here, and are the centroids of clusters and , respectively, and is the centroid of the merged cluster. This step is repeated until a stopping (linkage distance) is reached.
4.1.3. Meta-Heuristic Feature Selection
A key challenge when evaluating how different feature combinations affect model performance is the computational cost associated with these evaluations. Each unique subset of features must be used to train the model at least once, and as the number of features grows, the number of potential subsets expands exponentially. Due to their rapidly increasing runtime, traditional exhaustive or grid-search approaches become impractical in such scenarios. Sequential and Monte Carlo techniques can reduce this cost somewhat, but they still risk exploring too many unproductive states. Meta-heuristic algorithms offer a balanced exploration and exploitation strategy within fixed time and memory constraints. Rather than systematically enumerating all possibilities, they use randomness to sample from a vast search space, while methods such as mutation, crossover, or local search guide the process toward promising regions. The total computational cost often depends on the product of the number of iterations and the population size. This controlled and flexible exploration ensures that even complex feature selection problems can be tackled efficiently, leading to a near-optimal subset of features without an explosive increase in computation.
Meta-heuristic feature selection uses general-purpose optimization algorithms to search for the best combination of features. Inspired by natural processes such as evolution or swarm behavior, it systematically explores and refines potential solutions over multiple iterations. This approach helps uncover complex interactions between features and often identifies a more effective subset than basic methods, resulting in stronger and more efficient models.
In this study’s genetic algorithm approach, each potential solution was represented by a binary chromosome, where each gene indicates whether a particular feature was included (1) or excluded (0). The algorithm aimed to maximize the model’s performance, measured by the value of a neural network-based regressor containing two fully connected layers with 64 units. The number of agents, iteration size, crossover rate, and mutation rate were set to 30, 30, 0.8, and 0.2, respectively. A penalty term proportional to the number of active features was subtracted from the score to discourage the selection of too many features. Thus, the overall fitness function for a chromosome can be expressed as shown in Equation (4).
where is the coefficient of determination obtained from the neural network when trained on the selected features, is the number of active features in chromosome , and is a weight that controls how strongly we penalize larger feature sets among the total number of features. As the genetic algorithm iterates, it records the fitness calls, preserving a history of which feature subsets work best. These steps help reveal patterns, such as which features appear repeatedly in high-performing chromosomes, thereby guiding the identification of a reduced yet highly effective set of weather parameters.
4.2. Feature Importance
4.2.1. Tree-Based Feature Importance
Tree-based feature-importance methods rely on how often and effectively a feature is used to split the data within an ensemble of decision trees. Each node split is chosen to best separate the data based on a particular feature in a random forest or gradient-boosted tree. Consequently, if a feature repeatedly reduces prediction errors across the ensemble, it is deemed more significant, resulting in a higher importance score. One strength of this method is its ability to uncover complex relationships that simpler methods might miss. However, it may also be influenced by how a feature is encoded, particularly if it has many distinct values, necessitating careful interpretation of the results.
In this study, the random forest algorithm used for feature-importance measurement consisted of 100 estimators (trees). Additionally, the maximum depth of each tree and the maximum number of features used for splitting were tuned via a grid search to determine the most effective parameter values for this dataset. The model can strike an optimal balance between simplicity and flexibility by systematically testing different combinations of these hyperparameters. Once the best combination was identified, the random forest was restricted to these dominant parameter values in subsequent training sessions. Limiting the maximum depth, in particular, helps prevent overfitting because shallow trees are less likely to memorize training data. Instead, they learn more general patterns that can be applied to new, unseen examples. Likewise, an appropriate choice of max features can reduce the chance of focusing on a small subset of overly dominant parameters, thereby enhancing the diversity and robustness of the forest. These tuned hyperparameters help produce a more accurate and generalizable model while preserving interpretability through more stable feature-importance scores.
4.2.2. Information-Theory Feature Importance
In this approach, we created a pool of feature subsets by assigning each feature a binary (on/off) selection value. The pool members were generated randomly using a uniform distribution, aiming to cover a specified percentage of the entire feature combination space , where was the total number of features. A neural network (as described in the previous subsection) was trained and tested for each subset in the pool to obtain the performance metric. This random sampling strategy was more computationally feasible than exhaustively testing every possible subset while capturing a broad representation of feature combinations. To determine the overall contribution of each feature, we measured the change in model performance when the feature was present versus when it was absent. Let be the randomly generated subsets that include and the subsets that exclude features. We then computed the difference in the performance metric (e.g., ) and averaged these differences across all subsets. Equation (5) denotes the features’ information gain, representing the performance metric . Here is the set of common feature subsets, ignoring the feature . A larger value indicates that the feature provides greater unique information, contributing more significantly to the prediction task.
5. Results and Discussion
The following subsections present the results obtained by applying the methods mentioned in the previous section to the dataset.
5.1. Feature Selection Results
5.1.1. Variance Analysis Results
Figure 4 illustrates the variance of the normalized weather parameters. A variance threshold of 0.01, as recommended in several studies [96,97], was used to flag features with very low variability. Based on this criterion, precipitation and visibility were identified as low-variance features. Consequently, these parameters were removed from subsequent analyses to prevent them from diluting the model with near-constant values, thereby streamlining the feature set and focusing on variables that exhibit more meaningful fluctuations.
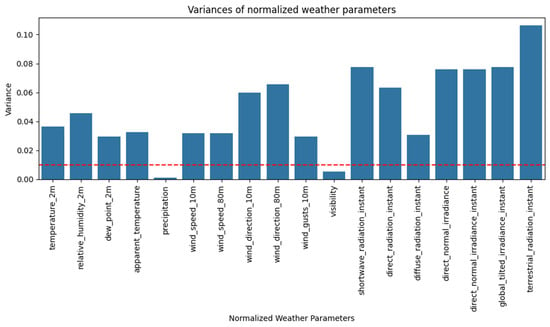
Figure 4.
The normalized variance of weather parameters.
5.1.2. Hierarchical Correlation Clustering Results
Figure 5 presents the correlation matrix of the weather parameters, clearly showing clusters of similar variables, for instance, groups related to temperature, wind, and radiation. The rationale behind this step is to pinpoint and eliminate features that largely overlap in the information they provide. Only those features contributing unique information are retained by applying Ward’s linkage distance to group parameters with strong correlation similarities. This filtering process not only streamlines the feature set but also helps minimize redundancy and reduce multicollinearity in the following stages of the analysis.
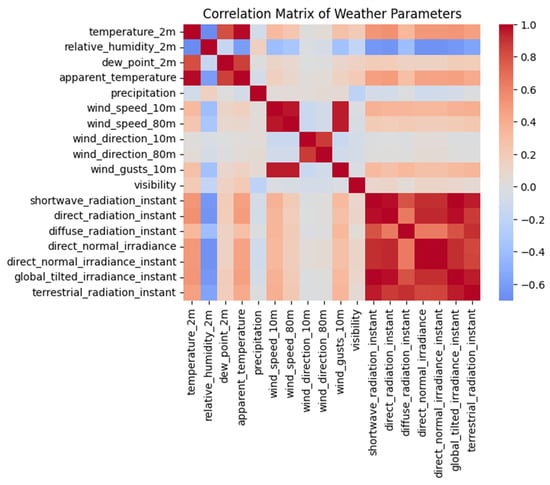
Figure 5.
The correlation between weather parameters.
A linkage distance matrix is initially computed using Ward’s method, translating correlation values into a distance measure. A clustering algorithm then partitions this matrix based on a specified distance threshold, grouping highly similar (i.e., correlated) parameters together. Each distance threshold effectively defines how strictly the parameters must differ to remain in the reduced set; if the correlation between two parameters surpasses ±0.7, they are considered highly correlated and thus potential candidates for removal. Figure 6 depicts how the maximum absolute correlation changes with different linkage distance thresholds. By finding the intersection point where the correlation threshold of 0.7 meets the Ward linkage distance, we identify an optimal cutoff that excludes parameters displaying excessive redundancy while preserving features that capture unique information.
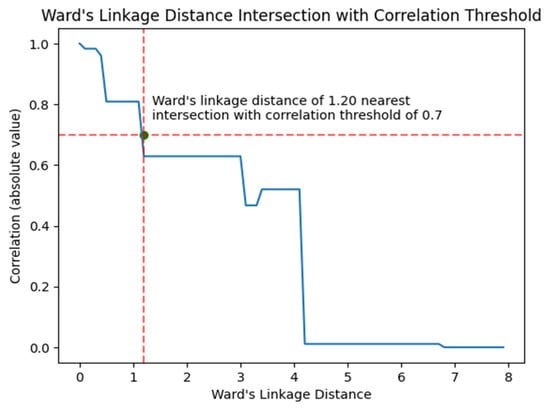
Figure 6.
The relationship between the linkage distance and the maximum correlation value.
Figure 7 shows a dendrogram containing clusters of weather parameters, along with their linkage distances. A distance of 1.2 was selected based on the results of the grid search. This threshold ensures that parameters with correlations exceeding ±0.7 are grouped, enabling the removal of redundant features. Within each cluster, only the parameter exhibiting the highest absolute correlation to the other members is retained, while the remaining parameters are discarded. This step ensures that each cluster is represented by a single, most relevant feature, preserving diversity in the dataset and minimizing duplication.
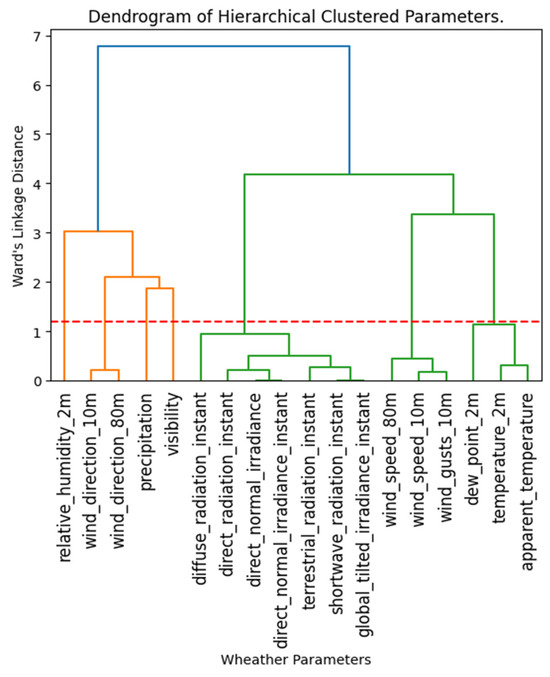
Figure 7.
The dendrogram of hierarchically clustered parameters showing the linkage distance.
Figure 8 presents the final set of weather parameters after the correlation-based selection process. Combining a linkage distance threshold and a strict correlation cutoff ensures that only a few redundant features are retained. Each cluster is represented by a single candidate feature, chosen for its higher absolute correlation with other parameters in that cluster. As a result, the dataset is streamlined to include the most informative variables, minimizing overlap while preserving a comprehensive picture of the underlying conditions.
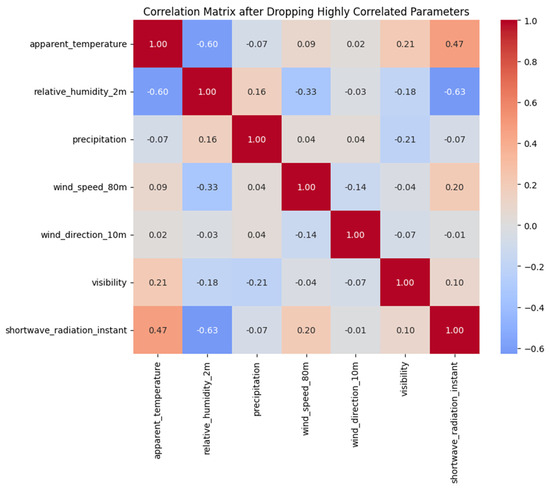
Figure 8.
The correlation matrix of the selected features using the hierarchical clustering method.
5.1.3. Meta-Heuristic Feature Selection Results
The utilized genetic algorithm’s objective function balances model accuracy and reduces the number of selected features. Specifically, the algorithm seeks to maximize while penalizing the fraction of features used. The resulting score reflects both the predictive power of the model and the efficiency of the feature set, thereby promoting solutions that are both accurate and concise. Figure 9 presents the convergence of the score over multiple iterations (fitness calls), illustrating how the population of candidate solutions evolves toward higher-scoring configurations. For clearer visualization, the rolling maximum scores obtained in each iteration, shown in Figure 9, are computed over a sliding window equal to the number of agents (30). As the genetic algorithm proceeds, it steadily refines the population’s feature subsets, leading to an optimal or near-optimal blend of strong predictive performance and minimized feature usage.
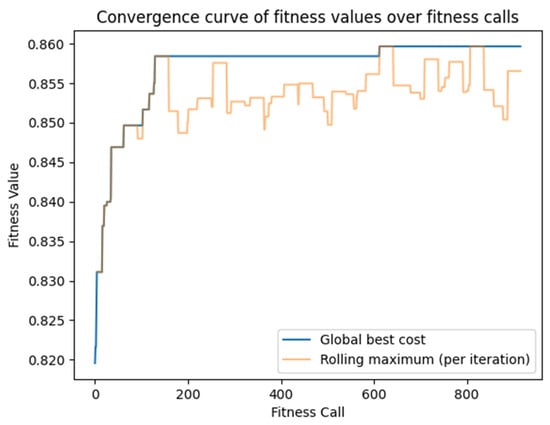
Figure 9.
Convergence of scores over 30 iterations for 30 agents.
Table 1 presents the top five agents produced by the genetic algorithm and their corresponding sets of selected features and average scores. Although the performances of these agents are extremely close, there is a noticeable overlap in the chosen features; specifically, apparent temperature and diffuse radiation appear consistently. This observation suggests that both parameters dominate in predicting PV output, making them prime candidates for inclusion in a streamlined yet effective feature set. Methods like genetic algorithms can converge rapidly within fixed time constraints by tuning factors such as iteration count, population size, and the duration spent training each model. However, they can be susceptible to getting stuck in local optima, which prevents them from finding the optimal combination of features. Additionally, interpreting the final feature subsets can be challenging, especially when balancing multiple objectives (e.g., maximizing while minimizing the number of features).

Table 1.
The top five agents by obtained from including features.
5.2. Feature-Importance Results
5.2.1. Tree-Based Feature-Importance Results
ML models can be seen as mathematical functions that map given inputs to desired outputs. Their performance depends on numerous factors, including the nature of the data, the underlying algorithm, and the chosen hyperparameters. Most algorithms offer hyperparameters that let users tune how the model learns, aiming for a balance between accurate predictions and generalizability. This study focuses on two key hyperparameters for our tree-based model: max_features and max_depth of the random forest regressor. This procedure can be generalized for other algorithms and their hyperparameters.
Figure 10 shows the heatmap of different combinations of ‘max_features’ and ‘max_depth’ values, with each color tone representing a clustered performance region. The dominant cells marked with * are those whose (max_features, max_depth) settings yield performance at least as good as all configurations to their right (increasing ‘max_features’) and below (increasing ‘max_depth’). Focusing on these dominant points ensures that we maintain or improve model accuracy while avoiding unnecessary complexity. In practice, selecting a dominant combination helps minimize training overhead and mitigate overfitting, ensuring that additional depth or features do not inflate model complexity without providing a meaningful performance boost.
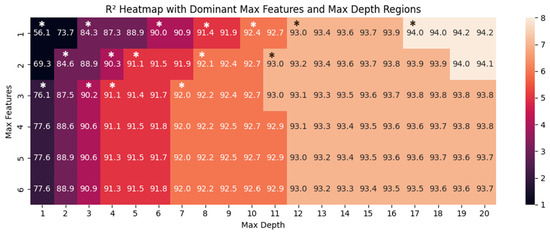
Figure 10.
Heatmap model performances as R2 percentage for hyperparameters. (The dominant cells are marked with *).
Each dominant combination of max_features and max_depth offers a valid option for training the model and evaluating feature importance. For example, a particularly effective configuration is set with max_features and max_depth values of 3 and 7, respectively, which achieves an R2 of roughly 92%. Because our random forest ensemble consists of 100 individual trees, we obtain 100 feature-importance evaluations, some of which are highly similar. Applying Principal Component Analysis (PCA) to these importance measurements helps us understand how many distinct “patterns” of feature importance truly exist among the ensemble. Figure 11 illustrates the resulting PCA plot, focusing on the first two principal components to reveal key clusters or groupings of feature-importance profiles.
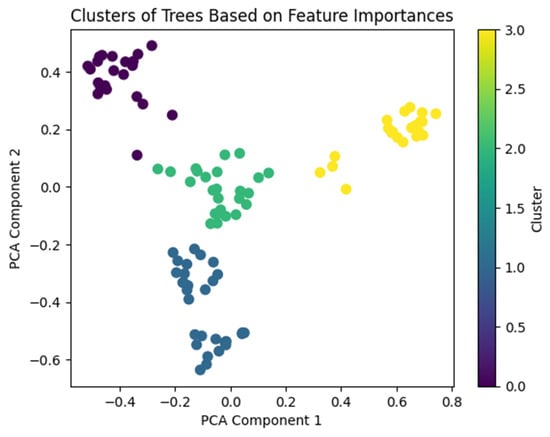
Figure 11.
PCA and clustering on feature-importance profiles.
Following the PCA analysis, four natural groupings emerged among the random forest’s feature-importance profiles. K-means clustering was applied with k = 4 to formalize these patterns, and the resulting clusters are shown by color in Figure 11. Each cluster represents a subset of estimators with a distinct view of which features contribute most strongly to the model’s accuracy. By identifying these clusters, we gain a better understanding of how different trees within the ensemble prioritize certain features over others.
Figure 12 provides a clearer picture of these variations by illustrating the average feature-importance values for each cluster. In some clusters, a few features dominate; in others, their importance is distributed more evenly among several parameters. This result demonstrates that even when overall performance metrics are similar, the paths to achieving those results can differ in how features are focused.
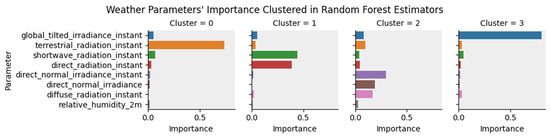
Figure 12.
Average features’ importance in clusters of the random forest estimators.
Each of the four feature clusters identified through PCA and K-means demonstrates a distinct strategy for leveraging available information. Cluster 0’s primary driver is terrestrial radiation instant, indicating that these trees focus heavily on that parameter to achieve good predictive performance. Cluster 1, on the other hand, emphasizes shortwave and direct radiation instants. Meanwhile, Cluster 2 incorporates broader features, such as direct normal irradiance instant, direct normal irradiance, diffuse radiation instant, and smaller contributions from global tilted irradiance and terrestrial radiation instants. Finally, Cluster 3 centers its predictions on the global tilted irradiance instant. Across all clusters, the trees have a maximum depth of seven levels, and their splitting thresholds are fine-tuned to optimize the Gini criterion, reflecting unique ways of capturing the most relevant aspects of the data.
Figure 13 presents a snapshot of the first two levels (depths) of a single decision tree within the random forest. This visualization clarifies how specific parameters, such as different types of radiation, are used in early splits to predict active power. While a random forest aggregates the predictions of all its trees, focusing on one tree at a time can help us understand how certain features drive splits and influence outcomes. Interpreting ML models involves more than just reviewing their internal splits. It also requires domain knowledge about PV power generation and environmental factors. By matching model decisions (e.g., “if direct_normal_irradiance > threshold, then …”) with real-world context (e.g., “High direct normal irradiance usually leads to increased power output”), we can form more meaningful insights. This combination of data-driven modeling and subject-matter expertise is essential for explaining why the model behaves as it does and for identifying potential improvements or inconsistencies in the model’s reasoning.
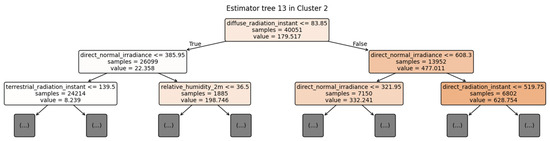
Figure 13.
An example of a decision tree estimator within a trained random forest model.
5.2.2. Information-Theory Feature-Importance Results
The information gained from each weather parameter quantifies its overall impact on predicting active power. In this study, 1036 feature combinations are evaluated, each represented by a binary indicator (0 for exclusion, 1 for inclusion). For each weather parameter, we split the combinations into two groups: those that contain the parameter and those that exclude it. By training and testing an ML model on both groups and observing the performance difference, we determine how crucial that parameter is to the prediction task.
Figure 14 illustrates both the information gain (IG) of each weather parameter (left plot) and the frequency with which each feature is included (right plot). Notably, shortwave radiation instant, direct radiation instant, global tilted irradiance instant, and terrestrial radiation instant show the highest IG values, indicating that their presence significantly improves the model’s performance when predicting active power. In contrast, wind speed at 10 m and wind direction at 10 m exhibit negative IG values. On average, including these features leads to a slight decrease in predictive accuracy compared to models that omit them. This outcome can occur if the added features introduce noise, are only weakly related to the target, or overlap with other features that confuse rather than clarify the model. It does not necessarily indicate that these parameters have no real-world influence; in the context of this dataset and modeling approach, their inclusion does not help, and may even hinder, the model’s ability to generalize.
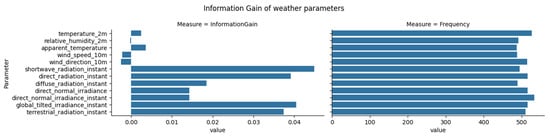
Figure 14.
Information gain and the frequency of involvement for each weather parameter.
6. Conclusions
In conclusion, achieving highly accurate active power predictions requires expert knowledge in the solar energy domain and sophisticated data science techniques. While module sensor data (e.g., irradiance and temperature) often deliver more precise models with lower errors, these measurements are not always available in every region. Consequently, relying on local weather parameters, as demonstrated in a case study obtained from open meteo APIs, can be an effective alternative, providing coverage for a wider array of locations where on-site sensor data may be lacking or impractical to collect.
This work demonstrates that short-term PV power can be accurately forecasted with high fidelity and interpretability, without the need for exhaustive on-site instrumentation. By coupling a three-stage feature-selection pipeline (variance filtering, hierarchical correlation clustering, and a genetic algorithm wrapper) with complementary importance metrics (permutation scores and information gain), we reduced the original 27 weather variables to an eight-feature core dominated by irradiance and apparent temperature. The trimmed input space preserved a mean R2 ≅ 0.91 on unseen 15 min data from a 1 MW array in Çanakkale, Türkiye, while halving model training time. Beyond raw accuracy, the framework exposes the parameters behind PV output: global-tilted, direct, and diffuse shortwave irradiance emerged as the principal drivers, whereas wind speed, direction, and most humidity metrics exhibited marginal or negative informational value. These insights provide plant operators with a data-backed rationale for prioritizing irradiance sensors over costly wind or aerosol instrumentation and refining inverter-level controls during periods of rapid shortwave variability.
Our results confirm that transparent feature reduction and explainable AI co-exist with state-of-the-art PV forecast accuracy, enlightening the way for scalable, sensor-agnostic deployment in emerging solar grids.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app15148005/s1, apw.xlsx excel and *.ipynb files.
Author Contributions
Conceptualization, S.N. and V.E.; methodology, S.N. and V.E.; validation, S.N. and V.E.; formal analysis, S.N.; investigation, V.E.; resources, V.E.; data curation, V.E.; writing—original draft, S.N. and V.E.; visualization, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by Istanbul Topkapi University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The utilized dataset and code are publicly available at https://github.com/sajjad-nematzadeh/Photovoltaic. Accessed on 3 July 2025.
Acknowledgments
We would like to thank Bülent ORAL and Şafak SAĞLAM for their guidance and support with their suggestions throughout the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, K.; Qi, X.; Liu, H. Photovoltaic Power Forecasting Based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Gao, M.; Li, J.; Hong, F.; Long, D. Day-Ahead Power Forecasting in a Large-Scale Photovoltaic Plant Based on Weather Classification Using LSTM. Energy 2019, 187, 115838. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time Series Forecasting of Solar Power Generation for Large-Scale Photovoltaic Plants. Renew Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.; Ahn, H.-K. Prediction Model for PV Performance with Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.-J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Esen, V.; Sağlam, Ş.; Oral, B.; Esen, Ö.C. Toward Class AAA LED Large Scale Solar Simulator with Active Cooling System for PV Module Tests. IEEE J. Photovolt. 2021, 12, 364–371. [Google Scholar] [CrossRef]
- Hajjaj, C.; El Ydrissi, M.; Azouzoute, A.; Oufadel, A.; El Alani, O.; Boujoudar, M.; Abraim, M.; Ghennioui, A. Comparing Photovoltaic Power Prediction: Ground-Based Measurements vs. Satellite Data Using an ANN Model. IEEE J. Photovolt. 2023, 13, 998–1006. [Google Scholar] [CrossRef]
- Pretto, S.; Ogliari, E.; Niccolai, A.; Nespoli, A. A New Probabilistic Ensemble Method for an Enhanced Day-Ahead PV Power Forecast. IEEE J. Photovolt. 2022, 12, 581–588. [Google Scholar] [CrossRef]
- Sangrody, H.; Zhou, N.; Zhang, Z. Similarity-Based Models for Day-Ahead Solar PV Generation Forecasting. IEEE Access 2020, 8, 104469–104478. [Google Scholar] [CrossRef]
- Alaraj, M.; Kumar, A.; Alsaidan, I.; Rizwan, M.; Jamil, M. Energy Production Forecasting from Solar Photovoltaic Plants Based on Meteorological Parameters for Qassim Region, Saudi Arabia. IEEE Access 2021, 9, 83241–83251. [Google Scholar] [CrossRef]
- Liu, R.; Wei, J.; Sun, G.; Muyeen, S.M.; Lin, S.; Li, F. A Short-Term Probabilistic Photovoltaic Power Prediction Method Based on Feature Selection and Improved LSTM Neural Network. Electr. Power Syst. Res. 2022, 210, 108069. [Google Scholar] [CrossRef]
- Yang, L.; Cui, X.; Li, W. A Method for Predicting Photovoltaic Output Power Based on PCC-GRA-PCA Meteorological Elements Dimensionality Reduction Method. Int. J. Green Energy 2024, 21, 2327–2340. [Google Scholar] [CrossRef]
- Guo, W.; Xu, L.; Wang, T.; Zhao, D.; Tang, X. Photovoltaic Power Prediction Based on Hybrid Deep Learning Networks and Meteorological Data. Sensors 2024, 24, 1593. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Zhang, T.; Qu, W.; Wang, W. Photovoltaic Power Prediction Based on VMD-BRNN-TSP. Mathematics 2023, 11, 1033. [Google Scholar] [CrossRef]
- Wang, C. A Prediction Model of Photovoltaic Power Generation Based on Association Rules and BP-AdaBoost Algorithm. In Proceedings of the Proceedings—2024 2nd International Conference on Mechatronics, IoT and Industrial Informatics, ICMIII, Melbourne, Australia, 12 June 2024; Institute of Electrical and Electronics Engineers Inc.: Melbourne, Australia, 2024; pp. 1–6. [Google Scholar]
- Atencio Espejo, F.E.; Grillo, S.; Luini, L. Photovoltaic Power Production Estimation Based on Numerical Weather Predictions. In Proceedings of the 2019 IEEE Milan PowerTech, PowerTech, Milan, Italy, 23–27 June 2019; Institute of Electrical and Electronics Engineers Inc.: Milan, Italy, 2019. [Google Scholar]
- Harrou, F.; Kadri, F.; Sun, Y.; Harrou, F.; Kadri, F.; Sun, Y. Forecasting of Photovoltaic Solar Power Production Using LSTM Approach. In Advanced Statistical Modeling, Forecasting, and Fault Detection in Renewable Energy Systems; IntechOpen: London, UK, 1 April 2020. [Google Scholar]
- Zhao, B.; Ge, X.; Xue, M.; Zhang, X.; Xu, W. Research on Model for Photovoltaic System Power Forecasting. In Proceedings of the ICED 2010 Proceedings, Nanjing, China, 13–16 September 2010; pp. 9–13. [Google Scholar]
- Mayer, M.J.; Gróf, G. Extensive Comparison of Physical Models for Photovoltaic Power Forecasting. Appl. Energy 2021, 283, 116239. [Google Scholar] [CrossRef]
- Li, B.; Chen, X.; Jain, A. Enhancing Power Prediction of Photovoltaic Systems: Leveraging Dynamic Physical Model for Irradiance-to-Power Conversion. arXiv 2024, arXiv:2402.11897. [Google Scholar]
- Jogunuri, S.; FT, J.; Stonier, A.A.; Peter, G.; Jayaraj, J.; Ganji, V. Random Forest Machine Learning Algorithm Based Seasonal Multi-step Ahead Short-term Solar Photovoltaic Power Output Forecasting. IET Renew. Power Gener. 2024, 19, e12921. [Google Scholar] [CrossRef]
- Tuncar, E.A.; Sağlam, Ş.; Oral, B. A Review of Short-Term Wind Power Generation Forecasting Methods in Recent Technological Trends. Energy Rep. 2024, 12, 197–209. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M. Photovoltaic Power Forecasting Using Statistical Methods: Impact of Weather Data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, N.; Gong, L.; Jiang, M. Prediction of Photovoltaic Power Output Based on Similar Day Analysis, Genetic Algorithm and Extreme Learning Machine. Energy 2020, 204, 117894. [Google Scholar] [CrossRef]
- Graditi, G.; Ferlito, S.; Adinolfi, G. Comparison of Photovoltaic Plant Power Production Prediction Methods Using a Large Measured Dataset. Renew. Energy 2016, 90, 513–519. [Google Scholar] [CrossRef]
- Sun, C.; Chu, X.; Ye, H. A Bayesian Structural Time Series Approach for Forecasting Photovoltaic Power Generation. In Proceedings of the IEEE 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–6. [Google Scholar]
- Serrano Ardila, V.M.; Maciel, J.N.; Ledesma, J.J.G.; Ando Junior, O.H. Fuzzy Time Series Methods Applied to (In) Direct Short-Term Photovoltaic Power Forecasting. Energies 2022, 15, 845. [Google Scholar] [CrossRef]
- Sumorek, M.; Idzkowski, A. Time Series Forecasting for Energy Production in Stand-Alone and Tracking Photovoltaic Systems Based on Historical Measurement Data. Energies 2023, 16, 6367. [Google Scholar] [CrossRef]
- Chen, X.; Xie, B.; Zhang, P.; Qiu, X. Research on Wind and Solar Power Generation Forecasting Based on SARIMA-LSTM Model. In Proceedings of the IEEE 2023 3rd International Conference on New Energy and Power Engineering (ICNEPE), Huzhou, China, 24–26 November 2023; pp. 695–699. [Google Scholar]
- Li, Y.; Su, Y.; Shu, L. An ARMAX Model for Forecasting the Power Output of a Grid Connected Photovoltaic System. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Gaboitaolelwe, J.; Zungeru, A.M.; Yahya, A.; Lebekwe, C.K.; Vinod, D.N.; Salau, A.O. Machine Learning Based Solar Photovoltaic Power Forecasting: A Review and Comparison. IEEE Access 2023, 11, 40820–40845. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar Power Generation Forecasting Using Ensemble Approach Based on Deep Learning and Statistical Methods. Appl. Comput. Inform. 2024, 20, 231–250. [Google Scholar] [CrossRef]
- Zazoum, B. Solar Photovoltaic Power Prediction Using Different Machine Learning Methods. Energy Rep. 2022, 8, 19–25. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Ayadi, O.; Adeeb, J.; Alrbai, M.; Qawasmeh, B.R. Extreme Learning Machines for Solar Photovoltaic Power Predictions. Energies 2018, 11, 2725. [Google Scholar] [CrossRef]
- Nespoli, A.; Leva, S.; Mussetta, M.; Ogliari, E.G.C. A Selective Ensemble Approach for Accuracy Improvement and Computational Load Reduction in Ann-Based Pv Power Forecasting. IEEE Access 2022, 10, 32900–32911. [Google Scholar] [CrossRef]
- Amiri, A.F.; Chouder, A.; Oudira, H.; Silvestre, S.; Kichou, S. Improving Photovoltaic Power Prediction: Insights through Computational Modeling and Feature Selection. Energies 2024, 17, 3078. [Google Scholar] [CrossRef]
- Abdulai, D.; Gyamfi, S.; Diawuo, F.A.; Acheampong, P. Data Analytics for Prediction of Solar PV Power Generation and System Performance: A Real Case of Bui Solar Generating Station, Ghana. Sci. Afr. 2023, 21, e01894. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Aruna, M.; Elumalai, P.V.; Karthik, K.; Khan, S.A.; Asif, M.; Rao, K.S. Advancing Solar PV Panel Power Prediction: A Comparative Machine Learning Approach in Fluctuating Environmental Conditions. Case Stud. Therm. Eng. 2024, 59, 104459. [Google Scholar] [CrossRef]
- Tahir, M.F.; Yousaf, M.Z.; Tzes, A.; El Moursi, M.S.; El-Fouly, T.H.M. Enhanced Solar Photovoltaic Power Prediction Using Diverse Machine Learning Algorithms with Hyperparameter Optimization. Renew. Sustain. Energy Rev. 2024, 200, 114581. [Google Scholar] [CrossRef]
- Ganesh, R.; Saha, T.K.; Kumar, M.L.S.S. Implementation of Optimized Extreme Learning Machine-Based Energy Storage Scheme for Grid Connected Photovoltaic System. J. Energy Storage 2024, 88, 111611. [Google Scholar] [CrossRef]
- Tercha, W.; Tadjer, S.A.; Chekired, F.; Canale, L. Machine Learning-Based Forecasting of Temperature and Solar Irradiance for Photovoltaic Systems. Energies 2024, 17, 1124. [Google Scholar] [CrossRef]
- AlSharabi, K.; Bin Salamah, Y.; Aljalal, M.; Abdurraqeeb, A.M.; Alturki, F.A. Long-Term Forecasting of Solar Irradiation in Riyadh, Saudi Arabia, Using Machine Learning Techniques. Big Data Cogn. Comput. 2025, 9, 21. [Google Scholar] [CrossRef]
- Matsushima, F.; Aoki, M.; Nakamura, Y.; Verma, S.C.; Ueda, K.; Imanishi, Y. Multi-Timescale Voltage Control Method Using Limited Measurable Information with Explainable Deep Reinforcement Learning. Energies 2025, 18, 653. [Google Scholar] [CrossRef]
- Andrew, N. Machine Learning Yearning: Technical Strategy for AI Engineers, in the Era of Deep Learning, 1st ed.; Deeplearning.AI: Palo Alto, CA, USA, 2018; Volume 1. [Google Scholar]
- Li, G.; Wang, H.; Zhang, S.; Xin, J.; Liu, H. Recurrent Neural Networks Based Photovoltaic Power Forecasting Approach. Energies 2019, 12, 2538. [Google Scholar] [CrossRef]
- Kermia, M.H.; Abbes, D.; Bosche, J. Photovoltaic Power Prediction Using a Recurrent Neural Network RNN. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 545–549. [Google Scholar]
- Kusuma, V.; Privadi, A.; Budi, A.L.S.; Putri, V.L.B. Photovoltaic Power Forecasting Using Recurrent Neural Network Based on Bayesian Regularization Algorithm. In Proceedings of the 2021 IEEE International Conference in Power Engineering Application (ICPEA), Shah Alam, Malaysia, 8–9 March 2021; pp. 109–114. [Google Scholar]
- Narayanan, S.; Kumar, R.; Ramadass, S.; Ramasamy, J. Hybrid Forecasting Model Integrating RNN-LSTM for Renewable Energy Production. Electr. Power Compon. Syst. 2024, 1–19. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate Photovoltaic Power Forecasting Models Using Deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Dhaked, D.K.; Dadhich, S.; Birla, D. Power Output Forecasting of Solar Photovoltaic Plant Using LSTM. Green Energy Intell. Transp. 2023, 2, 100113. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Sodsong, N.; Yu, K.M.; Ouyang, W. Short-Term Solar PV Forecasting Using Gated Recurrent Unit with a Cascade Model. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 February 2019; pp. 292–297. [Google Scholar]
- Gao, Y.; Qi, S.; Ponoćko, J. Assessing Critical Data Types for Deep Leaming-Based PV Generation Forecasting. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–6. [Google Scholar]
- Zameer, A.; Jaffar, F.; Shahid, F.; Muneeb, M.; Khan, R.; Nasir, R. Short-Term Solar Energy Forecasting: Integrated Computational Intelligence of LSTMs and GRU. PLoS ONE 2023, 18, e0285410. [Google Scholar] [CrossRef] [PubMed]
- Thipwangmek, N.; Suetrong, N.; Taparugssanagorn, A.; Tangparitkul, S.; Promsuk, N. Enhancing Short-Term Solar Photovoltaic Power Forecasting Using a Hybrid Deep Learning Approach. IEEE Access 2024, 12, 108928–108941. [Google Scholar] [CrossRef]
- Qu, J.; Qian, Z.; Pei, Y. Day-Ahead Hourly Photovoltaic Power Forecasting Using Attention-Based CNN-LSTM Neural Network Embedded with Multiple Relevant and Target Variables Prediction Pattern. Energy 2021, 232, 120996. [Google Scholar] [CrossRef]
- Lim, S.-C.; Huh, J.-H.; Hong, S.-H.; Park, C.-Y.; Kim, J.-C. Solar Power Forecasting Using CNN-LSTM Hybrid Model. Energies 2022, 15, 8233. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-Term Self Consumption PV Plant Power Production Forecasts Based on Hybrid CNN-LSTM, ConvLSTM Models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A Review and Evaluation of the State-of-the-Art in PV Solar Power Forecasting: Techniques and Optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Li, P.; Zhou, K.; Lu, X.; Yang, S. A Hybrid Deep Learning Model for Short-Term PV Power Forecasting. Appl. Energy 2020, 259, 114216. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Y.; Liu, Q.; Ye, X. A Hybrid Machine Learning Forecasting Model for Photovoltaic Power. Energy Rep. 2024, 11, 5125–5138. [Google Scholar] [CrossRef]
- Thaker, J.; Höller, R. Hybrid Model for Intra-Day Probabilistic PV Power Forecast. Renew. Energy 2024, 232, 121057. [Google Scholar] [CrossRef]
- Asiedu, S.T.; Nyarko, F.K.A.; Boahen, S.; Effah, F.B.; Asaaga, B.A. Machine Learning Forecasting of Solar PV Production Using Single and Hybrid Models over Different Time Horizons. Heliyon 2024, 10, e28898. [Google Scholar] [CrossRef] [PubMed]
- Tercha, W.; Zahraoui, Y.; Mekhilef, S.; Korõtko, T.; Rosin, A. A Hybrid Model ANN-LSTM Architecture for PV Power Forecasting: A Review and Implementation. In Technological and Innovative Progress in Renewable Energy Systems: Proceedings of the 2024 International Renewable Energy Days (IREN Days’ 2024); Springer: Berlin/Heidelberg, Germany, 2024; pp. 43–47. [Google Scholar]
- Yang, S.; Luo, Y. Short-Term Photovoltaic Power Prediction Based on RF-SGMD-GWO-BiLSTM Hybrid Models. Energy 2025, 316, 134545. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Alrbai, M.; Alahmer, H.; Rinchi, B.; Alahmer, A. Enhancing Solar Photovoltaic Energy Production Prediction Using Diverse Machine Learning Models Tuned with the Chimp Optimization Algorithm. Sci. Rep. 2024, 14, 18583. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Peng, S.-T.; Wu, P.-S.; Tseng, M.-L. High-Accuracy Photovoltaic Power Prediction under Varying Meteorological Conditions: Enhanced and Improved Beluga Whale Optimization Extreme Learning Machine. Energies 2024, 17, 2309. [Google Scholar] [CrossRef]
- Radhi, S.M.; Al-Majidi, S.D.; Abbod, M.F.; Al-Raweshidy, H.S. Machine Learning Approaches for Short-Term Photovoltaic Power Forecasting. Energies 2024, 17, 4301. [Google Scholar] [CrossRef]
- Li, D.; Zhu, D.; Tao, T.; Qu, J. Power Generation Prediction for Photovoltaic System of Hose-Drawn Traveler Based on Machine Learning Models. Processes 2023, 12, 39. [Google Scholar] [CrossRef]
- Kiani, F.; Nematzadeh, S.; Anka, F.A.; Findikli, M.A. Chaotic Sand Cat Swarm Optimization. Mathematics 2023, 11, 2340. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Kiani, F.; Torkamanian-Afshar, M.; Aydin, N. Tuning Hyperparameters of Machine Learning Algorithms and Deep Neural Networks Using Metaheuristics: A Bioinformatics Study on Biomedical and Biological Cases. Comput. Biol. Chem. 2022, 97, 107619. [Google Scholar] [CrossRef] [PubMed]
- Anka, F.; Agaoglu, N.; Nematzadeh, S.; Torkamanian-afshar, M.; Gharehchopogh, F.S. Advances in Artificial Rabbits Optimization: A Comprehensive Review. Arch. Comput. Methods Eng. 2024, 32, 2113–2148. [Google Scholar] [CrossRef]
- Haupt, T.; Trull, O.; Moog, M. PV Production Forecast Using Hybrid Models of Time Series with Machine Learning Methods. Energies 2025, 18, 2692. [Google Scholar] [CrossRef]
- Guo, Y.; Song, Y.; Lai, Z.; Wang, X.; Wang, L.; Qin, H. Learning Coupled Meteorological Characteristics Aids Short-Term Photovoltaic Interval Prediction Methods. Energies 2025, 18, 308. [Google Scholar] [CrossRef]
- Thipwangmek, N.; Woradit, K.; Suetrong, N.; Promsuk, N. Feature Selection Approaches for Short-Term Solar Photovoltaic Power Forecasting. In Proceedings of the IEEE 2024 13th International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 9–13 November 2024; pp. 252–257. [Google Scholar]
- Miao, J.; Niu, L. A Survey on Feature Selection. Procedia Comput. Sci. 2016, 91, 919–926. [Google Scholar] [CrossRef]
- Al Iqbal, R. Empirical Learning Aided by Weak Domain Knowledge in the Form of Feature Importance. In Proceedings of the 2011 International Conference on Multimedia and Signal Processing, Guilin, China, 14–15 May 2011; Volume 1, pp. 126–130. [Google Scholar]
- Massaoudi, M.; Chihi, I.; Sidhom, L.; Trabelsi, M.; Refaat, S.S.; Oueslati, F.S. PV Power Forecasting Using Weighted Features for Enhanced Ensemble Method. arXiv 2019, arXiv:1910.09404. [Google Scholar]
- Open-Meteo Historical Weather. Available online: https://open-meteo.com/en/docs/historical-weather-api (accessed on 8 March 2025).
- Google Earth. Available online: https://earth.google.com/web/search/ (accessed on 27 February 2025).
- Keddouda, A.; Ihaddadene, R.; Boukhari, A.; Atia, A.; Arıcı, M.; Lebbihiat, N.; Ihaddadene, N. Photovoltaic Module Temperature Prediction Using Various Machine Learning Algorithms: Performance Evaluation. Appl. Energy 2024, 363, 123064. [Google Scholar] [CrossRef]
- Sharma, P.; Goyal, P. Analysing the Effects of Solar Insolation and Temperature on PV Cell Characteristics. Mater. Today Proc. 2021, 45, 5539–5543. [Google Scholar]
- Ayadi, F.; Colak, I.; Genc, N.; Bulbul, H.I. Impacts of Wind Speed and Humidity on the Performance of Photovoltaic Module. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 229–233. [Google Scholar]
- Plyta, F. Optical Design of a Fully LED-Based Solar Simulator. Doctoral Thesis, Loughborough University, Loughborough, UK, 2015. [Google Scholar]
- Burduhos, B.-G.; Vişa, I.; Duţă, A.; Neagoe, M. Analysis of the Conversion Efficiency of Five Types of Photovoltaic Modules during High Relative Humidity Time Periods. IEEE J. Photovolt. 2018, 8, 1716–1724. [Google Scholar] [CrossRef]
- Berk, Z. Chapter 22—Dehydration. In Food Process Engineering and Technology; Berk, Z., Ed.; Academic Press: San Diego, CA, USA, 2009; pp. 459–510. ISBN 978-0-12-373660-4. [Google Scholar]
- Del Pero, C.; Aste, N.; Leonforte, F. The Effect of Rain on Photovoltaic Systems. Renew. Energy 2021, 179, 1803–1814. [Google Scholar] [CrossRef]
- Sengupta, S.; Sengupta, S.; Chanda, C.K.; Saha, H. Modeling the Effect of Relative Humidity and Precipitation on Photovoltaic Dust Accumulation Processes. IEEE J. Photovolt. 2021, 11, 1069–1077. [Google Scholar] [CrossRef]
- Ghazi, S.; Ip, K. The Effect of Weather Conditions on the Efficiency of PV Panels in the Southeast of UK. Renew. Energy 2014, 69, 50–59. [Google Scholar] [CrossRef]
- Boettcher, F.; Renner, C.H.; Waldl, H.-P.; Peinke, J. On the Statistics of Wind Gusts. Bound. Layer Meteorol. 2003, 108, 163–173. [Google Scholar] [CrossRef]
- Vasel, A.; Iakovidis, F. The Effect of Wind Direction on the Performance of Solar PV Plants. Energy Convers. Manag. 2017, 153, 455–461. [Google Scholar] [CrossRef]
- Liang, S.; Wang, J. (Eds.) Chapter 5– Solar Radiation. In Advanced Remote Sensing, 2nd ed.; Academic Press: New York, NY, USA, 2020; pp. 157–191. ISBN 978-0-12-815826-5. [Google Scholar] [CrossRef]
- Kirk, A.P. Chapter 2—From Nuclear Fusion to Sunlight. In Solar Photovoltaic Cells; Kirk, A.P., Ed.; Academic Press: Oxford, UK, 2015; pp. 9–24. ISBN 978-0-12-802329-7. [Google Scholar] [CrossRef]
- Bozsik, N.; Szeberényi, A.; Bozsik, N. Impact of Climate Change on Electric Energy Production from Medium-Size Photovoltaic Module Systems Based on RCP Climate Scenarios. Energies 2024, 17, 4009. [Google Scholar] [CrossRef]
- Povinec, P.P.; Hirose, K.; Aoyama, M.; Tateda, Y. Chapter 8—Summary. In Fukushima Accident, 2nd ed.; Povinec, P.P., Hirose, K., Aoyama, M., Tateda, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 519–531. [Google Scholar] [CrossRef]
- Ferré, J.; Rokem, A.; Buffalo, E.A.; Kutz, J.N.; Fairhall, A. Non-Stationary Dynamic Mode Decomposition. IEEE Access 2023, 11, 117159–117176. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.K.; Tiwari, M. Fusion of Chi-Square and Z-Test Statistics for Feature Selection with Machine Learning Techniques in Intrusion Detection. In International Conference on Advanced Network Technologies and Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2023; pp. 206–224. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).