Abstract
The time fluctuations of forest fires occurring in Basilicata, a region situated in Southern Italy, between 2004 and 2023 were investigated using various analytical approaches. Analysis revealed a clustering of fire occurrences over time, as indicated by a significantly high coefficient of variation. This suggests that the fire sequence does not follow a Poisson distribution and instead exhibits a clustered structure, largely driven by the heightened frequency of events during the summer seasons. The analysis of monthly forest fire occurrences and total burned area indicates a significant correlation between the two. This correlation is reinforced by shared patterns, notably an annual cycle that appears to be influenced by meteorological factors, aligning with the yearly fluctuations in the region’s weather conditions typical of a Mediterranean climate. Furthermore, the relationship between the Standardized Precipitation Evapotranspiration Index (SPEI) and forest fires revealed that the accumulation period of the SPEI corresponds to the cycle length of the fires: longer cycles in fire occurrences align with higher accumulation periods in SPEI data.
1. Introduction
Forest fires could be considered as natural processes that play a crucial role in sustaining various life cycles and maintaining the biodiversity of numerous ecosystems [1]; however, they are undoubtedly perceived as destructive natural phenomena [2] causing land degradation [3], facilitating alien plant invasion and patch homogenization, and creating positive feedback mechanisms favoring fuel loading, and fire spreading and intensity [3,4]. Although fires have long been utilized as a manner of fertilizing soil and controlling plant growth, they can change vegetation, increase soil erosion, and are one of the factors causing desertification of previously fertile areas [5].
Investigating the time dynamics of fire sequences in a specific region is of great importance, since it could reveal features of fire dynamics linked with the meteo-climatic variability of that region or with the identification of the anthropogenic mechanisms of fire ignition. Thus, the application of robust methodologies allowing to extract features hidden in the complex time fluctuations of fire sequences is crucial. Telesca et al. [6] analyzed the fire sequence that occurred in Ticino (Switzerland) by using the Allan Factor method [7] revealing several features of fire dynamics like (1) the Poissonian behavior of the time distribution of the sequence at small timescales and the non-Poissonian character at larger timescales (or time clustering), suggesting the existence of “memory phenomena” in the time distribution of the fires; (2) the presence at low altitudes of two different fire regimes that tend to merge into one single fire regime at higher altitudes, suggesting the mixing of natural and anthropogenic mechanisms, with the predominance of natural-caused (lightning) fires at higher altitudes; (3) the existence of daily periodicities that respond to the diurnal weather changes, like the increase and decrease in temperature and solar radiation, influencing the daily fluctuation of the dead fuel moisture content of open woodland fuel [8,9]; and (4) the presence of the yearly cycle, which is the typical seasonal variability, as a result of the cumulative impact of weather and climate as well as vegetation, specifically, the litter and herb layer in the forest stand understory, which follows a seasonal growth cycle. Similar temporal patterns were found in other regions of southern Europe, such as Tuscany [10] and Portugal [11].
The temporal clustering of fires suggests a correlation among them: a fire in a previously unburned area creates a mosaic of burned and unburned vegetation patches, leading to feedback behavior that influences the likelihood of the occurrence of subsequent fires [12,13].
Although human-induced fires are dominant in most Mediterranean regions [14], the fuel amount and moisture that depend on climate variability govern the conditions of fire ignition and its characteristics [15], like its intensity, spread, and propagation that are also influenced by wind [16,17].
In the future, fires in Europe are expected to increase in number of events and intensity, and the climate has been recognized as one of the main drivers for future fire regimes [18,19]. In fact, projected climate scenarios indicate an increase in the duration and the severity of fire seasons due to the strengthening of warming and the increase in drought events for most southern European countries [20]. The fuel amount and moisture can be considered as the manifestation of the link between climate and fire [21,22,23]; in fact, fire spread is limited by fuel amount during high-drought periods, and by fuel moisture during low-drought periods, and both conditions play an important role in shaping fire regimes, especially in Mediterranean-type ecosystems [24]. The close link between climate and fires was analyzed in several works; in particular, it was suggested that drought conditions concomitantly with high temperatures could provoke the occurrence of larger fires [25,26,27,28,29,30]. However, climate can impact on fire activity across multiple timescales. For instance, Pausas (2004) [31] found that in southeastern Spain year-to-year variations were anticorrelated with concurrent summer rainfalls and positively correlated with summer rainfalls that occurred 2 years before. Similarly, significant correlation was revealed between forest fire activity and lagged climate variables in several southern European countries [17,26,30]. Turco et al. [32], using a large, high-quality database provided by the European Forest Fire Information System (EFFIS) [33], analyzed the impact of concomitant drought and previous wet conditions on the summer burned area in Mediterranean Europe by modeling the relationship between the Standardized Precipitation Evapotranspiration Index (SPEI) and the burned area; they found a statistically significant relationship between fire and same-summer droughts, while antecedent climate conditions appear to impact fire activity much less.
From the above, it is evident that forest fires represent a complex natural phenomenon that cannot be disentangled by other factors, like climate and weather, anthropogenic activities, and vegetation conditions [15].
Forest fires, as a complex phenomenon, require advanced statistical methodologies to be thoroughly investigated from multiple perspectives. And in this context the objectives of this study are twofold: (1) To integrate different statistical approaches for the analysis of forest fire temporal dynamics, employing a combination of advanced techniques that, to our knowledge, have not been jointly applied in previous researches. While individual methods have been used in isolated cases, this study integrates them to explore the time dynamics of fire sequences and to investigate both short- and long-term relationships between fire activity and climatic variables, thereby offering a deeper and more holistic understanding of the underlying processes. (2) To conduct a high-resolution, localized analysis focused specifically on the Basilicata region (Southern Italy), representing the first study to investigate the temporal behavior of forest fires and their climatic drivers at fine spatial and temporal scales. Unlike most previous studies that analyze broader areas (e.g., entire countries or ecoregions) and rely on coarse temporal aggregations (e.g., annual or decadal), our study provides a detailed view capable of capturing fine-scale patterns and regional specificities.
This paper is organized as follows. Section 2 presents the study area, the forest fire dataset, and the Standardized Precipitation Evapotranspiration Index (SPEI), a well-known drought indicator. Section 3 outlines the statistical methods employed to investigate the fire sequence and its relationship with the SPEI. The results and a discussion of the main findings are provided in Section 4 and Section 5, respectively, while the conclusions are presented in Section 6.
2. Data
2.1. Study Area
The study area is the Basilicata region located in Southern Italy (Figure 1). The regional territory is about 10,000 km2 mostly characterized by mountains (47%) and hills (45%) with a small flat percentage (8%). The climate is prevailing Mediterranean humid in the Apennine Mountain range and Mediterranean dry in the hilly and flat areas. The Regional Forest Atlas reports for the forest area of the Basilicata an extent of around 355,409 hectares, in full accordance with the National Inventory being drawn up by Forests and Carbon Reservoirs which attributes approximately 345,000 hectares of wooded area to the Basilicata region. Deciduous oak forests occupying 51.8% of the territory represent the majority of the forest cover, followed by beech forest (8.4%), Mediterranean macchia (7.9%), shrublands (6.9%), and other deciduous broad-leaved forests (5.5%); the remaining 19.5% are mainly made up of evergreen broad-leaved forests, Mediterranean pine forests, chestnut stands, hygrophilous forests, and garrigue. The rest of the territory is mainly devoted to agricultural activities.
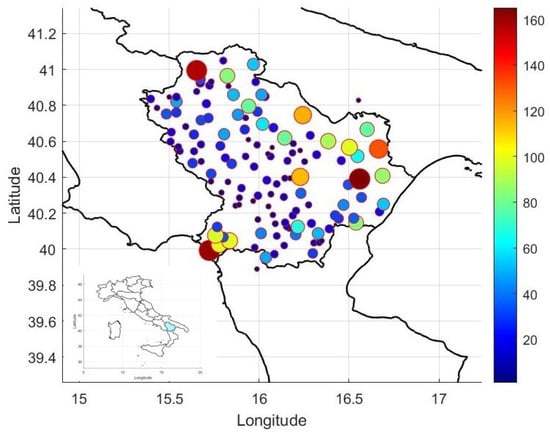
Figure 1.
Spatial distribution of fires. Each circle represents the location of events within a specific municipality within Basilicata region. The size of the circles is proportional to the average burned area, while the color of the circles represents the number of fires that occurred in the event location. Larger circles indicate a greater average area, and the color gradient, ranging from blue to red, indicates an increasing number of events.
2.2. Forest Fire Catalogue
The catalogue of forest fires is freely available at https://rsdi.regione.basilicata.it/ (accessed on 20 March 2025). For each fire event, the catalogue reports the date of occurrence, the location, and the extent of the burned area, along with other information. The fire data were pre-processed to produce the interevent times (i.e., the time interval between two consecutive fire events in days) and the monthly number of fires and monthly total burned area.
2.3. The Standardized Precipitation Evapotranspiration Index
The Standardized Precipitation Evapotranspiration Index (SPEI) is an index used to estimate drought intensity. The SPEI relies on a monthly climatic water balance, which involves subtracting potential evapotranspiration from precipitation. Details of the calculation of the SPEI can be found in [34]. If the SPEI is positive, this indicates above-normal wet conditions, while if it negative, this identifies dry situations.
The SPEI was obtained from http://sac.csic.es/spei/database.html (accessed on 20 March 2025), which contains data at the global scale, with a 0.5 degrees spatial resolution and a monthly time resolution. The SPEI is provided with accumulation times () ranging from 1 to 48 months starting in January 1901.
For our purposes, we extracted the SPEI for from 1 to 48 months at location (40.25°, 16.25°), which is included in the investigated area. The extracted SPEIB from May 2004 to November 2018 (that is the period of investigation of the fire sequence) is representative of the climatic (wet/dry) conditions of the area under study. Figure 2 shows the time variation of SPEIB for some typical .
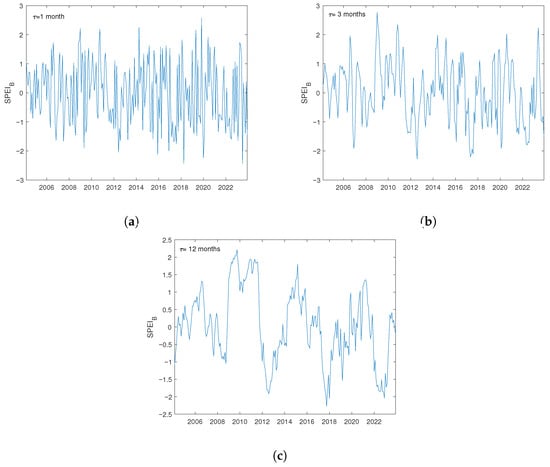
Figure 2.
SPEI at (40.44°, 16.17°) from 2004 to 2023 for accumulation times of (a) 1 month, (b) 3 months, and (c) 12 months. The data were downloaded from http://sac.csic.es/spei/database.html (accessed on 20 March 2025).
3. Methods
A fire sequence of N events can be represented as a temporal point process marked by the burned area A
where is the time of occurrence of the fire i with burned area and is the Dirac’s delta function that is zero for all t except .
After choosing a specific time window, such as one month or one year, an alternative representation of the fire occurrence is the time series depicting the count of fires or the cumulative burned area within that window.
3.1. The Coefficient of Variation
The coefficient of variation [35] is a simple quantity used to investigate the time structure of a sequence; in particular, it allows to discern if the sequence is periodic or quasi-periodic, purely random, or time-clusterized. A periodic or quasi-periodic sequence is characterized by events that occur regularly or almost regularly on time. In a purely random sequence, the events occur randomly on time, like a Poisson process; in this case the events occur homogeneously in time and the occurrence rate is almost constant. In a time-clusterized sequence, the events occur in clusters and not homogeneously; thus, the frequency of event occurrence changes with the time. The coefficient of variation is defined as
where is the standard deviation and is the average of the set of time intervals between two consecutive fire events known as interevent intervals.
For a Poissonian sequence is 1. If the set of events is governed by cyclic or quasi-periodic dynamics, . If the sequence is time-clustered, . The 95% confidence interval of the estimate of can be calculated by generating a huge number of surrogate Poissonian sequences with the same number of events and same mean interevent time of the original one.
It should be emphasized that while a Poisson process implies a equal to 1, the converse is not necessarily true; that is, a of 1 does not necessarily imply that the process is Poissonian. The coefficient of variation can be considered a global measure of the time structure of a sequence.
3.2. The Allan Factor
The Allan Factor (AF) is a tool commonly employed to analyze the temporal dynamics of various natural phenomena [36]. Compared to the coefficient of variation (), it provides a more refined assessment of the temporal structure within a sequence. While can distinguish between Poissonian, clustered, or regular event patterns, the AF additionally identifies the specific temporal scales at which these behaviors occur. To compute the AF, the time axis is partitioned into contiguous, equally sized intervals of duration , referred to as the timescale. Within each interval, the number of events is counted, yielding a sequence where denotes the number of events falling in the k-th window [37]. The Allan Factor is then defined by the following formula:
where indicates the average value. A Poissonian sequence, whose events are uncorrelated and independent, is characterized by the AF being rather flat for all the investigated timescales assuming a value around 1, except for very large timescales due to finite-size effects [38]. A decrease in the AF at a specific timescale indicates that the sequence exhibits periodic behavior at that scale [39]. Conversely, a time-clustered sequence is characterized by a scale-dependent AF; in particular, for a fractal (self-similar) process, the AF increases with the timescale following a power-law relationship:
A power-law behavior of the AF indicates that the sequence is characterized by correlation among the events [37]. The exponent is called the fractal exponent and quantifies the intensity of the time clusterization or time correlation. Thus, if the null hypothesis is not rejected against the alternative hypothesis , the sequence of interevent intervals is assumed to follow a Poissonian behavior. Conversely, if there is sufficient evidence to reject the null hypothesis , the sequence is assumed to exhibit a time-clustered pattern.
In order to investigate the significance of the AF, random sequences can be generated with two surrogate methods: (1) the Poissonian surrogate method, consisting of generating Poisson-distributed sequences with the same rate as the original one; and (2) the random permutating method [40], consisting of generating random shuffles of the interevent times of the original sequence; with the second surrogate method, the distribution of the original interevent times does not change. After calculating the AF for each surrogate, the distribution of AF values for each timescale is computed. For instance, by setting a confidence level of 97.5%, the 97.5% confidence curve corresponds to the envelope of all 97.5th percentiles. If the AF is significantly above the Poissonian confidence level, it indicates a notable deviation from Poissonian behavior. Similarly, if it is well above the confidence curve derived from random shuffles of interevent times, this suggests that the clustering behavior is not driven by the probability density of interevent times.
3.3. The Schuster’s Spectrum
The Schuster test has been used to investigate periodic patterns in natural point processes [41]. Assuming that the probability of event occurrences follows a sinusoidal function with period T, each occurrence time of the k-th event can be associated with a phase . This transforms the sequence of N occurrence times into a two-dimensional unit-length random walk, where each step changes direction according to the phase .
Let D be the distance between the starting point and the endpoint of this walk. The probability p of obtaining a distance greater than or equal to D under the null hypothesis of uniformly distributed occurrence times corresponds to the probability that such a pattern could arise by chance. This probability is referred to as Schuster’s p-value, and it is given by:
Therefore, the likelihood of a periodicity at period T increases as the Schuster’s p-value decreases. The number M of Schuster’s tests performed is given by [42]
where and are, respectively, the minimum and the maximum of the periods to be tested, and is usually 1.
As demonstrated in [42], if the Schuster p-value of a periodicity T is significantly lower than , then T can be considered to be not due to chance.
3.4. The Correlogram-Based Periodogram
The power spectrum of a time series represents the frequency distribution of series’ power at different frequency bands. It is commonly employed to discern cyclic patterns within time series data, as manifested by peaks in the power spectrum corresponding to the periods of these cycles. In the case of purely random processes, such as white noise, the power spectrum remains approximately constant across all frequencies; this signifies that the series is entirely uncorrelated, with each value being completely independent of the others.
In this study, since the time series we will analyze are short, we will employ the correlogram-based periodogram, which has proven to be an efficient method for estimating the power spectrum of short time series with only a few dozen samples [43].
The simple model of periodic series is:
with , , distributed as a uniform random variable in , and denoting a sequence of uncorrelated random variables with zero mean and standard deviation , independent of .
The classical periodogram is given by
with N being the length of the series, and it is calculated for
where and indicates the integer part of x. If a strong cycle with frequency modulates the series, the periodogram peaks at , while, if the series is uncorrelated , according to Priestley [44], the classical periodogram is uniformly distributed across the frequencies. To improve the detection of periodic components in a time series, Ahdesmäki et al. [43] introduced the correlogram-based periodogram, which has been shown to be a more effective tool for identifying cyclic patterns compared to the traditional approach. The periodogram is equivalent to the correlogram:
where
estimates the autocorrelation function. By using the sample autocorrelation function
where indicates the mean, the correlogram-based periodogram proposed by Ahdesmäki et al. [43] for estimating the power spectral density of a series is the following:
where the real part of x is indicated by , the series’ length by N, and the biased Spearman rank correlation coefficient by . If the classical periodogram is always positive, the correlogram-based periodogram could be negative; therefore, the absolute value is taken.
To test the significance of a frequency , the g-statistics could be used:
A large value of g at a specific frequency indicates that this frequency carries substantial power in the signal, suggesting it is statistically significant. The statistical significance of a tested frequency can be evaluated using a simulation-based approach [43]. Specifically, by employing Equation (7), we generate a set of random time series, and for each simulated series, the corresponding g-value is computed using Equation (14). The collection of these g-values is then used to approximate the distribution of the g-statistic, from which the associated p-value is estimated. A low p-value indicates a strong presence of the tested frequency in the original series.
3.5. Empirical Mode Decomposition
The Empirical Mode Decomposition (EMD), introduced by Huang et al. [45], is a method designed to decompose a time series into a set of components known as Intrinsic Mode Functions (IMFs). These IMFs must fulfill two criteria: (1) the count of local extrema and zero-crossings can differ by no more than one; and (2) at every point in time, the mean of the upper and lower envelopes—constructed from the local maxima and minima, respectively—is zero. While Empirical Mode Decomposition (EMD) was adopted in this study due to its adaptive and data-driven nature, it is worth noting that other signal decomposition techniques, such as the Wavelet Transform (WT) [46] and Singular Spectrum Analysis (SSA) [47], are also commonly employed. EMD offers the advantage of not requiring a priori selection of basis functions or decomposition levels (as in WT), or the number of components (as in SSA), making it particularly suitable for non-linear and non-stationary time series such as those analyzed in this work.
To decompose a series into the IMFs, the following sifting algorithm is employed [48]:
- Detect all minima and maxima points of the original signal .
- Form the lower envelope and upper envelope by using the cubic spline interpolation technique for minima and maxima data points.
- Calculate the mean envelope .
- Compute the signal .
- Verify the two conditions for to determine if it qualifies to be an IMF.
- If qualifies to be an IMF, then set and repeat the procedure from step (1) for the residual signal ; otherwise, replace with and repeat the procedure.
- Repeat steps (1) to (6) until a monotonic residual signal is obtained.
4. Results
We analyzed the sequence of fires that occurred in the Basilicata region (Southern Italy) from 2004 to 2023 (Figure 3a).
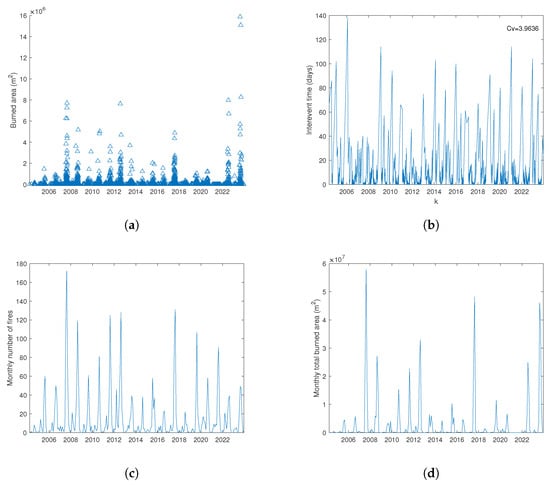
Figure 3.
Characteristics of the fire time series (2004–2023) in the Basilicata region, Southern Italy: (a) burned area; (b) interevent time; (c) monthly number of fires; and (d) monthly burned area (m2).
Considering the series of the interevent times (Figure 3b), we found . To calculate the 95% confidence interval of this estimate, a total of 1000 Poisson surrogate fire sequences were generated, each having the same number of fires and the same mean interevent time as the original series. The resulting 95% confidence interval for is given by , where the lower and upper bounds correspond to the 2.5th and 97.5th percentiles, respectively, of the distribution obtained from the Poissonian surrogate sequences. As can be seen, the fire series is highly time-clusterized at a global scale, being well beyond the 95% confidence interval. The time clustering of the fire sequence is rather high due to the temporal occurrence pattern of fire events, which is much denser during the summer months; therefore, considering the entire sequence, there is an increase in frequency during the summer, structuring the entire sequence as composed of a set of clusters.
Figure 3c,d display the monthly number of fires and the monthly total burned area, respectively; the two variables are very similar, as confirmed by the relationship between them (Figure 4).
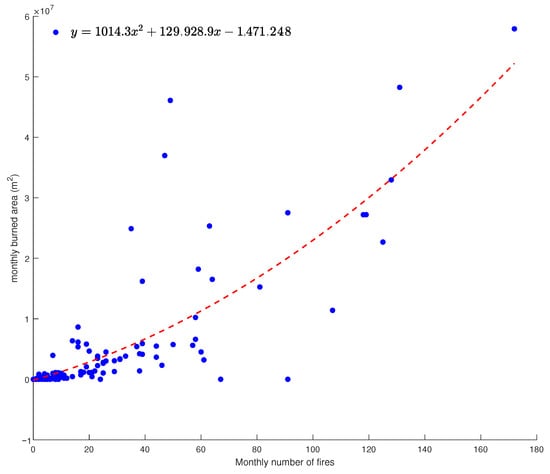
Figure 4.
Monthly total burned area versus monthly number of fires.
Figure 5a shows the AF for the analyzed fire sequence and the 97.5% confidence level calculated for 100 random sequences obtained with the Poissonian surrogate method and the random permutating method. The confidence envelopes were constructed from the pointwise 97.5th percentiles of the surrogate ensemble. No additional smoothing was applied to the confidence bands, in order to preserve their natural variability and accurately reflect the statistical variability across timescales. The AF of the original sequence of fires increases with , indicating that the sequence is clusterized in time. The AF is well above the confidence curve obtained by Poissonian surrogates, suggesting that its non-Poissonian character is significant for all the investigated timescales. The AF falls below the confidence level for the random shuffles of interevent times up to approximately one week; this suggests that the clustering behavior is influenced by the probability density of interevent times within this shorter timescale range. Conversely, for longer timescales, the clustering behavior depends on the ordering of interevent times. At the 1-year timescale, the AF exhibits a drop, indicating the presence of annual periodic fluctuations in the fire sequence. Between about 2 weeks and 3 months, we can identify a fractal behavior, revealed by the power-law increase of the AF with ; within this timescale range the fractal exponent , which indicates that the fire series is characterized by correlation among the events.
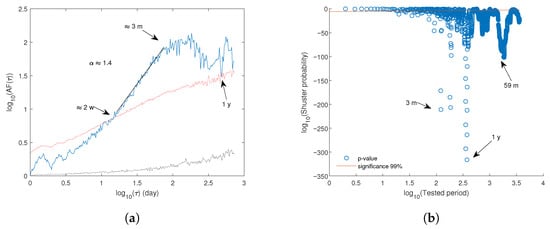
Figure 5.
Relationship between (a) the Allan Factor (AF) and the windows of duration and (b) the Schuster’s spectrum and the tested period. The AF and Schuster’s spectrum were used to characterize the time dynamics of fires (2004–2023) in the Basilicata region, Southern Italy. The arrows indicate the characteristics timescales and periodicities of the fire sequence. The black and red dotted lines in (a) represent the 97.5% confidence curves for Poissonian and random shuffles, respectively.
Figure 5b displays the Schuster spectrum. For each tested period, ranging from 1 day up to half the total duration of the observation period, the corresponding p-value (represented by circles) was computed. Several periods exhibit p-values below the 99% confidence threshold (indicated by the red line). Notably, periods of approximately 3 months and 1 year stand out as having the lowest p-values, indicating a strong periodic component at these timescales. The yearly period is in agreement with the annual timescale identified in the previous AF analysis, signaling the presence of the 1-year periodicity in the time dynamics of the fires. In addition, a period of about 5 years is revealed in Schuster’s spectrum.
We applied the EMD analysis to the monthly number of fires and the monthly total burned area. Figure 6 shows results of the EMD of the monthly counts, while Figure 7 shows the correlogram-based periodogram (CBP) of the IMFs. The CBP’s evidence period is significant at 95% (hollow circles) and at 99% (red circles). Among the peaks significant at 99%, the highest ones signal the characteristic modulating frequencies of the IMFs. IMF1 exhibits periodicities of 4 months and 6 months; IMF2 is marked by an annual periodicity, while IMF3 shows periodicities of about 12 months and 25 months; IMF4 is marked by periods of 28, 36 and 53 months, while IMF5 by a cycle of 60 months. IMF6 and IMF7 represent the long-term components of the monthly counts, since they are modulated by periods corresponding approximately to the length of the series.
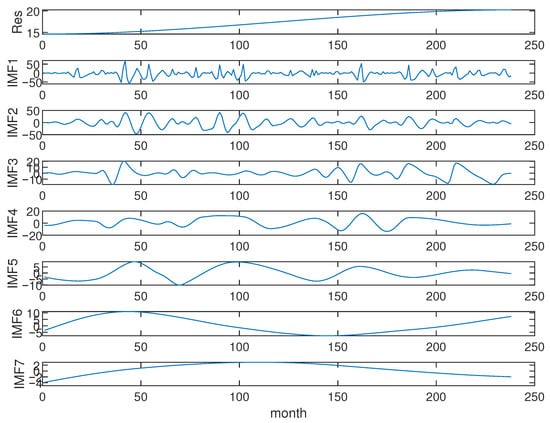
Figure 6.
Residual and Intrinsic Mode Functions (IMFs) after applying Empirical Mode Decomposition (EMD) to the monthly number of fires (2004–2023) in the Basilicata region, Southern Italy.
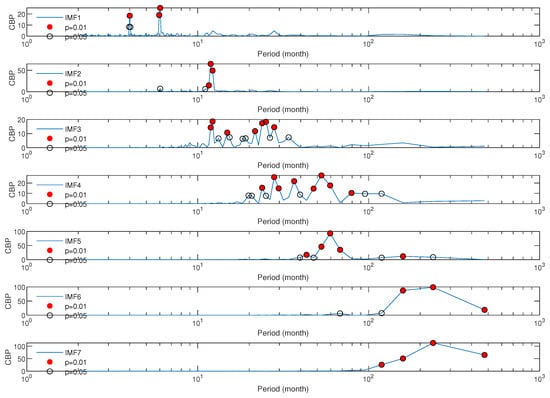
Figure 7.
Correlogram-based periodogram (CBP) of the Intrinsic Mode Functions (IMFs) for the monthly number of fires in the Basilicata region, Southern Italy. The plots from (top) to (bottom) correspond to the Intrinsic Mode Functions (IMF1 to IMF7), respectively. The periods significant at the 0.01 level are marked by filled red circles; those significant at 0.05, by hollow circles.
Figure 8 shows the results of the EMD of the monthly total area, and Figure 9 shows the CBP of the IMFs. The first two IMFs are characterized by the same modulating frequencies as the first two IMFs in the monthly counts. The third IMF shows only one main characteristic periodicity at 12 months. The fourth IMF is mainly modulated by 26-month and 48-month periodicities, while the fifth one mainly by a 60-month periodicity. IMF6 and IMF7 represent the long-term components of the monthly burned area as for the monthly counts. Table 1 shows the main periodicities for each IMF of the monthly number and burned area series (the highest one is in bold).
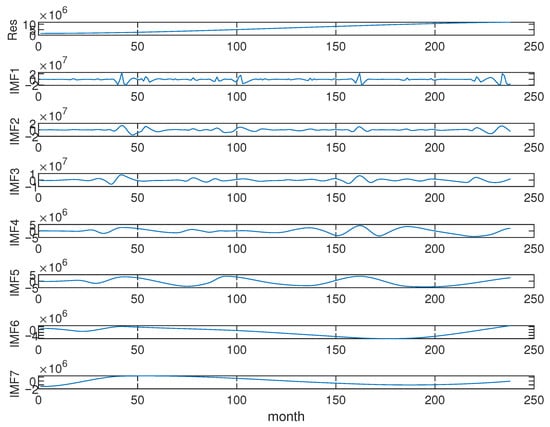
Figure 8.
Residual and Intrinsic Mode Functions (IMF1-IMF7) after applying Empirical Mode Decomposition (EMD) to the monthly total burned area (2004–2023) in the Basilicata region, Southern Italy.
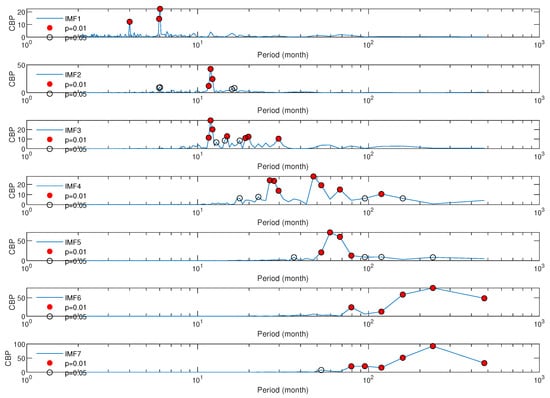
Figure 9.
Correlogram-based periodogram (CBP) of the Intrinsic Mode Functions (IMFs) for the monthly total burned area in the Basilicata region, Southern Italy. The plots from (top) to (bottom) correspond to IMF1 to IMF7, respectively. The periods significant at the 0.01 level are marked by filled red circles; those significant at 0.05, by hollow circles.

Table 1.
Main periodicities of the IMFs of the monthly number of fires and monthly burned area (the highest ones are bolded).
The monthly counts and the monthly total burned area unveil various components: intra-annual, with the main modulating periods at 4 and 6 months; annual; quasi-bi-annual; intermediate-term, with the main modulating periods from about 3 to 5 years; and long-term, with the main modulating periods at about 20 years.
We explored the relationship between SPEIB (calculated for the Basilicata region) and the IMF components of monthly counts and total burned area derived from EMD. Pearson’s correlation coefficient was computed between each for and each IMF. The left panels of Figure 10 and Figure 11 illustrate the correlation coefficient as a function of for the monthly counts and monthly total burned area, respectively. At the top of each plot in the left panel, the maximum , its p-value, and the corresponding accumulation time are displayed. The right panels of Figure 10 and Figure 11 exhibit the comparison between the SPEIB at alongside the corresponding IMF. Taking into account only the correlation coefficients with a p-value less than 0.05, the of SPEIB that exhibit correlations with the IMFs of the monthly counts are 1, 3, 10, 30, 36, and 48 months. Similarly, the significant timescales of SPEIB that show correlations with the IMFs of the monthly total burned area are 2, 13, 43, and 48 months. Table 2 and Table 3 summarize the results of the correlation analysis between SPEIB and IMFs of the monthly number of fires and total burned area, respectively.
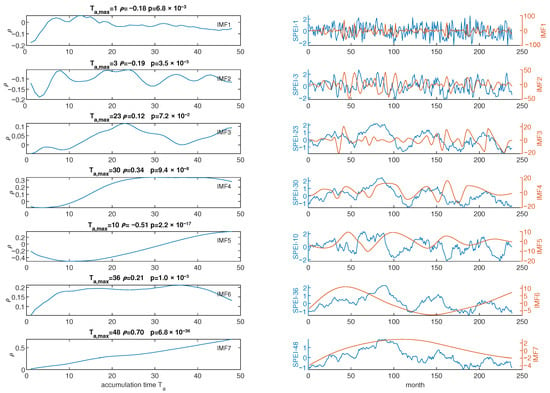
Figure 10.
Estimated Pearson’s correlation coefficient computed between the Standardized Precipitation Evapotranspiration Index (SPEI) calculated over accumulation times ranging from 1 to 48 months and the components of the Empirical Mode Decomposition (EMD) derived from monthly fire counts series (2004–2023) in the Basilicata region, Southern Italy (left panel). The (right panel) shows the SPEI corresponding to the maximum absolute Pearson’s correlation value (blue) with the specific EMD component (red). The maximum for each IMF, the corresponding (), and respective p-values (p) are shown above each individual graph. The (right panel) shows the SPEI corresponding to the maximum (blue line) and the respective EMD component (red line) as a function of time (month).
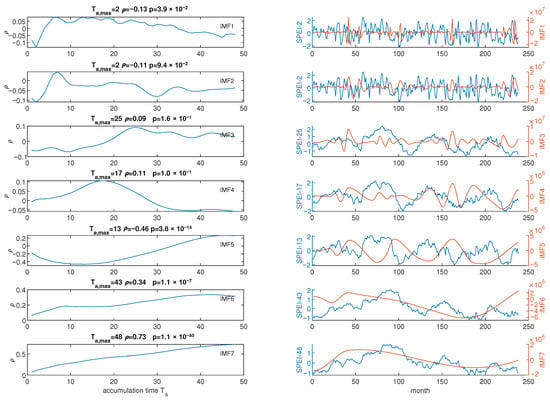
Figure 11.
Estimated Pearson’s correlation coefficient computed between the Standardized Precipitation Evapotranspiration Index (SPEI) calculated over accumulation times ranging from 1 to 48 months and the components of the Empirical Mode Decomposition (EMD) derived from monthly total burned area series (2004–2023) in the Basilicata region, Southern Italy (left panel). The (right panel) shows the SPEI corresponding to the maximum absolute Pearson’s correlation value (blue) with the specific EMD component (red). The maximum for each IMF, the corresponding (), and respective p-values (p) are shown above each individual graph. The (right panel) shows the SPEI corresponding to the maximum (blue line) and the respective EMD component (red line) as a function of time (month).

Table 2.
Results of correlation analysis between SPEIB and the IMF of the monthly number of fires.

Table 3.
Results of correlation analysis between SPEIB and the IMF of the monthly total burned area.
5. Discussion
This study was conducted to explore the time dynamics of the sequence of forest fires recorded in Basilicata (Southern Italy). The occurrence of forest fires can be modeled as a stochastic point process, where each event is defined by its time of occurrence and the extent of the burned area. By employing various representations of the fire process, including interevent times and count series, alongside several statistical measures, we examined the fire regimes in the investigated sequence.
5.1. Time-Clustering
The fire activity exhibits time-clusterized or non-Poissonian behavior, as evidenced by the coefficient of variation significantly larger than 1, and by the non-flat behavior of the AF curve across all timescales. This finding suggests the existence of time-clustered behavior within the dynamics of fires, indicating correlated structures in the temporal distribution of fire events. For timescales shorter than ≈2 weeks, the time-clustering is influenced by the probability density function of the interevent times. This suggests that the time dynamics of fires is primarily determined by the distribution of short and long intervals between consecutive fires. On larger timescales, the time-clustering depends upon the ordering of interevent times. This implies that the temporal structure of events is primarily shaped by the specific succession of fires. In particular, between ≈2 weeks () and 3 months (), the time-clustering of the fire activity is characterized by a scaling behavior (power law in log-log scales) with scaling exponent that indicates the existence of a fractal or self-similar structure in the time distribution of the fire events. The fractal structure is very common in many natural phenomena, and thus, it could be reasonably considered a natural behavior of the fire time dynamics. The fractal nature of fire activity across timescales ranging from a few days to a few months indicates that fire occurrences exhibit a consistent temporal structure that remains unchanged regardless of the scale considered; in other words, the time distribution of fire events remains nearly constant as we move from larger to smaller timescales.
If a scaling exponent 0 indicates that the process is Poissonian, and thus characterized by independent and uncorrelated events, a value of 1.4 suggests a rather high degree of clusterization and correlation among the fire events. In a joint analysis of wildfire occurrences and weather conditions in Japan, Ref. [49] discovered that there is a significant likelihood of fire occurrence when the average humidity drops below 60%, indicating a strong correlation between fire events and climate; and Ref. [50] in their analysis of the temporal clustering of humidity events (identified by instances when humidity drops below 60%), discovered that the temporal clustering of the humidity process exhibits fractal behavior with an exponent approximately equal to 1.07, in agreement with that of Japanese wildfires.
The found fractal behavior of our fire dataset agrees with that discovered in other fire sequences, and it is very likely that its behavior might be induced by similar meteo-climatic patterns.
5.2. Characteristic Timescales
The timescale weeks is consistent with the findings of [6,50] focused on fire activities that occurred in several areas of the world, and could have an anthropic origin [50]; indeed, activities related, for instance, to agriculture, such as burning stubble during the summer months, might be scheduled on a quasi-weekly basis and this could have an effect by exerting the quasi-weekly timescale. Ref. [51] used statistical methodologies well suited for detecting weekly periodicities in time series of fire counts and for identifying the weekday with the lowest number of fires; their study revealed how the anthropogenic activity impacts on the seasonal character of global vegetation burning, by precisely individuating a global fire activity cycle with a minimum on weekends. Such a minimum was presumably due to labor laws in most countries and the influence of the Christian religion that prescribes Sunday as the weekday of rest. However, it cannot be excluded that weekly meteo-climatic factors could affect fuel moisture in a site-specific way [52].
The increased occurrence of fires during the summer months might lead to the emergence of the timescale months, representing the upper timescale of the fractal regime in the time distribution of fire events, but also linked with the seasonality of the meteo-climatic conditions of the investigated area. Until a timescale of about 3 months, fire events exhibit consistent scaling properties, likely driven by similar meteo-climatic conditions. However, beyond , there may occur a blending of various temporal dynamics influenced by different meteo-climatic conditions, causing the time distribution of fires to deviate from fractal behavior, as evidenced by the lack of scaling observed in the AF curve for timescales larger than .
5.3. Cycles
The annual cycle stands out as the most apparent periodicity in the analyzed fire sequence, evidenced by the drop in the AF curve occurring approximately over a one-year timescale. This is also reflected in Schuster’s spectrum, where the most significant period (corresponding to the lowest p-value) aligns with one year. The annual cycle is also discernible in the second IMF of the EMD applied to the monthly fire number and the monthly total burned area. The nature of the yearly cycle is undoubtedly meteorological, as it mirrors the annual periodicity of the meteorological and climatic conditions in the investigated area, characterized by a Mediterranean climate that follows a yearly cycle.
Both the monthly number of fires and the total burned area exhibit a similar average annual bell-shaped pattern: fires are at their lowest in winter, gradually increase in spring, peak in summer, and then decrease in autumn (Figure 12). The striking similarity between the two patterns confirms a high correlation between the number of fires and the burned area, as illustrated in Figure 4. Forest fires are primarily influenced by factors such as relatively high temperatures and human activities related to land management, like the burning of stubble after harvesting crops. These factors typically reach their peak during the summer months, particularly in August.
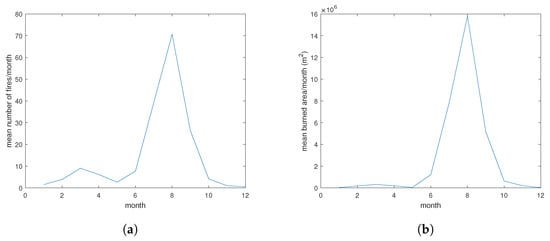
Figure 12.
Monthly average number of fires (a) and total burned area (b).
In addition to the annual cycle, the other cycles identified in the IMFs (i.e., sub-annual, interannual, and decadal) can also be considered as induced by the meteo-climatic seasonality of the investigated area.
5.4. Relationship Between Fires and SPEI
The inter-relationship between fires and climate has always been a subject of paramount importance in the scientific context devoted to fires. While fires undoubtedly affect climate change, climatic factors, like rainfall and temperature, not only directly impact the probability of fires but can also indirectly alter vegetation productivity (i.e., fuel abundance), consequently affecting the intensity of fires [53,54,55]. In regions abundant with biomass, the primary factors driving wildfire activity are typically high temperatures and seasonal drought conditions [56,57]. Extreme and prolonged droughts, induced by abnormal fluctuations in the climate system like El Niño, have consistently served as significant catalysts for regional fires [54,58]. On a global scale, greater seasonal variation with summer and autumn being the seasons with the most frequent fire occurrence worldwide was found by using satellite data and investigating the spatial distribution, intensity, emission changes, and meteorological differences between fires in different fire-active and fire-prone regions [59].
The SPEI is a well-known drought driver and its link with fires was demonstrated in several studies. For instance, it was statistically shown that same-summer-drought conditions play a dominant role for fires in Mediterranean Europe [26]; in particular, the correlation between burned area and coincident SPEI3 (i.e., calculated for an accumulation period = 3 months) for July and August (when usually the temperature reaches its highest value) is large in all the Mediterranean ecosystems that are characterized by a relatively high abundance of fine fuels able to dry out quickly during a single summer [32]. A correlation analysis between the SPEI (decomposed in trend and season through the LOESS method [60]) and fires in inland areas of Spain showed that short-term droughts (SPEI3 and SPEI6) have a more significant impact on fire occurrence than prolonged droughts (SPEI12 and SPEI24), while the seasonal cycles of burned area seem to be strongly associated to SPEI24, thus with prolonged dry conditions [61].
The monthly fire counts in the Basilicata region, investigated in the present study, exhibit cycles that show significant correlations (with a p-value less than 0.05) with SPEI at specific accumulation periods (Table 2). Specifically, short-term cycles (4 and 6 months) governing the first IMF are negatively correlated with SPEI1, representing the one-month accumulation period of drought. The second IMF, reflecting the annual cycle, shows a significant negative correlation with SPEI3. Additionally, SPEI10, with a longer accumulation period (10 months), is strongly negatively correlated with the fifth IMF, which is dominated by the 5-year cycle. Conversely, the 4–5 year long cycle, modulating the fourth IMF, exhibits a good positive correlation with a long accumulation period, SPEI30. Similarly, the long-term IMFs (IMF6 and IMF7) are positively correlated with SPEI36 and SPEI48 that are characterized by the longest accumulation time . Likewise, the monthly total burned area displays correlations with SPEI at nearly identical accumulation periods (Table 3). The first IMF, governed by the 4 and 6 month periodicities, shows a negative correlation with SPEI2. Similarly, the annual cycle is negatively correlated with SPEI2. The interannual cycle (≈5 years) governing the fifth IMF’s time variation is strongly correlated with SPEI13. Furthermore, IMF6 and IMF7, characterized by fluctuations dominated by the 20 year cycle, exhibit a positive correlation with SPEI43 and SPEI48, similarly to the monthly number of fires. Figure 13 shows the relationship between cycles in fires (monthly number and total burned area) and accumulation periods of the SPEI; such a relationship suggests that the larger the periodicity in fires, the longer the accumulation period of the SPEI. As shown in [62], the temporal evolution of the SPEI exhibits increasing smoothness with longer accumulation periods; thus, at shorter periods, it appears to fluctuate akin to random noise, while at longer periods, it varies smoothly with time exhibiting a certain persistence. Hence, it is plausible that the SPEI at shorter accumulation periods would amplify the influence of smaller cycles in fires, whereas those at longer accumulation periods would primarily drive the larger cycles in fires.
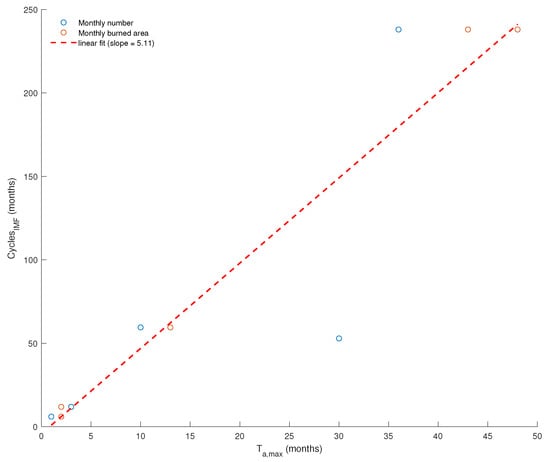
The negative correlation between the SPEI (at accumulation periods less than 10 months) and fires (both monthly occurrence and total burned area) is unsurprising, as negative SPEI values signify hot and dry conditions. Therefore, the negative correlation between the SPEI and fires suggests that as meteorological and climatic conditions become hotter and drier in the studied area, the total burned area increases and the frequency of fire occurrences rises. Conversely, humid conditions would restrict the spread and extent of fires. This pattern is characteristic of IMFs modulated by periodicities spanning from 4 months to 5 years. On the contrary, the IMF with the long-term behavior reveals the most robust positive correlation with SPEIn (n from 30 to 48), indicating that over decadal temporal scales, prolonged periods of hot and dry conditions would counteract the occurrence and spatial extent of fires, while persistent humid conditions would favor them. This could be interpreted in connection with the accumulation of burnable biomass under favorable conditions.
6. Conclusions
The diverse analyses conducted in this study enabled us to characterize the dynamic temporal patterns of fire occurrence and their relationship with drought in the Basilicata region of Southern Italy. We discovered that the fire sequence exhibits clustering over time, with characteristic timescales ranging from weekly, likely stemming from anthropogenic causes, to 3 months, attributed to meteorological and climatic influences. These distinct timescales overlay a clustered, non-Poissonian behavior that exhibits fractal properties between them. The comparative analysis of the monthly number of fires and the total burned area reveals a strong correlation between them. This correlation is further supported by the common cycles, especially the annual one evident in the second IMF of their EMD. This cycle clearly originates from meteorological factors, as it mirrors the annual cycle of the meteo-climatic conditions of the region under study, featured by the Mediterranean climate. The links between the SPEI and fire activity were investigated by analyzing the correlations between SPEI values (computed over accumulation periods ranging from 1 to 48 months) and the IMFs obtained from the EMD of both the monthly number of fires and the total burned area; the correlation analysis unveiled that the accumulation time of the SPEI corresponds to the cycle length of the fire time series: the longer the cycle of the fire time series, the higher the accumulation time of the SPEI (Figure 13).
Author Contributions
Conceptualization, L.T. and R.L.; Methodology, L.T.; Software, L.T.; Formal analysis, L.T.; Investigation, L.T. and R.L.; Resources, R.L.; Data curation, R.L.; Writing—original draft, L.T.; Writing—review & editing, L.T. and R.L.; Visualization, L.T.; Project administration, R.L.; Funding acquisition, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project DRAGON 6 project ID 95387 Multi-Sensor Remote Sensing for Cultural Heritage Climate Change Resilience funded by European Space Agency and by the project Firesat (2024-2025) funded by Civil Protection Department of Regione Bsasilicata.
Data Availability Statement
The catalogue of forest fires is freely available at https://rsdi.regione.basilicata.it/ (accessed on 20 March 2025). The SPEI data are available at https://spei.csic.es/ (accessed on 20 March 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pausas, J.G.; Keeley, J.E. Wildfires as an ecosystem service. Front. Ecol. Environ. 2019, 17, 289–295. [Google Scholar] [CrossRef]
- Doerr, S.H.; Santin, C. Global trends in wildfire and its impacts: Perceptions versus realities in a changing world. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150345. [Google Scholar] [CrossRef] [PubMed]
- Vila, M.; Lloret, F.; Ogheri, E.; Terradas, J. Positive fire-grass feedback in Mediterranean basin shrubland. For. Ecol. Manag. 2001, 147, 3–14. [Google Scholar] [CrossRef]
- Cochrane, M.; Alencar, A.; Schulze, M.; Souza, C., Jr.; Nepstad, D.; Lefebvre, P.; Davidson, E. Positive feedback in the fire dynamic of closely canopy tropical forests. Science 1999, 284, 1832. [Google Scholar] [CrossRef] [PubMed]
- Santín, C.; Doerr, S.H. Fire effects on soils: The human dimension. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L.; Kanevski, M.; Tonini, M.; Boris Pezzatti, G.; Conedera, M. Temporal patterns of fire sequences observed in Canton of Ticino (southern Switzerland). Nat. Hazards Earth Syst. Sci. 2010, 10, 723–728. [Google Scholar] [CrossRef]
- Allan, D. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- Pippen, B.G. Predicting Fine Fuel Moisture in Shrubby Vegetation. Bachelor’s Thesis, Australian National University, Canberra, Australia, 1999. [Google Scholar]
- Plucinski, M.P. The Investigation of Factors Governing Ignition and Development of Fires in Heathland Vegetation. Ph.D. Thesis, University of New South Wales, ADFA, Kensington, Australia, 1999. [Google Scholar]
- Telesca, L.; Lasaponara, R. Emergence of temporal regimes in fire sequences. Phys. A 2006, 359, 747–751. [Google Scholar] [CrossRef]
- Telesca, L.; Pereira, M.G. Time-clustering investigation of fire temporal fluctuations in Portugal. Nat. Hazards Earth Syst. Sci. 2010, 10, 661–666. [Google Scholar] [CrossRef]
- Gill, A.M.; Allan, G.; Yates, C. Fire-created patchiness in Australian savannas. Int. J. Wildland Fire 2003, 12, 323–331. [Google Scholar] [CrossRef]
- Malamud, B.D.; Millington, J.D.A.; Perry, G.L.W. Characterizing wildfire regimes in the USA. Proc. Natl. Acad. Sci. USA 2005, 102, 4694–4699. [Google Scholar] [CrossRef] [PubMed]
- Ganteaume, A.; Camia, A.; Jappiot, M.; San-Miguel-Ayanz, J.; Long-Fournel, M.; Lampin, C. A review of the main driving factors of forest fire ignition over Europe. Environ. Manag. 2013, 51, 651–662. [Google Scholar] [CrossRef] [PubMed]
- Bowman, D.M.J.S.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; D’Antonio, C.M.; DeFries, R.S.; Doyle, J.C.; Harrison, S.P.; et al. Fire in the Earth System. Science 2009, 324, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Goulden, M.L.; Faivre, N.; Veraverbeke, S.; Sun, F.; Hall, A.; Hand, M.S.; Hook, S.; Randerson, J.T. Identification of two distinct fire regimes in southern California: Implications for economic impact and future change. Environ. Res. Lett. 2015, 10, 094005. [Google Scholar] [CrossRef]
- Ruffault, J.; Moron, V.; Trigo, R.; Curt, T. Daily synoptic conditions associated with large fire occurrence in Mediterranean France: Evidence for a wind-driven fire regime. Int. J. Climatol. 2016, 37, 524–533. [Google Scholar] [CrossRef]
- Mouillot, F.; Rambal, S.; Joffre, R. Simulating climate change impacts on fire frequency and vegetation dynamics in a Mediterranean-type ecosystem. Glob. Change Biol. 2002, 8, 423–437. [Google Scholar] [CrossRef]
- Moriondo, M.; Good, P.; Durao, R.; Bindi, M.; Giannakopoulos, C.; Corte-Real, J. Potential impact of climate change on fire risk in the Mediterranean area. Clim. Res. 2006, 31, 85–95. [Google Scholar] [CrossRef]
- Wu, M.; Knorr, W.; Thonicke, K.; Schurgers, G.; Camia, A.; Arneth, A. Sensitivity of burned area in Europe to climate change, atmospheric CO2 levels, and demography: A comparison of two fire-vegetation models. J. Geophys. Res. Biogeosci. 2015, 120, 2256–2272. [Google Scholar] [CrossRef]
- Pausas, J.G.; Bradstock, R.A. Fire persistence traits of plants along a productivity and disturbance gradient in Mediterranean shrublands of south-east Australia. Glob. Ecol. Biogeogr. 2007, 16, 330–340. [Google Scholar] [CrossRef]
- Meyn, A.; White, P.S.; Buhk, C.; Jentsch, A. Environmental drivers of large, infrequent wildfires: The emerging conceptual model. Prog. Phys. Geogr. 2007, 31, 287–312. [Google Scholar] [CrossRef]
- Krawchuk, M.A.; Moritz, M.A. Constraints on global fire activity vary across a resource gradient. Ecology 2010, 92, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Pausas, J.G.; Paula, S. Fuel shapes the fire-climate relationship: Evidence from Mediterranean ecosystems. Glob. Ecol. Biogeogr. 2012, 21, 1074–1082. [Google Scholar] [CrossRef]
- Urbieta, I.R.; Zavala, G.; Bedia, J.; Gutiérrez, J.M.; San Miguel-Ayanz, J.; Camia, A.; Keeley, J.E.; Moreno, J.M. Fire activity as a function of fire-weather seasonal severity and antecedent climate across spatial scales in southern Europe and Pacific western USA. Environ. Res. Lett. 2015, 10, 114013. [Google Scholar] [CrossRef]
- Turco, M.; Llasat, M.C.; von Hardenberg, J.; Provenzale, A. Impact of climate variability on summer fires in a Mediterranean environment (northeastern Iberian Peninsula). Clim. Change 2013, 116, 665–678. [Google Scholar] [CrossRef]
- Trigo, R.M.; Sousa, P.M.; Pereira, M.G.; Rasilla, D.; Gouveia, C.M. Modelling wildfire activity in Iberia with different atmospheric circulation weather types. Int. J. Climatol. 2016, 36, 2761–2778. [Google Scholar] [CrossRef]
- Ruffault, J.; Moron, V.; Trigo, R.; Curt, T. Objective identification of multiple large fire climatologies: An application to a Mediterranean ecosystem. Environ. Res. Lett. 2016, 11, 075006. [Google Scholar] [CrossRef]
- Masala, F.; Bacciu, V.; Sirca, C.; Spano, D. Fire-weather relationship in the Italian peninsula. In Modelling Fire Behaviour and Risk; Università di Sassari: Sassari, Italy; Euro-Mediterranean Center for Climate Changes (CMCC): Sassari, Italy, 2012; pp. 56–62. [Google Scholar]
- Koutsias, N.; Xanthopoulos, G.; Founda, D.; Xystrakis, F.; Nioti, F.; Pleniou, M.; Mallinis, G.; Arianoutsou, M. On the relationships between forest fires and weather conditions in Greece from long-term national observations (1894–2010). Int. J. Wildland Fire 2013, 22, 493–507. [Google Scholar] [CrossRef]
- Pausas, J.G. Changes in Fire and Climate in the Eastern Iberian Peninsula (Mediterranean Basin). Clim. Change 2004, 63, 337–350. [Google Scholar] [CrossRef]
- Turco, M.; von Hardenberg, J.; AghaKouchak, A.; Llasat, M.C.; Provenzale, A.; Trigo, R. On the key role of droughts in the dynamics of summer fires in Mediterranean Europe. Sci. Rep. 2017, 7, 81. [Google Scholar] [CrossRef] [PubMed]
- San-Miguel-Ayanz, J.; Schulte, E.; Schmuck, G.; Camia, A.; Strobl, P.; Liberta, G.; Giovando, C.; Boca, R.; Sedano, F.; Kempeneers, P.; et al. Comprehensive Monitoring of Wildfires in Europe: The European Forest Fire Information System (EFFIS). In Approaches to Managing Disaster—Assessing Hazards, Emergencies and Disaster Impacts; Tiefenbacher, J., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 5. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Kagan, Y.Y.; Jackson, D.D. Long-Term Earthquake Clustering. Geophys. J. Int. 1991, 104, 117–134. [Google Scholar] [CrossRef]
- Telesca, L.; Amatulli, G.; Lasaponara, R.; Lovallo, M.; Santulli, A. Time-scaling properties in forest-fire sequences observed in Gargano area (southern Italy). Ecol. Model. 2005, 185, 531–544. [Google Scholar] [CrossRef]
- Thurner, S.; Lowen, S.; Feurstein, M.; Heneghan, C.; Feichtinger, H.; Teich, M. Analysis, synthesis, and estimation of fractal-rate stochastic point processes. Fractals 1997, 5, 565–596. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. On the sampling distribution of Allan factor estimator for a homogeneous Poisson process and its use to test inhomogeneities at multiple scales. Phys. A Stat. Mech. Its Appl. 2013, 392, 1080–1089. [Google Scholar] [CrossRef]
- Gebber, G.L.; Orer, H.S.; Barman, S.M. Fractal Noises and Motions in Time Series of Presympathetic and Sympathetic Neural Activities. J. Neurophysiol. 2006, 95, 1176–1184. [Google Scholar] [CrossRef] [PubMed]
- Ernst, M.D. Permutation Methods: A Basis for Exact Inference. Stat. Sci. 2004, 19, 676–685. [Google Scholar] [CrossRef]
- Tanaka, S.; Sato, H.; Matsumura, S.; Ohtake, M. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan. Tectonophysics 2006, 417, 69–80. [Google Scholar] [CrossRef]
- Ader, T.J.; Avouac, J.P. Detecting periodicities and declustering in earthquake catalogs using the Schuster spectrum, application to Himalayan seismicity. Earth Planet. Sci. Lett. 2013, 377–378, 97–105. [Google Scholar] [CrossRef]
- Ahdesmäki, M.; Lähdesmäki, H.; Pearson, R.; Huttunen, H.; Yli-Harja, O. Robust detection of periodic time series measured from biological systems. BMC Bioinform. 2005, 6, 117. [Google Scholar] [CrossRef] [PubMed]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press: London, UK; New York, NY, USA, 1981; p. 890. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Patil, A.; Soni, G.; Prakash, A. Chapter Five—Extremum center interpolation-based EMD approach for fault detection of reciprocating compressor. In Smart Electrical and Mechanical Systems; Sehgal, R., Gupta, N., Tomar, A., Sharma, M.D., Kumaran, V., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 109–122. [Google Scholar]
- Song, W.; Wang, J.; Satoh, K. Distribution and correlation analysis of wildfire and weather data in Japan. Prog. Nat. Sci. 2005, 15, 363–367. [Google Scholar] [CrossRef]
- Wang, J.; Song, W.; Zheng, H.; Telesca, L. Temporal scaling behavior of human-caused fires and their connection to relative humidity of the atmosphere. Ecol. Model. 2010, 221, 85–89. [Google Scholar] [CrossRef]
- Pereira, J.M.C.; Amaral Turkman, M.A.; Turkman, K.F.; Oom, D. Anthromes displaying evidence of weekly cycles in active fire data cover 70% of the global land surface. Sci. Rep. 2019, 9, 11424. [Google Scholar] [CrossRef] [PubMed]
- Gray, M.E.; Zachmann, L.J.; Dickson, B.G. A weekly, continually updated dataset of the probability of large wildfires across western US forests and woodlands. Earth Syst. Sci. Data 2018, 10, 1715–1727. [Google Scholar] [CrossRef]
- Engelmann, R.; Ansmann, A.; Ohneiser, K.; Griesche, H.; Radenz, M.; Hofer, J.; Althausen, D.; Dahlke, S.; Maturilli, M.; Veselovskii, I.; et al. Wildfire smoke, Arctic haze, and aerosol effects on mixed-phase and cirrus clouds over the North Pole region during MOSAiC: An introduction. Atmos. Chem. Phys. 2021, 21, 13397–13423. [Google Scholar] [CrossRef]
- Kloss, C.; Berthet, G.; Sellitto, P.; Ploeger, F.; Bucci, S.; Khaykin, S.; Jégou, F.; Taha, G.; Thomason, L.W.; Barret, B.; et al. Transport of the 2017 Canadian wildfire plume to the tropics via the Asian monsoon circulation. Atmos. Chem. Phys. 2019, 19, 13547–13567. [Google Scholar] [CrossRef]
- Yu, Y.; Ginoux, P. Enhanced dust emission following large wildfires due to vegetation disturbance. Nat. Geosci. 2022, 15, 878–884. [Google Scholar] [CrossRef]
- Bowman, D.; Williamson, G.; Yebra, M.; Lizundia-Loiola, J.; Pettinari, M.L.; Shah, S.; Bradstock, R.; Chuvieco, E. Wildfires: Australia needs national monitoring agency. Nature 2020, 584, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Requia, W.J.; Amini, H.; Mukherjee, R.; Gold, D.R.; Schwartz, J.D. Health impacts of wildfire-related air pollution in Brazil: A nationwide study of more than 2 million hospital admissions between 2008 and 2018. Nat. Commun. 2021, 12, 6555. [Google Scholar] [CrossRef] [PubMed]
- Andela, N.; van der Werf, G. Recent trends in African fires driven by cropland expansion and El Niño to La Niña transition. Nat. Clim. Change 2014, 4, 791–795. [Google Scholar] [CrossRef]
- Fan, H.; Yang, X.; Zhao, C.; Yang, Y.; Shen, Z. Spatiotemporal variation characteristics of global fires and their emissions. Atmos. Chem. Phys. 2023, 23, 7781–7798. [Google Scholar] [CrossRef]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A Seasonal-Trend Decomposition Procedure Based on Loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Jiménez-Ruano, A.; Rodrigues Mimbrero, M.; Jolly, W.M.; de la Riva Fernández, J. The role of drought length and magnitude in the temporal evolution of fire occurrence and burned area size in mainland Spain. In Proceedings of the Geophysical Research Abstracts, EGU General Assembly 2018, Vienna, Austria, 8–13 April 2018. [Google Scholar]
- Telesca, L.; Vicente-Serrano, S.M.; López-Moreno, J.I. Power spectral characteristics of drought indices in the Ebro river basin at different temporal scales. Stoch. Environ. Res. Risk Assess. 2013, 27, 1155–1170. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).