Deep Reinforcement Learning-Based Deployment Method for Emergency Communication Network

Abstract

Emergency communication networks play a crucial role in disaster relief operations. Current automated deployment strategies based on rule-driven or heuristic algorithms struggle to adapt to the dynamic and heterogeneous network environments in disaster scenarios, while manual command deployment is constrained by personnel expertise and response time requirements, leading to suboptimal trade-offs between deployment efficiency and reliability. To address these challenges, this study proposes a novel deep reinforcement learning framework with a fully convolutional value network architecture, which achieves breakthroughs in multi-dimensional spatial decision-making through end-to-end feature extraction. This design effectively mitigates the “curse of dimensionality” inherent in traditional reinforcement learning methods for topology planning. Experimental results demonstrate that the proposed method effectively accomplishes the planning tasks of emergency communication hub elements, significantly improving deployment efficiency while maintaining robustness in complex environments.

1. Introduction

In recent years, global emergencies and major natural disasters have exhibited composite risk characteristics marked by high frequency, wide scope, and strong destructive impact. Their unpredictability, urgency, and high uncertainty have significantly threatened economic production and social stability, with resulting economic losses and secondary hazards being difficult to quantify [1,2,3,4]. After decades of practical development, emergency communication systems have gradually established a multi-dimensional heterogeneous communication support framework centered on satellite communication, microwave communication, 5G mobile networks, and trunked communication [5,6]. This system has initially achieved basic communication coverage in disaster scenarios, providing critical support for rescue operations. However, with the increasing frequency of extreme climate events and accelerated urbanization, existing systems still face severe challenges in adapting to dynamic environments.

To enhance robustness, current emergency communication networks widely adopt multi-modal network integration strategies, forming multi-path redundant architectures through collaborative deployment of satellite links, terrestrial base stations, and wireless relays. This network architecture leverages 5G and cluster communication to achieve full-area coverage in disaster-affected core areas while establishing high-bandwidth transmission channels with the rear command center through satellite, microwave, and fiber-optic links [7]. It should be noted that although this complex network topology significantly enhances survivability against infrastructure damage, it imposes dual challenges for deployment planning: On one hand, physical constraints such as terrain features, disaster evolution, and communication coverage radii must be dynamically balanced; on the other hand, interference and resource competition between heterogeneous devices need to be avoided while meeting differentiated service demands like low-latency video backhaul and high-reliability command scheduling. Constrained by the dynamic nature of field environments and the urgency of decision-making timelines, traditional deployment models relying on manual experience struggle to rapidly generate globally optimal solutions. This results in a temporal mismatch between communication hub activation efficiency and the critical rescue window period, which has become a core bottleneck restricting the improvement of emergency communication effectiveness.

To overcome the above limitations, this paper proposes an intelligent deployment method based on deep reinforcement learning (DRL) to achieve rapid deployment optimization of emergency communication networks. The widespread applications of DRL in UAV deployment [8] have demonstrated its ability to effectively address complex state spaces and dynamically changing environments. By leveraging powerful deep neural networks (DNNs) for decision-making, DRL has proven capable of delivering excellent performance across numerous learning tasks even under conditions of severe domain knowledge scarcity. However, applying DRL to solve emergency communication network deployment challenges is non-trivial. Traditional DRL algorithms, such as Deep Q Network (DQN) [9], utilize convolutional neural networks (CNNs) to estimate Q values for each state–action pair. The fully connected layers in CNNs limit the DQN to handling only very limited action spaces, severely constraining the decision-making capabilities of the agent.

To address the challenges of rapid deployment and efficient communication in emergency communication networks under disaster scenarios, this thesis proposes a DRL-based intelligent deployment method. Targeting the dynamic characteristics of disaster environments and the complexity of heterogeneous network organization, this method innovatively integrates a fully convolutional neural network with deep reinforcement learning algorithms. By expanding the reinforcement learning action decision space through high-dimensional state perception capability, the method achieves dynamic adaptation to complex environments. Compared to earlier studies [10], this experiment optimized the action space design and conducted comparative experiments with the classic greedy strategy under the same benchmark environment. Meanwhile, we systematically analyzed the impact of key hyperparameters on performance, revealing the correlation between hyperparameter configurations and convergence efficiency.

Experimental simulations demonstrate that this approach significantly enhances network deployment efficiency and the rationality of emergency communication resource allocation in post-disaster dynamic environments, outperforming traditional modeling planning methods in robustness and adaptability. The research further validates the feasibility of applying DRL to solve network deployment problems in emergency communication fields, providing a novel technical pathway for communication restoration during disaster relief processes that balances real-time responsiveness with optimization performance.

2. Relevant Work

In this section, we will briefly introduce current research achievements and elaborate on our innovative contributions.

The deployment problem of the emergency communication network is a type of Hub Location Problem (HLP), which is an important research area in operations research. It primarily focuses on selecting optimal locations for establishing hubs within a given network to achieve predefined optimization objectives. This problem widely arises in various fields such as transportation, spatial planning, and military deployment. Many studies have been conducted to address the hub location problem, and the existing methods can generally be categorized into three types: rule-based, heuristic, and machine learning-based methods.

2.1. Rule-Based Deployment Method

The rule-based deployment methods primarily select actions according to predefined behavioral rules of the agents during deployment. These methods do not involve data-driven training or optimization of strategies during the deployment process. In rule-based methods, the decision-making mechanism typically extracts relevant features from the initial state and quantitatively evaluates the global impact of deploying in a certain area. Subsequent deployment plans are then selected based on predefined rules. Meyer et al. [11] proposed a two-stage branch-and-bound algorithm to solve the single-allocation p-hub location problem. Additionally, Ernst et al. [12] applied the branch-and-bound algorithm to address both uncapacitated single-allocation and multi-allocation p-hub center problems.

The advantage of rule-based methods lies in their ability to find the globally optimal solution for the current scenario, making them effective when the candidate site space is relatively small. However, as the deployment space increases, the computational complexity grows significantly, making it nearly impossible to find an optimal solution within a reasonable time frame. Moreover, due to the limited adaptability of predefined rules, this approach is unable to provide reasonable site selection solutions in complex and dynamically changing environments.

2.2. Heuristic Deployment Method

To address hub location challenges in complex scenarios, researchers widely employ heuristic and metaheuristic algorithms to approximate optimal solutions. These methods transform the problem into a combinatorial optimization framework through mathematical modeling, designing iterative search strategies based on objective functions and constraints.

Shuang Wang et al. [13] propose stratified single-allocation hub location problems with various extensions and develop an efficient neighborhood-search algorithm to solve them, demonstrating the importance of considering demand stratification in hub-and-spoke network design. Nan Yu et al. [14] study the multi-allocation hub-and-spoke network design problem for flight flow routing (HURO) aiming to maximize airline profit utility and propose a two-level algorithm framework with a constant approximation ratio and approximation algorithms for related variants. Simulation and field experiments demonstrate the effectiveness of the proposed methods. Bollapragada et al. [15] employed the greedy algorithm to solve the hub location problem. They dynamically adjusted the hub positions through phased decision-making to maximize the coverage of demands. The core of their approach lies in integrating two-stage planning with hub movement strategies and optimizing the Q value calculation by efficiently solving the maximum flow problem.

Heuristic methods, with their global search capabilities and convergence guarantees, have become dominant for large-scale hub location problems. However, traditional heuristic algorithms suffer from poor scalability and insufficient real-time performance, limiting their applicability to offline policy generation in dynamic environments.

2.3. Machine Learning-Based Deployment Method

Machine learning (ML)-based deployment methods primarily rely on data-driven training to iteratively optimize strategies in self-play. The core idea of ML lies in continuous trial and error within an environment, refining behavioral policies based on acquired rewards without relying on explicit models or prior knowledge. Traditional RL methods model problems through Q value tables, but these are limited to small-scale, simple scenarios. By integrating deep neural networks, agents can iteratively optimize policies in simulated environments, making them highly suitable for tackling complex, dynamically changing problems with challenging mathematical formulations. In recent years, RL-based methods have been widely applied to fields such as board games, UAV deployment, spatial planning, and building layout design, as summarized in

Table 1. Typical applications in intelligent deployment.

Model	Method	Core Idea
AlphaGo, AlphaZero [16,17]	Neural Networks + Monte Carlo Tree Search	Achieve game-playing capabilities without human prior knowledge.
DRL-EC [18]	DQN Algorithm	Optimize UAV hovering positions to maximize communication coverage and endurance.
DRL-Urban-Planning [19]	GNN-based Reinforcement Learning	Allocate land and road positions to enhance urban space utilization.
TorchCraft AI [20]	FCN-based Reinforcement Learning	Select optimal building sites based on terrain features.

.

In summary, ML-based methods have demonstrated significant potential in addressing challenges within complex, dynamic, and uncertain environments. However, their application to emergency communication network deployment remains limited and lacks in-depth exploration.

Our contributions are primarily reflected in the following aspects:

• We comprehensively consider the impacts of various environmental factors on different hub elements, quantify them, and establish an evaluation reward function.
• We propose a deep reinforcement learning model based on a fully convolutional network (FCN). By adopting an FCN as the value network, the model effectively expands the agent’s action space while preserving spatial topological features.
• Experimental results demonstrate that our method significantly improves the overall deployment effectiveness of emergency communication networks compared to existing approaches.

3. Preliminary

In this section, we first systematically elaborate on the emergency communication network deployment problem and conduct an in-depth analysis of its core challenges. Subsequently, we formalize the problem into a mathematical model to establish a theoretical foundation for subsequent optimization and solution processes.

3.1. Problem Description

The emergency communication network serves as the core supporting system for post-disaster rescue operations, where its deployment efficiency and operational reliability directly impact life-saving effectiveness and the control of disaster losses. In complex and dynamic disaster scenarios, such networks must possess rapid networking capabilities, multi-service support, and high robustness to enable diverse communication services—including messaging, audio, and video—while meeting multi-dimensional requirements for on-site command coordination, medical collaboration, and resource allocation [2].

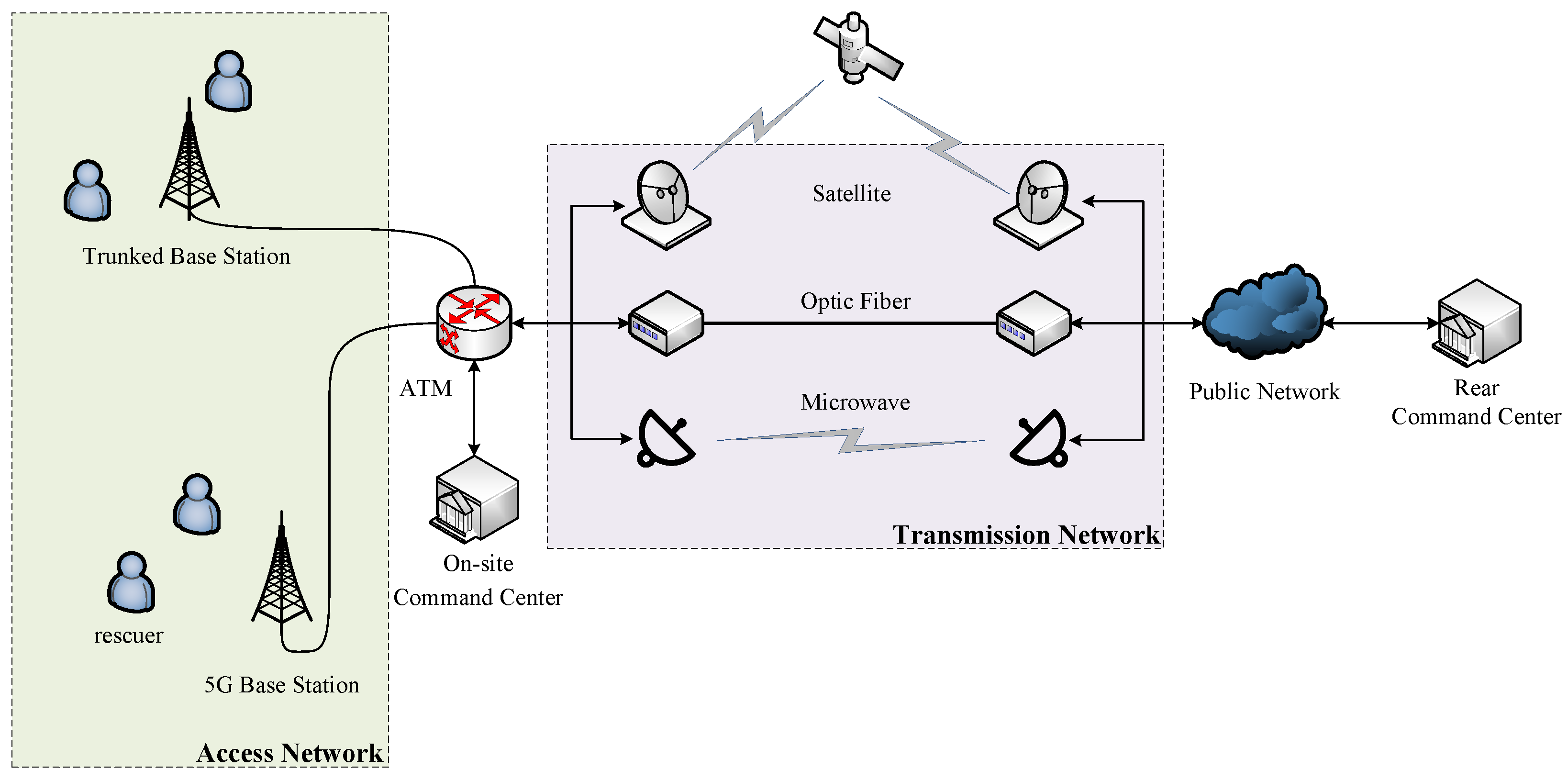
As illustrated in Figure 1, the network architecture of an emergency communication system is jointly composed of a transmission network and an access network [21]. The access network focuses on rapid connectivity of field terminal devices, utilizing technologies like trunked intercoms and 5G mobile networks to provide rescuers with messaging, voice, and low-latency data services, ensuring real-time command at the front line. The transmission network adopts a redundant architecture integrating multiple links such as satellite, microwave, and fiber-optic cables, and can forward data through public network to establish an efficient and stable high-speed information transmission channel between the rear command center and the disaster site [7]. This multi-dimensional transport mode not only significantly enhances video transmission quality but also ensures communication continuity in extreme environments through redundant link backup mechanisms.

To enhance the deployment efficiency and communication reliability of emergency communication networks, scientific planning of the deployment locations for critical components—including field command centers, ATM switches, satellite communication vehicles, microwave relay vehicles, optical terminal equipment, 5G base stations, and trunked base stations—is required. The deployment strategy should comprehensively account for geographical environments and communication methods to achieve a dynamic balance between communication quality and coverage efficiency.

3.2. System Model

To further analyze the deployment challenges of emergency communication networks, it is essential to systematically quantify and model key environmental indicators. The core environmental factors affecting hub element deployment can be categorized into the following aspects.

• Terrain. In this problem, the geographical environment is the core factor determining the feasibility of site selection for large mobile equipment. Therefore, terrain features need to be evaluated: areas with mobility advantages D such as roads, flat terrains, or grasslands are assigned a reward value of +1, while complex terrains or ecologically sensitive zones are penalized with −1 through spatial constraint algorithms to improve deployment efficiency.

  $$R_1=\left\{\begin{array}{cc}1,\hfill & a_t\in D\hfill \\ -1,\hfill & a_t\notin D\hfill \end{array}\right.$$

  (1)
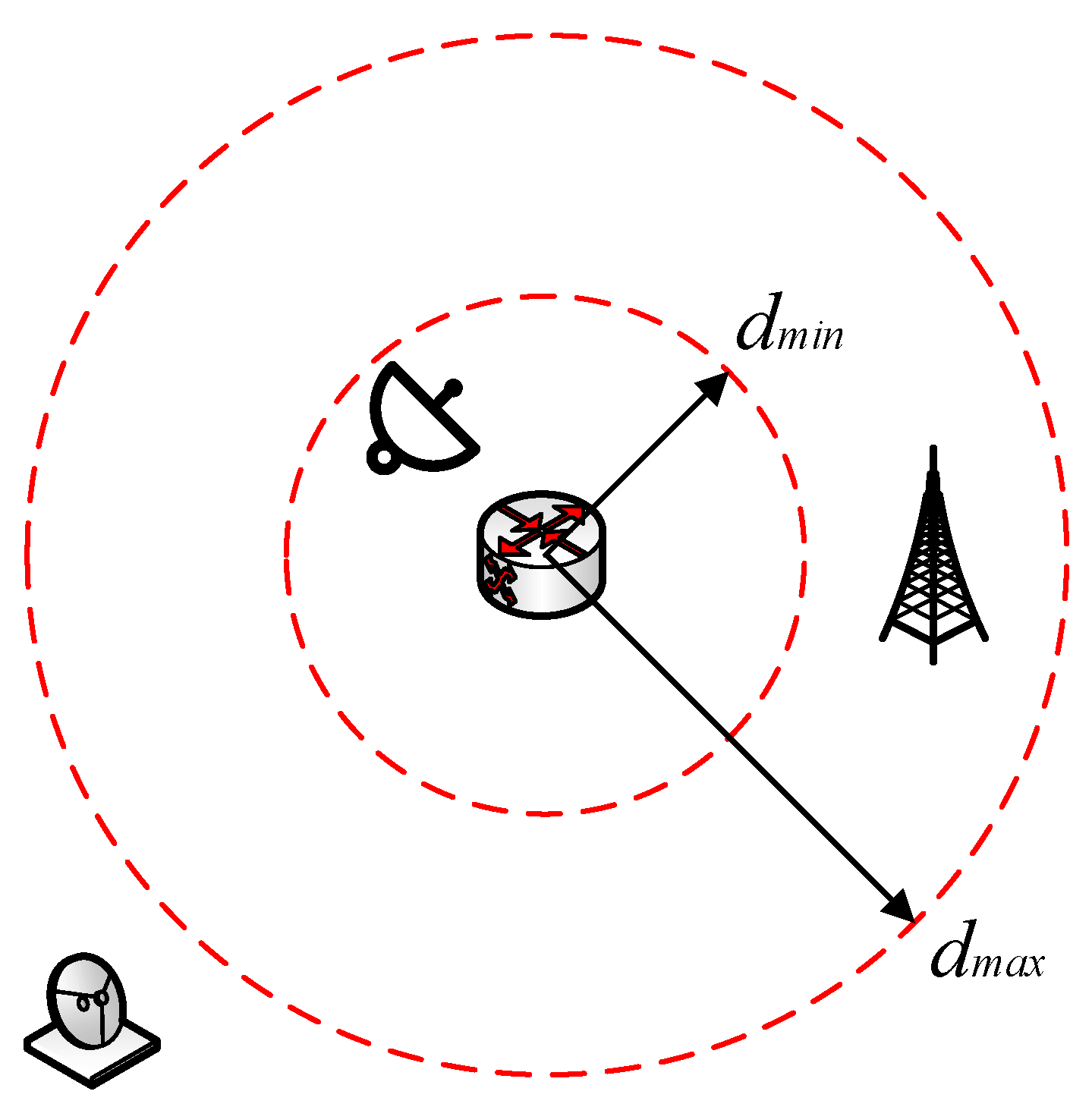
• Deployable range. As presented in Figure 2, the spatial distribution of elements must satisfy dual constraints, avoiding exceeding the maximum communication distance $d_{max}$ while preventing signal interference caused by overly close proximity $d_{min}$. To address this, a dynamic reward function is constructed using a Gaussian formulation.

  $$R_2=e^{-{\displaystyle \frac{{\left(d-\frac{d_{max}-d_{min}}{2}\right)}^2}{2{c_1}^2}}}$$

  (2)
• Distance from optical cable access point. To minimize the potential damage to exposed optical cables from secondary disasters and ensure stable optical communication, the optical terminal unit should be deployed in close proximity to the optical cable access point. The corresponding reward function is formulated as follows:

  $$R_3=e^{-{\displaystyle \frac{d^2}{2{c_2}^2}}}$$

  (3)
• Microwave direction. By employing the free-space path loss model for microwave transmission, the transmission distance d between microwave transceiver sites is leveraged to compute the propagation loss using the electromagnetic attenuation formula. This loss metric is subsequently transformed into a dynamically adjustable reward signal, which guides the optimization of transceiver deployment positions.

  $$R_4={\alpha }_4{\displaystyle \frac{G_t{G}_r{C}^2}{16{\pi }^2{d}^2{f}^2}}$$

  (4)
• Radio coverage. To ensure full communication coverage for rescue personnel at the disaster site, both 5G and cluster base stations should be deployed in a manner that maximizes their signal reach over the affected area. The rationality of their placement can be assessed by computing the Intersection over Union (IoU) between the communication coverage area of each base station and the disaster-affected region.

  $$R_5={\alpha }_5{\displaystyle \frac{\left|A_{com}\cap A_{dis}\right|}{\left|A_{com}\cup A_{dis}\right|}}$$

  (5)

The frequently used notations are listed in the

Table 2. Frequently used notations.

Notation	Explanation
$t,T$	the index of an element, the total number of elements
$G_t,G_r$	transmit and receive antenna gains
$C,f$	speed of light, carrier frequency
$c_1,c_2$	standard deviation of the Gaussian function
$R_i$	quantified reward function for each factor
$S_t,a_t,R_t$	state, action, and reward in t-th epoch
${\alpha }_i$, ${\beta }_i$	adjustment coefficients of the subtotal and total reward function
D	set composed of road areas
d	distance between two points
$d_{max},d_{min}$	maximum and minimum communication range among elements
$A_{com},A_{dis}$	effective communication coverage area and affected region
$ϵ$	denotes the exploration probability

:

4. Proposed DRL-Based Method

In this section, we first outline the overall architecture of the methodology, subsequently construct the value network, then define the state, action, and reward mechanisms, and finally elaborate on the reinforcement learning algorithm employed.

4.1. Overview

The emergency communication network deployment model we propose is based on an improved Double DQN (DDQN) [22] algorithm, with a core architecture comprising three major parts: agent, experience replay buffer, and environment, as illustrated in Figure 3.

The value network is constructed using a lightweight fully convolutional neural network (FCN). This network takes the current deployment state $S_t$ as input, extracts features through multiple convolutional layers, and ultimately outputs a Q value matrix $Q_w(S_t,a)$ aligned with the input resolution. Each position in the matrix corresponds to the value of a different deployment location, thereby achieving an end-to-end mapping from the high-dimensional state space to action values.

Then, the agent adopts an $ϵ$-greedy strategy to dynamically balance exploration and exploitation. Based on the Q value matrix generated from the current state, the agent selects the location $a_t$ with the highest value for deploying communication elements. After executing an action, the system receives an immediate reward through environmental feedback, which is then stored in the experience replay buffer. Each transition sample $\{S_t,a_t,R_t,S_{t+1}\}$ is stored using a prioritized experience replay mechanism. During training, the model maintains a separation between the parameters of the target network and the training network through an asynchronous parameter update strategy. Combined with the dual-network structure, this approach reduces the correlation in Q value estimation, thereby enhancing policy stability in complex and dynamic environments.

4.2. Architecture of Value Network

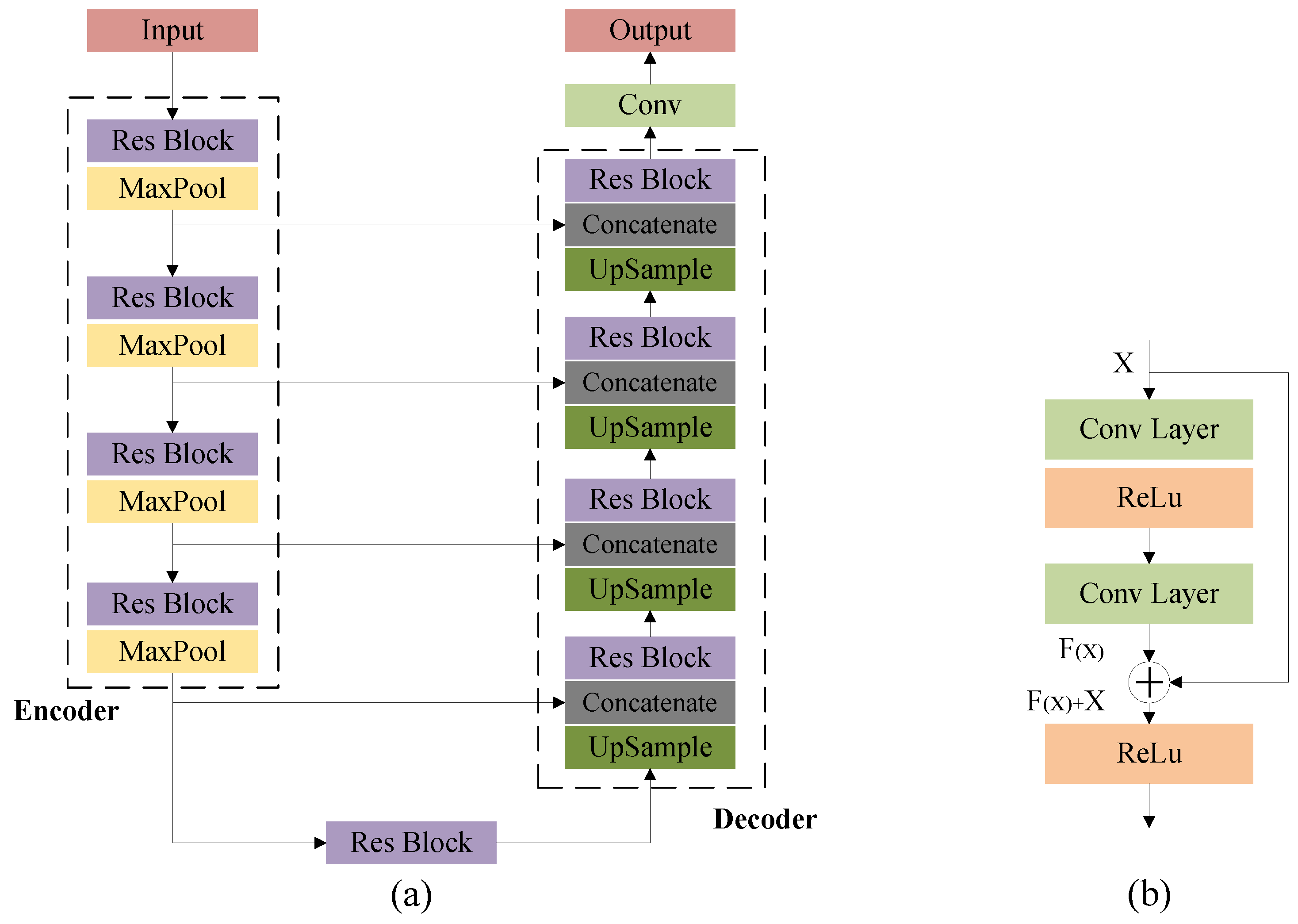
As shown in Figure 4a, we employ an FCN to construct the value network architecture, aiming to enhance the action space of reinforcement learning agents and improve decision-making capabilities in complex environments. This architecture implements high-dimensional state–action value function mapping through an encoder–decoder framework, drawing design inspiration from multi-scale feature fusion techniques in point cloud completion [23], semantic segmentation domains [24], and correspondence learning [25]. Specifically, the fully connected layers in traditional CNNs are replaced with convolutional layers, enabling the network to accept arbitrary-sized inputs and output resolution-matched value distribution maps through full convolutionalization.

The encoder is built upon the ResNet-50 [26] backbone network, extracting multi-level feature maps through four-stage downsampling operations from input states. Among them, Figure 4b shows the residual block structure. This multi-scale feature extraction inherits the advantages of the FCN in semantic segmentation tasks, effectively capturing composite features across spatial and semantic dimensions while representing both local details and global scene information. In decoder design, a Feature Pyramid Network (FPN) architecture is introduced to achieve cross-level feature fusion via lateral connections and a top-down pathway. Low-level features are fused with upsampled high-level semantic features through skip connections, progressively restoring spatial resolution while preserving semantic consistency. The final output value distribution map maintains pixel-level alignment with the input state, where each spatial location corresponds to the Q value of its action.

4.3. Design of State, Action and Reward

4.3.1. State

In the deep reinforcement learning framework, the state is defined as a complete observable description of the current environmental conditions. For this problem, the state design is primarily composed of the following parts:

• Terrain: Based on a rasterized topographic map, a binary encoding scheme is applied to distinguish deployable areas from restricted zones. Roads, flatlands, and grasslands are classified as deployable regions and assigned 1, while buildings, water, and forests are marked as restricted zones with 0.
• Deployable Range: Determine the communication range between adjacent elements based on the network topology, with values in the range [0, 1].
• Optical Cable Access Point: When the deployment element is the optical terminal equipment, the area within a certain range around the optical cable access point is set to 1, while other areas are set to 0.
• Microwave Directionality: For microwave relay vehicle deployment scenarios, a directional weight matrix is constructed, where the value increases as it approaches the direction of the opposite microwave terminal. The range of values is [0, 1].
• Type: The requested element type as an integer corresponding to the index of current element.

4.3.2. Action

In this problem, each selected deployment location for the current element is defined as an action $a_t$. Specifically, the deployable area is divided into an $n\times n$ grid, where each cell corresponds to a distinct action. Consequently, the action space A contains $n\times n$ discrete actions $a_t$. The agent processes the current state $S_t$ through a value network and outputs a Q value matrix $Q_w(S_t,a)$, which quantifies the expected cumulative reward for selecting action $a_t$ under state $S_t$. During decision-making, a greedy strategy is employed to select the optimal action corresponding to the maximum Q value in the matrix:

$$a_t=\underset{A}{argmax}{Q}_w\left(S_t,a\right)$$

(6)

4.3.3. Reward

In practice, multiple factors significantly impact the deployment efficiency of emergency communication networks and the channel quality of heterogeneous communication methods. To address the deployment problem of emergency communication network elements using reinforcement learning, it is essential to first model the environment and design a rational reward function.

In this problem, environmental rewards for different elements can originate from four key aspects: geographic environment, disaster directionality, communication distances between elements, and spatial separation distances. Detailed calculation methods for each reward component are revisited in Section 3.2. This design actively suppresses the occurrence of invalid or harmful behaviors by pre-limiting invalid decisions in the action space, thereby eliminating the reliance on negative rewards. This approach avoids manual design of penalty terms and significantly reduces redundant computational overhead during decision-making.

For elements, a dynamic weighting mechanism is required to allocate weights to individual reward components. The total reward function can be expressed as

$$R_t=\sum _{i=5}^n{\beta }_i{R}_i,$$

(7)

where ${\beta }_i$ is the correction coefficient of each reward sub-item in the total reward function, and $R_i$ is each reward sub-item. The correction coefficients of each reward sub-item in this total reward function are adjusted according to the type of element.

• ATM switch, satellite communication vehicle: ${\beta }_1$ = ${\beta }_2$ = 0.5, ${\beta }_3$ = ${\beta }_4$=${\beta }_5$ = 0.
• Optical terminal equipment: ${\beta }_1$ = ${\beta }_2$ = 0.3, ${\beta }_3$ = 0.4, ${\beta }_4$ = ${\beta }_5$ = 0.
• Microwave relay vehicle: ${\beta }_1$ = ${\beta }_2$ = 0.3, ${\beta }_4$ = 0.4, ${\beta }_3$ = ${\beta }_5$ = 0.
• 5G and trunked base stations: ${\beta }_1$ = ${\beta }_2$ = 0.3, ${\beta }_5$ = 0.4, ${\beta }_3$ = ${\beta }_4$ = 0.

4.4. Introduction of Algorithm

The basic idea of our algorithm has been introduced in Section 4.1. The training process of the algorithm, as shown in Algorithm 1, can be roughly divided into three stages.

Initial stage. The parameters w of the value network are randomly initialized and then copied to the target network to generate its initial parameters. Subsequently, the training environment is loaded, and an experience replay buffer is established to store interaction data. To enhance algorithmic stability, the update frequency of the target network parameters is constrained by a threshold $\tau$.

Exploration stage. To expand the scale of the neural network training dataset, the agent performs D element deployments within a single iteration cycle. Each epoch initializes the environment and state $S_0$ by randomly generating an initial point. Then, the agent follows a predefined priority sequence to deploy elements. During each deployment, the agent employs an $\epsilon$-greedy strategy for action decision-making $a_t$: with probability $\epsilon$, it explores random actions, and with probability $1-\epsilon$, it selects the current optimal policy. The environment returns an immediate reward value $r_t$ based on the action execution result and transitions the state from $S_t$ to a new state $S_{t+1}$. After completing a single element deployment, the system injects the experience data tuple $\{S_t,a_t,R_t,S_{t+1}\}$ into the replay buffer for storage.

Algorithm 1: Details of the Algorithm

1 Randomly initialize value network $Q_w\left(S_t,a\right)$ with weights w;  2 Initialize target network $Q_{w^{-}}\left(S_t,a\right)$ with weights $w^{-}$;  3 Initialize experience replay buffer B and environment;  4 for epoch m:= 1,…, M do  5  Initialize state $S_0$;  6  for episode e:= 1,…,E do  7   Select the random position for the first element;  8   for element t:= 1,…,T do  9     Select element type and generate $S_t$; 10    Predict the value matrix $Q_t$ by $Q_w\left(S_t,a\right)$; 11    According to $Q_t$, action a is adopted by $ϵ$-greedy strategy; 12    Obtain reward $R_t$ from environment; 13    $S_t$ transforms to $S_{t+1}$; 14    Store data $\left\{S_t,a_t,R_t,S_{t+1}\right\}$ into B; 15   end for 16  end for 17  Sample a random batch H of data $\{S_t,a_t,R_t,S_{t+1}\}$ from B; 18  Calculate the next value $Q_{t+1}$ by TD; 19  Calculate the TD target $R_t+\gamma Q_{t+1}$; 20  Calculate the loss by Equation (9); 21  Update w by minimizing the loss; 22  If m modulo updating interval P equals 0, then 23   Duplicate w to $w^{-}$; 24  end if 25 end for

Training stage. The parameters w, $w^{-}$ of the value network and target network are updated through an experience replay buffer B. Specifically, H transition samples $\{S_t,a_t,R_t,S_{t+1}\}$ are randomly sampled from B to form a mini-batch for neural network training. The Temporal Difference (TD) target is calculated as shown in Equation (8). However, since $Q_{t+1}$ is an $n\times n$ matrix, traversing all $n^2$ actions directly would lead to excessive computational complexity, degrading algorithm efficiency. To address this, a two-stage optimization strategy is proposed.

1.

Action Space Dimensionality Reduction: A grid sampling strategy with a step size of two reduces the original $n^2$ action space to $n^2/4$ candidate actions. Combining the geographic environment encoding matrix (deployable areas marked as 1, obstacles as 0), only valid deployment regions $A^{\prime }$ are retained for value evaluation to further reduce redundant computations.

2.

Value Matrix Reconstruction: For the next state $S_{t+1}$, the optimal action $a_{\max }=\underset{A^{\prime }}{argmax}{Q}_w(S_{t+1},a)$ is computed via the target network, and its corresponding value $q_{t+1}=Q_{w^{-}}(S_{t+1},a_{\max })$ is extracted to construct the reduced-value set $Q_{t+1}^{\prime }$. Bilinear interpolation then restores $Q_{t+1}^{\prime }$ to $n\times n$ resolution $Q_{t+1}$, balancing efficiency and precision.

Finally, the target value matrix ${\widehat{Q}}_t=R_t+\gamma Q_{t+1}$ is generated using the TD equation [27]. By Equation (9), the mean squared error between the estimated Q value $Q_w\left(S_t,a\right)$ and target Q value ${\widehat{Q}}_t$ serves as the loss function, updating the value network parameters $w^{\ast }$ via stochastic gradient descent.

$$q_{t+1}=\left\{\begin{array}{cc}{Q}_{w^{-}}[S_{t+1},\underset{A^{\prime }}{argmax}{Q}_w\left(S_{t+1},a\right)],\hfill & a\in A^{\prime }\hfill \\ 0,\hfill & a\notin A^{\prime }\hfill \end{array}\right.$$

(8)

$$w^{\ast }=argmin{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left[Q_w\left(S_t,a\right)-\left(R_t+\gamma Q_{t+1}\right)\right]}^2$$

(9)

5. Performance Evaluation

In this section, we first set up the simulation environment, conducted comparative experiments on the proposed DRL-based method, and then presented and analyzed the results.

5.1. Experiment Settings

In this experiment, we utilize the ground truth of semantic segmentation from the BLU dataset [28] as the digital terrain model of the deployment area, which is fed into the model to support deployment decisions for emergency communication network elements. For computational convenience, the area is divided into a $256\times 256$ pixel grid, where each pixel corresponds to a physical space of approximately 5.5 m in edge length. The fiber-optic access points and disaster epicenters are randomly generated within the deployment area, while the locations of the remote microwave nodes are set outside the deployment region, also randomly generated, to enhance the diversity and generalization capability of the training samples. The simulation involves sequentially deploying seven types of communication network elements while taking into account dynamic environmental factors such as disaster direction.

To evaluate the algorithm’s performance, we use the total reward $R_{total}$ obtained from all deployed elements in each episode as the key evaluation metric. The definition of $R_{total}$ is as shown in Equation (10).

$$R_{total}=\sum _{t=1}^T{R}_t,$$

(10)

where t denotes the index of the communication element, T is the total number of communication elements, and $R_t$ represents the reward obtained when deploying the t-th communication element.

Based on this scenario, the algorithm is trained for 1000 episodes, with 60 environment explorations conducted in each episode. All simulations are conducted on an NVIDIA RTX 3090Ti GPU with Ubuntu 22.04.4 LTS as the operating system. The implementation is based on Python 3.10 and the PyTorch 2.3 deep learning framework.

5.2. Results and Analysis

In this section, we first design multidimensional comparative experiments to benchmark our method against reinforcement learning algorithms and neural network architectures. The experimental framework comprehensively assesses performance through metrics such as cumulative reward curves and policy convergence speed, thereby validating the effectiveness of the proposed method. Subsequently, we conduct a systematic evaluation of model hyperparameters to reveal how key parameters influence the stability of emergency communication network.

5.2.1. Comparison with Other Methods

To explore the optimal model architecture for emergency communication network deployment tasks, this study integrates two classical value-based reinforcement learning algorithms—the DQN and DDQN—and incorporates two mainstream deep neural network structures in the design of the value network: the stacked convolutional modules of VGG and the residual-connected ResNet modules. By constructing four distinct algorithm-network combinations and conducting performance comparisons under identical experimental conditions, the study aims to identify the most suitable model configuration for the given task.

Meanwhile, we compared the proposed framework with a widely adopted baseline method—the greedy algorithm. The greedy strategy extends the classical greedy algorithm, which prioritizes locally optimal decisions at each deployment stage without considering long-term consequences. Specifically, during each site selection process, this method chooses the location with the highest immediate reward value (i.e., the optimal point under current network conditions) for deployment. This approach aligns with the greedy heuristic of selecting the “best” option available at each step, though it may not guarantee globally optimal solutions.

A.

Quantitative Analysis

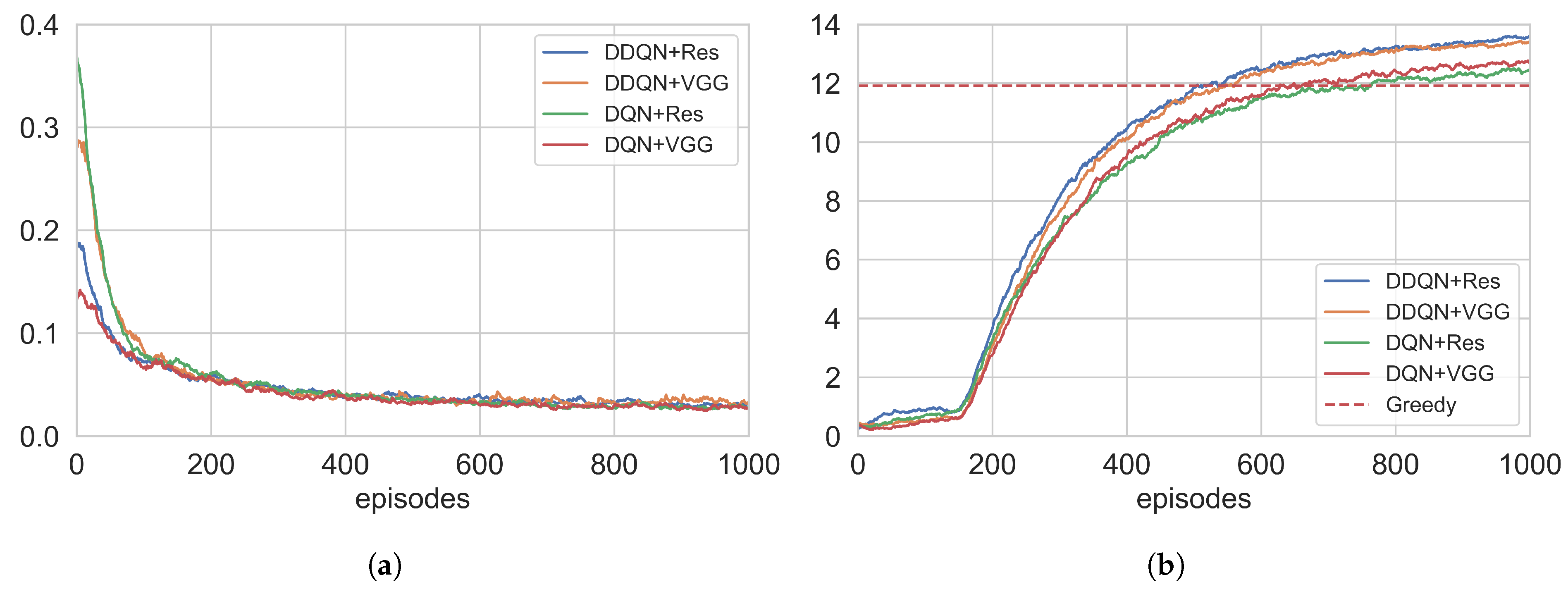
As shown in Figure 5a, the four combinations exhibit similar convergence characteristics in loss function trends, indicating minimal differences in convergence speed. However, the long-term performance comparison in Figure 5b reveals that the DDQN significantly outperforms the DQN after training stabilization. The improved average cumulative reward demonstrates the DDQN’s superior capabilities in strategy optimization and long-term return potential. Further analysis of value network structures shows that ResNet-based models achieve better overall performance compared to VGG modules, which correlates with ResNet’s residual architecture enabling stronger approximation capabilities for complex value functions.

To validate the limitations of greedy strategies, we conducted 100 experiments using the greedy algorithm, achieving an average deployment reward of 11.98. Although the greedy method demonstrates computational efficiency advantages, its myopic decision-making mechanism tends to fall into local optima—a defect particularly pronounced in combinatorial optimization tasks. In contrast, reinforcement learning-based methods balance immediate rewards and long-term returns, effectively overcoming the inherent drawbacks of greedy heuristics and exhibiting superior global optimization capabilities.

B.

Visual Analysis

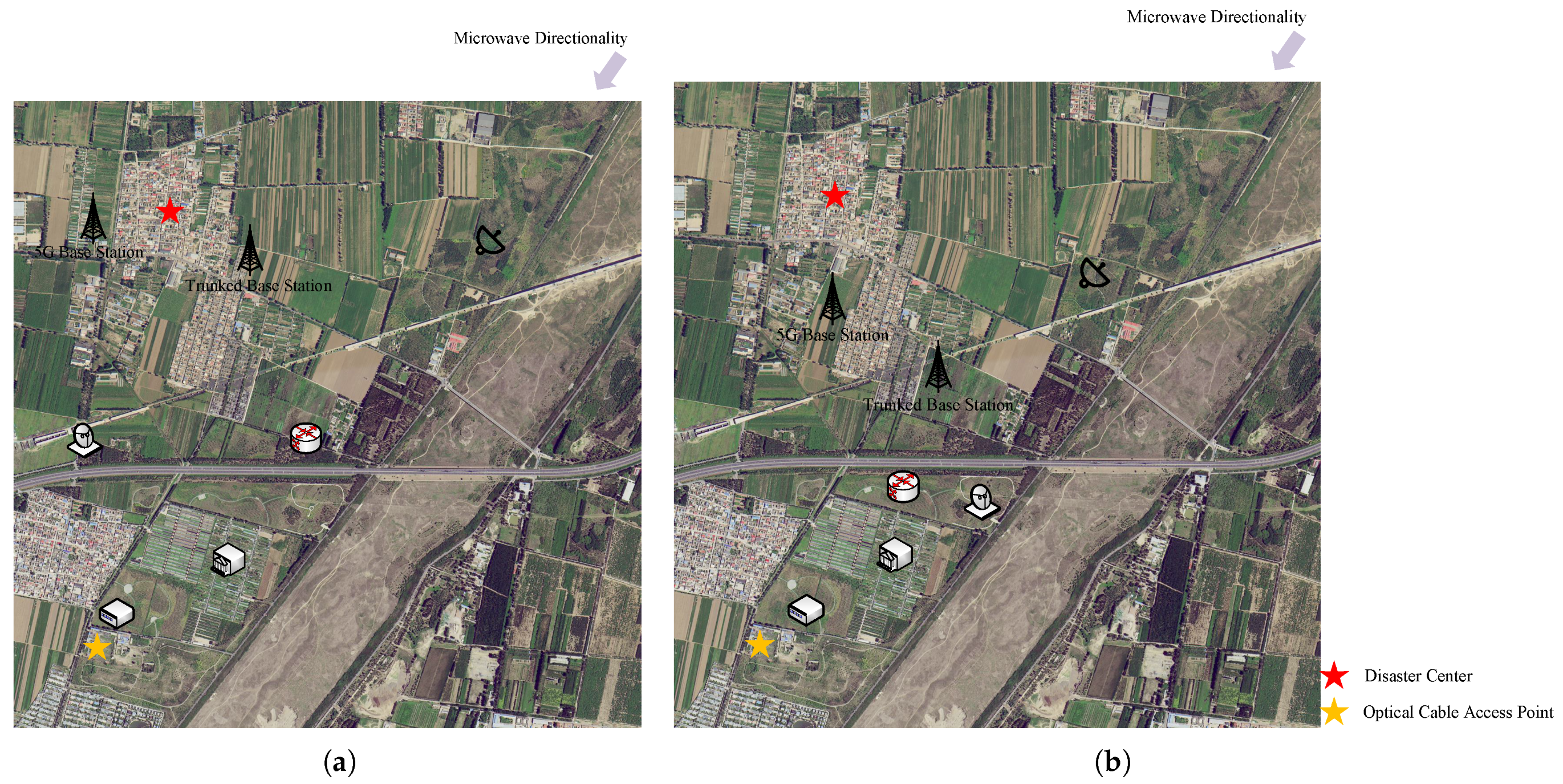
To provide a more intuitive comparison of performance differences in emergency communication network deployment between the proposed model and the greedy strategy, we conducted a visual comparative analysis of deployment results generated by both algorithms. To ensure experimental comparability, both groups adopted identical parameters, including microwave direction, disaster center, optical cable access point, on-site command center, and deployment terrain.

As illustrated in Figure 6, the two strategies demonstrate significant differences. The greedy strategy focuses solely on optimizing individual deployment elements, leading to a fragmented distribution pattern of deployed components. This over-dispersed layout not only increases inter-node connectivity costs but also substantially raises the complexity of network topology construction. In contrast, reinforcement learning demonstrates advantages in holistic network performance optimization. By sacrificing partial local optimality of 5G and microwave nodes, it achieves lower overall deployment difficulty and a more rational topology structure. This trade-off strategy effectively balances conflicting requirements between network efficiency and deployment feasibility. The comparative analysis validates the systematic optimization capability of the proposed model in complex scenarios, with its decision-making pattern better aligning with the practical emergency communication network deployment principle of “global optimality prioritized over local optimality”.

In summary, based on all experimental results, the combination of the DDQN algorithm and ResNet architecture demonstrates superior decision-making performance in this task. This hybrid approach enables more efficient and stable completion of dynamic emergency communication resource deployment tasks while exhibiting stronger practical application potential.

5.2.2. Impact of Hyper-Parameters

To further investigate the impact of different hyperparameters on model performance, we designed systematic comparative experiments, focusing on the functional mechanisms of three key parameters: experience replay buffer size, learning rate, and target network update interval.

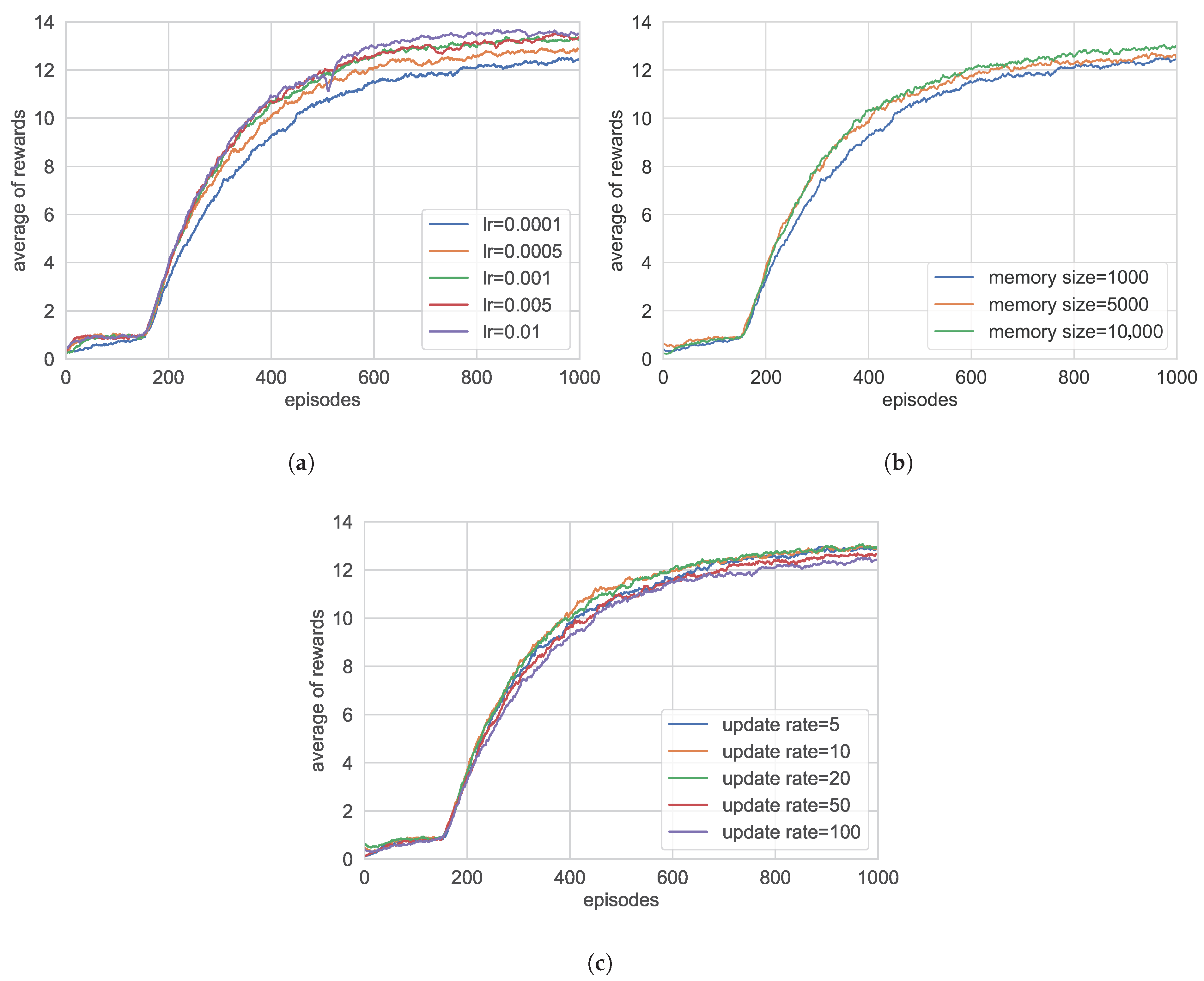
The sensitivity analysis of the learning rate reveals a clear convergence boundary effect, as illustrated in Figure 7a. When the learning rate is too low (lr = 0.0001), insufficient weight updates slow down convergence; conversely, an excessively high learning rate (lr = 0.01) causes parameter oscillations, leading to significant fluctuations in the average reward during the convergence process. This phenomenon confirms the strong constraint of the learning rate on the gradient descent path in reinforcement learning. Therefore, during the training process, the training effect is the best when the learning rate is set to 0.005 or 0.001.

As shown in Figure 7b, by comparing the effects of different experience replay capacities on the agent’s average global reward, we find that when the storage space is set to 10,000, the larger sampling range effectively breaks data correlation, resulting in significantly better training stability compared to other capacity configurations. However, it should be noted that an excessively large experience replay buffer can lead to a sharp increase in video memory usage. Experimental results show that when the storage space exceeds the system’s memory threshold, a dynamic data replacement strategy must be adopted to maintain training efficiency.

As shown in Figure 7c, experimental results regarding the target network update interval indicate that adopting a longer update cycle (update rate = 100) slows down the model’s convergence speed, while an excessively short update cycle (update rate = 5) also hinders convergence. This finding is consistent with the theoretical analysis of policy synchronization in reinforcement learning. Specifically, within the deep reinforcement learning framework, the update frequency of the target network directly affects the synchronization level between the policy network and the target network, thereby influencing the stability and efficiency of the overall learning process. When the update interval is too long, the target network parameters lag behind those of the policy network, leading to significant estimation bias in the target values and weakening the guiding effect during learning, which in turn reduces the convergence speed. Conversely, if the update interval is too short, the frequent changes in the target network result in unstable learning signals, making the training process prone to oscillation and negatively affecting the model’s stable convergence. As a result, setting the update rate to 10 yields optimal convergence behavior.

6. Conclusions

In the paper, we address the critical challenges in emergency communication network (ECN) deployment by proposing a deep reinforcement learning (DRL) framework with a fully convolutional value network architecture. Emergency communication networks face significant complexities in disaster scenarios, including dynamic environmental changes, heterogeneous infrastructure availability, and the urgent need for rapid deployment. Traditional rule-based and heuristic approaches struggle to adapt to these dynamic conditions, often resulting in suboptimal resource allocation and delayed response times, while manual deployment is constrained by limited expertise and prolonged decision-making processes. The proposed architecture leverages end-to-end feature extraction to overcome the “curse of dimensionality” inherent in topology planning, enabling multi-dimensional spatial decision-making that accounts for factors such as network resilience, resource constraints, and coverage requirements. By integrating deep value networks, the framework dynamically evaluates potential hub placements in real-time, prioritizing critical areas while balancing trade-offs between connectivity, latency, and energy efficiency.

Experimental results demonstrate that the proposed method is highly effective in planning emergency communication hub elements, achieving faster convergence speed and more robust performance in complex environments compared to traditional strategies. This approach aligns with the emerging trends in deep reinforcement learning-driven network optimization, which has shown promise in addressing challenges such as resource scheduling in aerial-assisted networks and resilient routing in hybrid sensor systems. By overcoming critical limitations in scalability, adaptability, and operational efficiency under high-stress disaster conditions, this research contributes to the deployment of emergency communication networks. Furthermore, with appropriate adjustments to the establishment function and input states, the method can be adapted to other scenarios, such as logistics distribution center site selection and urban infrastructure planning, highlighting its strong generalization capability and broad applicability.