Abstract
Computational fluid dynamics (CFD) has aided the development, design, and analysis of hypersonic airbreathing propulsion technologies, such as scramjets. The complex flow field in a scramjet isolator has been the subject of intense interest and study for several decades. Many features of this flow field also occur in supersonic wind-tunnel nozzles and diffusers. Computational analysis of these topics has frequently provided immense insight into the actual functionality and performance. Research presented in this work supports scientific investigation and understanding of a less-researched topic, which is shock–shock interference and interaction with the boundary layer in supersonic internal flows, as well as the passive control of its adverse effects to prevent the onset of unstart in a scramjet isolator. This computational investigation is conducted on a backpressured isolator and a modified three-dimensional shock-tube to represent a scramjet isolator with ram effects provided by high-pressure gas and high-speed flow provided by a supersonic inflow. Computational results for the backpressured isolator have been validated against available measured time-averaged wall pressure data. The modified shock-tube provided an opportunity to study the shock–shock interference and shock–boundary-layer interaction effects that would occur in a scramjet isolator or a ram-accelerator when the high-speed flow from the inlet interacted with the shock produced due to the combustor pressure traveling and meeting in the isolator. An assessment of wall cooling effects on these phenomena is presented for both the backpressured isolator and the modified shock-tube.
1. Introduction
A scramjet engine provides high-speed airbreathing propulsion for hypersonic vehicles. Major segments of a scramjet engine internal flowpath consist of an inlet, an isolator, a combustor, and a nozzle. A notable differentiating feature of scramjets from gas-turbines is that air compression is achieved by successive shocks in the inlet without the use of any rotating parts, such as a multi-stage compressor [1,2,3,4]. One of the primary issues involving scramjet engines is the unstart and the resulting limitations of operability, which have been discussed in several papers [5,6,7,8,9,10]. Unstart can occur in the inlet, isolator, or combustor. The isolator is a conduit of either rectangular or circular cross-section that separates (i.e., isolates) the inlet from the combustor. Throughout the combustion process, heat is released, leading to a pressure increase in the combustion chamber. The pressure rise in the combustor induces an adverse pressure gradient in the isolator, which results in thickening of the boundary layer, formation of the pseudo-shock-train in the isolator, and could also result in separation of the boundary layer, especially if the boundary layer is laminar [10]. In addition, high-speed flow entering the isolator from the inlet interacts with the pseudo-shock-train and separated or thickened boundary layer, leading to the generation of shock interference as well as flow instability in the isolator. The role of the isolator in the scramjet engine is shown in Figure 1.
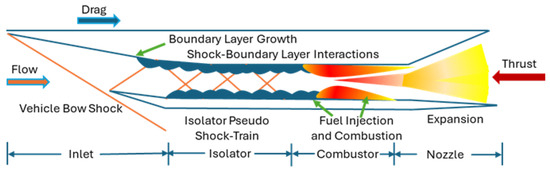
Figure 1.
Schematic of scramjet flow-path and position of the isolator [10].
Shock–shock interference is defined as the phenomenon that occurs when two or more shock waves of different types and strengths intersect with each other. The shock interference can manifest in terms of planar and curved shock interaction and/or curved–curved shock interaction. However, each type of interference can result in a sudden increase in surface pressure and heat transfer and can induce boundary-layer transition [11,12,13,14]. Edney [15] performed a comprehensive investigation of curved–curved shock interactions. This was carried out through experimental and theoretical studies of the impingement of an oblique shock on a bow shock formed in front of a blunt body. From this work, Edney coined the six types of distinct shock interference, titled Type I to Type VI, each type with a unique flow structure, which depend upon the intensity and direction of the intersecting shock waves. Most of the studies conducted on the investigation of shock interference have focused on external flows over conical shapes in the form of a blunt nose or round leading edges. However, shock interference can also occur in the scramjet flow path due to shocks generated by different parts in the flow field, leading to increased pressure and heating, which can affect the onset of unstart in the scramjet flow path. Investigation of shock interference in a supersonic internal flow path has not been reported in the open literature. The research presented in this paper addresses this technical gap. Shock-interference and interaction of shocks with boundary layer can lead to sudden unsteady disruption of the flow, resulting in the onset of “unstart” of the engine [8,10], depending upon a combination of Reynolds number, magnitude of adverse pressure gradient, extent of boundary-layer separation, flow unsteadiness, turbulence intensity, and the boundary-layer thickness, and types of shocks interacting with each other and the boundary-layer.
Due to the detrimental effects of unstart, the topic has been widely studied, but many challenging aspects remain open, including the root cause of the onset of unstart and how to prevent the onset of unstart, so that the operability envelope of modern scramjets can be maintained and expanded. Onset of unstart in the full scramjet flow path during flight can occur due to additional factors including pressure perturbations at the isolator exit due to combustion dynamics, distortion of the incoming inlet flow due to an unexpected change in the angle of attack or the ingestion of exhaust gases, and/or changes in wall conditions such as damage to or removal of thermal protection coating. In order to prevent unstart and maintain operability, active and passive control methods have been developed for the mitigation of the onset of scramjet isolator unstart by preventing any sudden disruption of the flow in the isolator by controlling the effects of shock interference and interaction with the boundary layer on the pseudo-shock-train in the isolator. SBLI is shown at the start of the shock-train in Figure 2.
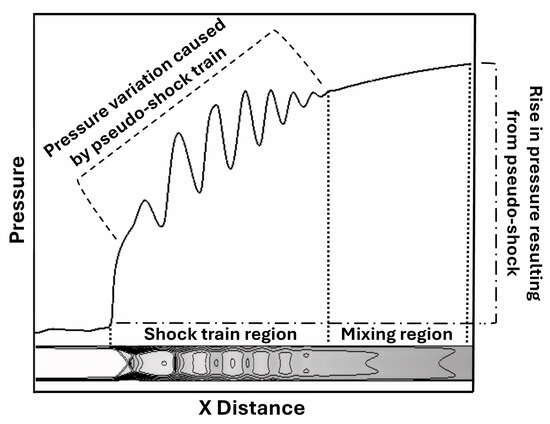
Figure 2.
Schematic of shock-train with trailing mixing region.
By controlling the shock-interference interaction with the boundary layer, the pseudo-shock-train in the isolator can be controlled. There are many methods of shock-train control by controlling the SBLI. The active boundary-layer control methods include: boundary-layer suction/bleed, micro-jets, plasma jets, and air vortex generators. Vortex generator implemented upstream of the interaction [16], creates a vortex, energizing the flow, and ultimately delaying the separation. Boundary-layer suction or bleed removes the low-momentum fluid closer to the wall by a mass flow outlet, leaving only higher-momentum fluid within the flow. The higher-momentum fluid is less likely to separate; therefore, flow separation is also delayed in this case, ultimately reducing the adverse consequences of strong SBLI [17]. Boundary-layer suction has been proven by Sethuraman et al. [18] to reduce shock-train oscillations and the length of the shock-train. Passive control methods include: porous cavity, splitter plate, bumps, recirculation cavity, and wall cooling. Theoretically, it has been shown that wall cooling can reduce wall boundary-layer thickness and therefore, can reduce the potential of boundary-layer separation due to SBLI phenomena.
1.1. Objectives
The major objective of the research presented in this work is to build scientific understanding of shock-interference interaction with the boundary layer in supersonic internal flow path and passive control of the adverse effects of such interactions to prevent the onset of unstart in a scramjet isolator. Specific objectives are as follows:
- To perform code verification and model validation with existing experimental data.
- To perform computational investigations of shock interference by utilizing both scale-resolving computational methods, such as large eddy simulation, and mean flow resolving methods, such as unsteady Reynolds Averaged Navier–Stokes method.
- To compare the effect of wall cooling on boundary-layer control for both backpressured isolator and modified shock-tube with crossflow.
1.2. Technical Approach
Computational fluid dynamics (CFD) is a useful approach for developing an in-depth understanding of such a complicated and unique flow field observed in the scramjet isolator. There are multiple approaches to solve the Navier–Stokes equations, including Reynolds Averaged Navier–Stokes (RANS) and a scale-resolving approach called Large Eddy Simulation (LES). RANS approach has a variation called Unsteady-RANS (URANS) in which the periodic oscillations of mean turbulent flow with time can be simulated. URANS does not resolve turbulent fluctuations, for which closure models have been developed to be utilized in both RANS and URANS approaches. RANS methods resolve the mean flow field and require modeling of the complete energy cascade and turbulent dissipation by utilizing zero, one-, two-, or three-equation models for the turbulence transport and dissipation phenomena. These equations are known as turbulence closure models. Multiple turbulence closure models of increasing complexity have been developed to capture the turbulent flow field for both external and internal aerodynamics with RANS and URANS as documented on NASA Langley Turbulence Modeling repository [19]. RANS has been a computationally affordable practical tool for the design, evaluation, planning, and assessment for most hypersonic flight applications, as well as high-speed wind-tunnel tests, but no single model has shown predictive capability, especially when applied to a range of flow phenomena encountered in hypersonic flows [20].
In order to observe turbulence scales and related characteristics of the turbulent flow, a Large Eddy Simulation (LES) method can also be used. LES is a higher fidelity and scale-resolving method, which requires a higher computational cost. However, it can resolve all turbulence above the Kolmogorov length scale () and only models the energy dissipation at the smallest turbulent scales near the Kolmogorov length scales. LES enables filtering of the Navier–Stokes equations so that scales of turbulence up to the dissipation scale can be solved by numerical solution of these equations. Turbulence closure of certain terms in the transport equations is still required, but it only models the dissipation of energy at the smallest scales of turbulence. In contrast, RANS turbulence closure models the energy cascade process in a turbulent flow.
In order to perform LES simulation, the Kolmogorov length scale and the associated Kolmogorov time scale have been calculated. The time step utilized for the simulation was set to the Kolmogorov time scale. Calculations of and are shown below. Equation (1) is used to find the Reynolds number, , of the flow, where is density, u is velocity, D is characteristic length, and is dynamic viscosity.
Equation (2) calculates the time for the flow to travel the length of the fluid domain.
Using both of those values, Equations (3) and (4) can be applied to obtain the Kolmogorov time and length scales, respectively.
1.2.1. Computational Methods and Mesh
Both LES and RANS represent two distinct approaches for turbulence modeling and provide different fidelity in resolving the energetics of turbulence. While LES resolves turbulent energy transport and requires modeling of turbulence dissipation only, the computational cost associated with it is multiple orders of magnitude higher than the RANS approach. Therefore, it is significant that RANS should be compared with LES to determine its ability to capture certain flow phenomena related to shock interference and interaction with the boundary layer. Such a comparison provides guidance to the vehicle designers on computational cost versus the value proposition of using either method.
A standard computational investigation includes verification and validation (V&V) steps. Verification is performed to quantify the accuracy of the numerical methods utilized in the calculations, and validation is performed to assess the applicability and validity of the closure models that are utilized in the calculations. In other words, code verification establishes if the CFD code is solving the equations correctly, and model validation is utilized to establish if the CFD code is solving the correct equations. Both code verification and model validation have been performed, and the results are presented in the following sections. Three geometries have been considered in this paper:
- Verification: A one-dimensional shock-tube problem, also known as Sod’s shock-tube problem [21] has been chosen for verification as the exact solution for this problem is known.
- Validation: A backpressured isolator from NASA Langley Research Center’s Isolator Dynamics Research Lab [22] has been utilized for model validation since the time-averaged measured wall pressures have been available.
- Demonstration and Investigation: Once the computational code and model have been verified and validated, a modified shock-tube (a shock-tube with square cross-section and open ends) has been utilized to investigate shock interference and interaction with boundary-layer phenomena. This shock-tube was modified to generate the effects of air entering an isolator from the inlet, and a pseudo-shock-train was generated due to the combustor backpressure and thermal choking.
1.2.2. Turbulence Closure Models
As mentioned earlier in this paper, there are two computational approaches to solve the turbulent flow field, called LES and RANS. These methods provide different fidelity in resolving the energetics of turbulence, with RANS requiring modeling of energy transport and dissipation at all turbulence scales, whereas LES requires modeling of turbulent dissipation occurring near Kolmogorov scales. However, it has become increasingly known that RANS turbulence closure models demonstrate significant variability in terms of predictions of shock physics.
While many turbulence closure models are available for RANS, a two-equation k-omega model called Wilcox 1998 [23] was utilized for turbulence closure in this work. In this model, turbulence closure is achieved via the formulation of two equations for turbulent kinetic energy, k, and specific dissipation rate, omega. This model has been found to predict the behavior of attached compressible boundary layers subjected to adverse pressure gradients more accurately than traditional turbulence kinetic energy dissipation rate models.
For LES, the Smagorinsky model [24] has been utilized to close the anisotropic residual-stress tensor, which is represented as a product of fluid velocity gradient and a modeling term known as eddy viscosity (sometimes referred to as turbulent viscosity). Eddy viscosity is calculated by assuming that it is proportional to the product of the square of the mesh size and the magnitude of the velocity gradient. The proportionality constant is typically between 0.1 and 0.2, depending on the flow evolution. This is the simplest model and has been proven to perform reasonably well. The Smagorinsky model assumes that there is equilibrium between the energy production and dissipation at the small scales. There are a few shortcomings with the Smagorinsky model, one of which is that there is no provision to account for energy transfer from the smallest scales to the larger scales. However, there is no evidence that such a transfer is occurring in the problem addressed by the current work. Another shortcoming is that there is no clear guidance on the value of the proportionality constant utilized in eddy viscosity calculations, which casts a degree of modeling uncertainty. Despite this issue, the Smagorinsky model is still a simple and reliable model for LES, and therefore, it has been utilized in this work.
2. Code Verification
Verification is needed to assess the accuracy of the numerical scheme for a relevant problem. In order to perform verification, one-dimensional Sod’s shock-tube problem [21], also known as the initial value problem for the linear advection equation, was utilized. Two tests were performed with different initial conditions. The numerical solution was compared with the exact solution. The overall setup for this problem is shown in Figure 3. The mesh and numerical methods used are shown in the next subsection.
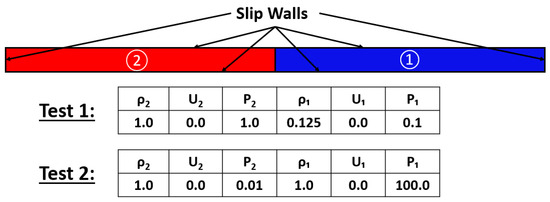
Figure 3.
Computational domain and initial conditions for one-dimensional Sod’s shock-tube.
2.1. Mesh
A structured mesh was utilized for code verification with a total mesh count of 1,587,808. The grid was uniform with a cell size of just over 20, where is the Kolmogorov length scale, calculated by Equation (4). As described earlier, the Kolmogorov scale is the smallest length scale of turbulence at which turbulent kinetic energy is dissipated into thermal energy by the fluid viscosity. In this case, Kolomogorov length scale, was equal to 2.32 × m, so the mesh used a cell size of 5.3 × m. Mesh resolution affects numerical error, and the finest mesh was utilized for code verification to establish numerical error. If there is a significant difference between the numerical and exact solutions, then further mesh refinement will be needed. As shown in the following sections, it was found that there is a close comparison between numerical and exact solutions, which means that the combined discretization and numerical method error due to mesh resolution is negligible. Based upon such observation, it can be concluded that the mesh resolution was sufficient in the context of reducing the numerical error to a minimum. Therefore, no further mesh refinement is needed from a numerical error perspective for the shock-tube problem.
2.2. Numerical Methods
The purpose of code verification is to quantify the accuracy of the numerical methods and quantify the numerical error that arises due to discretizations of partial differential equations over a mesh, the numerical methods such as inviscid flux reconstruction scheme, flux limiters, discretizations of viscous fluxes and time marching methods that are utilized in the CFD code. For this reason, an initial value problem, which does not contain turbulence modeling or viscous terms, was selected for this process. Therefore, the walls of the shock-tube were kept as slip walls, which do not require the terms related to viscosity (both kinematic and turbulent). An elliptic region solver with an active status was utilized. Reconstruction of cell interface variables achieved via the Monotone Upstream-Centered Scheme for Conservation Laws (MUSCL) [25]. A 3rd-order upwind-biased scheme (MUSCL parameter, k = ) was used to reconstruct the flow variables. This scheme used the Koren TVD limiter. The inviscid flux scheme applied in this case was an Edwards Low Dissipation Flux Split Scheme (LDFSS). A Runge–Kutta scheme was used to update equations. A fixed time step of 1.0 × s was implemented. Koren TVD limiter, van Albada limiter, and van Leer limiter were all used in the second verification test. An incomplete LU (ILU) decomposition scheme was used with a CFL number for pseudo-time marching.
2.3. Results of Code Verification
The results from the first code verification study are shown in Figure 4. In this figure, the results from the exact solution, which was obtained using the method of characteristics, and the results from the CFD solution of the same equation are shown at time = 0.25 s. Specifically, these plots show the comparisons between the numerical and exact solutions of density, axial velocity, pressure, and internal energy. A close comparison between these results is shown, demonstrating that the numerical methods are able to capture the formation and propagation of normal shock, expansion fan, and compression waves.
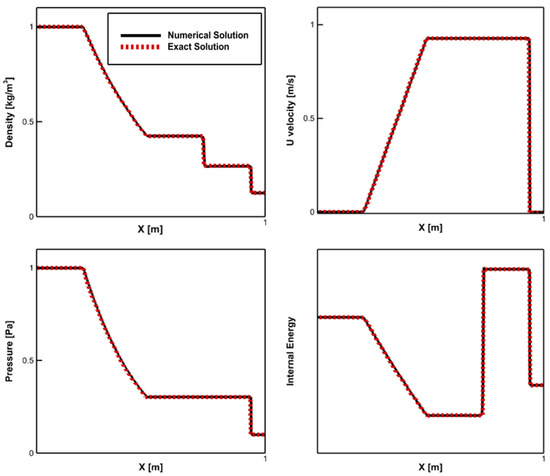
Figure 4.
Code Verification: Comparison of numerical results with exact solution at t = 0.25 s.
The results from the second code verification study are shown in Figure 5. In this figure, the results from the exact solution and the CFD solutions of the same equation are shown at time = 0.035 s. These plots show the comparisons between the exact and numerical solutions using Koren TVD, van Albada, and van Leer flux limiters. Comparisons of density, axial velocity, pressure, and internal energy are shown. The results varied slightly between the different limiters, but they were equal in terms of comparison with the exact solution.
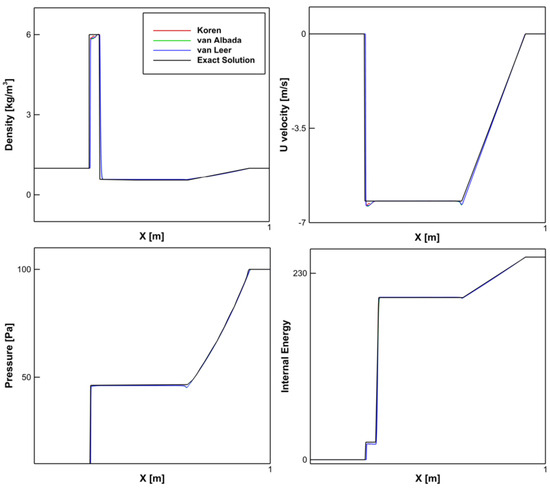
Figure 5.
Code Verification: Comparison of numerical results with exact solution at t = 0.035 s.
Close comparisons between the numerical and exact solutions showed that the combined discretization and numerical method error due to mesh resolution is negligible.
3. Model Validation
A backpressured isolator with a Mach 2.5 inflow was utilized as a configuration to perform model validation. The measurements of wall pressure at multiple axial locations were obtained at the Isolator Dynamics Research Laboratory (IDRL) at NASA Langley Research Center (NASA LaRC) [22]. Specifications of this facility, as well as a detailed description of the setup used (for the computational and experimental studies), can be found in the work by Baurle et al. [22]. These data were utilized for model validation in the current paper. In the previous work of Acharya et al. [9], a comparison between computed wall pressures and NASA LaRC IDRL calculations done by Baurle et al. [22], for this experimental set, has been presented. It should be noted that multiple boundary conditions for this setup have been published, but in this work, the boundary conditions for the computational investigations were obtained from those published in Acharya et al. [9].
In the published experimental work, a backpressure of 304.51 kPa was obtained from measurements (by averaging the 20 surface pressure measurements taken around the periphery of the isolator duct at the x = 22 h station) when a pressure plug was used at the isolator exit. Likewise, the time-averaged values of wall pressure obtained from sensors mounted at multiple locations were reported, which have been utilized for comparison with the time-averaged RANS calculations of the same setup. It is likely that the implementation of a pressure plug to generate backpressure at the isolator exit could have contributed to initial transience and low-amplitude oscillations throughout the steady-state operation and resulted in experimental uncertainty. However, the uncertainty in experimental results and experimental error were not reported in the published data on the experimental case. Since time-averaged experimental data without error and uncertainty were reported, RANS was utilized for the simulation of the time-averaged flow field in this isolator.
3.1. Computational Domain and Mesh
The IDRL backpressured isolator was 24 inches long, 2 inches wide, and 1 inch high. The structured mesh dimensions for this isolator were 1000 × 80 × 104. The streamwise spacing was held fixed at 0.02 × isolator height (h) for the front half of the isolator to resolve the region where the shock-train was expected to reside, and was stretched in the second half of the isolator to a value of 0.05 h at the isolator exit. The maximum grid spacing in the vertical (y) and spanwise (z) directions was 0.02 h (adjacent to the planes of symmetry). The grid was split into a total of 1488 grid blocks with 95% load balance on 720 processors. Grid sensitivity studies were performed with three structured grids (Grid 1: 1.3 million, Grid 2: 10 million, and Grid 3: 85 million). It was found in a previous work by Baurle et al. [22] that grid resolution with Grid 2: 10 million structured produced the same results as Grid 3: 85 million structured mesh, within measurement error. Therefore, it was determined that Grid 2, with 10 million grid points, is appropriate for this demonstration. The isolator schematic with the inflow, outflow, and symmetry planes is shown in Figure 6. In this work, the facility nozzle was not simulated, but the isentropic nozzle exit flow conditions were utilized as the boundary condition.
Figure 6.
Computational Domain: Schematic of quarter section of the backpressured isolator with boundary conditions.
3.2. Numerical Methods
All computational results were obtained using the Viscous Upwind aLgorithm for Complex flow ANalysis (VULCAN) Navier–Stokes code. Pseudo-time-step advancement was achieved using an incomplete LU factorization scheme with planar relaxation. A Courant-Friedrichs-Lewy (CFL) number of 100 was utilized. The inviscid flux differencing was evaluated using a Low-Diffusion Flux Splitting Scheme of Edwards, with cell interface variable reconstruction achieved via the k = Monotone Upstream-centered Scheme for Conservation Laws (MUSCL) [25]. The Koren flux limiter was utilized to avoid spurious oscillations during this reconstruction process. The viscous fluxes were evaluated using 2nd-order accurate central differences with the viscosity of air computed from Sutherland’s Law [26]. The molecular and turbulent Prandtl numbers were set to 0.72 and 0.9, respectively.
For the model validation study, an adiabatic no-slip condition was applied at all solid surfaces. An extrapolation boundary condition was used at the isolator exit for all variables (except for static pressure). The static pressure was set to 304.5 kPa, which was a value obtained by averaging the 20 surface pressure measurements taken around the periphery of the isolator duct at the x = 22 h station, as mentioned earlier in this paper. Details regarding the isolator dimensions, mesh, solution methodology, and turbulence modeling are summarized in Table 1.

Table 1.
Numerical methods, mesh, and model specifications utilized for model validation.
In the experimental work presented in Baurle et al. [22], facility flow conditions used for model validation were presented. These values are shown in Table 2 alongside the flowfield conditions used in this current work. It should be mentioned that this 2013 work contained multiple facility conditions. However, in a later publication of Acharya et al. [8], the conditions corresponding to the model validation were presented, which are utilized in this work. Due to the absence of a nozzle in this work, isentropic relations were utilized to calculate the total pressure and temperature at the nozzle exit using the plenum conditions reported in earlier work. The nozzle exit conditions served as isolator entrance conditions in this current work. All variables are consistent between the two, other than the minor variation in total temperature at the entry.

Table 2.
Flow variables.
3.3. Results
The computed static pressure along the top-wall centerline and side wall centerline is compared with the experimental results shown in Acharya et al. [22] in Figure 7. There are several metrics for comparing these two results, including: (1) location of the foot of the pseudo-shock-train, (2) length of the pseudo-shock-train, (3) maximum pressure rise across the isolator walls, and (4) number of oblique shocks formed in the pseudo-shock-train. An analysis of the computational results was performed for both centerlines. The shock location, max pressure rise, and shock-train length are displayed in Table 3. On the top wall, the shock location was 0.52 inches farther downstream in this work. This is approximately 2% of the total isolator length. The shock location on the side wall was 0.86 inches farther downstream in the current work. This is approximately 3.5% of the total isolator length. The maximum pressure rise and the number of oblique shocks on the top-wall centerline are equal between the two sets of results.
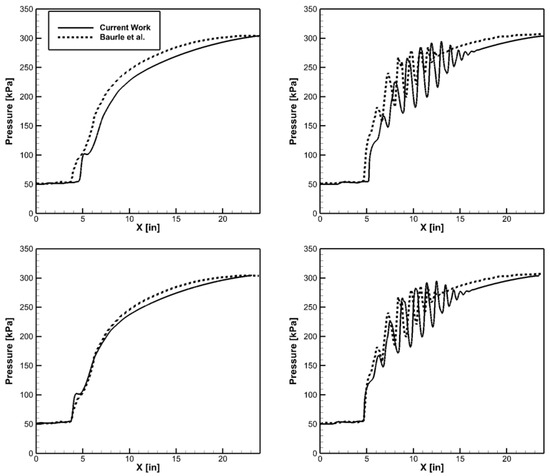
Figure 7.
Model validation with IDRL isolator—static pressure on side wall centerline (left) and top-wall centerline (right), Baurle et al. [22].

Table 3.
Quantitative comparison between measured and computational results.
To compare the pseudo-shock-train length, the computed results were translated so that the foot of the shock-train aligns with the measured data. This is shown in Figure 7, and consistency with the validation data is achieved. The side wall pressure has very good agreement with the validation case. The top-wall centerline static pressure distribution shows that the calculated shock-train has a similar structure to the validation data, but it is slightly longer. The slight differences can be attributed to two sources: first course could be the experimental error and uncertainty, which were not reported in the published data. Secondly, the elimination of the facility nozzle in front of the isolator results in a change in the incoming flow profile, which has a small effect on the shock location and shock-train structure. Within the typical experimental error and uncertainty, and the error arising due to differences between the inflow turbulent flow profile between calculations and experiments, there is a very close comparison between the measured and computed wall pressures.
From this computational investigation, the detailed flow features that are relevant to the understanding of shock–boundary-layer interaction are shown in Figure 8. These plots show the side wall and slices at multiple streamwise locations. The static pressure contour plot in Figure 8a clearly shows the pseudo-shock-train in the middle of the backpressured isolator. An investigation of the eddy viscosity ratio in Figure 8b shows that higher turbulent viscosity is generated at the corners where corner shocks originate. These regions grow as the flow progresses and eventually merge, affecting the centerline. Additionally, the formation of separation shocks can be observed in the divergence of the velocity contour in Figure 8c. The separation shocks appear on the side walls slightly upstream of where they appear on the centerline. The unfavorable flow separation can be observed in the velocity contour plot in Figure 8d. There is significant reverse flow occurring at the corners, and a noticeable separation bubble is formed at the centerline.
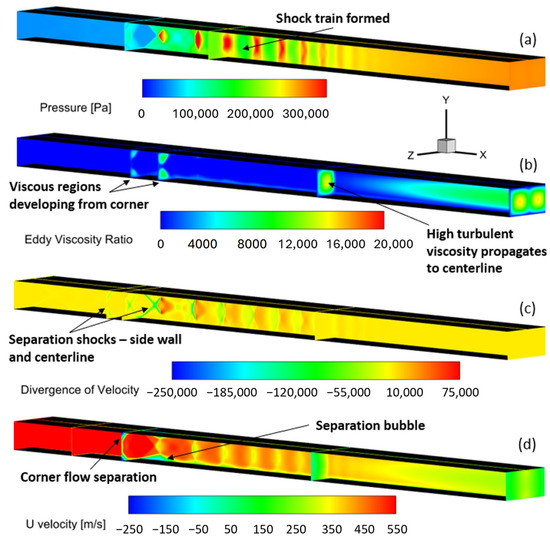
Figure 8.
Isolator contours: (a) static pressure, (b) eddy viscosity ratio, (c) divergence of velocity, (d) axial velocity.
3.4. Effect of Wall Cooling
Shock-induced flow separation could result in several adverse effects on scramjet performance, including loss of aerodynamic and propulsive efficiency and onset of unstart. Due to these reasons, it is important to control or reduce the boundary-layer separation and/or situate the pseudo-shock-train farther from the isolator entrance (which will be the inlet exit in a scramjet). As shown previously in Figure 8, a significant separation bubble is formed at the top and bottom walls along the centerline of the isolator. There is a theoretical basis that wall cooling could result in reducing the boundary-layer thickening and, therefore, could impact boundary-layer separation. To investigate this further, computational investigations were performed, and the results are presented in this section. All conditions were kept the same in this study as the model validation computations shown above, with the exception of the wall boundary condition, which was changed from adiabatic walls to isothermal walls at 150 K static temperature. Detailed flow features that are relevant to the understanding of shock–boundary-layer interaction are shown in Figure 9.
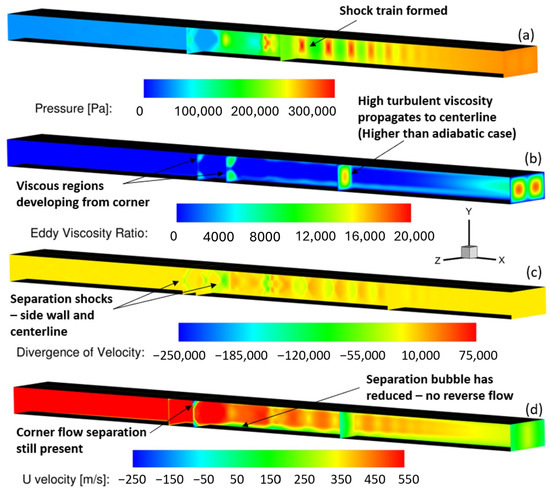
Figure 9.
Isolator contours with isothermal walls: (a) static pressure, (b) eddy viscosity ratio, (c) divergence of velocity, (d) U-Velocity.
These plots show the side wall and slices at multiple streamwise locations. The isothermal walls resulted in the pseudo-shock-train situating farther downstream the isolator than in the case with adiabatic walls. In addition, a higher eddy viscosity ratio was generated. The isothermal walls had a very positive effect on the flow separation observed in the case with the adiabatic walls. Corner flow separation is visible in both cases, but the separation bubble is significantly reduced, and there is no reverse flow present in this area with the isothermal walls. Furthermore, static temperature contours were also evaluated for both cases. The effect of the wall cooling in this contour is very clear. As shown in Figure 10, there is a high temperature region associated with the separation bubble in the case with adiabatic walls. As the Mach number of the flow decreases due to the pseudo-shock-train, much of the kinetic energy is transferred to thermal energy, resulting in the high temperature zone at the walls. With the isothermal walls with temperature fixed at 150 K, the boundary-layer growth is less dramatic, which reduces the size of the separation bubble, allowing for the flow to maintain more speed than that with adiabatic walls. With this maintained flow speed, much kinetic energy is preserved, resulting in lower conversion into thermal energy.
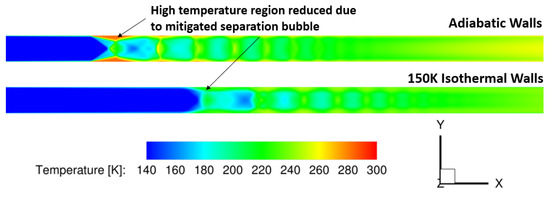
Figure 10.
Effect of cooled walls on static temperature.
A deeper investigation into the physical effects of wall cooling is shown in Figure 11. From this figure, it can be observed that the divergence of velocity is lower in the initial portion of the pseudo-shock-train when the walls are cooled.
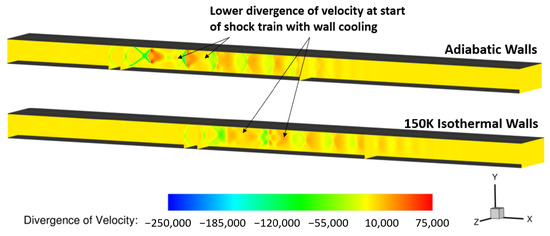
Figure 11.
Effect of wall cooling on divergence of velocity.
The flow improvement caused by the isothermal wall cooling is illustrated in Figure 12, through the mass flux at the isolator exit. It is very clear that the mass flux distribution in the isolator cross-section is more uniform after the wall cooling has been implemented, particularly at the centerline. A more uniform profile can be observed with isothermal walls, compared to adiabatic walls. Mass flux is another good metric to observe for this study, as an increase in mass flux leaving the isolator can be attributed to decreased boundary-layer effects, which is a result of the wall cooling. Higher mass flux at the exit is desirable in this system to optimize performance.
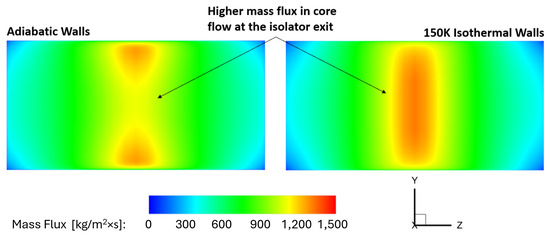
Figure 12.
Effect of wall cooling on mass flux at isolator exit.
The static temperature at the exit is also shown in Figure 13. These results show that the wall region is much warmer with adiabatic walls, as expected. The core flow is also cooler in the case of isothermal wall cooling. These results show just how large the impact of the walls can be on the entire flowfield. With adiabatic walls, the thermal energy of the system is growing. With the numerical implementation of wall cooling, less energy is converted to thermal, resulting in the sustained kinetic energy needed for the system to optimally function.
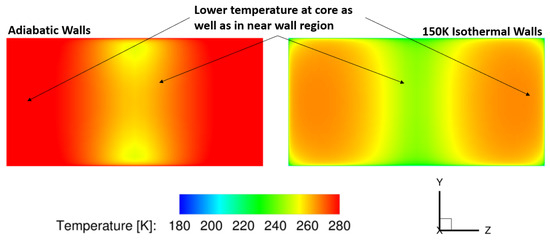
Figure 13.
Effect of isothermal cooled walls on static temperature at isolator exit.
An observation of the pressure at the walls of the isolator very clearly shows the effectiveness of the isothermal walls on the flow physics within the domain. This can be shown in Figure 14. The maximum pressure rise within the shock-train on the top wall is 84.4 kPa, compared to the 100.26 kPa shown with adiabatic wall, providing a maximum pressure rise reduction of over 15%. The shock-train along the top wall is about 12.5% shorter with the wall cooling implementation. The shock-train was measured at 9.85 inches with cooling, while it is about 11.26 inches without it. Additionally, the shock-train is shown to initiate approximately 3.5 inches further downstream along both the side and top walls. This is beneficial for an isolator as it will reduce the risk of the shocks backing into the inlet if some pressurization were to occur downstream.
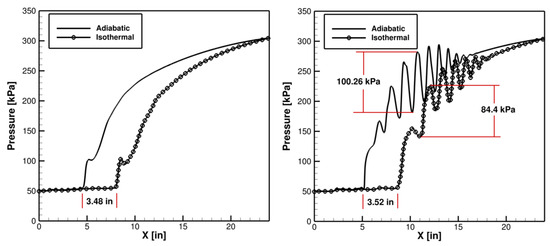
Figure 14.
Effect of isothermal cooled walls side (left) and top (right) centerline wall pressure.
4. Shock Interference in Modified Shock-Tube
The IDRL configuration provided model validation in terms of comparison between measured and computed steady-state wall pressure values on the side-wall centerline and top-wall centerline. Such a comparison provided a significant insight into the ability of models utilized in computational code to capture key shock-physics metrics. However, the insight into the detailed temporal evolution of shock physics and the impact of wall cooling to control undesirable phenomena could not be obtained from the above case. In order to assess processes such as shock interference and the ability of wall cooling to mitigate the adverse effects of shock interference and shock–boundary-layer interactions under conditions at higher Mach numbers, a modified shock-tube was utilized. Since RANS only captures the mean flow characteristics, and a study of the temporal evolution of shock physics was desired, LES was utilized as it has the capability of resolving scales. Companion simulations with Unsteady-RANS (URANS) are also presented for comparison between URANS and LES methodologies in the context of their abilities to capture the transient shock physics.
As mentioned earlier, a typical Sod’s shock-tube consists of a one-dimensional inviscid flow in rectangular tube with closed ends containing two different fluids separated by a diaphragm in the middle of this shock-tube, where the fluid at the left side of this diaphragm (called the driver section) is typically at a higher pressure/density than the fluid at the right side of this diaphragm (called the driven section). Once the diaphragm breaks, a one-dimensional inviscid flow pattern including normal shock, compression waves, and expansion waves is established in the shock-tube. Sod’s shock-tube problem does not account for viscous effects or inflow/outflow from either end of the tube. In this work, the Sod’s shock-tube is modified so that shock–shock and shock–boundary-layer interactions that are likely to be observed in a scramjet isolator can be computationally investigated. This is accomplished by replacing the right and left walls with a high-speed velocity inlet and pressure outlet, respectively. This computational domain was 1 m long, with 0.03 m height and width. This configuration is longer and has a larger cross-section than the IDRL isolator utilized in the model validation study. It has a square cross-section versus the rectangular cross-section of the IDRL backpressured isolator. Initially, the driver and driven sections of the tube were set to 50 kPa and 5 kPa, respectively. The velocity inlet produced an incoming speed of 736.5 m/s or 3 Mach, with an outflow gauge and initial static pressure of 50 kPa, as well as a temperature of 150 K. A supersonic outflow boundary was specified so that the variables at the outlet were obtained using a 1st order extrapolation. The walls were adiabatic, no-slip walls. For the isothermal wall case, the wall temperature was fixed at 200 K. The flow entering the shock-tube created a boundary layer and a pseudo-shock-train. A schematic of the modified shock-tube with square cross-section is shown below in Figure 15. The interference of high-speed flow entering from the right-side end of this shock-tube with square cross-section and a right-traveling shockwave generated due to the high-pressure region in the left-half of this duct can also result in Richtmyer–Meshkov-like instability. Any perturbation on that interface is susceptible to the shock acceleration and is expected to grow in amplitude.
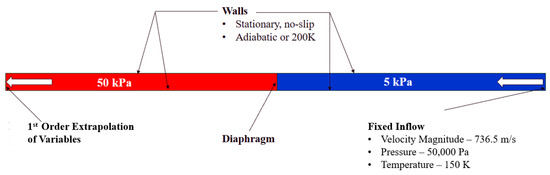
Figure 15.
Computational Domain: Modified shock-tube with a velocity inlet and pressure outlet.
4.1. Mesh
The mesh utilized for the computational investigations of this configuration was a three-dimensional, structured mesh with a cell size of 5.3 × m, which is approximately 20 times the Kolmogorov scale calculated previously, which is the same as the model validation study. As mentioned earlier, the computational domain was 1 m long and 0.015 m in both height and width. Since the flow is symmetric in both y- and z-planes, only a quarter section of the modified shock-tube was simulated with the front and top boundaries as walls and the back and bottom boundaries as symmetry. Doing so resulted in significant savings in computational time than if the entire geometry was used initially.
4.2. Numerical Methods
Similar to the model validation case, the region solver type was elliptic with an active status. Solution methodology was the same as presented in Table 1, other than the CFL number, which was held constant at 1.0 in this study. Sutherland’s Law was utilized for laminar viscosity calculations; the molecular and turbulent Prandtl numbers were constant at 0.72 and 0.9, respectively. The time step was obtained using the CFL number to determine a spatially varying time step. For LES, the Smagorinsky closure model was selected [27] and the time step was obtained using the global method. This means that the minimum local time step at each iteration was used. The local time did not exceed 5.2 × s, which is lower than the Kolmogorov time scale. The associated Kolmogorov time scale was 1.1 × s. This was determined using the process described earlier.
4.3. Results
In order to assess the ability of URANS and LES to capture the transient shock-physics evolution, first comparisons between the calculated results from URANS and LES for the first 0.6 ms of the flow have been made in terms of static temperature, density, and shadowgraph contours. As this modified shock-tube has a square cross-section, only centerplane (or symmetry plane) contours are shown for comparison between the two computational approaches. The static temperature contours at the symmetry plane calculated with URANS and LES are shown below in Figure 16 and Figure 17 at various times, respectively. There are several differences between URANS and LES results that can be observed from these plots. LES results show higher static temperature values as well as faster progression of the left-to-right waves in comparison to the URANS results. It can also be observed that a thicker boundary-layer development in URANS calculations results in larger curvature of shocks on both right and left sides as compared to the LES results, where the left shock remains planar. The shock–shock interference was greatly developed after approximately 4.228 × seconds in the URANS results in comparison to the LES results at the same time. As mentioned in an earlier section, the LES results show a more detailed shock–shock interference as well as shock–boundary-layer interaction as compared to URANS results.
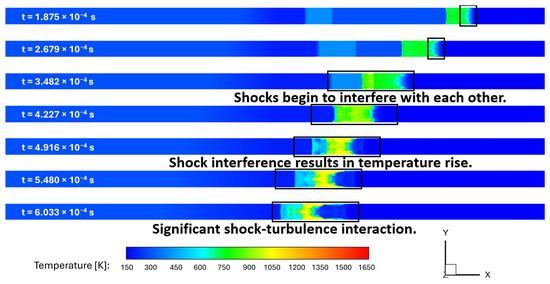
Figure 16.
Static temperature contours at symmetry plane: adiabatic walls with LES.
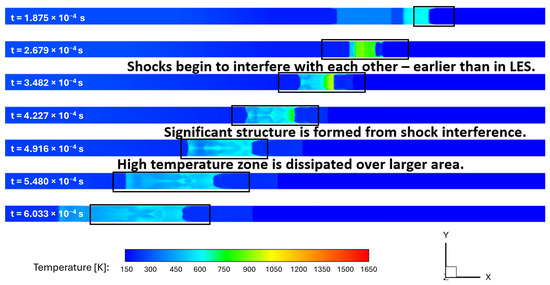
Figure 17.
Static temperature contours at symmetry plane: adiabatic walls with URANS-SA.
In addition to the static temperature, density contours at the wall calculated with LES and URANS are shown in Figure 18 and Figure 19 at various times, respectively. These results show remarkable differences between the temporal evolution of the flow phenomena between URANS and LES calculations, and show a clear evolution of shock–shock interference as calculated by LES versus URANS.
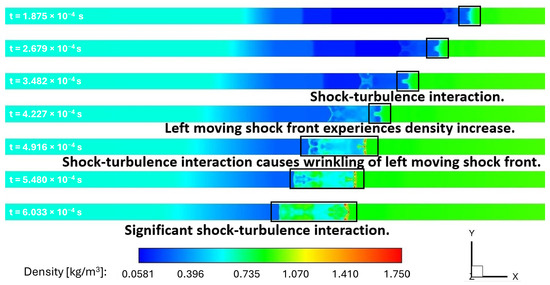
Figure 18.
Density contours at the wall: adiabatic walls with LES.
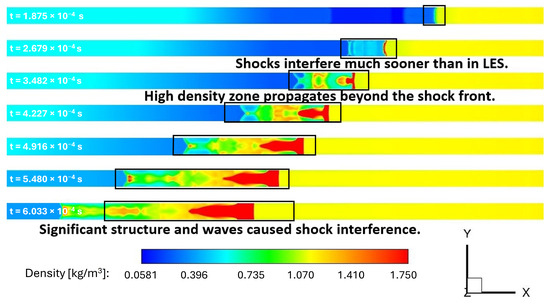
Figure 19.
Density contours at the wall: adiabatic walls with URANS-SA.
The required mesh size is primarily dependent on the Reynolds number. Given the minimal Reynolds number variation in Figure 20, the initial mesh is still considered adequate. The change in scales from the initial assumption is minor, on the order of 10% or less, as abstracted from the contour plot provided.
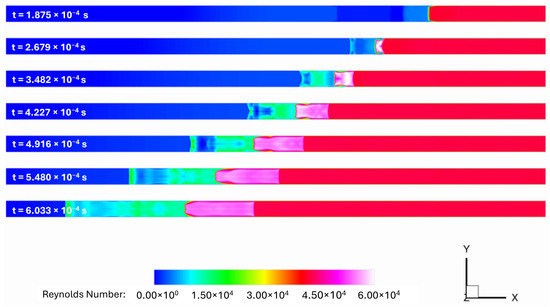
Figure 20.
Reynolds number contours at the centerplane: adiabatic walls with URANS-SA.
The dimensionless values along the solid walls are shown below in Figure 21. This contour displays that the value at a given point becomes significantly higher as the incoming flow develops over that area. In addition to this, Figure 22 shows the ratio of the grid resolution to the Kolmogorov scale, . The Kolmogorov scale will not be resolved with LES, so being within 100 times is adequate for this simulation. This plot shows that the Kolmogorov scale does change with time, but not so drastically that the physics cannot be resolved. These images provide justification for the mesh resolution used in this study.
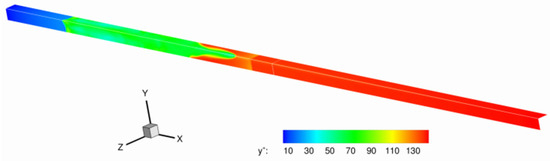
Figure 21.
Contour of along the walls of quarter cut: adiabatic walls with URANS-SA.
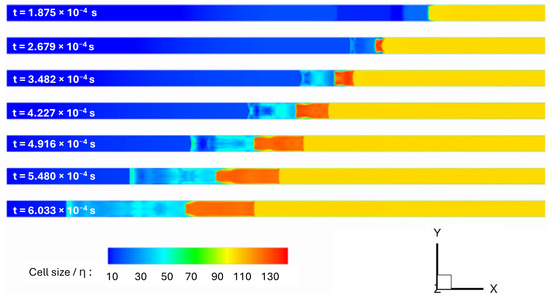
Figure 22.
Ratio of cell size to Kolmogorov scale () at the centerplane: adiabatic walls with URANS-SA.
To observe how the density and static temperature evolve, the results at a later time are shown. Figure 23 shows the comparison of URANS and LES results at a later time. This shows the flow after the shocks had interacted with each other in the LES case. The density was lower in this area in the LES case compared to RANS. Richtmyer–Meshkov instability can also be observed in the LES results in comparison to the URANS results.
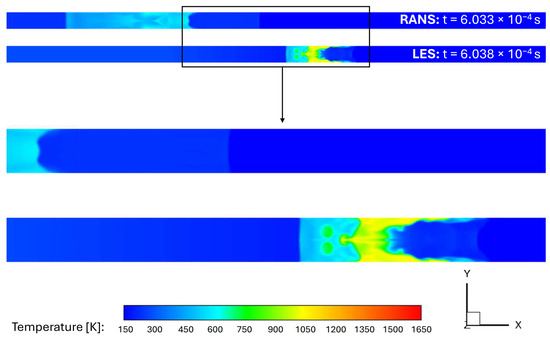
Figure 23.
Static temperature contours of developed flow: adiabatic walls (RANS-SA vs. LES).
The temperature contours also showed significant differences between the URANS and LES results. These differences include a higher temperature zone appearing near the wall, shown in the LES results. The Richtmyer–Meshkov instability was shown in both density and temperature contours. These contours displayed the advantages of LES simulations, as they showed significantly more details that are not captured by URANS.
Contours of shadowgraphs were created for the LES and URANS cases to compare the two techniques. These are shown below in Figure 24 and Figure 25, respectively. These plots further demonstrate the significant differences in results obtained with URANS and LES methods over the identical mesh. The RANS results showed only major features, while the LES results showed much finer details of the flowfield. LES calculations showed smaller structures within the larger structures—something that was not captured by the URANS calculations. In addition to this, the rotational effects are shown in the LES case, but not in the URANS case. The shock–shock interaction represented by URANS showed a curved and curved shock interference, whereas the LES results show that the left shock front remained planar with only curvature at the wall, resulting in planar-curved shock interactions. The interactions between turbulence and shock resulted in shock wrinkling.
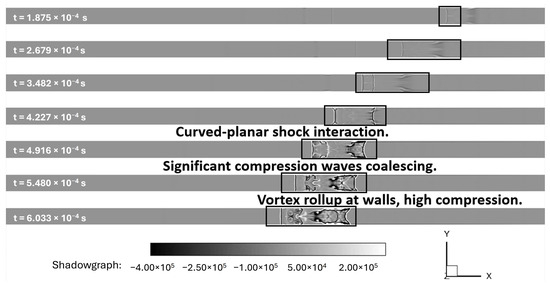
Figure 24.
LES shadowgraph: adiabatic walls.
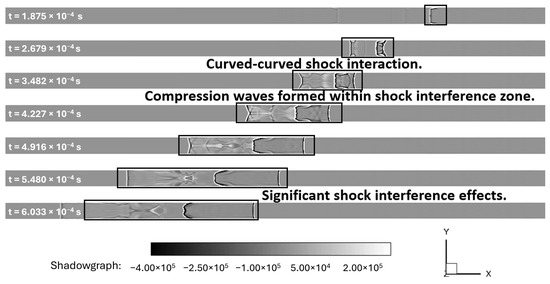
Figure 25.
RANS shadowgraph: adiabatic walls.
The Mach number contours at the symmetry plane from LES calculations are shown in Figure 26 at progressive times. These results show that there are two shock fronts traveling towards each other including (1) a normal shock formed in the middle of the shock-tube due to high-pressure driver gas in the left half and low-pressure driven gas in the right half of this tube, and (2) a compression wave traveling from right to left due to 3 Mach supersonic flow entering the shock-tube. Shock–shock interference begins to form at 0.3482 ms, and it develops with time. As indicated in this figure, the region of shock interference expands and moves to the left under the influence of a 3 Mach supersonic flow pushing the fluid from right to left in the shock-tube.
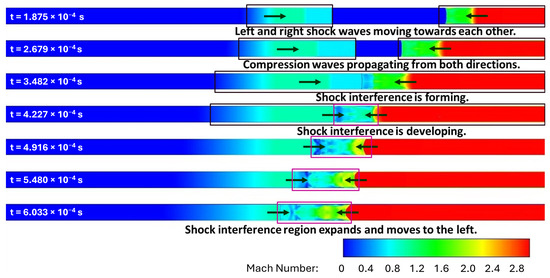
Figure 26.
Mach number contours at symmetry plane: adiabatic walls with LES.
The static pressure contours at the symmetry plane from LES calculations are shown in Figure 27 at progressive times. In addition to the pressure gradients along the axial direction, significant pressure gradients in lateral directions as well, evolving in mushroom-like structures that appear to be forming Richtmyer–Meshkov instability. This instability is manifested when a shock interacts with an interface separating fluids of two different densities, similar to this current scenario. This can be further illustrated by the eddy viscosity ratio contours at the wall shown in Figure 28. As shown in this figure, it can be observed that turbulence-shock interaction resulting in wrinkling of the shock fronts, therefore resulting in a complex flowfield in this shock-tube, which has been captured by LES.
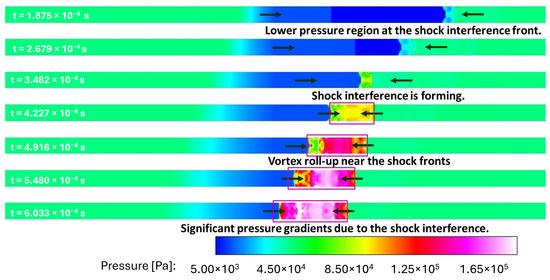
Figure 27.
Pressure contours at symmetry plane: adiabatic walls with LES.
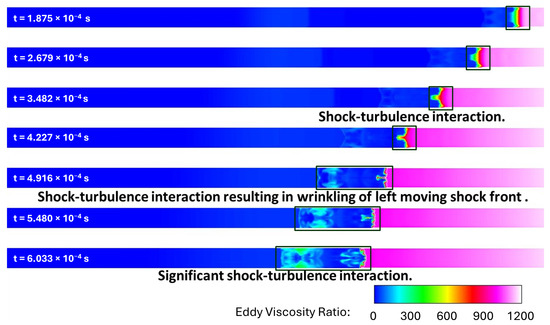
Figure 28.
Eddy viscosity ratio contours at the wall: adiabatic walls with LES.
4.4. Effect of Wall Temperature on Shock Interference
Comparisons of wall pressure contours with adiabatic and isothermal walls (at 200 K) calculated with LES are shown in Figure 29. The results with isothermal walls show differences from the results with adiabatic walls, including lower overall wall pressure with isothermal walls. These results also show that isothermal walls result in a reduction of lower pressures at the wall corners where both the y- and z-walls meet. In addition, the pressure peak at the centerline is reduced significantly as well.
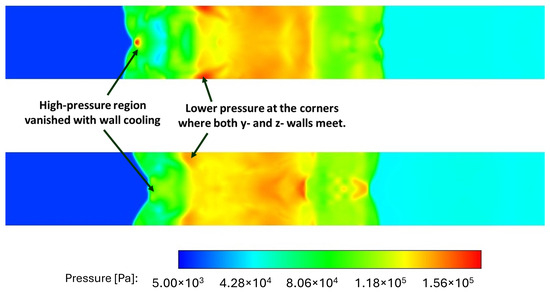
Figure 29.
Wall pressure contours with adiabatic (top) and isothermal (bottom) walls calculated with LES.
Figure 30 displays temperature and pressure line plots at a time of 4.228 × s. These variables were plotted at the wall and the centerline of the modified shock-tube. As shown in Figure 29, the pressure at the wall has lower peaks in the case with isothermal walls due to cooling. The pressure peaks were also at different locations within the shock structure. The centerline temperature distribution with isothermal wall appears to be heated at some locations while cooled in the region where shock interference is occurring. This is due to the fact that the air entering from the inlet is at 150 K, whereas the wall temperature is higher at 200 K. The centerline pressure shows that the case with the cooled walls actually had a substantially higher peak pressure. In this case, the pressure at the wall was reduced, but the pressure at the centerline increased.
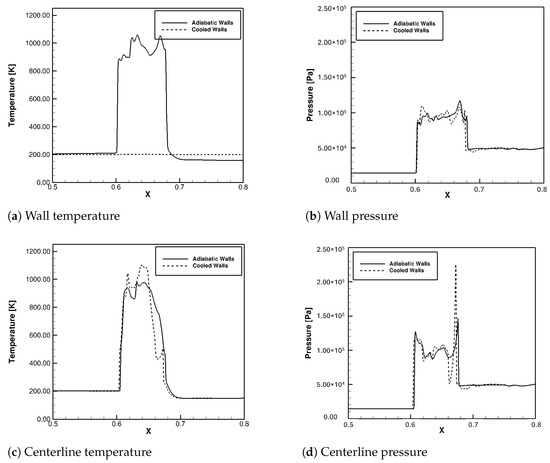
Figure 30.
Static temperature and pressure distribution at t ≈ 4.228 × s.
Figure 31 shows the same quantities as discussed above except at a time of 4.909 × s. Again, the walls were obviously cooler with the isothermal walls than they were with the adiabatic walls. The pressure at the wall also had a lower peak and less variation in the cooled walls case. The centerline was heated in some portions as mentioned above. At this time, however, the shock-train was dampened at the centerline in the cooled walls case. At the previous time, the pressure peak was noticeably higher. The shock-train near the wall is also shorter in the cooled wall case.
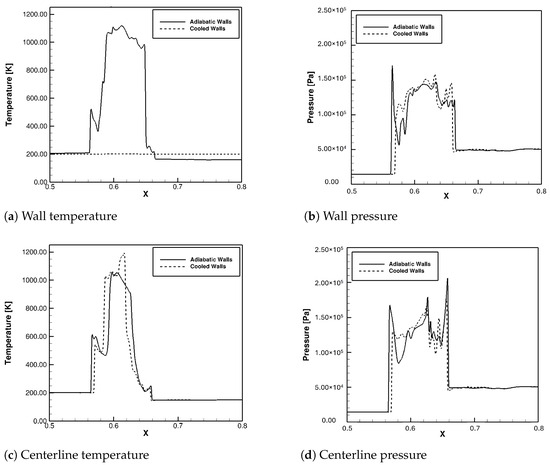
Figure 31.
Static temperature and pressure distribution at t ≈ 4.909 × s.
Theoretically, wall cooling results in boundary-layer thickness reduction, resulting in less compression of the core flow due to thinner boundary-layer and therefore, weaker and/or shorter pseudo-shock-train. Figure 32 shows two plots. One is the u-velocity at z = 0, which was the centerline of the z-axis (width). The other plot shows the u-velocity at z = 0.0075, which was halfway between the centerline of the z-axis and the front wall of the modified shock-tube. These data were extracted at the same x-location within the shock structure, after it had developed. The boundary layer at the centerline of the z-axis was slightly thicker in the cooled walls case. This helps to provide an explanation as to why the pressure in the cooled walls case is not very different than the adiabatic case, at the centerline. It was observed previously that the effects of the wall cooling were significantly more prevalent at the wall. The plot in Figure 32b further supports this as the boundary layer in the cooled case was much thinner than that of the adiabatic case. This shows that the technique of cooling the walls does reduce the thickness of the boundary layer, as expected.
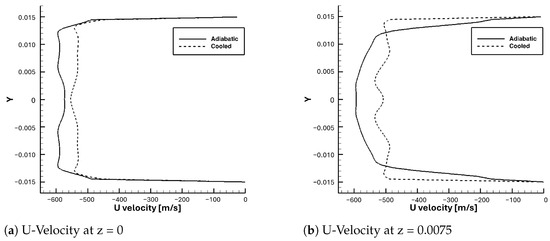
Figure 32.
Displacement boundary-layer thickness with adiabatic and cooled walls.
The LES calculations were again performed with a higher inflow temperature to observe if the cooling effects were amplified with a higher temperature difference between the inflow and walls. Results with 300 K inflow are shown in Figure 33.
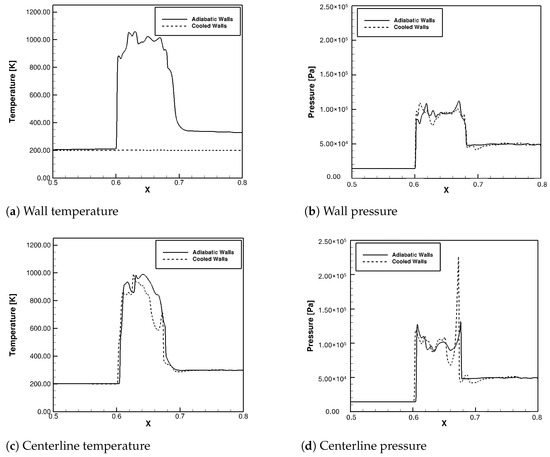
Figure 33.
Static temperature and pressure distribution at t ≈ 4.225 × s with 300 K Inflow.
These plots were from approximately the same time as the previous calculations. Initially, the inflow was 150 K and the isothermal walls were 200 K, so the walls were heating the flow that was entering through the velocity inlet on the left, but cooling the flow was the shock interference is occurring. This case with 300 K inflow was used to ensure that the flow was being cooled at all locations, and to observe any differences that this made. The wall pressure followed the same trend as the previous case. The peak is slightly lower with other different fluctuations, but no drastic difference. The temperature at the centerline in the case with cooled walls was almost never higher than that of the case with adiabatic walls. This was the objective with the higher inflow temperature. Although the temperature at the centerline was lower in the case with cooled walls, the significantly higher pressure spike is still visible. The dip in pressure after the initial spike was lower in the cooled walls case as well.
At a later time, the effect of cooled walls can be observed more, but mainly at the wall itself. Figure 34 shows the same plots as Figure 31, but with the 300 K inflow. Again, the wall pressure had a lower peak in the case with the cooled walls. At this later time, it was also apparent that the shock-train itself was slightly shorter. This is consistent with the previous case. Even though the temperature at the centerline was lower in the cooled walls case almost everywhere, the centerline pressure did not decrease all around. The peak pressure was lower, and the variation was different, but the changes were not substantially advantageous.
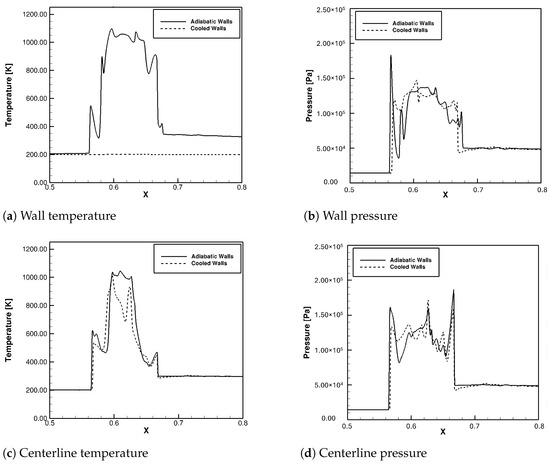
Figure 34.
Static temperature and pressure distribution at t ≈ 4.905 × s with 300K Inflow.
Isothermally cooled walls have some effect on the shock-train in all of these cases. At the earlier time studied (t ≈ 4.23 × s), the case with adiabatic walls actually had a lower peak pressure at the centerline. This was the opposite in both cases at the later time (t ≈ 4.91 × s). These results showed that the isothermally cooled walls had a greater impact on the pressure at the wall than at the centerline. This is as expected because the walls were the portion that was isothermal and cooled. The centerline was influenced by more of the surrounding flow. The cooled walls seemed to slightly reduce the length of the shock-train. This conclusion was supported by two different inflow temperatures. Although this is true, the effect of the cooled walls was minimal. The effect was even less at the centerline. These data show that although isothermally cooled walls did have a damping effect on the shock-train, there may be a better way to accomplish more. The maximum difference between the wall temperature and the inflow temperature was 100 K, as shown in the case with 300 K inflow. It is possible that the wall cooling effects would be amplified if the temperature difference were greater. More work would need to be done in this area to determine if that is true.
5. Conclusions
Computational analysis presented in this work supports scientific understanding of shock interference and passive control of the adverse effects of shockwave boundary-layer interaction to prevent the onset of unstart in a scramjet isolator for a backpressured isolator and a modified three-dimensional shock-tube. Model validation of the steady-state RANS calculations for the backpressured isolator was performed with experimental data. In addition, the modified shock-tube provided an opportunity to study the shock interference and shock–boundary-layer interaction effects that would occur in a scramjet isolator or a ram-accelerator when the high-speed flow from the inlet interacted with the shock produced due to the combustor pressure traveling and meeting in the isolator. An assessment of wall cooling effects on these phenomena is presented for both the backpressured isolator and the modified shock-tube. Wall cooling showed significant success in reducing the boundary-layer separation and the length and beginning of the pseudo-shock-train. In the case of the modified shock-tube, the static pressure comparison along the centerline of the tube demonstrated that the cooling of the walls only had minor effects on the shock-train; the effect was significant at the wall.
It is well known that there are many differences between the underlying assumptions made in formulating URANS and LES methods. Both methodologies utilized a common structured mesh where the resolution (both spatial and time-step) was kept closer to the Kolmogorov scale to support large eddy simulation. In general, both URANS and LES results show shock–boundary-layer and shock–shock interference, and RANS with an appropriate mesh and turbulence closure model shows the ability to capture steady-state shock-structure, as shown in the model validation section. However, there are significant quantitative differences between the two methodologies in the form of differences in maximum pressure, temperature, and turbulence production. These differences include a higher temperature zone appearing near the wall, display of Richtmyer–Meshkov instability, and shock wrinkling due to interaction with small-scale turbulence, shown in LES results.
Reporting has been scarce on the investigation of shock–shock interference and interaction with the boundary layer in high-speed internal flows, and therefore, it is difficult to perform a comparison of the results presented in this paper with other experimental or numerical studies. However, a few conclusions can be made based on the theoretical knowledge of turbulence and Richtmyer–Meshkov instability. It is well known that the prediction of boundary-layer development and thickness varies between RANS and LES, which clearly affects the formation of shocks inside the modified shock-tube. Similarly, vortex formation and roll-up near the walls are expected, but it is not captured by RANS methodology. LES is able to capture the vortex roll-up phenomena and displays a Richtmyer–Meshkov type instability, which can be expected under these conditions. Due to these reasons, LES is likely better suited to capture the shock physics in this case.
This conclusion comes with a set of limitations. The LES approach gave a clear view of how shocks interact with the boundary layer, but its high computational cost limited broader parametric and sensitivity studies. While RANS is unable to capture the complex phenomena observed in the modified shock-tube, it is able to capture the time-averaged wall pressures in the isolator, where there is small shock interference.
These results show that passive wall cooling could be a practical way to delay the onset of shock trains and reduce flow separation in scramjet isolators, helping to keep the engine stable under changing backpressure conditions. However, perfectly cooled walls have cost implications for practical aviation systems and are a slower process. To build on these findings, future work should investigate more flexible cooling approaches, such as varying the cooling intensity along the wall and flow control methods. Future work must also investigate how they might perform alongside active control methods. Ultimately, experimental testing under realistic, unsteady conditions will be key to understanding how well these cooling strategies perform in actual flight systems.
Author Contributions
Conceptualization, R.A.; Investigation, R.A.; Writing—original draft, C.A.; Writing—review & editing, R.A.; Supervision, R.A.; Funding acquisition, R.A. All authors have read and agreed to the published version of the manuscript.
Funding
The funding for this effort was provided by the Office of Naval Research (ONR) and Eric Marineau via ONR grant number N00014-22-1-2457.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to acknowledge the support from Office of Naval Research (ONR) and Eric Marineau via ONR grant number N00014-22-1-2457. This paper is an extended version of our paper published in Alexander, C.; Acharya, R. Computational Investigations of Shock Interference in a Scramjet Isolator. In Proceedings of the AIAA Aviation Forum and Ascend 2024, Las Vegas, NV, USA, 29 July–2 August 2024 [28].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Heiser, W.H.; Pratt, D.T. (Eds.) Hypersonic Airbreathing Propulsion; AIAA Education Series; AIAA: New York, NY, USA, 1994. [Google Scholar]
- Curran, E.T. Scramjet Engines: The First Forty Years. J. Propuls. Power 2001, 17, 1138–1148. [Google Scholar] [CrossRef]
- Waltrup, P.; White, M.E.; Zarlingo, F.; Gravlin, E.S. History of U.S. Navy Ramjet, Scramjet, and Mixed-Cycle Propulsion Development. J. Propuls. Power 2002, 18, 14–27. [Google Scholar] [CrossRef]
- Fry, R.S. A Century of Ramjet Propulsion Technology Evolution. J. Propuls. Power 2004, 20, 27–58. [Google Scholar] [CrossRef]
- Do, H.; Im, S.-K.; Mungal, M.G.; Cappelli, M.A. The influence of boundary layers on supersonic inlet flow unstart induced by mass injection. Exp. Fluids 2011, 51, 679–691. [Google Scholar] [CrossRef]
- Rodi, P.E.; Emami, S.; Trexler, C.A. Unsteady Pressure Behavior in a Ramjet/Scramjet Inlet. J. Propuls. Power 1996, 12, 486–493. [Google Scholar] [CrossRef]
- Carroll, B.; Dutton, J.C. Turbulence Phenomena in a Multiple Normal Shock Wave/Turbulent Boundary-Layer Interaction. AIAA J. 1992, 30, 43–48. [Google Scholar] [CrossRef]
- Acharya, R.; Palies, P.; Schetz, J.; Schmisseur, J. Development of Uncertainty Quantification Framework Applied to Scramjet Unstart Challenge. In Proceedings of the 23rd AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Montreal, QC, Canada, 10–12 March 2020. [Google Scholar] [CrossRef]
- Acharya, R.; Schetz, J.; Schmisseur, J.D. Non-Intrusive Computational Method and Uncertainty Quantification for Isolator Operability Calculations: Part 1. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Acharya, R. Identification and Assessment of Scramjet Isolator Unstart and Operability Metrics. Aerospace 2025, 12, 503. [Google Scholar] [CrossRef]
- Weiting, A. Multiple shock-shock interference on a cylindrical leading edge. AIAA J. 1992, 30, 2073. [Google Scholar] [CrossRef]
- Boldyrev, S.M.; Borovoy, V.Y.; Chinilov, A.Y.; Gusev, V.N.; Krutiy, S.N.; Struminskaya, I.V.; Yakovleva, L.V.; Délery, J.; Chanetz, B. A thorough experimental investigation of shock/shock interferences in high Mach number flows. Aerosp. Sci. Technol. 2001, 5, 167–178. [Google Scholar] [CrossRef]
- Grasso, F.; Purpura, C.; Chanetz, B.; Délery, J. Type III and type IV shock/shock interferences: Theoretical and experimental aspects. Aerosp. Sci. Technol. 2003, 7, 93–106. [Google Scholar] [CrossRef]
- Cardona, V.; Joussot, R.; Lago, V. Shock/shock interferences in a supersonic rarefied flow: Experimental investigation. Exp. Fluids 2021, 62, 135. [Google Scholar] [CrossRef]
- Edney, B. Anomalous Heat Transfer and Pressure Distributions on Blunt Bodies at Hypersonic Speeds in the Presence of an Impinging Shock. FFA Report 115; 1968. Available online: https://www.osti.gov/biblio/4480948 (accessed on 24 May 2025).
- Valdivia, A.; Yuceil, K.B.; Wagner, J.L.; Clemens, N.T.; Dolling, D.S. Control of Supersonic Inlet-Isolator Unstart Using Active and Passive Vortex Generators. AIAA J. 2014, 52, 1207–1218. [Google Scholar] [CrossRef]
- Sethuraman, V.R.P.; Kim, T.H.; Kim, H.D. Control of the oscillations of shock train using boundary layer suction. Aerosp. Sci. Technol. 2021, 118, 1872–1873. [Google Scholar] [CrossRef]
- Sethuraman, V.R.P.; Yang, Y.; Kim, J.G. Low-frequency shock train oscillation control in a constant area duct. Phys. Fluids 2022, 34, 016105. [Google Scholar] [CrossRef]
- NASA LaRC. Turbulence Modeling Resource. Available online: https://turbmodels.larc.nasa.gov/ (accessed on 29 June 2025).
- Harris, N.; Stokes, T.M.; Acharya, R. A Comparison of Turbulence Models for Scramjet Isolator Unstart Estimation. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 0711. [Google Scholar]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Baurle, R.A.; Middleton, T.F.; Wilson, L.G. Reynolds-Averaged Turbulence Model Assessment for a Highly Back-Pressured Isolator Flowfield. In Proceedings of the 33rd Airbreathing Propulsion Joint Subcommittee Meeting, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar]
- Wilcox, D.C. Comparison of two-equation turbulence models for boundary layers with pressure gradient. AIAA J. 1993, 31, 1414–1421. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Sutherland, W. LII. The viscosity of gases and molecular force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather. Rev. 1963, 91, 99. [Google Scholar] [CrossRef]
- Alexander, C.; Acharya, R. Computational Investigations of Shock Interference in a Scramjet Isolator. In Proceedings of the AIAA Aviation Forum and Ascend 2024, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).