Enhancing Security of Error Correction in Quantum Key Distribution Using Tree Parity Machine Update Rule Randomization
Abstract
1. Introduction
2. Overview
2.1. Quantum Cryptography
2.1.1. Quantum Key Distribution
2.1.2. Key Distillation
2.2. Artificial Neural Networks
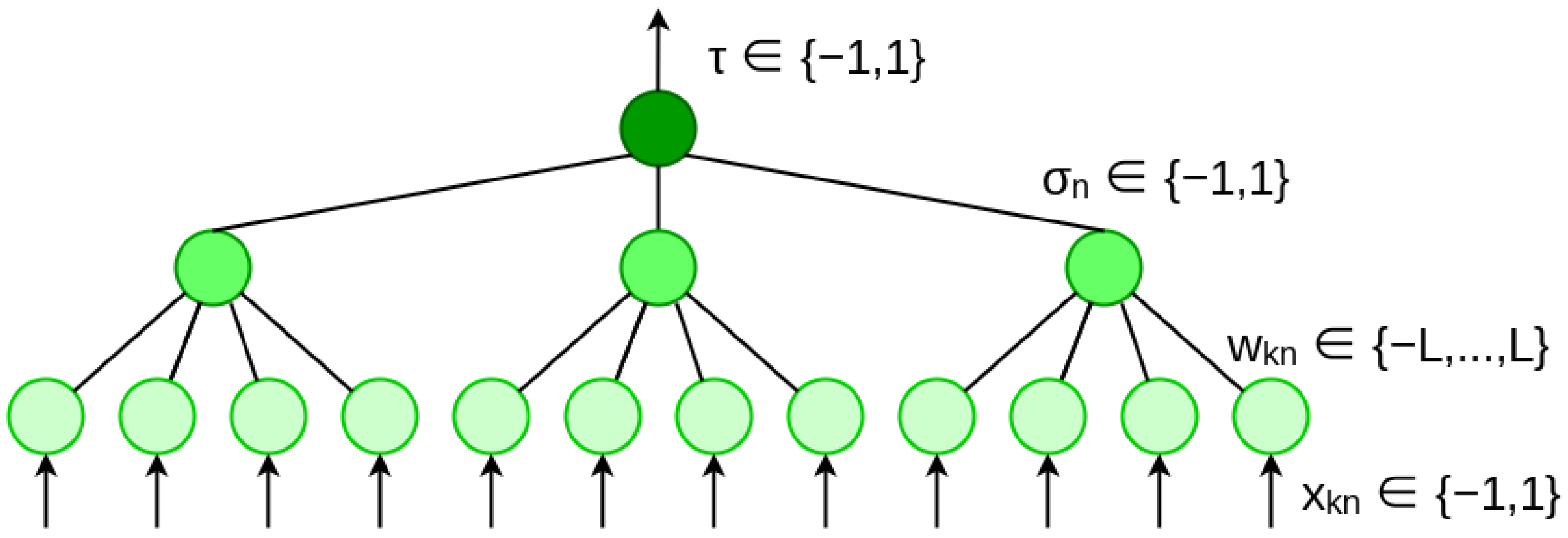
2.2.1. Tree Parity Machine
2.2.2. TPMs in Cryptography
- —in this case, does not matter, as the sender and receiver do not update their weights.
- —in this case, the sender and receiver update their weights, but the attacker does not.
- —this is the only case in which the attacker’s weights are updated.
2.2.3. TPMs in Quantum Cryptography Error Correction
3. Materials and Methods
3.1. Methodology
- dynamic_rows,
- dynamic_matrix.
- where: V is the chosen vector (which may be a part or the entirety of the input vector). and floor function rounds the value to the largest integer that is less than or equal to that value.
3.2. Testbed
- The number of updates between synchronizing TPMs,
- The percentage synchronization value between the attacker’s and victims’ machines,
- The number of attacker’s TPM updates.
- K value,
- N value,
- L value,
- QBER value in %,
- Chosen update algorithm,
- Attacker’s update algorithm (optional, used in case of new, dynamic update algorithms).
3.3. Parameters
- All parties: hebbian;
- Victims: dynamic_rows, attacker: hebbian;
- Victims: dynamic_matrix, attacker: hebbian;
- All parties: random walk;
- Victims: dynamic_rows, attacker: random walk;
- Victims: dynamic_matrix, attacker: random walk;
- Victims: dynamic_rows, attacker: random rule;
- Victims: dynamic_matrix, attacker: random rule.
- In how many cases did the dynamic algorithms result in the attacker retrieving less information when the attacker chose the hebbian rule?
- In how many cases did the dynamic algorithms result in the attacker retrieving less information when the attacker chose the random walk rule?
- In how many cases did the dynamic algorithms result in the attacker retrieving less information when the attacker chose a random update rule at each iteration?
4. Results
4.1. Scenario 1
- K: {5,7,9,11},
- N: {5},
- L: {2,4,6},
- QBER: {3,5,7}
4.1.1. First Example Test
4.1.2. Second Example Test
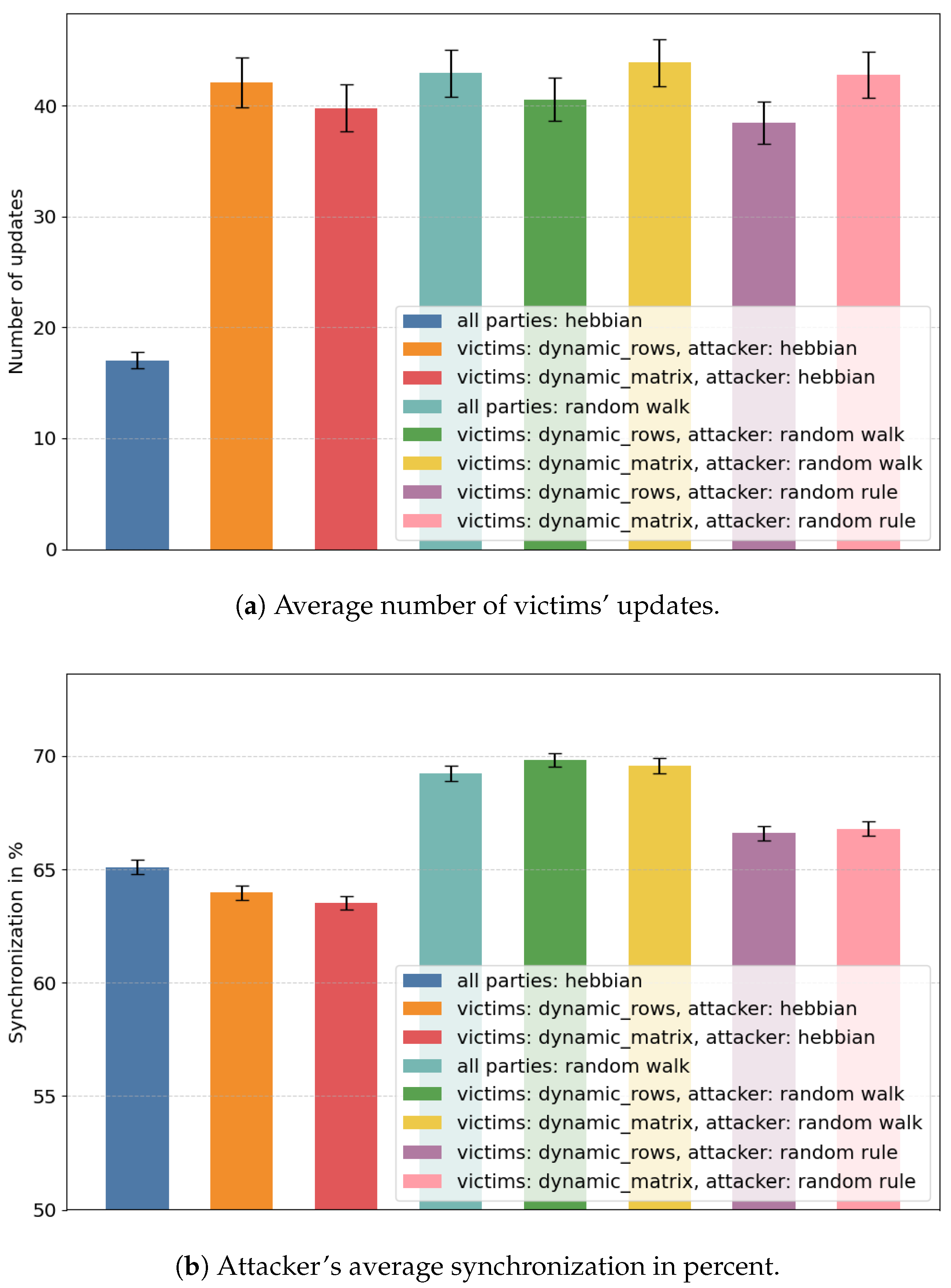
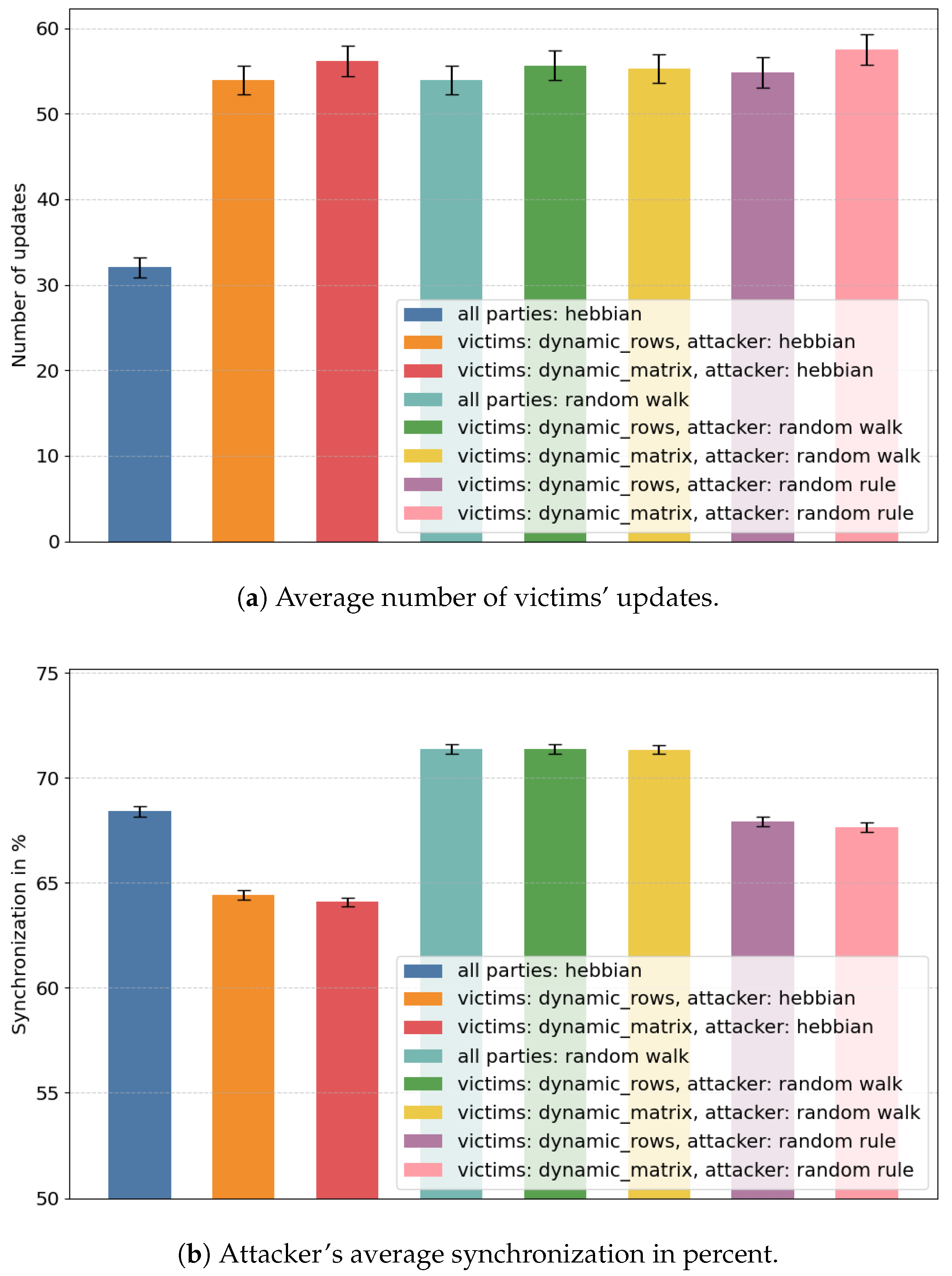
- In hebbian-oriented tests, the attacker was able to obtain less information when the victims were using dynamic_rows or dynamic_matrix (≈59% in both cases), compared to the scenario in which all parties used the hebbian algorithm.
- The attacker’s synchronization percentage is lower when they choose the update rule randomly, while the victims choose dynamic_rows or dynamic_matrix (≈63.5% in both cases), compared to any combination in which the attacker uses the random walk algorithm (≈69% on average). The values are also comparable with the attacker’s synchronization when all parties use the hebbian algorithm (≈63.5%), although the confidence intervals are not narrow enough to definitely conclude which of these combinations is more beneficial for the victims.
- Additionally, compared to previously presented tests, in this case, the mean value of the attacker’s synchronization was lower when the attacker used the random walk rule, and the victims used either dynamic_rows or dynamic_matrix (≈68% and ≈69%, respectively), compared to all parties using random walk (≈69%). However, in the case of dynamic_matrix, this observation is not conclusive, due to the width of the confidence intervals.
4.1.3. Comparative Analysis
4.2. Scenario 2
- K: {5},
- N: {5,13,34,89},
- L: {2,4,6},
- QBER: {3,5,7}
4.2.1. First Example Test
4.2.2. Second Example Test
4.2.3. Comparative Analysis
- Comparison of scenarios in which all parties are using hebbian versus scenarios in which victims change their update algorithms to proposed solutions.
- Comparison of scenarios in which all parties are using random walk versus scenarios in which victims change their update algorithms to proposed solutions.
- Comparison of scenarios in which all parties are using hebbian versus scenarios in which victims change their update algorithms to proposed solutions and the attacker chooses their update rule randomly.
- Comparison of scenarios in which all parties are using random walk versus scenarios in which victims change their update algorithms to proposed solutions and the attacker chooses their update rule randomly.
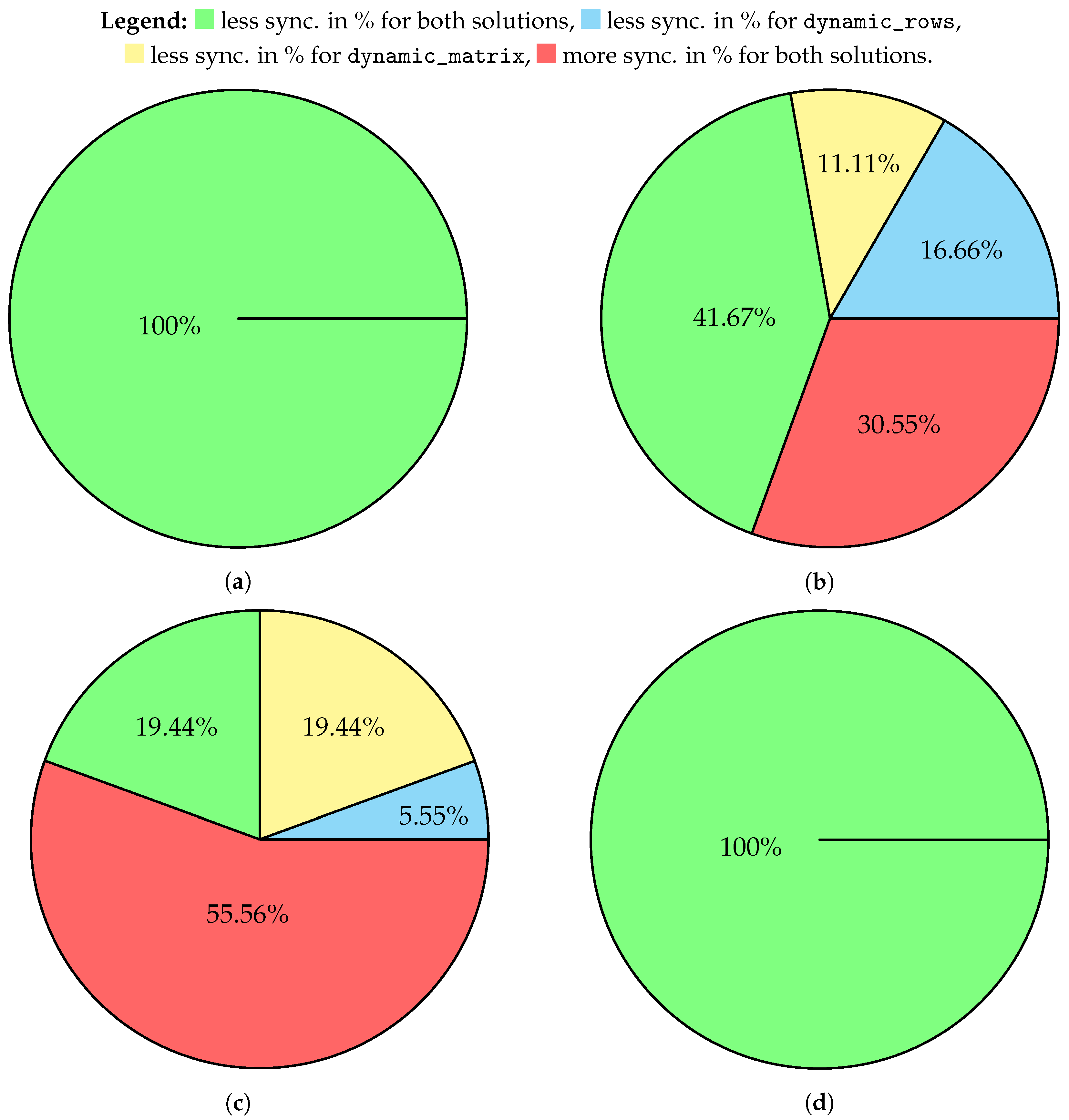
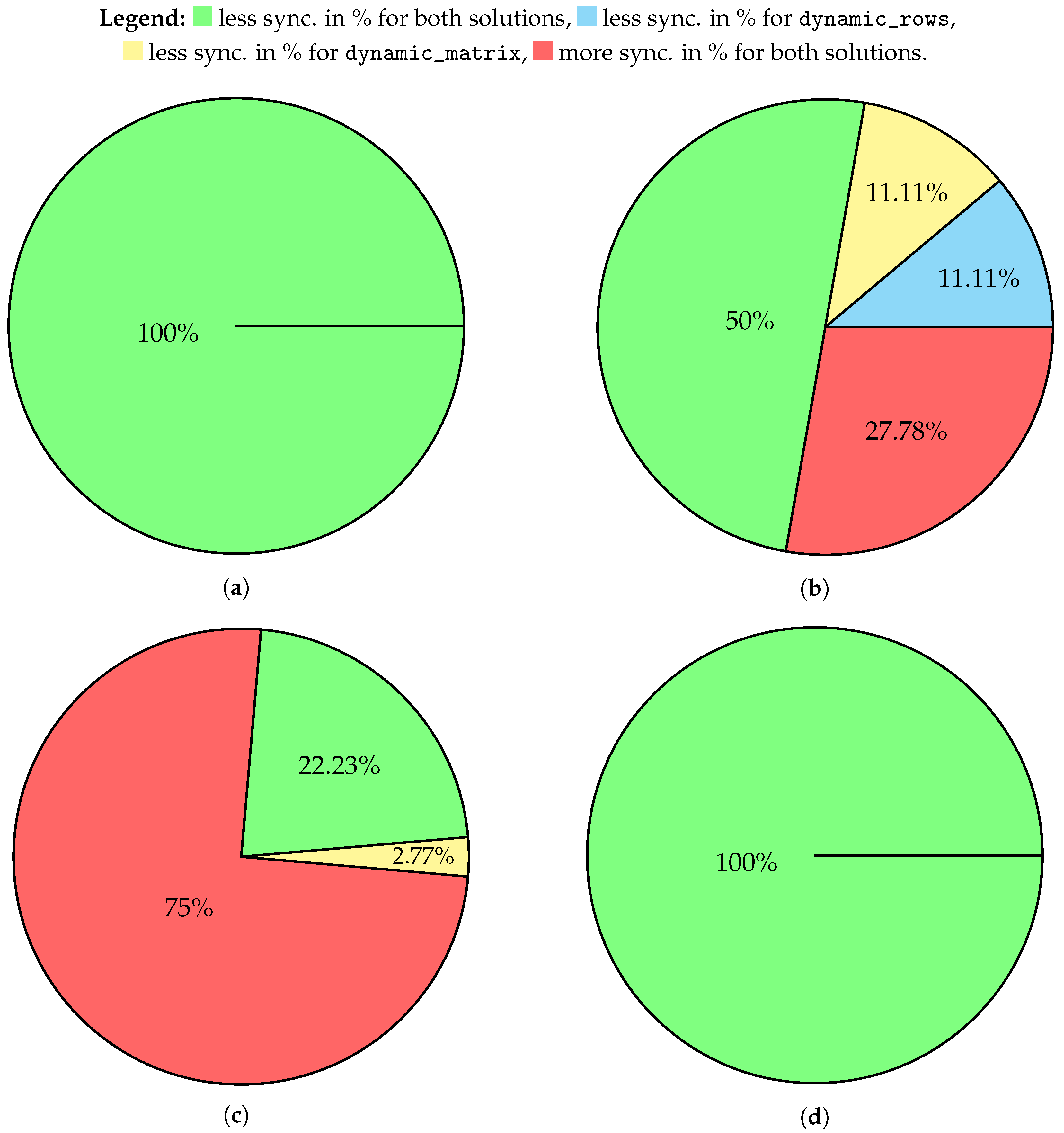
- If the victims have suspicion that the attacker is using hebbian, it is always better to use any of the dynamic approaches;
- If the victims have suspicion that the attacker is using random walk, in general dynamic_matrix or dynamic_rows are better (about of all cases);
- If the attacker is using random update rule, dynamic algorithms perform worse compared to hebbian-only synchronization;
- If the attacker is using random update rule, it is always better to use dynamic update rule compared to all parties synchronizing with random walk.
5. Discussion
- In the vast majority of cases, it is more secure to use either dynamic_rows or dynamic_matrix if we are sure that the attacker will use a static update rule (in case they are using hebbian rule, it is always more profitable).
- If the communicating parties would want to use random walk as the update rule, in the vast majority of cases it is more secure to use dynamic approaches, no matter what the attacker’s approach is (in case they are using random update rule, it is always more profitable).
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Barker, E.; Dang, Q. Recommendation for Key Management, Part 3: Application-Specific Key Management Guidance; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Wood, G. Encryption Security for a Post Quantum World. Available online: https://csis.org/blogs/strategic-technologies-blog/encryption-security-post-quantum-world (accessed on 4 July 2025).
- AtomC. Quantum Startup Atom Computing First to Exceed 1000 Qubits. Available online: https://atom-computing.com/quantum-startup-atom-computing-first-to-exceed-1000-qubits/ (accessed on 4 July 2025).
- IBM. Expanding the IBM Quantum Roadmap to Anticipate the Future of Quantum-Centric Supercomputing (Updated 2024). Available online: https://research.ibm.com/blog/ibm-quantum-roadmap-2025 (accessed on 4 July 2025).
- Opiłka, F.; Niemiec, M.; Gagliardi, M.; Kourtis, M.A. Performance Analysis of Post-Quantum Cryptography Algorithms for Digital Signature. Appl. Sci. 2024, 14, 4994. [Google Scholar] [CrossRef]
- Hughes, R.J.; Alde, D.M.; Dyer, P.; Luther, G.G.; Morgan, G.L.; Schauer, M. Quantum cryptography. Contemp. Phys. 1995, 36, 149–163. [Google Scholar] [CrossRef][Green Version]
- Mehic, M.; Niemiec, M.; Rass, S.; Ma, J.; Peev, M.; Aguado, A.; Martin, V.; Schauer, S.; Poppe, A.; Pacher, C.; et al. Quantum key distribution: A networking perspective. ACM Comput. Surv. 2020, 53, 96. [Google Scholar] [CrossRef]
- Ekert, A.; Gisin, N.; Huttner, B.; Inamori, H.; Weinfurter, H. Quantum Cryptography. In The Physics of Quantum Information; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Bennett, C.; Brasard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 10–19 December 1984. [Google Scholar]
- Bennett, C. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121–3124. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Dušek, M.; Lütkenhaus, N.; Hendrych, M. Quantum cryptography. Prog. Opt. 2006, 49, 381–454. [Google Scholar]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Devitt, S.; Munro, W.; Nemoto, K. Quantum error correction for beginners. Rep. Prog. Phys. 2013, 7, 076001. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Dixon, A.R.; Dynes, J.F.; Lucamarini, M.; Fröhlich, B.; Sharpe, A.W.; Plews, A.; Tam, S.; Yuan, Z.L.; Tanizawa, Y.; Sato, H.; et al. 77 day field trial of high speed quantum key distribution with implementation security. In Proceedings of the 6th International Conference on Quantum Cryptography (QCrypt), Washington, DC, USA, 12–16 September 2016. [Google Scholar]
- Niemiec, M.; Pach, A. The measure of security in quantum cryptography. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012. [Google Scholar]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Jennewein, T.; Simon, C.; Weihs, G.; Weinfurter, H.; Zeilinger, A. Quantum Cryptography with Entangled Photons. Phys. Rev. Lett. 2000, 84, 4729–4732. [Google Scholar] [CrossRef] [PubMed]
- Brassard, G.; Salvail, L. Secret-Key Reconciliation by Public Discussion. In Advances in Cryptology—EUROCRYPT ’93; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Niemiec, M. Error correction in quantum cryptography based on artificial neural networks. Quantum Information Processing 2019, 18, 174. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Maurer, U.M. Generalized privacy amplification. IEEE Trans. Inf. Theory 1995, 41, 1915–1923. [Google Scholar] [CrossRef]
- Mehic, M.; Rass, S.; Fazio, P.; Voznak, M. Quantum Key Distribution Networks: A Quality of Service Perspective; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Sobti, R.; Geetha, G. Cryptographic hash functions: A review. Int. J. Comput. Sci. Issues 2012, 9, 461–479. [Google Scholar]
- Kasiviswanathan, S.P.; Lee, H.K.; Nissim, K.; Raskhodnikova, S.; Smith, A. What Can We Learn Privately? In Proceedings of the 49th Annual IEEE Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 25–28 October 2008.
- Feldman, V.; Mironov, I.; Talwar, K.; Thakurta, A. Privacy Amplification by Iteration. In Proceedings of the 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS), Paris, France, 7–9 October 2018. [Google Scholar]
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hansel, D.; Sompolinsky, H. Learning from examples in a single-layer neural network. EPL (Europhys. Lett.) 1990, 11, 687. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Barkai, E.; Hansel, D.; Kanter, I. Statistical mechanics of a multilayered neural network. Phys. Rev. Lett. 1990, 65, 2312–2315. [Google Scholar] [CrossRef] [PubMed]
- Ruttor, A.; Kinzel, W.; Naeh, R.; Kanter, I. Genetic attack on neural cryptography. Phys. Rev. E 2006, 73, 036121. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kanter, I.; Kinzel, W.; Kanter, E. Secure exchange of information by synchronization of neural networks. Europhys. Lett. (EPL) 2002, 57, 141–147. [Google Scholar] [CrossRef]
- Dourlens, S. Neuro-Cryptographie Appliquée et Neuro-Cryptanalyse du DES. Ph.D. Thesis, Paris 8 University, Paris, France, 1995. [Google Scholar]
- Kinzel, W.; Kanter, I. Neural cryptography. In Proceedings of the 9th International Conference on Neural Information Processing (ICONIP), Singapore, 18–22 November 2002. [Google Scholar]
- Javurek, M.; Turčanik, M. Synchronization of two tree parity machines. In Proceedings of the 2016 New Trends in Signal Processing (NTSP), Demanovska Dolina, Slovakia, 12–14 October 2016. [Google Scholar]
- Klein, E.; Mislovaty, R.; Kanter, I.; Ruttor, A.; Kinzel, W. Synchronization of neural networks by mutual learning and its application to cryptography. In Proceedings of the NIPS, Vancouver, BC, Canada, 13–18 December 2004. [Google Scholar]
- Aleksandrov, M.; Bashkov, Y. Factors Affecting Synchronization Time of Tree Parity Machines in Cryptography. In Proceedings of the 2020 IEEE 2nd International Conference on Advanced Trends in Information Theory (ATIT), Kyiv, Ukraine, 25–27 November 2020. [Google Scholar]
- Dolecki, M.; Kozera, R. Distribution of the Tree Parity Machine Synchronization Time. Adv. Sci. Technol. Res. J. 2013, 7, 20–27. [Google Scholar] [CrossRef]
- farizrahman4u. GitHub–NeuralKey. Available online: https://github.com/farizrahman4u/neuralkey (accessed on 6 June 2025).
- bgdowski_agh. GitHub–Dynamic TPM Update. Available online: https://github.com/bgdowski-agh/dynamic_TPM_update (accessed on 4 July 2025).
- Ruttor, A. Neural Synchronization and Cryptography. Ph.D. Thesis, Julius Maximilian University of Würzburg, Würzburg, Germany, 2009. [Google Scholar]
- Dolecki, M.; Kozera, R. The Impact of the TPM Weights Distribution on Network Synchronization Time. In Computer Information Systems and Industrial Management. CISIM 2015; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Teodoro, A.; Gomes, O.S.M.; Saadi, M.; Silva, B.A.; Rosa, R.L.; Rodríguez, D.Z. An FPGA-Based Performance Evaluation of Artificial Neural Network Architecture Algorithm for IoT. Wirel. Pers. Commun. 2022, 127, 1085–1116. [Google Scholar] [CrossRef]
- Niemiec, M.; Widlarz, T.; Mehic, M. Secure Synchronization of Artificial Neural Networks Used to Correct Errors in Quantum Cryptography. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023. [Google Scholar]
- Stypiński, M.; Niemiec, M. Synchronization of Tree Parity Machines Using Nonbinary Input Vectors. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 1423–1429. [Google Scholar] [CrossRef] [PubMed]
| Update Rules | Victims’ Updates | Attacker’s Synchronization |
|---|---|---|
| all parties: hebbian | 17.02 ± 0.72 | 65.09 ± 0.31 |
| victims: dynamic_rows, attacker: hebbian | 42.10 ± 2.25 | 63.98 ± 0.31 |
| victims: dynamic_matrix, attacker: hebbian | 39.8 ± 2.15 | 63.52 ± 0.3 |
| all parties: random walk | 42.94 ± 2.11 | 69.24 ± 0.32 |
| victims: dynamic_rows, attacker: random walk | 40.56 ± 1.94 | 69.82 ± 0.31 |
| victims: dynamic_matrix, attacker: random walk | 43.91 ± 2.12 | 69.58 ± 0.32 |
| victims: dynamic_rows, attacker: random rule | 38.46 ± 1.91 | 66.6 ± 0.31 |
| victims: dynamic_matrix, attacker: random rule | 42.79 ± 2.09 | 66.79 ± 0.32 |
| Update Rules | Victims’ Updates | Attacker’s Synchronization |
|---|---|---|
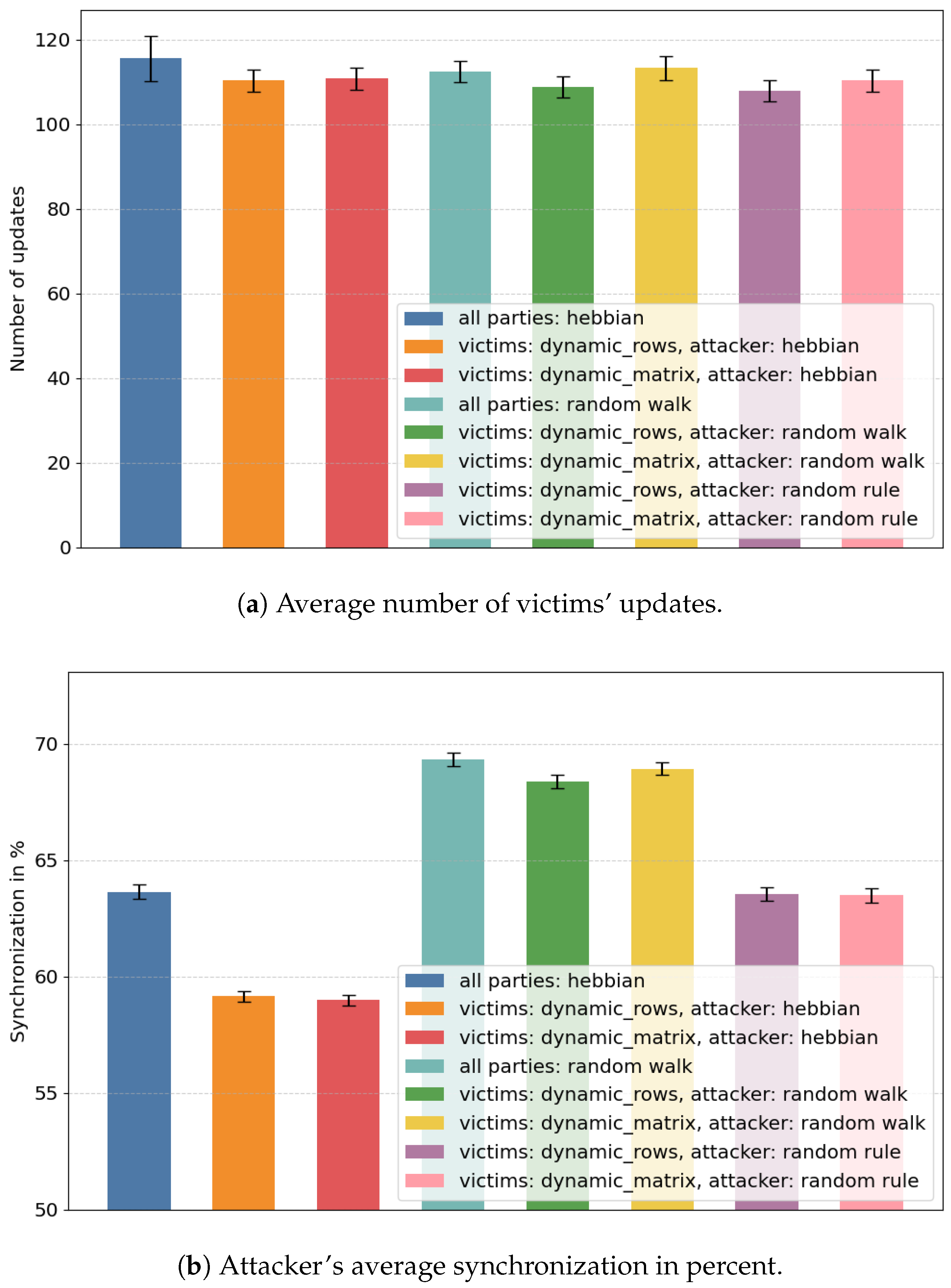
| all parties: hebbian | 115.62 ± 5.27 | 63.62 ± 0.1 |
| victims: dynamic_rows, attacker: hebbian | 110.32 ± 2.56 | 59.13 ± 0.25 |
| victims: dynamic_matrix, attacker: hebbian | 110.78 ± 2.60 | 58.97 ± 0.24 |
| all parties: random walk | 112.5 ± 2.56 | 69.31 ± 0.29 |
| victims: dynamic_rows, attacker: random walk | 108.8 ± 2.52 | 68.35 ± 0.29 |
| victims: dynamic_matrix, attacker: random walk | 113.28 ± 2.76 | 68.92 ± 0.27 |
| victims: dynamic_rows, attacker: random rule | 107.93 ± 2.6 | 63.55 ± 0.29 |
| victims: dynamic_matrix, attacker: random rule | 110.35 ± 2.56 | 63.48 ± 0.31 |
| Update Rules | Victims’ Updates | Attacker’s Synchronization |
|---|---|---|
| all parties: hebbian | 33.06 ± 1.19 | 68.41 ± 0.24 |
| victims: dynamic_rows, attacker: hebbian | 53.95 ± 1.69 | 64.42 ± 0.21 |
| victims: dynamic_matrix, attacker: hebbian | 56.16 ± 1.84 | 64.08 ± 0.21 |
| all parties: random walk | 53.95 ± 1.64 | 71.39 ± 0.23 |
| victims: dynamic_rows, attacker: random walk | 55.65 ± 1.71 | 71.38 ± 0.22 |
| victims: dynamic_matrix, attacker: random walk | 55.26 ± 1.69 | 71.35 ± 0.21 |
| victims: dynamic_rows, attacker: random rule | 54.88 ± 1.79 | 67.92 ± 0.26 |
| victims: dynamic_matrix, attacker: random rule | 57.5 ± 1.86 | 67.64 ± 0.23 |
| Update Rules | Victims’ Updates | Attacker’s Synchronization |
|---|---|---|
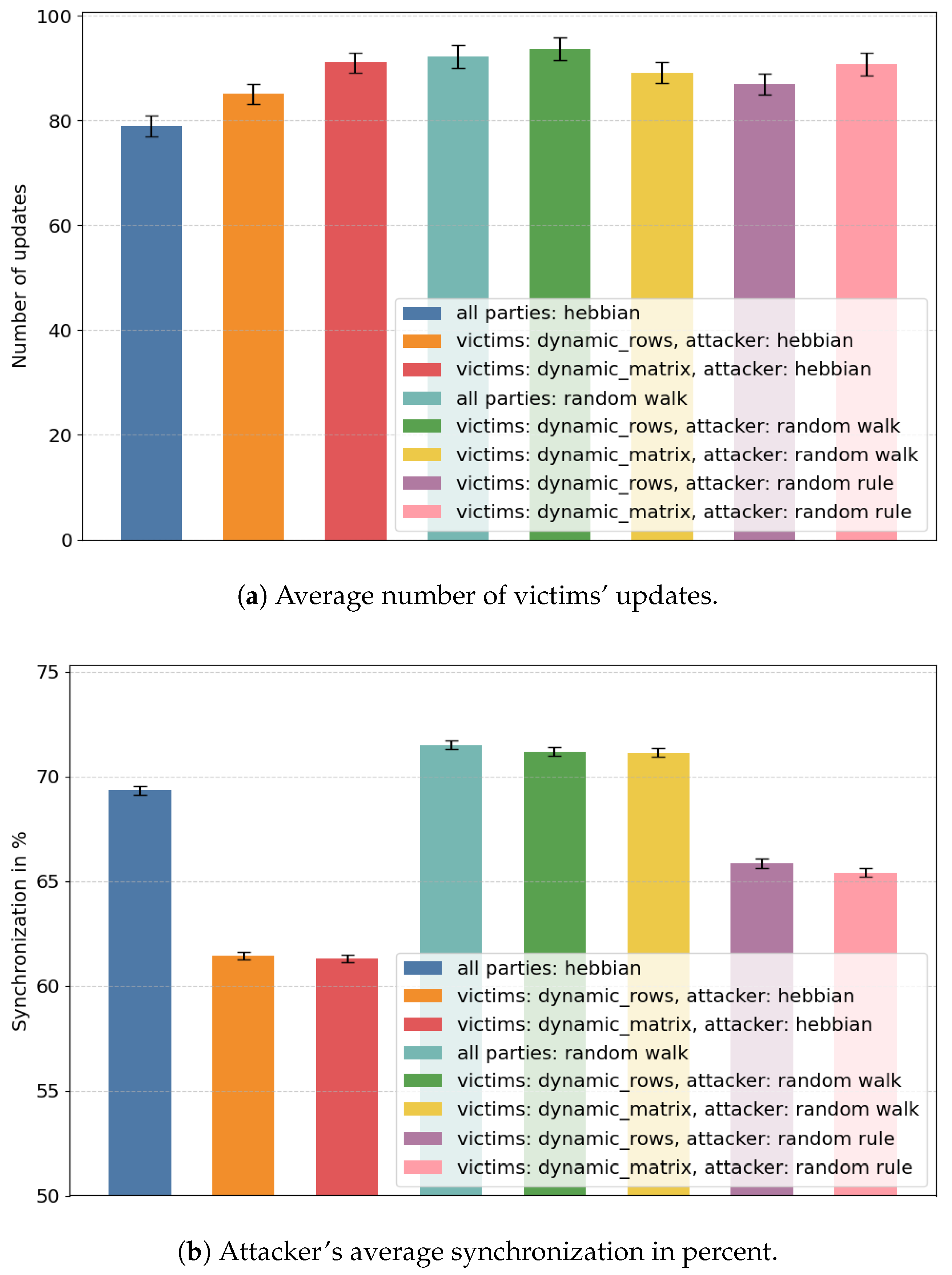
| all parties: hebbian | 78.94 ± 2.06 | 69.32 ± 0.22 |
| victims: dynamic_rows, attacker: hebbian | 85.05 ± 1.89 | 61.42 ± 0.18 |
| victims: dynamic_matrix, attacker: hebbian | 91.08 ± 1.95 | 61.28 ± 0.18 |
| all parties: random walk | 92.15 ± 2.17 | 71.5 ± 0.2 |
| victims: dynamic_rows, attacker: random walk | 93.71 ± 2.23 | 71.17 ± 0.2 |
| victims: dynamic_matrix, attacker: random walk | 89.12 ± 2.06 | 71.13 ± 0.21 |
| victims: dynamic_rows, attacker: random rule | 87.02 ± 2 | 65.85 ± 0.21 |
| victims: dynamic_matrix, attacker: random rule | 90.76 ± 2.17 | 65.41 ± 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gdowski, B.; Mehic, M.; Niemiec, M. Enhancing Security of Error Correction in Quantum Key Distribution Using Tree Parity Machine Update Rule Randomization. Appl. Sci. 2025, 15, 7958. https://doi.org/10.3390/app15147958
Gdowski B, Mehic M, Niemiec M. Enhancing Security of Error Correction in Quantum Key Distribution Using Tree Parity Machine Update Rule Randomization. Applied Sciences. 2025; 15(14):7958. https://doi.org/10.3390/app15147958
Chicago/Turabian StyleGdowski, Bartłomiej, Miralem Mehic, and Marcin Niemiec. 2025. "Enhancing Security of Error Correction in Quantum Key Distribution Using Tree Parity Machine Update Rule Randomization" Applied Sciences 15, no. 14: 7958. https://doi.org/10.3390/app15147958
APA StyleGdowski, B., Mehic, M., & Niemiec, M. (2025). Enhancing Security of Error Correction in Quantum Key Distribution Using Tree Parity Machine Update Rule Randomization. Applied Sciences, 15(14), 7958. https://doi.org/10.3390/app15147958








