Mechanical Behavior Characteristics of Sandstone and Constitutive Models of Energy Damage Under Different Strain Rates
Abstract
1. Introduction
2. Experiment Preparation
3. Experimental Result Analysis
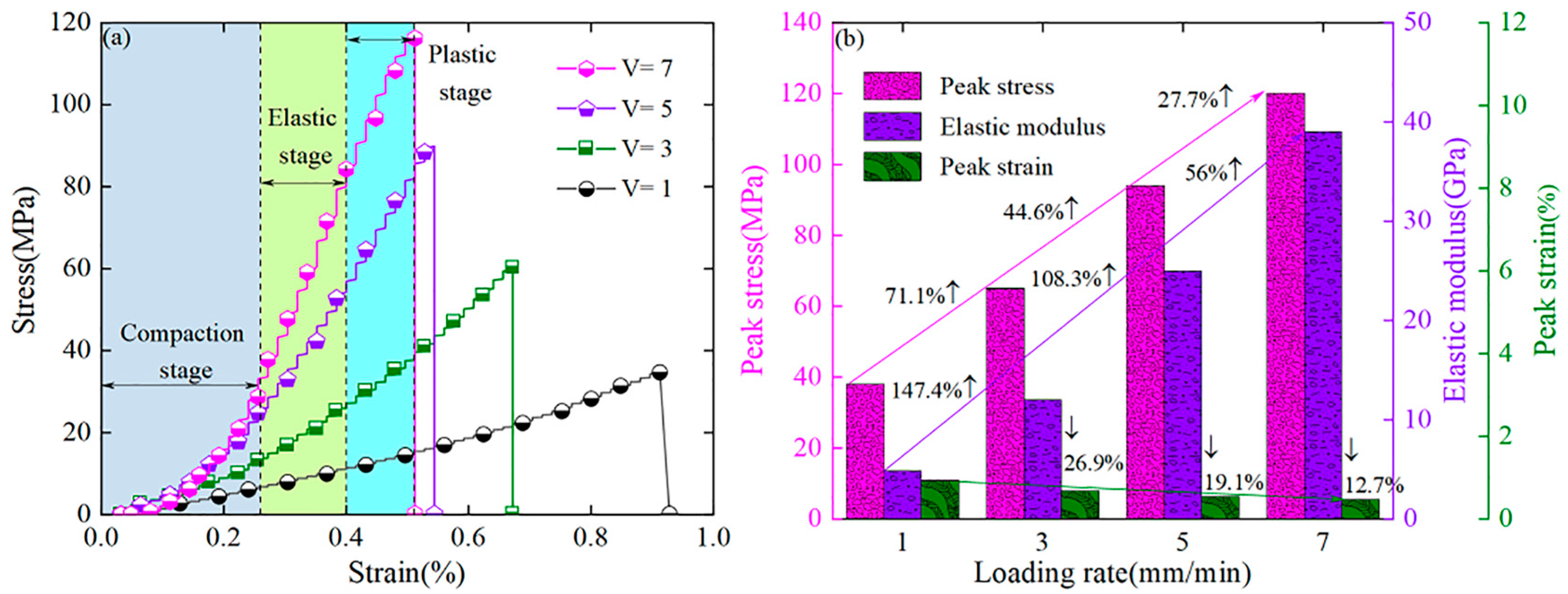
3.1. Strength and Deformation Characteristics
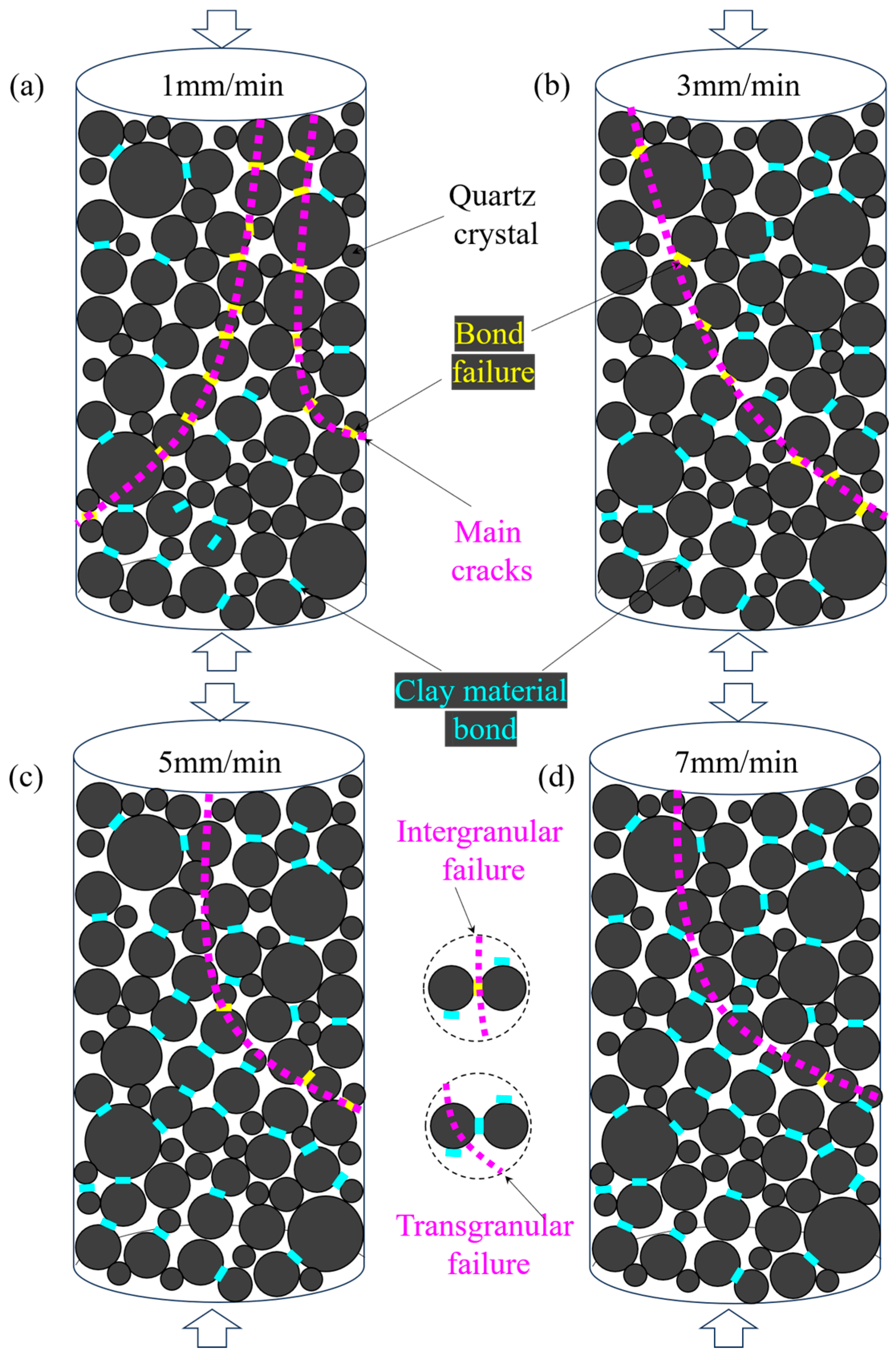
3.2. Failure Characteristics
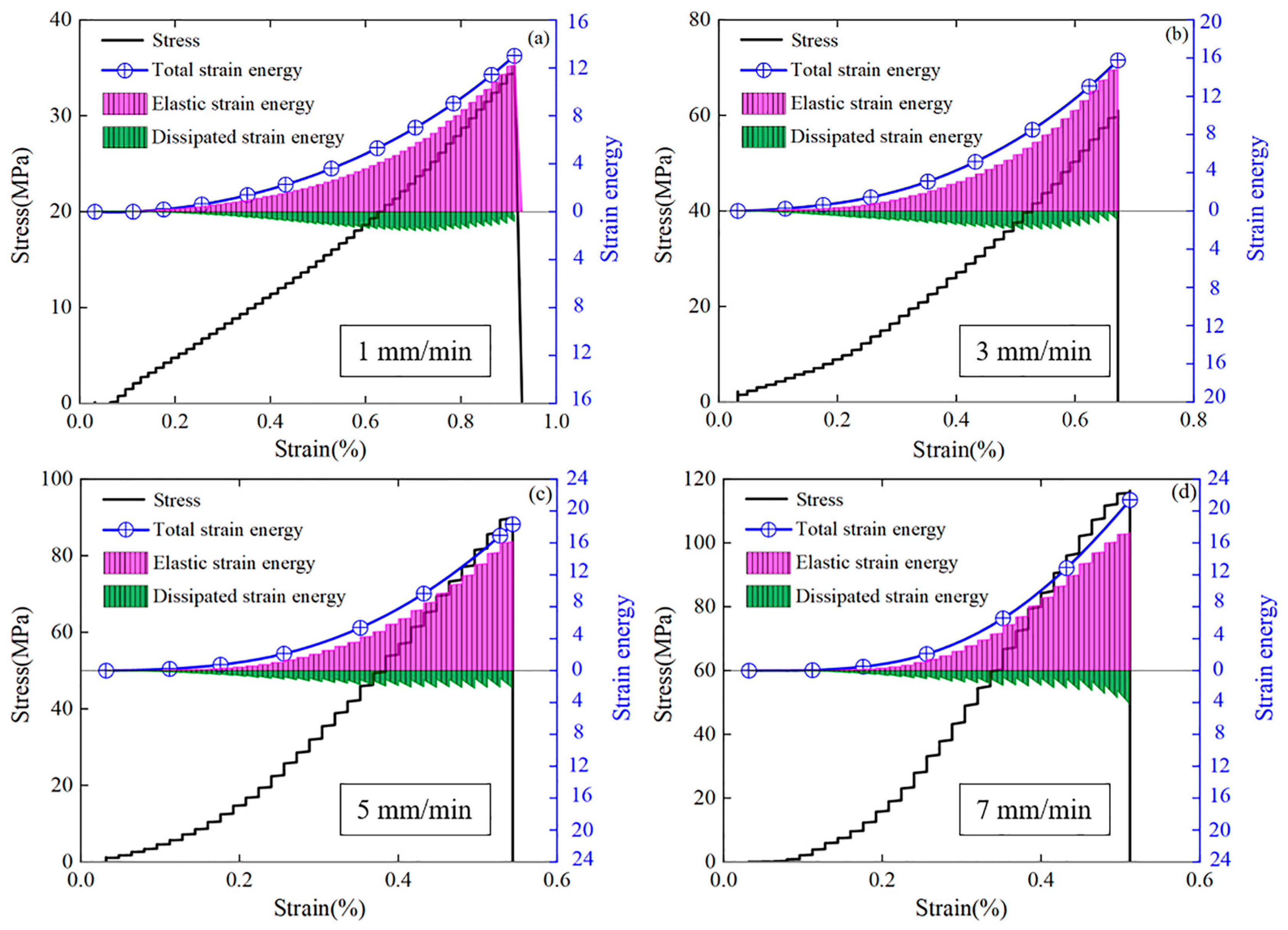
3.3. Energy Characteristics
3.3.1. Energy Calculation
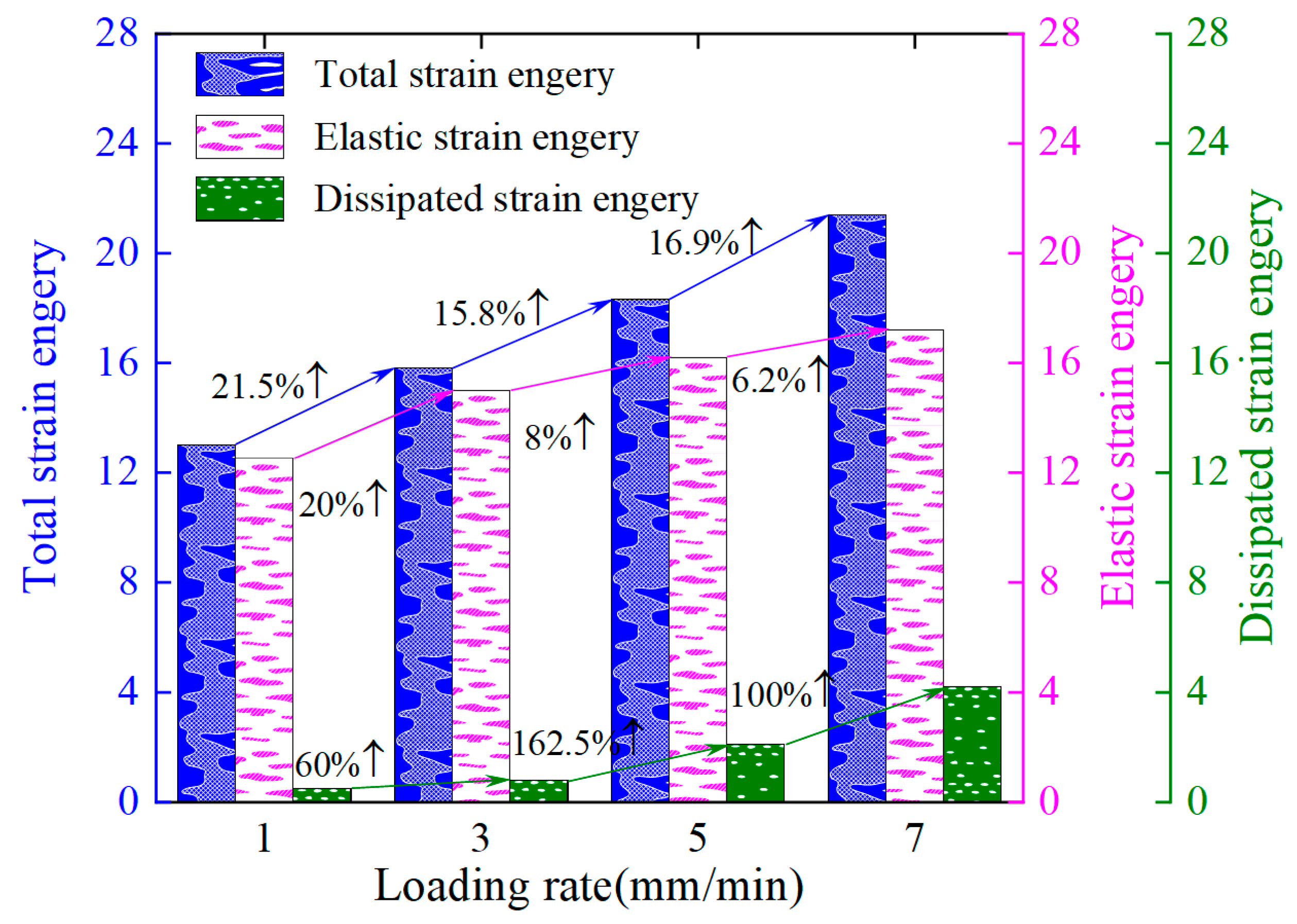
3.3.2. Energy Conversion Characteristics
3.3.3. Relationship Between Energy and Failure Mechanism
4. Discussion
4.1. Constructing Constitutive Model
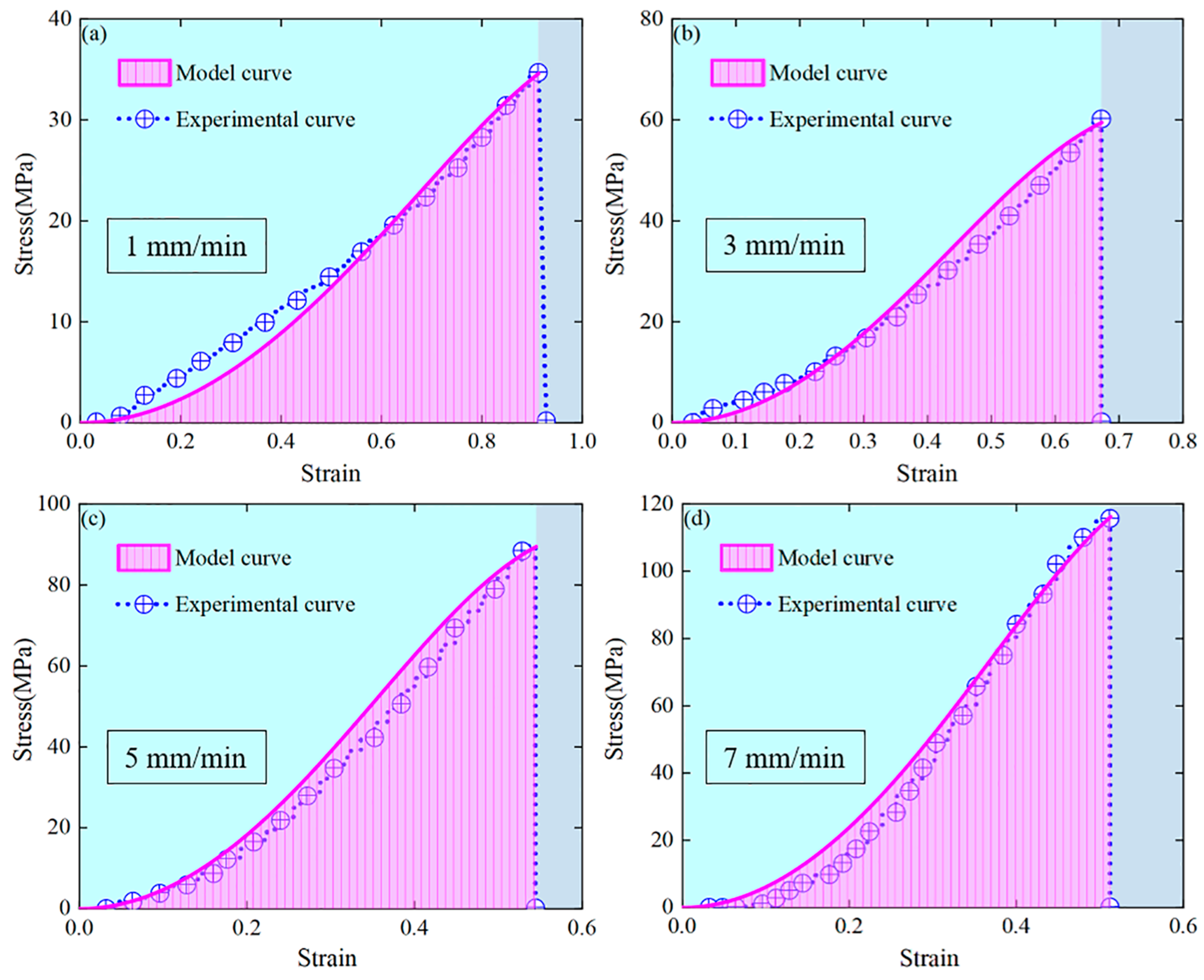
4.2. Constitutive Model Rationality
4.3. Constitutive Model Prediction
5. Conclusions
- (1)
- The strain rate has a significant influence on the mechanical behavior of rock samples. Both the peak stress and the elastic modulus show a monotonically increasing trend with the increase in the strain rate. When the strain rate increased from 1 mm/min to 3 mm/min, the growth ratios of the peak stress and the elastic modulus were the largest, increasing by 71.1% and 147.4%, respectively. The peak strain, however, shows a monotonically decreasing law with the increase in the strain rate, presenting an evolution trend opposite to the peak stress and elastic modulus. The particle size distribution of the destroyed rock blocks varies under different strain rates. Under a low strain rate, large-sized complete rock blocks of the rock samples dominate, while rock samples with a high strain rate retain more small-sized fragmented rock blocks. This difference stems from the variation of secondary crack propagation characteristics.
- (2)
- Rocks exhibit phased energy transformation characteristics during the loading process. In the early stage of loading, the axial stress prompts the closure of the primary fissures. The increase in dissipated strain energy with strain mainly results from the frictional slip of the fissures and the fragmentation of minerals. Entering the middle stage of loading, the residual fissures are compacting and maintaining the continuous increase in the dissipated strain energy, but the energy-dominated mechanism undergoes a transformation. The accelerated bifurcation propagation of secondary cracks in the later stage of loading exacerbated the accumulation of the dissipated strain energy, but the elastic energy storage still dominated. When the secondary crack expands to the critical length, the elastic strain energy is suddenly released, causing macroscopic brittle failure of the rock sample. The energy is dissipated in the forms of crack propagation, clastic kinetic energy, and acoustic emission.
- (3)
- With the increase in the loading stress, secondary cracks preferentially select the propagation path and slowly expand along the clay–quartz interface. The elastic strain energy is slowly released in the form of frictional heat, eventually forming a penetrating main crack that extends along the boundary of the quartz crystal, resulting in the failure of the rock sample along the crystal. At a high strain rate, the energy transfer mechanism changes, the stress relaxation ability of the clay is suppressed, and the energy is forced to transfer to the quartz crystal. Driven by the high elastic strain energy, the tip of the secondary crack rapidly breaks through the energy threshold of the mineral interface and directly penetrates the internal lattice structure of the quartz crystal, resulting in the transgranular failure of the rock sample.
- (4)
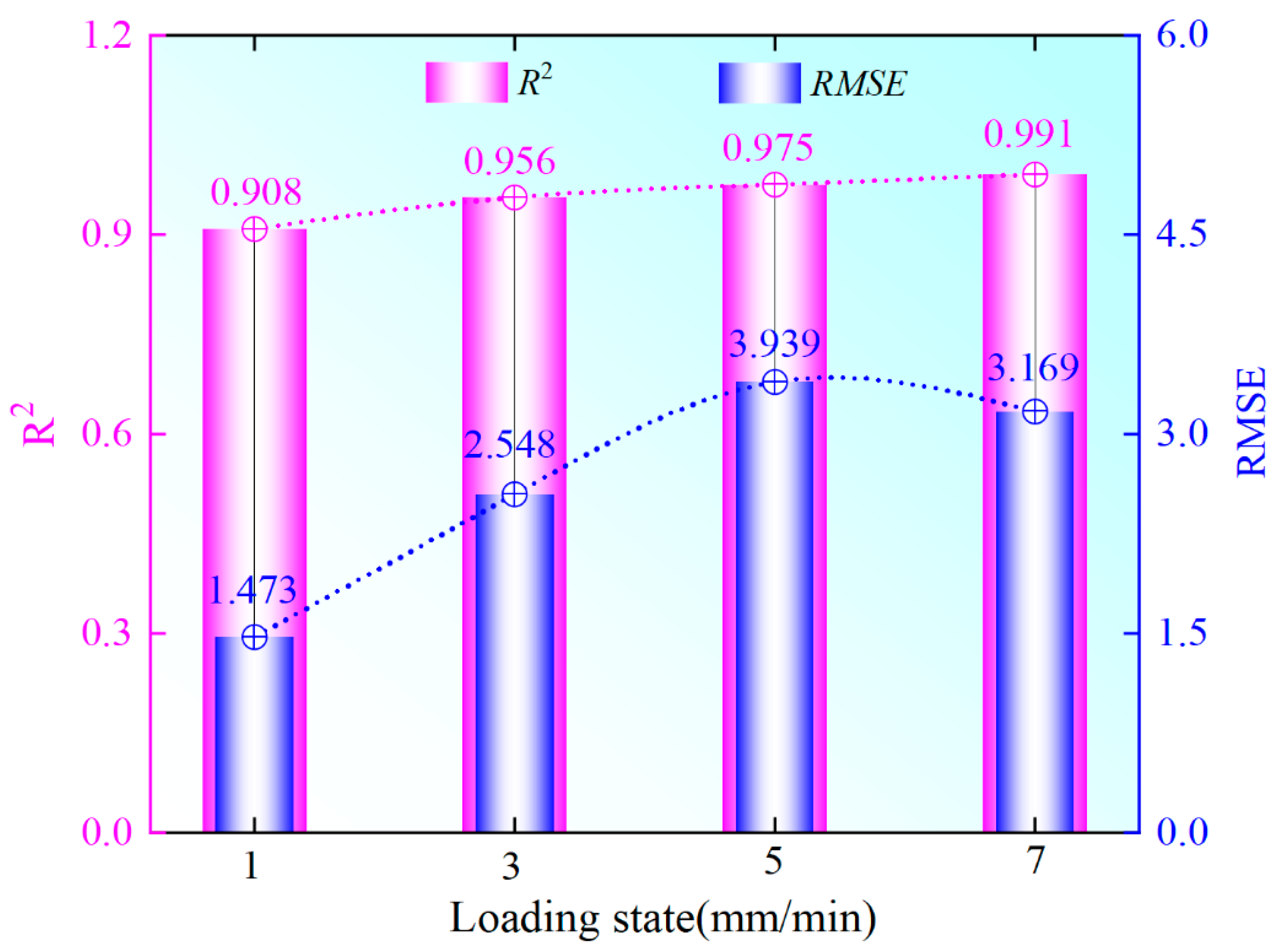
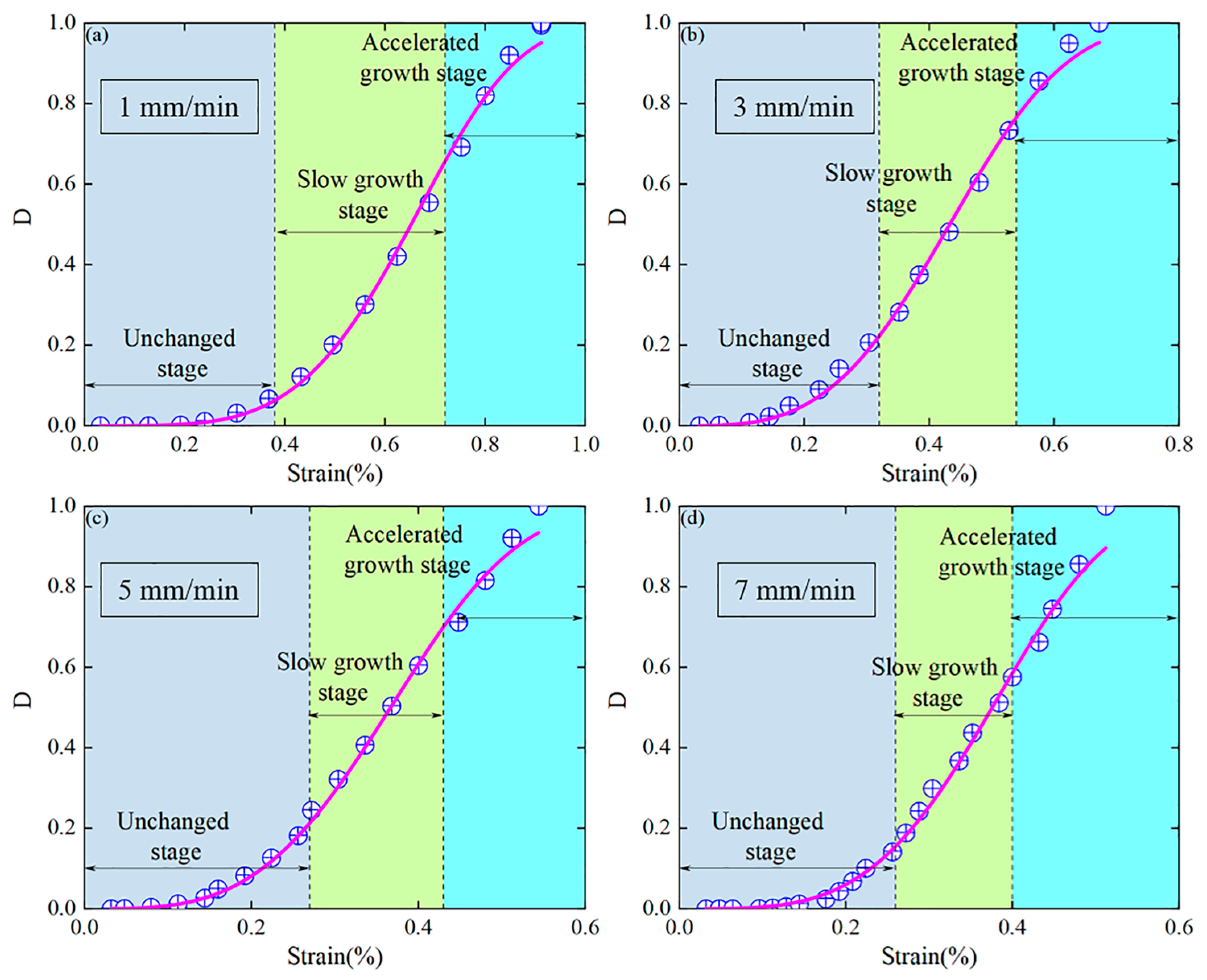
- Judging from R2 and RMSE, the constitutive model of energy damage constructed in this paper is reasonable. With the increase in the strain rate, the fitting degree among rock samples with different strain rates gradually increases, and all are greater than 0.908. This model can not only accurately characterize the nonlinear hardening characteristics of the rock sample in the compaction stage under different strain rates, but also respond well to the strength and deformation laws of the rock sample. Based on the evolution characteristics of the damage variables of this model, its evolution process can be divided into the unchanged stage, the slow growth stage, and the accelerated growth stage. The characteristics of this stage reveal the sudden change mechanism from the dissipation of elastic strain energy of rock samples to the unstable propagation of secondary cracks, clarify the influence of strain rate on damage accumulation, and provide a theoretical basis for the dynamic assessment of surrounding rock damage and disaster early warning when the mine roof is crushed.
6. Further Research Plan
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| U | total input strain energy |
| Ud | dissipative strain energy |
| Ue | elastic strain energy |
| Uh | energy consumed in the form of heat exchange |
| σ | stress |
| ε | strain |
| E | elastic modulus |
| D | damage variable |
| λ, k | parameters of the Weibull distribution |
| N | destruction of microunits |
| NP | total number of microunits |
| U | cumulative dissipated strain energy at a certain moment |
| UP | cumulative dissipated strain energy at the peak stress |
| εn | peak strain corresponding to peak stress |
| εm | the yield strain |
| m1 and m2 | experimental coefficients |
| μ | correction coefficient |
| n | total amount of data |
| σt | measured value of the stress corresponding to the t-th data point |
| theoretical value of the stress corresponding to the t-th data point | |
| average measured stress of the total data quantity |
References
- Gao, X.X.; Shi, X.Y.; Guo, W.B. Case Study on the Mechanism of Influence of Stoppage on Ground Pressure under Different Rates of Advance. Adv. Civ. Eng. 2021, 2021, 5574693. [Google Scholar] [CrossRef]
- Ardehjani, E.A.; Ataei, M.; Rafiee, R. Estimation of First and Periodic Roof Weighting Effect Interval in Mechanized Longwall Mining Using Numerical Modeling. Int. J. Geomech. 2020, 20, 04019164. [Google Scholar] [CrossRef]
- Wang, S.G.; Yuan, C.; Li, L.X.; Su, X.W.; Wang, C. Application of Research on Risk Assessment of Roadway Roof Falls Based on Combined Weight Matter Element Extension Model. Appl. Sci. 2024, 14, 4111. [Google Scholar] [CrossRef]
- Chen, T.; Yao, Q.; Wei, F.; Chong, Z.; Zhou, J.; Wang, C.; Li, J. Effects of water intrusion and loading rate on mechanical properties of and crack propagation in coal-rock combinations. J. Cent. South Univ. 2017, 24, 423–431. [Google Scholar] [CrossRef]
- Gong, F.; Ye, H.; Luo, Y. The Effect of High Loading Rate on the Behaviour and Mechanical Properties of Coal-Rock Combined Body. Shock Vib. 2018, 2018, 4374530. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J. The effect of loading rate on the behavior of samples composed of coal and rock. Int. J. Rock Mech. Min. Sci. 2013, 61, 23–30. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.; Han, L.; Pu, H.; Chen, Y.L. Experimental research on the influence of loading rate on the mechanical properties of limestone in a high-temperature state. Bull. Eng. Geol. Environ. 2019, 78, 3479–3492. [Google Scholar] [CrossRef]
- Wang, J.B.; Zhang, Q.; Song, Z.P.; Zhang, Y.W.; Liu, X.R. Mechanical properties and damage constitutive model for uniaxial compression of salt rock at different loading rates. Int. J. Damage Mech. 2021, 30, 739–763. [Google Scholar] [CrossRef]
- Komurlu, E. Loading rate conditions and specimen size effect on strength and deformability of rock materials under uniaxial compression. Int. J. Geo-Eng. 2018, 9, 17. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, E. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Ma, C.; Tan, G.; Lv, Z.; Yang, W.; Zhang, J. Fracture Mechanism of Sandstone Under Triaxial Extension at Different Loading Rates. Rock Mech. Rock Eng. 2023, 56, 3429–3450. [Google Scholar] [CrossRef]
- Suo, Y.; Zhao, Y.-J.; Fu, X.-F.; He, W.-Y.; Pan, Z.-J. Mixed-mode fracture behavior in deep shale reservoirs under different loading rates and temperatures. Pet. Sci. 2023, 20, 3037–3047. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, L.; Fan, L. Investigation of the characteristics of rock fracture process zone using coupled FEM/DEM method. Eng. Fract. Mech. 2018, 200, 355–374. [Google Scholar] [CrossRef]
- Zhao, K.; Yu, X.; Zhou, Y.; Wang, Q.; Wang, J.Q.; Hao, J.L. Energy evolution of brittle granite under different loading rates. Int. J. Rock Mech. Min. Sci. 2020, 132, 104392. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Yu, R.; Hu, L.; Irfan, M. Effect of Loading Rate on the Felicity Effect of Three Rock Types. Rock Mech. Rock Eng. 2017, 50, 1673–1681. [Google Scholar] [CrossRef]
- Wei, Y.L.; Zhao, L.Y.; Yuan, T.; Liu, W. Study on Mechanical Properties of Shale Under Different Loading Rates. Front. Earth Sci. 2022, 9, 815616. [Google Scholar] [CrossRef]
- Zhang, J.W.; Ding, L.J.; Song, Z.X.; Fan, W.B.; Wang, S.Y. Mechanical properties of deep sandstones under loading rate effect. J. Cent. South Univ. 2022, 29, 1933–1944. [Google Scholar] [CrossRef]
- Gao, H.; Xie, H.; Zhang, R.; Zhang, Z.; Gao, M.; Lu, J.; Wu, M.; Li, Y.; Xie, H. Effect of True Triaxial Loading and Unloading Rates on the Mechanical Properties of Deep Rock. Rock Mech. Rock Eng. 2025, 1–25. [Google Scholar] [CrossRef]
- Li, X.; Liu, C. Mechanical Properties and Damage Constitutive Model of High Water Material at Different Loading Rates. Adv. Eng. Mater. 2018, 20, 1701098. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, W.; Peng, W.; Wang, Y.; Zhou, Y.; Peng, Z. Uniaxial compressive damage evolution and constitutive modeling of fissure-like rocks under different loading rates based on acoustic emission. Sci. Rep. 2025, 15, 2119. [Google Scholar] [CrossRef] [PubMed]
- GB/T 50266-2013; Ministry of Housing and Urban-Rural Development of the People’s Republic of China, Standard for Test Methods of Engineering Rock Masses. China Planning Press: Beijing, China, 2013.
- Dai, B.; Shan, Q.-W.; Chen, Y.; Luo, X.-Y. Mechanical and energy dissipation characteristics of granite under cyclic impact loading. J. Cent. South Univ. 2022, 29, 116–128. [Google Scholar] [CrossRef]
- Dehestani, A.; Kazemi, F.; Abdi, R.; Nitka, M. Prediction of fracture toughness in fibre-reinforced concrete, mortar, and rocks using various machine learning techniques. Eng. Fract. Mech. 2022, 276, 108914. [Google Scholar] [CrossRef]
- Chen, G.Q.; Li, T.B.; Wang, W.; Zhu, Z.F.; Chen, Z.Q.; Tang, O.L. Weakening effects of the presence of water on the brittleness of hard sandstone. Bull. Eng. Geol. Environ. 2019, 78, 1471–1483. [Google Scholar] [CrossRef]
- Xie, H.; Ju, Y.; Li, L. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Chen, J.H.; Zeng, B.Q.; Xu, W.Y.; Hu, S.S.; Wang, S.J.; Wang, K.; Zhang, W.B.; Wu, S.K.; Song, Z.X. Mechanical behaviour and damage constitutive model of semi-circular arch tunnels with straight walls under soaking conditions. Eng. Fail. Anal. 2025, 169, 109137. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.J.; Han, P.H.; Zhang, T.; Zhang, L.; Wang, F.T. Acoustic emission and splitting surface roughness of sandstone in a Brazilian splitting test under the influence of water saturation. Eng. Geol. 2024, 329, 107369. [Google Scholar] [CrossRef]
- Wang, J.; Ma, D.; Li, Z.; Huang, Y.; Du, F. Experimental investigation of damage evolution and failure criterion on hollow cylindrical rock samples with different bore diameters. Eng. Fract. Mech. 2022, 260, 108182. [Google Scholar] [CrossRef]
- Chen, J.H.; Zeng, B.Q.; Xu, W.Y.; Wang, K.; Liu, P.; Hu, S.S.; Wang, S.J.; Song, Z.X.; Wu, S.K.; Bai, X.Y. Deterioration mechanism and dynamic constitutive model of coal-rock assemblages considering chemical corrosion and impact damage. Int. J. Min. Sci. Technol. 2025, 35, 837–862. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; He, M.; Shen, R.; Gu, Z.; Cheng, T.; Xiao, Y.; Tang, J. Effect of water saturation on dynamic behavior of sandstone after wetting-drying cycles. Eng. Geol. 2023, 319, 107109. [Google Scholar] [CrossRef]
- Stavropoulou, M.; Xiroudakis, G. Fracture Frequency and Block Volume Distribution in Rock Masses. Rock Mech. Rock Eng. 2020, 53, 4673–4689. [Google Scholar] [CrossRef]
- Chen, J.H.; Zeng, B.Q.; Xu, W.Y.; Wang, K.; Wang, S.J.; Hu, S.S.; Song, Z.X.; Wu, S.K. Progressive failure characteristics and damage constitutive model of rock samples under immersion conditions. J. China Coal Soc. 2024, 2024, 1–19. [Google Scholar] [CrossRef]
- Shen, P.; Tang, H.; Ning, Y.; Xia, D. A damage mechanics based on the constitutive model for strain-softening rocks. Eng. Fract. Mech. 2019, 216, 106521. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.J.; Tan, Y.l.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Han, P.; Wang, K.; Pang, J.; Ji, X.; Zhang, C. Response properties of geometries of coal penetrating fracture on seepage behavior. Int. J. Min. Sci. Technol. 2025, 35, 191–211. [Google Scholar] [CrossRef]

| Rock Samples | Loading Rate (mm/min) | Ultrasonic Wave (km/s) | Weight (g) | Height (mm) | Diameter (mm) |
|---|---|---|---|---|---|
| A1-1 | 1 | 3.02 | 504.53 | 100.32 | 49.89 |
| A2-1 | 3.05 | 506.71 | 99.83 | 49.97 | |
| A3-1 | 2.99 | 503.97 | 100.6 | 49.7 | |
| A1-3 | 3 | 2.97 | 503.95 | 99.79 | 49.72 |
| A2-3 | 3.03 | 504.89 | 99.94 | 49.91 | |
| A3-3 | 2.98 | 504.24 | 99.87 | 49.95 | |
| A1-5 | 5 | 3.04 | 505.24 | 100.51 | 49.96 |
| A2-5 | 3.02 | 504.76 | 99.75 | 49.87 | |
| A3-5 | 2.97 | 504.18 | 100.48 | 49.97 | |
| A1-7 | 7 | 3.00 | 504.23 | 99.83 | 49.94 |
| A2-7 | 3.04 | 505.58 | 100.52 | 49.86 | |
| A3-7 | 3.02 | 504.61 | 100.46 | 49.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhang, C. Mechanical Behavior Characteristics of Sandstone and Constitutive Models of Energy Damage Under Different Strain Rates. Appl. Sci. 2025, 15, 7954. https://doi.org/10.3390/app15147954
Xu W, Zhang C. Mechanical Behavior Characteristics of Sandstone and Constitutive Models of Energy Damage Under Different Strain Rates. Applied Sciences. 2025; 15(14):7954. https://doi.org/10.3390/app15147954
Chicago/Turabian StyleXu, Wuyan, and Cun Zhang. 2025. "Mechanical Behavior Characteristics of Sandstone and Constitutive Models of Energy Damage Under Different Strain Rates" Applied Sciences 15, no. 14: 7954. https://doi.org/10.3390/app15147954
APA StyleXu, W., & Zhang, C. (2025). Mechanical Behavior Characteristics of Sandstone and Constitutive Models of Energy Damage Under Different Strain Rates. Applied Sciences, 15(14), 7954. https://doi.org/10.3390/app15147954








