Mechanical Properties and Failure Mechanisms of Sandstone Under Combined Action of Cyclic Loading and Freeze–Thaw
Abstract
1. Introduction
2. Materials and Methods
2.1. Indoor Testing Program
2.2. Numerical Modeling
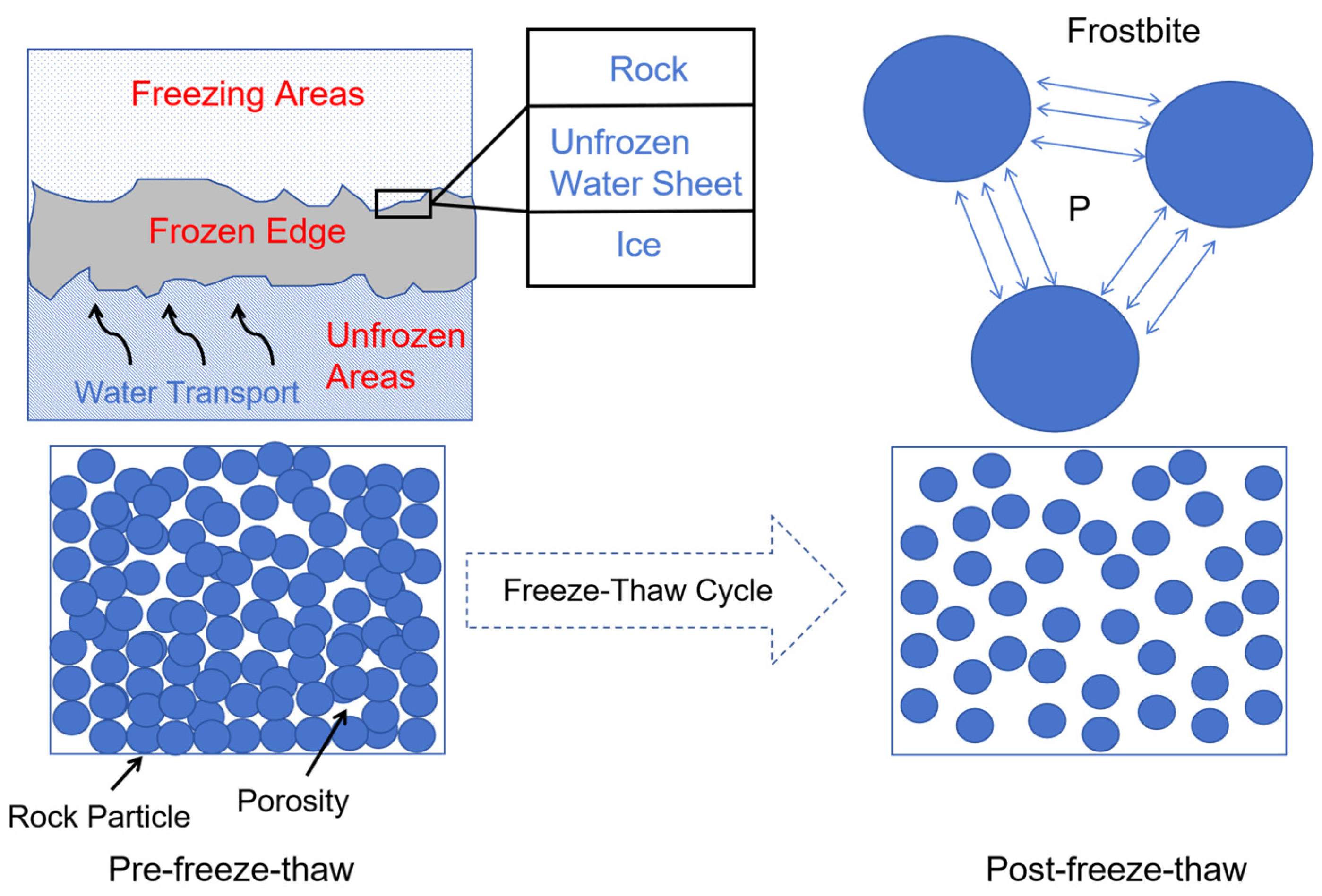
2.3. Freeze–Thaw Cycle Simulation
3. Results and Discussion
3.1. Mass and Wave Velocity Damage Analysis
3.2. Analysis of Numerical Simulation Results
3.2.1. Crack Extension Analysis
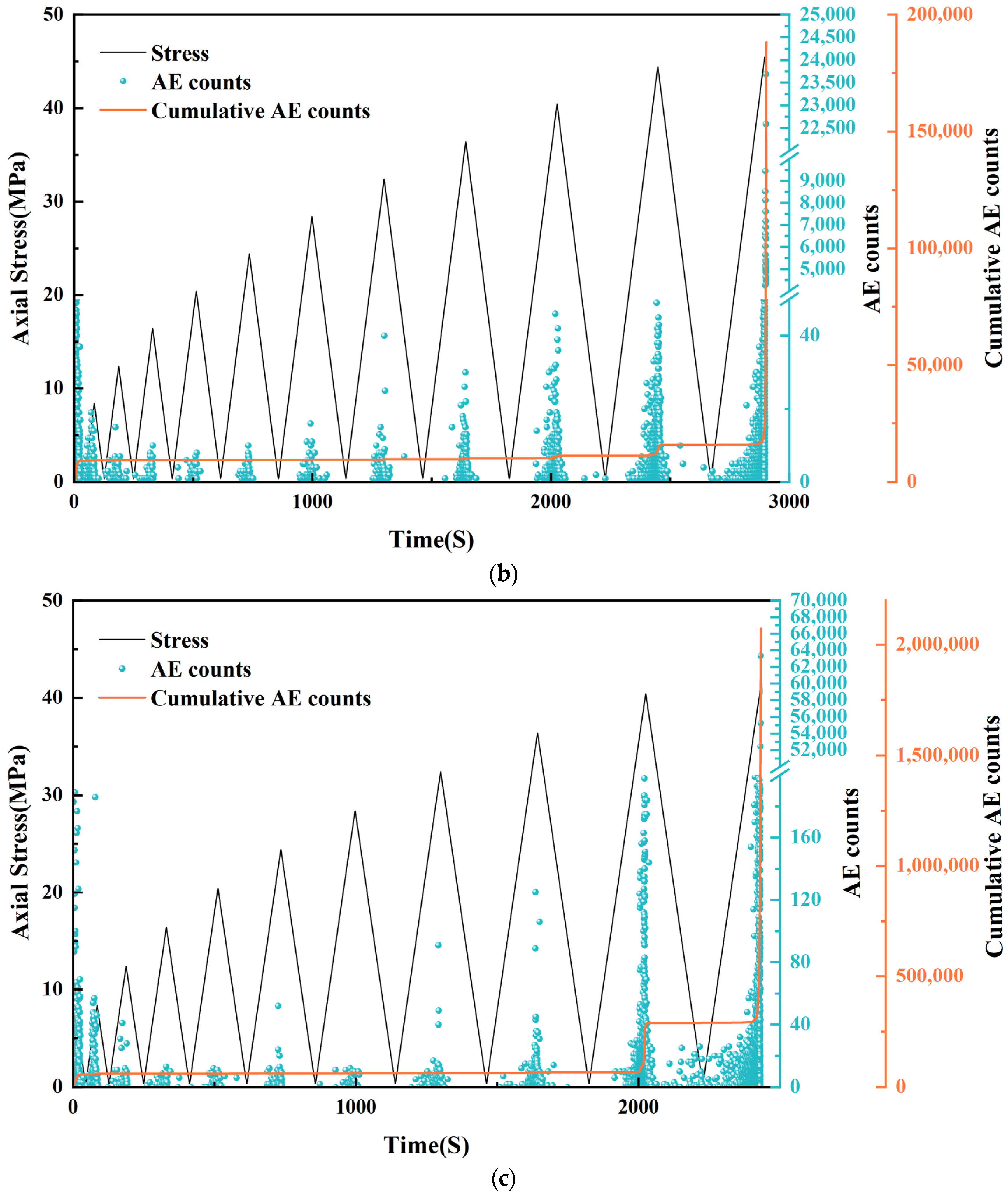
3.2.2. Energy Analysis
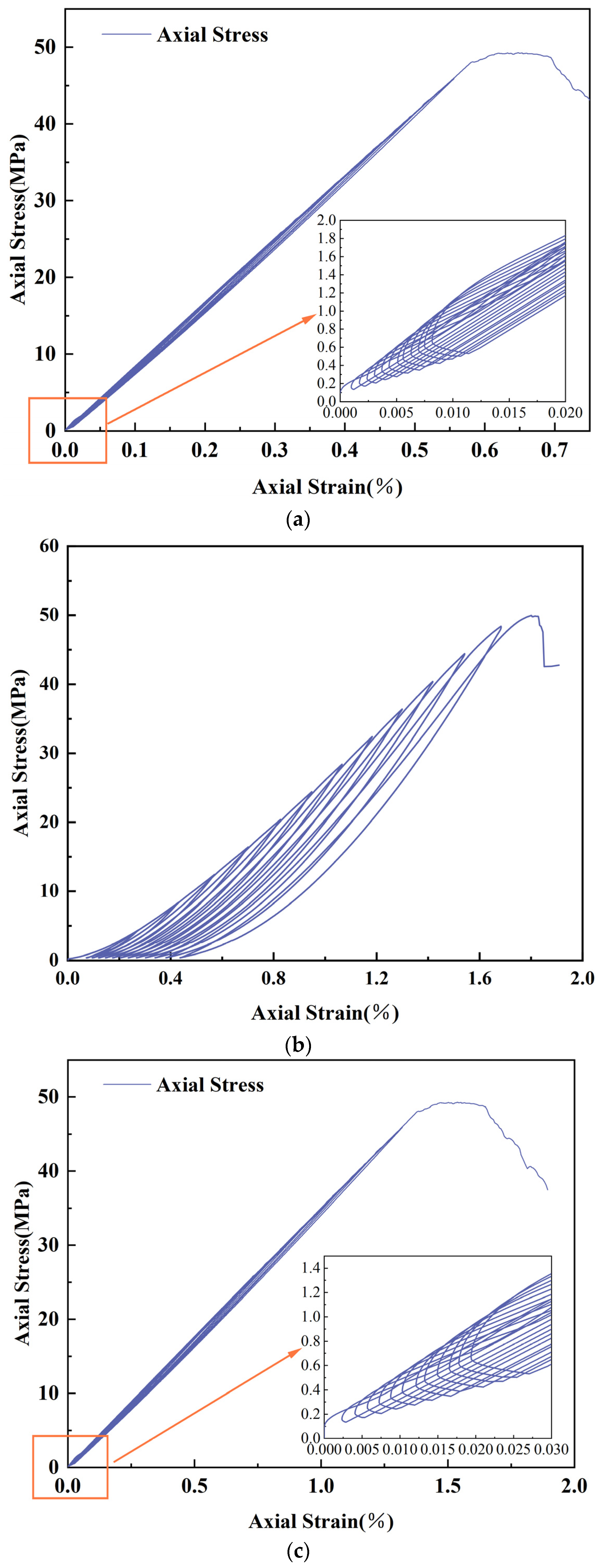
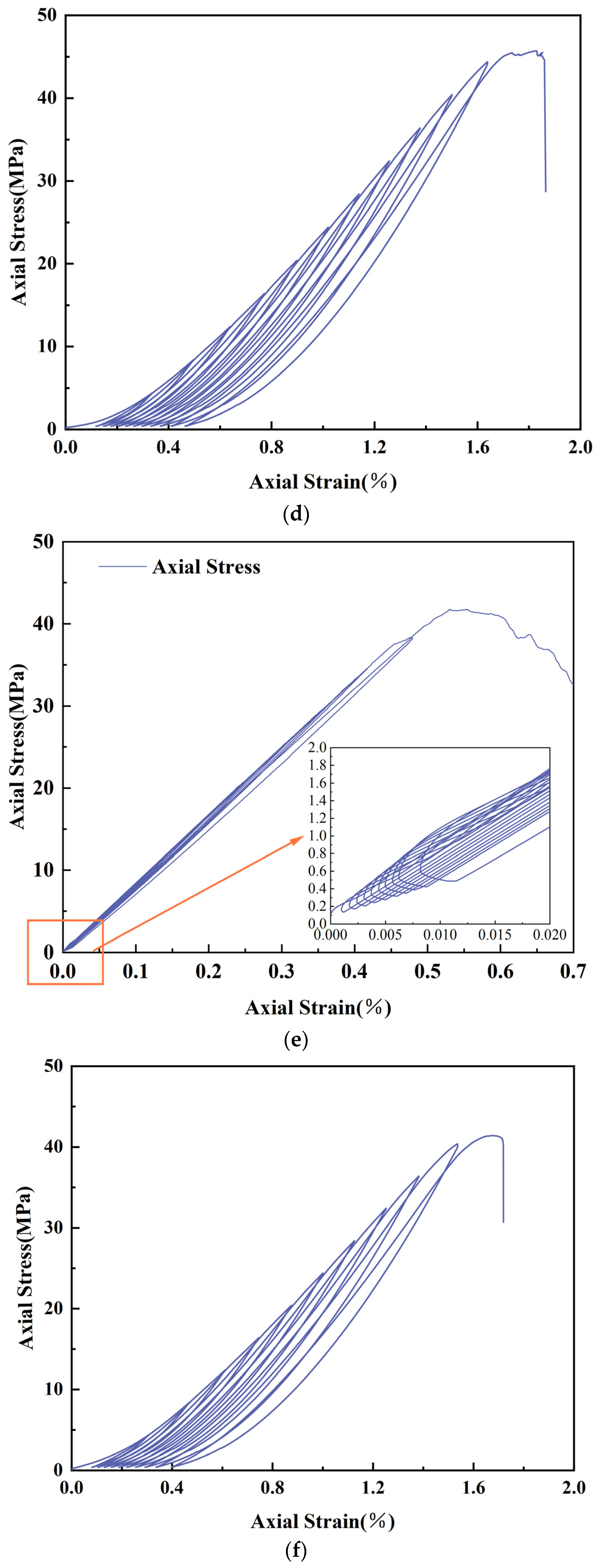
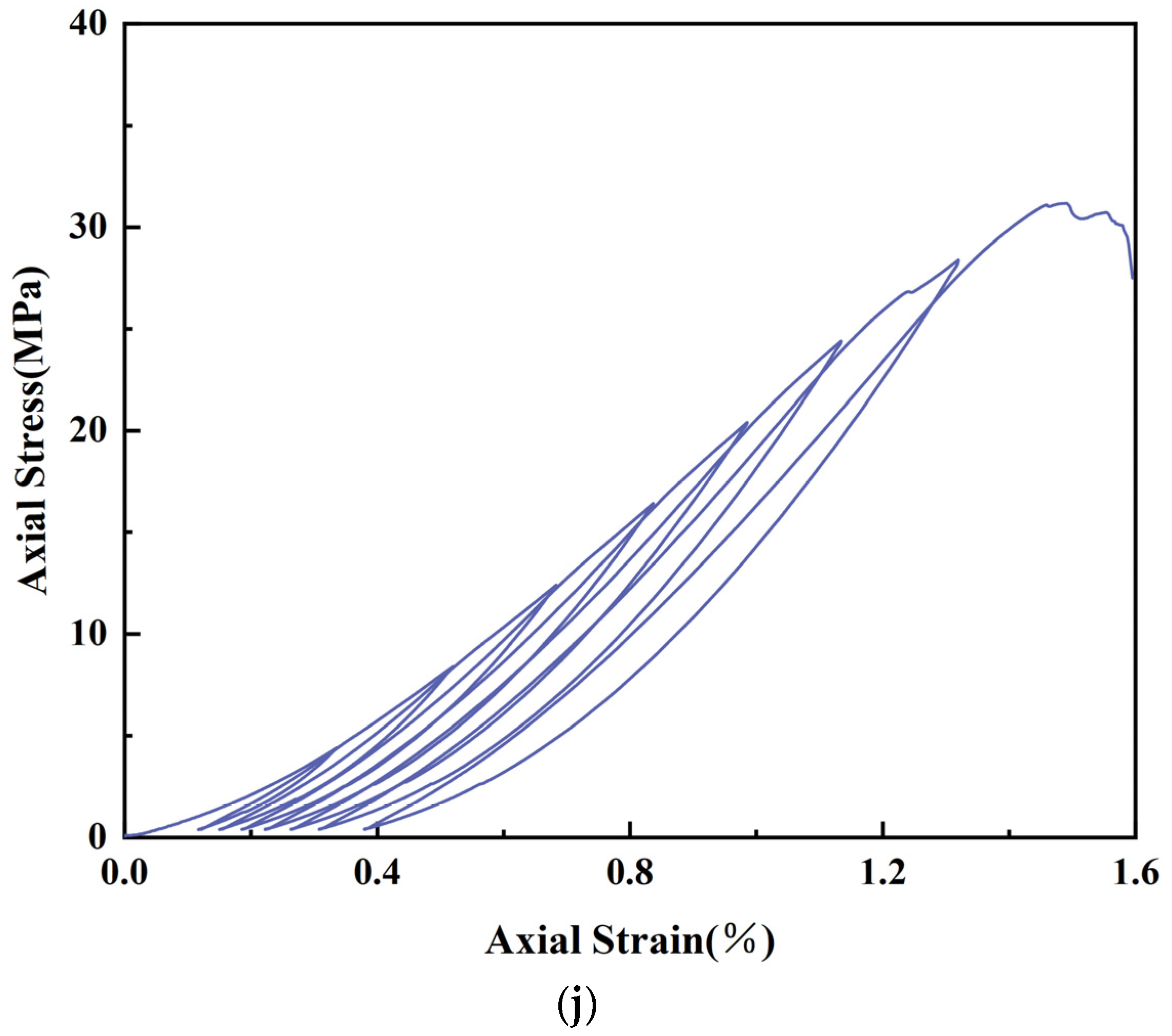
3.2.3. Cyclic Loading and Unloading Stress–Strain Analysis
3.2.4. Analysis of Damage Patterns of Specimens
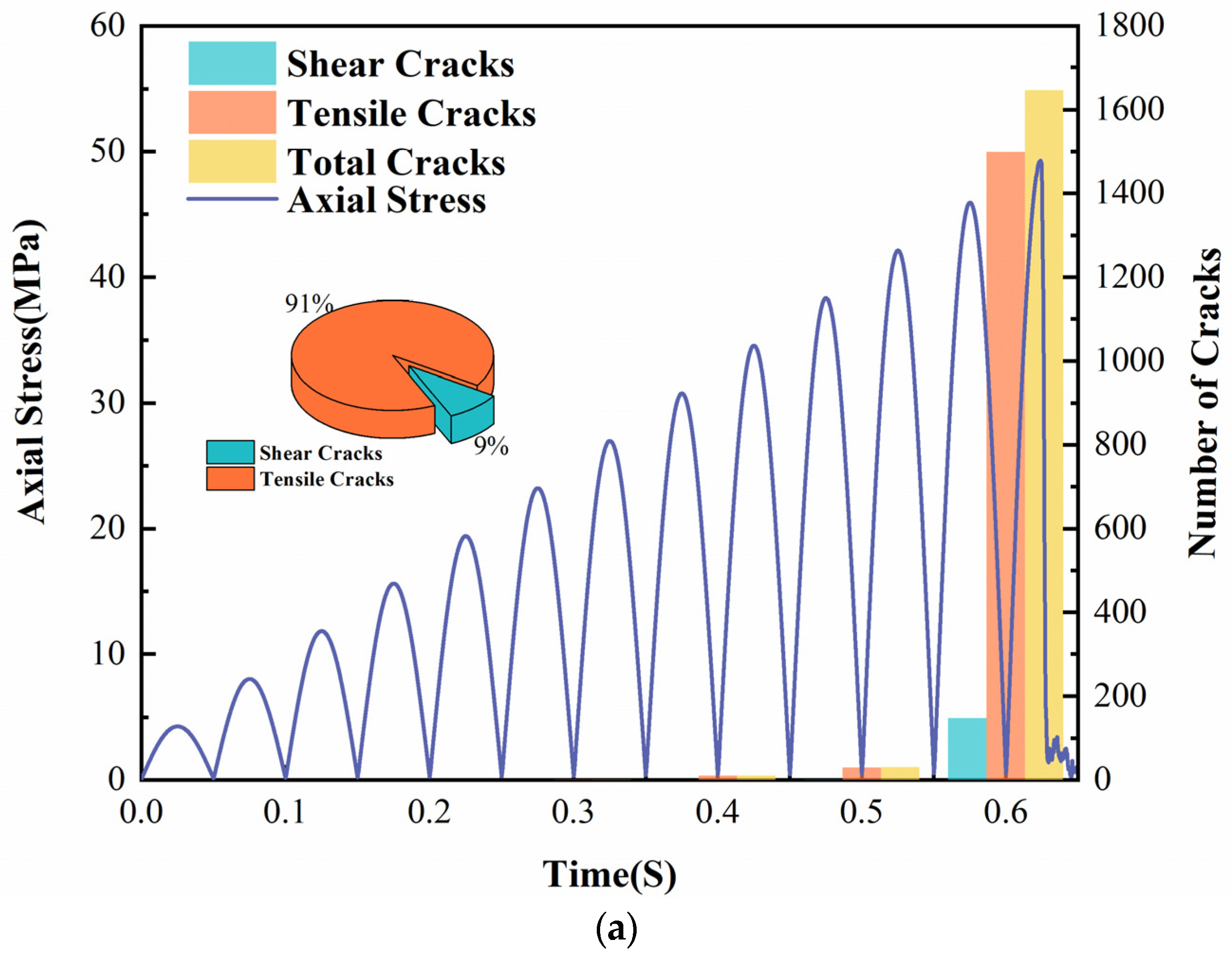
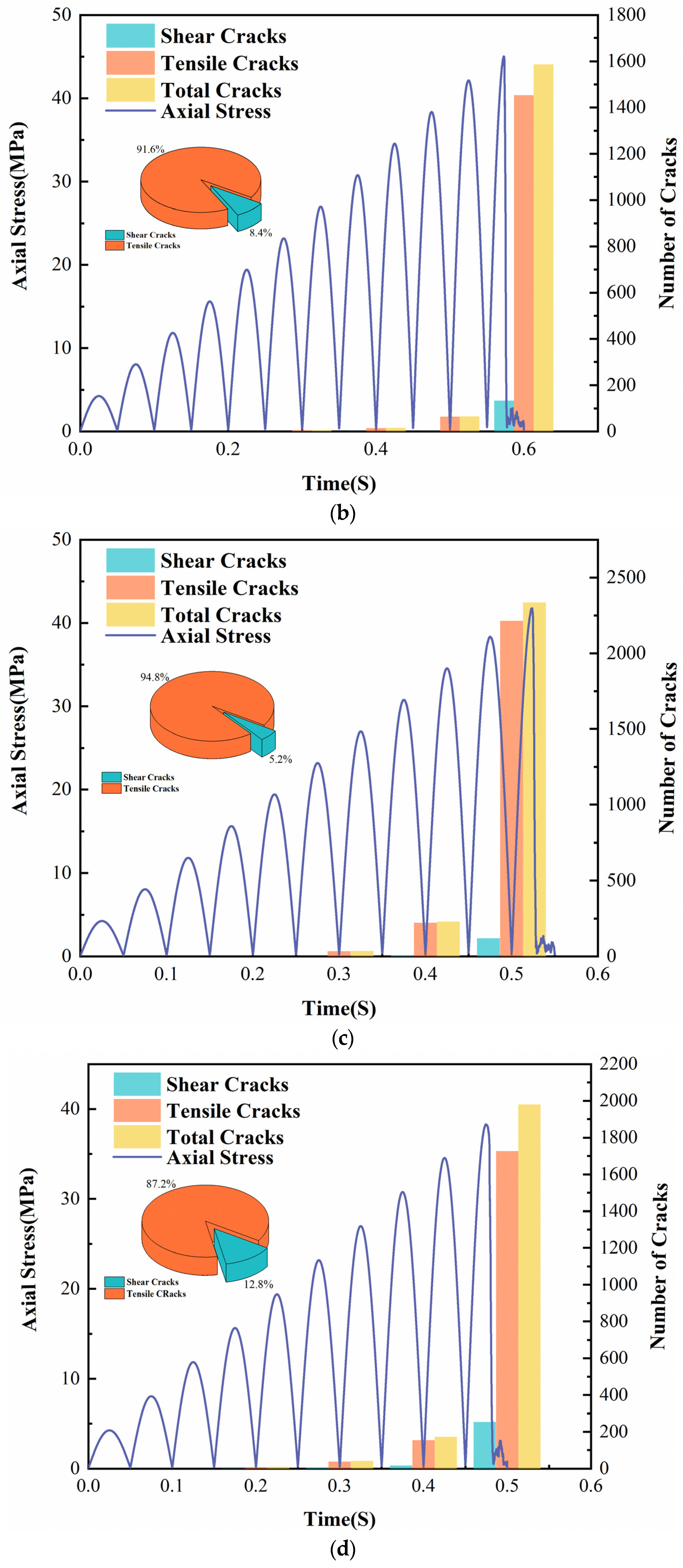
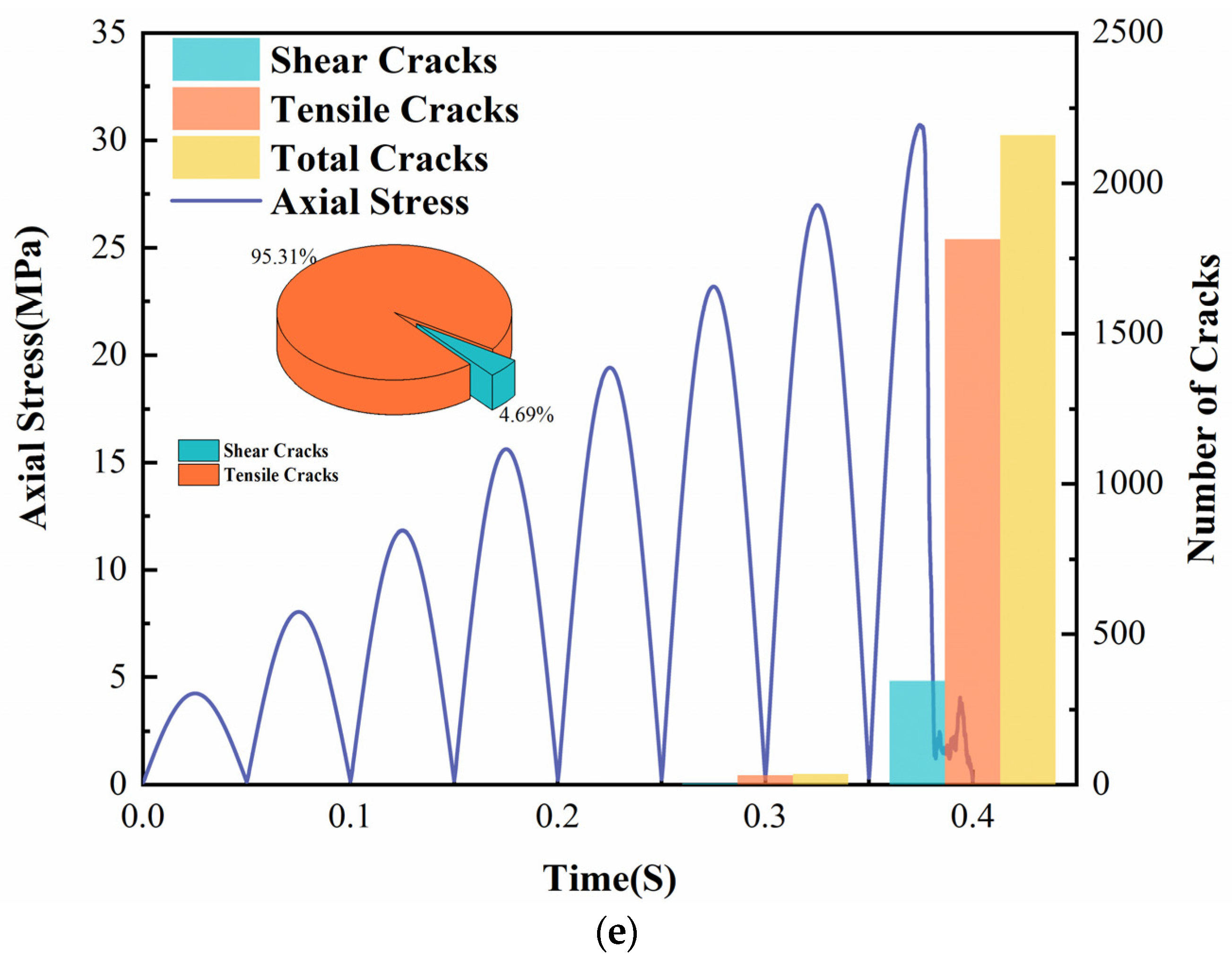
3.2.5. Analysis of Crack Extension During Cyclic Loading and Unloading Simulation
4. Conclusions
- The Wave Velocity Damage Factor () increases linearly throughout the cycle period. It provides that the wave propagation velocity within the sandstone is sensitive to changes in the freeze–thaw cycles. In contrast, the Mass Damage Factor () shows a significant change only at a higher number of freeze–thaw cycles.
- The PFC thermal calculation module was used to simulate the freeze–thaw cycle process of sandstone, and the model agreed with the experimental results. Combined with the energy analysis, the model continues accumulating energy due to the freezing and swelling effect. At specific moments, the energy undergoes a drastic and rapid release. Subsequently, the specimen enters the next energy accumulation period, and the frequency of energy release increases as the number of freeze–thaw cycles increases.
- Cyclic loading leads to the accumulation of internal damage in the specimen, resulting in a gradual weakening of the load-bearing capacity of the specimen. The average value of the Cumulative Strain Difference () is calculated to be 20.57%, which is within a reasonable range. Moreover, the trend of Cumulative Strain Difference () reflects that the difference between simulated and measured plastic strains decreases with the increase in cycle level.
- The crack extension pattern inside the specimen changes significantly with increased freeze–thaw cycles. When the number of freeze–thaw cycles is higher, the specimen is more likely to form X-shaped conjugate shear damage. When the number of freeze–thaw cycles is less, the specimen is more likely to have monoclinic shear damage. The freezing and swelling forces destroy the mineral particle cementation and reduce its strength. The freeze–thaw destroys the specimen from the outside to the inside, so the cracks are more inclined to expand to the outer surface, leading to block spalling on the outer surface of the specimen. These two factors combine to influence the damage pattern of the rock.
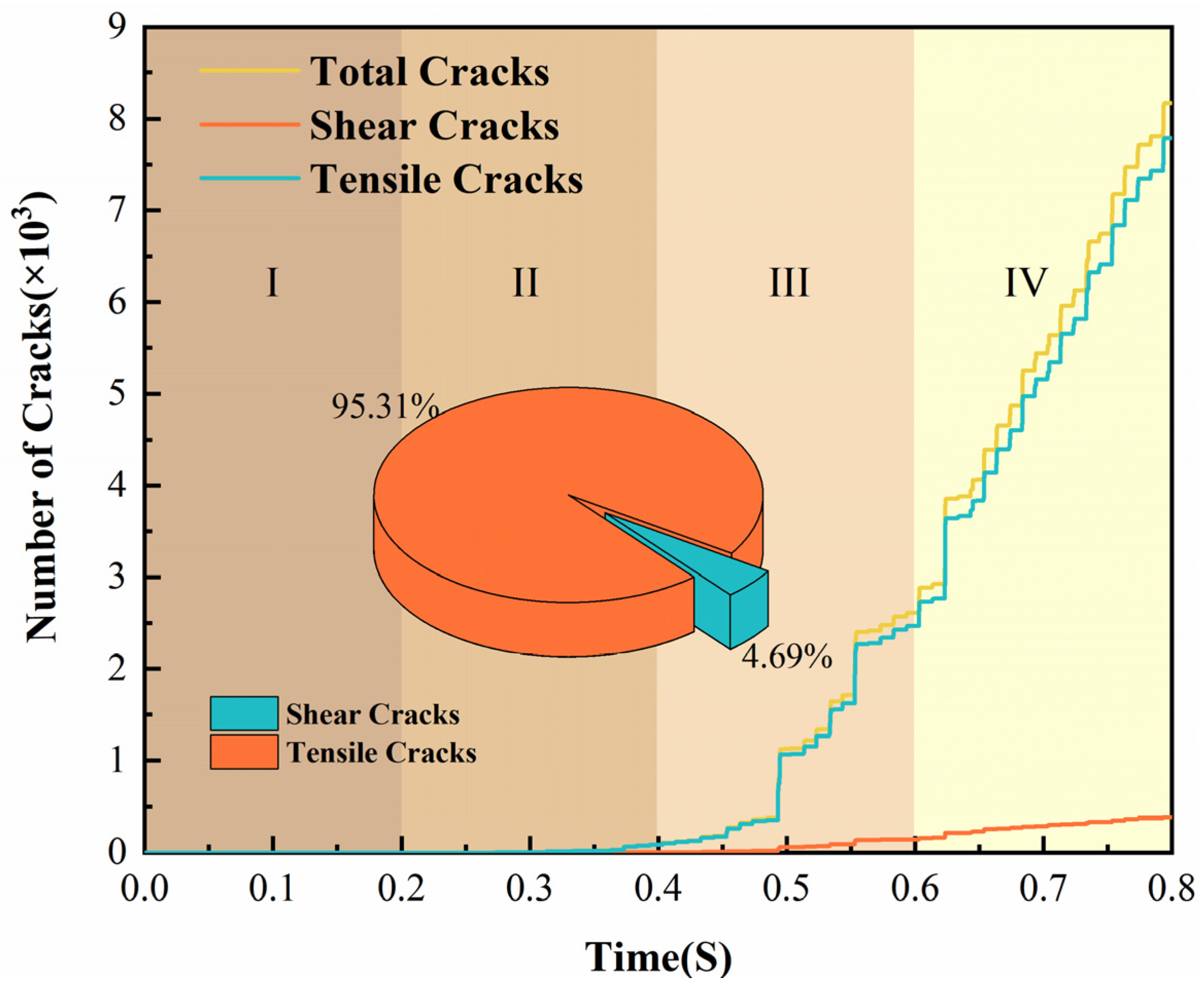
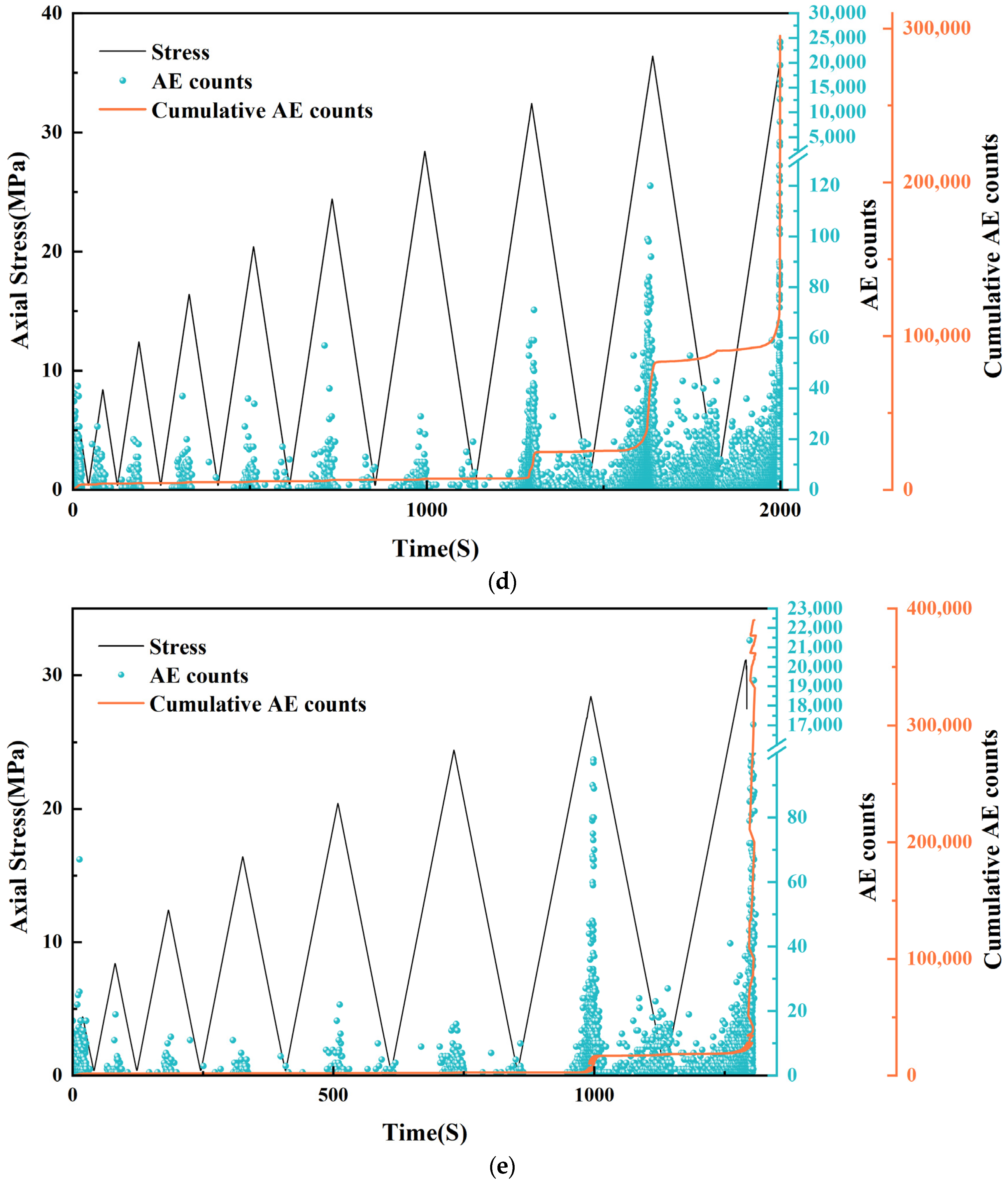
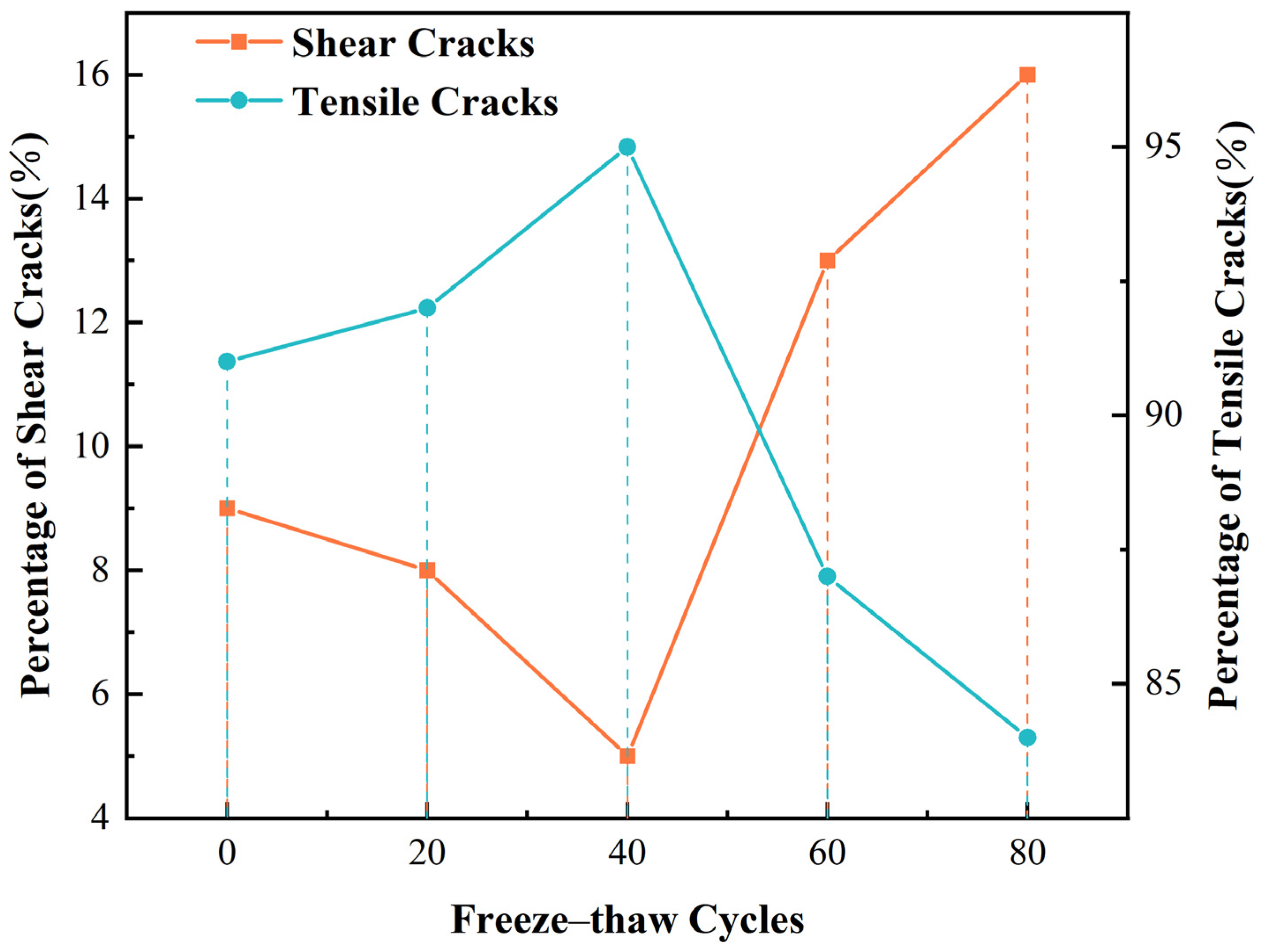
- The emergence of cracks in the cyclic loading process shows a significant correlation with the magnitude of axial stress, and a large number of cracks appear in the late stage of cyclic loading. The number of tensile cracks dominated the whole loading and unloading process. However, after the 50th freeze–thaw cycle, the proportion of tensile cracks decreased, and the proportion of shear cracks gradually increased. It clarified that the sandstone was more prone to shear damage with increased freeze–thaw cycles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.L.; Zhou, K.P.; Liu, W.J.; Deng, H.W. NMR research on deterioration characteristics of microscopic structure of sandstones in freeze-thaw cycles. Trans. Nonferr. Met. Soc. China 2016, 11, 2997–3003. [Google Scholar]
- Liu, Y.Z.; Cai, Y.T.; Huang, S.B.; Guo, Y.L.; Liu, G.F. Effect of water saturation on uniaxial compressive strength and damage degree of clay-bearing sandstone under freeze-thaw. Bull. Eng. Geol. Environ. 2020, 79, 2021–2036. [Google Scholar] [CrossRef]
- Martínez-Martínez, J.; Benavente, D.; Gomez-Heras, M.; Marco-Castaño, L.; García-del-Cura, M.Á. Non-linear decay of building stones during freeze–thaw weathering processes. Constr. Build. Mater. 2013, 38, 443–454. [Google Scholar] [CrossRef]
- Song, Y.; Tan, H.; Yang, H.; Shaojie, C.; Yongxin, C.; Jiaxing, C. Fracture evolution and failure characteristics of sandstone under freeze-thaw cycling by computed tomography. Eng. Geol. 2021, 294, 106370. [Google Scholar] [CrossRef]
- Jiang, D.-Y.; Zhang, S.-L.; Chen, J.; Yang, T.; Wang, X.-S.; Xie, K.-N.; Jiang, X. Low filed NMR and acoustic emission probability density study of freeze-thaw cycles damage for sandstone. Rock Soil Mech. 2019, 40, 436–444. (In Chinese) [Google Scholar]
- Chen, Y.-L.; Zhang, K.; Sun, H. Meso-research on the development of rock surface crack under freeze-thaw cycles. China Civ. Eng. J. 2019, 52 (Suppl. S1), 1–7. (In Chinese) [Google Scholar]
- Ke, B.; Zhang, C.Y.; Liu, C.J.; Ding, L.; Zheng, Y.; Li, N.; Wang, Y.; Lin, H. An experiment study on characteristics of impact compression of freeze-thaw granite specimens under four different states considering moisture content and temperature difference. Environ. Earth Sci. 2021, 80, 661. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, J. Effect of creep load on fatigue behavior and acoustic emission characteristics of sandstone containing pre-existing crack during fatigue loading. Theor. Appl. Fract. Mech. 2022, 119, 103296. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, J. Energy Evolution and Fracture Behavior of Sandstone Under the Coupling Action of Freeze–Thaw Cycles and Fatigue Load. Rock Mech. Rock Eng. 2023, 56, 1321–1341. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, J.; Chen, J.; Lin, H.; Cao, P. Experimental and numerical study on fracture characteristics and constitutive model of sandstone under freeze-thaw-fatigue. Int. J. Fatigue 2023, 166, 107236. [Google Scholar]
- Liu, T.Y.; Zhang, C.Y.; Li, J.T.; Keping, Z.; Ping, C. Detecting freeze–thaw damage degradation of sandstone with initial damage using NMR technology. Bull. Eng. Geol. Environ. 2021, 80, 4529–4545. [Google Scholar] [CrossRef]
- Song, Y.-J.; Sun, Y.-W.; Li, C.-J.; Yang, H.M.; Zhang, L.T.; Xie, L.J. Meso-fracture evolution characteristics of freeze-thaw sandstone based on discrete element method simulation. Rock Soil Mech. 2023, 44, 3602–3616. (In Chinese) [Google Scholar] [CrossRef]
- Abdolghanizadeh, K.; Hosseini, M.; Saghafiyazdi, M. Effect of freezing temperature and number of freeze-thaw cycles on mode I and mode II fracture toughness of sandstone. Theor. Appl. Fract. Mech. 2020, 105, 102428. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, X.F.; Li, P.; Cai, M.F.; Sun, T. Macro-meso damage cracking and volumetric dilatancy of fault block-in-matrix induced by freeze-thaw-multistage constant amplitude cyclic (F-T-MSCAC) loads. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 2990–3008. [Google Scholar] [CrossRef]
- Song, Z.Y.; Konietzky, H.; Wu, Y.F.; Kun, D.; Xin, C. Mechanical behaviour of medium-grained sandstones exposed to differential cyclic loading with distinct loading and unloading rates. J. Rock Mech. Geotech. Eng. 2022, 14, 1849–1871. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, D.; Li, B.; Wang, H.Y.; Tang, Q.Q.; Zhang, Z.Z. Fatigue Damage Mechanism and Deformation Behaviour of Granite Under Ultrahigh-Frequency Cyclic Loading Conditions. Rock Mech. Rock Eng. 2021, 54, 4723–4739. [Google Scholar] [CrossRef]
- Xiong, F.; Liu, X.; Zhou, X.; Lin, G.Y.; Liu, D.S.; Han, Y.F.; Xu, B.; He, C.M.; Wang, Z.J. Mechanical behaviours of sandstone containing intersecting cracks under uniaxial compression. J. Rock Mech. Geotech. Eng. 2022, 14, 460–476. [Google Scholar] [CrossRef]
- Bian, K.; Chen, Y.-A.; Liu, J.; Cui, D.S.; Li, Y.R.; Liang, W.D.; Han, X. The unloading failure characteristics of shale under different water absorption time using the PFC numerical method. Rock Soil Mech. 2020, 41 (Suppl. S1), 355–367. (In Chinese) [Google Scholar]
- Aliha, M.R.M.; Ayatollahi, M.R.; Smith, D.J.; Pavier, M.J. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading. Eng. Fract. Mech. 2010, 77, 2200–2212. [Google Scholar] [CrossRef]
- Al-Shayea, N. Crack propagation trajectories for rocks under mixed mode I-II fracture. Eng. Geol. 2005, 81, 84–97. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Deng, J.H. A new method for determining the crack classification criterion in acoustic emiss ion parameter analysis. Int. J. Rock Mech. Min. Sci. 2020, 130, 104323. [Google Scholar] [CrossRef]
- Aldandooh, M.A.A.; Bunnori, N.M. Crack classification in reinforced concrete beams with varying thicknesses by mean of acoustic emission signal features. Constr. Build. Mater. 2013, 45, 282–288. [Google Scholar] [CrossRef]
- Shi, Z.C.; Li, J.T.; Wang, J. Research on the fracture mode and damage evolution model of sandstone containing pre-existing crack under different stress paths. Eng. Fract. Mech. 2022, 264, 108299. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, K.; Gao, F.; Gu, Z.Y.; Yang, C. Research on the Mechanical Characteristics of Cyclic Loading and Unloading of Rock Based on Infrared Thermal Image Analysis. Math. Probl. Eng. 2021, 2021, 5578629. [Google Scholar] [CrossRef]
- Zhuang, Y.; Cui, X.; Zhang, S.; Dai, G.L.; Zhao, X.L. The load transfer mechanism in reinforced piled embankment under cyclic loading and unloading. Eur. J. Environ. Civ. Eng. 2020, 26, 1364–1378. [Google Scholar] [CrossRef]
- Xiao, F.; Jiang, D.; Wu, F.; Zou, Q.L.; Chen, J.; Chen, B.; Sun, Z.G. Effects of prior cyclic loading damage on failure characteristics of sandstone under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 2020, 132, 104379. [Google Scholar] [CrossRef]
- Zeng, P. Experimental Study on Macro-Meso Mechanical Properties of Limestone Under Multi-Level Cyclic Loading and Unloading. Master’s Thesis, Central South University, Changsha, China, 2022. (In Chinese). [Google Scholar]
- Wang, H.; Gao, Y.; Zhou, Y. Experimental and numerical studies of brittle rock-like specimens with unfilled cross fissures under uniaxial compression. Theor. Appl. Fract. Mech. 2022, 117, 103167. [Google Scholar] [CrossRef]
- Cao, K.W.; Ma, L.Q.; Wu, Y.; Khan, N.M.; Spearing, A.J.S.; Hussain, S.; Yang, J. Cyclic fatigue characteristics of rock failure using infrared radiation as precursor to violent failure: Experimental insights from loading and unloading response. Fatigue Facture Eng. Mater. Struct. 2020, 44, 584–594. [Google Scholar]
- Meng, Q.B.; Liu, J.F.; Ren, L.; Pu, H.; Chen, Y.L. Experimental Study on Rock Strength and Deformation Characteristics Under Triaxial Cyclic Loading and Unloading Conditions. Rock Mech. Rock Eng. 2020, 54, 777–797. [Google Scholar] [CrossRef]
- PFC Documentation, Version PFC 6.0; PFC 6.0 © 2019; Itasca: Minneapolis, MN, USA, 2019.
- Huang, G.; Yang, Y.; Liu, M.; Zhang, J.; Liu, F.; Mwangi, A.D.; Ye, H. Numerical Study on Mechanical Properties of the Freezing–Thawing Cycle of Tailings Based on Particle Discrete Element Method. Minerals 2022, 12, 904. [Google Scholar] [CrossRef]
- Mardoukhi, A.; Mardoukhi, Y.; Hokka, M.; Kuokkala, V.T. Effects of Test Temperature and Low Temperature Thermal Cycling on the Dynamic Tensile Strength of Granitic Rocks. Rock Mech. Rock Eng. 2020, 54, 443–454. [Google Scholar] [CrossRef]
- Xing, K.; Zhou, Z.; Yang, H.; Liu, B. Macro–meso freeze–thaw damage mechanism of soil–rock mixtures with different rock contents. Int. J. Pavement Eng. 2020, 21, 9–19. [Google Scholar] [CrossRef]
- Yue, Z.; Song, Y.; Li, P.; Tian, S.; Ming, X.; Chen, Z. Applications of Digital Image Correlation (DIC) and the Strain Gage Method for Measuring Dynamic Mode I Fracture Parameters of the White Marble Specimen. Rock Mech. Rock Eng. 2019, 52, 4203–4216. [Google Scholar] [CrossRef]
- Cao, P.; Cao, R.-H.; Zhao, Y.-L.; Zhang, K.; Pu, C.Z.; Fan, W.C. Propagation-coalescence and rheologic fracture behavior of rock cracks. Chin. J. Nonferr. Met. 2016, 26, 1737–1762. (In Chinese) [Google Scholar]
- Dong, L.J.; Zhang, Y.H.; Bi, S.J.; Ma, J.; Yan, Y.; Cao, H. Uncertainty investigation for the classification of rock micro-fracture types using acoustic emission parameters. Int. J. Rock Mech. Min. Sci. 2023, 162, 105292. [Google Scholar] [CrossRef]
- Tan, H.; Li, J.T.; Shi, Z.M.; Wang, M.; Wang, J.; Li, J. Damage evolution and failure characteristics of red sandstone with prefabricated crack under coupled dry-wet cycle-fatigue loading. Int. J. Fatigue 2023, 175, 107751. [Google Scholar] [CrossRef]
- Song, H.; Zhang, H.; Kang, Y.; Huang, G.; Fu, D.; Qu, C. Damage evolution study of sandstone by cyclic uniaxial test and digital image correlation. Tectonophysics 2013, 608, 1343–1348. [Google Scholar] [CrossRef]
- Liu, T.Y.; Zhang, C.Y.; Cao, P.; Zhou, K. Freeze-thaw damage evolution of fractured rock mass suing nuclear magnetic resonance technology. Cold Reg. Sci. Technol. 2020, 170, 102951. [Google Scholar] [CrossRef]
- Jensen, P.R.; Plesha, E.M.; Edil, B.T.; Bosscher, P.J.; Kahla, N.B. DEM Simulation of Particle Damage in Granular Media—Structure Interfaces. Int. J. Geomech. 2001, 1, 21–39. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Liu, T.Y.; Jiang, C.; Chen, Z.; Zhou, K.; Chen, L. The Freeze-Thaw Strength Evolution of Fiber-Reinforced Cement Mortar Based on NMR and Fractal Theory: Considering Porosity and Pore Distribution. Materials 2022, 15, 7316. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Li, J.; Zhao, Y. Study on damage evolution and constitutive model of sandstone under the coupled effects of wetting-drying cycles and cyclic loading. Eng. Fract. Mech. 2021, 253, 107883. [Google Scholar] [CrossRef]
- Peng, K.; Wang, Y.; Zou, Q.; Liu, Z.; Mou, J. Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
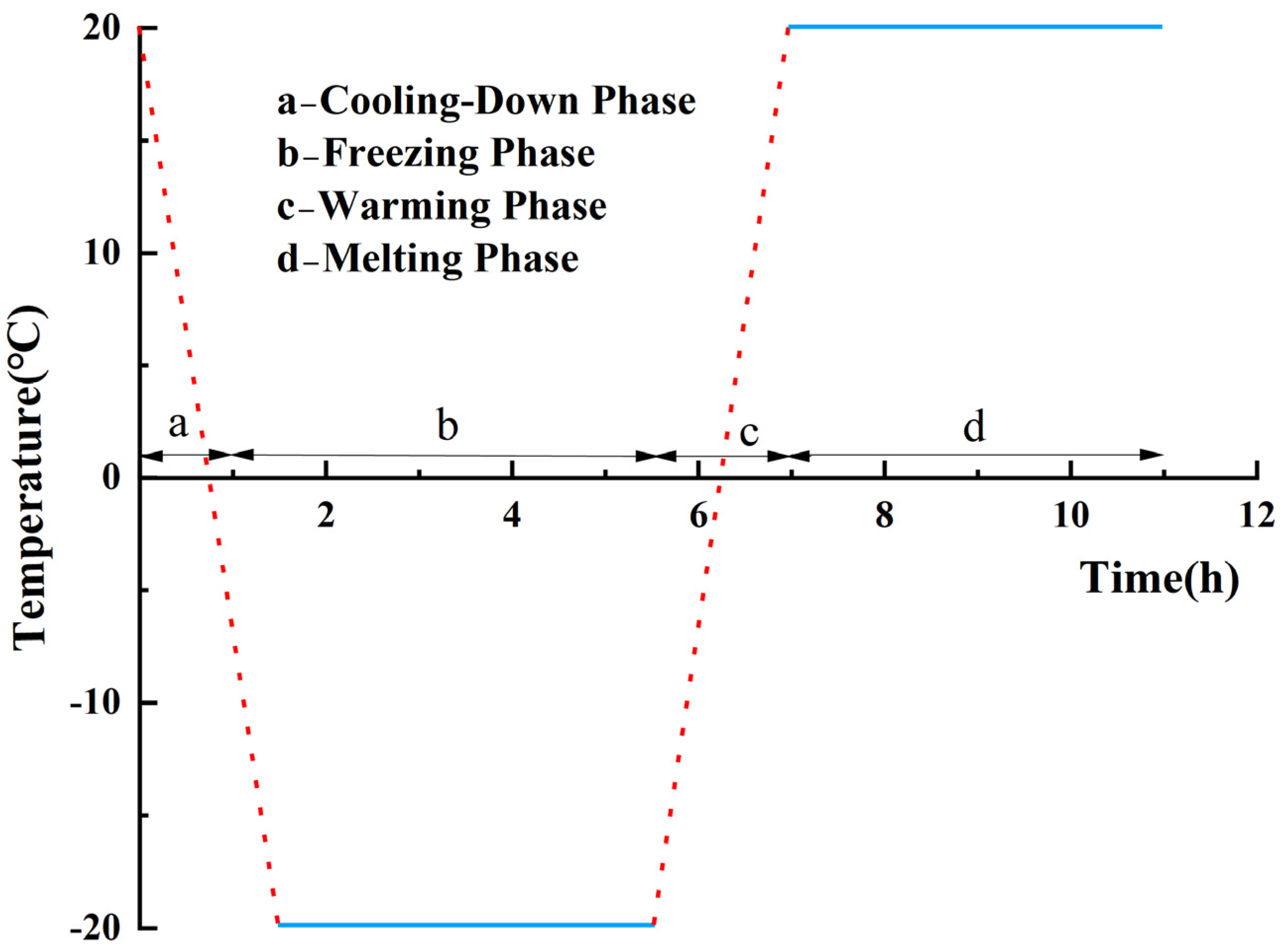


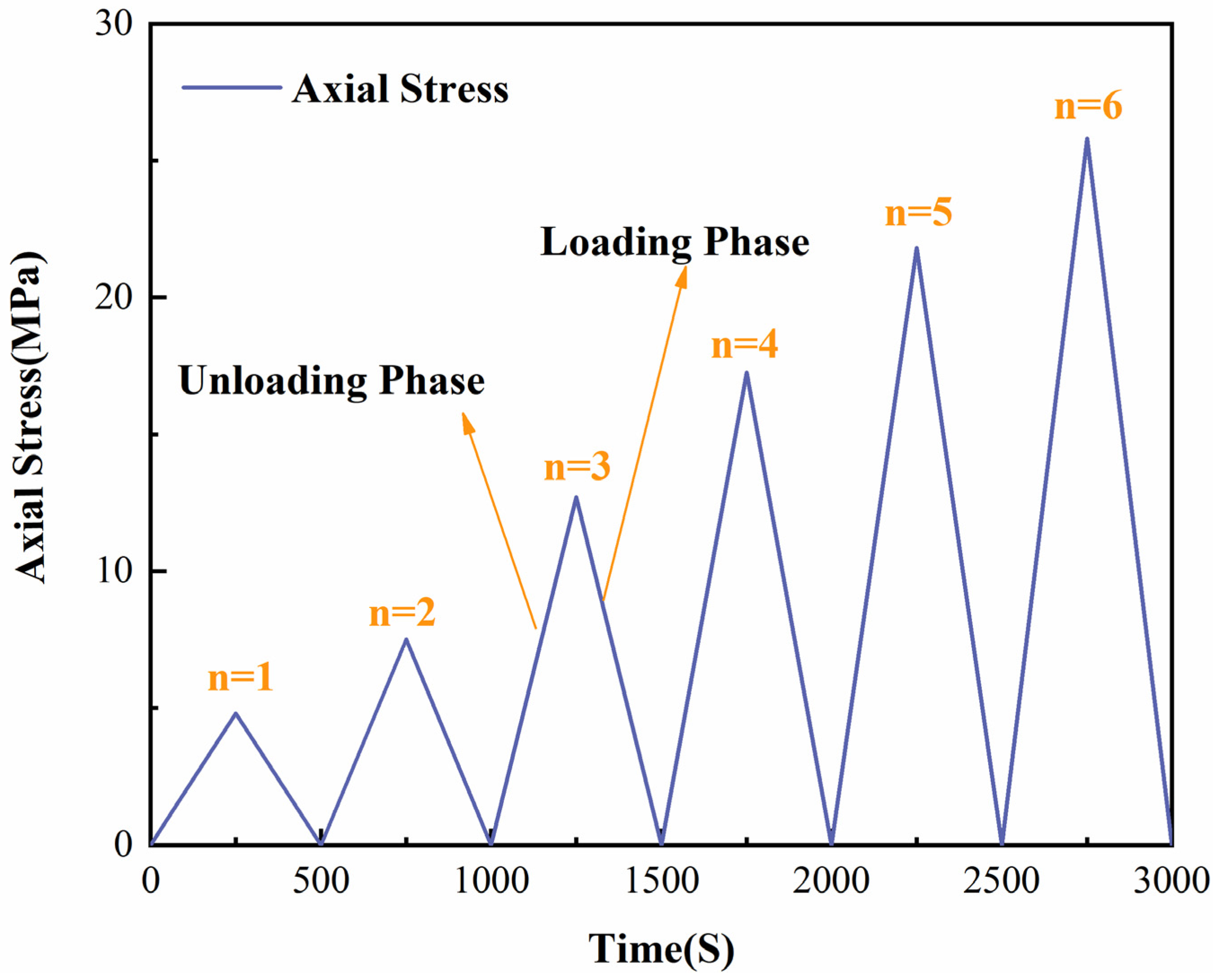
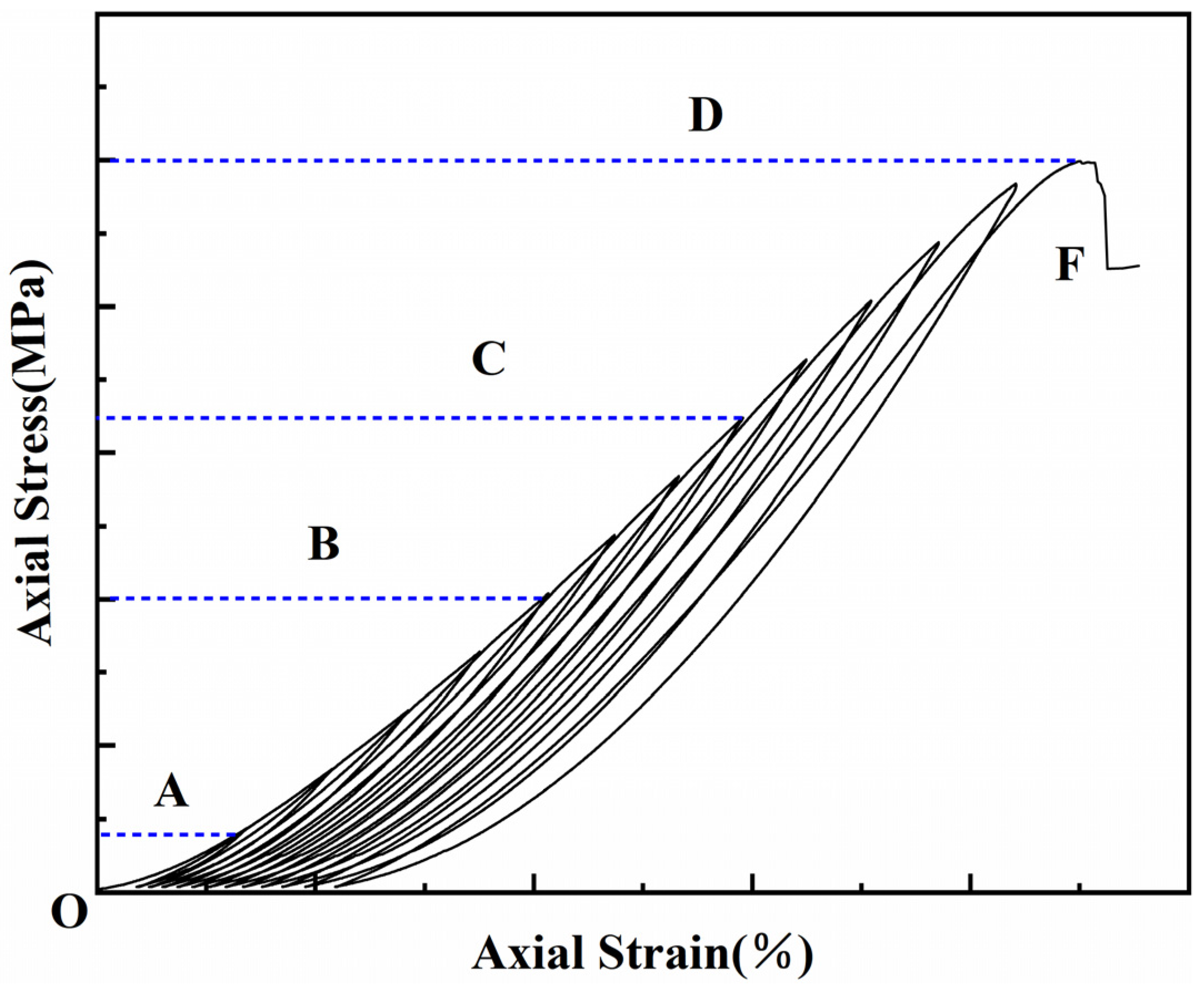


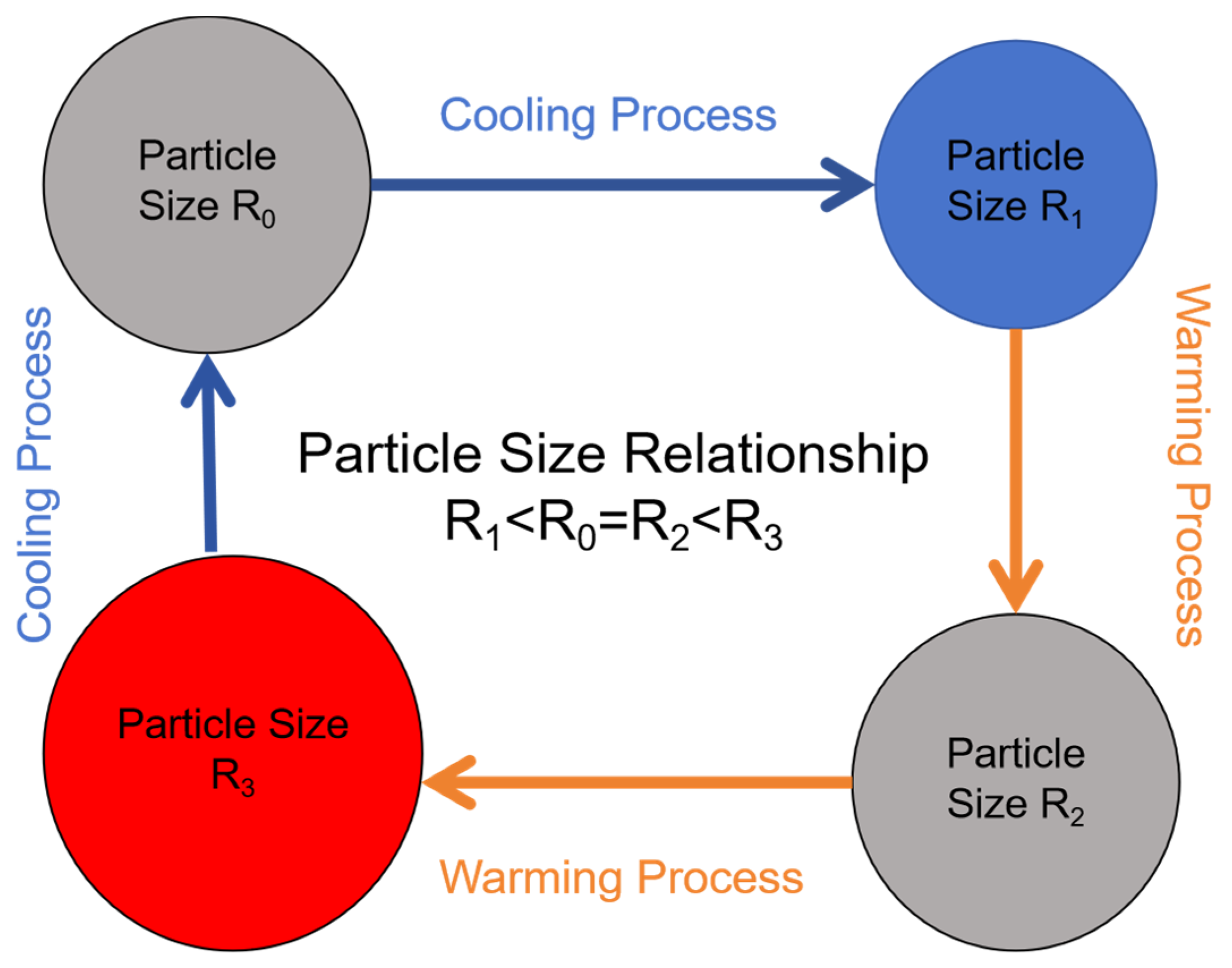









| Rock Specimen Number | Uniaxial Compressive Strength/MPa | Modulus of Elasticity/GPa |
|---|---|---|
| 1 | 45.70 | 3.56 |
| 2 | 44.47 | 3.71 |
| 3 | 43.99 | 3.90 |
| Pb_fa/° | Emod/GPa | Fric | Pb_ten/MPa | Pb_coh/MPa |
|---|---|---|---|---|
| 44.72 | 3.72 | 0.55 | 20 | 30 |
| Particle Type | Parameters | ||
|---|---|---|---|
| /(1 °C−1) | m−1) | °C−1) | |
| Rock particle | 0.053 | 2.59 | 878 |
| Water particle | 2.080 | 1.00 | 4216 |
| Specimen Number | Pre-Freeze–Thaw Mass/g | Post-Freeze–Thaw Mass/g | Mass Loss/% | Pre-Freeze–Thaw Wave Speed/m·s−1 | Post-Freeze–Thaw Wave Speed/m·s−1 | Wave Speed Loss/% |
|---|---|---|---|---|---|---|
| F-T-20-1 | 589.56 | 587.86 | 0.288 | 3225.66 | 3212.76 | 0.4 |
| F-T-20-2 | 594.20 | 592.52 | 0.283 | 3456.98 | 3446.61 | 0.3 |
| F-T-20-3 | 591.89 | 590.29 | 0.270 | 3015.28 | 2994.17 | 0.7 |
| Average value | 591.88 | 590.22 | 0.280 | 3232.64 | 3217.85 | 0.5 |
| F-T-40-1 | 595.66 | 593.66 | 0.336 | 3456.78 | 3415.30 | 1.2 |
| F-T-40-2 | 588.98 | 587.18 | 0.306 | 3598.58 | 3537.40 | 1.7 |
| F-T-40-3 | 590.27 | 588.57 | 0.288 | 3569.28 | 3515.74 | 1.5 |
| Average value | 591.60 | 589.80 | 0.310 | 3541.55 | 3489.48 | 1.5 |
| F-T-60-1 | 589.75 | 587.15 | 0.441 | 3426.20 | 3350.82 | 2.2 |
| F-T-60-2 | 590.70 | 588.3 | 0.406 | 3265.10 | 3173.68 | 2.8 |
| F-T-60-3 | 592.30 | 589.6 | 0.456 | 3356.12 | 3295.71 | 1.8 |
| Average value | 590.92 | 588.35 | 0.434 | 3349.14 | 3273.40 | 2.3 |
| F-T-80-1 | 590.22 | 586.02 | 0.712 | 3567.55 | 3446.25 | 3.4 |
| F-T-80-2 | 591.26 | 586.76 | 0.761 | 3055.12 | 2966.52 | 2.9 |
| F-T-80-3 | 595.10 | 590.40 | 0.790 | 3099.70 | 3000.51 | 3.2 |
| Average value | 592.19 | 587.73 | 0.754 | 3240.79 | 3137.76 | 3.2 |
| Simulated Peak Stress/Mpa | Measured Peak Stress/Mpa | Simulated Strain/% | Measured Strain/% | Stress Difference/Mpa | Strain Relief/% | Single-Axis Simulated Strain Differential/% | Uniaxial Simulation of Peak Stress/MPa | Cumulative Strain Difference/% |
|---|---|---|---|---|---|---|---|---|
| 4.40 | 4.80 | 0.001 | 0.075 | 0.40 | 0.074 | 0.23 | 45 | 36.20 |
| 8.40 | 7.50 | 0.0025 | 0.10 | 0.90 | 0.0975 | 21.20 | ||
| 12.40 | 12.70 | 0.0026 | 0.053 | 0.30 | 0.0504 | 32.87 | ||
| 16.40 | 17.25 | 0.004 | 0.15 | 0.85 | 0.146 | 33.61 | ||
| 20.40 | 21.80 | 0.005 | 0.175 | 1.40 | 0.17 | 23.76 | ||
| 24.40 | 25.80 | 0.006 | 0.21 | 1.40 | 0.204 | 28.51 | ||
| 28.40 | 32.50 | 0.007 | 0.23 | 4.10 | 0.223 | 10.64 | ||
| 32.20 | 36.125 | 0.0075 | 0.275 | 3.925 | 0.2675 | 13.33 | ||
| 36.40 | 41.10 | 0.0085 | 0.30 | 4.70 | 0.2915 | 12.13 | ||
| 40.40 | 49.00 | 0.01 | 0.34 | 8.60 | 0.33 | 7.51 | ||
| 44.40 | 48.40 | 0.0105 | 0.38 | 4.00 | 0.3695 | 18.07 | ||
| 48.40 | 40.00 | 0.0107 | 0.40 | 8.40 | 0.3892 | 9.07 | ||
| Average cumulative strain difference/% | 20.57 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Li, H.; Dong, L.; Cao, P. Mechanical Properties and Failure Mechanisms of Sandstone Under Combined Action of Cyclic Loading and Freeze–Thaw. Appl. Sci. 2025, 15, 7942. https://doi.org/10.3390/app15147942
Liu T, Li H, Dong L, Cao P. Mechanical Properties and Failure Mechanisms of Sandstone Under Combined Action of Cyclic Loading and Freeze–Thaw. Applied Sciences. 2025; 15(14):7942. https://doi.org/10.3390/app15147942
Chicago/Turabian StyleLiu, Taoying, Huaheng Li, Longjun Dong, and Ping Cao. 2025. "Mechanical Properties and Failure Mechanisms of Sandstone Under Combined Action of Cyclic Loading and Freeze–Thaw" Applied Sciences 15, no. 14: 7942. https://doi.org/10.3390/app15147942
APA StyleLiu, T., Li, H., Dong, L., & Cao, P. (2025). Mechanical Properties and Failure Mechanisms of Sandstone Under Combined Action of Cyclic Loading and Freeze–Thaw. Applied Sciences, 15(14), 7942. https://doi.org/10.3390/app15147942





