A Comprehensive Method for Calculating Maritime Radar Identification Probability Using 3D Marine Geographical Feature Models

Abstract

To overcome the limitations of existing maritime radar identification analysis methods, which are only applicable to sea-skimming aircraft and fail to quantitatively calculate the probability of radar correctly identifying the target under electromagnetic influence from marine geographical features (MGFs), an advanced method is proposed for calculating the radar identification probability in marine areas using 3D MGF models. The method first established the radar identification criteria in 3D space, considering radar line of sight (LOS), radar target adhesion (RTA), and radar resolutions in range, azimuth angle, and elevation angle. It then comprehensively analyzed errors from both the aircraft and MGFs. Finally, the probability of a target at a specific marine location being correctly identified by radar was calculated using the Monte Carlo method. Theoretical derivations and simulation results demonstrated that: (1) Unlike existing methods limited to sea-skimming aircraft, the proposed method is applicable to aircraft at any altitude, better aligning with current aircraft performance and requirements; (2) While existing methods provide only a binary result of “identified” or “unidentified,” the proposed method offers a probability value. For the same marine location point T_a, the proposed method yields radar identification probabilities of 0.0877 for sea-skimming aircraft and 0.5887 for high-altitude aircraft, providing more precise and intuitive decision-making support for mission planners.

1. Introduction

Radar systems on maritime aircrafts, especially those used for anti-ship missiles, frequently encounter significant detection challenges when the target is close to marine geographical features (MGFs) such as islands and offshore drilling platforms with pronounced electromagnetic characteristics. The challenges arise primarily from two aspects:

(1) The detection blind zones caused by MGFs. MGFs can create physical obstructions that block the radar beam, resulting in areas where the radar cannot detect targets. This is particularly problematic for sea-skimming aircraft when the target is located behind MGFs.

(2) The radar target adhesion (RTA) problem caused by MGFs. Even when the target is within the radar line of sight (LOS), the limitations in radar resolution and the electromagnetic interference from MGFs may also lead to the RTA problem. In this case, the target can be mistakenly merged with MGFs and identified as a single target [1].

To address these challenges, current technical research primarily focuses on ensuring that target signals can be detected by radar as well as avoiding the RTA problem. Efforts include improving radar resolution and imaging capabilities [2,3] and developing relevant algorithms [4,5,6,7,8,9,10,11,12,13,14]. While these research directions are theoretically significant, there are still several technical barriers and hardware limitations for their practical application.

From a tactical perspective, optimizing aircraft operations is crucial for overcoming these challenges. This can be achieved by selecting appropriate radar activation points and flight directions to improve the ability of radar correctly identifying the target, even with limited radar resolution and LOS conditions. In this context, several studies have made notable contributions: Hou, Chen, and Dong [15,16,17] simplified MGFs and targets into point mass models, providing a theoretical basis for evaluating target identification conditions based on radar range and azimuth angle resolution. However, this method can introduce significant errors, especially for complex MGFs like large islands. To address these limitations, based on the 2D contour data of MGFs, Wang [18] attempted to enhance radar’s ability to distinguish targets from MGFs by adjusting the aircraft’s search direction, and Xie [19] assessed the number of “false targets” that coastlines may generate in a radar system with radar azimuth angle resolution; Wu [20] proposed a strategy to optimize the aircraft’s searching direction, ensuring the radar search range covers the target while avoiding MGFs using radar range resolution. Despite these efforts, existing methods still have notable limitations:

(1) They do not account for the influence of MGFs’ elevation data and radar elevation angle resolution, limiting their applicability to sea-skimming aircraft and making them unsuitable for advanced high-altitude aircraft;

(2) They ignore potential errors, such as radar activation point errors and MGF position errors. So, they can only provide a binary result of “identified” or “unidentified” and cannot quantitatively calculate the probability of the target being correctly identified by radar at a specific marine location.

With the developments in equipment technology, the usage of advanced high-altitude aircraft is increasing due to their broader field of view, faster speed, and longer range. As for the radar LOS and RTA problems with analysis of high-altitude aircraft in 3D space, it is essential to incorporate the 3D model of MGFs, radar elevation angle resolution, and related errors. Therefore, this paper proposes a method to calculate the radar identification probability (P_ident) for a target at a specific marine location. Compared to the existing methods, the proposed method has advantages as follows:

(1) The proposed method further considers the influence of MGFs’ elevation data and radar elevation angle resolution, so that it can be applied to aircraft at any altitude, better aligning with the advanced aircraft’s performance and requirements.

(2) The proposed method integrates errors from both the MGFs and the aircraft and employs the Monte Carlo method to obtain P_ident, instead of the binary result from the existing method, providing more accurate and intuitive decision-making support for the mission planning of maritime aircraft.

2. Principle of Radar Identification Probability Calculation

2.1. Criteria for Radar Identification in 3D Space

As previously discussed, the challenges of radar identification caused by MGFs stem from two main aspects: radar detection blind zones and the RTA problem. To address the former, it is essential to ensure that the target is within the radar LOS. In terms of the RTA problem, it primarily depends on the radar resolution.

Radar resolution can be categorized into range and angular resolutions in the spatial domain. Range resolution refers to the minimum distance between two adjacent targets that the radar can distinguish, primarily determined by the radar signal’s bandwidth and pulse width. Angular resolution can be further divided into azimuth angle resolution and elevation angle resolution, which refer to the minimum angles for radar to distinguish two adjacent targets in horizontal and vertical directions, respectively. These are mainly dependent on the radar antenna’s beamwidth.

Existing methods [15,16,17,18,19,20] have mostly simplified MGFs to point masses or relied solely on their 2D contour data, focusing mainly on radar range and azimuth angle resolution within a 2D plane. However, these methods did not fully consider the influence of elevation angle resolution. To extend the research scope from 2D to 3D for advanced high-altitude aircraft, this paper introduces radar elevation angle resolution and an MGF 3D model.

When considering only the spatial domain and ignoring factors such as Doppler resolution, the RTA problem occurs when two or more objects are within the radar LOS and their differences in range, azimuth angle, and elevation angle relative to the radar are all smaller than the respective resolutions.

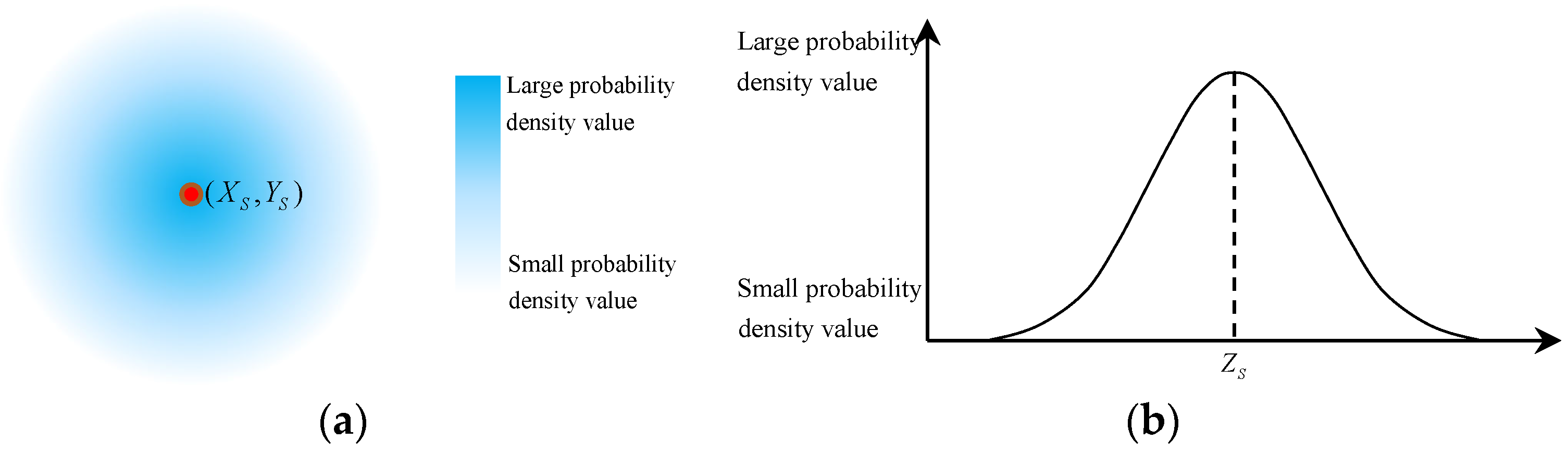
To more precisely quantify and describe the criteria for the RTA problem in 3D space, this paper establishes a local Cartesian coordinate system with the due north direction as the X-axis, the due east direction as the Y-axis, the instantaneous sea surface as the XOY plane, and the Z-axis pointing vertically upward. Two targets are denoted as the points T₁(X_T1, Y_T1, Z_T1) and T₂(X_T2, Y_T2, Z_T2), and the radar position is denoted as the point S(X_S, Y_S, Z_S). The schematic diagram of the relative positional relationship between these points is shown in Figure 1.

In Figure 1, d_ST1 and d_ST2, A_ST1 and A_ST2, and E_ST1 and E_ST2 represent the distances, azimuth angles and elevation angles from point S to points T₁ and T₂, respectively. According to the definition of RTA, given the radar range resolution R_res, azimuth angle resolution A_res, and elevation angle resolution E_res, when both T₁ and T₂ are within the radar LOS, the condition for the radar to misidentify T₁ and T₂ as a single target is that Equations (1)–(3) are simultaneously satisfied.

$$\left|d_{S{T}_1}-d_{S{T}_2}\right|\le R_{res}$$

(1)

$$\left|A_{S{T}_1}-A_{S{T}_2}\right|\le A_{res}$$

(2)

$$\left|E_{S{T}_1}-E_{S{T}_2}\right|\le E_{res}$$

(3)

The terms in Equations (1)–(3) are as follows:

$$\left\{\begin{array}{l}{d}_{S{T}_1}=\sqrt{{\left(X_S-X_{T_1}\right)}^2+{\left(Y_S-Y_{T_1}\right)}^2+{\left(Z_S-Z_{T_1}\right)}^2}\hfill \\ d_{S{T}_2}=\sqrt{{\left(X_S-X_{T_2}\right)}^2+{\left(Y_S-Y_{T_2}\right)}^2+{\left(Z_S-Z_{T_2}\right)}^2}\hfill \\ A_{S{T}_1}=\arctan {\displaystyle \frac{Y_{T_1}-Y_S}{X_{T_1}-X_S}}\hfill \\ A_{S{T}_2}=\arctan {\displaystyle \frac{Y_{T_2}-Y_S}{X_{T_2}-X_S}}\hfill \\ E_{S{T}_1}=\arctan {\displaystyle \frac{\sqrt{{\left(X_S-X_{T_1}\right)}^2+{\left(Y_S-Y_{T_1}\right)}^2}}{Z_S-Z_{T_1}}}\hfill \\ E_{S{T}_2}=\arctan {\displaystyle \frac{\sqrt{{\left(X_S-X_{T_2}\right)}^2+{\left(Y_S-Y_{T_2}\right)}^2}}{Z_S-Z_{T_2}}}\hfill \end{array}\right.$$

(4)

Therefore, in this paper, the conditions for a target to be correctly identified by the radar are:

(1) The target is within the radar LOS;

(2) If there are any interfering objects within the radar LOS in addition to the target, Equations (1)–(3) are not simultaneously satisfied.

After establishing the radar identification criteria in 3D space, the potential errors from both the MGF and the maritime aircraft are further analyzed in the following section.

2.2. Error Analysis

In addition to the limitations of radar LOS and resolution, potential errors can also affect radar identification. This paper focuses on errors from two sources: the MGF and the maritime radar (aircraft). For MGF data, the errors are mainly due to the accuracy of geospatial surveys. There are planar position errors (ΔX_B, ΔY_B) and elevation data error ΔZ_B. (ΔX_B, ΔY_B) are assumed to follow a 2D normal distribution with independent directions, an expected value of 0, and a standard deviation of σ_BXY for both directions. ΔZ_B is assumed to follow a normal distribution with an expected value of 0 and a standard deviation of σ_BZ:

$$(\Delta X_B,\Delta Y_B)\sim \mathrm{N}(0,{\sigma }_{B_{XY}};0,{\sigma }_{B_{XY}};0)$$

(5)

$$\Delta Z_B\sim \mathrm{N}(0,{\sigma }_{B_Z})$$

(6)

The errors from the radar (aircraft) mainly stem from the radar system’s hardware precision and the navigation errors of the aircraft and its launch platform. They primarily consist of three aspects: the planar position error of the aircraft launch platform (ΔX_L, ΔY_L), the planar position error (ΔX_S, ΔY_S), and the elevation error ΔZ_S of the radar activation point. Similarly, these errors are assumed to follow the normal distributions:

$$(\Delta X_L,\Delta Y_L)\sim \mathrm{N}(0,{\sigma }_L;0,{\sigma }_L;0)$$

(7)

$$(\Delta X_S,\Delta Y_S)\sim \mathrm{N}(0,{\sigma }_{S_{XY}};0,{\sigma }_{S_{XY}};0)$$

(8)

$$\Delta Z_S\sim \mathrm{N}(0,{\sigma }_{S_Z})$$

(9)

To simplify the calculations, this paper combines (ΔX_S, ΔY_S), (ΔX_L, ΔY_L), and (ΔX_B, ΔY_B) as shown in Equation (10), so that (ΔX_S, ΔY_S) can be equivalently considered to follow the 2D normal distribution as shown in Equation (11):

$${{\sigma }_{m_{XY}}}^2={{\sigma }_{S_{XY}}}^2+{\sigma }_L^2+{{\sigma }_{B_{XY}}}^2$$

(10)

$$(\Delta X_S,\Delta Y_S)\sim \mathrm{N}(0,{\sigma }_{m_{XY}};0,{\sigma }_{m_{XY}};0)$$

(11)

Similarly, ΔZ_B and ΔZ_S are combined as follows:

$${{\sigma }_{m_Z}}^2={{\sigma }_{S_Z}}^2+{{\sigma }_{B_Z}}^2$$

(12)

$$\Delta Z_S\sim \mathrm{N}(0,{\sigma }_{m_Z})$$

(13)

In summary, the errors from both the MGF and the radar (aircraft) are combined and equivalently regarded as the errors of S, whose planar error (ΔX_S, ΔY_S) and elevation error ΔZ_S follow the normal distributions shown in Equations (11) and (13), respectively. Based on that, the actual radar activation point with errors S′(X_S′, Y_S′, Z_S′) and its distribution are shown in Equations (14)–(16), and the schematic diagram of that is shown in Figure 2.

$$\left\{\begin{array}{l}{X}_S^{\prime }=X_S+\Delta X_S\hfill \\ Y_S^{\prime }=Y_S+\Delta Y_S\hfill \\ Z_S^{\prime }=Z_S+\Delta Z_S\hfill \end{array}\right.$$

(14)

$$(X_S^{\prime },Y_S^{\prime })\sim \mathrm{N}(X_S,{\sigma }_{m_{XY}};Y_S,{\sigma }_{m_{XY}};0)$$

(15)

$$Z_S^{\prime }\sim \mathrm{N}(Z_S,{\sigma }_{m_Z})$$

(16)

In Equations (14)–(16) and Figure 2, S(X_S, Y_S, Z_S) is the theoretical radar activation point.

With the error analysis completed, the detailed steps for calculating the radar identification probability using the Monte Carlo method would be presented.

2.3. Calculation Steps

In this paper, the actual radar operation process is simplified since we paid more attention to the impact of the limitations of radar resolutions and electromagnetic interference from MGFs, and the relevant assumptions are as follows:

Assumption 1. 

All objects mentioned in this paper are within the theoretical searching range of the radar.

Assumption 2. 

If the line connecting radar and target is occluded by an MGF, the target would be out of radar LOS and cannot be detected or identified.

Assumption 3. 

If there is no LOS limitation or RTA problem, the target would be correctly identified by the radar, regardless of the dynamic environmental factors, such as sea state or weather.

Assumption 4. 

The result probability P_ident only corresponds to the moment when the radar is activated at point S.

Based on these assumptions, the process of calculating the probability P_ident is shown in Figure 3.

In Figure 3, the specific implementation process of each step is as follows:

Step 1: Input Data. Based on the 3D model of MGFs, extract the points with pronounced electromagnetic characteristics, denoted as B_i(X_Bi, Y_Bi, Z_Bi) (i = 1,2, …, N), and input their planar position and elevation error standard deviation σ_BXY and σ_BZ. According to the aircraft’s mission planning and performance parameters, input the radar activation point S(X_S, Y_S, Z_S) and its planar position and elevation error standard deviation σ_SXY and σ_SZ (for sea-skimming aircraft, Z_S and σ_SZ can be set as 0), aircraft launch platform planar position error standard deviation σ_L, radar range resolution R_res, elevation angle resolution E_res, and azimuth angle resolution A_res. Finally, input the marine location point T(X_T,Y_T) where P_ident is to be calculated.

Step 2: Monte Carlo Simulation. Set the Monte Carlo repetition times M_repeat and initialize the counter M_ident = 0. In each simulation:

(1) Randomly generate the radar position point S′(X_S′, Y_S′, Z_S′) based on the theoretical values and errors from Step 1 using Equations (5)–(16).

(2) Determine whether T is within the LOS of S′. If it is, proceed to the next step; otherwise, proceed to the next simulation.

(3) Sequentially determine whether S′, T, and each B_i simultaneously satisfy Equations (1)–(3). If none of them satisfies the condition, increment M_ident by 1; otherwise, proceed to the next simulation.

Repeat the simulation M_repeat times.

Step 3: Calculate P_ident. Calculate the ratio of M_ident to M_repeat to obtain P_ident, as shown in Equation (17):

$$P_{ident}={\displaystyle \frac{M_{ident}}{M_{repeat}}}$$

(17)

Due to the instability of the Monte Carlo method, the accuracy of P_ident can be improved by increasing M_repeat in Step 2.

By inputting the marine location points around the MGF and repeating the above steps, the distribution of P_ident around the MGF can be visually expressed.

3. Simulation and Analysis

3.1. Data Input

To validate the effectiveness and applicability of the proposed method across different scenarios, a series of simulation experiments were conducted. According to the calculation process of P_ident shown in Figure 3, the experiment first required the input of data.

To simplify the simulation, it was assumed that all points of the MGF possess pronounced electromagnetic characteristics. Based on this assumption, the experiment used points read from the MGF’s stl file as the B_i(X_Bi,Y_Bi,Z_Bi) (i = 1,2, …, N) for data input. The stl format is a file format that describes the surface geometry of a 3D object with multiple triangular facets. Its binary format is shown in

Table 1. stl binary format.

Name	Data Type	Offset/Byte	Notes
Header	String	0	File header
Number of triangles	UInt32	80	Number of triangular facets
Normal vector of triangle M	Single(3)	50(M − 1) + 84	Normal vector of the M-th triangular facet
Vertex1 of triangle M	Single(3)	50(M − 1) + 96	Coordinates of the 1st vertex of the M-th triangular facet
Vertex2 of triangle M	Single(3)	50(M − 1) + 108	Coordinates of the 2nd vertex of the M-th triangular facet
Vertex3 of triangle M	Single(3)	50(M − 1) + 120	Coordinates of the 3rd vertex of the M-th triangular facet
Attribute	UInt16	50(M − 1) + 142	Attribute of the M-th triangular facet

.

Since the triangular facets of the MGF were obtained using the file format in Table 1, it was accessible to determine whether the marine location point was within the radar LOS by checking whether the line connecting the radar position point and the marine location point intersected with any of the triangular facets. The B_i(X_Bi, Y_Bi, Z_Bi) (i = 1, 2, …, N) data could be used to determine whether the RTA problem occurred.

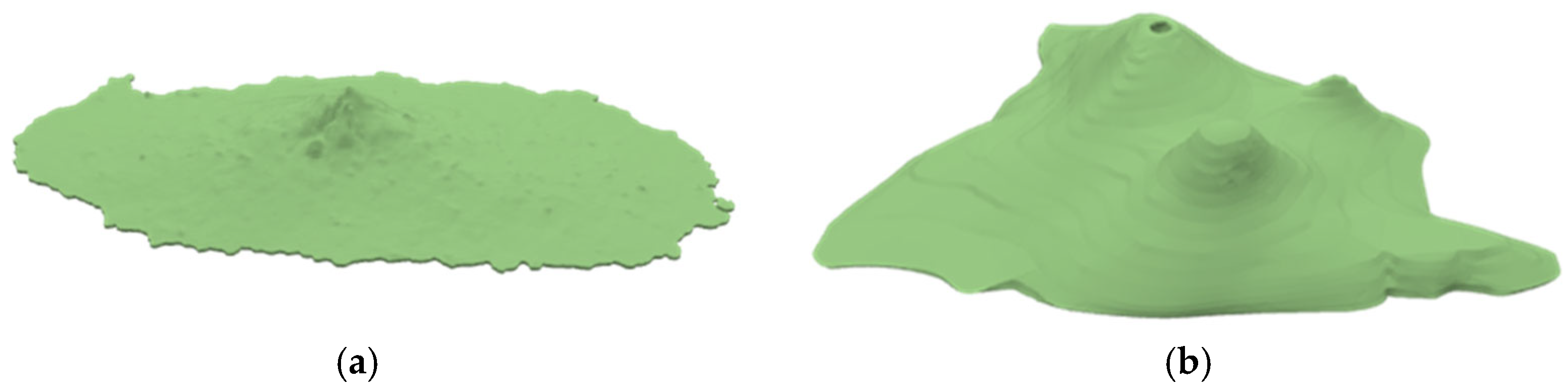
Based on that, two islands of different shapes were used as the MGFs for the experiment. The 3D models and parameters of the MGFs are shown in Figure 4 and

Table 2. Parameters of MGFs for experiment.

Parameter	Value of Narrow-Shaped Island	Value of Triangular-Shaped Island	Notes
[Xmin, Xmax]	[−0.8718 km, 0.9056 km]	[−0.3424 km, 0.6201 km]	The range of MGF along X-axis
Xmax − Xmin	1.7774 km	0.9625 km	The length of MGF along X-axis
[Ymin, Ymax]	[−0.5638 km, 0.4370 km]	[−0.5162 km, 0.5892 km]	The range of MGF along Y-axis
Ymax − Ymin	1.0008 km	1.1054 km	The length of MGF along Y-axis
[Zmin, Zmax]	[0 km, 0.1998 km]	[0, 0.1971 km]	The range of MGF along Z-axis
Zmax − Zmin	0.1998 km	0.1971 km	The length of MGF along Z-axis
Planar area	1.1220 km2	0.6582 km2	The planar area of the MGF under the current tide
Number of facets	74,157	35,080	The number of triangle facets that make up the MGF
Number of vertices	37,988	17,542	The number of points that make up the MGF

.

Since the planar geometric center of the experimental MGFs are close to the coordinate origin, for the convenience of subsequent calculations and explanations, the distance, azimuth angle, and elevation angle between the radar and the coordinate origin are considered as those between the radar and the MGFs for the experiment.

In addition to the MGF, the experiment simulated reasonable types of virtual maritime aircraft and the onboard radar. The specific parameters of them and other parameters for the simulation are shown in

Table 3. Simulation parameters.

Parameter	Value	Notes
Rres	0.5 km	Radar range resolution
Ares	1°	Radar azimuth angle resolution
Eres	1°	Radar elevation angle resolution
σL	0.5 km	Standard deviation of the aircraft launch platform planer position error
σSXY	0.1 km	Standard deviation of the radar activation point planer position error
σSZ	0.01 km for high-altitude aircraft 0 km for sea-skimming aircraft	Standard deviation of the radar activation point elevation error
σBXY	0.5 km	Standard deviation of the MGF planer position error
σBZ	0.005 km	Standard deviation of the MGF elevation error

Note: All values in the table are hypothetical.

.

To verify the applicability of the proposed method to aircraft at any altitude, three groups of radar position points were constructed, as shown in

Table 4. Radar positions.

Group	Point Name	XS /km	YS /km	ZS /km	Aircraft State	Relative Positional Relationship with the MGFs for Experiment
						Elevation Angle/°	Azimuth Angle/°	Distance /km
➀	S1	18	0	0.01	Sea-skimming	0	0	18
	S2	15	0	10	High-altitude	34
➁	S3	0	18	0.01	Sea-skimming	0	90
	S4	0	15	10	High-altitude	34
➂	S5	12.7	12.7	0.01	Sea-skimming	0	45
	S6	10.5	10.5	10	High-altitude	34

.

3.2. Result Calculation

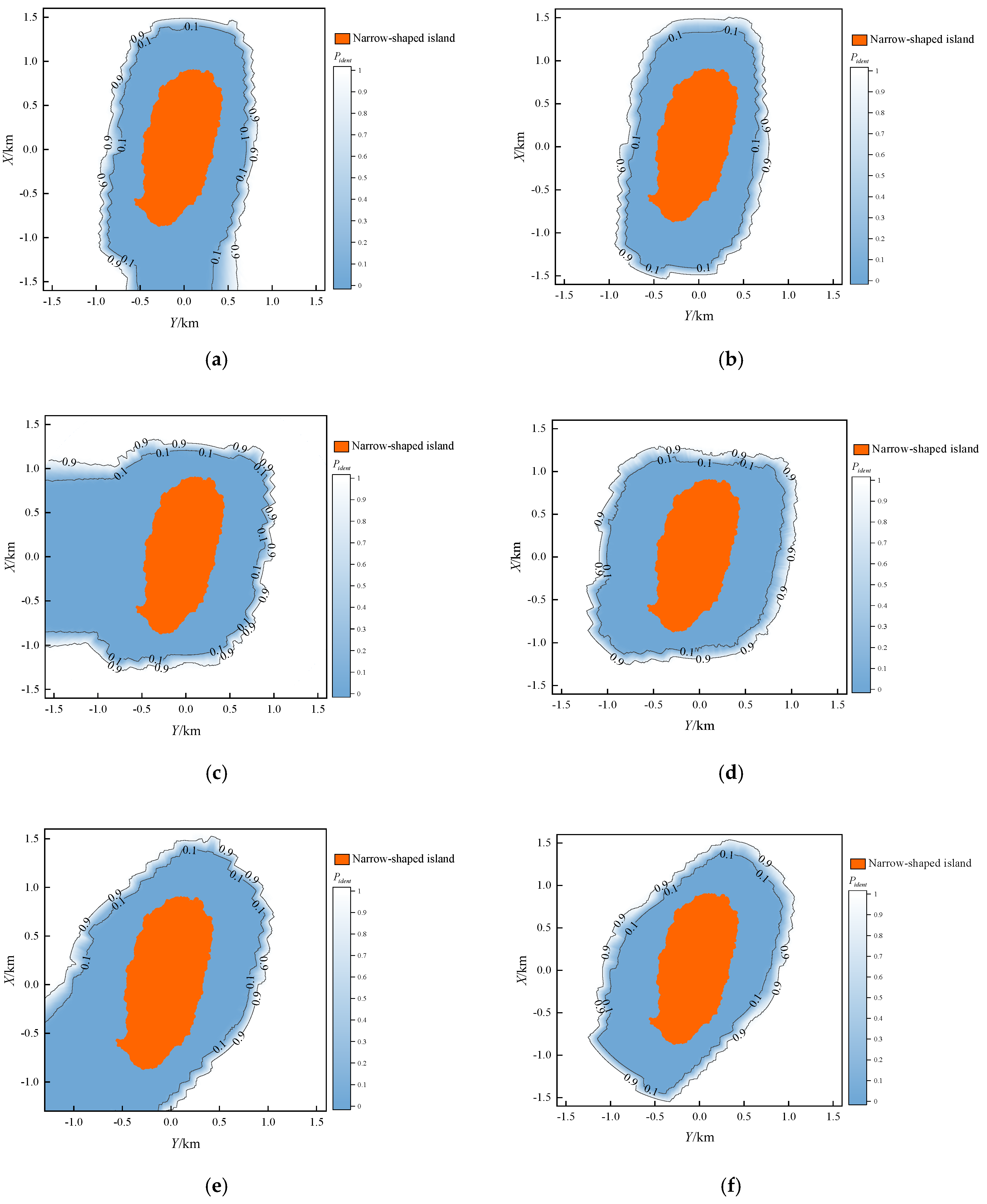
With M_repeat set to 10,000 and the input data from Section 3.1, we calculated and visualized the P_ident distribution around the MGFs for the experiment under the radar points from S₁ to S₆. The results are shown in Figure 5 and Figure 6.

3.3. Result Analysis

For ease of description, in this paper, the marine areas around the MGF for the experiment were denoted as different levels according to their value of P_ident as shown in

Table 5. Marine area level.

Value of Pident	Level of Region
Pident < 0.1	Level I
0.9 ≥ Pident ≥ 0.1	Level II
Pident > 0.9	Level III

.

As illustrated in Figure 5 and Figure 6, the proposed method effectively calculates and visualizes the P_ident distribution around the MGFs for both sea-skimming and high-altitude scenarios.

Combining Figure 5 and Figure 6 and Table 4, it can be observed that, the Level I and II regions always mirror the MGF’s outline but are stretched along the radar’s azimuth bearing. For example, when the radar is north of MGFs (0° azimuth) in Figure 5b and Figure 6b, the Level I and II regions extend along the X-axis as “enlarged copies” of both narrow-shaped island and triangular-shaped island; when radar moves east (90° azimuth) in Figure 5d and Figure 6d, they lengthen along the Y-axis. These are consistent with physical expectations and provide an initial validation of the proposed method.

Furthermore, Given the same distance and azimuth angle between the MGF and the radar, the changes in elevation angle caused by the decrease in Z_S (from high-altitude to sea-skimming) also result in the shapes of the Level I and Level II regions extending towards the azimuth direction of the aircraft. This indicates that the threat level of the marine areas around the MGF is enhanced, consistent with the radar detection blind zones caused by MGF occlusion for sea-skimming aircraft, further demonstrating the effectiveness of the proposed method in this paper.

In addition to the overall result, we selected marine location points T_a (0.6 km, −0.8 km) for the narrow-shaped island and T_b (0.6 km, −0.6 km) for the triangular-shaped island as individual cases since they were always within the LOS of radar at the point of S₁, S₂, S₅, and S₆. The corresponding probabilities were extracted and shown in

Table 6. P_ident of T_a and T_b under different radar position points.

Point Name	Aircraft State	Pident at Ta with the Interference of Narrow-Shaped Island	Pident at Tb with the Interference of Triangular-Shaped Island
S1	Sea-skimming	0.9564	0.0505
S2	High-altitude	0.9990	0.3833
S5	Sea-skimming	0.0877	0.9625
S6	High-altitude	0.5887	0.9997

.

From Table 6, it can be seen that, even for T_a and T_b which always satisfied the radar LOS condition, changes in the aircraft state still have a significant impact on P_ident. For S₅ and S₆, under the interference of the narrow-shaped island, the change in aircraft state from sea-skimming to high-altitude increased the P_ident of T_a by 0.5010; for S₁ and S₂, under the interference of the triangular-shaped island, the change in aircraft state from sea-skimming to high-altitude increased the P_ident of T_b by 0.3328. This indicates the importance of introducing the radar elevation angle resolution and MGF 3D model, and the necessity of the proposed method.

3.4. Practical Application

In actual application scenarios, the complex relationship between radar activation point, MGF data, and P_ident is further compounded by dynamic maritime environment, aircraft performance, and specific mission requirement. Owing to the non-linear interaction among these factors, analytically determining the single optimal radar activation point, either by maximizing P_ident at a given target location or by minimizing the combined extent of Level I and Level II regions, is computationally intractable and often operationally impractical.

The proposed method circumvents this difficulty by providing planners with an explicit, probability-based comparison of candidate configurations. The Inputs consist of

(1) The 3D MGF model;

(2) The area around the MGF whose P_ident needs be calculated;

(3) Radar resolution parameters;

(4) Errors mentioned in Section 2.2;

(5) A discrete set of candidate radar activation points that satisfy the constraints.

The proposed method would then return the corresponding P_ident values, and the mission planners can select the most operationally suitable radar activation point from candidates without recourse to exhaustive numerical optimization.

Example. Consider the narrow-shaped island scenario with two candidate radar activation points S₂ and S₆ due to the constraints. If surveillance intelligence indicates that a target is expected at location T_a, and the computed probabilities are P_ident(S₂) = 0.9990 and P_ident(S₆) = 0.5887. The planner therefore selects S₂, achieving a substantial increase in identification confidence.

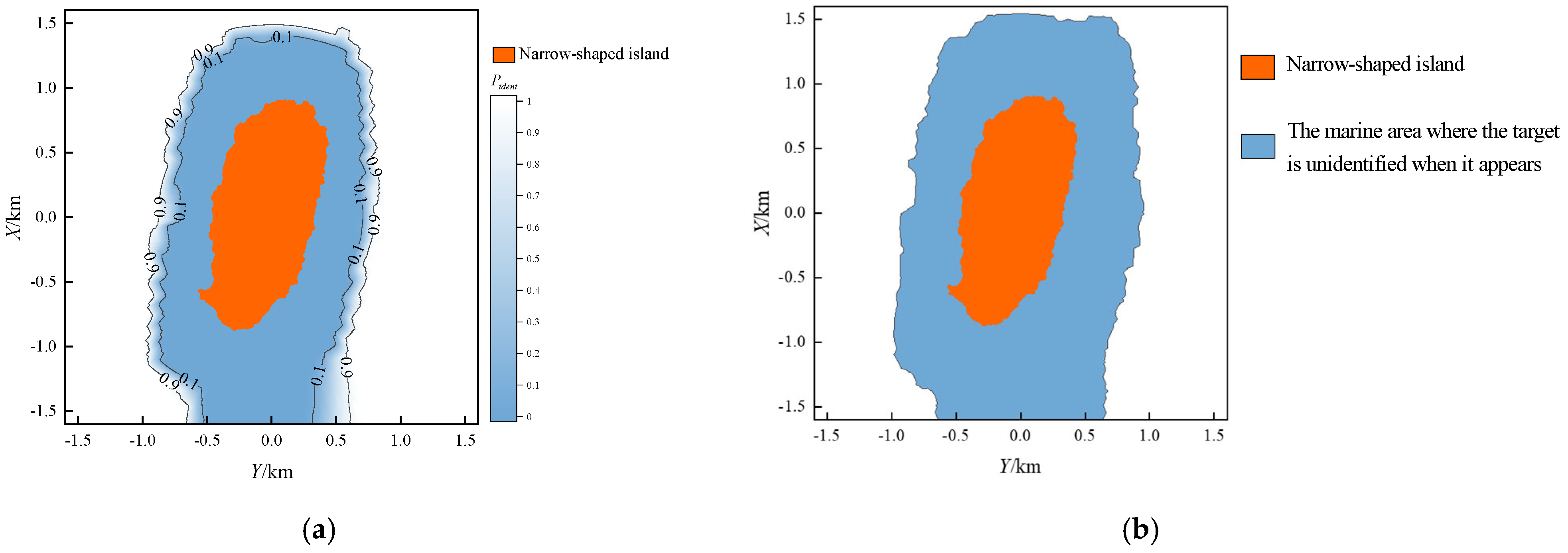
3.5. Result Comparison

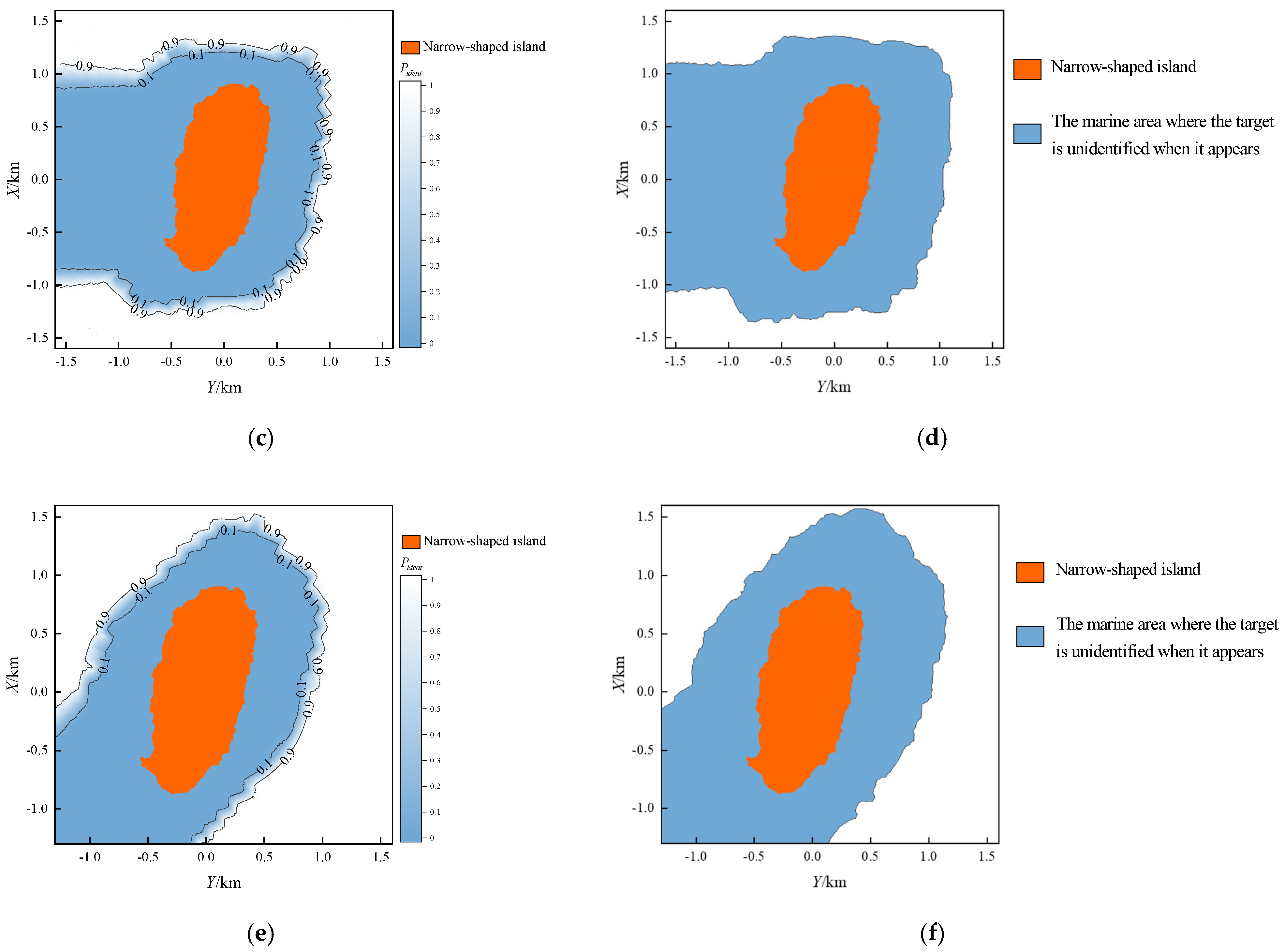
To compare the results from the proposed method and existing methods, we first need to clarify the calculation principle of the existing methods. Existing methods predominantly utilize the 2D contour data of MGFs and are limited to sea-skimming aircraft. These methods do not account for potential errors and merely provide a binary result of “identified” or “unidentified” rather than a probability of identification. The relevant calculation is based on the 2D contour data of MGFs, using the LOS condition and Equations (1) and (2), while neglecting the impact of radar elevation angle resolution (Equation (3)). As these methods do not incorporate error considerations, there is no requirement for Monte Carlo simulation.

To further illustrate the differences between the proposed method and existing methods, we selected radar position points S₁, S₃, and S₅ as examples (sea-skimming aircraft), and calculated and visualized the binary result surrounding the narrow-shaped island. The comparison of these results with those obtained from the proposed method is shown in Figure 7.

From Figure 7, it can be seen that the shape and area of the “unidentified” region from existing methods is similar to those of the sum of Level I and Level II regions from the proposed method, which validates the effectiveness of the proposed method from a different angle.

Besides that, the proposed method not only can be applied to aircraft at any altitude, but it can also take more errors into consideration, and the probability result rather than the binary result provides more precise and intuitive decision-making support for aircraft mission planners.

The detailed comparison between the proposed method and the existing methods in terms of RTA determination conditions, MGF data utilization, and other factors is shown in

Table 7. Comparison of two methods.

Method	RTA Determination Factors	MGF Data Utilization	Applicable Range	Error Consideration	Result
Existing methods	Range resolution Azimuth angle resolution	2D contour	Sea-skimming aircraft	No	Binary
Proposed method	Range resolution Azimuth angle resolution Elevation angle Resolution	3D model	Aircraft at any altitude	Yes	Probability

.

In summary, the proposed method, which incorporates radar elevation angle resolution and the MGF 3D model, is applicable to aircraft at any altitude in 3D space. It can quantitatively calculate the probability of radar correctly identifying a target at a specific marine location, providing more precise and intuitive decision-making support for aircraft mission planners. Compared with existing methods, it better aligns with the current performance and requirements of aircraft.

4. Conclusions

Based on theoretical derivation and simulation analysis, the conclusions are as follows:

(1) In contrast to existing methods limited to sea-skimming aircraft, the proposed method offers a significant advancement by being applicable to aircraft at any altitude.

(2) With the input parameters, the proposed method can effectively calculate the probability P_ident of the target closed to MGF being correctly identified by the radar, rather than a binary result of “identified” or “unidentified” from existing methods, which helps provide more precise and intuitive decision-making support for aircraft mission planners.

However, we acknowledge that our current model does not account for dynamic environmental factors such as sea state or weather conditions, nor does it consider the correlations between the mentioned errors. Future work will focus on incorporating these elements to enhance model accuracy and robustness. Specifically, we plan to analyze error correlations to refine our method, which means that the distribution for actual radar activation point S′(X_S′, Y_S′, Z_S′) would consider the covariances between MGFs and aircraft caused by dynamic environmental factors, and each Monte Carlo simulation would then sample from this refined distribution, yielding more accurate and robust probability results.