Parallels Between Models of Gyrotron Physics and Some Famous Equations Used in Other Scientific Fields
Abstract
1. Introduction
2. Adler’s Equation and Phase Locking and Synchronization of Gyrotrons
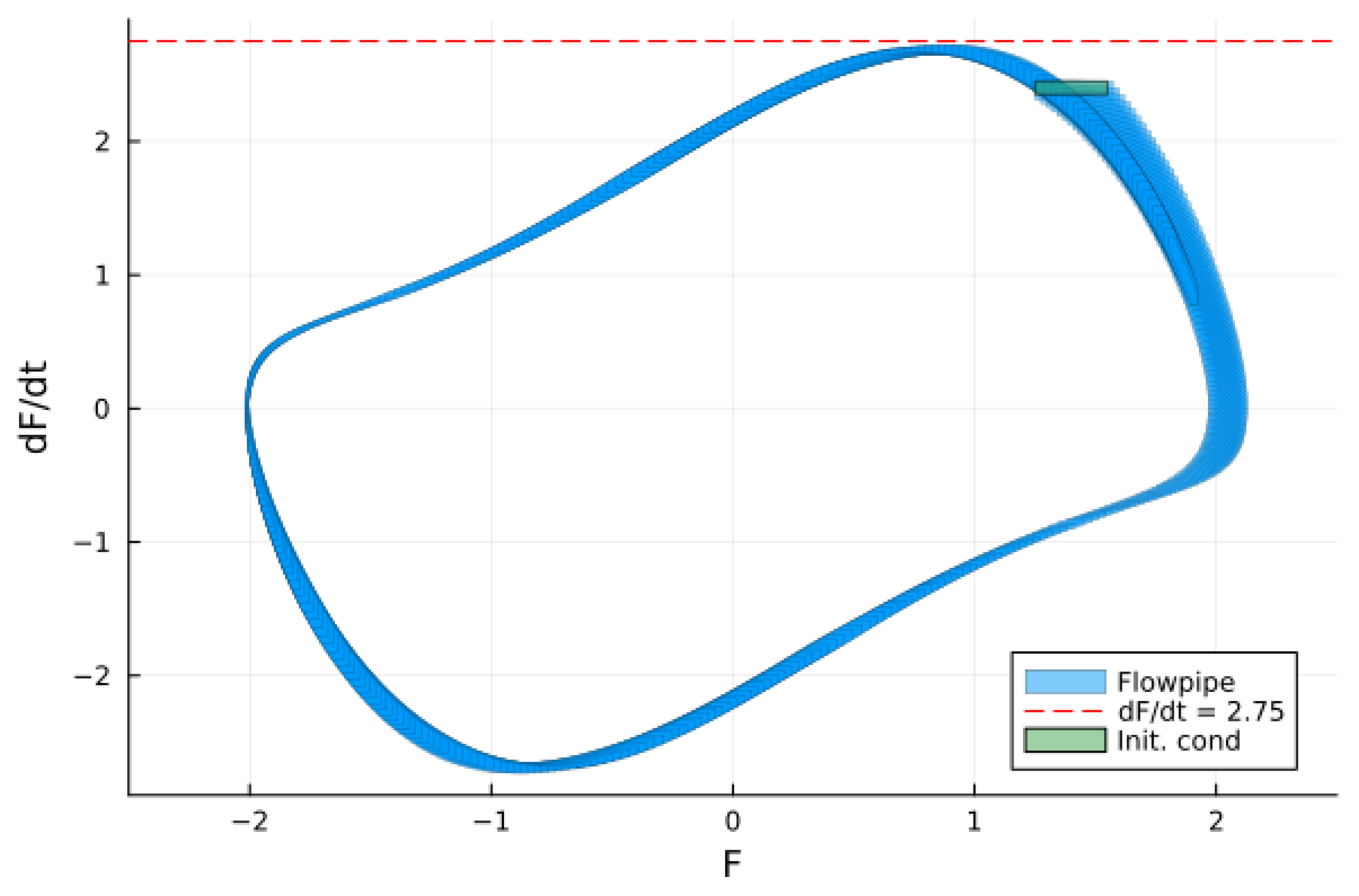
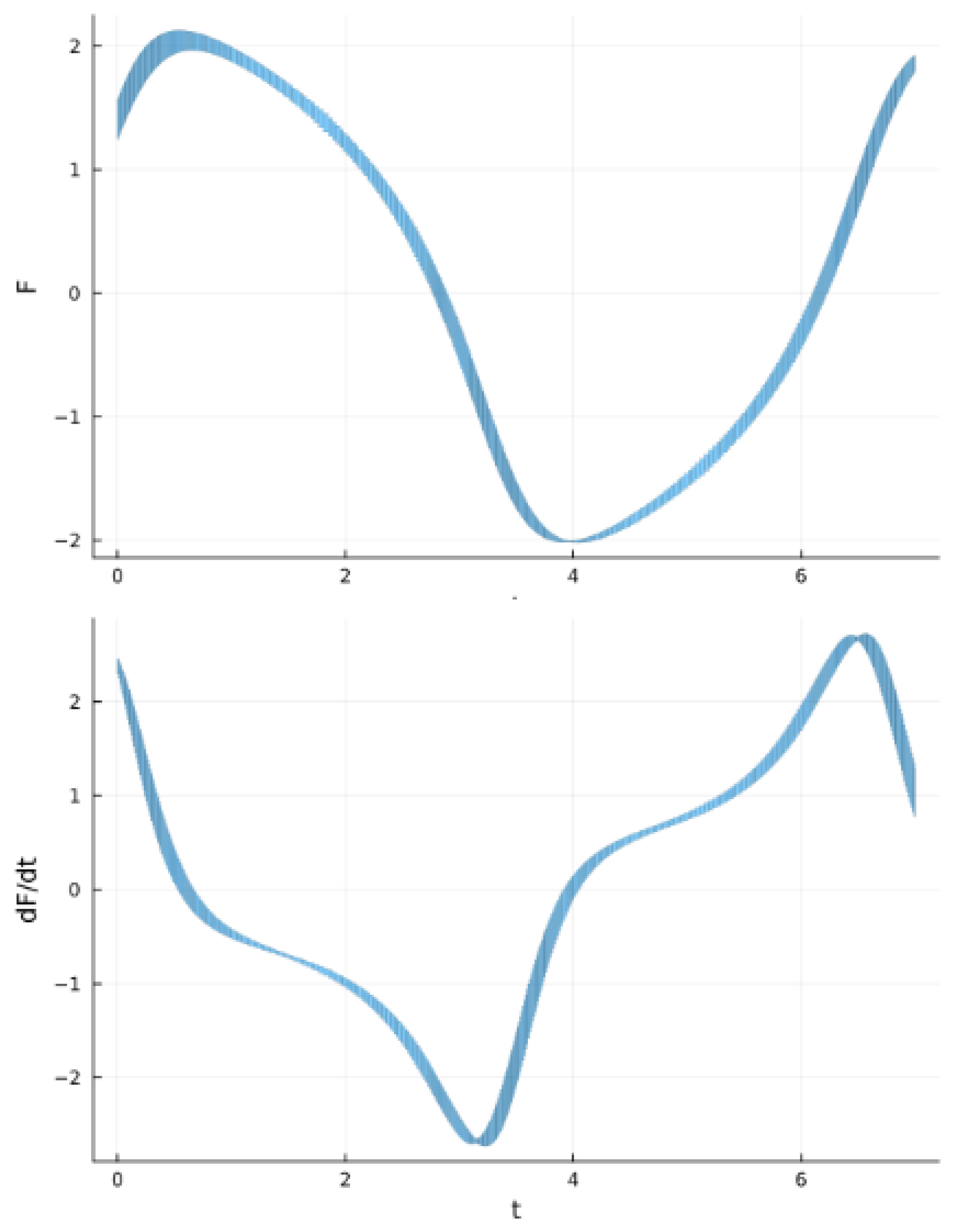
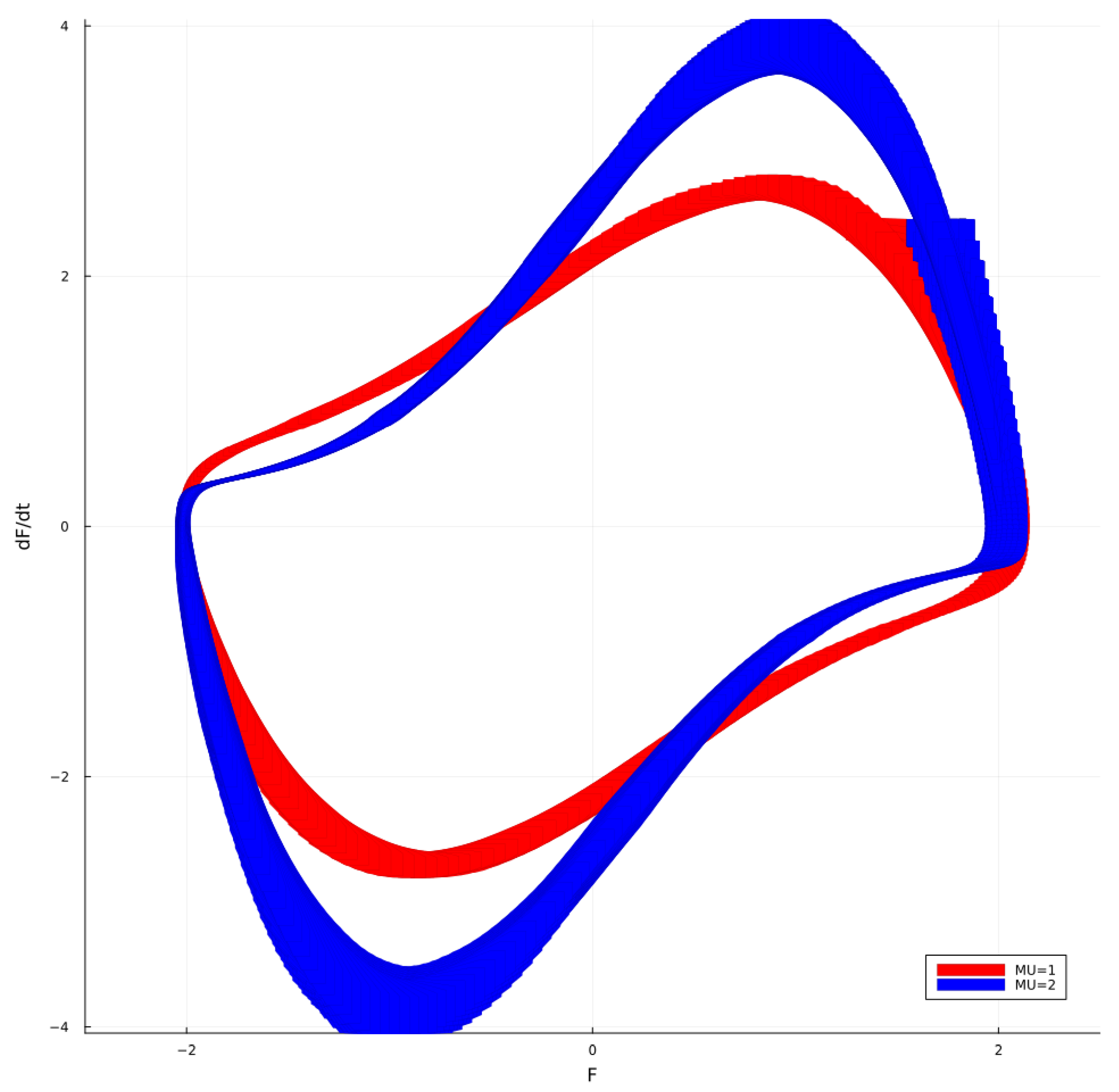
3. Van der Pol Equation and the Analysis of Gyrotron Oscillators
4. From the Equations of Adler and Van der Pol to the Kuramoto Model of Synchronization
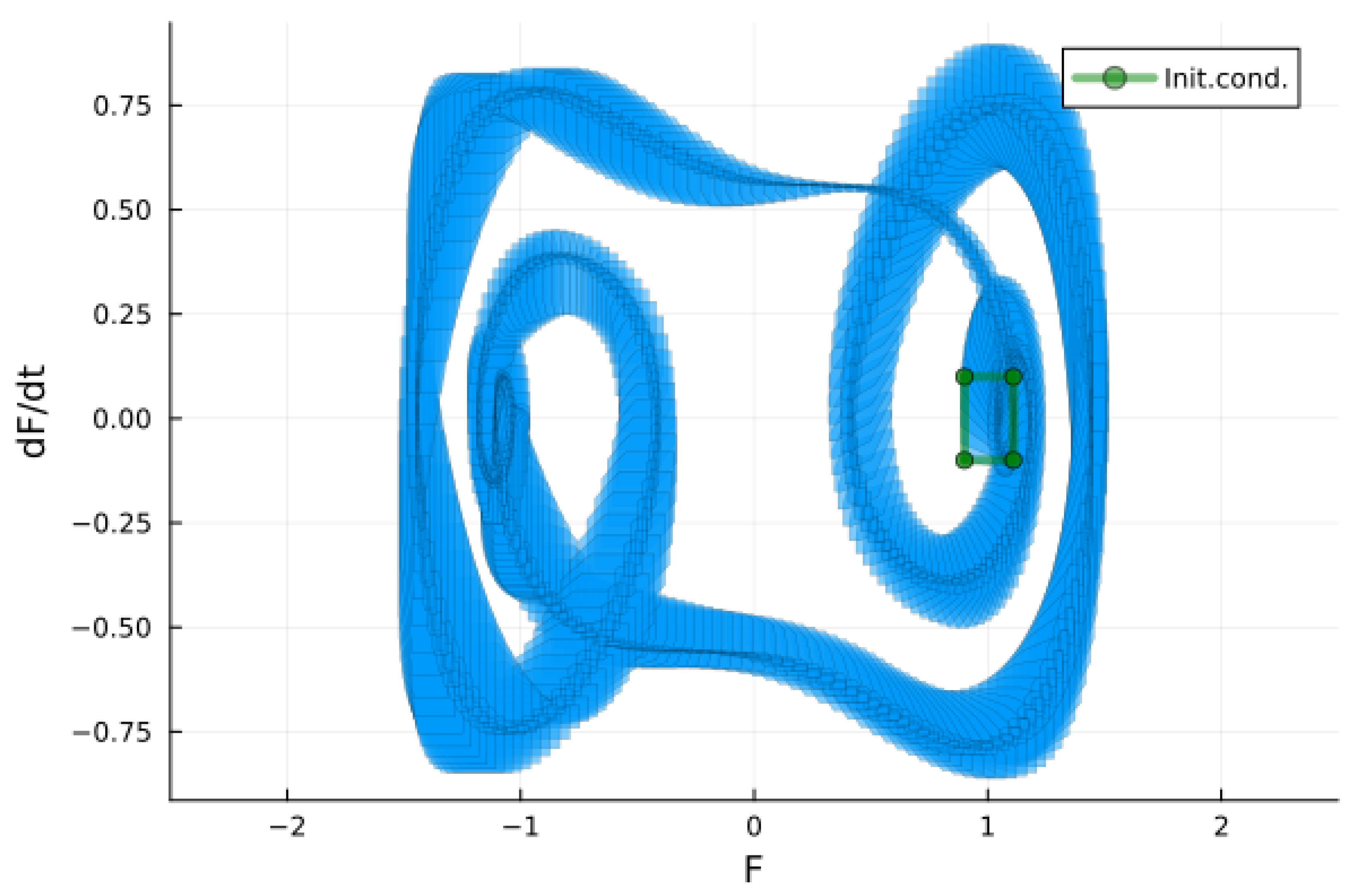
5. Parallels of the Models of Mode Interaction in Gyrotrons and the Models of Population Dynamics in Ecological Systems
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maler, O. Computing Reachable Sets: An Introduction; French National Center of Scientific Research: Paris, France, 2008; pp. 1–8. Available online: https://www-verimag.imag.fr/~maler/Papers/reach-intro.pdf (accessed on 10 May 2025).
- Althoff, M.; Frehse, G.; Girard, A. Set propagation techniques for reachability analysis. Annu. Rev. Control Robot. Auton. Syst. 2021, 4, 369–395. [Google Scholar] [CrossRef]
- ReachabilityAnalysis.jl. Methods to Compute Sets of States Reachable by Dynamical Systems. 2025. Available online: https://juliareach.github.io/ReachabilityAnalysis.jl/dev/ (accessed on 10 May 2025).
- Bogomolov, S.; Forets, M.; Frehse, G.; Potomkin, K.; Schilling, C. JuliaReach: A toolbox for set-based reachability. In Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control, Montreal, QC, Canada, 16–18 April 2019; pp. 39–44. [Google Scholar] [CrossRef]
- Nusinovich, G. Review of the theory of mode interaction in gyrodevices. IEEE Trans. Plasma Sci. 1999, 27, 313–326. [Google Scholar] [CrossRef]
- Sabchevski, S.; Glyavin, M.; Nusinovich, G. The Progress in the Studies of Mode Interaction in Gyrotrons. J. Infrared Millim. Terahertz Waves 2022, 43, 1. [Google Scholar] [CrossRef]
- Temkin, R. Development of terahertz gyrotrons for spectroscopy at MIT. Terahertz Sci. Technol. 2014, 7, 1. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, U.; Bera, A.; Sinha, A. A review on the sub-THz/THz gyrotrons. Infrared Phys. Technol. 2016, 76, 38. [Google Scholar] [CrossRef]
- Glyavin, M.; Sabchevski, S.; Idehara, T.; Mitsudo, S. Gyrotron-Based Technological Systems for Material Processing-Current Status and Prospects. J. Infrared Millim. Terahertz Waves 2020, 41, 1022. [Google Scholar] [CrossRef]
- Idehara, T.; Sabchevski, S.; Glyavin, M.; Mitsudo, S. The Gyrotrons as Promising Radiation Sources for THz Sensing and Imaging. Appl. Sci. 2020, 10, 980. [Google Scholar] [CrossRef]
- Sabchevski, S.; Glyavin, M.; Mitsudo, S.; Tatematsu, Y.; Idehara, T. Novel and Emerging Applications of the Gyrotrons Worldwide: Current Status and Prospects. J. Infrared Millim. Terahertz Waves 2021, 42, 715. [Google Scholar] [CrossRef]
- Litvak, A.G.; Denisov, G.; Glyavin, M. Russian Gyrotrons: Achievements and Trends. IEEE J. Microwaves 2021, 1, 260. [Google Scholar] [CrossRef]
- Karmakar, S.; Mudiganti, J. Gyrotron: The Most Suitable Millimeter-Wave Source for Heating of Plasma in Tokamak. In Plasma Science and Technology; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Sabchevski, S.; Glyavin, M. Development and Application of THz Gyrotrons for Advanced Spectroscopic Methods. Photonics 2023, 10, 189. [Google Scholar] [CrossRef]
- Kartikeyan, M.; Borie, E.; Thumm, M. GYROTRONS High Power Microwave and Millimeter Wave Technology; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Nusinovich, G. Introduction to the Physics of Gyrotrons; The Johns Hopkins University Press: Baltimore, MD, USA, 2004. [Google Scholar] [CrossRef]
- Chu, K.R. The Electron Cyclotron Maser. Rev. Mod. Phys 2004, 76, 489. [Google Scholar] [CrossRef]
- Tsimring, S.E. Electron Beams and Microwave Vacuum Electronics; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Du, H.; Du, C.-H.; Liu, P.-K. Millimeter-Wave Gyrotron Traveling-Wave Tube Amplifiers; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Gilmour, A.S. Klystrons, Traveling Wave Tubes, Magnetrons, Crossed-Field Amplifiers, and Gyrotrons; Artech House: Norwood, MA, USA, 2011. [Google Scholar]
- Grigoriev, A.D.; Ivanov, V.; Molokovsky, S. Microwave Electronics; Springer Series in Advanced Microelectronics; Springer: Berlin/Heidelberg, Germany, 2018; Volume 61. [Google Scholar] [CrossRef]
- Dattoli, G.; Palma, E.; Sabchevski, S.; Spassovsky, I. An overview of the gyrotron theory. In High Frequency Sources of Coherent Radiation for Fusion Plasmas; IOP Publishing: Bristol, UK, 2021; p. 51. [Google Scholar] [CrossRef]
- Tarakanov, V. Code KARAT Simulations Power Microw. Sources Incl. Cherenkov Plasma Devices, Vircators, Orotron, E-Field Sensor, Calorimeter Etc. EPJ Web Conf. 2017, 149, 04024. [Google Scholar] [CrossRef]
- Goplen, B.; Ludeking, L.; Smithe, D.; Warren, G. User-configurable MAGIC for electromagnetic PIC calculations. Comput. Phys. Commun. 1995, 87, 54. [Google Scholar] [CrossRef]
- Nguyen, T. Modeling of gyroklystrons with MAGY. IEEE Trans. Plasma Sci. 2000, 28, 867. [Google Scholar] [CrossRef]
- Jain, R.; Kartikeyan, M. Design of a 60 GHz, 100 kW CW gyrotron for plasma diagnostics: GDS V.01 simulations. Prog. Electromagn. Res. B 2010, 22, 379. [Google Scholar] [CrossRef]
- Sabchevski, S.; Zhelyazkov, I.; Thumm, M.; Illy, S.; Piosczyk, B.; Tran, T.-M.; Pagonakis, J.G. Recent evolution of the simulation tools for computer aided design of electron-optical systems for powerful gyrotrons. Comput. Model. Eng. Sci. 2007, 20, 203. [Google Scholar] [CrossRef]
- Sabchevski, S.; Idehara, T.; Saito, T.; Ogaw, I.; Mitsudo, S.; Tatematsu, Y. Physical Models and Computer Codes of the GYROSIM (GYROtron SIMulation) Software Package; FIR Center Report FIR FU-99; IOP Publishing: Bristol, UK, 2010. [Google Scholar]
- Braunmueller, F.; Tran, T.; Vuillemin, Q.; Alberti, S.; Genoud, J.; Hogge, J.P.; Tran, M. TWANG-PIC, a novel gyro-averaged onedimensional particle-in-cell code for interpretation of gyrotron experiments. Phys. Plasmas 2015, 22, 063115. [Google Scholar] [CrossRef]
- Wang, P.; Chen, X.; Xiao, H.; Dumbrajs, O.; Qi, X.; Li, L. GYROCOMPU: Toolbox Designed for the Analysis of Gyrotron Resonators. IEEE Trans. Plasma Sci. 2020, 48, 3007. [Google Scholar] [CrossRef]
- Sawant, A.; Choi, E. Development of the Full Package of Gyrotron Simulation Code. J. Korean Phys. Soc. 2018, 73, 1750. [Google Scholar] [CrossRef]
- Belousov, V.l.; Ergakov, V.S.; Moiseev, M.A. Two-cavity CRM at harmonics of electron cyclotron frequency. Electronnaya Tech. Ser. 1 Electron. SVCh 1978, 5, 41–50. [Google Scholar]
- Ergakov, V.S.; Moiseev, M.A. Theory of synchronization of oscillations in a cyclotron resonance maser monotron by an external signal. Radiophys. Quantum Electron. 1975, 18, 89–97. [Google Scholar] [CrossRef]
- Bazhanov, V.S.; Ergakov, V.S.; Moiseev, M.A. Synchronization of CRM-monotron by by electron beam modulation. Radiophys. Quantum Electron. 1977, 20, 90–95. [Google Scholar] [CrossRef]
- Nusinovich, G.S. Efficiency of the mode nonlinear selection methods in CRM-Oscillators. Radio Eng. Electron. Phys. 1977, 22, 151. [Google Scholar]
- Read, M.E.; Seeley, R.; Manheimer, W.M. Observations of Phase Locking in a Single-Cavity Gyrotron Oscillator. IEEE Trans. Plasma Sci. 1985, 13, 398–403. [Google Scholar] [CrossRef][Green Version]
- Fliflet, A.W.; Manheimer, W.M. Nonlinear theory of phase-locking gyrotron oscillators driven by an external signal. Phys. Rev. A 1989, 39, 3432–3443. [Google Scholar] [CrossRef] [PubMed]
- Latham, P.E.; Granatstein, V.L.; Carmel, Y. Phase locking and bandwidth in a gyrotron oscillator. Int. J. Infrared Millim. Waves 1993, 14, 1217–1227. [Google Scholar] [CrossRef]
- Guo, H.; Hoppe, D.; Rodgers, J.; Perez, R.; Tate, J.; Conroy, B.; Granatstein, V.; Bhanji, A.; Latham, P.; Nusinovich, G.; et al. Phase-locking of a second-harmonic gyrotron oscillator using a quasi-optical circulator to separate injection and output signals. IEEE Trans. Plasma Sci. 1995, 23, 822–832. [Google Scholar] [CrossRef]
- Rodgers, J.; Guo, H.; Granatstein, V.; Chen, S.; Nusinovich, G.; Walter, M.; Zhao, J. High efficiency, phase-locked operation of the harmonic-multiplying inverted gyrotwystron oscillator. IEEE Trans. Plasma Sci. 1999, 27, 412–421. [Google Scholar] [CrossRef]
- Rodgers, J.; Guo, H.; Nusinovich, G.; Granatstein, V. Experimental study of phase deviation and pushing in a frequency doubling, second harmonic gyro-amplifier. IEEE Trans. Electron Devices 2001, 48, 2434–2441. [Google Scholar] [CrossRef]
- Glyavin, M.Y.; Denisov, G.; Kulygin, M.; Melnikova, M.; Novozhilova, Y.V.; Ryskin, N. Gyrotron frequency stabilization by a weak reflected wave. Radiophys. Quantum Electron. 2016, 58, 673–683. [Google Scholar] [CrossRef]
- Denisov, G.G.; Kuftin, A.N.; Manuilov, V.N.; Zavolsky, N.A.; Chirkov, A.V.; Soluyanova, E.A.; Tai, E.M.; Bakulin, M.I.; Tsvetkov, A.I.; Fokin, A.P.; et al. Design of master oscillator for frequency locking of a complex of megawatt level microwave sources. Microw. Opt. Technol. Lett. 2020, 62, 2137–2143. [Google Scholar] [CrossRef]
- Denisov, G.; Kuftin, A.; Glyavin, M.; Tsvetkov, A.; Golubiatnikov, G.; Tai, E.; Soluyanova, E.; Bakulin, M.; Fokin, A.; Shmelev, M.; et al. Experimental tests of a high-stable 170 GHz/25 kW gyrotron as a master oscillator for frequency locking of megawatt level microwave sources. In Proceedings of the 2021 22nd International Vacuum Electronics Conference (IVEC), Rotterdam, The Netherlands, 27–30 April 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Krier, L.; Avramidis, K.A.; Braune, H.; Gantenbein, G.; Illy, S.; Ioannidis, Z.; Jelonnek, J.; Laqua, H.P.; Marsen, S.; Moseev, D.; et al. Frequency Stabilization of Megawatt-Class 140 GHz Gyrotrons at W7-X Using an Off-the-Shelf PLL System. In Proceedings of the 2021 46th International Conference on Infrared, Millimeter and Terahertz Waves (IRMMW-THz), Chengdu, China, 29 August–3 September 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Grigorieva, N.V.; Ryskin, N.M. A study of gyrotron synchronization in the hard-excitation regime on the basis of the modified quasilinear model. Radiophys. Quantum Electron. 2022, 65, 371–383. [Google Scholar] [CrossRef]
- Adilova, A.B.; Ryskin, N.M. The phase-locking of high-power delay-coupled gyrotron oscillators with hard excitation. In Proceedings of the 2022 IEEE 8th All-Russian Microwave Conference (RMC), Moscow, Russia, 23–25 November 2022. [Google Scholar] [CrossRef]
- Denisov, G.G.; Zotova, I.V.; Zheleznov, I.V.; Malkin, A.M.; Ginzburg, N.S.; Sergeev, A.S.; Semenov, E.S.; Glyavin, M.Y. Phase-Locking of Second-Harmonic Gyrotrons for Providing MW-Level Output Power. IEEE Trans. Electron Devices 2022, 69, 754–758. [Google Scholar] [CrossRef]
- Rozental, R.M.; Zotova, I.V.; Sergeev, A.S.; Ginzburg, N.S.; Denisov, G.G. Concept of Gyrotron Complexes With Serial Phase and Frequency Locking. IEEE Trans. Electron Devices 2023, 70, 2161–2164. [Google Scholar] [CrossRef]
- Fokin, A.P.; Kuftin, A.N.; Belousov, V.I.; Chirkov, A.V.; Shmelev, M.Y.; Golubiatnikov, G.Y.; Movshevich, B.Z.; Tai, E.M.; Glyavin, M.Y.; Denisov, G.G. First Experiments on Frequency Locked Operation of the 170 GHz/1 MW Gyrotron. In Proceedings of the 2024 Photonics and Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Spigler, R. The Remote Control and Beyond: The Legacy of Robert Adler. SIAM News 2007, 40, 613. [Google Scholar]
- Adler, R. A Study of Locking Phenomena in Oscillators. Proc. IRE 1946, 34, 351–357. [Google Scholar] [CrossRef]
- Lai, X.; Roychowdhury, J. Analytical equations for predicting injection locking in LC and ring oscillators. In Proceedings of the IEEE 2005 Custom Integrated Circuits Conference, San Jose, CA, USA, 21 September 2005; pp. 461–464. [Google Scholar] [CrossRef]
- Razavi, B. A study of injection pulling and locking in oscillators. In Proceedings of the IEEE 2003 Custom Integrated Circuits Conference, San Jose, CA, USA, 24 September 2003; pp. 305–312. [Google Scholar] [CrossRef]
- Nusinovich, G.S.; Dumbrajs, O. Technical noise in gyroklystrons and phase-locked gyrotron oscillators. Phys. Plasmas 1997, 4, 1424–1433. [Google Scholar] [CrossRef]
- Bakunin, V.L.; Denisov, G.G.; Novozhilova, Y.V. Phase locking of a gyrotron with low-frequency voltage and current fluctuations by an external monochromatic signal. Radiophys. Quantum Electron. 2020, 63, 392–402. [Google Scholar] [CrossRef]
- Bakunin, V.L.; Denisov, G.G.; Kuftin, A.N.; Novozhilova, Y.V.; Fokin, A.P.; Zuev, A.S.; Semenov, E.S. Stabilization of the radiation frequency of a gyrotron with a remote reflector under the conditions of interaction of the equidistant-spectrum modes. Radiophys. Quantum Electron. 2023, 65, 566–577. [Google Scholar] [CrossRef]
- Adilova, A.B.; Ryskin, N.M. Theory of Peer-to-Peer Locking of High-Power Gyrotron Oscillators Coupled with Delay. Electronics 2022, 11, 811. [Google Scholar] [CrossRef]
- Kuftin, A.N.; Golubiatnikov, G.Y.; Vilkov, V.A.; Fokin, A.P.; Novozhilova, Y.V.; Glyavin, M.Y.; Denisov, G.G. Experimental Study of Extended Operating Zone of a 170-GHz/1-MW Gyrotron Locked by a Narrowband External Signal. IEEE Trans. Electron Devices 2024, 71, 7061–7065. [Google Scholar] [CrossRef]
- Gaponov-Grekhov, A.V.; Rabinovich, M.I. L. I. Mandel’shtam and the modern theory of nonlinear oscillations and waves. Sov. Phys. Uspekhi 1979, 22, 590. [Google Scholar] [CrossRef]
- Nusinovich, G.S. To the theory of gyrotrons with confocal resonators. Phys. Plasmas 2019, 26, 053107. [Google Scholar] [CrossRef]
- Barroso, J.J. Cavity Excitation Described by the van der Pol Equation in Transit-Time Tubes. IEEE Trans. Electron Devices 2007, 54, 3085–3091. [Google Scholar] [CrossRef]
- Ryskin, N.M.; Shigaev, A.M. Complex dynamics of a simple distributed self-oscillatory model system with delay. Tech. Phys. 2002, 47, 795–802. [Google Scholar] [CrossRef]
- Koronovsky, A.A.; Trubetskov, D.I.; Khramov, A.E. Transient Processes in the Distributed Active Medium “Helical Electron Beam–Counterpropagating Electromagnetic Wave”. Radiophys. Quantum Electron. 2004, 47, 332–340. [Google Scholar] [CrossRef]
- Reachability Computations for Dynamical Systems in Julia. 2025. Available online: https://github.com/juliareach (accessed on 10 May 2025).
- Mathematica Tutorial for the Second Course. Part III: Van der Pol Equations. 2025. Available online: https://www.cfm.brown.edu/people/dobrush/am34/Mathematica/ch3/pol.html (accessed on 10 May 2025).
- Kanamaru, T. Van der Pol oscillator. Sch. J. 2007, 2, 2202. [Google Scholar] [CrossRef]
- Lynch, J.; York, R. Stability of mode locked states of coupled oscillator arrays. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 413–418. [Google Scholar] [CrossRef]
- Wirkus, S.; Rand, R. The Dynamics of Two Coupled van der Pol Oscillators with Delay Coupling. Nonlinear Dyn. 2002, 30, 205–221. [Google Scholar] [CrossRef]
- Balakin, M.I.; Ryskin, N.M. Bifurcational mechanism of formation of developed multistability in a van der Pol oscillator with time-delayed feedback. Nelineinaya Din. 2017, 13, 151–164. [Google Scholar] [CrossRef]
- Balakin, M.I.; Ryskin, N.M. Multistability and complex oscillatory regimes in a microwave generator with delayed reflection from the load. Tech. Phys. Lett. 2019, 45, 278–280. [Google Scholar] [CrossRef]
- Kuznetsov, A.P.; Stankevich, N.V.; Turukina, L.V. Coupled Van der Pol and Van der Pol–Duffing oscillators: Dynamics of Phase and Computer Simulation. Izv. VUZ 2008, 16, 101–136. [Google Scholar] [CrossRef]
- Korsch, H.J.; Jodl, H.J.; Hartmann, T. The duffing oscillator. In Chaos; Springer: Berlin/Heidelberg, Germany, 2008; pp. 157–184. [Google Scholar]
- Brand, G.F.; Ideharaj, T.; Tatsukawa, T.; Ogawa, I. Mode competition in a high harmonic gyrotron. Int. J. Electron. 1992, 72, 745–758. [Google Scholar] [CrossRef]
- Dumbrajs, O.; Idehara, T.; Iwata, Y.; Mitsudo, S.; Ogawa, I.; Piosczyk, B. Hysteresis in gyrotrons. In Proceedings of the Twenty Seventh International Conference on Infrared and Millimeter Waves, San Diego, CA, USA, 26 September 2002; pp. 331–332. [Google Scholar] [CrossRef]
- Dumbrajs, O.; Idehara, T.; Iwata, Y.; Mitsudo, S.; Ogawa, I.; Piosczyk, B. Hysteresis-like effects in gyrotron oscillators. Phys. Plasmas 2003, 10, 1183–1186. [Google Scholar] [CrossRef]
- Dumbrajs, O.; Khutoryan, E.M.; Idehara, T. Hysteresis and frequency tunability of gyrotrons. J. Infrared Millim. Terahertz Waves 2016, 37, 551–560. [Google Scholar] [CrossRef]
- Blokhina, E.V.; Rozhnev, A.G. Chaos and hyperchaos in a gyrotron. Radiophys. Quantum Electron. 2006, 49, 799–810. [Google Scholar] [CrossRef]
- Nusinovich, G.S.; Sinitsyn, O.V. Interpretation of the nonlinear mode excitation in the ITER gyrotron. Phys. Plasmas 2007, 14, 113103. [Google Scholar] [CrossRef]
- Blokhina, E.V.; Kuznetsov, S.P.; Rozhnev, A.G. High-Dimensional Chaos in a Gyrotron. IEEE Trans. Electron Devices 2007, 54, 188–193. [Google Scholar] [CrossRef]
- Fedotov, A.E.; Rozental, R.M.; Isaeva, O.B.; Rozhnev, A.G. Chaos and Hyperchaos in a Ka-Band Gyrotron. IEEE Electron Device Lett. 2021, 42, 1073–1076. [Google Scholar] [CrossRef]
- Ishchenko, A.S.; Novozhilova, Y.V.; Petelin, M.I. Theory of locking of a Van der Pol oscillator by delayed reflection from a resonant load. Radiophys. Quantum Electron. 2006, 49, 485–498. [Google Scholar] [CrossRef]
- Usacheva, S.A.; Ryskin, N.M. Phase locking of two limit cycle oscillators with delay coupling. Chaos 2014, 24, 023123. [Google Scholar] [CrossRef] [PubMed]
- Rozental, R.M.; Ginzburg, N.S.; Glyavin, M.Y.; Sergeev, A.S.; Zotova, I.V. Mutual synchronization of weakly coupled gyrotrons. Phys. Plasmas 2015, 22, 093118. [Google Scholar] [CrossRef]
- Kuramoto, Y. Self-entrainment of a population of coupled non-linear oscillators. In International Symposium on Mathematical Problems in Theoretical Physics; Springer: Berlin/Heidelberg, Germany, 1975; pp. 420–422. [Google Scholar] [CrossRef]
- Kuramoto, Y. Phase- and Center-Manifold Reductions for Large Populations of Coupled Oscillators with Application to Non-Locally Coupled Systems. Int. J. Bifurc. Chaos 1997, 07, 789–805. [Google Scholar] [CrossRef]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life, 1st ed.; Hyperion: New York, NY, USA, 2003. [Google Scholar]
- Acebrón, J.A.; Bonilla, L.L.; Pérez Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Rosenblum, M.; Pikovsky, A. Synchronization: From pendulum clocks to chaotic lasers and chemical oscillators. Contemp. Phys. 2003, 44, 401–416. [Google Scholar] [CrossRef]
- Dirk Brockman and Steven Strogatz, “Ride My Kuramoto Cycle”. 2025. Available online: https://www.complexity-explorables.org/explorables/ride-my-kuramotocycle (accessed on 10 May 2025).
- Subbarao, D.; Arora, M.; Uma, R.; Phanendra, M.V.R.; Singh, K.K. Computer simulation of gyrophase self-organisation in a magnetoplasma. Comput. Phys. Commun. 2004, 164, 477–481. [Google Scholar] [CrossRef]
- Zapevalov, V.E.; Nusinovich, G.S. The theory of amplitude-phase mode interactions in electron masers. Radiophys. Quantum Electron. 1989, 32, 269–276. [Google Scholar] [CrossRef]
- Adilova, A.B.; Balakin, M.I.; Gerasimova, S.A.; Ryskin, N.M. Bifurcation analysis of multistability of synchronous states in the system of two delay-coupled oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 113103. [Google Scholar] [CrossRef] [PubMed]
- Provansal, M.; Mathis, C.; Boyer, L. Bénard-von Kármán instability: Transient and forced regimes. J. Fluid Mech. 1987, 182, 1. [Google Scholar] [CrossRef]
- D’Huys, O.; Vicente, R.; Danckaert, J.; Fischer, I. Amplitude and phase effects on the synchronization of delay-coupled oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 043127. [Google Scholar] [CrossRef] [PubMed]
- Nusinovich, G.S. Mode interaction in gyrotrons. Int. J. Electron. 1981, 51, 457–474. [Google Scholar] [CrossRef]
- Zavol’skii, N.A.; Nusinovich, G.S. Interaction of modes in gyrotrons with a high-frequency field whose longitudinal structure is variable. Radiophys. Quantum Electron. 1990, 33, 627–632. [Google Scholar] [CrossRef]
- Wangersky, P.J. Lotka-Volterra Population Models. Annu. Rev. Ecol. Syst. 1978, 9, 189–218. [Google Scholar] [CrossRef]
- Berryman, A.A. The Orgins and Evolution of Predator-Prey Theory. Ecology 1992, 73, 1530–1535. [Google Scholar] [CrossRef]
- Nusinovich, G. Mode competition in a gyromonotron with a distorted axial symmetry. Radiotekhnika I Elektron. 1974, 19, 1788–1790. [Google Scholar]
- Gashturi, A.P.; Nusinovich, G.S.; Zotova, I.V.; Semenov, E.S.; Sabchevski, S.P.; Glyavin, M.Y. Nonlinear excitation of parasitic modes in harmonic gyrotrons. Phys. Plasmas 2020, 27, 063304. [Google Scholar] [CrossRef]
- Sabchevski, S.; Nusinovich, G.; Glyavin, M. Harmonic Gyrotrons: Pros and Cons. J. Infrared Millim. Terahertz Waves 2024, 45, 184–207. [Google Scholar] [CrossRef]
- Maynard-Smith, J. Models in Ecology; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Nusinovich, G. Methods of voltage feeds for a pulsed gyromonotron which ensure high-efficiency in a single-mode operation. Elektron. Teknh. Elektron. SVCh 1974, 3, 44–49. [Google Scholar]
- Ginoux, J.M. History of Nonlinear Oscillations Theory in France (1880–1940); Springer: Berlin/Heidelberg, Germany, 2017; Volume 49. [Google Scholar]
- Landa, P.S. Nonlinear Oscillations and Waves in Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2013; Volume 360. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurths, J.; Synchronization, A. A Universal Concept in Nonlinear Sciences; Cambridge University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Strogatz, S.H. From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Phys. D Nonlinear Phenom. 2000, 143, 1–20. [Google Scholar] [CrossRef]
- Strogatz, S.H. Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life; Grand Central Publishing: New York, NY, USA, 2012. [Google Scholar]
- Spigler, R. The mathematics of Kuramoto models which describe synchronization phenomena. Mat. Cult. E Società. Riv. Dell’Unione Mat. Ital. 2016, 1, 123–132. [Google Scholar]
- JuliaReach—Summer of Code. 2025. Available online: https://julialang.org/jsoc/gsoc/juliareach/ (accessed on 10 May 2025).



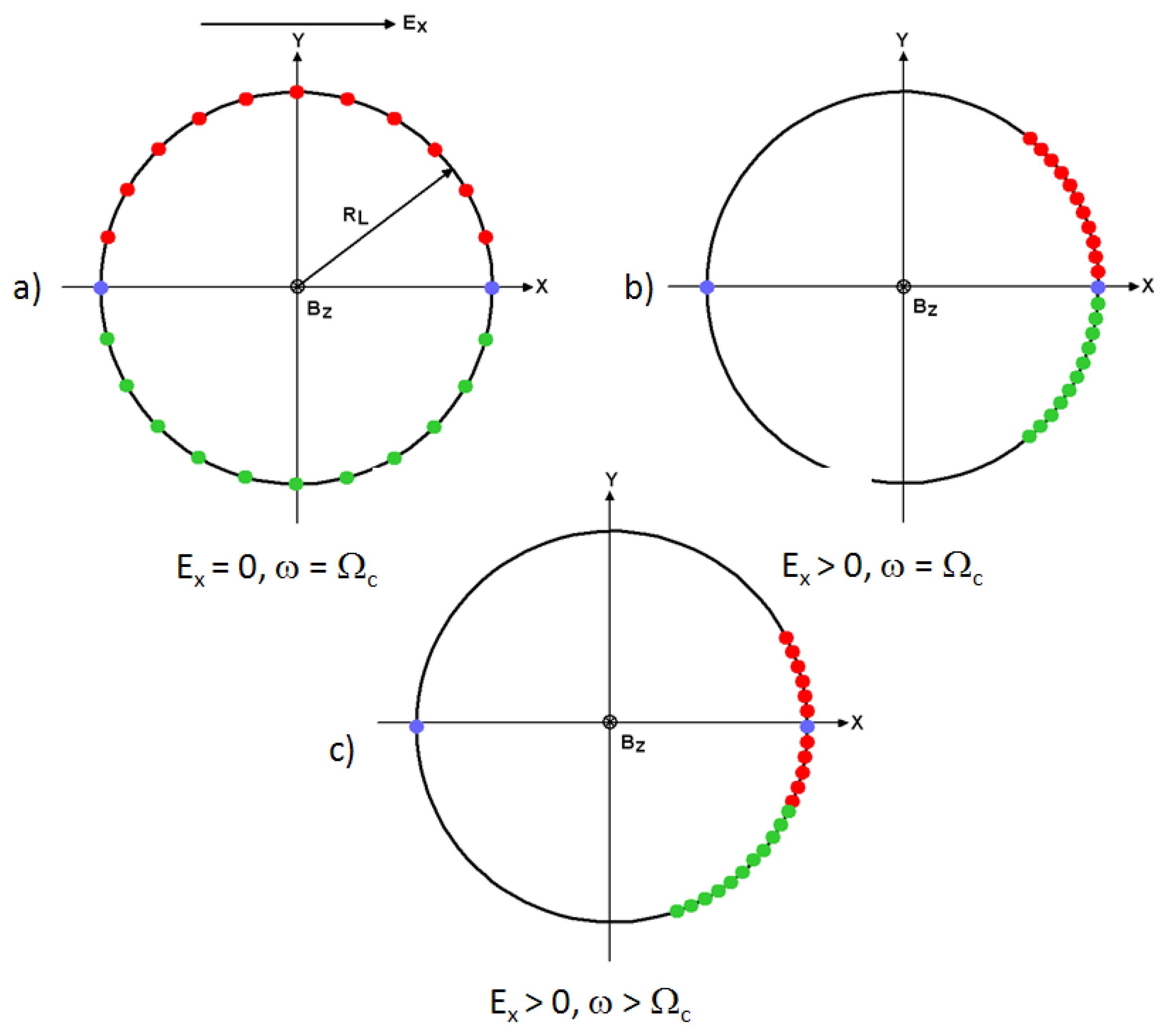
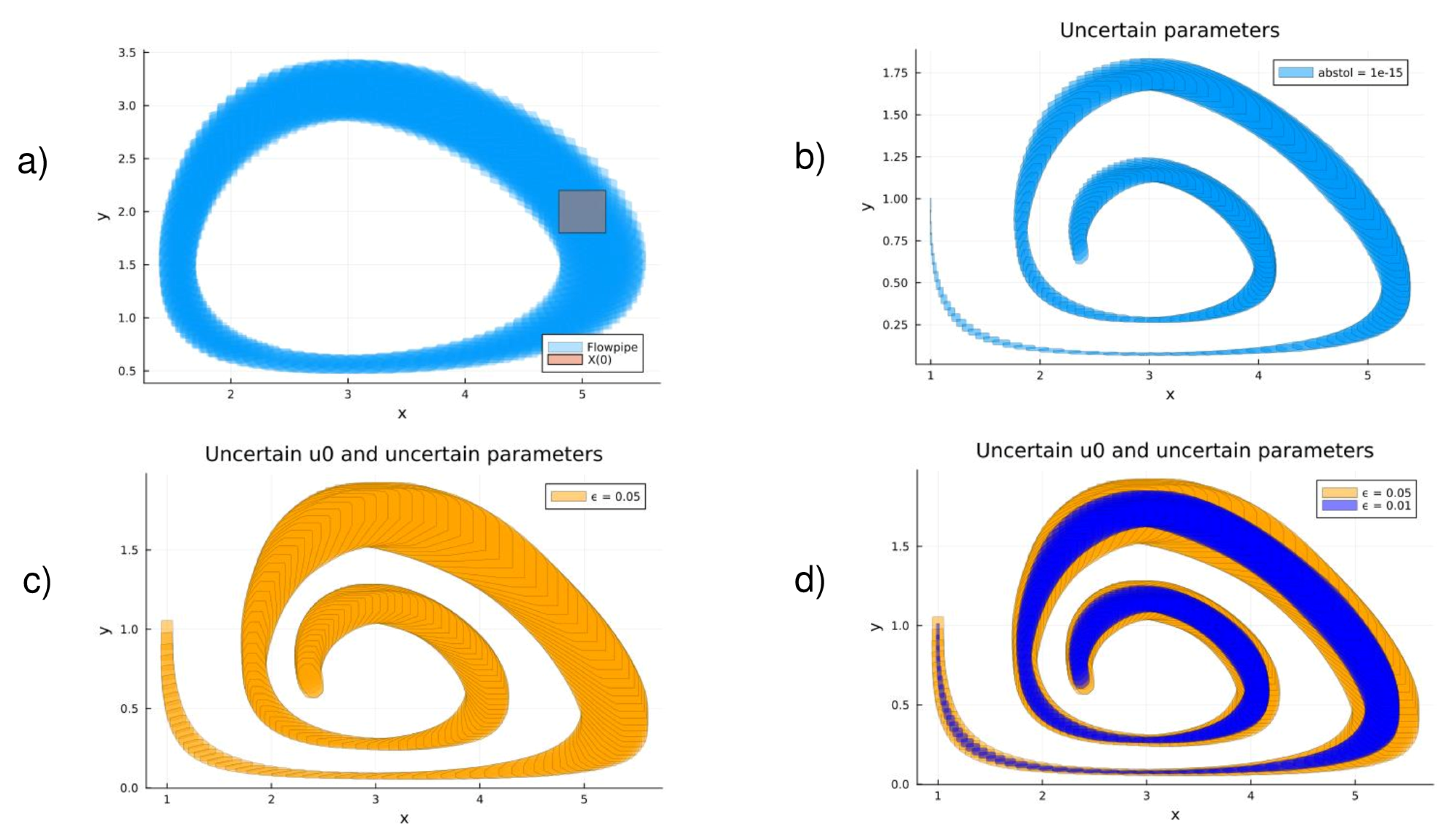
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabchevski, S. Parallels Between Models of Gyrotron Physics and Some Famous Equations Used in Other Scientific Fields. Appl. Sci. 2025, 15, 7920. https://doi.org/10.3390/app15147920
Sabchevski S. Parallels Between Models of Gyrotron Physics and Some Famous Equations Used in Other Scientific Fields. Applied Sciences. 2025; 15(14):7920. https://doi.org/10.3390/app15147920
Chicago/Turabian StyleSabchevski, Svilen. 2025. "Parallels Between Models of Gyrotron Physics and Some Famous Equations Used in Other Scientific Fields" Applied Sciences 15, no. 14: 7920. https://doi.org/10.3390/app15147920
APA StyleSabchevski, S. (2025). Parallels Between Models of Gyrotron Physics and Some Famous Equations Used in Other Scientific Fields. Applied Sciences, 15(14), 7920. https://doi.org/10.3390/app15147920





