Particle-Scale Insights into Extraction Zone Development During Block Caving: Experimental Validation and PFC3D Simulation of Gradation-Dependent Flow Characteristics

Abstract

To investigate the evolution trend of the extraction zone above the drawbell in block caving, an experimental apparatus incorporating the drawbell structure was designed. Ore drawing experiments were conducted using materials with varying particle size gradations. The results demonstrate that the extraction zones for all three gradations exhibit an ellipsoidal shape in the vertical direction, with elliptical cross-sections. As the draw height increases, both the major and minor axes of the extraction zone’s maximum cross-section continuously enlarge, stabilizing beyond a draw height of 80 cm. The ore fragment size significantly influences the extraction zone dimensions. Gradation I, characterized by the smallest average particle size, yielded the largest extraction zone, whereas Gradation III, with the largest average particle size, resulted in the smallest. Numerical simulations of ore drawing for the different particle sizes were performed using PFC3D. The extent of the extraction zone in the numerical results was determined by reconstructing the initial positions of the drawn particles. The simulations show good agreement with the experimental findings, particularly regarding how the major and minor axes of the extraction zone cross-section vary with increasing draw height. Moreover, the simulations confirm that smaller average particle sizes enhance particle flowability, leading to larger extraction zones, as anticipated.

1. Introduction

The block caving method exploits the distribution characteristics of joints and the low-strength properties of the ore/rock. Undercutting—blasting at the base of the ore block—creates a free surface, inducing gravity-driven caving of the ore [1]. This process involves stages including undercutting, initial caving, and continuous caving until the collapse propagates to the surface. Block caving is an efficient underground mining method well suited to specific geological conditions, offering significant economic benefits and technical advantages [2]. However, its successful implementation depends critically on precise draw control strategies. Understanding draw theory and its associated control techniques is paramount for elucidating the movement laws of caved ore within the surrounding rock cover. Furthermore, it plays a vital role in predicting ore loss and dilution, thereby enhancing economic outcomes [3,4].

Numerous researchers have conducted extensive indoor experiments, numerical simulations, and theoretical studies on draw problems in metal mines. Various ore draw theories have been developed to date, including the ellipsoid theory, quasi-ellipsoid theory, random medium theory, and inverted drop theory. Concurrently, indoor draw experiments have garnered significant interest among scholars, and their findings have proven indispensable in mining research. For instance, Sanchez [5] developed a large-scale ore draw test apparatus and utilized it to investigate the influence of moisture content and particle size on extraction zone (EZ) morphology. Power [6] and Castro [7] systematically conducted three-dimensional physical draw experiments using gravel as a granular medium to examine the morphological evolution of the extraction zone and ore flow patterns under 3D conditions. Castro et al. [8] performed multiple laboratory experiments to quantify variations in internal stress within the drawpoint structure under consistent rock mass gradation but different draw strategies. Their results revealed that the vertical stress during drawing fluctuated between 0.3 and 2.8 times the initial vertical stress, with variations closely linked to factors such as the draw strategy and spatial location within the draw zone. Jin [9] conducted isolated draw experiments, the results of which demonstrated a distinct longitudinal asymmetry in the EZ shape, deviating from a standard ellipsoid. The migration zone (MZ) exhibited an inverted droplet shape, corroborating the inverted drop theory. Building on this, Jin proposed a novel method for characterizing EZ geometry and development. Bridgwater and Hashim et al. [10,11] constructed a physical model featuring a draw funnel and tested various coarse-to-fine material ratios, coarse particle distributions, and material heights to assess the effects of key variables on fine particle migration. Janelid [12] examined the migration patterns of caved ore and rock under different influencing factors, such as draw column height, drawpoint size, and vertical stress.

Furthermore, with the continuous advancement of computer technology and ore draw theory, numerical simulation methods are poised to play an increasingly critical and indispensable role in studying ore draw problems. Among these methods, PFC (particle flow code) is particularly well suited for investigating ore draw phenomena due to its unique capability to analyze the movement laws of granular media, such as caved ore, from a microscopic perspective [13,14]. Currently, researchers have achieved significant results in studying near-field mining issues in metal mines using PFC software. For instance, Jin [15] investigated the shape of the Isolated Extraction Zone (IEZ) and its key influencing factors through isolated physical draw experiments. After validating the reliability of Particle Flow Code (PFC) for draw simulations, Jin constructed various numerical models to examine the flow behaviors of caved ore and rock under multiple drawpoint conditions. The findings indicate that the influence of the particle size, drawpoint size, and caved ore column height on the IEZ shape is negligible, being primarily governed by draw control. The ore loss rate decreases with increasing drawpoint size and caved ore column height but increases with larger drawpoint spacing. Sun et al. [16] proposed a method for generating irregular particle clusters using PFC and explored the variation patterns of IEZ shape and caved ore/rock fragment size under conditions considering secondary fragmentation. Song et al. [17] employed the Particle Flow Code (PFC) to define different block categories to characterize the irregularity of caved rock shapes. Using numerical analysis, they studied the influence of rock particle shape on the morphology and quality of the IEZ. Rafiee et al. [18] utilized discrete element numerical simulation to assess the rock mass cavability under various factors prior to far-field mining initiation. They reported that in situ stress and the hydraulic radius are the primary factors influencing rock cavability in block caving. Dai et al. [19] established a void diffusion model based on stochastic medium theory, introducing the concept of the draw fragmentation index. Programming algorithms were then used for simulations to analyze the flow characteristics of caved rock under varying draw heights and fragmentation conditions. Chen et al. [20] conducted numerical simulations using PFC2D to investigate the evolution characteristics of force chains within granular media flow beneath a flexible isolation layer. By integrating contact mechanics and statistical mechanics, they studied the evolution of internal force chain attributes—including length, quantity, strength, orientation, and quasi-linear count—during multi-drawpoint mining. Lapčević Veljko [21] applied the discrete element numerical simulation method to analyze the effects of ore friction and fragmentation on ore dilution and recovery. Wu et al. [22] constructed a caved rock model with uniformly distributed block sizes via PFC3D. They explored the optimization of sublevel caving method structural parameters, the shape of the extraction zone under different granular medium conditions, and the optimal cave step distance.

Previous research has predominantly focused on the shape of the extraction zone in caving methods. However, most studies characterize release points based on single-hole configurations, neglecting drawbell conditions. In the block caving method, ore is drawn from both ends of the drawbell. The flow mechanisms induced by the interaction between these two outlets create a distinct extraction zone morphology, inevitably differing from prior conclusions drawn under single-hole conditions. Additionally, variations in rock mass structure lead to differences in fragmented rock sizes across zones. Such size disparities directly impact rock flowability, thereby altering the extraction zone dimensions above the drawbell and resulting in divergent overlap patterns. Consequently, designing ore extraction drift spacing in block caving must account for these influences. Investigating the migration laws of caved ore and rock during the draw process is therefore of paramount importance for refining the ore draw methodology in block caving operations.

2. Description of the Isolated Draw Test

2.1. Experimental Materials

The particle size distribution (PSD) of loose particles within caved ore is a critical factor influencing ore flowability. To ensure that the results of laboratory-scale physical draw experiments closely approximate those at actual mining sites, the particle size ratio of the materials selected for this experiment was based on fragmentation test results obtained from in situ caved ore. As illustrated in Figure 1, on-site fragmentation testing of ore was conducted at three underground stopes selected within the Pulang copper mine.

Photographs of the ore heap at the stope were captured. Ore particles visually discernible in the photographs, possessing measurable block sizes, were annotated. The size distribution was subsequently calculated. The ore particles were treated as equivalent circular particles. The area of each particle was determined based on its particle size, and Equation (1) was employed to compute the percentage for each size grade.

$$\eta =(S^{\prime }/S)\times 100\%$$

(1)

Here, η denotes the area percentage, S′ represents the area of ore particles within a specific size grade, and S is the total area.

As shown in Figure 2, the fragmentation distribution results obtained from the three test points are as follows: For Test Point I, the proportion of small fragments in the corresponding ore fragmentation is the highest. Conversely, for Test Point III, the proportion of large fragments is the highest within its particle size distribution (Gradation III).

The particle size distribution tables shown in

Table 1. Particle size distribution I.

Particle size	0–1.5 mm	1.5–4.5 mm	4.5–7.5 mm	7.5–10.5 mm	10.5–15 mm	15–45 mm
Percentage	4%	23%	21%	22%	10%	20%

,

Table 2. Particle size distribution II.

Particle size	0–3.0	3.0–6.0	6.0–10.5	10.5–15	15–45	45–90
Percentage	10%	30%	23%	17%	16%	4%

and

Table 3. Particle size distribution III.

Particle size	0–3.0	3.0–6.0	6.0–10.5	10.5–15	15–45	45–90
Percentage	8%	11%	16%	15%	40%	10%

are converted according to the particle size distribution in Figure 2. Notably, the particle size distributions in Table 1, Table 2 and Table 3 are all converted according to a 1:66 similarity ratio.

Following the conversion process, rock materials approximating the natural angle of repose of the ore were selected. Based on the gradation results presented in Table 1, Table 2 and Table 3, stone particles of corresponding sizes were screened. Subsequently, material mixing and preparation were conducted according to the proportions of crushed stones for each size fraction specified in the tables, as illustrated in Figure 3.

2.2. Experimental Process

Following material preparation, a series of uniform draw experiments were conducted on the two ore outlets of the drawbell using materials of different particle sizes. The ore draw test apparatus is depicted in Figure 4. The boundaries of the apparatus consist of transparent glass plates. The bottom opening accommodates the drawbell, and the model’s four corners and ends are welded together using steel plates. The internal dimensions of the ore draw test apparatus are length × width × height = 400 mm × 200 mm × 1200 mm. A photograph of the physical draw apparatus and the characteristics of its ore outlet are shown in Figure 4.

To quantify EZ morphology and characteristic parameters under uniform draw conditions within the drawbell, marker particles must be placed at various positions inside the model prior to drawing. Marker particles were fabricated from particles with diameters ranging from 6 to 8 mm. The arrangement of the marker particles within each layer is depicted in Figure 5, with an inter-particle spacing of 3 cm. Positioning was achieved using a combination of laser pens and measuring scales; explicit quantification of the positioning error (±1 mm accuracy) would concretely characterize the controllability.

The draw process during the experiment involves continuously shoveling loose particles out of the drawbell openings at both ends using a small shovel to simulate the balanced and continuous extraction characteristic of a shovel loader.

3. Analysis of Experimental Results

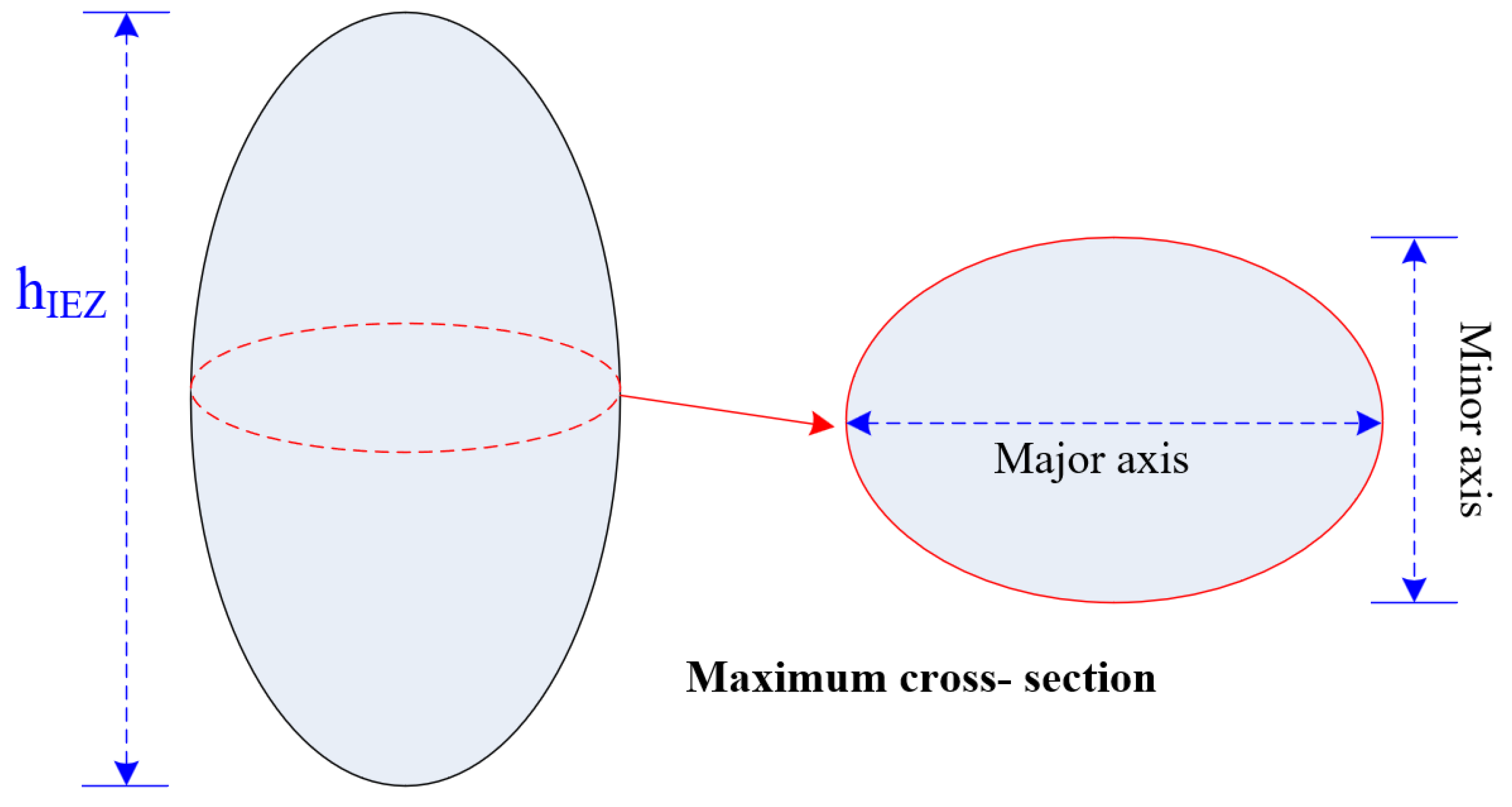
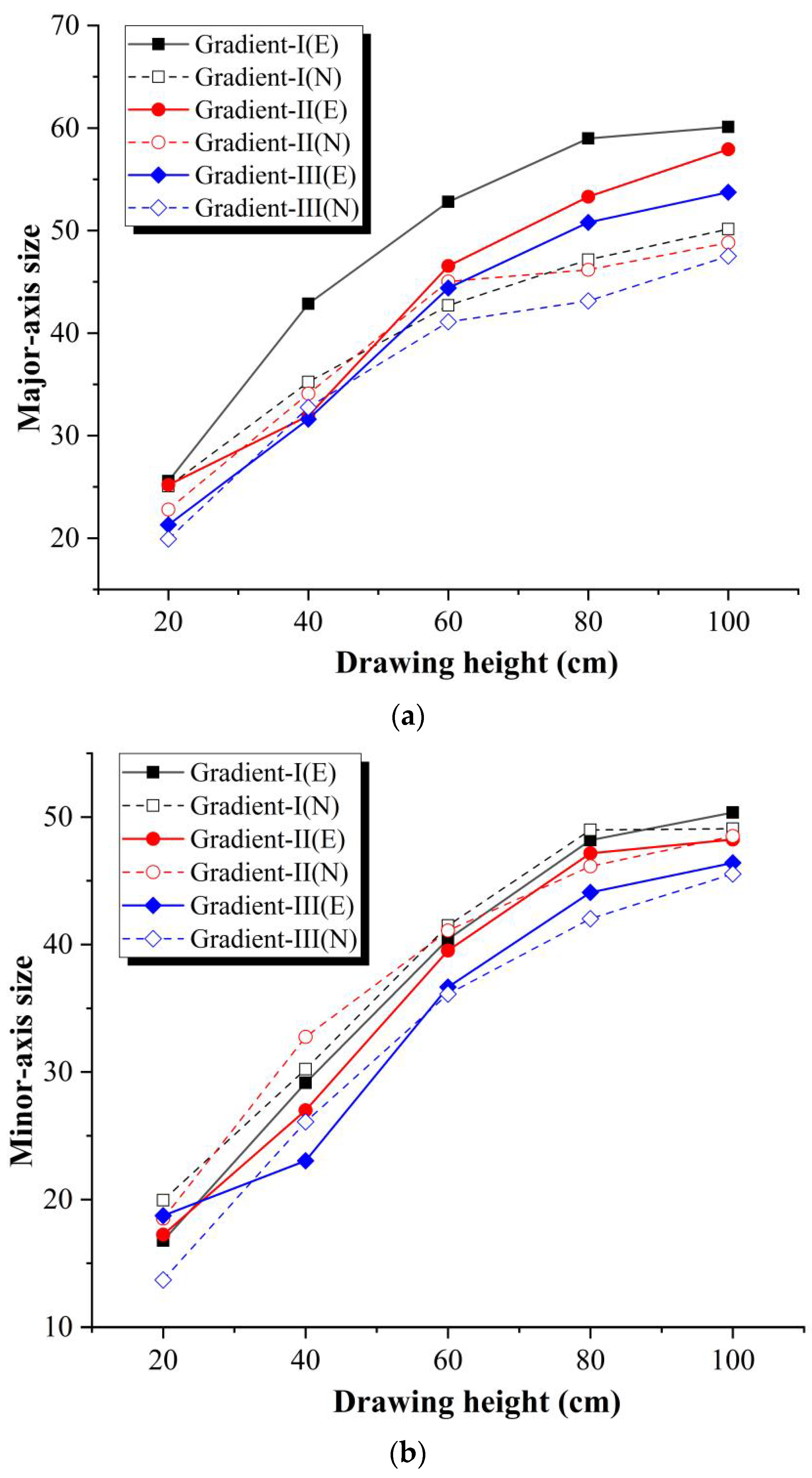
3.1. 3D EZ Shapes with Different Particle Sizes

As shown in Figure 6, the three-dimensional (3D) morphology of the extraction zone (Gradation II) was obtained by weighing the drawn ore and recording the number of labeled marker particles. Figure 6 clearly demonstrates that the resulting 3D extraction zone exhibits an ellipsoidal shape in the height direction. Furthermore, both its side and top views reveal that the cross-section of this 3D extraction zone is elliptical.

Figure 7 shows the fitting curves of the volume Q (mass drawn) and height of the extraction zone during the draw process for gradient-II.

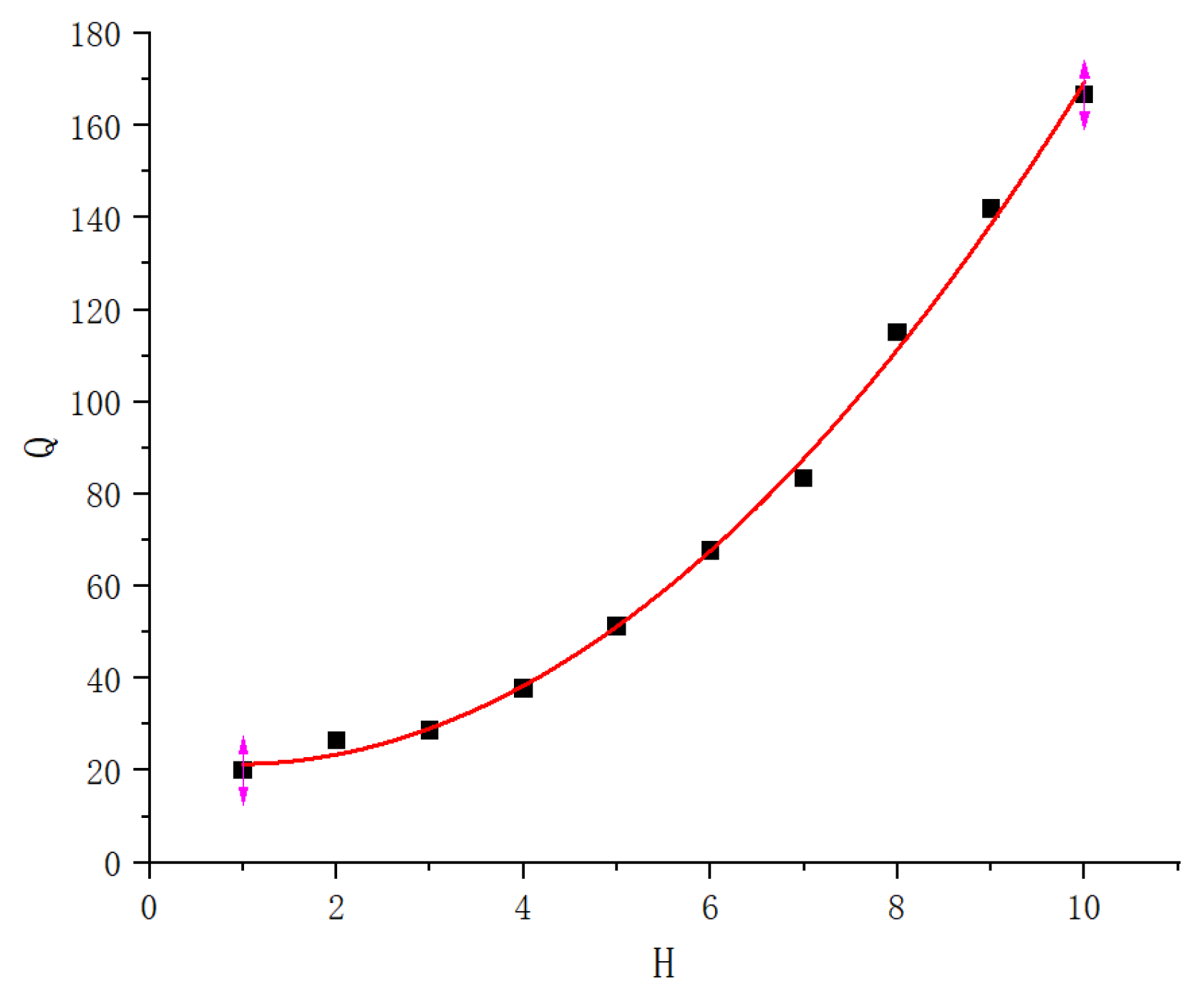
3.2. Relationship Between the Particle Size and Radius of the EZ

As mentioned earlier, under uniform draw conditions in a single drawbell, the extraction zone exhibits an ellipsoidal shape in the height direction, with an elliptical cross-section. Thus, to evaluate the differences between extraction zones formed by different particle gradations, it is necessary to compare and analyze their characteristic parameters. As shown in Figure 8, the extracted feature parameters characterizing the size of the extraction zone are the semi-major and semi-minor axis sizes of the maximum cross-sectional ellipse.

Different draw heights correspond to distinct extraction zones. To compare and analyze the size differences of the extraction zone at various draw heights, the semi-major and semi-minor axis dimensions of the maximum cross-section were extracted at ten different draw heights, as shown in Figure 9 and Figure 10, respectively. As the draw height increases, the semi-major axis dimension of the maximum cross-section continuously increases. Upon reaching a draw height of 80 cm, further increases in the draw height result in a slower growth rate of the semi-major axis size, which eventually stabilizes. Furthermore, comparing the results of draw tests with three different particle gradations revealed that the semi-major axis size of the extraction zone exhibited a decreasing trend as the average particle size increased. This indicates that changes in particle gradation significantly affect the size of the extraction zone.

Similar to the established trend for the semi-major axis dimension of the maximum cross-section, the variation of another characteristic parameter—the semi-minor axis size—with draw height is fundamentally consistent with that of the semi-major axis size. The semi-minor axis sizes obtained under different particle gradations also exhibit slight changes upon reaching a draw height of 80 cm, progressively stabilizing with further increases in draw height.

As previously stated, the experimental similarity ratio in this study is 1:66. The major and minor axis dimensions of the maximum cross-section within the extraction zone under varying particle sizes were obtained through testing. These maximum cross-sectional dimensions were scaled according to the similarity ratio and projected onto the actual mine bottom structure, at a draw height of 46.2 m, as illustrated in Figure 11. The figure clearly demonstrates that during multi-drawbell operations, the overlap degree of extraction zones is highest for Gradient-I and lowest for Gradient-III.

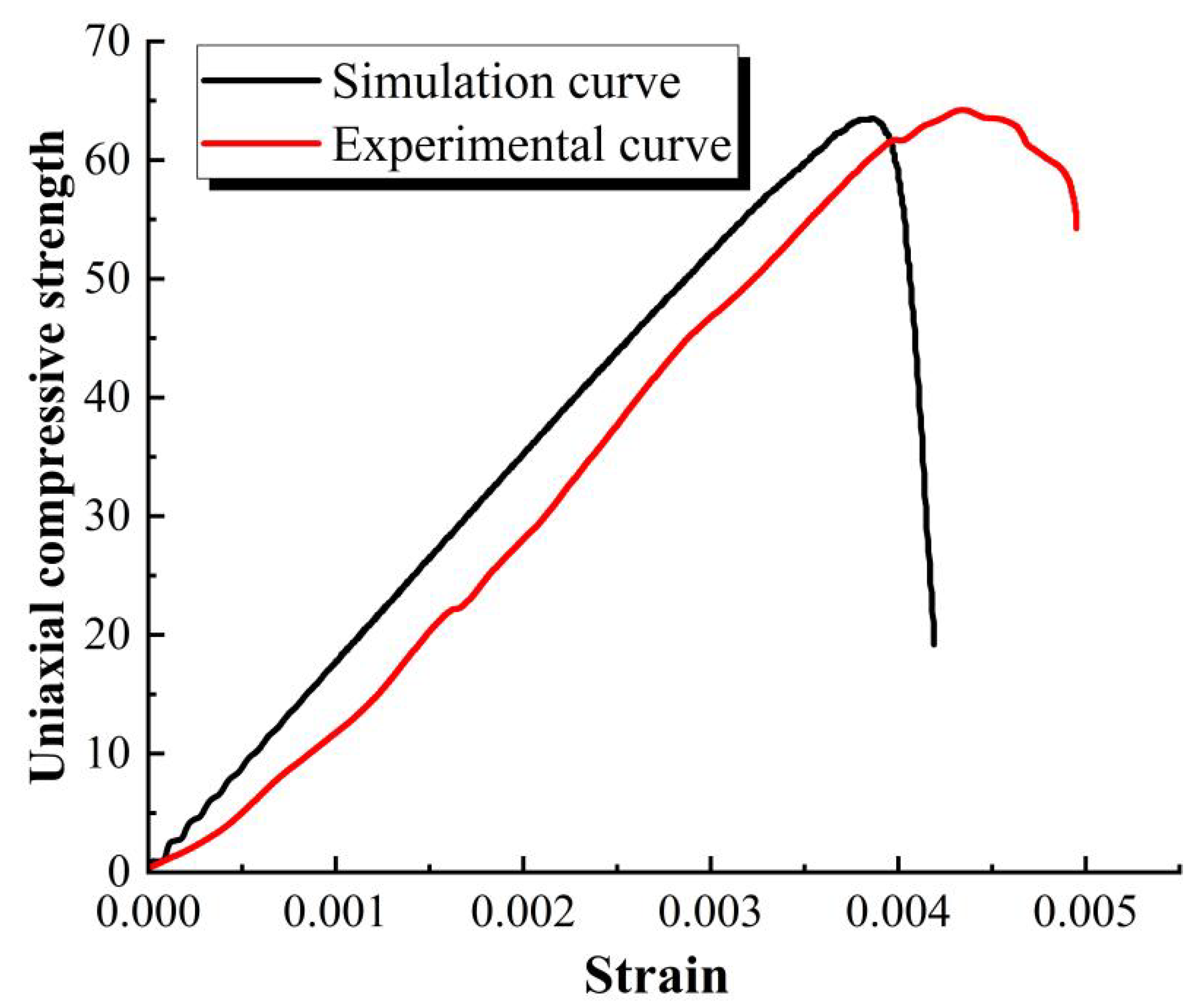
4. Numerical Simulation

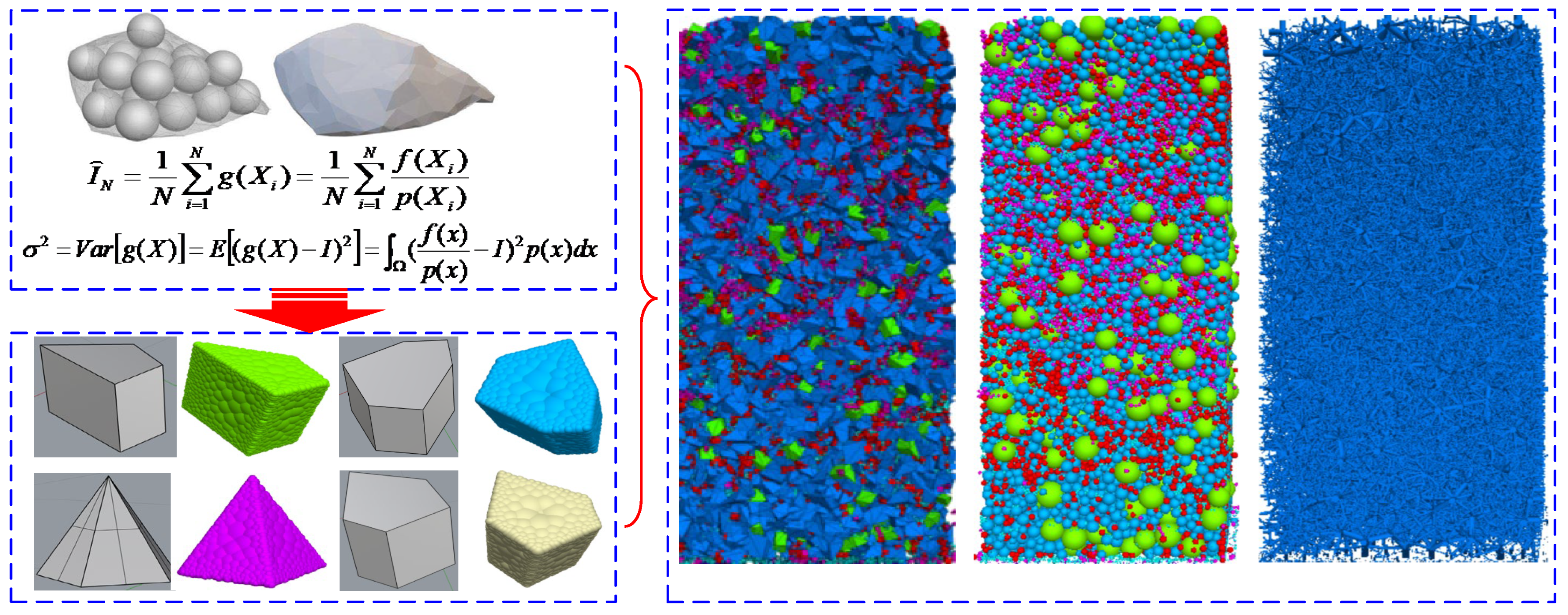
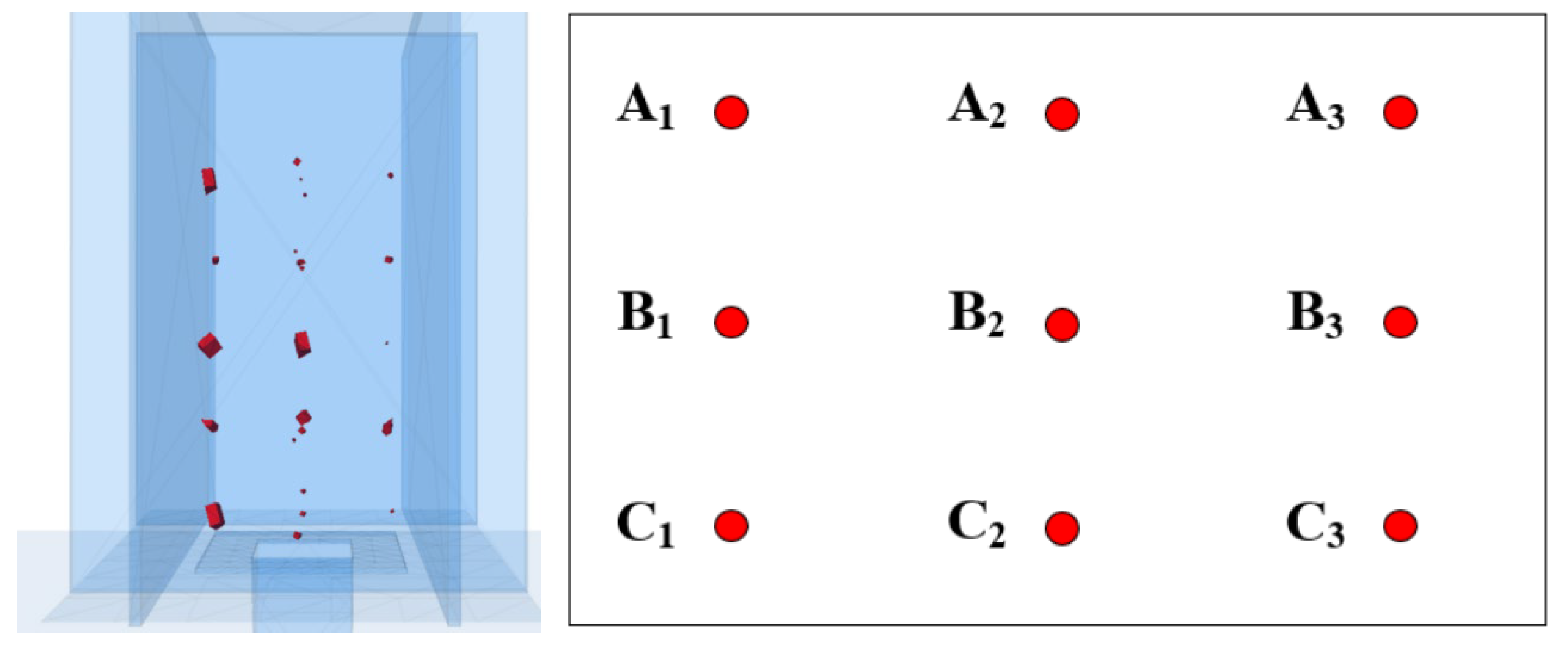
4.1. Model Setup

In this work, PFC3D was employed to simulate the ore draw process of a single drawbell with different particle size distributions. Prior to drawing, a numerical model must be established. The draw apparatus dimensions are consistent with those of the experimental apparatus; specifically, the internal dimensions are length × width × height = 700 mm × 550 mm × 1600 mm. Furthermore, to better characterize the extraction zone features and particle flow behavior under irregular particle conditions, the ore particles in this numerical simulation scheme were also modeled as randomly generated irregular blocks, as shown in Figure 12. This approach successfully circumvents the issue associated with spherical particles: their excessively smooth surfaces prevent the development of sufficient internal locking forces between particles, thereby failing to reasonably characterize the morphology and evolution of the extraction zone. In the experimental tests, ore extraction was achieved by continuously shoveling ore particles out from the outlets at both ends of the drawbell. The depth of shovel penetration into the model outlets was consistently maintained at 2.1 cm. In the numerical simulation, this extraction approach was replicated. However, the key difference lies in the simulation method: a 2.1 cm long wall section was removed from the bottom structure at the ore outlets to create space for particle movement, thereby simulating the ore extraction process.

For the construction of irregular blocks, we begin by modeling a three-dimensional ore unit geometry in Rhino and exporting it as an STL file and then utilize the command in PFC3D to construct complex block units. As shown in Figure 13, the ore draw model was generated based on a rigid block model and different particle size ratios within the specified gradations. Figure 13a represents the initial ore draw model under Gradation I conditions. Although discerning particle gradation within the model visually is challenging, careful observation reveals that the number of large blocks in Figure 13a is significantly lower than in the numerical models depicted in Figure 13b,c.

The microscopic parameters of the particles significantly influence the numerical simulation outcomes. Therefore, a series of iterative calibration trials need to be conducted prior to the main draw experiments to obtain microscopic parameters capable of characterizing the flow behavior of the fragmented rock during the draw process. The parameter calibration procedure in this numerical simulation comprises two sequential steps: first, assigning particle density parameters based on the actual rock density and then iteratively adjusting the friction coefficient until the extracted zone (EZ) height-versus-mass curve aligns with experimental data to determine the particle friction coefficient (Figure 14). Subsequently, using the calibrated friction coefficient and incorporating the rock’s uniaxial compressive strength curve, numerical simulations of rock compression tests are performed while continuously tuning other microscopic parameters until the simulated strength curve converges with the experimental measurements, thereby obtaining the remaining particle strength parameters (Figure 15). The particle microscopic parameters obtained after these preliminary draw calibrations are presented in

Table 4. Microscopic parameters used in the numerical simulation.

Parameters	Value
Normal stiffness/shear stiffness	1.2
Solid density (kg/m3)	2700
Elastic modulus (GPa)	7.1
Friction coefficient	0.35
Normal damping coefficient, βn	0.5
Tangential normal damping coefficient, βs	0.1

.

The fitting relationship between the extraction zone (EZ) height and the mass of drawn ore under the parameter conditions in Table 4 is shown in Figure 14. The overall trend of the EZ height vs. mass drawn curve from the numerical simulation results is the same as that of the experimental test results, and the data are also relatively close. The differences between experiments and numerical simulations may be caused by boundary effects or limitations of label resolution. Overall, the microscopic parameters in Table 4 effectively characterize the flow characteristics of granular materials.

4.2. Drawing Process and Characteristics

Figure 16 demonstrates the progressive particle depletion characteristics within the Gradation II model under varying drawn ore masses. Initial displacement measurements at 24.75 kg extraction mass reveal minimal upper section movement. Progressive mass increase to 62.47 kg induces substantial vertical particle depletion, manifesting as a pronounced concave displacement recession surface. This phenomenon confirms the quasi-ellipsoidal nature of the extraction zone, where lower boundary particles maintain positional stability despite upper material discharge.

The numerical framework implements unique particle identification tracking, enabling post-extraction spatial reconstruction of discharged materials for precise extraction zone profiling at multiple elevations. Figure 17 chronologically documents the extraction zone evolution across different discharge quantities. Initial 24.75 kg extraction produces limited zone dimensions, while subsequent mass increments (up to 110.75 kg) demonstrate progressive vertical expansion and lateral enlargement, with transverse dimension stabilization becoming evident beyond 110.75 kg discharge.

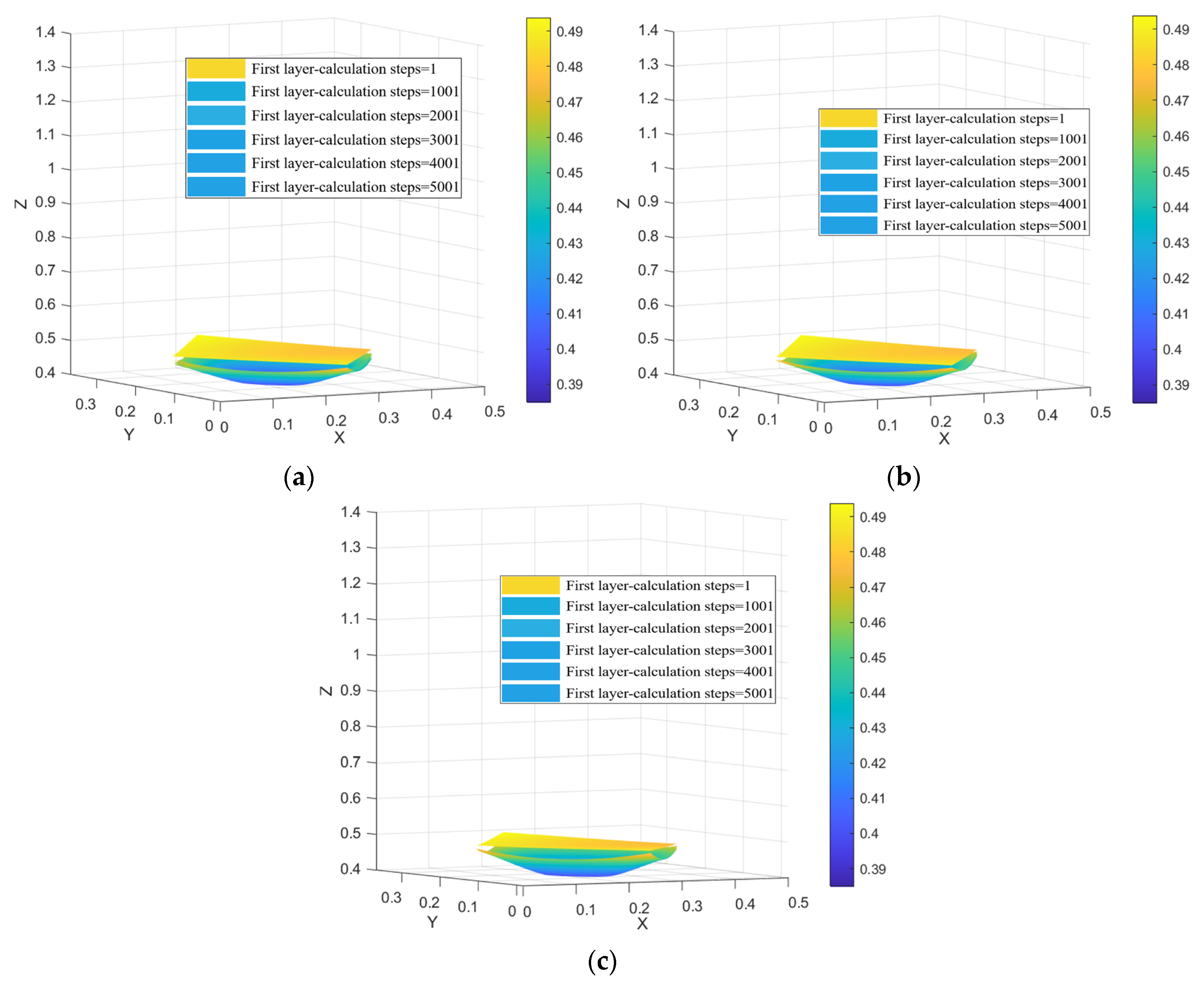
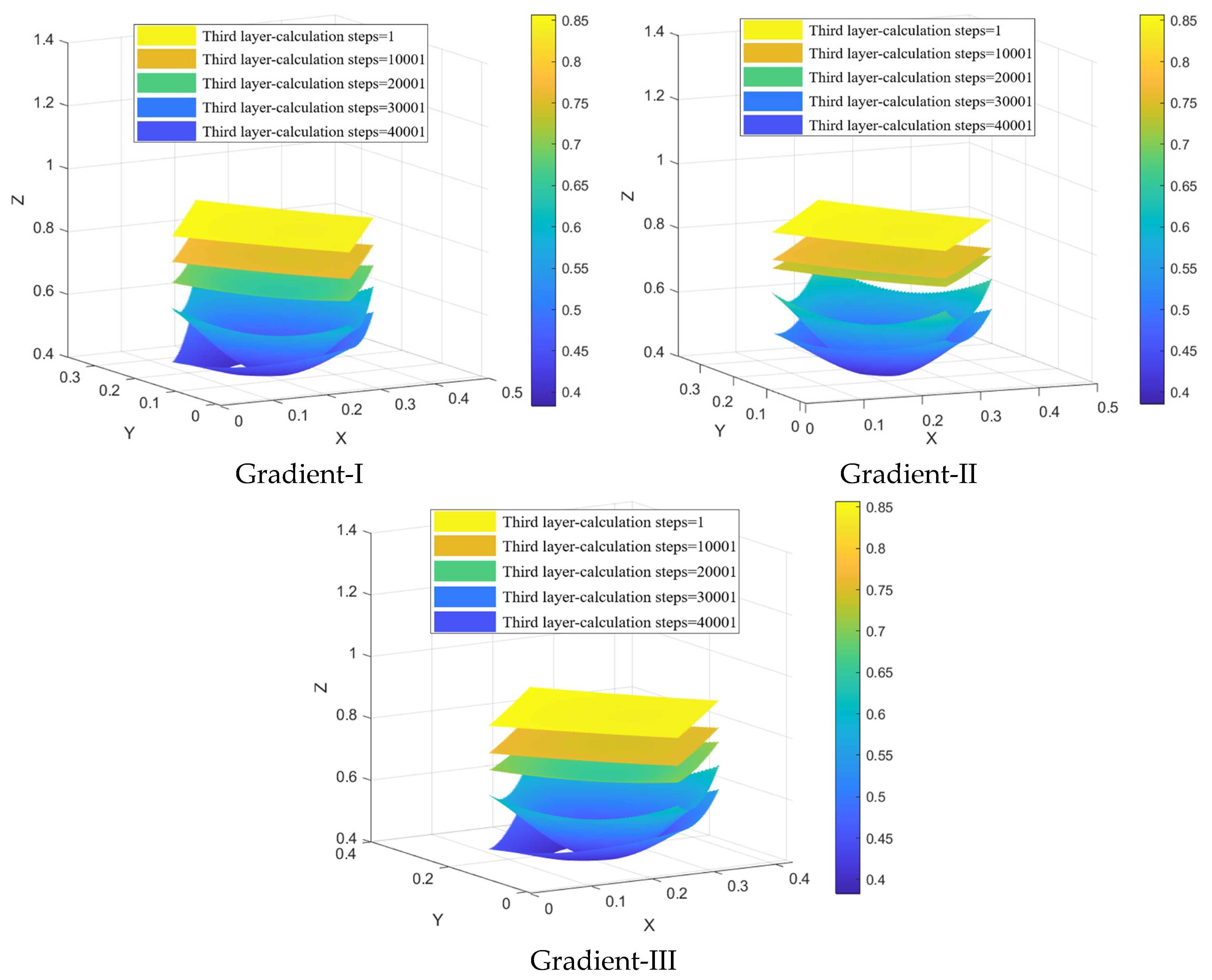
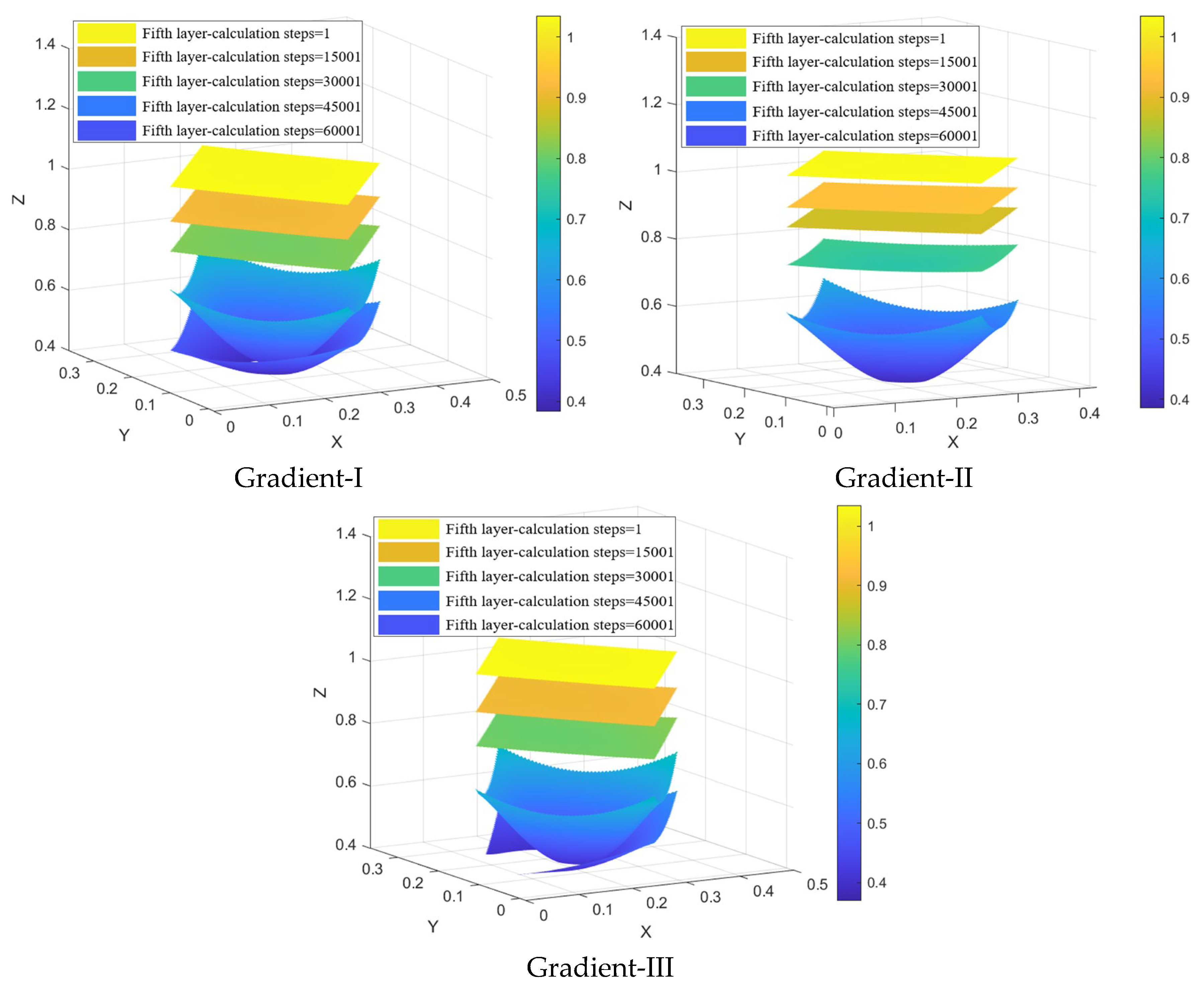
4.3. 3D Isolated Extraction Zones with Different Particle Sizes in the Numerical Simulation

Three-dimensional zone reconstruction employing segmented boundary panels reveals height-dependent morphological development in Figure 18. The extraction zones spanning 20 cm to 100 cm heights exhibit consistent ellipsoidal vertical profiles across all three gradation types.

Figure 18 demonstrates that across the examined draw heights, not only do the characteristics of the drawn ore vary with draw height, but comparisons of the drawn ore under different particle gradations also reveal that changes in gradation lead to distinct differences in the released material. Shown in Figure 19 is the comparison of the relationships between the drawn height and the volume of extraction zone with different particle gradient. The calculation of the volume of extraction zone with different particle gradations and drawing heights shows that the larger the drawing height, the larger the volume of extraction zone. Meanwhile, the smaller the particle size, the larger the volume of the extraction zone.

Figure 20 presents comparative cross-sectional profiles of extraction zones under three distinct particle gradation configurations. The visualization conclusively demonstrates transverse elliptical morphology across all gradation types, maintaining congruence with the experimental cross-sectional characteristics observed in the physical tests.

Comparative analysis with experimental data confirms the predominant elliptical geometry in numerical simulations. Quantitative evaluation of the dimensional parameters was conducted through systematic extraction of cross-sectional major/minor semi-axis measurements, with Figure 21a and Figure 21b, respectively, illustrating major and minor axis evolution patterns. All three gradations exhibit progressive dimensional expansion along both axes with increasing draw height. Crucially, the computational model reveals an inverse correlation between ore particle size and extraction zone dimensions, showing 12–18% reductions in semi-axis sizes with coarser gradations, a trend that aligns precisely with the experimental findings. This dimensional contraction mechanism is attributed to degraded particle mobility resulting from increased large-block proportions, which effectively constrains material flow propagation.

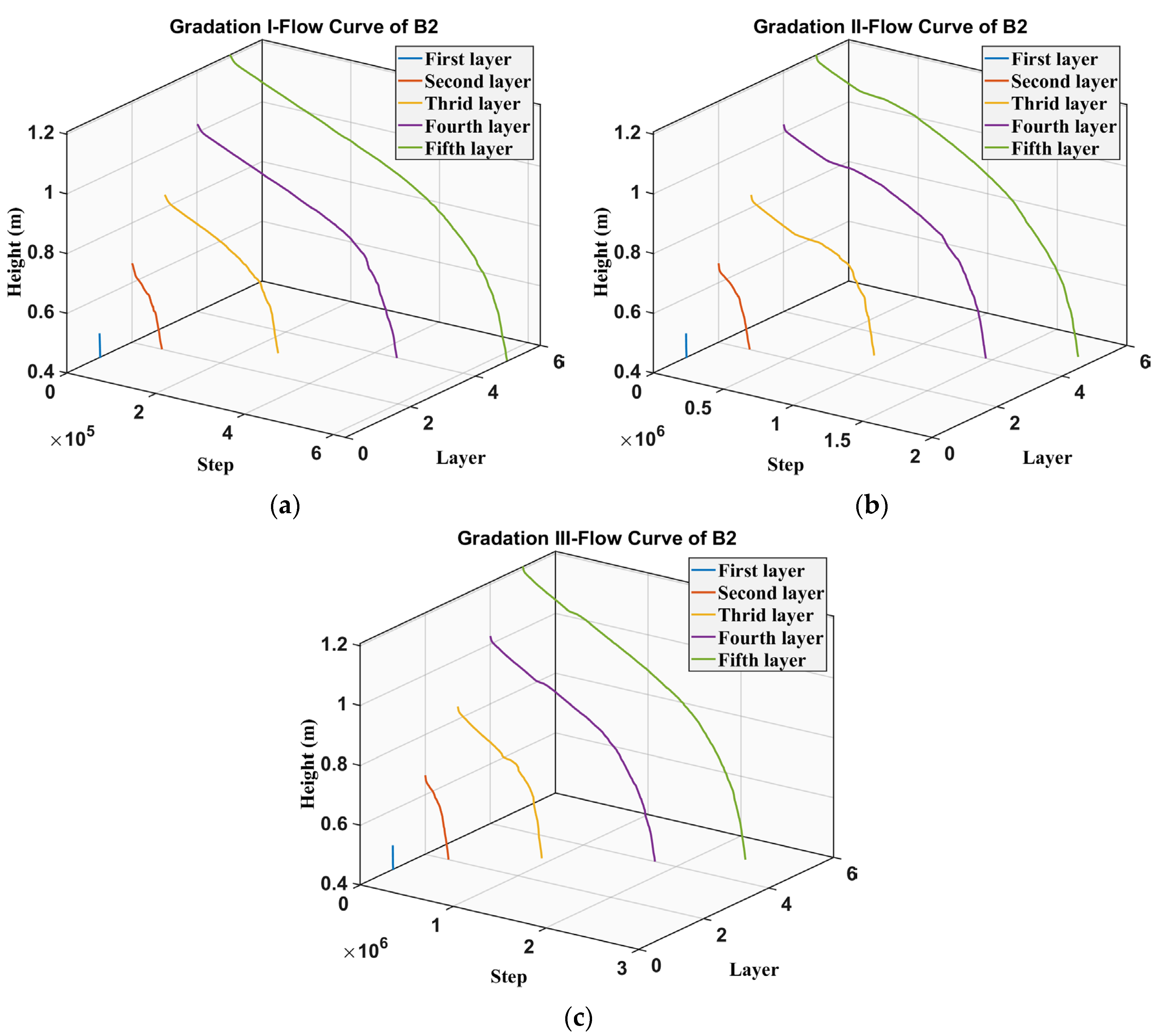
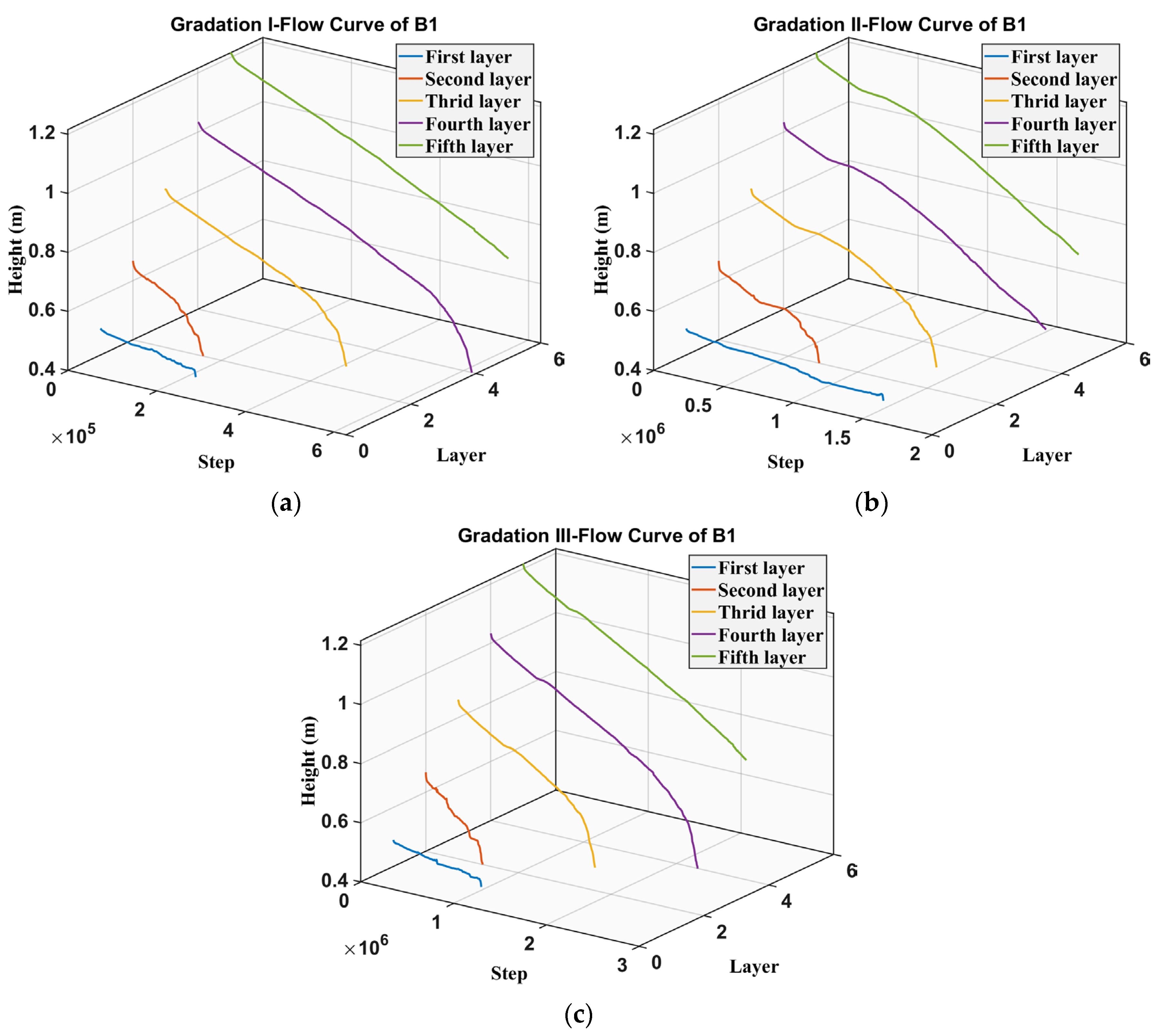
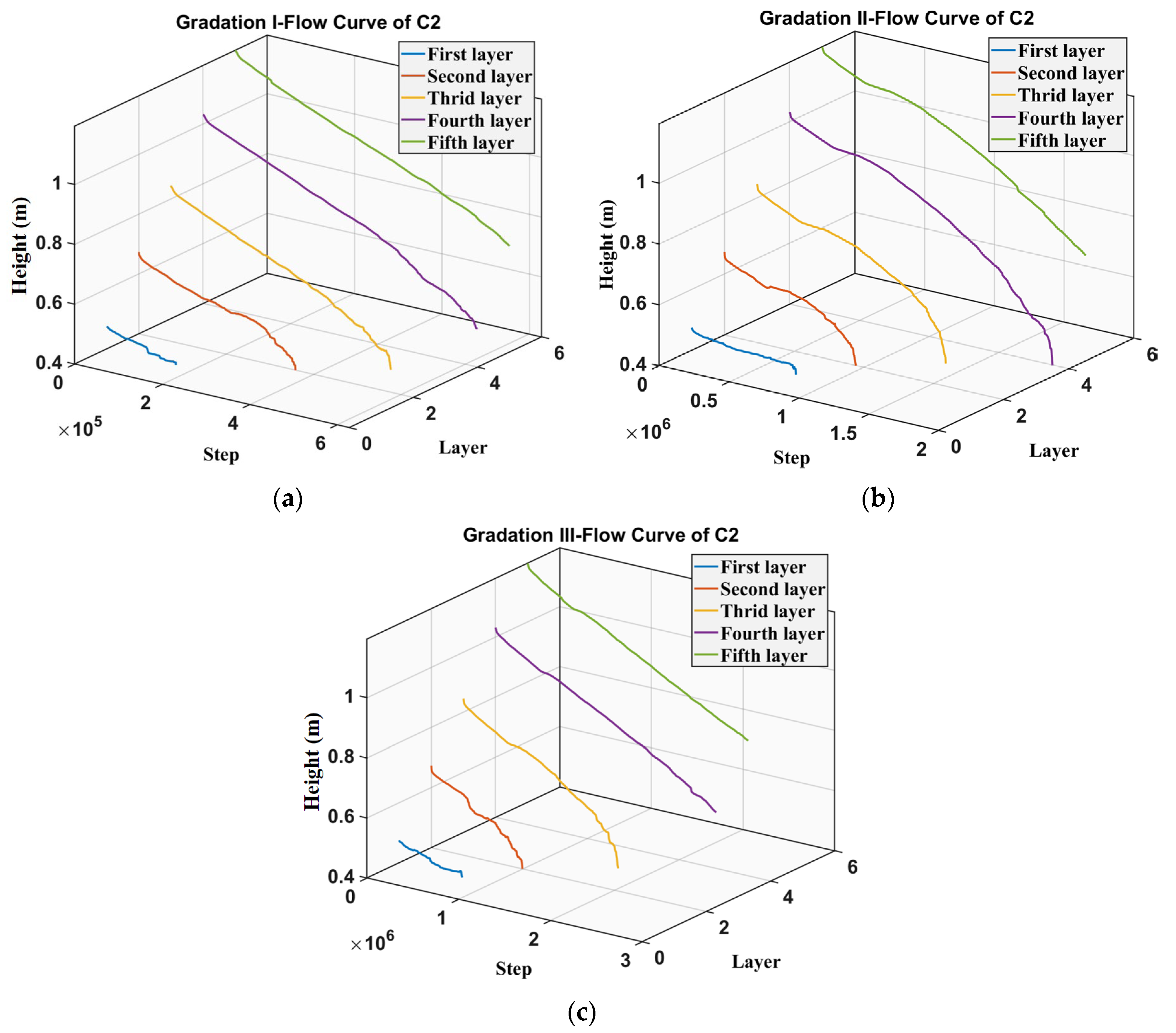
4.4. Particle Flow Characteristics Under Different Gradations

To evaluate the flowability of particles within the model under different particle size distributions, five monitoring surfaces were established inside the model prior to ore drawing. Nine monitoring points were arranged on each surface, as shown in Figure 22. During the draw process, real-time tracking of the particle height was performed at all 45 monitoring points.

The particle height-versus-calculation step curves for different monitoring points within the model are presented in Figure 23, Figure 24 and Figure 25. These curves illustrate the variation in monitoring point height with the calculation step. A particle’s height is considered to be 0 when it descends continuously until it reaches the top plane of the drawbell opening. The cumulative calculation step count at which its height becomes 0 represents the number of steps required for it to move from its initial position to the drawbell opening. The ore extraction process demonstrates queuing behavior, requiring each ore unit to sequentially await clearance of the discharge outlet by preceding rocks before passing through. The computed step count directly equates to ore queuing duration, where fewer steps indicate enhanced flow efficiency, while increased steps lead to longer release times for individual ore units. This cumulative step count can therefore serve as a quantitative indicator for evaluating particle flowability.

Figure 23 presents the height-versus-calculation step curves for the central monitoring point B2 in each layer. As the initial height of the monitoring point increases from layer 1 to layer 5, the calculation steps required to reach the top plane of the drawbell opening exhibit a continuous increase. However, comparing the numerical simulation results across different particle sizes reveals that Gradation I, possessing the smallest average particle size, also requires the fewest calculation steps for its central monitoring points B2 (layers 1–5) to reach the drawbell opening. Conversely, Gradation II ranks second, and Gradation III, owing to its largest average particle size, necessitates the highest number of calculation steps.

The height-versus-calculation step curves for the left monitoring point B1 (shown in Figure 24) and the lower monitoring point C2 (shown in Figure 24) are similar to those presented in Figure 23. For particle Gradation I, the calculation steps required for each monitoring point to reach the bottom layer are fewer than those for corresponding points in the other two gradation models. Notably, in the monitoring curve of Figure 25, the time required for the B1 monitoring point in layer 1 to reach the bottom layer exceeds that of the B1 point in layer 2. The primary reason for this is that the layer 1 B1 point is situated outside the boundary of the extraction zone, where the flow velocity is lower than that of particles within the extraction zone. In particle size Gradation III (which has the largest average particle size), the time required for its left monitoring point B2 to reach the bottom layer is longer than that for its monitoring points B2-3 in layer 3.

The height-versus-calculation step curve for monitoring point C2 in Figure 23 is similar to those in Figure 23 and Figure 24 mentioned above, with the exception that the height parameter of the layer 1 C2 point showed no significant change as ore drawing progressed. This indicates that its location is largely outside the boundary of the extraction zone and remained largely static during the draw process. Consequently, it ultimately became part of the accumulation zone after subsequent drawing was completed.

After extracting data from the nine monitoring points within each layer, the positions of these points were connected and fitted onto a surface. This allows the flow resistance of particles within the model to be characterized based on changes in the concavity degree of this surface. The movement surfaces for the first-layer particles under the three different particle gradations are shown in Figure 26. Compared to deeper layers, the movement surfaces exhibited by first-layer particles across the three gradations show minimal variation. This limited difference is attributed to the inherent proximity of the first monitoring layer to the draw source.

The movement surfaces for monitoring points at different depths within the model are presented in Figure 27 and Figure 28. The spatial extent (size) of these movement surfaces indicates the range of particle movement inside the model during ore drawing and serves as an indicator of particle flowability. The movement surfaces for monitoring points in the first and fifth layers reveal that as particle size increases, the spatial extent of the movement surface decreases. This indicates that smaller particle sizes correspond to larger flow ranges within different regions of the model.

Contrasted with the movement surface of the first-layer monitoring points in Figure 26, the surface for the third-layer points (Figure 27) exhibits increasing concavity with progression in the calculation steps. This trend is even more pronounced in the movement surface of the fifth-layer monitoring point shown in Figure 28. These observations demonstrate that increasing the particle size within the ore draw model deteriorates ore flowability. Consequently, the spatial extent and concavity of the surface formed by flowing particles diminish.

5. Conclusions

To investigate the influence of different ore fragment sizes on release and flow characteristics during block caving draw, this study employed ore draw experiments and PFC3D numerical simulations. The evolution of the shape and cross-sectional size of the extraction zone from a single drawbell under varying particle gradations was analyzed. Furthermore, numerical simulations were utilized to examine differences in ore flow behavior across these gradations. The principal conclusions are as follows:

(1)

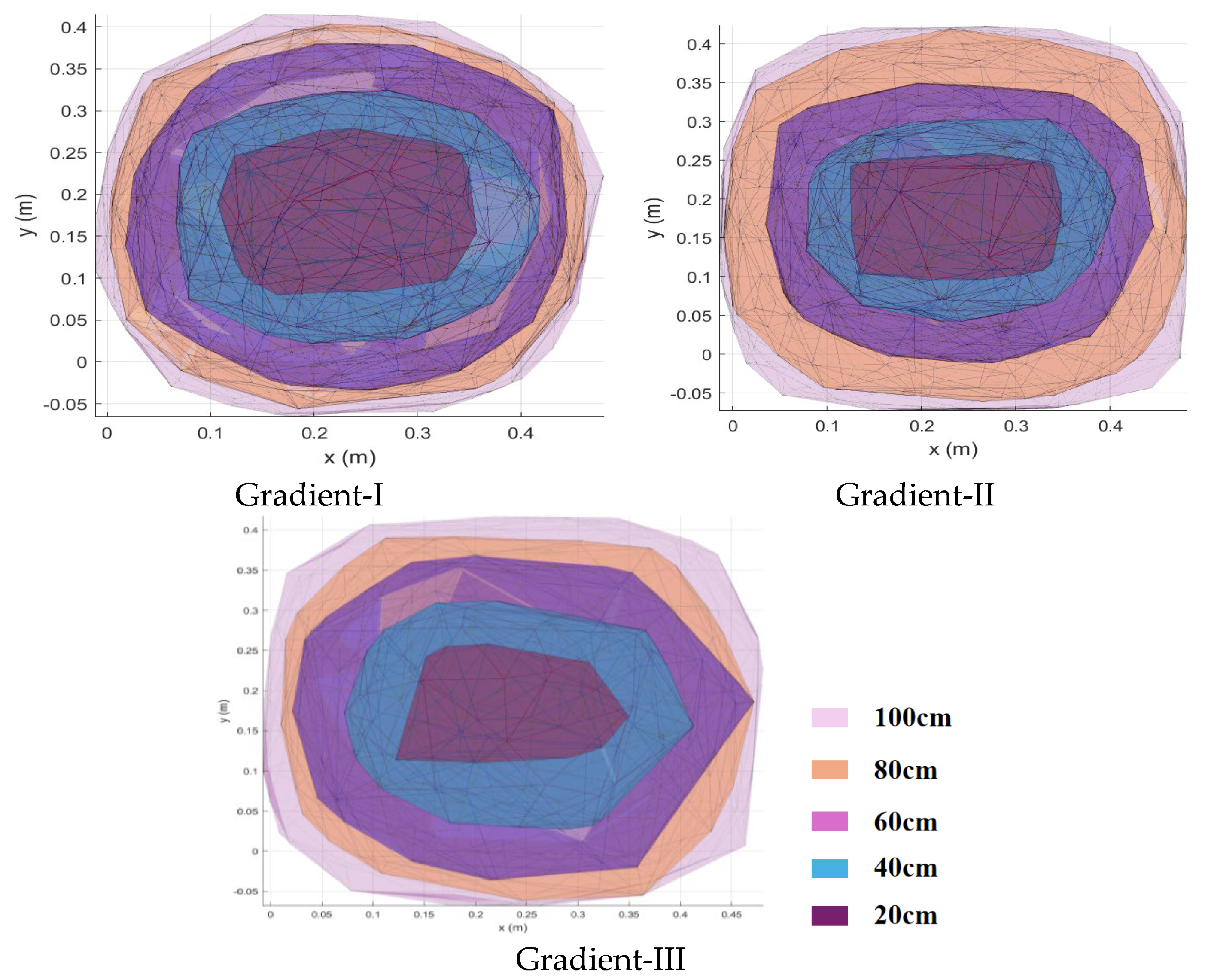
Based on in situ fragmentation testing, three distinct particle gradations were established. From Gradation I to Gradation III, the average ore fragment size increased progressively. Experimental draw tests for these three gradations demonstrate that the extraction zone exhibits an ellipsoidal shape in the vertical direction, with elliptical cross-sections at different heights.

(2)

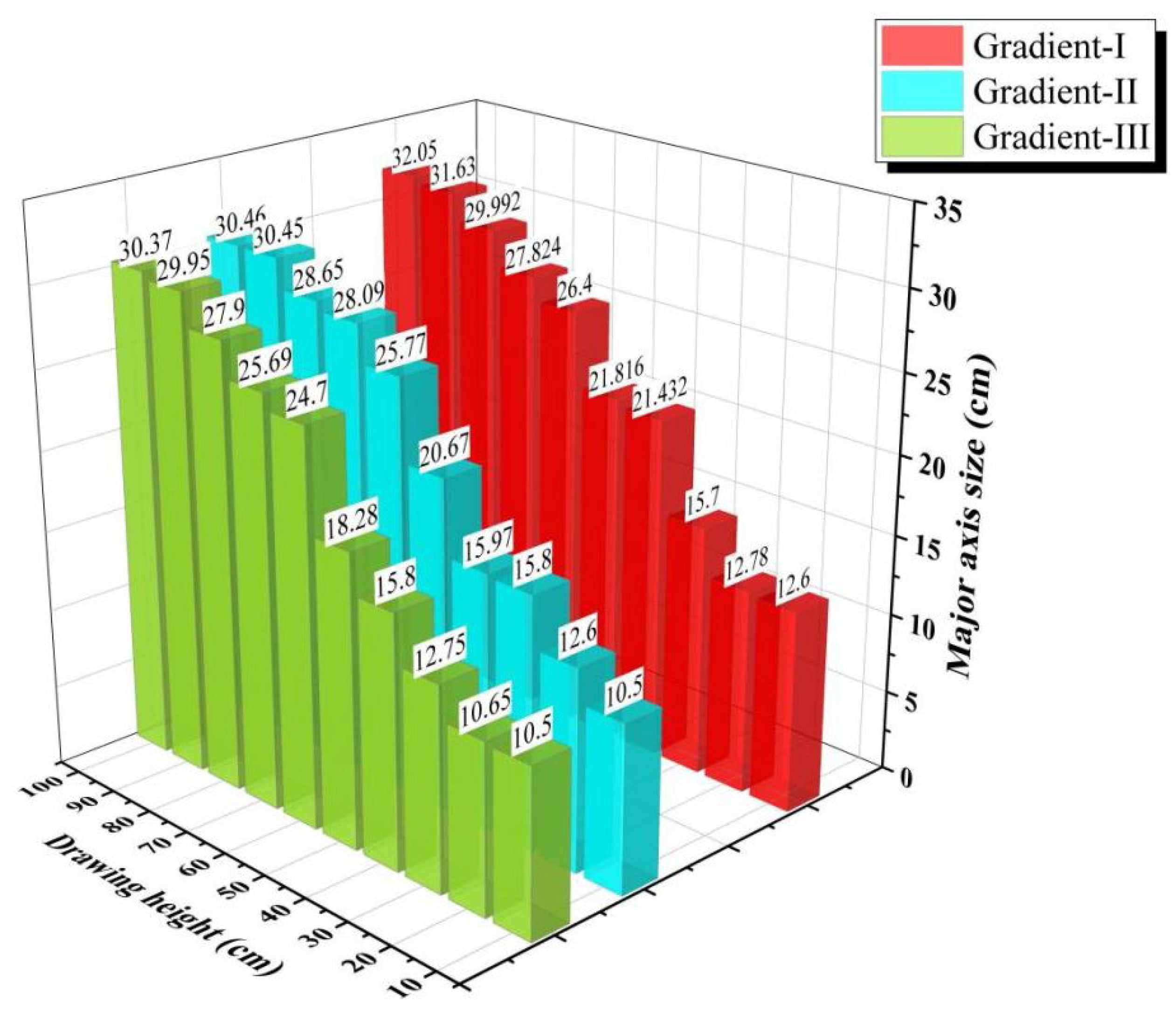
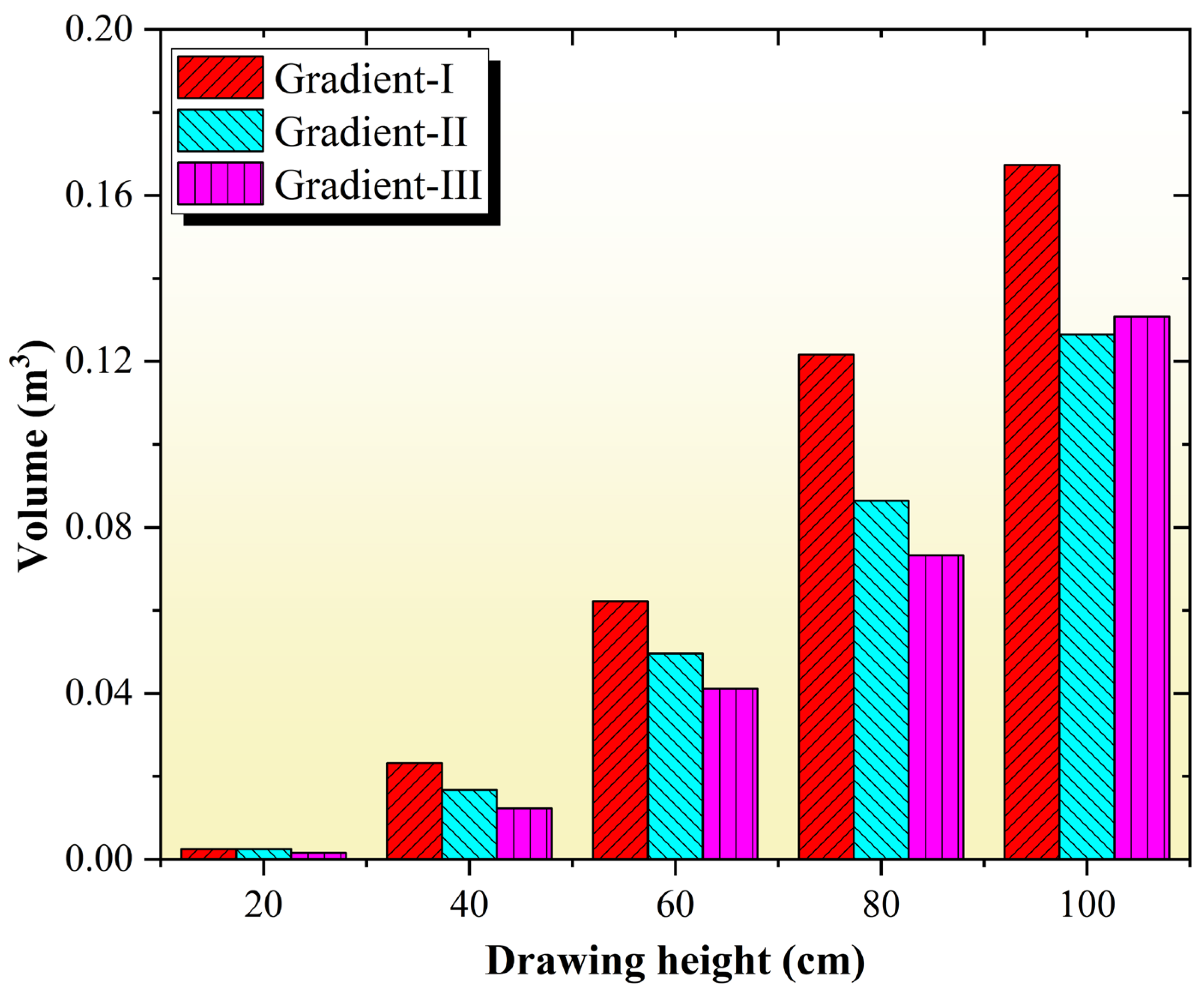
The semi-major and semi-minor axis dimensions of the extraction zone cross-section increase with the draw height, stabilizing when a draw height of 80 cm is reached. The ore fragment size significantly impacts the size of the extraction zone. Gradation I, with the smallest average particle size, yields the largest extraction zone. Conversely, Gradation III, characterized by the largest average particle size, produces the smallest extraction zone.

(3)

The numerical simulation results show excellent agreement with the experimental findings. Flow characteristics of ore particles under different gradations were evaluated using multiple monitoring points within the model. The results indicate that Gradation I exhibits the best particle flowability, attributable to its smallest average particle size. As the particle size increases, the spatial extent of the movement surface derived from monitoring points diminishes. This signifies that smaller particle sizes correspond to larger flow ranges within different regions of the model.

6. Discussion

As previously mentioned, existing research on extraction zone morphology has predominantly employed experimental and numerical simulations based on single-hole ore discharge configurations, typically yielding inverted droplet-shaped or ellipsoidal extraction zones. Crucially, the inclination angle of the drawbell in the block caving method is not consistent in the direction parallel to and perpendicular to the laneway. In this scheme, the inclination angle parallel to the laneway direction is 90^°, and the angle perpendicular to the laneway direction is 70°. Higher inclination angles correlate with increased ore flow rates, and this directional flow differential fundamentally generates elliptical extraction zone cross-sections, a finding that markedly contrasts with prior results and conclusively demonstrates the profound influence of drawbell geometry on extraction zone contours. At the same time, in the block caving method, the bottom structure typically incorporates multiple drawbells arranged systematically. When these drawbells operate concurrently, their respective extraction zones progressively expand with increasing draw height, leading to gradual convergence and overlap between adjacent zones. Research has demonstrated that overlapping extraction zones between neighboring drawbells are essential for maintaining uniform ore release rates and mitigating ore dilution during production. Notably, the ore flow velocity correlates positively with the extent of this overlap, a critical factor in optimizing subsequent extraction drift layouts. This study employs a 1:66 similarity ratio for experimental modeling, when applied to the Pulang copper mine’s bottom structure design at a draw height of 46.2 m, Gradation-I conditions yield maximal zone overlap, whereas Gradation-III exhibits minimal overlap due to larger rock fragmentation sizes. While these findings offer theoretical guidance for block caving infrastructure design, two key limitations warrant attention:

(1)

The predefined angles of drawbell orientations (parallel/perpendicular to the laneway) directly influence inclination and directional ore flow velocities, thereby modifying extraction zone morphology.

(2)

Practical mining scenarios involve simultaneous multi-drawbell operations where drift spacing and laneway intervals dynamically alter overlap characteristics, and multi-drawbell simulations are planned as part of ongoing work.