Operational Reliability of Steel Ropes in Terms of Mechanical Properties of Wires Using Control Charts
Abstract
1. Introduction
2. Literature Review
3. Problem Formulation
- Class I included ropes that met the highest quality standard, with wire strength class dispersion within ±4% of the mean—representing optimal selection of input material;
- Class II comprised ropes that conformed to the criteria set by the now obsolete DIN 21254 or STN 02 4301 standards, with a strength class dispersion tolerance of ±10%;
- Class III included ropes meeting the current EN 12385-1 requirements, which allow for a dispersion range of −50 MPa to +15%;
- Class IV consisted of ropes that failed to meet the minimum requirements defined by EN 12385-1.
4. Materials and Method
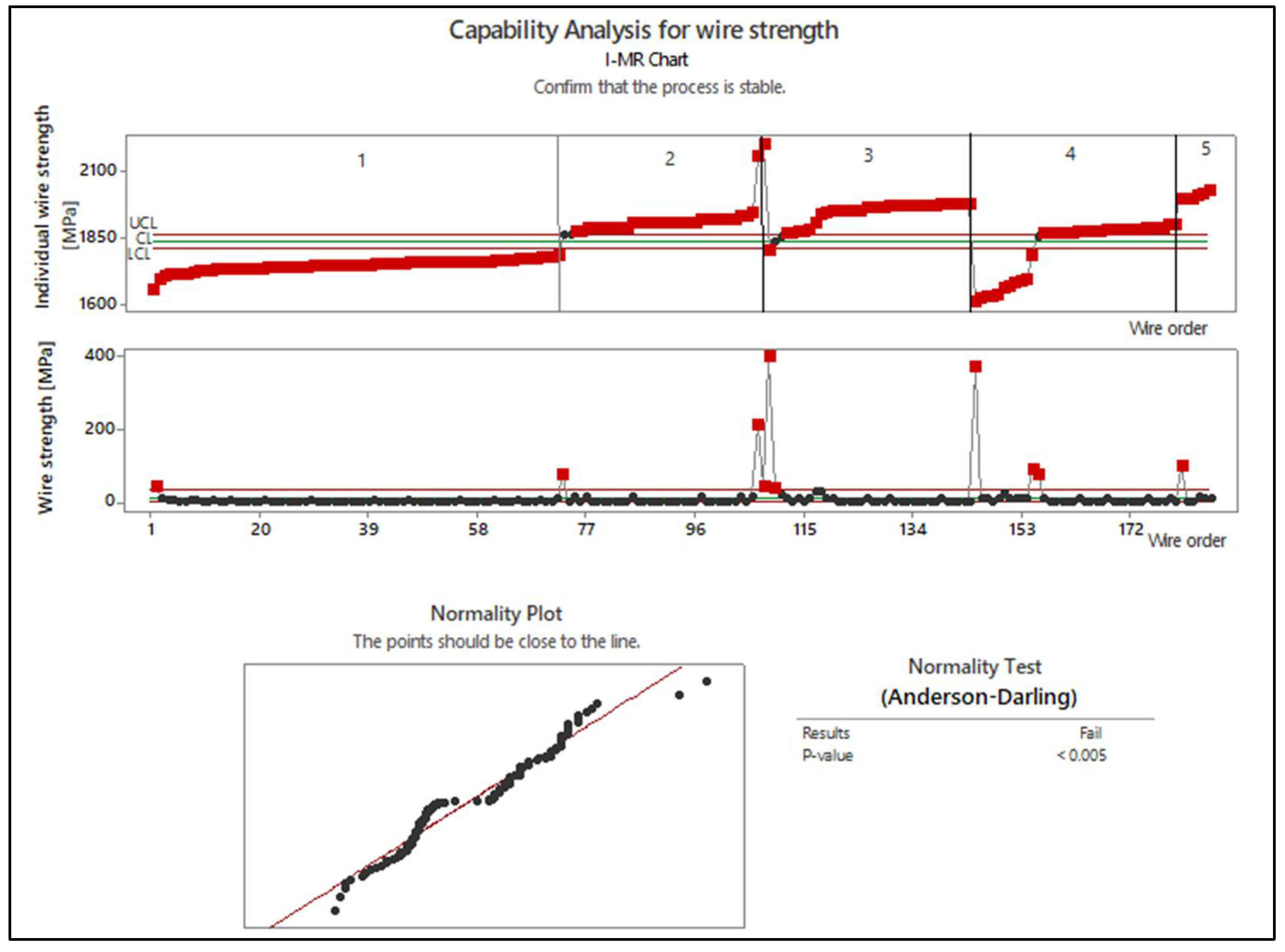
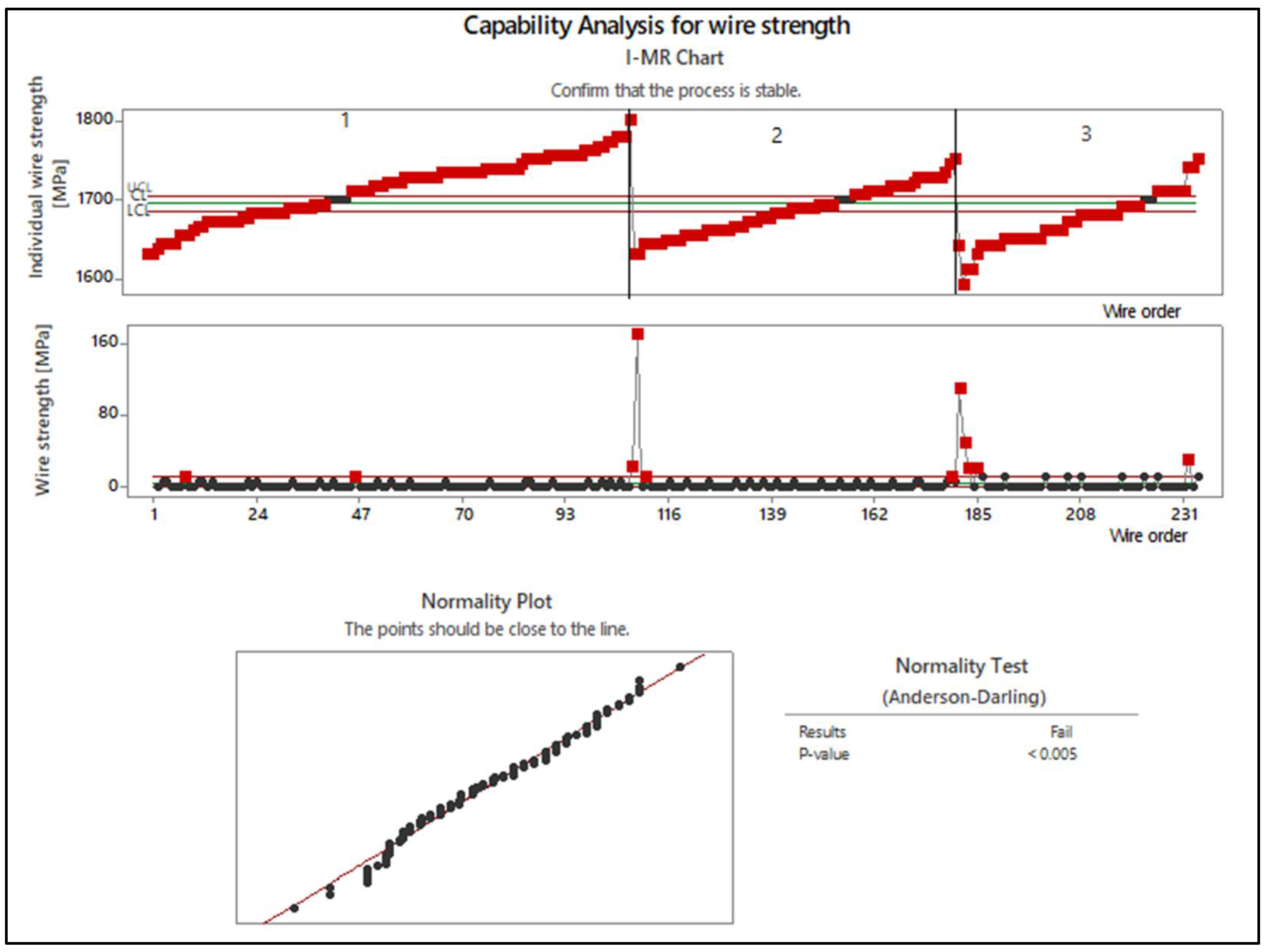
4.1. Application of Statistical Quality Control Methods
- Verification of the normality of the measured data using normality tests, such as the Anderson–Darling test;
- Constancy of the process mean across the observed dataset;
- Constancy of the process standard deviation, indicating homoscedasticity;
- Independence of observations, ensuring that the data points are not autocorrelated.
4.1.1. Anderson–Darling Test for Normality Assessment
- The significance level was set at α = 0.05.
- Establishing the null hypothesis H0: The data are normally distributed.
- 4.
- The critical value for the test is determined by the p-value:
- If AD > 0.05, the null hypothesis is not rejected, and the data are considered to follow a normal distribution;
- If AD < 0.05, the null hypothesis is rejected, indicating that the data do not follow a normal distribution.
4.1.2. Implementation of Control Charts for Process Monitoring
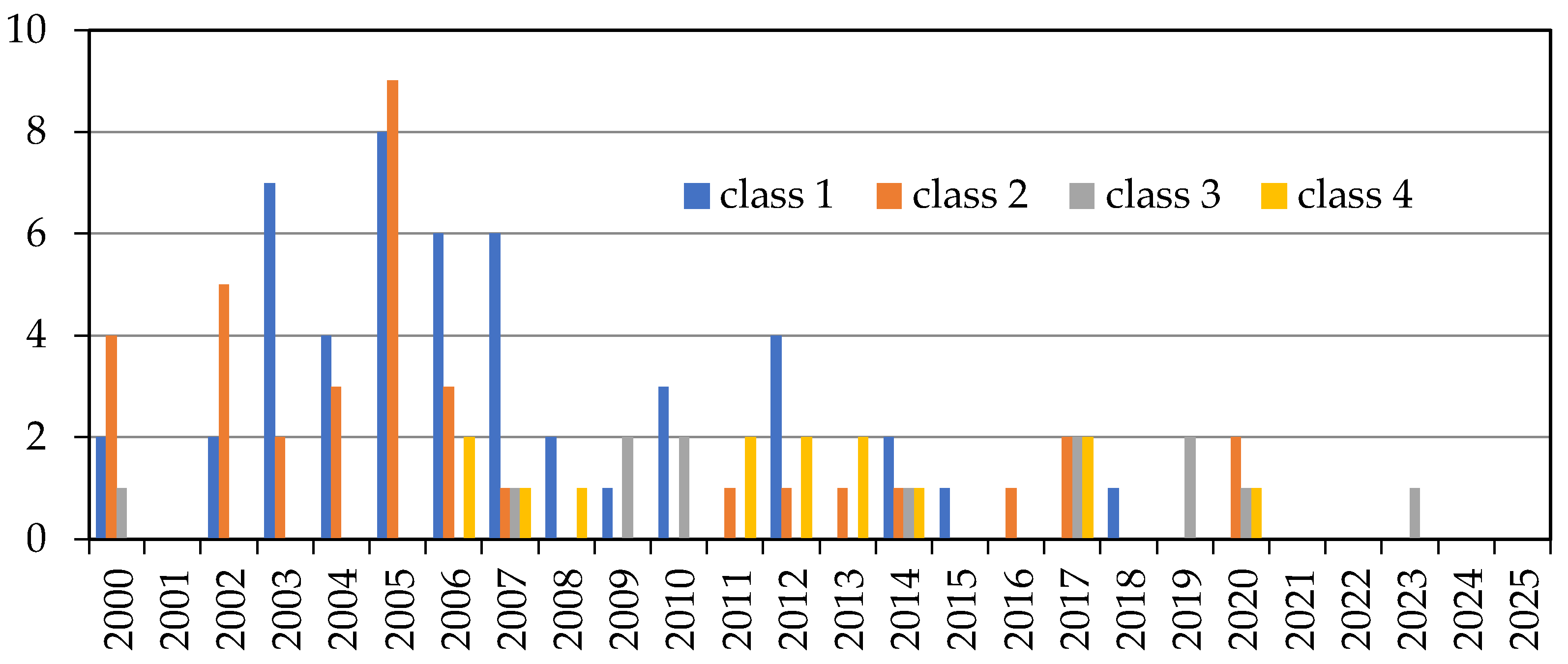
5. Results
- First quality class—30 8x26 WS IWRC 1960 B sZ;
- Second quality class—22.4 6x27 NS SFC 1570 U sZ;
- Third quality class—42.5 6x39 NFC 1570 B zZ;
- Fourth quality class—25 6x31 WS SFC 1770 B sZ.
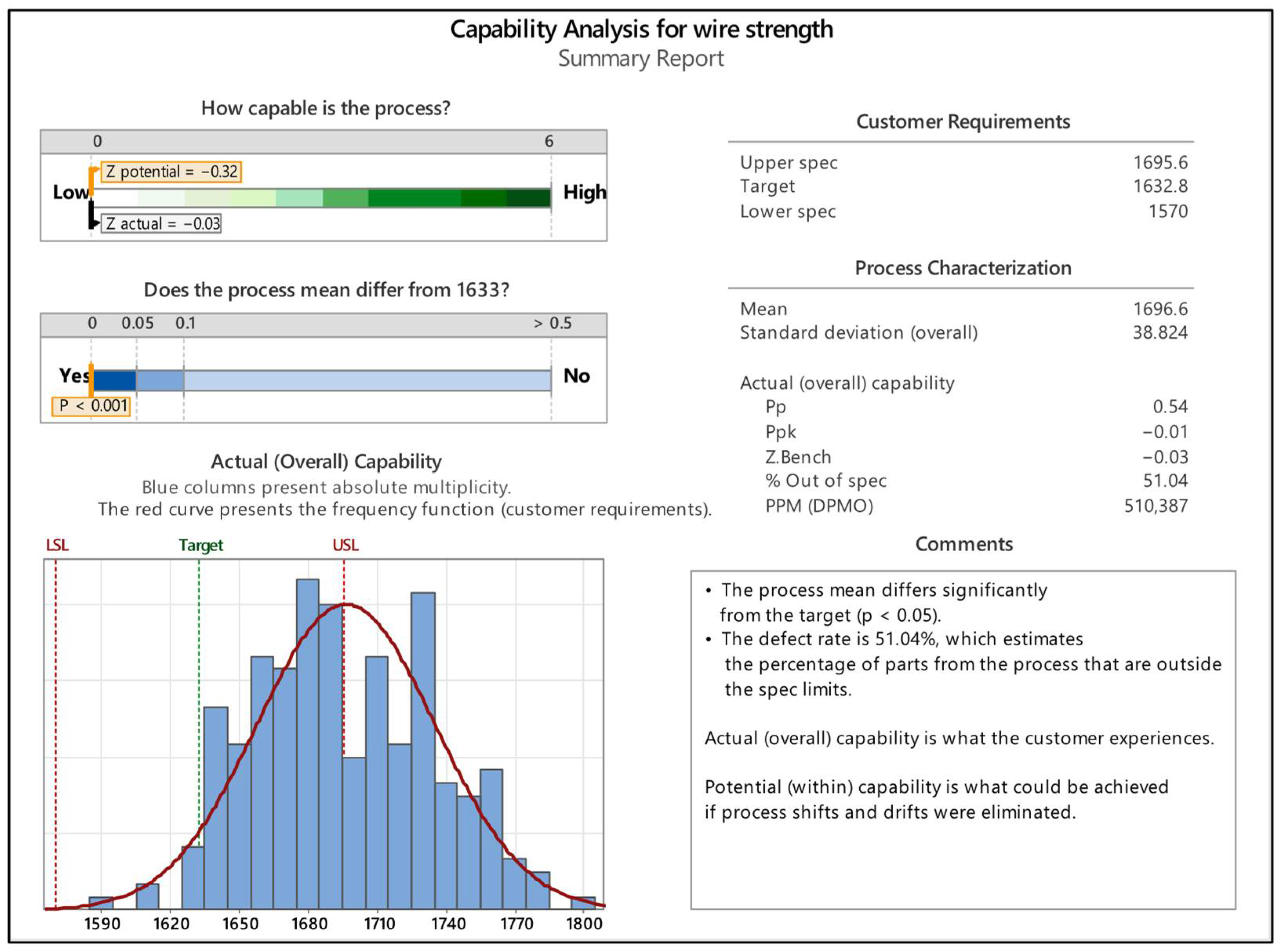
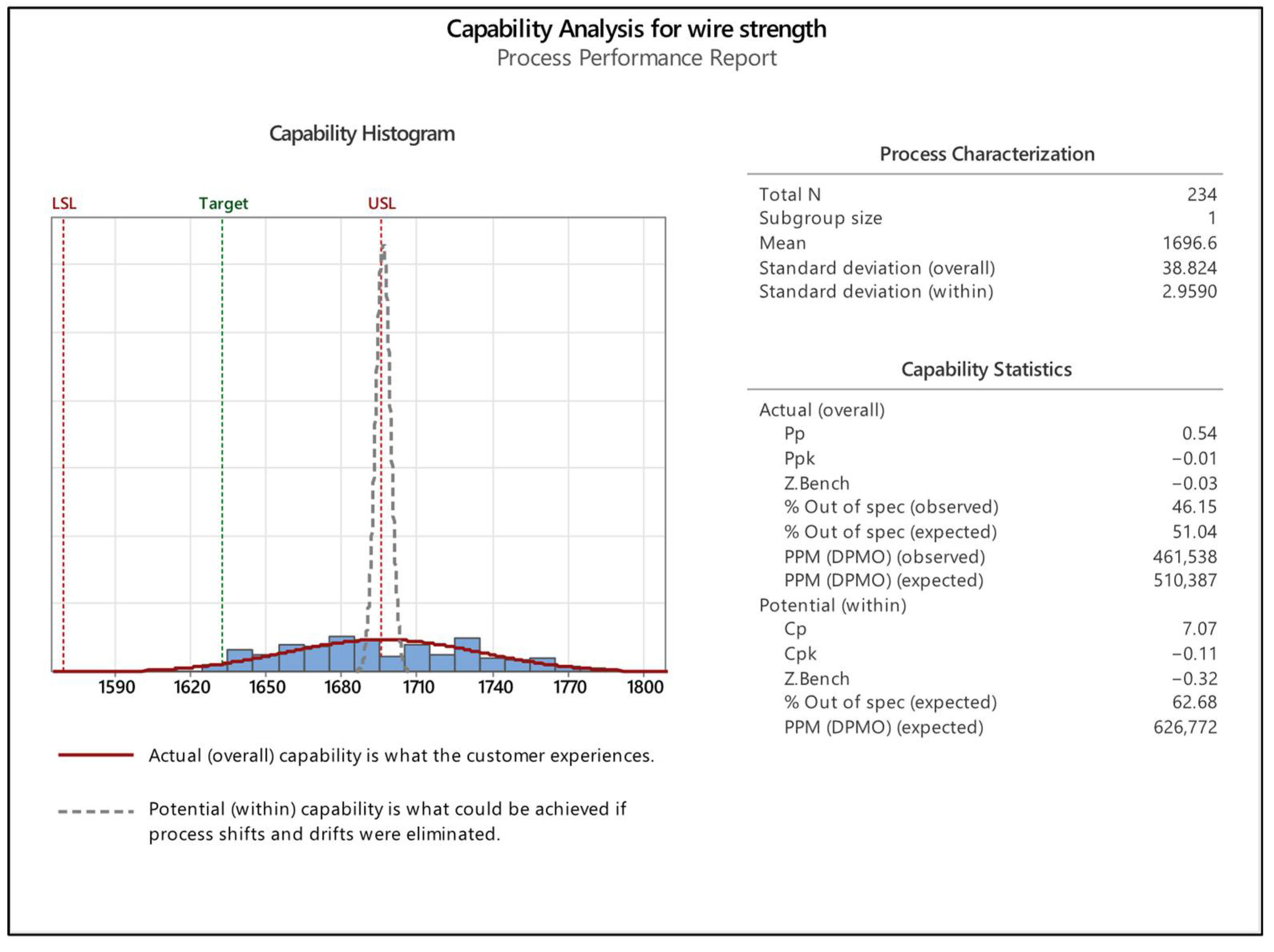
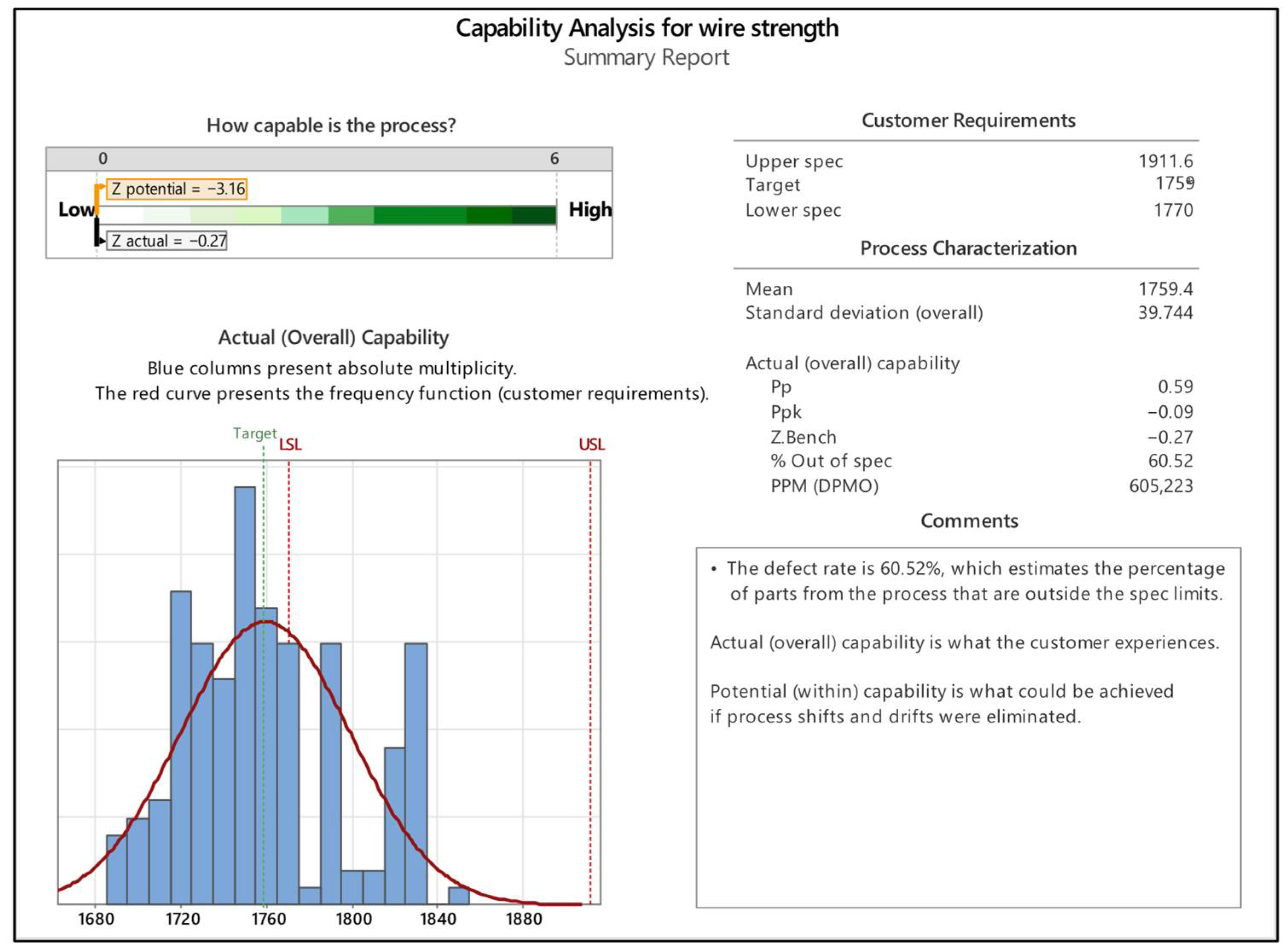
5.1. Analysis of Rope in the Fourth Quality Class
5.2. Analysis of Rope in the Third Quality Class
5.3. Analysis of Rope in the Second Quality Class
5.4. Analysis of Rope in the First Quality Class
6. Conclusions
- Rope of quality class No. 1—25 6x31 WS SFC 1770 B sZ;
- Rope of quality class No. 2—42.5 6x39 NFC 1570 B zZ;
- Rope of quality class No. 3—22.4 6x27 NS SFC 1570 U sZ;
- Rope of quality class No. 4—30 8x26 WS IWRC 1960 B sZ.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PVF | Plastic valley filled |
| NDT | Non-destructive testing |
| SQC | Statistical quality control |
| AD | Anderson–Darling |
| SPC | Statistical process control |
| CDF | Cumulative distribution function |
References
- Hrabovsky, L.; Fries, J.; Kudrna, L.; Gaszek, J. Determination of the coefficient of friction in a pulley groove by the indirect method. Coatings 2022, 12, 606. [Google Scholar] [CrossRef]
- Hrabovsky, L.; Ucen, O.; Kudrna, L.; Cepica, D.; Frydrysek, K. Laboratory device detecting tensile forces in the rope and coefficient of friction in the rope sheave groove. Machines 2022, 10, 590. [Google Scholar] [CrossRef]
- Wang, D.; Chong, H.; Ge, S.; Wu, K.; Wang, B.; Li, C.; Ji, W.; Zhang, J.; Chen, J.; Deng, H.; et al. Bending tribo-fatigue behaviors between steel wire rope and rope groove material of offshore rig winch drum. Tribol. Int. 2025, 204, 110477. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Tan, H.; Xu, J.; He, Y.; Wang, S. Study on the tribological performance at the interface between a steel wire rope and groove during a twisting process. J. Non-Linear Mech. 2024, 166, 104829. [Google Scholar] [CrossRef]
- Čereška, A.; Zavadskas, E.K.; Bucinskas, V.; Podvezko, V.; Sutinys, E. Analysis of steel wire rope diagnostic data applying multi-criteria methods. Appl. Sci. 2018, 8, 260. [Google Scholar] [CrossRef]
- Pawar, G.; Qureshi, U. Review of wire rope analysis, construction and testing. Int. J. Sci. Prog. Res. (IJSPR) 2018, 43, 54–56. [Google Scholar]
- Changsha Aulone Construction Machinery Co., Ltd. What Is Wire Rope? Understanding the Specifications and Construction. Available online: https://loadmate.in/blog/what-is-wire-rope-understanding-the-specifications-and-construction/ (accessed on 18 May 2025).
- Mazurek, P. A Comprehensive Review of steel wire rope degradation mechanisms and recent damage detection methods. Sustainability 2023, 15, 5441. [Google Scholar] [CrossRef]
- da Silva, F.A.C. Steel wire ropes service life. Limitations of the application of ISO 4308 on the design of storage and retrieval machines. J. Fail. Anal. Prev. 2022, 22, 1924–1935. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, H.; Tian, J.; He, H.; Ji, Z.; He, X. Research on quantitative identification method for wire rope wire breakage damage signals based on multi-decomposition information fusion. J. Saf. Sustain. 2024, 1, 89–97. [Google Scholar] [CrossRef]
- Rosaa, C.; Silvaa, F.J.G.; Ferreiraa, L.P. Improving the quality and productivity of steel wire-rope assembly lines for the automotive industry. In Proceedings of the 27th International Conference on Flexible Automation and Intelligent Manufacturing, FAIM2017, Modena, Italy, 27–30 June 2017. [Google Scholar]
- Slesarev, D.; Vorontsov, A. Consideration of NDT results ambiguity while estimating rope residual strength by an example of drilling rig rope monitoring system. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Mouradi, H.; El Barkany, A.; El Biyaali, A. Reliability estimation of non-rotating ropes based on cumulative damage. Int. J. Perform. Eng. 2016, 12, 471–480. [Google Scholar]
- Mazumder, S.; Paul, A.; Chandra Dey, N.; Chakraborty, K.; Banerjee, S. Performance analysis of PVF and Non-PVF ropes using Statistical Process Control (SPC) and Customer Value Management (CVM) techniques in respect of opencast mines. J. Inst. Eng. Ser. D 2021, 102, 461–472. [Google Scholar] [CrossRef]
- Yordanova, R.; Yankova, S. Evaluation of the mechanical properties of steel wire rope during its operation in the mining industry. J. Chem. Technol. Metall. 2025, 60, 163–172. [Google Scholar] [CrossRef]
- EN 12385; Steel Wire Ropes—Safety—Part 1: General Requirements. DIN: Berlin, Germany, 2009.
- Costello, G.A. Theory of Wire Rope, 2nd ed.; Springer Sciences and Business Media: New York, NY, USA, 1997; pp. 87–98. [Google Scholar]
- DIN 21 254; Förderseile, Technische Lieferbedingungen, Invalid Standard. DIN: Berlin, Germany, 1969.
- STN 02 4301; Oceľové Laná, Technické Dodacie Predpisy, Invalid Slovak Standard. SUTN: Bratislava, Slovakia, 1974.
- Žitkov, E.I.; Pospechov, F.P. Staľnyje Konaty Dlja Podzemnotransportnych Mašin, 1st ed.; Metalurgizdet: Moscow, Russia, 1953; pp. 48–56. [Google Scholar]
- Molnár, V.; Boroška, J.; Dečmanová, J. Mechanical properties of steel rope wires—Quality test assurance. Acta Montan. Slovaca 2010, 15, 23–30. [Google Scholar]
- Boroška, J.; Krešák, J.; Peterka, P. Estimation of quality for steel wire ropes according to their mechanical properties. Acta Montan. Slovaca 1997, 2, 37–42. [Google Scholar]
- Andrejiova, M. Statistical Methods in Practise, [Štatistické Metódy v Praxi], 1st ed.; Technical University of Košice: Košice, Slovakia, 2016; pp. 249–271. [Google Scholar]
- Das, K.R.; Rahmatullah Imon, A.H.M. A Brief Review of Tests for Normality. Am. J. Theor. Appl. Stat. 2016, 5, 5–12. [Google Scholar]
- Jäntschi, L.; Bolboaca, S.D. Computation of Probability Associated with Anderson–Darling Statistic. Mathematics 2018, 6, 88. [Google Scholar] [CrossRef]
- Berlinger, M.; Stefan Kolling, S.; Schneider, J. A generalized Anderson–Darling test for the goodness-of-fit evaluation of the fracture strain distribution of acrylic glass. Glass Struct. Eng. 2021, 6, 195–208. [Google Scholar] [CrossRef]
- Malindzakova, M.; Garaj, P.; Trpčevská, J.; Malindzak, D. Setting MRP parameters and optimizing the production planning process. Processes 2022, 10, 690. [Google Scholar] [CrossRef]
- Malindzakova, M.; Čulková, K.; Trpčevská, J. Shewhart Control Charts implementation for quality and production management. Processes 2023, 11, 1246. [Google Scholar] [CrossRef]
- Plura, J. Quality Planning and Continuous Quality Improvement, [Plánování a Neustálé Zlepšování Jakosti], 1st ed.; Computer Press: Praha, Czech Republic, 2001; pp. 107–113. [Google Scholar]
- EN 8258:1995; Shewhart Control Charts. SUTN: Bratislava, Slovakia, 1995.
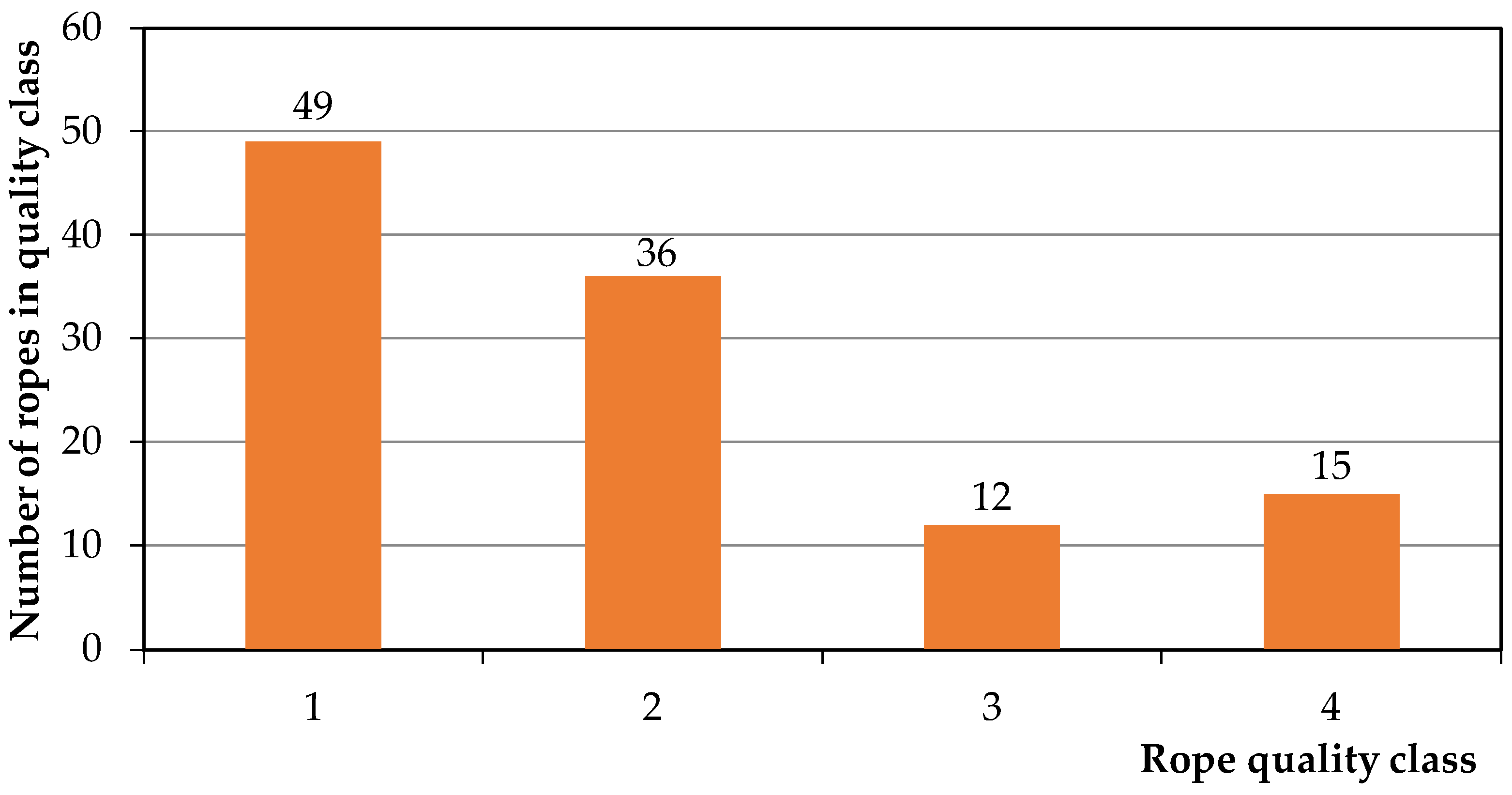







| Quality Class | Rope Construction | Nominal Accuracy |
|---|---|---|
| Class I | 30 8x26 WS IWRC 1960 B sZ | |
| Class II | 22.4 6x27 NS SFC 1570 U sZ | |
| Class III | 42.5 6x39 NFC 1570 B zZ | |
| Class IV | 25 6x31 WS SFC 1770 B sZ |
| Wire 1 | Wire 2 | Wire 3 | Wire 4 | Wire 5 | |
|---|---|---|---|---|---|
| Mean [MPa] | 1746.41 | 1919.26 | 1941.51 | 1814.01 | 2008.82 |
| Maximum value [MPa] | 1786.43 | 2201.95 | 1981.60 | 1899.62 | 2027.66 |
| Minimum value [MPa] | 1657.05 | 1863.19 | 1804.67 | 1614.27 | 1997.51 |
| Variation range (Vx) [MPa] | 129.38 | 338.76 | 176.93 | 285.35 | 1230.15 |
| Standard deviation (s) [MPa] | 20.53 | 67.02 | 48.34 | 103.70 | 1313.27 |
| Variance (s2) [MPa] | 421.60 | 4491.17 | 2336.54 | 10,754.72 | 176.14 |
| Wire 1 | Wire 2 | Wire 3 | |
|---|---|---|---|
| Arithmetic mean [MPa] | 1714.38 | 1686.46 | 1674.37 |
| Maximum value [MPa] | 1802.67 | 1751.65 | 1751.59 |
| Minimum value [MPa] | 1632.60 | 1632.60 | 1592.36 |
| Variation range (Vx) [MPa] | 170.06 | 119.04 | 159.24 |
| Standard deviation (s) [MPa] | 38.95 | 29.98 | 32.75 |
| Variance (s2) [MPa] | 1516.77 | 898.87 | 1072.45 |
| Wire 1 | Wire 2 | Wire 3 | Wire 4 | |
|---|---|---|---|---|
| Arithmetic mean [MPa] | 1725.84 | 1782.17 | 1769.84 | 1804.67 |
| Maximum value [MPa] | 1754.35 | 1847.13 | 1791.40 | 1831.21 |
| Minimum value [MPa] | 1692.64 | 1694.27 | 1691.88 | 1771.50 |
| Variation range (Vx) [MPa] | 61.71 | 152.87 | 99.52 | 59.71 |
| Standard deviation (s) [MPa] | 14.73 | 42.07 | 23.49 | 24.11 |
| Variance (s2) [MPa] | 217.00 | 1769.66 | 551.83 | 581.07 |
| Wire 1 | Wire 2 | Wire 3 | Wire 4 | Wire 5 | Wire 6 | Wire 7 | Wire 8 | Wire 9 | Wire 10 | Wire 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Arithmetic mean [MPa] | 2035.22 | 2035.81 | 2066.49 | 2045.12 | 2072.15 | 2033.40 | 2010.06 | 1987.16 | 2045.27 | 2022.16 | 2023.68 |
| Maximum value [MPa] | 2124.32 | 2070.09 | 2102.93 | 2111.15 | 2121.88 | 2069.04 | 2173.26 | 2113.46 | 2098.16 | 2084.26 | 2023.68 |
| Minimum value [MPa] | 1940.82 | 1947.92 | 2013.92 | 1988.08 | 2046.10 | 1930.13 | 1920.56 | 1911.38 | 1957.11 | 1950.97 | |
| Variation range (Vx) [MPa] | 183.50 | 122.17 | 89.01 | 123.07 | 75.78 | 138.91 | 252.70 | 202.08 | 141.05 | 133.30 | |
| Standard deviation (s) [MPa] | 34.51 | 24.10 | 18.17 | 41.15 | 26.67 | 24.39 | 49.99 | 83.18 | 42.15 | 47.35 | |
| Variance (s2) [MPa] | 1190.84 | 581.02 | 330.06 | 1693.62 | 711.44 | 595.08 | 2498.91 | 6919.74 | 1776.43 | 2241.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malindzakova, M.; Peterka, P. Operational Reliability of Steel Ropes in Terms of Mechanical Properties of Wires Using Control Charts. Appl. Sci. 2025, 15, 7875. https://doi.org/10.3390/app15147875
Malindzakova M, Peterka P. Operational Reliability of Steel Ropes in Terms of Mechanical Properties of Wires Using Control Charts. Applied Sciences. 2025; 15(14):7875. https://doi.org/10.3390/app15147875
Chicago/Turabian StyleMalindzakova, Marcela, and Pavel Peterka. 2025. "Operational Reliability of Steel Ropes in Terms of Mechanical Properties of Wires Using Control Charts" Applied Sciences 15, no. 14: 7875. https://doi.org/10.3390/app15147875
APA StyleMalindzakova, M., & Peterka, P. (2025). Operational Reliability of Steel Ropes in Terms of Mechanical Properties of Wires Using Control Charts. Applied Sciences, 15(14), 7875. https://doi.org/10.3390/app15147875







