Leading-Edge Noise Mitigation on a Rod–Airfoil Configuration Using Regular and Irregular Leading-Edge Serrations
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Volume Flow Solver
2.2. Acoustics Solver
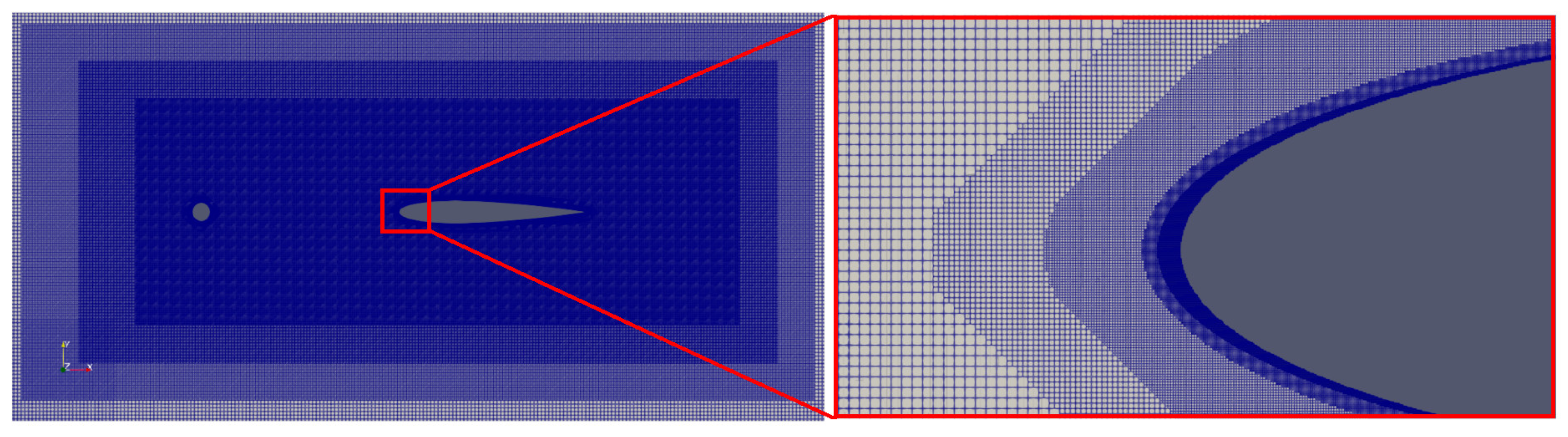
3. Computational Setup
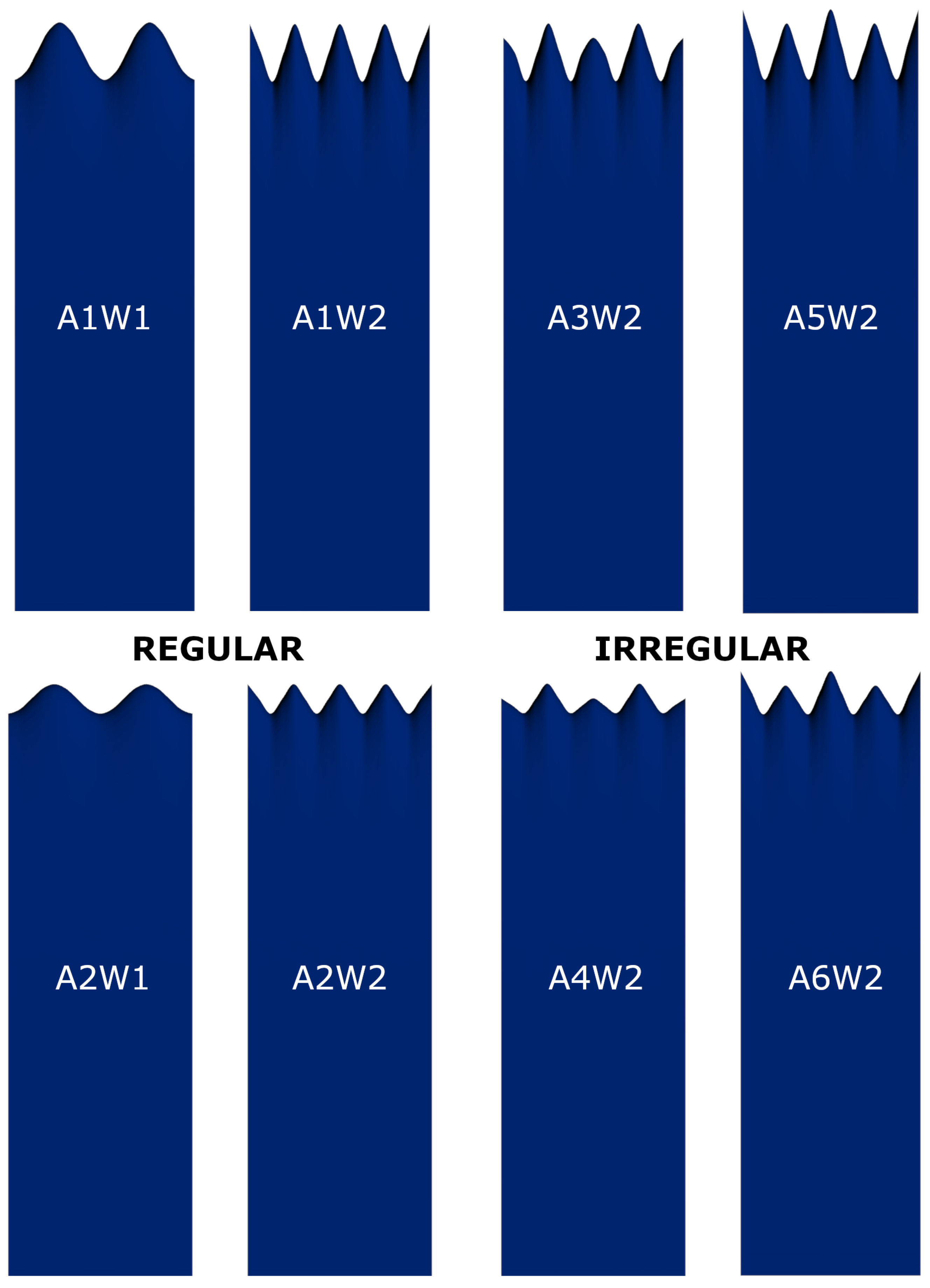
Serrated Leading-Edge Geometries
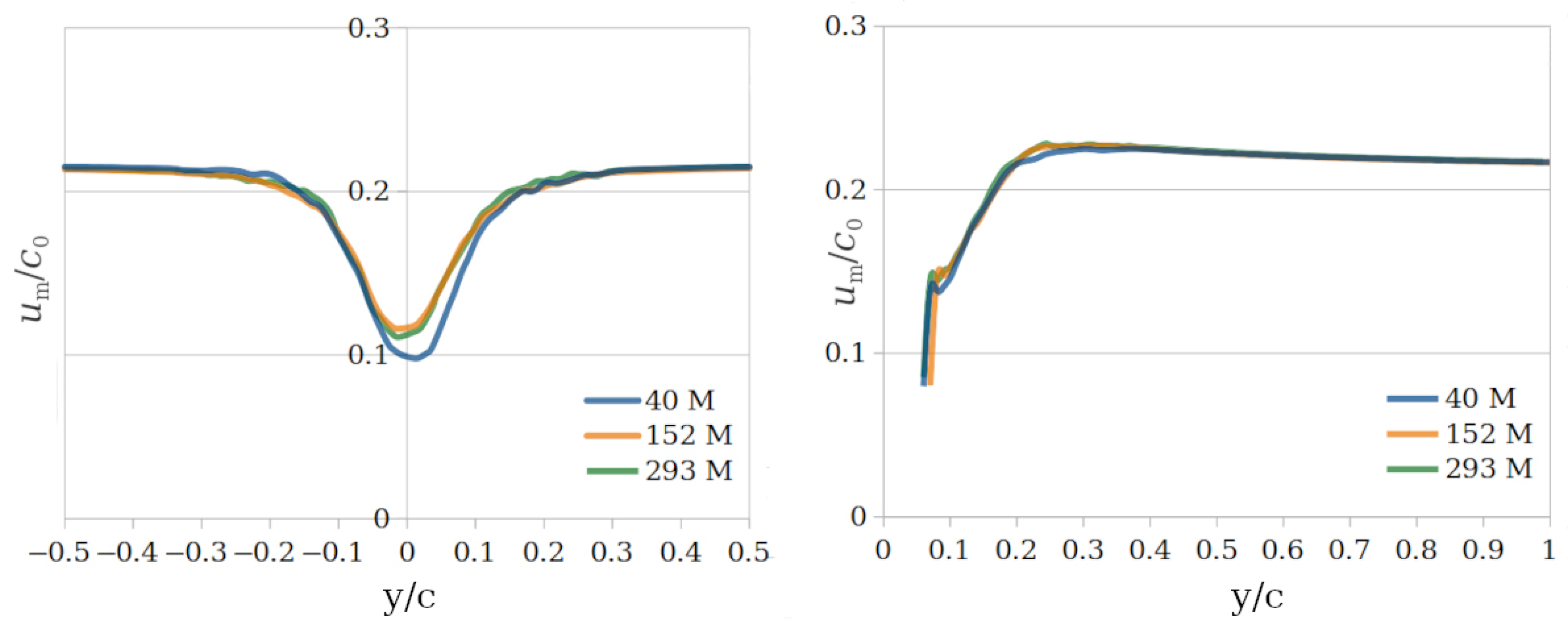
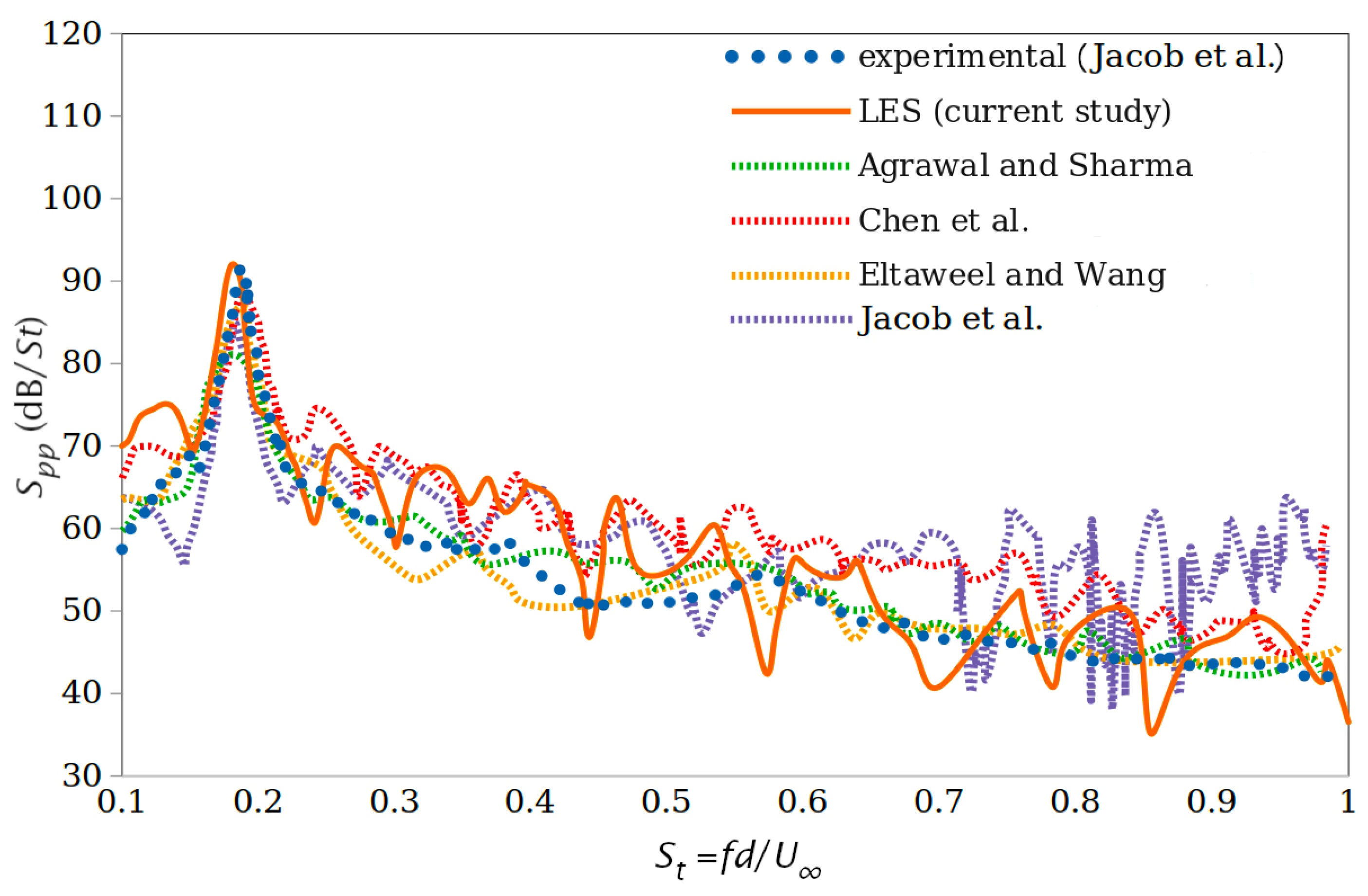
4. Validation
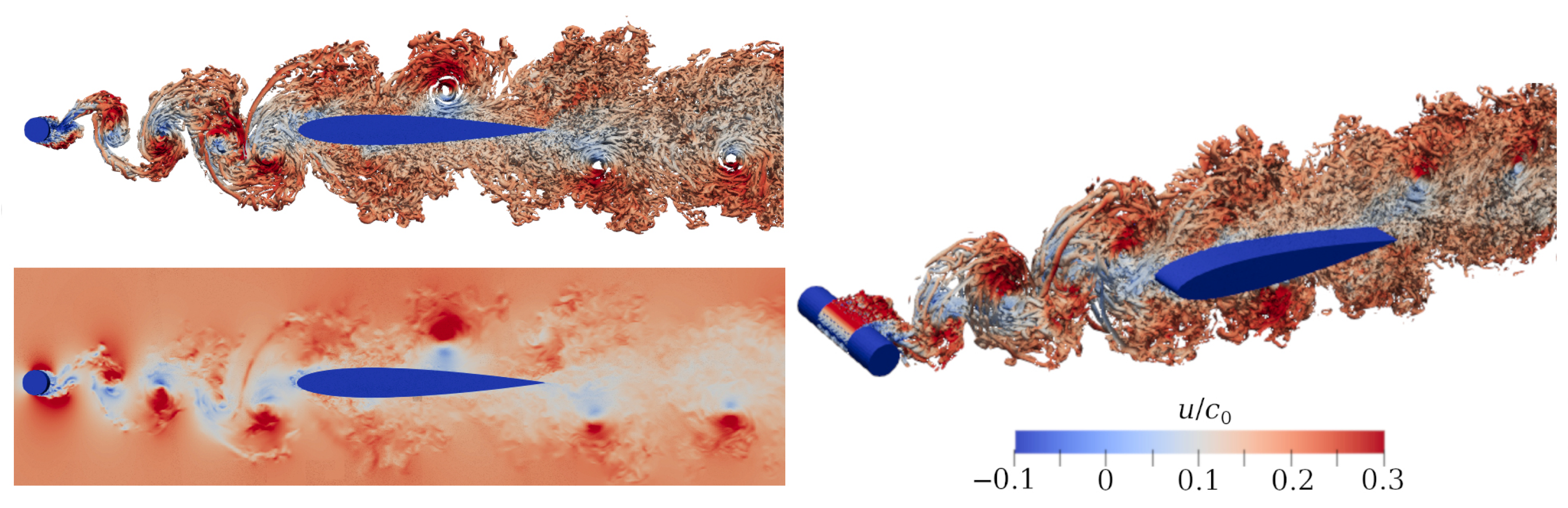
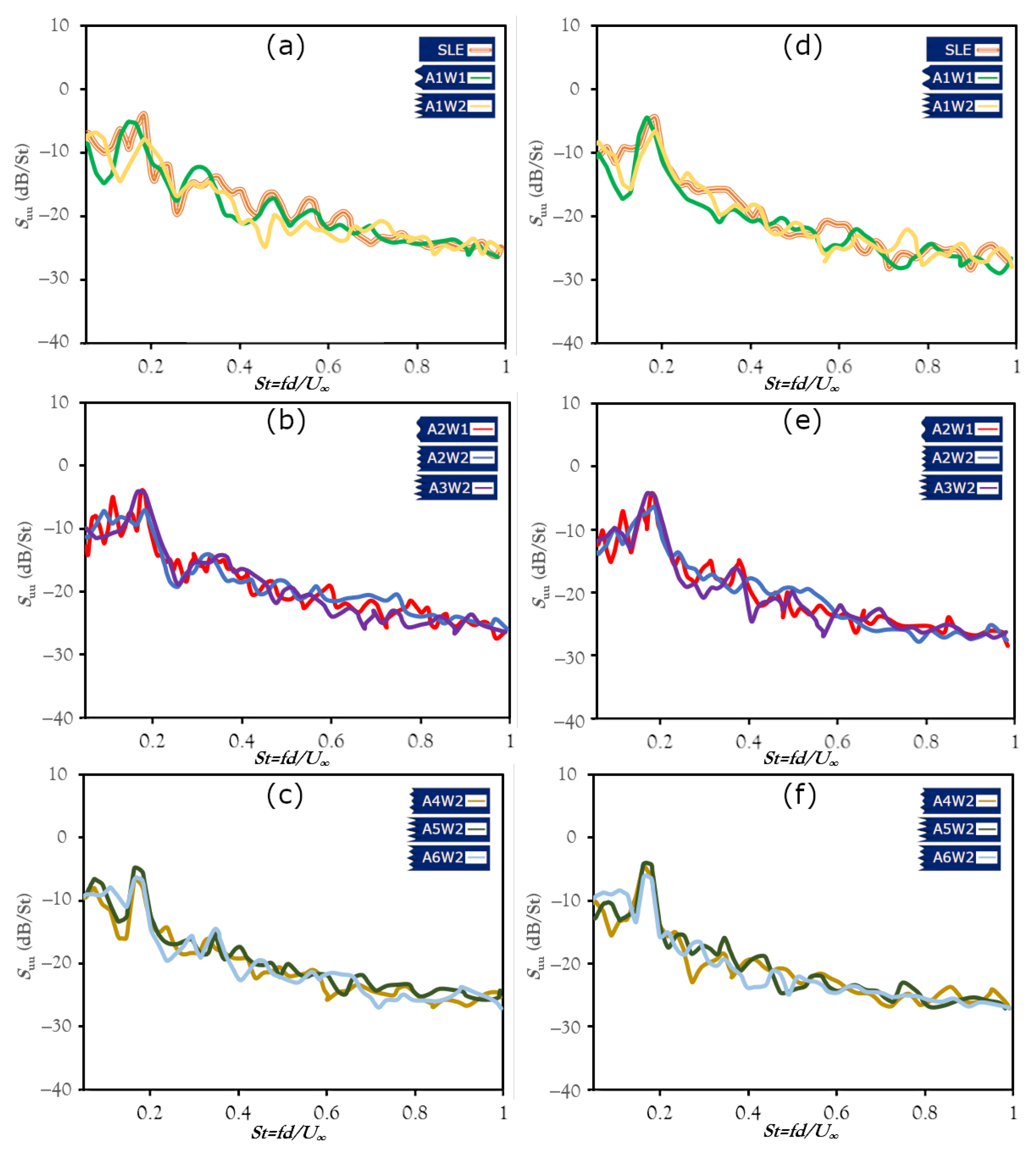
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jacob, M.C.; Boudet, J.; Casalino, D.; Michard, M. A Rod-Airfoil Experiment as a Benchmark for Broadband Noise Modeling. Theor. Comput. Fluid Dyn. 2005, 19, 171–196. [Google Scholar] [CrossRef]
- Moore, P.; Lorenzoni, V.; Scarano, F. Two Techniques for PIV-Based Aeroacoustic Prediction and Their Application to a Rod-Airfoil Experiment. Exp. Fluids 2010, 50, 877–885. [Google Scholar] [CrossRef]
- Giret, J.-C.; Sengissen, A.; Moreau, S.; Sanjose, M.; Jouhaud, J.-C. Noise Source Analysis of a Rod-Airfoil Configuration Using Unstructured Large-Eddy Simulation. AIAA J. 2015, 53, 1062–1077. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Chen, Z.; Zheng-chu, L. Experimental Study of Vortex-Structure Interaction Noise Radiated from Rod-Airfoil Configurations. J. Fluid Struct. 2014, 51, 313–325. [Google Scholar] [CrossRef]
- Jiang, M.; Li, X.; Zhou, J. Experimental and Numerical Investigation on Sound Generation from Airfoil-Flow Interaction. Appl. Math. Mech. 2011, 32, 765–776. [Google Scholar] [CrossRef]
- Jiang, Y.; Mao, M.-L.; Deng, X.-G.; Liu, H.-Y. Numerical Investigation on Body-Wake Flow Interaction Over Rod-Airfoil Configuration. J. Fluid Mech. 2015, 779, 1–35. [Google Scholar] [CrossRef]
- Sharma, S.; Geyer, T.F.; Giesler, J. Effect of Geometric Parameters on the Noise Generated by Rod-Airfoil Configuration. Appl. Acoust. 2021, 177, 107908. [Google Scholar] [CrossRef]
- Agrawal, B.R.; Sharma, A. Numerical Analysis of Aerodynamic Noise Mitigation via Leading Edge Serrations for a Rod-Airfoil Configuration. Int. J. Aeroacoust. 2016, 15, 734–756. [Google Scholar] [CrossRef]
- Chen, W.; Qiao, W.; Tong, F.; Wang, L.; Wang, X. Experimental Investigation of Wavy Leading Edges on Rod-Aerofoil Interaction Noise. J. Sound Vib. 2018, 422, 409–431. [Google Scholar] [CrossRef]
- Fan, T.; Qiao, W.; Chen, W.; Cheng, H.; Wei, R.; Wang, X. Numerical Analysis of Broadband Noise Reduction with Wavy Leading Edge. Chin. J. Aeronaut. 2018, 31, 1489–1505. [Google Scholar]
- Chen, W.; Qiao, W.; Tong, F.; Wang, L.; Wang, X. Numerical Investigation of Wavy Leading Edges on Rod-Airfoil Interaction Noise. AIAA J. 2018, 56, 2553–2567. [Google Scholar] [CrossRef]
- Teruna, C.; Avallone, F.; Casalino, D.; Ragni, D. Numerical Investigation of Leading Edge Noise Reduction on a Rod-Airfoil Configuration Using Porous Materials and Serrations. J. Sound Vib. 2021, 494, 115880. [Google Scholar] [CrossRef]
- Chen, W.; Lei, H.; Xing, Y.; Wang, L.; Zhou, T.; Qiao, W. On the airfoil leading-edge noise reduction using poro-wavy leading edges. Phys. Fluids 2024, 36, 035158. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, F.; Chen, Z.; Wang, C.; Jiang, S. Rod–Airfoil Interaction Noise Reduction Using Gradient Distributed Porous Leading Edges. Appl. Sci. 2022, 12, 4941. [Google Scholar] [CrossRef]
- Gao, R.; Chen, W.; Tong, H.; Zhang, Y.; Zhang, L.; Wang, X.; Qiao, W. Aerodynamic performance of a fan with porous-wavy leading edge. Phys. Fluids 2025, 37, 047128. [Google Scholar] [CrossRef]
- Yu, F.-Y.; Wan, Z.-H.; Hu, Y.-S.; Sun, D.-J.; Lu, X.-Y. Effects of leading-edge serration shape on noise reduction in rod-airfoil interactions. J. Acoust. Soc. Am. 2025, 157, 215–233. [Google Scholar] [CrossRef]
- Paruchuri, C.C.; Narayanan, S.; Joseph, P.; Kim, J.W. Leading Edge Serration Geometries for Significantly Enhanced Leading Edge Noise Reductions. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 2736. [Google Scholar]
- Schlottke-Lakemper, M.; Yu, H.; Berger, S.; Meinke, M.; Schröder, W. A Fully Coupled Hybrid Computational Aeroacoustics Method on Hierarchical Cartesian Meshes. Comput. Fluids 2017, 144, 137–153. [Google Scholar] [CrossRef]
- Institute of Aerodynamics. m-AIA, 2024, 13350586. Available online: https://doi.org/10.5281/zenodo.13350586 (accessed on 20 October 2024).
- Boris, J.P.; Grinstein, F.F.; Oran, E.S.; Kolbe, R.L. New Insights into Large Eddy Simulation. Fluid Dyn. Res. 1992, 10, 199. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme. V. A Second-Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Schneiders, L.; Günther, C.; Meinke, M.; Schröder, W. An Efficient Conservative Cut-Cell Method for Rigid Bodies Interacting with Viscous Compressible Flows. J. Comput. Phys. 2016, 311, 62–86. [Google Scholar] [CrossRef]
- Cetin, M.O.; Koh, S.R.; Meinke, M.; Schröder, W. Numerical Analysis of the Impact of the Interior Nozzle Geometry on Low Mach Number Jet Acoustics. Flow Turbul. Combust. 2017, 98, 417–443. [Google Scholar] [CrossRef]
- Ewert, R.; Schröder, W. Acoustic Perturbation Equations Based on Flow Decomposition via Source Filtering. J. Comput. Phys. 2003, 188, 365–398. [Google Scholar] [CrossRef]
- Xiao, C.; Tong, F. Experiment on Noise Reduction of a Wavy Cylinder with a Large Spanwise Wavelength and Large Aspect Ratio in Aeroacoustic Wind Tunnels. Appl. Sci. 2023, 13, 6061. [Google Scholar] [CrossRef]
- Wang, Y.; Zuo, K.; Guo, P.; Zhao, K.; Kopiev, V.F. Experimental Investigation of Airfoil Instability Tonal Noise Reduction Using Structured Porous Trailing Edges. Appl. Sci. 2024, 14, 2992. [Google Scholar] [CrossRef]
- Al-Okbi, Y.; Chong, T.P.; Stalnov, O. Leading Edge Blowing to Mimic and Enhance the Serration Effects for Aerofoil. Appl. Sci. 2021, 11, 2593. [Google Scholar] [CrossRef]
- Eltawcel, A.; Wang, M. Numerical Simulation of Broadband Noise from Airfoil-Wake Interaction. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, OR, USA, 5–8 June 2011; p. 2802. [Google Scholar]
- Yu, F.-Y.; Wan, Z.-H.; Hu, Y.-S.; Sun, D. Effects of the wavy leading-edge wavelength on the reduction in the noise of the rod–airfoil configuration. JUSTC 2025, 55, 0202. [Google Scholar] [CrossRef]








| # | Rod Diam. (mm) | Gap (mm) | Exp./CFD | Flow Speed (m/s) | Airfoil Geometry Mod. and/or Additional Note | Acoustic Method | Reference |
|---|---|---|---|---|---|---|---|
| 1 | 10, 16 | 100 | Exp. | 30.5, 61, 72, 115 | No, benchmark study | Exp. | [1] |
| 2 | 6 | 220 | Exp. | 15 | No | Curle’s acc. an. | [2] |
| 3 | 10 | 100 | CFD | 72 | No | FWH 1 | [3] |
| 4 | 10 | 100 | Exp. & CFD | 72 | No | Exp. | [5] |
| 5 | 10 | 20–100 | CFD | 72 | No | FWH | [6] |
| 6 | 5, 16 | 86, 124 | Exp. & CFD | 26 | No | FWH | [7] |
| 7 | 10 | 100 | CFD | 72 | Yes, LE serrations | FWH | [8] |
| 8 | 10, 15, 20 | 150 | Exp. | 72 | Yes, LE serrations | Exp. | [9] |
| 9 | 10 | 100 | CFD | 40 | Yes, LE serrations | Generalized Lighthill Eq. | [10] |
| 10 | 10 | 100 | CFD | 72 | Yes, LE serrations | FWH | [11] |
| 11 | 10 | 100 | CFD | 72 | Yes, LE porous-serrations | FWH | [12] |
| 12 | 15 | 150 | CFD | 40 | Yes, LE porous-serrations | FWH | [13] |
| 13 | 10 | 100 | CFD | 72 | Yes, regular and irregular LE serrations | APE-4 2 | Present study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, M.N.; Satcunanathan, S.; Meinke, M.; Schröder, W. Leading-Edge Noise Mitigation on a Rod–Airfoil Configuration Using Regular and Irregular Leading-Edge Serrations. Appl. Sci. 2025, 15, 7822. https://doi.org/10.3390/app15147822
Kaya MN, Satcunanathan S, Meinke M, Schröder W. Leading-Edge Noise Mitigation on a Rod–Airfoil Configuration Using Regular and Irregular Leading-Edge Serrations. Applied Sciences. 2025; 15(14):7822. https://doi.org/10.3390/app15147822
Chicago/Turabian StyleKaya, Mehmet Numan, Sutharsan Satcunanathan, Matthias Meinke, and Wolfgang Schröder. 2025. "Leading-Edge Noise Mitigation on a Rod–Airfoil Configuration Using Regular and Irregular Leading-Edge Serrations" Applied Sciences 15, no. 14: 7822. https://doi.org/10.3390/app15147822
APA StyleKaya, M. N., Satcunanathan, S., Meinke, M., & Schröder, W. (2025). Leading-Edge Noise Mitigation on a Rod–Airfoil Configuration Using Regular and Irregular Leading-Edge Serrations. Applied Sciences, 15(14), 7822. https://doi.org/10.3390/app15147822







