Predicting Olympic Medal Performance for 2028: Machine Learning Models and the Impact of Host and Coaching Effects

Abstract

This study develops two machine learning models to predict the medal performance of countries at the 2028 Olympic Games while systematically analyzing and quantifying the impacts of the host effect and exceptional coaching on medal gains. The dataset encompasses records of total medals by country, event categories, and athletes’ participation from the Olympic Games held between 1896 and 2024. We use K-means clustering to analyze medal trends, categorizing 234 nations into four groups (${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$). Among these, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ represent medal-winning countries, while ${\alpha }_4$ consists of non-medal-winning nations. For the $\alpha$1, $\alpha$2, and $\alpha$3 groups, 2–3 representative countries from each are selected for trend analysis, with the United States serving as a case study. This study extracts ten factors that may influence medal wins from the dataset, including participant data, the number of events, and medal growth rates. Factor analysis is used to reduce them into three principal components: Factor analysis condenses ten influencing factors into three principal components: the event scale factor (F1), the medal trend factor (F2), and the gender and athletic ability factor (F3). An ARIMA model predicts the factor coefficients for 2028 as 0.9539, 0.7999, and 0.2937, respectively. Four models (random forest, BP Neural Network, XGBoost, and SVM) are employed to predict medal outcomes, using historical data split into training and testing sets to compare their predictive performance. The research results show that XGBoost is the optimal medal predicted model, with the United States projected to win 57 gold medals and a total of 135 medals in 2028. For non-medal-winning countries (${\alpha }_4$), a three-layer fully connected neural network (FCNN) is constructed, achieving an accuracy of 85.5% during testing. Additionally, a formula to calculate the host effect and a Bayesian linear regression model to assess the impact of exceptional coaching on athletes’ medal performance are proposed. The overall trend of countries in the $\alpha$1 group is stable, but they are significantly affected by the host effect; the trend in the $\alpha$2 group shows an upward trend; the trend in the $\alpha$3 group depend on the athletes’ conditions and whether the events they excel in are included in that year’s Olympics. In the $\alpha$4 group, the probabilities of the United Arab Republic (UAR) and Mali (MLI) winning medals in the 2028 Olympic Games are 77.47% and 58.47%, respectively, and there are another four countries with probabilities exceeding 30%. For the eight most recent Olympic Games, the gain rate of the host effect is 74%. Great coaches can bring an average increase of 0.2 to 0.5 medals for each athlete. The proposed models, through an innovative integration of clustering, dimensionality reduction, and predictive algorithms, provide reliable forecasts and data-driven insights for optimizing national sports strategies. These contributions not only address the gap in predicting first-time medal wins for non-medal-winning nations but also offer guidance for policymakers and sports organizations, though they are constrained by assumptions of stable historical trends, minimal external disruptions, and the exclusion of unknown athletes.

1. Introduction

As the world’s highest-level international sports event, the Olympic Games have evolved into a top-tier sporting extravaganza encompassing over 200 participating countries and more than 40 major sports disciplines [1,2] It is not only a concentrated manifestation of the highest levels of competitive sport but also serves as a crucial platform for countries to showcase their comprehensive national strength and resource allocation strategies. With the continuous expansion of the event scale and the increase in the variety of events—for instance, the 2020 Tokyo Olympics added five new events such as skateboarding and surfing—sports management departments of various countries have attached greater importance to using scientific methods to predict the distribution of medals [3]. The aim is to maintain competitiveness in dominant events and achieve breakthroughs in emerging ones. Accurate medal prediction not only helps optimize the allocation of training resources, but also provides a quantitative basis for the formulation of national sports policies and strategic planning, which holds significant practical importance for enhancing comprehensive sports competitiveness.

Machine learning (ML) excels at uncovering nonlinear relationships within vast historical datasets, overcoming the limitations of traditional statistical models that rely on predefined equations [4,5], and has been widely applied in fields such as finance, healthcare, and advertising [6,7] As a core ML technique, neural networks exhibit powerful adaptive learning capabilities, excelling in handling nonlinear relationships and high-dimensional data with exceptional generalization and fault tolerance. By comparing multiple ML models, precise predictions can be achieved for complex dynamic systems such as Olympic medal outcomes [8,9,10]. Additionally, K-means clustering effectively segments data by maximizing intra-cluster similarity and inter-cluster differences [11,12], while factor analysis reduces highly correlated variables into a few independent principal components, revealing latent data patterns and mitigating multicollinearity [13,14]. By integrating K-means clustering and factor analysis into the ML pipeline, this study constructs an innovative framework that significantly enhances the efficiency of analyzing global medal performance trends. Furthermore, a Fully Connected Neural Network (FCNN) is employed to predict the probability of non-medal-winning nations achieving their first medal at the 2028 Olympic Games, achieving an impressive 85.5% accuracy on the test set.

The impacts of the host effect and the great coach effect on athletes medal wins cannot be underestimated. The host effect significantly enhances the medal competitiveness of the host country through various mechanisms, such as increasing the number of participants, optimizing venue adaptability, and boosting athletes’ morale [15]. The introduction of renowned coaches can not only improve the strength of domestic athletes through technical guidance and psychological support but can also weaken the competitiveness of competitors through strategic analysis, resulting in a situation of relative gain and loss [16,17]. This study quantifies the host effect and the great coach effect separately. It proposes a formula for the host effect and evaluates the coach effect factors by segments. Moreover, this study designs a coach effect scoring system, which assesses the extent to which the introduction of coaches enhances the overall strength of athletes in a project through Bayesian linear regression, providing data support for the optimal allocation of coaching teams.

Although prior studies have established a theoretical foundation for Olympic medal prediction, challenges such as limited research volume, overly simplistic models, and insufficient data diversity persist [18,19,20,21]. These issues result in significant gaps in predicting medal distributions at the national or individual level. The Medal Predict XGBoost Model (MPXG) and First Medal Prediction Model (FMPM) proposed in this study not only forecast global medal trends across countries but also specifically address the likelihood of non-medal-winning nations achieving their first medal. Furthermore, the formula for calculating the host effect and the coach effect scoring system provide a scientific basis for countries to optimize their preparation strategies.

The innovations of this study are listed as follows:

(1)

Classifying global countries into four categories based on Olympic participation and medal outcomes, with an analysis of their 2028 medal trends.

(2)

Integrating factor analysis, time series, and four machine learning methods into the MPXG model to predict individual country medal outcomes.

(3)

Employing a FCNN to predict the probability of non-medal-winning countries winning their first medal in the next competition.

(4)

Quantifying the host effect value for the past eight Olympic Games.

(5)

Developing a Bayesian linear regression-based coach effect scoring system to evaluate the extent to which coaches enhance the overall strength of athletes in a discipline.

(6)

Ensuring the universal applicability of all models, allowing for data updates to analyze various events beyond the Olympics.

2. Related Work

The prediction of Olympic medal outcomes has evolved through several key methodological breakthroughs. In 2004, Bernard pioneered the application of Cobb–Douglas production functions to medal forecasting, developing national-level prediction models based on macroeconomic indicators such as population size and GDP [3]. In 2007, Lin Yinping advanced the field by introducing time series analysis techniques through ARIMA models to predict China’s medal count at the 2008 Beijing Olympics [22], though these linear approaches showed limitations in capturing nonlinear relationships.

In 2008, Wu Dianting’s research team made a significant contribution by quantitatively establishing the host country effect, determining specific coefficients for home advantage (C = 0.298) and population size (P = 1.000) [23]. In 2010, Li Kun developed specialized analytical methods through the gray relational analysis of technical indicators for China’s men’s basketball team, marking a shift toward sport-specific modeling [24]. In 2011, Wang Guofan’s team achieved a methodological breakthrough by combining genetic algorithms with regression analysis, significantly enhancing prediction adaptability [25].

The field saw further specialization in 2012 when Huang Changmei applied gray prediction modeling to Olympic track and field performance analysis [26]. In 2013, Zhang Long expanded the spatial dimension of research through the dynamic evolution analysis of gold medal distributions in Olympic track and field events [27]. Most recently in 2022, Schlembach et al. revolutionized the field by introducing machine learning approaches, using random forest models to not only improve prediction accuracy but also reveal the mechanistic roles of socioeconomic factors through feature importance analysis [28].

While existing research has established fundamental theories for Olympic medal forecasting, significant limitations persist in terms of research scope, model sophistication, and data heterogeneity [18,19,20,21]. These shortcomings have resulted in notable gaps in predicting medal distributions at both national and individual event levels, with compromised accuracy in current projections. Building upon recent advancements in neural network algorithms, our study incorporates deep learning techniques to enhance predictive precision. The Medal Predict XGBoost Model (MPXG) and the First Medal Prediction Model (FMPM) not only forecast overall national medal standings but also specifically evaluate the probability of non-medal-winning nations securing their inaugural Olympic honors. Furthermore, our quantitative framework for host effect assessment and the coach effect evaluation metric provide data-driven insights for optimizing national training strategies.

3. Methodology

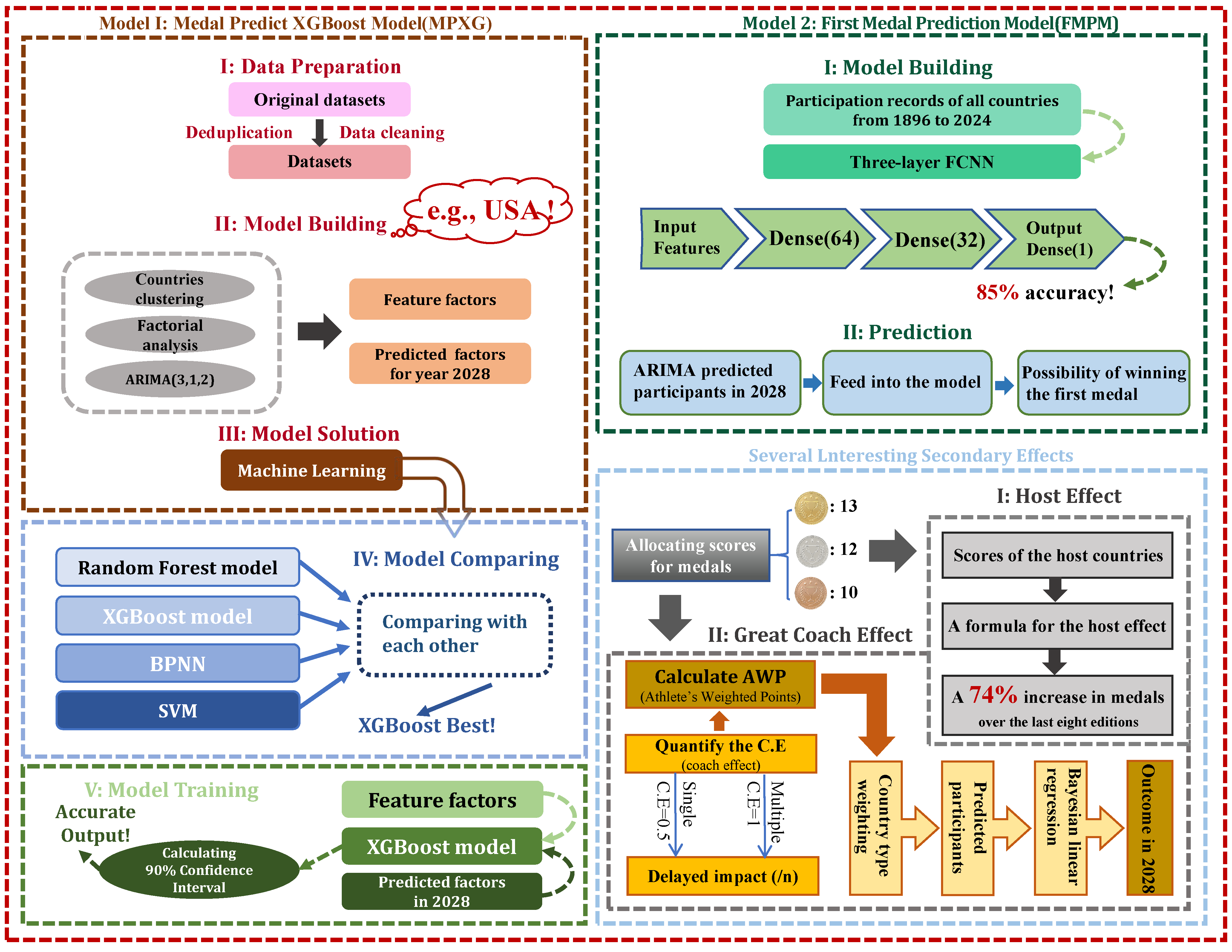
As shown in Figure 1, we establish the MPXG model to predict the medal counts of countries ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ in the 2028 Olympics. Subsequently, we develop the FMPM model to predict the probability of countries that have never won medals before achieving a podium finish in the 2028 Olympics. Finally, we discover and quantify interesting effects: the host effect and the great coach effect.

3.1. MPXG

To analyze medal trends, we employ K-means clustering to categorize 234 nations into four groups ($\alpha$1, $\alpha$2, $\alpha$3, $\alpha$4), with $\alpha$1, $\alpha$2, and $\alpha$3 comprising countries with prior medal wins and $\alpha$4 consisting of those without. For the $\alpha$1, $\alpha$2, and $\alpha$3 groups, we select 2–3 representative countries from each for trend analysis, with the United States serving as a case study. Factor analysis condenses ten influencing factors into three principal components. We use an ARIMA model to predict the factor coefficients for 2028. We compare the predictive performance of four models (RF, BPNN, XGBoost, and SVM). Among them, XGBoost(2.1.4) achieves the highest accuracy and the best evaluation metrics. Consequently, we select the XGBoost model to predict the medal counts for representative countries in 2028, providing a 90% confidence interval and speculatively forecasting the medal trends for each of the $\alpha$1, $\alpha$2, and $\alpha$3 groups.

3.2. FMPM

Countries in the ${\alpha }_4$ category have never won medals. We compile the participation records of ${\alpha }_4$ countries from 1896 to 2024. Then, we employ a three-layer neural network algorithm, achieving a high accuracy of 85.5%. Using the participation values predicted by the ARIMA model for 2028, we feed them into the model to calculate the probability of each ${\alpha }_4$ country winning its first medal.

3.3. Interesting Effects

We identify two intriguing phenomena: the host effect and the great coach effect. For the host effect, we quantify gold, silver, and bronze medals into scores of 13, 12, and 10, respectively, and construct a formula for the host effect. Our findings reveal that host countries experience a 74% increase in medal counts within 30 years.

For the great coach effect, we first classify and quantify the C.E. (Coach Effect) based on whether the great coach is active or retired, and whether they coach a single project or multiple projects, assigning values of 1.0, 0.5, and 0.25 accordingly. Next, we propose the AWP (Athlete’s Weighted Points) formula to calculate the AWP value. Then, based on the four country categories derived from K-means, we assign different values to $s_k$, such as 0.4, 0.3, and 0.1. Finally, we use Bayesian linear regression to predict the outcome for 2028.

4. Medal Predict XGBoost Model (MPXG)

4.1. National Classification

Given the complexity of individually analyzing medal counts and performance trends across all 234 countries, we first identified 78 nations that have never won Olympic medals as a distinct group. Subsequently, we applied K-means clustering to classify the remaining 156 countries. K-means clustering is a widely used distance-based algorithm designed to partition datasets into K clusters, offering efficient processing of large-scale datasets without requiring pre-labeled categories [11,12]. Here, we selected each country’s total Olympic participations and total medal counts as clustering metrics.

4.1.1. Determining the Number of Clusters

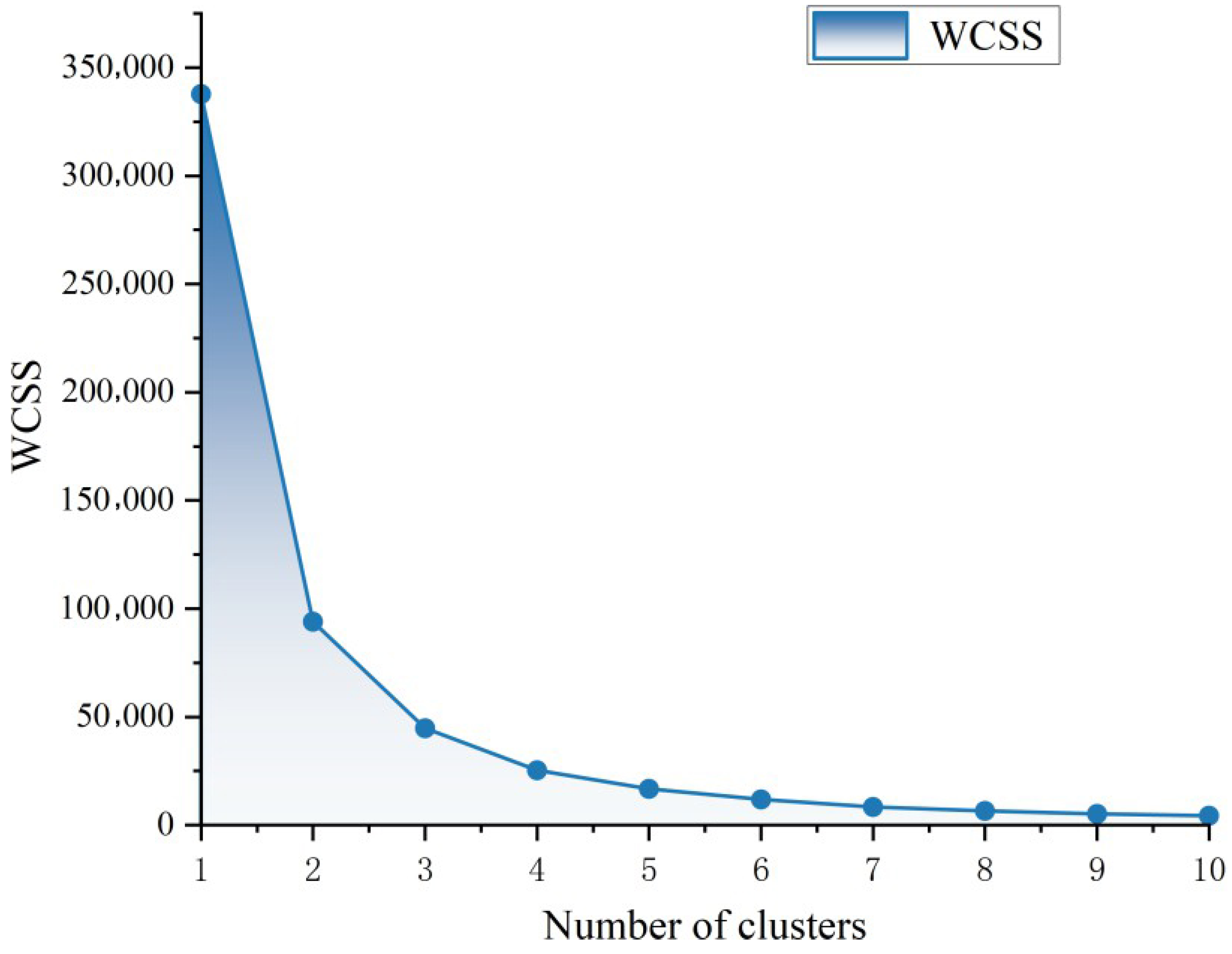
We employed the elbow method to determine the optimal K value. The elbow method identifies the most suitable number of clusters by observing the inflection point in the curve of Within-Cluster Sum of Squares (WCSS) values corresponding to different K values. This inflection point indicates the optimal cluster count. The calculation formula for WCSS is shown in Equation (1).

$$\mathrm{WCSS}=\sum _{i=1}^k\sum _{x\in C_i}{∥x-{\mu }_i∥}^2$$

(1)

where $C_i$ represents the i-th cluster, and ${\mu }_i$ denotes the centroid of the cluster. The comparative results of optimal cluster numbers determined by the elbow method are illustrated in Figure 2.

As shown in Figure 2, the WCSS decreases as the number of clusters (K) increases. When K increases from 1 to 3, the WCSS declines rapidly, indicating that adding more clusters significantly reduces within-cluster variance. However, from $K=4$ to $K=10$, the decreasing trend slows and eventually stabilizes. This suggests that the “elbow point” occurs around $K=3$, where the marginal benefit of adding more clusters begins to diminish. Therefore, we select $K=3$ as the optimal number of clusters. Combined with the pre-identified group of non-medal-winning countries, the 234 nations are ultimately classified into four distinct categories.

4.1.2. Cluster Results

The classification results for each country and their corresponding annotations on the maps are presented in Figure 3 and Figure 4. In Figure 4, the stars represent the cluster centroids of each group. $\alpha$1 represents established sports powerhouses, with a total of 35 countries, including the United States, the United Kingdom, etc. These countries have rich experience in participating in the Olympics and strong sports strength, and have accumulated a large number of medals. $\alpha$2 refers to countries of moderate strength, with a total of 50 countries, such as China, Belarus (BLR), etc. These countries have relatively fewer participations in the Olympics, but have achieved a substantial number of medals. $\alpha$3 is composed of 71 underdeveloped countries. These countries have participated in the Olympics many times, but generally have a low number of medals. $\alpha$4 includes 78 countries that have never won a medal. Countries within the same category exhibit similar characteristics in terms of the number of Olympic participations and the number of medals. To a certain extent, the medal prediction trends of a few representative countries in each group can reflect the trends of the remaining countries in that group.

4.2. Machine Learning Prediction (United States as an Example)

The United States, as an $\alpha$1 category country and also the host nation in 2028, will be used as an example to demonstrate our machine learning prediction process. The factors related to medals and number of medals is shown in

Table 1. U.S. Olympic key metrics.

Yr	N	W	M	Nu. W	T. E	T. D	T. S	G. R	S. R	B. R	Gold	Total
1896	27	0	27	20	43	10	11	0.00	0.00	0.00	11	20
1900	135	9	126	48	97	22	20	0.73	1.00	6.50	19	48
1904	1109	16	1093	231	95	18	16	3.00	4.57	4.13	76	231
1906	81	0	81	0	76	13	11	-	-	-	0	0
1908	219	0	219	47	110	25	22	1.00	1.00	1.00	23	47
1912	364	0	364	64	102	18	14	0.13	0.58	0.58	26	64
1920	473	22	451	95	156	29	22	0.58	0.42	0.42	41	95
1924	459	35	424	99	126	23	17	0.10	0.00	0.00	45	99
1928	426	54	372	56	109	20	14	−0.51	−0.33	−0.41	22	56
1932	743	124	619	110	117	20	14	1.00	1.00	0.88	44	110
1936	487	58	429	57	129	25	19	−0.45	−0.42	−0.60	24	57
1948	424	58	366	84	136	23	17	0.58	0.29	0.58	38	84
1952	451	99	352	76	149	23	17	0.05	−0.30	−0.11	40	76
1956	443	98	345	74	151	23	17	−0.20	0.32	0.00	32	74
1960	428	102	326	71	150	23	17	0.06	−0.16	−0.06	34	71
1964	492	136	356	90	163	25	19	0.06	0.24	0.75	36	90
1968	529	152	377	107	172	24	18	0.25	0.08	0.21	45	107
1972	578	155	423	94	195	28	21	−0.27	0.11	−0.12	33	94
1976	554	182	372	94	198	27	21	0.03	0.13	−0.17	34	94
1980	-	-	-	-	203	27	21	0.72	0.37	0.10	58.5	134
1984	693	256	437	174	221	29	21	0.42	0.27	0.09	83	174
1988	715	284	431	94	237	31	23	−0.57	−0.49	−0.10	36	94
1992	734	280	454	108	257	34	25	0.03	0.10	0.37	37	108
1996	839	361	478	101	271	37	25	0.19	−0.06	−0.32	44	101
2000	764	340	424	93	300	40	27	−0.16	−0.25	0.28	37	93
2004	726	340	386	101	301	40	27	−0.03	0.63	−0.19	36	101
2008	596	285	311	112	302	39	26	0.00	0.05	0.19	36	112
2012	530	269	261	104	302	39	26	0.00	−0.08	0.03	46	104
2016	719	369	350	121	306	42	28	−0.04	0.42	0.26	46	121
2020	856	456	400	113	339	50	33	−0.15	0.10	−0.13	39	113
2024	854	451	403	126	329	48	32	0.02	0.07	0.27	40	126

Note: N, W, M, Nu. W, T. E, T. D, T. S, G. R, S. R, and B. R represent number of participants, women, men, number of award winners, total events, total disciplines, total sports, gold medal growth rate, silver medal growth rate, and bronze medal growth rate, respectively.

.

4.2.1. Factor Analysis

To simplify the complexity of the Medal Predict XGBoost Model (MPXG) and enhance its effectiveness, we attempt to reduce the dimensionality of the ten main factors (Nu., W, M, Nu. W, T. E, T. D, T. S, G. R, S. R, and B. R) through factor analysis. The formula for the medal growth rate is defined as follows: (current year’s medal count − previous year’s medal count)/previous year’s medal count. The KMO and Bartlett tests are used to determine whether the data is suitable for factor analysis [29]. A KMO value greater than 0.6 indicates that the data is appropriate for factor analysis, while a KMO value less than 0.5 suggests that factor analysis should be abandoned. In the Bartlett test, if the p-value is less than 0.05, the null hypothesis is rejected, indicating that factor analysis can be performed. The KMO and Bartlett test results are shown in

Table 2. KMO test and Bartlett’s test results.

Test	Value
KMO Value	0.707
Bartlett’s test of sphericity p	<0.0001

.

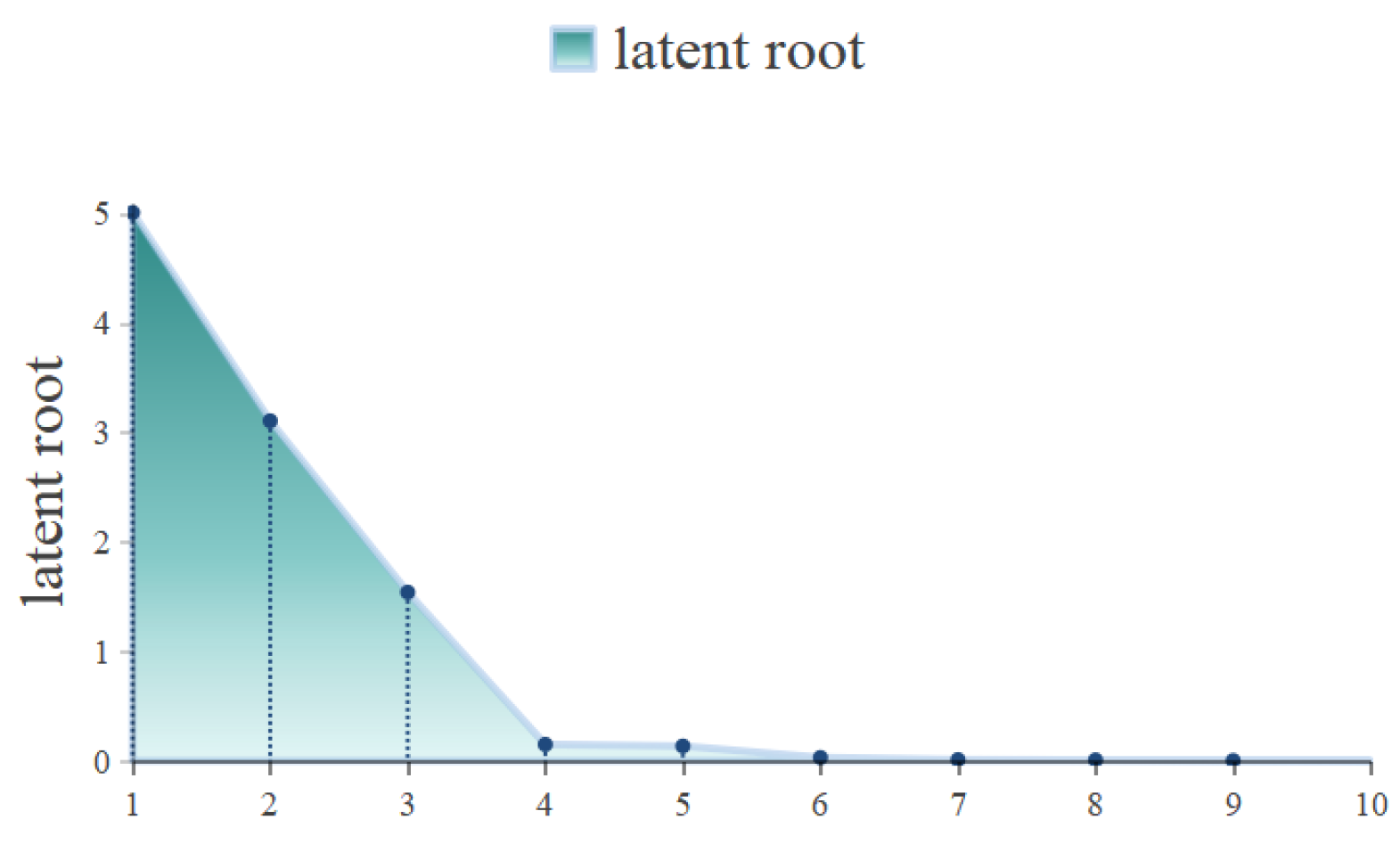
The results showed that the value of KMO was 0.707 (>0.6), while the Bartlett’s p-value was significantly less than 0.05, indicating that the use of factor analysis was effective. Next, we plotted the fragments of these 10 raw variables. Its function is to confirm the number of principal components of the factor to be selected based on the slope of the eigenvalue decline, as shown in Figure 5. It can be seen that the turning point of the fold line is before factor 4, so the number of principal components of the factor is determined to be three.

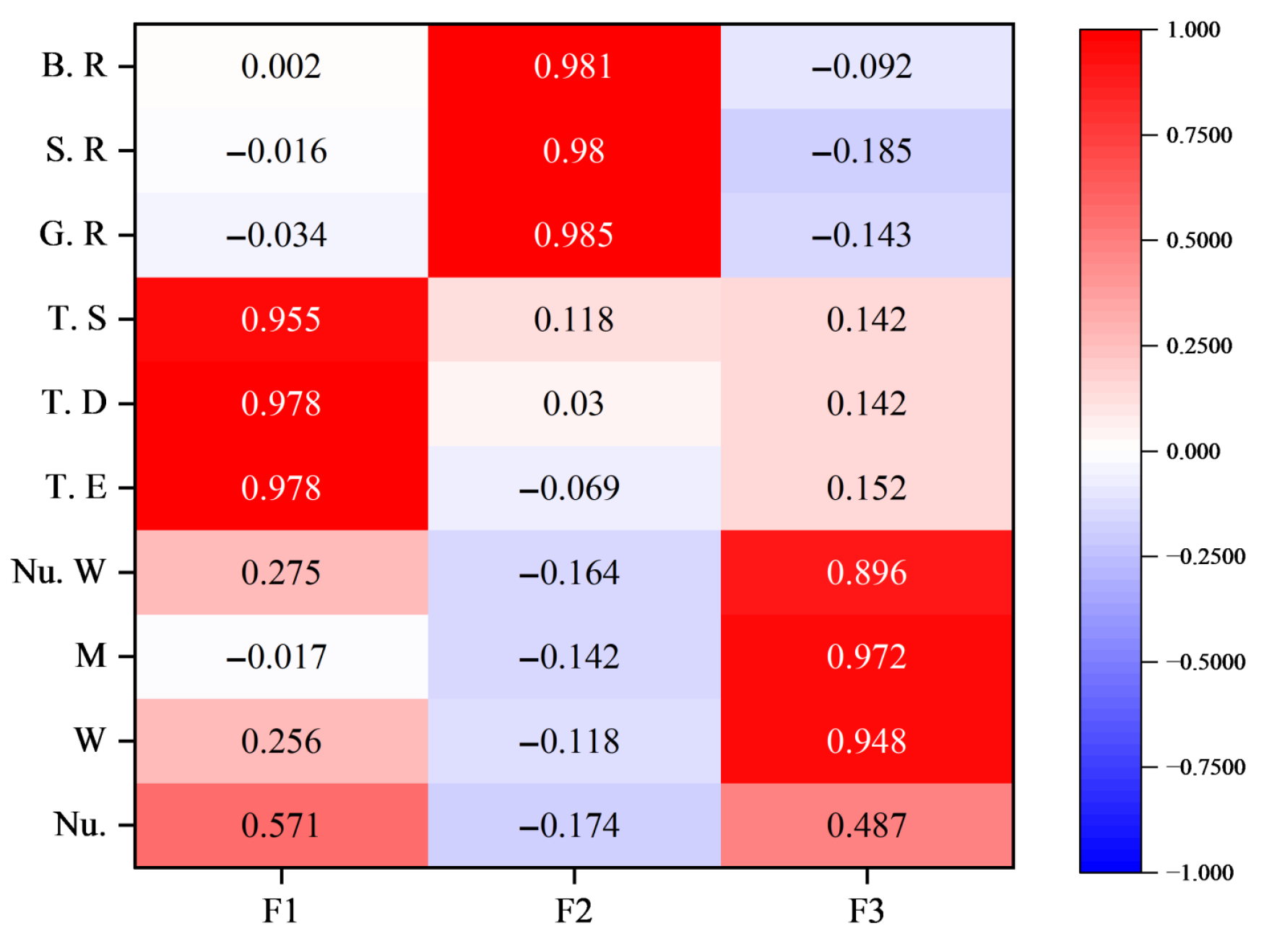
After determining the three main factors, we used the rotated factor loading coefficients to generate a heatmap of the factor loading matrix, visually illustrating the importance of principal component factors 1, 2, and 3 in relation to the original 10 variables before dimensionality reduction, as shown in Figure 6. To ensure consistent dimensions during calculation, the ten main factors are standardized. Factor 1, with positive coefficients near 1 for T. E, T. D, T. S, and Nu., shows a strong positive correlation with these variables and a low correlation with G. R, S. R, and B. R, thus defining it as the “Event scale factor”. Factor 2, highly correlated (approximately 1) with G. R, S. R, and B. R, is termed the “Medal trend factor” for its link to medal growth trends. Factor 3, with strong correlations to M, W, and Nu. W, is interpreted as the “Gender and award-winning capability factor”. The derived principal component calculation formulas are presented in Equation (2).

$$\left(\begin{array}{c}{F}_1\\ F_2\\ F_3\end{array}\right)=\left(\begin{array}{cccccccccc}0.70& -0.15& -0.80& -0.16& 0.29& 0.29& 0.28& -0.03& -0.01& -0.03\\ 0.09& -0.06& 0.17& 0.13& -0.04& -0.01& 0.03& 0.37& 0.36& 0.38\\ -0.62& 0.43& 1.26& 0.47& -0.14& -0.13& -0.10& 0.13& 0.09& 0.15\end{array}\right)\left(\begin{array}{c}\mathrm{Nu}.\\ \mathrm{W}\\ \mathrm{M}\\ \mathrm{Nu}.\mathrm{W}\\ \mathrm{T}.\mathrm{E}\\ \mathrm{T}.\mathrm{D}\\ \mathrm{T}.\mathrm{S}\\ \mathrm{G}.\mathrm{R}\\ \mathrm{S}.\mathrm{R}\\ \mathrm{B}.\mathrm{R}\end{array}\right)$$

(2)

4.2.2. ARIMA Model

For machine learning-based medal prediction at the 2028 Olympics, we use ARIMA to predict the unknown values of key factors (such as F1, F2, F3) [30,31]. The prediction process for factor Nu. serves as an example, with all other factors being predicted analogously.

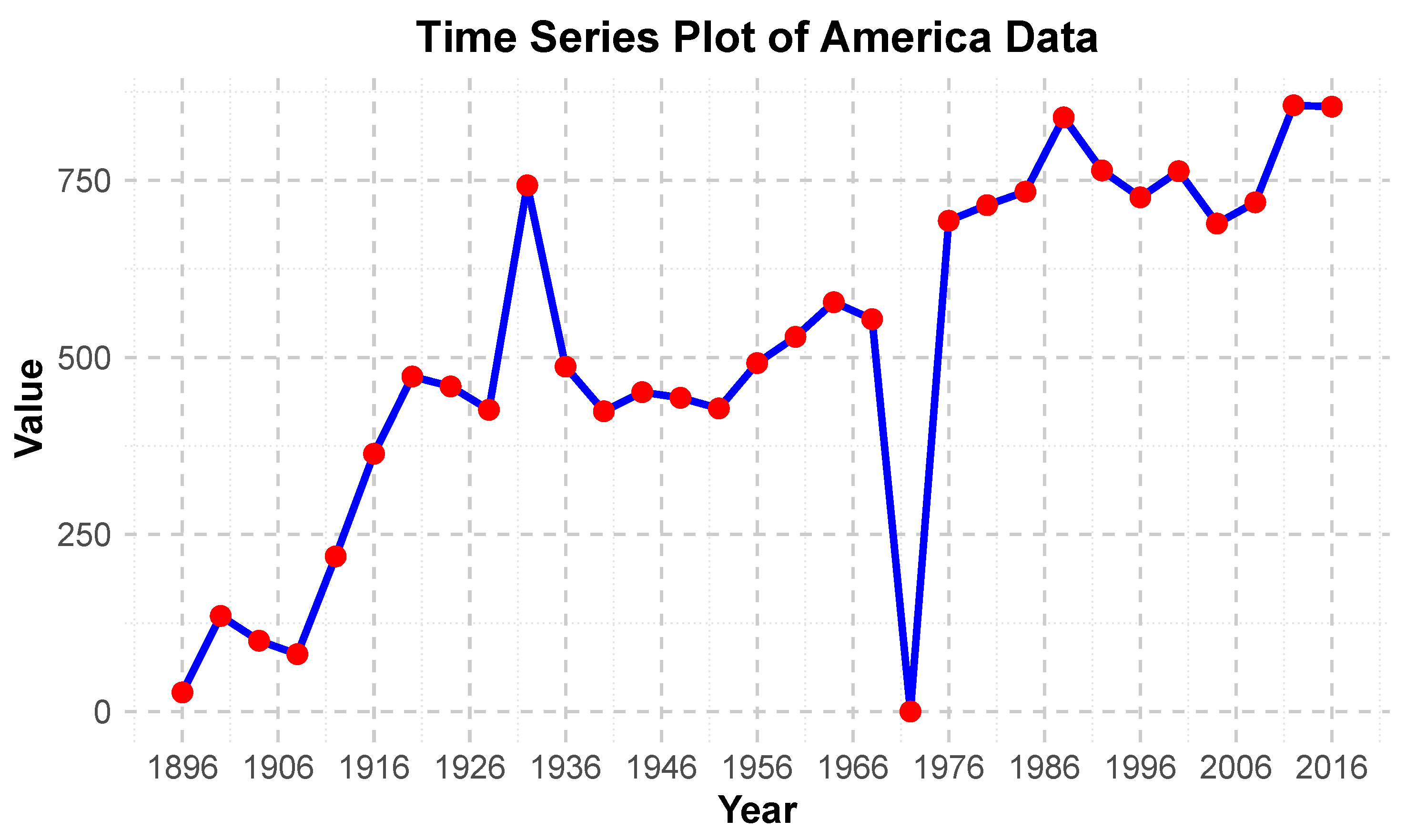
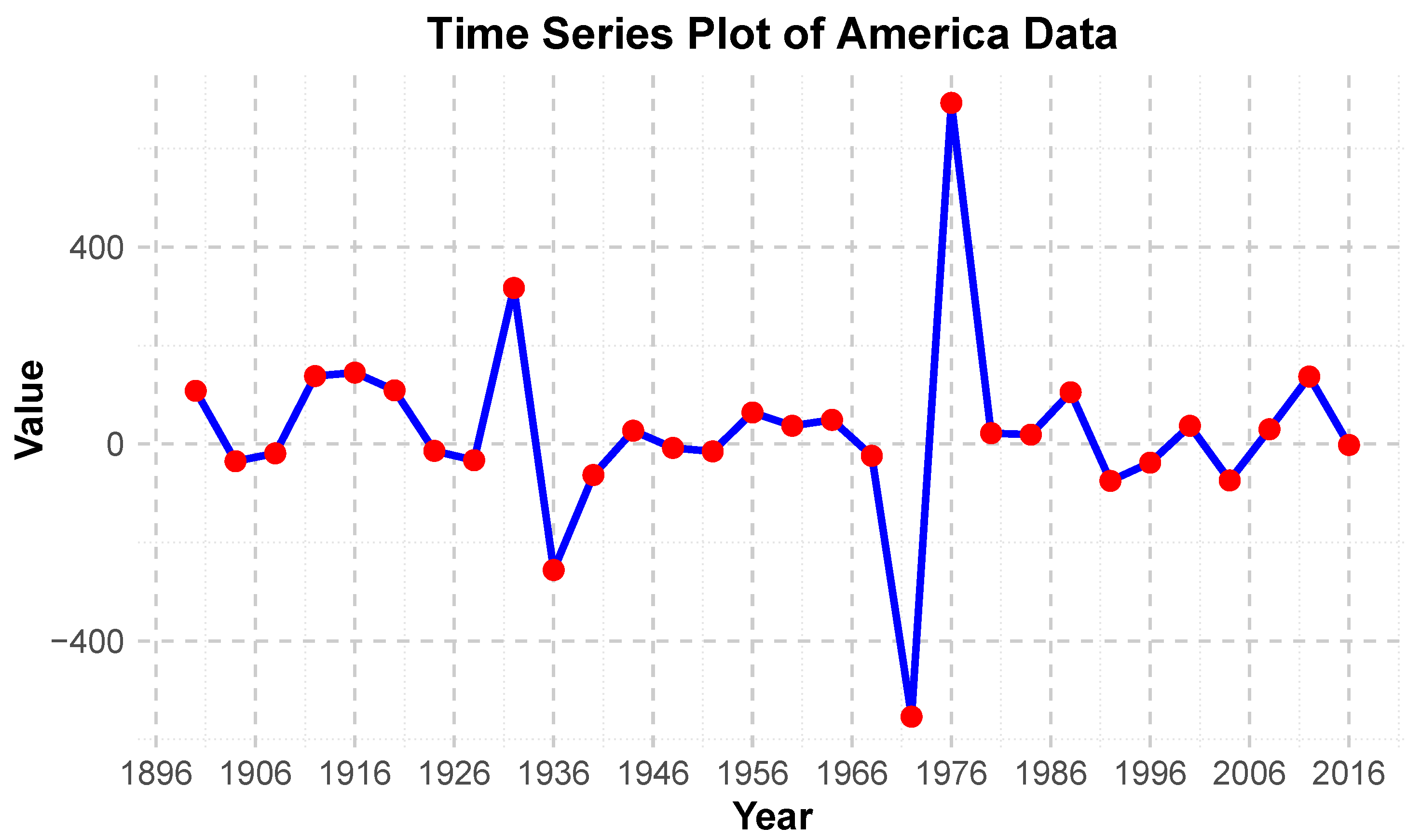
The ARIMA model requires stationary data for prediction. The stationarity of the data can be assessed through the characteristics of time series plots and autocorrelation plots, which indicate that the series exhibits non-stationary behavior, as shown in Figure 7 and Figure 8. Therefore, a first-order differencing was applied, resulting in a stationary series, as shown in Figure 9 and Figure 10. Subsequently, the randomness of the differenced series was tested using the Q-statistic. The resulting p-value was 0.043, which is less than 0.05, leading to the rejection of the null hypothesis that the series is white noise. This indicates that the Nu. series, after first-order differencing, exhibits significant autocorrelation, meeting the conditions for ARIMA modeling. The fitted model was determined to be ARIMA (3,1,2). Based on this model, the number of U.S. participants at the 2028 is forecasted to be 871. Furthermore, the predicted values for the principal component factors F1, F2, and F3 are 0.9539, 0.7999, and 0.2937, respectively.

4.2.3. The Best Machine Learning Model

Machine learning models each have their unique strengths: random forest (RF) excels at predicting nonlinear relationships in high-dimensional data, leveraging ensemble decision trees to reduce overfitting while enabling feature importance analysis [32]. Back propagation neural network (BPNN) demonstrates superior capability in modeling complex nonlinear patterns and large-scale data structures by automatically learning intrinsic data representations through deep architectures [33]. XGBoost shows outstanding performance in the precise modeling of structured data prediction tasks, achieving computational efficiency and strong generalization through its gradient boosting framework with regularization techniques [34]. SVM performs exceptionally well in classifying high-dimensional small sample data by employing kernel functions to address linearly inseparable problems [35]. This study compares the predictive performance of these four model types to identify the optimal solution for the target dataset.

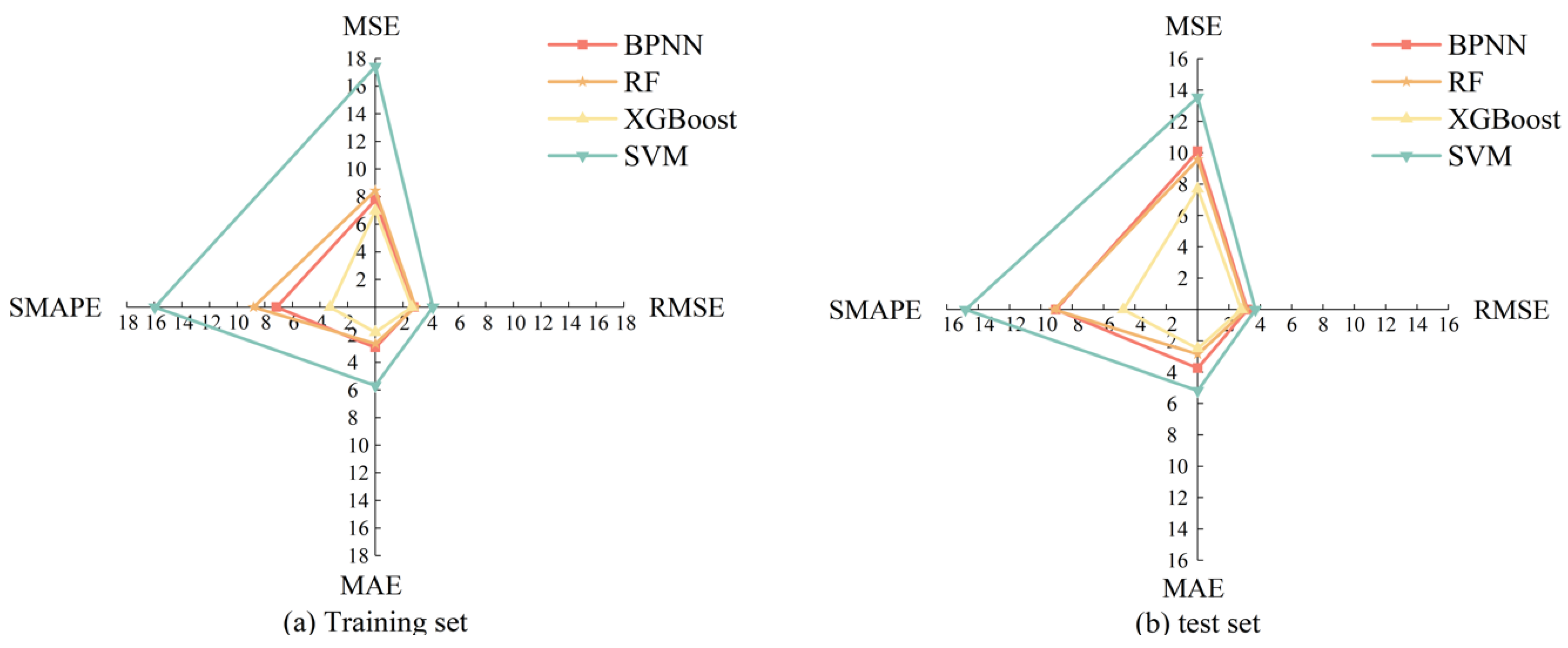
We select Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Symmetric Mean Absolute Percentage Error (SMAPE) as evaluation metrics. Among them, SMAPE, which measures relative error in percentage terms and is robust to scale variations, is particularly suitable for comparing prediction accuracy across countries with diverse medal counts. These metrics effectively assess the predictive performance of regression models by quantifying the error between predicted and actual values, as shown in Figure 11.

Observing Figure 11, the minimal performance discrepancies between training and test sets across all models indicate no overfitting occurred. Notably, XGBoost demonstrates the most balanced and superior performance, achieving the best metrics (MSE = 7.7, RMSE = 2.7, MAE = 2.4, SMAPE = 4.7 in the test set) with all absolute error indicators (MAE) and relative error indicators (SMAPE) significantly below 10. This robust performance confirms XGBoost’s reliability for predicting medal counts in the 2028 Olympic Games. FCNN and random forest show moderately good performance, though with slightly higher errors compared to XGBoost. In contrast, SVM exhibits the weakest predictive capability with substantially higher error values. In conclusion, XGBoost is identified as the optimal model for Olympic medal prediction due to its optimal accuracy and stability.

4.2.4. MPXG Model

Next, based on the trained XGBoost model, we predict the number of gold medals and total medals for the United States at the 2028 Olympic Games. Quantile regression is employed by training multiple XGBoost models to estimate the target value at different quantiles, thereby constructing a 90% confidence interval to assess the accuracy of the predictions [36]. The prediction results are presented in

Table 3. National medal prediction results.

Category	Country	Gold Medals	90% PI (Gold)	Total Medals	90% PI (Total)
${\alpha }_1$	USA	57.47	(41.31, 68.50)	135.4	(108.91, 140.23)
	Japan	20.82	(10.13, 24.70)	49.27	(38.35, 56.18)
	Italy	14.66	(9.94, 20.37)	40.19	(29.77, 47.20)
${\alpha }_2$	China	43.19	(25.1, 60.3)	97.56	(86.4, 123.6)
	Kenya	5.16	(3.05, 7.18)	13.82	(10.58, 15.05)
${\alpha }_3$	Qatar	0.618	(0.482, 1.017)	1.893	(1.211, 2.525)
	Kyrgyz.	0.111	(0.024, 0.219)	3.512	(2.158, 5.001)

. Following the previous process, we selected two representative countries from each of $\alpha$1, $\alpha$2, and $\alpha$3 to make predictions in order to obtain the medal-winning trends for each group (excluding the host country effect), as shown in

Table 4. The 2020, 2024, and 2028 national medal results.

Category	Country	Gold Medals			Total Medals
		2020	2024	2028	2020	2024	2028
${\alpha }_1$	American	39	40	57.57	113	126	135.4
	Japan	27	20	20.82	58	45	49.27
	Italy	10	12	13.66	40	40	40.19
${\alpha }_2$	China	38	40	43.19	89	91	97.56
	Kenya	4	4	5.16	10	11	13.82
${\alpha }_3$	Qatar	2	0	0.618	3	1	1.893
	Kyrgyzstan	0	0	0.114	3	3	3.512

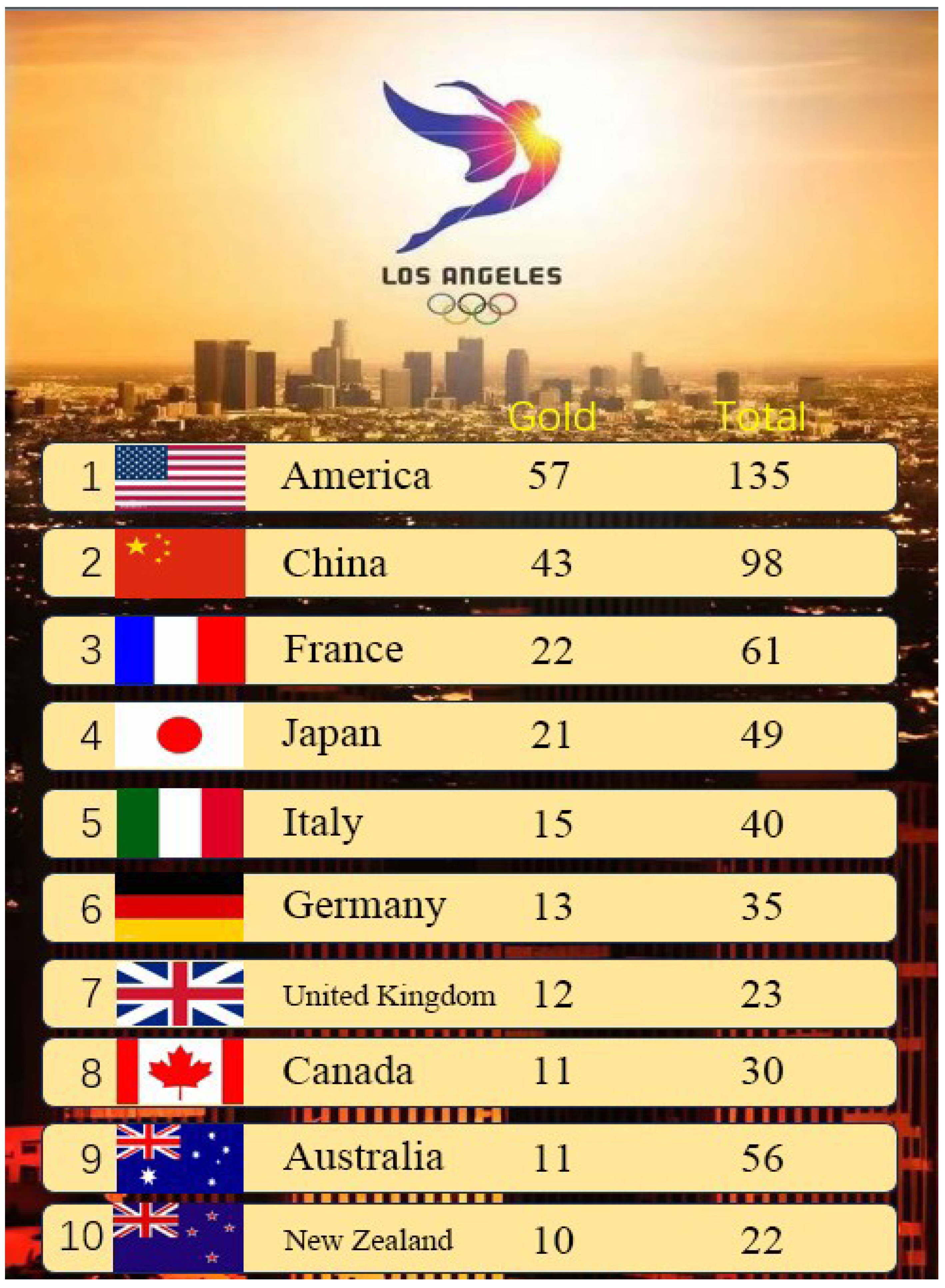
. Additionally, we predict the medal table for the 2028 Olympics, as shown in Figure 12.

By examining Table 3, we observe that the predicted results fall within the 90% prediction interval, indicating a high level of accuracy in our model. Analyzing the U.S. data, we find that the projected number of gold medals for 2028 (57.47) is significantly higher than the previous two Olympics (39 in 2024 and 40 in 2020), and the total medal count (135) substantially surpasses those of the prior two games (113 in 2024 and 126 in 2020). This suggests that, as a sports powerhouse, the U.S. benefits greatly from home-field advantages (e.g., familiar venues and climate, logistical convenience, dominance in favored events, and enthusiastic support from local audiences). These factors enable the U.S. to significantly increase its medal haul, particularly in gold medals, while maintaining stable overall strength. Table 4 presents the medal performance of representative countries in recent Olympics. It can be observed that Group $\alpha$1 countries generally exhibit a stable trend, with very slight fluctuations compared to the previous two Olympic Games. This indicates that, as traditional Olympic powerhouses, these countries have consistent athlete quality and national investment, and their medal outcomes may depend more on individual athlete performance, competition venues, and whether their strong events are included—objective factors inherent to the Olympics. Countries in Group $\alpha$2 show an upward trend in both gold and total medals. As emerging Olympic nations with strong athletic capabilities but limited Olympic experience, their increasing participation in the games leads to a growing number of medals. Group $\alpha$3 countries, with fewer medals overall despite rich Olympic experience, rely on elite athletes in specific events to win medals. Their success hinges on athletes’ performance and whether their strong events are included in the games. Group $\alpha$4 countries, which have never won a medal, will be analyzed using a different model to predict whether they can secure their first medal in 2028.

5. First Medal Prediction Model (FMPM)

Group ${\alpha }_4$ comprises 78 countries that have never won an Olympic medal, with 37% of them having participated fewer than 10 times. Analyzing medal-winning countries’ journeys—like Peru, which broke its 48-year medal drought at the 1948 Olympics after increased participation—reveals key patterns. We aim to model the relationship between a country’s Olympic participations, athlete numbers, and medal success to predict potential breakthroughs in the 2028 Games.

5.1. Partitioning of Datasets

We extract the key features from all national participation records (3123 entries in total), including the number of participants, each country’s total participations, the year of participation, and the medal-winning outcome (0 or 1). To ensure consistency in category distribution, we employ stratified sampling to divide the datasets into training (2498 records) and testing (625 records) sets at an 8:2 ratio. During this partitioning process, we ensure data integrity by ensuring records from the same country were not split across both sets, thereby preserving the independence of the test set.

5.2. Construction of the Neural Network Model

A neural network is a computational model inspired by biological nervous systems, which is widely used in machine learning tasks such as pattern recognition, classification, and regression [9,10]. It has a powerful nonlinear modeling ability and performs excellently in prediction tasks, such as financial market prediction and medical diagnosis.

In this study, a three-layer fully connected neural network is employed to predict the probability of winning Olympic medals [37]. Features are utilized to capture the complex relationships between these factors and the medal-winning results. The implementation is carried out using the TensorFlow framework, and the pseudo-code is as follows:

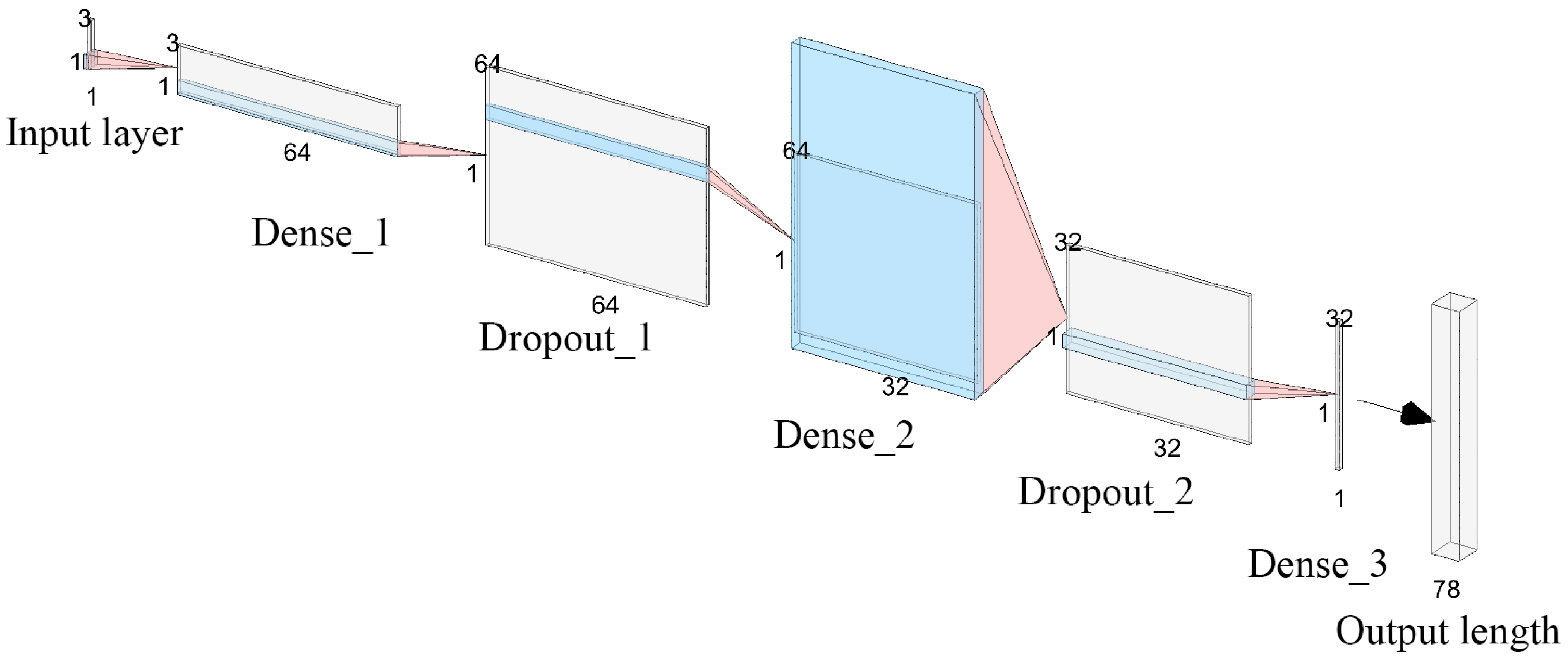
Algorithm 1 describes the process of constructing and training a three-layer fully connected neural network to predict the probability of winning Olympic medals. The visualization result of the structure is shown in Figure 13. Lines 1–14 define the model structure, which consists of layers with 64, 32, and 1 neuron, respectively. The ReLU and Sigmoid activation functions are used, and Dropout (with a dropout rate of 0.2) is introduced to prevent overfitting. Lines 15–18 configure the model, using the Adam optimizer and binary cross-entropy loss. Lines 19–29 outline the training process, which iterates for 50 epochs with a batch size of 32. The parameters are updated through back propagation, and the validation metrics are tracked. This algorithm effectively learns the relationship between the features and the medal results.

Algorithm 1: Fully connected neural network (FCNN) training.

5.3. Results of Performance Evaluation

The comprehensive performance and confusion matrix of the model on the independent test set (a total of 688 records) are shown in

Table 5. Model evaluation results.

Class	Precision	Recall	F1-Score	Support
0 (No Award)	0.85	0.90	0.88	352
1 (Awarded)	0.86	0.80	0.83	236

and

Table 6. Confusion matrix.

	Predicted 0	Predicted 1
Actual 0	352	40
Actual 1	60	236

.

Table 5 shows the classification performance indicators of the model on the test set, and the confusion matrix is presented in Table 6. For the non-medal-winning category (0), the model has a precision of 0.85, a recall of 0.90, and an F1-score of 0.88, indicating that the model can effectively identify non-medal-winning samples with a low false-positive rate (40/432). For the medal-winning category (1), the precision is 0.86, the recall is 0.80, and the F1-score is 0.83, suggesting that the model is a bit conservative in predicting medal-winning samples and has a relatively high false-negative rate (60/296).

The confusion matrix further reveals that the model correctly predicted 352 non-medal-winning samples and 236 medal-winning samples, but there were some misclassifications: 40 non-medal-winning samples were misjudged as medal-winning, and 60 medal-winning samples were misjudged as non-medal-winning. It is possible that due to the class imbalance in the dataset, the model performs better on the non-medal-winning category than on the medal-winning category. However, overall, the model is accurate and can be used to predict which countries will win medals for the first time in the 2028 Olympics.

5.4. Prediction Application and Conclusion

The trained neural network model is deployed in the medal prediction process for the 2028 Olympics, based on the prediction data of 78 countries that have never won a medal. The ARIMA model is used to generate the prediction of the number of participants. For countries with a cumulative number of participations of less than three, the number of participants is set to the value of their most recent Olympic Games by default. The prediction results are shown in Figure 14.

According to Figure 14, among the 78 countries that have never won a medal, only two countries (UAR and MLI) have a medal-winning probability of over 50% in the 2028 Olympics, which are 77.47% for UAR and 58.47% for MLI, respectively. Specifically, UAR is expected to send 26 athletes, with the country having a total of 3 participations; MLI is expected to send 25 athletes, with the country’s having a total of 14 participations. The relatively high medal-winning probabilities of these two countries may be related to their stable number of participants and gradually increasing participation experience.

In addition, six countries have a medal-winning probability of over 30%, including Guatemala (48.50%) and Senegal (45.70%), showing a certain potential to win medals. However, more than 85% of the countries have a medal-winning probability of less than 40%. Among them, the countries with the lowest probabilities (UHN and UNK, approximately 3.16%) plan to send only one athlete or not participate at all, which reflects the limitations of the insufficient participation scale and experience on the possibility of winning medals.

6. Special Effects Affecting Medal Outcomes

Apart from the direct influencing factors (Nu., W, M, Nu. W, T. E, T. D, T. S, G. R, S. R, and B. R), we also identify several interesting secondary effects that similarly impact award outcomes.

6.1. Host Effect

We observe that most host countries achieve better results. For example, China won 100 medals at the 29th Beijing Olympics, compared to only 63 medals at the 28th Olympic Games. The host effect positively influences athlete performance to varying degrees. Studies have shown that home athletes exhibit higher levels of testosterone and cortisol compared to non-home athletes [38]. Additionally, factors such as familiar venues, convenient transportation, enthusiastic home crowds, and the inclusion of favorable events contribute to better athlete conditions and an increased likelihood of winning medals.

We establish a model to validate the existence of the host effect and to quantify its impact on medal achievements. The medal performances of all host countries are scored accordingly, as shown in

Table 7. Scoring sheet of the host countries.

NOC	Year	Gold	Silver	Bronze	Total	Total Score (S)
Greece	1896	10	18	19	47	536
France	1900	27	39	37	103	1189
United States	1904	76	78	77	231	2694
United Kingdom	1908	56	51	39	146	1730
Sweden	1912	23	25	17	65	769
Belgium	1920	14	11	11	36	424
France	1924	13	15	10	38	449
Netherlands	1928	6	9	4	19	226
United States	1932	44	36	30	110	1304
Germany	1932	5	12	7	24	279
United Kingdom	1948	3	14	6	23	267
Finland	1952	6	3	13	22	244
Australia	1956	13	8	14	35	405
Italy	1960	13	10	13	36	419
Japan	1964	16	5	8	29	348
Mexico	1968	3	3	3	9	105
West Germany	1972	13	11	16	40	461
Canada	1976	0	5	6	11	120
Soviet Union	1980	80	69	46	195	2328
United States	1984	83	61	30	174	2111
South Korea	1988	12	10	11	33	386
Spain	1992	13	7	2	22	273
United States	1996	44	32	25	101	1206
Australia	2000	16	25	17	58	678
Greece	2004	6	6	4	16	190
China	2008	48	22	30	100	1188
Switzerland	2012	2	2	0	4	50
Brazil	2016	7	6	6	19	223
Japan	2020	27	14	17	58	689
France	2024	16	26	22	64	740

. It is widely accepted in the academic community that gold, silver, and bronze medals can be assigned scores of 13, 12, and 10 points, respectively.

Additionally, we assign scores to the host countries’ medal performances in the two editions before and after hosting, and formulate an equation to calculate the Host Effect Coefficient (AS), which reflects the relative increase or decrease in scores during the hosting year compared to the average scores of non-hosting years, as shown in Equation (3).

$$AS={\displaystyle \frac{{\overline{S}}_{\mathrm{host}}-{\overline{S}}_{\mathrm{non}-\mathrm{host}}}{{\overline{S}}_{\mathrm{non}-\mathrm{host}}}}$$

(3)

where ${\overline{S}}_{\mathrm{host}}$ represents the total score of the host country in the Olympic year it hosts, and ${\overline{S}}_{\mathrm{non}-\mathrm{host}}$ represents the average total score of the host country in non-host Olympic years, as shown in Equation (4).

$${\overline{S}}_{\mathrm{non}-\mathrm{host}}={\displaystyle \frac{{\sum }_{i\in \mathrm{non}-\mathrm{host}\mathrm{years}}{S}_i}{N}}$$

(4)

Here, $S_i$ represents the total score of the host country in the i-th year. N represents the number of non-host years. We correct the host advantage effect to ensure that the host country has a higher probability of winning medals in the host year compared to non-host years. Specifically, we set the probability of winning to the average level during the host year; we make the probability of winning lower than the average level during favorable years; and we characterize the probability of winning by the average level during zero years.

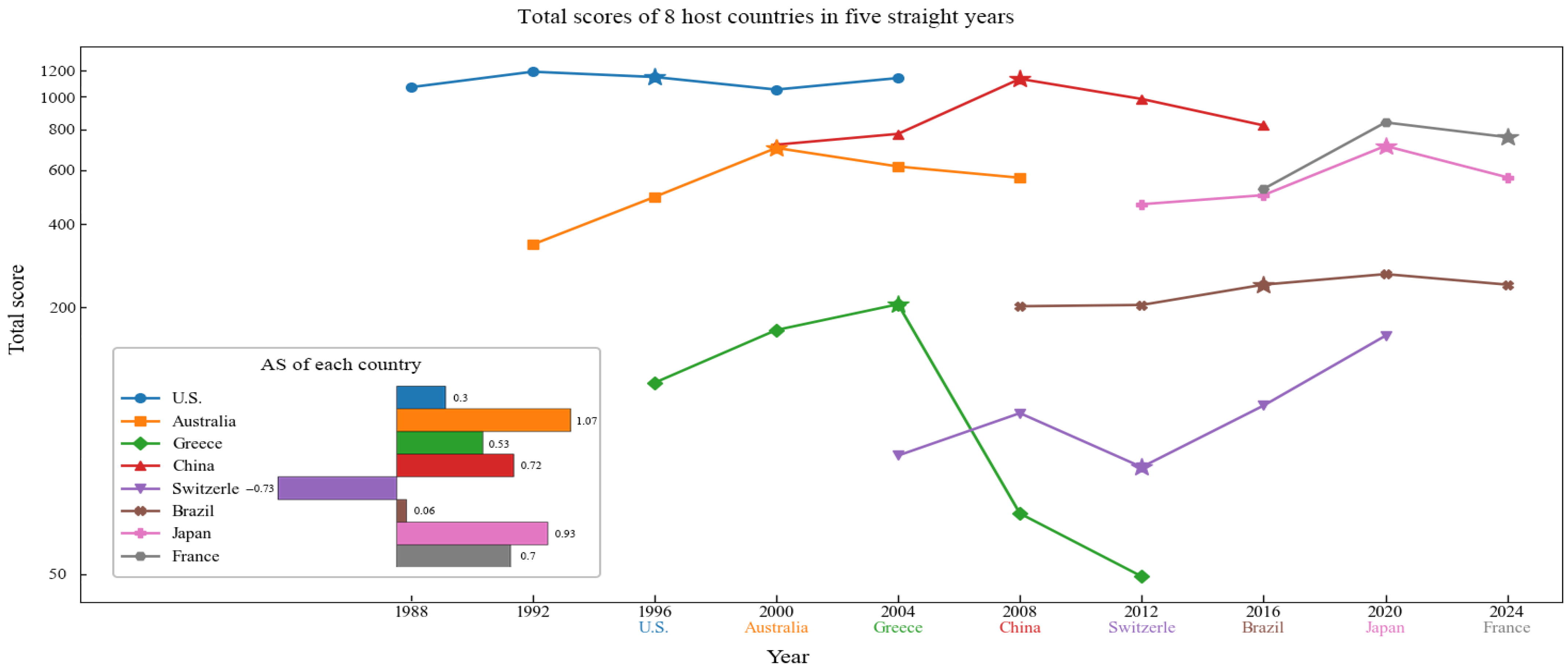
We compile the medal score coefficients for all countries hosting the Olympics from 1896 to 2024. Due to significant differences between early Olympics and modern ones in terms of event scale, number of participating countries, and international political contexts, we select data from only the last eight Olympic Games to more accurately reflect the current host effect, as shown in

Table 8. Host country scores and average total scores.

Year	Host Country	Host Score	Avg. Total Score	AS
1996	United States	1206	930.38	0.30
2000	Australia	678	327.63	1.07
2004	Greece	190	123.86	0.53
2008	China	1188	691.60	0.72
2012	United Kingdom	65	241.56	$-0.73$
2016	Brazil	223	210.50	0.06
2020	Japan	689	356.43	0.93
2024	France	740	435.00	0.70

and Figure 15. The statistical analysis of the medal score coefficients for host countries in these Olympic Games shows that, over the past 30 years, the host nation’s medal score increases by an average of approximately 74% during the Olympics they host.

6.2. Great Coach Effect

The Olympic Games have given birth to many legendary athletes, and behind them there are often excellent coaches who can significantly improve a country’s medal performance in specific events. For example, the performance of the Chinese men’s epee fencer Lei Sheng fluctuated significantly during the 2008–2016 Olympic Games. After Coach Wang Haibin took charge of the Chinese epee fencing program in 2010, Lei Sheng won the first individual gold medal in men’s epee fencing for China at the 2012 Olympics, achieving a historic breakthrough. However, Wang Haibin’s departure in 2013 directly led to Lei Sheng not winning a medal at the 2016 Olympics. Similarly, the coach of the Chinese women’s volleyball team, Lang Ping, with her outstanding guidance, led the team to win the gold medal at the 2016 Olympics, ending a 12-year championship drought.

6.2.1. Great Coach in Fencing

Italy, China, and South Korea are established countries in the fencing event. Among them, Italy and China introduced great coaches in 2004 and 2012, respectively, which led to an increase in medal scores [39]. We have summarized their medal-winning situations and participation data in the fencing event for some years, as shown in

Table 9. Analysis of AWP and coaching effect by country.

Country	Year	AWP	Nu	C.E	Type (${\mathit{s}}_{\mathit{k}}$)
Italy	2000	5.31	29	0	0.4
	2004	7.22	18	1	0.4
	2008	6.64	25	0.5	0.4
	2016	0	5	0	0.4
Korea	2020	0	16	0	0.4
	2024	0.42	24	0	0.4
	2008	1.8	32	0.25	0.2
	2012	2.6	25	0.5	0.2
China	2020	0.54	24	0	0.2
	2024	0	24	0	0.2

.

Italy introduced an excellent coach for the 2004 Olympics, leading to a 30% decrease in participants. Despite the decreased participants, the average score increased by nearly two points compared to the previous Olympics, equivalent to each athlete winning an average of an additional one-fifth of a bronze medal. The average score in the 2008 Olympics was also 1.33 points higher than that before the coach was hired. Thus, the influence of a great coach is evident. Next, we will estimate and predict the scoring results of China (as a gold medal contender) and South Korea (which participates frequently but has mediocre performance) after investing in excellent coaches.

6.2.2. Model Building

We innovatively propose Athlete’s Weighted Points (AWP) as an evaluation indicator, which is shown in Equation (5). It can comprehensively reflect the overall level of athletes in a certain sport and demonstrate the influence of the great coach effect.

$$\mathrm{AWP}={\displaystyle \frac{(\mathrm{Gold}\times 13)+(\mathrm{Silver}\times 11)+(\mathrm{Bronze}\times 10)}{\mathrm{Nu}}}$$

(5)

Since there are many events in a class of disciplines and a single coach has limited ability, we quantify the coach effect (C.E) who coach a single event and those who have the ability to coach multiple events as 0.5 and 1, respectively, as shown in

Table 10. Coaching effect data.

Coach Effect	Single Event	Multiple Events
Current	1.00	0.50
Next	0.50	0.25

. For example, at the Beijing games in 2008, Wang Haibin was a great coach but only specialized in the men’s foil event in fencing.

Since he could not coach other events, his impact was limited to improving medals in foil, not in other disciplines. Furthermore, the great coaching effect may have a delayed impact influence. For example, Lang Ping began coaching the U.S. women’s volleyball team in 2006, leading them to consistent medal success. Her great coaching impact continues to influence the team’s performance to some extent even today.

In addition, we also introduce the national category factor $s_k$ according to the classification results of K-means, and the scoring result is shown in Equation (6).

$$s_k=\left\{\begin{array}{cc}0.4,\hfill & \mathrm{if}k=1,\mathrm{class}{\alpha }_1\hfill \\ 0.2,\hfill & \mathrm{if}k=2,\mathrm{class}{\alpha }_2\hfill \\ 0.1,\hfill & \mathrm{if}k=3,\mathrm{class}{\alpha }_3\hfill \end{array}\right.$$

(6)

Given that the dataset is relatively small (with only eight groups of observations), we employ Bayesian linear regression. By utilizing the prior distribution to enhance parameter estimation, it outperforms traditional linear regression in scenarios with small samples. The model incorporates an error term $ϵ\sim N(0,{\sigma }^2)$ to improve the prediction accuracy. After fitting the model, the resulting formula is shown in Equation (7).

$$y=-0.5+0.099\times Nu.+4.022\times C.E+0.45\times S_k+ϵ$$

(7)

The model uses the default prior. To verify the robustness of the model, we calculate the Variance Inflation Factor (VIF), and the results are all less than 10, indicating that there is no significant multicollinearity. The analysis of the posterior distribution shows that the coefficient of the great coach effect is 4.022, the standard deviation is 0.921, and the 95% credible interval is significantly non-zero, highlighting its significant contribution to the AWP.

6.2.3. Prediction in 2028

In order to predict the fencing performance of China and South Korea after introducing excellent coaches in 2028, ARIMA is used to predict the Nu. in 2028. Then, the predicted Nu, C.E (1 or 0.5), and $s_k$ is substituted into Equation (7) to obtain the prediction result table, as shown in

Table 11. 2028 Olympic projections.

Country	Year	Nu.	C.E	Type (${\mathit{s}}_{\mathit{k}}$)	Projection
Korea	2028	25	1.0	0.4	4.997
Korea	2028	25	0.5	0.4	2.986
China	2028	27	1.0	0.2	5.115
China	2028	27	0.5	0.2	3.104

.

By observing Table 11 it is shown that if China and South Korea hire top coaches to provide comprehensive guidance for the fencing program in 2028, as traditional participating countries in the fencing event, the AWP are expected to increase from 4 to 6. That is to say, on average, each athlete can win half a bronze medal more. If focusing on specific events (such as the Chinese men’s epee fencing and the South Korean men’s sabre fencing), the coaches can still increase the AWP to 2 to 4, which means that on average, each athlete can win one-fourth of a bronze medal more.

7. Results

7.1. Data Collection

This study compiles a comprehensive dataset encompassing 33 editions of Olympic Games data from 1896 to 2024, 3 of which were canceled due to global conflicts. The dataset includes critical variables such as the number of participating countries, distributions of gold, silver, bronze, and total medal counts, as well as detailed records of events, disciplines, and sports featured in each Olympic edition. Additionally, participation records for 252,565 athletes were collected, capturing attributes such as athlete names, gender, nationality, year of participation, host city, events, and medal outcomes. These data were sourced from official Olympic records and verified through cross-referencing with international sports databases to ensure accuracy and reliability.

7.2. Data Cleaning and Standardization

To ensure the integrity of the dataset, a rigorous data preprocessing pipeline was implemented:

• Missing Data Handling: Missing entries, particularly in early Olympic records (before 1920), were addressed using imputation techniques based on historical trends or exclusion where imputation was infeasible. For instance, incomplete athlete participation records were supplemented with average participation rates for the respective country and era.
• Data Merging for Temporarily Divided Nations: Political divisions, such as those of East and West Germany (1949–1990), required merging medal counts and participation records to treat them as a single entity (Germany) for consistent analysis. Similar unifications were applied to other temporarily divided nations, such as the Soviet Union and its successor states, ensuring continuity in longitudinal trends.
• Outlier Detection and Correction: Outliers, such as anomalous medal counts due to boycotts (e.g., the 1980 and 1984 Olympics), were identified using statistical methods (e.g., Z-scores) and adjusted by referencing alternative data sources or contextual historical context to prevent skewing model predictions.
• Standardization of Variables: All numerical variables, including participation counts and medal growth rates, were standardized to a common scale (mean = 0, standard deviation = 1) to facilitate factor analysis and machine learning model training. Categorical variables, such as event types, were encoded using one-hot encoding to ensure compatibility with the K-means clustering and neural network models.

7.3. Assumptions

To facilitate analysis and ensure the applicability of the prediction model, this study proposes the following assumptions:

• Continuity of Historical Trends: We assume that the patterns observed in Olympic medal distributions and athlete performance from 1896 to 2024 will continue through 2028. This assumption is supported by the consistent evolution of Olympic performance, driven by macro-level factors such as advancements in training methodologies, sports science, and global competition dynamics. For instance, the steady increase in medal counts for emerging nations (e.g., China’s rise since 1984) suggests a predictable trajectory that can be modeled using historical data. However, this assumption acknowledges potential variations due to minor rule changes or the inclusion of new events, which are accounted for in the ARIMA model’s forecasting of principal components.
• Consistency in National Sports Investment: We assume that countries will maintain their levels of investment in sports infrastructure, athlete training, and talent development over the decade leading up to 2028. This assumption is critical for non-medal-winning nations (Group ${\alpha }_4$), where significant policy shifts could disrupt predictive accuracy. Historical data supports this assumption, as most countries exhibit stable sports funding patterns unless influenced by major economic or political upheavals, which are not anticipated based on current global trends. For example, nations like Kenya have shown consistent investment in athletics, leading to predictable medal outcomes.
• Controllability of External Factors: The model assumes that the 2028 Los Angeles Olympics will proceed without significant disruptions, such as wars, pandemics, or major rule changes, which could alter event structures or participation. This assumption is necessary to ensure that predictions are based on a stable operational environment, consistent with the majority of Olympic Games in history since 1896. Historical disruptions (e.g., the cancellations of the 1916, 1940, and 1944 Games) are rare, and recent global stability supports the feasibility of this assumption. The model incorporates robustness checks, such as sensitivity analyses, to mitigate the impact of minor unforeseen events.
• Historical Data Sufficiency and Exclusion of Unknown Athletes: We assume that historical Olympic data from 1896 to 2024 is sufficient to predict the medal performance of countries in 2028, and that the impact of unknown (i.e., emerging) athletes on national medal tallies is negligible. Given the study’s focus on the overall performance of 234 countries, the models (MPXG and FMPM) rely on systemic factors such as participation trends, medal growth rates, and national investment, which are comprehensively captured in historical data. Although exceptional individual performances (e.g., Usain Bolt’s emergence in 2008) can have a significant impact in rare cases, these occurrences are statistically infrequent and lack predictive precursors in existing datasets, and are thus excluded from the model to maintain focus on systemic factors. Including such unpredictable events would introduce noise and reduce the model’s generalizability.
• Stability of Data Quality: We assume that the quality and structure of Olympic data available for 2028 will be consistent with historical datasets (1896–2024). This includes the accuracy of participation records, medal counts, and event categorizations, as well as the availability of comparable input metrics for model inputs. This assumption is supported by the International Olympic Committee’s standardized data collection practices, which have improved significantly since the mid-20th century. Any minor inconsistencies in future data are expected to be addressed through preprocessing techniques similar to those applied in this study, ensuring model reliability.

7.4. Findings

This study yields several key findings through multiple predictive models and analytical frameworks. In the MPXG model, the Olympic medal prediction system based on the XGBoost algorithm demonstrates optimal performance, forecasting that the United States will win 57 gold medals and 135 total medals at the 2028 Olympics. The analysis reveals significant variations among different national groupings: ${\alpha }_1$ countries exhibit stable performance but are notably affected by host nation effects, ${\alpha }_2$ countries show an upward trend, while the performance of ${\alpha }_3$ countries heavily depends on athletes’ competitive form and whether their dominant events are included in that Olympic Games.

The FMPM model, which adopts an FCNN architecture, achieves an accuracy of 85.5% in predicting medal potential for traditionally non-medal-winning nations (${\alpha }_4$ group). Notably, the United Arab Republic (UAR) has a 77.47% probability of podium success, while Mali (MLI) stands at 58.47%. Additionally, four other ${\alpha }_4$ countries exceed the 30% probability threshold for winning medals.

A significant quantitative finding regarding the Host Effect Coefficient (AS) is presented in Equations (3) and (4). Historical data analysis indicates that, over the past three decades, host nations have experienced an average increase of approximately 74% in medal performance during their hosted Olympics.

The Bayesian linear regression model for coaching effects introduces the Athlete Weighted Points (AWP) metric to quantitatively assess coaches’ influence on athletes’ medal potential. The AWP calculation incorporates coefficients based on coaches’ employment status and specialization (C.E. = 0.25, 0.5, or 1) as well as national grouping factors ($s_k$ = 0.4, 0.2, or 0.1), as detailed in Equation (6). The model results show that hiring top-tier coaches for comprehensive guidance can elevate AWP scores to reach 4–6 points, while specialized training for specific events can still raise AWP to 2–4 points. Together, these findings establish a robust quantitative analytical framework, providing critical insights into the dynamics of Olympic performance across different national contexts and systemic factors.

8. Discussion

In early Olympic medal count forecasting studies, researchers first adopted economic production models. In 2004, Bernard employed a Cobb–Douglas function, using national population and GDP to predict each country’s medal tally [3]. Subsequently, time series approaches emerged. In 2007, Lin Yinping applied ARIMA to China’s medal count trajectory but found that linear models were insensitive to nonlinear dynamics [22]. In 2008, Wu Dianting’s team quantified home-field advantage ($C=0.298$) and population effects within a regression framework [23]. In 2010, Li Kun and in 2012, Huang Changmei introduced gray relational analysis and gray forecasting models, respectively, into analyses of specific sports and athletics events [24,26]. In 2011, Wang Guofan combined genetic algorithms with regression to enhance model adaptability [25]. More recently, Schlembach et al. (2022) showed that random forests not only improved predictive accuracy but also, via feature-importance rankings, illuminated the socioeconomic drivers of Olympic success [28]. Despite these advances, traditional single-model methods still face limitations in handling model complexity, heterogeneous data sources, and “first-medal” predictions for historically non-medal-winning nations.

This study achieves significant breakthroughs on both methodological and theoretical levels. First, we innovatively integrate K-means clustering with a three-layer fully connected neural network (FMPM), enabling, for the first time, probabilistic forecasts of inaugural Olympic medals for countries with no prior medals. Second, our MPXG framework organically combines factor analysis, ARIMA, and XGBoost—precisely fitting linear trends while flexibly capturing complex nonlinear relationships while yielding narrower confidence intervals than ARIMA or univariate regression approaches and allowing trend inferences for entire clusters of nations based on limited samples. Third, we employ Bayesian linear regression to convert host country and coaching effects from simple dummy variables into quantifiable marginal contribution coefficients, deepening the quantitative interpretation of these key factors. Together, these innovations not only enhance model interpretability and generalizability but also establish a cross-disciplinary paradigm for sports big data and event prediction research.

Our research also offers substantial practical value, providing actionable decision support tools for national sports authorities and event organizers. By forecasting the probability of a nation’s first medal, governing bodies can swiftly identify and support potential dark horse contenders. Combining medal trend analysis with clustering enables the precise targeting of each country’s strengths under budget constraints, optimizing training programs and funding allocation. Finally, the quantified host country and coaching effect coefficients supply objective, data-driven criteria for host nation preparations and coaching staff selection, thereby comprehensively enhancing overall competitive performance.

This research also makes significant contributions to interdisciplinary fields involving sports. It can intersect with public policy by guiding equitable resource allocation to underrepresented nations, promoting social inclusion through sports development. In sports economics, clustering and trend analysis tools can optimize event planning, ensuring sustainable economic benefits for host cities while minimizing environmental impact [3]. In the field of education, the methodology for quantifying coaching effects can be adapted to assess teacher performance, improving training programs and enhancing student outcomes. Additionally, predictive models can be applied to sports-related public health initiatives, such as forecasting participation trends to design community fitness programs, fostering a healthier society [40]. By connecting sports events with these domains, the research provides actionable, data-driven tools that enhance inclusivity, economic efficiency, and societal well-being.

9. Conclusions

This study developed a hybrid machine learning framework to predict Olympic medal performance for the 2028 Games, incorporating the impacts of host and coaching effects. The key findings are summarized as follows:

• Classifying global countries into four categories based on Olympic participation and medal outcomes, with an analysis of their 2028 medal trends. To simplify the analysis of 234 countries, we categorized them based on shared characteristics using the K-means clustering method. The algorithm divided the nations into four distinct clusters (${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$). The first three clusters (${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$) contain countries with Olympic medal achievements, while the fourth cluster (${\alpha }_4$) consists of nations without any medals.
• Integrating factor analysis, time series, and four machine learning methods into the MPXG model to predict individual country medal outcomes. From each of the medal-winning clusters, we selected 2–3 representative nations for detailed examination, using the United States as a primary example for comparative analysis. Through dimensionality reduction analysis, ten original variables were consolidated into three principal components: competition scale factor (F1), medal distribution trend factor (F2), and the gender–athletic performance composite factor (F3). The ARIMA forecasting model yielded 2028 coefficient estimates of 0.9539, 0.7999, and 0.2937 for these factors, respectively. A comparative evaluation of four predictive algorithms (random forest, back propagation neural network, XGBoost, and Support Vector Machine) revealed XGBoost’s superior predictive accuracy with minimal error margins. This methodological framework establishes a robust foundation for nation-specific medal outcome projections.
  Based on predictive modeling, the United States is projected to secure 57 gold medals, with an estimated total medal count reaching 135 in the 2028 Olympic Games. The analysis of the overall performance trends among ${\alpha }_1$ group nations reveals relatively stable competitive levels. The ${\alpha }_2$ group demonstrates a clear upward trajectory in athletic performance. Meanwhile, competitive outcomes for ${\alpha }_3$ group nations primarily depend on two key factors: athletes’ competitive condition and the inclusion of their specialty events in the Olympic program.
• Employing a FCNN to predict the probability of non-medal-winning countries winning their first medal in the next competition. For non-medal-winning nations, we developed a three-layer fully connected neural network architecture that attained 85.5% prediction accuracy during validation. Within the ${\alpha }_4$ cluster, probabilistic modeling indicates distinct medal prospects for the 2028 Olympics: the United Arab Republic (UAR) shows a 77.47% likelihood of podium achievement, while Mali (MLI) demonstrates a 58.47% probability. Furthermore, four additional nations in this group exhibit success probabilities surpassing the 30% threshold.
• Quantifying the host effect value for the past eight Olympic Games. We developed a weighted scoring system (gold = 13, silver = 12, bronze = 10 points) and a quantitative host advantage model. Analysis shows that host nations achieve 74% higher weighted scores than non-host years, based on 30 years of data.
• Developing a Bayesian linear regression-based coach effect scoring system to evaluate the extent to which coaches enhance the overall strength of athletes in a discipline. We introduce the Athletic Winning Potential (AWP) metric to quantify the impact of elite coaching. The Coaching Effectiveness (C.E.) index is stratified into three distinct tiers (1.0, 0.5, 0.25), determined by the coach’s current professional status (active/retired) and their specialization scope (single event/multi-event). National teams were systematically classified into ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ clusters, each associated with specific scaling coefficients $s_k$ (0.4, 0.2, 0.1, respectively). Case studies featuring South Korea and China demonstrate the model’s predictive capabilities. Our findings indicate that elite coaching contributes to a measurable enhancement in athlete performance. When implementing comprehensive guidance by a great coach, the AWP (Athlete Winning Probability) improves by 4–6 points, indicating an average increase of 0.5 bronze medal equivalent per athlete. However, when focusing on event-specific coaching, the improvement is limited to 2–4 points, translating to an average gain of 0.25 bronze medal equivalent per athlete.

While the model demonstrates strong performance, several limitations remain noteworthy. The study relied on historical data under the assumption of continuity in trends and national sports policies, which may fail to account for sudden geopolitical or economic disruptions. While host and coaching effects were quantified, they could be further refined with more granular data, such as individual athlete performance metrics or country-specific policy changes. The model’s predictions for ${\alpha }_4$ nations, though promising, are based on limited historical data, warranting caution in interpretation.

Moreover, this study suggests several promising directions for future research. The study suggests expanding the dataset to include more granular variables such as athlete-specific performance metrics and real-time training data, incorporating advanced techniques like reinforcement learning to dynamically adapt predictions based on emerging trends, exploring the cultural and socioeconomic dimensions of medal performance to offer a more holistic understanding of Olympic success, and adapting the MPXG and FMPM models for medal prediction in other major sporting events (such as the Winter Olympics, Asian Games, and Commonwealth Games) with sport-specific modifications.