Application of a Bi-Mamba Model for Railway Subgrade Settlement Prediction During Pipe-Jacking Tunneling
Abstract
1. Introduction
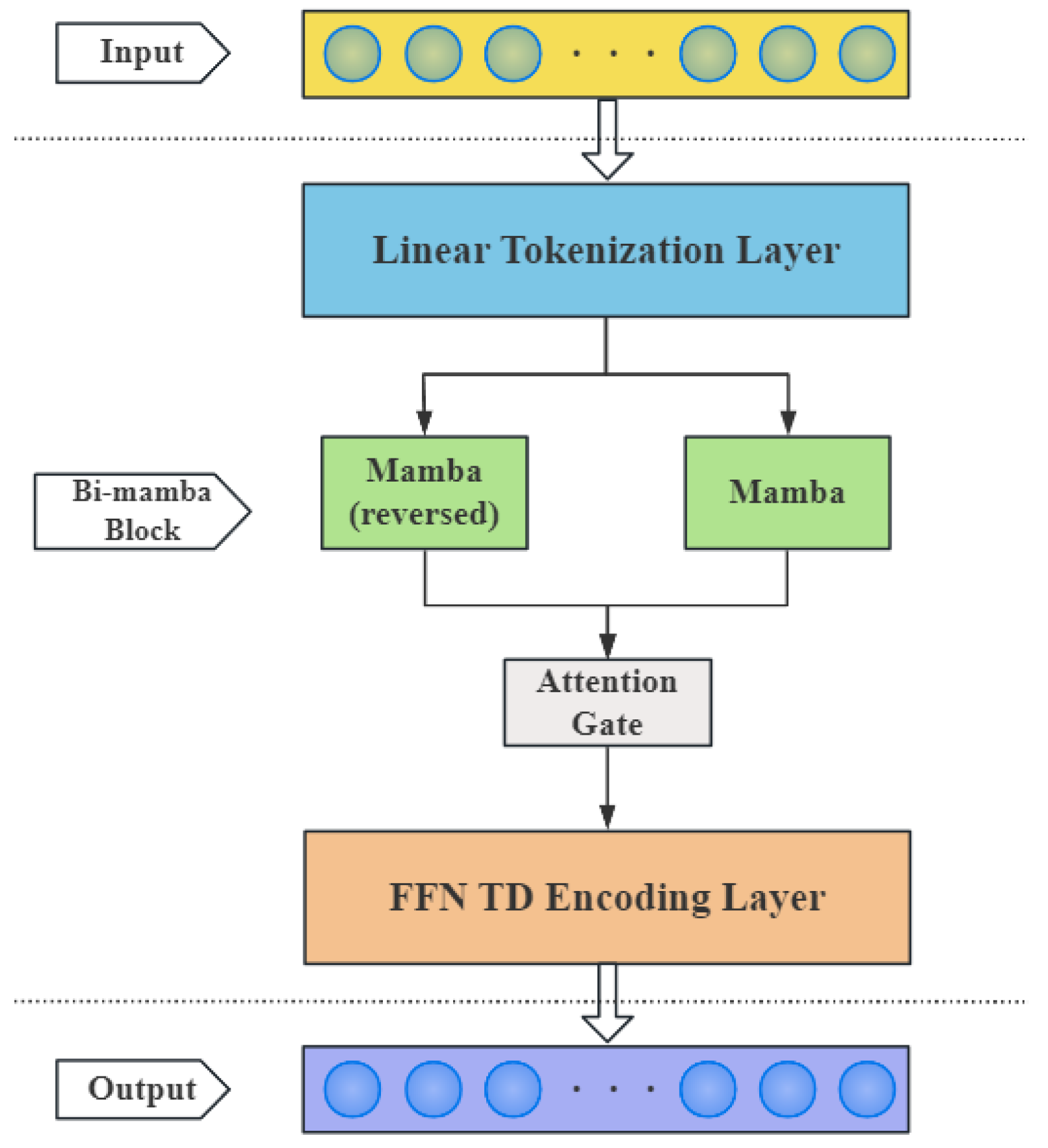
2. Monolithic Framework
3. The Establishment of Railway Subgrade Settlement Model Based on Bi-Mamba
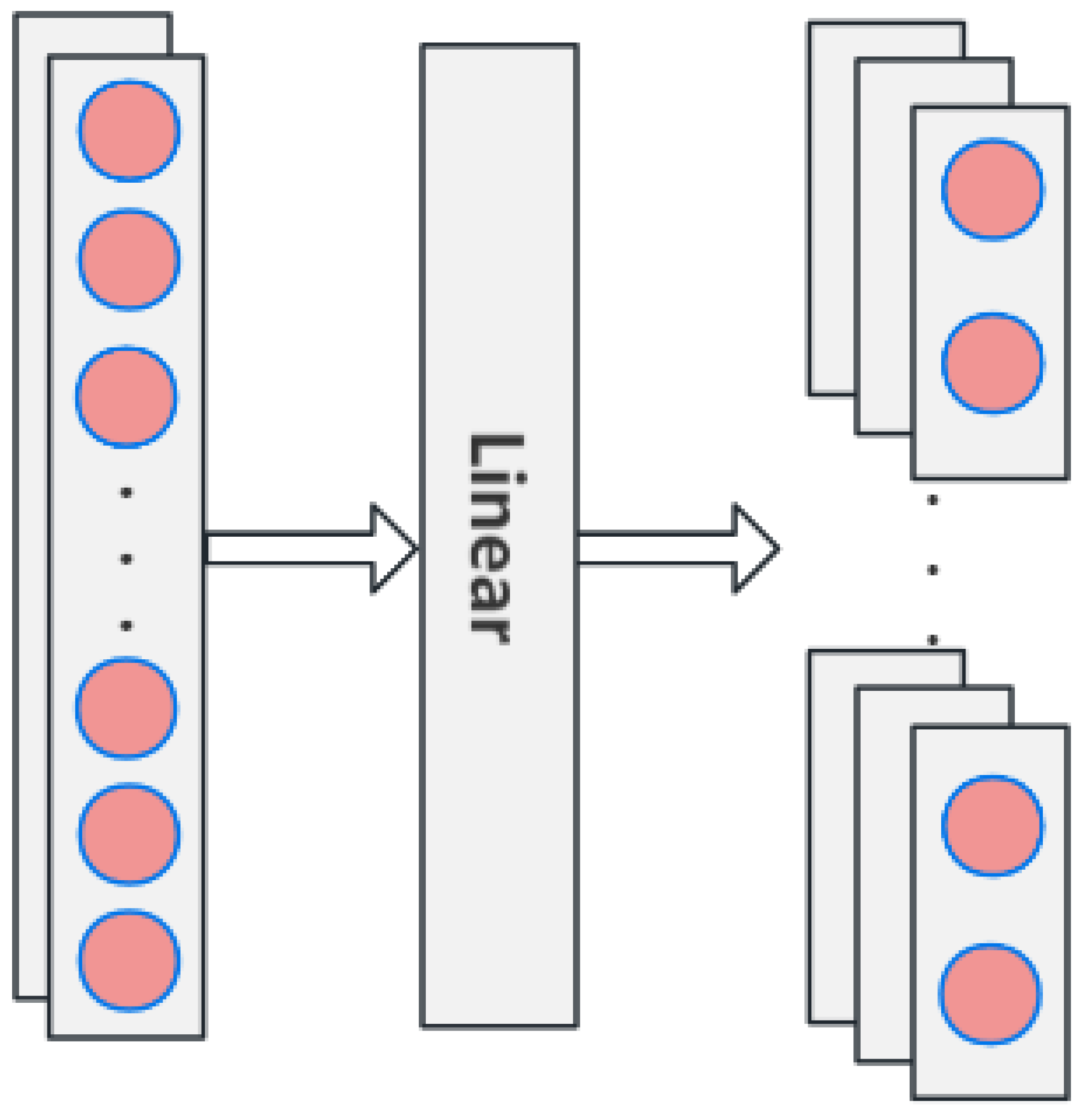
3.1. Linear Tokenization Layer
3.2. Bi-Mamba Block
3.3. Attention Gate
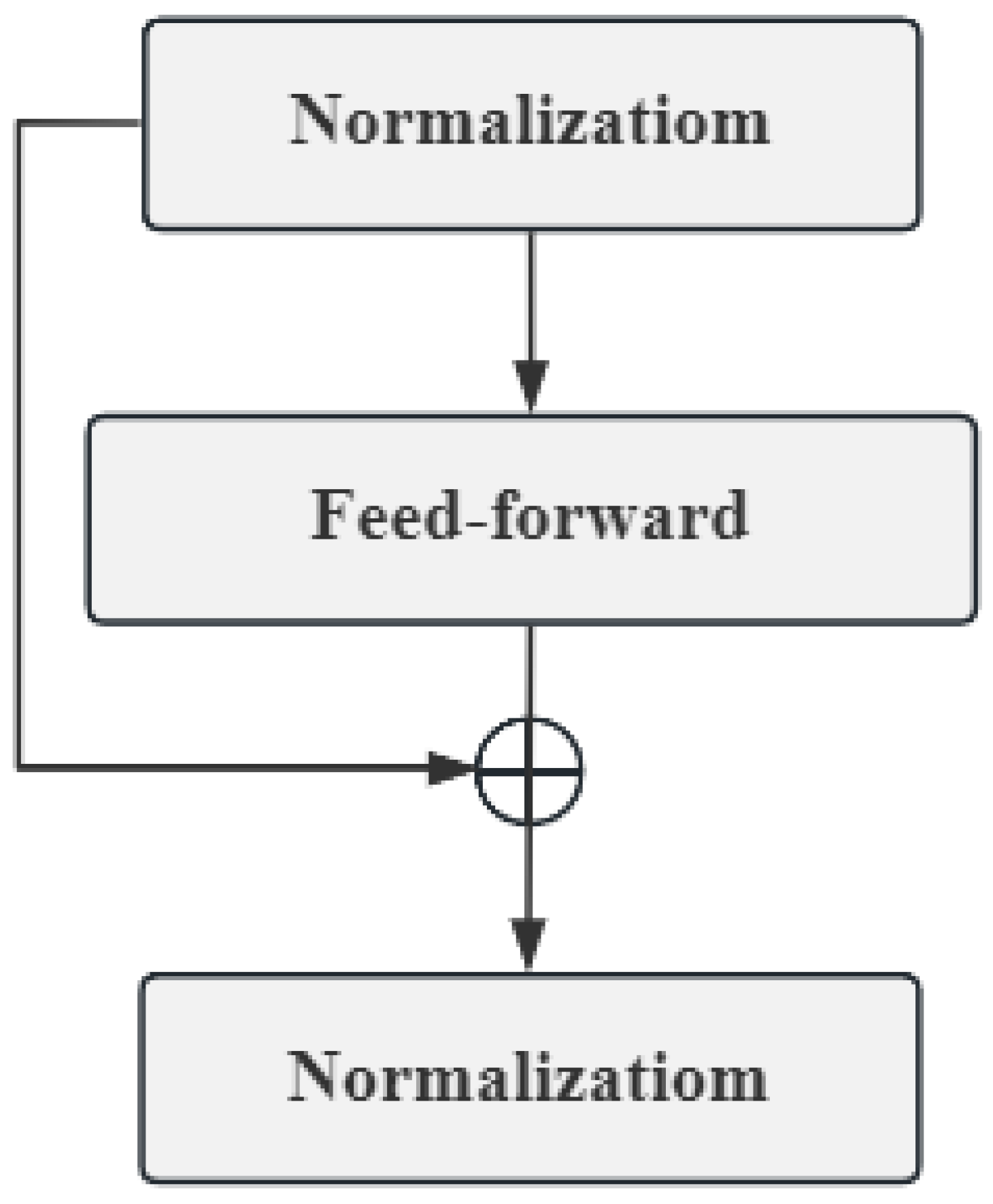
3.4. FFN TD Encoding Layer
4. Project Examples
4.1. Project Overview
4.2. Data Acquisition
4.3. Experimental Analysis
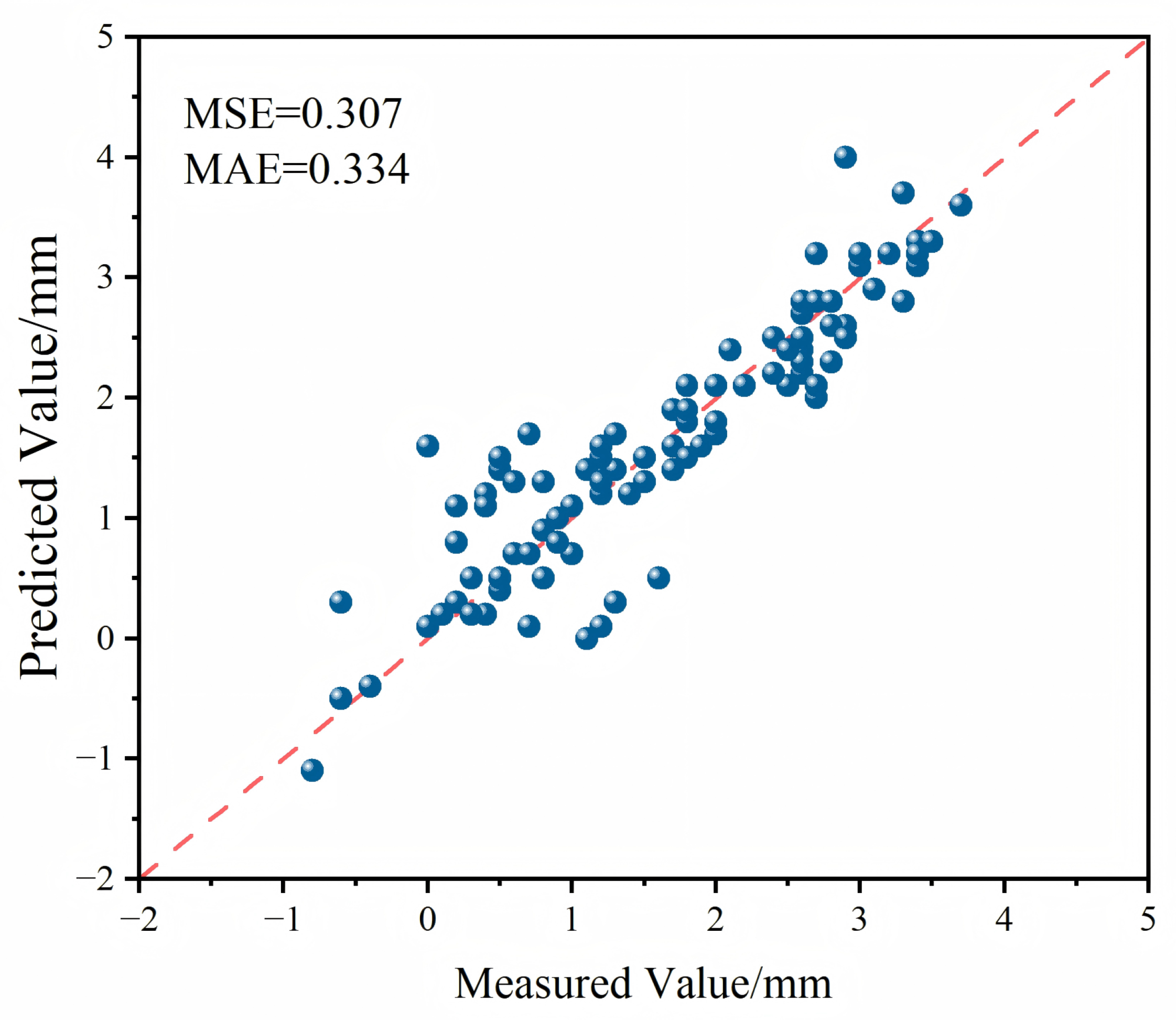
4.3.1. Model Evaluation Metrics
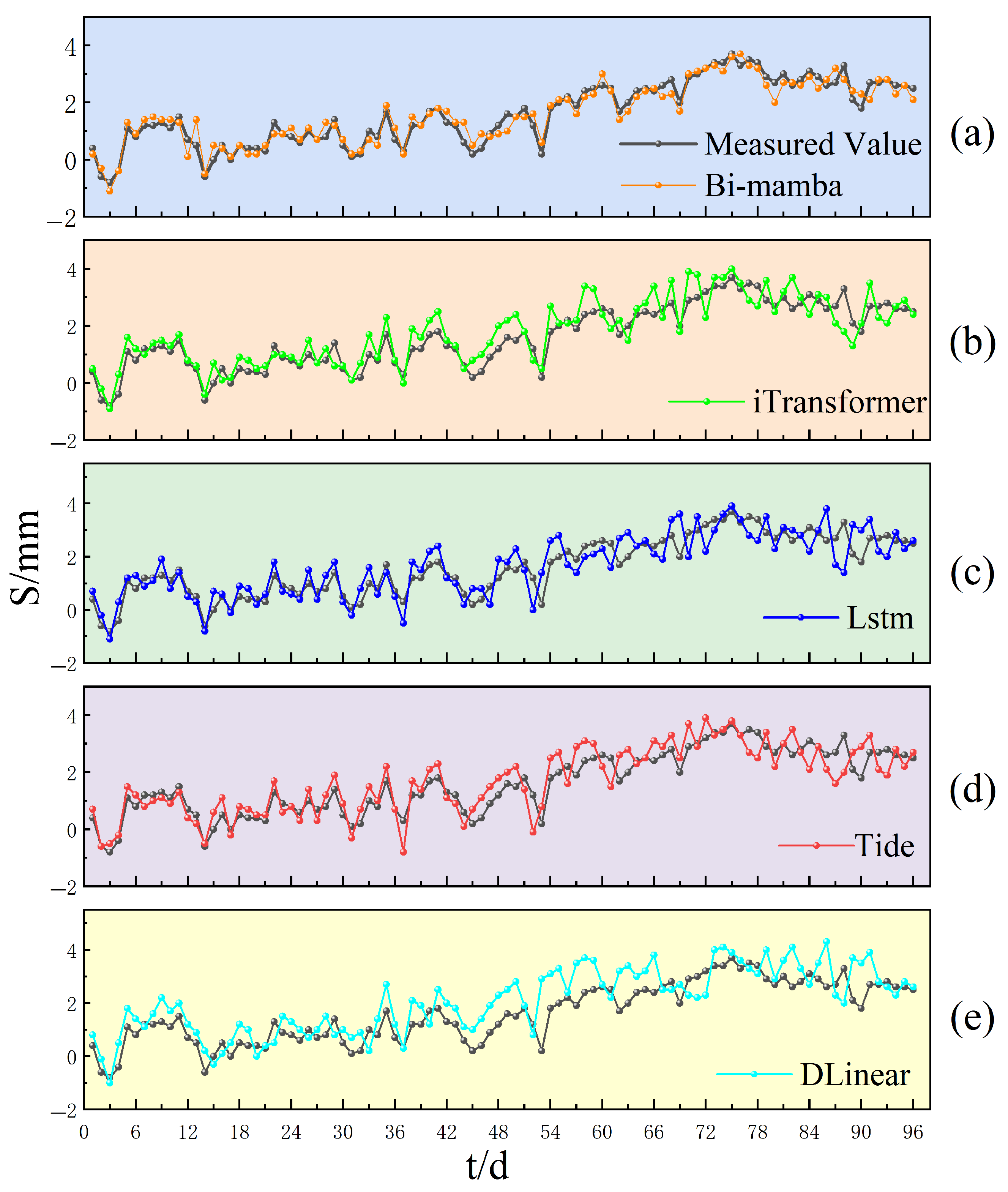
4.3.2. Prediction Results
4.3.3. Model Comparison Experiment
4.3.4. Ablation Experiment
5. Conclusions
- (1)
- The Bi-Mamba model demonstrates excellent alignment between predicted and actual settlement values, effectively capturing the relationship between pipe jacking progress and surface subsidence. For long-sequence predictions, the model achieves MSE and MAE of 0.279 and 0.27,6 respectively, outperforming iTransformer, LSTM, Tide, and DLinear models in predictive accuracy. These results establish Bi-Mamba as a novel methodological approach for subgrade settlement prediction.
- (2)
- The Attention Gate mechanism significantly enhances model performance by dynamically adjusting feature fusion weights through computed attention coefficients.
- (3)
- The study could further incorporate soil information; for example, the cohesion of soil layers can be incorporated as input variables into the model, to predict foundation settlement under different geological conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, R.; Wang, Z.; Wu, H. Risk assessment for shield tunneling beneath buildings based on interval improved TOPSIS method and FAHP method. J. Shanghai Jiao Tong Univ. 2022, 56, 1710–1719. [Google Scholar]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, H.; Zhang, G.; Xiong, W.; Wang, L. The Prediction of Ground Settlement of a Box Culvert Jacked Under the Action of an Ultra-Shallow Buried Pipe Curtain. Arab. J. Sci. Eng. 2022, 47, 12423–12438. [Google Scholar] [CrossRef]
- Li, J.; Yan, B.; Shi, Y. The monitoring and analysis of surface subsidence of Soft soil rock large section of subway tunnel shield construction. In Proceedings of the 2nd International Conference on Energy Materials and Material Application, Changsha, China, 5–7 December 2013; pp. 78–82. [Google Scholar]
- Hamza, M.; Ata, A.; Roussin, A. Ground movements due to the construction of cut-and-cover structures and slurry shield tunnel of the Cairo Metro. Tunn. Undergr. Space Technol. 1999, 14, 281–289. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. Stability of plane strain tunnel headings in soils with tensile strength cut-off. Tunn. Undergr. Space Technol. 2020, 95, 103138. [Google Scholar] [CrossRef]
- Ding, D.; Yang, X.; Lu, W.; Liu, W.; Yan, M. Numerical Analysis on Deformation of Adjacent Structures due to Metro Station Construction by Enlarging Large-diameter Shield Tunnel. In Proceedings of the International Conference on Civil Engineering and Building Materials, Kunming, China, 31 October–3 November 2011; pp. 1196–1200. [Google Scholar]
- Huang, Y.; Zhang, T.; Yu, T.; Wu, X. Support vector machine model of settlement prediction of road soft foundation. Rock Soil Mech. 2005, 26, 1987–1990. [Google Scholar]
- Kirts, S.; Nam, B.H.; Panagopoulos, O.P.; Xanthopoulos, P. Settlement prediction using support vector machine (SVM)-based compressibility models: A case study. Int. J. Civ. Eng. 2019, 17, 1547–1557. [Google Scholar] [CrossRef]
- Santos, O.J.; Celestino, T.B. Artificial neural networks analysis of São Paulo subway tunnel settlement data. Tunn. Undergr. Space Technol. 2008, 23, 481–491. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Wu, H.; Wang, Z.; Zhong, Z. Prediction of shield tunneling-induced ground settlement using machine learning techniques. Front. Struct. Civ. Eng. 2019, 13, 1363–1378. [Google Scholar] [CrossRef]
- Li, T.; Tang, T.; Liu, B.; Chen, Q. Surface settlement prediction of subway tunnels constructed by step method based on VMD-GRU. J. Huazhong Univ. Sci. Technol. 2023, 51, 48–54+62. [Google Scholar]
- Hu, Y.; Gu, C.; Meng, Z.; Shao, C.; Min, Z. Prediction for the Settlement of Concrete Face Rockfill Dams Using Optimized LSTM Model via Correlated Monitoring Data. Water 2022, 14, 2157. [Google Scholar] [CrossRef]
- Su, J.; Wang, Y.; Niu, X.; Sha, S.; Yu, J. Prediction of ground surface settlement by shield tunneling using XGBoost and Bayesian Optimization. Eng. Appl. Artif. Intell. 2022, 114, 105020. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhang, P.; Kang, X.; Zhong, Z.Q.; Liu, Y.; Wu, H.N. Prediction of maximum surface settlement caused by earth pressure balance (EPB) shield tunneling with ANN methods. Soils Found. 2019, 59, 284–295. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W.; Zhang, Y.; Xiao, Y.; Xiang, Y. Determination of earth pressure balance tunnel-related maximum surface settlement: A multivariate adaptive regression splines approach. Bull. Eng. Geol. Environ. 2018, 77, 489–500. [Google Scholar] [CrossRef]
- Wang, C.; Tsepa, O.; Ma, J.; Wang, B. Graph-mamba: Towards long-range graph sequence modeling with selective state spaces. arXiv 2024, arXiv:2402.00789. [Google Scholar]
- Ma, X.; Zhang, X.; Pun, M.O. Rs 3 mamba: Visual state space model for remote sensing image semantic segmentation. IEEE Geosci. Remote Sens. Lett. 2024, 21, 6011405. [Google Scholar] [CrossRef]
- Chen, K.; Chen, B.; Liu, C.; Li, W.; Zou, Z.; Shi, Z. Rsmamba: Remote sensing image classification with state space model. IEEE Geosci. Remote Sens. Lett. 2024, 21, 8002605. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, H.; Zhang, X.; Xiao, P.; Bai, L.; Ouyang, W. Rs-mamba for large remote sensing image dense prediction. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5633314. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Bai, L.; Li, W.; Ouyang, W.; Zou, Z.; Shi, Z. Mambads: Near-surface meteorological field downscaling with topography constrained selective state space modeling. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4112615. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Wang, Z.; Kong, F.; Feng, S.; Wang, M.; Yang, X.; Zhao, H.; Wang, D.; Zhang, Y. Is mamba effective for time series forecasting? Neurocomputing 2025, 619, 129178. [Google Scholar] [CrossRef]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Raffel, C.; Ellis, D.P.W. Feed-forward networks with attention can solve some long-term memory problems. arXiv 2015, arXiv:1512.08756. [Google Scholar]
- Li, Z.; Peng, Y.; Li, J.; Tang, Z. Composite Foundation Settlement Prediction Based on LSTM-Transformer Model for CFG. Appl. Sci. 2024, 14, 732. [Google Scholar] [CrossRef]
- Das, A.; Kong, W.; Leach, A.; Mathur, S.K.; Sen, R.; Yu, R. Long-term forecasting with tide: Time-series dense encoder. Trans. Mach. Learn. Res. 2023, arXiv:2304.08424. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? Proc. Aaai Conf. Artif. Intell. 2023, 37, 11121–11128. [Google Scholar] [CrossRef]


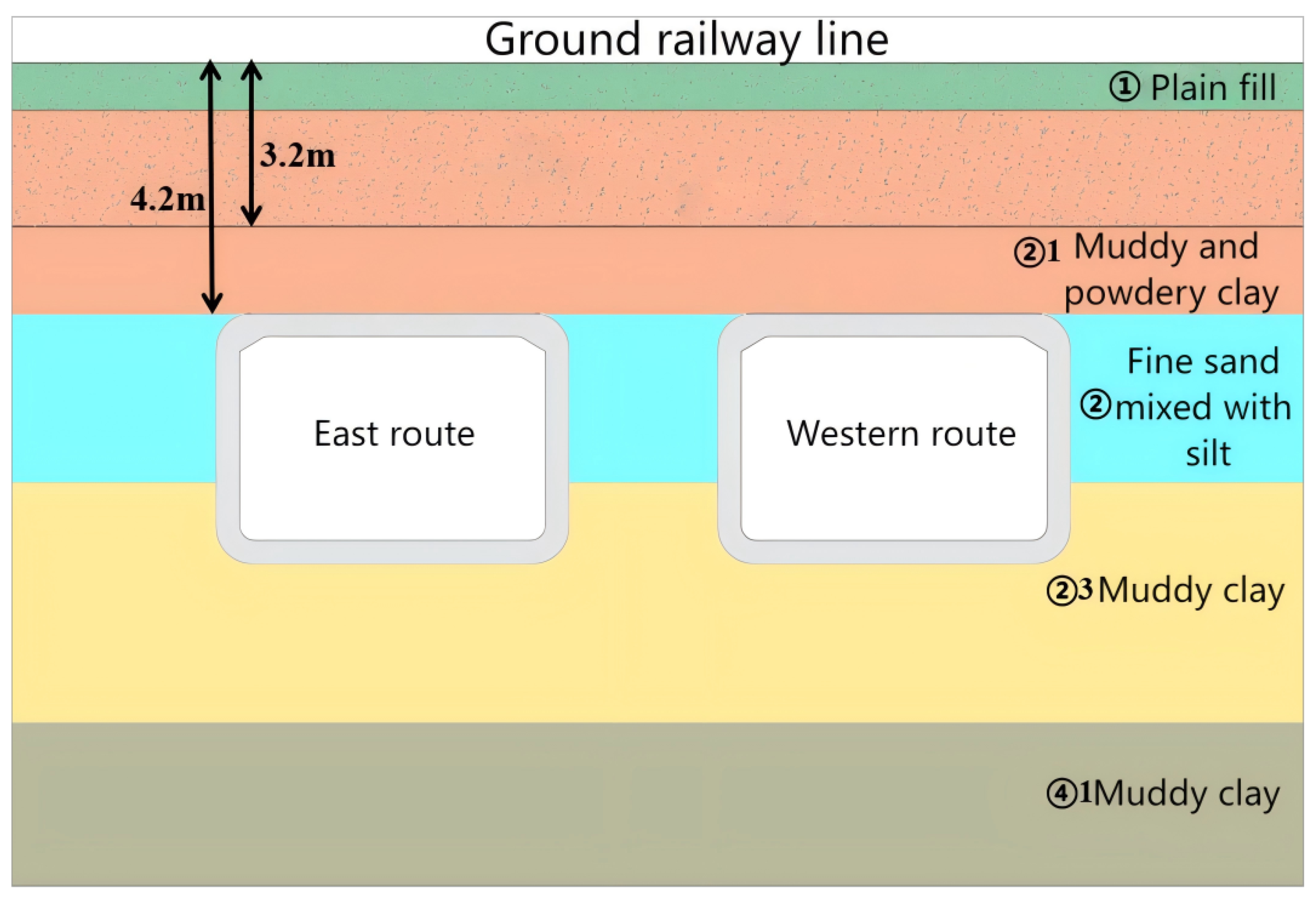




| Name of Soil Layer | Characteristic Value of Bear Capacity/kpa | Compression Modulus/Mpa | Cohesion/kpa | Friction Angle/° | Void Ratio |
|---|---|---|---|---|---|
| Plain fill | / | / | / | / | / |
| Muddy and powdery clay | 60 | 4.5 | 12.2 | 10.5 | 1.028 |
| Fine sand mixed with silt | 110 | 6.6 | 12.2 | 19.5 | 0.648 |
| Muddy clay | 60 | 2.8 | 10.9 | 8.6 | 1.217 |
| Muddy clay | 65 | 2.7 | 15.9 | 9.8 | 1.330 |
| Model | Bi-Mamba | iTransformer | LSTM | Tide | DLinear | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| The Forecast Length | 16 | 0.173 | 0.213 | 0.325 | 0.373 | 0.272 | 0.175 | 0.573 | 0.318 | 0.294 | 0.259 |
| 32 | 0.203 | 0.234 | 0.398 | 0.428 | 0.432 | 0.258 | 0.624 | 0.339 | 0.452 | 0.264 | |
| 64 | 0.255 | 0.273 | 0.435 | 0.455 | 0.681 | 0.382 | 0.641 | 0.341 | 0.723 | 0.402 | |
| 96 | 0.279 | 0.276 | 0.606 | 0.498 | 0.753 | 0.525 | 0.675 | 0.394 | 1.030 | 0.560 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Zhou, N.; Wang, B.; Gan, H. Application of a Bi-Mamba Model for Railway Subgrade Settlement Prediction During Pipe-Jacking Tunneling. Appl. Sci. 2025, 15, 7790. https://doi.org/10.3390/app15147790
Peng Y, Zhou N, Wang B, Gan H. Application of a Bi-Mamba Model for Railway Subgrade Settlement Prediction During Pipe-Jacking Tunneling. Applied Sciences. 2025; 15(14):7790. https://doi.org/10.3390/app15147790
Chicago/Turabian StylePeng, Yipu, Ning Zhou, Bin Wang, and Hongjun Gan. 2025. "Application of a Bi-Mamba Model for Railway Subgrade Settlement Prediction During Pipe-Jacking Tunneling" Applied Sciences 15, no. 14: 7790. https://doi.org/10.3390/app15147790
APA StylePeng, Y., Zhou, N., Wang, B., & Gan, H. (2025). Application of a Bi-Mamba Model for Railway Subgrade Settlement Prediction During Pipe-Jacking Tunneling. Applied Sciences, 15(14), 7790. https://doi.org/10.3390/app15147790






