A Novel Hierarchical Multi-Stable Cylindrical Structure with Superior Energy Trapping
Abstract
1. Introduction
2. Structural Design
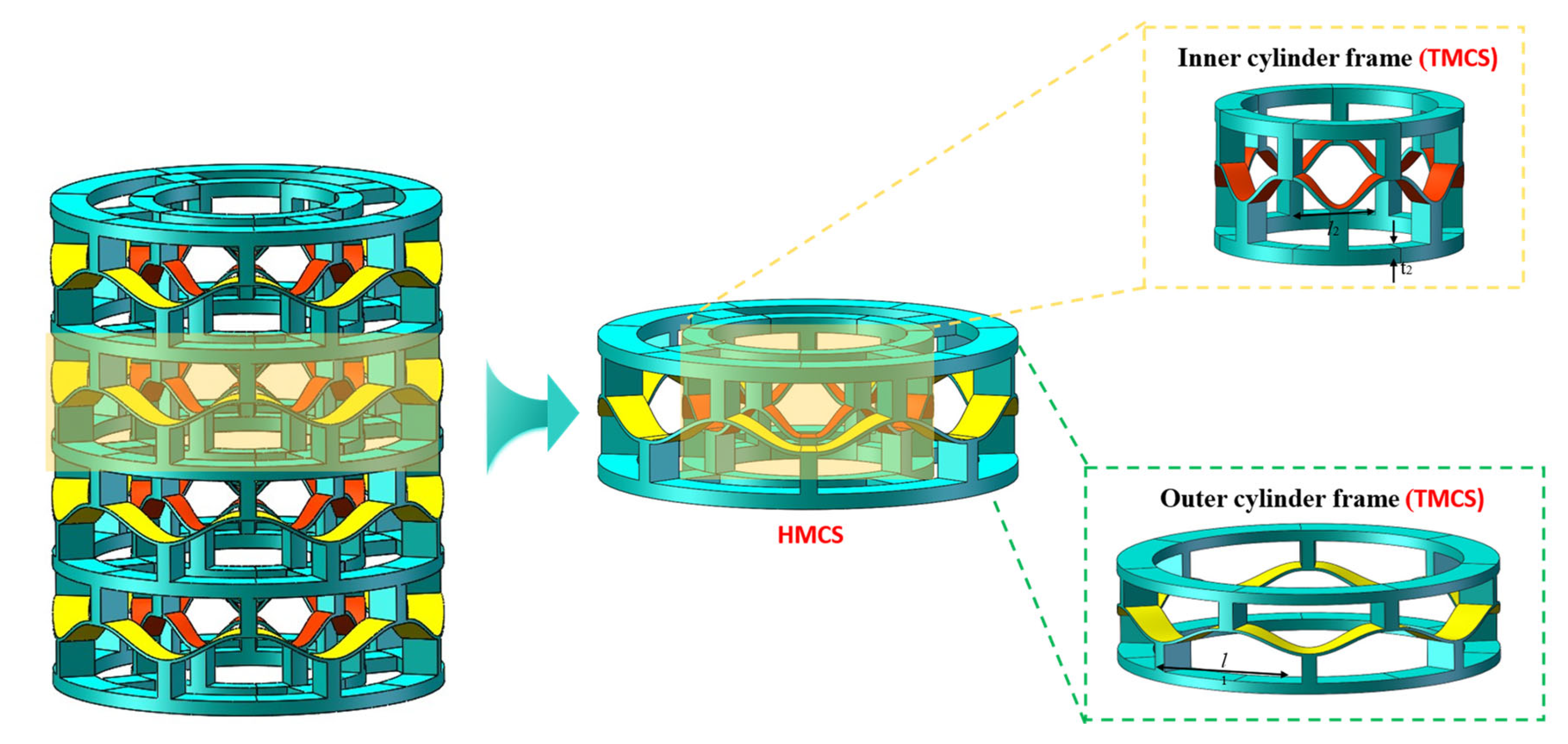
2.1. Design of the Bi-Stable Unit Cell
2.2. Design of Hierarchical Multi-Stable Cylindrical Structure (HMCS)
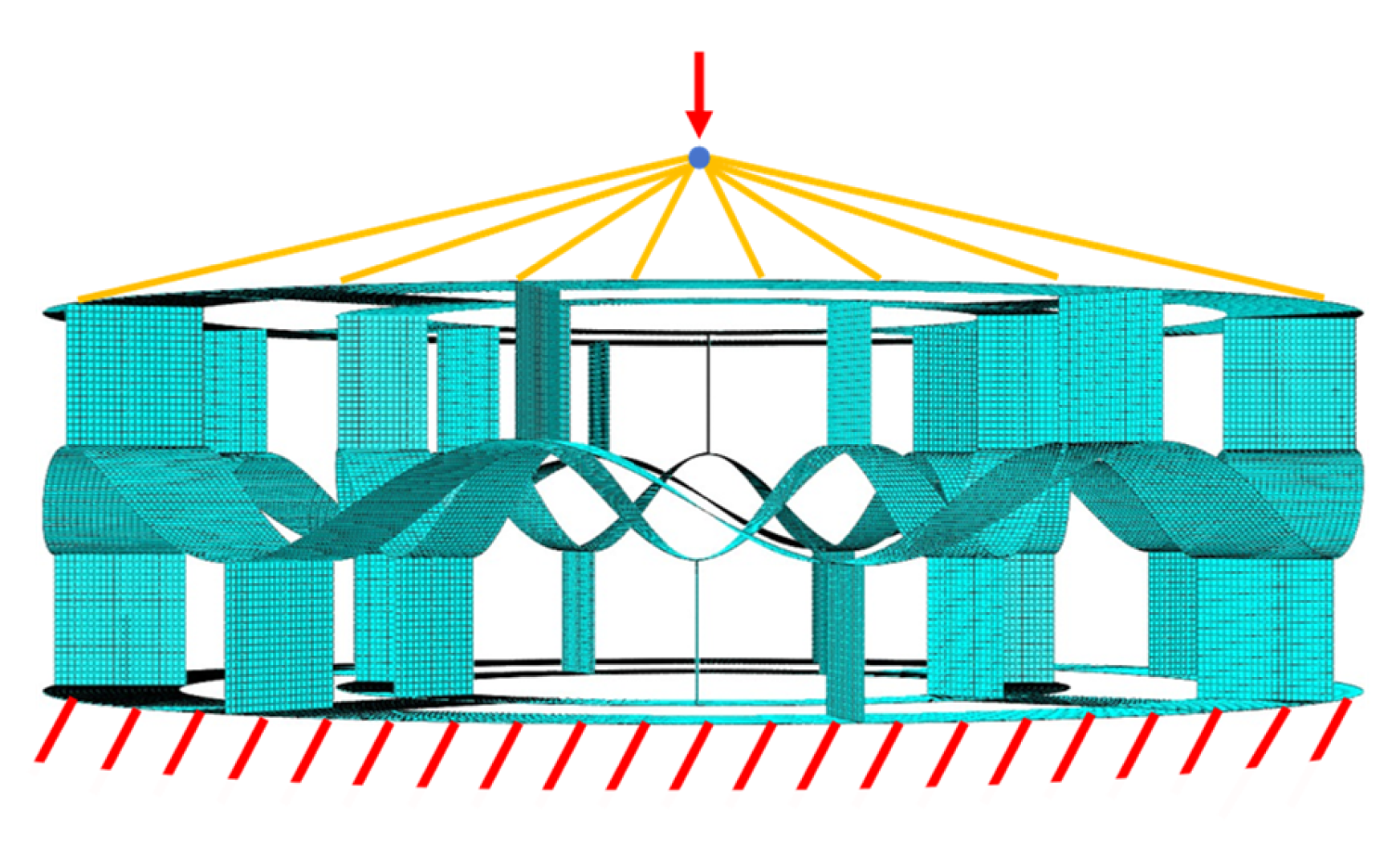
3. Numerical Simulation
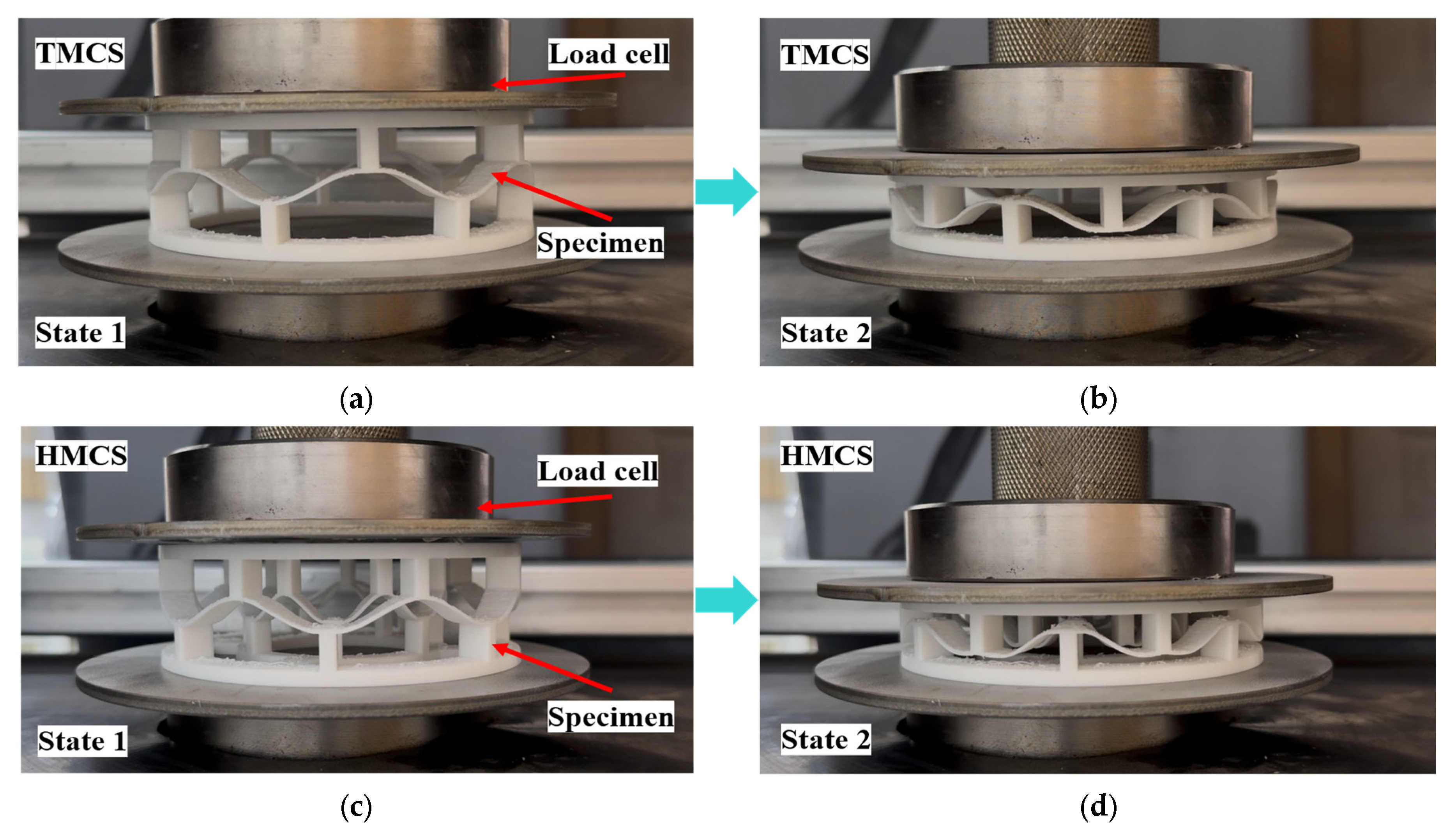
4. Experiments
5. Results and Discussion
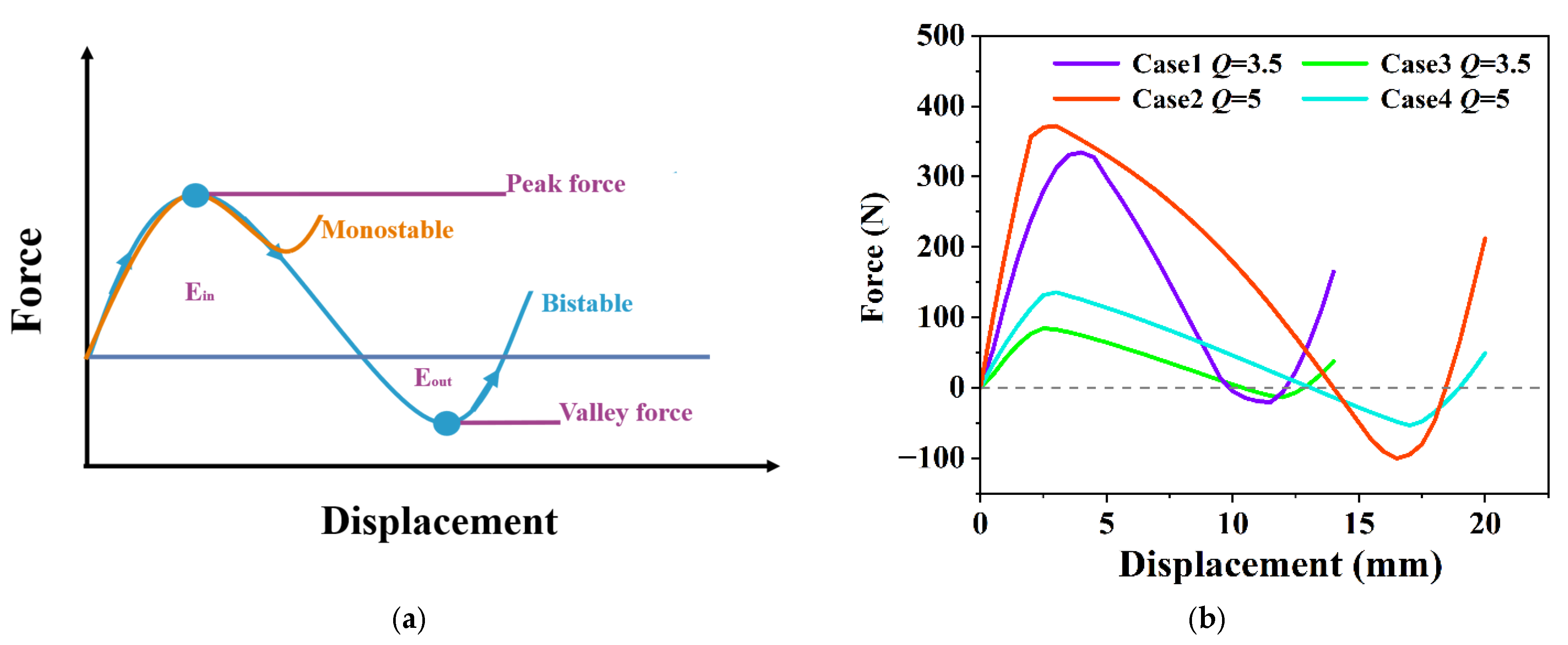
5.1. Energy Trapping and Load-Bearing Behavior
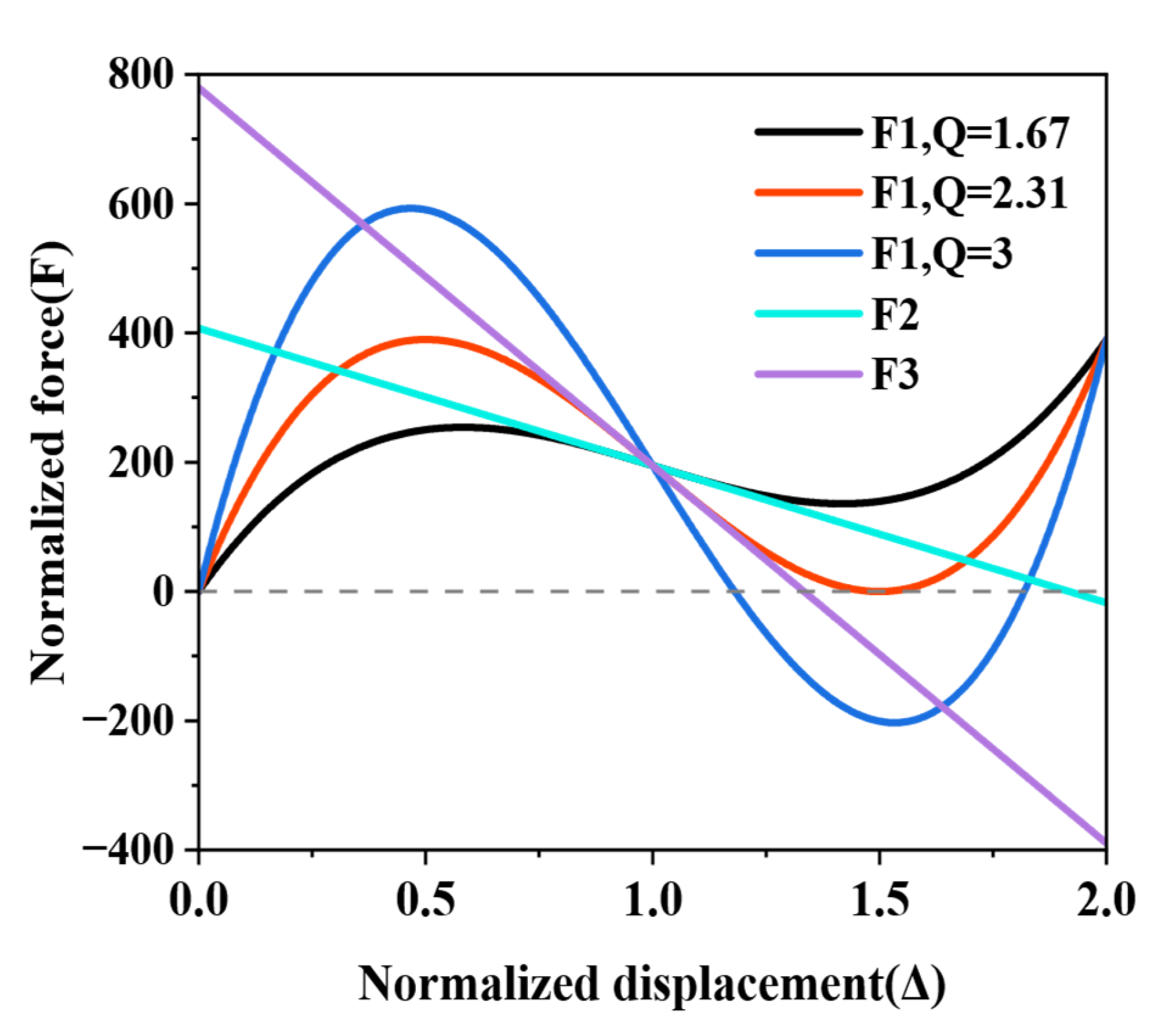
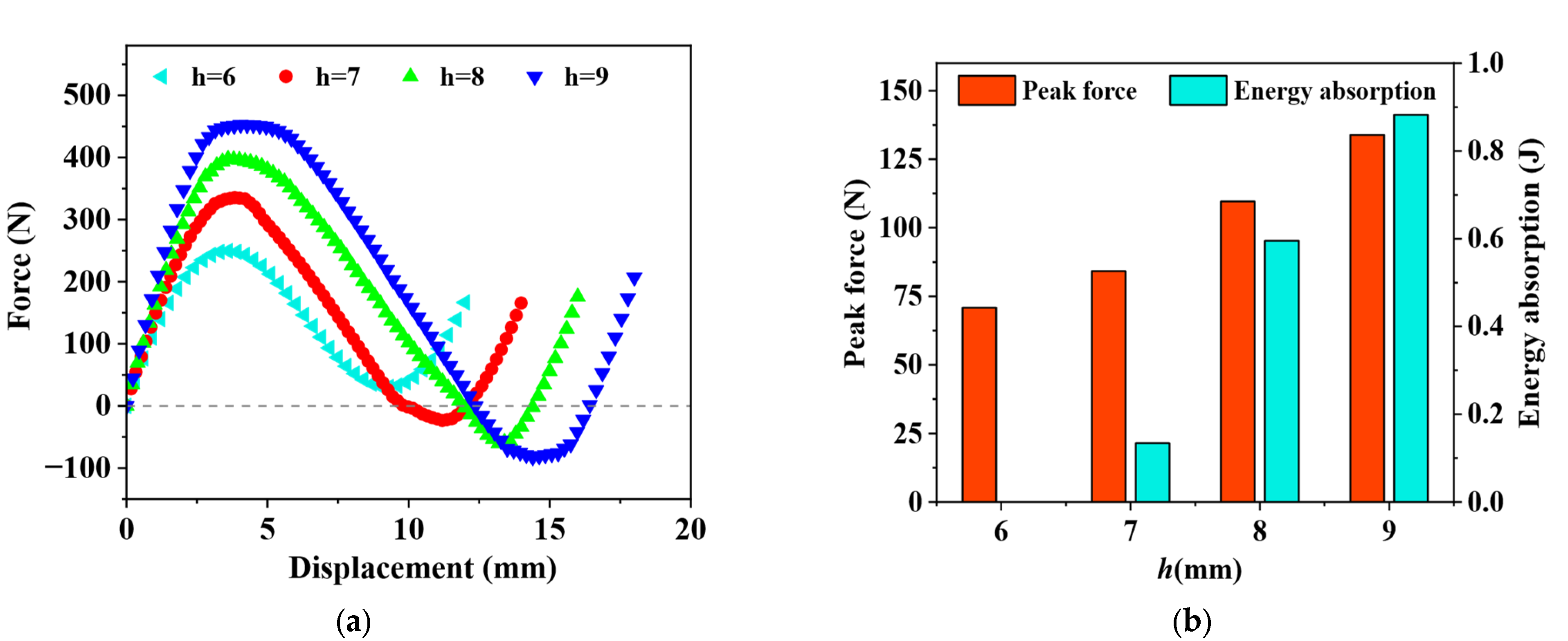
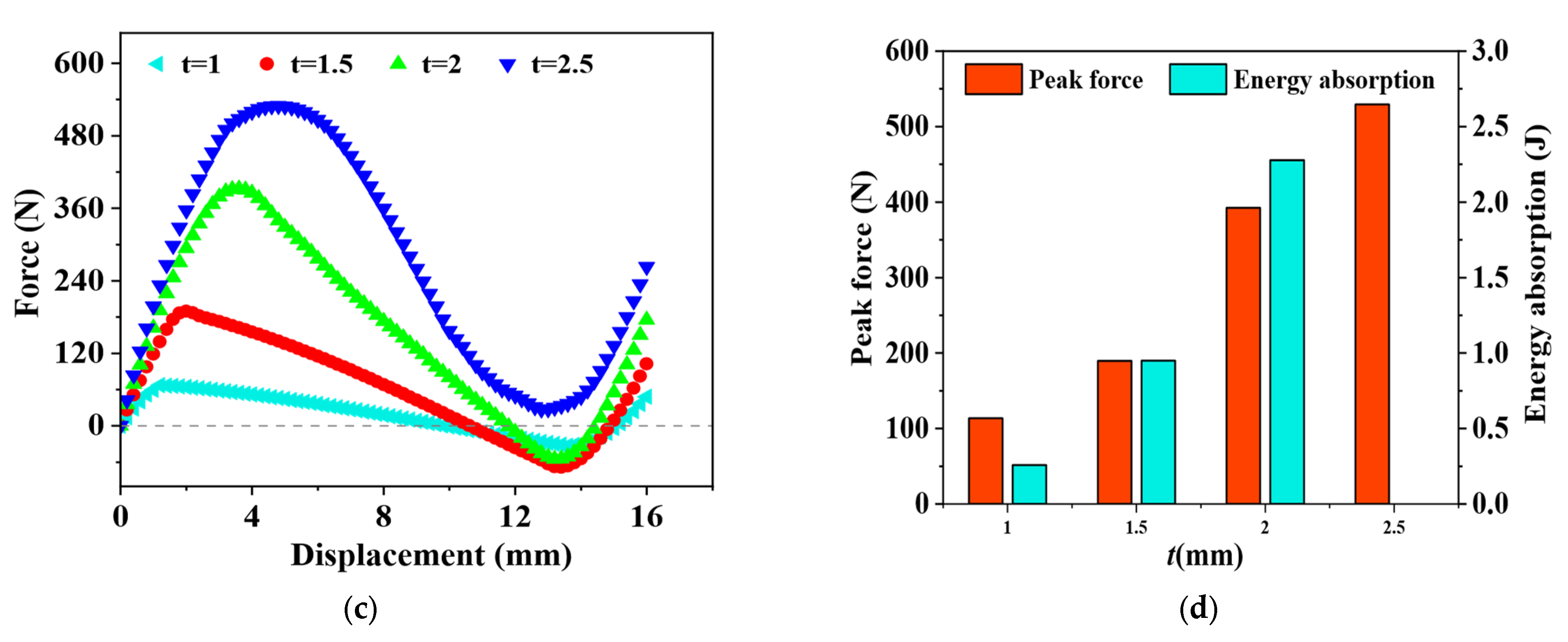
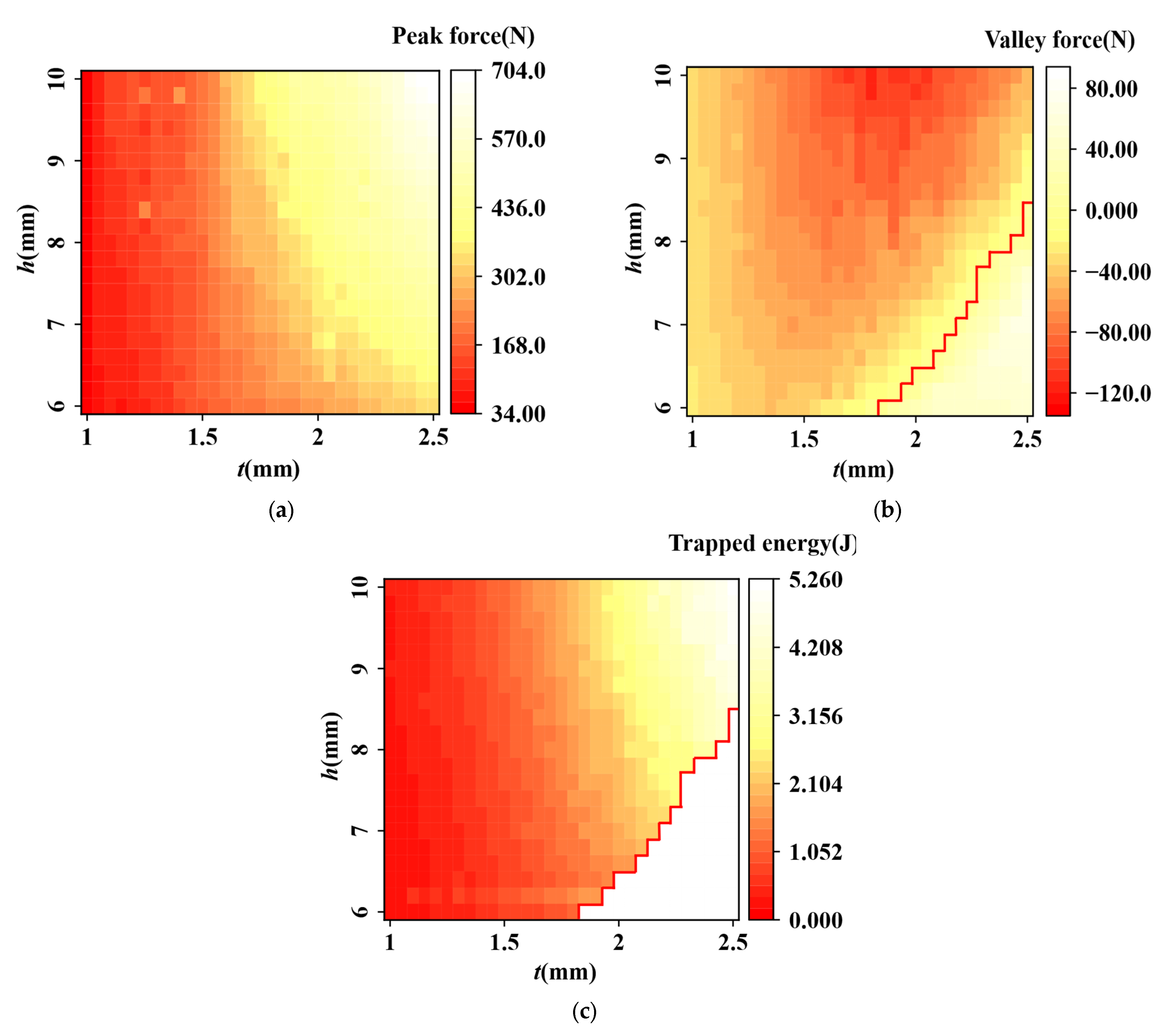
5.2. The Effect of Structural Parameters
5.3. Tuning Snap-Through Sequence
6. Conclusions
- (1)
- The HMCS inherits all the characteristic mechanical behaviors of traditional multi-stable cylindrical structures (TMCSs), including energy absorption and snap-through behaviors. Compared with the TMCS, the proposed HMCS has significant increases in both total and specific energy absorption. Specifically, in the case tested, the HMCS exhibited approximately a 200% increase in load-carrying capacity, and achieved a total energy trapping of 485% and a specific energy trapping gain of 225% compared to the TMCS.
- (2)
- The height h and thickness t of the curved beams are identified as critical parameters influencing the performance of the HMCS. While the peak force and energy absorption exhibit relatively straightforward correlations with h and t, the valley force shows a more complex relationship with beam thickness. A critical parameter ratio of h/t ≈ 3.69 was determined, serving as a threshold for distinguishing between mono-stable and bi-stable responses.
- (3)
- A tuning snap-through sequence design of a multilayer HMCS is achieved by tailoring the thickness of the curved beams. The results reveal that the thicknesses of the curved beams dominate the snap-through behavior in multilayer structures. Deformation initiates from the layer with the lowest stiffness and progresses sequentially through layers with increasing beam thickness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, T.; Lin, C.; Zhang, Y.; Cai, J.; Yang, J. Viscoelastic negative stiffness metamaterial with multistage load bearing and programmable energy absorption ability. Int. J. Smart Nano Mater. 2024, 16, 1–23. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, Y.; Xu, W.; Wei, R.; Chen, M.; Jiang, H. A bistable honeycomb mechanical metamaterial with transformable Poisson’s ratio and tunable vibration isolation properties. Thin-Walled Struct. 2024, 198, 111718. [Google Scholar] [CrossRef]
- Li, N.; Liu, S.; Wu, X.; Wang, J.; Han, Y.; Zhang, X. Mechanical characteristics of a novel rotating star-rhombic auxetic structure with multi-plateau stages. Thin-Walled Struct. 2023, 191, 111081. [Google Scholar] [CrossRef]
- Mizzi, L.; Grasselli, L.; Spaggiari, A.; Gatt, R.; Farrugia, P.S.; Grima, J.N. Design of isotropic 2D chiral metamaterials based on monohedral pentagonal tessellations. Thin-Walled Struct. 2023, 187, 110739. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, J.; Chen, L.; Liu, T.; Li, W. Negative stiffness metamaterial with directional stability in uniform fields. Thin-Walled Struct. 2024, 194B, 111302. [Google Scholar] [CrossRef]
- Ren, L.; Wu, Q.; Li, J.; He, Y.; Zhang, Y.; Zhou, X.; Wu, S.; Liu, Q.; Li, B. 4D printing of customizable and reconfigurable mechanical metamaterials. Int. J. Mech. Sci. 2024, 270, 109112. [Google Scholar] [CrossRef]
- Khajehtourian, R.; Kochmann, D.M. Soft Adaptive Mechanical Metamaterials. Front. Robot. AI 2021, 8, 673478. [Google Scholar] [CrossRef]
- Wan, M.; Yu, K.; Sun, H. 4D printed programmable auxetic metamaterials with shape memory effects. Compos. Struct. 2022, 279, 114791. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. Novel metamaterial structures with negative thermal expansion and tunable mechanical properties. Int. J. Mech. Sci. 2024, 261, 108692. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, H.; Wei, N.; Tao, R.; Luo, Z. Design optimization of multifunctional metamaterials with tunable thermal expansion and phononic bandgap. Mater. Des. 2021, 209, 109990. [Google Scholar] [CrossRef]
- Coulais, C.; Teomy, E.; de Reus, K.; Shokef, Y.; van Hecke, M. Combinatorial design of textured mechanical metamaterials. Nature 2016, 535, 529–532. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Wang, K.; Zhao, H.; Shi, W.; Xue, J.; Zhou, Y.; Li, Q.; Wang, G.; Yan, B. Energy dissipation and shock isolation using novel metamaterials. Int. J. Mech. Sci. 2022, 218, 107464. [Google Scholar] [CrossRef]
- Gholikord, M.; Etemadi, E.; Imani, M.; Hosseinabadi, M.; Hu, H. Design and analysis of novel negative stiffness structures with significant energy absorption. Thin-Walled Struct. 2022, 181, 110137. [Google Scholar] [CrossRef]
- Jiang, H.; Bednarcyk, B.A.; Le Barbenchon, L.; Chen, Y. Elastically anisotropic architected metamaterials with enhanced energy absorption. Thin-Walled Struct. 2023, 192, 111115. [Google Scholar] [CrossRef]
- Li, Y.; Deng, Z.; Yan, G.; Gao, G. Wave propagation in two-dimensional elastic metastructures with triangular configuration. Thin-Walled Struct. 2022, 181, 110043. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, H.; Cai, C.; Xu, D. Tunable ultralow frequency wave attenuations in one-dimensional quasi-zero-stiffness metamaterial. Int. J. Mech. Mater. Des. 2021, 17, 285–300. [Google Scholar] [CrossRef]
- Bobbert, F.S.L.; Janbaz, S.; van Manen, T.; Li, Y.; Zadpoor, A.A. Russian doll deployable meta-implants: Fusion of kirigami, origami, and multi-stability. Mater. Des. 2020, 191, 108624. [Google Scholar] [CrossRef]
- Bodaghi, M.; Liao, W.H. 4D printed tunable mechanical metamaterials with shape memory operations. Smart Mater. Struct. 2019, 28, 045019. [Google Scholar]
- Yang, H.; Ma, L. 1D and 2D snapping mechanical metamaterials with cylindrical topology. Int. J. Solids Struct. 2020, 204–205, 220–232. [Google Scholar] [CrossRef]
- Zhang, Y.; Tichem, M.; van Keulen, F. A novel design of multi-stable metastructures for energy dissipation. Mater. Des. 2021, 212, 110234. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, F.; Ma, Y.; Yang, K.; Guo, S.; Chen, Y. Bistable reconfigurable origami metamaterials with high load-bearing and low state-switching forces. Extreme Mech. Lett. 2023, 63, 102064. [Google Scholar] [CrossRef]
- Hu, H.; Xia, Z.; Tao, Q.; Ye, Z.; Yuan, K.; Song, L. Self-unfolding properties of smart grid-reinforced membrane origami. J. Compos. Sci. 2024, 8, 64. [Google Scholar] [CrossRef]
- Sun, Y.; Song, K.; Ju, J.; Zhou, X. Curved-creased origami mechanical metamaterials with programmable stabilities and stiffnesses. Int. J. Mech. Sci. 2024, 262, 108729. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, D.; Wang, L.; Xiang, P.; Jia, L.-J. Cushioning performance of origami negative Poisson’s ratio honeycomb steel structure. Thin-Walled Struct. 2024, 204, 112284. [Google Scholar] [CrossRef]
- Li, Z.; Xie, C.; Li, F.; Wu, D.; Hu, N. Heterogeneous geometric designs in auxetic composites toward enhanced mechanical properties under various loading scenarios. Compos. Commun. 2023, 38, 101499. [Google Scholar] [CrossRef]
- Danish, B.; Anilkumar, P.M.; Rao, B.N. Suppression of cross-well vibrations of a bistable square cross-ply laminate using an additional composite strip. Int. J. Dyn. Control 2023, 11, 2680–2690. [Google Scholar] [CrossRef]
- Zhang, K.; Qi, L.; Zhao, P.; Zhao, C.; Deng, Z. Buckling induced negative stiffness mechanical metamaterial for bandgap tuning. Compos. Struct. 2023, 304, 116421. [Google Scholar] [CrossRef]
- Liu, T.; Deng, R.; Zhang, Y.; Yang, J.; Cai, J. Composite negative stiffness structure with tunable and temperature-dependent properties induced by viscoelastic and shape-memory materials. Compos. Commun. 2024, 48, 101937. [Google Scholar] [CrossRef]
- Debeau, D.A.; Seepersad, C.C.; Haberman, M.R. Impact behavior of negative stiffness honeycomb materials. J. Mater. Res. 2018, 33, 290–299. [Google Scholar] [CrossRef]
- Zhang, Y.; Tichem, M.; van Keulen, F. Concept and design of a metastructure-based multi-stable surface. Extrem. Mech. Lett. 2022, 51, 101553. [Google Scholar] [CrossRef]
- Chen, B.; Chen, L.; Du, B.; Liu, H.; Li, W.; Fang, D. Novel multifunctional negative stiffness mechanical metamaterial structure: Tailored functions of multi-stable and compressive mono-stable. Compos. B Eng. 2021, 204, 108501. [Google Scholar] [CrossRef]
- Qiu, J.; Lang, J.H.; Slocum, A.H. A curved-beam bistable mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- Hua, J.; Zhou, Y.; Chen, C.Q. Design and analysis of a tunable multistable mechanical metamaterial. Int. J. Mech. Sci. 2024, 272, 109170. [Google Scholar] [CrossRef]
- Hua, J.; Lei, H.; Gao, C.F.; Guo, X.; Fang, D. Parameters analysis and optimization of a typical multistable mechanical metamaterial. Extreme Mech. Lett. 2020, 35, 100640. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Tian, R.; Xue, Q.; Guan, H.; Yang, X. Quasi-static compression and dynamic crushing behaviors of novel hybrid re-entrant auxetic metamaterials with enhanced energy-absorption. Compos. Struct. 2022, 288, 115399. [Google Scholar] [CrossRef]
- Che, K.; Rouleau, M.; Meaud, J. Temperature-tunable time-dependent snapping of viscoelastic metastructures with snap-through instabilities. Extreme Mech. Lett. 2019, 32, 100528. [Google Scholar] [CrossRef]
- Yan, S.; Wu, L.; Wen, Y.; Sun, J.; Zhou, J. Snap-through instability in mechanical metamaterials. Respons. Mater. 2025, 3, e20240035. [Google Scholar]
- Seyedkanani, A.; Akbarzadeh, A. Magnetically assisted rotationally multistable metamaterials for tunable energy trapping–dissipation. Adv. Funct. Mater. 2022, 32, 2207581. [Google Scholar] [CrossRef]
- Dong, T.; Zhang, W.; Dong, M. The novel morphing airfoil based on the bistable composite laminated shell. Nonlinear Dyn. 2023, 111, 17667–17685. [Google Scholar] [CrossRef]
- Che, K.; Yuan, C.; Wu, J.; Qi, H.J.; Meaud, J. Three-dimensional-printed multistable mechanical metamaterials with a deterministic deformation sequence. J. Appl. Mech. 2017, 84, 011004. [Google Scholar] [CrossRef]
- Meaud, J.; Che, K. Tuning elastic wave propagation in multistable architected materials. Int. J. Solids Struct. 2017, 122–123, 69–80. [Google Scholar] [CrossRef]
- Che, K.; Yuan, C.; Qi, H.J.; Meaud, J. Viscoelastic multistable architected materials with temperature-dependent snapping sequence. Soft Matter 2018, 14, 2492–2499. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; An, N.; Wang, G.; Li, M.; Zhou, J. A novel bistable structure with temperature-dependent transition. J. Appl. Phys. 2021, 129, 044903. [Google Scholar] [CrossRef]
- Zouhri, K.; Mohamed, M.; Erol, A.; Liu, B.; Appiah-Kubi, P. Innovative bistable composites for aerospace and high-stress applications: Integrating soft and hard materials in experimental, modeling, and simulation studies. Materials 2024, 17, 4280. [Google Scholar] [CrossRef]
- Mozafari, H.; Distefano, F.; Epasto, G.; Gu, L.; Linul, E.; Crupi, V. Design of an innovative hybrid sandwich protective device for offshore structures. J. Mar. Sci. Eng. 2022, 10, 1385. [Google Scholar] [CrossRef]
- Wang, L.; Kim, H. Bistable CFRP structures for automotive crash boxes: Experimental and numerical validation. Thin-Walled Struct. 2023, 182, 110234. [Google Scholar]
- Wang, C.; Guo, H.; Liu, R.; Deng, Z.; Chen, Y.; You, Z. Reconfigurable origami-inspired multistable metamorphous structures. Sci. Adv. 2024, 10, eadk8662. [Google Scholar] [CrossRef]
- Ji, S.; Wang, F.; Wang, J.; Wang, Z.; Wang, C.; Wei, Y. Dynamic responses and energy absorption of mechanical metamaterials composed of buckling beams. J. Vib. Eng. Technol. 2024, 12, 1249–1261. [Google Scholar] [CrossRef]
- Tan, S.; Pan, D.; Wu, Z. Multi-stable metastructure with multi-layer and multi-degree of freedom: A numerical and experimental investigation. Mater. Des. 2024, 240, 112859. [Google Scholar] [CrossRef]
- Ju, X.; Li, S.; Zhang, Y.; Wu, P.; Li, Y. Design of multi-stable metamaterial cell with improved and programmable energy trapping ability based on frame reinforced curved beams. Thin-Walled Struct. 2024, 202, 112120. [Google Scholar] [CrossRef]
- Yao, X.; Liu, K.; Dong, Q.; Li, X.; Ma, C.; Hu, N. Tunable and recoverable energy absorption of foam-embedded architected cellular composite material at multiple strain rates. Compos. Struct. 2024, 329, 117745. [Google Scholar] [CrossRef]
- Song, Y.; Ruan, S.; Hao, N.; Liu, Y.; Zhang, S. A novel cylindrical sandwich plate inspired by beetle elytra and its compressive properties. Sci. China Technol. Sci. 2024, 67, 3465–3476. [Google Scholar] [CrossRef]
- Dong, Y.; Yu, T.; Zhang, Z. Design and mechanical analysis of 3D negative-stiffness curved domes with Bessel-functional profile. Compos. Struct. 2023, 30, 116422. [Google Scholar] [CrossRef]
- Tan, X.; Wang, B.; Wang, L.; Zhu, S.; Chen, S.; Yao, K.; Xu, P. Effect of beam configuration on its multistable and negative stiffness properties. Compos. Struct. 2022, 286, 115308. [Google Scholar] [CrossRef]
- Li, Y.H.; Dong, Y.H.; Qin, Y.; Lv, H.W. Nonlinear forced vibration and stability of an axially moving viscoelastic sandwich beam. Int. J. Mech. Sci. 2018, 138–139, 131–145. [Google Scholar] [CrossRef]
- Guan, Y.; Ge, X. Dynamic modeling and analysis of the central rigid body-Timoshenko beam model based on unconstrained modes. Appl. Math. Mech. 2022, 43, 156–165. [Google Scholar]
- Wang, Y.; Fang, Y.; Li, L.; Zhang, D.; Liao, W.H.; Fang, J. Dynamic modeling and vibration suppression of a rotating flexible beam with segmented active constrained layer damping treatment. Aerospace 2023, 10, 1010. [Google Scholar] [CrossRef]
- Hohimer, C.; Christ, J.; Aliheidari, N.; Mo, C.; Ameli, A. 3D printed thermoplastic polyurethane with isotropic material properties. Proc. SPIE 2017, 10168, 101680E. [Google Scholar]
- Tan, X.; Wang, B.; Chen, S.; Zhu, S.; Sun, Y. A novel cylindrical negative stiffness structure for shock isolation. Compos. Struct. 2019, 214, 397–405. [Google Scholar] [CrossRef]






| Case | h | t | Q | |
|---|---|---|---|---|
| Hierarchical multi-stable cylindrical structure | 1 | 7 mm | 2 mm | 3.5 |
| 2 | 10 mm | 2 mm | 5 | |
| Traditional multi-stable cylindrical structure | 3 | 7 mm | 2 mm | 3.5 |
| 4 | 10 mm | 2 mm | 5 |
| Case | t1 | t2 | t3 | t4 |
|---|---|---|---|---|
| 1 | 1.3 mm | 1.2 mm | 1.1 mm | 1.0 mm |
| 2 | 1.2 mm | 1.3 mm | 1.1 mm | 1.0 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, M.; Tao, Q.; Chen, X.; Wang, J.; Ji, Q. A Novel Hierarchical Multi-Stable Cylindrical Structure with Superior Energy Trapping. Appl. Sci. 2025, 15, 7748. https://doi.org/10.3390/app15147748
Wang Y, Huang M, Tao Q, Chen X, Wang J, Ji Q. A Novel Hierarchical Multi-Stable Cylindrical Structure with Superior Energy Trapping. Applied Sciences. 2025; 15(14):7748. https://doi.org/10.3390/app15147748
Chicago/Turabian StyleWang, Yu, Maosheng Huang, Qiang Tao, Xiaoyu Chen, Jirong Wang, and Qingxiang Ji. 2025. "A Novel Hierarchical Multi-Stable Cylindrical Structure with Superior Energy Trapping" Applied Sciences 15, no. 14: 7748. https://doi.org/10.3390/app15147748
APA StyleWang, Y., Huang, M., Tao, Q., Chen, X., Wang, J., & Ji, Q. (2025). A Novel Hierarchical Multi-Stable Cylindrical Structure with Superior Energy Trapping. Applied Sciences, 15(14), 7748. https://doi.org/10.3390/app15147748







