Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes
Abstract
1. Introduction
2. Materials and Methods
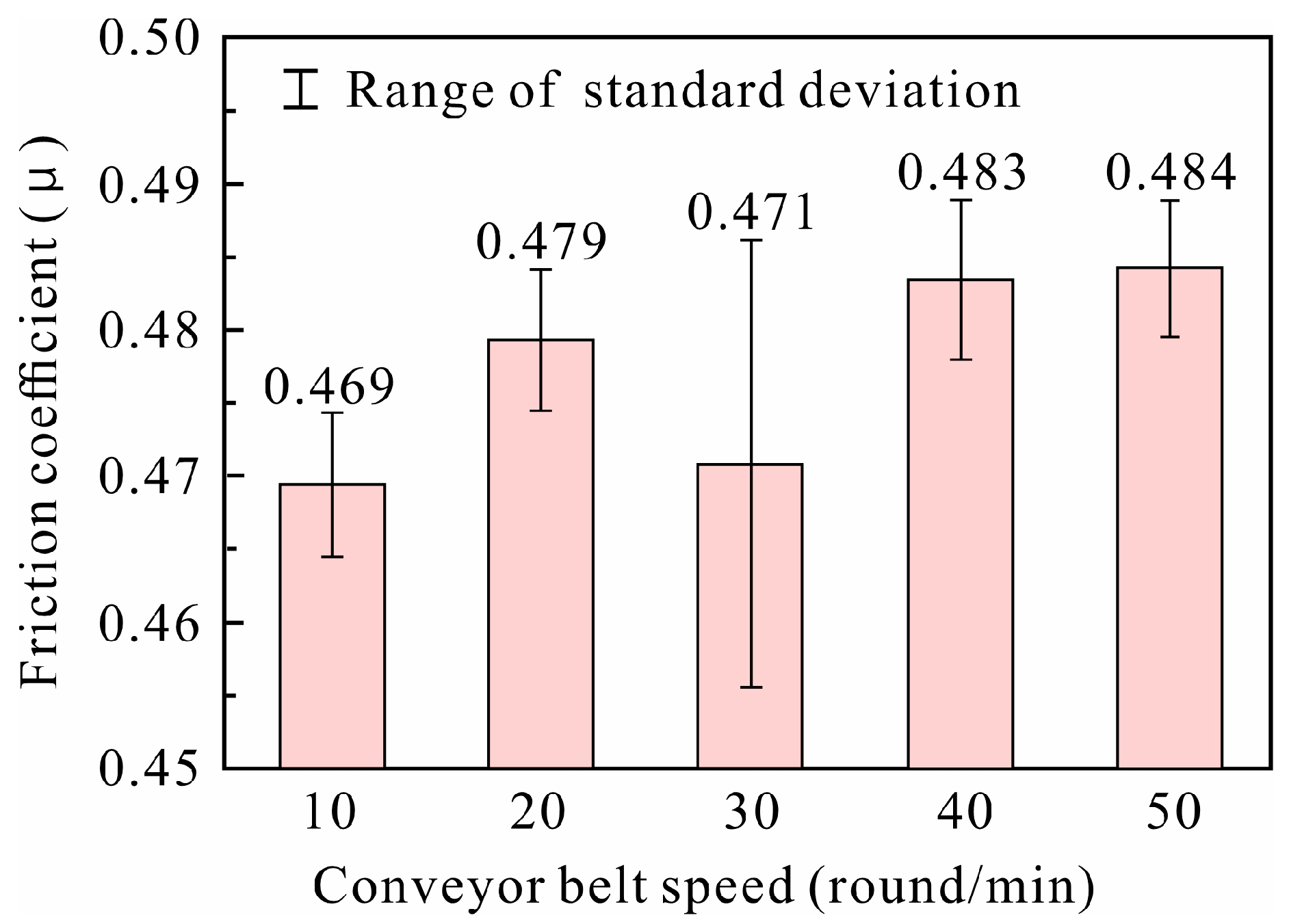
2.1. Model Test Theory
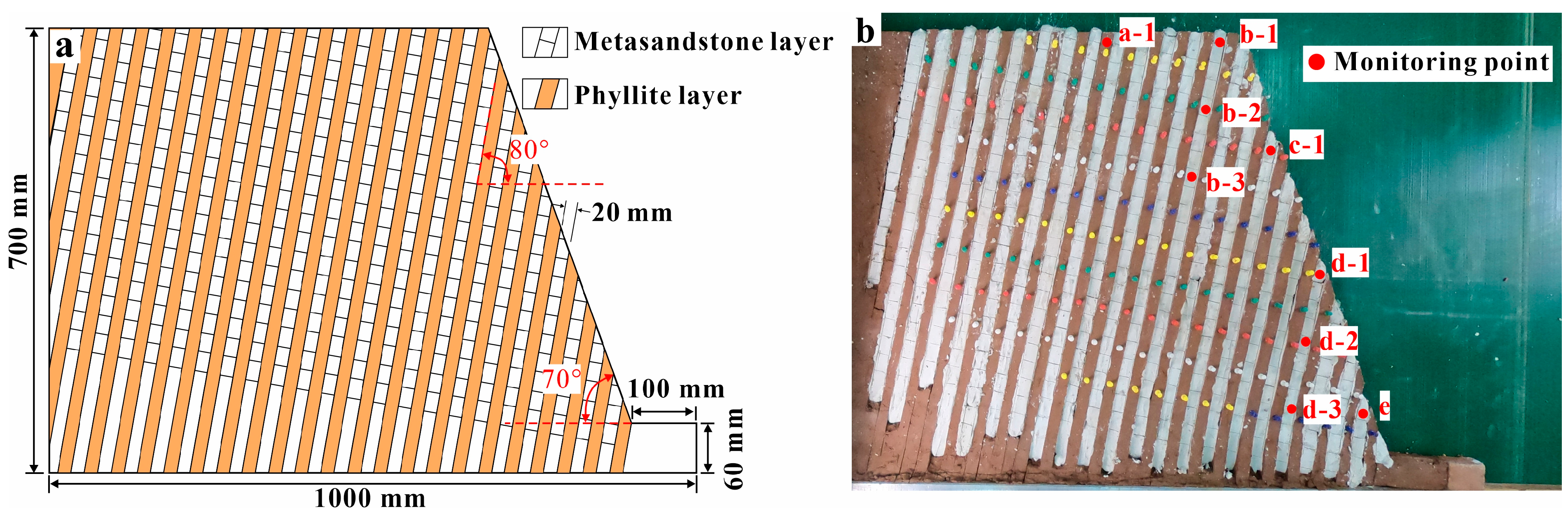
2.2. Model Configuration
2.3. Model Establishment and Test Process
3. Results
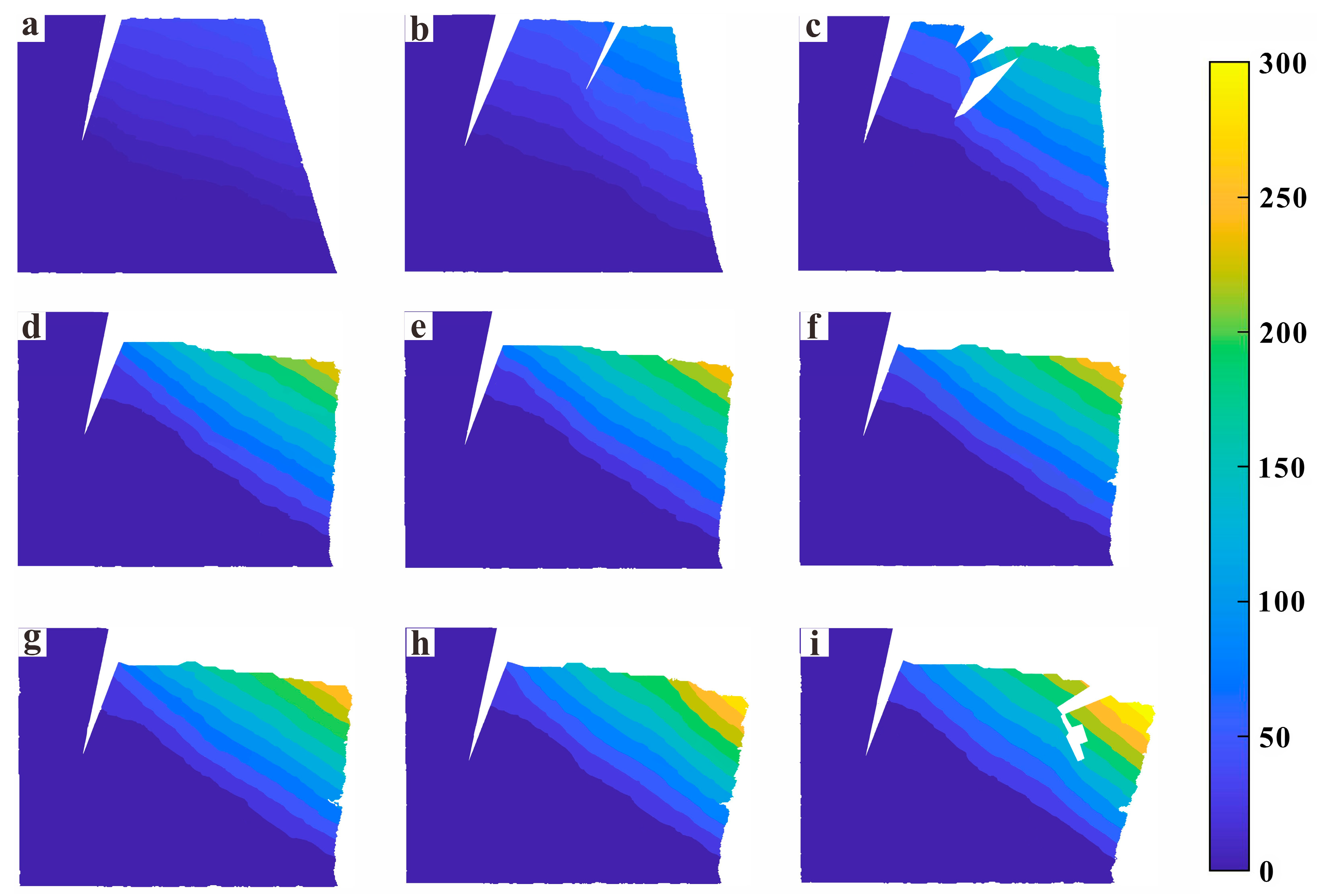
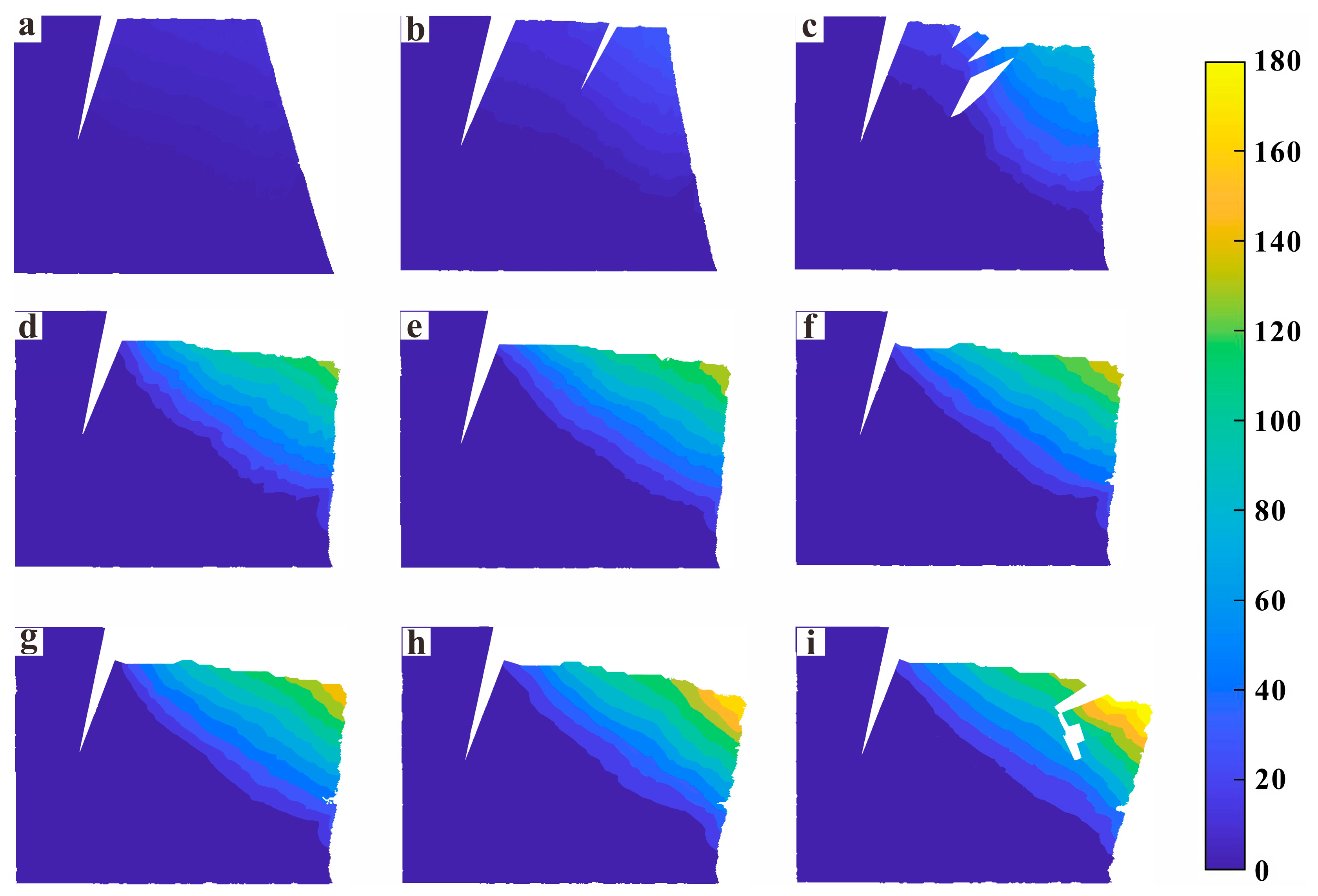
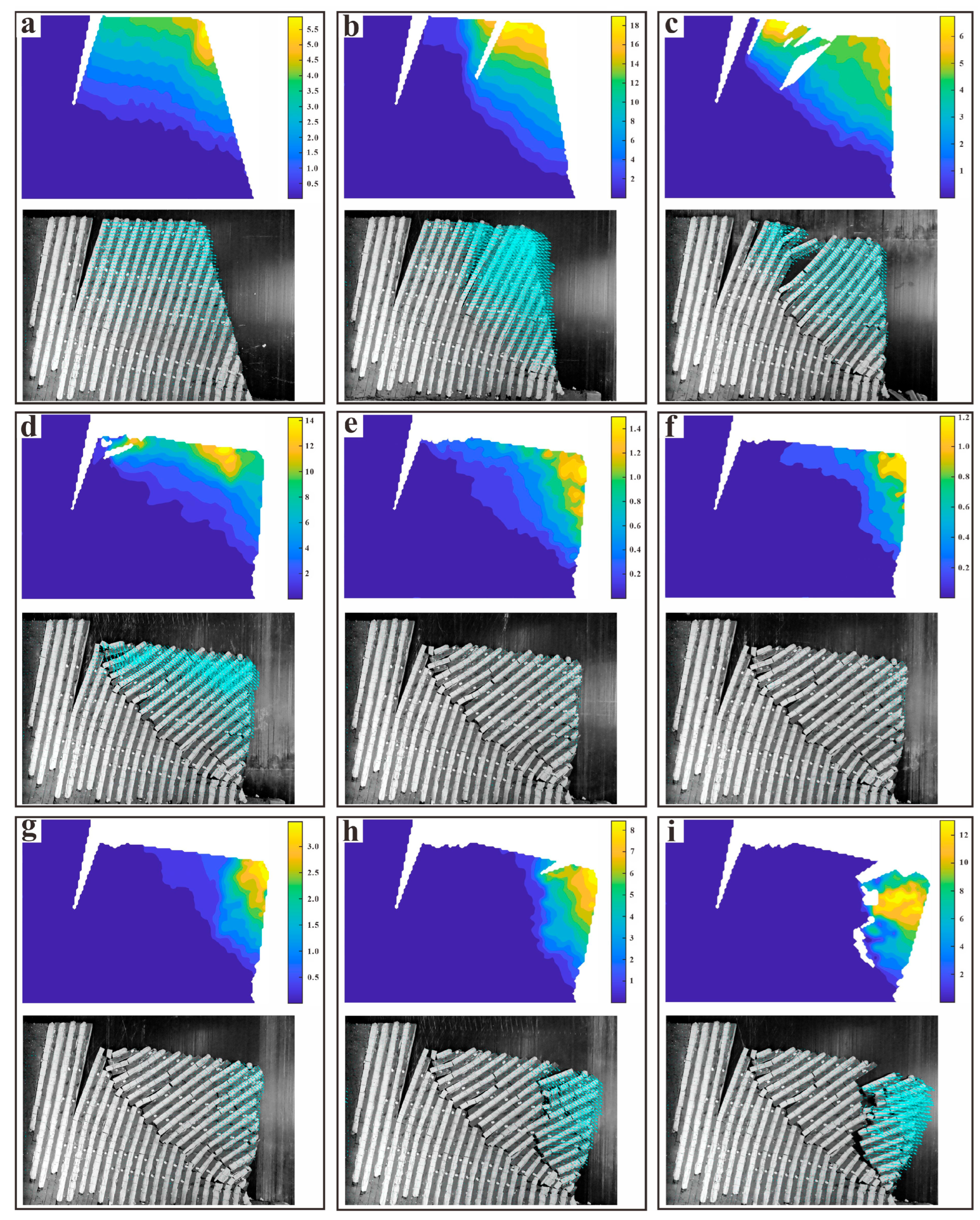
3.1. Deformation and Failure Process
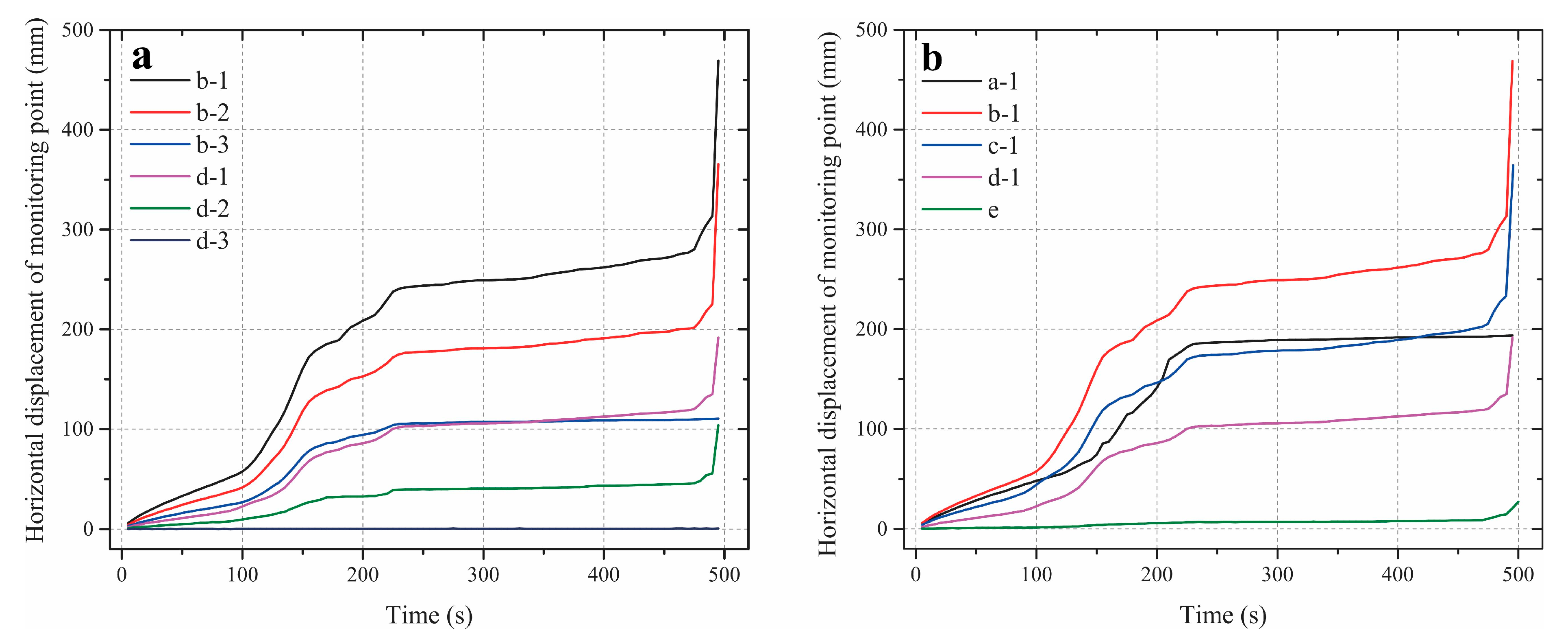
3.2. Evolution of the Slope Displacement
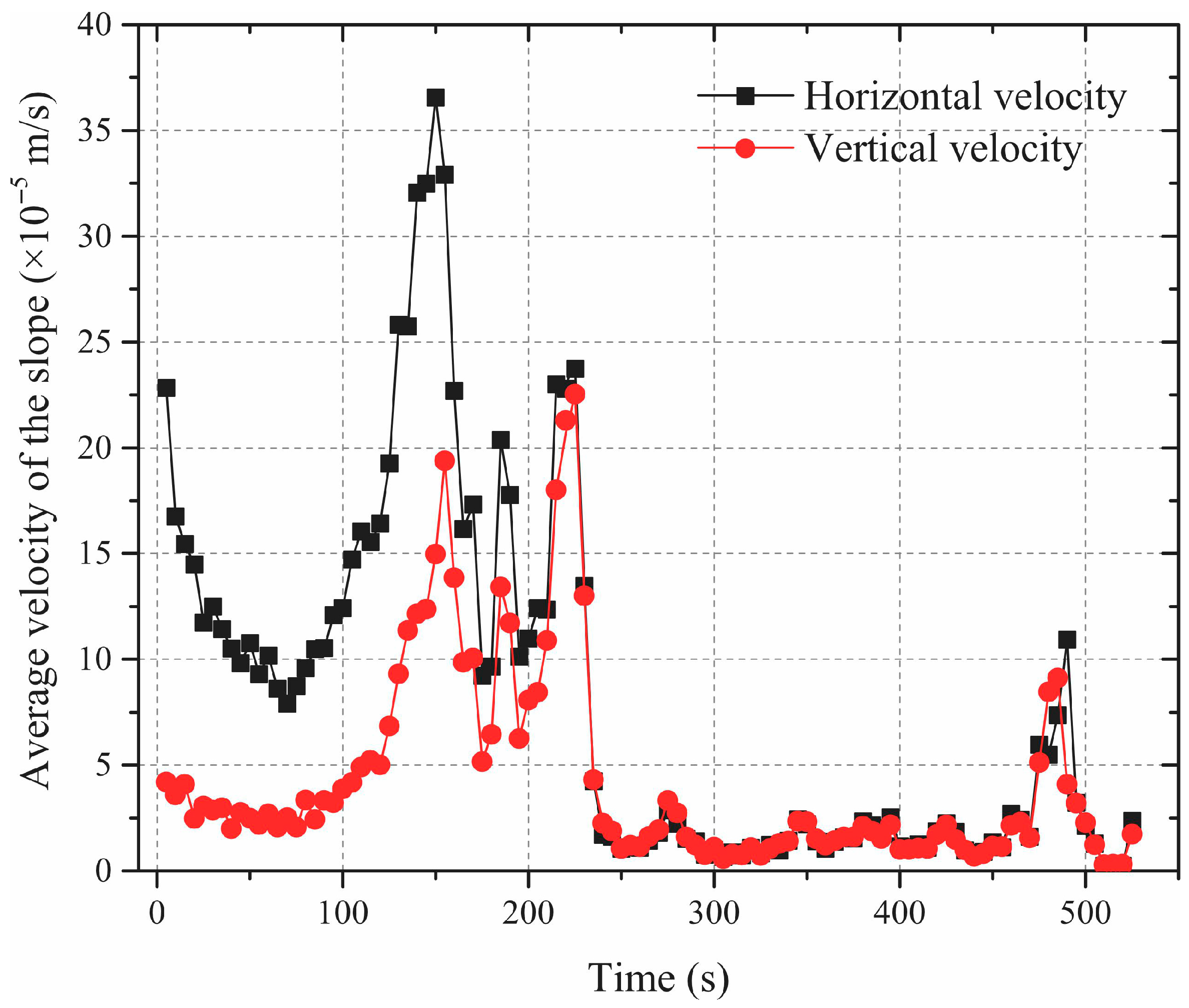
3.3. Evolution of the Slope Velocity
4. Discussion
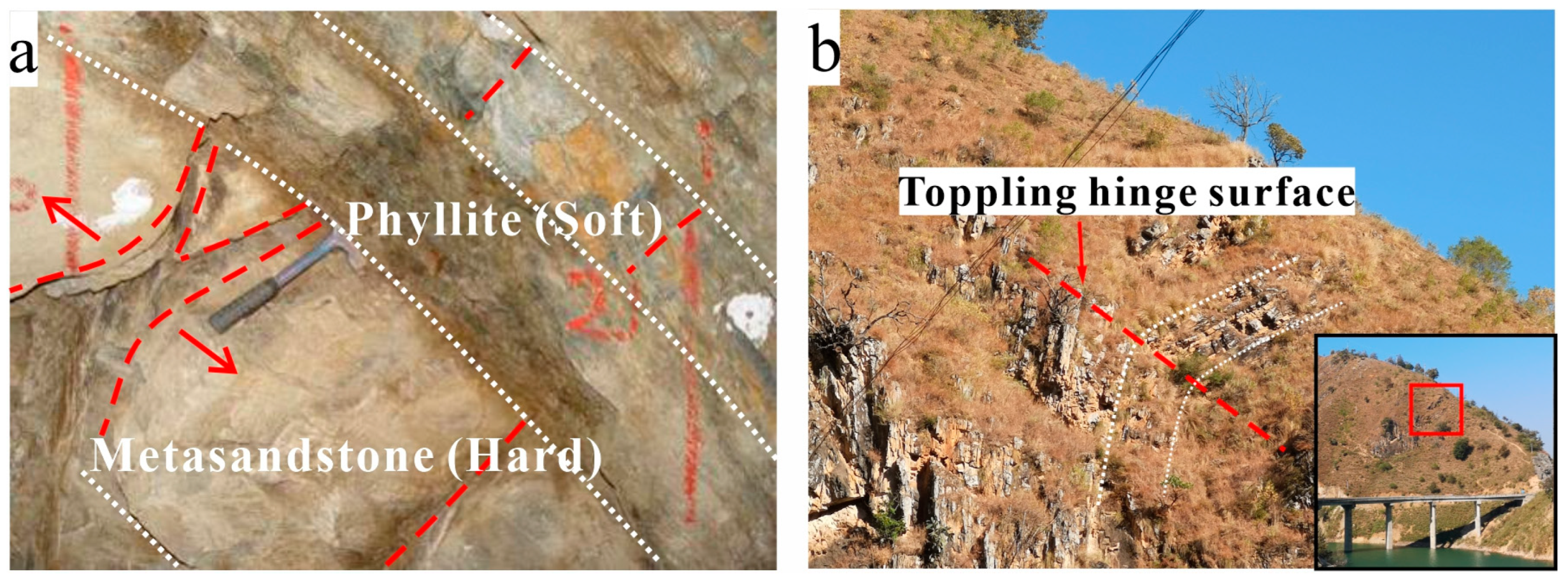
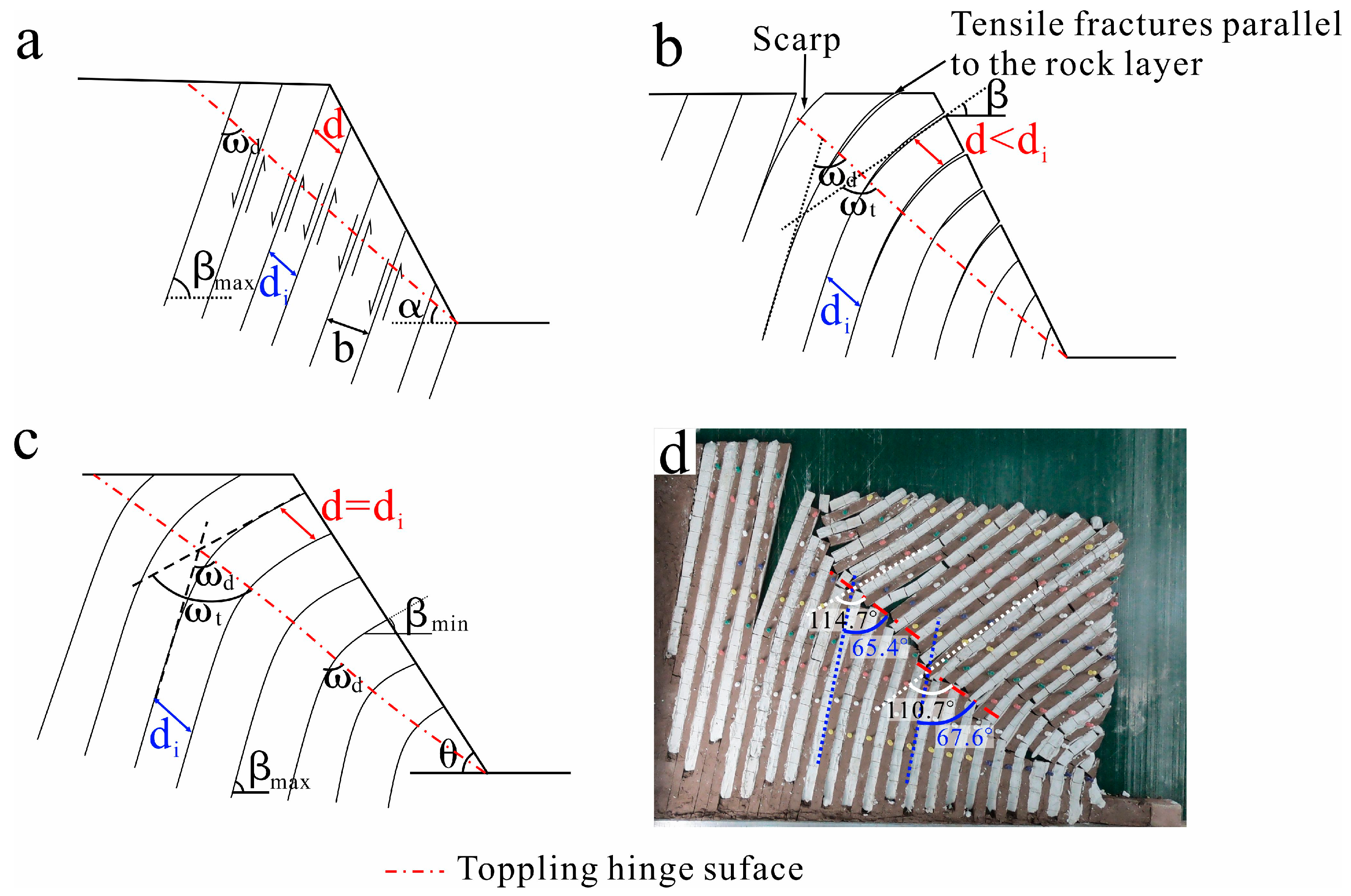
4.1. Uniqueness of the Interbedded Toppling
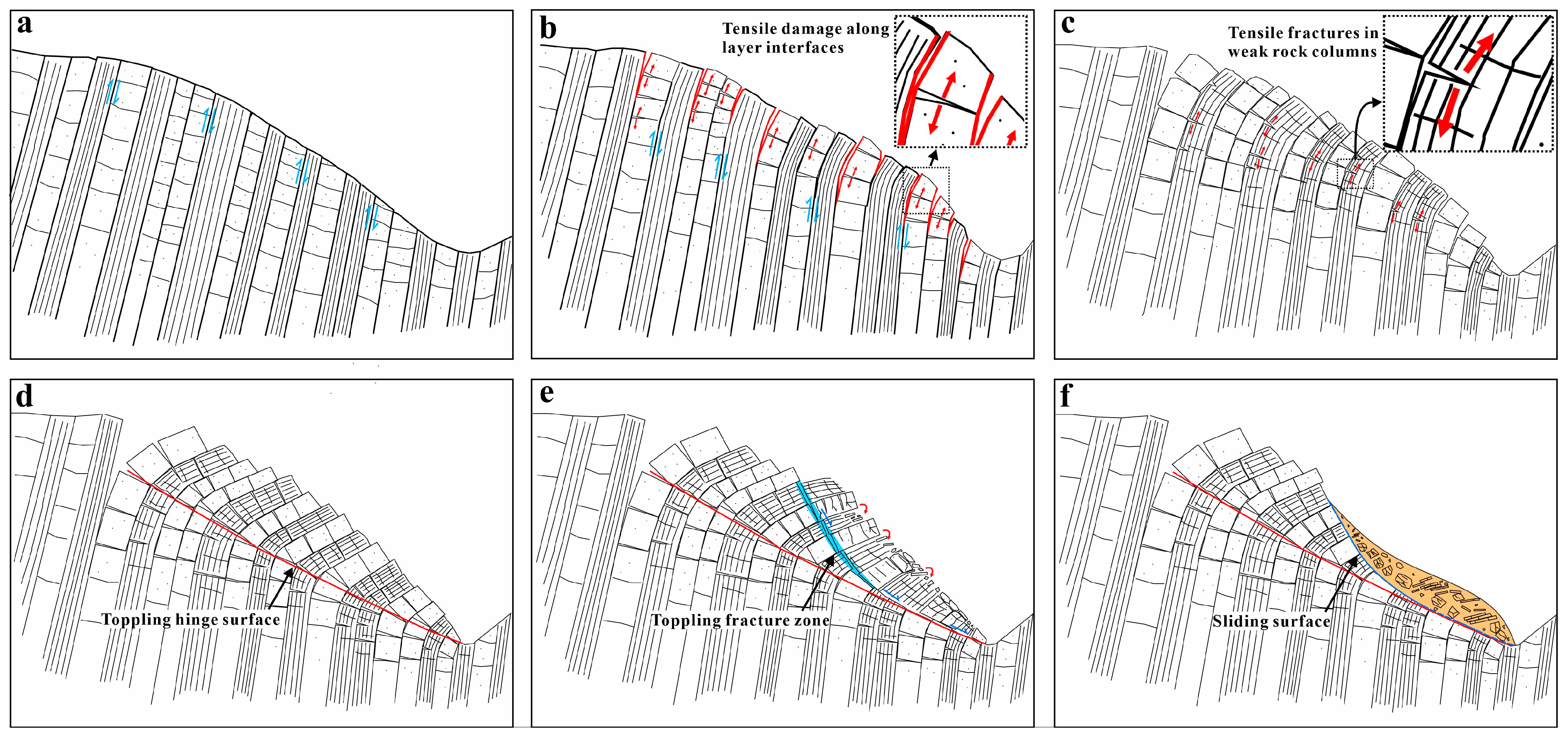
4.2. Evolution Process of the Interbedded Toppling
- (1)
- Initial shearing stage (Figure 13a)
- (2)
- Free rotation stage (Figure 13b,c)
- (3)
- Creep stage (Figure 13d)
- (4)
- Progressive failure stage (Figure 13e,f)
4.3. Limitations of the Model Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| THS | Toppling hinge surface |
| DIC | Digital Image Correlation |
| PIV | Particle Image Velocimetry |
References
- Goodman, R.E.; Bray, J.W. Toppling of rock slopes. In Proceedings of the Special Conference on Rock Engineering for Foundations and Slopes, ASCE, Boulder, CO, USA, 15–18 August 1976; Volume 1, pp. 201–234. [Google Scholar]
- Dong, M.; Zhang, F.; Lv, J.; Hu, M.; Li, Z. Study on deformation and failure law of soft-hard rock interbedding toppling slope base on similar test. Bull. Eng. Geol. Environ. 2020, 79, 4625–4637. [Google Scholar] [CrossRef]
- De Freitas, M.H.; Watters, R.J. Some field examples of toppling failure. Geotechnique 1973, 23, 495–513. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Y.; Zhang, P.; Tang, T.; Liu, Y.; An, Y. Deformation characteristics of anti-dip rock slope controlled by discontinuities: A case study. Bull. Eng. Geol. Environ. 2021, 80, 905–915. [Google Scholar] [CrossRef]
- Huang, D.; Ma, H.; Huang, R.; Peng, J.; Luo, S. Deep-seated toppling deformations at the dam site of the Miaowei Hydropower Station, Southwest China. Eng. Geol. 2022, 303, 106654. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, P.Z.; Chu, W.J.; Zhou, Y.; Liu, N.; Sheng, Q. Deformation mechanism and reinforcement design for the flexural toppled slope of Miaowei HPP. Bull. Eng. Geol. Environ. 2023, 82, 39. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Giraud, A.; Rochet, L.; Antoine, P. Processes of slope failure in crystallophyllian formations. Eng. Geol. 1990, 29, 241–253. [Google Scholar] [CrossRef]
- Glueer, F.; Loew, S.; Manconi, A.; Aaron, J. From toppling to sliding: Progressive evolution of the Moosfluh Landslide, Switzerland. J. Geophys. Res. Earth Surf. 2019, 124, 2899–2919. [Google Scholar] [CrossRef]
- Tu, G.; Deng, H. Formation and evolution of a successive landslide dam by the erosion of river: A case study of the Gendakan landslide dam on the Lancang River, China. Bull. Eng. Geol. Environ. 2020, 79, 2747–2761. [Google Scholar] [CrossRef]
- Tu, G.; Deng, H.; Shang, Q.; Zhang, Y.; Luo, X. Deep-seated large-scale toppling failure: A case study of the Lancang slope in Southwest China. Rock Mech. Rock Eng. 2020, 53, 3417–3432. [Google Scholar] [CrossRef]
- Ning, Y.; Tang, H.; Zhang, G.; Smith, J.V.; Zhang, B.; Shen, P.; Chen, H. A complex rockslide developed from a deep-seated toppling failure in the upper Lancang River, Southwest China. Eng. Geol. 2021, 293, 106329. [Google Scholar] [CrossRef]
- Fang, K.; Miao, M.; Tang, H.; Jia, S.; Dong, A.; An, P.; Zhang, B. Insights into the deformation and failure characteristic of a slope due to excavation through multi-field monitoring: A model test. Acta Geotech. 2023, 18, 1001–1024. [Google Scholar] [CrossRef]
- Fang, K.; Tang, H.; Li, C.; Su, X.; An, P.; Sun, S. Centrifuge modelling of landslides and landslide hazard mitigation: A review. Geosci. Front. 2023, 14, 101493. [Google Scholar] [CrossRef]
- Fang, K.; An, P.; Tang, H.; Tu, J.; Jia, S.; Miao, M.; Dong, A. Application of a multi-smartphone measurement system in slope model tests. Eng. Geol. 2021, 295, 106424. [Google Scholar] [CrossRef]
- Amini, M.; Golamzadeh, M.; Khosravi, M. Physical and theoretical modeling of rock slopes against block-flexure toppling failure. Int. J. Min. & Geo-Eng. 2015, 49, 155–171. [Google Scholar]
- Amini, M.; Ardestani, A.; Khosravi, M.H. Stability analysis of slide-toe-toppling failure. Eng. Geol. 2017, 228, 82–96. [Google Scholar] [CrossRef]
- Alejano, L.R.; Carranza-Torres, C.; Giani, G.P.; Arzúa, J. Study of the stability against toppling of rock blocks with rounded edges based on analytical and experimental approaches. Eng. Geol. 2015, 195, 172–184. [Google Scholar] [CrossRef]
- Alejano, L.R.; Sánchez–Alonso, C.; Pérez–Rey, I.; Arzúa, J.; Alonso, E.; González, J.; Beltramone, L.; Ferrero, A.M. Block toppling stability in the case of rock blocks with rounded edges. Eng. Geol. 2018, 234, 192–203. [Google Scholar] [CrossRef]
- Zhu, C.; He, M.; Karakus, M.; Cui, X.; Tao, Z. Investigating toppling failure mechanism of anti-dip layered slope due to excavation by physical modelling. Rock Mech. Rock Eng. 2020, 53, 5029–5050. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, C.; Liu, T.; Xia, K.; Liu, X. Stability analysis of rock slopes against sliding or flexural-toppling failure. Bull. Eng. Geol. Environ. 2018, 77, 1383–1403. [Google Scholar] [CrossRef]
- Ding, B.; Han, Z.; Zhang, G.; Beng, X.; Yang, Y. Flexural toppling mechanism and stability analysis of an anti-dip rock slope. Rock Mech. Rock Eng. 2021, 54, 3721–3735. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Dyskin, A.V.; Jewell, R.J. Modelling of flexural toppling failures of rock slopes. In Proceedings of the International Society for Rock Mechanics Congress, ISRM, Tokyo, Japan, 25–30 September 1995; pp. 25–29. [Google Scholar]
- Adhikary, D.P.; Dyskin, A.V.; Jewell, R.J.; Stewart, D.P. A study of the mechanism of flexural toppling failure of rock slopes. Rock Mech. Rock Eng. 1997, 30, 75–93. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Dyskin, A.V. Modelling of progressive and instantaneous failures of foliated rock slopes. Rock Mech. Rock Eng. 2007, 40, 349–362. [Google Scholar] [CrossRef]
- Pant, S.R.; Adhikary, D.P.; Dyskin, A.V. Slope failure in a foliated rock mass with non-uniform joint spacing: A comparison between numerical and centrifuge model results. Rock Mech. Rock Eng. 2015, 48, 403–407. [Google Scholar] [CrossRef]
- Bray, J.W.; Goodman, R.E. The theory of base friction models. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 453–468. [Google Scholar] [CrossRef]
- Aydan, Ö.; Shimizu, Y.; Ichikawa, Y. The effective failure modes and stability of slopes in rock mass with two discontinuity sets. Rock Mech. Rock Eng. 1989, 22, 163–188. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Chiu, M.A. Study on failure mechanism of toppling by physical model testing. In Proceedings of the 38th U.S. Rock Mechanics Symposium, Washington, DC, USA, 7–10 July 2001; pp. 989–995. [Google Scholar]
- Aydan, Ö.; Kawamoto, T. The stability of slopes and underground openings against flexural toppling and their stabilisation. Rock Mech. Rock Eng. 1992, 25, 143–165. [Google Scholar] [CrossRef]
- Adachi, T.; Ohnishi, Z.; Arai, K. Investigation of toppling slope failure at Route 305 in Japan. In Proceedings of the 7th ISRM Congress, Aachen, Germany, 16–20 September 1991. [Google Scholar]
- Tu, G.; Deng, H.; Li, M. Development and evolution of deep-seated toppling landslide by rapid river downcutting. Bull. Eng. Geol. Environ. 2023, 82, 185. [Google Scholar] [CrossRef]
- Li, Q.; Shi, W.; Yu, L.; Yang, C.; Zhu, C. Test evaluation of slope deformation and fissure network with different surface shapes under the action of underground mining. Bull. Eng. Geol. Environ. 2024, 83, 477. [Google Scholar] [CrossRef]
- Ning, Y.; Tang, H.; Zhang, B.; Ding, B.; Shen, P.; Xia, D.; Chen, H. Evolution process and failure mechanism of a deep-seated toppling slope in the Lancang River Basin. Chin. J. Rock Mech. Eng. 2021, 40, 2199–2213. [Google Scholar]
- Zhang, L.; Chen, Z.; Nian, G.; Bao, M.; Zhou, Z. Base friction testing methodology for the deformation of rock masses caused by mining in an open-pit slope. Measurement 2023, 206, 112235. [Google Scholar] [CrossRef]
- Wang, R.; Zheng, Y.; Chen, C.; Zhang, W. Theoretical and numerical analysis of flexural toppling failure in soft-hard interbedded anti-dip rock slopes. Eng. Geol. 2023, 312, 106923. [Google Scholar] [CrossRef]
- Huang, D.; Ma, H.; Huang, R. Deep-seated toppling deformations of rock slopes in western China. Landslides 2022, 19, 809–827. [Google Scholar] [CrossRef]
- Ning, Y.; Tang, H.; Wang, F.; Zhang, G. Sensitivity analysis of toppling deformation for interbedded anti-inclined rock slopes based on the Grey relation method. Bull. Eng. Geol. Environ. 2019, 78, 6017–6032. [Google Scholar] [CrossRef]
- Ning, Y.; Zhang, G.; Tang, H.; Shen, W.; Shen, P. Process analysis of toppling failure on anti-dip rock slopes under seismic load in southwest China. Rock Mech. Rock Eng. 2019, 52, 4439–4455. [Google Scholar] [CrossRef]
- Wang, S.N.; Xu, W.Y.; Shi, C.; Chen, H.J. Run-out prediction and failure mechanism analysis of the Zhenggang deposit in southwestern China. Landslides 2017, 14, 719–726. [Google Scholar] [CrossRef]
- Lv, J.; Shan, Z.; Yin, F.; Chen, L.; Dong, M.; Zhang, F. Deformation Characteristics and Stability Prediction of Mala Landslide at Miaowei Hydropower Station under Hydrodynamic Action. Water 2023, 15, 3942. [Google Scholar] [CrossRef]
- Mai, Z.; Hu, X.; Li, L.; Hou, J. Deformation characteristics and mechanism of Mala paleo-landslide during the Miaowei reservoir initial impoundment period. Sci. Rep. 2024, 14, 5059. [Google Scholar] [CrossRef]
- Ning, Y.; Tang, H.; Zhang, B.; Shen, P.; Zhang, G.; Xia, D. Investigation of the rock similar material proportion based on orthogonal design and its application in base friction physical model tests. Rock and Soil Mech. 2020, 41, 2009–2020. [Google Scholar]
- Fumagalli, E. Geomechanical models of dam foundation. In Proceedings of the International Colloquium on Physical and Geomechanical Models, Bergamo, Italy, 29–30 March 1979. [Google Scholar]
- Zhu, W.; Li, Y.; Li, S.; Wang, S.; Zhang, Q. Quasi-three-dimensional physical model tests on a cavern complex under high in-situ stresses. Int. J. Rock Mech. Min. Sci. 2011, 48, 199–209. [Google Scholar]
- Ning, Y.; Tang, H.; Peng, J.; Shen, Y.; Smith, J.V.; Ding, T. Study of the initiating and resisting mechanisms of toppling deformations in anti-inclined rock slopes. Bull. Eng. Geol. Environ. 2025, 84, 167. [Google Scholar] [CrossRef]
- Smith, J.V. Self-stabilization of toppling and hillside creep in layered rocks. Eng. Geol. 2015, 196, 139–149. [Google Scholar] [CrossRef]
- Ning, Y.; Tang, H.; Peng, J.; Shen, Y.; Smith, J.V.; Zhang, B. A stability evaluation method for deep-seated toppling in the upper Lancang River, Southwestern China. J. Rock Mech. Geotech. Eng. 2024, 16, 2388–2410. [Google Scholar] [CrossRef]




| Material Type | Density (kg/m3) | Elastic Modulus (GPa) | Cohesion (Mpa) | Internal Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Phyllite | 2700 | 6.0 | 3.0 | 40.0 | 5.0 |
| Target value 1 | 2700 | 2.9 × 10−3 | 1.45 × 10−3 | 40.0 | 2.4 × 10−3 |
| Similar material 1 | 2636 | 4.8 × 10−3 | 2.82 × 10−3 | 43.3 | 4.5 × 10−3 |
| Metasandstone | 2600 | 11.0 | 7.0 | 45.0 | 9.0 |
| Target value 2 | 2600 | 5.3 ×10−3 | 3.4 × 10−3 | 45.0 | 4.3 × 10−3 |
| Similar material 2 | 2480 | 6.7 × 10−3 | 4.8 × 10−3 | 48.7 | 6.1 × 10−3 |
| Material Type | Cohesion (Pa) | Internal Friction Angle (°) |
|---|---|---|
| Rock layer | 1.0 × 105 | 20 |
| Target value 3 | 48.4 | 20 |
| Similar material 3 | 68.7 | 18.8 |
| Cross joint | 3.0 × 105 | 30 |
| Target value 3 | 145.2 | 30 |
| Similar material 4 | 178.6 | 24.3 |
| Monitoring Point | Displacement (mm) | Velocity (m/s) | ||||
|---|---|---|---|---|---|---|
| Monitoring Value | True Value | Relative Error (%) | Monitoring Value | True Value | Relative Error (%) | |
| a-1 | 221.3 | 225.6 | −1.9 | 5.8 × 10−5 | 5.5 × 10−5 | 6.1 |
| b-1 | 375.2 | 391.7 | −4.2 | 6.9 × 10−4 | 7.5 × 10−4 | −7.7 |
| c-1 | 275.8 | 286.5 | −3.7 | 10.3 × 10−4 | 10.8 × 10−4 | −4.6 |
| d-1 | 158.6 | 164.8 | −3.8 | 8.5 × 10−4 | 9.0 × 10−4 | −5.0 |
| e | 10.7 | 11.1 | −4.0 | 1.5 × 10−4 | 1.4 × 10−4 | 8.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, Y.; Shen, Y.; Ding, T.; Xu, P.; Duan, F.; Zhang, B.; Zhang, B.; Smith, J.V. Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes. Appl. Sci. 2025, 15, 7727. https://doi.org/10.3390/app15147727
Ning Y, Shen Y, Ding T, Xu P, Duan F, Zhang B, Zhang B, Smith JV. Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes. Applied Sciences. 2025; 15(14):7727. https://doi.org/10.3390/app15147727
Chicago/Turabian StyleNing, Yibing, Yanjun Shen, Tao Ding, Panpan Xu, Fenghao Duan, Bei Zhang, Bocheng Zhang, and John Victor Smith. 2025. "Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes" Applied Sciences 15, no. 14: 7727. https://doi.org/10.3390/app15147727
APA StyleNing, Y., Shen, Y., Ding, T., Xu, P., Duan, F., Zhang, B., Zhang, B., & Smith, J. V. (2025). Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes. Applied Sciences, 15(14), 7727. https://doi.org/10.3390/app15147727






