Abstract
Image-based human age estimation has been a hot topic in the field of face attribute recognition. As the greatest dilemma of age estimation is the similar appearance of adjacent age labels, this paper presents a two-stage age estimation model based on the idea of coarse-to-fine decision strategy and fine-grained feature learning mechanism. In the first stage, Swin Transformer is employed to perform global age estimation for each image, and then an adaptive age range is obtained by local adjusted the global age estimation result. This stage gives a relative age trend of the input image. In the second stage, a local regressor is performed on the generated age range based on a sub-network combining semantic attention mechanism and hierarchical fine-grained feature pooling. The proposed semantic attention provides a guidance of age-sensitive regions for distinguishing fine-grained age-relevant feature in the second stage. The formulation of the proposed two-stage framework is intuitive and end-to-end trainable, and experiments on three popular age estimation benchmarks achieve the state-of-the-art results.
1. Introduction
Automatic age estimation is a crucial problem in biometrical recognition, and has plenty of practical applications, such as security verification, public-safety surveillance and border control. In [1], the authors illustrate that automatic age estimation supports the identification of undocumented individuals, accelerates the search for missing children and assists immigration officers in verifying the age of travelers or asylum applicants. Moreover, user profiling on social media, market analysis and human–computer interaction are further important application domains for automatic age estimation [2]. Although a lot of work has been made, effective human age estimation is still very challenging. As we all know, the aging process is slow and determined by many intrinsic and extrinsic factors, including identity, expression, pose illumination and so on. Therefore, there is an inherent ambiguity in the mapping between face image and its age label. Recent advances in age estimation have been made by deep learning models, which usually employ a one-stage network and can provide an overall estimation. However, it is still insufficient to perform accurate age estimation. As shown in Figure 1, the facial appearances tend to be very similar at adjacent ages, and errors frequently happen when distinguishing adjacent age labels. Despite the difficulties of accurate age estimation, it is relatively easy to achieve an accurate age range estimation of an unknown person and then perform finer age estimation within that range.

Figure 1.
Samples of facial images at adjacent ages.
Hierarchical age estimation is a successful method to perform the above from-coarse-to-fine decision strategy. A given face image is firstly classified into one of a number of age groups by a global estimation, then the precise age estimation is performed within the age group. Generally speaking, hierarchical age estimation is likely to result in better performance. Nevertheless, the existing works usually divide the age spectrum into several fixed age groups, such as [3,4], and improper quantization of age groups will also lead to large age estimation errors. On the other hand, the global estimation may provide prior knowledge to pick up some discriminative regions for better distinguishing adjacent age labels with subtle appearance differences. Therefore, refined age estimation from a small local range could benefit from more distinctive features learned from those age-sensitive areas. However, previous studies of hierarchical age estimation usually neglect the above guidance information.
In brief, we aim to design a new two-stage model that overcomes the limitations of fixed age group partitioning and the underutilization of global information in local refinement found in previous methods. By introducing an adaptive age range in the first stage and leveraging a semantic attention mechanism in the second stage, our model dynamically adjusts to age-specific ranges and focuses on age-sensitive facial regions, enabling more precise and flexible age estimation.
This paper proposes a novel two-stage deep model for age estimation. Our model sequentially performs a coarse estimation by relaxing the global age prediction to a local age range, and then refines the estimation from the local age range by semantic attention mechanism and fine-grained feature learning. At the first age estimation stage, an adaptive age range is obtained for each image by local adjustment of the global deep model prediction, which is learned based on Swin Transformer [5], to take advantage of global information during aging. At the second stage, we perform refined age estimation from local age range with the help of a semantic attention mechanism, which is a fine-grained classification task. The semantic attention aims to exploit global prediction as prior knowledge to locate more age-sensitive regions and features. During training, we define two losses for the two stages and jointly learn our model.
To recapitulate briefly, the contributions of our work are as follows:
(1) A novel hierarchical age estimation network is proposed, which consists of two sequential processes: global estimation and local estimation. Different from existing hard quantization of age groups, an adaptive age range is obtained by relaxing the global estimation. And at local age estimation, local feature interactions from multi-layers are learned to obtain the complementary information for fine-grained adjacent age label distinguishing.
(2) We propose a semantic attention mechanism by integrating semantic information of global estimation into the fine-grained feature representation at local estimation, which is beneficial to select the most useful features from age-sensitive regions.
(3) Extensive experimental comparisons and analysis about the role of local adjustment and semantic attention are conducted on the challenging age estimation benchmarks.
The remainder of the paper is organized as follows. Section 2 reviews related work about age estimation. Section 3 describes the proposed two-stage age estimation model in detail. Section 4 presents experimental results and comparative analysis. Section 5 discusses the strengths and limitations of the proposed method and suggests areas for future improvement. Section 6 summarizes the work.
2. Related Works
2.1. Deep Age Estimation
With the advancement of deep learning, age estimation is commonly formulated as a classification or regression problem. While early studies relied heavily on convolutional neural networks (CNNs) for extracting multi-scale deep features, recent approaches have begun to explore more powerful alternatives. For instance, Yi et al. [6] learned an ensemble of CNNs from multi-scale patches generated from facial landmarks, while Malli et al. [7] employed age-group-based CNN models for apparent age estimation. However, these CNN-based approaches often struggle to fully capture long-range dependencies and global facial context, which are critical for modeling aging patterns.
Recently, transformer-based architectures have gained attention for age estimation due to their ability to model global relationships and fine-grained visual dependencies. Among them, the Swin Transformer [8] introduces a hierarchical window-based self-attention mechanism, enabling effective multi-scale feature learning with reduced computation. Its success in general vision tasks has inspired its adoption in age estimation frameworks. In [9], the DAA model integrated delta age encoding into a binary code transformer using AdaIN operations, allowing the model to better represent age progression. In [10], a cross spatial and cross-scale Swin Transformer is proposed, which can extract fine-grained age-related features. In [11], the Scale-Adaptive Deformable Transformer (SADT) enhances the flexibility of attention across varying scales, improving model robustness in vision tasks. Similarly, ref. [12] introduced TopNet, utilizing Adaptive-Length Sliding Window Attention (AL-SWA) to efficiently capture both local and global dependencies. In [13], the TADFormer dynamically adapts to task-specific input contexts by performing fine-grained feature adaptation, improving multi-task learning efficiency and accuracy. Transformer-based models not only outperform CNNs in modeling contextual cues but also provide a flexible mechanism to incorporate auxiliary supervision, such as ordinal constraints and label distributions. These designs have shown strong generalization in real-world aging scenarios with high inter-subject variability.
2.2. Hierarchical Age Estimation
Hierarchical model which is a coarse-to-fine estimation process has been proved to be an effective age estimation framework by many works [14,15,16,17,18,19]. In [14], a hierarchical mixture model is constructed for facial age prediction by partitioning the age spectrum into multiple groups and subsequently training an expert network for each group. The work in [15] proposed a stage-wise soft regression network called SSR-Net, by which the age is estimated from coarse to fine. In [16], a multi-stage deep neural network was designed, which performs age estimation progressively through several cascaded stages. Each stage extracts and refines features at different levels, enabling a coarse-to-fine prediction process. Similarly, in [17], evolutionary label distribution learning and evolutionary slack regression were incorporated into a Coupled Evolutionary Network (CEN) to constantly refine the age estimation results from the last decision. In [18], a two-points representation of age label was proposed to assign an age group distribution to each age label and age estimation problem was then implemented by a cascaded age group estimation and age value estimation model. In [19], the proposed BridgeNet consisted of several local regressors, and the mixture of weighted regression results produced the final estimation. The weights were learned from the gating networks by employing the bridge-tree structure to enforce the similarity between neighbor local regressors. GroupFace [20] constructed a multi-hop attention graph convolutional network with group-aware margin optimization to handle data imbalance across age ranges, achieving state-of-the-art results on benchmark datasets.
2.3. Fine-Grained Visual Classification
Fine-grained classification focuses on recognizing visual objects from subordinate categories. Some approaches use two or more deep networks to make a better distinction of highly similar fine-grained images. The work in [21] proposed a bilinear model from two independent CNNs which are integrated by outer product to obtain more discriminating image features. The bilinear model is able to capture the pairwise feature interactions, which has proved its effectiveness for fine-grained visual classification task. Furthermore, in the work of [22], Yu et al. proposed a hierarchical bilinear pooling (HBP) model for fine-grained visual classification by exploiting relations of features from different layers.
Attention mechanism is another fine-grained classification scheme by finding the most discriminative regions of the images [23,24,25]. A representative work of this category is the Squeeze and Excitation (SE) module introduced in [26]. In order to obtain attention feature maps, SE module re-weighted the feature channels of the deep model by multi-layer perception. The work in [25] proposed an attribute-aware attention model which used attribute information to select important category features from different regions. The learned features contained more category relevant information for image recognition. There are also small inter-class differences between the adjacent ages in local age range, hence, accurate age estimation can be solved by fine-grained learning framework. In [27], the attention Long Short-Term Memory (LSTM) was combined into the CNN to capture the local features of age-sensitive areas for age group classification problem. Additionally, Wang et al. [28] proposed an attention-based dynamic patch fusion strategy that adaptively focused on the most age-relevant facial regions, effectively improving robustness to occlusion and pose variations. The authors of [29] proposed a multi-attention model, in which spatial attentions and channel attentions can be inferred in both self-attention and mutual-attention way.
3. Hierarchical Age Estimation with Semantic Attention
In this section, we propose a hierarchical age estimation model based on deep neural networks, as shown in Figure 2. The architecture consists of two main networks: a global network for coarse age prediction and a sub-network for local refined age estimation. In the first stage, the input image is processed through the Swin Transformer architecture, which extracts hierarchical features using patch partitioning and multiple transformer blocks. This global network performs an initial age prediction. The prediction errors are then corrected by a local adjustment module in the second stage, which incorporates semantic attention module and fine-grained feature learning to refine the prediction. The total loss function is designed by combining both global prediction and local prediction losses, optimizing the overall model performance for more accurate age estimation.
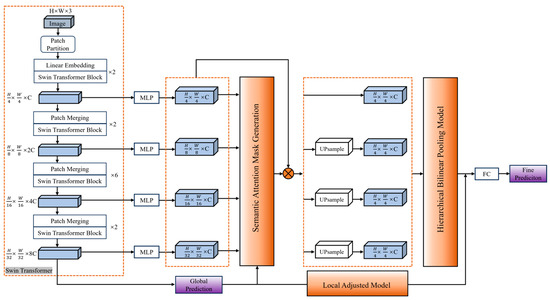
Figure 2.
Network architecture of proposed approach.
3.1. Swin Transformer Based Global Regression
3.1.1. Swin Transformer Architecture
Swin Transformer introduces a hierarchical model that builds feature map at various scales, and the window-based self-attention mechanism allows it to capture long-range dependencies in images that significantly enhance modeling power. Its core structure includes patch partition, linear embedding, shifted window-based multi-head self-attention (SW-MSA), window-based multi-head self-attention (W-MSA), and patch merging modules.
In this work, we adopt the Swin Transformer as the global feature extractor due to its great modeling power. Initially, the input image is partitioned into non-overlapping patches (patch partition), and each patch is projected into a high-dimensional embedding through a linear layer. The network is composed of multiple Swin Transformer Blocks, each consisting of a window-based attention layer followed by a shifted window attention layer. This design significantly improves information exchange across neighboring windows without significantly increasing computational complexity.
The Swin Transformer follows a four-stage hierarchical structure, with feature map resolutions progressively reduced from the input size of 224 × 224 to 56 × 56, 28 × 28, 14 × 14, and finally 7 × 7. This pyramid-like architecture enables multi-scale feature extraction, which is advantageous for age estimation tasks that require capturing features such as wrinkles, facial contours, and skin texture.
Compared with conventional convolutional models, Swin Transformer better models global contextual information and exhibits strong generalization capability in visual tasks, especially those requiring age-related reasoning across facial regions. In our model, the output of the fourth stage of the Swin Transformer serves as the input to the global regression branch, where label distribution learning and expectation regression are applied.
However, inferior global age estimation will lead to worse refined age estimation. In order to utilize the correlation among adjacent labels and improve the global age estimation performance, one solution is to perform label distribution learning for global age estimation, which firstly converts real-value age label to a Gaussian distribution, then a softmax layer is employed to obtain the prediction age distribution. Finally, an expected value over the predicted distribution is taken as the final global estimation. The final global age prediction is computed as the expected value of the predicted distribution :
3.1.2. Local Adjusted Decision
Although Swin Transformer effectively captures global semantic information, the inherent ambiguity and visual similarity between neighboring age labels make sole reliance on global prediction insufficient. To address this, we incorporate a local adjustment module to refine the global age prediction and improve estimation accuracy. Motivated by [30], errors mainly occurred around the global estimation. To enable more precise local regression, we construct a dynamic age range around the global estimation based on the local adjustment decision strategy. This local range is defined as:
where is the predicted global age and is the neighborhood radius. The radius is dataset-dependent and can be adaptively tuned. For instance, the optimal radius for Morph II and CACD is 10, while for MegaAge-Asian it is 15. More detailed analysis of the impact of the radius are discussed in the experimental section. This flexible adjustment strategy narrows the search space for local estimation, mitigates the global prediction errors and enhances the model’s focus on relevant age intervals.
3.2. Local Feature Learning and Semantic Attention Mechanism
3.2.1. Semantic Attention Mask Generation
Supposing the size of global feature maps from the last feature layer is , and global age estimation probability is , we firstly exploit a linear transformation layer to transform to a semantic guided feature weighting vector. Specially, it can be achieved by a fully connected layer that mapping the overall age label probability to a semantic guided feature channel weighting vector.
where and are model parameters. As a result, this global prediction guided semantic feature weighting vector provide an attention that denotes the importance of feature channels from global feature map.
In order to transfer the semantic attention to local age estimation, the intuition is to convert the feature weighting vector to a regional attention, which aims to select most age-sensitive local regions. For this purpose, we introduce an attention map by performing the 1 × 1 convolutional layer on the global feature map. The attention map can represent the visual patterns of facial patches and can be further used to produce the regional attention. By reshaping the size of attention map to , where , the regional attention mask is computed as follows:
where is the sigmoid function. The generated regional attention mask reflects the correlations between the local patches and the feature channels, and also describes the importance of the regions for age estimation. It can be easily propagated to the second local age estimation stage for fine-grained feature learning.
Specifically, given the regional attention mask obtained in Equation (4) we first broadcast it along the channel dimension to form . The broadcasted mask matches the shape of each local feature map and is applied through element-wise multiplication:
where denotes the attention-enhanced local feature and denotes element-wise multiplication. This spatial reweighting explicitly highlights age-sensitive areas, such as eye corners, forehead wrinkles and nasolabial folds, thus guiding the subsequent local branch to focus on the most informative regions for robust age estimation. This design is further supported by the attention heatmaps in Figure 3, which show that the semantic attention mechanism consistently emphasizes these key facial regions, confirming its effectiveness in guiding local refinement.

Figure 3.
Original maps and attention heatmaps of three faces. The red areas represents the most age-sensitive regions.
3.2.2. Local Feature Learning
Local age estimation is essentially a fine-grained visual classification task due to the subtle differences in facial appearance between neighboring ages. In this section, we propose a local feature learning strategy that utilizes multi-scale feature extraction and cross-layer interaction to improve the accuracy of age estimation.
In particular, we designed a sub-network that first projects the four-stage multi-scale features of the Swin Transformer to a unified channel width with individual MLP layers; then, the enhanced local feature is obtained by semantic attention mechanism. Subsequently, the Transformer bilinearly upsamples the lower-resolution maps so that every feature attains the common spatial size
Finally, the attention-enhanced feature set is fed to the hierarchical bilinear pooling module. As has been proved by the HBP work in [22], inter-layer part feature interaction and fine-grained feature learning are mutually correlated and can reinforce each other. Therefore, we employed hierarchical bilinear pooling (HBP), which computes pairwise bilinear interactions across layers. Let x,y,z,o ∈ RC be the channel-wise descriptors obtained by global average-pooling the local feature maps F1,F2,F3,F4 and U,V,S,R ∈ Rc × d be learnable projection matrices that map each descriptor into a common d-dimensional sub-space. Thus, the fused feature is calculated as:
This operation captures complementary information across layers and enhances feature discriminability.
3.3. Joint Training
The training procedure is conducted in two stages: the global estimation stage and the local estimation stage. The learning of global estimation is combined by the label distribution learning and expectation regression. The Kullback–Leibler (KL) divergence is employed to measure the difference between ground-truth label distribution and the global prediction distribution . As in [31], the ground-truth label distribution is assumed to be Gaussian distribution and the loss is adopted for expectation regression. Therefore, we define the total loss for global estimation as follows:
where is the prediction age at the global estimation stage. At local estimation stage, the learning of the local regression model is implemented by minimizing the loss between ground truth age label and the prediction of the final age as follows:
where is the prediction age at the local estimation stage. The second term in Equation (7) urges the local regressed age lie in an interval . Finally, the total loss for our model is defined as follows:
where is a parameter to balance the importance of the global estimation result and the local estimation result.
4. Experimental Results and Analysis
This section experimentally evaluates the performance of our two-stage network on three challenging age datasets. It is noteworthy that all comparison results reported in this section are obtained under the same conditions and are directly taken from the corresponding original papers. Firstly, the three datasets, evaluation protocol and implementation details employed in the experiments are introduced. Secondly, the results of the experiments are reported and analyzed, which validate the proposed two-stage model. Thirdly, the ablation experiments are discussed, exploring the role of each module and parameter settings of the proposed model. Finally, the speed analysis and qualitative results are presented to intuitively explain our model.
4.1. Datasets
The proposed age estimation framework involves five datasets: IMDB-WIKI [32], Morph II [33], MegaAge-Asian [34], CACD [35] and ImageNet [36].
IMDB-WIKI is currently the largest publicly available age estimation benchmark. It has 523,051 facial images in total, with 460,723 images from IMDB and the remaining images from Wikipedia. The age in IMDB-WIKI ranges from 0 to 100. Since the images from IMDB-WIKI contain too much noise, it is not suitable for evaluating the performance of the age estimation study. IMDB-WIKI is used for pre-training in most previous human age estimation works, e.g., SSR [15] and DEX [32].
ImageNet is a large-scale image classification dataset that contains 1.2 million training images and 50,000 validation images of 1000 classes. It is widely used to pre-train deep convolutional neural networks. Although ImageNet does not contain age-specific labels, pre-training on this dataset helps the model to learn general visual features. Therefore, it was employed to fine-tuned our basic Swin Transformer for age estimation task.
Morph II is the most widely used human age estimation dataset; it includes 55,134 facial images from 13,617 subjects. The ages range from 16 to 77. Popular experimental protocol used for Morph is 80% for training and 20% for testing. Since Morph II is large enough to carry out real age estimation, we employ it to evaluate the effectiveness of our model and compare with the state-of-the-arts.
MegaAge-Asian is another large-scale age estimation benchmark, which has 40,000 facial images with multiple image variations involving illumination, pose and expression. Different from Morph II, MegaAge-Asian is collected from Asians. The age ranges from 0 to 70 and we employ 3945 images for testing and the remaining ones for the training.
CACD is a publicly available cross-age face dataset containing 166,417 images collected from 2000 celebrities, with ages ranging from 14 to 62 years. The dataset is divided into three subsets: the training set consists of 1800 celebrities, the testing set includes 120 celebrities, and the validation set contains 80 celebrities. Given that the dataset includes a variety of facial expressions, illumination, and pose variations, it provides a rich and diverse source of data for training age estimation models. Following previous works, we train our model on the training subset and report its performance on the test subset
4.2. Evaluation Protocol
As in most previous age estimation work, it is fair to evaluate the performance of our two-stage network with the widely used Mean Absolute Error (MAE) for Morph II dataset and Cumulative Score (CS) for MegaAge-Asian dataset. MAE calculates the average of absolute errors between the real ages and the estimated ages, which is represented as shown below:
where and denote the real age and estimation age of the -th test image. CS is defined as the number of test images whose absolute error is smaller than , which is represented as follows:
The better age estimation performance will possess lower MAE and higher CS.
4.3. Implementation Details
In all the experiments, the images are cropped according to facial landmarks and resized into 224 × 224 as the inputs to our model. The commonly used random sampling and horizontal flipping is also performed to augment data during the training. We firstly pre-train our global Swin Transformer network on ImageNet dataset and then fine-tune the complete two-stage network separately on each age-estimation benchmark dataset, AdamW optimizer is employed simultaneously. The base learning-rate is 0.0001, it is linearly warmed up for five epochs, and then cosine-decayed to . The momentum and the weight decay are set to 0.9 and 0.005, respectively. There are 200 epochs for training, and the batch size is set to be 64. The factors , in the loss function are set to 4,4 in all the experiments.
4.4. Comparisions with State-of-the-Arts
4.4.1. Experiments on Morph II Dataset
The proposed framework is first compared with recent state-of-the-art methods on the Morph II benchmark. Among non-hierarchical methods, the MV [37] reports an MAE of 2.16, with CS(3) at 75.00% and CS(5) at 89.90%, while DAA [9] achieves an MAE of 2.06 by combining delta-age encoding with a binary transformer. Classic ensembles of models such as DEX [32] achieves an MAE of 2.68. In hierarchical architectures, SSR-Net [15] reaches an MAE above 3.1, with CS(5) remaining below 80%. The compact ALD-Net [38], which uses no additional pre-training, achieves an MAE of 2.65. Transformer-based methods further improve the performance; for example, GroupFace [20] couples multi-hop graph attention with group-aware margins and attains 2.01 MAE. Table 1 summarizes these results in terms of MAE, CS(3), CS(5). Benefiting from its semantic attention guided two-stage design, the proposed model achieves an MAE of 2.18 with ImageNet pre-training, comparable to MV [37] and surpassing most hierarchical and CNN ensemble baseline methods. For cumulative scores, our model reaches 79.93% for CS(3) and 90.96% for CS(5), demonstrating superior performance in distinguishing adjacent age labels.

Table 1.
Comparison results for age estimation on Morph II.
Our proposed method follows a coarse-to-fine hierarchical strategy by first predicting a global age and then refining it locally. Compared to most methods, our framework achieves better performance through several key improvements. Instead of relying solely on the final CNN features, we extract multi-stage features from a Swin Transformer backbone and fuse them using enhanced bilinear pooling, capturing fine-grained age cues more effectively. Moreover, we introduce a lightweight semantic attention mechanism that leverages global age predictions to guide local feature refinement, allowing the model to focus on age-sensitive regions. The integration of multi-scale feature extraction, global context enhancement, and adaptive feature weighting further boosts the model’s capacity to distinguish adjacent ages under varied conditions. All modules are jointly optimized in an end-to-end fashion, ensuring coherent learning between the global and local stages.
4.4.2. Experiments on MegaAge-Asian Dataset
To verify the performance of our framework on other races, we also conduct experiments on the MegaAge-Asian dataset. Facial images in Morph II are usually from Whites and Blacks, but MegaAge-Asian dataset only contains Asians. In Table 2, we report the comparison results in terms of MAE, CS(3) and CS(5).

Table 2.
Comparison results for age estimation on MegaAge-Asian.
As reported in Table 2, it can be seen that our model achieves an MAE of 3.09, with CS(3) at 63.11% and CS(5) at 82.30%. The performance is competitive when compared with other state-of-the-arts. Among non-hierarchical methods, this translates into about 15~40% relative improvement in CS(3) and 11~36% in CS(5) over classical CNN baselines such as MobileNet [15] and DenseNet [15]. Compared with recent label-distribution and hierarchical methods such as SSR-Net [15] and ALD-Net [38], our model also exhibits noticeable gains on both CS(3) and CS(5). Although DAA [9] achieves the best CS(3) 68.82% and CS(5) 84.89% by combining extra IMDB-WIKI pre-training, binary age-code supervision and multi-stage incremental training, these additional mechanisms substantially increase model complexity and training overhead.
4.4.3. Experiments on CACD Dataset
We also conduct experiments on the CACD dataset, which is a widely used cross-age face dataset containing a large number of celebrity face images ranging from 14 to 62 years old. To comprehensively evaluate the performance of our method, we also use three evaluation metrics: MAE, CS(3) and CS(5), for comparison with other methods. Detailed comparisons are made among non-hierarchical and hierarchical methods to demonstrate the effectiveness of our proposed model on the CACD dataset.
The experimental results on the CACD dataset are reported in Table 3. Our method achieves an MAE of 4.47, significantly outperforming most competing methods. Among non-hierarchical methods, Soft softmax [44] reaches an MAE of 5.19, dLDLF [45] reaches 6.16, DEX [32] reaches 6.52, CasCNN [46] reaches 5.23 and RNDF [47] reaches 4.59; all of them are clearly higher in MAE than our method. Meanwhile, our model also demonstrates strong competitiveness among hierarchical methods. ADPF [28] achieves an MAE of 5.39 and MoE [14] achieves 5.19, but our model achieves a lower MAE of 4.47, outperforming these hierarchical methods. Additionally, our model also excels in cumulative scores, achieving 52.91% for CS(3) and 77.63% for CS(5), both of which are significantly higher than other methods. Though GroupFace [20] achieves the lowest MAE, this should be attributed to its complex multi-hop graph attention and group-aware margin coupling technology. These comparative results clearly demonstrate the superiority of our method on the CACD dataset, showing its ability to better handle age estimation tasks for cross-age faces.

Table 3.
Comparison results for age estimation on CACD.
4.5. Ablation Study
4.5.1. Impact of Each Module
To validate the effectiveness of our proposed framework, we conducted a thorough empirical study to investigate the role of each individual module within the network. Table 4 summarizes the comparison results in MAE and CS(3) among different module configurations evaluated on the Morph II, MegaAge-Asian and CACD datasets.

Table 4.
Comparison of role of each module in our framework.
The first row reports the baseline performance when only the Swin Transformer is employed for global age estimation, achieving 2.33 MAE and 72.99% CS(3) on Morph II, 3.18 MAE and 61.98% CS(3) on MegaAge-Asian and 5.15 MAE and 42.91% CS(3) on CACD, which already provides a solid starting point thanks to the strong representation power of Swin Transformer.
In the second row, the inclusion of the local adjustment module refines the global prediction, the MAE drops slightly to 2.31 and CS(3) increases to 74.53% on Morph II, while the MAE improves to 3.12 but CS(3) falls marginally to 60.23% on MegaAge-Asian. On CACD, the inclusion of local adjustment reduces the MAE to 5.02 and increases CS(3) to 43.80%. This shows that narrowing the search space of age is often helpful for age estimation.
The third row replaces the local adjustment module with the semantic attention mechanism. It yields 2.28 MAE and 74.37% CS(3) on Morph II, 3.20 MAE and 59.49% CS(3) on MegaAge-Asian and 5.11 MAE and 42.74% CS(3) on CACD, confirming that semantic attention enhances discrimination for age on Morph II, although its benefit is less pronounced on the MegaAge-Asian set and CACD.
The fourth row combines both local adjustment and semantic attention, significantly boosting accuracy. It yields 2.25 MAE and 74.27% CS(3) on Morph II, 3.06 MAE and 61.12% CS(3) on MegaAge-Asian and 4.51 MAE and 47.73% CS(3) on CACD. The joint use of the two modules clearly outperforms either one alone in terms of MAE and CS on all datasets.
Finally, the last row shows the performance of our full model, which integrates Swin Transformer, local adjustment, semantic attention, and hierarchical bilinear pooling (HBP). The addition of HBP allows for effective cross-layer feature interactions, enriching the local feature representation. This comprehensive framework achieves the best results, with an MAE of 2.18 and a CS(3) of 79.93% on the Morph II dataset, a competitive MAE of 3.09 and CS(3) of 63.11% on MegaAge-Asian and 4.47 MAE and 52.91% CS(3) on CACD. Compared with the baseline Swin Transformer, all metrics show significant improvements across the three datasets.
Overall, these results clearly demonstrate that each module contributes positively to the age estimation task. The global estimation stage with Swin Transformer provides a rough but solid prediction of the true age. The local adjustment module effectively refines this prediction by focusing on a narrowed age range. The semantic attention mechanism further enhances performance by selecting more discriminative, age-sensitive facial regions for fine-grained local feature learning. Finally, HBP complements the pipeline by capturing complementary information across feature layers. Together, this hierarchical design significantly improves the accuracy and robustness of age estimation, validating the effectiveness of our two-stage framework.
4.5.2. Impact of Radius in Local Adjustment
We also investigate the effect of the radius parameter in the local adjustment module. To demonstrate the impact across different races and individuals, the experiment is conducted on Morph II, MegaAge-Asian and CACD datasets. As shown in Table 5, the radius is varied from 5 to 20. For the Morph II and CACD dataset, the best age estimation performance is achieved when the radius is set to 10. It reaches 2.18 MAE and 79.93% CS(3) on Morph II and 4.47 MAE and 52.91% CS(3) on CACD. For the MegaAge-Asian dataset, however, the optimal radius is 15, which yields an MAE of 3.18 and a CS(3) of 64.55%. These results suggest that the population in the MegaAge-Asian dataset appears to age more slowly compared to that in Morph II and CACD. When comparing the characteristics of the three datasets, MegaAge-Asian contains more diverse image variations, such as differences in lighting, cluttered backgrounds, glasses, and makeup. These factors likely influence the optimal radius setting, aligning with the common perception that Asians seem to age more slowly, partly due to makeup. In summary, we conclude that the radius parameter in the local adjustment module significantly affects the age estimation results, and the optimal radius should be carefully tuned according to the specific characteristics of each dataset.

Table 5.
Comparison of local adjustment at different radius settings.
4.5.3. Impact of Multi-Task Learning with Parameters and
We further explore the influence of hyperparameters and within our loss function, aiming to identify the optimal balance among local regression loss and the interval penalty in the two-stage estimation scenario. We conduct experiments on Morph II by fixing one parameter at its optimal value and varying the other to study its impact. It is important to note that cannot be set to 0, as this would result in the disappearance of the local regression module, leading to the loss of local adjustment information. Figure 4a illustrates the performance trend as increases from 1 to 8, while is fixed at 4. It is clear that the network achieves its lowest MAE around 2.2 and highest CS(3) of approximately 80% when = 4. This indicates that an appropriate weight on the regression loss effectively fine-tunes the local age predictions, while excessively large or small values may impair the model’s capability to accurately capture fine-grained age-related features. Figure 4b shows the model performance variation as changes from 0 to 8 with fixed at 4. The results demonstrate a clear initial improvement in MAE and CS(3) as increases up to 4, after which the performance declines. This trend suggests that an appropriate interval penalty effectively constrains predictions to reasonable local age intervals, while overly strict or overly relaxed interval penalties reduce prediction performance.
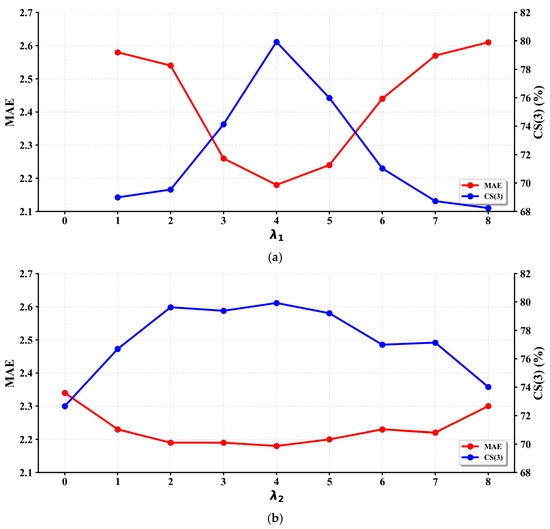
Figure 4.
MAE and CS(3) on Morph II using (a) different and fixed = 4, and (b) different and fixed = 4.
Based on the above analyses, we finalize our choice as = 4 and = 4, striking an optimal balance between local regression precision and interval constraint stability, thus yielding the best overall age estimation results.
4.6. Speed Analysis
In this section, we evaluate the inference speed of our model on an NVIDIA RTX 4090 GPU (24 GB GDDR6X) and 16-core AMD EPYC 7502 CPU using three metrics: runtime per image in milliseconds, frames per second (FPS), and model complexity measured by million multiply-accumulate operations (MACC). The runtime denotes the average processing time over images from test set, and the FPS is calculated as the number of images inferred per second. The MACC is the total number of multiply-accumulate operations (in millions) required by the model, reflecting its computational cost. Table 6 compares these metrics for various combinations of the four modules: the baseline Swin Transformer alone and variants that incorporate the local adjustment module, the semantic attention module, and the hierarchical bilinear pooling (HBP) module, either individually or jointly.

Table 6.
Speed analysis.
As shown in Table 6, the computational demands vary noticeably depending on which modules are included. The baseline Swin Transformer model achieves a runtime of 1.69 ms (≈591 FPS) with 47.82 M MACC. Adding the local adjustment module increases the runtime to 1.97 ms (507 FPS) and MACC to 48.16 M, indicating a modest overhead. Similarly, incorporating the semantic attention module yields a runtime of 1.91 ms (523 FPS) and 47.99 M MACC. When both the local adjustment and semantic attention modules are combined, the runtime further rises to 2.14 ms (467 FPS) with 48.33 M MACC. In contrast, after incorporating the HBP module, the full model incurs the largest additional cost. Specially, the full model requires 3.52 ms per image (284 FPS) and 50.51 M MACC, roughly doubling the base inference time. Nonetheless, this full configuration achieves the best accuracy for the MAE on Morph II improving to 2.18 from 2.33 for the base model. These results demonstrate that while our full model incurs higher computational cost due to the integration of all modules, it achieves a significant breakthrough in accuracy. The performance gain justifies the added complexity, making the overall computation–effectiveness trade-off highly acceptable.
4.7. Qualitative Results
Qualitative results on the three datasets are also given in Figure 5. The images from the first row and the third row are from Morph II, MegaAge-Asian and CACD, respectively. By the first three images of each row, our model is able to perform age estimation task very precisely although the race is different. By the last three images of each row, we also show a number of face images where our model fails. There are several possible reasons. Firstly, the aging speed during middle ages is slow; it is difficult to accurately discriminate adjacent ages from visual similar appearances. Secondly, some images are under extreme conditions, such as illumination variations, glasses, clutters and makeup of girls.

Figure 5.
Examples from test sets of three datasets.
5. Discussion
Compared to prior approaches, the proposed method exhibits clear advantages in addressing key age estimation challenges. CNN-based hierarchical models such as SSR-Net [10] and BridgeNet [14] pioneered coarse-to-fine prediction pipelines, but they rely on fixed age group partitions that can introduce quantization errors. In contrast, our two-stage network dynamically adjusts the local age range around each face’s initial age prediction, mitigating rigid group boundary issues and directly tackling the ambiguity between neighboring age labels. Furthermore, whereas SSR-Net and BridgeNet do not leverage global context to guide fine-grained predictions, our model integrates a semantic attention mechanism that uses the global age estimate to focus on discriminative, age-sensitive facial regions. This guided refinement of local features enables the proposed method to distinguish subtle differences between adjacent ages more effectively than previous CNN-based methods. Transformer-based architectures have also advanced age estimation performance. By leveraging a Swin Transformer in the global stage, our model similarly benefits from rich contextual modeling, attaining a competitive MAE of 2.18 on the same benchmark and surpassing most existing frameworks. Notably, the proposed approach achieves superior cumulative score for closely spaced age labels, as demonstrated by a CS(5) of 90.96% on the Morph II dataset, underscoring its strength in fine-grained age differentiation and further validating the effectiveness of the semantic attention-guided hierarchical design.
Automatic age estimation remains crucial in biometric recognition and various real-world applications, which underscores the value of further improving accuracy and robustness. Despite its strong performance, the proposed two-stage model has a few limitations. First, the neighborhood radius for refinement is manually defined for each dataset, which may not optimally adapt to every individual. Second, the incorporation of a Transformer backbone and a dual-stage architecture results in a relatively large model, potentially hindering deployment on resource-limited devices. In future work, we plan to explore adaptive mechanisms that learn an optimal neighborhood radius dynamically and to investigate model simplification or compression techniques to reduce the parameter count. Addressing these issues would further enhance the practicality and applicability of the proposed approach in real-world settings.
6. Conclusions
In this paper, we proposed a two-stage age-estimation network that comprises a coarse stage followed by a refined stage. During the coarse stage, a global branch predicts a full label distribution and its expectation, thus exploiting information from neighboring ages. This prediction is then softly adjusted to form an image-specific local age range. Guided by that range, the refined stage combines fine-grained feature learning with a lightweight semantic attention mechanism to produce the final estimate. Experiments on three large-scale benchmarks, Morph II, MegaAge-Asian and CACD, verified the superiority of the proposed framework. However, the neighborhood radius used in the local adjusted module is still selected manually, and the full model architecture keeps the parameter count in the tens of millions, so future work will focus on learning an adaptive neighborhood radius per image and reducing the overall model size to improve inference speed.
Author Contributions
Conceptualization, C.H.; methodology, X.Q.; software, X.Q.; validation, B.Q.; writing—original draft preparation, X.Q.; writing—review and editing, C.H.; visualization, B.Q.; supervision, C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grants 62376109.
Institutional Review Board Statement
Ethical review was waived as this study solely utilized publicly available anonymized datasets.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article and the data supporting the findings are openly accessible. Further information is available from the corresponding author upon request.
Acknowledgments
All authors gratefully acknowledge the reviewing experts for their constructive feedback and professional guidance.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rahman, A.; Aonty, S.S.; Deb, K.; Sarker, I.H. Attention-Based Human Age Estimation from Face Images to Enhance Public Security. Data 2023, 8, 145. [Google Scholar] [CrossRef]
- Zhang, Y.; Shou, Y.; Meng, T.; Ai, W.; Li, K. A Multi-view Mask Contrastive Learning Graph Convolutional Neural Network for Age Estimation. Knowl. Inf. Syst. 2024, 66, 7137–7162. [Google Scholar] [CrossRef]
- Tan, Z.; Wan, J.; Lei, Z.; Zhi, R.; Guo, G.; Li, S.Z. Efficient Group-n Encoding and Decoding for Facial Age Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2610–2623. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, R.; Aarabi, P. Continuous Face Aging via Self-estimated Residual Age Embedding. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15003–15012. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar] [CrossRef]
- Yi, D.; Lei, Z.; Li, S.Z. Age Estimation by Multi-scale Convolutional Network. In Computer Vision—ACCV 2014, Proceedings of the 2014 Asian Conference on Computer Vision (ACCV), Singapore, 1–5 November 2014; Springer: Singapore, 2014; pp. 144–158. [Google Scholar]
- Malli, R.C.; Aygun, M.; Ekenel, H.K. Apparent Age Estimation Using Ensemble of Deep Learning Models. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 714–721. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the 2021 9th International Conference on Learning Representations (ICLR), Virtually, 3–7 May 2021. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, X.; Li, Y.; Tao, J.; Xiao, B.; Wang, B.; Jiang, Z. DAA: A Delta Age AdaIN operation for age estimation via binary code transformer. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 15836–15845. [Google Scholar]
- Xu, L.; Hu, C.; Shu, X.; Yu, H. Cross spatial and Cross-Scale Swin Transformer for fine-grained age estimation. Comput. Electr. Eng. 2025, 123, 110264. [Google Scholar] [CrossRef]
- He, X.; Quan, Y.; Xu, R.; Ji, H. A Universal Scale-Adaptive Deformable Transformer for Image Restoration across Diverse Artifacts. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR) 2025, Nashville, TN, USA, 11–15 June 2025; pp. 12731–12741. [Google Scholar]
- Wang, X.; Zhang, Y.; Liu, T.; Liu, X.; Xu, K.; Wan, J.; Guo, Y.; Wang, H. TopNet: Transformer-Efficient Occupancy Prediction Network for Octree-Structured Point Cloud Geometry Compression. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 27305–27314. [Google Scholar]
- Baek, S.; Lee, S.; Jo, H.; Choi, H.; Min, D. TADFormer: Task-Adaptive Dynamic TransFormer for Efficient Multi-Task Learning. arXiv 2025, arXiv:2501.04293. [Google Scholar]
- Zhao, Q.; Liu, J.; Wei, W. Mixture of deep networks for facial age estimation. Inf. Sci. 2024, 679, 121086. [Google Scholar] [CrossRef]
- Yang, T.-Y.; Huang, Y.-H.; Lin, Y.-Y.; Hsiu, P.-C.; Chuang, Y.-Y. SSR-Net: A Compact Soft Stagewise Regression Network for Age Estimation. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; International Joint Conferences on Artificial Intelligence Organization: Stockholm, Sweden, 2018; pp. 1078–1084. [Google Scholar]
- Bekhouche, S.E.; Benlamoudi, A.; Dornaika, F.; Telli, H.; Bounab, Y. Facial Age Estimation Using Multi-Stage Deep Neural Networks. Electronics 2024, 13, 3259. [Google Scholar] [CrossRef]
- Li, P.; Hu, Y.; He, R.; Sun, Z. A Coupled Evolutionary Network for Age Estimation. arXiv 2018, arXiv:1809.07447. [Google Scholar]
- Zhang, C.; Liu, S.; Xu, X.; Zhu, C. C3AE: Exploring the Limits of Compact Model for Age Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12579–12588. [Google Scholar]
- Li, W.; Lu, J.; Feng, J.; Xu, C.; Zhou, J.; Tian, Q. BridgeNet: A Continuity-Aware Probabilistic Network for Age Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1145–1154. [Google Scholar]
- Zhang, Y.; Shou, Y.; Ai, W.; Meng, T.; Li, K. GroupFace: Imbalanced Age Estimation Based on Multi-Hop Attention Graph Convolutional Network and Group-Aware Margin Optimization. IEEE Trans. Inf. Forensics Secur. 2025, 20, 605–619. [Google Scholar] [CrossRef]
- Lin, T.-Y.; RoyChowdhury, A.; Maji, S. Bilinear CNN Models for Fine-Grained Visual Recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1449–1457. [Google Scholar]
- Yu, C.; Zhao, X.; Zheng, Q.; Zhang, P.; You, X. Hierarchical Bilinear Pooling for Fine-Grained Visual Recognition. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 11220, pp. 595–610. ISBN 978-3-030-01269-4. [Google Scholar]
- Xu, D.; Tang, Z.; Xu, W. Salient Object Detection Based on Regional Contrast and Relative Spatial Compactness. KSII Trans. Internet Inf. Syst. 2013, 7, 2737–2753. [Google Scholar] [CrossRef]
- Jiao, Y.; Li, Z.; Huang, S.; Yang, X.; Liu, B.; Zhang, T. Three-Dimensional Attention-Based Deep Ranking Model for Video Highlight Detection. IEEE Trans. Multimed. 2018, 20, 2693–2705. [Google Scholar] [CrossRef]
- Han, K.; Guo, J.; Zhang, C.; Zhu, M. Attribute-Aware Attention Model for Fine-grained Representation Learning. In Proceedings of the 26th ACM international conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; ACM: New York, NY, USA, 2018; pp. 2040–2048. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA; pp. 7132–7141. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, N.; Yuan, X.; Guo, X.; Gao, C.; Zhao, Z.; Ma, Z. Fine-Grained Age Estimation in the Wild With Attention LSTM Networks. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 3140–3152. [Google Scholar] [CrossRef]
- Wang, H.; Sanchez, V.; Li, C.-T. Improving Face-Based Age Estimation with Attention-Based Dynamic Patch Fusion. IEEE Trans. Image Process. 2022, 31, 1084–1096. [Google Scholar] [CrossRef]
- Hu, C.; Gao, J.; Chen, J.; Jiang, D.; Shu, Y. Fine-Grained Age Estimation With Multi-Attention Network. IEEE Access 2020, 8, 196013–196023. [Google Scholar] [CrossRef]
- Yu, H.; Mu, C.; Sun, C.; Yang, W.; Yang, X.; Zuo, X. Support vector machine-based optimized decision threshold adjustment strategy for classifying imbalanced data. Knowl.-Based Syst. 2015, 76, 67–78. [Google Scholar] [CrossRef]
- Gao, B.-B.; Xing, C.; Xie, C.-W.; Wu, J.; Geng, X. Deep Label Distribution Learning With Label Ambiguity. IEEE Trans. Image Process. 2017, 26, 2825–2838. [Google Scholar] [CrossRef]
- Rothe, R.; Timofte, R.; Gool, L.V. DEX: Deep EXpectation of Apparent Age from a Single Image. In Proceedings of the 2015 IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015; pp. 252–257. [Google Scholar]
- Ricanek, K.; Tesafaye, T. MORPH: A Longitudinal Image Database of Normal Adult Age-Progression. In Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition (FGR06), Southampton, UK, 10–12 April 2006; pp. 341–345. [Google Scholar]
- Zhang, Y.; Liu, L.; Li, C.; Loy, C. change Quantifying Facial Age by Posterior of Age Comparisons. arXiv 2017, arXiv:1708.09687. [Google Scholar]
- Chen, B.-C.; Chen, C.-S.; Hsu, W.H. Face Recognition and Retrieval Using Cross-Age Reference Coding With Cross-Age Celebrity Dataset. IEEE Trans. Multimed. 2015, 17, 804–815. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Pan, H.; Han, H.; Shan, S.; Chen, X. Mean-Variance Loss for Deep Age Estimation From a Face. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 5285–5294. [Google Scholar]
- He, J.; Hu, C.; Wang, L. Facial age estimation based on asymmetrical label distribution. Multimed. Syst. 2023, 29, 753–762. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, C.; Dong, M.; Le, J.; Rao, M. Using Ranking-CNN for Age Estimation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 742–751. [Google Scholar]
- Liu, N.; Zhang, F.; Duan, F. Age estimation by extracting hierarchical age-related features. J. Vis. Commun. Image Represent. 2023, 95, 103884. [Google Scholar] [CrossRef]
- Bao, Z.; Luo, Y.; Tan, Z.; Wan, J.; Ma, X.; Lei, Z. Deep domain-invariant learning for facial age estimation. Neurocomputing 2023, 534, 86–93. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, X.; Yao, X.; Yang, J. Ordinal Label Distribution Learning. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 23424–23434. [Google Scholar]
- Li, P.; Hu, Y.; Wu, X.; He, R.; Sun, Z. Deep label refinement for age estimation. Pattern Recognit. 2020, 100, 107178. [Google Scholar] [CrossRef]
- Tan, Z.; Zhou, S.; Wan, J.; Lei, Z.; Li, S.Z. Age Estimation Based on a Single Network with Soft Softmax of Aging Modeling. In Computer Vision—ACCV 2016, Proceedings of the 13th Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; Lai, S.-H., Lepetit, V., Nishino, K., Sato, Y., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10113, pp. 203–216. ISBN 978-3-319-54186-0. [Google Scholar]
- Shen, W.; Zhao, K.; Guo, Y.; Yuille, A. Label Distribution Learning Forests. In Proceedings of the 30th Conference on Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Wan, J.; Tan, Z.; Lei, Z.; Guo, G.; Li, S.Z. Auxiliary Demographic Information Assisted Age Estimation With Cascaded Structure. IEEE Trans. Cybern. 2018, 48, 2531–2541. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Cheng, K.T. Facial Age Estimation by Deep Residual Decision Making. arXiv 2019, arXiv:1908.10737. [Google Scholar]
- Shen, W.; Guo, Y.; Wang, Y.; Zhao, K.; Wang, B.; Yuille, A. Deep Regression Forests for Age Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2304–2313. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).