Abstract
The main objective of proton beam therapy is to precisely irradiate diseased tissue while minimizing damage to healthy cells. For effective treatment, the linear energy transfer (LET) is a key parameter in ensuring the destruction of diseased cells, and both the dose and LET are typically represented as functions of depth. The distribution of dose and LET in the target depends on the beam properties, including beam energy, energy spread, beam size, and beam emittance. The aim of this work is to present the method used to characterize the proton beam properties obtained from the machine employed in the simulation and to determine the dose and dose-averaged LET (LETd) values, including their peak positions in depth. These results are used to predict the dose and LETd at different depth positions under experimental conditions. We utilized GEANT4, a Monte Carlo (MC) simulation-based software, to examine the integral depth-dose position and the peak position of the LETd. The proton source was obtained from a cyclotron accelerator, specifically the Varian ProBeam Compact spot scanning system at King Chulalongkorn Memorial Hospital in Bangkok, Thailand. The system provides proton energies ranging from 70 MeV to 220 MeV. In this study, four proton energies—70 MeV, 100 MeV, 150 MeV, and 220 MeV—were chosen to characterize the beam properties. The 80%–20% distal fall-off obtained from the simulation was used to determine the energy spread for each selected energy by matching the depth-dose peak with the measurement data. The optimal energy spreads were found to be 1.5%, 1.25%, 1%, and 0.5% for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV, respectively. These energy spreads ensure that the difference in the depth-dose profile is below 1% when comparing the simulated and measured depth-dose profiles. Furthermore, the peak LETd was found to be approximately 1 mm away from the R80 position, a depth that corresponds to 80% of maximum dose, for each energy. This information can be used to guide the desired LETd position by utilizing the R80 depth position.
1. Introduction
In modern medicine, radiation therapy remains a cornerstone in cancer treatment. As the most widely established modality, it benefits from decades of clinical research and extensive infrastructure in radiotherapy centers worldwide. Over time, the field has evolved from individualized anatomical treatments toward a more sophisticated, personalized approach that integrates technological advancements for precise dose delivery with biological insights into tumor characteristics and resistance mechanisms [1]. Photon therapy is a conventional method that uses ionizing X-ray radiation to target and eradicate cancerous tissues. The primary mechanism involves damaging the DNA of malignant cells, leading to cell death and ultimately controlling or eliminating tumor growth. However, a significant limitation of X-ray therapy is its inability to selectively target tumors at varying depths while sparing adjacent healthy tissue. This issue arises from the inherent nature of photon energy deposition in tissue, where, after a brief accumulation, the radiation dose increases with depth, potentially resulting in unintended damage to healthy tissues beyond the tumor site [2].
To address this limitation, particle beam therapy, using protons and heavy ions, has emerged as a more precise modality, offering enhanced protection for normal tissues by concentrating energy deposition at a specific depth. Proton therapy, a leading form of particle therapy, was first introduced in a clinical setting at Loma Linda University Medical Center (CA) in 1990. By the end of 2022, over 300,000 patients had been treated with proton therapy [3]. Currently, more than 140 proton therapy facilities are operating worldwide, with more than 20 additional centers under construction [4].
Proton therapy has gained attention because of its superior dose-distribution properties. As protons travel through tissue, their velocity decreases as energy is lost through inelastic Coulombic interactions with atomic nuclei. Near the end of their path, protons deposit most of their energy, resulting in a low entrance dose, followed by a sharp increase at the maximum peak, and a steep fall-off at the end of the range. This peak, known as the “Bragg peak”, occurs near the end of the proton beam range, which is determined by the energy of the protons [5].
As illustrated in Figure 1, which compares the depth-dose distribution characteristics of the X-rays and the proton beam, the peak of the proton depth-dose distribution occurs at a specific depth. The position of this peak can be adjusted by varying the proton energy to target a desired depth. In addition, the Bragg peak profile characterizes the depth-dose distribution of a proton beam, highlighting key dosimetric parameters. The range at 100% dose (RBP) marks the location of the peak dose deposition. The range at 80% dose (R80) is commonly used to define the clinical target position due to its stability and reproducibility [6]. The distal fall-off width (W80–20), defined as the distance between the 80% and 20% dose levels on the distal edge of the Bragg peak, reflects the sharpness of dose fall-off and is critical for assessing beam precision and minimizing dose to surrounding healthy tissues.

Figure 1.
Comparison of relative depth-dose distributions for protons and photons in tissue (left), and beam characteristics of the Bragg peak, illustrating the range at 100% dose (RBP), the range at 80% dose (R80), and the distal fall-off width between 80% and 20% dose levels (W80–20) (right).
This unique feature allows for precise targeting of the tumor while protecting surrounding healthy tissue [7], potentially reducing collateral damage to healthy cells. With the advancement of pencil beam scanning, protons can now be precisely directed using intensity-modulated proton therapy (IMPT) [8]. This advanced technique enables controlled energy deposition within the tumor at a predetermined depth or over a narrow range, minimizing exposure to healthy tissues around the tumor. These characteristics make proton and other charged-particle therapies more advantageous for cancer radiation therapy than conventional photon beams.
Additionally, from a radiobiological perspective, charged particle beams provide a high linear energy transfer (LET) around the Bragg peak [9]. LET refers to the energy that charged particles deposit per unit length as they move through a material or tissue. LET increases progressively as the particles approach the Bragg peak and reaches a sharp peak near the distal end due to energy loss from successive nuclear and electromagnetic interactions. This high LET region creates dense ionization clusters that effectively damage DNA and are less influenced by oxygen levels. This characteristic allows it to overcome the radioresistance of hypoxic tumor cells, which is a limitation of conventional photon therapy [10].
In radiobiological studies, LET is typically averaged based on dose deposition (LETd) rather than track length (LETt). A systematic review of 354 proton therapy publications revealed that 69% reported LETd [11]. However, calculating LET accurately is challenging because primary protons continuously lose energy and produce secondary particles. Additionally, researchers have different methods for averaging, specifying mediums, normalizing densities, and including secondary particles. These variations can result in significantly different LET values, hindering the development of reliable relative biological effectiveness (RBE) models. RBE evaluates therapeutic efficacy by comparing clinical outcomes with those achieved using standard radiation, usually Co-60 and X-ray irradiation. However, the RBE of particle therapy remains poorly quantified due to its dependence on multiple factors, including LET [12,13,14,15].
Since LET is strongly correlated with RBE—and directly correlates under constant radiobiological conditions—accurate LET characterization is crucial for conducting RBE-weighted dose calculations in treatment planning systems (TPSs) [16,17]. However, most clinical TPSs rely on a fixed RBE value of 1.1 [18], which may underestimate the true effectiveness of high-LET areas at the distal Bragg peak and increase the risk of damage to surrounding healthy tissues. This limitation presents a critical gap in ensuring that the tumor receives the optimal dose and the appropriate LET distribution. Addressing this gap requires the implementation of MC simulations, which offer the precision necessary to correlate the Bragg peak with LET positioning. Further investigation is required to refine these correlations and enhance TPS accuracy in clinical applications. The purpose of this study is to characterize the proton beam energy and energy spread obtained from the proton cyclotron accelerator at King Chulalongkorn Memorial Hospital in Bangkok, Thailand. The objective parameters include the Bragg peak position, R80, distal fall-off, and LETd values.
2. Materials and Methods
To establish beam parameters for machine setup, comparison with TPSs, and other experimental planning, MC simulations were implemented to provide high accuracy in dose calculations. These simulations account for secondary particles, such as neutrons, light ions, electrons, X-rays, and gamma rays, generated during the tracking process, which significantly influence the dose distribution, LET, and DNA damage. For realistic simulation conditions, beam parameters were obtained from measurements of the cyclotron proton accelerator at King Chulalongkorn Memorial Hospital.
2.1. Cyclotron Accelerator Specifications
The cyclotron accelerator at King Chulalongkorn Memorial Hospital is the Varian ProBeam Compact spot scanning system (Varian Medical Systems, Palo Alto, CA, USA). This system utilizes a pencil beam scanning technique to deliver IMPT, enabling precise dose distribution around the target volume. The energy is varied using an energy degrader, providing an energy range of 220 MeV down to 70 MeV, corresponding to an increase in the transverse beam size () from approximately 3.5 to 6.0 mm with a decreasing beam energy after exiting the windows [19].
Degradation directly influences the beam properties in the exit windows, including energy spread (), transverse beam size (), and the divergence. In this work, we focus on the energy spread and the transverse beam size. The measured Bragg peak in the water phantom was used to characterize the energy spread, and the measured transverse beam size at the target entrance was incorporated into the MC simulations to optimize the beam size at the defined source position, ensuring precise modeling and accurate dose calculations.
2.2. Monte Carlo Simulation: GEANT4 Simulations
A key challenge of this study lies in integrating machine parameters from the cyclotron accelerator, such as the average beam energy (Emean), the energy spread () and the influence of the transverse beam size, dose, and LET, into the simulation. These parameters are rigorously examined, and their impacts are presented in this paper. In the simulation, the source of the beam is defined as a virtual source located at the treatment head before the exit window. As can be seen in Figure 2, the distance from the source to the phantom surface was set at 420 mm. For this study, a cubic water phantom (50 × 50 × 40 cm3), which matches the dimensions of a standard phantom used in beam commissioning, was modeled. A virtual sensitive detector, positioned immediately in front of the exit window, was used to capture the beam profile data.

Figure 2.
A diagram of the setup in the GEANT4 simulation, illustrating the positioning based on the actual experimental configuration, with a distance of 420 mm from the source, where the beam exits from the vacuum into the air, to the target in air.
The simulation was performed using GEANT4 (version 11.0) [20], a widely recognized open source tool, to model the treatment process. The QGSP_BIC_HP reference physics list was used for all simulations in this study, which is a comprehensive physics list that covers a wide range of hadronic interactions. It is used to simulate the interaction of high-energy protons and neutrons with tissue in radiation therapy applications. To measure depth-dose and beam profiles, the water phantom was subdivided into 1400 thin slabs, each 0.25 mm thick, arranged across a total depth of 350 mm, sufficient to cover the full range of proton energies used in this study. Proton particles were generated using the G4ParticleGun() class. The particle gun was positioned at the center of the vacuum tube to generate a focused beam with a defined beam size and energy spread.
To generate particles with a Gaussian distribution of beam size and energy spread, the function G4RandGauss::shoot(mean, sigma) was employed, where the mean and sigma were defined to cover the values of interest in this study.
3. Energy and Energy Spread Characterization
The proton energy significantly influences the depth position of the Bragg peak. The impact of energy spread on the depth-dose distribution is well documented in the literature [21]. This effect is characterized by a decrease in peak intensity and a shift in the Bragg peak position as the energy spread increases. To investigate these phenomena, we conducted an MC simulation. In this simulation, a round beam was initialized at the source position, with the transverse beam properties modeled as a Gaussian distribution, resulting in a beam size of 4 mm, as illustrated in Figure 3. The initial beam parameters are summarized in Table 1. Proton beam energies were varied from 70 MeV to 220 MeV, with an energy spread modeled as a Gaussian distribution with a standard deviation of up to 5%.

Figure 3.
Transverse profile distribution of the proton beam at the source position, with a beam size of 4.0 mm in both horizontal and vertical directions (left), and the energy distribution of the 70 MeV proton beam, with an energy spread of 0.62 MeV corresponding to 0.88% (right).

Table 1.
Initial proton parameters used in GEANT4 simulation for energy spread investigations.
The simulated results of the energy spread investigation are shown in Figure 4. The results are presented as the dose profile per proton particle as a function of depth position, with the left plot representing 220 MeV and the right plot displaying energies ranging from 70 MeV to 220 MeV. A shift in the Bragg peak position to lower depths occurs as the energy spread increases, accompanied by a decrease in peak intensity with increasing energy spread.

Figure 4.
The depth-dose distribution per proton particle with varying energy spreads ranging from 0% to 5% for 220 MeV (left) and for 70 MeV, 80 MeV, 100 MeV, 120 MeV, 140 MeV, 160 MeV, 180 MeV, 200 MeV, and 220 MeV (right).
As listed in Table 2, for the 220 MeV proton beam, the Bragg peak position shifts to a lower depth by approximately 23 mm when the energy spread increases to 5%. Simultaneously, the peak dose intensity decreases by 50%. The energy spread has less influence on the R80 position, which more reliably represents the range position for each mean energy than the Bragg peak position.

Table 2.
The Bragg peak position (RBP), intensity, and distal fall-off width (W80–20) for each energy spread, ranging from 0% to 5% of the proton beam at an energy of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.
Subsequently, the distal fall-off length increases linearly with increasing energy spread. These values, along with the distal fall-off length, will be used to match the depth-dose profile obtained from experiments conducted with a water phantom. This matching process provides the energy spread of the proton beam at the exit window for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.
In addition to its impact on Bragg peak position, energy spread also significantly influences the linear energy transfer dose (LETd), as illustrated in Figure 5. The results demonstrate that LETd decreases with increasing proton energy. Specifically, lower-energy protons (e.g., 70 MeV) exhibit higher LETd values due to their shorter range and denser energy deposition, whereas higher-energy protons (e.g., 220 MeV) show lower LETd values as they travel further with less energy deposited per unit length. This behavior aligns with the well-established physical characteristics of proton interactions in matter. Furthermore, an increase in energy spread results in a reduction in the peak LETd, highlighting the importance of beam quality in treatment planning.
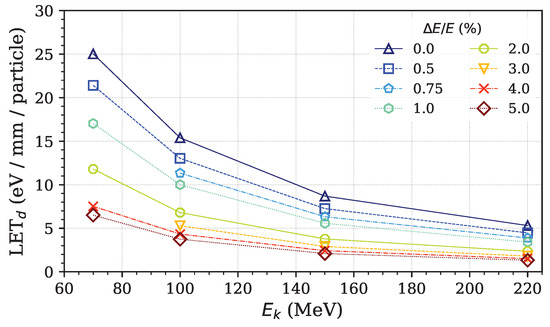
Figure 5.
Peak LETd per proton particle with varing energy spreads, ranging from 0% to 5%, for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.
The measured integral depth doses correspond to beam energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV. Their normalized dose profiles are shown in Figure 6. The Bragg peak positions, R80, and distal fall-offs were analyzed and are listed in Table 3. Due to the lesser influence of energy spread on R80, the Bragg peak and distal fall-off are utilized to match the depth-dose distribution and determine the energy spread of the proton beam.

Figure 6.
Measured integral depth-dose curves normalized to relative values for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.

Table 3.
The Bragg peak position (RBP), intensity, and distal fall-off width (W80–20) of the proton beam were analyzed from the measured integral depth doses at energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.
The simulated integral depth doses for each energy spread are normalized and plotted against the measured depth-dose profile for the proton energy of 220 MeV. The calculated distal fall-off for each energy was used to match the depth-dose distribution. For example, the measured depth dose of the 220 MeV proton beam closely matches the shape of the simulated energy spread of 0.5%, as indicated in Figure 7.

Figure 7.
The depth-dose distribution per proton particle with varying energy spread ranging from 0% to 5% for 220 MeV.
The Gamma Index () is a widely used quantitative metric in radiotherapy for evaluating the agreement between a calculated dose distribution—typically generated by a treatment planning system (TPS)—and a measured or reference dose distribution [22]. This metric simultaneously considers both the dose difference () and the spatial distance () between corresponding points in the two distributions, providing a comprehensive assessment of dosimetric accuracy. In this study, the reference distribution corresponds to the measured dose, while the evaluated distribution is derived from simulation results. The -index is computed for each point in the reference distribution by identifying the minimum Euclidean distance in the evaluated distribution that satisfies both the dose and distance criteria. Mathematically, the -index at a reference point is defined as
where
Here, denotes the spatial location in the experimental (measured) dose distribution, while represents the corresponding location in the simulated distribution. The term is the spatial distance between the evaluated point and the reference point , and is the dose difference between the experimental and simulated values at those points. A reference point is considered to pass the gamma test if , indicating that at least one evaluated point lies within the acceptance ellipsoid defined by the criteria. The most commonly adopted acceptance criteria are a 3% dose difference and a 3 mm distance-to-agreement (3%/3 mm), as originally proposed by Low et al. [23].
By applying the -index analysis using Equations (1) and (2), with the standard criteria of mm and , the results—illustrated in the right plot of Figure 8—demonstrate that the -index remains below 1 for all comparison points. This confirms that the beam energy spread of 0.5% at 220 MeV satisfies the acceptance criteria, indicating a high level of agreement between the simulated and measured dose distributions. Furthermore, the optimal energy spreads determined for other investigated proton energies are 1.5%, 1.25%, and 1% for beams of 70 MeV, 100 MeV, and 150 MeV, respectively.

Figure 8.
The relative depth-dose distribution comparing the measured depth dose and the simulated depth dose (left). The results of the -index for and , set to 3 mm and 3%, respectively, are shown in the right plot for a proton beam energy of 220 MeV (right).
To investigate the depth-dose distribution, Bragg peak position, and peak LETd position for each proton energy, the resulting energy spreads for the four energies were collected and used as the initial proton beam energy spreads for the MC simulation. The Bragg peak positions, R80, peak LETd positions, and distal fall-off were monitored and are summarized in Table 4 and Table 5. Typically, R80 is considered and defined as the target position [6,19]. The variation in peak position and R80 is less than 1% compared to the measured data for all the considered energies.

Table 4.
The simulated depth of the Bragg peak (RBP) and R80 were analyzed for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV and compared against the measurement data.

Table 5.
The depths of R80 and the peak positions of LETd were analyzed for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV.
The peak position of the LETd value shifts approximately 1 mm away from R80, as illustrated in Table 5. This information will be utilized as a guide for predicting the position of the desired peak LETd for each proton beam energy, using the R80 depth position, which is crucial for effectively killing cancer cells.
4. Conclusions
The proton beam characterization included energy spread, transverse beam size, and transverse beam emittance. This study initially focused on the energy spread, which directly influences the depth-dose distribution in terms of the intensity and depth position of RBP, R80, as well as the distal fall-off length. To investigate this effect, the energy spread of the proton beam was examined for proton energies of 70 MeV, 100 MeV, 150 MeV, and 220 MeV. The depth-dose distribution was simulated using GEANT4-based Monte Carlo simulations. The proton beam energy and energy spread were varied over the ranges of 70 MeV to 220 MeV and 0% to 5%, respectively.
Two key effects of the energy spread on the depth-dose distribution were observed. First, the dose intensity decreases as the energy spread increases. Second, the shape of the dose profile changes, with the Bragg peak shifting to a shallower depth as the energy spread increases. The RBP, R80, and distal fall-off were analyzed, revealing that the energy spread has a stronger influence on the Bragg peak position and distal fall-off than on R80. This confirms why R80 is widely used to define the depth position.
The distal fall-off length from the simulation was utilized to match the measured W80–20 length in order to determine the energy spread corresponding to each energy. Matching results indicated that the optimal energy spreads for 70 MeV, 100 MeV, 150 MeV, and 220 MeV are 1.5%, 1.25%, 1%, and 0.5%, respectively. These optimized energy spreads provide close agreement between the simulated and measured Bragg peak and R80 positions, with a relative error of less than 1%.
Author Contributions
Conceptualization, P.T. and S.W.; Methodology, P.T., E.K., K.T. and P.K.; Formal analysis, E.K.; Writing—original draft, P.T. and E.K.; Writing—review & editing, P.T., E.K. and N.C.; Visualization, E.K. and K.T.; Project administration, W.P.; Funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Thailand Science Research and Innovation (TSRI), and National Science, Research and Innovation Fund (NSRF) grant number 4161655.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We would like to thank Sirinya Ruangchan and Taweap Sanghangthum for their invaluable assistance in facilitating the beam measurement at the King Chulalongkorn Memorial Hospital. Their critical insights into the impact of proton beam parameters on treatment planning systems also offered valuable perspectives from a medical standpoint.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MC | Monte Carlo |
| IMPT | Intensity-Modulated Proton Therapy |
| LET | Linear Energy Transfer |
| LETd | Dose-Averaged Linear Energy Transfer |
| LETt | Track-Averaged Linear Energy Transfer |
| RBP | Depth in Water of 100% Depth Dose or Bragg Peak Position |
| R80 | Depth in Water of 80% Depth Dose |
| W80–20 | Distal Fall-Off Width between 80% and 20% dose levels |
| NIST | National Institute of Standards and Technology |
| TPS | Treatment Planning System |
References
- Baumann, M.; Krause, M.; Overgaard, J.; Debus, J.; Bentzen, S.M.; Daartz, J.; Bortfeld, T. Radiation Oncology in the Era of Precision Medicine. Nat. Rev. Cancer 2016, 16, 234–249. [Google Scholar] [CrossRef] [PubMed]
- Lomax, A.J. Charged Particle Therapy: The Physics of Interaction. Cancer J. 2009, 15, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Vincini, M.G.; Zaffaroni, M.; Schwarz, M.; Marvaso, G.; Mastroleo, F.; Volpe, S.; Bergamaschi, L.; Mazzola, G.C.; Corrao, G.; Orecchia, R.; et al. More than Five Decades of Proton Therapy: A Bibliometric Overview of the Scientific Literature. Cancers 2023, 15, 5545. [Google Scholar] [CrossRef]
- PTCOG. Particle Therapy Co-Operative Group. Available online: https://www.ptcog.site (accessed on 31 March 2025).
- Newhauser, W.D.; Zhang, R. The Physics of Proton Therapy. Phys. Med. Biol. 2015, 60, R155. [Google Scholar] [CrossRef]
- Paganetti, H. Range Uncertainties in Proton Therapy and the Role of Monte Carlo Simulations. Phys. Med. Biol. 2012, 57, R99–R117. [Google Scholar] [CrossRef]
- Jäkel, O. State of the Art in Hadron Therapy. AIP Conf. Proc. 2007, 958, 70–77. [Google Scholar]
- Kooy, H.M.; Grassberger, C. Intensity Modulated Proton Therapy. Br. J. Radiol. 2015, 88, 20150195. [Google Scholar] [CrossRef]
- Deng, W.; Yang, Y.; Liu, C.; Bues, M.; Mohan, R.; Wong, W.W.; Foote, R.H.; Patel, S.H.; Liu, W. A critical review of LET-based intensity-modulated proton therapy plan evaluation and optimization for head and neck cancer management. Int. J. Part. Ther. 2021, 8, 36–49. [Google Scholar] [CrossRef]
- Hall, E.J.; Giaccia, A.J. Radiobiology for the Radiologist, 8th ed.; Wolters Kluwer: Philadelphia, PA, USA, 2018. [Google Scholar]
- Kalholm, F.; Grzanka, L.; Traneus, E.; Bassler, N. A Systematic Review on the Usage of Averaged LET in Radiation Biology for Particle Therapy. Radiother. Oncol. 2021, 161, 211–221. [Google Scholar] [CrossRef]
- Grassberger, C.; Trofimov, A.; Lomax, A.; Paganetti, H. Variations in Linear Energy Transfer within Clinical Proton Therapy Fields and the Potential for Biological Treatment Planning. Int. J. Radiat. Oncol. Biol. Phys. 2011, 80, 1559–1566. [Google Scholar] [CrossRef]
- Jones, B.; Underwood, T.S.A.; Dale, R.G. The Potential Impact of Relative Biological Effectiveness Uncertainty on Charged Particle Treatment Prescriptions. Br. J. Radiol. 2011, 84, S61–S69. [Google Scholar] [CrossRef] [PubMed]
- Paganetti, H. Relative Biological Effectiveness (RBE) Values for Proton Beam Therapy: Variations as a Function of Biological Endpoint, Dose, and Linear Energy Transfer. Phys. Med. Biol. 2014, 59, R419. [Google Scholar] [CrossRef] [PubMed]
- Gridley, D.S.; Pecaut, M.J.; Mao, X.W.; Wroe, A.J.; Luo-Owen, X. Biological Effects of Passive Versus Active Scanning Proton Beams on Human Lung Epithelial Cells. Technol. Cancer Res. Treat. 2015, 14, 81–98. [Google Scholar] [CrossRef] [PubMed]
- Grün, R.; Friedrich, T.; Traneus, E.; Scholz, M. Is the Dose-Averaged LET a Reliable Predictor for the Relative Biological Effectiveness? Med. Phys. 2019, 46, 1064–1074. [Google Scholar] [CrossRef]
- Kanematsu, N.; Matsufuji, N.; Inaniwa, T. Estimation of Linear Energy Transfer Distribution for Broad-Beam Carbon-Ion Radiotherapy at the National Institute of Radiological Sciences, Japan. Radiol. Phys. Technol. 2018, 11, 242–247. [Google Scholar] [CrossRef]
- ICRU. Prescribing, Recording, and Reporting Proton-Beam Therapy. J. ICRU 2007, 7, ndm021. [Google Scholar] [CrossRef]
- Thasasi, P.; Ruangchan, S.; Oonsiri, P.; Oonsiri, S. Determination of Integral Depth Dose in Proton Pencil Beam Using Plane-parallel Ionization Chambers. Int. J. Particle Ther. 2022, 9, 1–9. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Nucl. Instrum. Methods Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Konefał, A.; Szaflik, P.; Zipper, W. Influence of the Energy Spectrum and Spatial Spread of Proton Beams Used in Eye Tumor Treatment on the Depth-Dose Characteristics. Nukleonika 2010, 55, 313–316. [Google Scholar]
- Hussein, M.; Clark, C.H.; Nisbet, A. Challenges in Calculation of the Gamma Index in Radiotherapy—Towards Good Practice. Eur. J. Med. Phys. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Low, D.A.; Harms, W.B.; Mutic, S.; Purdy, J.A. A Technique for the Quantitative Evaluation of Dose Distributions. Med. Phys. 1998, 25, 656–661. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).