A Finite Element Approach to the Upper-Bound Bearing Capacity of Shallow Foundations Using Zero-Thickness Interfaces
Abstract
1. Introduction
2. Upper-Bound Limit Analysis Theorem
2.1. Cohesive Soils
2.2. C-Phi Soils
3. Theoretical Analysis and Programming of Zero-Thickness Interface Elements
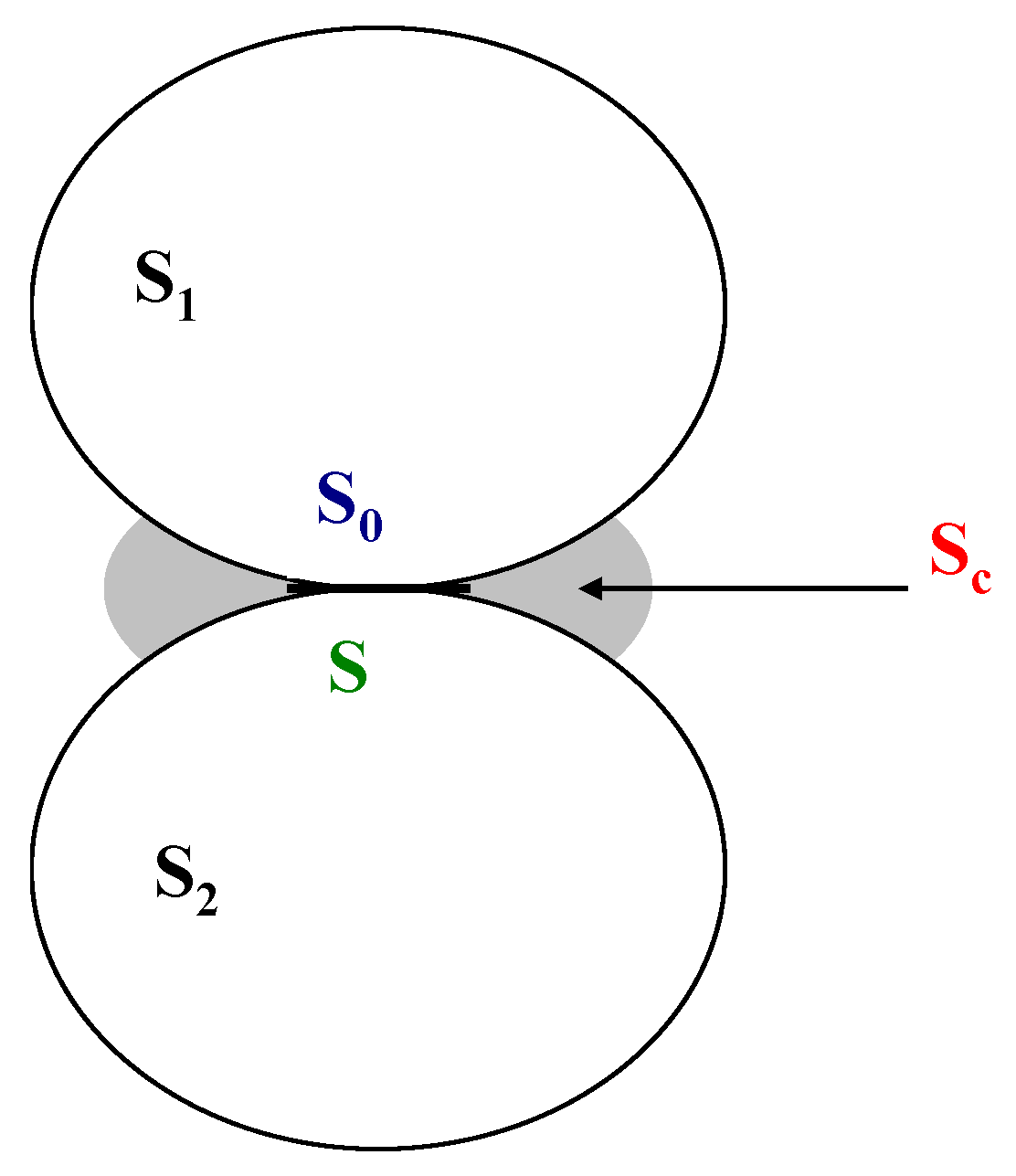
3.1. Zero-Thickness Interface Model
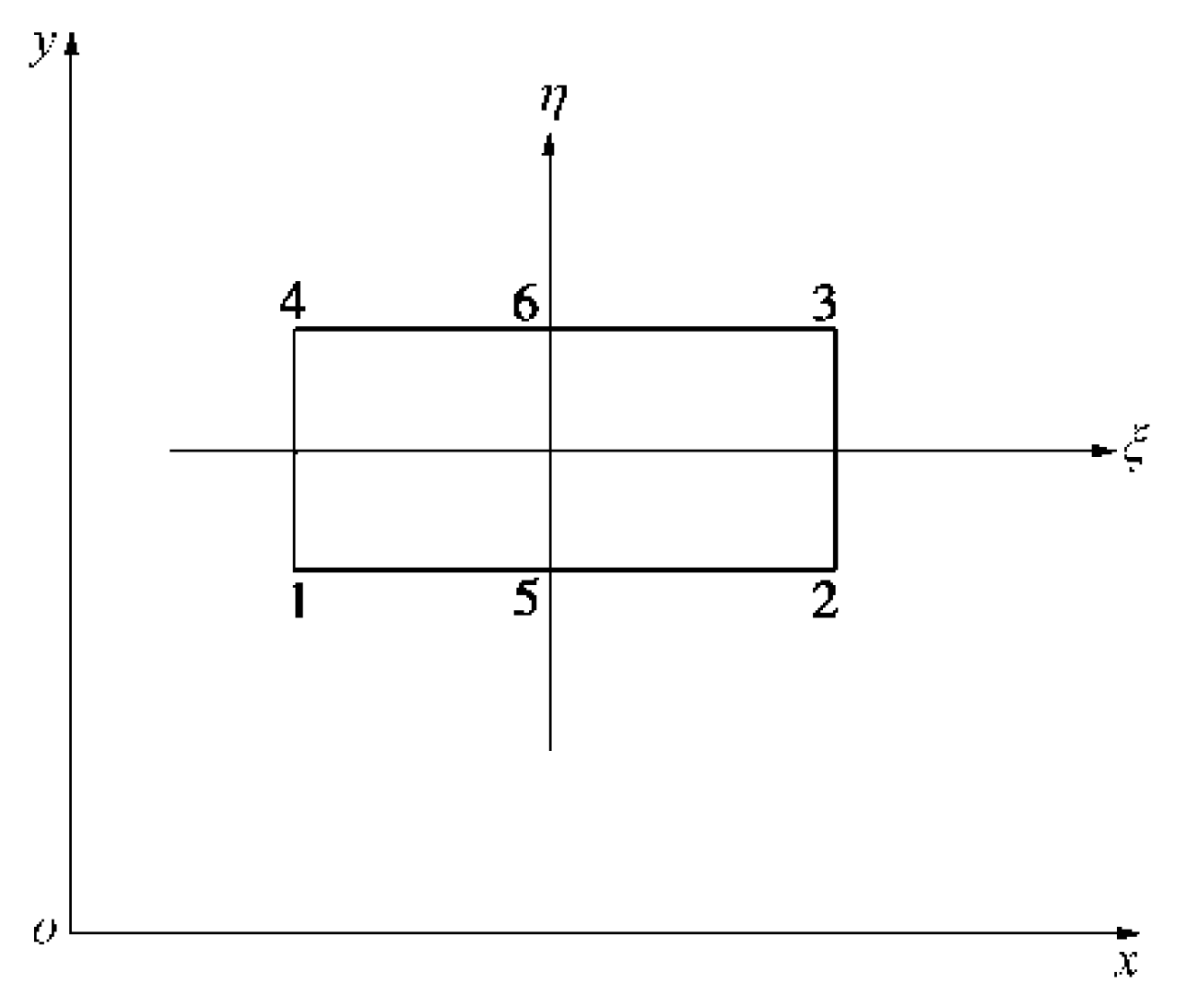
3.2. Establishment of Zero-Thickness Interface Elements in Finite Element Analysis
- (1)
- Constitutive law: stress–strain relationship
- (2)
- Compatibility: strain–displacement relationship
- (3)
- Equilibrium: Energy conservation equations
3.3. Application Principle and Operation Process of Zero-Thickness Interface Elements
4. Verification Between Numerical and Analytical Results
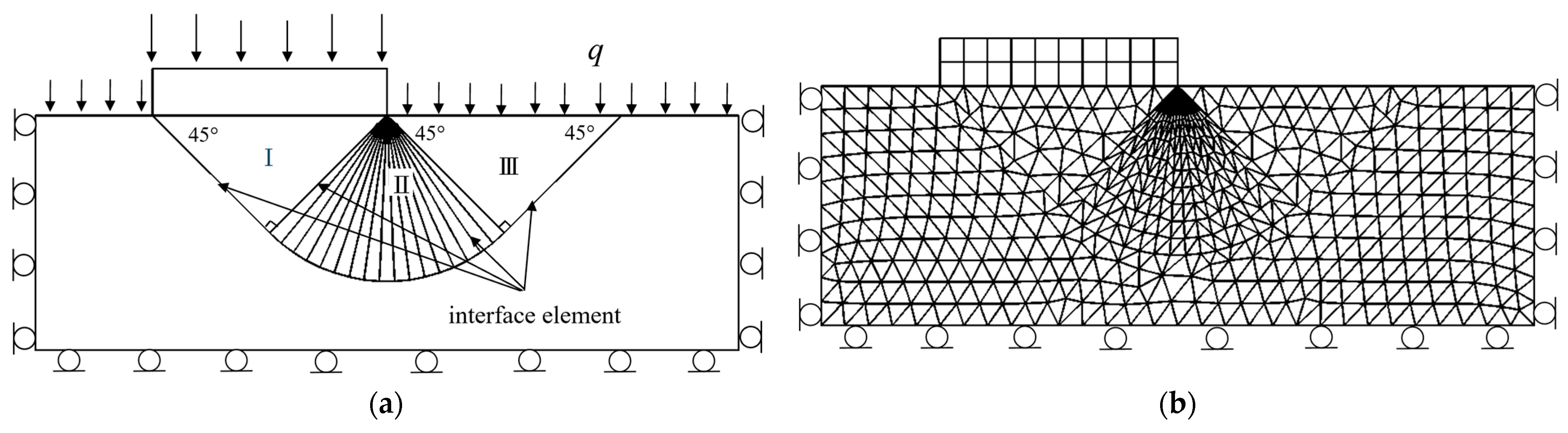
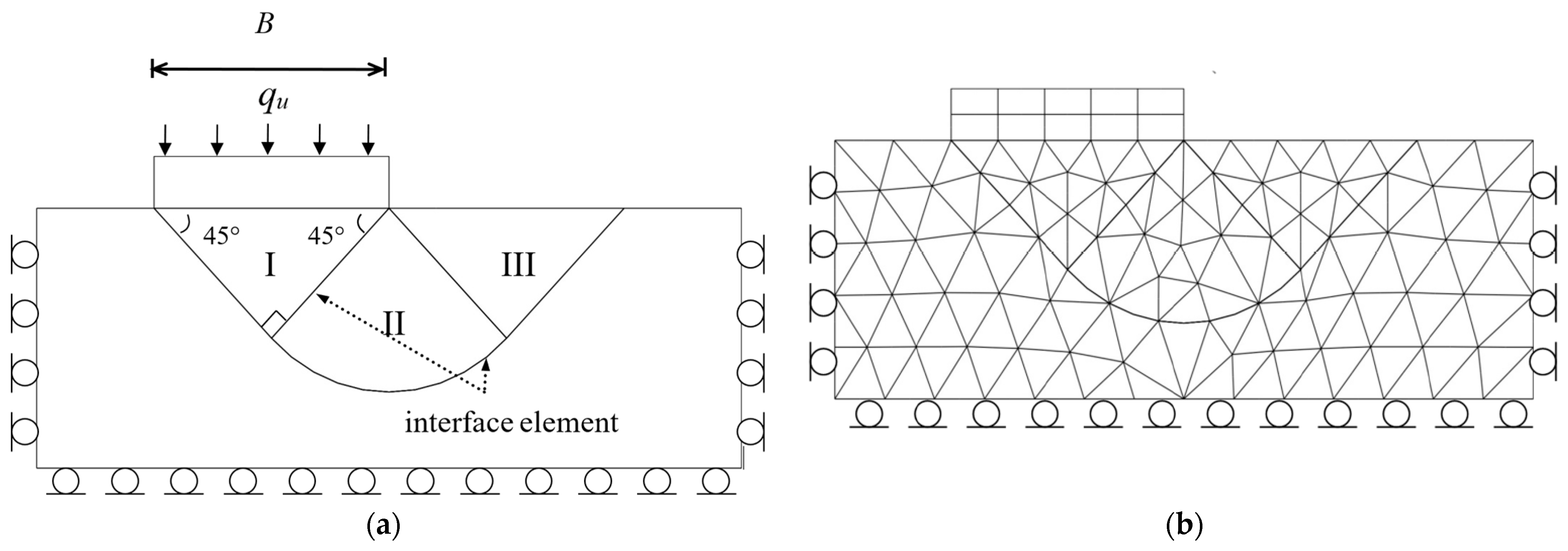
4.1. Analysis of the Ultimate Bearing Capacity of Shallow Foundations in Cohesive Soils
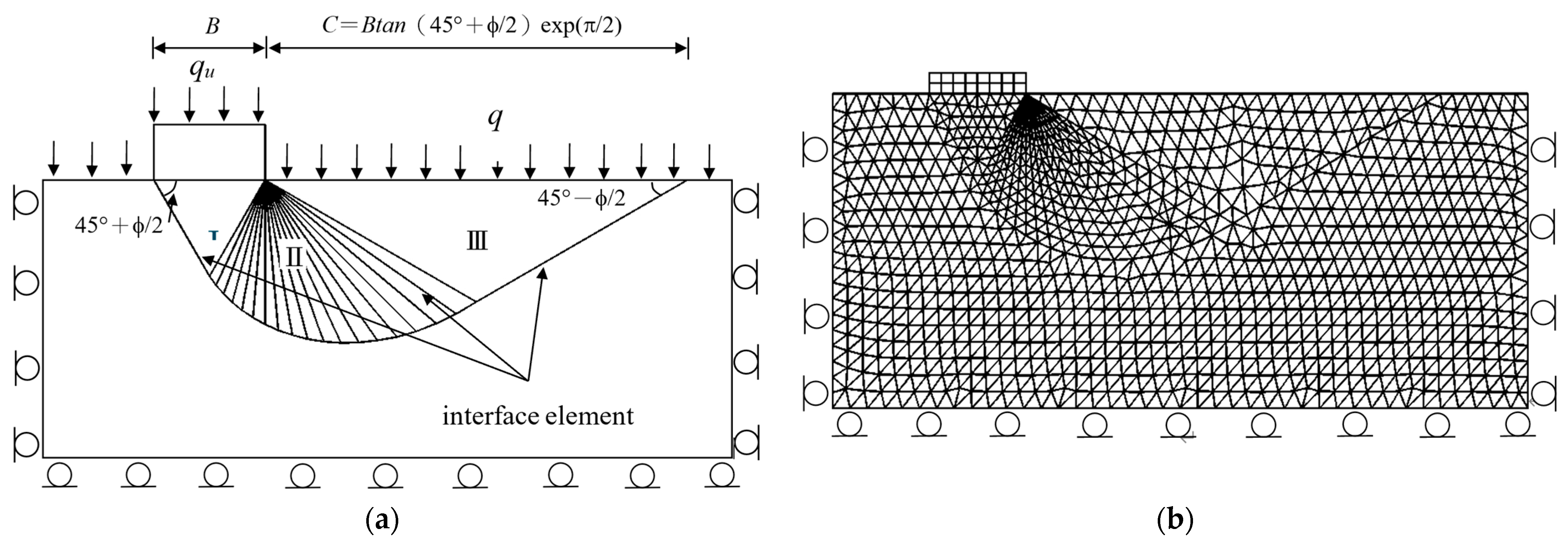
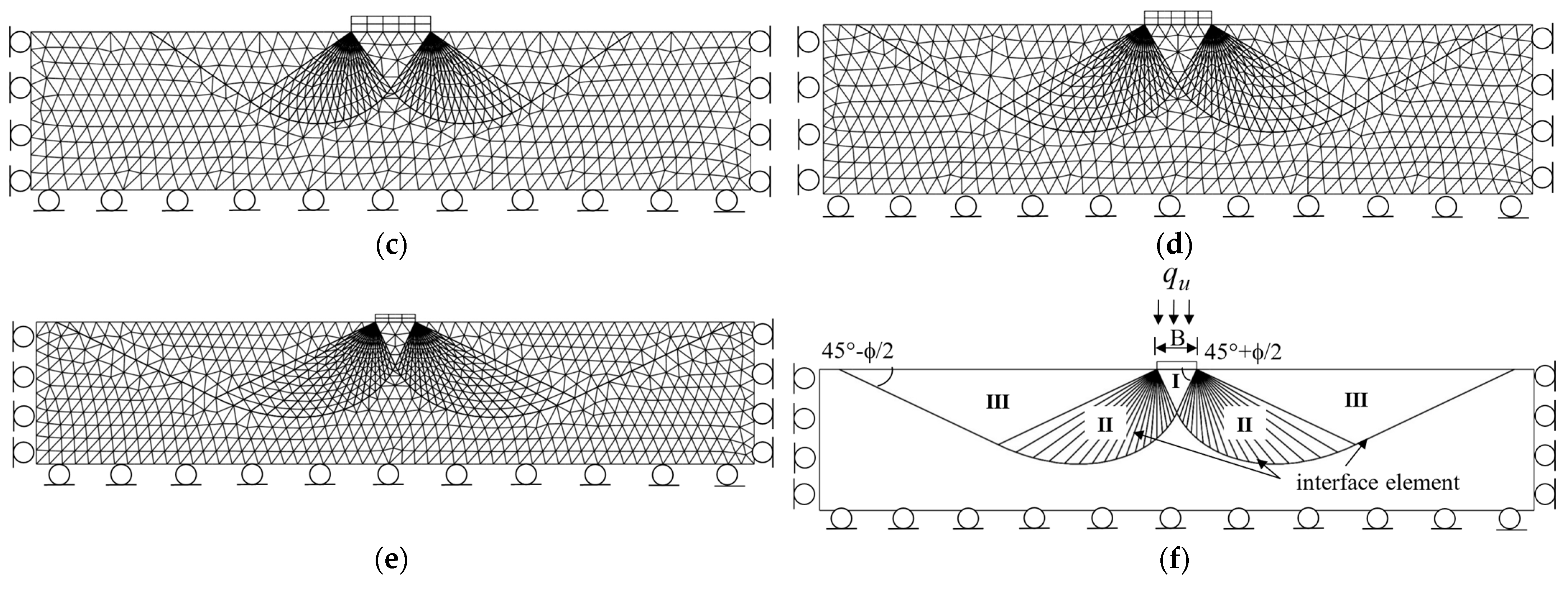
4.2. Analysis of the Ultimate Bearing Capacity of Shallow Foundations in C-Phi Soils
5. Discussion
5.1. Cohesive Soils
5.2. C-Phi Soils
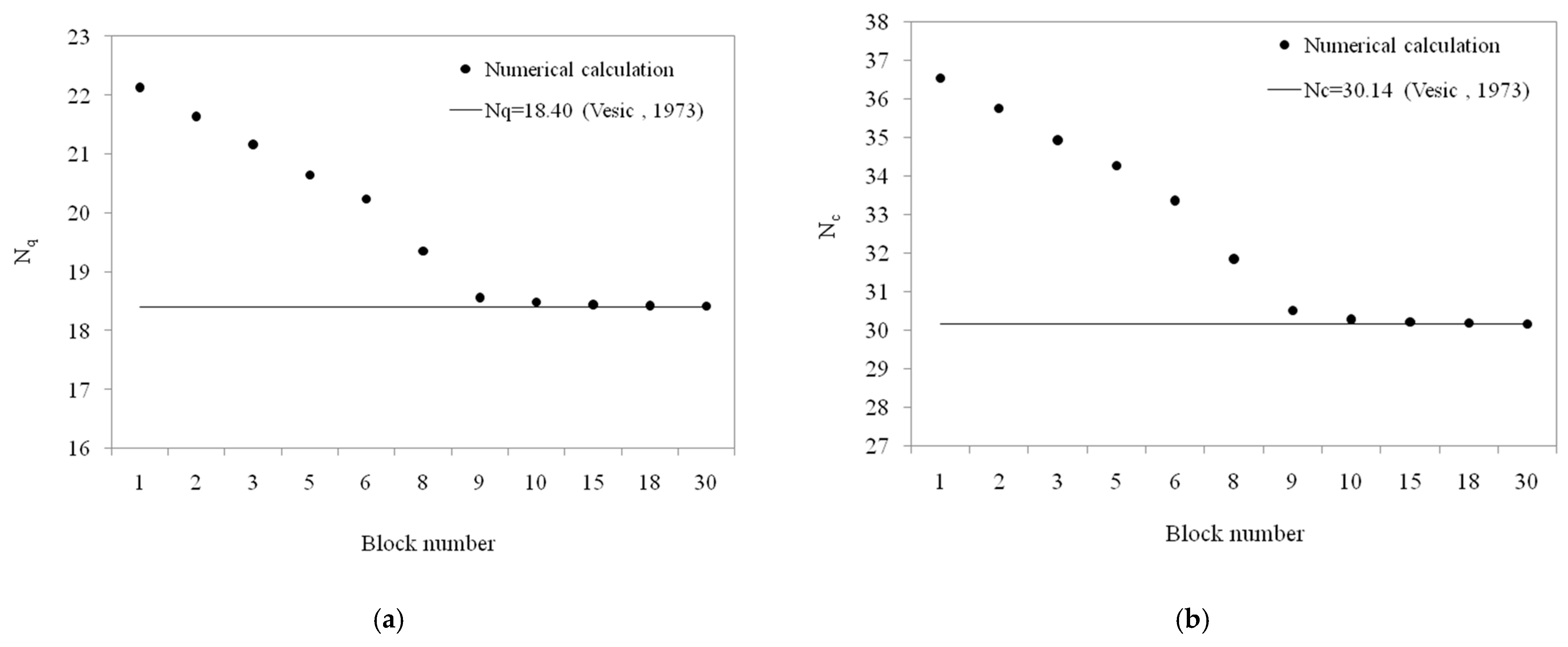
5.3. Discussion of the Bearing Capacity Factors Nq and Nc
6. Conclusions
- (1)
- Failure Mechanisms: For purely cohesive soils, the optimal failure mechanism comprises two triangular zones and a circular sector. For C-phi soils, it consists of two triangular zones and a logarithmic spiral sector.
- (2)
- Verification: Numerical results for both soil types show an excellent agreement with the upper-bound solutions by Atkinson (1981) [16], validating the modeling approach.
- (3)
- Transition Zone Accuracy: When the transition zone is discretized into 18 blocks, the computed bearing capacity factors closely match Vesic’s (1973) [4] theoretical values, with errors ranging from 0.1% to 0.19%.
- (4)
- Frictional Soils: For friction angles between 10° and 40°, the computed Nc and Nq values deviate by only 0.04–0.19% and 0.12–2.43%, respectively, from analytical solutions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Fazio, N.; Placidi, L.; Tomassi, A.; Fraddosio, A.; Castellano, A.; Paparella, N. Different mechanical models for the study of ultrasonic wave dispersion for mechanical characterization of construction materials. Int. J. Solids Struct. 2025, 315, 113352. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Meyerhof, G.G. The ultimate bearing capacity of foundations. Geotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Vesic, A.S. Analysis of ultimate loads of shallow foundations. J. Soil Mech. Found. Div. 1973, 99, 45–73. [Google Scholar] [CrossRef]
- Silvestri, V. A Limit equilibrium solution for bearing capacity of strip foundations on sand. Can. Geotech. J. 2003, 40, 351–361. [Google Scholar] [CrossRef]
- Bolton, M.D.; Lau, C.K. Vertical bearing capacity factors for circular and footing foundations on Mohr-Coulomb soil. Can. Geotech. J. 1993, 30, 1024–1033. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, X.H.; Lo, K.W. Influence of anisotropic damage on ultimate load of plane strain problems for foundation. Comput. Geotech. 2003, 30, 41–60. [Google Scholar] [CrossRef]
- Zheng, H.; Tham, L.G.; Liu, D. On two definitions of the factor of safety commonly used in the finite element slope stability analysis. Comput. Geotech. 2006, 33, 188–195. [Google Scholar] [CrossRef]
- Soubra, A.H. Upper-bound solutions for bearing capacity of foundations. J. Geotech. Geoenviron. Eng. 1999, 125, 59–68. [Google Scholar] [CrossRef]
- Michalowski, R.L. An estimate of the influence of soil weight on bearing capacity using limit analysis. Soils Found. 1997, 37, 57–64. [Google Scholar] [CrossRef]
- Sloan, S.W. Upper bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 263–282. [Google Scholar] [CrossRef]
- Sloan, S.W.; Kleeman, P.W. Upper bound limit analysis using discontinuous velocity fields. Comput. Methods Appl. Mech. Eng. 1995, 127, 293–314. [Google Scholar] [CrossRef]
- Zhu, D.Y.; Lee, C.F.; Jiang, H.D. A numerical study of the bearing capacity factor Nγ. Can. Geotech. J. 2001, 38, 1090–1096. [Google Scholar] [CrossRef]
- Griffiths, D.V. Computation of bearing capacity factors using finite elements. Geotechnique 1982, 32, 195–202. [Google Scholar] [CrossRef]
- Ugai, K.; Leshchinsky, D. Three-dimensional limit equilibrium and finite element analyses: A comparison of results. Soils Found. 1995, 35, 1–7. [Google Scholar] [CrossRef]
- Atkinson, J.H. Foundations and Slopes: An Introduction to Applications of Critical State Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Cheng, W.F.; Liu, X.L. Limit Analysis in Soil Mechanics; Elsevier: London, UK, 1990. [Google Scholar]
- Salençon, J. Handbook of Limit Analysis; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Sloan, S.W. Lower bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1988, 12, 61–77. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Sloan, S.W. Upper bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 181–216. [Google Scholar] [CrossRef]
- Izadi, A.; Nalkiashari, L.A.; Payan, M.; Chenari, R.J. Bearing capacity of shallow strip foundations on reinforced soil subjected to combined loading using upper bound theorem of finite element limit analysis and second-order cone programming. Comput. Geotech. 2023, 160, 105550. [Google Scholar] [CrossRef]
- Firouzeh, S.H.; Shirmohammadi, S.; Zanganeh Ranjbar, P.; Payan, M.; Jamsawang, P.; Keawsawasvong, S. Upper bound finite element limit analysis of the response of shallow foundations subjected to dip-slip reverse fault rupture outcrop. Transp. Infrastruct. Geotechnol. 2024, 11, 3256–3292. [Google Scholar] [CrossRef]
- Jin, L.X.; Qin, T.; Liu, P.T. Upper bound solution analysis of the ultimate bearing capacity of two-layered strip foundation based on improved radial movement optimization. Appl. Sci. 2023, 13, 7299. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V.; Sloan, S.W. Formulation and solution of some plasticity problems as conic programs. Int. J. Solids Struct. 2007, 44, 1533–1549. [Google Scholar] [CrossRef]
- Makrodimopoulos, A.; Martin, C.M. Upper bound limit analysis using simplex strain elements and second-order cone programming. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 681–701. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Day, R.A.; Potts, D.M. Zero thickness interface elements—Numerical stability and application. Int. J. Numer. Anal. Methods Geomech. 1994, 18, 689–708. [Google Scholar] [CrossRef]
- Smith, C.; Gilbert, M. Application of discontinuity layout optimization to plane plasticity problems. Proc. Math. Phys. Eng. Sci. 2007, 463, 2461–2484. [Google Scholar] [CrossRef]
- He, L.W.; Schiantella, M.; Gilbert, M.; Smith, C. A Python script for discontinuity layout optimization. Struct. Multidisc. Optim. 2023, 66, 152. [Google Scholar] [CrossRef]
- Milani, G.; Lourenço, P.B. A discontinuous quasi-upper bound limit analysis approach with sequential linear programming mesh adaptation. Int. J. Mech. Sci. 2009, 51, 89–104. [Google Scholar] [CrossRef]
- Desai, C.S.; Zaman, M.M.; Lightner, J.G.; Siriwardane, H.J. Interface element for joint and crack modeling. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 19–43. [Google Scholar] [CrossRef]
- Sharma, K.G.; Desai, C.S. Analysis and implementation of thin-layer element for interface and joints. J. Eng. Mech. 1992, 118, 2442–2462. [Google Scholar] [CrossRef]
- Potts, D.M.; Zdravković, L. Finite Element Analysis in Geotechnical Engineering: Theory; Thomas Telford: London, UK, 1999. [Google Scholar]
- ABAQUS Documentation. User’s Manual for Cohesive Elements and Contact Interactions, 2024, Dassault Systèmes. Available online: http://130.149.89.49:2080/v2016/pdf_books/CAE.pdf (accessed on 3 July 2025).
- Smith, I.M.; Griffiths, D.V. Programming the Finite Element Method, 5th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Sachdeva, T.D.; Ramakrishnan, C.V. A finite element solution for the two-dimensional elastic contact problems with friction. Int. J. Numer. Meth. Eng. 1981, 17, 1257–1271. [Google Scholar] [CrossRef]





















| Analysis Case | Failure Mechanism | Upper-Bound Limit of the Ultimate Bearing Capacity of Shallow Foundations, qu | |
|---|---|---|---|
| Atkinson (1980) [16] | F.E.M. | ||
| Cohesive soil (q = 0, c = cu, φ = 0) | Two triangular and fan-shaped groups | (2 + π) cu | 5.14 cu |
| C-phi soil (q, c = 0, φ = 30°) | Two triangular and logarithmic spirals | 1.84 q | 1.84 q |
| Block Number (n) | Ultimate Bearing Capacity (F.E.M.), qu/cu | Error Percentage * (%) | Calculation Time ** |
|---|---|---|---|
| 1 | 6.51 | 26.65 | 39.18 s |
| 2 | 5.74 | 11.67 | 37.88 s |
| 3 | 5.50 | 7.00 | 53.52 s |
| 5 | 5.33 | 3.70 | 1 min 15.77 s |
| 6 | 5.29 | 2.92 | 2 min 0.04 s |
| 8 | 5.25 | 2.14 | 1 min 28.61 s |
| 9 | 5.23 | 1.75 | 2 min 57.73 s |
| 10 | 5.22 | 1.56 | 4 min 37.85 s |
| 15 | 5.18 | 0.78 | 15 min 43.50 s |
| 18 | 5.15 | 0.19 | 19 min 52.12 s |
| 30 | 5.14 | 0.00 | 52 min 44.78 s |
| Block Number (n) | Ultimate Bearing Capacity (F.E.M.), qu/cu | Error Percentage * (%) | Calculation Time ** |
|---|---|---|---|
| 1 | 22.13 | 20.27 | 1 h 23 min |
| 2 | 21.64 | 17.61 | 1 h 17 min |
| 3 | 21.16 | 15 | 1 h 20 min |
| 5 | 20.64 | 12.17 | 1 h 15 min |
| 6 | 20.23 | 9.95 | 1 h 25 min |
| 8 | 19.35 | 5.16 | 1 h 14 min |
| 9 | 18.56 | 0.87 | 1 h 18 min |
| 10 | 18.48 | 0.43 | 1 h 27 min |
| 15 | 18.44 | 0.22 | 2 h 25 min |
| 18 | 18.42 | 0.11 | 2 h 39 min |
| 30 | 18.41 | 0.05 | 6 h 17 min |
| Block Number (n) | Ultimate Bearing Capacity (F.E.M.), qu/cu | Error Percentage * (%) |
|---|---|---|
| 1 | 36.53 | 21.20 |
| 2 | 35.75 | 18.61 |
| 3 | 34.92 | 15.86 |
| 5 | 34.26 | 13.67 |
| 6 | 33.35 | 10.65 |
| 8 | 31.84 | 5.64 |
| 9 | 30.50 | 1.19 |
| 10 | 30.27 | 0.43 |
| 15 | 30.21 | 0.23 |
| 18 | 30.17 | 0.1 |
| 30 | 30.15 | 0.03 |
| Friction Angle, φ (°) | Vesic (1973) [4], Nq | F.E.M. | Error Percentage * (%) |
|---|---|---|---|
| 10 | 2.47 | 2.53 | 2.43 |
| 20 | 6.40 | 6.44 | 0.63 |
| 30 | 18.40 | 18.48 | 0.43 |
| 40 | 64.20 | 64.28 | 0.12 |
| Friction Angle, φ (°) | Vesic (1973) [4], Nc | F.E.M. | Error Percentage * (%) |
|---|---|---|---|
| 0 | 5.14 | 5.15 | 0.19 |
| 10 | 8.35 | 8.39 | 0.48 |
| 20 | 14.83 | 14.86 | 0.20 |
| 30 | 30.14 | 30.16 | 0.07 |
| 40 | 75.31 | 75.34 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-L.; Huang, Y.-T.; Lee, C.-M.; Hsu, T.-H.; Zhu, M.-L. A Finite Element Approach to the Upper-Bound Bearing Capacity of Shallow Foundations Using Zero-Thickness Interfaces. Appl. Sci. 2025, 15, 7635. https://doi.org/10.3390/app15147635
Lee Y-L, Huang Y-T, Lee C-M, Hsu T-H, Zhu M-L. A Finite Element Approach to the Upper-Bound Bearing Capacity of Shallow Foundations Using Zero-Thickness Interfaces. Applied Sciences. 2025; 15(14):7635. https://doi.org/10.3390/app15147635
Chicago/Turabian StyleLee, Yu-Lin, Yu-Tang Huang, Chi-Min Lee, Tseng-Hsing Hsu, and Ming-Long Zhu. 2025. "A Finite Element Approach to the Upper-Bound Bearing Capacity of Shallow Foundations Using Zero-Thickness Interfaces" Applied Sciences 15, no. 14: 7635. https://doi.org/10.3390/app15147635
APA StyleLee, Y.-L., Huang, Y.-T., Lee, C.-M., Hsu, T.-H., & Zhu, M.-L. (2025). A Finite Element Approach to the Upper-Bound Bearing Capacity of Shallow Foundations Using Zero-Thickness Interfaces. Applied Sciences, 15(14), 7635. https://doi.org/10.3390/app15147635






