Performance Comparison of Multi-Objective Optimizers for Dynamic Balancing of Six-Bar Watt Linkages Using a Fully Cartesian Model
Abstract
1. Introduction
2. Mechanical Analysis
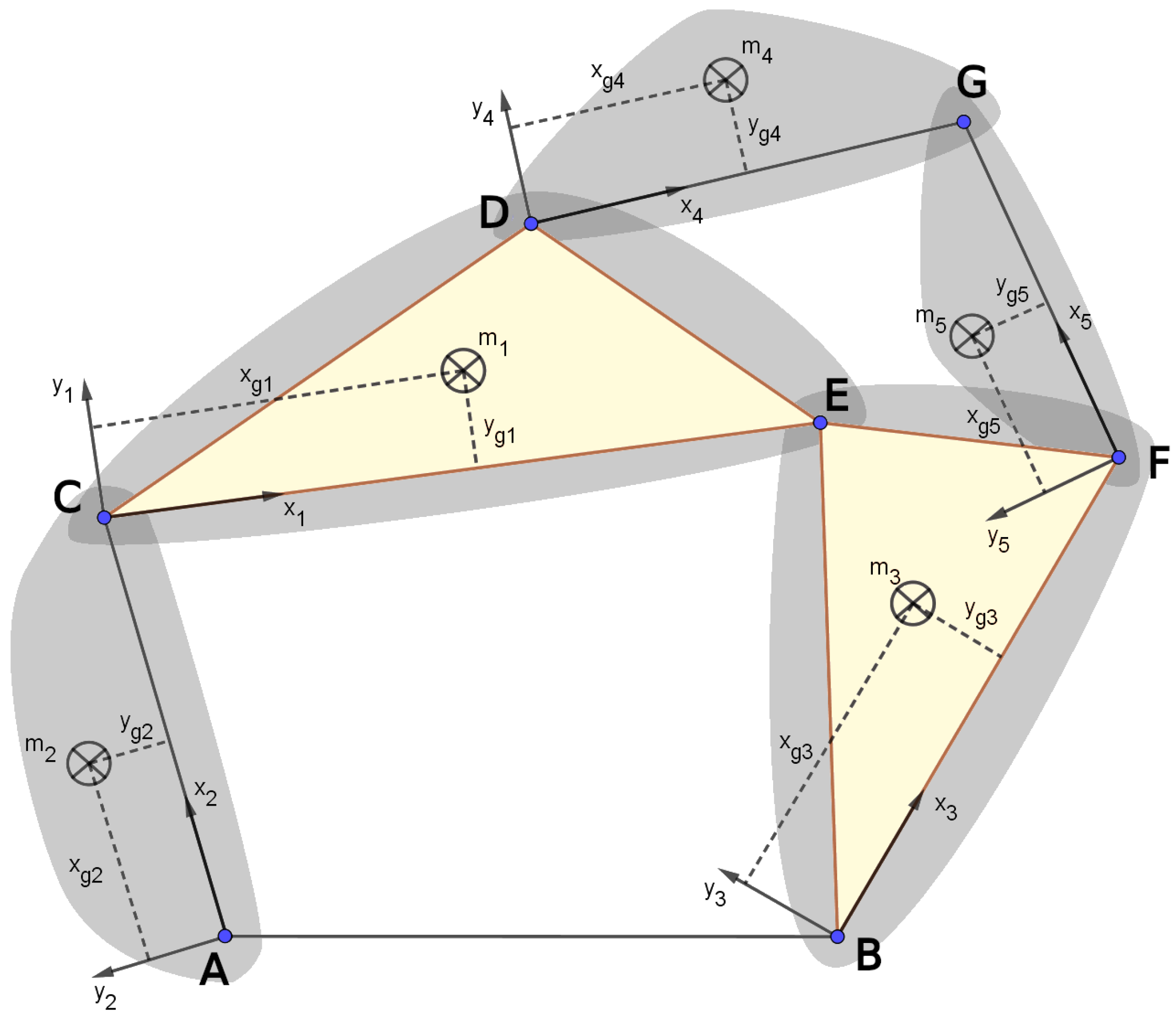
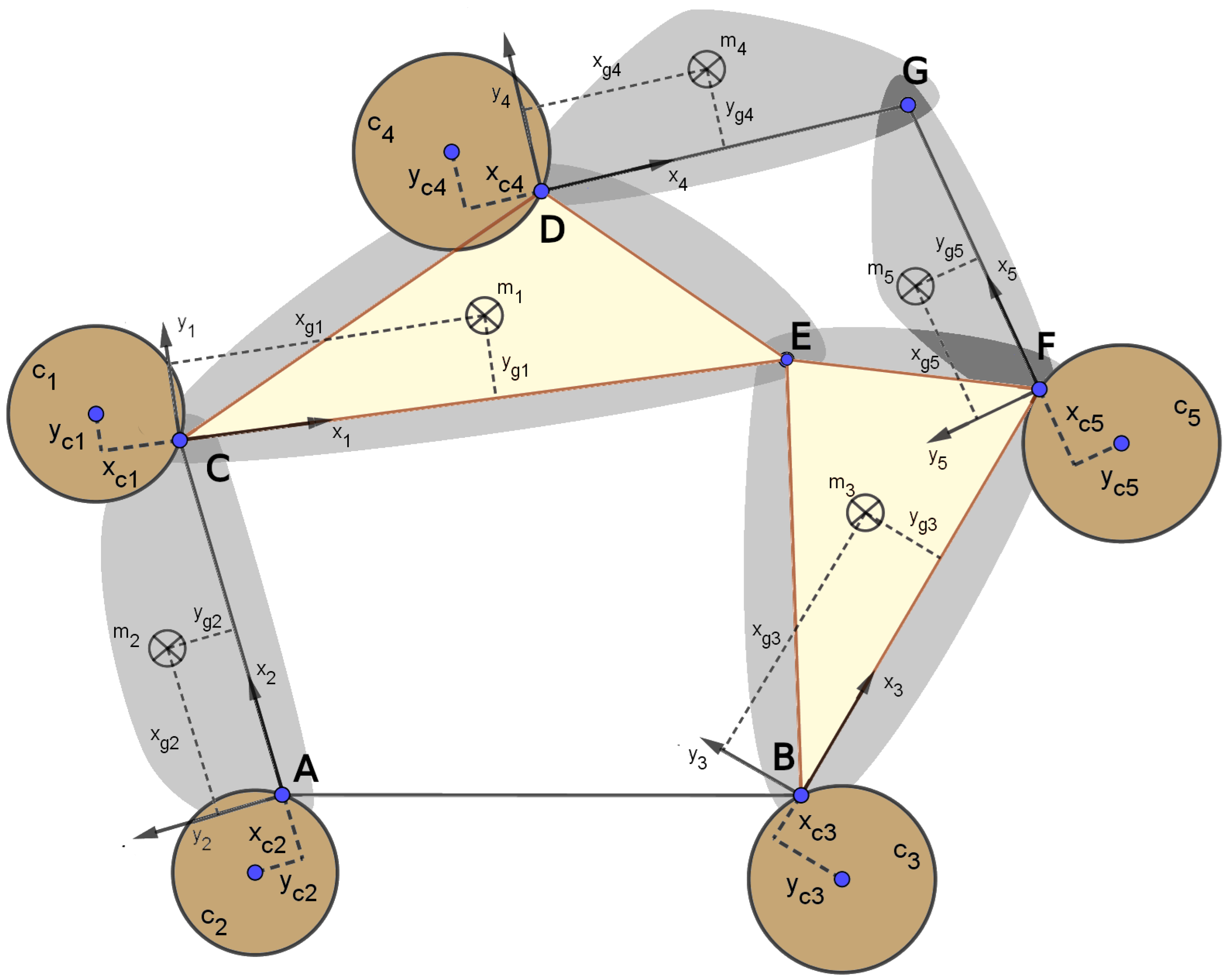
2.1. Mass-Matrix Characterization of a Six-Bar Watt Linkage Using FCC
2.2. Shaking Force and Shaking Moment
3. Optimization
3.1. Objective Functions and Boundaries
3.2. Single- and Multi-Objective Optimization
- is at least as good as in all objectives.
- is strictly better than in at least one objective.
3.3. Algorithms
3.3.1. Single-Objective Optimization Algorithms
3.3.2. Multi-Objective Optimization Algorithms
4. Experiments and Results
4.1. Physical Properties of the Six-Bar Watt Linkage Without Counterweights
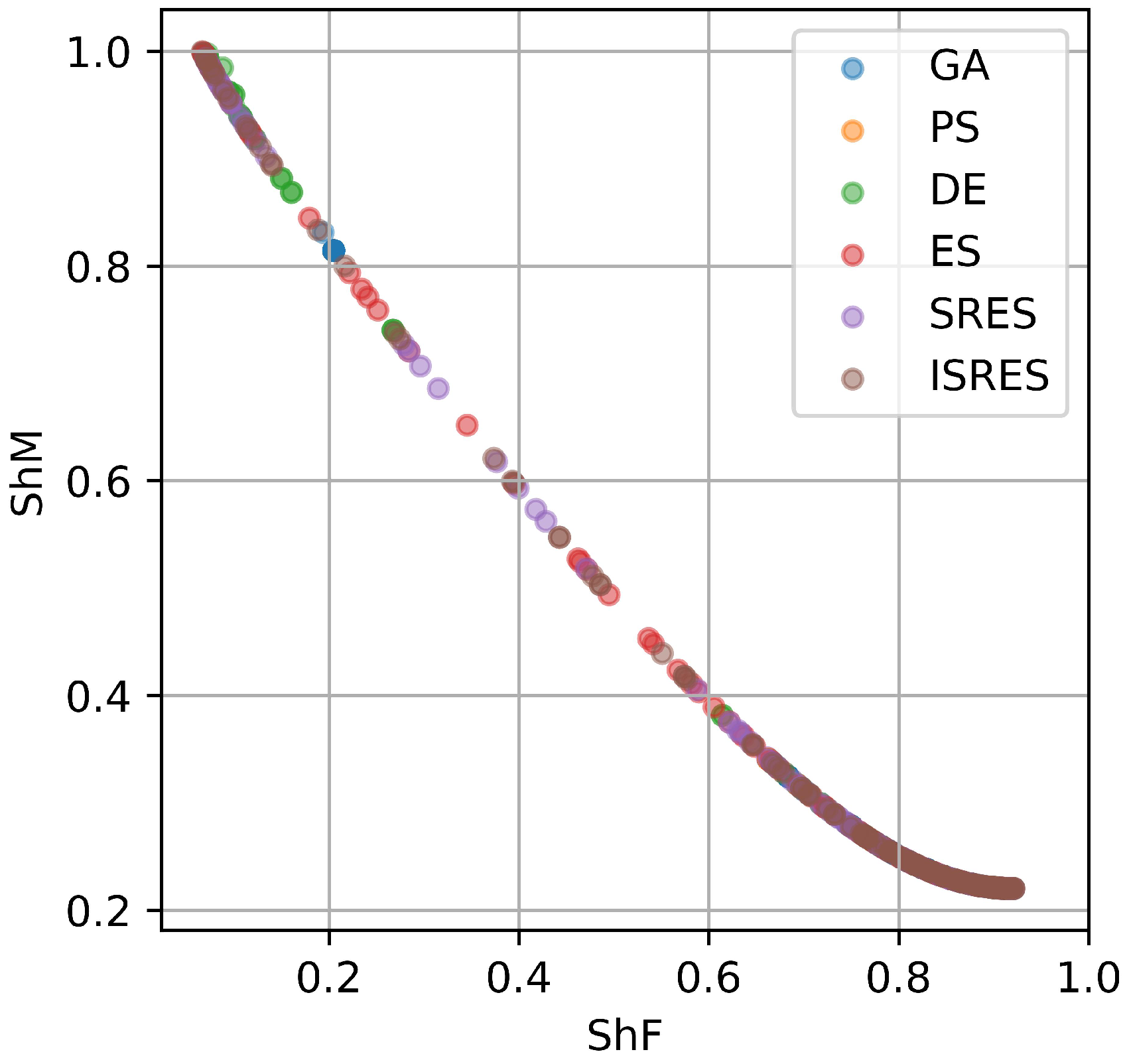
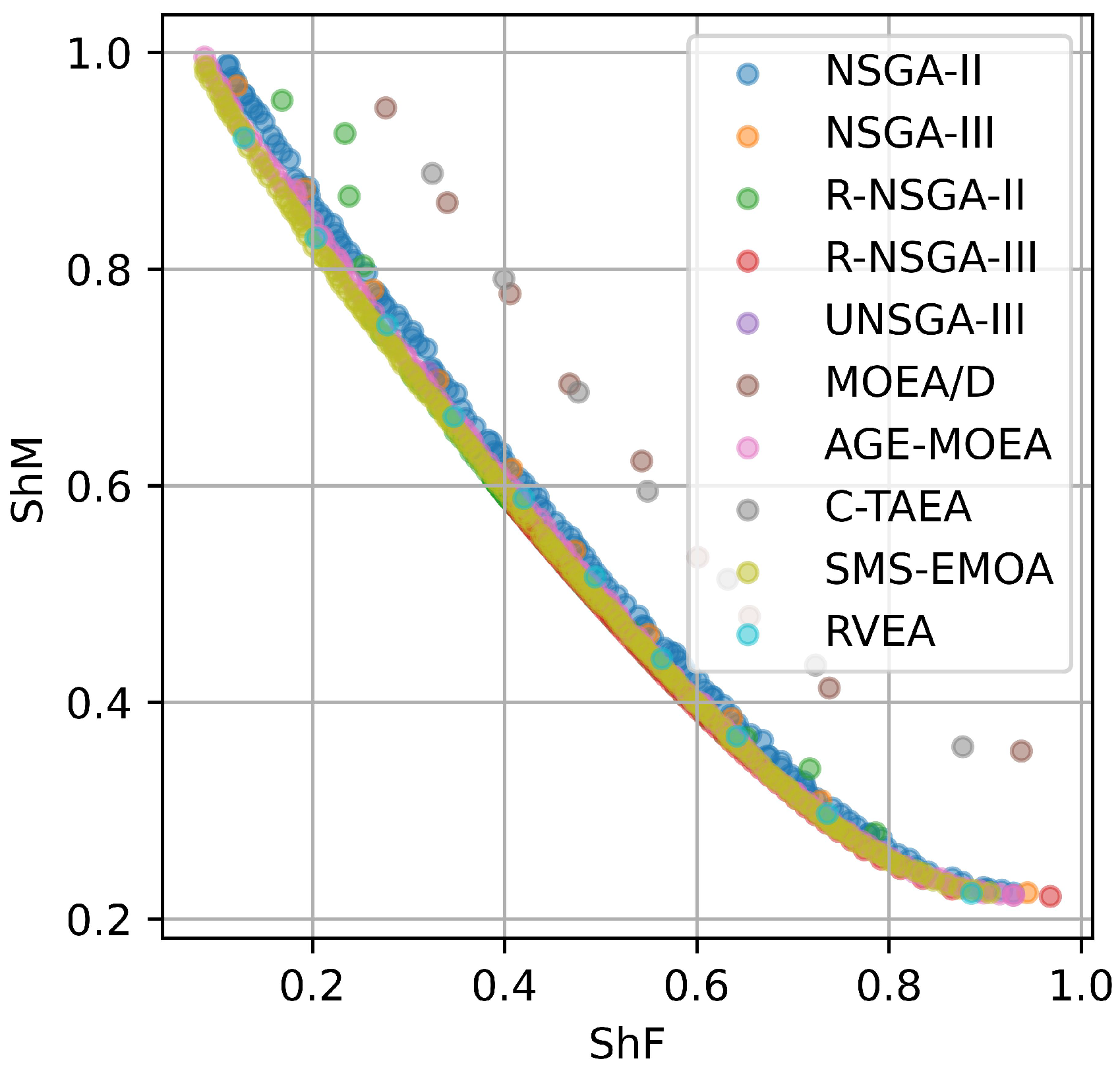
4.2. Comparison of Different Optimization Algorithms
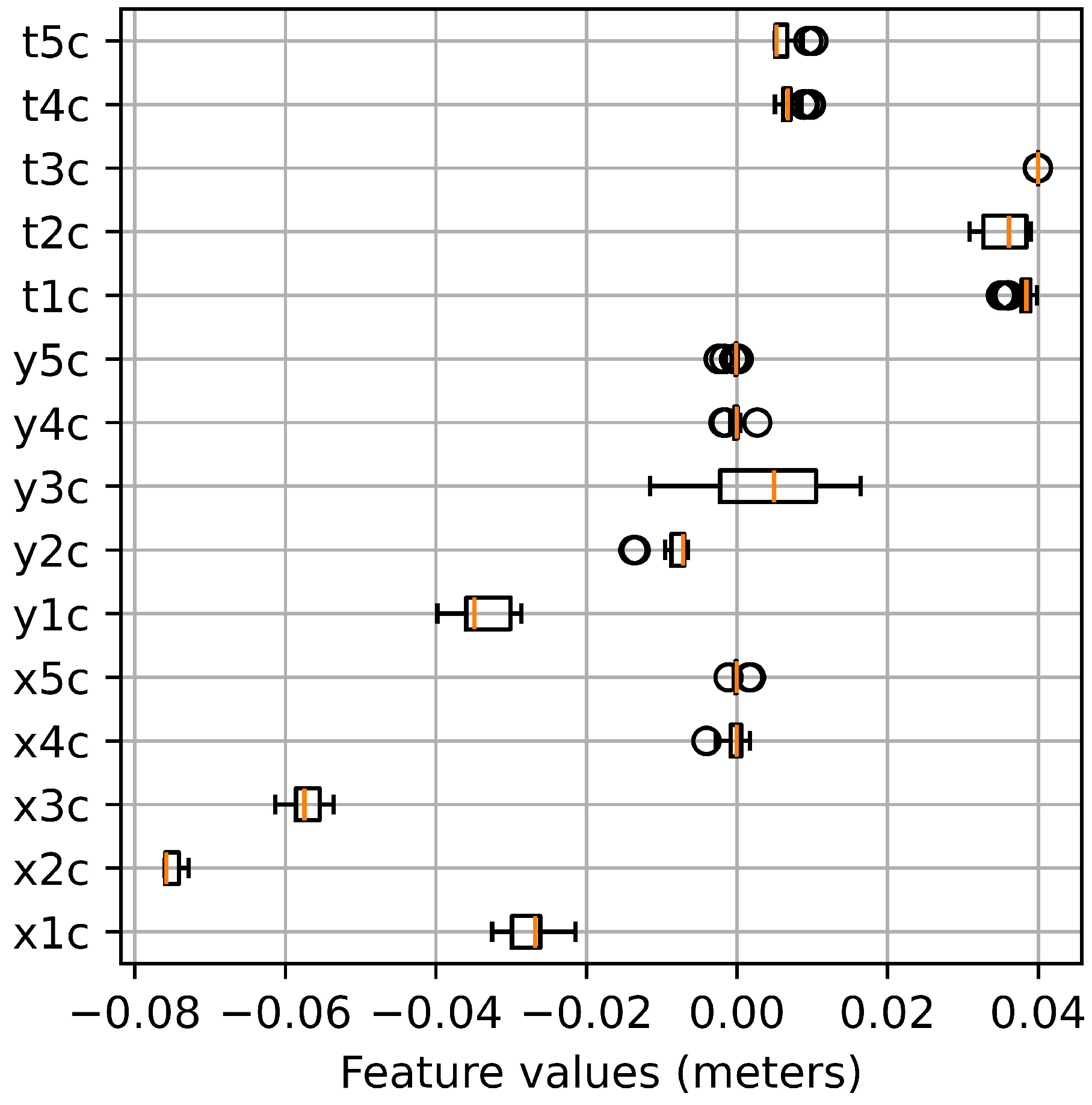
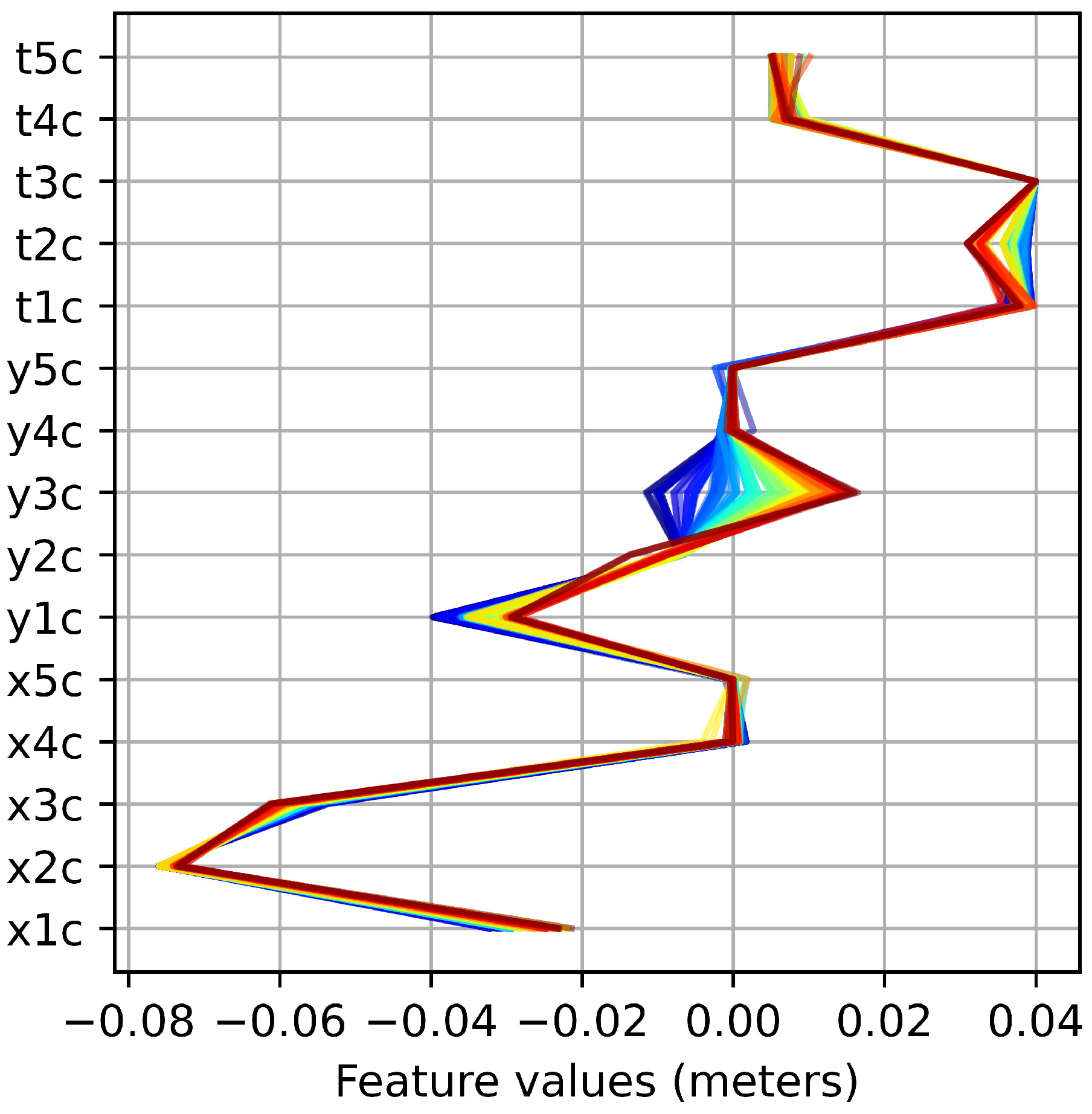
4.3. Analysis of Solutions Obtained with the Best Algorithm
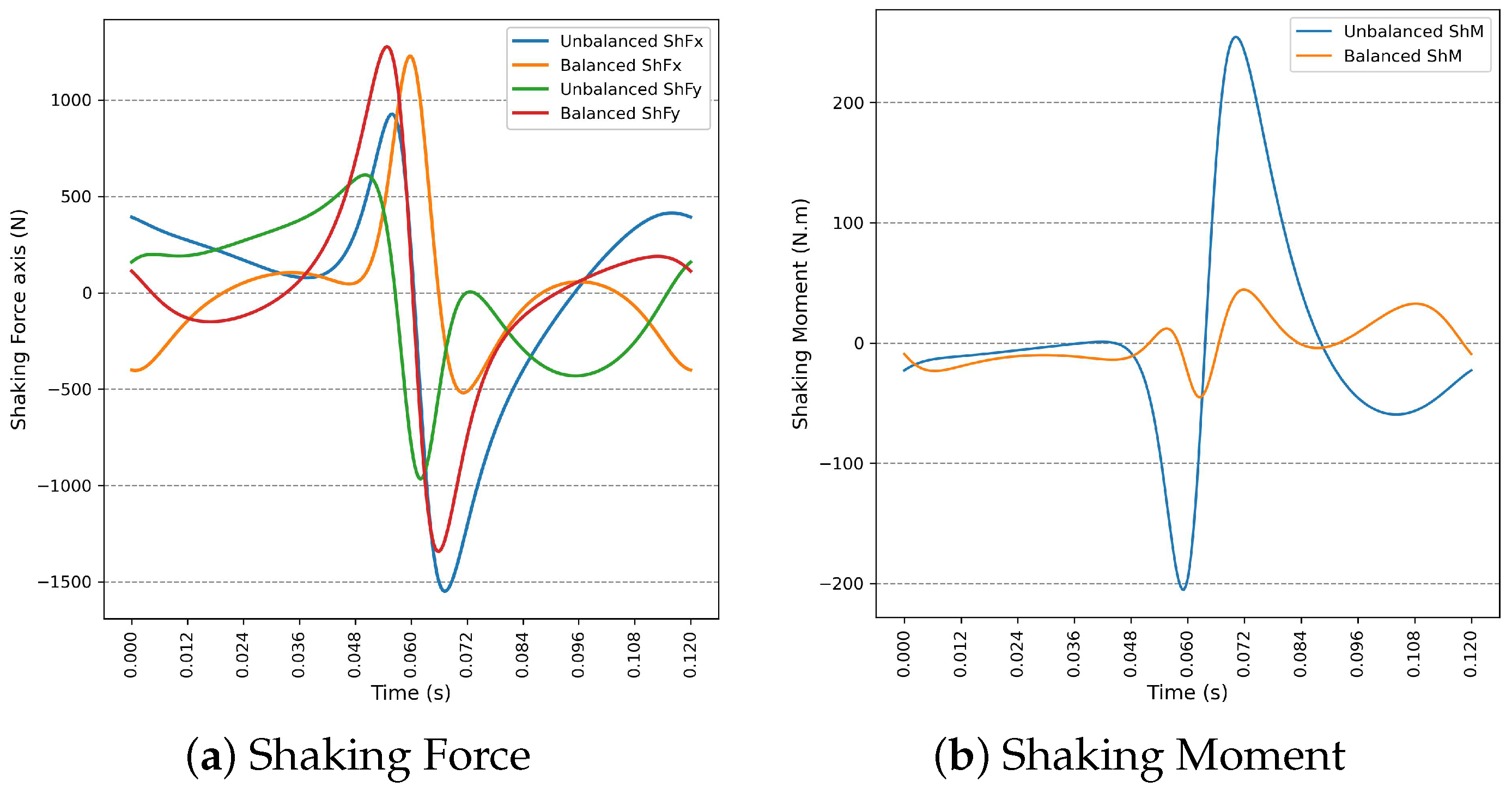
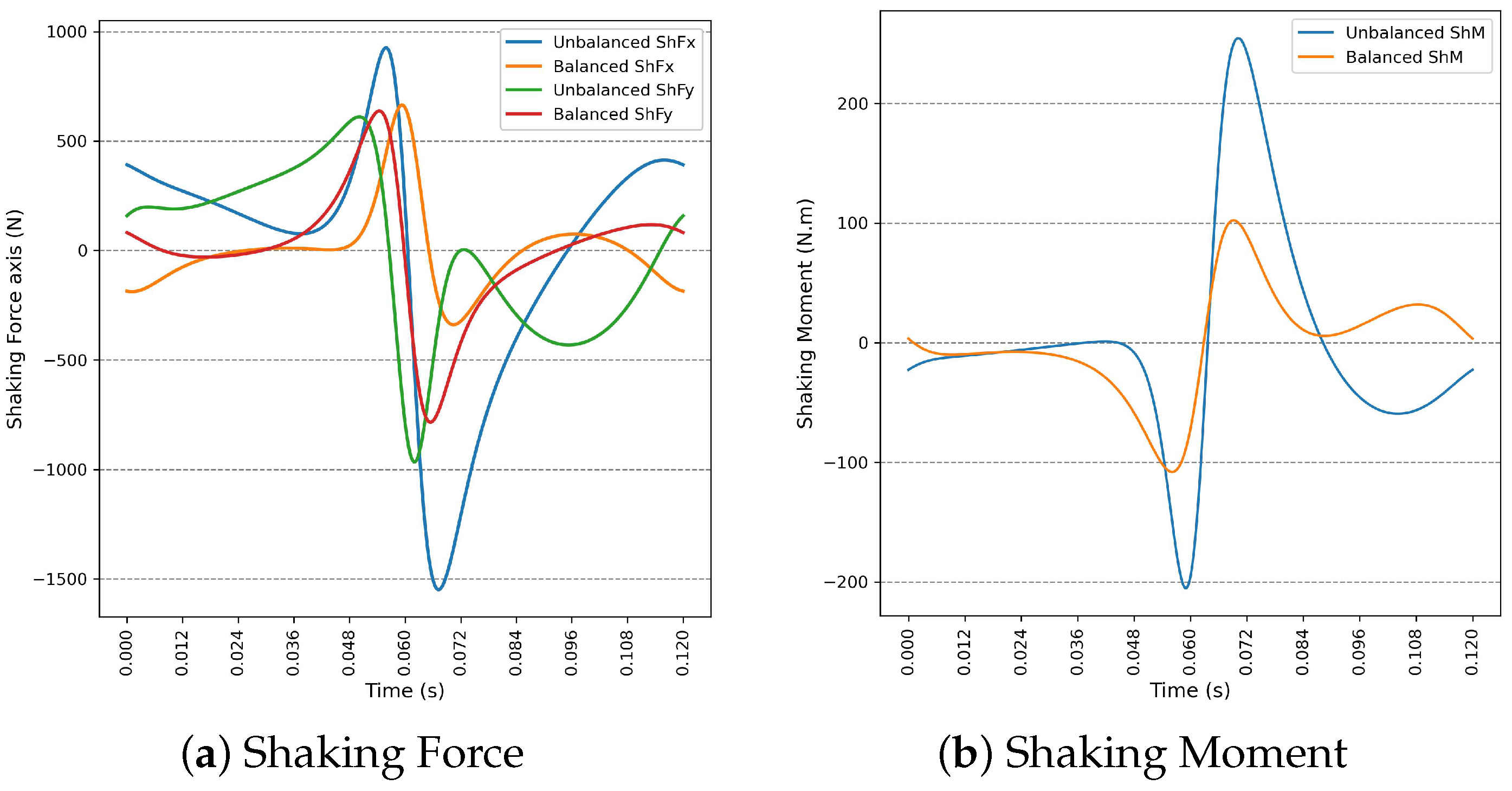
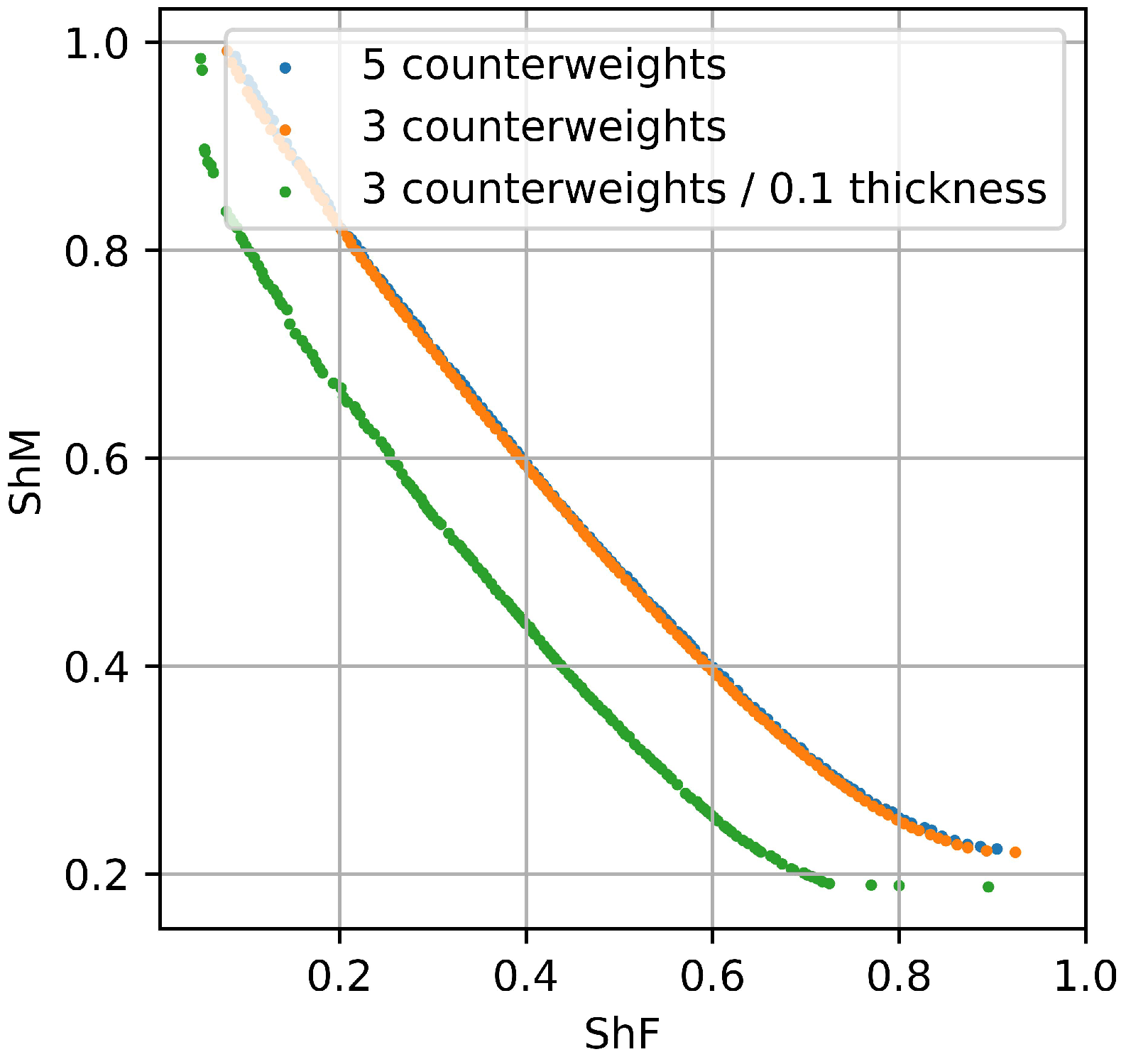
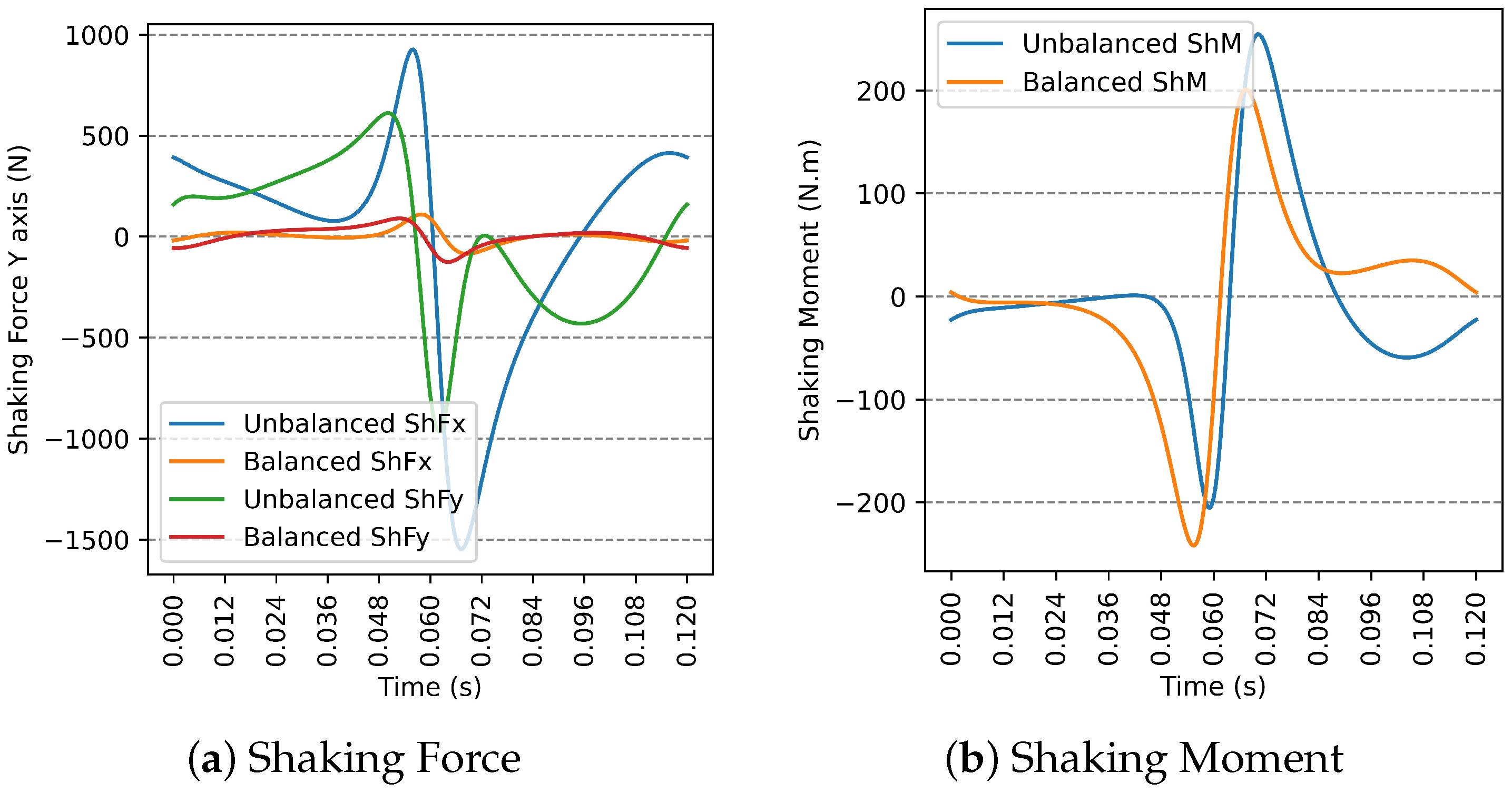
5. Balancing Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FCC | Fully Cartesian Coordinates |
| ShF | Shaking Force |
| ShFx | Shaking Force X axis |
| ShFy | Shaking Force Y axis |
| ShM | Shaking Moment |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
| ES | Evolution Strategy |
| SRES | Stochastic Ranking for Constrained Evolutionary Optimization |
| ISRES | Improved Stochastic Ranking Evolution Strategy |
| PS | Pattern Search |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| NSGA-III | Non-Dominated Sorting Genetic Algorithm III |
| MOGA | Multi-Objective Genetic Algorithm |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| R-NSGA-II | Reference-point NSGA-II |
| R-NSGA-III | Reference-point NSGA-III |
| UNSGA-III | Unified NSGA-III |
| MOEA/D | Multi-objective Evolutionary Algorithm based on Decomposition |
| AGE-MOEA | Adaptive Geometry Estimation based MOEA |
| C-TAEA | Convergence and Trade-off-based Multi-objective Evolutionary |
| SMS-EMOA | S-Metric Selection Evolutionary Multi-objective Optimization Algorithm |
| RVEA | Reference Vector Guided Evolutionary Algorithm |
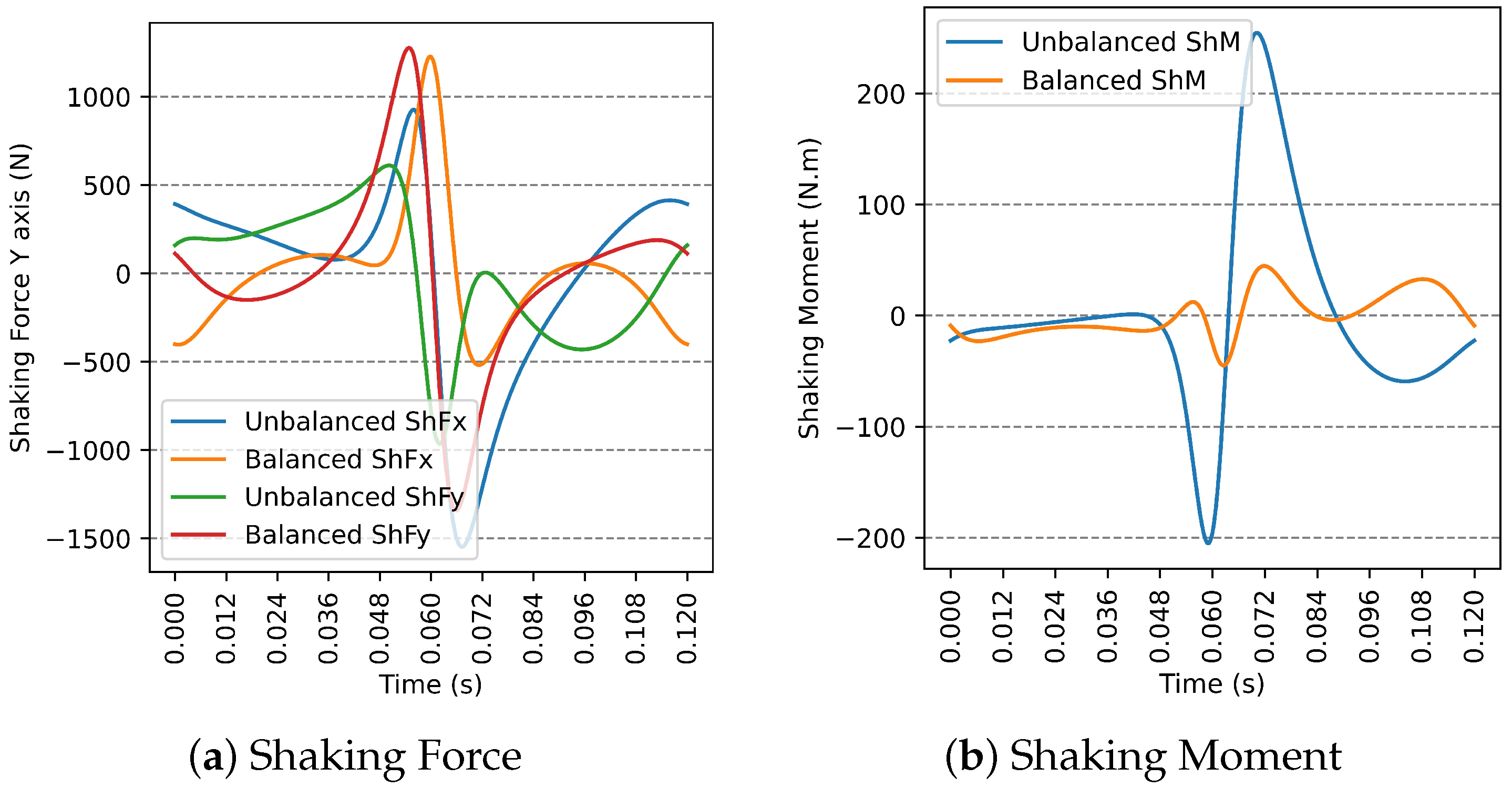
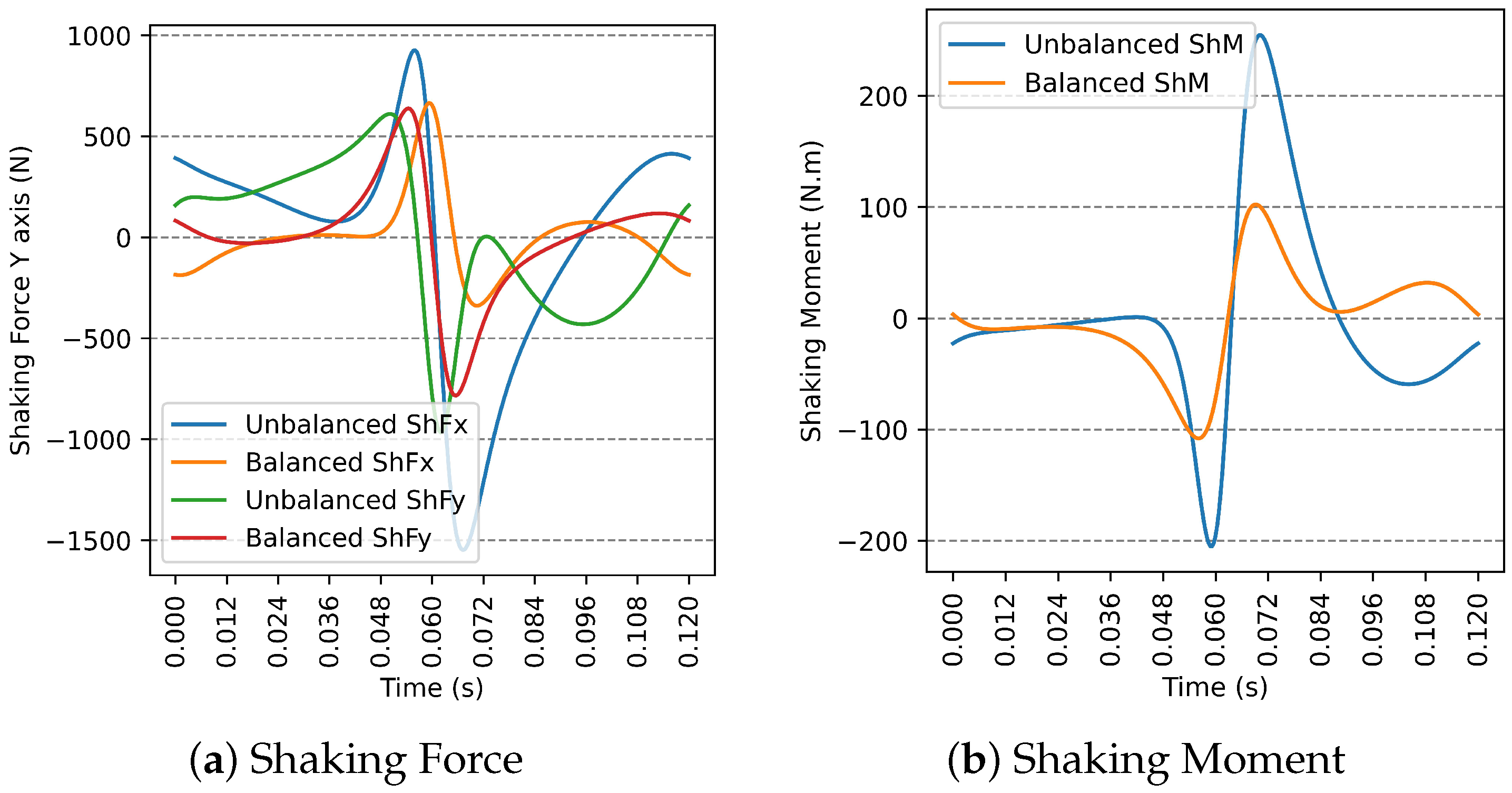
Appendix A. Dynamical Results When Using Only Three Counterweights

References
- Arakelian, V.; Dahan, M.; Smith, M. A Historical Review of the Evolution of the Theory on Balancing of Mechanisms. In International Symposium on History of Machines and Mechanisms Proceedings HMM 2000; Springer: Dordrecht, The Netherlands, 2000; pp. 291–300. [Google Scholar] [CrossRef]
- Arakelian, V.H.; Smith, M.R. Shaking force and shaking moment balancing of mechanisms: A historical review with new examples. J. Mech. Des. 2005, 127, 334–339. [Google Scholar] [CrossRef]
- Orvañanos-Guerrero, M.T.; Sánchez, C.N.; Rivera, M.; Acevedo, M.; Velázquez, R. Gradient descent-based optimization method of a four-bar mechanism using fully cartesian coordinates. Appl. Sci. 2019, 9, 4115. [Google Scholar] [CrossRef]
- Porter, B.; Sanger, D.J. Synthesis of dynamically optimum four-bar linkages. In Proc. Conf. on Mechanisms, Paper C69/72; Institution of Mechanical Engineers: London, UK, 1972; pp. 24–28. [Google Scholar]
- Mayne, R.W.; Sadler, J.P.; Conte, F.L.; George, G.R. Optimum Mechanism Design Combining Kinematic and Dynamic-Force Considerations. J. Eng. Ind. 1975, 97, 662–670. [Google Scholar] [CrossRef]
- Dresig, H.; Schönfeld, D. Rechnergestützte Optimierung der Antribs-und Gestellkraftgrössen ebene. Koppelgetriebe-Teil 1. Mech. Mach. Theory 1976, 11, 363–370. [Google Scholar] [CrossRef]
- Dresig, H.; Schönfeld, S. Rechnergestützte Optimierung der Antriebs- und Gestellkraftgrössen ebener Koppelgetriebe—Teil II. Mech. Mach. Theory 1976, 11, 371–379. [Google Scholar] [CrossRef]
- Walker, M.J.; Haines, R.S. A study of counterweight synthesis for a 6-bar chain. Mech. Mach. Theory 1982, 17, 327–334. [Google Scholar] [CrossRef]
- Rao, S.S.; Kaplan, R.L. Optimal Balancing of High-Speed Linkages Using Multiobjective Programming Techniques. ASME J. Mech. Trans. Autom. 1986, 108, 454–460. [Google Scholar] [CrossRef]
- Qi, N.M.; Pennestri, E. Optimum balancing of four-bar linkages. Mech. Mach. Theory 1991, 26, 337–348. [Google Scholar] [CrossRef]
- Chaudhary, H.; Saha, S.K. Balancing of shaking forces and shaking moments for planar mechanisms using the equimomental systems. Mech. Mach. Theory 2008, 43, 310–334. [Google Scholar] [CrossRef]
- Erkaya, S. Investigation of balancing problem for a planar mechanism using genetic algorithm. J. Mech. Sci. Technol. 2013, 27, 2153–2160. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Minimization of Shaking Force and Shaking Moment in Multiloop Planar Mechanisms. In Proceedings of the 1st International and 16th National Conference on Machines and Mechanisms, Roorkee, India, 18–20 December 2013. [Google Scholar]
- Chaudhary, K.; Chaudhary, H. Dynamic balancing of planar mechanisms using genetic algorithm. J. Mech. Sci. Technol. 2014, 28, 4213–4220. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Shape Optimization of Dynamically Balanced Planar Four-bar Mechanism. Procedia Comput. Sci. 2015, 57, 519–526. [Google Scholar] [CrossRef][Green Version]
- Chaudhary, K.; Chaudhary, H. Optimum Dynamic Balancing of a Planar Five-Bar Mechanisms Using Genetic Algorithm. In Proceedings of the International Conference on Advances in Materials and Product Design (AMPD-2015), Sardar Vallabhbhai Patel Institute of Technology, Surat, Gujarat, India, 10–11 January 2015. [Google Scholar]
- Chaudhary, H.; Chaudhary, K. Design of Reactionless Mechanisms Based on Constrained Optimization Procedure. In Dynamic Balancing of Mechanisms and Synthesizing of Parallel Robots; Springer: Cham, Switzerland, 2016; pp. 273–298. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Optimal dynamic design of planar mechanisms using teaching-learning-based optimization algorithm. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2016, 230, 3442–3456. [Google Scholar] [CrossRef]
- Feng, B.; Morita, N.; Torii, T. A new optimization method for dynamic design of planar linkage with clearances at joints—Optimizing the mass distribution of links to reduce the change of joint forces. J. Mech. Des. 2002, 124, 68–73. [Google Scholar] [CrossRef]
- Belleri, B.K.; Kerur, S.B. Balancing of planar six-bar mechanism with genetic algorithm. J. Mech. Energy Eng. 2021, 4, 303–308. [Google Scholar] [CrossRef]
- Orvananos-Guerrero, M.T.; Sanchez, C.N.; Davalos-Orozco, O.; Rivera, M.; Velazquez, R.; Acevedo, M. Using Fully Cartesian Coordinates to Calculate the Support Reactions of Multi-Scale Mechanisms. In Proceedings of the 2018 Nanotechnology for Instrumentation and Measurement, NANOfIM 2018, Mexico City, Mexico, 7–8 November 2018; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Orvañanos-Guerrero, M.T.; Acevedo, M.; Sánchez, C.N.; Campos-Delgado, D.U.; Ghavifekr, A.A.; Visconti, P.; Velázquez, R. Complete Balancing of the Six-Bar Mechanism Using Fully Cartesian Coordinates and Multiobjective Differential Evolution Optimization. Mathematics 2022, 10, 1830. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Farmani, M.R.; Jaamiolahmadi, A. Optimization of Force and Moment Balance of a Four-Bar Linkage using Multi-Objective Genetic Algorithm. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009. [Google Scholar] [CrossRef]
- García-Nieto, J.; López-Camacho, E.; García Godoy, M.J.; Nebro, A.J.; Durillo, J.J.; Aldana-Montes, J.F. A Study of Archiving Strategies in Multi-objective PSO for Molecular Docking. In Swarm Intelligence: 10th International Conference, ANTS 2016, Brussels, Belgium, 7–9 September 2016, Proceedings 10; Dorigo, M., Birattari, M., Li, X., López-Ibañez, M., Ohkura, K., Pinciroli, C., Stützle, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 40–52. [Google Scholar] [CrossRef]
- Li, X. Better Spread and Convergence: Particle Swarm Multiobjective Optimization Using the Maximin Fitness Function. In Genetic and Evolutionary Computation—GECCO 2004 Genetic and Evolutionary Computation Conference Seattle, WA, USA, 26–30 June 2004, Proceedings, Part I; Deb, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 117–128. [Google Scholar] [CrossRef]
- Farmani, M.R.; Jaamialahmadi, A.; Babaie, M. Multiobjective optimization for force and moment balance of a four-bar linkage using evolutionary algorithms. J. Mech. Sci. Technol. 2011, 25, 2971–2977. [Google Scholar] [CrossRef]
- Mejia-Rodriguez, R.; Villarreal-Cervantes, M.G.; Rodríguez-Molina, A.; Pérez-Cruz, J.H.; Silva-García, V.M. Evolutionary Multiobjective Design Approach for Robust Balancing of the Shaking Force, Shaking Moment, and Torque under Uncertainties: Application to Robotic Manipulators. Mathematics 2023, 11, 1776. [Google Scholar] [CrossRef]
- Collette, Y.; Siarry, P. Multiobjective Optimization, Principles and Case Studies; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A Survey on the Hypervolume Indicator in Evolutionary Multiobjective Optimization. IEEE Trans. Evol. Comput. 2021, 25, 1–20. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Hooke, R.; Jeeves, T. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM (JACM) 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolution Strategy: Nature’s Way of Optimization. In Optimization: Methods and Applications, Possibilities and Limitations— Proceedings of an International Seminar Organized by Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), Bonn, Germany, June 1989; Bergmann, H.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 106–126. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Stochastic Ranking for Constrained Evolutionary Optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Search biases in constrained evolutionary optimization. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2005, 35, 233–243. [Google Scholar] [CrossRef]
- Deb, K.; Sundar, J.; Bhaskara Rao, U.N.; Chaudhuri, S. Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ’06), Seattle, WA, USA, 8–12 July 2006; Technical Report 3. ACM: New York, NY, USA, 2006. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. U-NSGA-III: A Unified Evolutionary Algorithm for Single, Multiple, and Many-Objective Optimization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guimaraes, Portugal, 29 March–1 April 2015; pp. 34–49. [Google Scholar] [CrossRef]
- Vesikar, Y.; Deb, K.; Blank, J. Reference Point Based NSGA-III for Preferred Solutions. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1587–1594. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Panichella, A. An adaptive evolutionary algorithm based on non-euclidean geometry for many-objective optimization. In Proceedings of the GECCO 2019—Proceedings of the 2019 Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; ACM: New York, NY, USA, 2019; pp. 595–603. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 303–315. [Google Scholar] [CrossRef]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]

| Link n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Mass [kg] | 0.6935 | 0.1022 | 0.9636 | 0.1825 | 0.1679 |
| Length [m] | 0.19 | 0.14 | 0.1341640 | 0.25 | 0.23 |
| Inertia [kg · m2] | 0.0011616 | - | 0.0062264 | - | - |
| Inertia [kg · m2] | 0.0055653 | - | 0.0065733 | - | - |
| Inertia [kg · m2] | - | 0.0006685 | - | 0.0038036 | 0.0029620 |
| Inertia [kg · m2] | 0.0016759 | - | 0.0052291 | - | - |
| CoM [m] | 0.08 | 0.07 | 0.0775170 | 0.125 | 0.115 |
| CoM [m] | 0.0333333 | 0.0 | 0.0655913 | 0.0 | 0.0 |
| [m] | 0.05 | - | 0.0983869 | - | - |
| [m] | 0.1 | - | 0.1966773 | - | - |
| Algorithm | Type | Hypervolume |
|---|---|---|
| GA | Single | 0.327 |
| PS | Single | 0.24 |
| DE | Single | 0.39 |
| ES | Single | 0.452 |
| SRES | Single | 0.441 |
| ISRES | Single | 0.448 |
| NSGA-II | Multi | 0.438 |
| NSGA-III | Multi | 0.405 |
| R-NSGA-II | Multi | 0.427 |
| R-NSGA-III | Multi | 0.387 |
| UNSGA-III | Multi | 0.201 |
| MOEA/D | Multi | 0.297 |
| AGE-MOEA | Multi | 0.454 |
| C-TAEA | Multi | 0.291 |
| SMS-EMOA | Multi | 0.458 |
| RVEA | Multi | 0.422 |
| Algorithm | Time per Repetition (min) | No. of Repetitions | Total Time (min) |
|---|---|---|---|
| GA | 13.43 | 200 | 2686.0 |
| PS | 2.66 | 200 | 532.0 |
| DE | 13.3 | 200 | 2660.0 |
| ES | 26.62 | 200 | 5324.0 |
| SRES | 26.62 | 200 | 5324.0 |
| ISRES | 26.48 | 200 | 5296.0 |
| NSGA-II | 13.15 | 1 | 13.15 |
| NSGA-III | 10.86 | 1 | 10.86 |
| R-NSGA-II | 10.23 | 1 | 10.23 |
| R-NSGA-III | 21.09 | 1 | 21.09 |
| UNSGA-III | 10.32 | 1 | 10.32 |
| MOEA/D | 0.96 | 1 | 0.96 |
| AGE-MOEA | 10.56 | 1 | 10.56 |
| C-TAEA | 0.87 | 1 | 0.87 |
| SMS-EMOA | 10.44 | 1 | 10.44 |
| RVEA | 10.43 | 1 | 10.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orvañanos-Guerrero, M.T.; Sánchez, C.N.; Robles-Jiménez, L.E.; Gómez-Delgado, S.C. Performance Comparison of Multi-Objective Optimizers for Dynamic Balancing of Six-Bar Watt Linkages Using a Fully Cartesian Model. Appl. Sci. 2025, 15, 7543. https://doi.org/10.3390/app15137543
Orvañanos-Guerrero MT, Sánchez CN, Robles-Jiménez LE, Gómez-Delgado SC. Performance Comparison of Multi-Objective Optimizers for Dynamic Balancing of Six-Bar Watt Linkages Using a Fully Cartesian Model. Applied Sciences. 2025; 15(13):7543. https://doi.org/10.3390/app15137543
Chicago/Turabian StyleOrvañanos-Guerrero, María T., Claudia N. Sánchez, Luis Eduardo Robles-Jiménez, and Sara Carolina Gómez-Delgado. 2025. "Performance Comparison of Multi-Objective Optimizers for Dynamic Balancing of Six-Bar Watt Linkages Using a Fully Cartesian Model" Applied Sciences 15, no. 13: 7543. https://doi.org/10.3390/app15137543
APA StyleOrvañanos-Guerrero, M. T., Sánchez, C. N., Robles-Jiménez, L. E., & Gómez-Delgado, S. C. (2025). Performance Comparison of Multi-Objective Optimizers for Dynamic Balancing of Six-Bar Watt Linkages Using a Fully Cartesian Model. Applied Sciences, 15(13), 7543. https://doi.org/10.3390/app15137543







