Abstract
Balancing mechanisms require the minimization of both the Shaking Moment () and Shaking Force (), a complex multi-criteria challenge often tackled using single-objective algorithms. However, these methods face difficulties in navigating competing objectives. In contrast, multi-objective algorithms provide a more efficient and adaptable framework, while Fully Cartesian Coordinates () simplify the balancing equations compared to conventional Cartesian formulations. This study focuses on optimizing the dynamic balance of a six-bar Watt linkage using . A wide set of optimization methods is analyzed and compared, and among them, the S-Metric Selection Evolutionary Multi-objective Optimization Algorithm (SMS-EMOA) demonstrates superior performance. This algorithm achieves the most significant hypervolume value in only 10.44 min of execution. The results indicate that multi-objective algorithms outperform single-objective approaches, offering faster and more diverse optimization solutions. Additionally, this study introduces an analytical method that enables the straightforward identification of removable counterweights, achieving an equally effective balance while minimizing the number of counterweights required.
1. Introduction
Balancing mechanisms have been a significant research focus in mechanical engineering, as effective balancing reduces vibrations, noise, and wear, enhancing both the performance and lifespan of mechanical systems. The primary objective is to minimize—or, ideally, eliminate—the reaction forces and moments acting on the mechanism’s base (Shaking Force () and Shaking Moment ()), improving dynamic performance and operational stability while reducing maintenance costs. Various techniques have been developed to achieve optimal balance, including mass redistribution and the strategic use of counterweights [1]. Arakelian and Smith [2] explored the application of optimization algorithms and computational methods to achieve the dynamic balancing of mechanisms. They emphasized that optimization techniques enable precise mass distribution and fine-tune geometric parameters, leading to optimal balance, enhanced performance, and reduced vibrations.
This document reviews recent advancements in multi-objective optimization algorithms for balancing mechanisms, categorizing them based on the type of algorithm employed, with particular emphasis on whether they are inherently multi-objective or rely on a weighted combination of objectives. Furthermore, it examines the mathematical processes involved in deriving balancing equations. Most optimization studies have implemented these algorithms using Cartesian coordinates incorporating angular parameters. However, as demonstrated by Orvañanos et al. [3], it is possible to formulate these equations using —eliminating angles and associated trigonometric functions—resulting in more computationally efficient optimization processes.
In 1972, Porter et al. [4] presented one of the earliest studies on dynamic balance optimization. They investigated a four-bar mechanism, formulating the objective function as a weighted sum of s, s, and joint loads. Similarly, Sadler and Mayne [5] analyzed a four-bar mechanism with counterweights, modeling the counterweights as point masses with no predefined upper limits. Their approach involved optimizing a single performance criterion while enforcing constraints on another. In 1976, Dresig et al. [6,7] developed a computer-based system called KOGEOP to optimize linkage dynamics. Their research focused on minimizing an objective function’s mean square and peak values, integrating s, s, and driving torque. Additionally, they explored the performance of various search algorithms in the optimization process.
Walker et al. [8] applied optimization techniques using a nonlinear programming approach combined with the Simplex algorithm. They developed the MEDIC program, which iteratively adjusts counterweight parameters to achieve optimal balance. Their methodology employs an objective function that assigns weights to multiple criteria. Rao et al. [9] applied multi-objective optimization techniques, including goal programming, goal attainment, the lexicographic method, and the bounded objective function method, to balance a four-bar linkage mechanism. These approaches aim to simultaneously minimize s and moments by employing weighted-sum methods to construct the objective function. Qi et al. [10] introduced a numerically efficient technique for optimizing the dynamic balance of linkages. Their method integrates Newton’s equations with the virtual work principle to decouple the link equilibrium equations, facilitating an efficient dynamic analysis. Optimization is achieved through a weighted-sum approach to construct the objective function.
Multi-objective optimization techniques, which utilize methods not inherently designed for multi-objective problems in combination with mathematical approaches like weighted factors, are widely employed to explore a range of potential solutions and identify the optimal configuration that simultaneously minimizes both the and . These techniques are particularly advantageous due to their ability to address the complex, nonlinear nature of the balancing problem, offering a set of Pareto-optimal solutions, the most suitable of which can be selected based on specific performance criteria. Such advanced optimization methods have been shown to significantly enhance the dynamic performance of mechanisms, leading to improved stability and extended operational lifespan. Recent studies have introduced various approaches for optimizing the balancing of planar mechanisms using these methods. Key contributions in this field include [11,12,13,14,15,16,17,18,19,20]. All these optimization approaches employ traditional Cartesian coordinates methods to formulate the objective function.
Orvananos-Guerrero et al. [3,21] introduced a methodology for optimizing the balance of a four-bar mechanism by formulating the objective functions exclusively in . Subsequently, they extended this approach to optimize a six-bar Watt linkage [22], employing a similar technique that relies on . Both studies used weighted factors to integrate the s and moments into the optimization process, enabling a balanced consideration of these dynamic parameters through a weighted combination.
Optimizing the balance of and through multi-objective optimization algorithms can handle the problem as a set of objectives that must be minimized simultaneously. This approach eliminates the need to weigh the objectives and offers a more comprehensive solution to the balancing challenge. Notable examples of such research include the application of the Non-Dominated Sorting Genetic Algorithm II (NSGA-II [23]), an enhanced version of the original NSGA [24], and the Multi-Objective Genetic Algorithm (MOGA) to optimize the force and moment balance of a four-bar linkage, as demonstrated by Farmani et al. [25]. In subsequent studies, Multi-Objective Particle Swarm Optimization (MOPSO [26,27]) and NSGA-II to were employed to achieve similar objectives [28]. Additionally, Mejia-Rodriguez et al. [29] proposed a method utilizing the NSGA-II algorithm to perform robust balancing of , , and torque in robotic manipulators.
While numerous studies have demonstrated the efficacy of various optimization algorithms in mechanism balancing, comparative analyses remain relatively scarce. This paper seeks to address this gap by conducting a comprehensive evaluation of diverse multi-objective optimization algorithms, including NSGA-II, NSGA-III, R-NSGA-II, R-NSGA-III, UNSGA-III, MOEA/D, AGE-MOEA, C-TAEA, SMS-EMOA, and RVEA. Specifically, the study minimizes the and moment in a six-bar Watt linkage. The governing equations for the optimization are derived using a mathematical method based on , ensuring a straightforward yet robust and precise formulation of the dynamic problem. In addition, this document proposes a methodology to analyze the sensitivity of counterweights to determine if it is possible to reduce them.
The rest of this manuscript is organized as follows. Section 2 describes the mechanical analysis and how the mathematical equations are calculated. The optimization foundations and algorithms are introduced in Section 3. Section 4 shows the experiments and results, including a comparison of algorithms and a sensitivity analysis. Section 5 describes the balancing optimization results. Finally, Section 6 concludes this document.
2. Mechanical Analysis
Most existing methods for the optimization of mechanism balancing rely on Cartesian coordinates, which inherently involve angles and trigonometric functions for the characterization of the mechanisms and formulation of the corresponding balancing equations.
This section outlines the methodology for deriving the mass matrix that characterizes a six-bar Watt linkage using , a formulation previously introduced in [22] and briefly explained in this section.
2.1. Mass-Matrix Characterization of a Six-Bar Watt Linkage Using FCC
Figure 1 depicts a six-bar Watt linkage consisting of five moving links and one degree of freedom. Each link is associated with a local coordinate system ( axis and axis), where the origin is positioned at point i and the x-axis is oriented toward point j. The physical properties of each link include its mass and a center of gravity defined by the local coordinates for .
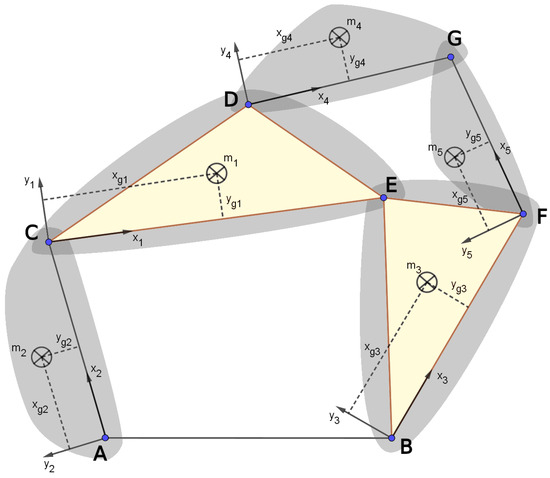
Figure 1.
Six-bar Watt linkage to be optimized.
Three important vectors must be defined to characterize the mass matrix of the mechanism: vector (Equation (1)), which represents the position of the basic points; vector (Equation (2)), which represents the velocity of the basic points; and vector Equation (3)), which represents the acceleration of the basic points.
The mechanical method proposed to optimize dynamic balance in this research consists of adding fixed counterweights to each of the bars to redistribute the mass, thereby shifting the center of mass of the linkage to improve balancing. Figure 2 illustrates the mechanism with the added counterweights for each linkage. The physical properties of each counterweight include its mass () and a center of gravity located at the local coordinates of its corresponding link, i.e., for .
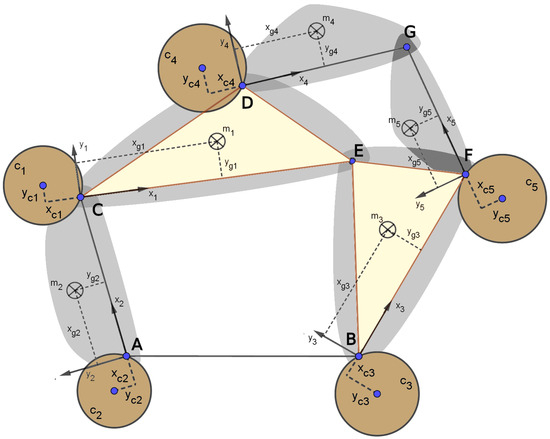
Figure 2.
Six-bar Watt linkage with counterweights.
After defining the mass matrix [22] for each linkage (considering the bar-counterweight system), it is possible to derive the mass matrix that characterizes the entire mechanism.
Equation (4) presents the mass matrix (M) of the mechanism depicted in Figure 2, where , , …, represent the elements of the individual mass matrices for each linkage, with .
The definitions of , , , , , , , , , and , where the n suffix denotes the corresponding linkage number, can be found in [22].
2.2. Shaking Force and Shaking Moment
The mass matrix (M; Equation (4)) is notable for being constant, as it is not expressed in terms of the mechanism’s movement. Due to this property, it is possible to derive the equations that define the linear momentum (L) in both the x-axis and y-axis using Equation (5).
where is a matrix composed of identity matrices corresponding to the number of basic points in the mechanism (Equation (6)).
The shaking force ( and ) (Equation (7)) can be computed by taking the time derivative of the equations and (Equation (5)).
Similarly, the shaking moment () (Equation (9)) is derived by differentiating the angular momentum equation (H) (Equation (8)) with respect to time.
Consider the following:
3. Optimization
Numerical optimization involves identifying the optimal solution (maximum or minimum) to a mathematical problem by systematically evaluating and refining candidate solutions using numerical methods. Such problems typically comprise an objective function dependent on one or more variables, subject to constraints. In the present context, the objective functions to be optimized are the ShF and ShM. The design variables consist of the positions and thicknesses of the counterweights.
This section formally defines the objective functions, variables, and constraints. Furthermore, it details the various single- and multi-objective optimization algorithms employed to optimize the six-bar Watt linkage.
3.1. Objective Functions and Boundaries
This study considers the shaking force () and the shaking moment () as the objective functions for the optimization of the balance of the mechanism. To ensure dimensionless quantities for and , normalization factors and are introduced, defined as follows:
(Equation (12)) is defined as the ratio of the root mean square (RMS) value of the reaction for the optimized mechanism () to the RMS value of the for the original, unbalanced mechanism (), both evaluated over time period T. The values of , , and for each time step (k) can be obtained through direct kinematics or by modeling the original mechanism using CAD software such as Solidworks 2023.
Analogously, (Equation (13)) is determined by a similar ratio, where oShM(X)
represents the of the optimized mechanism and is a constant representing the of the unbalanced mechanism.
A solution to the problem (X; Equation (14)) is a vector comprising all the design variables associated with the five counterweights.
The constraints on the design variables, corresponding to the position of the mass center (, ) and the thickness () of each counterweight (), are imposed based on the physical limitations of the model and are defined in Equation (15).
3.2. Single- and Multi-Objective Optimization
Numerical optimization algorithms can be broadly classified as single- or multi-objective. Single-objective optimization algorithms aim to optimize (minimize or maximize) a single objective function. As previously defined, the problem of balancing the six-bar Watt linkage involves two objective functions: and . Prior work [3,22] employed a single-objective optimization approach by constructing a linear combination of the objectives, as shown in Equation (16), where is a hyperparameter ranging from 0 to 1, controlling the relative weight assigned to each objective function.
However, this research compares the performance of single- and multi-objective algorithms.
Multi-objective optimization algorithms address problems involving two or more conflicting objectives [30], as is the case with and . These algorithms aim to identify a set of solutions that balance these competing objectives. A single, universally “best” solution rarely exists in multi-objective optimization. Instead, a given solution may excel for one objective but perform poorly with respect to another.
To assess solution quality, solutions are categorized as either dominated or non-dominated. A solution () is considered to be dominated by another solution () if the following two conditions are met:
- is at least as good as in all objectives.
- is strictly better than in at least one objective.
A solution is considered non-dominated if no other solution exists that dominates it. Non-dominated solutions are also called Pareto-optimal solutions, representing trade-offs where improvement in one objective necessitates a degradation in the other.
Hypervolume is a widely adopted indicator in multi-objective optimization for the evaluation of the quality of a solution set. The hypervolume indicator quantifies the “size of the space covered” [31]. Higher hypervolume values indicate a superior solution set, implying a larger region of dominance and typically better proximity to the Pareto-optimal front. This metric simultaneously assesses two key aspects: convergence, reflecting how close the solutions are to the Pareto-optimal front, and diversity, indicating how well the solutions are distributed across the front.
3.3. Algorithms
This research optimizes the balancing of a six-bar Watt linkage, comparing the performance of sixteen optimization algorithms: six single-objective algorithms and ten multi-objective algorithms.
The single-objective algorithms evaluated in this study include Differential Evolution (DE), Evolution Strategy (ES), the Genetic Algorithm (GA), Improved Stochastic Ranking Evolution Strategy (ISRES), Stochastic Ranking Evolution Strategy (SRES), and Pattern Search (PS). The investigated multi-objective optimization algorithms are the Non-dominated Sorting Genetic Algorithm II (NSGA-II), NSGA-III, R-NSGA-II, R-NSGA-III, UNSGA-III, the Multi-objective Evolutionary Algorithm based on Decomposition (MOEA/D), the Adaptive Geometric-based Multi-objective Evolutionary Algorithm (AGE-MOEA), the Convergence and Trade-off-based Multi-objective Evolutionary Algorithm (C-TAEA), the S-Metric Selection Evolutionary Multi-objective Optimization Algorithm (SMS-EMOA), and the Reference Vector Guided Evolutionary Algorithm (RVEA).
Section 3.3.1 concisely describes each single-objective optimization algorithm employed in this research. Conversely, Section 3.3.2 details the multi-objective optimization algorithms.
3.3.1. Single-Objective Optimization Algorithms
The Genetic Algorithm (GA) was introduced by Holland, J. in the 1960s and formalized in his 1975 book [32]. Inspired by natural selection in biological evolution, it employs selection, crossover, and mutation to iteratively refine solutions.
The Pattern Search (PS) algorithm [33], introduced by Hooke, R., et al. in 1961, is a direct search method. It iteratively evaluates candidate solutions within a structured pattern, adjusting the search area based on the observed results. Pattern search is particularly well-suited for objective functions that are non-smooth, non-linear, or noisy.
The Evolution Strategy (ES) algorithm [34], developed by Rechenberg, I. in 1978, is another evolutionary algorithm that aims to evolve a population of candidate solutions to identify the optimal one. This algorithm is based on Gaussian random mutations with optional recombination and often employs self-adaptive step sizes for local exploration.
Differential Evolution (DE) [35], developed by Kenneth Price and published in 1994, is a biologically inspired optimization algorithm that maintains a population of candidate solutions. It generates new candidate solutions using mathematical operations based on differences between randomly selected individuals within the population and ensures the preservation of superior solutions.
In 2000, Runarsson, T.P. and Yao, X., developed the Stochastic Ranking for Constrained Evolutionary Optimization (SRES) algorithm [36]. This derivative-free global optimization method is designed to solve constrained optimization problems by combining fitness values and constraint violation information into a single ranking system.
The Improved Stochastic Ranking Evolution Strategy (ISRES) algorithm [37], proposed by Runarsson, T.P., et al. in 2005, is specifically tailored for constrained optimization and is particularly effective in addressing non-linear problems. This algorithm combines stochastic search and evolutionary strategies.
3.3.2. Multi-Objective Optimization Algorithms
The Non-dominated Sorting Genetic Algorithm II (NSGA-II), developed by Kalyanmoy et al. [23] in 2002, is characterized by non-dominated sorting, crowding distance calculation, elitism, fast computation, and genetic operations such as crossover and mutation to generate new solutions.
In 2006, Kalyanmoy et al. [38] introduced R-NSGA-II, incorporating decision-maker preferences through reference points to more effectively guide the search for desirable solutions.
Kalyanmoy and Himanshu developed NSGA-III [39] in 2013. This algorithm modifies specific selection mechanisms of NSGA-II to enhance the diversity of the resulting solutions.
The Unified NSGA-III (UNSGA-III) algorithm [40], an extension of NSGA-III developed by Seada and Kalyanmoy in 2015, aims to improve performance and broaden applicability in multi-objective optimization. It integrates several techniques and concepts for more efficient handling of multi-objective problems, including a unified approach for diversity maintenance, reference-point management, and solution selection, thereby enhancing its versatility.
The Reference point-based NSGA-III (R-NSGA-III) algorithm [41], designed by Vesikar et al. in 2018, builds upon NSGA-III by incorporating user-defined reference points. This allows users to specify preferred regions within the objective space, guiding the search towards solutions of interest.
A distinct approach to multi-objective optimization was introduced by Zhang and Li in 2007, with the Multi-objective Evolutionary Algorithm based on Decomposition (MOEA/D) [42]. This method decomposes a multi-objective optimization problem into a set of scalar optimization subproblems, then solves them concurrently by integrating evolutionary algorithms with a decomposition strategy.
In 2019, Panichella introduced the Adaptive Geometry Estimation-based MOEA (AGE-MOEA) [43], an adaptive, generalized, multi-objective evolutionary algorithm. While it follows the general structure of NSGA-II, it employs a modified crowding distance calculation. This algorithm incorporates an adaptive framework that adjusts parameters or strategies based on the evolving optimization process.
Also in 2019, Li et al. introduced the Convergence and Trade-off-based Multi-objective Evolutionary Algorithm (C-TAEA) [44] for solving multi-objective problems. This algorithm emphasizes both convergence to the Pareto front and the maintenance of a well-distributed set of solutions.
The S-Metric Selection Evolutionary Multi-objective Optimization Algorithm (SMS-EMOA), introduced by Beume et al. [45] in 2007, is specifically designed to maximize the dominated hypervolume during the optimization process. It employs the s-metric (referring to the hypervolume measure) as a central component in its selection process, effectively guiding the population of solutions toward a diverse and high-quality representation of the Pareto front.
The Reference Vector Guided Evolutionary Algorithm (RVEA), presented by Cheng et al. [46] in 2016, utilizes reference vectors in the objective space to guide the population toward the Pareto front while maintaining diversity. It incorporates an angle penalty function to dynamically balance convergence and diversity.
4. Experiments and Results
This section presents the experiments and results obtained by optimizing the dynamic balance of a six-bar Watt linkage modeled using . It is organized into three subsections to facilitate the analysis and interpretation of the performance of different optimization algorithms and the sensitivity of key features.
Section 4.1 details the physical properties of the six-bar Watt linkage in its uncompensated state (i.e., without counterweights). Section 4.2 analyzes the performance of various optimization techniques, encompassing single-objective and multi-objective algorithms. Finally, Section 4.3 presents a sensitivity analysis of the solutions identified by the most effective algorithm.
4.1. Physical Properties of the Six-Bar Watt Linkage Without Counterweights
Table 1 presents the physical properties of the six-bar Watt linkage illustrated in Figure 1. The links are assumed to be fabricated from steel with a density of 7800 kg/m3, while the counterweights are brass, with a density of kg/m3.

Table 1.
Parameters of the six-bar Watt linkage. Parameters indicated with a ‘-’ are unnecessary for the numerical analysis.
The behaviors of the (along the x and y axes) and the before balance optimization are illustrated in Figure 3.
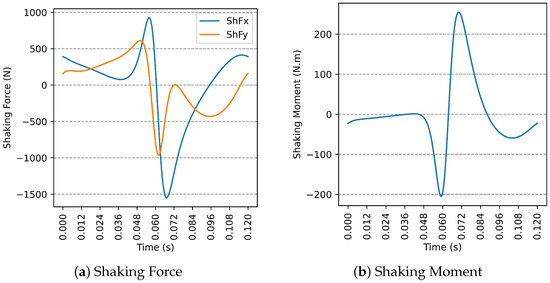
Figure 3.
Unbalanced dynamic response.
4.2. Comparison of Different Optimization Algorithms
This subsection compares the performance of various single-objective (GA, DE, ES, SRES, ISRES, and PS) and multi-objective (NSGA-II, NSGA-III, R-NSGA-II, R-NSGA-III, UNSGA-III, MOEA/D, AGE-MOEA, C-TAEA, SMS-EMOA, and RVEA) algorithms when applied to the dynamic balance optimization of a six-bar Watt linkage.
The optimization algorithms were implemented in Python using the Pymoo library [47]. A consistent set of hyperparameters was employed for all algorithms: a population size of 150 individuals and 500 generations. All other hyperparameters were set to their default values.
The multi-objective optimization algorithms were executed once, generating solutions that constitute the Pareto front. Conversely, each single-objective optimization algorithm was executed 200 times, each run employing a randomly selected value of (ranging from 0 to 1) to define the objective function, as described in Equation (16).
Figure 4 and Figure 5, along with Table 2, present the performance of the single- and multi-objective optimization algorithms with respect to and , visualized through the Pareto fronts of the obtained solutions. Figure 5 shows that the multi-objective algorithms identified a larger number of solutions. Most solutions found by the single-objective algorithms lie along or near the Pareto front. Visual comparison of Figure 4 and Figure 5 does not readily reveal a single best-performing algorithm. However, analysis of the multi-objective algorithms suggests that NSGA-III, R-NSGA-III, AGE-MOEA, and SMS-EMOA demonstrate strong performance. Table 2 presents the hypervolume metric calculated from the Pareto front solutions obtained by each algorithm. We defined the reference point as [1.0, 1.0]. This metric identifies SMS-EMOA as the most effective algorithm for the optimization of the and objective functions.
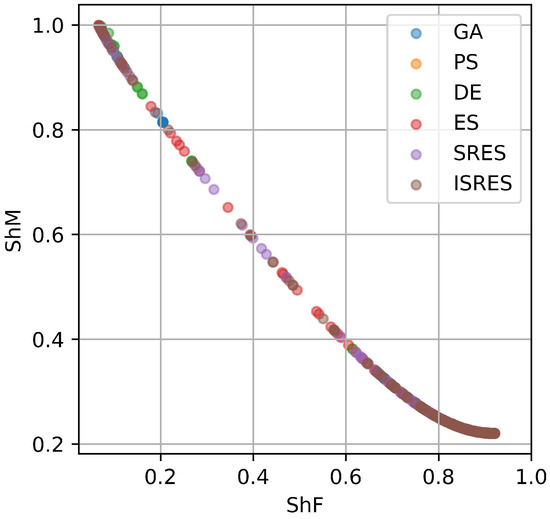
Figure 4.
Performance of single-objective optimization algorithms in terms of and .
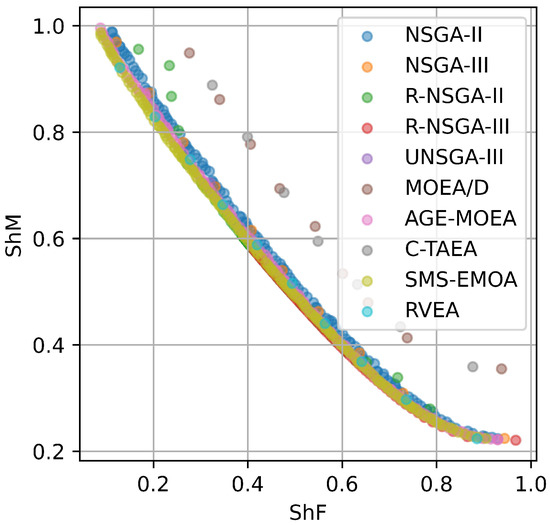
Figure 5.
Performance of multi-objective optimization algorithms in terms of and .

Table 2.
Hypervolumes of different optimization algorithms. Bold letters indicate the best performance.
Table 3 presents the execution times for both single- and multi-objective optimization algorithms. All the experiments were executed on a Dell Latitude 7440 laptop with a 13th Gen Intel(R) Core(TM) i7-1365U processor, 1.80 GHz, and 32 GB RAM. A significant difference in execution times is observed between the two categories. This disparity arises because single-objective algorithms require multiple executions to generate a set of solutions approximating the Pareto front. Conversely, multi-objective algorithms can generate a diverse set of solutions within a single execution. Among the tested algorithms, C-TAEA and MOEA/D exhibited the shortest execution times; however, as illustrated in Figure 5, their performance in terms of solution quality was not optimal. In contrast, SMS-EMOA, which demonstrated the best performance with respect to and (see Table 2), had an execution time of 10.44 min—considerably faster than the single-objective algorithms, which required over 500 min to complete their multiple runs.

Table 3.
Execution times of different multi-objective optimization algorithms.
4.3. Analysis of Solutions Obtained with the Best Algorithm
The previous experiment identified SMS-EMOA as the best-performing multi-objective optimization algorithm, achieving the highest hypervolume, with an execution time of 10.44 min. The solutions generated by this algorithm (shown in Figure 5) were subsequently used for sensitivity analysis.
Figure 6 displays boxplots of the feature values corresponding to the best solutions identified by SMS-EMOA. It is observed that the x and y values for counterweights 4 and 5 are near zero. Furthermore, the thicknesses of these counterweights are very small, approaching the minimum bound (see Equation (15)); the average thicknesses are 0.0068 and 0.0059 for counterweights 4 and 5, respectively. This suggests that these counterweights contribute minimally to the optimization of the and objective functions. Some features exhibit more significant variance than others; for instance, assumes both negative and positive values.
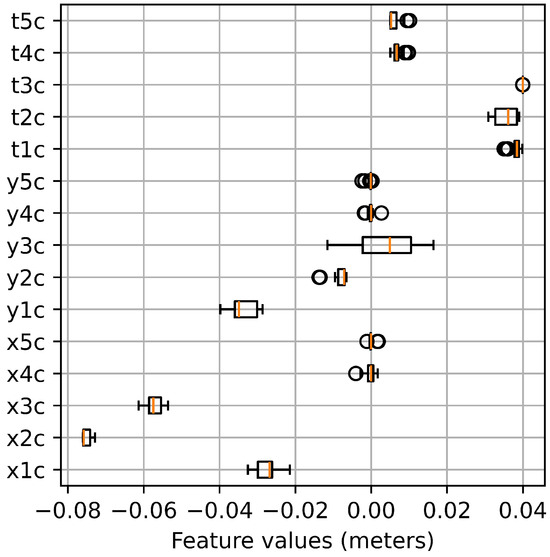
Figure 6.
Boxplots of feature values for the best solutions obtained with SMS-EMOA.
Figure 7 presents the feature values, categorized according to the corresponding and values. It is observed that the values of play a critical role in determining whether the mechanism tends to optimize or : negative values correspond to optimization, while positive values favor optimization. A similar pattern is evident for . A trend is also observed for : lower thickness values tend to correlate with optimization, whereas higher thickness values are more effective for optimization.
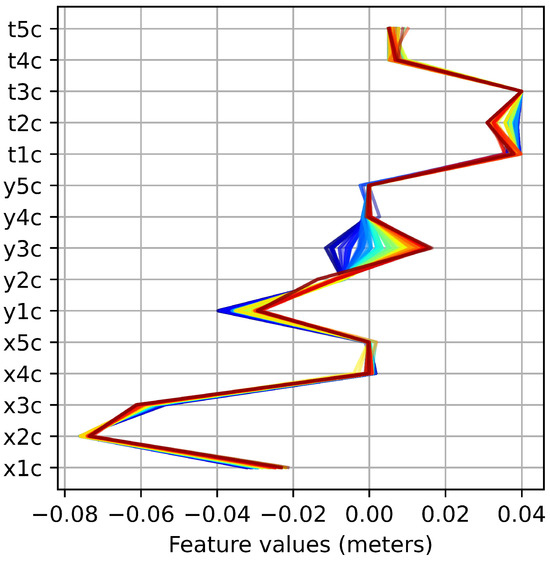
Figure 7.
Feature values of the best solutions obtained with SMS-EMOA Based on and . Each line represents a solution. The bluer the line, the lower the value of , while the redder the line, the higher the value of . Conversely, the bluer the line, the higher the value of , and the redder the line, the lower the value of .
As shown in Figure 6, counterweights four and five tend to be minimized or effectively eliminated. Therefore, the SMS-EMOA algorithm was re-executed with modified parameters. First, counterweights four and five were removed while maintaining the original constraints. Subsequently, a second experiment was conducted in which counterweights four and five were removed, and the thickness constraint was increased, allowing a maximum value of 0.10. This adjustment was implemented because the thickness values of counterweights one, two, and three are close to the maximum allowable value (see Figure 6 and Figure 7).
Figure 8 presents the results of these experiments. It can be observed that using only the first three counterweights and including all five yield comparable results in terms of and optimization. This finding is significant, suggesting that two counterweights can be eliminated without compromising the optimization performance. A detailed justification about eliminating these counterweights can be found in the Appendix A. Furthermore, increasing the maximum allowable thickness () to 0.10 m enables smaller and values to be achieved. While a thickness of 0.10 m may not be practical for the current mechanism design, this observation provides valuable insight for future work, suggesting the exploration of alternative designs or materials.
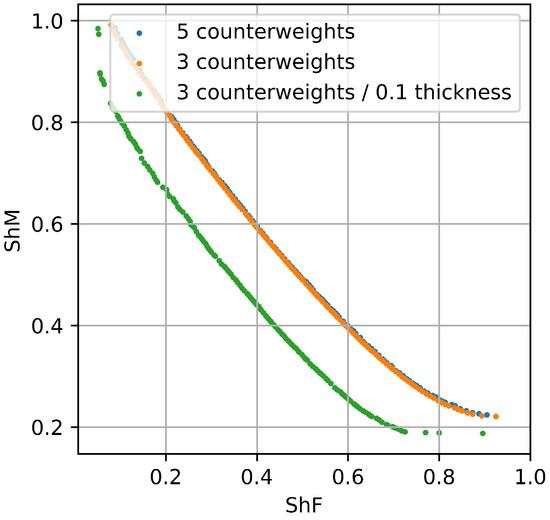
Figure 8.
Comparison of the use of five and three counterweights and incrementing the thickness constraint.
5. Balancing Optimization Results
The optimal solution for the balancing of a six-bar Watt linkage is application-dependent. Solutions can be selected from the Pareto front, enabling a choice that prioritizes either or minimization or achieves a balanced reduction in both.
For example, consider the solution obtained by SMS-EMOA (Equation (19)), corresponding to and . This solution yields a reduction of 91. 19% in , while is only reduced by 1.33%.
Figure 9 compares the unbalanced and balanced (both and ) and the unbalanced and balanced using the solution vector provided in Equation (19).
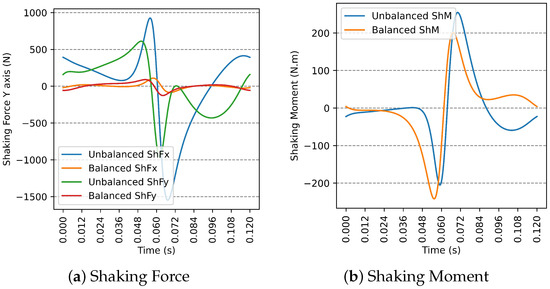
Figure 9.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (19).
Alternatively, consider the solution obtained by SMS-EMOA (Equation (20)), corresponding to and . This solution yields a 77.60% reduction in , while is reduced by 9.54%.
Figure 10 illustrates a comparison between the unbalanced and balanced (both and ) and the unbalanced and balanced using the solution vector presented in Equation (20).
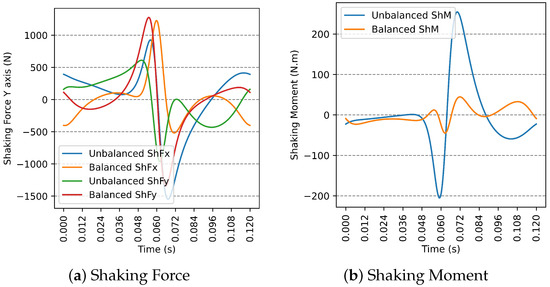
Figure 10.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (20).
Finally, consider the solution obtained by SMS-EMOA (Equation (21)), corresponding to and . This solution yields a 50.43% reduction in and a 50.44% reduction in .
Figure 11 presents a comparison between the unbalanced and balanced (both and ) and between the unbalanced and balanced using the solution vector provided in Equation (21).
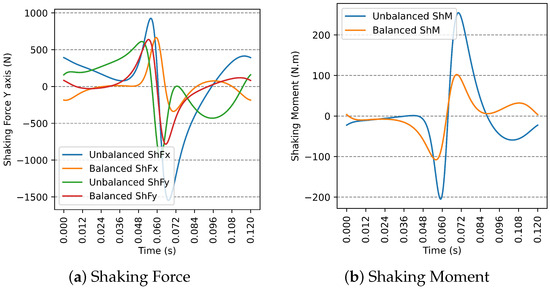
Figure 11.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (21).
6. Conclusions
This paper presented the dynamic balance optimization of a six-bar Watt linkage modeled using (also known as natural coordinates), comparing the performance of single- and multi-objective optimization algorithms. While much of the current state-of-the-art mechanism balancing optimization relies on Cartesian coordinates and single-objective algorithms, the balancing problem involves two quantities: and . Using multi-objective algorithms offers a more efficient approach to balancing optimization, enabling the identification of a wider range of solutions in a shorter time frame.
This research compared the performance of single-objective (GA, ES, DE, SRES, and ISRES) and multi-objective (NSGA-II, NSGA-III, R-NSGA-II, R-NSGA-III, UNSGA-III, MOEA/D, AGE-MOEA, C-TAEA, SMS-EMOA, and RVEA) algorithms. SMS-EMOA emerged as the top performer, exhibiting the highest hypervolume and an execution time of 10.44 min. The experiments demonstrated that multi-objective algorithms are significantly more efficient at identifying diverse solutions than single-objective algorithms, establishing them as the preferred method for balancing mechanical systems.
Sensitivity analysis revealed that two counterweights could be eliminated without affecting the optimization performance achieved with all five counterweights. Further analysis identified the y position of the third counterweight and the thickness (t) of the second counterweight as critical parameters influencing whether the optimization prioritizes or reduction.
The analysis presented in this research demonstrates that the SMS-EMOA optimization algorithm can achieve either a 91.19% reduction in (with a corresponding 1.33% reduction in ) or a 77.60% reduction in (with a corresponding 9.54% reduction in ).
Author Contributions
Conceptualization, M.T.O.-G. and C.N.S.; methodology, M.T.O.-G. and C.N.S.; software—mechanical development, M.T.O.-G.; software—optimization, C.N.S., L.E.R.-J. and S.C.G.-D.; validation, M.T.O.-G. and C.N.S.; formal analysis, M.T.O.-G. and C.N.S.; investigation, M.T.O.-G., C.N.S., L.E.R.-J. and S.C.G.-D.; writing—original draft preparation, M.T.O.-G. and C.N.S.; writing—review and editing, M.T.O.-G. and C.N.S.; supervision, M.T.O.-G. and C.N.S.; project administration, M.T.O.-G. and C.N.S.; funding acquisition, M.T.O.-G., through the Instituto de Ciencia y Tecnología del Estado de Aguascalientes (INCyTEA) and the Faculty of Engineering at Universidad Panamericana, Aguascalientes campus. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Instituto de Ciencia y Tecnología del Estado de Aguascalientes (INCyTEA FEIT-2024-MTOG) and the Faculty of Engineering, Universidad Panamericana, Aguascalientes campus.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the Instituto de Ciencia y Tecnología del Estado de Aguascalientes (INCyTEA) for equipment procurement through the project titled “Análisis y optimización del balanceo de mecanismos utilizando coordenadas naturales”. María T. Orvañanos-Guerrero extends her sincere appreciation to INCyTEA for their generous support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FCC | Fully Cartesian Coordinates |
| ShF | Shaking Force |
| ShFx | Shaking Force X axis |
| ShFy | Shaking Force Y axis |
| ShM | Shaking Moment |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
| ES | Evolution Strategy |
| SRES | Stochastic Ranking for Constrained Evolutionary Optimization |
| ISRES | Improved Stochastic Ranking Evolution Strategy |
| PS | Pattern Search |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| NSGA-III | Non-Dominated Sorting Genetic Algorithm III |
| MOGA | Multi-Objective Genetic Algorithm |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| R-NSGA-II | Reference-point NSGA-II |
| R-NSGA-III | Reference-point NSGA-III |
| UNSGA-III | Unified NSGA-III |
| MOEA/D | Multi-objective Evolutionary Algorithm based on Decomposition |
| AGE-MOEA | Adaptive Geometry Estimation based MOEA |
| C-TAEA | Convergence and Trade-off-based Multi-objective Evolutionary |
| SMS-EMOA | S-Metric Selection Evolutionary Multi-objective Optimization Algorithm |
| RVEA | Reference Vector Guided Evolutionary Algorithm |
Appendix A. Dynamical Results When Using Only Three Counterweights
This appendix provides a more detailed justification for disregarding counterweights whose thickness is close to zero. In addition, it reports the balancing results obtained when the mechanism operates with only three counterweights instead of five, illustrating that the dynamic response remains practically unchanged when the removed counterweights are assumed to have negligible thickness. For direct comparison, exactly the three solution vectors examined in Section 5 are reconsidered.
A detailed examination of the constituent terms of the mass matrix (Equation (4)) shows that every entry involving counterweight parameters is directly proportional to the corresponding thickness. Consequently, when a counterweight’s thickness approaches zero, the associated terms vanish, and the counterweight ceases to influence either the or the . The explicit expressions demonstrating this proportionality are provided in [22], thereby validating the cancellation criterion.
The results for the representative cases selected in Section 5 are presented below. They confirm that removing counterweights 4 and 5—whose computed thicknesses are close to zero—yields a balancing performance virtually indistinguishable from that obtained with the complete five-counterweight configuration.
The first solution corresponds to the vector given in Equation (19). The associated performance indices are and , representing reductions of 91.19% in the shaking force (ShF) and 1.33% in the shaking moment (ShM), respectively.
After removing counterweights four and five, the reduced solution vector becomes:
Substituting this vector into Equations (12) and (13) yield and , corresponding to the reductions of in ShF and in ShM.
Figure A1 displays the shaking force (ShF) and shaking moment (ShM) obtained with this solution. Compared with the balanced-mechanism response shown in Figure 9, the two curves are virtually indistinguishable.
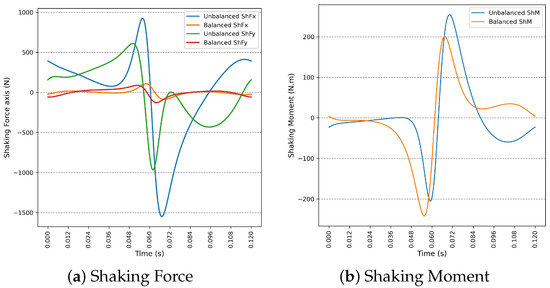
Figure A1.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (19) using three counterweights.
Alternatively, consider the solution obtained by SMS-EMOA (Equation (20)), corresponding to and . This solution yields a 77.60% reduction in ShM, while ShF is reduced by 9.54%.
By discarding counterweights four and five, the solution vector can be represented according to (Equation (A2)).
Substituting this vector into (Equations (12) and (13)) yield and , which corresponds to a reduction of in ShM, and a reduction of in ShF.
It can be seen that the ShF and ShM responses (Figure A2) are practically the same as the responses shown when using five counterweights (Figure 10).
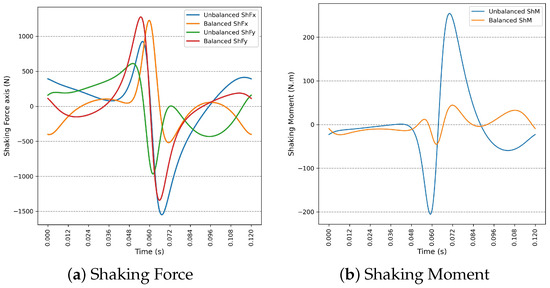
Figure A2.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (20) using three counterweights.
Finally, consider the third solution obtained by SMS-EMOA (Equation (21)), corresponding to and . This solution yields a 50.44% reduction in ShM and a 50.43% reduction in ShF.
When discarding counterweights four and five, the solution vector can be represented with Equation (A3)
Substituting this vector into Equations (12) and (13) yield and , which corresponds to a reduction of in ShM, and a reduction of in ShF.
Figure A3 shows the balanced and obtained when using only three counterweights. When comparing these results with the ones obtained using five counterweights (Figure 11), it can be seen that they are almost identical.
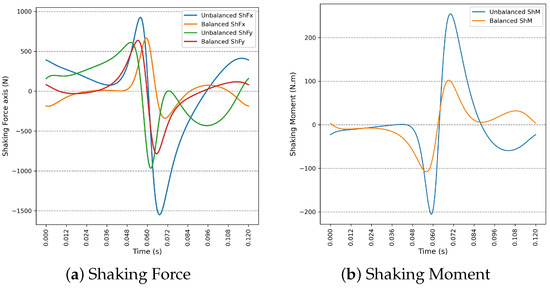
Figure A3.
Comparison between unbalanced and balanced dynamics for the solution vector in Equation (21) using three counterweights.
References
- Arakelian, V.; Dahan, M.; Smith, M. A Historical Review of the Evolution of the Theory on Balancing of Mechanisms. In International Symposium on History of Machines and Mechanisms Proceedings HMM 2000; Springer: Dordrecht, The Netherlands, 2000; pp. 291–300. [Google Scholar] [CrossRef]
- Arakelian, V.H.; Smith, M.R. Shaking force and shaking moment balancing of mechanisms: A historical review with new examples. J. Mech. Des. 2005, 127, 334–339. [Google Scholar] [CrossRef]
- Orvañanos-Guerrero, M.T.; Sánchez, C.N.; Rivera, M.; Acevedo, M.; Velázquez, R. Gradient descent-based optimization method of a four-bar mechanism using fully cartesian coordinates. Appl. Sci. 2019, 9, 4115. [Google Scholar] [CrossRef]
- Porter, B.; Sanger, D.J. Synthesis of dynamically optimum four-bar linkages. In Proc. Conf. on Mechanisms, Paper C69/72; Institution of Mechanical Engineers: London, UK, 1972; pp. 24–28. [Google Scholar]
- Mayne, R.W.; Sadler, J.P.; Conte, F.L.; George, G.R. Optimum Mechanism Design Combining Kinematic and Dynamic-Force Considerations. J. Eng. Ind. 1975, 97, 662–670. [Google Scholar] [CrossRef]
- Dresig, H.; Schönfeld, D. Rechnergestützte Optimierung der Antribs-und Gestellkraftgrössen ebene. Koppelgetriebe-Teil 1. Mech. Mach. Theory 1976, 11, 363–370. [Google Scholar] [CrossRef]
- Dresig, H.; Schönfeld, S. Rechnergestützte Optimierung der Antriebs- und Gestellkraftgrössen ebener Koppelgetriebe—Teil II. Mech. Mach. Theory 1976, 11, 371–379. [Google Scholar] [CrossRef]
- Walker, M.J.; Haines, R.S. A study of counterweight synthesis for a 6-bar chain. Mech. Mach. Theory 1982, 17, 327–334. [Google Scholar] [CrossRef]
- Rao, S.S.; Kaplan, R.L. Optimal Balancing of High-Speed Linkages Using Multiobjective Programming Techniques. ASME J. Mech. Trans. Autom. 1986, 108, 454–460. [Google Scholar] [CrossRef]
- Qi, N.M.; Pennestri, E. Optimum balancing of four-bar linkages. Mech. Mach. Theory 1991, 26, 337–348. [Google Scholar] [CrossRef]
- Chaudhary, H.; Saha, S.K. Balancing of shaking forces and shaking moments for planar mechanisms using the equimomental systems. Mech. Mach. Theory 2008, 43, 310–334. [Google Scholar] [CrossRef]
- Erkaya, S. Investigation of balancing problem for a planar mechanism using genetic algorithm. J. Mech. Sci. Technol. 2013, 27, 2153–2160. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Minimization of Shaking Force and Shaking Moment in Multiloop Planar Mechanisms. In Proceedings of the 1st International and 16th National Conference on Machines and Mechanisms, Roorkee, India, 18–20 December 2013. [Google Scholar]
- Chaudhary, K.; Chaudhary, H. Dynamic balancing of planar mechanisms using genetic algorithm. J. Mech. Sci. Technol. 2014, 28, 4213–4220. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Shape Optimization of Dynamically Balanced Planar Four-bar Mechanism. Procedia Comput. Sci. 2015, 57, 519–526. [Google Scholar] [CrossRef][Green Version]
- Chaudhary, K.; Chaudhary, H. Optimum Dynamic Balancing of a Planar Five-Bar Mechanisms Using Genetic Algorithm. In Proceedings of the International Conference on Advances in Materials and Product Design (AMPD-2015), Sardar Vallabhbhai Patel Institute of Technology, Surat, Gujarat, India, 10–11 January 2015. [Google Scholar]
- Chaudhary, H.; Chaudhary, K. Design of Reactionless Mechanisms Based on Constrained Optimization Procedure. In Dynamic Balancing of Mechanisms and Synthesizing of Parallel Robots; Springer: Cham, Switzerland, 2016; pp. 273–298. [Google Scholar] [CrossRef]
- Chaudhary, K.; Chaudhary, H. Optimal dynamic design of planar mechanisms using teaching-learning-based optimization algorithm. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2016, 230, 3442–3456. [Google Scholar] [CrossRef]
- Feng, B.; Morita, N.; Torii, T. A new optimization method for dynamic design of planar linkage with clearances at joints—Optimizing the mass distribution of links to reduce the change of joint forces. J. Mech. Des. 2002, 124, 68–73. [Google Scholar] [CrossRef]
- Belleri, B.K.; Kerur, S.B. Balancing of planar six-bar mechanism with genetic algorithm. J. Mech. Energy Eng. 2021, 4, 303–308. [Google Scholar] [CrossRef]
- Orvananos-Guerrero, M.T.; Sanchez, C.N.; Davalos-Orozco, O.; Rivera, M.; Velazquez, R.; Acevedo, M. Using Fully Cartesian Coordinates to Calculate the Support Reactions of Multi-Scale Mechanisms. In Proceedings of the 2018 Nanotechnology for Instrumentation and Measurement, NANOfIM 2018, Mexico City, Mexico, 7–8 November 2018; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Orvañanos-Guerrero, M.T.; Acevedo, M.; Sánchez, C.N.; Campos-Delgado, D.U.; Ghavifekr, A.A.; Visconti, P.; Velázquez, R. Complete Balancing of the Six-Bar Mechanism Using Fully Cartesian Coordinates and Multiobjective Differential Evolution Optimization. Mathematics 2022, 10, 1830. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Farmani, M.R.; Jaamiolahmadi, A. Optimization of Force and Moment Balance of a Four-Bar Linkage using Multi-Objective Genetic Algorithm. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009. [Google Scholar] [CrossRef]
- García-Nieto, J.; López-Camacho, E.; García Godoy, M.J.; Nebro, A.J.; Durillo, J.J.; Aldana-Montes, J.F. A Study of Archiving Strategies in Multi-objective PSO for Molecular Docking. In Swarm Intelligence: 10th International Conference, ANTS 2016, Brussels, Belgium, 7–9 September 2016, Proceedings 10; Dorigo, M., Birattari, M., Li, X., López-Ibañez, M., Ohkura, K., Pinciroli, C., Stützle, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 40–52. [Google Scholar] [CrossRef]
- Li, X. Better Spread and Convergence: Particle Swarm Multiobjective Optimization Using the Maximin Fitness Function. In Genetic and Evolutionary Computation—GECCO 2004 Genetic and Evolutionary Computation Conference Seattle, WA, USA, 26–30 June 2004, Proceedings, Part I; Deb, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 117–128. [Google Scholar] [CrossRef]
- Farmani, M.R.; Jaamialahmadi, A.; Babaie, M. Multiobjective optimization for force and moment balance of a four-bar linkage using evolutionary algorithms. J. Mech. Sci. Technol. 2011, 25, 2971–2977. [Google Scholar] [CrossRef]
- Mejia-Rodriguez, R.; Villarreal-Cervantes, M.G.; Rodríguez-Molina, A.; Pérez-Cruz, J.H.; Silva-García, V.M. Evolutionary Multiobjective Design Approach for Robust Balancing of the Shaking Force, Shaking Moment, and Torque under Uncertainties: Application to Robotic Manipulators. Mathematics 2023, 11, 1776. [Google Scholar] [CrossRef]
- Collette, Y.; Siarry, P. Multiobjective Optimization, Principles and Case Studies; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A Survey on the Hypervolume Indicator in Evolutionary Multiobjective Optimization. IEEE Trans. Evol. Comput. 2021, 25, 1–20. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Hooke, R.; Jeeves, T. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM (JACM) 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolution Strategy: Nature’s Way of Optimization. In Optimization: Methods and Applications, Possibilities and Limitations— Proceedings of an International Seminar Organized by Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), Bonn, Germany, June 1989; Bergmann, H.W., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 106–126. [Google Scholar]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Stochastic Ranking for Constrained Evolutionary Optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef]
- Runarsson, T.P.; Yao, X. Search biases in constrained evolutionary optimization. IEEE Trans. Syst. Man Cybern. Part Appl. Rev. 2005, 35, 233–243. [Google Scholar] [CrossRef]
- Deb, K.; Sundar, J.; Bhaskara Rao, U.N.; Chaudhuri, S. Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ’06), Seattle, WA, USA, 8–12 July 2006; Technical Report 3. ACM: New York, NY, USA, 2006. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. U-NSGA-III: A Unified Evolutionary Algorithm for Single, Multiple, and Many-Objective Optimization. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guimaraes, Portugal, 29 March–1 April 2015; pp. 34–49. [Google Scholar] [CrossRef]
- Vesikar, Y.; Deb, K.; Blank, J. Reference Point Based NSGA-III for Preferred Solutions. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1587–1594. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Panichella, A. An adaptive evolutionary algorithm based on non-euclidean geometry for many-objective optimization. In Proceedings of the GECCO 2019—Proceedings of the 2019 Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; ACM: New York, NY, USA, 2019; pp. 595–603. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-Archive Evolutionary Algorithm for Constrained Multiobjective Optimization. IEEE Trans. Evol. Comput. 2019, 23, 303–315. [Google Scholar] [CrossRef]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).