DICTION: DynamIC robusT whIte bOx Watermarking Scheme for Deep Neural Networks

Abstract

Deep neural network (DNN) watermarking is a suitable method for protecting the ownership of deep learning (DL) models. It secretly embeds an identifier within the model, which can be retrieved by the owner to prove ownership. In this paper, we first provide a unified framework for white-box DNN watermarking schemes that encompasses current state-of-the-art methods and outlines their theoretical inter-connections. Next, we introduce DICTION, a new white-box dynamic robust watermarking scheme derived from this framework. Its main originality lies in a generative adversarial network (GAN) strategy where the watermark extraction function is a DNN trained as a GAN discriminator, while the target model acts as a GAN generator. DICTION can be viewed as a generalization of DeepSigns, which, to the best of our knowledge, is the only other dynamic white-box watermarking scheme in the literature. Experiments conducted on four benchmark models (MLP, CNN, ResNet-18, and LeNet) demonstrate that DICTION achieves a zero bit error rate (BER) while maintaining model accuracy within 0.5% of the baseline. DICTION shows superior robustness, tolerating up to 95% weight pruning compared to 80% for existing methods, and it demonstrates complete resistance to fine-tuning and overwriting attacks where competing methods fail, with a BER of >0.3.

1. Introduction

Deep Learning (DL) [1] has enabled significant and rapid progress in signal analysis and applications such as speech recognition [2], natural language processing [3], and diagnostic support [4,5]. However, building a deep learning model is increasingly becoming an expensive process that requires (i) large amounts of data; (ii) substantial computational resources (such as GPUs); (iii) expertise from DL specialists to carefully define the network topology and correctly set training hyperparameters (such as learning rate, batch size, weight decay, etc.); and (iv) domain experts with specialized knowledge (sometimes, these experts are very rare, as in the medical field). Consequently, the illegal copying and redistribution of such models represents a significant financial loss for their creators.

Watermarking has been proposed to protect the ownership of deep learning models. It consists of inserting a message (a watermark) into a host document by imperceptibly modifying some of its characteristics. For example, image watermarking [6,7,8,9,10,11] is based on slight modifications (or modulations) of pixel values to encode the message. This message can then help verify the origin/destination of the document it protects in the context of copyright protection or data leak prevention [12,13]. DL model watermarking relies on the same principles while taking into account the specific features and operating constraints of neural networks. A DL model differs from a multimedia document in many fundamental ways.

Problem definition: Designing an effective and efficient DNN watermarking scheme must meet the following six key criteria [14,15,16,17,18]:

• Fidelity—the performance of the model should be well preserved after watermarking;
• Integrity—the watermarking scheme’s ability to produce minimal false alarms and ensure that the watermarked model can be uniquely identified using the appropriate watermarking key;
• Robustness—the watermark cannot be easily removed when the model is attacked;
• Security—the watermark cannot be easily detected by malicious attackers;
• Capacity—the scheme’s ability to effectively embed an amount of data (payload—size of the watermark) into the protected model;
• Efficiency—the computation cost of watermark embedding and extraction must be kept reasonably low.

In practice, most existing schemes achieve only a partial compromise between these criteria. For instance, while the watermark should not degrade the model performance, it must simultaneously resist to attacks aimed at detecting or removing it. Among these attacks, the most common are the following:

• The pruning attack (PA), where model weights whose absolute values are below a threshold are set to zero;
• The fine-tuning attack (FTA), which retrains and updates the model without decreasing its accuracy;
• The overwriting attack (OWA), where the attacker embeds their own watermark to suppress the original one;
• The Wang and Kerschbaum attack (WKA), which analyzes the weight distribution of the watermarked model to detect watermark presence;
• The Property Inference Attack (PIA), which trains a discriminator capable of differentiating watermarked from non-watermarked models by analyzing their statistical properties.

Note that removal attacks are considered effective and efficient only if the watermark is completely removed while maintaining high test accuracy and requiring significantly fewer computational resources than retraining a model from scratch. Currently, the literature lacks both a formal unified definition of white-box watermarking schemes and a watermarking method that simultaneously satisfies all the requirements mentioned above. To address these gaps, we first present a formal unified framework for white-box watermarking algorithms. We then propose DICTION, a novel, dynamic white-box algorithm that overcomes the limitations of existing methods. In particular, we propose using a neural network following a generative adversarial-based strategy to map activation maps of the target model to the watermark space, rather than using a static projection matrix, as in DeepSigns.

To embed a watermark b in a target model, DICTION first considers the initial portion of the target model up to layer l as a generative adversarial network (GAN) generator [19] and then trains a projection neural network (acting as a GAN discriminator) concurrently with the generator model. This joint training ensures that the trigger set activation maps of the watermarked model are mapped to the desired watermark b, while those of the non-watermarked model (i.e., the original/initial one) are mapped to random watermarks. To detect the watermark, it is sufficient to use the trigger set samples as model input and verify that the projection neural network outputs the watermark from the corresponding activation maps.

Using a neural network for mapping activation-maps-to-watermarking space, significantly expands the ability to embed robust watermarks while increasing the capacity. Additionally, our projection neural network can be trained either while embedding the watermark into a pretrained model or during initial training, whereas DeepSigns requires a trained target model. Another key innovation of our proposal is the use of a trigger set composed of samples from a latent space defined by its mean and standard deviation. DICTION can insert watermarks into the activation maps of a single layer or a combination of multiple layers. The concatenation of these activation maps forms a tensor where each channel represents the output from a hidden layer of the model. This strategy propagates the watermark across all model layers, better preserving model accuracy and avoiding potential misclassification of real images, as observed in DeepSigns.

This approach also simplifies detection, as one only needs to generate samples from the latent space to constitute the trigger set. DICTION is thus independent of selecting a set of real samples (e.g., images) as a trigger set. Moreover, very few parameters need to be stored (only the mean and standard deviation of the latent distribution). In some cases, model accuracy is even improved because our watermarking proposal acts as a regularization term. As we demonstrate, our proposal is highly resistant to all the attacks listed previously (PA, FTA, OWA, WKA, and PIA) and outperforms the DeepSigns white-box dynamic watermarking scheme in terms of both watermark robustness and watermarked model accuracy.

• Our main contributions are the following:
  • Unified framework: We present the first unified mathematical framework for white-box DNN watermarking that encompasses all existing schemes and reveals their theoretical inter-connections;
  • Novel dynamic scheme: We propose DICTION, a new GAN-based dynamic watermarking approach that uses a neural network projection function instead of static linear projections;
  • Latent space innovation: We introduce the use of latent space triggers (Gaussian noise) instead of training data subsets, eliminating storage requirements and enabling unlimited trigger generation;
  • Superior performance: DICTION demonstrates significant improvements over state-of-the-art methods in capacity, robustness, and security while maintaining computational efficiency.

The rest of this paper is organized as follows. Section 2 presents the background and related work. Section 3 introduces our unified white-box watermarking framework that encompasses the most recent static and dynamic schemes, illustrating their advantages and weaknesses through theoretical unification. Section 4 presents DICTION, our novel, dynamic white-box watermarking scheme that generalizes DeepSigns with significantly improved performance. Section 5 provides the experimental results and a comparative evaluation of our scheme against state-of-the-art solutions. Section 6 discusses the limitations and future work, while Section 7 concludes this paper.

2. Related Work and Background

2.1. Background: Deep Neural Networks

In this work, we focus on classical DNN architectures for image classification, as the vast majority of DNN watermarking schemes have been developed and evaluated in this context. As depicted in Figure 1, a DNN model M is a stack of layers that transforms an input layer holding data X to classify into an output layer holding the label scores Y. Different types of layers are commonly used:

• Fully connected (FC) layer—It consists of a set of neurons such that each neuron of layer ${\mathrm{FC}}^m$ is connected to all neurons of the previous layer ${\mathrm{FC}}^{m-1}$. More precisely, an FC layer of $I_m$ neurons connected to a previous layer of $I_{m-1}$ neurons receives as input a vector $a^{(m-1)}$ of size $I_{m-1}$ and provides as output a vector $a^{\left(m\right)}$ with $I_m$ components that serves as input to the next layer. This computation can be expressed as

  $$a^{\left(m\right)}=g_m(W^{\left(m\right)}{a}^{(m-1)}+b^{\left(m\right)})$$

  (1)

  where $W^{\left(m\right)}$ is the matrix of neuron weights of shape $I_m\times I_{m-1}$, $b^{\left(m\right)}\in {\mathbb{R}}^{I_m}$ is the bias vector, and $g_m(·)$ is a nonlinear activation function applied component-wise (e.g., ReLU, sigmoid, and Tanh…).
• Convolutional layer $\mathrm{Conv}(O_m,P_m,Q_m)$—As illustrated in Figure 1, such a layer receives as input a feature map $A^{(m-1)}$ of $O_{m-1}$ channels and computes as output a new feature map $A^{\left(m\right)}$ composed of $O_m$ channels. The output at each channel is called an activation map and is computed as

  $$A_o^{\left(m\right)}=g_m\left(\sum _k{W}_{ok}^{\left(m\right)}\ast A_k^{(m-1)}+b_o^{\left(m\right)}\right)$$

  (2)

  where ∗ denotes the 2D convolution operation, $W_{ok}^{\left(m\right)}$ is the filter weight matrix of shape $P_m\times Q_m$, and $b_o^{\left(m\right)}\in \mathbb{R}$ is the bias term. The matrix $W_{ok}^{\left(m\right)}$ parameterizes a spatial filter that is automatically tuned during training to detect or enhance specific features from $A^{(m-1)}$.
• Pooling (PL) layers—These implement spatial dimensionality reduction operations in DNNs. The most common pooling layers are max pooling and average pooling. Max-Pooling$(n,n)$ is a patch kernel operator of size $n\times n$ applied to $A^{\left(m\right)}$ that outputs the maximum value found in each $n\times n$ patch of $A^{\left(m\right)}$. For average pooling, the average of the values in a patch is computed. The appropriate choice of pooling function can make the model more robust to input distortions. In any case, a PL layer reduces the number of trainable parameters for subsequent layers.
• Flatten layer—This corresponds to a special reshaping operation required to transition from bidimensional (or multidimensional) layers to one-dimensional, fully connected layers.
• Batch normalization (BN) layers—These layers normalize inputs so as to have zero mean and unit variance, which helps stabilize and accelerate the training process. BN layers contain learnable parameters (scale and shift) that have been utilized in some watermarking schemes, particularly in passport-based methods [20], where watermarks are embedded in these normalization parameters.

Architecting a DNN involves developing a suitable sequence of convolutional, pooling, batch normalization, and fully connected layers, along with their hyperparameters (e.g., learning rate, momentum, and weight decay). Typical architectures, as shown in Figure 1, introduce a pooling layer after one or more convolutional layers, defining a convolutional block that is repeated until the activation map size is small enough to feed fully connected layers.

A typical DNN training is based on two iterative phases: feed-forward and back-propagation. Before the first feed-forward phase begins, all model parameters are initialized (e.g., with random values). The training data are then fed into the DNN in batches, where the batch size is the number of samples used to perform a single forward and backward pass. The difference between the original labels $\left(Y_{\mathrm{Train}}\right)$ and those computed by the DNN is calculated using an objective function (also known as the loss function $E(·)$), such as cross-entropy for classification or mean squared error for regression. This error is then used in the back-propagation phase to update all model parameters using optimization techniques such as stochastic gradient descent (SGD) or AdamW [21].

Once the DNN model is trained (i.e., when model parameters converge and accuracy stabilizes), it can be used to classify new data during the inference phase. This classification process consists of applying the feed-forward phase with new data (Test-set) as input, where the DNN output provides the predicted class of the input data.

Figure 1. CNN architecture for image classification using the MNIST dataset [22], with two convolutional layers, two max-pooling layers, and two fully connected layers.

Figure 1. CNN architecture for image classification using the MNIST dataset [22], with two convolutional layers, two max-pooling layers, and two fully connected layers.

2.2. Related Work

DNN watermarking methods can be classified into black-box (BBx) and white-box (WBx) schemes [14,15,23,24,25,26]. By definition, a black-box watermark can be extracted by querying only the model’s outputs. The watermarked message is retrieved by examining the outputs of the watermarked model for carefully designed and crafted inputs referred to as the “trigger set” [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. These methods have zero-bit capacity, as they can only detect the presence of a given watermark in a protected model. This is equivalent to extracting a message b of one bit equal to “1” if the watermark is detected or “0” otherwise.

In contrast, white-box (WBx) watermarking schemes [45,46,47,48,49,50,51,52,52] require access to the complete model parameters to extract the watermark. These schemes have multi-bit capacity, allowing the encoding of messages containing several bits of information. In other words, the message $b={\left\{m_i\right\}}_{i=1..N}$, with $m_i\in \{0,1\}$, can be chosen by the user. WBx schemes can be further differentiated based on whether the watermark is read directly from the network parameters (called “static watermarking” schemes) or by examining the values of the intermediate activation maps for specific inputs (called “dynamic watermarking” schemes) [51].

WBx watermarking schemes can be further classified based on their embedding methodology. The first category involves modifying secretly selected model parameters through classical multimedia watermarking modulation techniques. To maintain model accuracy, these approaches fine-tune the network by updating non-watermarked parameters until the original performance is restored. The second category alters the model’s training process by incorporating regularization terms into the loss function, enabling watermark insertion into weights, activation maps, or passport layers.

2.2.1. Parameter Modification Methods

For example, Song et al. [53] embed the watermark in the least-significant bits or signs of the model parameters. They developed a correlated-value-encoding method to maximize the correlation between model parameters and a given secret. Feng et al. [46] randomly select model weights and apply an orthogonal transformation. The watermark is then embedded using a binarization method on the obtained coefficients, followed by applying the inverse orthogonal transformation. Fine-tuning is performed on the non-watermarked weights to restore accuracy. Similarly, Kuribayashi et al. [54] embed the watermark into the discrete cosine transform (DCT) coefficients of secretly selected weights using dither modulation and quantization index modulation (DM-QIM). Tartaglione et al. [48] proposed a different approach using real-valued watermarks instead of binary strings. The watermark is embedded into a secret subset of model parameters using an affine transformation and replica-based approach. The weights carrying the watermark remain frozen during training, enabling easy extraction.

2.2.2. Regularization-Based Methods

The second class of watermarking techniques modifies the model’s loss function by adding a regularization term. This approach allows for a principled trade-off between watermark strength and overall model performance. By adjusting the regularization hyperparameter, one can control the balance between embedding a strong watermark and maintaining the model’s accuracy. This flexibility ensures effective watermark embedding without sacrificing the model’s predictive capabilities. Although we examine these schemes in detail within our unified framework in Section 3, we provide an overview of their technical evolution here.

Uchida et al. [45] proposed one of the first explicit watermarking schemes of this kind. They insert a binary string as a watermark in model parameters by training or fine-tuning the model using a loss function composed of the model’s original loss, along with an embedding regularizer. Embedding the watermark by introducing a regularizer term manages a trade-off between watermark robustness and preservation of model accuracy. However, this method is not robust against overwriting attacks (OWA). Li et al. [47] extended this approach and proposed a DNN watermarking algorithm based on spread-transform dither modulation (ST-DM). The DNN is trained with a loss function explicitly designed with a regularizer to ensure the correlation of the DNN weights with a given spreading sequence. Li et al. [55] propose inserting the watermark into fused kernels instead of using them separately to resist parameter-shuffling attacks. Because this strategy reduces capacity, the authors introduce a capacity expansion mechanism using a MappingNet to map fused kernels into a higher-dimensional space capable of hosting the watermark. However, it should be noted that the shuffling attack is not effective, since it degrades model performance.

Wang and Kerschbaum [56] demonstrated that the aforementioned approaches based on the scheme by Uchida et al. [45] do not fulfill the requirement of watermark secrecy because they introduce easily detectable changes in the statistical distribution of model parameters. To address this limitation, Wang and Kerschbaum [57] proposed a strategy to create undetectable watermarks in a white-box setting using generative adversarial networks (GANs). In this approach, the watermarked model serves as the generator while the watermark detector acts as a discriminator, detecting changes in the statistical distribution of model parameters.

2.2.3. Passport-Based Methods

Unlike previous studies, different methods for verifying the ownership of DNN based on passports have been proposed, e.g., in [20,52,58]. These methods increase the connection between network performance and correct passports by embedding passports in special normalization layers, resulting in enhanced watermark resistance to ambiguity attacks. An ambiguity attack consists of forging a new watermark on a given model without necessarily preventing the legitimate model owner from successfully verifying the watermark in a stolen model instance. However, it creates an ambiguity where, for an external entity such as a legal authority, it becomes impossible to decide which party has watermarked the given model. Thus, the attack prevents the legitimate owner from successfully claiming copyright of the intellectual property. This attack can be solved by either using an authorized time server or a decentralized consensus protocol with which an author authorizes their timestamp to the verification community before publishing the DNN model [59].

2.2.4. Dynamic Watermarking Methods

Rouhani et al. [51] introduced DeepSigns, the first scheme that embeds a sequence of bits as a watermark into the probability density function (PDF) of the activation maps of multiple layers in a model, contrary to previous schemes that work with model parameters. This is accomplished through a fine-tuning process that relies on a trigger dataset (a secretly selected subset of input samples) and the use of specialized regularizers to balance model accuracy and watermark detection. The fundamental idea behind DeepSigns is to cluster the activation maps of the model training set and embed the watermark within a secret subset of the clustered classes. To insert the message, the mean of each of these classes is computed on the trigger dataset and modified through fine-tuning such that its projection in a secret space defined by a matrix matches the watermark. The extraction procedure only requires knowledge of the trigger dataset, calculating the statistical mean of each class’s activation maps, and their projection in the secret space to extract the watermark. Although DeepSigns achieves good model accuracy after watermarking, it suffers from poor insertion capacity and significant vulnerabilities to certain attacks, such as FTA, PA, and OWA, as the watermark size increases.

2.2.5. Summary and Extensions to Federated Learning

Table 1. Taxonomy of ML watermarking schemes. Classification criteria include access type (white-box vs. black-box), watermark type (static vs. dynamic), embedding stage (training vs. fine-tuning), and secret key components required for watermark extraction.

Existing Works	White-Box		Black-Box	Stages of Application		Secret Key
	Dynamic	Static	Dynamic	Training	Fine-Tuning
Uchida et al. [45]		✓		✓	✓	Matrix
DeepSigns [51]	✓		✓		✓	TriggerSet, Matrix
RIGA [57]		✓		✓	✓	DNN
Li et al. [47]		✓		✓	✓	Matrix
Tartaglione et al. [48]		✓			✓	Matrix
Kuribayashi et al.  [54]		✓			✓	Matrix
Feng et al.  [46]		✓			✓	Matrix
EncryptResist [55]		✓		✓	✓	DNN, Matrix
Fan et al. [52]		✓	✓	✓	✓	Passport layer and Matrix
DICTION (our work)	✓			✓	✓	TriggerSet, DNN

summarizes the taxonomy of existing schemes according to their access requirements (white-box vs. black-box), temporal characteristics (static vs. dynamic), embedding methodology (training vs. fine-tuning), and secret key parameters. Note that these algorithms have been developed primarily for centralized learning scenarios. Extensions to federated learning, where training is distributed among clients with private data, have also been proposed [42,60,61]. These federated schemes represent extensions of the above methods adapted to the unique challenges of distributed model training.

3. Unified White-Box ML Watermarking Framework

Contribution overview: This section presents our first major contribution, a unified framework that encompasses all existing white-box watermarking schemes. This unification reveals the theoretical connections between different approaches and provides the foundation for our novel DICTION scheme. We present the most efficient static schemes [45,55,57] and, to our knowledge, the only dynamic scheme [51] within our unified framework.

3.1. White-Box Watermarking Framework

As previously stated, there are two classes of white-box watermarking schemes: static and dynamic. The former encompasses methods that embed the watermark by directly modifying the weights of a trained model [46,62] using classical watermarking modulation techniques similar to those used for images. In the second class [45,47,51,55,57], the watermark is inserted during the training of the model for its original task. The idea is that the watermark-insertion process does not reduce the performance of the host model. From our perspective, these methods can be integrated within a unified white-box watermarking framework that describes any of these schemes according to the following two main steps:

• Feature extraction: Given a target model M, a secret parameterized feature extraction function $\mathrm{Ext}(M,K_{\mathrm{ext}})$ is applied using a secret key $K_{\mathrm{ext}}$. As we will demonstrate, such features can be a subset of the model weights. In that case, $K_{\mathrm{ext}}$ simply indicates the indices of the model weights to select. Alternatively, features can be model activation maps for secretly selected input data from a trigger set. These features are then used for watermark insertion and extraction.
• Watermark embedding: The embedding of a watermark message b consists of regularizing M with a specific watermarking regularization term $E_{\mathrm{wat}}$ added to the model loss such that the projection function $\mathrm{Proj}(·,K_{\mathrm{Proj}})$ applied to the selected features encodes b in a given watermark space, where the space depends on the secret key $K_{\mathrm{Proj}}$. The objective is that after training, we have

  $$\mathrm{Proj}(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}}),K_{\mathrm{Proj}})=b$$

  (3)

  where $M^{\mathrm{wat}}$ is the watermarked version of the target model M.

The watermarking regularization term $E_{\mathrm{wat}}$ depends on a distance measure $\delta$ defined in the watermark space, such as Hamming distance, Hinge loss, or cross-entropy in the case of a binary watermark (i.e., a binary string of length l where $b\in {\{0,1\}}^l$). $E_{\mathrm{wat}}$ is, thus, defined as

$$E_{\mathrm{wat}}=\delta (\mathrm{Proj}(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}}),K_{\mathrm{Proj}}),b)$$

(4)

To preserve the accuracy of the target model, the watermarked model $M^{\mathrm{wat}}$ is generally derived from M through a fine-tuning operation parameterized with the following loss function:

$$E=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+\lambda E_{\mathrm{wat}}$$

(5)

where $E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})$ represents the original loss function of the network, and $\lambda$ is a parameter for adjusting the trade-off between the original loss term and the watermarking regularization term. Here, $E_0$ ensures good performance on the classification/main task while $E_{\mathrm{wat}}$ ensures correct watermark insertion.

Watermark extraction: The watermark retrieval is straightforward. It consists of using both the feature extraction $\mathrm{Ext}(·,K_{\mathrm{ext}})$ and the projection $\mathrm{Proj}(·,K_{\mathrm{Proj}})$ functions as follows:

$$b^{\mathrm{ext}}=\mathrm{Proj}(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}}),K_{\mathrm{Proj}})$$

(6)

where $b^{\mathrm{ext}}$ is the watermark or message extracted from $M^{\mathrm{wat}}$. $K_{\mathrm{ext}}$ and $K_{\mathrm{Proj}}$ are the secret parameters or keys for the watermarking.

In the following subsections, we describe the following methods: Uchida et al. [45], RIGA [57], ResEncrypt [55], and DeepSigns [51] according to our framework.

3.2. Static White-Box Watermarking Schemes

3.2.1. Uchida et al. Scheme [45]

In the scheme of Uchida et al. [45], the feature extraction function $\mathrm{Ext}(·,K_{\mathrm{ext}})$ corresponds to the mean value of secretly selected filter weights. More precisely, based on $K_{\mathrm{ext}}$, a convolutional layer is selected. Let $(s,s)$, d, and n represent the kernel size of the layer filters, the number of input channels, and the number of filters, respectively. Let $\mathbf{W}\in {\mathbb{R}}^{d\times n\times s\times s}$ denotes the tensor containing all the weights of these filter layers. The feature extraction function then includes the following steps:

• Calculate the mean values of the filter coefficients at the same position: ${\overline{W}}_{ikh}={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{W}_{ijkh}$, obtaining $\overline{\mathbf{W}}\in {\mathbb{R}}^{d\times s\times s}$.
• Flatten $\overline{\mathbf{W}}$ to produce a vector $\mathbf{w}\in {\mathbb{R}}^v$ with $v=d\times s\times s$.

The Uchida et al. projection function $\mathrm{Proj}(·,K_{\mathrm{Proj}})$ is designed to insert an l-bit watermark $b\in {\{0,1\}}^l$ and is defined as

$$\mathrm{Proj}(\mathbf{w},K_{\mathrm{Proj}})=\sigma \left(\mathbf{w}A\right)\in {\{0,1\}}^l$$

(7)

where $K_{\mathrm{Proj}}=A$ is a secret random matrix of size $\left(\right|\mathbf{w}|,l)$ and $\sigma (·)$ is the sigmoid function:

$$\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(8)

As the distance measure $\delta$ for the watermarking regularizer $E_{\mathrm{wat}}$, Uchida et al. [45] use binary cross-entropy:

$$\delta (b,y)=-\sum _{j=1}^l(b_{j}log\left(y_j\right)+(1-b_j)log(1-y_j))$$

(9)

Based on $\delta$, $\mathrm{Proj}(·,K_{\mathrm{Proj}})$, and $\mathrm{Ext}(·,K_{\mathrm{ext}})$, one can compute the loss $E_{\mathrm{wat}}$, as given in (5), to watermark a target model M.

Framework interpretation: It is interesting to note that the projection function $\mathrm{Proj}(·)$ (7) corresponds to a simple perceptron with sigmoid activation and parameter set $\theta$ that includes null biases and weights $\left|\mathbf{w}\right|$. The embedding process of the scheme by Uchida et al. is equivalent to training a perceptron ${\mathrm{Proj}}_{\theta }(·)$ over the dataset ${(A_i,b_i)}_{i=1\dots l}$, where the $i^{\mathrm{th}}$ column of A, denoted $A_i$, corresponds to a training sample with label $b_i$ (the $i^{\mathrm{th}}$ bit of b), with batch size l (the watermark size).

Within our framework, the scheme by Uchida et al. can be reformulated as the training of a perceptron ${\mathrm{Proj}}_{\theta }(·)$, where $\theta =\mathrm{Ext}(M,K_{\mathrm{ext}})$. The global loss becomes

$$E=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+\lambda (\delta ({\mathrm{Proj}}_{\theta }\left(A\right),b)+\left|\right|\theta -\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\left|\right|)$$

(10)

This formulation enables the joint training of $M^{\mathrm{wat}}$ and ${\mathrm{Proj}}_{\theta }(·)$ with different optimization parameters while maintaining a performance equivalent to the original scheme.

Watermark extraction: The watermark extraction can be expressed through hard thresholding the result of the $\mathrm{Proj}(·,·)$ function applied to ${\mathbf{w}}^{\mathrm{wat}}=\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})$:

$$b_i^{\mathrm{ext}}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{Proj}{({\mathbf{w}}^{\mathrm{wat}},K_{\mathrm{Proj}})}_i={\mathrm{Proj}}_{{\mathbf{w}}^{\mathrm{wat}}}\left(A_i\right)\ge 0.5\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

where $\mathrm{Proj}{({\mathbf{w}}^{\mathrm{wat}},K_{\mathrm{Proj}})}_i$ is the $i^{\mathrm{th}}$ component of the projection output and $b_i^{\mathrm{ext}}$ is the $i^{\mathrm{th}}$ bit of the extracted watermark.

Advantages and limitations: The scheme by Uchida et al. demonstrates robustness to fine-tuning and pruning attacks and provides substantial watermark capacity. However, it is vulnerable to watermark detection attacks, such as the Wang and Kerschbaum attack (WKA) and Property Inference Attack (PIA), because it modifies weight distributions in detectable ways. The watermark can be erased without knowing $K_{\mathrm{ext}}$ [56]. Additionally, it is not resistant to overwriting attacks, as the linear projection has low mapping capacity, making it susceptible to adversarial overwrites.

3.2.2. Wang et al. Scheme (RIGA) [57]

RIGA (Robust whIte-box GAn watermarking) [57] is a static scheme proposed to overcome the weaknesses of the approach by Uchida et al. [45] against WKA, PIA, and overwriting attacks. The main innovation of RIGA is the use of a DNN ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ with parameters $\theta$ as the projection function, instead of the perceptron of Uchida et al. ${\mathrm{Proj}}_{\theta }$, and associating it with another DNN $F_{\det }$ to preserve the distance between watermarked and non-watermarked weight distributions for WKA robustness.

Feature extraction: The feature extraction function of RIGA is similar to that of Uchida et al. [45]:

• Calculate mean values ${\overline{W}}_{ikh}={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{W}_{ijkh}$, obtaining $\overline{\mathbf{W}}\in {\mathbb{R}}^{d\times s\times s}$ and flattening it to vector $\mathbf{w}\in {\mathbb{R}}^v$;
• From $\mathbf{w}$, RIGA secretly extracts a subset of elements: ${\mathbf{w}}_s=\mathrm{Ext}(M,K_{\mathrm{ext}})=\mathbf{w}{K}_{\mathrm{ext}}$, where $K_{\mathrm{ext}}$ is a selection matrix.

Training strategy: RIGA trains ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ with the dataset $(({\mathbf{w}}_s^{\mathrm{wat}},b),({\mathbf{w}}_s,b_r))$, where ${\mathbf{w}}_s^{\mathrm{wat}}$ and ${\mathbf{w}}_s$ are features from watermarked and original models, respectively, and b and $b_r$ are the owner’s and random watermarks, respectively. This prevents the trivial mapping problem, where the projection function always outputs b regardless of the input.

Loss function: RIGA watermarks a target model M through fine-tuning under the global loss:

$$\begin{array}{cc}\hfill E=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+{\lambda }_1{E}_{\mathrm{wat}}^{\prime }& + {\lambda }_2{E}_{\det }\hfill \\ & =E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+{\lambda }_1{E}_{\mathrm{wat}}^{\prime }-{\lambda }_{2}log\left(F_{\det }\left({\mathbf{w}}^{\mathrm{wat}}\right)\right)\hfill \end{array}$$

(12)

where ${\lambda }_1$ and ${\lambda }_2$ are adjustment parameters, and $F_{\det }$ is a binary classifier discriminating between watermarked and non-watermarked weights.

Advantages and limitations: RIGA demonstrates resistance to fine-tuning, pruning, and overwriting attacks, as well as robustness to watermark detection attacks (PIA and WKA) due to $F_{\det }$. However, its main limitations include the following: (i) Computational complexity from training three models simultaneously, (ii) contradictory objectives between watermark embedding and distribution preservation, leading to slow convergence, and (iii) requirement for 500+ non-watermarked models to train $F_{\det }$, making it extremely costly for large-scale applications.

3.2.3. Li et al. Scheme (ResEncrypt) [55]

ResEncrypt, proposed by Li et al. [55], is a static white-box watermarking scheme. Unlike the Uchida et al. and RIGA schemes that embed watermarks in filter parameter means, ResEncrypt inserts watermarks into kernel means to resist parameter-shuffling attacks. However, this strategy reduces the insertion capacity, prompting the authors to propose a DNN model called MappingNet to map fused kernels into higher-dimensional spaces.

Feature extraction: The feature extraction of ResEncrypt $\mathrm{Ext}(·,K_{\mathrm{ext}})$ works as follows:

• Calculate the mean values of the kernel coefficients: ${\overline{W}}_{ij}={\displaystyle \frac{1}{n\times d}}{\sum }_{i=1}^n{\sum }_{j=1}^d{W}_{ijkh}$, obtaining $\overline{\mathbf{W}}\in {\mathbb{R}}^{s\times s}$;
• Use MappingNet $F_{\mathrm{map}}(·)$ to map the fused kernel to higher dimensions: ${\mathbf{W}}^{\mathrm{map}}=F_{\mathrm{map}}\left(\overline{\mathbf{W}}\right)$.

Projection function: Similar to Uchida et al., the projection function is

$$\mathrm{Proj}({\mathbf{W}}^{\mathrm{map}},K_{\mathrm{Proj}})=\sigma ({\mathbf{W}}^{\mathrm{map}}\times A)\in {\{0,1\}}^l$$

(13)

where $K_{\mathrm{Proj}}=A$ is a secret random matrix.

Advantages and limitations: ResEncrypt aims to resist parameter-shuffling attacks through kernel fusion. However, the shuffling attack is not effective, as it degrades model performance. Moreover, being based on the same strategy as Uchida et al., ResEncrypt suffers from similar problems: The projection function has low linear mapping capacity, making it vulnerable to overwriting attacks.

3.3. Dynamic White-Box Watermarking Schemes

Rouhani et al. Scheme (DeepSigns) [51]

Unlike previous works that directly embed watermarks into static model content (weights), DeepSigns embeds watermarks into the probability density functions (PDFs) of activation maps of a secret selected layer. The watermarking process is both data- and model-dependent, meaning the watermark is embedded into the dynamic behavior of the DNN, triggered only by passing specific input data to the model.

Feature extraction process: DeepSigns watermarks model layers independently through the following steps:

• Feed the model with all training data $(X_{\mathrm{train}},Y_{\mathrm{train}})$ to obtain activation maps ${\left\{f^l(x,w)\right\}}_{x\in X_{\mathrm{train}}}$ for layer l, where $f^l(x,w)\in {\mathbb{R}}^m$;
• Define a Gaussian Mixture Model (GMM) of S Gaussians fitted to the activation maps, where S equals the number of classification classes;
• Secretly select s Gaussians from the mixture, identified by indices T, and compute their mean values ${\left\{{\mu }_l^i\right\}}_{i\in T}$;
• Secretly select a subset of training data to build the trigger set $(X_{\mathrm{key}},Y_{\mathrm{key}})$ from the Gaussian classes selected.

Framework integration: In our framework, the extraction function of DeepSigns is defined as:

$$\mathrm{Ext}(M,K_{\mathrm{ext}})={\{{\{f^l(x,w)\}}_{x\in X_{\mathrm{key}}\&y_{\mathrm{train}}=i}\}}_{i\in T}$$

(14)

where T indexes secretly selected GMM classes, and $K_{\mathrm{ext}}$ corresponds to the trigger set.

Loss function: The global DeepSigns loss function is

$$E=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+{\lambda }_1{E}_{\mathrm{wat}}-{\lambda }_2{E}_{\mathrm{sep}}$$

(15)

where $E_{\mathrm{sep}}$ prevents watermarked parameters from converging to non-watermarked GMM means.

Advantages and limitations: DeepSigns provides higher security than static methods by relying on the secret matrix and trigger set and secretly selected GMM classes. It demonstrates resistance to fine-tuning, pruning, and overwriting attacks for small insertion capacities. However, its main weakness lies in its limited insertion capacity, where increasing watermark length makes it vulnerable to FTA and overwriting attacks. Additionally, the method’s reliance on GMM clustering becomes questionable for large watermark capacities due to the lack of constraints, ensuring that watermarked parameters remain close to the original GMM means.

3.4. Motivation for DICTION

Our analysis of existing white-box watermarking schemes within the unified framework reveals fundamental limitations that DICTION addresses:

• Detection vulnerability: Static schemes such as Uchida et al. and ResEncrypt modify weight distributions in detectable ways. DICTION uses latent space triggers to preserve the original distributions.
• Limited projection capacity: Linear projection methods suffer from low mapping capacity. DICTION employs DNN as a projection function with significantly higher representational power.
• Training data dependency: DeepSigns relies on training set samples as triggers, creating overfitting risks. DICTION uses generated latent space samples, enabling unlimited trigger generation.
• Computational complexity: RIGA requires training multiple models with complex hyperparameter tuning. DICTION achieves robustness with simpler two-model training.

Building on this framework analysis, Section 4 presents DICTION, which can be viewed as a generalization of DeepSigns that overcomes these limitations through the use of adversarial training and latent space generation.

4. DICTION: Proposed Methodology

4.1. Architectural Overview

DICTION is a novel, dynamic white-box watermarking scheme for DNN that inserts watermarks into the activation maps of one or multiple concatenated layers of the target model. Its originality lies in two key innovations.

First, to ensure the fidelity requirement (i.e., preserving the target model’s performance while embedding the watermark), DICTION uses a trigger set from a distribution different from the training set. Our key insight is that if the trigger set is out-of-distribution from the training data, such as data from a latent space defined as a Gaussian distribution similar to GAN generators [19] and Variational AutoEncoder (VAE) decoders [63], we can better preserve the probability density function of the activation maps of the training samples. This approach consequently maintains the accuracy of the target model while increasing watermark robustness.

Second, to achieve an optimal trade-off between insertion capacity and watermark robustness against PA, FTA, OWA, WKA, and PIA attacks, the projection function of DICTION is defined as a DNN that learns to map the activations of the target model $M^{\mathrm{wat}}$ to a watermark b and the activations of the non-watermarked model to a random watermark $b_r$ using the trigger set. This projection function is analogous to the discriminator of a GAN model trained to distinguish (for samples in the latent space) the activation maps produced by a watermarked model from those of a non-watermarked model.

DICTION workflow: The workflow of DICTION is illustrated in Figure 2. In each training round, it follows these steps to produce a watermarked model:

• Latent space generation: Generate a trigger set image LS of the same size as the training set images from a latent space following a Gaussian distribution with mean $\mu$ and standard deviation $\sigma$.
• Activation map extraction: Feed LS to both the original (non-watermarked) model M and the watermarked model under training $M^{\mathrm{wat}}$ to compute, for a given layer l, the activation maps $f^l(\mathrm{LS},w^{\mathrm{wat}})$ and $f^l(\mathrm{LS},w)$, where $w^{\mathrm{wat}}$ are the weights of $M^{\mathrm{wat}}$ and w are those of M, respectively. Note that at the first round, $M^{\mathrm{wat}}$ is initialized with the parameters of M.
• Projection model training: Use $f^l(\mathrm{LS},w)$ and $f^l(\mathrm{LS},w^{\mathrm{wat}})$ to train the projection model ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ by assigning the following labels: the watermark b for the activation maps of $M^{\mathrm{wat}}$ and a random watermark $b_r$ for those of M. This dual-label training prevents ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ from becoming a trivial function that maps any input to b (addressing the integrity requirement described in Section 1).
• Model training: To ensure fidelity requirements, train the target model $M^{\mathrm{wat}}$ on the training set $(X_{\mathrm{Train}},Y_{\mathrm{Train}})$ at each round. The original model M remains frozen during the watermarking process.

These steps are repeated until the bit error rate (BER) between the extracted watermark $b^{\mathrm{ext}}$ from $M^{\mathrm{wat}}$ and the embedded watermark b is equal to zero while maintaining good accuracy for the target model $M^{\mathrm{wat}}$.

GAN-like training strategy: Our embedding process is analogous to GAN training, where the projection model acts as a discriminator that learns to classify the activation maps of the original model M as $b_r$ and those of the target model $M^{\mathrm{wat}}$ as b. The first l layers of the target model $M^{\mathrm{wat}}$ function as the generator, trained to produce appropriate activation maps for the discriminator while maintaining main task performance (i.e., classification). The original model M is not trained during the embedding process, and its activation maps are fed to the projection model to prevent trivial solutions. The watermarked model $M^{\mathrm{wat}}$ and the projection model ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ are trained simultaneously to achieve fast convergence.

4.2. Formal Definition of DICTION

We formulate our scheme following the unified framework presented in Section 3.1 for state-of-the-art white-box schemes through its embedding regularization term $E_{\mathrm{wat}}$. Consider a trigger set defined as a latent space from a normal distribution $N(\mu ,\sigma )$ with the mean $\mu$ and standard deviation $\sigma$. From this perspective, the feature extraction function for a given target model M is

$$\mathrm{Ext}(M,K_{\mathrm{ext}})=f^l(\mathrm{LS},w)\odot Z$$

(16)

where $K_{\mathrm{ext}}=\{l,Z,\mathrm{LS}\}$ is the secret extraction key composed of the following: l (the index of the layer to be watermarked), Z (a permutation matrix used to secretly select a subset of features from $f^l(\mathrm{LS},w)$ and order them), and LS (a sample from the latent space, i.e., an image whose pixel values follow a normal distribution).

As illustrated in Figure 2, our projection function ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ is a DNN that takes as input the extracted features $\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})$ and outputs the watermark b. The input and output dimensions are equal to the size of the extracted features $\left|\mathrm{Ext}\right(M,K_{\mathrm{ext}}\left)\right|$ and the watermark size $\left|b\right|$, respectively. To embed b in the secretly selected layer l of the target model, our watermarking regularization term is defined as

$$E_{\mathrm{wat}}=\delta ({\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)+\delta ({\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}\left(\mathrm{Ext}(M,K_{\mathrm{ext}})\right),b_r)$$

(17)

where $M^{\mathrm{wat}}$ is the watermarked version of M, $b_r$ is a random watermark, and $\delta$ is a watermark distance measure. The random watermark $b_r$ ensures that ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ projects the desired watermark b only for $M^{\mathrm{wat}}$. Note that $\delta$ depends on the watermark type: for binary sequences, cross-entropy is appropriate, while for images, pixel mean squared error is more relevant. Our global embedding loss is

$$E=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+\lambda E_{\mathrm{wat}}$$

(18)

where $\lambda$ adjusts the trade-off between the original target model loss term $E_0$ and the watermarking regularization term $E_{\mathrm{wat}}$, and $(X_{\mathrm{Train}},Y_{\mathrm{Train}})$ is the training set. Importantly, $E_{\mathrm{wat}}$ depends only on the trigger set, not on $(X_{\mathrm{Train}},Y_{\mathrm{Train}})$.

Parameter updates: The parameters of $M^{\mathrm{wat}}$ are updated according to the following regularization term from E:

$$E_{w^{\mathrm{wat}}}=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+\lambda \delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)$$

(19)

This ensures that the parameters $w^{\mathrm{wat}}$ of $M^{\mathrm{wat}}$ are updated to maintain the accuracy of the original target model while minimizing the distance between the projection of the activation maps and the watermark b.

Note that the projection model ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ serves as a discriminator that associates the projection of the trigger set activation maps of $M^{\mathrm{wat}}$ to b and those of M to $b_r$. The shared term $\delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)$ in Equations (19) and (20) allows for an optimal compromise between the parameters $w^{\mathrm{wat}}$ and $\theta$, ensuring that the activation maps projection is close to b without impacting accuracy and remains unique for $M^{\mathrm{wat}}$. In practice, $M^{\mathrm{wat}}$ and ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ are trained simultaneously for fast convergence. The parameters of ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ are updated based on

$$E_{\theta }=\lambda (\delta ({\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)+\delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M,K_{\mathrm{ext}})\right),b_r))$$

(20)

Watermark detection: The watermark detection process works as follows. Given a suspicious model $M^{*}$, and using the feature extraction key $K_{\mathrm{ext}}=\{l,Z,\mathrm{LS}\}$, the projection key $K_{\mathrm{proj}}={\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$, and the latent space $N(\mu ,\sigma )$, the watermark extraction is given as

$$b^{\mathrm{ext}}=\mathrm{HT}\left(\underset{\mathrm{LS}\sim N(\mu ,\sigma )}{\mathrm{mean}}{\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}\left(\mathrm{Ext}(M^{*},K_{\mathrm{ext}})\right)\right)$$

(21)

where HT is the Hard Thresholding operator at 0.5. In contrast to DeepSigns, which uses a fixed subset of the training set (see Equation (14)), DICTION extraction can sample an unlimited number of latent space images. This approach makes the watermarked model and projection function extremely resistant to attacks, such as fine-tuning, pruning, and overwriting, because they overfit to the latent space rather than a few specific images.

Advantages of latent space triggers: The use of latent space triggers provides several benefits:

• Storage efficiency: Reduces storage complexity, as only latent space parameters (mean and standard deviation) need to be recorded, rather than storing trigger images;
• Distribution preservation: Preserves the distribution of the weights and activation maps of the watermarked model.
• Computational simplicity: Avoid the need for additional DNN like $F_{\det }$ in the RIGA scheme, which requires complex hyperparameter tuning and increased computational complexity.

4.3. Projection Model Design

The projection function ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ is a DNN with an input dimension $\left|\mathrm{Ext}\right(M,K_{\mathrm{ext}}\left)\right|$ and an output dimension $\left|b\right|$ (watermark size). In this work, we employ a two-layer, fully-connected network:

$${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}\left(x\right)=\sigma (W_2·\mathrm{ReLU}(W_1·x+b_1)+b_2)$$

(22)

where $\sigma$ is the sigmoid function for binary watermark output, $W_1,W_2$ are weight matrices, and $b_1,b_2$ are bias vectors.

Architecture Details:

• Hidden layer: A total of 256 neurons with ReLU activation, and a dropout rate of 0.3;
• Learning rates: A total of ${10}^{-3}$ for ${\mathrm{Proj}}_{\theta }$ and ${10}^{-4}$ for $M^{\mathrm{wat}}$;
• Alternative architectures: ResNet-style or CNN-based architectures can be used for applications requiring higher capacity.

Joint training strategy: The projection model and watermarked model are trained jointly through alternating optimization:

$$\mathrm{Update}\theta :\underset{\theta }{min}{E}_{\theta }=\lambda (\delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)+\delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M,K_{\mathrm{ext}})\right),b_r))$$

(23)

$$\mathrm{Update}{w}^{\mathrm{wat}}:\underset{w^{\mathrm{wat}}}{min}{E}_{w^{\mathrm{wat}}}=E_0(X_{\mathrm{Train}},Y_{\mathrm{Train}})+\lambda \delta ({\mathrm{Proj}}_{\theta }\left(\mathrm{Ext}(M^{\mathrm{wat}},K_{\mathrm{ext}})\right),b)$$

(24)

This alternating optimization ensures that both the projection function learns to discriminate correctly between watermarked and non-watermarked activation maps, while the watermarked model maintains its primary task performance and embeds the watermark effectively.

5. Experimental Results

We evaluated DICTION in terms of its (1) impact on model performance (fidelity); (2) robustness against three watermark removal techniques (overwriting, fine-tuning, and weight pruning); and (3) resilience to watermark detection attacks (security). For all attacks, we considered the most challenging threat model, assuming that the attacker has access to or knowledge of the training data and the watermarked layer.

5.1. Datasets and Models

Our experiments were conducted on two well-known public benchmark image datasets for image classification: CIFAR-10 [64] and MNIST [22]. We utilized four distinct DNN architectures as target models: three previously experimented on with DeepSigns [51] (MLP, CNN, and ResNet-18) and one with RIGA [57] (LeNet).

Table 2. Benchmark DNN: architectures, number of epochs, and classification baseline accuracies on two public datasets (CIFAR-10 [64] and MNIST [22]). Model notation: ‘64C3(1)’ denotes a convolutional layer with 64 output channels and $3\times 3$ filters applied with stride 1; ‘MP2(1)’ indicates a max-pooling layer over $2\times 2$ regions with stride 1; ‘512FC’ refers to a fully connected layer with 512 output neurons; ‘BN’ stands for batch normalization. ReLU and sigmoid activation functions are used across all benchmarks.

Benchmark ID	Dataset	Baseline Acc	Training Epochs	Model Type	Architecture
1	MNIST	98.06%	50	MLP	784-512FC-512FC-10FC
2	CIFAR-10	87.17%	100	CNN	3×32×32-32C3(1)-32C3(1)-MP2(1)-64C3(1)-64C3(1)-MP2(1)-512FC-10FC
3	CIFAR-10	91.7%	200	ResNet-18	Please refer to [65]
4	MNIST	99.16%	50	LeNet	1×28×28-24C3(1)-BN-24C3(1)-BN-128FC-64FC-10FC

summarizes their topologies, training epochs, and corresponding baseline accuracies.

Throughout the experimental section, we use the following abbreviations for our four benchmark configurations: BM1: MLP architecture on the MNIST dataset, BM2: CNN architecture on the CIFAR-10 dataset, BM3: ResNet-18 architecture on the CIFAR-10 dataset, and BM4: LeNet architecture on the MNIST dataset. The implementations of DeepSigns [51], ResEncrypt [55], and DICTION, along with their configurations, are publicly available at https://github.com/Bellafqira/DICTION, accessed on 15 June 2025.

5.2. Experimental Configuration

In all experiments, we embedded a 256-bit watermark b in the second-to-last layer of the target model, following the approach used in DeepSigns. This watermark could represent, for example, the hash of the model owner’s identifier generated using the SHA-256 hash function. We used the bit error rate (BER) to measure the discrepancy between the original and extracted watermarks:

$$\mathrm{BER}(b^{\mathrm{ext}},b)={\displaystyle \frac{1}{n}}\sum _{i=1}^{l}I(b_i^{\mathrm{ext}}\ne b_i)$$

(25)

where $b^{\mathrm{ext}}$ is the extracted watermark, I is the indicator function returning 1 if the condition is true and 0 otherwise, and l is the watermark size ($l=256$). A BER close to 0 indicates identical watermarks, while a BER close to 0.5 indicates uncorrelated watermarks.

DICTION configuration: We used a simple two-layer fully connected neural network as the architecture for the DICTION projection function ${\mathrm{Proj}}_{\theta }$ in our experiments. The normal distribution $N(\mu ,\sigma )=N(0,1)$ serves as a latent space to embed the watermark, and the selection matrix Z serves as the identity. We used the Adam optimizer with a learning rate of ${10}^{-3}$, a batch size of 100, and a weight decay of ${10}^{-4}$ to train the DICTION projection function. We set $\lambda =1$ in Equation (18). We used 10 epochs for each benchmark to embed the watermark.

Baseline method configurations: Regarding the implementation of DeepSigns, we used the second-to-last layer for embedding, as in its original version. ${\lambda }_1$ and ${\lambda }_2$ were set to 0.01 to obtain a BER equal to zero. The number of watermarked classes s equals 2, N was 128 (i.e., a watermark of 256 bits), and the watermark projection matrix A was generated based on the standard normal distribution $N(0,1)$. The trigger set corresponds to 1% of the training data.

For ResEncrypt, we used two-layer, fully connected neural networks as the architecture for MappingNet. We recall that the role of MappingNet is to expand the size of the selected weights to the watermark. In our implementation, we used an expansion factor equal to 2 for LeNet and 1 for the other benchmarks.

5.3. Fidelity Analysis

By definition, watermarked model accuracy should not be degraded compared to the target model.

Table 3. BER and accuracy of watermarking schemes for the four benchmarks after embedding a 256-bit watermark. Best results are highlighted in bold.

Benchmark ID	Baseline Acc	DICTION		DeepSigns		ResEncrypt
		BER	Model Accuracy	BER	Model Accuracy	BER	Model Accuracy
1	98.06%	0	98.06%	0	97.73%	0	97.57%
2	87.17%	0	85.65%	0	85.18%	0	84.98%
3	91.7%	0	91.58%	0	91.36%	0	90.84%
4	99.16%	0	99.1%	0	98.75%	0	98.68%

presents the accuracy of watermarked models after embedding a 256-bit watermark. The results show that the watermarked model accuracies are very close to those of the non-watermarked models for all three methods (DeepSigns, ResEncrypt, and DICTION), indicating successful optimization of both model accuracy and watermark embedding (minimizing the watermark loss term $E_{\mathrm{wat}}$, as discussed in Section 4). In particular, DICTION achieves the best accuracy preservation across all benchmarks.

5.4. Robustness Evaluation

We evaluated our scheme’s robustness against the three contemporary removal attacks discussed in Section 1.

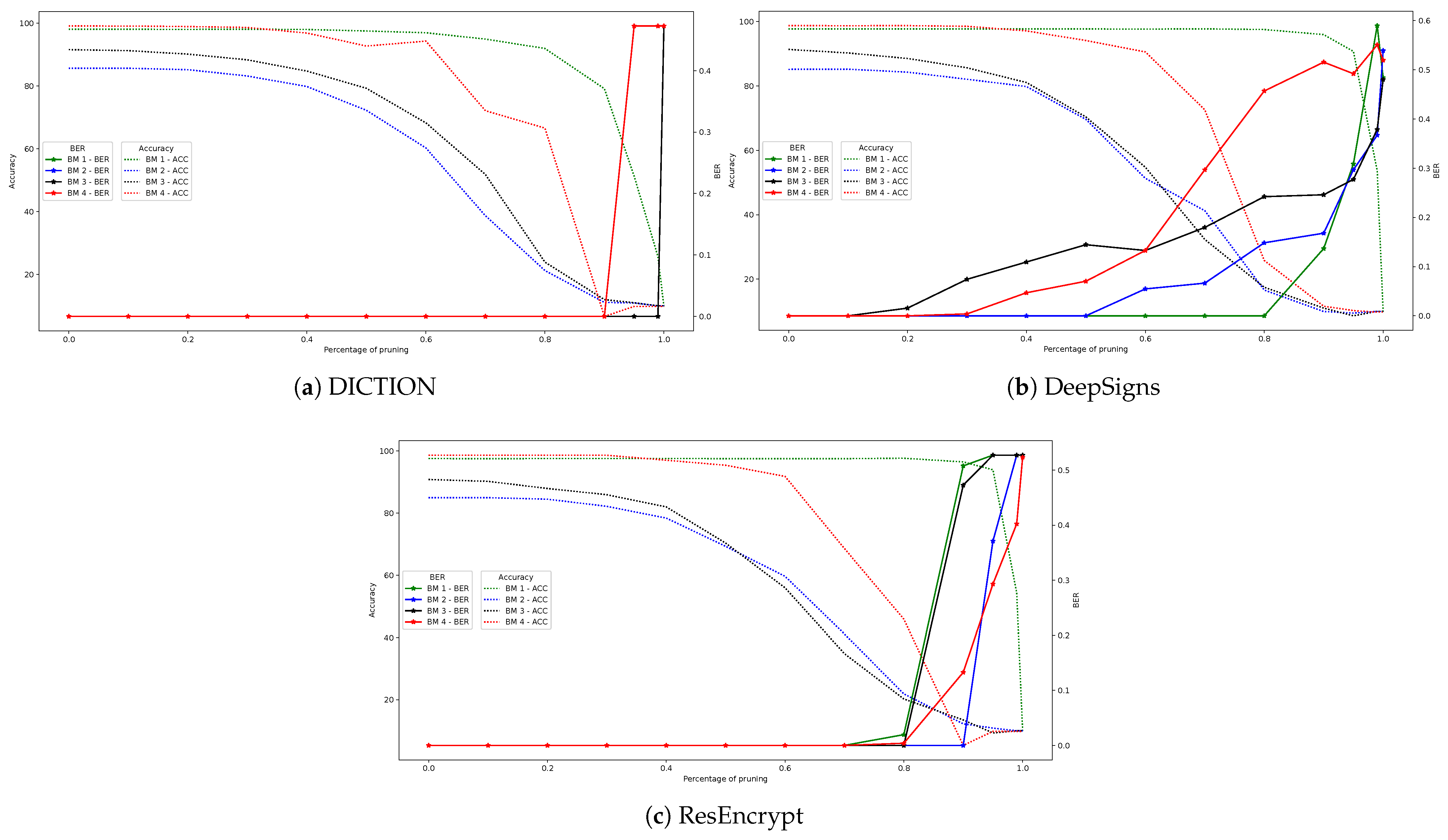
Pruning attack: We employed the pruning approach proposed by Han et al. [66] to compress watermarked models. For each layer, this method sets the $\alpha \%$ of the weights with the lowest absolute values to zero. Figure 3 illustrates the impact of pruning on watermark extraction/detection and model accuracy for different values of $\alpha$. DICTION demonstrates superior robustness, tolerating up to 90-95% pruning across all benchmark networks, compared to 80% for ResEncrypt. DeepSigns shows increased vulnerability when a 256-bit watermark is inserted. Importantly, when pruning achieves substantial BER values, the attacked watermarked model suffers significant accuracy loss compared to the baseline, indicating that watermark removal comes at the cost of model performance degradation.

Fine-tuning attack: Fine-tuning represents another transformation attack that adversaries might use to remove watermarks. In its most effective implementation, the watermarked model is fine-tuned using original training data and the target model’s loss function (conventional cross-entropy in our case), without exploiting watermarking loss functions $E_{\mathrm{wat}}$. Fine-tuning deep learning models causes convergence to different local minima that may not be equivalent to the original in terms of prediction accuracy.

Our fine-tuning attack protocol multiplies the last training learning rate by a factor of 10, then divides it by 10 after 20 epochs, allowing the model to explore new local minima.

Table 4. Robustness of watermarking schemes against fine-tuning attacks. Best results are highlighted in bold.

Benchmarks	BM1		BM2		BM3		BM4
Epochs	50	100	50	100	50	100	50	100
ACC DICTION	98.27%	98.3%	86.81%	86.69%	91.59%	91.58%	99.17%	99.16%
BER DICTION	0	0	0	0	0	0	0	0
ACC DeepSigns	98.53%	97.83%	86.9%	87.49%	90.89%	91.48%	99.14%	99.14%
BER DeepSigns	0.0977	0.1445	0	0.0234	0.1406	0.1641	0.3398	0.3320
ACC ResEncrypt	98.54%	98.64%	87.37%	87.3%	91.31%	90.98%	99.17%	99.2%
BER ResEncrypt	0	0	0	0	0	0	0.5234	0.5273

summarizes the impact of fine-tuning on watermark detection rates (expressed as BER) for all benchmark models. DICTION successfully detects watermarks even after extensive fine-tuning, unlike DeepSigns or ResEncrypt. The poor performance of ResEncrypt on BM4 can be attributed to the small number of parameters in the watermarked layer, while the limited capacity of DeepSigns makes 256-bit watermark insertion vulnerable to fine-tuning attacks.

Overwriting attack: Assuming that the attacker knows the watermarking technique, they may attempt to damage the original watermark by embedding a new watermark in the watermarked model. In practice, attackers lack knowledge about watermarked layer locations. However, considering the worst-case scenario, we assume that the attacker knows the watermark location but not the original watermark or projection function. To perform the overwriting attack, the attacker follows the protocol described in Section 4 to embed a new watermark of the same size (256 bits) or larger size (512 bits) using different or identical latent spaces.

Table 5. BER of watermarking schemes for the four benchmarks after an overwriting attack with 256-bit or 512-bit watermarks using different keys. Best results are highlighted in bold.

Benchmark ID	DICTION		DeepSigns		ResEncrypt
	256 bits	512 bits	256 bits	512 bits	256 bits	512 bits
1	0	0	0.199	0.277	0.527	0.527
2	0	0	0.367	0.418	0	0
3	0	0	0.391	0.438	0	0
4	0	0	0.484	0.484	0.406	0.418

presents the results against this attack for all four benchmarks. DICTION demonstrates robustness against overwriting attacks and successfully detects the original embedded watermark in overwritten models, while the DeepSigns and ResEncrypt watermarks are perturbed and sometimes completely erased (achieving a BER close to 50%), especially with shallower models such as BM1 and BM4.

5.5. Security Analysis (Watermark Detection Attacks)

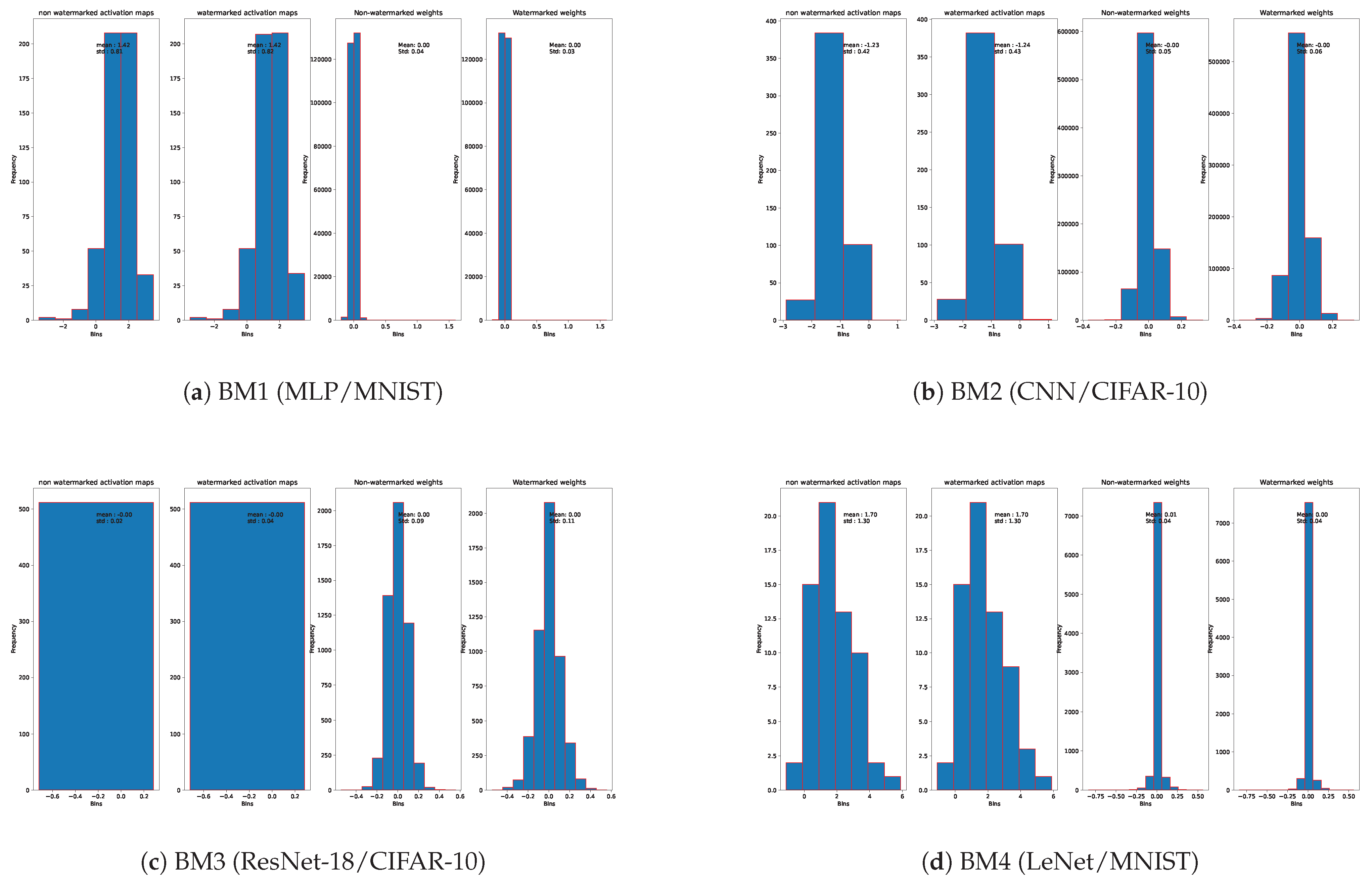
We tested all schemes against the attack proposed by Wang et al. [56] and Property Inference Attack (PIA). Watermark embedding should not leave noticeable changes in the probability distribution of the watermarked model. Figure 4 illustrates histograms of activation maps from watermarked and non-watermarked models. DICTION preserves the model’s distribution while robustly embedding the watermark. The range of activation maps is not deterministic across different models and cannot be used by malicious users to detect watermark existence.

Table 6. Mean and standard deviation of weight and activation map distributions for baseline and watermarked models. Values closest to baseline are highlighted in bold.

	BM1		BM2		BM3		BM4
	Act. Maps	Weights	Act. Maps	Weights	Act. Maps	Weights	Act. Maps	Weights
Baseline	1.42 ± 0.81	0 ± 0.04	−1.23 ± 0.42	0 ± 0.05	0 ± 0.02	0 ± 0.09	1.70 ± 1.30	0.01 ± 0.04
DICTION	1.42 ± 0.82	0 ± 0.03	−1.24 ± 0.43	0 ± 0.06	0 ± 0.04	0 ± 0.11	1.70 ± 1.30	0 ± 0.04
DeepSigns	−0.01 ± 0.38	0 ± 0.02	−0.04 ± 0.12	0 ± 0.05	0 ± 0.11	0 ± 0.11	0.22 ± 0.47	0 ± 0.05
ResEncrypt	0 ± 0.53	−0.01 ± 0.02	−1.64 ± 0.45	0 ± 0.06	0 ± 0.01	0 ± 0.10	−0.18 ± 1.74	−0.02 ± 0.06
Uchida	−2.49 ± 1.47	0.01 ± 0.28	−1.96 ± 0.44	0 ± 0.07	0 ± 0.01	0.03 ± 0.35	−2.91 ± 2.56	0 ± 0.02

provides the mean and standard deviation of the parameter distributions and activation maps of the watermarked layer for all watermarking schemes. DICTION minimally disturbs the distribution of model parameters across all four benchmarks, demonstrating superior security properties.

Property Inference Attack (PIA): We evaluated PIA with a watermark detector $F_{\mathrm{Det}}$ trained on multiple watermarked and non-watermarked models. We assumed the worst-case scenario where the attacker knows the training data, the exact model architecture of $M^{\mathrm{wat}}$, and the feature extraction key. While this threat model is overly strong, we use it to demonstrate our watermark scheme’s effectiveness.

For the PIA evaluation, we trained 700 watermarked and 700 non-watermarked LeNet models on MNIST with different keys, plus 100 models of each type as test sets. We tested PIA only on LeNet due to the attack’s high complexity, requiring the training and watermarking of 800 models. The detector $F_{\mathrm{Det}}$ was trained on watermarking features labeled according to the model’s watermarking status. All generated models achieved good accuracy with correctly embedded watermarks. The detector $F_{\mathrm{Det}}$ achieved only 60% accuracy on training data and around 50% on testing after 50 epochs, equivalent to random guessing. This demonstrates the resistance of DICTION to property inference attacks.

5.6. Integrity and Efficiency Analysis

Integrity: The integrity requirement refers to the watermarking scheme’s ability to minimize false alarms. DICTION achieves this through its generative adversarial network (GAN) strategy. We trained the projection model ${\mathrm{Proj}}_{\theta }$ to map the activation maps of the watermarked target model $M^{\mathrm{wat}}$ to the intended watermark and those of the original model M to a random watermark $b_r$. This approach enables DICTION to effectively meet integrity requirements.

Computational efficiency: We analyzed the overhead incurred by the watermark-embedding process in terms of computational and communication complexities. DICTION introduces no communication overhead for watermark embedding since the process is conducted locally by the model owner. The additional computational cost depends on the target model topology $M^{\mathrm{wat}}$, projection model ${\mathrm{Proj}}_{\theta }(·)$, and the number of epochs required for watermark embedding while maintaining high accuracy.

Our experiments show that 30 epochs are sufficient for ${\mathrm{Proj}}_{\theta }(·)$ convergence with satisfactory target model accuracy. The projection model topology is modest compared to the target model, enabling efficient watermark embedding.

Table 7. Computational cost for training and watermarking across all benchmarks.

Benchmark	Training		Watermarking
	Run Time	Epochs	Run Time	Epochs
BM1	02:44 min	50	02:00 min	30
BM2	09:42 min	100	03:09 min	30
BM3	48:57 min	200	05:39 min	30
BM4	03:17 min	50	02:22 min	30

provides computation times for the model training and watermarking processes. DICTION incurs reasonable overhead, with a maximum of 30 epochs for all benchmarks, suggesting high efficiency.

Complexity comparison: Our embedding complexity remains higher than the Uchida [45] and DeepSigns [51] methods because their projection functions are based solely on secret matrix multiplication. However, our method has similar complexity to ResEncrypt [55], as both train an additional model (${\mathrm{Proj}}_{\theta }(·)$ and MappingNet, respectively), which is less expensive than RIGA [57] since we do not require a third model to preserve weight distribution.

6. Discussion and Limitations

In this section, we discuss the properties, strengths, and limitations of DICTION, providing a comprehensive analysis of our proposed methodology.

6.1. DICTION Parameterization and Flexibility

The DICTION scheme depends on several key parameters, particularly the layers selected for calculating activation maps and the architecture of the ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$ projection function. In

Table 8. Ablation study: BER results after watermarking Benchmark 3 using different CNN layers and projection architectures under various attacks.

CNN Layers	Fine-Tuning (50 Epochs)	Overwriting (Same Layers)	Pruning (80%)
FC1	0	0	0
Conv4	0	0	0
Conv3	0	0	0
Mix of all layers	0	0	0
FC1 with deep Projθ	0	0	0

, we varied all these parameters for BM3 (ResNet-18/CIFAR-10), which contains both convolutional and fully connected layers. The results demonstrate that regardless of the watermarked layer or the architecture of the ${\mathrm{Proj}}_{\theta }$ model, our watermark resists all evaluated attacks, achieving zero BER across fine-tuning, overwriting, and pruning scenarios. This flexibility makes DICTION adaptable to various network architectures and deployment requirements.

6.2. Trigger Set Generation Strategies

While trigger sets are predominantly used in black-box watermarking where verifiers lack access to model parameters. Various methods have been proposed for trigger set generation in the literature, particularly for out-of-distribution scenarios and could be used in this work as well:

• Random database selection: Images chosen randomly from public databases or images with added patterns [30,67,68] (e.g., company logo).
• Diffusion-based generation: As demonstrated in [69] for image watermarking, where trigger images begin as noise (similar to DICTION) with patterns added to their Fourier transform domain.
• Cryptographic primitives: Methods like [70] that generate random images and labels serving as seeds for trigger set generation using a customized hash function.

The latent space approach of DICTION eliminates the need for storing specific trigger images while providing unlimited trigger generation capability, representing a significant advancement over traditional methods.

6.3. Watermark Generation and Encoding

Watermarks in DICTION can be either randomly generated or derived from meaningful messages (e.g., model owner and receiver identifiers). When the identifier’s encoding space does not match the watermark space, cryptographic hashing, such as HMAC [10], serves as an effective solution. An interesting enhancement involves including a frozen part of the original model in the hash calculation, creating a watermark that attests to both the user’s identifier and the link between the original and watermarked models, and providing additional authenticity verification.

6.4. Multi-Layer Activation Map Processing

DICTION supports concatenating activation maps from multiple layers to create comprehensive tensors containing information from selected layers, which are then processed by ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$. This strategy captures information encoded across all model layers but increases the computational complexity of ${\mathrm{Proj}}_{\theta }^{\mathrm{DNN}}$. Table 8 demonstrates that DICTION with a three-hidden-layer ${\mathrm{Proj}}_{\theta }$ using ReLU activation functions achieves zero BER against all attacks, confirming the method’s robustness across different architectural configurations.

The projection model architecture can be adapted to various designs, such as ResNet-50 or VGG-16, by modifying the final layer to match the size of the binary watermark. Moreover, if the watermark is an image or text, the projection function could employ a diffusion model [69] or an NLP model, such as BERT or GPT, respectively. Nevertheless, choosing a deeper and more complex model will increase the computational complexity of the watermarking process, requiring a trade-off based on available computational resources.

6.5. Study Limitations and Computational Considerations

Two-model training requirement: The watermarking process of DICTION requires training two models (the target model and projection network), unlike methods such as those of Uchida et al. and DeepSigns, which only require single-model training. This represents the computational cost for ensuring robust watermarking properties. The impact is particularly significant for large models like GPT, but several mitigating factors exist: (i) Offline processing: Watermarking occurs in offline mode, eliminating runtime overhead for end users. (ii) One-time cost: The computational overhead is incurred only during watermarking, not during model deployment or inference. (iii) Deployment efficiency: Once watermarked and deployed, the model operates with identical performance characteristics to the original.

6.6. Future Research Directions

Building on the promising results of DICTION, we identify several key directions for future research that could significantly enhance the framework’s applicability and robustness.

Large language models and transformer architectures: Extending DICTION to transformer architectures and large language models like GPT and BERT represents a critical next step. This requires adapting the activation-based watermarking approach to attention mechanisms and token embeddings, which presents unique challenges given the fundamentally different computational structure of transformers compared to traditional neural networks. The growing importance of language models in practical applications makes this extension particularly valuable for ensuring model ownership protection in NLP domains.

Federated learning applications: The adaptation of DICTION for federated learning environments presents another promising direction. This involves addressing the unique challenges of decentralized model ownership verification while preserving watermark integrity across multiple clients. In federated settings where data privacy is paramount, the watermarking mechanism must maintain its effectiveness without compromising the privacy guarantees that make federated learning attractive. This includes developing protocols for watermark verification that do not require centralized access to client models.

Advanced attack resistance: Developing enhanced robustness against emerging attacks remains crucial for practical deployment. This includes defending against model extraction attacks, as studied by Kinakh et al. [71], where adversaries attempt to steal model functionality through query access. Additionally, architectural modification attacks that add dummy neurons, as analyzed by Yan et al. [72], pose unique challenges that require watermarking schemes to be invariant to such structural changes. Furthermore, gradient inversion and other privacy-focused attacks that attempt to extract training data or watermark information through gradient analysis must be considered in future defense mechanisms.

Real-world deployment and integration: Practical deployment considerations warrant a thorough investigation to transition DICTION from research prototype to a production-ready solution. This encompasses integration with existing ML pipelines and frameworks such as TensorFlow, PyTorch, and MLflow, ensuring minimal overhead on training and inference processes. Performance optimization for large-scale deployment becomes critical when dealing with models serving millions of requests. Additionally, conducting comprehensive cost–benefit analyses for industrial applications will help organizations understand the trade-offs between watermarking overhead and intellectual property protection. Finally, working toward standardization and ensuring compatibility with existing watermarking protocols will facilitate broader adoption across the machine learning community.

7. Conclusions

In this paper, we present a unified framework that encompasses all existing white-box watermarking algorithms for DNN models. This framework establishes theoretical connections between previous works on white-box watermarking for DNN models. From this framework, we derived DICTION, a novel white-box dynamic robust watermarking scheme that relies on a GAN strategy. Its main innovation lies in a watermark extraction function that is a DNN trained using latent space triggers as an adversarial network.

We subjected DICTION to a comprehensive evaluation against several watermark detection and removal attacks, and demonstrated that it is significantly more robust than existing works with superior embedding and extraction efficiency. DICTION achieves a zero bit error rate while maintaining model accuracy within 0.5% of the baseline, tolerates up to 95% weight pruning compared to 80% for existing methods, and shows complete resistance to fine-tuning and overwriting attacks where competing methods fail.

In future work, we plan to broaden the scope of our evaluation by incorporating additional machine learning applications, such as natural language processing, and learning strategies, such as federated learning.